I
T
P
W
ZPT
1
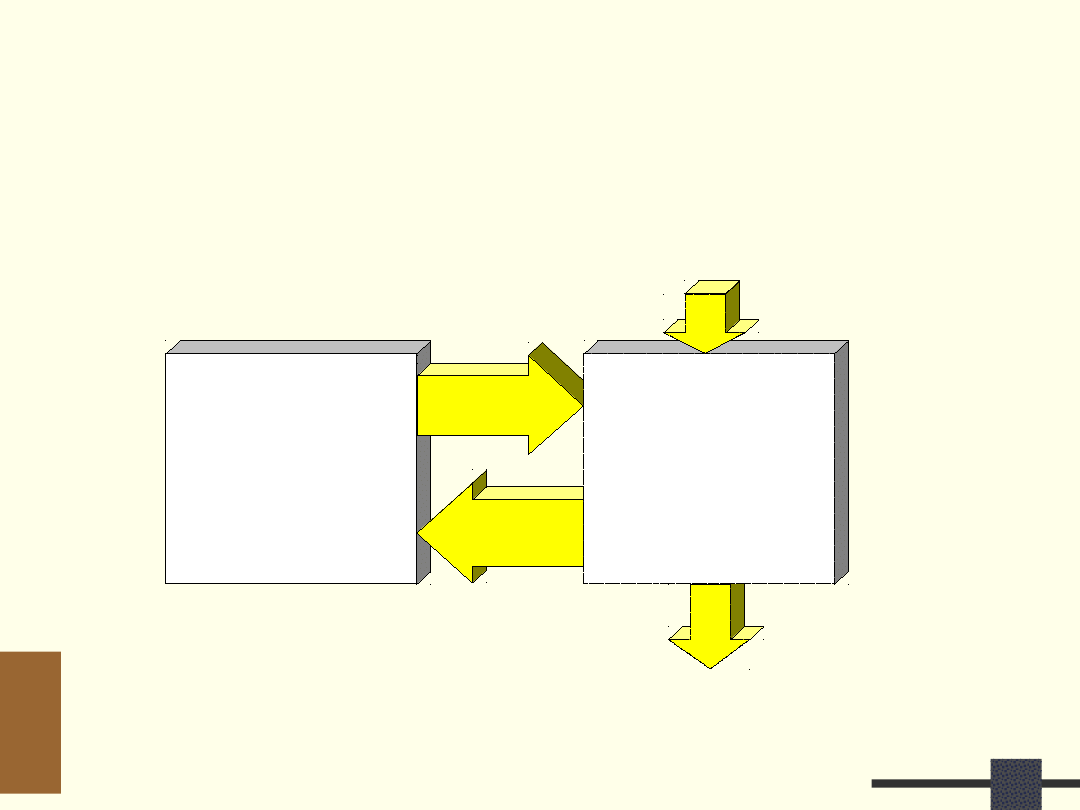
Układ
sterujący
(kontroler
)
Dane wyjściowe
Dane
wejściowe
Sygnały
sterujące
Stan części
operacyjnej
Układ operacyjny
(Datapath)
System cyfrowy
Mikrooperac
je
wywoływane przez
sygnały sterujące
I
T
P
W
ZPT
2
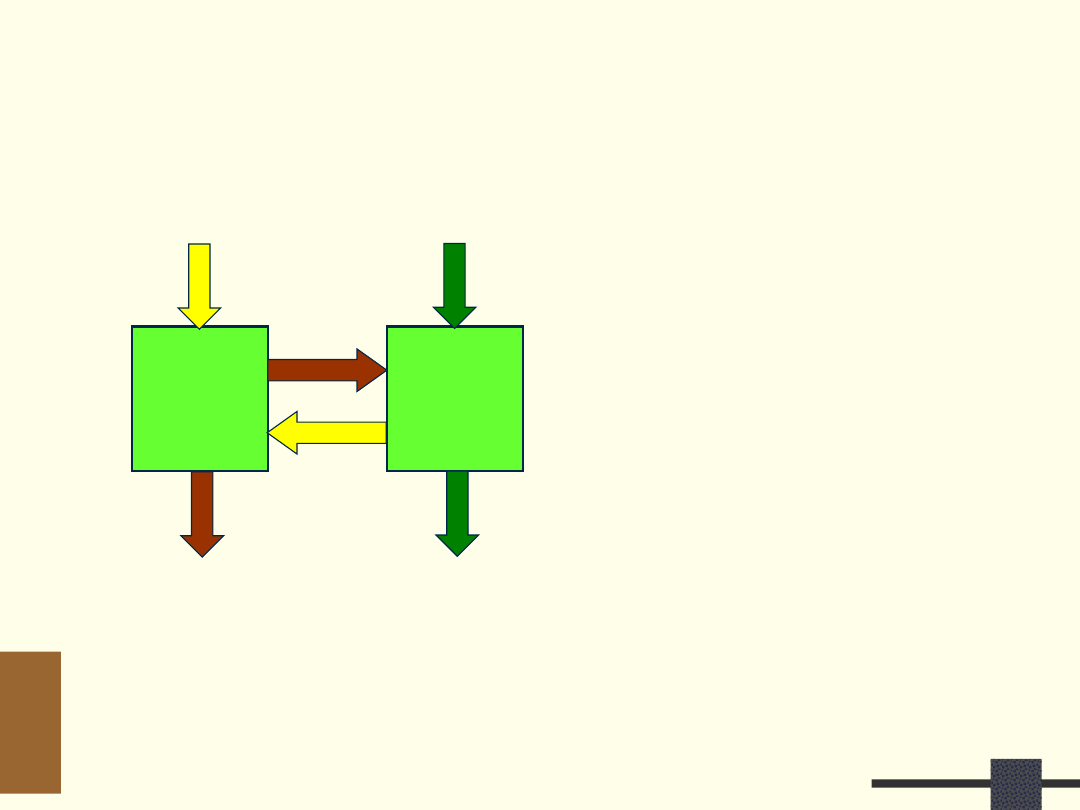
System cyfrowy - realizacja
UO – z bloków funkcjonalnych
US – automat lub układ
mikroprogramowany
X
Z
X
P
Z
Y
Z
D
F
US
UO

I
T
P
W
ZPT
3
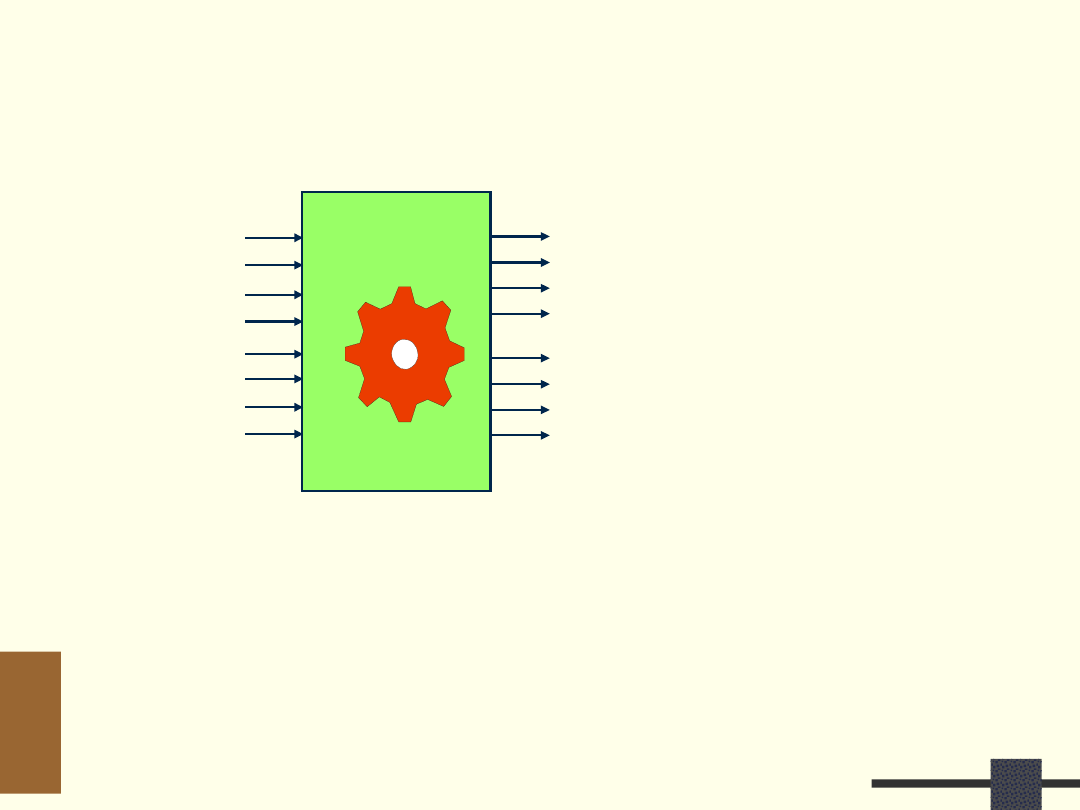
Przykład syntezy strukturalnej
W kodzie BCD (Binary Coded Decimal) każda
cyfra liczby zapisanej w kodzie dziesiętnym
jest przedstawiana czterobitową liczbą binarną
Konwerter kodu binarnego na kod
BCD:
4 8 9
Np. liczba 489 zostanie zapisana jako
wektor binarny z wykorzystaniem 12 bitów
(3 4 bity)
BCD
0100 1000 1001
I
T
P
W
ZPT
4
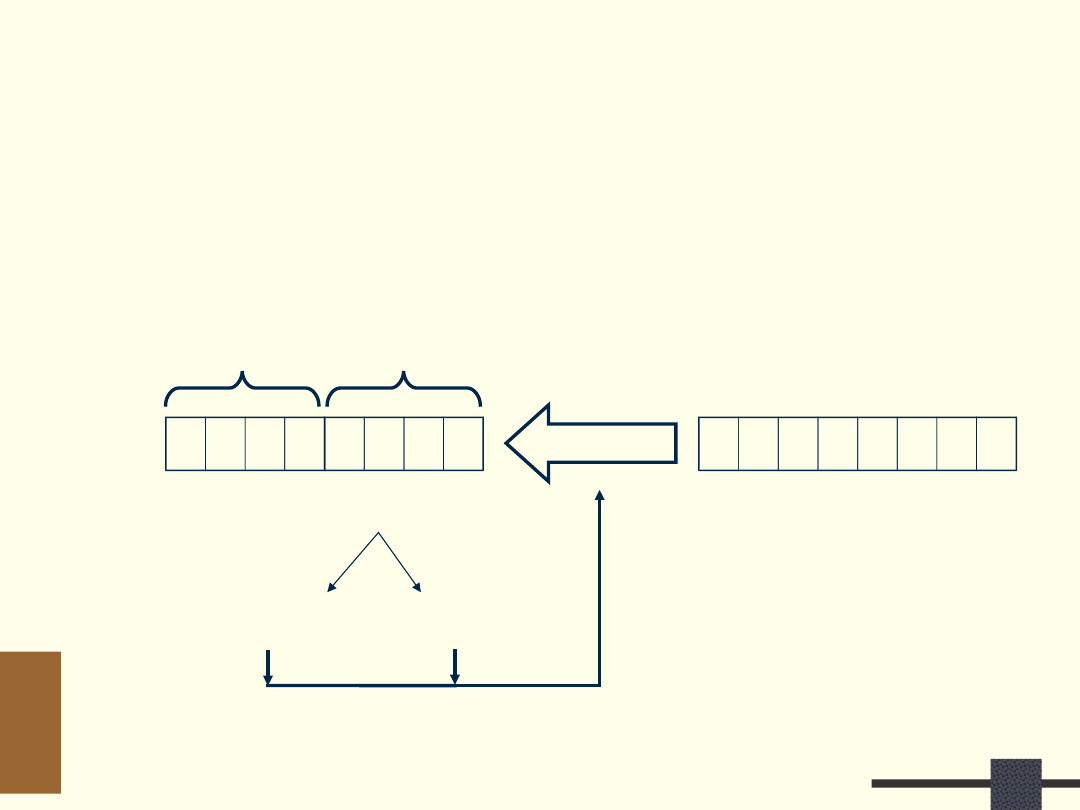
Konwerter Bin2BCD
BIN/BCD
0 liczby 99
0
0
0
1
1
0
1
1
27
BI
N
Celem jest pokazanie różnych metod
projektowania
27
BCD
0
0
1
0
0
1
1
1
I
T
P
W
ZPT
5
0
0
0 0 0 0 0 0
0
0
0 1 1 0 1 1
27
LDA
LDB
LB
=
0
0
0 0 0 0 0 0
LDB 5
LDB := LDB+3
NIE
TAK
LDB := LDB
8
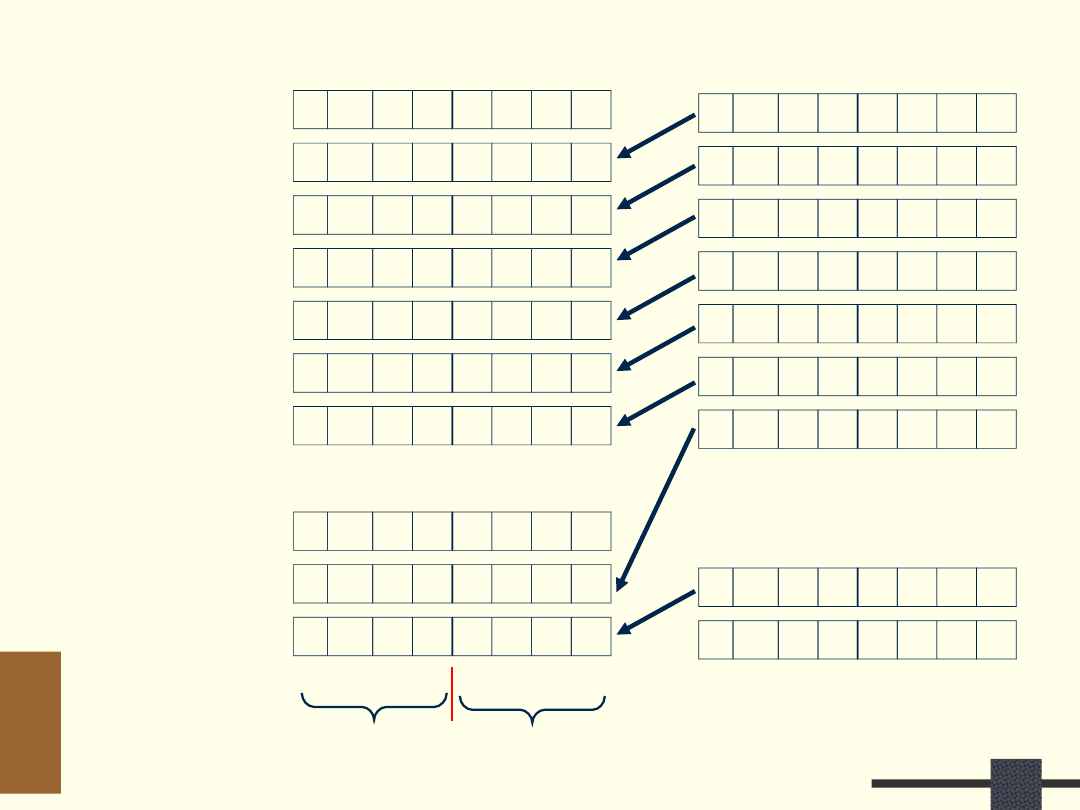
Metoda +3
I
T
P
W
ZPT
6
0
0
0 1 1 0 1 1
LDA
LDB
LB
0
0
0 0 0 0 0 0
0
0
0
0
0 0 0 0 0 0
0
0
0
0 0 0 0 0 0
0
0
0 0 0 0 0 0
0
0
0 0 0 0 0 1
0
0
0 0 0 0 1 1
0
0
0 0 0 1 1 0
0 0 1 1
0
0
0 0 1 0 0 1
0 1 1
0
0
0 1 0 0 1 1
0
0
1 0 0 1 1 1
LDB < 5
LDB < 5
LDB < 5
LDB < 5
LDB < 5
LDB < 5
LDB 5
+
LDB < 5
1
2
3
4
5
6
7
8
1 1 0 1 1
1 1 0 1 1
1 1 0 1 1
1 0 1 1
1 1
1
0
0
1 0 0 1 1 1
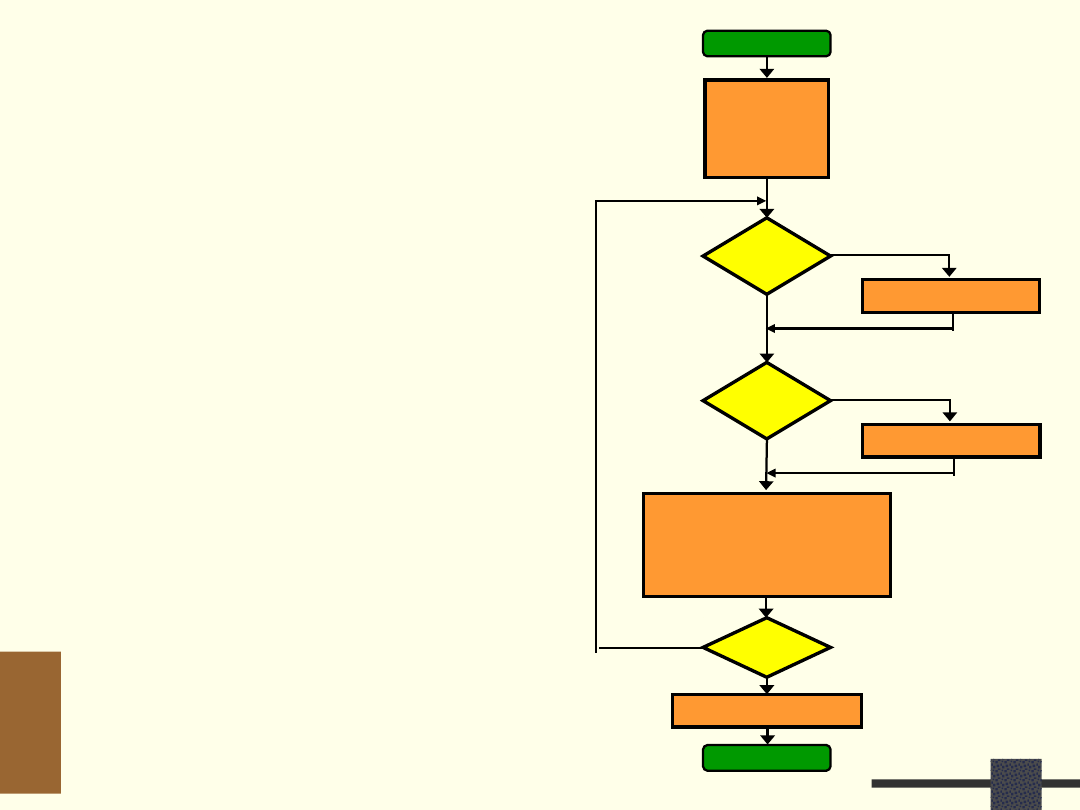
LD
BCD
=
2
7
= 27
I
T
P
W
ZPT
7
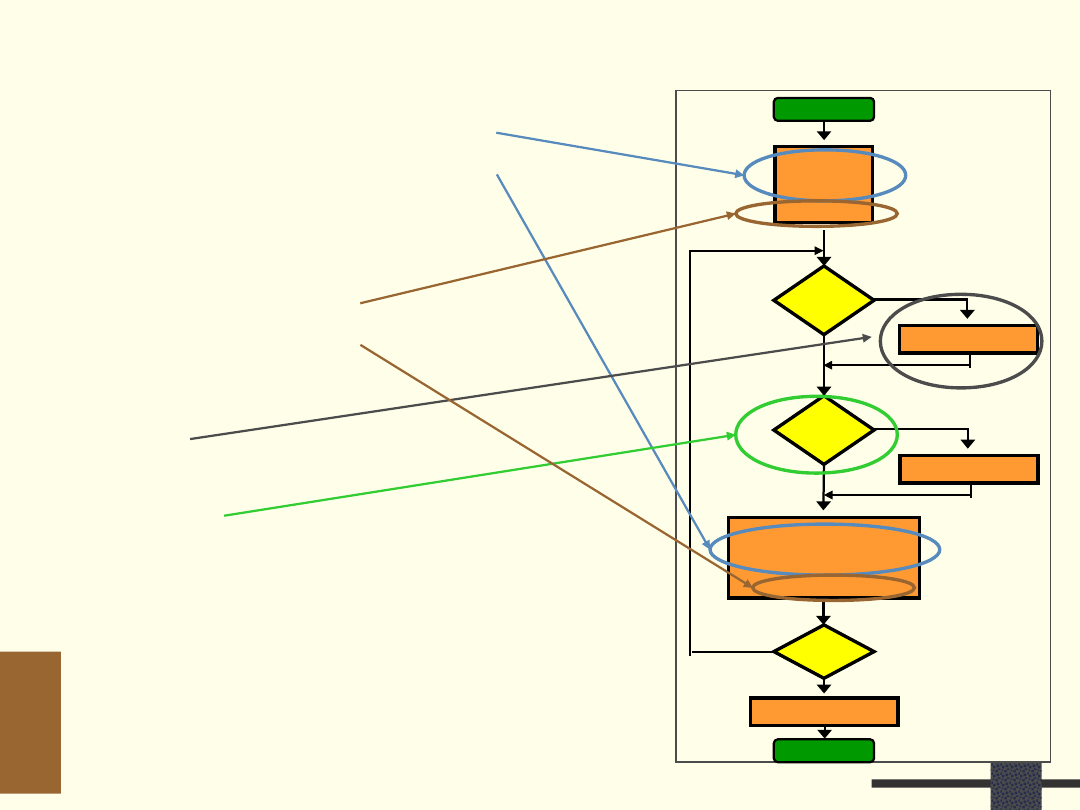
Algorytm
konwersji
z kodu BIN na
BCD
KONIEC
LOAD (LB)
LDA := 0
LDB := 0
LK := 8
LDB 5
LDB := LDB + 3
LDA := LDA + 3
LDA 5
START
LDA := SHL(LDA,LDB
3
)
LDB := SHL(LDB,LB
7
)
LB := SHL(LB)
LK := DEC(LK)
LD := LDA
LDB
LK =
0
NIE
TAK
NIE
NIE
TAK
TAK
Liczba konwertowana
zapisana jest w postaci
binarnej
Przekształcenie polega na
wykonaniu określonej liczby
prostych operacji
Przy konwersji liczb z zakresu
0 – 99 można algorytm
uprościć
Wykorzystuje proste operacje
na liczbach binarnych:
przesunięcie w lewo,
zwiększenie o 3,
porównanie ze stałą.
I
T
P
W
ZPT
8
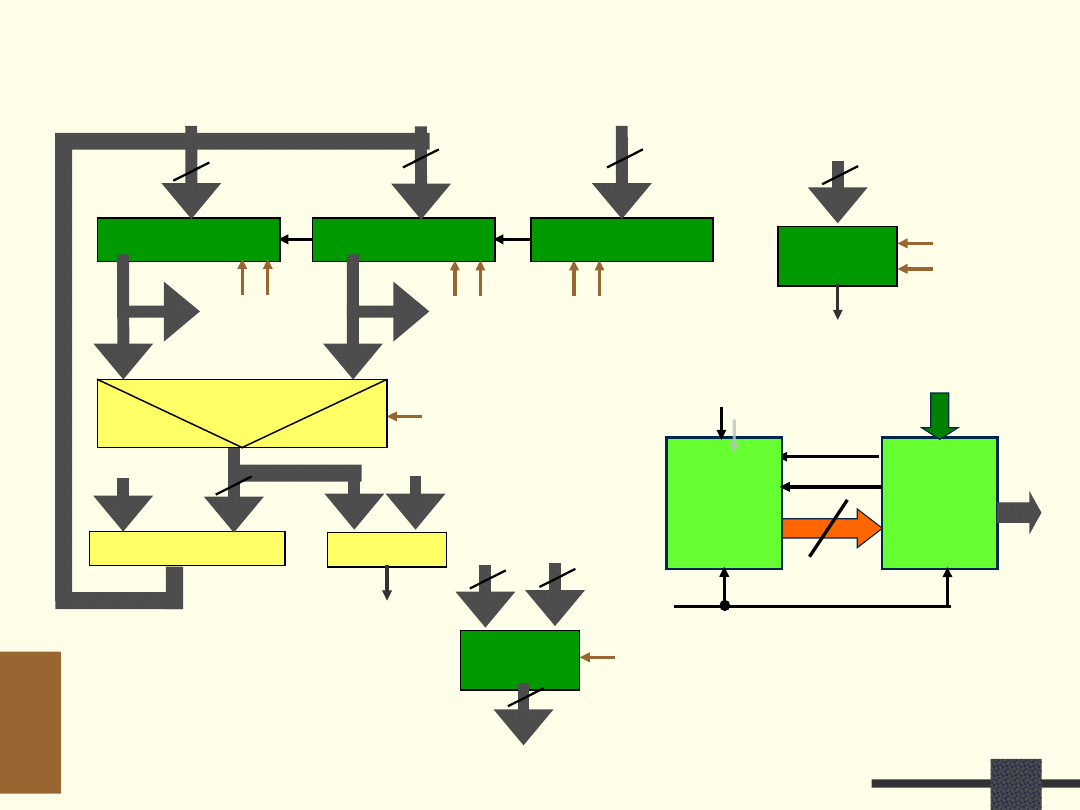
Algorytm
konwersji
Rejestry LB, LDA, LDB z
operacjami:
zeruj
wpisz,
przesuń.
Licznik LK z operacjami:
ustaw,
zmniejsz o 1.
Sumator
Komparator
KONIEC
LOAD (LB)
LDA := 0
LDB := 0
LK := 8
LDB 5
LDB := LDB + 3
LDA := LDA + 3
LDA 5
START
LDA := SHL(LDA,LDB
7
)
LDB := SHL(LDB,LB
7
)
LB := SHL(LB)
LK := DEC(LK)
LD := LDA
LDB
LK =
0
NIE
TAK
NIE
NIE
TAK
TAK
I
T
P
W
ZPT
9
Opis strukturalny
R3
R2
R1
K
S3
S2
S1
A
B
8
4
4
4
„3”
„5”
K 5
LK
4
„8”
LOAD1
DEC
LK = 0
R4
LOAD2
8
Y = LD
UO
LB
Y
LK = 0
10
US
S
K 5
MUX
1
0
MUX
4
A
B
4
LB
I
T
P
W
ZPT
10
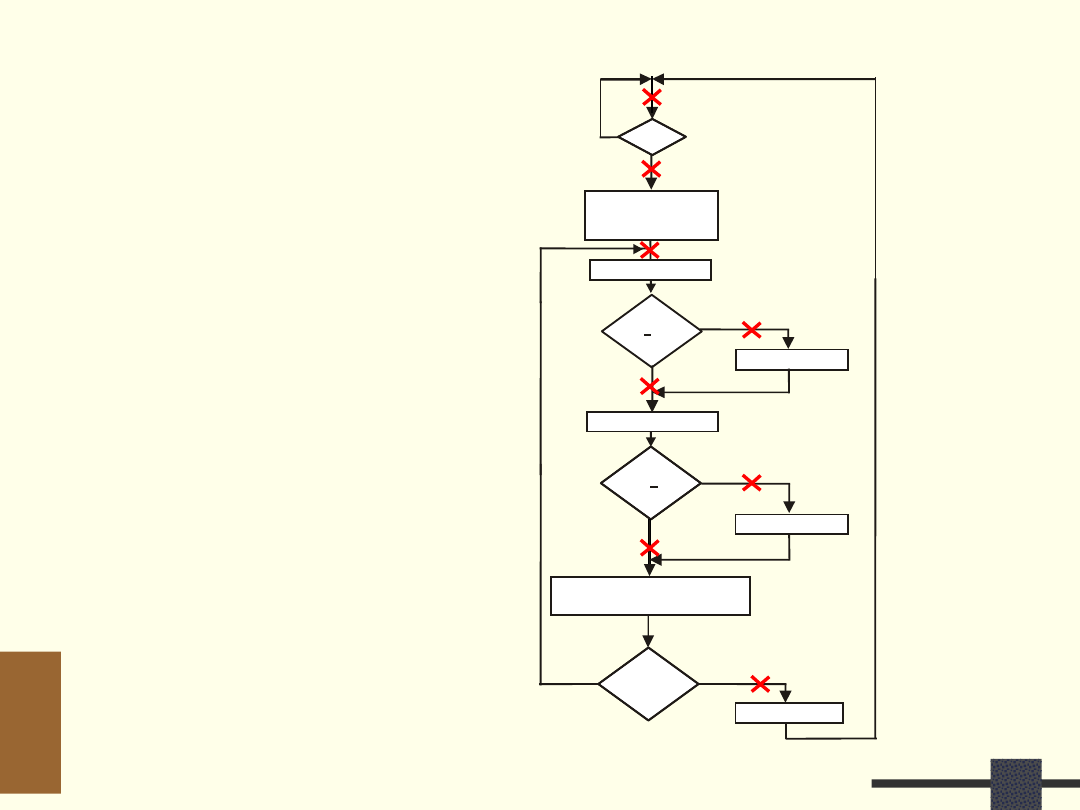
Sieć działań
z uwzględnieniem UO
LK = 0
0
0
SHL 1, SHL 2, SHL 3,
DEC (LK)
MUX := 0
MUX := 1
LOAD 4
LOAD 2
LOAD 3
S
0
1
1
0
1
1
LOAD 1
CLEAR 2,3
LOAD (LK)
K > 5
K > 5
A
0
A
1
A
3
A
4
A
5
A
6
A
7
A
2
Synteza układu
sterującego!
Numeracja stanów
wewnętrznych
I
T
P
W
ZPT
11
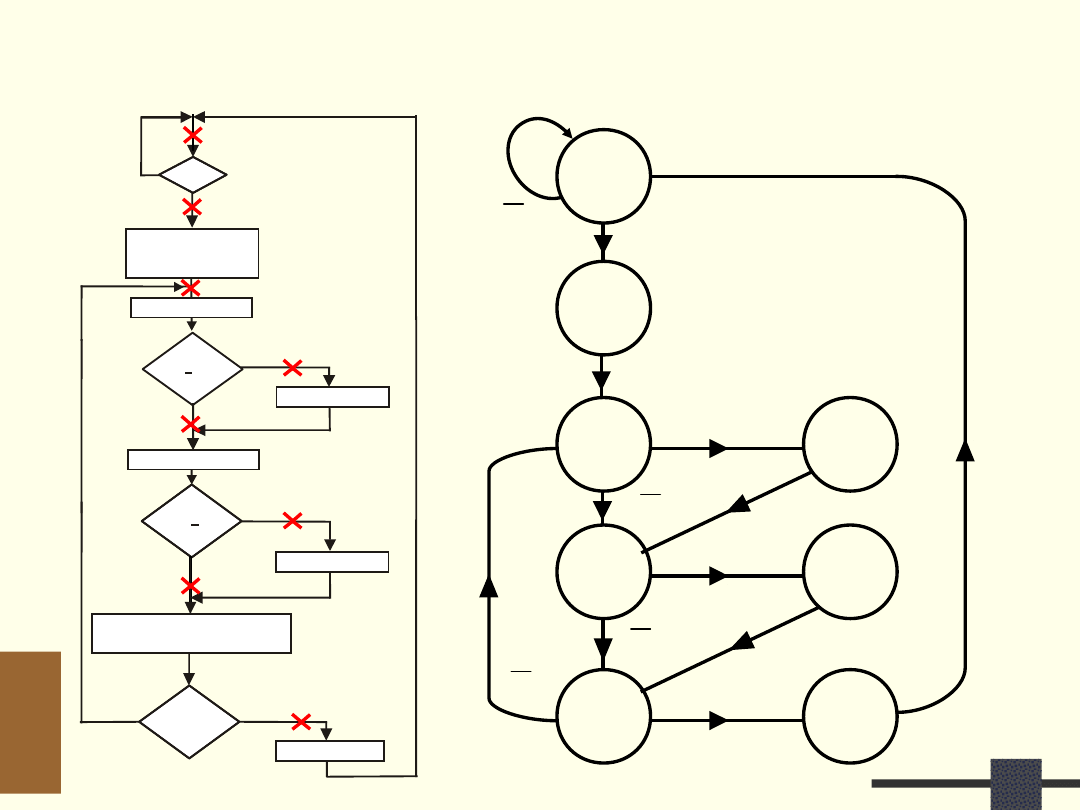
Zamiana SD na automat sterujący
LK = 0
0
0
SHL 1, SHL 2, SHL 3,
DEC (LK)
MUX := 0
MUX := 1
LOAD 4
LOAD 2
LOAD 3
S
0
1
1
0
1
1
LOAD 1
CLEAR 2,3
LOAD (LK)
K > 5
K > 5
A
0
A
1
A
2
A
3
A
4
A
5
A
6
A
7
A
0
/Z
0
A
1
/Z
1
A
2
/Z
2
A
3
/Z
3
A
4
/Z
6
A
6
/Z
4
A
7
/Z
5
A
5
/Z
7
x
1
x
1
x
0
x
2
0
x
1
x
1
x
2
x
Zamiana SD na automat sterujący
Nowe oznaczenia
sygnałów
predykatowych
I
T
P
W
ZPT
12
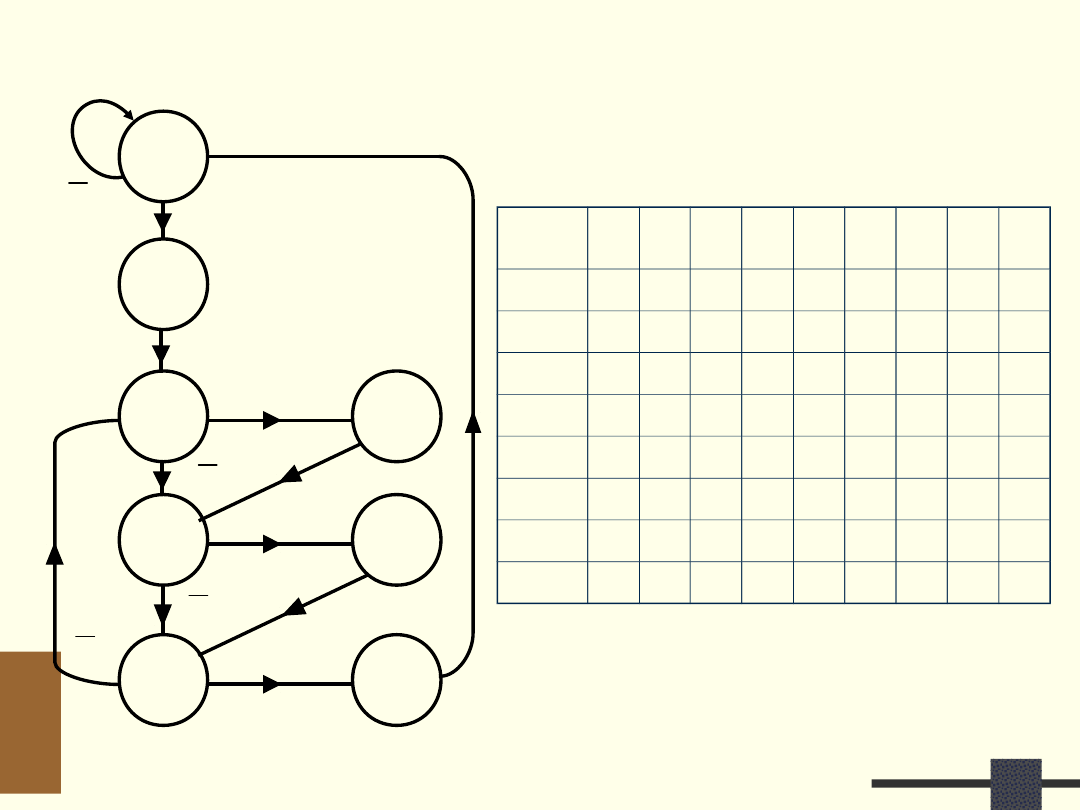
Tablica p-w automatu sterującego
x
2
x
1
x
0
S
00
0
00
1
01
1
01
0
11
0
11
1
10
1
10
0
Z
A
0
Z
0
A
1
Z
1
A
2
Z
2
A
3
Z
3
A
4
Z
6
A
5
Z
7
A
6
Z
4
A
7
Z
5
A
0
/Z
0
A
1
/Z
1
A
2
/Z
2
A
3
/Z
3
A
4
/Z
6
A
6
/Z
4
A
7
/Z
5
A
5
/Z
7
x
1
x
1
x
0
x
2
0
x
1
x
1
x
2
x
A
0
A
0
A
0
A
0
A
1
A
1
A
1
A
1
A
2
A
2
A
2
A
2
A
2
A
2
A
2
A
2
A
6
A
6
A
6
A
6
A
3
A
3
A
3
A
3
A
4
A
4
A
7
A
7
A
7
A
7
A
4
A
4
A
2
A
5
A
5
A
2
A
2
A
5
A
5
A
2
A
0
A
0
A
0
A
0
A
0
A
0
A
0
A
0
A
3
A
3
A
3
A
3
A
3
A
3
A
3
A
3
A
4
A
4
A
4
A
4
A
4
A
4
A
4
A
4
Tablica p-w wystarcza
do realizacji automatu!
I
T
P
W
ZPT
13
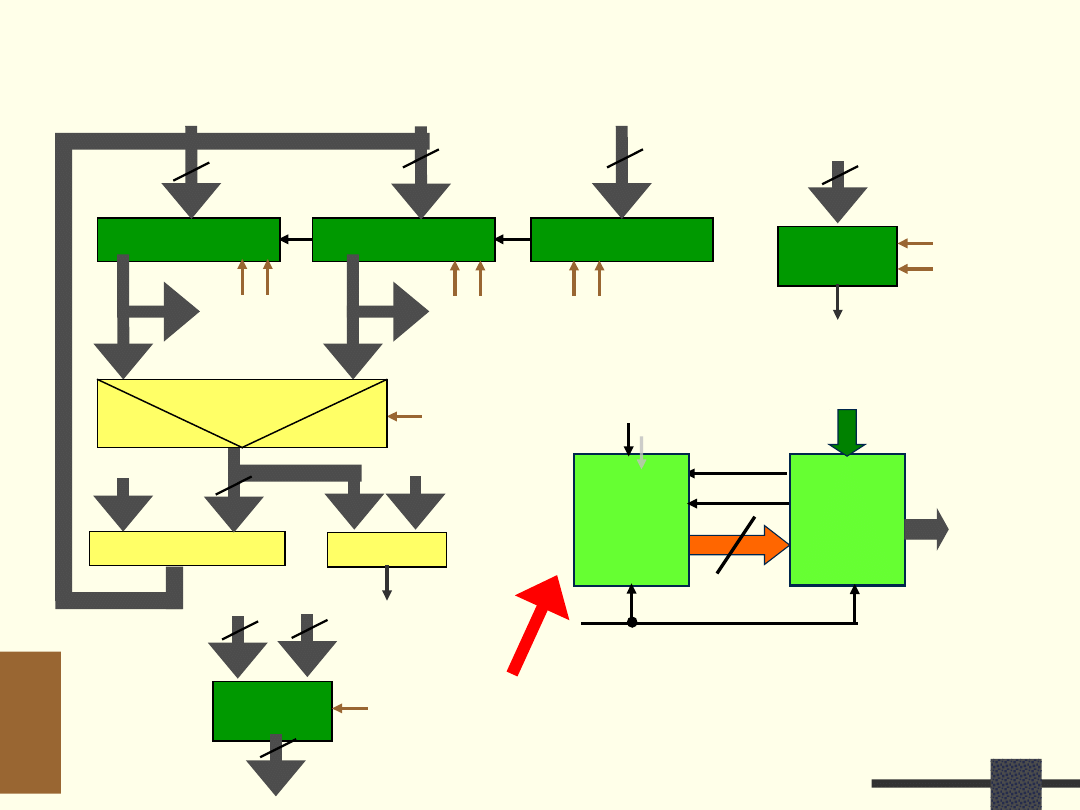
Opis strukturalny
R3
R2
R1
K
S3
S2
S1
A
B
8
4
4
4
„3”
„5”
K 5
LK
4
„8”
LOAD1
DEC
LK = 0
R4
LOAD2
8
Y = LD
UO
LB
Y
LK = 0
10
US
S
K 5
MUX
1
0
MUX
4
A
B
4
LB
Zrealizowany automat
jest Układem
Sterującym
I
T
P
W
ZPT
14
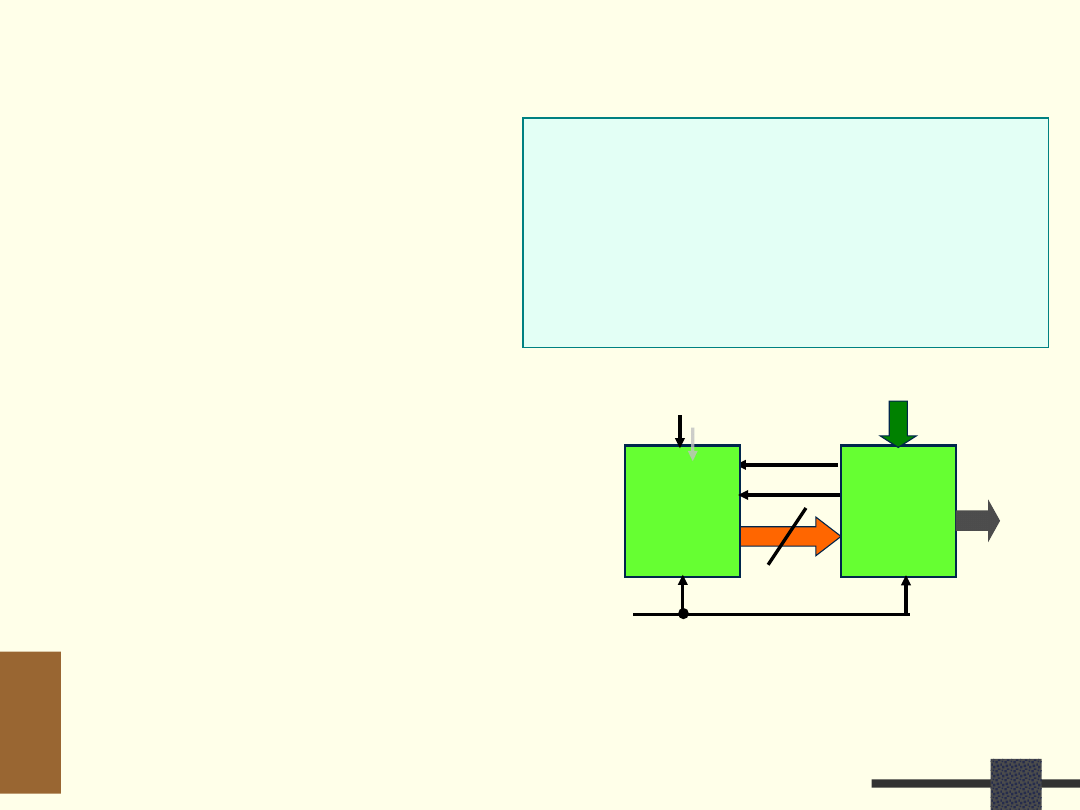
Bin2BCD – opis strukturalny
-- Kowersja liczby binarnej na liczbe bcd (lb<99)
------------------------------------------------
library
ieee;
use
ieee.std_logic_1164.all;
entity
bin2bcd
is
port
(
start, zegar
:
in
std_logic;
lb
:
in
std_logic_vector(7
downto
0);
ld
:
out
std_logic_vector(7
downto
0);
koniec
:
out
std_logic);
end
bin2bcd;
architecture
structure
of
bin2bcd
is
component
uo
port
(
lb
:
in
std_logic_vector(7
downto
0);
st
:
in
std_logic_vector(9
downto
0);
zegar
:
in
std_logic;
ld
:
out
std_logic_vector(7
downto
0);
lk_s, k_s :
out
std_logic);
end
component
;
component
us
port
(
start, lk :
in
std_logic;
k,zegar :
in
std_logic;
s
:
out
std_logic_vector(9
downto
0);
koniec :
out
std_logic);
end
component
;
signal
a : std_logic_vector(1
downto
0);
signal
b : std_logic_vector(9
downto
0);
begin
k1 : uo
port
map (lb => lb, st => b, zegar => zegar,
ld => ld, lk_s => a(1), k_s => a(0));
k2 : us
port
map (start => start, lk => a(1), k => a(0),
zegar => zegar, s => b, koniec => koniec);
end
structure;
UO
LB
Y
LK = 0
10
US
S
K 5
I
T
P
W
ZPT
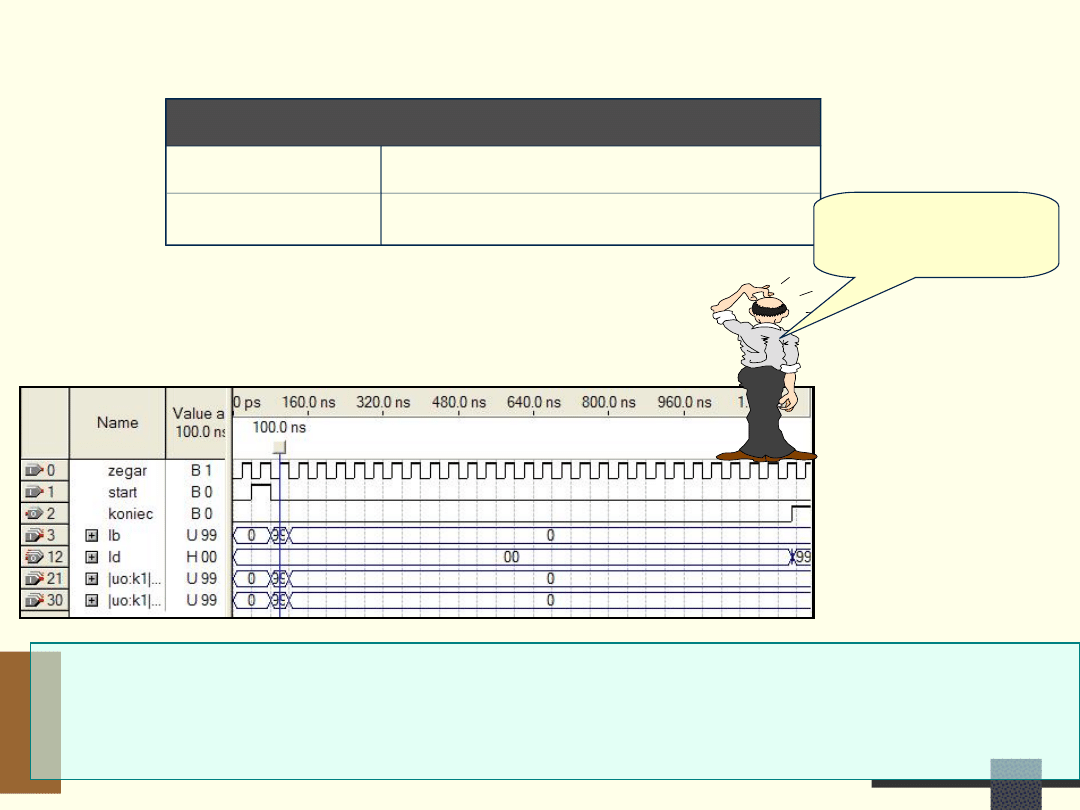
15
Wyniki realizacji – FLEX10K10
• Liczba jest konwertowana w (około) 29 cyklach zegarowych
• Przepustowość =
56,82
* 10
6
/ 29
=
1,959
mln liczb binarnych na sekundę
EPF10K10LC84-3
LC’s
69 (12 %)
f
MAX
56,82 MHz (17,6 ns )
Niewielki procent
wykorzystania
zasobów układu
I
T
P
W
ZPT
16
Bin2BCD – opis funkcjonalny
-- Konwersja liczby binarnej na liczbe bcd (lb<99)
------------------------------------------------
library
ieee;
use
ieee.std_logic_1164.all;
-- USE ieee.std_logic_arith.all;
use
ieee.std_logic_unsigned.all;
entity
bin2bcd
is
port
(
start, clk :
in
std_logic;
lb
:
in
std_logic_vector(7
downto
0);
koniec :
out
std_logic;
ld
:
out
std_logic_vector(7
downto
0));
end
b
in
2bcd;
architecture
behavior
of
bin2bcd
is
begin
process
(clk)
variable
lk
: integer
range
0
to
8;
variable
lda, ldb : std_ligic_vec
to
r(3
downto
0);
variable
lb_r
: std_ligic_vec
to
r(7
downto
0);
begin
if
(rising_edge(clk))
then
if
start = '1'
then
lda := "0000";
ldb := "0000";
ld <= "00000000";
lb_r := lb;
lk := 8;
koniec <= '0';
else
if
lk > 0
then
if
ldb >= 5
then
lda := (lda(2
downto
0) & '1');
ldb := ((ldb(2
downto
0) + "011") & lb_r(7));
else
lda := (lda(2
downto
0) & '0');
ldb := (ldb(2
downto
0) & lb_r(7));
end
if
;
lb_r := (lb_r(6
downto
0) & '0');
lk := lk - 1;
else
ld <= (lda & ldb);
koniec <= '1';
end
if
;
end
if
;
end
if
;
end
process
;
end
behavior;

I
T
P
W
ZPT
17
Wyniki realizacji – FLEX10K10
• Liczba jest konwertowana w (około) 10 cyklach zegarowych
• Przepustowość = 69,93 * 10
6
/ 10
= 6,993 mln liczb binarnych na sekundę
EPF10K10LC84-3
LC’s
43 (7 %)
f
MAX
69,93 MHz (14,3
ns )
Jeszcze mniejsze
wykorzystanie
zasobów układu
I
T
P
W
ZPT
18
Inna rodzina układów FPGA
Dla realizacji opisanej funkcjonalnie:
Przepustowość =
392,77
* 10
6
/ 10
=
39,277
mln liczb binarnych na sekundę
EP1S10F484C5
Strukturalny
Funkcjonalny
LC’s
54 ( < 1 % )
34 ( < 1 % )
f
MAX
392,77 MHz (2,546
ns )
371,20 MHz (2,694 ns
)
Znacznie więcej
niż nowoczesny
komputer!
I
T
P
W
ZPT
19
.type fr
.i 9
.o 8
.p 100
000000000 0000
0000
000000001 0000
0001
000000010 0000
0010
000000011 0000
0011
000000100 0000
0100
000000101 0000
0101
000000110 0000
0110
000000111 0000
0111
000001000 0000
1000
000001001 0000
1001
000001010 0001
0000
000001011 0001
0001
000001100 0001
0010
000001101 0001
0011
* * *
001100001 1001
0111
001100010 1001
1000
001100011 1001
1001
.e
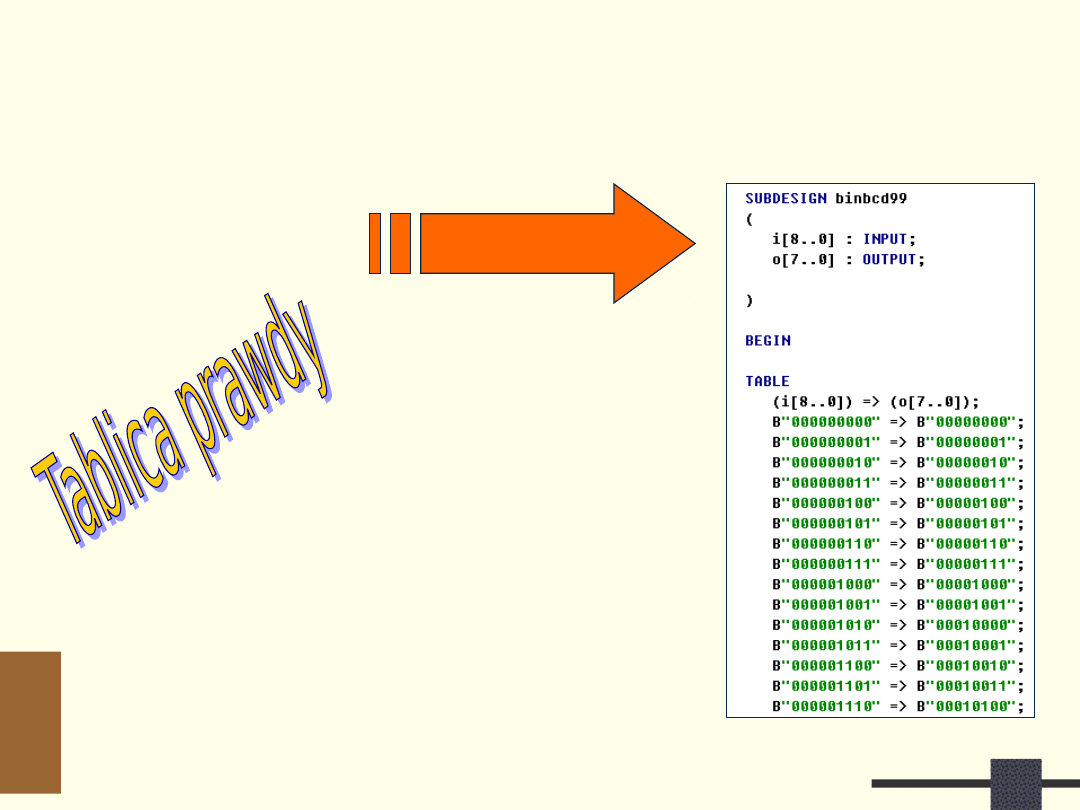
Konwerter Bin2BCD na poziomie
Konwerter Bin2BCD na poziomie
logicznym
logicznym
AHDL/VHDL
I
T
P
W
ZPT
20
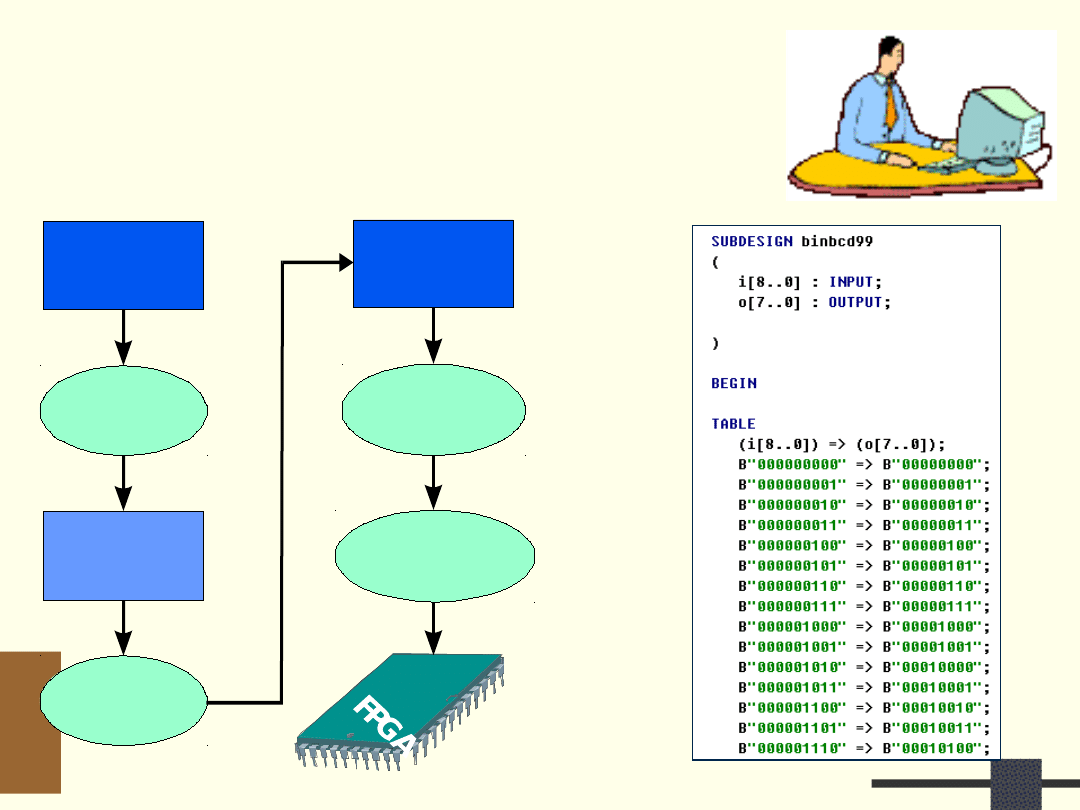
Komputerowe projektowanie…
20
SPECYFIKACJA
FUNKCJONALNA
(HDL)
SYNTEZA
FUNKCJONALNA
OPIS RTL
TRANSLACJE
SPECYFIKACJI
SIEĆ
LOGICZNA
OPTYMALIZACJA
LOGICZNA
ODWZOROWANIE
TECHNOLOGICZN
E
24 LEs ─ 313
mln/sek
I
T
P
W
ZPT
21
.type fr
.i 9
.o 8
.p 100
000000000 0000
0000
000000001 0000
0001
000000010 0000
0010
000000011 0000
0011
000000100 0000
0100
000000101 0000
0101
000000110 0000
0110
000000111 0000
0111
000001000 0000
1000
000001001 0000
1001
000001010 0001
0000
000001011 0001
0001
000001100 0001
0010
000001101 0001
0011
* * *
001100001 1001
0111
001100010 1001
1000
001100011 1001
1001
.e
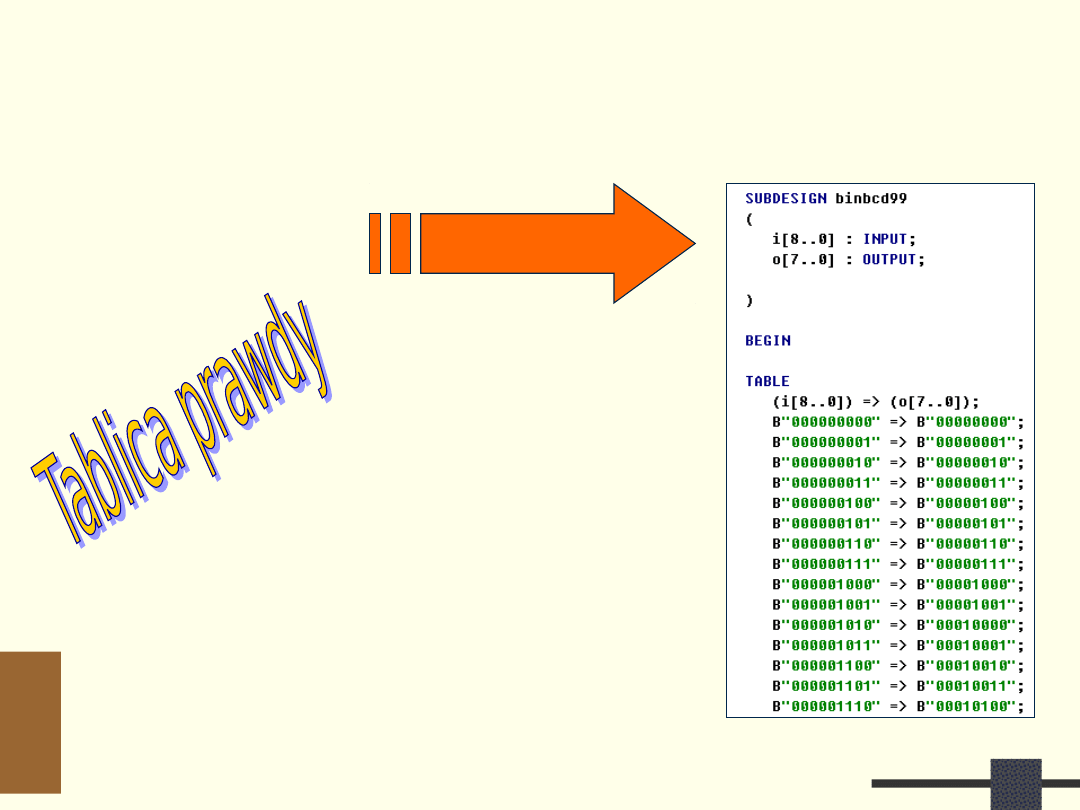
Konwerter Bin2BCD na poziomie
Konwerter Bin2BCD na poziomie
logicznym
logicznym
AHDL/VHDL
I
T
P
W
ZPT
22
Tablica prawdy – bin2bcd
TITLE " Decomposed project: bin2bcd ";
% Translated from DEMAIN format %
% Warsaw University of Technology %
% Institute of Telecommunications %
SUBDESIGN A
(
in_1, in_2, in_3, in_4
:INPUT;
in_5, in_6, in_7
:INPUT;
out_1, out_2, out_3, out_4 :OUTPUT;
out_5, out_6, out_7, out_8 :OUTPUT;
)
VARIABLE
g1_1, g1_2, g1_3, g3_1
:LCELL;
g2_1, g2_2
:LCELL;
BEGIN
---- Level 1 ----
TABLE
(in_1, in_2, in_3, in_4) => (g1_1);
B"1000" => B"0";
B"0011" => B"0";
.................
B"0001" => B"1";
B"1011" => B"1";
END TABLE;
TABLE
(in_6, g1_1, g2_1, g2_2) => (out_7);
B"0X10" => B"0";
.................
B"1011" => B"1";
END TABLE;
END;
# Konwerter
bin2bcd
.type fr
.i 7
.o 8
.p 100
0000000 00000000
0000001 00000001
0000010 00000010
0000011 00000011
0000100 00000100
0000101 00000101
. . . ..........
1011111 10010101
1100000 10010110
1100001 10010111
1100010 10011000
1100011 10011001
.e
Procedura
dekompozycji
13 komórek
(!!!)
22
352
mln/sek

I
T
P
W
ZPT
23
Realizacja programowa
Algorytm zapisany w języku
C++
Kompilacja w systemie
Windows XP
Specyfikacja komputera:
Procesor AMD Athlon™ 64X2 Dual Core
4200+ 2.2 GHz
Pamięć RAM 1,96 GB DDR2
Konieczność symulowania
operacji na rejestrach:
przesunięcie w lewo,
zwiększenie o 3,
porównanie ze stałą.
I
T
P
W
ZPT
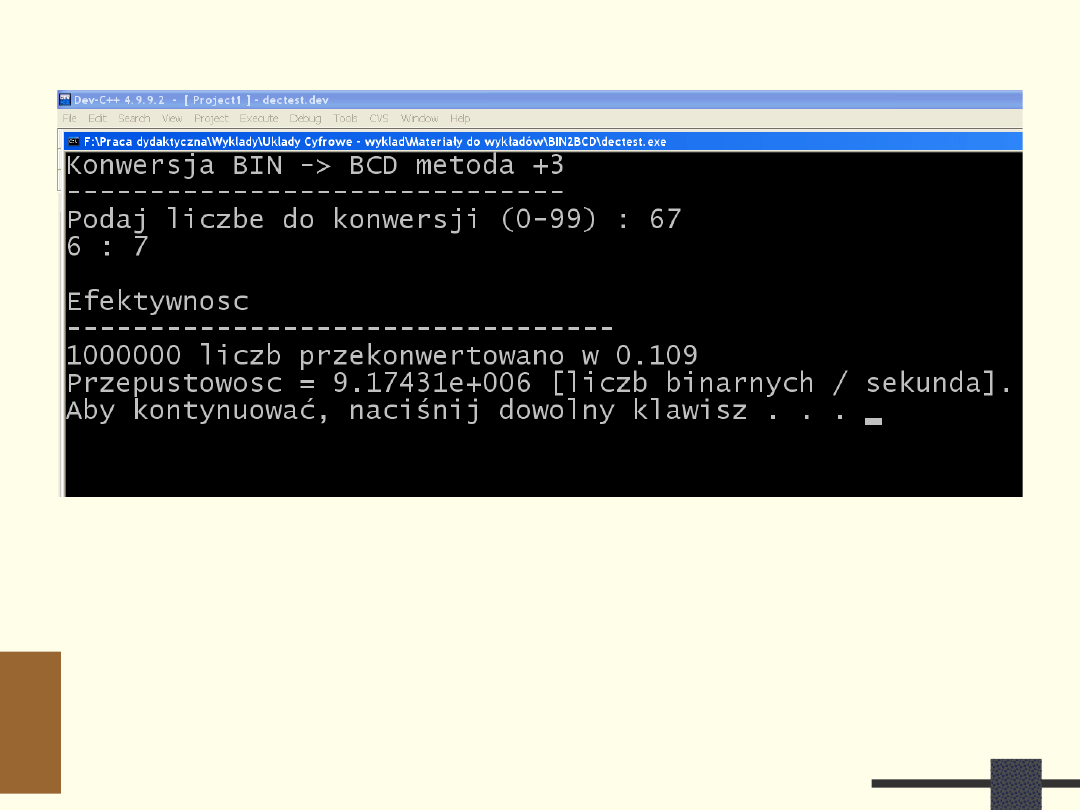
24
Efektywność realizacji
Szybkość działania szacowana liczbą konwersji na
sekundę
Przepustowość = 9,17 * 10
6
= 9,17 mln liczb binarnych na sekundę

I
T
P
W
ZPT
25
Porównanie realizacji BIN2BCD
Synteza strukturalna – 54 LEs ─ 33
mln/sek
Synteza logiczna:
system komercyjny Quartus – 24 LEs ─ 313
mln/sek
system specjalizowany – 13 LEs ─ 352
mln/sek
Liczba elementów logicznych ─ liczba
słów
Procesor AMD Athlon™ 64X2 Dual Core 4200+
2.2 GHz – 9,17 mln/sek
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
Wyszukiwarka
Podobne podstrony:
ELC met synt
ELC VHDL
ELC VHDL cz 1
ELC dek klas
Przyklad-bin2bcd-I
Przyklad-bin2bcd-II
ELC met synt
ELC bloki cz 1
ELC notatki (2)
ELC dek klas
ELC dek r p
ELC
Jednostka sterująca ELC drugiej
więcej podobnych podstron