
Programowanie
matematyczne
• Programowanie Liniowe
funkcja celu i funkcje ograniczeń
są liniowe
• Programowanie Nieliniowe
funkcja celu i/lub funkcje
ograniczeń są nieliniowe

Każde zadanie minimalizacji funkcji celu
można zapisać w równoważnej formie
Ograniczenie nierównościowe typu
można wyrazić w postaci
Ograniczenie nierównościowe można zamienić na ograniczenie
równościowe poprzez dodanie tzw. zmiennej osłabiającej
)
(
min x
x
f
)
(
max
)
(
min
x
x
x
x
f
f
n
k
n
k
dla
g
,...,
1
,
)
(
0
x
n
k
n
k
dla
g
,...,
1
,
)
(
0
x
rs
k
n
k
dla
g
,...,
1
,
)
(
0
s
x
2
0
s

Zadanie optymalizacji
• zbiór zmiennych decyzyjnych zadania
optymalizacji
• n=1,...,N
ilość zmiennych zadania
•
funkcja celu
•
ograniczenia równościowe
• ograniczenia
nierównościowe
T
n
x
x
}
,...,
{
1
x
)
(x
f
r
j
n
j
dla
h
,...,
1
,
)
(
0
x
n
k
n
k
dla
g
,...,
1
,
)
(
0
x

Sformułowanie zadania
optymalizacji
Znajdź x takie, że
przy ograniczeniach
)
(
min x
x
f
r
j
n
j
dla
h
,...,
1
,
)
(
0
x
n
k
n
k
dla
g
,...,
1
,
)
(
0
x
g
d
x
x
x

Podstawy matematyczne
macierz jest tablicą prostokątną o wymiarze nxm
ij
mn
m2
m1
2n
22
21
1n
12
11
a
a
...
a
a
a
...
a
a
a
...
a
a
A
Macierz diagonalna
mn
22
11
a
...
0
0
0
...
a
0
0
...
0
a
A
Macierz jednostkowa
1
...
0
0
0
...
1
0
0
...
0
1
I
Macierz trójkątna górna
mn
2n
22
1n
12
11
a
...
0
0
a
...
a
0
a
...
a
a
A
mn
2n
1n
m2
22
12
m1
21
11
T
a
...
a
a
a
...
a
a
a
...
a
a
A
•Macierz A jest symetryczna gdy
A=A
T
tzn.
a
ij
=a
ij
•Macierz A jest skośnosymetryczna gdy
a
ij
=-a
ij

Działania na macierzach
ij
mn
m2
m1
2n
22
21
1n
12
11
a
a
...
a
a
a
...
a
a
a
...
a
a
A
mn
mn
m2
m2
m1
m1
2n
2n
22
22
21
21
1n
1n
12
12
11
11
mn
m2
m1
2n
22
21
1n
12
11
mn
m2
m1
2n
22
21
1n
12
11
a
b
...
a
b
a
b
a
b
...
a
b
a
b
a
b
...
a
b
a
b
a
...
a
a
a
...
a
a
a
...
a
a
b
...
b
b
b
...
b
b
b
...
b
b
A
B
32
23
22
22
12
21
31
23
21
22
11
21
32
13
22
12
12
11
31
13
21
12
11
11
32
31
22
21
12
11
23
22
21
13
12
11
a
b
a
b
a
b
a
b
a
b
a
b
a
b
a
b
a
b
a
b
a
b
a
b
a
a
a
a
a
a
b
b
b
b
b
b
*
* A
B
Iloczyn macierzy
Dodawanie macierzy
Mnożenie macierzy przez skalar
Dodawanie macierzy - własności
)
(
)
(
C
B
A
C
B
A
Prawo łączności
A
B
B
A
Prawo przemienności
B
A
B
A
A
A
A
)
(
)
(
Prawo rozdzielności
A
0
A
Mnożenie macierzy - własności
)
(
)
(
BC
A
C
AB
Prawo łączności
BA
AB
CB
CA
B
A
C
BC
AC
C
B
A
)
(
)
(
Prawa rozdzielności
A
IA
AI
B
A
B
A
AB
)
(
Uwaga !
T
T
T
A
B
AB
wyznacznik macierzy
12
21
33
11
23
32
13
22
31
32
21
13
31
23
12
33
22
11
33
32
31
23
22
21
13
12
11
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
A
1. Jeśli macierz posiada kolumnę lub wiersz złożony z samych
zer to
2. Wartość wyznacznika nie zmienia się jeśli zmienimy ze sobą
kolumny lub wiersze
3. Jeśli B powstaje przez zamianę dwóch kolumn lub wierszy to
4. Jeśli dwie kolumny lub wiersze macierzy B są równe to
5. Pomnożenie elementów wiersza lub kolumny przez k jest
równoznaczne z pomnożeniem wyznacznika przez k
6. Wartość wyznacznika nie podlega zmianie gdy do elementów
wiersza dodamy lub odejmiemy elementy innego wiersza
pomnożone przez k
0
A
A
B
0
B

Rzędem
macierzy A nazywamy stopień największej podmacierzy
kwadratowej której wyznacznik jest różny od zera
Gdy
macierz jest
osobliwa
Gdy
macierz jest
nieosobliwa
Minor
D
ij
elementu a
ij
jest wyznacznikiem otrzymanym z macierzy
kwadratowej przez wykreślenie i-tego wiersza i j-tej kolumny
Dopełnienie algebraiczne
A
ij
elementu a
ij
jest równe (-1)
i+j
D
ij
.
Macierzą dołączoną
macierzy A o wymiarach nxn jest macierz
J=[A
ij
] o wymiarach nxn, w której element i-tego wiersza i j-tej
kolumny jest dopełnieniem algebraicznym elementu w i-tym
wierszu i j-tej kolumnie macierzy A
0
A
0
A
33
32
31
23
22
21
13
12
11
a
a
a
a
a
a
a
a
a
A
13
31
33
11
33
31
13
11
22
a
a
a
a
a
a
a
a
D
22
2
2
22
D
A
)
1
(
33
32
31
23
22
21
13
12
11
A
A
A
A
A
A
A
A
A
J
Macierz B nazywamy
macierzą odwrotną
macierzy kwadratowej
A jeśli AB=I. Macierz odwrotną oznaczamy A
-1
Dla każdej nieosobliwej macierzy A istnieje jedna i tylko jedna
macierz odwrotna A
-1
taka, że
Gdy
to
Tylko nieosobliwe macierze kwadratowe mają macierze odwrotne
I
A
A
AA
1
1
0
A
J
A
A
1
1
1
1
1
A
B
AB

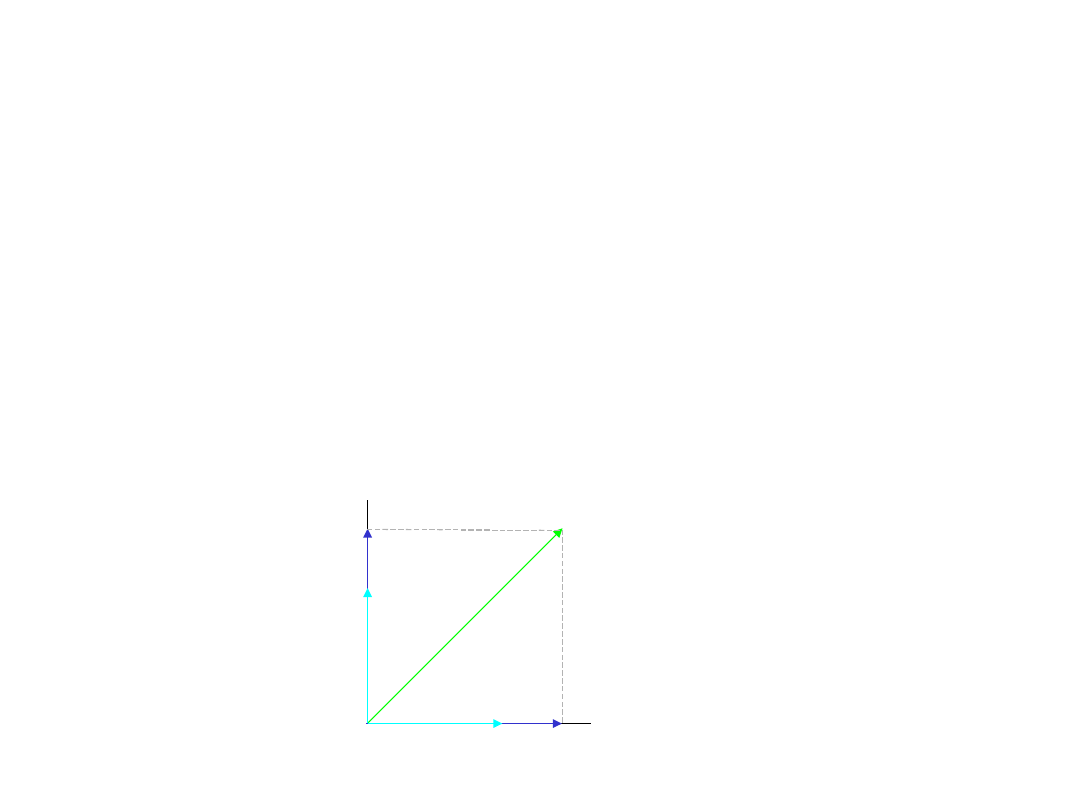
(0,0)
u
1
u
2
(u
1
,u
2
)
u
2
1
u
u
u
Własności wektorów w dwuwymiarowej przestrzeni euklidesowej E
2
u
u
)
(
Prawo łączności
v
u
v
u
u
u
u
)
(
)
(
Prawo rozdzielności
0
,
0
0
1
0
u
u
u
Mnożenie wektorów przez skalar - własności
2
1
2
1
)
(
u
u
u
u
u
u
u
u
u

u
v
v
u
Prawo przemienności
Dodawanie wektorów-własności
Prawo łączności
2
1
u
u
u
2
1
v
v
v
2
2
1
1
2
1
2
1
v
u
v
u
v
v
u
u
v
u
u
v
u-v
-v
u+v
w
v
u
w
v
u
W przestrzeni E
2
istnieje tylko jeden wektor
zerowy
0 zwany
punktem odniesienia
taki, że
u
0
u
dla każdego u w E
2
Dla każdego u w E
2
istnieje tylko jeden wektor
przeciwny
-u taki, że
0
u
u
dla każdego u w E
2

vu
uv
Prawo przemienności
Iloczyn skalarny
wektorów-własności
Wtedy i tylko wtedy gdy u=0
vw
uw
w
v
u
Każdej parze wektorów u i v w E
2
odpowiada liczba rzeczywista uv=u
1
v
1
+u
2
v
2
zwana iloczynem skalarnym u i v.
0
0
u
u
i
wtedy i tylko wtedy gdy u=0
Każdemu wektorowi u w E
2
odpowiada liczba rzeczywista
zwana długością wektora u
Nierówność trójkąta
0
0
uu
uu
i
Dla dowolnych skalarów , i wektorów u, v i w w E
2
Długość wektora
2
2
2
1
u
u
u
u
u
uu
u
v
u
v
u
dla każdego u, v w E
2
u
1
u
2
2
2
2
1
u
u
u
Zbiór wektorów U
1
,U
2
, U
3
,...,U
n
nazywamy
liniowo niezależnym
,
gdy dla wszystkich liczb
1
,
2
,...,
n
równość
pociąga
np.
W przeciwnym razie zbiór jest
liniowo zależny
0
U
U
U
n
2
2
...
n
1
1
U
1
=[1 0]
T
U
2
=[0 1]
T
0
n
...
2
1
0
1
1
U
0
0
1
1
0
1
2
1
2
2
1
U
U
1
1
1
2
U
0
0
2
2
1
0
1
1
U
0
0
1
1
1
0
0
1
3
2
1
3
3
2
2
1
1
U
U
U
1
0
2
U
0
0
3
2
3
1
1
1
3
U
1
U
1
=[
1
0]
T
2
U
2
=[0
2
]
T
1
U
1+
2
U
2
=[
1
2
]
T

n – wymiarowa przestrzeń euklidesowa
E
n
, jest zbiorem obiektów zwanych
wektorami, które posiadają własności opisane poprzednio; w przestrzeni E
n
istnieje
układ n niezależnych wektorów, ale każde n+1 wektorów
w jest układem liniowo zależnym.
Bazą
w E
n
jest zbiór liniowo niezależnych wektorów. Każdy wektor może być
jednoznacznie wyznaczony jako kombinacja liniowa wektorów danej bazy.
Zbiory wypukłe
Wypukłą kombinacją punktów U
1
,U
2
, U
3
,...,U
n
nazywamy punkt
U=
1
U
1
+
2
U
2
+...
n
U
n
gdzie
i
są skalarami spełniającymi warunki i . Podzbiór C
w E
n
jest wypukły wtedy i tylko wtedy, gdy dla każdej pary U
1
,U
2
w C każda
kombinacja wypukła
U=
1
U
1
+
2
U
2
lub
gdy
1
=1-
2
U= (1-
2
)U
1
+
2
U
2
,
również należy do C.
0
i
1
i
i
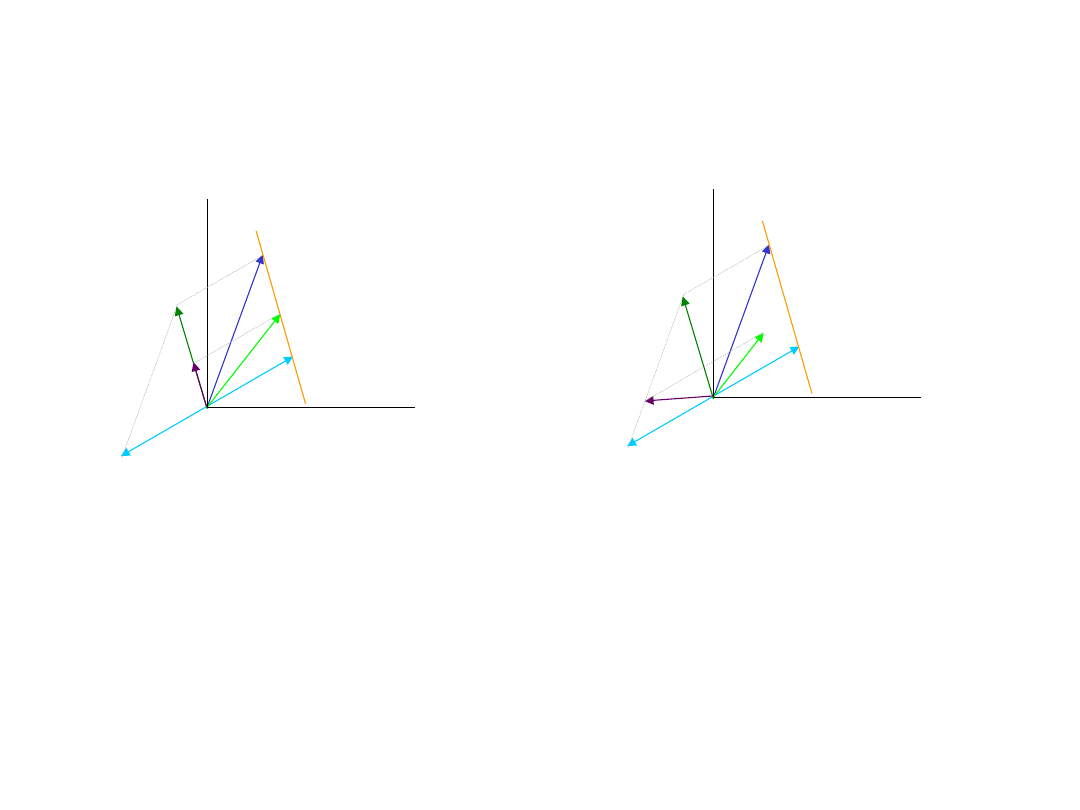
Twierdzenie 1
Dowolny punkt leżący na odcinku łączącym dwa punkty w E
n
może
być wyrażony jako kombinacja wypukła tych dwóch punktów.
Dowód
Oznaczmy dwa punkty przez U i V oraz punkt W leżący na odcinku
łączącym U i V.
Ponieważ kombinacja liniowa jest wypukła gdy spełnia warunek
W= (1-
2
)V+
2
U
dla każdego
przy
Więc dla
mamy W =V+
(U-V)
Zatem wektor W jest kombinacją wypukłą V i U.
U
V
U-V)
-V
W
U-V
0,1]
[
2
0,1]
[
2
U
V
W-V)
-V
W
U-V
1
i
i
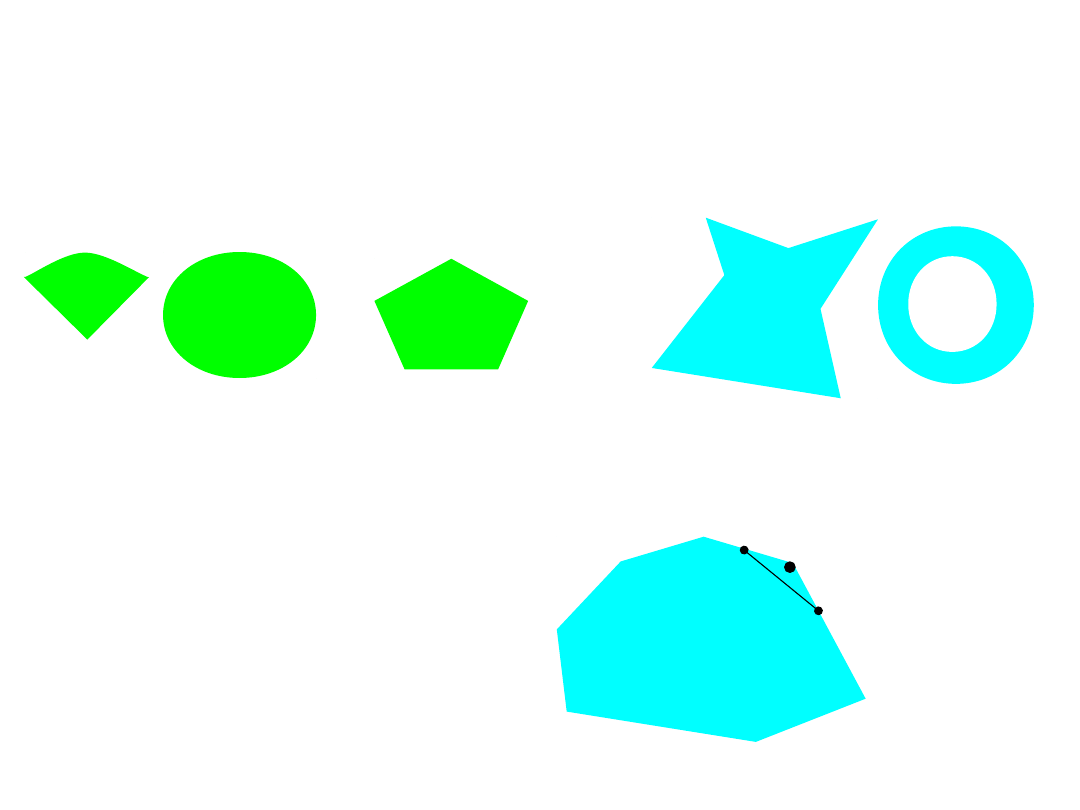
Twierdzenie 2 (odwrotne)
Dowolny punkt, który może być wyrażony jako
kombinacja wypukła dwóch punktów w E
n
, leżący na
odcinku łączącym te dwa punkty.
Zbiory wypukłe
Zbiory nie wypukłe
Punkt U zbioru wypukłego C nazywamy
wierzchołkiem
, jeśli
nie może być on wyrażony jako kombinacja wypukła dwóch różnych
punktów należących do C.
U
C
W
V
Punkt U nie leży na prostej łączącej punkty W i V.

Zbiór wektorów S nazywamy
stożkiem
, jeśli dla każdego wektora U
Należącego do S,
2
U także należy do S, gdzie
2
jest liczbą
nieujemną.
Przykładem stożków są całe przestrzenie, początek układu oraz zbiór
S
S.
Uwaga!
Stożek zawiera początek układu ponieważ
2
może być równe
zeru.
Sympleks
jest n-wymiarowym wielościanem wypukłym mającym
dokładnie n+1 wierzchołków. W przestrzeni E
0
sympleksem jest punkt,
w E
1
prosta, zaś w E
2
trójkąt.
S
S
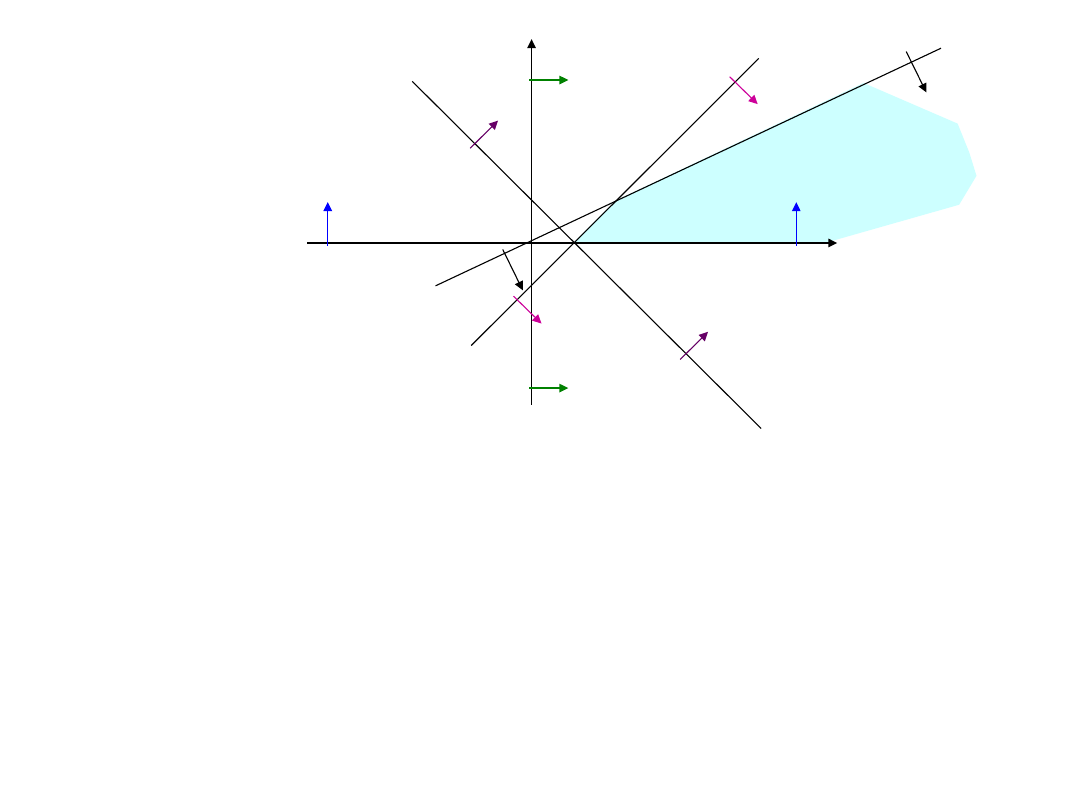
Nierówności liniowe
0
2
0
2
1
2
1
2
1
1
2
1
1
0
x
x
x
x
x
x
x
x
a)
b)
c)
d)
e)
(0,1)
(1,0)
(2,1)
b)
a)
c)
d)
e)
C
0
1
1
0
0
2
-
1
-
1
-
1
1
1
1
0
0
1
2
1
x
x
0
2
2
1
1
x
x
P
P
P
T
1
1
1
1
0
1
P
T
2
1
1
1
0
2
P
T
0
1
1
0
0
0
P
lub
gdzie
Obszar dopuszczalnych
rozwiązań
Układ nierówności
można zamienić na układ równości poprzez odjęcie
(dodanie)
zmiennej osłabiającej
takiej, że
wówczas
m
n
mn
2
m2
1
m1
2
n
2n
2
22
1
21
1
n
1n
2
12
1
11
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
m
m
n
mn
2
m2
1
m1
2
2
n
2n
2
22
1
21
1
1
n
1n
2
12
1
11
b
s
x
a
x
a
x
a
b
s
x
a
x
a
x
a
b
s
x
a
x
a
x
a
0
0,...,s
s
m
1
x
1
>0
x
1
-s
2
=0
s
2
Obszar dopuszczalnych
rozwiązań
x
1
=0
x
1
x
2

Twierdzenie Kroneckera-Capelli
m
m
mxn
b
X
A
m
mxn
r
b
A
A
)
(
)
(
mxn
r
rz
rz
A
A
Jeśli dla układu (*) równań liniowych spełniony jest warunek
to mogą zaistnieć trzy następujące przypadki:
•
rz(A)=n=m, istnieje tylko jedno rozwiązanie (*)
•
rz(A)=n<m, istnieje jedno rozwiązanie (*), lecz (m-n) równań jest zbędnych
(redukcja)
•
rz(A)=m<n, istnieje nieskończenie wiele rozwiązań układu (*), układ jest
nieoznaczony
Układ równań liniowych
(*)
ma rozwiązanie
wtedy i tylko wtedy, gdy rząd macierzy rozszerzonej
jest równy macierzy A, tj.
n
R
X
)
(
)
(
mxn
r
rz
rz
A
A
Przykład. Obliczyć rząd macierzy
2
6
1
6
)
(
0
1
6
0
0
0
0
1
0
6
0
0
0
0
0
0
0
0
0
0
0
6
0
1
0
3
0
0
0
0
0
2
0
0
0
1
3
2
0
6
0
1
0
3
0
0
0
3
0
2
0
0
0
1
4
3
3
6
2
0
3
3
1
0
0
3
1
0
2
0
0
0
1
1
4
,
1
3
,
1
2
3
5
3
3
3
1
0
0
1
3
2
2
1
1
1
1
A
rz
w
w
k
k
k
k
k
k
k
k

Metody rozwiązywania układów równań
b
Ax
6
3
2
3
3
3
2
x
x
x
x
x
x
x
x
x
2
1
2
1
2
1
b
A
x
1
1
1
1
1
1
2
1
1
1
A
3
2
1
x
x
x
x
6
3
2
b
1
2
1
1
P
1
1
2
1
P
1
1
-
1
-
3
P
6
2
0
3
P
ponieważ
Powyższy układ (*) można zapisać w postaci kombinacji liniowej
wektorów
0
3
3
2
2
1
1
P
P
P
P
x
x
x
(*)
(**)

Definiujemy n-1 czynników
Mnożymy pierwsze równanie przez m
21
a następnie odejmujemy je od
równania drugiego. Następnie mnożymy pierwsze równanie przez m
31
a
następnie odejmujemy je od równania trzeciego. Postępowanie to
kontynuujemy aż do ostatniego równania. W ten sposób otrzymujemy
Opisaną procedurę można zastosować do końcowych n-1 równań. W tym
celu definiujemy
Metoda Eliminacji Gaussa
m
n
mn
2
m2
1
m1
2
n
2n
2
22
1
21
1
n
1n
2
12
1
11
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
n
i
a
a
m
i
i
,...,
3
,
2
,
11
1
1
)
1
(
1
1
)
1
(
i
)
2
(
i
)
1
(
ij
1
)
1
(
ij
)
2
(
ij
)
m
(
n
)
n
(
mn
)
2
(
m2
)
2
(
2
)
n
(
2n
)
2
(
22
)
1
(
1
)
n
(
1n
)
2
(
12
)
1
(
11
,
b
m
b
b
a
m
a
a
gdzie
b
x
a
x
a
b
x
a
x
a
b
x
a
x
a
x
a
i
i
n
2
n
2
n
2
1
n
i
a
a
m
i
i
,...,
3,4
,
)
2
(
2
)
(
2
2
2
2
(*)
(**)

Mnożymy drugie równanie układu (**) przez m
i2
a następnie wynik odejmujemy od trzeciego
równania, czwartego równania,....., n-1 równania. W k-tym kroku procedury posługujemy się
Czynnikami
i obliczamy nowe współczynniki
Po wykonaniu n-1 kroków otrzymujemy trójkątny układ równań
Ostatnie równanie zawiera jedynie zmienną x
n
. Podstawienie jej do równania otrzymanego
wcześniej prowadzi do wyrażenia na zmienną x
n-1
, tzn. w ogólnym przypadku
n
i
a
a
m
k
kk
k
ik
i
,...,
2
k
1,
k
,
)
(
)
(
k
)
k
(
k
k
)
k
(
i
)
k
(
i
)
k
(
kj
k
)
k
(
ij
)
(
ij
b
m
b
b
a
m
a
a
i
i
k
1
1
)
m
(
n
)
n
(
mn
)
2
(
2
)
1
(
2n
)
2
(
22
)
1
(
1
)
1
(
1n
)
1
(
12
)
1
(
11
b
x
a
b
x
a
x
a
b
x
a
x
a
x
a
n
n
2
n
2
1
1
,...,
1
,
,
1
1
i
l
)
i
(
il
)
i
(
i
)
i
(
ii
n
n
i
x
a
b
a
x
n
l
i

Definiujemy n-1 czynników
Mnożymy pierwsze równanie przez m
21
a następnie odejmujemy je od
równania drugiego. Następnie mnożymy pierwsze równanie przez m
31
a
następnie odejmujemy je od równania trzeciego. W ten sposób otrzymujemy
Metoda Eliminacji Gaussa - przykład
1
1
,
3
,
2
,
11
1
1
11
1
1
11
1
1
a
a
m
a
a
m
i
a
a
m
i
i
3
3
2
2
1
2
(*)
3
2
1 ,
,
,
6
3
2
2
3
3
3
m
n
x
x
x
x
x
x
x
x
x
2
1
2
1
2
1
6
3
2
)
2(*m
3
3
21
3
x
x
x
x
x
x
x
x
x
2
1
2
1
2
1
6
3
2
4
-
3
3
3
x
x
x
x
x
x
x
x
x
2
1
2
1
2
1
2
2
2
6
7
4
-
2
2
2
3
3
3
)
1
(
)
2
(
x
x
x
x
x
x
x
x
2
1
2
2
1
w
w
1
3
Metoda Eliminacji Gaussa - przykład
6
3
2
)
2(*m
3
3
31
3
x
x
x
x
x
x
x
x
x
2
1
2
1
2
1
6
3
2
2
3
3
3
x
x
x
x
x
x
x
x
x
2
1
2
1
2
1
4
7
1
3
2
3
3
3
)
1
(
)
3
(
x
x
x
x
x
x
2
2
1
w
w
2
Ostatnie równanie zawiera jedynie zmienną x
n
. Podstawienie jej do równania
otrzymanego
wcześniej prowadzi do wyrażenia na zmienną x
n-1
, tzn. w ogólnym przypadku
1
)
2
)
1
(
3
1
(
2
1
1
)
(
2
1
1
2
1
1
,
1
3
2
)
1
(
7
3
1
)
(
7
3
1
,
1
2
0
0
4
2
1
4
2
1
,
1
1
,...,
1
,
,
1
3
)
1
(
13
2
)
1
(
12
2
l
)
1
(
1l
1
1
1
l
)
1
(
1l
)
1
(
1
)
1
(
11
1
3
3
l
3
)
2
(
23
2
1
2
l
)
2
(
2l
)
2
(
2
)
2
(
22
2
4
l
4
l
4
)
3
(
34
3
1
3
l
)
3
(
3l
)
3
(
3
)
3
(
33
3
1
i
l
)
i
(
il
)
i
(
i
)
i
(
ii
x
a
x
a
x
a
x
x
a
b
a
x
x
a
x
x
a
b
a
x
x
a
x
x
a
b
a
x
n
n
i
x
a
b
a
x
n
l
n
l
n
l
n
n
n
l
n
l
i
Określenie macierzy
odwrotnej
o
P
I
A
6
1
0
0
1
1
1
3
0
1
0
1
1
2
2
0
0
1
1
1
1
Krok 1:
Krok 2:
4
1
0
1
-
2
0
0
7
0
1
2
1
-
3
0
2
0
0
1
1
1
1
2
/
1
0
2
/
1
6
/
1
3
/
1
2
/
1
3
/
1
3
/
1
0
1
A
2
1/2
0
1/2
-
1
0
0
9
1/2
1
3/2
0
3
0
4
1/2
0
1/2
1
1
0
Krok 3:
2
1/2
0
1/2
-
1
0
0
3
1/6
1/3
1/2
0
1
0
1
1/3
1/3
-
0
0
0
1
Ponieważ macierz A jest
nieosobliwa
, układ wektorów P
1
, P
2
i P
3
jest
linowo niezależny
i wobec tego tworzy
bazę
w przestrzeni E
3
0
6
2
1
)
1
(
2
1
1
1
1
(-2)
-
1
1
1
-
(-1)
1
1
-
1
(-2)
(-1)
1
1
1
1
1
1
1
1
1
1
1
2
1
1
1
A
Policzmy wyznacznik macierzy A
0
6
A
0
P
P
P
n
n
2
2
1
1
...
0
n
...
2
1
Dowód nie wprost
Dla dowodu, że wektory P
1
, P
2
... P
n
macierzy nieosobliwej A tworzą układ liniowo
niezależny załóżmy najpierw, że układ ten jest liniowo zależny, wówczas dla pewnej
j
musi być spełniona równość
Przy czym przynajmniej jedno
j
musi być różne od zera.
0
P
P
P
n
n
2
2
1
1
...

. Przeczy to założeniu, że macierz A jest macierzą
nieosobliwą. W ten sposób założenie liniowej zależności prowadzi do
sprzeczności, więc wektory P
1
, P
2
i P
3
są
linowo niezależne
.
Podstawmy wartości wektora P
1
do macierzy A
3
3
2
2
1
P
P
P
1
1
1
1
1
1
-
3
2
3
2
3
2
3
2
3
2
3
2
3
2
3
3
2
2
1
-
1
1
1
-
1
1
1
P
P
P
Możemy wówczas jeden z wektorów przedstawić jako kombinację liniową pozostałych.
W rozważanym przykładzie mamy
Dodając do pierwszej kolumny
3
3
2
2
P
P
1
1
-
1
1
-
1
1
-
-
3
2
3
2
3
2
3
2
3
2
3
2
otrzymujemy
1
1
0
1
1
0
1
1
0
A
0
A
n
n
2
1
1
n
n
1
2
2
1
...
...
P
P
P
P
P
P
2

Kombinacja liniowa (**) wektorów P
1
, P
2
i P
3
równa P
0
przyjmuje postać
0
3
2
1
P
P
P
P
2
3
1
Ponieważ wektory P
1
, P
2
i P
3
tworzą bazę każdy inny wektor może być
wyznaczony jako kombinacja liniowa tych wektorów
Dla
otrzymujemy
Zatem P
4
został wyrażony jako kombinacja liniowa P
1
, P
2
i P
3
.
Wektor P
4
jest wektorem
osobliwym
gdyż jest wyznaczony przez mniej
niż n wektorów bazy
4
3
3
2
2
1
y
y
y
P
P
P
P
1
0
2
2
4
2
-
4
2
/
1
0
2
/
1
6
/
1
3
/
1
2
/
1
3
/
1
3
/
1
0
4
1
4
Y
P
A
Y
P
AY
T
4
2
4
4
P
4
3
2
1
0
2
2
P
P
P
P
4
2
1
2
2
P
P
P

Postać standardowa Zadania Programowania liniowego
Alternatywne zapisy
Znajdź wektor (x
1
,...,x
n
) który minimalizuje kombinację liniową
(funkcję celu)
(1.1)
Przy ograniczeniach
n
n
2
2
1
1
x
...
x
x
c
c
c
z
n
m
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
m
n
mn
2
m2
1
m1
2
n
2n
2
22
1
21
1
n
1n
2
12
1
11
n
j
,...,
2
,
1
,
0
x
j
n
j
c
z
1
j
j
x
n
j
i
j
ij
m
i
b
x
a
1
,...,
2
,
1
,
n
j
,...,
2
,
1
,
0
x
j
przy
ograniczeniach
Zminimalizować
funkcję
(1.2)
(1.3)

cX
z
b
AX
0
X
przy
ograniczeniach
Zminimalizować
funkcję
cX
z
0
X
przy
ograniczeniach
Zminimalizować
funkcję
0
n
n
2
2
1
1
x
...
x
x
P
P
P
P
gdzie P
j
dla j=1,...,n jest j-tą kolumną macierzy A, P
0
=b

Sprowadzenie ogólnych zadań programowania liniowego
do postaci standardowej
1. Pełne ograniczenie nierównościowe typu
ograniczenie sprowadzamy do postaci równościowej przez dodanie zmiennej
dopełniającej s>0
2. Pełne ograniczenie nierównościowe typu
ograniczenie sprowadzamy do postaci równościowej przez odjęcie zmiennej
dopełniającej s>0
Każde zadanie minimalizacji funkcji celu
można zapisać w równoważnej formie
b
AX
0
s
,
2
b
s
AX
b
AX
0
s
,
2
b
s
AX
)
(
min x
x
z
)
(
max
)
(
min
x
x
x
x
z
z
1
1
0
0
2
1
2
1
2
1
x
x
x
x
x
x
a)
b)
c)
d)
(0,1)
(1,0)
(2,1)
b)
a)
c)
d)
C
Obszar dopuszczalnych
rozwiązań
Podstawowe definicje
Def.1.
Rozwiązaniem dopuszczalnym zagadnienia PL jest wektor X=
(x
1
,...,x
n
) spełniający warunki (1.2) i (1.3).
Def.2a.
Macierzą bazową B układu równań AX=b , rz(A)=m, n>m, nazywamy
nieosobliwą macierz kwadratową o wymiarach mxm utworzoną z liniowo niezależnych
kolumn a
j
macierzy A.

Def.2a.
Rozwiązaniem bazowym układu równań AX=b , rz(A)=m,
n>m, nazywamy
wektor X
B
=B
-1
b utworzony ze zmiennych odpowiadających
kolumnom a
j
macierzy
bazowej B. Składowe wektora X
B
noszą nazwę zmiennych bazowych.
Uwaga!
Maksymalna ilość rozwiązań bazowych wynosi
)!
(
!
!
m
n
m
n
Def.2b.
Rozwiązaniem bazowym dopuszczalnym nazywamy
rozwiązanie bazowe, które spełnia warunek (1.2), czyli wszystkie
zmienne bazowe są nieujemne.
Def.3.
Niezdegenerowanym rozwiązaniem bazowym dopuszczalnym
nazywamy bazowe rozwiązanie dopuszczalne, w którym wszystkie
zmienne bazowe są dodatnie.
Def.4.
Minimalnym rozwiązaniem dopuszczalnym nazywamy
rozwiązanie dopuszczalne, które minimalizuje funkcję (1.1)
0
X
B
0
X
B

b
P
P
P
3
3
2
2
1
1
x
x
x
Przykład.
Znaleźć rozwiązanie bazowe układu równań
5
4
;
5
1
2
1
2
1
;
5
1
;
1
2
2
;
2
1
3
1
b
A
P
P
P
Maksymalna liczba rozwiązań bazowych
3
2
3
2
3
)!
(
!
!
Rząd macierzy A jest równy 2, zatem macierze B
i
, i=1,2,3,
odpowiadające kolejnym rozwiązaniom złożone będą z dwóch
kolumn macierzy A . Jeśli
to
i
B
X
1
2
2
1
,
2
1
1
P
P
B
1
2
5
4
1
2
2
1
1
2
1
1
3
1
1
1
b
B
X
B
B
B
x
x
stąd
0
3
1
x
x
x
x
x
B
B
,
,
2
1
2
1
1
Jeśl
i
to
5
2
1
1
,
3
1
2
P
P
B
1
-
5
5
4
1
2
1
5
3
1
1
2
2
2
1
2
b
B
X
B
B
B
x
x
stąd
0
,
,
2
3
2
2
1
2
1
x
x
x
x
x
B
B
Jeśl
i
to
5
1
1
2
,
3
2
3
P
P
B
2/3
5/3
5
4
2
1
1
5
9
1
1
3
2
3
1
3
b
B
X
B
B
B
x
x
stąd
0
,
,
1
3
3
2
2
3
1
x
x
x
x
x
B
B
Przykład
0
0
6
16
2
10
8
2
2
1
1
2
1
2
1
2
1
x
x
x
x
x
x
x
x
x
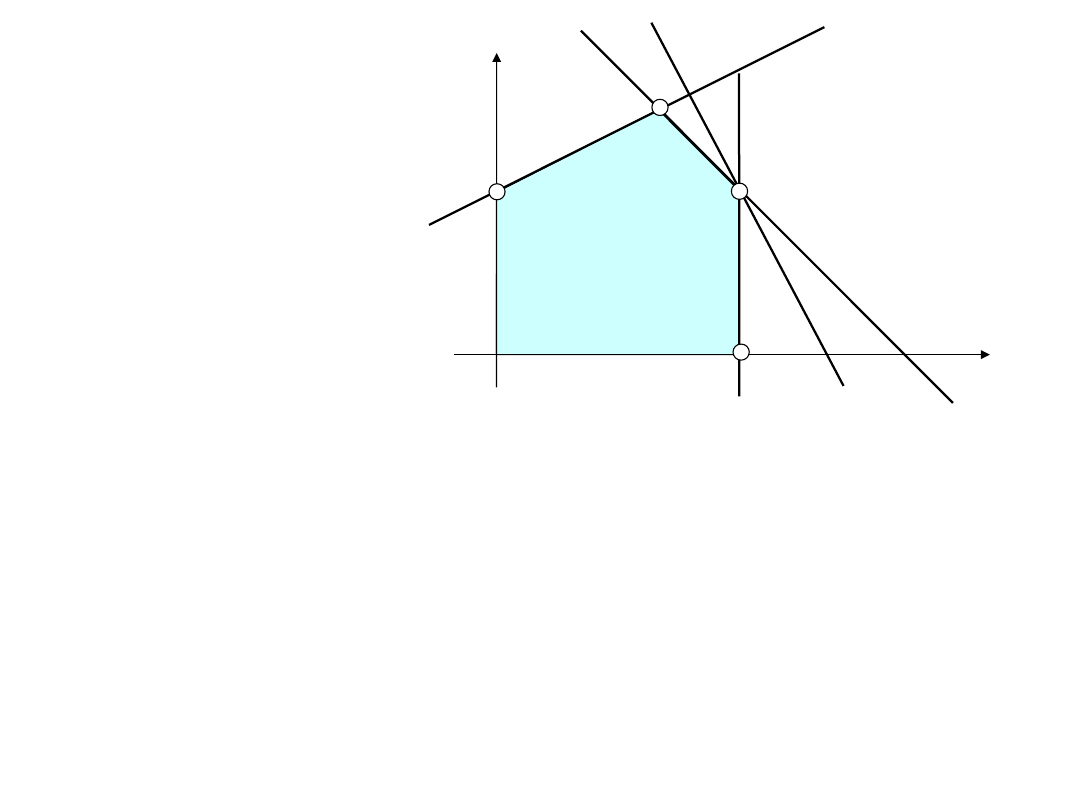
Wykażemy, że rozwiązania bazowe odpowiadają wierzchołkom wielościanu.
Sprowadzamy układ nierówności do postaci kanonicznej dodając zmienne dopełniające.
x
1
(0,6)
(0,4)
(6,0)
x
2
x
1
+x
2
=10
-
x
1
+2x
2
=8
2x
1
+x
2
=1
6
A
B
C
D
Zbiór rozwiązań
dopuszczalnych
1,..,6
j
0,
6
16
2
10
8
2
j
6
1
5
2
1
4
2
1
3
2
1
x
x
x
x
x
x
x
x
x
x
x
x
0
X
b
AX
1
0
0
0
0
1
0
1
0
0
1
2
0
0
1
0
1
1
0
0
0
1
2
1
A
6
16
10
8
b

Rząd macierzy A jest równy 4, zatem macierze bazowe B
i
utworzone będą z 4 kolumn
macierzy A, a każde niezdegenerowane dopuszczalne rozwiązanie bazowe
powinno zawierać 4 zmienne bazowe niezerowe.
1) Rozwiązanie bazowe związane z przecięciem się ograniczeń
Punkt wierzchołkowy B wynosi
2) Rozwiązanie bazowe związane z przecięciem się ograniczeń
Punkt wierzchołkowy D wynosi
0
X
B
1
0
0
1
0
1
1
2
0
0
1
1
0
0
2
1
,
,
,
6
5
2
1
B
P
P
P
P
B
2
2
6
4
1
B
6
B
5
B
2
B
1
1
b
B
X
B
B
B
B
B
x
x
x
x
lub
10
8,
2
2
1
2
1
x
x
x
x
2
2
6
4
6
5
2
1
B
x
x
x
x
B
X
2
2
0
0
6
4
6
5
4
3
2
1
x
x
x
x
x
x
X
0
6,
2
1
x
x
0
0
0
1
1
0
0
2
0
1
0
1
0
0
1
1
,
,
,
5
4
3
1
D
P
P
P
P
B
4
4
14
6
1
D
5
D
4
B
3
D
1
D
b
B
X
B
B
B
B
B
x
x
x
x
4
4
14
6
5
4
3
1
D
x
x
x
x
B
X
0
4
4
14
0
6
6
5
4
3
2
1
x
x
x
x
x
x
X

3) Rozwiązanie bazowe związane z przecięciem się ograniczeń
Punkt wierzchołkowy C wynosi
16
0,
6,
2
1
2
1
1
x
x
x
x
x
2
1
0
0
0
1
0
0
1
2
1
0
1
1
0
1
2
1
,
,
,
4
3
2
1
C
P
P
P
P
B
0
6
4
6
1
C
4
C
3
C
2
C
1
C
b
B
X
B
B
B
B
B
x
x
x
x
4
4
14
6
4
3
2
1
c
x
x
x
x
B
X
0
0
0
6
4
6
6
5
4
3
2
1
x
x
x
x
x
x
X
Rozwiązanie i ma cztery zmienne niezerowe jest więc rozwiązaniem
niezdegenerowanym. Rozwiązanie ma tylko trzy zmienne dodatnie jest więc
rozwiązaniem zdegenerowanym.
C
B
X
B
B
X
D
B
X

Właściwości rozwiązań zadania PL
Twierdzenie.1.
Zbiór wszystkich rozwiązań dopuszczalnych
zagadnienia PL jest zbiorem wypukłym.
Dowód. Należy wykazać, że każda wypukła kombinacja dwóch
rozwiązań dopuszczalnych jest również rozwiązaniem
dopuszczalnym. Załóżmy, że istnieją dwa rozwiązania X
1
i X
2
. Mamy
zatem A X
1
=b dla
i A X
2
=b dla
Dla
niech
będzie wypukłą kombinacja
liniową wektorów X
1
i X
2
. Zauważmy, że wszystkie elementy wektora
X są nieujemne, tj. . Zatem X jest rozwiązaniem dopuszczalnym
ponieważ
0
X
1
0
X
2
b
b
b
b
AX
AX
X
X
A
AX
2
1
2
1
)
(
)
)
(
(
1
1
1
0
)
)
1
(
(
2
1
X
X
X
0
X
C
X
1
X
2
Jeśli zbiór jest wypukły to prosta łącząca dwa dowolne punkty zbioru należy także
do zbioru.
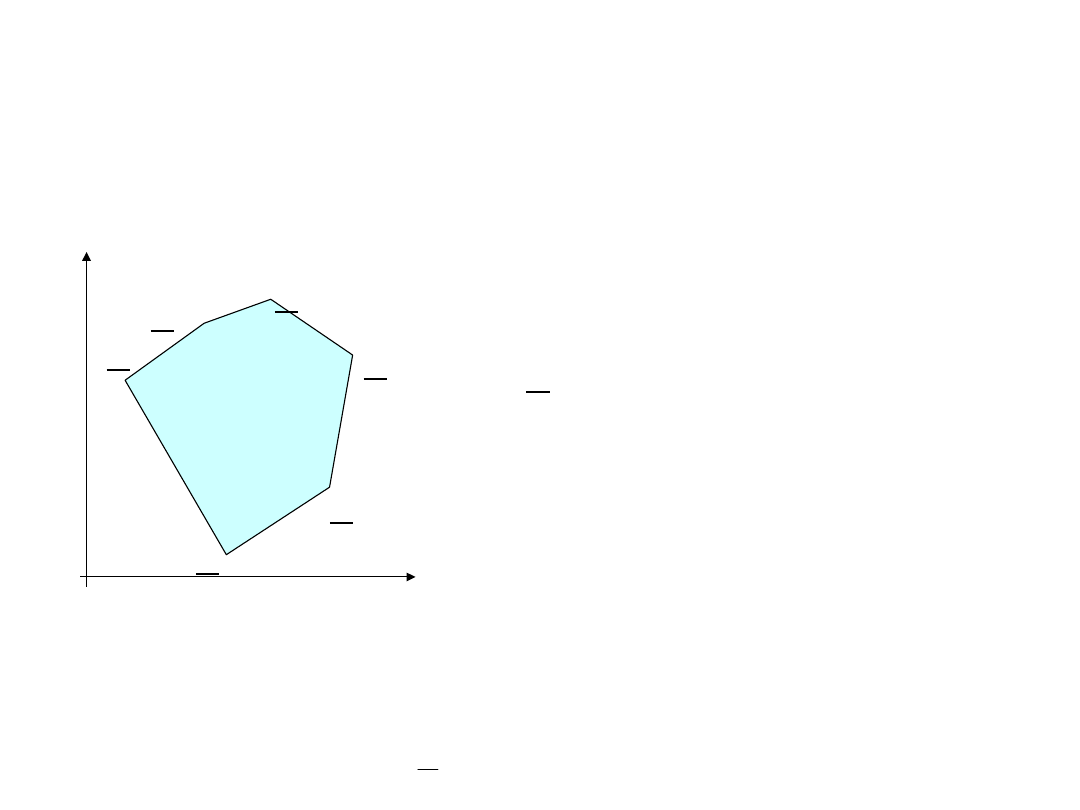
Twierdzenie.2.
Funkcja celu przyjmuje wartość minimalną w punkcie wierzchołkowym
zbioru wypukłego K, utworzonego na zbiorze rozwiązań dopuszczalnych zagadnienia
PL. Jeśli przyjmuje wartość minimalną w więcej niż jednym punkcie wierzchołkowym to
tę samą wartość przyjmuje dla każdej kombinacji liniowej tych punktów.
Dowód. Ponieważ K, jest zbiorem wypukłym ma skończoną ilość punktów
wierzchołkowych np.
x
1
x
2
X
1
X
2
X
3
X
4
X
5
X
6
X
o
K
X
o
minimalne rozwiązanie dopuszczalne
X
p
punkty wierzchołkowe, p=1,..,6
f(X)
funkcja celu
warunek minimalizacji
dla każdego K
Załóżmy, że X
o
nie jest punktem wierzchołkowym (patrz rys.) wtedy X
o
możemy
zapisać jako kombinację wypukłą wierzchołków zbioru K
1
0
,
1
1
p
i
i
i
p
i
i
i
o
i
dla
X
X
)
(
)
(
X
X
f
f
o
X

Ponieważ funkcja celu f(X) jest funkcjonałem liniowym, mamy
Zauważmy, że nie zwiększamy minimum jeśli za każde podstawimy najmniejszą
spośród wszystkich wartości . W związku z tym niech
Podstawiając do powyższej równości otrzymujemy
Z założenia mamy
dla wszystkich X należących do K, zatem musi być
spełniona równość
Istnieje zatem punkt wierzchołkowy w którym funkcja celu przyjmuje wartość
Minimalną.
min
)
(
...
)
(
)
(
)
...
,
(
)
(
p
p
2
2
1
1
2
2
1
1
1
X
X
X
X
X
X
X
X
f
f
f
f
f
f
p
p
p
i
i
i
o
i
i
m
f
f
X
X
min
)
(
i
f X
i
f X
1
i
i
o
f
f
f
f
f
),
(
)
(
...
)
(
)
(
)
(
m
m
p
m
2
m
1
X
X
X
X
X
)
(
)
(
X
X
f
f
o
min
)
(
)
(
m
X
X
f
f
o
m
f X

Twierdzenie.3.
Jeśli można znaleźć
wektorów P
1
, P
2
,..., P
k
liniowo niezależnych takich, że
oraz wszystkie
, to punkt
jest
punktem wierzchołkowym zbioru wypukłego rozwiązań
dopuszczalnych. X jest wektorem n-wymiarowym, którego n-k
ostatnich elementów jest równych zeru.
Dowód Załóżmy, że X nie jest punktem wierzchołkowym. Ponieważ
jest rozwiązaniem dopuszczalnym może być wyrażony jako
kombinacja wypukła dwóch dowolnych punktów X
1
i X
2
ze zbioru
K co zapisujemy
Ponieważ wszystkie elementy wektora X są nieujemne i
wektory X
1
i X
2
przyjmują postać
Ponieważ X
1
i X
2
są rozwiązaniami dopuszczalnymi zatem A X
1
=b i
A X
2
=b. W postaci wektorowej równania te przyjmują postać
Aby oba równania były zgodne musi być spełniony warunek
Wobec tego punkt X nie może być wyrażony jako kombinacja
wypukła X
1
i X
2
i musi być punktem wierzchołkowym
m
k
o
k
k
2
2
1
1
...
P
P
P
P
x
x
x
0
i
x
)
0
,...,
0
,
,...,
,
(
k
2
1
x
x
x
X
)
)
1
(
(
2
1
X
X
X
1
0
0
i
x
1
0
)
0
,...,
0
,
,...,
,
(
),
0
,...,
0
,
,...,
,
(
)
2
(
k
)
2
(
2
)
2
(
1
2
)
1
(
k
)
1
(
2
)
1
(
1
1
x
x
x
x
x
x
X
X
0
k
)
2
(
k
2
)
2
(
2
1
)
2
(
1
0
k
)
1
(
k
2
)
1
(
2
1
)
1
(
1
...
...
P
P
P
P
P
P
P
P
x
x
x
i
x
x
x
)
2
(
i
)
1
(
i
x
x
x
i

Twierdzenie.4.
Jeśli
jest punktem wierzchołkowym
zbioru K, to wektory odpowiadające dodatnim x
i
tworzą zbiór
liniowo niezależny. Dodatnich x
i
jest co najwyżej m.
Wniosek 1.
Każdemu punktowi wierzchołkowemu zbioru K
odpowiada zbiór m wektorów liniowo niezależnych z danego
zbioru P
1
, P
2
,..., P
n
.
Twierdzenie.5.
Punkt
jest punktem
wierzchołkowym zbioru K, wtedy i tylko wtedy, gdy w kombinacji
linowej wektorów niezależnych P
j
Współczynniki x
j
są dodatnie
Wnioski
1. Istnieje punkt wierzchołkowy zbioru K, w którym funkcja celu
przyjmuje minimum
2. Każde bazowe rozwiązanie dopuszczalne jest punktem
wierzchołkowym zbioru K
3. Każdemu punktowi wierzchołkowemu zbioru K odpowiada m
wektorów liniowo niezależnych z danego zbioru n wektorów
związanych z tym punktem.
)
,...,
,
(
n
2
1
x
x
x
X
)
,...,
,
(
n
2
1
x
x
x
X
n
j
o
j
j
x
1
P
P

Interpretacja geometryczna zadania PL
Zagadnienie PL można przedstawić w postaci kanonicznej gdzie
przestrzeń rozwiązań
jest przestrzenia działania
Znaleźć
takie, że
gdzie
lub w przestrzeni wektorów
, zwanej przestrzenią wymagań
(ograniczeń) w
postaci
Znaleźć
takie, że
gdzie
Hiperpłaszczyzną nazywamy obiekt określony jednym warunkiem
liniowym w E
n
cX
X
c
X
X
0
min
ˆ
n
m
n
R
R
czym
przy
R
c
b
0
b
AX
X
X
X
,
,
,
:
0
n
R
X
m
R
b
X
ˆ
X
ˆ
cX
X
c
X
X
0L
min
ˆ
ˆ
z
n
m
n
R
R
czym
przy
R
c
b
X
0
X
b
AX
X
X
,
,
,
,
,
:
0L
Interpretacja geometryczna zadania PL
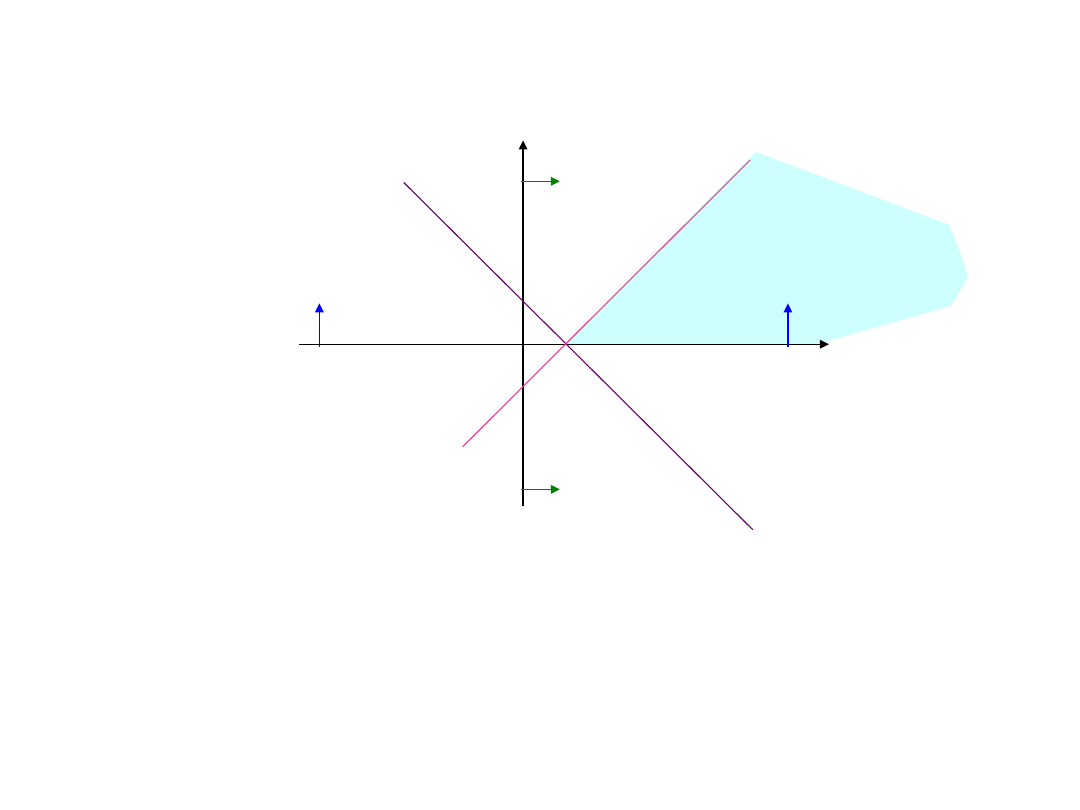
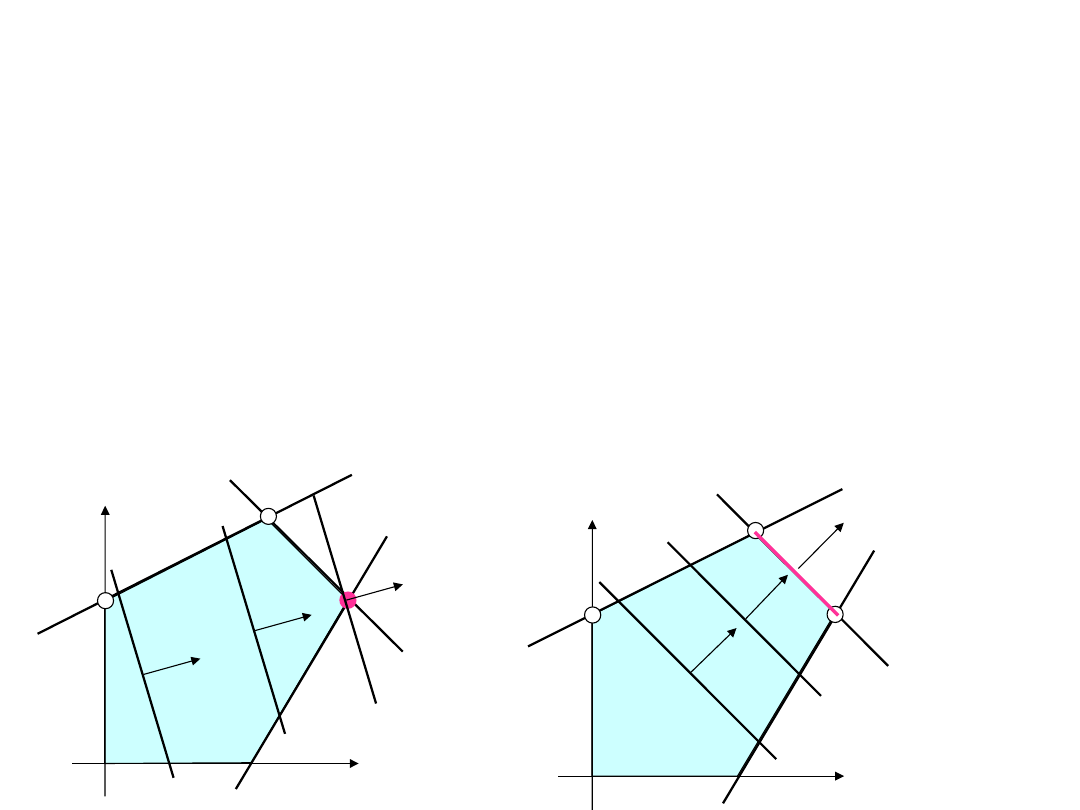
W przestrzeni działań jeśli zbiór rozwiązań dopuszczalnych
jest
ograniczony,
to tworzy on wielościan wypukły S. Wyrażenie z=cX określa w
przestrzeni R
n
rodzinę równoległych hiperpłaszczyzn, prz czym
wektor –c prostopadły do tych hiperpłaszczyzn wskazuje kierunek
malenia funkcji z. Wychodząc z pewnej hiperpłaszczyzny należącej
do tej rodziny i mającej wspólne punkty z wieloscianem S, przy
przesuwaniu jej rónolegle w kierunku malenia z, można dojść do
takiego jej położenia, że staje się ona hiperpłaszczyzną podpierającą.
Jeśli ta hiperpłaszczyzna ma tylko jeden punkt wspólny ze zbiorem
X
0
to punkt ten będzie punktem wierzchołkowym i zadanie PL ma
jedyne rozwiązanie optymalne.
n
m
n
R
R
czym
przy
R
c
b
0
b
AX
X
X
X
,
,
,
:
0
x
2
minimum
Zbiór
rozwiązań
dopuszczalnyc
h
x
1
-c
-c
-c
x
2
minimum
Zbiór
rozwiązań
dopuszczalnyc
h
x
1
-c
-c
-c
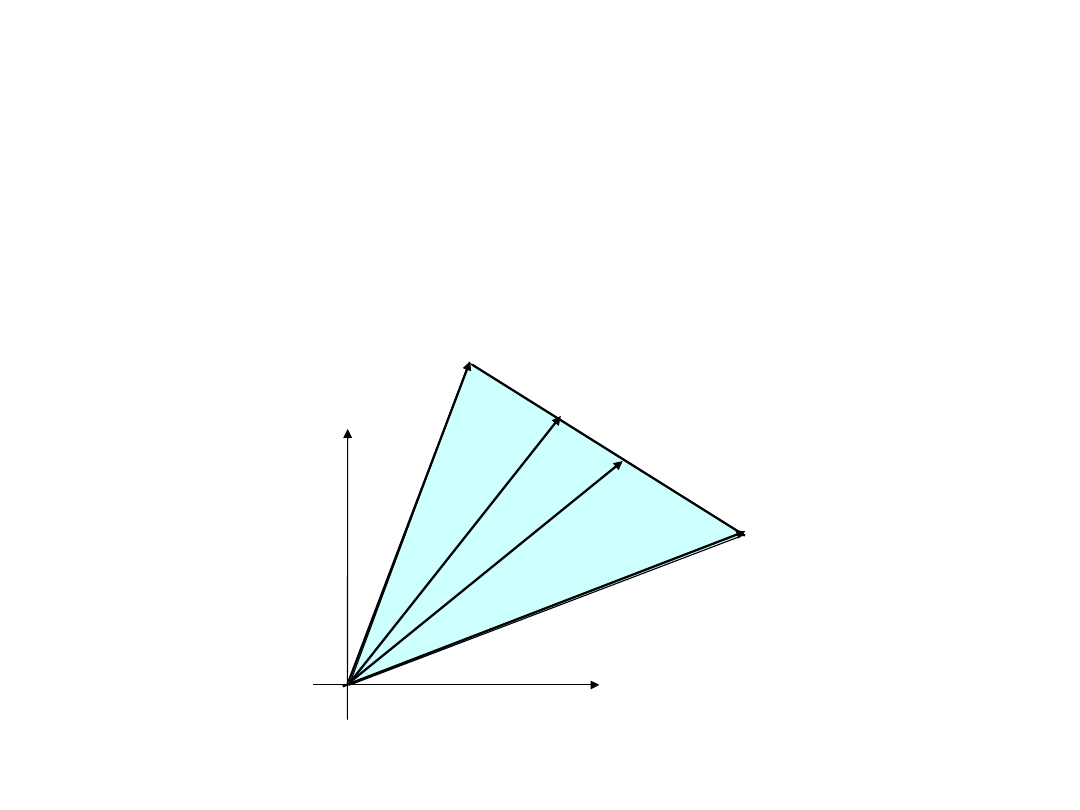
Interpretacja geometryczna zadania PL
W przestrzeni wymagań R
m
zbiór wektorach P
i
, i=1,...,n generuje
wypukły stożek wielościenny C. Jeśli wektor b (P
0
) zawarty jest w
tym stożku, to istnieje rozwiązanie dopuszczalne zadania PL. Przy
założeniu, że rząd macierzy A jest równy m więc liniowo
niezależnych wektorów P
i
jest tylko m, przy czym wektory te tworzą
bazę w R
m
. Jeśli wektor b (P
0
) należy do stożka rozpiętego na
wektorach P
i
, i=1,...,m to rozwiązanie dopuszczalne jest
rozwiązaniem bazowym jest ograniczony,
b
2
b
1
P
3
P
2
P
1
P
0

Metoda sympleksów
Rozwiązanie zadania PL metodą sympleksów polega na tym, że
poczynając od określonego wierzchołka wielościanu wypukłego,
będącego zbiorem rozwiązań dopuszczalnych, w kolejnych
krokach wybieramy wierzchołki położone coraz bliżej
wierzchołka optymalnego, tzn. odpowiadającemu optymalnemu
bazowemu rozwiązaniu dopuszczalnemu.
W metodzie sympleksów należy określić
1. Sposób przechodzenia z bazy do bazy
2. Kryterium zbieżności, kryterium zatrzymania procedury
3. Metodę wyznaczania początkowego bazowego rozwiązania
dopuszczalnego
4. Sposób postępowania przy pojawieniu się zdegenerowanych
rozwiązań bazowych

Metoda sympleks do rozwiązywania zadania PL
W programowaniu liniowym szukamy optimum poruszając się po punktach
ekstremalnych zbioru punktów dopuszczalnych Xo. W każdym punkcie ekstremalnym
przynajmniej n-m zmiennych przyjmuje wartość zero. Reszta jest określona równaniem
AX=b. Za pomocą metody sympleks przeszukujemy wierzchołki zbioru punktów
dopuszczalnych w uporządkowany sposób, generując kolejne punkty x
1
, x
2
, ... ,x
k
.
W każdym punkcie x
k
n-m zmiennych, które w punkcie x
k
mają wartości zerowe nazy-
wamy zmiennymi niebazowymi (zbiór indeksów tych zmiennych oznaczymy N
k
). Na-
tomiast pozostałe m zmiennych nazywamy zmiennymi bazowym (zbór indeksów B
k
).
Wektor zmiennych oznaczamy
X=[X
B
X
N
]
Odpowiednio macierz ograniczeń przyjmuje postać
A=[A
B
A
N
]

Macierz A
B
o wymiarze mxm nazywamy macierzą bazową, A
N
o wymiarze mx(n-m)
macierzą niebazową. Macierz A
B
nie może być osobliwa. Dla zmiennych niebazowych
Przyjmujemy wartość zero, a wartości zmiennych bazowych wybieramy tak, aby był
spełniony układ pełnych ograniczeń liniowych. Wówczas równanie AX=b można
zapisać
Jeśli zmienne bazowe także przyjmują wartość zero wówczas mówimy o rozwiązaniu
Zdegenerowanym. Punkt wierzchołkowy odpowiadający wybranej bazie ma następują-
ce wartości współczynników
0
,
k
N
N
N
B
B
N
B
N
B
X
b
X
A
X
A
X
X
A
A
b
A
b
0
b
X
X
X
1
B
k
k
N
B
k
gdzie ˆ
,
ˆ

Kryterium optymalności bazowego rozwiązania dopuszczalnego
Wartość funkcji celu w bazowym rozwiązaniu dopuszczalnym wyraża się wzorem
Funkcję bazową wyrażoną za pomocą zmiennych niebazowych f(X
N
) nazywamy
funkcją zredukowaną. Jeśli wszystkie współczynniki w zredukowanej funkcji celu są
większe lub równe zeru to rozwiązanie jest rozwiązaniem X
k
optymalnym.
jest oznacza ceny zredukowane w bazowym rozwiązaniu dopuszczalny. Kryterium
optymalności brzmi
punkt X
k
jest optymalny, jeśli
N
N
B
N
N
B
B
X
A
A
b
X
A
b
A
X
1
ˆ
1
b
c
x
c
ˆ
ˆ
T
B
k
T
f
N
N
N
N
B
T
B
T
N
N
N
B
T
B
N
T
N
N
T
N
N
N
B
T
B
N
T
N
B
T
B
B
f
f
f
f
X
c
X
A
A
c
c
X
A
A
c
X
c
X
c
X
A
A
b
c
X
c
X
c
X
ˆ
ˆ
ˆ
ˆ
ˆ
)
(
1
1
1
N
cˆ
0
c
N
ˆ

Wektor zmiennych bazowych dla nowej zmiennej x
q
jest wyrażony wzorem
Wektor a
q
oznacza kolumnę macierzy pełnych ograniczeń równościowych,
odpowiadającą zmiennej x
q
, którą wprowadzamy do bazy. Jeśli d
i
<0 to zwiększenie x
q
zmniejsza wartość zmiennej bazowej x
i
Zmienna x
i
osiąga wartość 0 gdy
Zatem indeks p zmiennej wyprowadzanej z bazy określa się jako
Wybór zmiennej wprowadzanej do bazy
i
N
i
q
c
c
ˆ
min
ˆ
Jeśli warunek
nie jest spełniony to wybieramy nową zmienną x
q
, która
wchodzi do bazy, przy czym ta zmienna jest wybierana na podstawie kryterium
0
c
N
ˆ
Wybór zmiennej wyprowadzanej z bazy
q
B
q
B
B
gdzie
a
A
d
d
b
a
A
b
X
1
1
,
ˆ
ˆ
q
q
x
x
i
i
q
d
b
x
ˆ
j
j
d
B
j
p
p
d
b
d
b
j
ˆ
min
ˆ
0
Tablicowa postać metody sympleks
Wykorzystywane równania
Organizacja danych
b
X
A
X
A
N
N
B
B
b
A
X
A
A
IX
1
B
N
N
B
B
1
b
A
0
c
B
T
f )
(
b
A
I
c
0
B
ˆ
ˆ
ˆ
ˆ
)
(
N
T
N
T
f
f
0
X
X
5
.
0
3
1
4
3
2
min
4
3
1
4
3
2
1
4
3
2
1
x
x
x
x
x
x
x
x
x
x
x
5
.
0
3
1
0
1
1
1
1
1
1
0
4
3
2
1
2
1
x
x
5
.
0
4
0
1
0
0.5
3
-
1
0
1
1.5
-
1
-
2
0
0
5
.
0
3
1
0
1
1
1
1
1
1
0
4
3
2
1
2
1
x
x
5
.
0
5
.
0
,
,
,
4
3
2
1
b
c
c
X
X
4
3
2
1
N
B
N
B
x
x
x
x
3
-
1
1
1
,
1
-
1
1
0
,
0
1
1
1
N
B
B
A
A
A
1
Dane:
k=1
b
A
I
c
0
B
ˆ
ˆ
ˆ
ˆ
)
(
N
T
N
T
f
f
N
B
T
B
T
N
N
A
A
c
c
c
1
ˆ
N
B
N
A
A
A
1
ˆ
b
A
b
1
ˆ
B
b
c ˆ
ˆ
T
B
f
gdzie
Wektor cen
zredukowanych
Sprawdzamy kryterium optymalności. Ponieważ jedna z cen nie jest dodatnia
wyznaczony punkt nie jest optymalnym. Zmienna dla której wchodzi do
nowej bazy. Jest to zmienna x
4
.
i
N
i
q
c
c
ˆ
min
ˆ

j
j
d
B
j
j
j
d
B
j
d
b
d
b
j
j
ˆ
max
lub
,
ˆ
min
0
0
W celu określenia zmiennej opuszczającej bazę sprawdzamy kryterium
W naszym przypadku otrzymujemy min(0.5/3; -0.5/4) jest (-0.5/4) stąd zmienna x
2
opuszcza bazę
k=2
5
.
0
4
0
1
0
0.5
3
-
1
0
1
1.5
-
1
-
2
0
0
8
/
1
1
0
1/4
0
7/8
0
1
3/4
1
3/8
-
0
2
1/4
0
4
1
x
x
Ponieważ wszystkie ceny zredukowane są dodatnie więc
wyznaczony punkt jest punktem optymalnym.

podsumowanie
c
i
- z
i
- wskaźniki optymalności. Dla zmiennych bazowych wskaźniki
optymalności są zawsze równe zero
Kryterium optymalności
Rozwiązanie jest optymalne, jeżeli wartości wszystkich wskaźników
optymalności są niedodatnie
Kryterium wejścia do bazy
Do bazy wchodzi zmienna, która ma największą wartość wskaźnika
optymalności. Jeżeli największa wartość wskaźnika optymalności
odpowiada więcej niż jednej zmiennej, wybieramy zmienną o
najniższym indeksie.
Kryterium wyjścia z bazy
Obliczamy ilorazy wyrazów wolnych (kolumna b
i
) przez elementy
(tylko dodatnie) kolumny zmiennej wchodzącej do bazy. Bazę
opuszcza ta zmienna, dla której obliczony iloraz jest najmniejszy.
Jeżeli najmniejsza wartość ilorazu występuje dla więcej niż jednej
zmiennej, to jako zmienną opuszczającą bazę można wybrać
dowolną zmienną.

Metoda sympleksów - Przykład
Standardowa postać zadania
Znajdź wektor (x
1
,...,x
n
) który maksymalizuje kombinację liniową
(funkcję celu)
Przy ograniczeniach
2
1
3x
2x
z
16
4
8
2
14
2
2
2
1
1
2
1
x
x
x
x
x
2
,
1
,
0
x
j
j
5
4
3
2
1
x
0
x
0
x
0
3x
2x
z
2,...,5
,
1
,
0
x
j
j
przy
ograniczeniach
n=5, m=3
Zminimalizować
funkcję
16
4
8
2
14
2
2
5
4
2
3
x
x
x
x
x
x
x
x
1
1
2
1
c
T
x
3
0
0
0
x
b
c
b
x
1
x
2
x
3
x
4
x
5
b
i
x
3
0
x
4
0
x
5
0
Zj
Cj-
zj
5
4
3
2
1
x
0
x
0
x
0
3x
2x
z

c
T
x
3
0
0
0
x
b
c
b
x
1
x
2
x
3
x
4
x
5
b
i
x
3
0
1
0
0
14
x
4
0
x
5
0
Zj
Cj-
zj
16
0
0
4
8
0
0
2
14
2
2
5
4
3
5
4
3
2
5
4
3
x
x
x
x
x
x
x
x
x
x
x
x
x
x
1
1
2
1
0
0
c
T
x
3
0
0
0
x
b
c
b
x
1
x
2
x
3
x
4
x
5
b
i
x
3
0
1
0
0
14
x
4
0
1
0
1
0
8
x
5
0
Zj
Cj-
zj
16
0
0
4
8
0
0
2
14
2
2
5
4
3
5
4
3
2
5
4
3
x
x
x
x
x
x
x
x
x
x
x
x
x
x
1
1
2
1
0
0
c
T
x
3
0
0
0
x
b
c
b
x
1
x
2
x
3
x
4
x
5
b
i
x
3
0
1
0
0
14
x
4
0
1
0
1
0
8
x
5
0
4
0
0
0
1
16
z
j
=
c
b
T
x
b
0*+0
*1+0*
4=0
0
0
0
0
cj-zj
-0=
3-
0=3
0
0
0
16
0
0
4
8
0
0
2
14
2
2
5
4
3
5
4
3
2
5
4
3
x
x
x
x
x
x
x
x
x
x
x
x
x
x
1
1
2
1
0
0
5
4
3
2
1
x
0
x
0
x
0
3x
2x
z
Kryterium wejścia do bazy: max (c
j
-
z
j
); max(2,3,0,0,0)=3
zatem zmienna x
2
wchodzi do bazy
wskaźnik
optymalności
16
0
0
4
8
0
0
2
14
2
2
5
4
3
5
4
3
2
5
4
3
x
x
x
x
x
x
x
x
x
x
x
x
x
x
1
1
2
1
0
0
5
4
3
2
1
x
0
x
0
x
0
3x
2x
z
Kryterium wyjścia z bazy: min (b
i
/x2); min(7,4,-,)=4
zatem zmienna x
4
opuszcza bazę
wskaźnik
optymalności
c
T
x
3
0
0
0
x
b
c
b
x
1
x
2
x
3
x
4
x
5
b
i
bi/x
x
3
0
1
0
0
14
14/
=7
x
4
0
1
0
1
0
8
8/
=4
x
5
0
4
0
0
0
1
16
-
z
j
=
c
b
T
x
b
0*+0
*1+0*
4=0
0
0
0
0
Cj-
zj
-0=
3-
0=3
0
0
0

Zatem zmienna
x
2
wchodzi do bazy na miejsce zmiennej
x
4
. Teraz
wektorami bazy są x
3
, x
2
, x
5
. Dla nowych wektorów bazowych należy
utworzyć macierz bazową
Def.2a.
Macierzą bazową B układu równań AX=b , rz(A)=m, n>m,
nazywamy
nieosobliwą macierz kwadratową o wymiarach mxm utworzoną z
liniowo niezależnych
kolumn a
j
macierzy A.
W tym celu odejmujemy od pierwszego wiersza drugi i dzieląc drugi
przez dwa otrzymujemy
Kryterium wejścia do bazy: max (c
j
-
z
j
); max(0.5,0,0,-1.5,0)=0.5
zatem zmienna x
1
wchodzi do bazy
c
T
x
3
0
0
0
x
b
c
b
x
1
x
2
x
3
x
4
x
5
b
i
bi/x
x
3
0
1
0
1
-1
0
6
x
2
3
1/2
1
0
1/2
0
4
x
5
0
4
0
0
0
1
16
z
j
=
c
b
T
x
b
Cj-
zj
1.5
3
0
1.5
0
0.5
0
0
-1.5
0
c
T
x
3
0
0
0
x
b
c
b
x
1
x
2
x
3
x
4
x
5
b
i
bi/x
x
3
0
1
0
1
-1
0
6
x
2
3
1/2
1
0
1/2
0
4
x
5
0
4
0
0
0
1
16
4
z
j
=
c
b
T
x
b
Cj-
zj
1.5
3
0
1.5
0
0.5
0
0
-1.5
0
6/1=6
8
Kryterium wyjścia z bazy: min (b
i
/x2); min(6,8,4,)=4
zatem zmienna x
5
opuszcza bazę
c
T
x
3
0
0
0
x
b
c
b
x
1
x
2
x
3
x
4
x
5
b
i
bi/x
x
3
0
0
0
1
-1
-
1/4
2
x
2
3
0
1
0
1/2
-
1/8
2
x
1
2
1
0
0
0
1/4
4
z
j
=
c
b
T
x
b
Cj-
zj
Zatem zmienna
x
1
wchodzi do bazy na miejsce zmiennej
x
5
. Teraz wektorami bazy są x
3
,
x
2
, x
1
. Przeprowadzamy obliczenia (2w)*2, (1w)-(2w), (3w)/4 i (2w)-(3w), (1w)+(2w)
i (2w)/2
2
3
0
1.5 1/8
0
0
0
-1.5 -1/8
Ponieważ wszystkie wskaźniki optymalności są mniejsze bądź równe
zero uzyskane rozwiązanie jest rozwiązaniem optymalnym,
x
1
=4
,
x
2
=2
, f(
x
1
, x
2
)=2*
4
+3*
2
=14
Programowanie nieliniowe bez ograniczeń
Minimum globalne
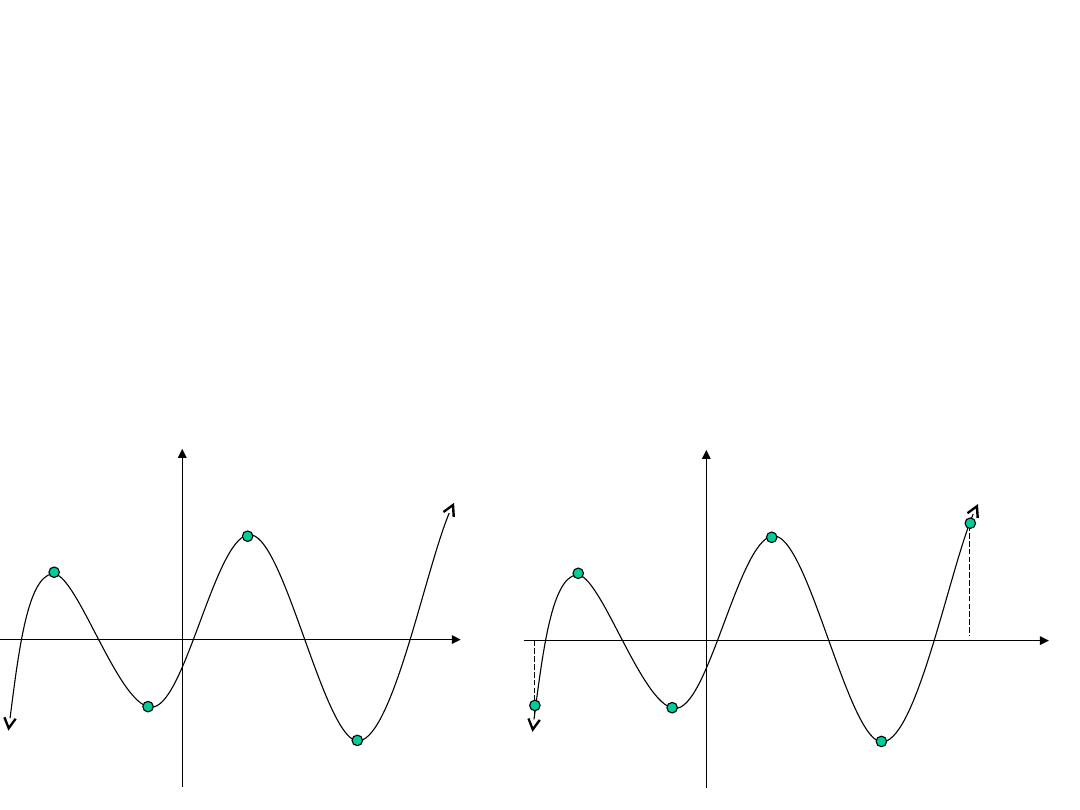
Funkcja f(X) osiąga minimum globalne w punkcie jeśli
dla każdego X należącego do zbioru rozwiązań dopuszczalnych S.
Minimum lokalne
Funkcja f(X) osiąga minimum lokalne w punkcie jeśli istnieje
otwarte otoczenie U
punktu , że
)
(
)
ˆ
(
X
X
f
f
X
ˆ
X
ˆ
X
ˆ
f(x)
x
A
B
C
D
x
A
B
C
D
f(x)
x=b
x=a
n
R
U
U
f
f
i
U
,
),
(
)
ˆ
(
ˆ
X
X
X
X
E
F

Gradient funkcji
Definicja
Jeżeli funkcja f(X) i jej wszystkie pierwsze pochodne są ciągłe na pewnym
podzbiorze E
n
to dla każdego punktu w tym podzbiorze określamy n-elementowy
wektor kolumnowy zwany gradientem f(X) w punkcie , jako
jest wektorem prostopadłym do warstwicy f(X) przechodzącej wrzez X
T
x
f
x
f
x
f
x
f
x
f
x
f
f
n
2
1
n
2
1
)
ˆ
(
)
ˆ
(
)
ˆ
(
)
ˆ
(
)
ˆ
(
)
ˆ
(
)
ˆ
(
X
X
X
X
X
X
X
X
ˆ
)
ˆ
(X
f
X
ˆ
)
ˆ
(X
f
x
2
x
1
x
2
f(x
1
,x
2
)=const
)
ˆ
(X
f
X
ˆ
x
3
x
1
X
ˆ
)
ˆ
(X
f
f(x
1
,x
2
,x
3
)=const
f(x)
x
0
)
(
2
x
x
x
f
0
)
(
1
x
x
x
f
Macierz Hessianu
Definicja
Jeżeli funkcja f(X) i jej wszystkie pierwsze i drugie pochodne są ciągłe
na pewnym podzbiorze E
n
to dla każdego punktu w tym podzbiorze określamy
nxn-elementową macierz zwaną macierzą Hessianu funkcji f(X)
w punkcie , jako
n
n
2
2
n
2
1
n
2
n
2
2
2
2
2
1
2
2
n
1
2
2
1
2
1
1
2
2
2
)
ˆ
(
)
ˆ
(
)
ˆ
(
)
ˆ
(
)
ˆ
(
)
ˆ
(
)
ˆ
(
)
ˆ
(
)
ˆ
(
ˆ
ˆ
)
ˆ
(
)
ˆ
(
x
x
f
x
x
f
x
x
f
x
x
f
x
x
f
x
x
f
x
x
f
x
x
f
x
x
f
f
f
X
X
X
X
X
X
X
X
X
X
X
X
X
X
ˆ
)
ˆ
(X
f
2
X
ˆ
)
ˆ
(
)
ˆ
(
2
X
X
H
f

Konieczne i wystarczające warunki optymalności
Warunki jakie musi spełniać punkt optymalny nazywane są
warunkami koniecznymi.
Jeśli punkt nie spełnia tych warunków to nie jest punktem
optymalnym. Spełnienie
jednak tych warunków nie wystarcza do tego aby określić czy punkt
jest optymalny.
Punkt spełniający warunki konieczne jest punktem podejrzanym o to,
że może być
optymalny .
Jeśli punkt spełniający warunki konieczne spełnia także warunki
wystarczające wówczas
Jest to punkt optymalny.
Podsumowanie
1. Punkt optymalny musi spełniać warunki konieczne optymalności.
Punkt, który nie s
pełnia tych warunków nie może być punktem optymalnym.
2. Punkt spełniający warunki konieczne nie musi być optymalny np.
punkty
nieoptymalne mogą spełniać warunki konieczne
3. Punkt podejrzany o optimum i spełniający warunki wystarczające
jest punktem
optymalnym.
4. Jeżeli warunki wystarczające nie mogą być użyte lub nie są one
spełnione to
wówczas nie jesteśmy w stanie nic powiedzieć o optymalności
punktu.
Warunki optymalności są wykorzystywane w dwóch przypadkach:
•
chcemy sprawdzić czy dany punkt projektowy może być punktem
optymalnym
•
warunków optymalności mogą być rozwiązane dla punktu, który
może być
optymalnym
Procedura określania warunków optymalności punktu spełniającego
minimum lokalne funkcji f jednej zmiennej
Warunki optymalności
są używane do określania
punktu minimum
funkcji f(x)
Warunki konieczne
optymalności muszą być spełnione w
punkcie
minimum
funkcji,
w przeciwnym wypadku punkt ten nie może być punktem minimum.
Niech będzie punktem lokalnego minimum funkcji f(x). Niech X
będzie bliskim sąsiadem punku . Zdefiniujmy przyrost d zmiennej
i wartości funkcji , oraz jej wartość w punkcie
xˆ
f
)
ˆ
(
)
(
,
ˆ
x
f
x
f
f
i
x
x
d
d
f
0
)
ˆ
(
)
(
x
f
x
f
f
warunek optymalności
Jeżeli jest punktem minimum to zaburzając położenie
nie zwiększamy wartości funkcji
xˆ
)
ˆ
(x
f
xˆ
xˆ
xˆ
xˆ
x

Warunek konieczny optymalności pierwszego rzędu
Rozwińmy w szereg Taylora funkcję f(x) w punkcie
Pomijając wyrazy wyższego rzędu otrzymujemy
Z warunku
otrzymujemy
Ponieważ d morze być zarówno dodatnie jak i ujemne więc aby był zawsze spełniony
powyższy warunek pochodna funkcji musi być równa zero, co zapisujemy
wówczas jest punktem minimum funkcji f.
R
d
x
d
x
f
d
d
x
d
x
df
x
f
x
f
R
x
x
x
d
x
f
d
x
x
x
d
x
df
x
f
x
f
f
d
d
2
2
2
2
2
2
ˆ
)
ˆ
(
2
1
ˆ
)
ˆ
(
)
ˆ
(
)
(
)
ˆ
(
ˆ
)
ˆ
(
2
1
)
ˆ
(
ˆ
)
ˆ
(
)
ˆ
(
)
(
d
x
d
x
df
f
ˆ
)
ˆ
(
0
)
ˆ
(
)
(
x
f
x
f
f
0
ˆ
)
ˆ
(
d
x
d
x
df
f
0
ˆ
)
ˆ
(
x
d
x
df
xˆ
xˆ
Warunek wystarczający optymalności
Punkt podejrzany o ekstremum musi spełniać konieczne warunki optymalności
Podstawiając do szeregu Taylora otrzymujemy
Z warunku
otrzymujemy
Warunek konieczny optymalności drugiego rzędu
Jeśli
wówczas nie możemy założyć, że punkt nie jest punktem minimum.
Należy sprawdzić warunek
jest to warunek konieczny drugiego rzędu.
Jeśli
punkt nie może być lokalnym minimum.
W przypadku gdy
należy sprawdzić jak zachowują się pochodne wyższych
rzędów. Wartość nieparzystej pochodnej mówi nam czy są spełnione warunki konieczne
optymalności, znak parzystej pochodnej mówi nam czy są spełnione warunki
wystarczające i czy punkt wyznacza minimum funkcji.
0
f
0
ˆ
)
ˆ
(
x
d
x
df
R
d
x
d
x
f
d
f
R
x
x
x
d
x
f
d
x
f
x
f
d
2
2
2
2
2
2
ˆ
)
ˆ
(
2
1
,
)
ˆ
(
ˆ
)
ˆ
(
2
1
0
)
ˆ
(
)
(
0
ˆ
)
ˆ
(
2
2
x
d
x
f
d
0
ˆ
)
ˆ
(
2
2
x
d
x
f
d
xˆ
0
ˆ
)
ˆ
(
2
2
x
d
x
f
d
0
ˆ
)
ˆ
(
2
2
x
d
x
f
d
xˆ
0
ˆ
)
ˆ
(
2
2
x
d
x
f
d

Przykład 1. Określenie punktu minimum przy użyciu warunków
koniecznych
4
4
2
x
x
x
f )
(
4
)
(
x
dx
x
df
2
0
4
)
(
2
2
2
x
dx
x
f
d
warunek
konieczny
2
x
0,
4
2
0
)
(
x
dx
x
df
warunek
wystarczający
Zatem x=2 jest minimum lokalnym funkcji f a jej wartość w tym
punkcie wynosi 0.
Przykład 2. Określenie punktu minimum przy użyciu warunków
koniecznych
4
4
)
(
3
x
x
x
x
f
2
4
2
-
3
)
(
2
x
x
dx
x
df
warunek
konieczny
8685
.
0
x
535,
.
1
x
0,
4
2
-
3
0
)
(
B
A
2
x
x
dx
x
df
2
x
)
(x
f
4
x
)
(x
f
1 2
5
-2
B
A
warunek
wystarczający
0
211
.
7
)
(
0,
.
7
)
(
2
2
2
2
B
A
x
x
dx
x
f
d
dx
x
f
d
211
Punkt B jest lokalnym maksimum, zaś punkt A lokalnym minimum
Przykład 3. Określenie punktu minimum przy użyciu warunków
koniecznych
4
)
(
x
x
f
2
2
2
3
1
)
(
,
4
)
(
x
dx
x
f
d
x
dx
x
df
2
0
)
(
1
)
(
0
2
2
2
0
2
x
dx
x
f
d
warunek
konieczny
0
3
x
0,
4
0
)
(
x
dx
x
df
warunek
wystarczający
Ponieważ druga pochodna funkcji f w punkcie x=0 jest równa zero
należy zbadać znak trzeciej pochodnej
Należy zatem policzyć kolejną pochodną
x
)
(x
f
Zatem punkt x=0 jest punktem lokalnego a także
globalnego minimum.
0
)
0
(
2
)
(
0
3
3
4
x
dx
x
f
d
0
24
)
(
0
4
4
x
dx
x
f
d

Warunki optymalności dla funkcji wielu zmiennych f(X)
Rozwińmy w szereg Taylora funkcję f(X) w punkcie
(*)
Załóżmy, że funkcja osiąga minimum w punkcie wtedy przyrost funkcji musi
zatem spełniać warunek
(**)
Pomijając wyrażenia wyższego rzędu zauważamy, że warunek (**) dla dowolnego d
jest spełniony gdy
(***)
(warunek konieczny I rzędu)
Punkt spełniający warunek (***) jest nazywany punktem stacjonarności. Podstawiając
(***) do wzoru (*) i uwzględniają (**) otrzymujemy dla dowolnego
(****)
(warunek konieczny II rzędu)
Warunek (****) jest spełniony jeżeli macierz H jest dodatnio określona
R
f
f
R
f
f
f
T
T
T
T
d
X
H
d
d
X
d
X
H
d
d
X
X
X
)
ˆ
(
2
1
)
ˆ
(
)
ˆ
(
2
1
)
ˆ
(
)
ˆ
(
)
(
X
ˆ
0
f
0
X
)
ˆ
(
f
0
)
ˆ
(
d
X
H
d
T
0
d
Określanie formy macierzy
Forma kwadratowa macierzy A wyrażona wzorem
może być
dodatnio określona, gdy
•dodatnio półokreślona, gdy
•niedodatnio określona, gdy
dla każdego
•niedodatnio półokreślona, gdy
•nieokreślona , gdy
AX
X
X
T
F
2
1
)
(
0
2
1
0
2
1
0
2
1
0
2
1
2
1
AX
X
AX
X
AX
X
AX
X
AX
X
T
T
T
T
T
0
0
X
Forma kwadratowa
AX
X
X
T
n
i
n
j
j
i
ij
x
x
p
F
2
1
2
1
)
(
1
1
1
3
3
2
2
1
2
3
2
2
2
1
2
2
2
2
)
(
x
x
x
x
x
x
x
x
x
F
3
X
np.
Przykład 1. Określenie punktu minimum przy użyciu warunków
koniecznych
8
2
2
2
)
(
2
1
2
2
2
1
2
1
x
x
x
x
x
x
x
f
warunek
konieczny
2
/
x
2,
/
x
,
0
0
1
4
2
2
2
2
0
)
(
2
1
2
1
2
1
3
5
x
x
x
x
d
df
X
X
Dla wszystkich X z wyjątkiem X=0 wyrażenie X
T
HX jest dodatnio
określone
warunek wystarczający
4
2
2
2
)
ˆ
(
)
ˆ
(
)
ˆ
(
)
ˆ
(
)
(
2
2
2
1
2
2
2
1
2
1
1
2
x
x
f
x
x
f
x
x
f
x
x
f
X
X
X
X
X
H
2
2
1
2
2
1
2
1
2
1
2
1
2
1
2
1
4
4
2
4
2
2
2
4
2
2
2
x
x
x
x
x
x
x
x
x
x
x
x
x
x
T
HX
X
x
2
x
1
10.0
8.0
6.0
5.0
X(2.5,-1.5)
F(2.5,-1.5)=4.75
0
HX
X
T
Metody numeryczne rozwiązywania zadań minimalizacji bez ograniczeń
Powody dla których korzysta się z metod numerycznych przy rozwiązywaniu zadania
optymalizacji:
•Zadanie optymalizacji posiada wiele zmiennych decyzyjnych
•Funkcja celu może cechować się nieliniowością wysokiego rzędu
•Funkcja celu może nie zależeć w sposób jawny od zmiennych decyzyjnych
Optymalizacja bez ograniczeń
Problem jednowymiarowy
Znaleźć skalar * , które minimalizuje
funkcję f()
Problem wielowymiarowy
Znaleźć punkt x* , który minimalizuje
funkcję f(x)
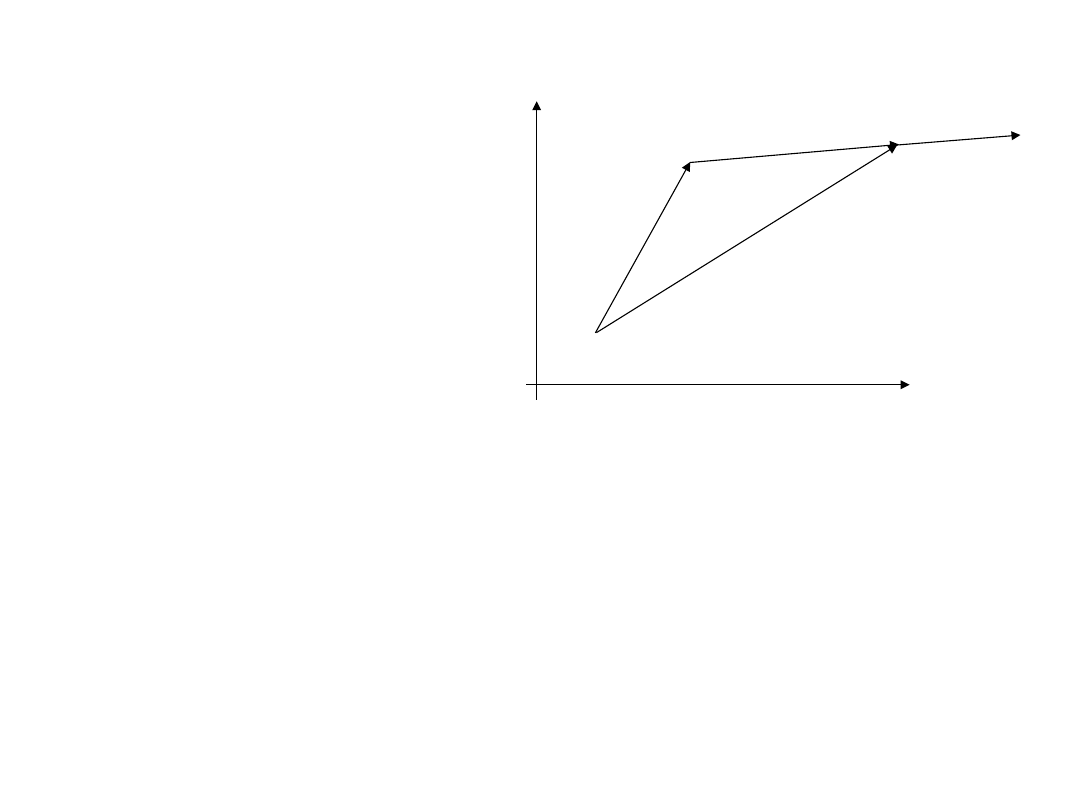
Główne zasady działania algorytmu numerycznego
Ogólny algorytm działania metod
k numer iteracji
d
(k)
dopuszczalny kierunek poszukiwań
długość kroku
Rozwiązywanie zadania optymalizacji przy użyciu metod numerycznych
polega na
przemierzaniu obszaru rozwiązań dopuszczalnych w poszukiwaniu
ekstremum funkcji
celu według iteracyjnego schematu
wektor
x
(k+1)=
x
(k)
+x
(k)
,
k=0,1,2,...
składowe
x
i
(k+1)=
x
i
(k)
+x
i
(k)
,
k=0,1,2,...
i=1 do n
gdzie
x
(k)
=
k
d
(k)
A
B
C
x
(k-1)
x
(k)
x
(k+1)
d
(k)
d
(k)

Procedury algorytmu numerycznego
Krok 1. Wybór punktu startowego x
(0)
. Iteracja początkowa k=0.
Krok 2. Obliczenie kierunku poszukiwań d
(k)
w przestrzeni
projektowej. Ten krok wymaga znajomości wartości funkcji celu i jej
gradientów, oraz ewentualnie gradientów funkcji ograniczeń przy
optymalizacji z ograniczeniami.
Krok 3. Sprawdzenie zbieżności algorytmu. Jeśli kryterium
zbieżności jest spełnione kończymy proces, w przeciwnym wypadku
przechodzimy do dalszych kroków.
Krok 4. Wyznaczenie długości kroku
k
.
Krok 5. Obliczenie nowego punktu projektowego jako
x
(k+1)=
x
(k)
+
k
d
(k)
,
teraz k=k+1 i powracamy do kroku 2.

Idea Procedury Iteracyjnej
Załóżmy, że minimalizujemy funkcję f(x). Załóżmy, że w k-tej iteracji
punkt x
(k)
nie jest punktem minimalnym. Nie są bowiem spełnione
kryteria optymalności dla tego punktu. Jeśli x
(k)
nie jest punktem
optymalnym należy znaleźć inny punkt x
(k+1)
dla którego wartość
funkcji będzie malała, co można zapisać
f(x
(k+1)
)<f(x
(k)
)
Jeśli do powyższego wyrażenia wprowadzimy zależność określającą
x
(k+1)
otrzymujemy
f(x
(k)
+
k
d
(k)
)<f(x
(k)
)
(*)
Rozwijając w szereg Taylora funkcję f(x
(k)
+
k
d
(k)
) względem punktu
x
(k)
otrzymujemy
pomijając człony wyższego rzędu i podstawiając do powyższej
nierówności (*) otrzymujemy
dla
k
>0
(**)
Ponieważ możemy określić gradient funkcji celu zatem kierunek
poszukiwań d
(k)
musi być dobrany tak aby spełniony był warunek (**)
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
k
k
k
k
k
k
f
d
df
f
x
d
x
x
x
R
d
f
d
d
df
f
f
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
2
)
(
)
(
)
(
2
)
(
)
(
2
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
2
1
)
(
)
(
)
(
)
(
x
d
x
x
x
x
d
x
x
x
x
d
x
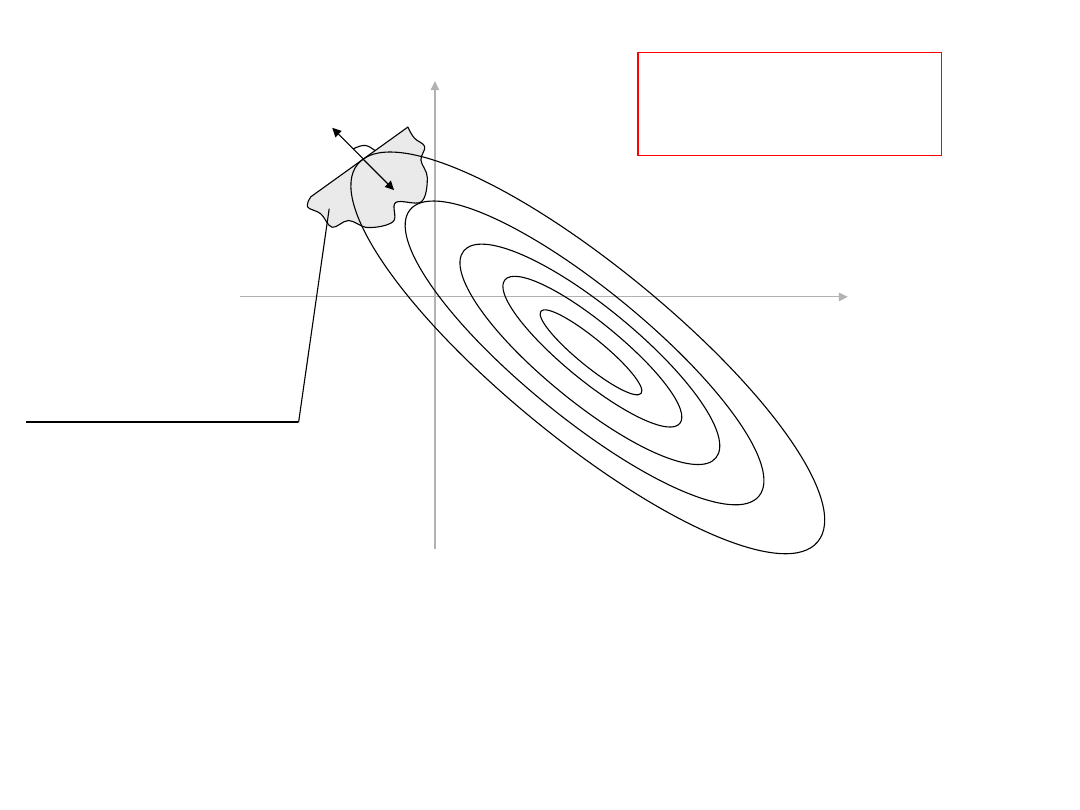
0
)
(
)
(
)
(
k
k
k
f
d
x
Kierunek d
(k)
jest dopuszczalnym kierunkiem poprawy gdy iloczyn
skalarny wektora d
(k)
i wektora gradientów funkcji celu
jest mniejszy od zera. Tzn. wektor d
(k)
należy do stożka
dopuszczalnych kierunków . Kąt pomiędzy d
(k)
i
musi
Się zawierać pomiędzy 90 a 270 stopni.
)
(k
f x
x
2
x
1
10.0
8.0
6.0
5.0
)
(
)
(k
f x
)
(k
d
stożek dopuszczalnych
kierunków poprawy
B
)
(k
f x
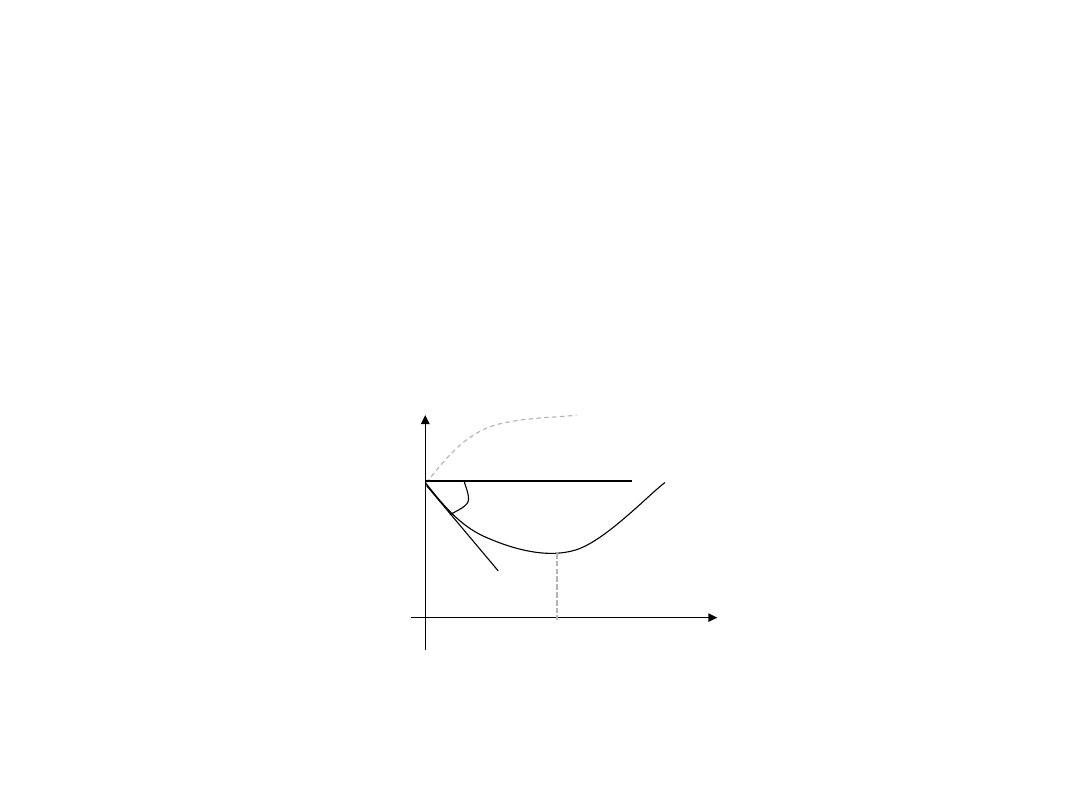
Problem określania długości kroku
Załóżmy, że funkcja f(x
(k)
+
k
d
(k)
) jest funkcją zmiennej tj. f=f().
Gdy =0, f(0)= f(x
(k)
). Gdy x
(k)
nie jest punktem minimum, wówczas
można znaleźć dopuszczalny kierunek poprawy d
(k)
. Małe zmiany
funkcji wzdłuż tego kierunku zmniejszają wartości funkcji.
Wykorzystując zależność (*) otrzymujemy
f()<f(0)
Aby spełnić powyższy warunek f() musi mieć ujemne nachylenie w
punkcie =0. Malejąco rosnący charakter funkcji f() wynika z
faktu, że musi być dodatnie.
f()
k
Analityczne metody określania długości kroku
Jeśli d
(k)
jest kierunkiem dopuszczalnym, wówczas musi być
zawsze dodatnie aby był spełniony warunek
Dla problemu jednowymiarowego należy określić =
k
takie aby
f() osiągała minimum. Jeżeli f() jest funkcją prostą można
wykorzystać warunki konieczne i dostateczne optymalności do
wyznaczenia . Przy czym warunek konieczny jest zdefiniowany w
postaci
(*)
zaś warunek wystarczający przyjmuje postać
Licząc
i podstawiając do
otrzymujemy
0
)
(
)
(
)
(
k
k
k
f
d
x
0
d
df
k
)
(
0
)
(
2
2
d
f
d
k
)
(
)
1
(
)
1
(
)
1
(
)
1
(
)
(
)
(
)
(
)
(
)
(
k
k
k
k
k
k
k
k
f
d
d
d
df
d
df
d
x
x
x
x
d
x
0
d
df
k
)
(
0
)
(
)
1
(
)
(
k
k
f
d
x

Przykład
7
2
2
)
(
2
2
2
1
2
1
x
x
x
x
f
3
x
w punkcie (1,2) i kierunku (-1,-1) określić długość kroku minimalizującą funkcję f(x)
na danym kierunku.
Dla punktu x
(k)
=(1,2), f(x
(k)
)=f(1,2)=3+4+8+7=22, oraz d
(k)
=(-1,-1). Najpierw
sprawdzamy, czy kierunek d
(k)
jest kierunkiem dopuszczalnym. W tym celu liczymy
Gradient
Z zależności
zatem d
(k)
jest kierunkiem
dopuszczalnym. Obliczamy następnie nową wartość zmiennej x
(k+1)=
x
(k)
+
k
d
(k)
,
Stąd x
1
(k+1)=
1
+
k
(-1),
oraz x
2
(k+1)=
2
+
k
(-1). Podstawiając otrzymujemy
)
,
(
4
2
,
2
6
)
(
)
,
(
2
1
2
1
)
(
10
10
2
1
x
x
x
x
f
k
x
0
20
10
1
10
)
1
(
)
(
)
(
)
(
)
(
k
k
f
d
x
1
-
1
-
2
1
)
(
)
(
2
1
)
1
(
2
1
k
k
k
k
k
x
x
x
x
d
22
20
7
7
)
1
(
2
)
2
)(
1
(
2
)
1
(
3
)
(
2
2
2
)
1
(
k
f x

22
20
7
)
(
2
f
f()
k
f(0)=22
0
20
)
(
)
(
)
(
k
k
f
d
x
0
14
)
(
7
10
-
0,
,
)
(
2
2
20
14
0
d
f
d
d
df
k
k
Warunek konieczny
Warunek dostateczny
Zatem nowy punkt projektowy
7
4
3
7
-
1
-
1
-
2
1
)
(
)
(
2
1
)
1
(
2
1
7
10
k
k
k
k
x
x
x
x
d
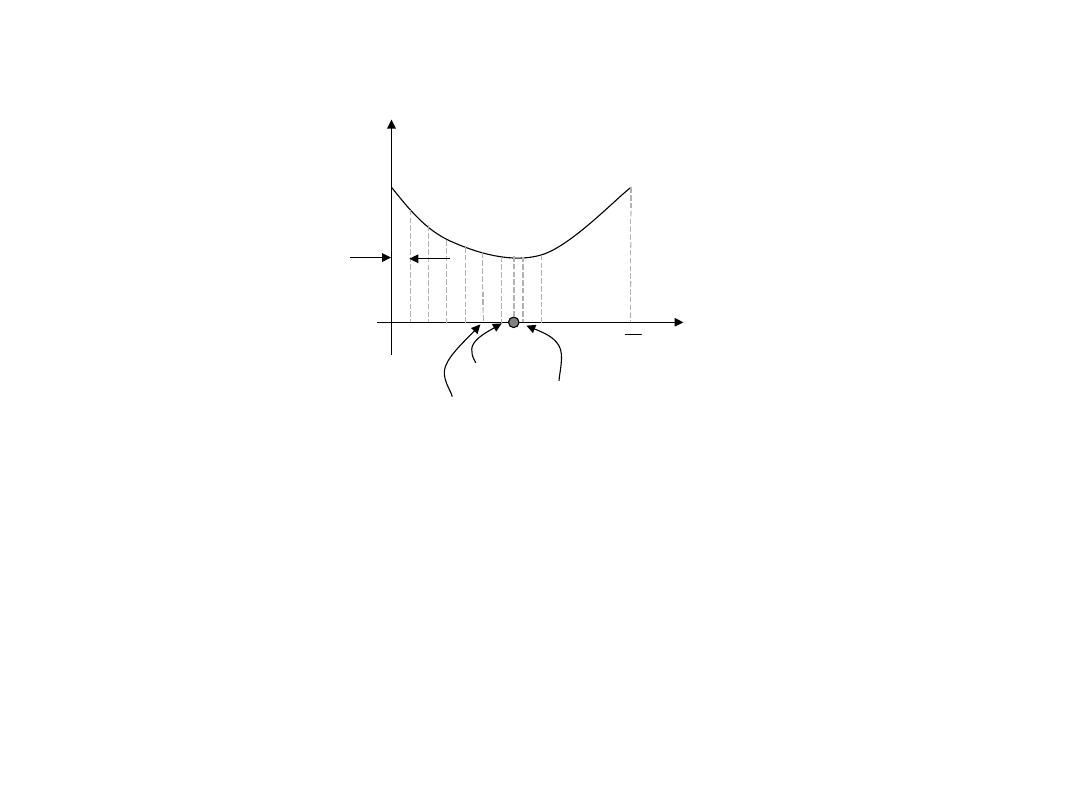
Numeryczne metody określania długości kroku
Metoda równego połowienia
f()
q
(q-1) (q+1)
Jeśli wartość funkcji w punkcie q jest większa niż w punkcie (q+1)
)
)
((
)
(
1
q
f
q
f
)
)
((
)
(
1
q
f
q
f
punkt optymalny jeszcze nie został osiągnięty
Jeśli wartość funkcji w punkcie q jest mniejsza niż w punkcie (q+1)
punkt optymalny został przekroczony. Aby wyznaczyć punkt optymalny można
wykorzystać metodę złotego podziału rozważając przedział od q do (q+1)
Metoda złotego podziału dla zadania jednowymiarowego
Niech punkt znajduje się w odległości od punktu
l
q
u
q
)
( 1
I
I
I
)
(
1
I
)
(
1
I
a
b
'
I
'
l
'
u
'
b
'
I
'
)
(
I
1
I
I
)
(
'
1
'
b
'
I
l
Po podstawieniu otrzymujemy równanie
I
I
'
0
I
I
I
2
którego rozwiązaniem są pierwiastki
1.927
0.618
2
5
1
2
,
1
Kolejne rozważane punktu określane są ze wzoru
j
q
j
q
0
0.618
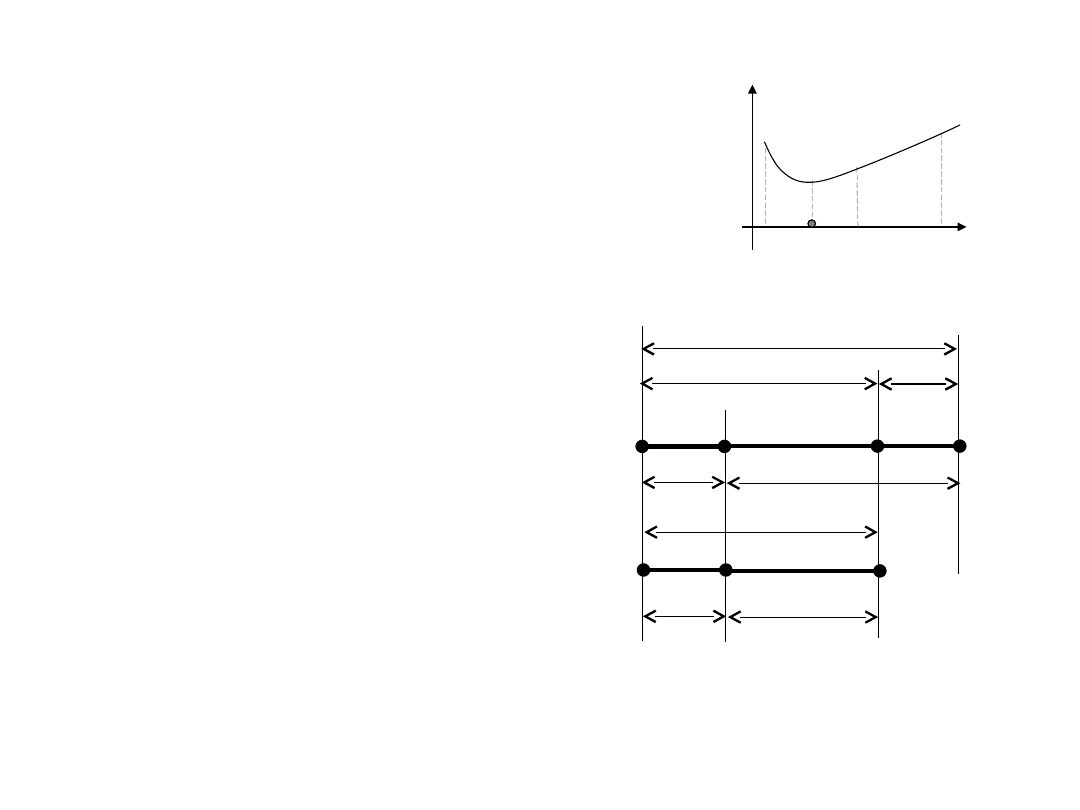
Algorytm metody złotego podziału dla zadania
jednowymiarowego
Obliczamy f(
a
) i f(
b
)
Krok 1
Dla wybranego małego kroku spełniającego
warunki
l
u
I
I
I)
(
1
I)
(
1
I
a
b
'
I
'
l
'
u
'
b
'
I
'
)
(
I
1
)
(
)
(
)
(
)
(
1
2
q
q
q
q
f
f
i
f
f
1
f()
(q-1) q
(q-2)
określamy
q
j
j
q
u
q
j
j
q
l
i
0
2
0
2
1.618
1.618
Krok 2
Krok 3
Jeśli
f(
a
) < f(
b
) wtedy punkt optymalny jest
pomiędzy
b
l
*
b
u
l
l
'
'
,
przyjmujemy
obliczamy
)
(
,
'
'
'
'
'
l
u
l
a
a
gdzie
f
0.382
Sprawdzamy kryteria zbieżności. Jeśli nie są spełnione powracamy do punktu 3.
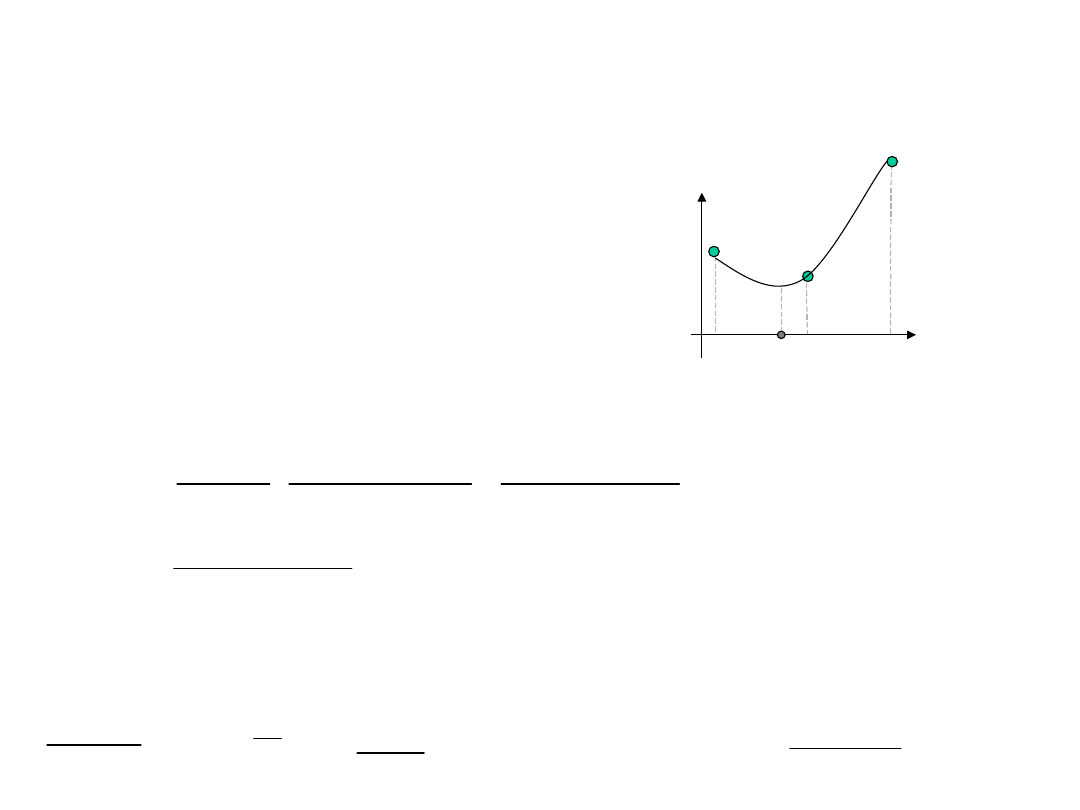
Interpolacja kwadratowa
funkcji
lub
Jeśli mamy zadane trzy punkty
l
,
u
i pośrednią zawartą pomiędzy nimi
i
oraz znamy
wartości funkcji w tych punktach f(
l
), f(
u
), f(
i
), to rozważaną krzywą możemy
aproksymować parabolą o równaniu
2
2
1
)
(
a
a
a
q
o
f()
(q-1) q
(q-2)
0
d
dq )
(
2
2
1
o
2
1
2
)
(
)
(
)
(
)
(
)
(
)
(
)
(
l
l
l
i
l
l
i
l
i
l
i
l
i
l
u
l
u
i
u
a
a
f
a
a
f
f
a
f
f
f
f
a
1
Położenie ekstremum paraboli q określamy z warunku
2
1
a
a
2
2
2
1
2
2
1
2
2
1
)
(
)
(
)
(
u
u
o
u
i
i
o
i
l
l
o
l
a
a
a
f
a
a
a
f
a
a
a
f
Po rozwiązaniu układu równań otrzymujemy
0
2
2
2
2
a
d
q
d
)
(
minimum gdy
Określanie minimum za pomocą Interpolacji
kwadratowej-przykład
Dane
5.236610
f
0.466464
f
1.648721
f
2.618034
1.309017,
0.5
u
i
l
u
i
l
,
,
,
Współczynniki paraboli wynoszą kolejno
3.957
0.5
2.410
0.5
5.821
1.648721
5.821
1.309017
0.5
2.410
0.5
1.309017
1.648721
0.466464
2.410
0.5
1.309017
1.648721
0.466464
0.5
2.618034
1.648721
5.236610
1.309017
2.618034
1
1
2
2
2
1
o
2
1
2
)
(
)
(
)
(
)
(
)
(
)
(
)
(
l
l
l
i
l
l
i
l
i
l
i
l
i
l
u
l
u
i
u
a
a
f
a
a
f
f
a
f
f
f
f
a

Określanie minimum za pomocą Interpolacji
kwadratowej-przykład
Następnie określamy ekstremum paraboli
Wartość funkcji w punkcie jest równa
1.2077
2.410
2
5.821
2
2
1
a
a
0.5149
f
Zauważamy, że
2.618034
1.2077
1.309017
1.2077
0.5
1.2077
u
i
l
5.236610
f
0.5149
0.466464
f
0.5149
1.648721
f
0.5149
u
i
l
f
f
f
)
(
)
(
)
(
Ponieważ należy przyjąć inny przedział poszukiwania ekstremum
jako równy
i
f
f
)
(
0.5
l
2.618034
u
1.309017
i
1.2077
u
u
i
l
'
'
'
1
Określanie minimum za pomocą Interpolacji
kwadratowej-przykład
Przechodzimy do drugiej iteracji
1.3464
2
2
1
a
a
2.618034
1.309017
1.2077
u
i
l
5.236610
f
0.466464
f
0.5149
f
u
i
l
Aktualizujemy współczynniki paraboli oraz punkt ekstremum i wartość funkcji
w tym punkcie
0.4579
)
(
f
0.5
2.618034
'
u
1.309017
'
i
1.2077
'
l
u
u
i
l
''
''
i
'
''
2.713
7.30547
5.3807
o
1
2
a
a
a
Metody gradientowe-optymalizacja w kierunku
największego spadku
Niech f(x) będzie różniczkowalne względem x. Kierunek spadku wartości funkcji dla
Dowolnego punktu jest okreslony
c
T
x
f
x
f
x
f
f
n
1
1
Algorytm optymalizacji w kierunku realizowany jest w następujących krokach
•
Określenie punktu startowego x
(o)
, ustalenie parametrów zbieżności >0.
•
Obliczenie gradientu funkcji f(x) w punkcie x
(k)
jako
Obliczenie . Jeśli przerwij proces iteracyjny i przyjmij, że x*=x
(k)
jest punktem optymalnym. W przeciwnym wypadku przejdź do punktu 3.
3. Określ kierunek poszukiwań w punkcie x
(k)
optimum jako
4. Oblicz długość kroku
k
poprzez minimalizację wyrażenia
5. Uaktualnij wartości zmiennych decyzyjnych wg. Wzoru
Przyjmij k=k+1 i powróć do punktu 2.
i
i
i
x
f
c
d
lub
c
d
)
(
)
(
)
(
k
k
f x
c
)
(k
c
)
(k
c
)
(
)
(
k
k
c
d
)
(
)
(
)
(
k
k
f
d
x
)
(
)
(
)
(
k
k
k
k
d
x
x
1

Metody gradientowe-optymalizacja w kierunku
największego spadku
Kierunek największego spadku jest prostopadły do gradientu funkcji
Długość kroku określamy z warunku
Otrzymujemy zatem
gdzie
)
(
)
(
)
(
)
1
(
)
1
(
)
(
,
k
k
k
k
k
k
i
f
d
d
x
x
x
x
c
1
)
1
(
)
1
(
)
1
(
)
(
)
(
k
T
k
k
f
f
x
x
x
x
0
)
1
(
)
(
k
k
c
c
0
0
)
(
)
1
(
)
(
)
1
(
lub
,
k
k
k
k
c
c
d
c
Optymalizacja w kierunku największego spadku-przykład
znajdź
Przyjmując, że punkt startowy ma współrzędne (1,0)
2
2
2
min
x
x
x
x
f
1
2
1
2
x
x
1. Określenie punktu startowego x
(o)
=(1,0) ustalenie parametrów zbieżności >0.
2. Obliczenie gradientu funkcji f(x) w punkcie x
(k)
jako
Obliczamy
3. Określamy kierunek poszukiwań w punkcie x
(k)
optimum jako
4. Obliczamy długość kroku
k
poprzez minimalizację wyrażenia
5. Uaktualnij wartości zmiennych decyzyjnych wg. Wzoru
Przyjmij k=k+1 i powróć do punktu 2.
2
-
2
2
2
2
2
)
0
,
1
(
1
2
2
1
)
(
)
(
)
(
x
x
x
x
f
o
o
x
c
0
2
2
2
2
2
)
0
(
2
c
)
(k
c
2
2
)
0
(
)
0
(
c
d
)
,
(
)
(
)
(
)
(
2
0
2
1
f
f
0
0
d
x
)
(
)
(
)
(
k
k
k
k
d
x
x
1
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
- Slide 58
- Slide 59
- Slide 60
- Slide 61
- Slide 62
- Slide 63
- Slide 64
- Slide 65
- Slide 66
- Slide 67
- Slide 68
- Slide 69
- Slide 70
- Slide 71
- Slide 72
- Slide 73
- Slide 74
- Slide 75
- Slide 76
- Slide 77
- Slide 78
- Slide 79
- Slide 80
- Slide 81
- Slide 82
- Slide 83
- Slide 84
- Slide 85
- Slide 86
- Slide 87
- Slide 88
- Slide 89
- Slide 90
- Slide 91
- Slide 92
- Slide 93
- Slide 94
- Slide 95
- Slide 96
- Slide 97
- Slide 98
- Slide 99
Wyszukiwarka
Podobne podstrony:
haccp cwiczenia pl
haccp-cwiczenia-pl
haccp cwiczenia pl
haccp cwiczenia pl
POPRAWA WSZYSTKICH KOLOKWIËW. 5fantastic.pl , Ćwiczenia
Osocze a mocz. 5fantastic.pl , Ćwiczenia
Zjazd5s1 v2. 5fantastic.pl , Ćwiczenia
cwwo27 word 2007 pl cwiczenia p Nieznany
Excel 2007 PL cwiczenia praktyczne cwex27
cwwvin 4 windows vista pl instalacja i naprawa cwiczenia praktycznie ebook promocyjny helion pl KJID
InDesign 2 0 PL Cwiczenia prakt Nieznany
Excel 2003 PL cwiczenia zaawansowane czex23
Ćwiczenie nr2, Studia PŁ, Ochrona Środowiska, Biochemia, laborki, sprawka
wykład 1. 5fantastic.pl , Ćwiczenia
więcej podobnych podstron