1

1

ĆWICZENIE

ĆWICZENIE

nr 2

POTRZEBY MATERIAŁOWE

– ilościowe metody prognozowania

2

2

PRZYKŁADY PROGNOZ

ZADANIE 1
W okresie 15 tygodni zanotowano w magazynie zaopatrzenia następujące
liczby samochodów dostarczających niezbędne do produkcji surowce :

Tydzień

Liczba samochodów

1

84

2

81

3

89

4

90

5

99

6

106

7

127

8

117

9

127

10

103

11

96

12

96

13

86

14

101

15

109

3

3

Określić przy wykorzystaniu metody naiwnej liczbę samochodów
obsługiwanych w terminalu
1. Zgodnie z modelem dla metody naiwnej prognozę można sporządzić dla
okresu tydzień 2 – tydzień 16; jej wartości są następujące:

Tydzień

Rzeczywista liczba

samochodów (D

t

)

Prognoza F

(t=1)

na

podstawie danych z

ostatniego okresu

Błąd prognozy

1

84

-

-

2

81

3

89

4

90

5

99

6

106

7

127

8

117

9

127

10

103

11

96

12

96

13

86

14

101

15

109

16

-

-

4

4

ZADANIE 2

Dla danych jak w ZADANIU 1 opracować prognozę dla 16. tygodnia opartą na
średniej ruchomej wartości danych dla danych z a) dwóch, b) czterech
okresów

Tydzień

Rzeczywista liczba

samochodów

PROGNOZA

(średnia z 2 okresów)

PROGNOZA

(średnia z 4 okresów)

1

84

-

-

2

81

-

-

3

89

-

4

90

-

5

99

6

106

7

127

8

117

9

127

10

103

11

96

12

96

13

86

14

101

15

109

16

-

średnia

wartość min

wartość max

5

5

Tabela wynikowa ma postać następującą:

Tydzień

Rzeczywista liczba

samochodów

PROGNOZA

(średnia z 2 okresów)

PROGNOZA

(średnia z 4 okresów)

1

84

-

-

2

81

-

-

3

89

-

4

90

-

5

99

6

106

7

127

8

117

9

127

10

103

11

96

12

96

13

86

14

101

15

109

16

-

średnia

wartość min

wartość max

6

6

ZADANIE 3

Dla danych z ZADANIA 1 obliczyć prognozę wielkości obsługi w 16. tygodniu
opartą na ważonej średniej ruchomej z a) dwóch, b) czterech okresów.

USTALENIE WAG przy średniej ruchomej z dwóch okresów:



waga przypisana bieżącemu okresowi



waga przypisana ostatniemu okresowi

PROGNOZA F

16

:

14

14

15

15

16

2

1

16

16

D

W

D

W

D

W

F

i

i

i





















F

16

bez wygładzania 105,0

USTALENIE WAG przy średniej ruchomej z czterech okresów okresów:



waga przypisana bieżącemu okresowi



waga przypisana okresowi (t + 1)

–

2



waga przypisana okresowi (t + 1)

–

3



waga przypisana ostatniemu okresowi (t+1) – 4

PROGNOZA F

16

:

 

 



































12

12

13

13

14

15

15

15

1

4

1

1

16

4

D

W

D

W

D

W

D

W

D

W

F

i

t

i

i

t

F

16

bez wygładzania 98,0

7

7

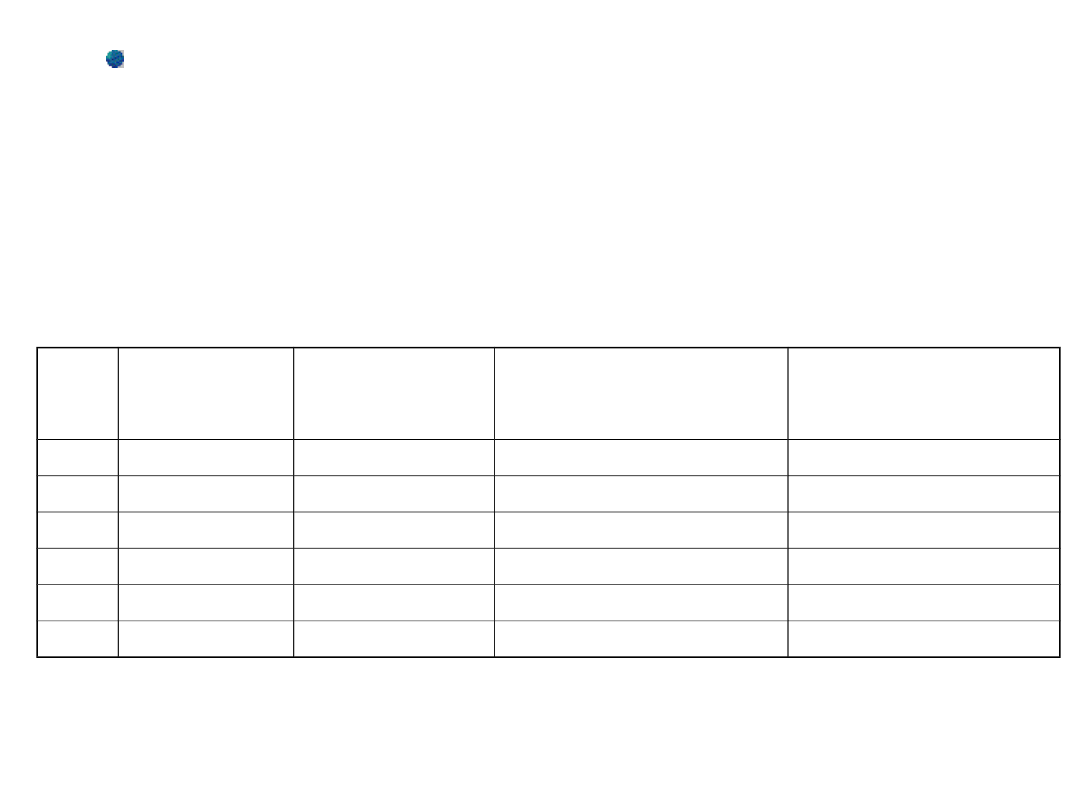
ZADANIE 4

Popyt na miedź elektrolityczną w tys. ton w 20 miesiącach kształtował się tak,
jak przedstawiono w poniższej tabeli. Obliczyć prognozę popytu wykorzystując
liniowy model wygładzania wykładniczego Holta (prognoza dostosowana)

Okres

Popyt w [tys. ton]

1

30

2

34

3

37

4

40

5

44

6

48

7

51

8

55

9

58

10

62

11

65

12

66

13

67

14

66

15

67

16

65

17

66

18

67

19

67

20

66

8

8

SPORZĄDZENIE PROGNOZY OPARTEJ NA MODELU WYGŁADZANIA
WYKŁADNICZEGO (prognoza niedostosowana)



przyjęto stałą wygładzania α = 0,3



postać modelu:

 





t

t

t

F

D

F













1

1



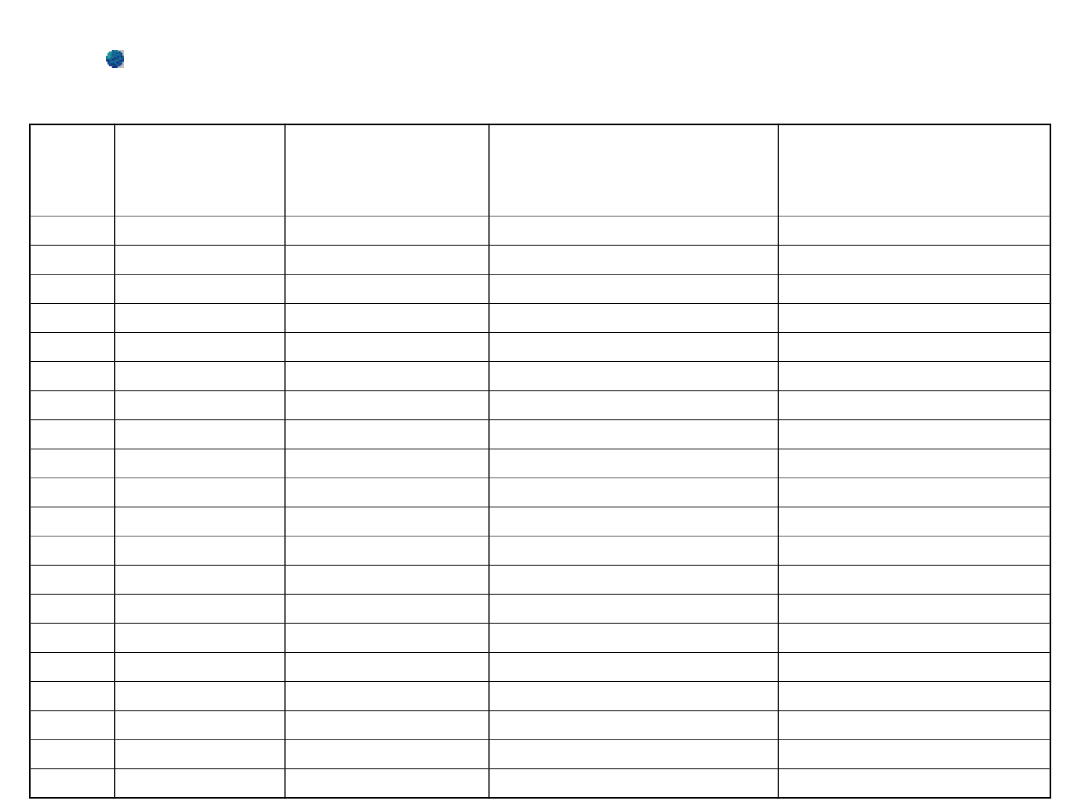
PROGNOZA NIEDOSTOSOWANA F

(t+1)

– model Browna

Okre

s (t)

Popyt (D

t

)

Prognoza

niedostosowana

1

30

-

-

27,00

2
3

⁞

19

65,58

20

t

D











t

t

t

F

F

F

















7

,

0

3

,

0

0

,

1

1



 





t

t

t

F

D

F

















1

1

SPORZĄDZENIE PROGNOZY OPARTEJ NA MODELU WYGŁADZANIA
WYKŁADNICZEGO (prognoza niedostosowana)

Okres

(t)

Popyt (D

t

)

Prognoza

niedostosowana

t

D











t

t

t

F

F

F

















7

,

0

3

,

0

0

,

1

1



 





t

t

t

F

D

F

















1

1

10

10



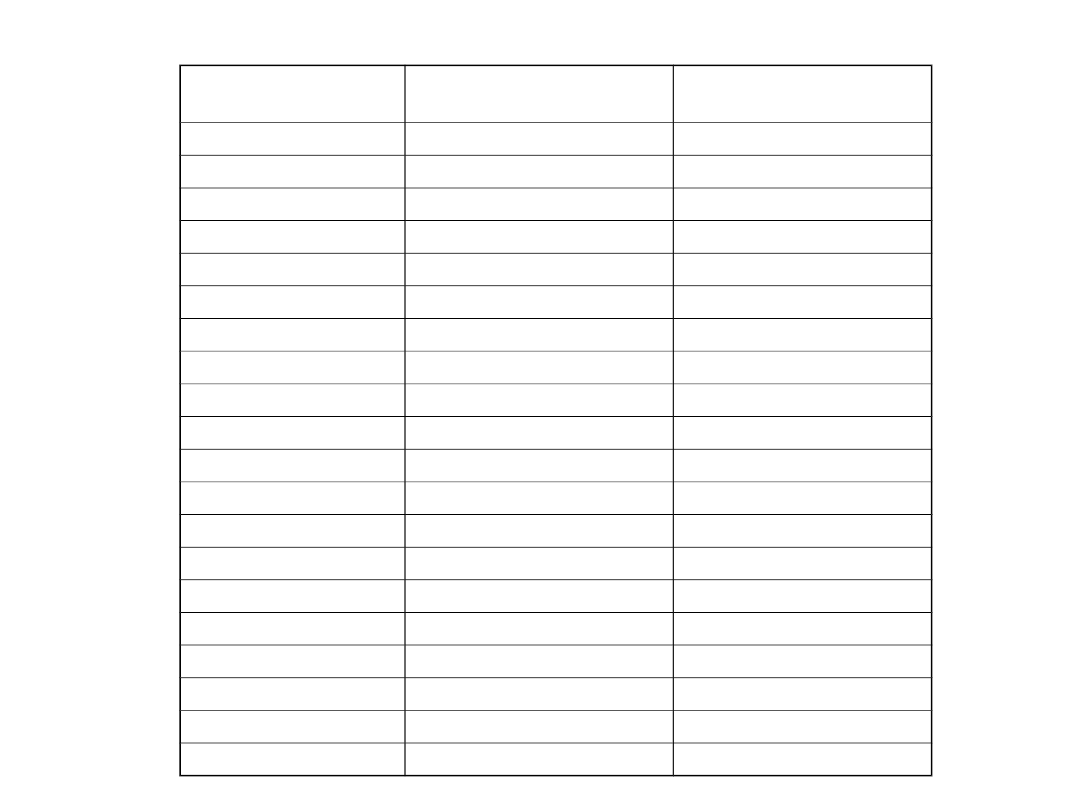
Postać tabeli wynikowej jest następująca:

Okres (t)

Popyt (D

t

)

Prognoza niedostosowana

F

t

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

11

11



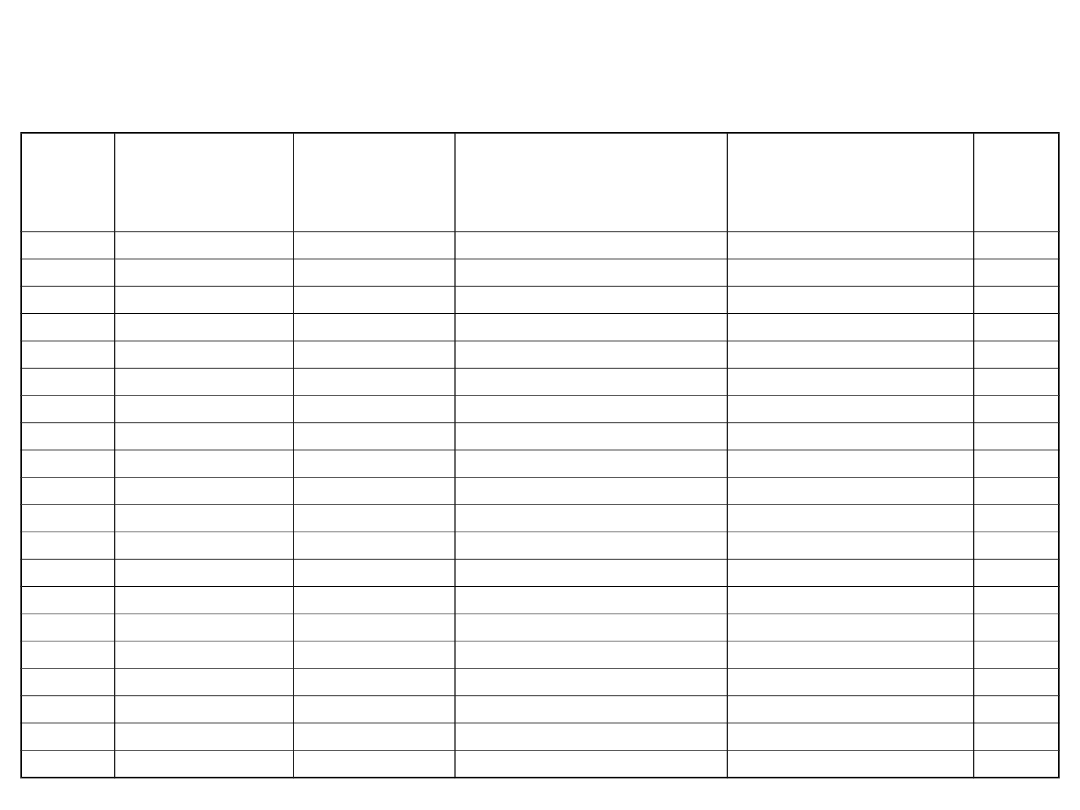
Przyjęcie współczynnika wygładzania trendu β = 0,6



Obliczenie współczynnika dostosowania do trendu T

t+1

Okre

s (t)

Prognoza

niedostosowa

na F

t

Trend

T

t

1

27,00

-

-

-

0,00

2
3
4

⁞

19

0,58

20

 

t

t

F

F



1

 





 





F

F

F

F

t

t

t













1

1

6

,

0











t

t

t

T

T

T

4

,

0

6

,

0

1

1

















Przyjęcie współczynnika wygładzania trendu β = 0,6



Obliczenie współczynnika dostosowania do trendu T

t+1

 

t

t

F

F



1

 





 





F

F

F

F

t

t

t













1

1

6

,

0











t

t

t

T

T

T

4

,

0

6

,

0

1

1















Okres

(t)

Prognoza

niedostosowa

na F

t

Trend

T

t

13

13



PROGNOZA DOSTOSOWANA AF(T+1) – model Holta

 

 

 

1

1

1











t

t

t

T

F

AF

Okres (t)

Popyt (D

t

)

Prognoza

niedostosowana F

t

Trend T

(t+1)

Prognoza

dostosowana

AF

(t+1)

1

30

27,00

0,00

-

2

34

3

37

4

40

5

44

6

48

7

51

8

55

9

58

10

62

11

65

12

66

13

67

14

66

15

67

16

65

17

66

18

67

19

67

20

66

14

14

ZADANIE 5
Firma zajmuje się sprzedażą nowoczesnych pojazdów specjalnych. W ciągu 10
miesięcy popyt kształtował się tak, jak przedstawiono w poniższej tabeli.
Obliczyć prognozę popytu w miesiącach 11 – 13 wykorzystując metodę regresji
liniowej.

Miesiąc (x)

Popyt (y)

1

8

2

12

3

25

4

40

5

50

6

65

7

36

8

61

9

88

10

63



Obliczenie wartości niezbędnych do szacunkowego określenia
parametrów funkcji liniowej

x

b

a

y

ˆ

ˆ

ˆ





15

15

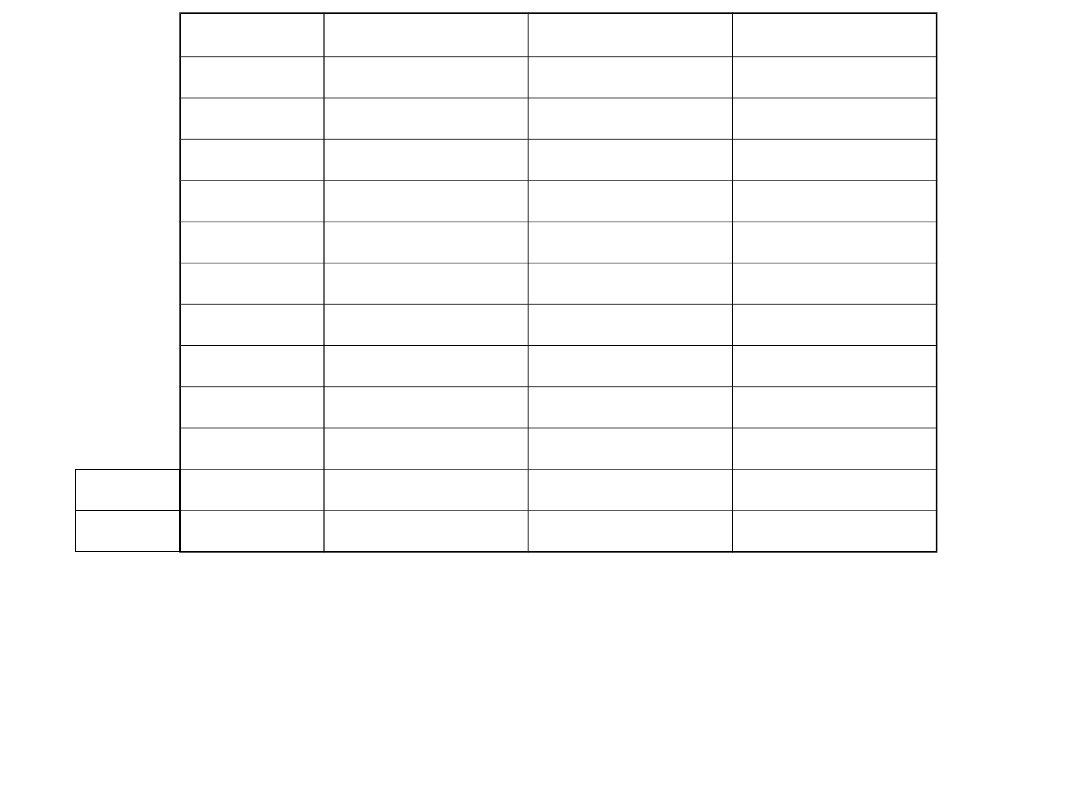
Miesiąc (x)

Popyt (y)

x

2

xy

1

8

2

12

3

25

4

40

5

50

6

65

7

36

8

61

9

88

10

63

-

suma

średnia



Oszacowanie wartości współczynnika kierunkowego

bˆ



bˆ

16

16



Oszacowanie wyrazu wolnego

aˆ







x

b

y

a

ˆ

ˆ

ˆ



Otrzymana funkcja regresji ma postać:



yˆ



Prognoza

- 11 miesiąc
- 12 miesiąc
- 13 miesiąc



11

ˆy



12

ˆy



13

ˆy

17

17



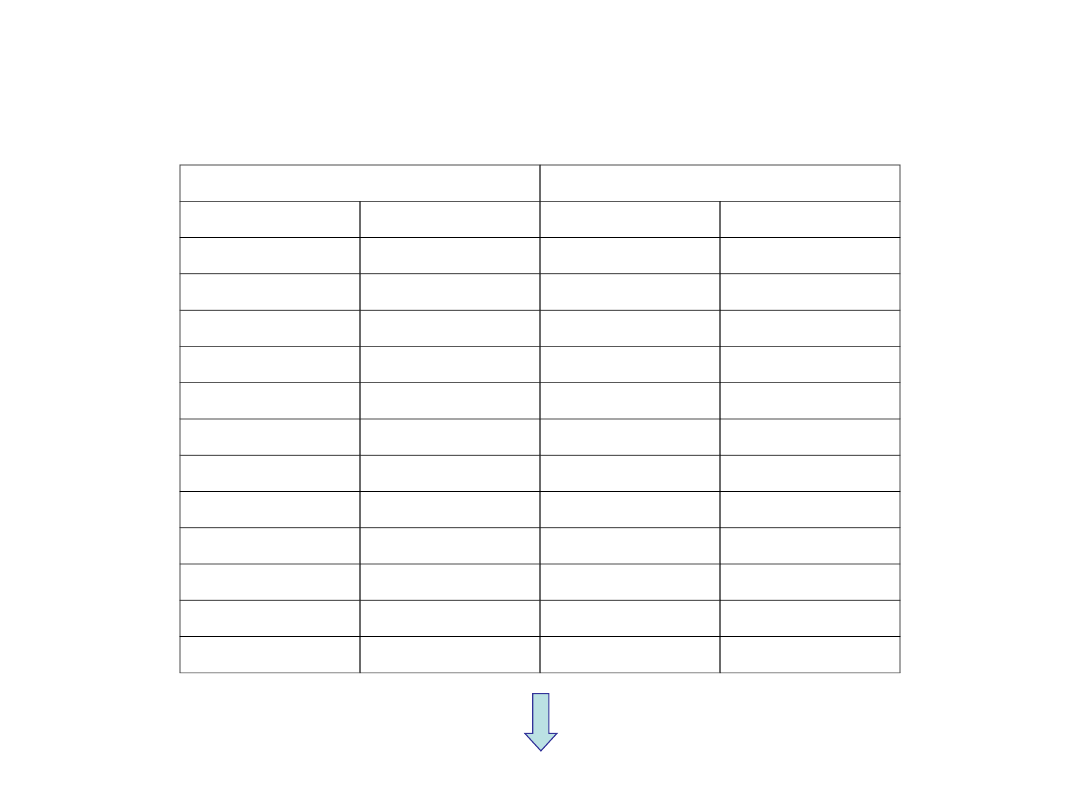
PRZYKŁAD – Regresja liniowa z dostosowaniem sezonowym

2009

2010

Miesiąc

Popyt

Miesiąc

Popyt

1

51

1

112

2

67

2

137

3

65

3

191

4

129

4

250

5

225

5

416

6

272

6

487

7

238

7

421

8

172

8

285

9

143

9

235

10

131

10

222

11

125

11

192

12

103

12

165

18

18

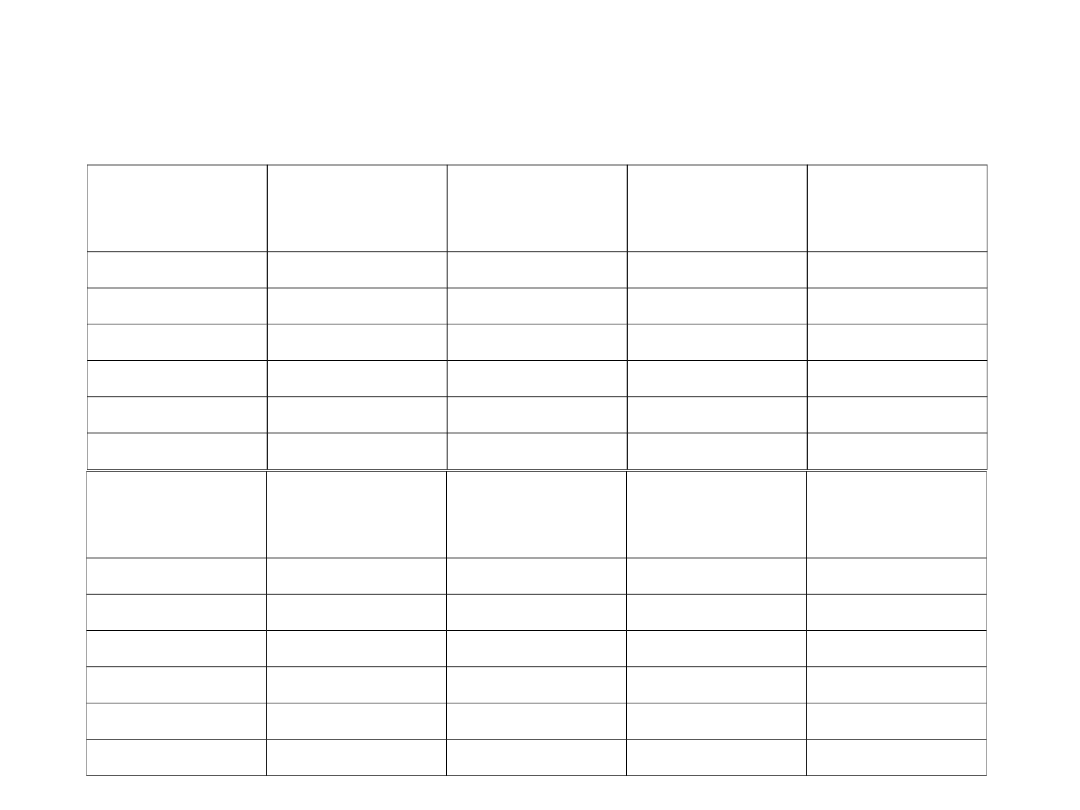
1. MODEL PROGNOZY OPARTY NA REGRESJI LINIOWEJ

x

y







22

,

8

71

,

98

ˆ

Miesiąc

Okres

Popyt

Prognoza

niedostosowan

a

Błąd prognozy

1’ 2009 r.

1

2

2

3

3

4

4

5

5

⁞

⁞

Miesiąc

Okres

Popyt

Prognoza

niedostosowan

a

Błąd prognozy

1’ 2010 r.

13

2

14

3

15

4

16

5

17

⁞

⁞

19

19

2. OBLICZENIE WARTOŚCI POPYT/PROGNOZA

styczeń 2009 r.

styczeń 2010 r.

3. OBLICZENIE MIESIĘCZNEGO WSKAŹNIKA SEZONOWOŚCI

styczeń



1

WS

4. OBLICZENIE PROGNOZY DOSTOSOWANEJ

styczeń 2009 r.

styczeń 2010 r.

DLA POZOSTAŁYCH MIESIĘCY SPOSÓB POSTĘPOWANIA JEST TAKI SAM