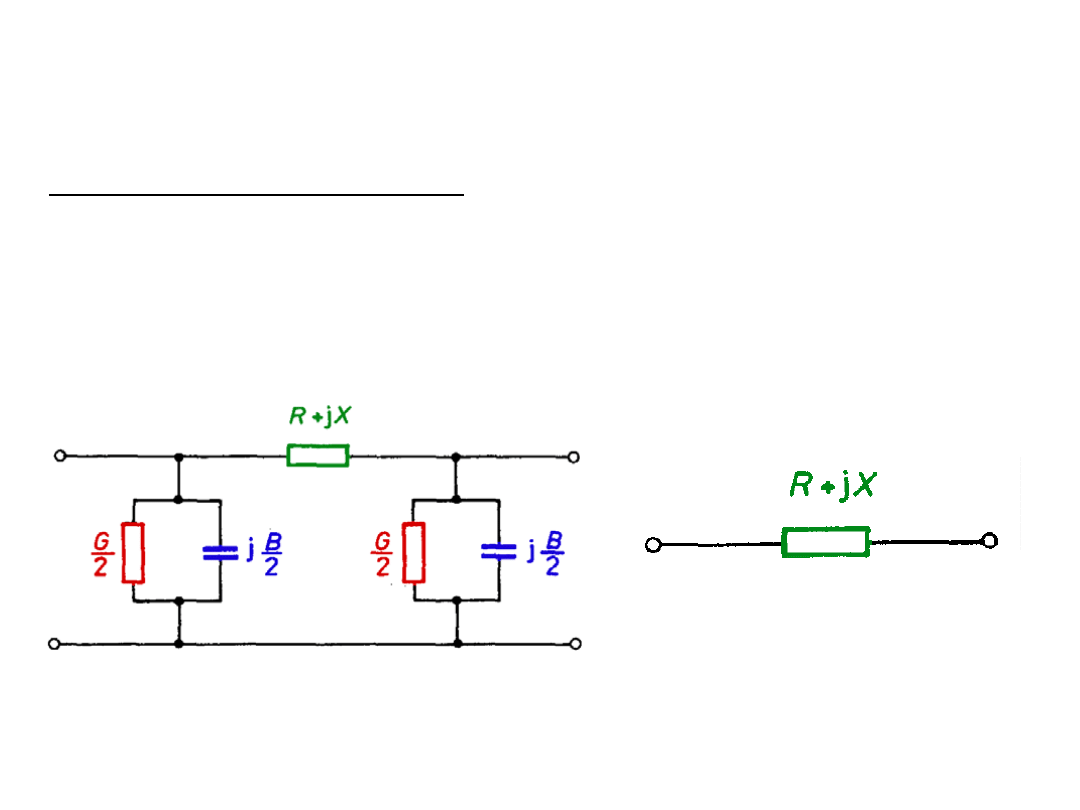
Schematy

Linie elektroenergetyczne

Impedancje i admitancje linii są, rozłożone równomiernie
wzdłuż linii, lecz musimy to uwzględnić jedynie w przypadku
długich linii NN (220kV i 400 kV) i UWN (750 kV).
W większości przypadków posługujemy się schematem
zastępczym w postaci czwórnika typu π lub nawet przy
obliczeniach uproszczonych linii nn, SN i WN schematem w
postaci dwójnika

Schemat zastępczy linii w
postaci czwórników typu π

Schemat zastępczy linii w
postaci dwójnika R, X

Wielkości jednostkowe

Wielkościami charakterystycznymi linii są impedancje i
admitancje
Jednostkowe: R', X', B', G' odniesione do 1 km długości linii.
Impedancje i admitancje całkowite otrzymuje się mnożąc
przez długość:

R = R’l

X = X’l

B = B’l

G = G’l

Rezystancję jednostkową linii odczytuje się z
tablic.
Dla linii napowietrznych z przewodami AFL będzie
to tabl. 5.1, a dla linii kablowych tabl. 5.2.

W przypadku braku tablic można ją obliczyć ze wzoru

gdzie:

γ

-przewodność właściwa materiału przewodowego

s – przekrój przewodu [mm2].

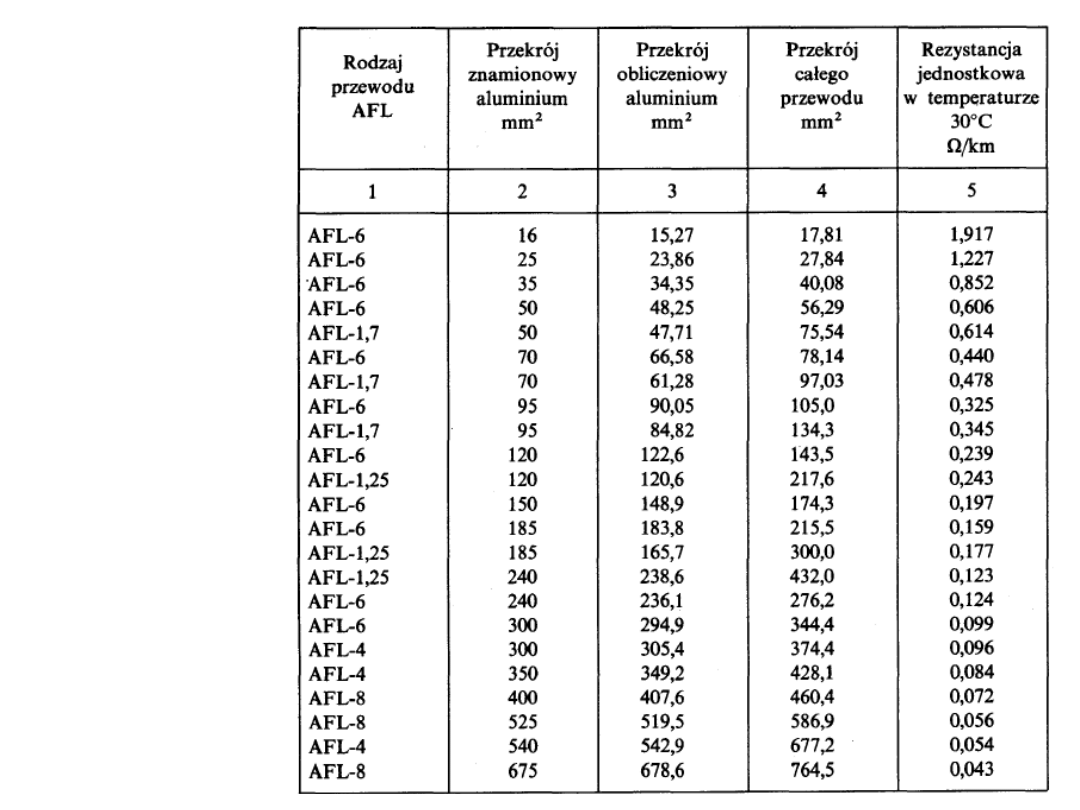
Tablica 5.1.
Rezystancje
jednostkowe R’
przewodów
stalowo-
aluminiowych
AFL

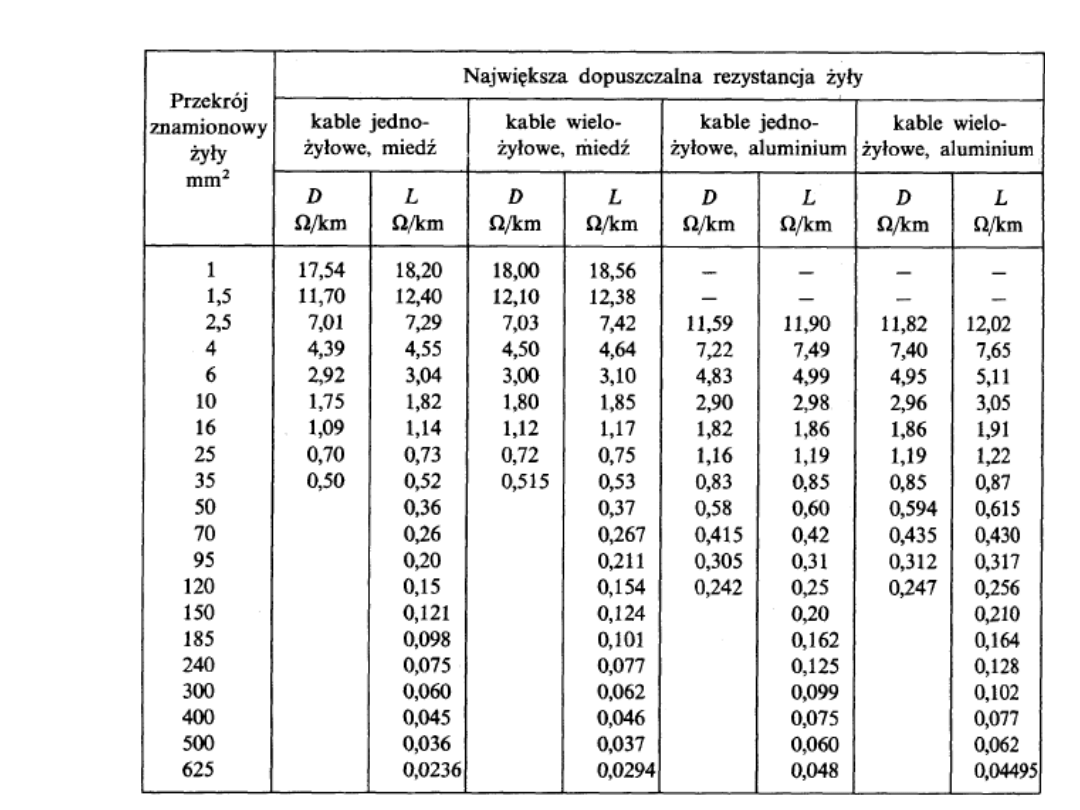
Tablica 5.2. Rezystancje jednostkowe R' linii kablowych

Reaktancja jednostkowa

W praktyce do wyznaczania reaktancji jednostkowych X'
korzystamy z odpowiednich wykresów i tablic.

Reaktancja jednostkowa przewodów linii napowietrznych
zależy od:
- odstępów między przewodami,
- układu przewodów na słupach, ich średnicy,
- konstrukcji przewodów i
- własności magnetycznych materiałów, z których są
wykonane przewody.

Na rys. 5.18 przedstawiono wykresy zmienności
jednostkowych reaktancji indukcyjnych przewodów stalowo -
aluminiowych AFL w linii 3-fazowej jednotorowej w funkcji
odstępu między przewodami.

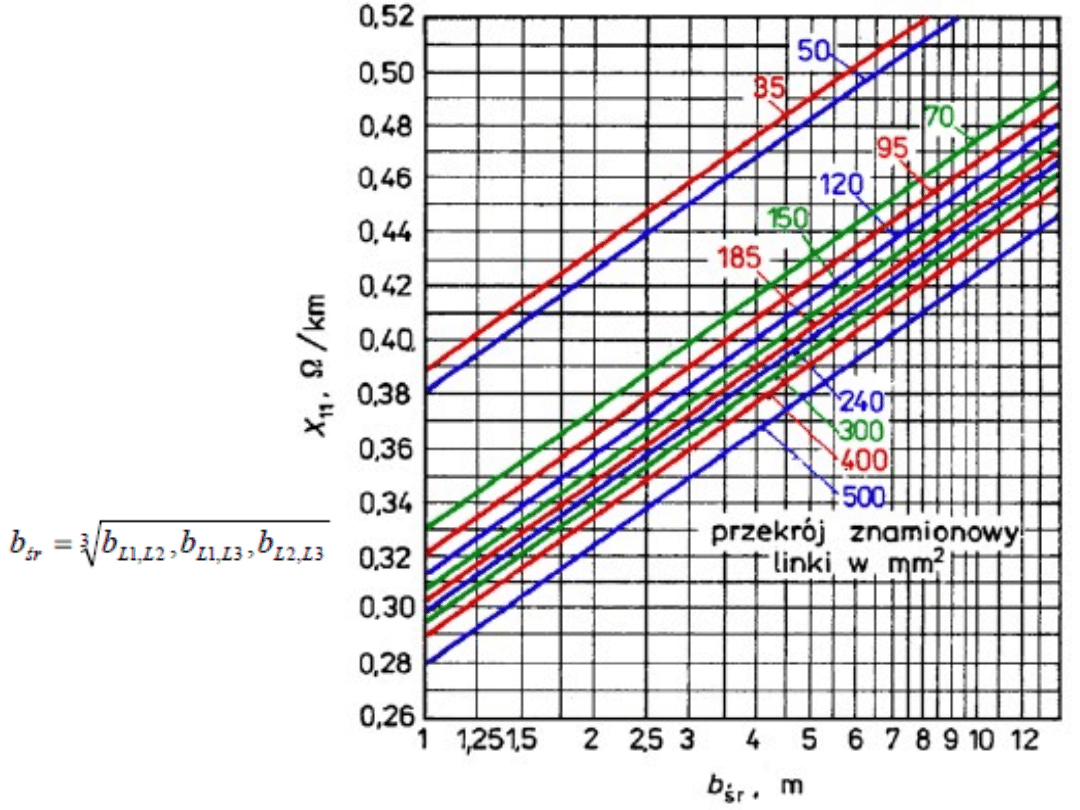
Reaktancje

indukcyjne

przewodów

stalowo-
aluminiowych linii
trójfazowych
jednotorowych w
zależności od
średniego odstępu
między przewodami
przy różnych
przekrojach
znamionowych

gdzie: b

L1,L2

, b

L1,L3

,

b

L2,L3

to odstępy

między
odpowiednimi
przewodami.

Rys. 5.18.

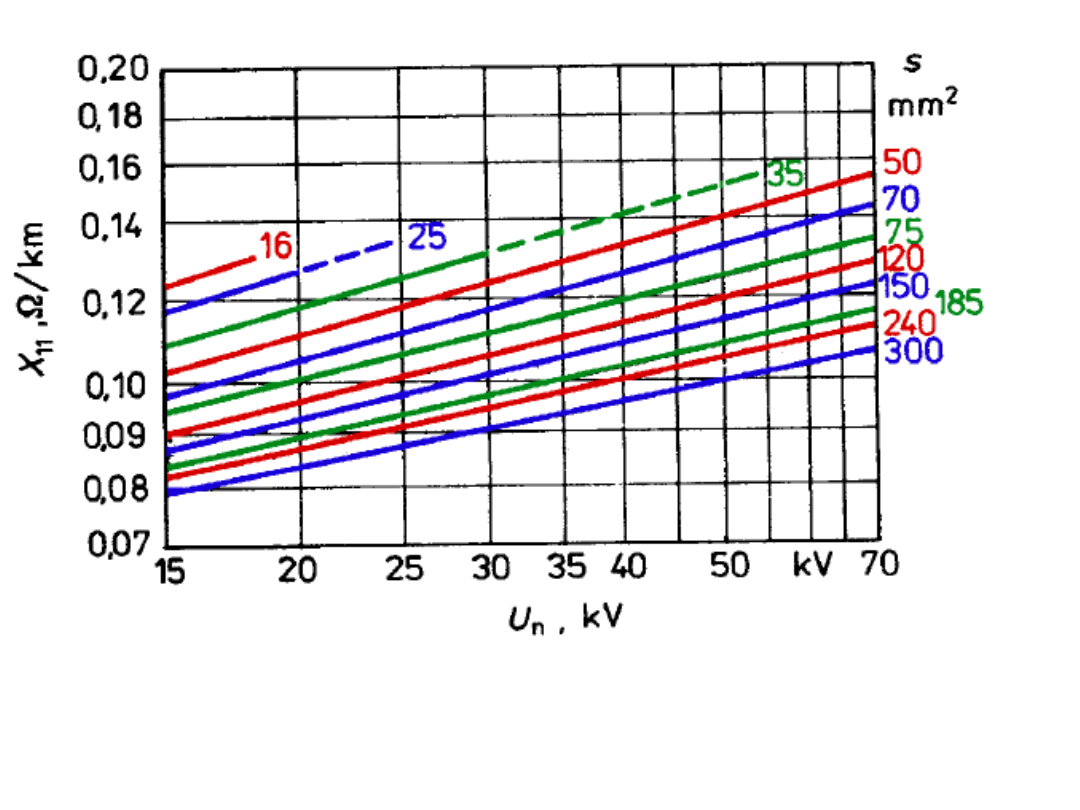
Rys. 5.20. Reaktancje jednostkowe indukcyjne kabli z żyłami ekranowymi

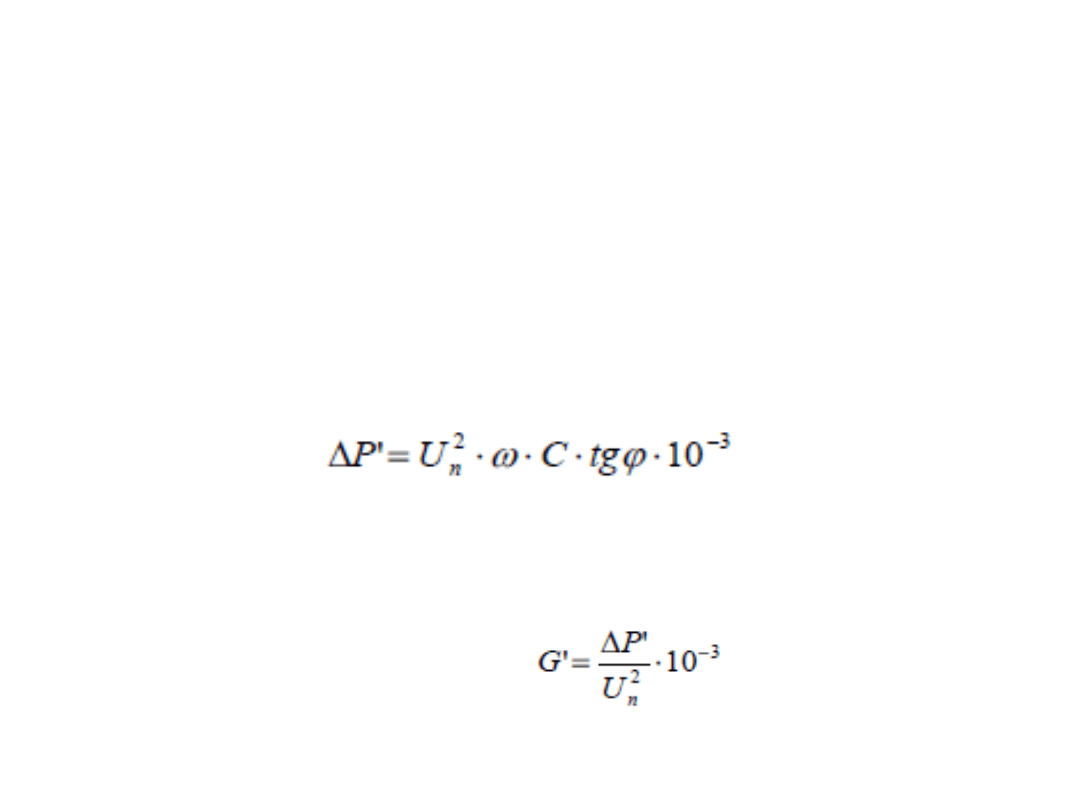
Konduktancja jednostkowa G' linii

Konduktancję G' w liniach napowietrznych wywołaną przez straty
ulotu, na
ogół pomija się.

W liniach kablowych występują straty na skutek jonizacji oraz
histerezy
dielektrycznej. Jonizacja powstaje w kablu wskutek istnienia
pęcherzyków powietrza w izolacji. Straty wskutek histerezy
dielektrycznej powstają przy zmianach natężenia pola elektrycznego.
Dla kabla 3-fazowego określa je wzór

gdzie: C - pojemność robocza żyły linii, tgφ - współczynnik stratności dielektrycznej

Konduktancję oblicza się ze wzoru

Susceptancja pojemnościowa linii B

Przewody wraz ze znajdującymi się między nimi warstwami izolacji
można
traktować jako układ kondensatorów.
Rozróżnia się dwa rodzaje pojemności:
- pojemność roboczą Cr jednej żyły kabla, niezbędną do obliczenia
prądu ładowania linii,
- pojemność dla składowej zerowej C

(0)

jednej żyły kabla,

potrzebną do obliczenia prądów ziemnozwarciowych.

Kable o polu promieniowym

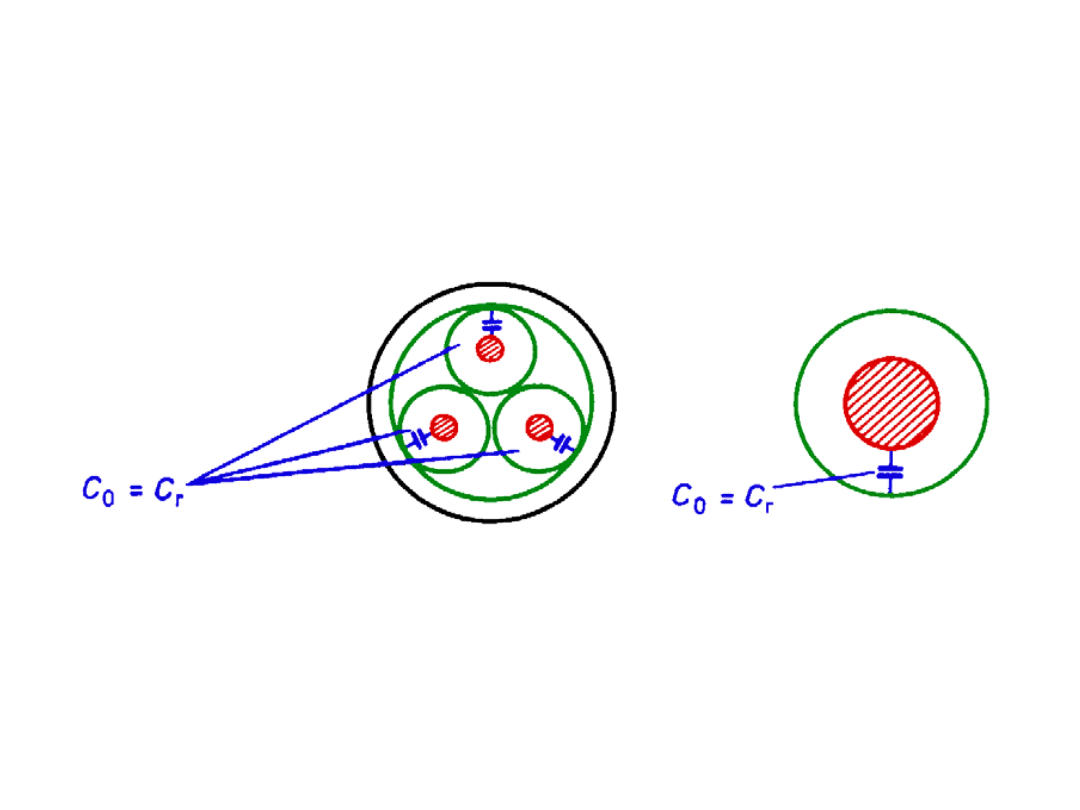
Izolacja żyły kabla o polu promieniowym może być traktowana jak
kondensator cylindryczny (rys. 5.21).
Wartości pojemności tych kabli podano w tabl. 5.3.

kable

Rys. 5.21. Pojemności poprzeczne
kabli o polu promieniowym:
trójżyłowego i
jednożyłowego

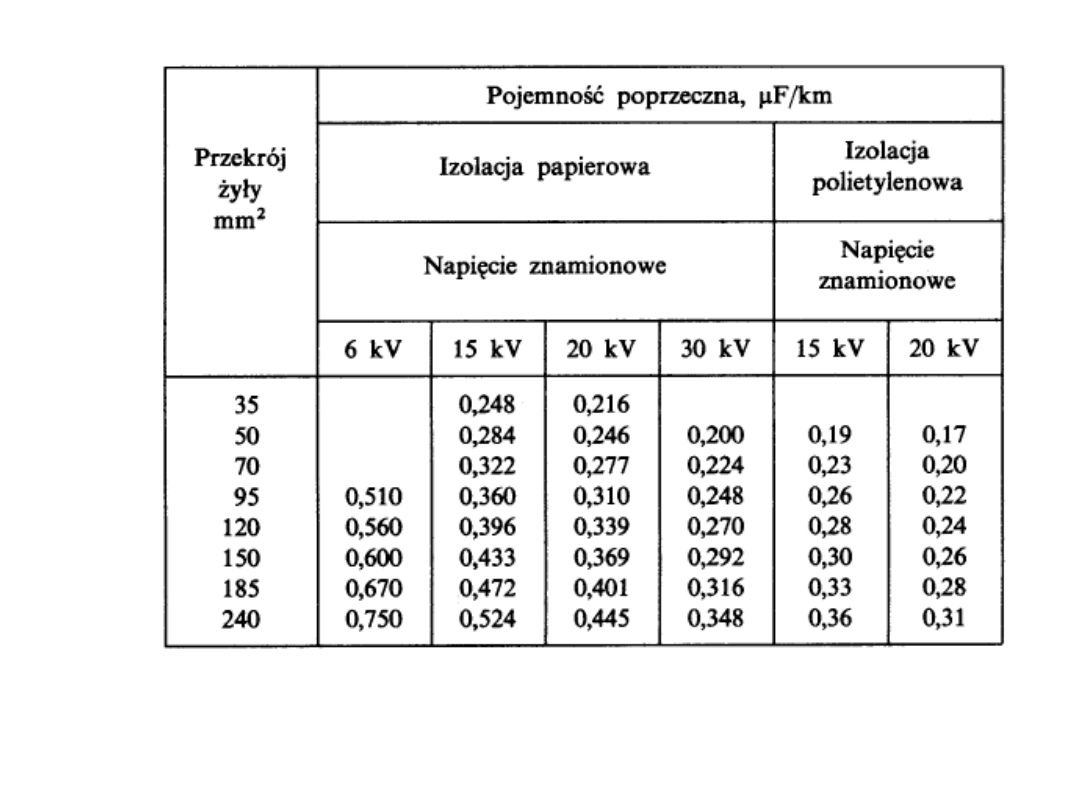
Tabl. 5.3. Pojemności jednostkowe poprzeczne kabli z izolacją promieniową

Pojemności dla składowej zerowej i roboczej kabla o polu
promieniowym są
jednakowe.

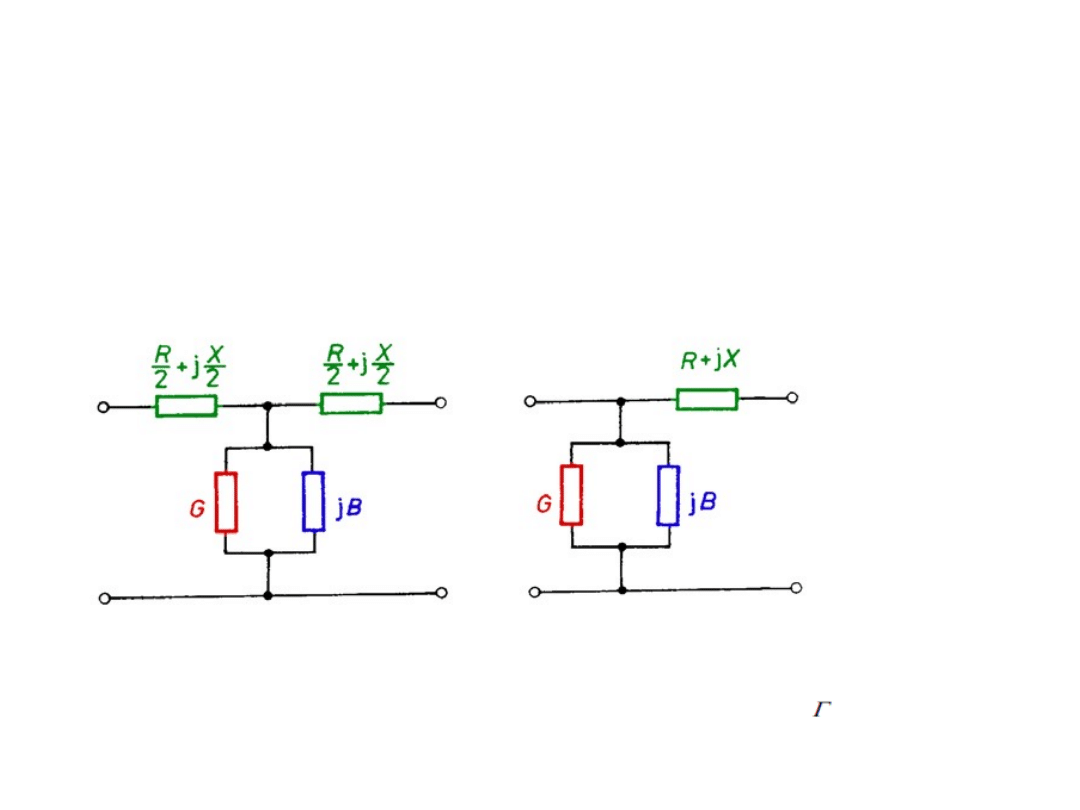
Transformatory

Transformatory dwuuzwojeniowe o górnym napięciu 110 kV i
wyższym przy
dokładnych obliczeniach odwzorowuje się za pomocą czwórników
typu T, lub typu Г (rys. 5.24).

Rys. 5.24. Schematy zastępcze transformatora
dwuuzwojeniowego w postaci czwórników: a) czwórnik typu T,
b) czwórnik typu

Transformatory

Wielkościami podstawowymi dla transformatorów są:
-napięcia znamionowe górne U

rH

i dolne U

rL

,

górne U

ng

i dolne U

nd

-przekładnia znamionowa t

r

, υ

n

-prądy znamionowe: górny I

rH

i dolny I

rL

,

górny I

ng

i dolny I

nd

,

-moc znamionowa S

rT

,

-napięcie zwarcia u

kr

,

-straty mocy czynnej w uzwojeniach P

krT

,

-straty mocy w rdzeniu transformatora P

Fe

oraz

-prąd biegu jałowego i

0

.

W obliczeniach sieciowych posługujemy się całkowitą rezystancją
R

T

i

całkowitą reaktancją X

T

transformatora, w zależności od

przyjętego napięcia odniesienia

R

g

= R

d

υ

n

2

X

g

= X

d

υ

n

2

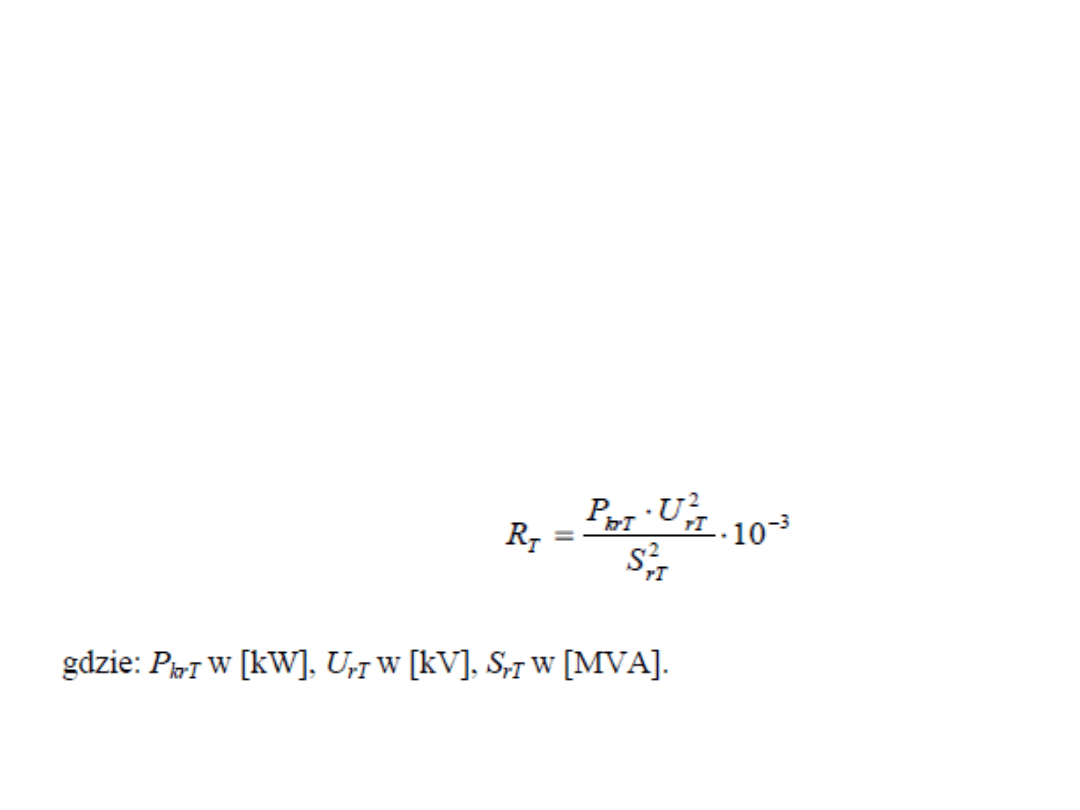
Transformatory

Wyznaczanie parametrów transformatora:

Rezystancję R

T

wyznacza się ze wzoru

Transformatory dwuuzwojeniowe przy mniej
dokładnych obliczeniach oraz transformatory o
napięciu górnym niższym od 110 kV odwzorowuje się
jako dwójniki R , X.

reaktancja

Przy czym

Konduktancja, susceptancja

Konduktancję odwzorowującą straty mocy czynnej w
rdzeniu transformatora oblicza się ze wzoru

Susceptancję wyznacza się ze wzoru
przybliżonego

Dławiki zwarciowe

Dławiki zwarciowe są produkowane o napięciach zwarcia 3% i 15%
oraz prądzie znamionowym do 2000 A. Stosuje się je w sieciach o
napięciach 6 i 20 kV i niekiedy 30 kV.
Rezystancja dławika stanowi zaledwie około 1% reaktancji
indukcyjnej dławika i praktycznie może być w obliczeniach
pomijana.
W związku z tym dławik odwzorowuje się jako dwójnik o reaktancji
X

R

Rys. 5.25. Schemat
zastępczy dławika
zwarciowego

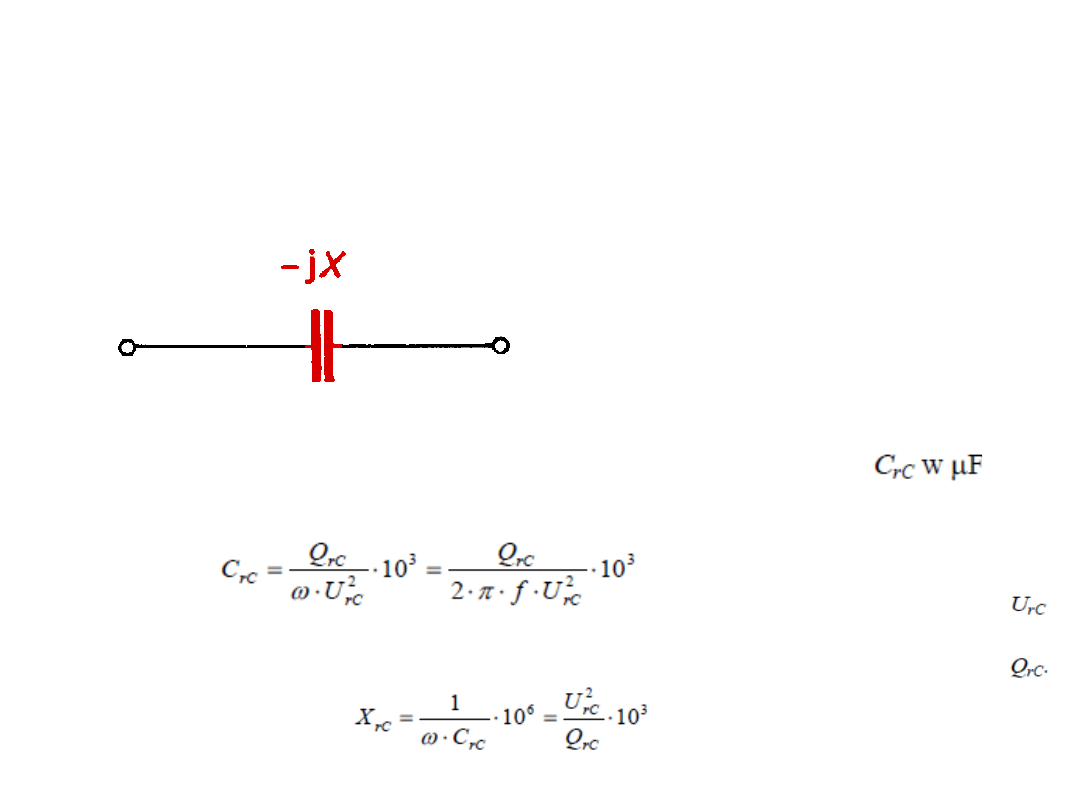
Kondensatory

Rezystancja kondensatora stanowi zaledwie 2‰ do 5‰ reaktancji
pojemnościowej i praktycznie może być w obliczeniach pomijana. W
związku z tym kondensator odwzorowuje się jako dwójnik o
reaktancji X

C

Schemat zastępczy kondensatora

Wielkościami podstawowymi dla kondensatora są: napięcie
znamionowe U

rC

i

moc znamionowa Q

rC

. Często podaje się pojemność znamionową

, którą przy mocy znamionowej w kvar i napięciu w kV można
wyznaczyć ze wzoru

Reaktancję oblicza się ze wzoru

Zadania

Zadania

Zadania