WYKŁAD 10 Drzewa Binarnych

Poszukiwań

Grażyna Mirkowska

Plan wykładu



Drzewa BST

–

Wyszukiwanie w BST

–

Koszt utworzenia drzewa BST

–

Wstawianie do BST

–

Usuwanie elementu z drzewa
BST

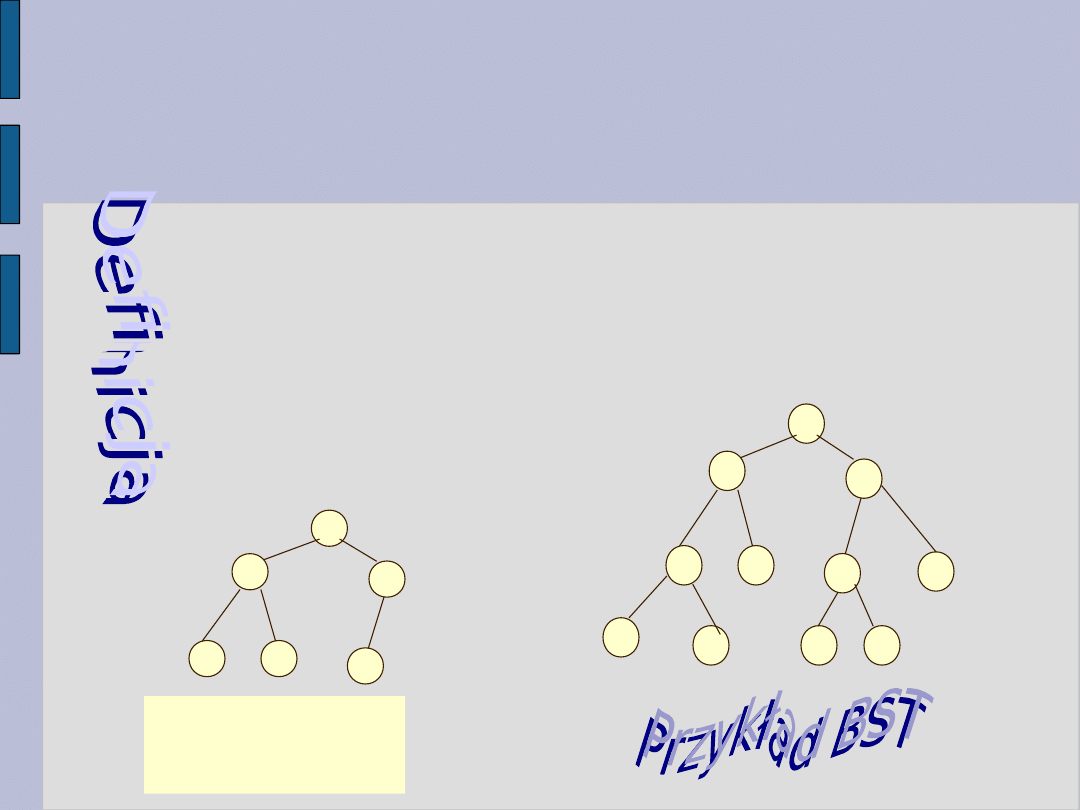
Drzewo binarnych poszukiwań

BST

Niech <ET,  > będzie niepustym, liniowo

uporządkowanym zbiorem. Drzewem binarnych
poszukiwań nazywamy etykietowane drzewo binarne
z wyróżnionym korzeniem D= <V, E, et> takie, że
et :V-> ET jest funkcją różnowartościową oraz dla
każdego wierzchołka v V,
(1) jeśli x  LD(v), to et(x) et(v)
(2) jeśli x  PD(v), to et(v)  et(x).

7

9

8

5

6

3

6

10

8

4

2

5

1

3

7 9

11

To nie jest
BST

Operacja wyszukiwania w BST

Rozpoczynając od korzenia, porównujemy
etykietę wierzchołka x z wyszukiwanym
elementem e.

Zbadać, czy element e należy do
zbioru etykiet drzewa D.

Member(D,e) wttw (xD.V) et(x) =

e

e<
x.et

Szukaj e w prawym
poddrzewie wierzchołka x

Szukaj e w lewym
poddrzewie x

x.et<
e

x.et=
e

Specyfikacja

Specyfikacja

Algorytm Wyszukiwania

{

bool := false;
while (not empty(x) and not
bool)
do
if x.e = e then bool :=
true
else
if x.e < e then
x := x.prawy
else
x := x.lewy
f
f
od;
return bool;
}

Jeżeli wartością zmiennej x
jest korzeń drzewa D, to
algorytm member zatrzymuje
się po skończonej liczbie
kroków oraz końcowa wartość
bool jest równa true wttw,
gdy e jest jedną z etykiet
drzewa D.

member : BST

member : BST





ET

ET





Bo

Bo

Przykład

6

10

8

4

2

5

1

3

7

9

11

Szukam
3

Szukam
8.5

pokaz

Koszt operacji member

Operacja dominująca = porównywanie

Operacja dominująca = porównywanie

elementów.

elementów.

Niech n = card(D.V). Ponumerujmy etykiety drzewa
liczbami naturalnymi 1,2,...,n i załóżmy, że
prawdopodobieństwo tego, że w korzeniu jest i-ta
etykieta (lub po prostu liczba i) wynosi 1/n.

A(n) średnia liczba
porównań dla
znalezienia elementu
e.

A(n) =



n

i=1

1/n (

średnia liczba porównań dla

znalezienia elementu e, o ile etykietą korzenia jest i

)

W(n) = O(n)

Prawdopodobieństwo tego, że

korzeniem drzewa jest i

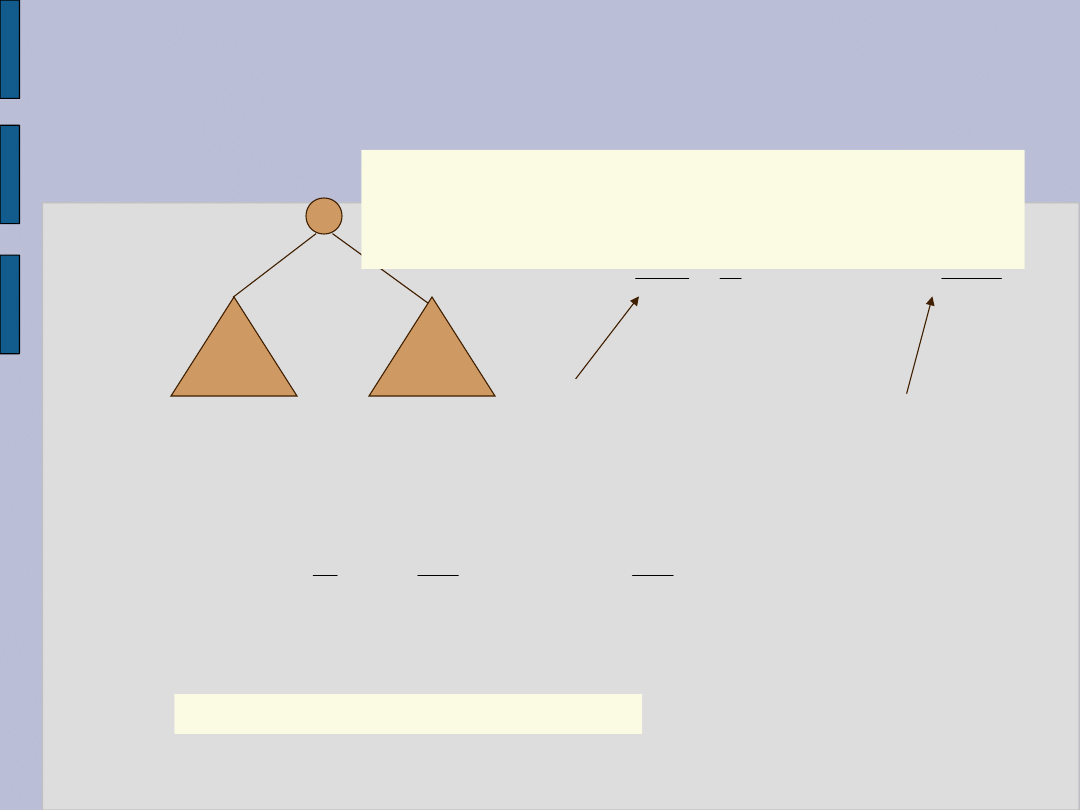
Cd. Koszt średni wyszukiwania

i

LD

LD

PD

PD

i-1
elem.

n-i
elem.

n

i

n

i

n

A

n

n

i

i

A

















)

1

)

(

(

1

1

)

1

)

1

(

(

Prawdopodobień
stwo tego, że e
jest w lewym
poddrzewie

Prawdop
odobieńst
wo tego,
że e jest
w
prawym
poddrzew
ie

Średnia liczba porównań potrzebna do
znalezienia elementu e w drzewie o
korzeniu i :

























1

1

2

1

1

2

1

)

(

2

1

)

(

2

1

1

)

(

n

i

n

i

n

i

i

iA

n

i

iA

n

n

n

A

Można pokazać przez
indukcję, że

stala

k

n

k

n

A





,

lg

)

(

Dowód w komentarzu do strony!

Operacja minimum w BST

Zadanie

Zadanie

Znaleźć etykietę o

najmniejszej wartości, w zbiorze
etykiet danego drzewa D.

Zejdź po ścieżce od
korzenia do liścia,
wybierając zawsze drogę w
lewo, o ile to możliwe.

public min (node x)
{
while (not x.lewy=
null)
{ x := x.lewy}
return x.e;
}

W(n) = O(n)

A(n) = O(lg n)

min: BST

min: BST





ET

ET

Wstawianie elementu do drzewa

BST

insert : BST

insert : BST





ET

ET





BST

BST

Rozpoczynając od korzenia drzewa D
przeglądamy wierzchołki tak, jak w operacji
wyszukiwania: Jeśli znajdziemy wierzchołek z
etykietą e, to wynikiem operacji jest dane drzewo
D. Jeśli nie, to zapamiętujemy ostatni wierzchołek
v, do którego doszliśmy w trakcie poszukiwań e,
tworzymy nowy wierzchołek z etykietą e i
dowiązujemy go

1. jako lewego syna wierzchołka v, gdy e< et(v) i
LP jest puste lub
2. jako prawego syna v, gdy et(v)< e, oraz PD
jest puste.

Zadanie

Zadanie

Do zbioru reprezentowanego przez

drzewo D dołączyć element e, o ile nie należy on
jeszcze do etykiet drzewa D.

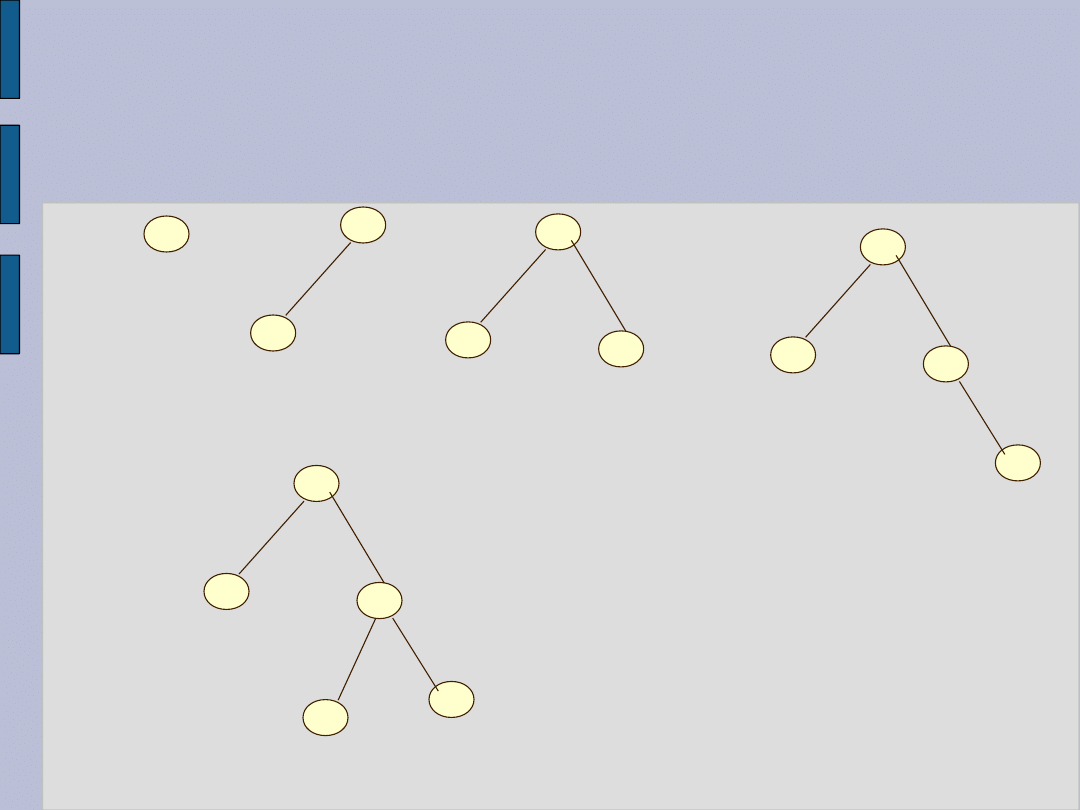
Przykład

6

6

5

6

5

9

6

5

9

12

6

5

9

12

8

Dodaj 5

Dodaj 9

Dodaj 8

Dodaj

12

Algorytm wstawiania

{

bool := false;

x:= root ;
while not bool {
if x.et= e then bool := true
else
if (e < x.et) then
if ( x.lewy <>null) then x :=
x.lewy
else y := New node(e);
x.lewy := y;
bool := true
f
else {//analogicznie dla prawego

//poddrzewa}

f
f }}

Algorytm insert
zatrzymuje się
dla wszystkich
danych
początkowych.
Otrzymane w
wyniku drzewo
ma w zbiorze
swoich etykiet e.

A(n) = O(lg n)

Koszt utworzenia drzewa BST

UWAGA

Koszt utworzenia i struktura drzewa

zależą od kolejności wkładanych elementów.

W(n) = O(n

2

)

Średni koszt utworzenia
drzewa BST o n
wierzchołkach wynosi O(n
lg n),

por. uzasadnienie

.

Najgorszy przypadek =

wkładane elementy tworzą

ciąg uporządkowany

9

8

7

6

Koszt utworzenia c.d.

Niech wkładane do drzewa elementy będą
permutacją liczb 1...n i niech prawdopodobieństwo
tego, że i-tym elementem jest k będzie takie samo dla
wszystkich k=1,2,...n.

i

LD

LD

PD

PD

)

(

1

)

(

1

poddrzew

utworzenia

koszt

n

n

A

n





))

(

)

1

(

)

(

)

1

(

(

1

)

(

1

i

n

i

i

n

A

i

A

n

n

A

n



















Każdy wkładany element
jest porównywany z
korzeniem









n

i

A

n

n

n

A

1

)

(

2

1

)

1

(

)

(

Stąd
A(n)  k * n *lg

n

Operacja usuwania elementu

delete : BST

delete : BST





Et

Et





BST

BST

(1) Znajdujemy wierzchołek x o etykiecie e
stosując algorytm member i zapamiętujemy
jego ojca y.

(2) Dalsze postępowanie zależy od liczby
następników x:
- Usuwamy wierzchołek x, jeśli jest on liściem.
- Zastępujemy wierzchołek x jego następnikiem,
jeśli x ma tylko jednego syna.
- Zastępujemy etykietę wierzchołka x,
najmniejszą etykietą w jego prawym
poddrzewie (lub największą w jego lewym
poddrzewie), a wierzchołek o tej etykiecie
usuwamy z drzewa, stosując zasadę (1) lub(2).

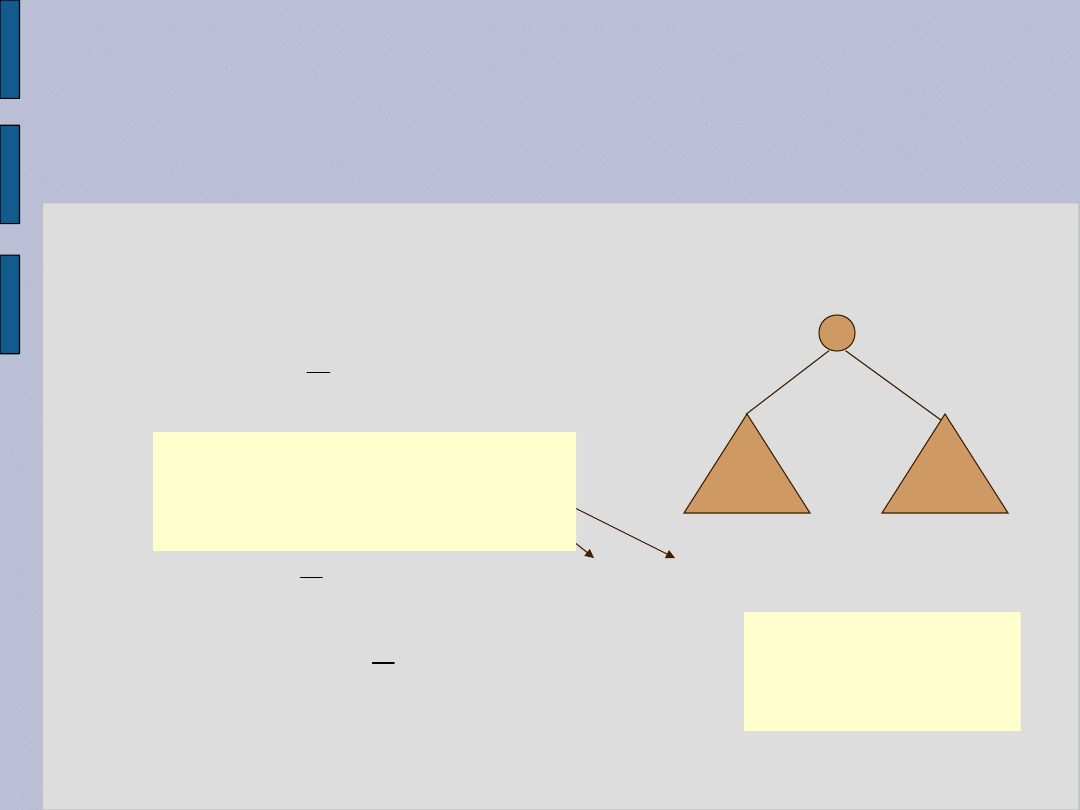
Usuwanie - ilustracja 1

1 Przypadek : x nie ma synów, tzn. jest
liściem (rz(x)=0)

Usuwamy

Usuwamy

wierzchołek x.

wierzchołek x.

y

PD

y

x

PD

y

x

LD

y

LD

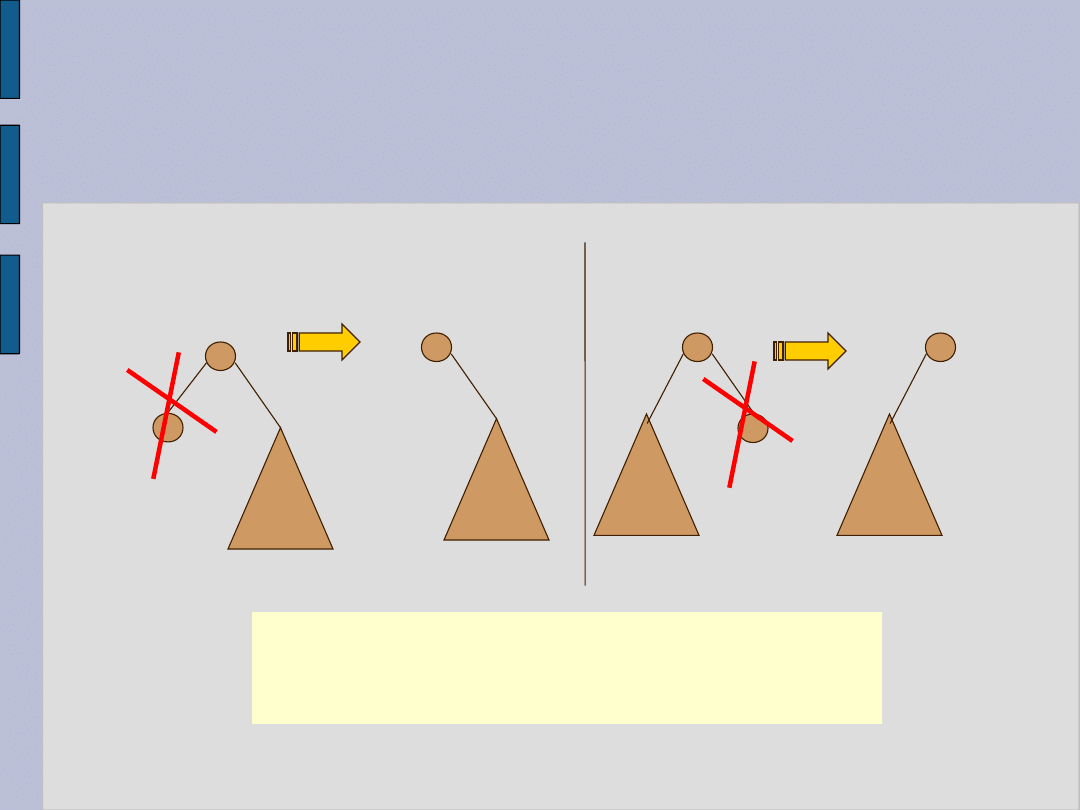
Usuwanie - ilustracja 2

2. Przypadek : x ma jednego syna, tzn.
rz(x) = 1.

Usuwamy

Usuwamy

wierzchołek x.

wierzchołek x.

y

x

PD

LD(x)

y

LD(x)

PD

Postępowanie jest analogiczne, gdy x ma tylko
prawego syna.

y.lewy :=
x.lewy;

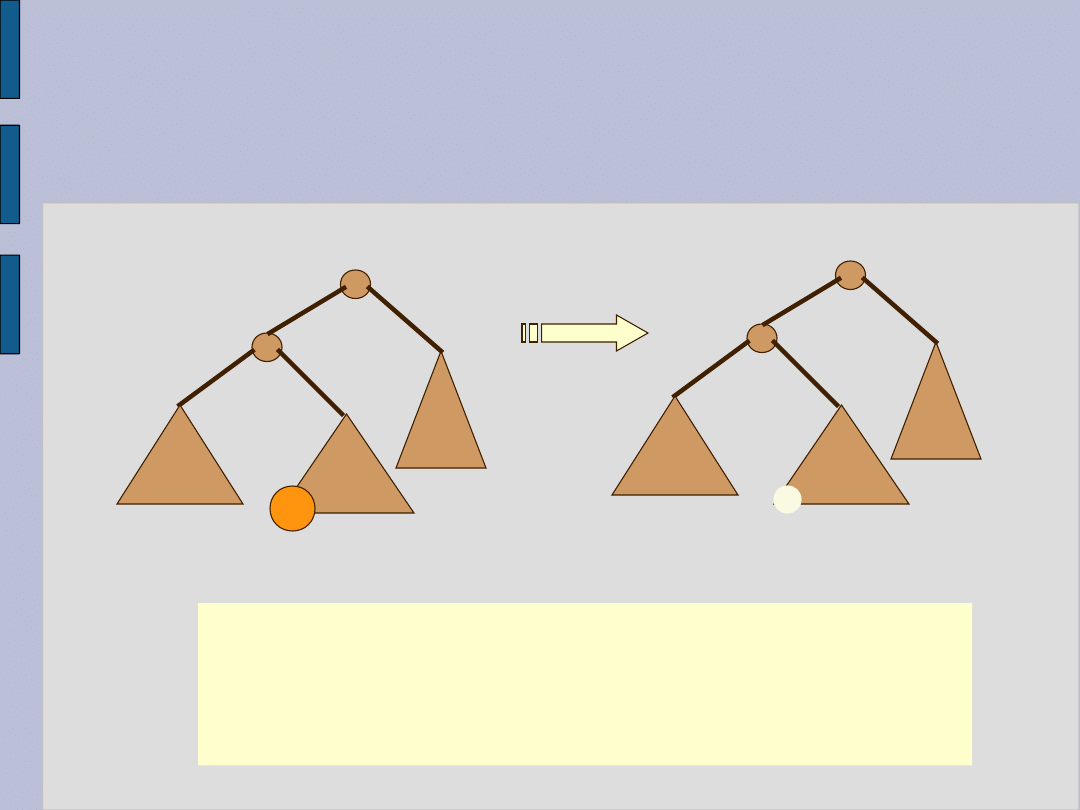
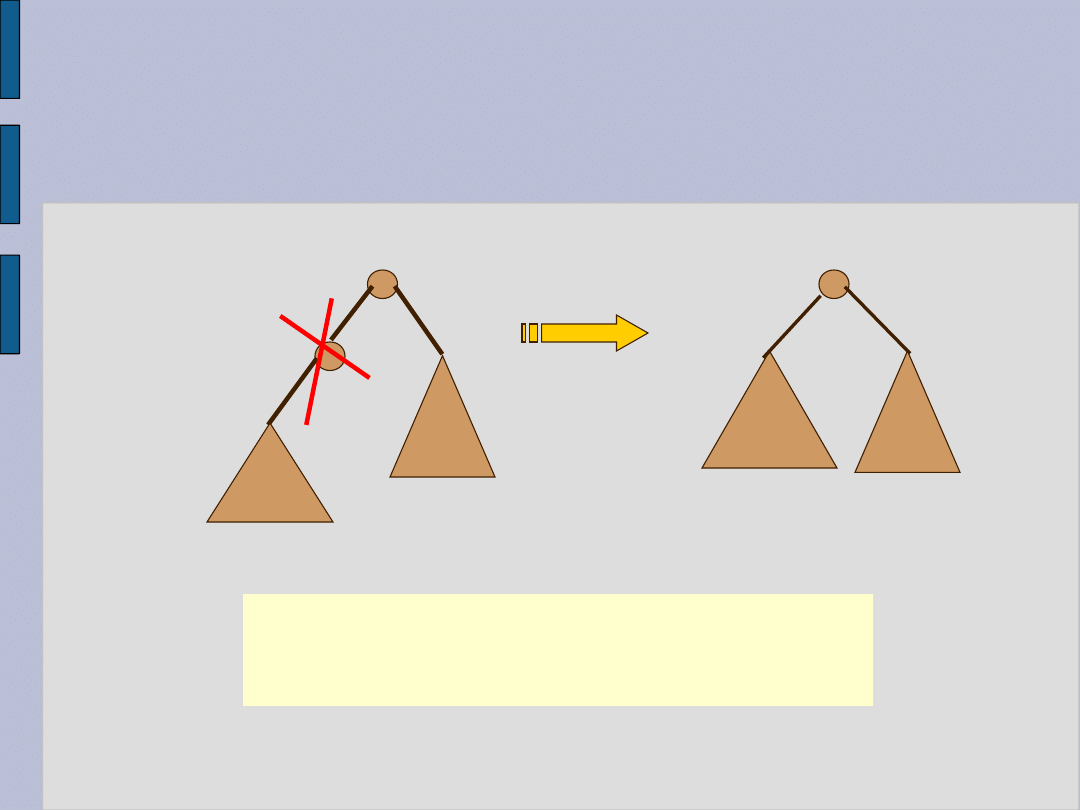
Usuwanie - ilustracja 3

Zastępujemy wierzchołek x

Zastępujemy wierzchołek x

jego bezpośrednim następnikiem w

jego bezpośrednim następnikiem w

drzewie .

drzewie .

3. Przypadek : x ma dwóch synów, tzn.
rz(x) = 2.

y

x

PD

LD(x)

PD(x)

z

y

x

PD

LD(x)

PD’(x)

Et(x)=Et(
z)

z := min(PD(x)); Et(x) := et(z); x.prawy:=
delete(PD(x), et(z));

Zastosowanie: wyszukiwanie i

sortowanie

Zadanie A

Dany jest zbiór n elementów

należących do pewnej liniowo
uporządkowanej przestrzeni. Zbadać, czy
dany element należy, czy nie należy do tego
zbioru.

Zadanie B

Dany jest zbiór n elementów

należących do pewnej liniowo
uporządkowanej

przestrzeni.

Uporządkować elementy tego zbioru w
porządku niemalejącym.

•

w tablicy

• z użyciem listy
dynamicznej

• z użyciem
drzewa BST

1.Zbudować

drzewo BST,

2.Odczytać jego

wierzchołki w
porządku
inorder
(infxowym)