1

POMIAR MOCY CZYNNEJ I 

BIERNEJ ODBIORNIKÓW 

TRÓJFAZOWYCH

        

prof. dr hab. inż. T. Niedziela

2

Pomiar mocy czynnej  

odbiorników trójfazowych

3

Do pomiaru 

mocy czynnej

 (

P

) w układach 

trójfazowych są stosowane watomierze.

 

Watomierz ma dwa uzwojenia: uzwojenie 

napięciowe, zwane często cewką napięciową, i 

uzwojenie prądowe, zwane cewką prądową.

4

Początki uzwojenia prądowego i napięciowego, 

powinny być ze sobą połączone ( zwarte) .

Sposób dołączenia cewki prądowej i cewki 

napięciowej watomierza wynika ze wzorów na 

moc czynną

 układu trójfazowego. 

5

    

Jeśli przykładowo chcemy zmierzyć 

moc czynną

 (

P

) 

pobraną przez fazę A odbiornika trójfazowego 

połączonego np. w gwiazdę, to zgodnie ze wzorem.

                          

P

A

  = U

A

 I

A

 cos φ

A

 
   

włączamy cewkę prądową  tak, aby przez nią 

płynął 

prąd fazowy I

A

 , a cewkę napięciową 

włączamy tak, aby na zaciskach cewki 

występowało 

napięcie fazowe U

A

 odbiornika. 

6

  
   

Obecnie zilustrowane zostaną 

schematy układów pomiarowych i 
wzory na moce odbiorników.

7

Pomiar mocy czynnej  

odbiorników 

niesymetrycznych

8

W układach trójfazowych czteroprzewodowych 
niesymetrycznych (Z

A

, Z

B

, Z

C

 ) do pomiaru 

mocy czynnej (P) stosujemy 3 watomierze . 

Każdy watomierz mierzy moc pobieraną przez 
odpowiednią fazę odbiornika.

Dodajemy więc uzyskane wskazania

 

i 

otrzymujemy wartość mocy pobieranej przez 
cały odbiornik.

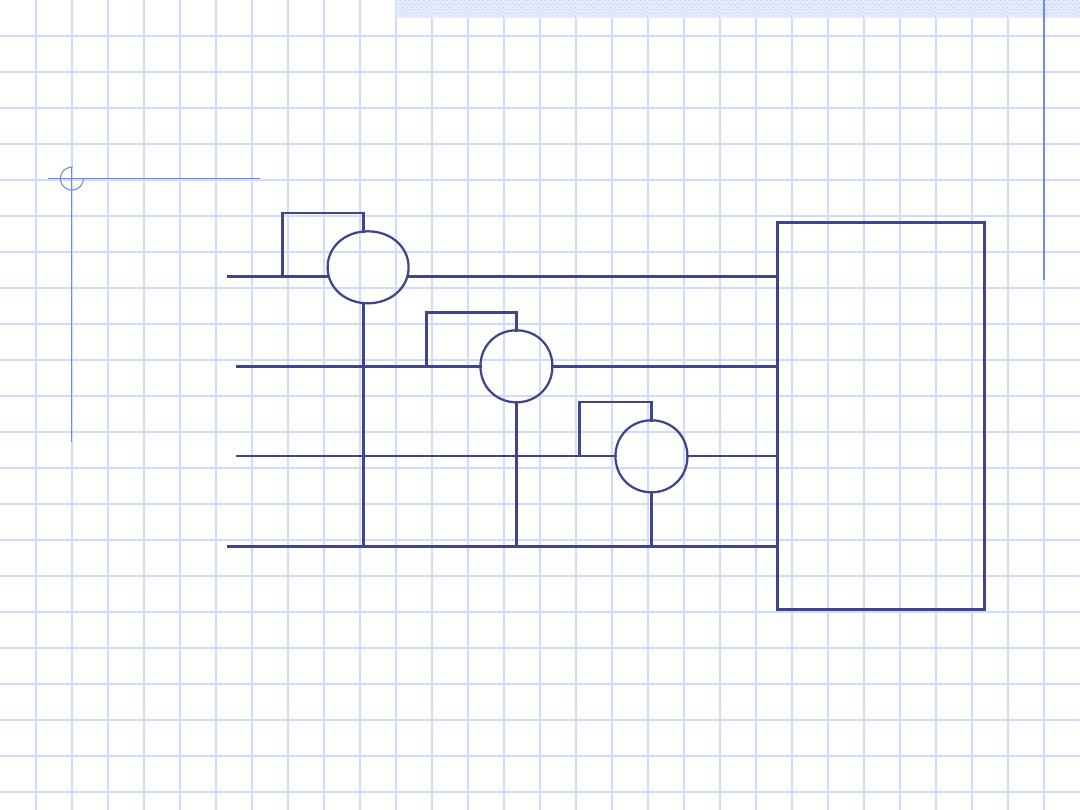
9

a)

Odbiorni

k 

niesyme-

tryczny 

czteroza-

ciskowy

W

1

W

2

W

3

L1

L2

L3

N

P = P

W1

 + P

W2

 + P

W3

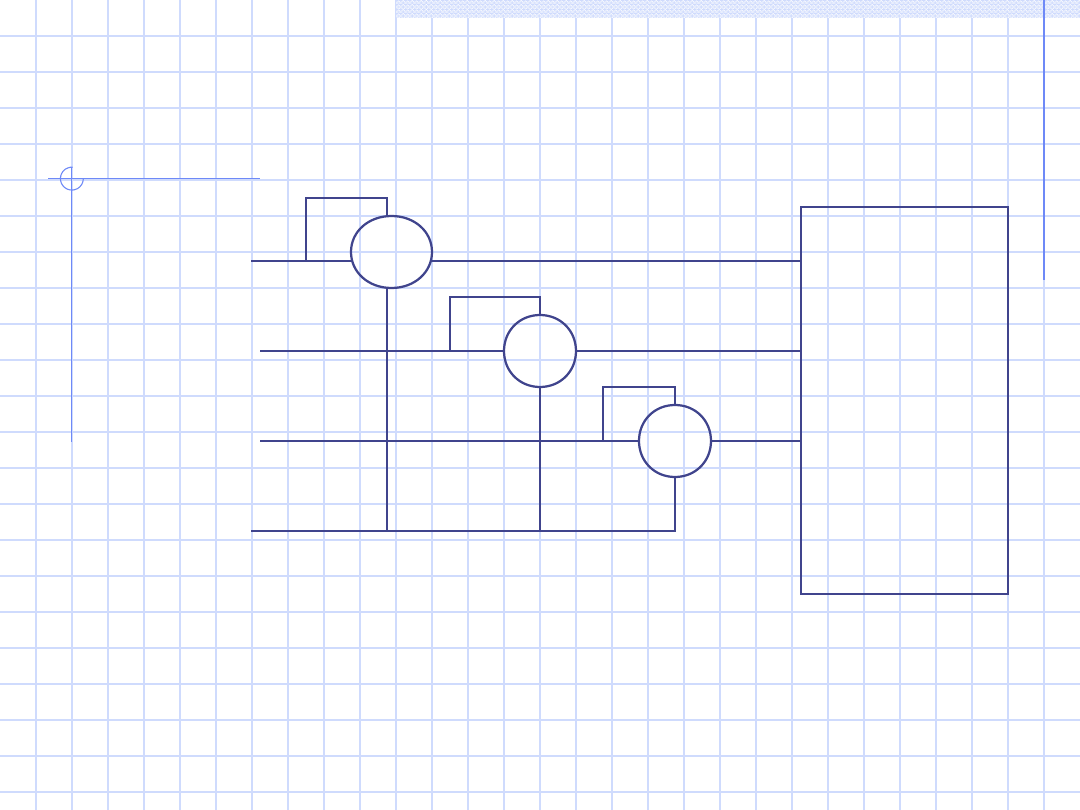
10

b1)

Odbiorni

k 

niesyme-

tryczny 

trzy-

zaciskow

y

W

1

W

2

W

3

L1

L2

L3

N

P = P

W1

 + P

W2

 + P

W3

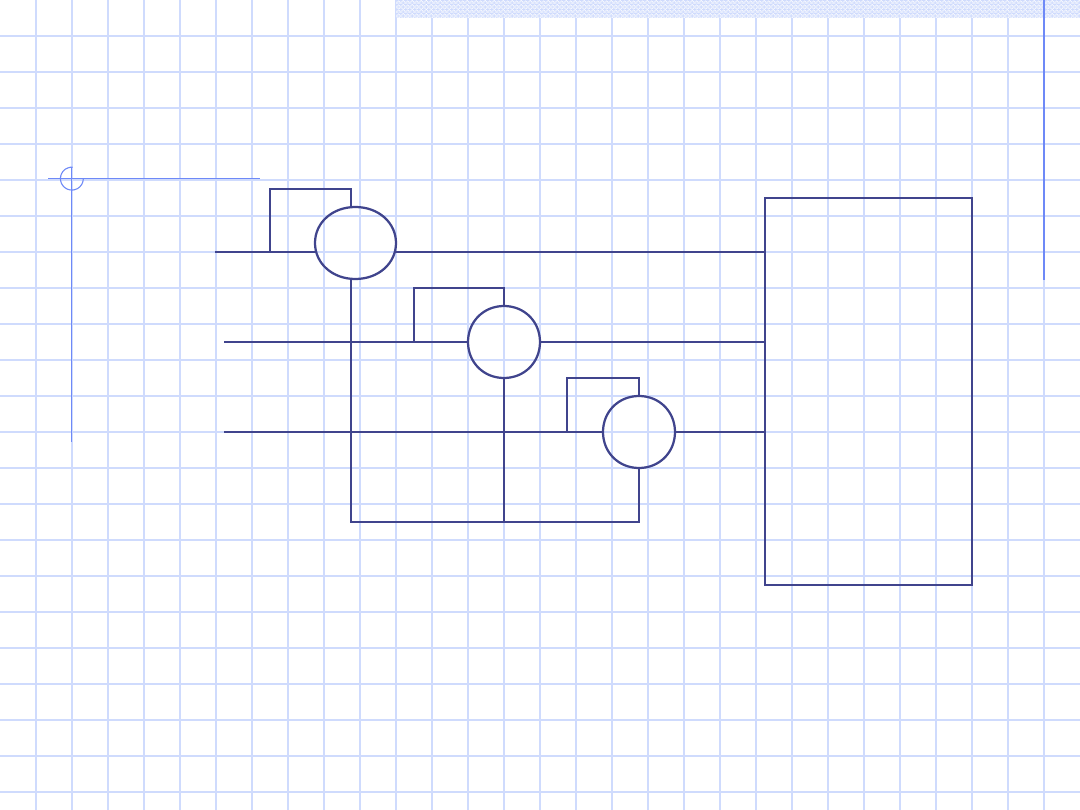
11

b2)

Odbiorni

k 

niesyme-

tryczny 

trzy-

zaciskow

y

W

1

W

2

W

3

L1

L2

L3

P = P

W1

 + P

W2

 + P

W3

12

   

Metodę dwóch watomierzy

 

stosuje się 

zarówno do pomiaru

 

mocy układów 

trójprzewodowych niesymetrycznych

 

(Z 

A

, 

Z

B

, Z

C

), 

   

jak i symetrycznych

 

(Z 

A

 = Z

B

 = Z

C

 = Z). 

   

Jest ona obecnie bardzo 

rozpowszechniona. 

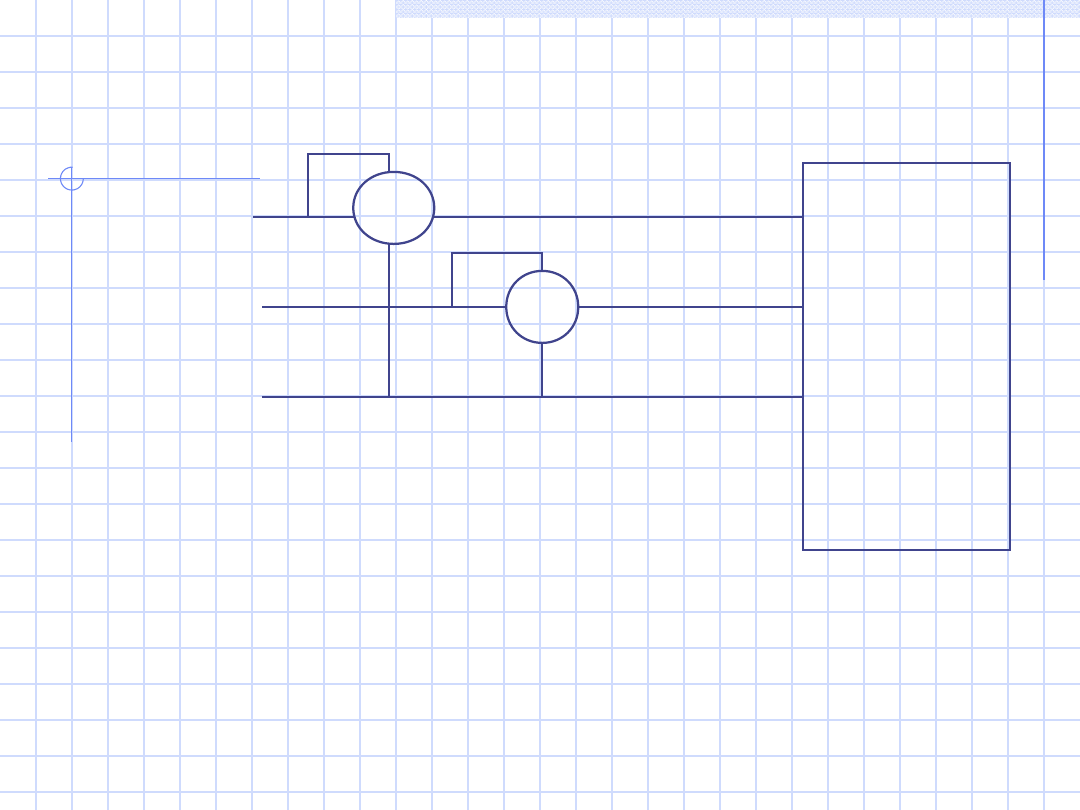
13

c)

Odbiorni

k 

niesyme-

tryczny 

trzy-

zaciskow

y

W

1

W

2

L1

L2

L3

(układ Arona)

P = P

W1

 + P

W2

 

14

Dla wyjaśnienia sposobu podłączenia watomierzy 

posłużymy się wzorem na

 

moc pozorną zespoloną

.

 

S = U

A

  I

A

 * + U

B

  I

B

* +U

C

 I

C

 * 

W układach trójfazowych trójprzewodowych

, 

zarówno symetrycznych jak i niesymetrycznych,

 

suma prądów przewodowych

 

jest równa zero,

  I

A

  + I

B

 + I 

C

= 0 

15

Jest oczywiste, że również

 

suma prądów przewodowych sprzężonych 

jest równa zero,

 czyli                       I

A

* 

+ I

B

* 

+ I

C

* 

= 0 

 Z równania powyższego otrzymujemy

                             I

C

* 

= - ( I

A

*  

+  I

B

*

) 

po podstawieniu 

moc pozorna

 

S

S = U

A

 I

A

* 

+ U

B

 I

B

* 

- U

C 

( I

A

* 

+ I

B

*

) = 

( U

A 

– U

C 

) I

A

* 

+ ( U

B 

– U

C 

) I

B

* 

= U

AC  

I

A

*

+ U

BC  

I

B

* 

= P + jQ  

gdyż

 

napięcia międzyfazowe

              

U

AC 

= U

A 

– U

C 

;    U

BC 

= U

B 

– U

C 

16

Ponieważ

 

moc czynna

 

(P)

 

jest częścią rzeczywistą mocy 

pozornej zespolonej, zatem dla odbiornika
 

P = U

AC  

I

A 

cos  φ

A

 + U

BC  

I

B  

cos φ

B 

= P

1

 + P

2

Stąd dwa watomierze W

1

 i W

2

 należy dołączyć tak, jak na to 

wskazują indeksy przy 

napięciach międzyfazowych

 (U

AC

, 

U

BC

) i 

prądach przewodowych

 (I

A

, I

B

), a mianowicie:

•

 

watomierz pierwszy musi mieć cewkę prądową dołączoną 

do fazy A, a cewkę napięciową miedzy fazą A i  fazą C

•

wwatomierz drugi musi mieć cewkę prądową dołączoną do 

fazy B, a cewkę napięciową  między fazą B i fazą C.

17

Istnieją jeszcze dwa inne warianty dołączania 

watomierzy związane z wyeliminowaniem 

odpowiednio prądu I

B

 oraz I

A

  (

proszę przećwiczyć 

w ramach pracy własnej

).

W każdym jednak przypadku zasada dołączania 

watomierzy jest jednakowa: 

    cewki prądowe są dołączone do dwóch 

przewodów fazowych a końce cewek napięciowych 

są dołączone do trzeciej wolnej fazy. 

18

    

Zatem sumie wskazań watomierzy w układzie 

Arona odpowiada moc czynna pobierana przez 

odbiornik 

 

P = P

W1

 + P

W2

 

    

Nie jest przy tym ważne, jak w rzeczywistości 

połączone są ze sobą elementy odbiornika, 

albowiem trójfazowy odbiornik o dowolnym 

układzie można zastąpić równoważnym 

odbiornikiem „gwiazdowym” .    

19

Pomiar mocy czynnej  

odbiorników symetrycznych 

20

Pomiar mocy czynnej (P) pobieranej przez 
odbiornik trójfazowy symetryczny

  

W odbiorniku symetrycznym napięcia 

międzyfazowe są sobie równe (U

AC

 = U

BC

 = U

p

) oraz 

prądy przewodowe są sobie równe (I

A

 = I

B

 = I

p

), 

zatem 

w szczególnym przypadku układów 

symetrycznych

   

P

 

= P

1

 + P

2

 = U

AC

 I

A

 cos 

1

 + U

BC

 I

B

 cos 

2

 = 

   U

p

 I

p

 cos ( -  / 6) + U

p

 I

p

 cos ( +  / 6) =

      

= 3

1/2

 U

p

 I

p 

cos 

 

21

W ten sposób uzyskujemy potwierdzenie, że

  

 suma wskazań watomierzy włączonych w 

układzie Arona jest równa mocy czynnej (P) 
pobieranej przez odbiornik trójfazowy 
symetryczny 

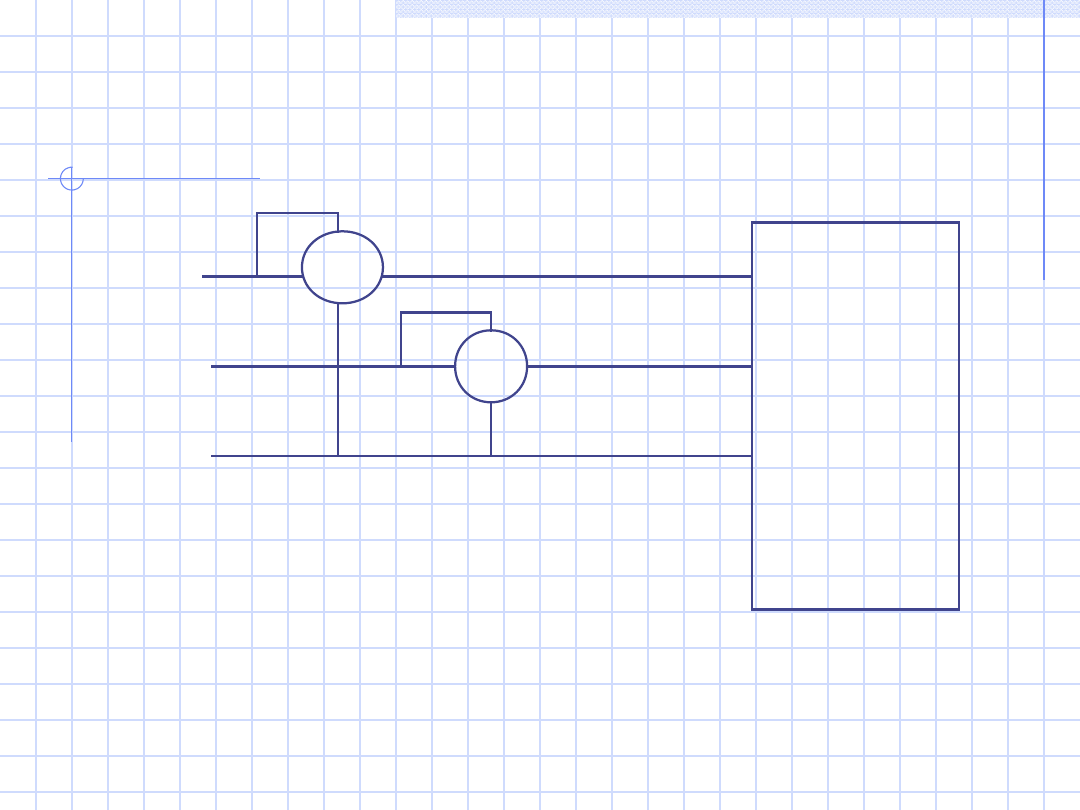
22

Odbiorni

k syme-

tryczny 

trzy-

zaciskow

y

W

1

W

2

L1

L2

L3

(układ Arona)

P = P

W1

 + P

W2

 

23

(

W układach trójfazowych czteroprzewodowych 

symetrycznych

 

Z

A

 = Z

B

 = Z

C

 = Z) do pomiaru

 

mocy czynnej (P)

 

stosujemy

 

jeden watomierz 

dołączony tak, jak pokazano na poniższym 

rysunku.

 

W układach tych, moc pobierana przez każdą fazę 

jest taka sama.

Wynik pomiaru mnożymy przez 3 i otrzymujemy 

wartość mocy pobieranej przez cały odbiornik 

trójfazowy.

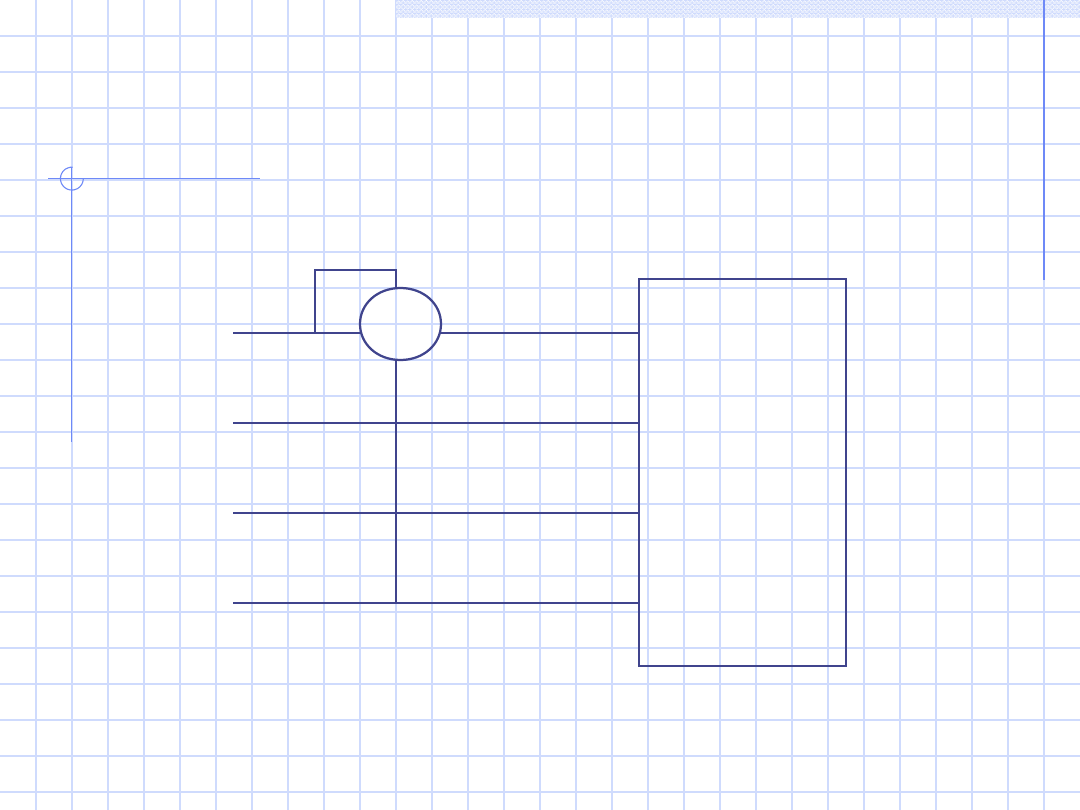
24

a)

Odbiorni

k syme-

tryczny 

czteroza-

ciskowy

W

1

P = 3P

W

L1

L2

L3

N

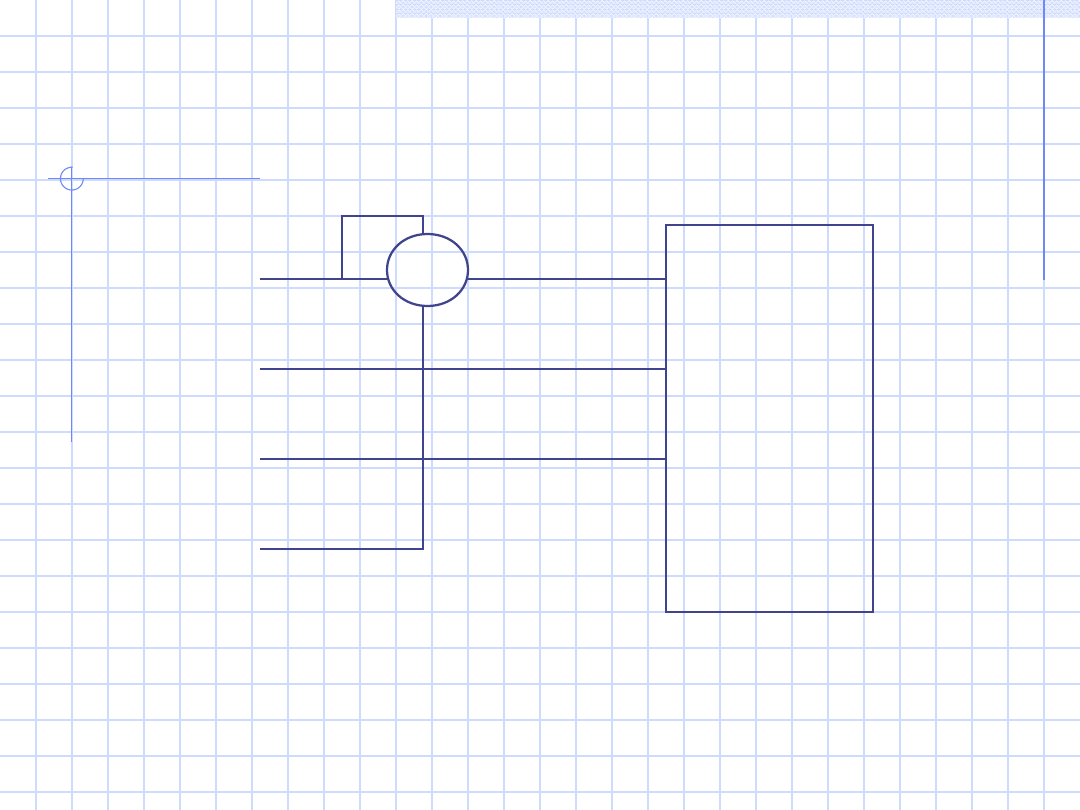
25

b)

Odbiorni

k syme-

tryczny 

trzyza-

ciskowy

W

1

P = 3P

W

L1

L2

L3

N

26

    

W układach trójfazowych trójprzewodowych 

symetrycznych (Z

A

 = Z

B

 = Z

C

 = Z)

, bez 

względu na sposób połączenia odbiornika (w 
trójkąt lub gwiazdę), do pomiaru mocy czynnej 
stosujemy albo

 jeden watomierz z 

dodatkowym układem rezystorów 

do 

utworzenia sztucznego punktu neutralnego 
albo 

dwa watomierze w układzie pomiarowym 

zwanym układem pomiarowym Arona. 

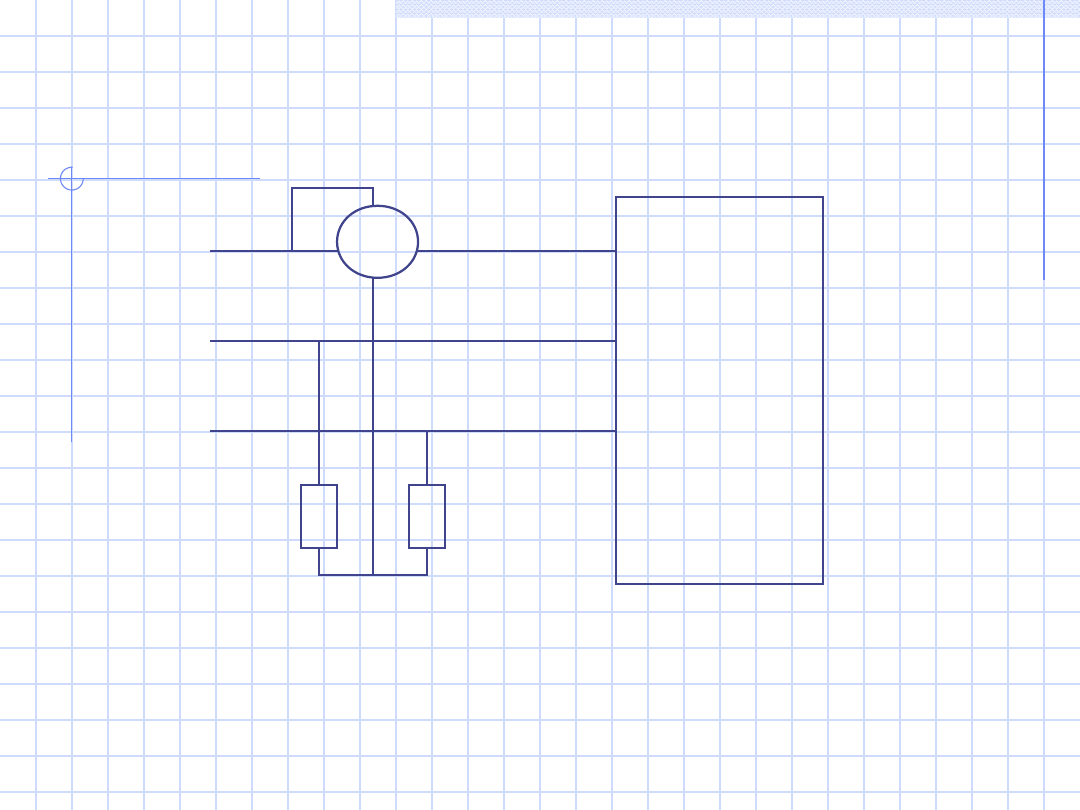
27

c)

Odbiorni

k syme-

tryczny 

trzyza-

ciskowy

W

1

P = 3P

W

L1

L2

L3

R

Wn

R

Wn

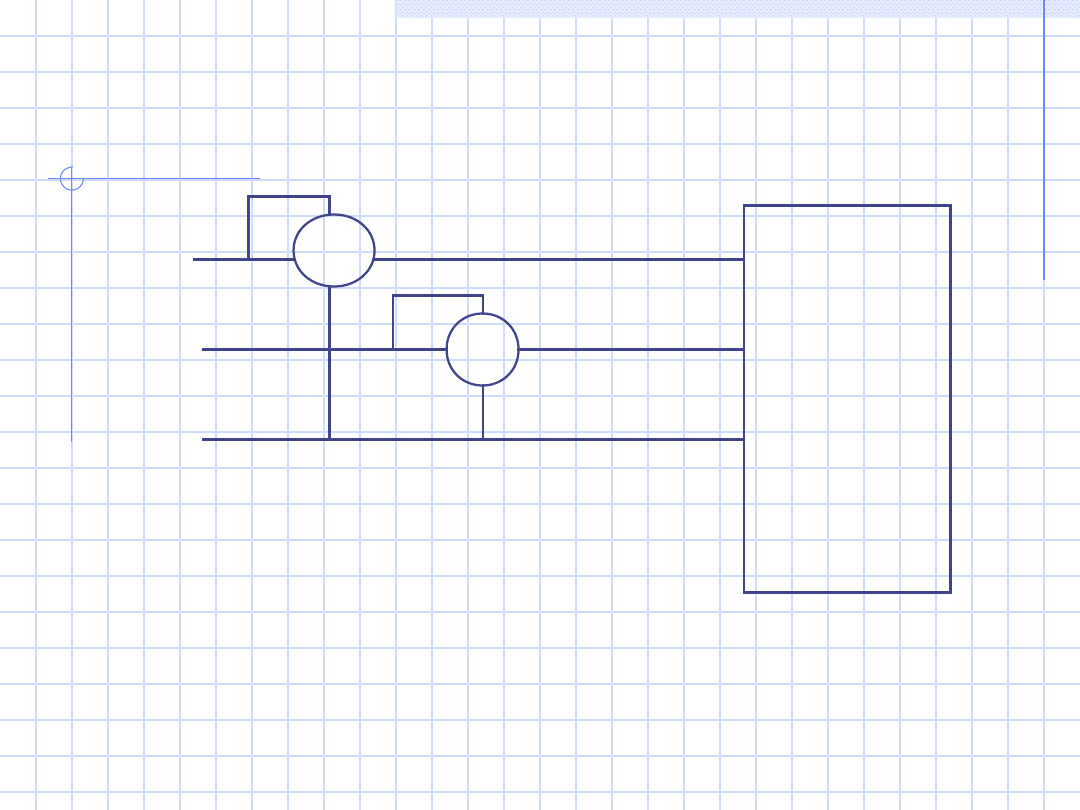
28

Odbiorni

k syme-

tryczny 

trzy-

zaciskow

y

W

1

W

2

L1

L2

L3

(układ Arona)

P = P

W1

 + P

W2

 

29

Podczas pomiaru mocy czynnej (P) jednym 

watomierzem

 

dobieramy tak wartości 

rezystancji dodatkowych R

d

, aby w fazie, w 

której jest włączona

 

cewka napięciowa 

watomierza

, wartość rezystancji wypadkowej 

była równa rezystancji włączonej do każdej z 

faz dodatkowych. 

Wtedy potencjał punktu N  utworzonej 

gwiazdy jest równy

 

0  i

 

cewka napięciowa 

jest włączona w napięcie fazowe

.

30

Uwagi

1.

W układzie „c” dołącza się dwie    

rezystancje R

Wn

 o wartościach równych 

rezystancji cewki napięciowej watomierza 

W, aby stworzyć 

sztuczny punkt neutralny

.

2.

Oczywiście, podane wcześniej układy do 

pomiaru mocy odbiorników 

niesymetrycznych mogą być stosowane w 

przypadku odbiorników symetrycznych, 

ale wtedy używa się więcej przyrządów i 

dokonuje więcej odczytów.   

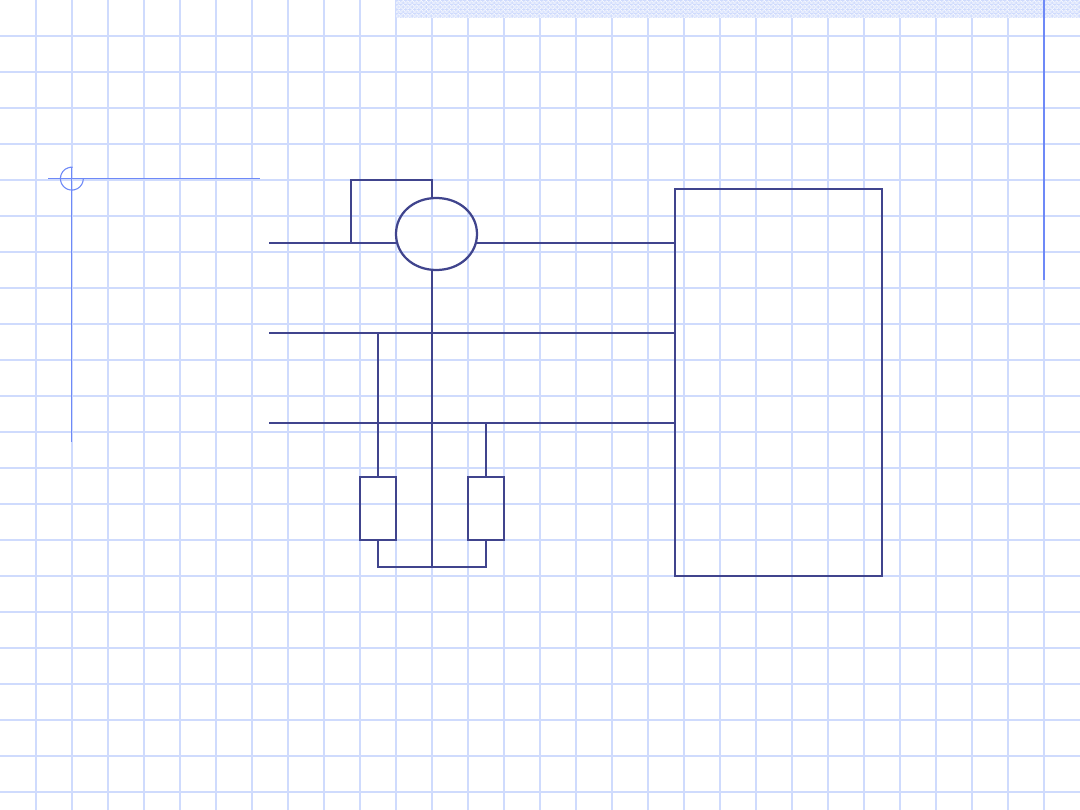
31

c)

Odbiorni

k syme-

tryczny 

trzyza-

ciskowy

W

1

P = 3P

W

L1

L2

L3

R

Wn

R

Wn

32

Pomiar mocy biernej 

odbiorników trójfazowych

33

   

Do pomiaru

 

mocy biernej (Q)

, przesyłanej 

lub odbieranej w obwodach trójfazowych, 

używa się również watomierzy. W tym celu, 

na cewki napięciowe

 

watomierza podaje się 

napięcia przesunięte w fazie o kąt –π/2,

 

względem napięć podawanych na nie w 

analogicznym układzie do pomiaru mocy 

czynnej

, co wynika ze wzorów: 

sinφ = cos(φ - 90°)   

φ= ψ

U

 –ψ

i

           (φ - 90°)=(ψ

U

 - 90°) – ψ

i 

 

34

   

Obecnie podane zostaną schematy 

przykładowych układów pomiarowych, 
wykresy wskazowe objaśniające wybór 
napięć podawanych na watomierze, 
oraz wzory na

 

moce bierne (Q) 

odbiorników

.

 

35

Pomiar mocy biernej (Q) 

odbiorników trójfazowych 

niesymetrycznych

 

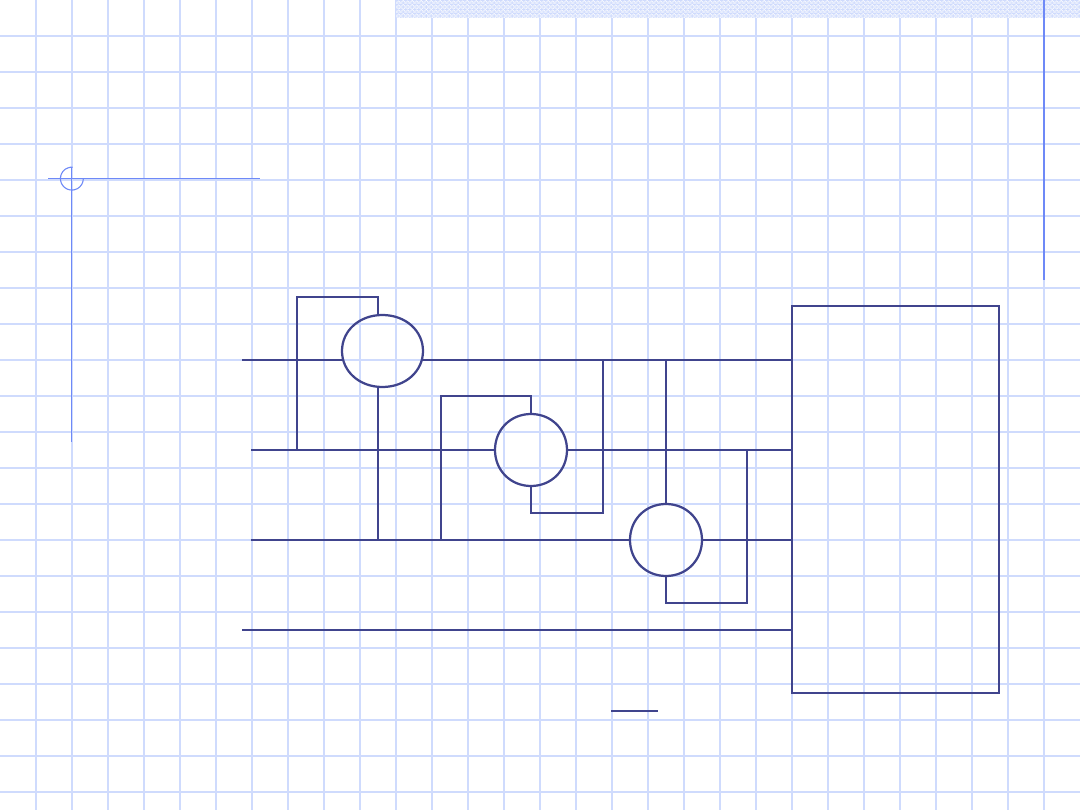
36

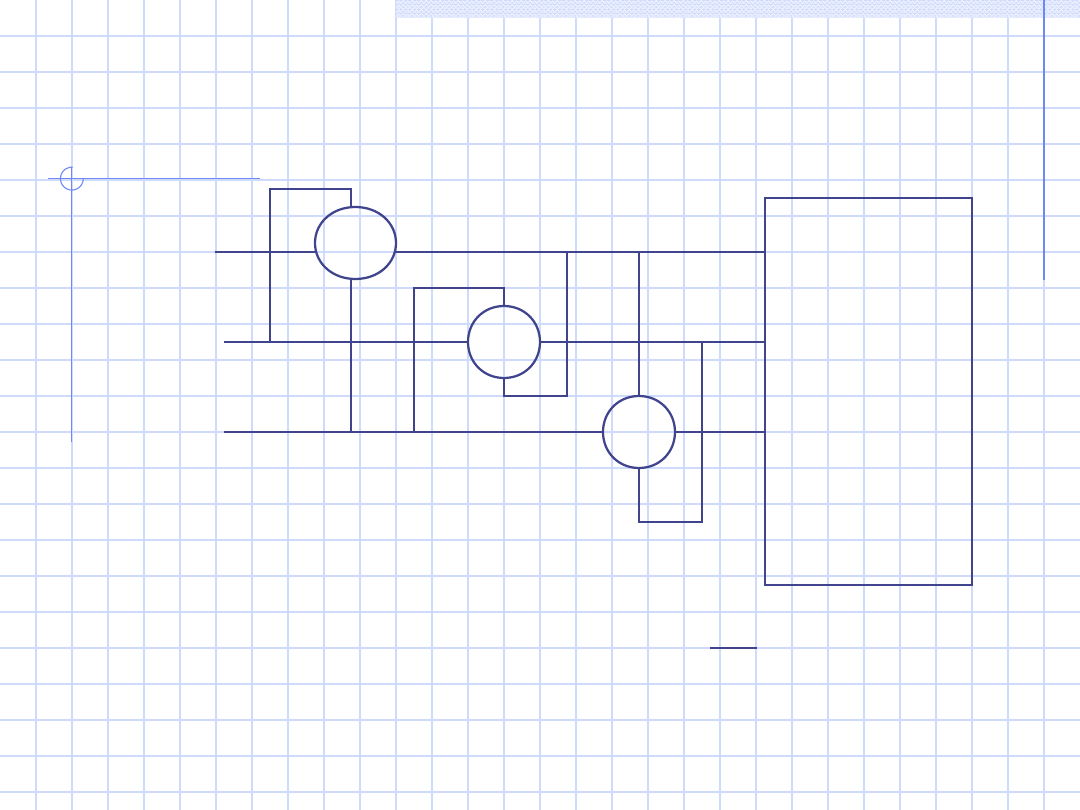
Na cewkach napięciowych – napięcia 
międzyfazowe.

a)

Odbiorni

k 

niesyme-

tryczny 

czteroza-

ciskowy

W

1

W

2

W

3

L1

L2

L3

N

Q = (P

W1

 + P

W2

 + P

W3

) · 1/ 3

37

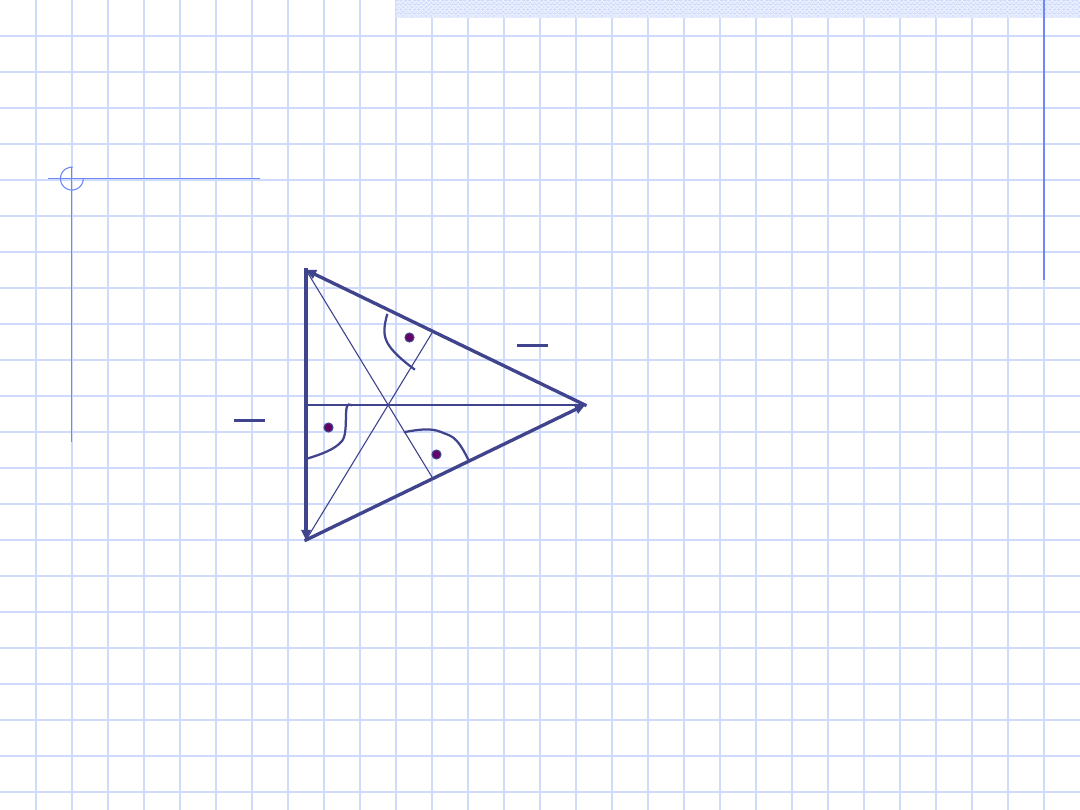
b)

Odbiorni

k 

niesyme-

tryczny 

trzy-

zaciskow

y

W

1

W

2

W

3

L1

L2

L3

Q = (P

W1

 + P

W2

 + P

W3

) · 1/ 3

Na cewkach napięciowych – napięcia 

międzyfazowe.

38

Wykres wskazowy do układów a i b 

U

23

U

1

39

Pomiar mocy biernej (Q) przy 

pomocy dwóch watomierzy

40

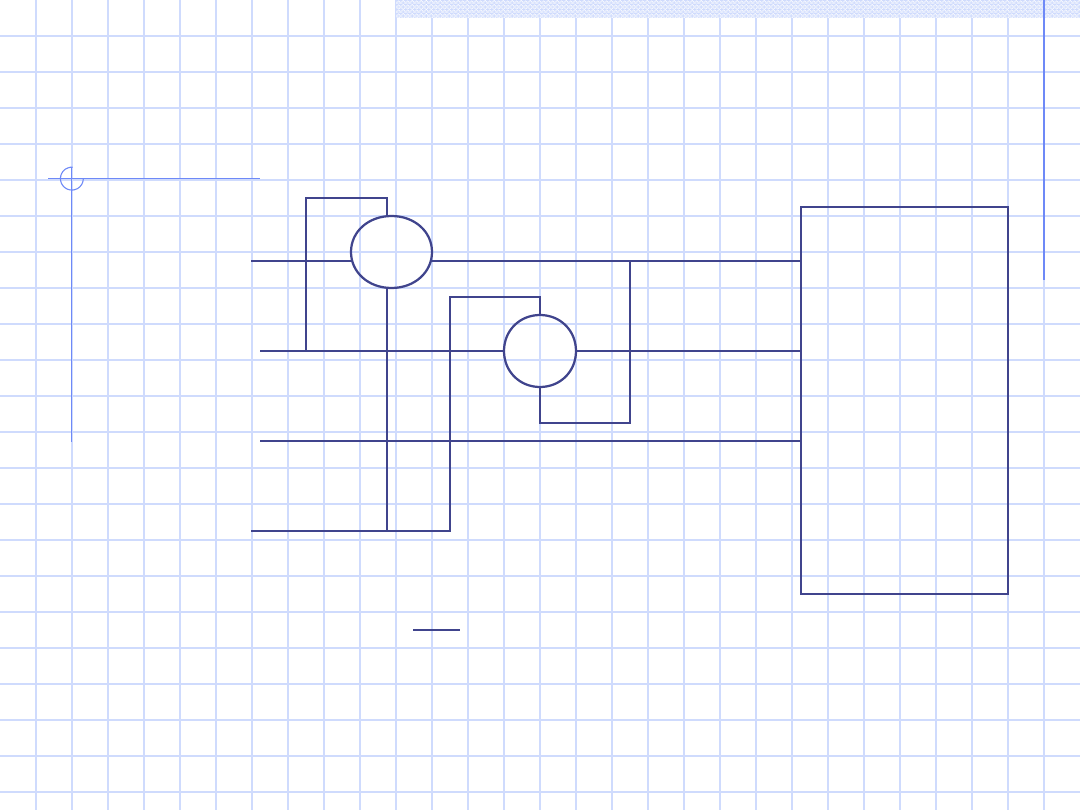
c1

Odbiorni

k 

niesyme-

tryczny 

trzy-

zaciskow

y

W

1

W

2

L1

L2

L3

N

Q = 3 · ( P

W1

 + P

W2

 )

Na cewkach napięciowych – napięcia 

fazowe

41

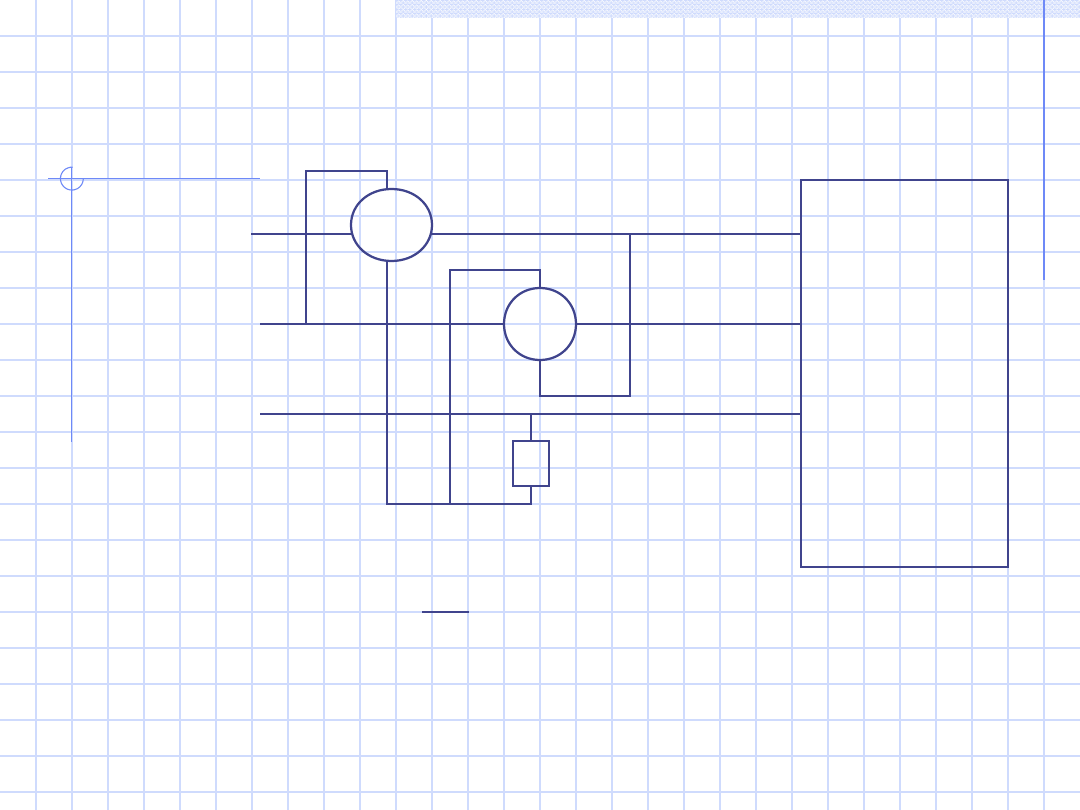
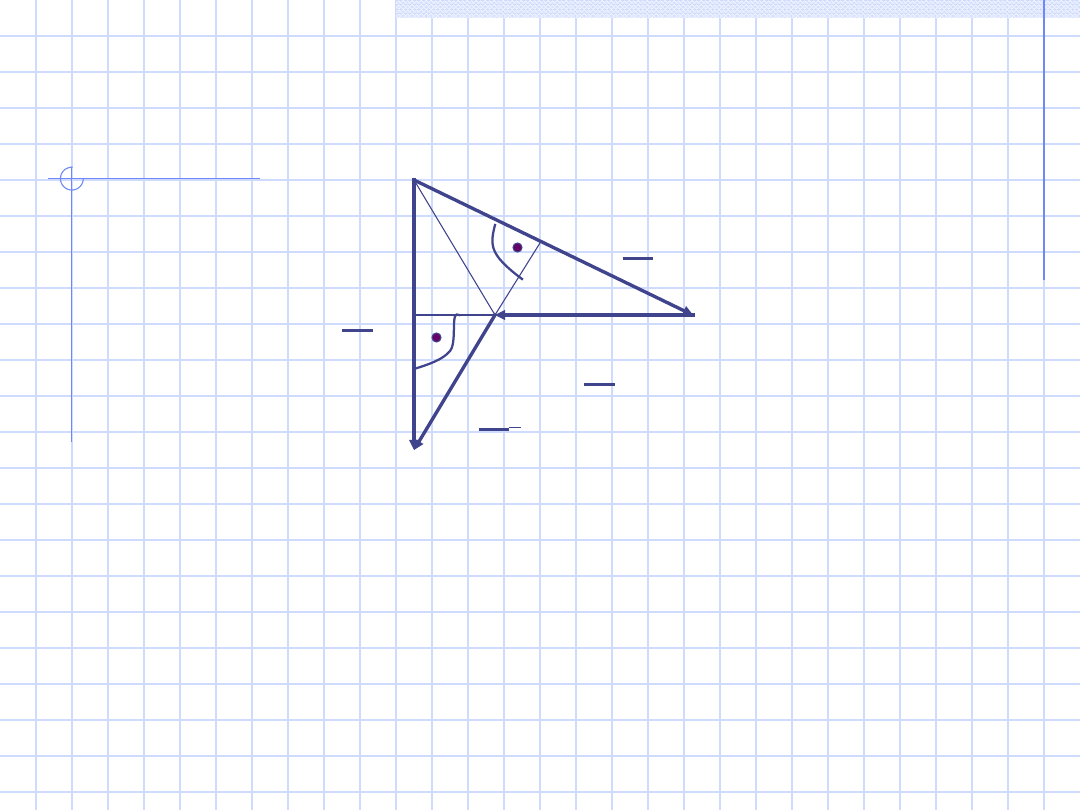
c2)

Odbiorni

k 

niesyme-

tryczny 

trzy-

zaciskow

y

W

1

W

2

L1

L2

L3

Q = 3 · ( P

W1

 + P

W2

 )

Na cewkach napięciowych – napięcia fazowe

R

Wn

42

Wykres wskazowy do układów c1 i c2

 

U

23

U

13

-U

1

U

2

Uwaga
Cewki napięciowe watomierzy W

1

 i W

2

 oraz 

rezystancja dołączona do układu „c2” musza 
mieć jednakową rezystancję, równą R

Wn 

(tworzą sztuczny punkt neutralny).

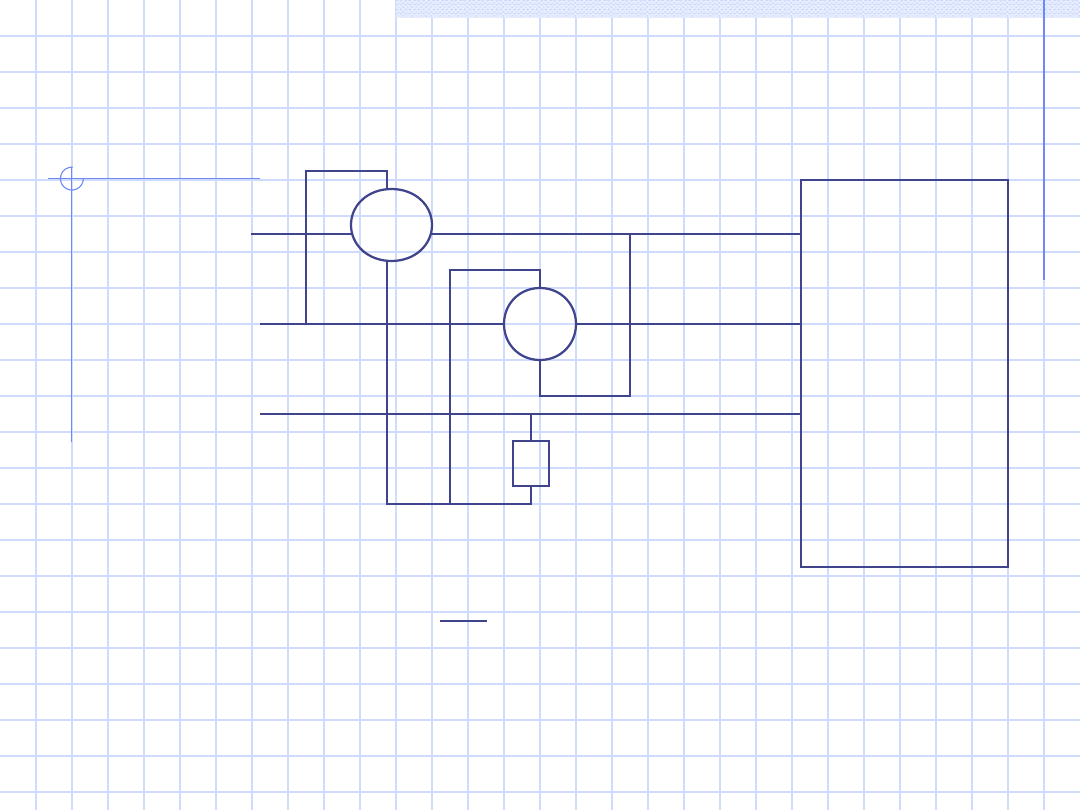
43

c2)

Odbiorni

k 

niesyme-

tryczny 

trzy-

zaciskow

y

W

1

W

2

L1

L2

L3

Q = 3 · ( P

W1

 + P

W2

 )

Na cewkach napięciowych – napięcia fazowe

R

Wn

44

Pomiar mocy biernej (Q) 

odbiorników  

symetrycznych

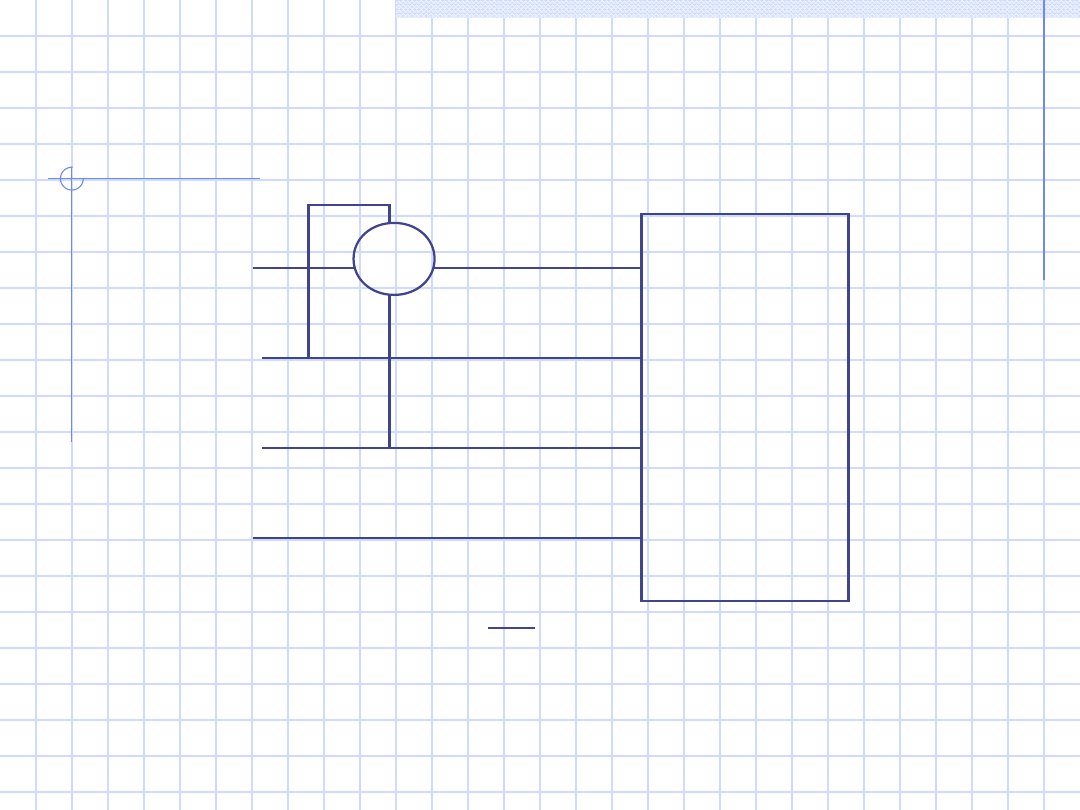
45

a)

Odbiorni

k syme-

tryczny 

czteroza-

ciskowy

W

1

L1

L2

L3

N

Q =  3 P

w

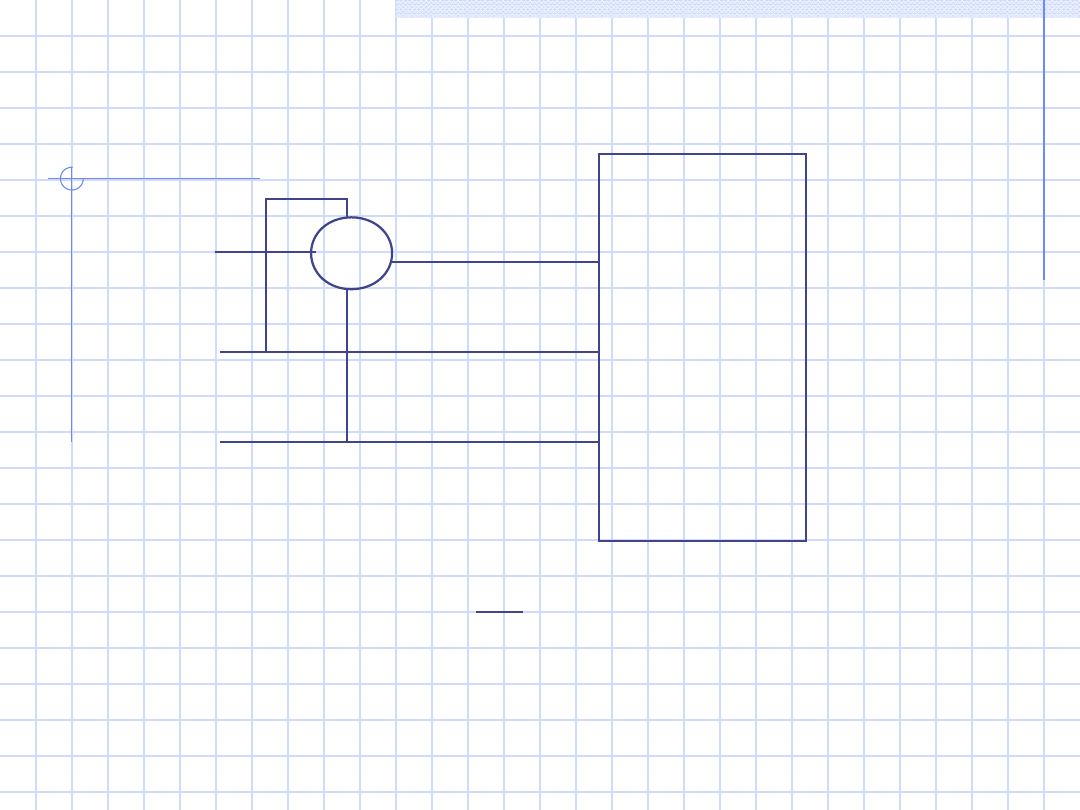
46

b)

Odbiorni

k syme-

tryczny 

trzy-

zaciskow

y

W

1

L1

L2

L3

Q =  3 P

w

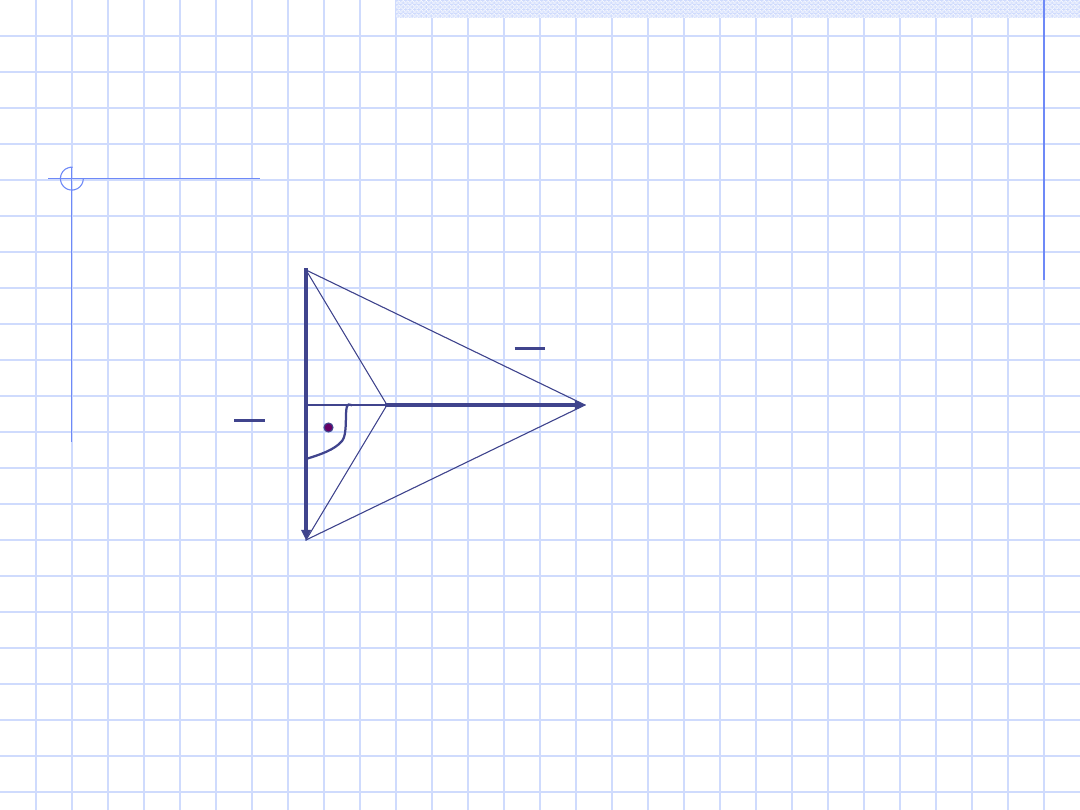
47

Wykres wskazowy do układów a i b 

U

23

U

1

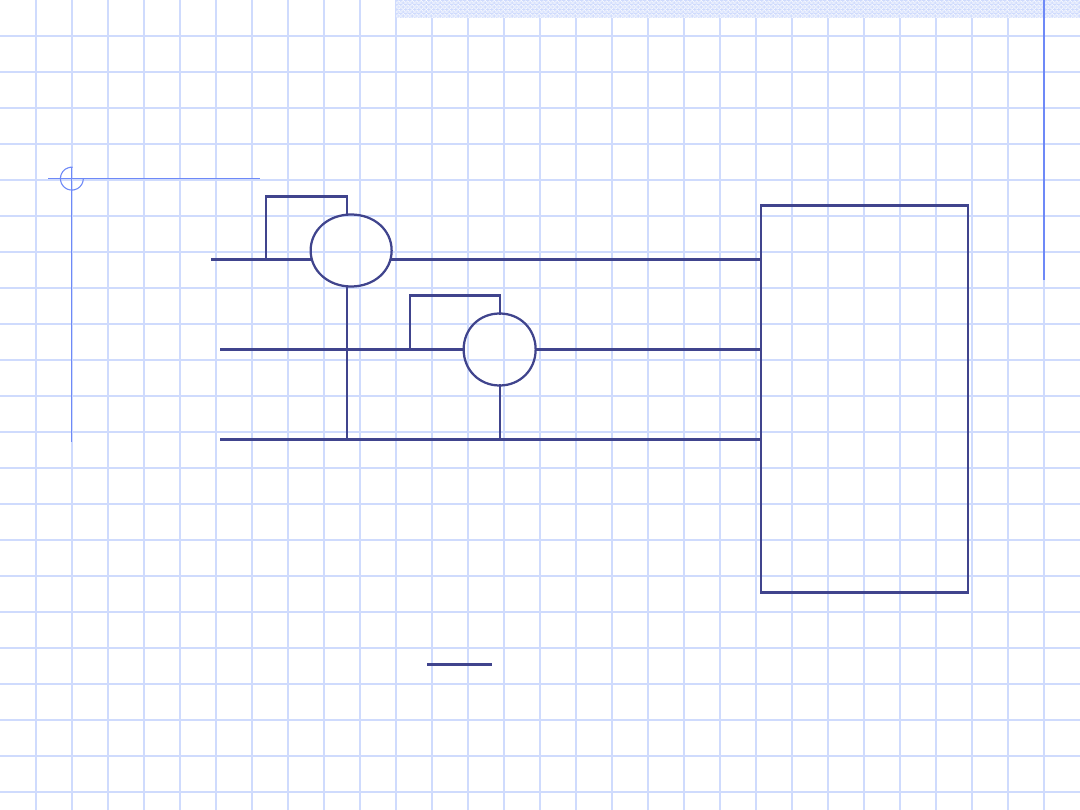
48

c)

Odbiorni

k syme-

tryczny 

trzy-

zaciskow

y

W

1

W

2

L1

L2

L3

(układ Arona)

Q = 3 ( P

W1

 - P

W2

 )

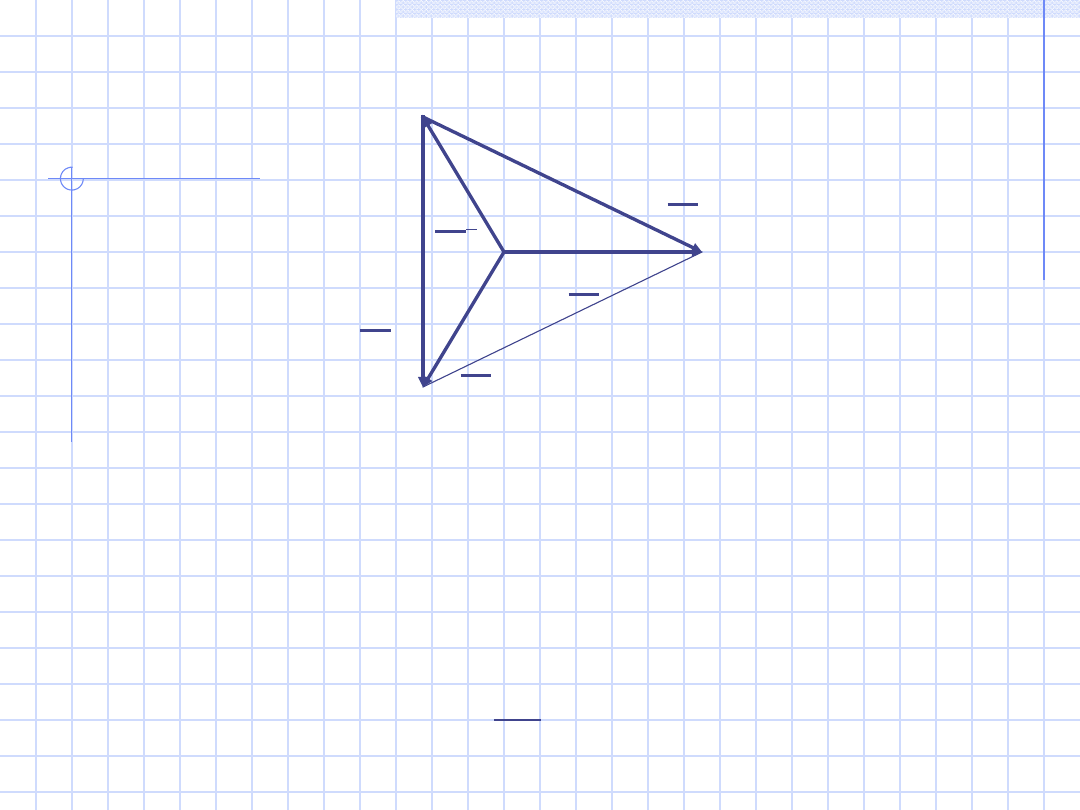
49

Wykres wskazowy do układu c 

U

23

U

1

U

13

U

3

U

2

50

   

W odbiorniku symetrycznym napięcia 

międzyfazowe są sobie równe (U

AC

 = U

BC

 = 

U

p

) oraz prądy przewodowe są sobie równe 

(I

A

 = I

B

 = I

p

), zatem

 

w szczególnym 

przypadku układów symetrycznych 

można 

mierzyć jednocześnie moc czynną i bierną.

 

51

Możliwość pomiaru mocy biernej wynika z 
następujących zależności:

P

W1

 = U

13

 · I

1

 · cos(φ- 30°) = U·I cos(φ - 30°)

P

W2

 = U

23

 · I

2

 · cos(φ+ 30°) = U·I cos(φ + 30°)

P

W1

 - P

W2

 

= -2U·I sinφ · sin(-30°)=

 

UI sinφ   

 

Q

=

 3 UI sinφ

Oczywiście, otrzymuje się również

P

W1

 +  P

W2

 

= 2U·I cosφ · cos(-30°) =

 

 3 UI cosφ 

= P 

   

52

Pomiar kąta fazowego odbiornika 
trójfazowego symetrycznego

tg  = 3

1/2

 (P

1

 - P

2

) / (P

1

 + P

2

)

ponieważ

P

1

 - P

2

 = U

p

 I

p  

sin  

P

1

 + P

2

 = 3

1/2

 U

p

 I

p 

cos  

 

53

P = U

AC

  I

A

 cos  φ

A

 + U

BC

  I

B

  cos φ

B

 

Wzór na

 

moc czynną (P) 

ma służyć glównie do wyjaśnienia 

sposobu dołączania watomierzy, ale może być też 
stosowan

y do 

obliczania mocy czynnej w układach 

trójprzewodowych, zarówno symetrycznych jak i 
niesymetrycznych

. 

Jeśli są znane napięcia międzyfazowe i prądy fazowe w 
układzie, to jedyną trudność stanowi wyznaczenie kątów φ

1

 

oraz φ

2

 

Kąty te najłatwiej wyznaczyć z wykresu wektorowego

. 

Wykonamy przykładowo wykres wektorowy dla odbiornika 
symetrycznego rezystancyjno-indukcyjnego .
 Napięcie fazowe fazy A przyjmiemy na osi odniesienia.

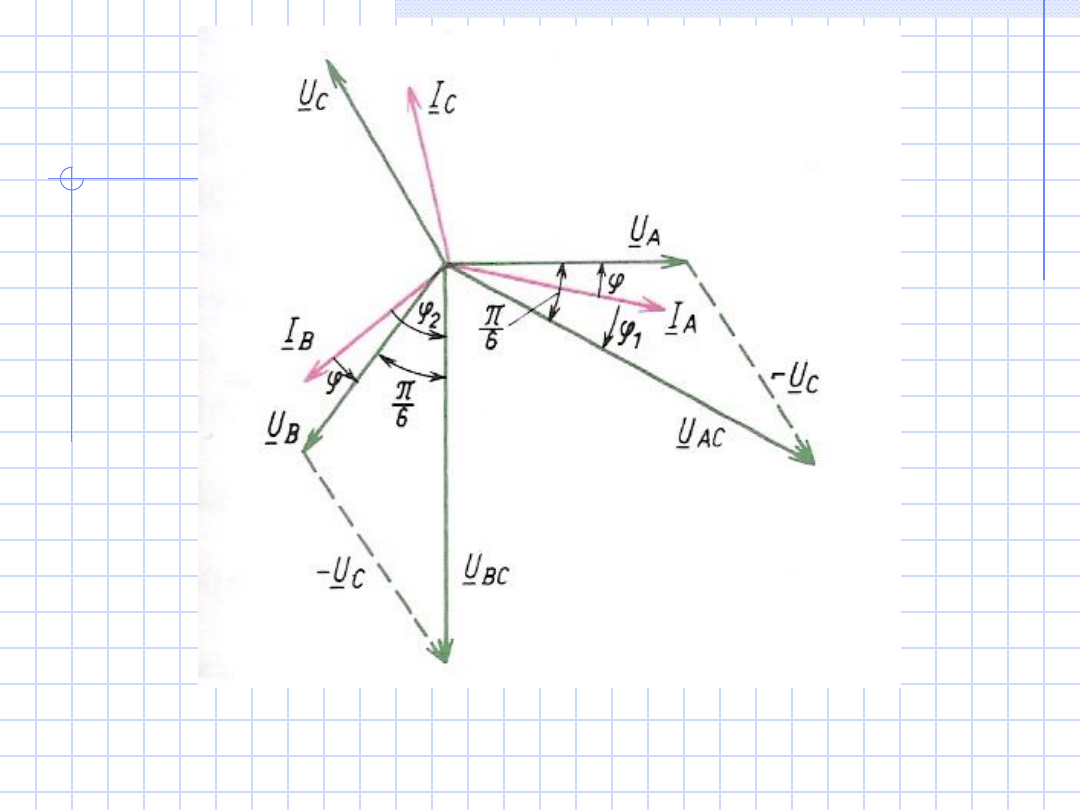
54

Rys.  Wykres wektorowy prądów i napięć ilustrujący sposób 
wyznaczania kątów przesunięcia fazowego 

φ

1

 i 

φ

2

 w odbiorniku 

symetrycznym rez.-ind

.

55

Wobec symetrii układu

, napięcia fazowe U

A , 

U

B

 

i U

C

 tworzą gwiazdę symetryczną, a prąd 

fazowy (równy przewodowemu) w każdej fazie 
jest opóźniony względem swojego napięcia 
fazowego o kąt φ, będący argumentem 
impedancji zespolonej odbiornika.

 

W odbiorniku symetrycznym

 

napięcia 

międzyfazowe są sobie równe oraz prądy 
przewodowe są sobie równe. 

56

Ze względu na to, że kąt φ  może być zawarty 
w granicach od 0 do 

π

/2 i jest

 

dodatni

 

- gdy

 

odbiornik ma charakter indukcyjny

, a

 

ujemny

 

- 

gdy

 

odbiornik ma charakter pojemnościowy

, 

jedno ze wskazań watomierzy może być 
ujemne.
 
Stąd wynika ważny wniosek, a mianowicie: 

wskazania watomierzy należy dodawać 
algebraiczne, czyli z uwzględnieniem znaku

. 

57

Podczas wykonywania pomiaru stwierdzamy 
wtedy, że wskazówka jednego z watomierzy 
odchyla się w przeciwną stronę niż wskazówka 
drugiego. 

Wynika drugi wniosek:

w ogólnym przypadku wskazania watomierzy są 
różne; jednakowe wskazania watomierzy będą 
tylko przy φ  = 0, czyli przy obciążeniu 
rezystancyjnym.

58

Dziękuję za uwagę