Statystyka

HIPOTEZY

Alicja Ganczarek-Gamrot

Testy istotności dla jednego parametru-
test dla wartości przeciętnej w populacji

Przykład 1

Na podstawie 10-elementowej próby
prostej oszacowano średni czas
dojazdu na uczelnię 27 min. i
odchylenie standardowe 3,5 min.
Zakładając, że czas dojazdu na
uczelnię ma rozkład normalny. Na
poziomie

istotności

0,02

zweryfikować

hipotezę,

że

przeciętny czas dojazdu na uczelnię
wynosi 30 min.

Testy istotności dla jednego parametru-
test dla wariancji w populacji

Przykład 2

Na bazie 20 elementowej losowej próby
studentów otrzymano następujące
wyniki:
- średnią liczbę punktów uzyskanych na
egzaminie z matematyki 30 punktów

-odchylenie standardowe 12 punktów.
a) Na poziomie istotności 0,05
zweryfikować hipotezę, że odchylenie
liczby uzyskanych punktów wynosi 10.
b) Jaka będzie decyzja na poziomie
istotności 0,1.

Testy istotności dla jednego parametru-
test dla wskaźnika struktury w populacji

Przykład 3

Wśród

650

wylosowanych

pracowników pewnego zakładu 440
zna podstawy obsługi komputera.
Czy można twierdzić na poziomie
istotności 0,05, że znający obsługę
komputera stanowią przynajmniej
65% załogi?

Test zgodności

2



Test zgodności

2



Test zgodności
Przykład 1

2



Dla losowo wybranych 100
klientów

PZU

poddano

analizie

liczbę

szkód

zgłoszonych

w

ciągu

ostatniego

roku

przez

klientów

Na poziomie istotności
0,05

zweryfikować

hipotezę, że rozkład liczby
szkód

jest

rozkładem

Poissona.

Liczba

Szkód

x

i

Liczba

klientów

n

i

0 10
1 30
2 25
3 20
4 15

Test zgodności
Przykład 1

2



Test zgodności
Przykład 1

2



8

,

1

100

180







x

i

n

i

x

i

*n

i

0

15

0

1

30

30

2

25

50

3

20

60

4

10

40

suma

100

180

!

)

(

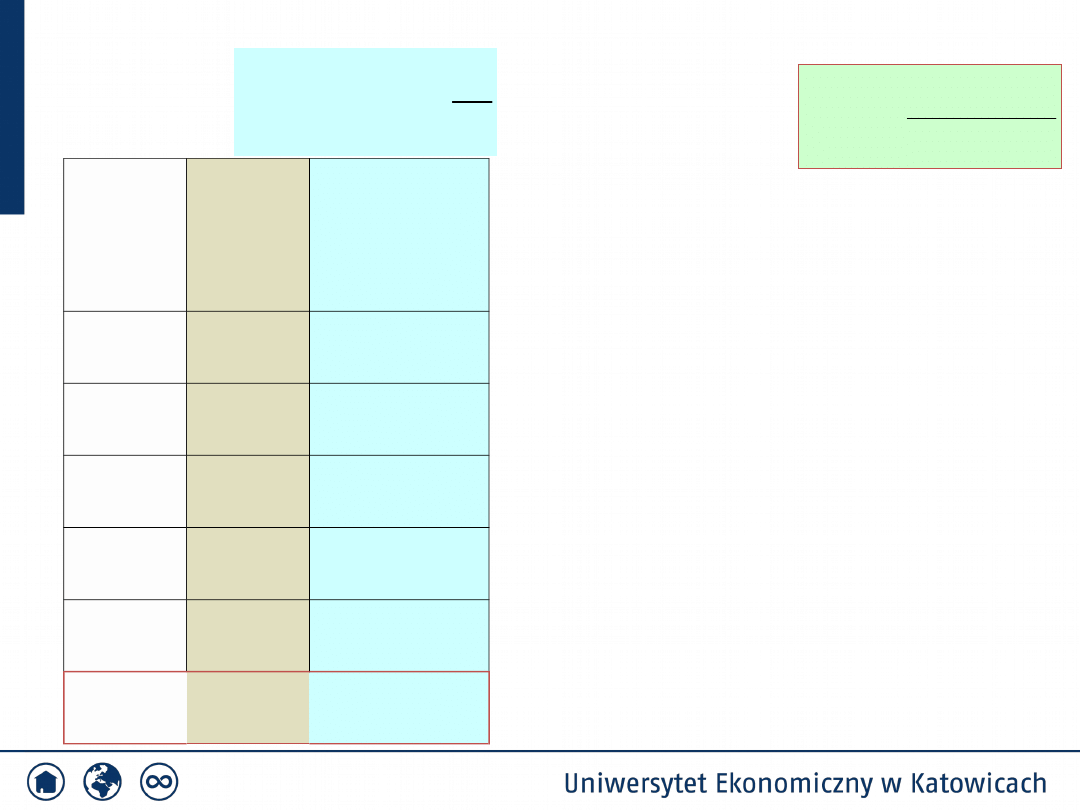
i

x

i

x

e

x

X

P

i



















r

i

i

i

i

np

)

np

n

(

1

2

2



x

i

n

i

P(X=x

i

)

0

15

0,1653

1

30

0,2975

2

25

0,2678

3

20

0,1607

4

10

0,1087

suma

100

1,0000

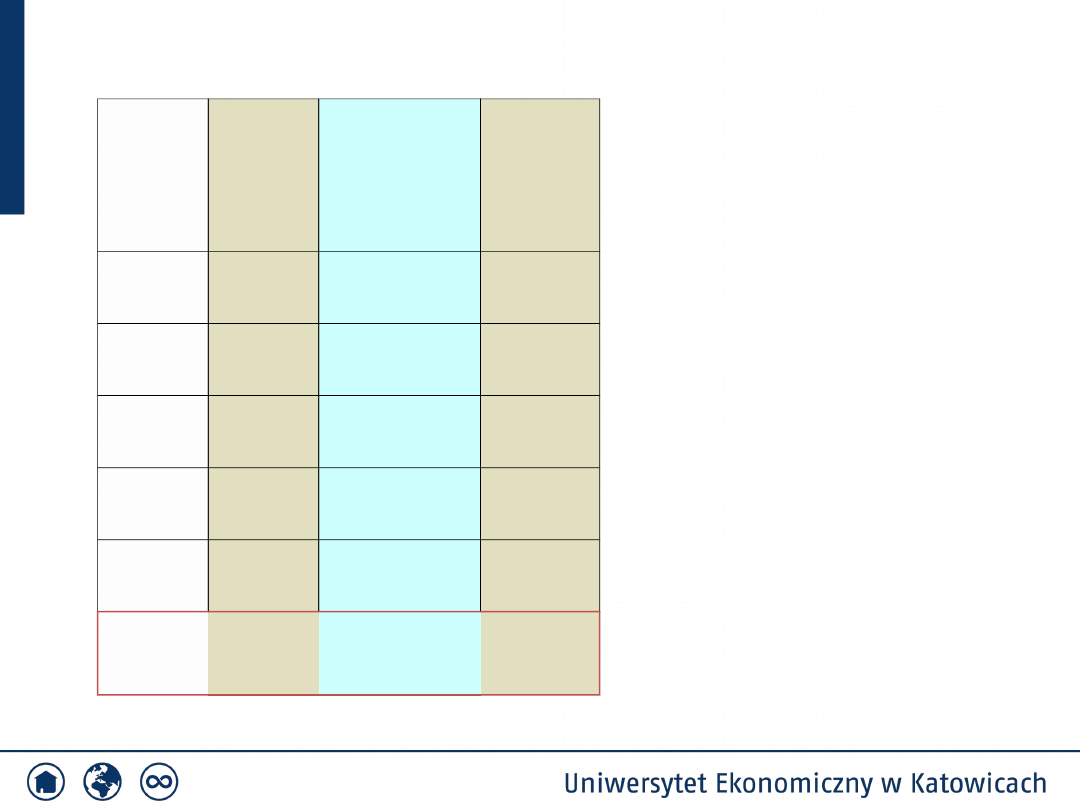
x

i

n

i

P(X=x

i

)

n*p

i

0

15

0,1653 16,53

1

30

0,2975 29,75

2

25

0,2678 26,78

3

20

0,1607 16,07

4

10

0,1087 10,87

suma

100

1,0000

100,0

0











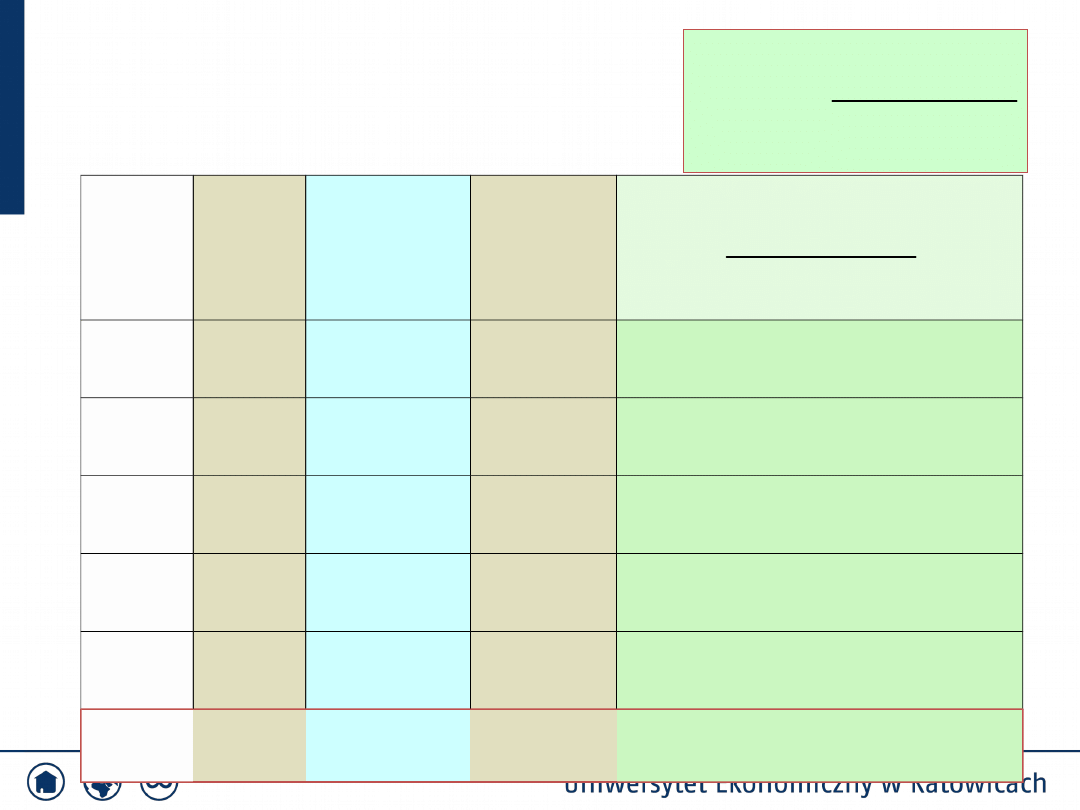
r

i

i

i

i

np

np

n

1

2

2

)

(

x

i

n

i

P(X=x

i

)

n*p

i

0

15

0,1653

16,53

0,14

1

30

0,2975

29,75

0,00

2

25

0,2678

26,78

0,12

3

20

0,1607

16,07

0,96

4

10

0,1087

10,87

0,07

suma

100

1,0000

100,00

1,29

i

i

i

np

np

n

2

)

( 

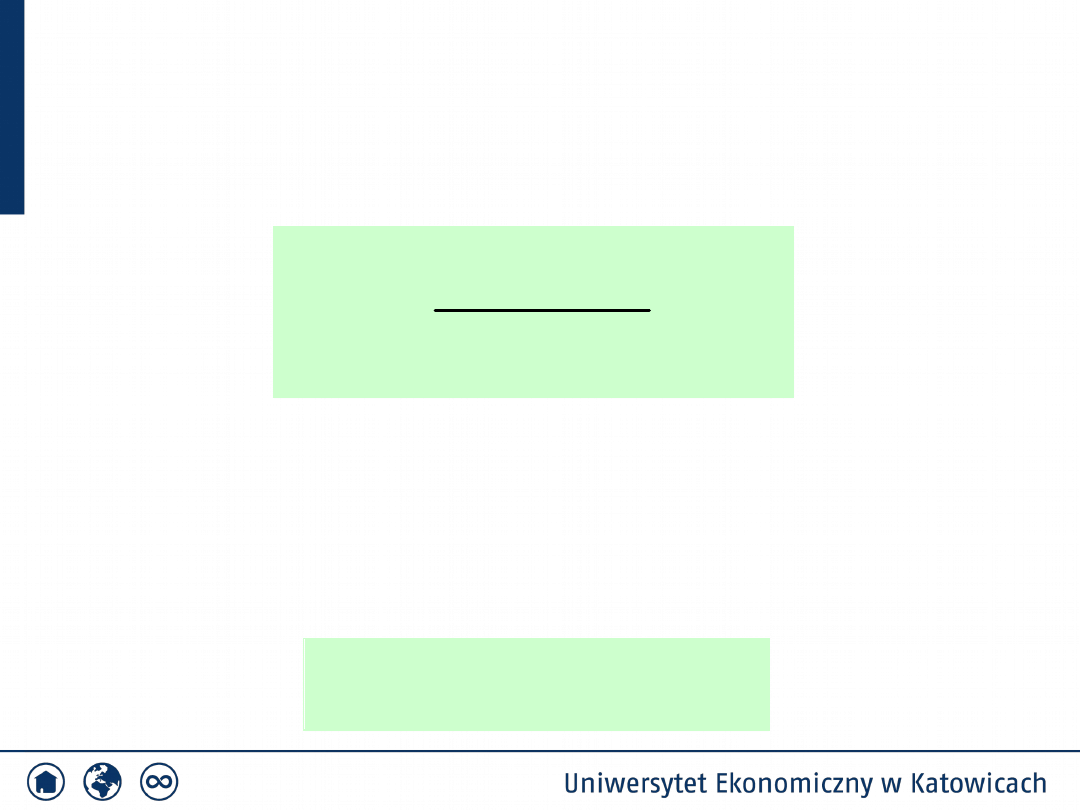
29

,

1

)

(

1

2

2











r

i

i

i

i

np

np

n



815

,

7

2

1

1

5

,

05

,

0

2

,













 k

Przykład 1

7305

,

0

)

29

,

1

(

2





k

P



Test zgodności
Przykład 2

2



Koszty

produkcji

pewnego

wyrobu w wylosowanych 400
zakładach były następujące (w
mln zł).

Na poziomie istotności 0,05
zweryfikować

hipotezę,

że

rozkład kosztów przy produkcji
tego wyrobu jest N(540,200)

Koszt

materiałowy

(x

i

; x

i+1

>

Liczba

zakładów

n

i

350

450

90

450

550

120

550

650

80

650

750

60

750

850

50

400

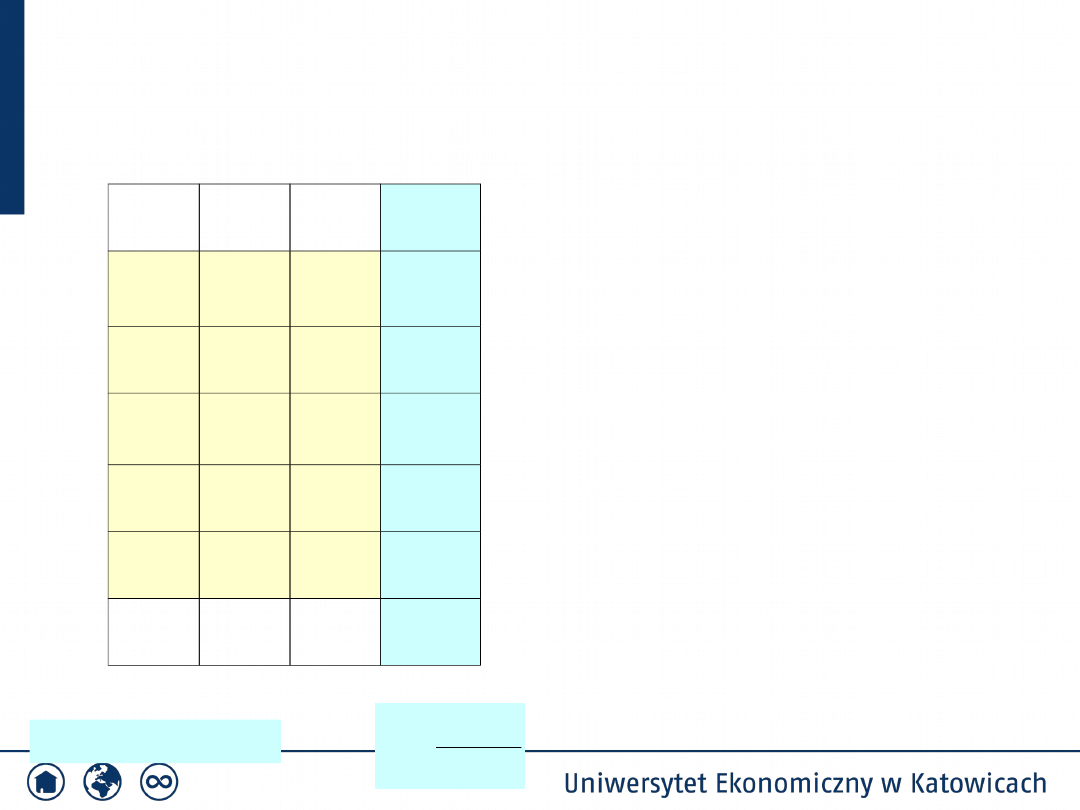
Test zgodności
Przykład 2

2











X

U

N(540,200)

x

id

x

ig

n

i

u

i

350

450

90 -0,45

450

550

120

0,05

550

650

80

0,55

650

750

60

1,05

750

850

50

1,55

 

 

400  

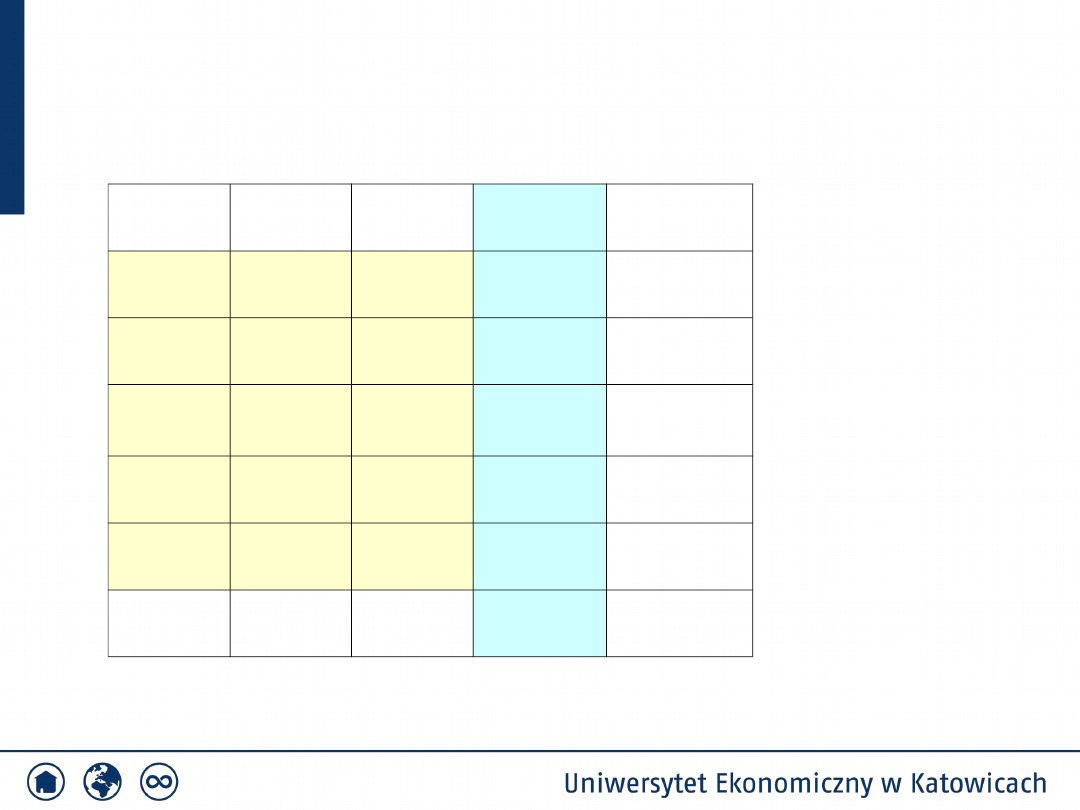
Test zgodności
Przykład 2

2



x

id

x

ig

n

i

u

i

F(u

i

)

350

450

90

-0,45

0,3264

450

550

120

0,05

0,5199

550

650

80

0,55

0,7088

650

750

60

1,05

0,8531

750

850

50

1,55

1,0000

 

 

400  

 

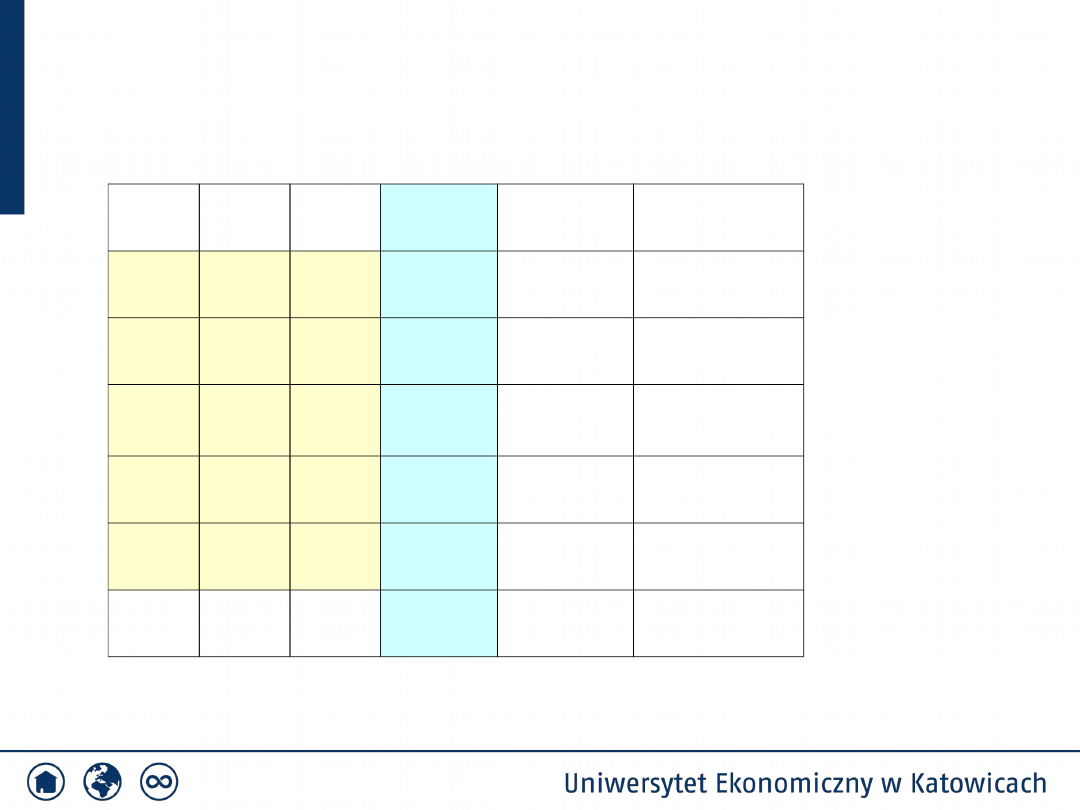
Test zgodności
Przykład 2

2



x

id

x

ig

n

i

u

i

F(u

i

)

p

i

350

450

90

-0,45

0,3264

0,3264

450

550

120

0,05

0,5199

0,1935

550

650

80

0,55

0,7088

0,1889

650

750

60

1,05

0,8531

0,1443

750

850

50

1,55

1,0000

0,1469

 

 

400  

 

1,00

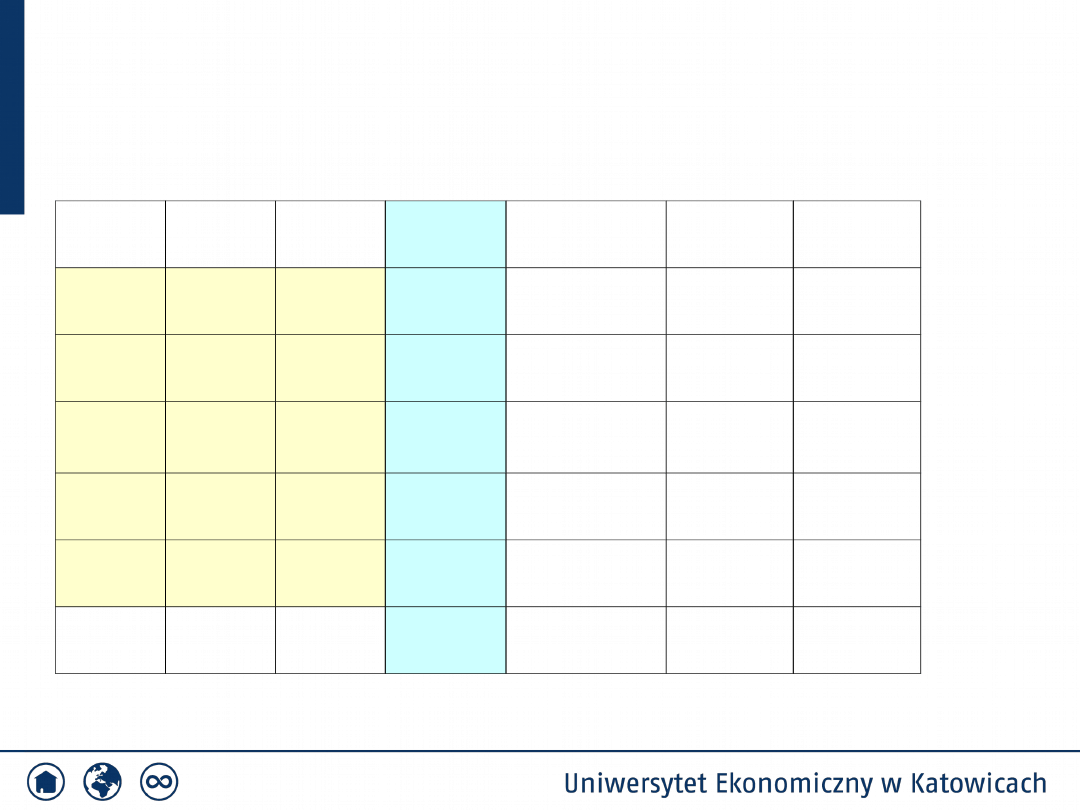
Test zgodności
Przykład 2

2



x

id

x

ig

n

i

u

i

F(u

i

)

p

i

np

i

350

450

90

-0,45

0,3264

0,3264

130,56

450

550

120

0,05

0,5199

0,1935

77,40

550

650

80

0,55

0,7088

0,1889

75,56

650

750

60

1,05

0,8531

0,1443

57,72

750

850

50

1,55

1,0000

0,1469

58,76

 

 

400  

 

1,00

400,00

Test zgodności
Przykład 2

2



x

id

x

ig

n

i

u

i

F(u

i

)

p

i

np

i

350

450

90

-0,45

0,3264 0,3264 130,56

12,60

450

550

120

0,05

0,5199 0,1935

77,40

23,45

550

650

80

0,55

0,7088 0,1889

75,56

0,26

650

750

60

1,05

0,8531 0,1443

57,72

0,09

750

850

50

1,55

1,0000 0,1469

58,76

1,31

 

 

400  

 

1,00 400,00

37,71

i

i

i

np

np

n

2

)

( 

Test zgodności
Przykład 2

2



71

,

37

)

(

1

2

2











r

i

i

i

i

np

np

n



488

,

9

2

1

5

,

05

,

0

2

,











 k

03

0

00000

,

0

)

71

,

37

(

2





k

P

