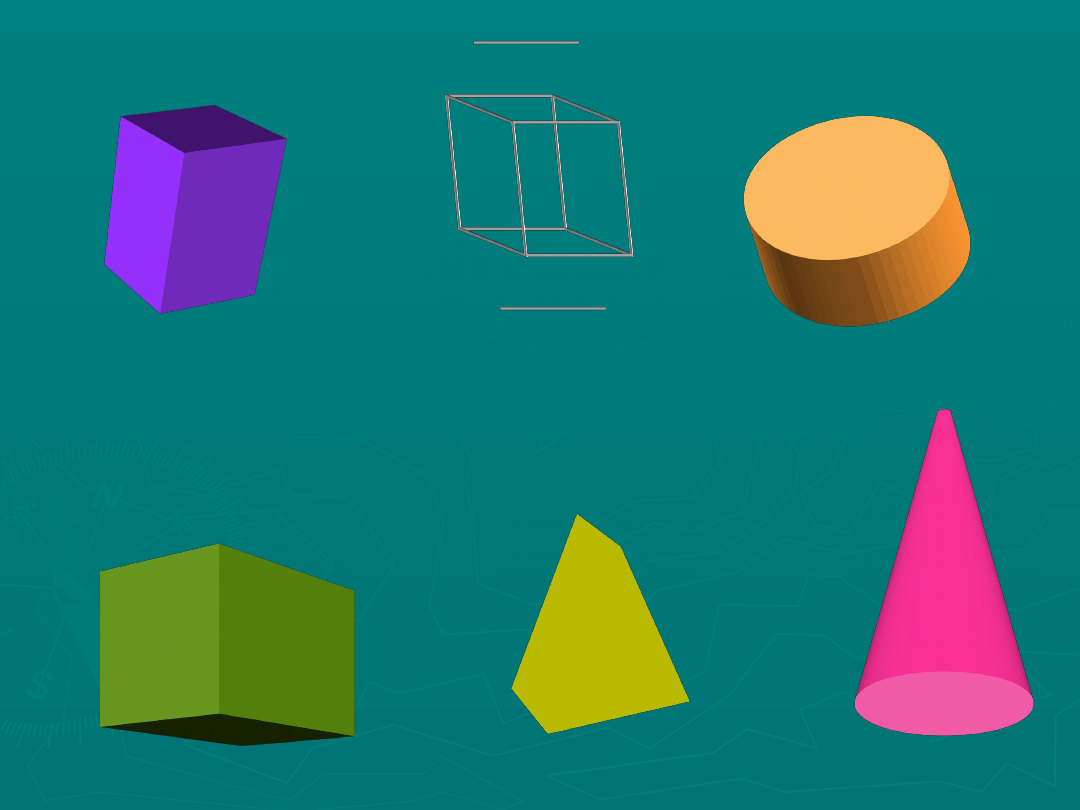
FIGURY
FIGURY
PRZESTRZENNE
PRZESTRZENNE
FIGURY
FIGURY
PRZESTRZENNE
PRZESTRZENNE
GRANIASTOSŁUPY
GRANIASTOSŁUPY
Graniastosłup (wielościan)
Graniastosłup (wielościan)
jest figurą przestrzenną, której
jest figurą przestrzenną, której
obie podstawy są równoległymi wielokątami przystającymi,
obie podstawy są równoległymi wielokątami przystającymi,
a ściany boczne są równoległobokami. Krawędzie boczne
a ściany boczne są równoległobokami. Krawędzie boczne
graniastosłupa są równoległe i mają jednakową długość.
graniastosłupa są równoległe i mają jednakową długość.
Wysokość
Wysokość
graniastosłupa jest to
graniastosłupa jest to
odcinek prostopadły do podstaw i
odcinek prostopadły do podstaw i
zawarty między obydwoma podstawami.
zawarty między obydwoma podstawami.
Przekątna
Przekątna
graniastosłupa jest to
graniastosłupa jest to
odcinek łączący dwa wierzchołki nie
odcinek łączący dwa wierzchołki nie
leżące na jednej ścianie (np.: BD
leżące na jednej ścianie (np.: BD
1
1
).
).
Graniastosłupy proste
Graniastosłupy proste
Graniastosłup prosty
Graniastosłup prosty
to taki
to taki
graniastosłup, w którym
graniastosłup, w którym
wszystkie ściany boczne są
wszystkie ściany boczne są
prostokątami.
prostokątami.
Graniastosłupem prostym
Graniastosłupem prostym
jest m.in. sześcian,
jest m.in. sześcian,
prostopadłościan.
prostopadłościan.
Wzór na objętość graniastosłupa
Wzór na objętość graniastosłupa
prostego:
prostego:
- pole powierzchni
- pole powierzchni
- wysokość graniastosłupa
- wysokość graniastosłupa
P
h
Ph
V
Wzór na pole powierzchni siatki
Wzór na pole powierzchni siatki
graniastosłupa prostego:
graniastosłupa prostego:
-
pole powierzchni
pole powierzchni
-
wysokość graniastosłupa
wysokość graniastosłupa
- obwód podstawy
- obwód podstawy
P
lh
S
2
l
h
P
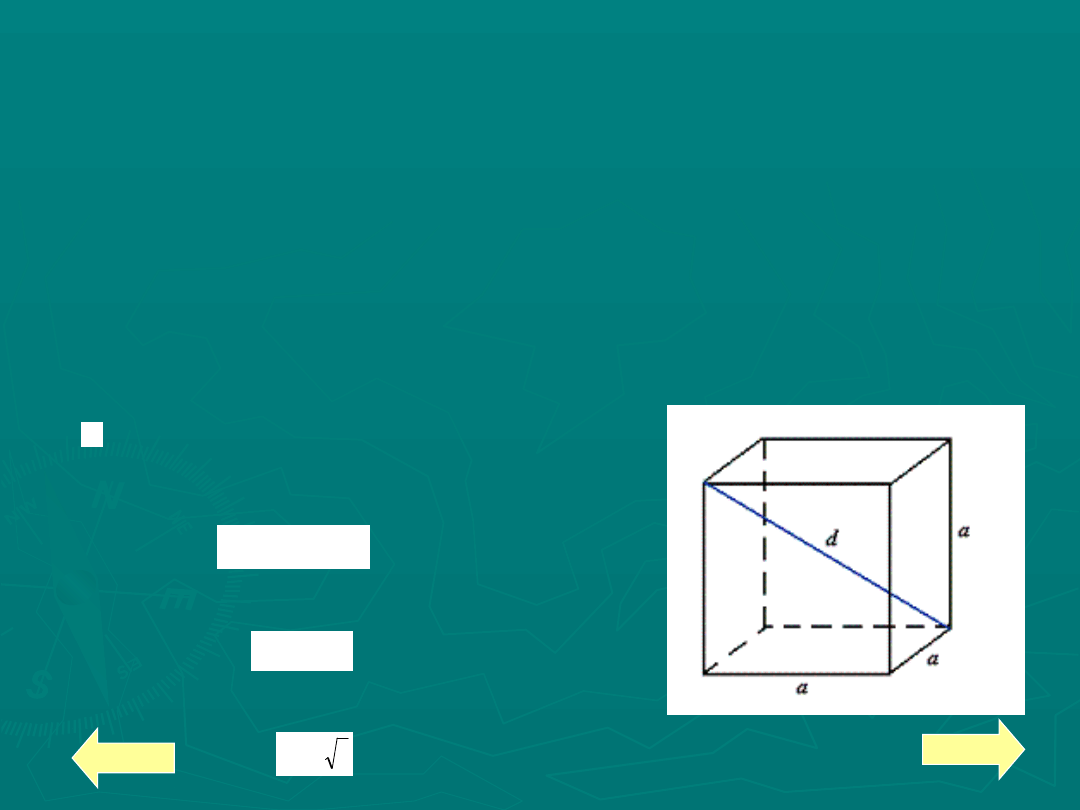
Sześcian
Sześcian
Sześcian (inaczej heksaedr)
Sześcian (inaczej heksaedr)
– wielościan foremny o sześciu
– wielościan foremny o sześciu
ścianach w kształcie identycznych kwadratów. Posiada 12
ścianach w kształcie identycznych kwadratów. Posiada 12
krawędzi, 8 wierzchołków i 4 przekątne.
krawędzi, 8 wierzchołków i 4 przekątne.
a
Kąt między ścianami sześcianu jest kątem prostym.
Kąt między ścianami sześcianu jest kątem prostym.
Sześcian jest także szczególnym przypadkiem graniastosłupa
Sześcian jest także szczególnym przypadkiem graniastosłupa
prawidłowego, hipersześcianu, prostopadłościanu i
prawidłowego, hipersześcianu, prostopadłościanu i
romboedru.
romboedru.
a
- długość jednej krawędzi sześcianu
- długość jednej krawędzi sześcianu
Wzór na objętość sześcianu:
Wzór na objętość sześcianu:
Wzór na pole powierzchni:
Wzór na pole powierzchni:
Wzór na długość przekątnej sześcianu:
Wzór na długość przekątnej sześcianu:
2
6a
S
3
a
a
a
a
V
3
a
d
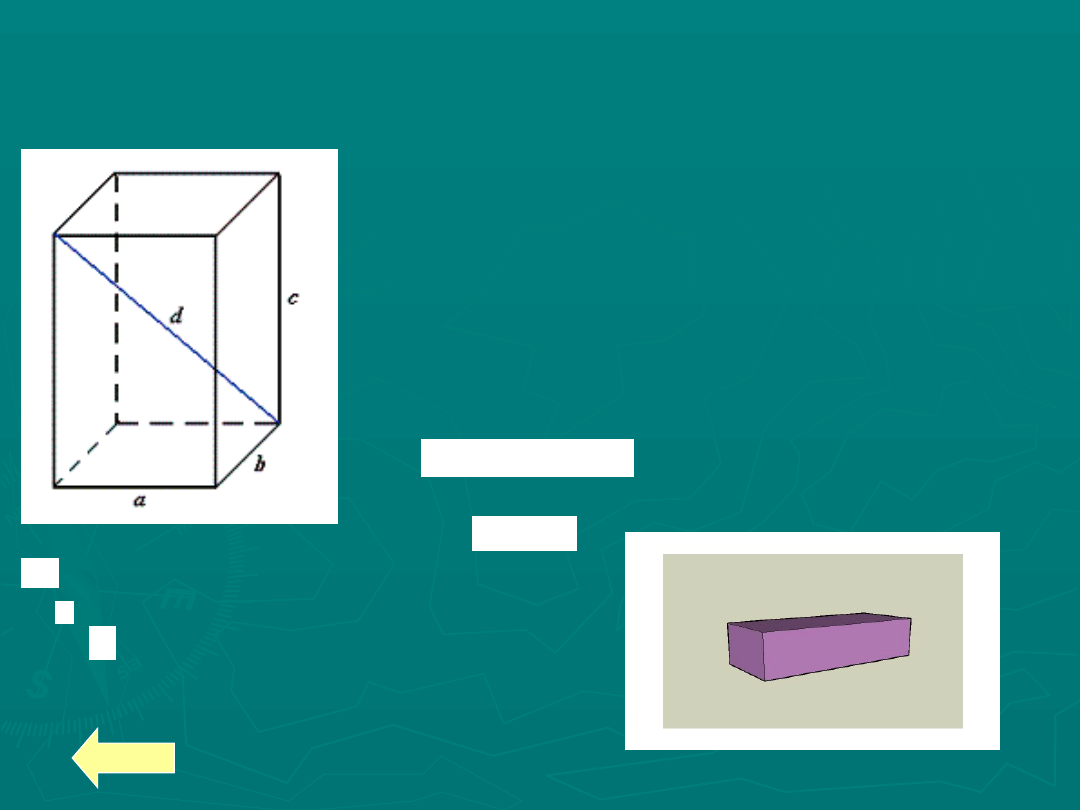
Prostopadłościan
Prostopadłościan
Graniastosłup prosty, którego podstawy są
Graniastosłup prosty, którego podstawy są
prostokątami nazywamy
prostokątami nazywamy
prostopadłościanem.
prostopadłościanem.
Prostopadłościan ma trzy wymiary:
Prostopadłościan ma trzy wymiary:
długość, szerokość i wysokość (
długość, szerokość i wysokość (
a
a
,
,
b
b
,
,
c
c
).
).
Każdy prostopadłościan ma 6 ścian (4
Każdy prostopadłościan ma 6 ścian (4
ściany boczne i 2 podstawy), 8
ściany boczne i 2 podstawy), 8
wierzchołków i 12 krawędzi.
wierzchołków i 12 krawędzi.
Pole powierzchni całkowitej
Pole powierzchni całkowitej
Objętość prostopadłościanu:
Objętość prostopadłościanu:
- krawędzie
- krawędzie
podstawy
podstawy
- krawędź boczna
- krawędź boczna
- przekątna
- przekątna
prostopadłościanu
prostopadłościanu
abc
V
ac
bc
ab
P
c
2
2
2
d
c
b
a,
Graniastosłupy pochyłe
Graniastosłupy pochyłe
Graniastosłup pochyły
Graniastosłup pochyły
to taki
to taki
graniastosłup, w którym krawędzie
graniastosłup, w którym krawędzie
boczne nie są prostopadłe do
boczne nie są prostopadłe do
podstaw, ale są do siebie
podstaw, ale są do siebie
równoległe.
równoległe.
W graniastosłupie pochyłym długość
W graniastosłupie pochyłym długość
wysokości jest mniejsza od długości
wysokości jest mniejsza od długości
krawędzi bocznej.
krawędzi bocznej.
Pole powierzchni i objętość takiej
Pole powierzchni i objętość takiej
figury obliczam z takiego samego
figury obliczam z takiego samego
wzoru, jak dla graniastosłupa
wzoru, jak dla graniastosłupa
prostego.
prostego.
OSTROSŁUPY
OSTROSŁUPY
P
C
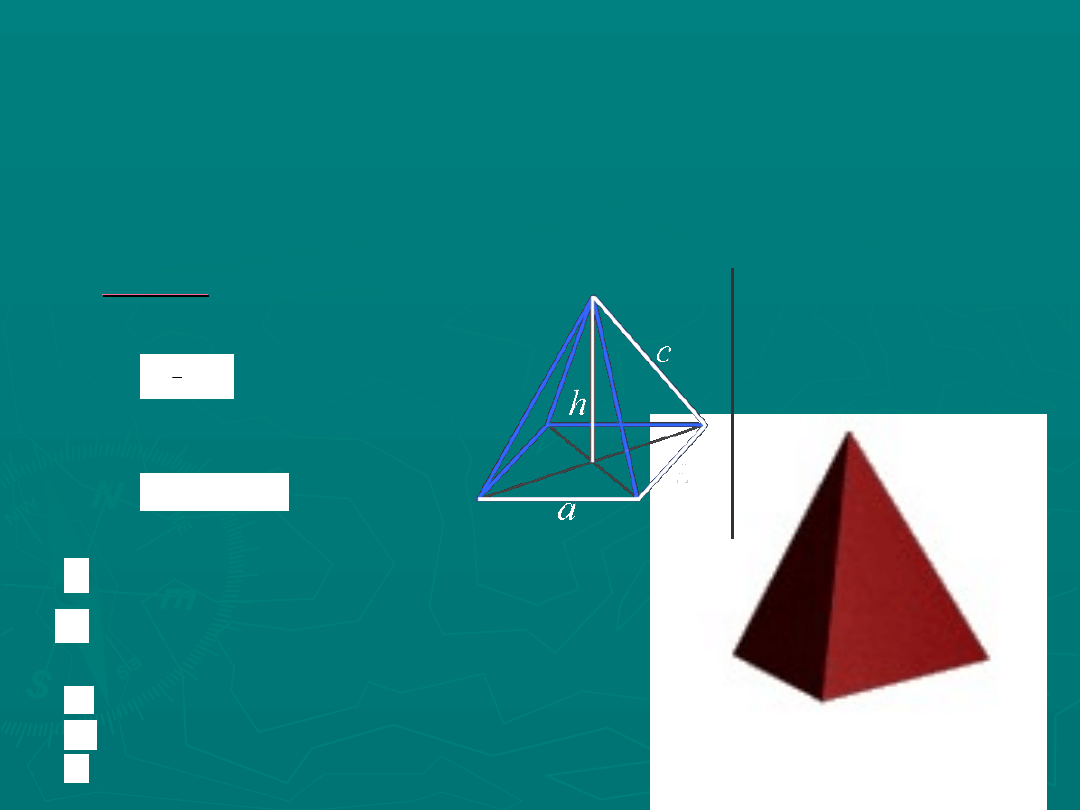
Ostrosłup
Ostrosłup
– bryła geometryczna w postaci wielościanu,
– bryła geometryczna w postaci wielościanu,
którego wszystkie ściany prócz podstawy zbiegają się w
którego wszystkie ściany prócz podstawy zbiegają się w
jednym punkcie zwanym wierzchołkiem.
jednym punkcie zwanym wierzchołkiem.
Wzory
Wzory
na objętość:
na objętość:
na pole powierzchni:
na pole powierzchni:
gdzie:
gdzie:
–
–
długość wysokości ostrosłupa,
długość wysokości ostrosłupa,
–
–
pole powierzchni bocznej (suma pól ścian
pole powierzchni bocznej (suma pól ścian
bocznych),
bocznych),
–
–
pole podstawy ostrosłupa,
pole podstawy ostrosłupa,
–
–
pole powierzchni całkowitej ostrosłupa,
pole powierzchni całkowitej ostrosłupa,
–
–
objętość ostrosłupa.
objętość ostrosłupa.
P
b
h
V
P
P
3
1
P
P
P
P
b
c
h
V
P
P
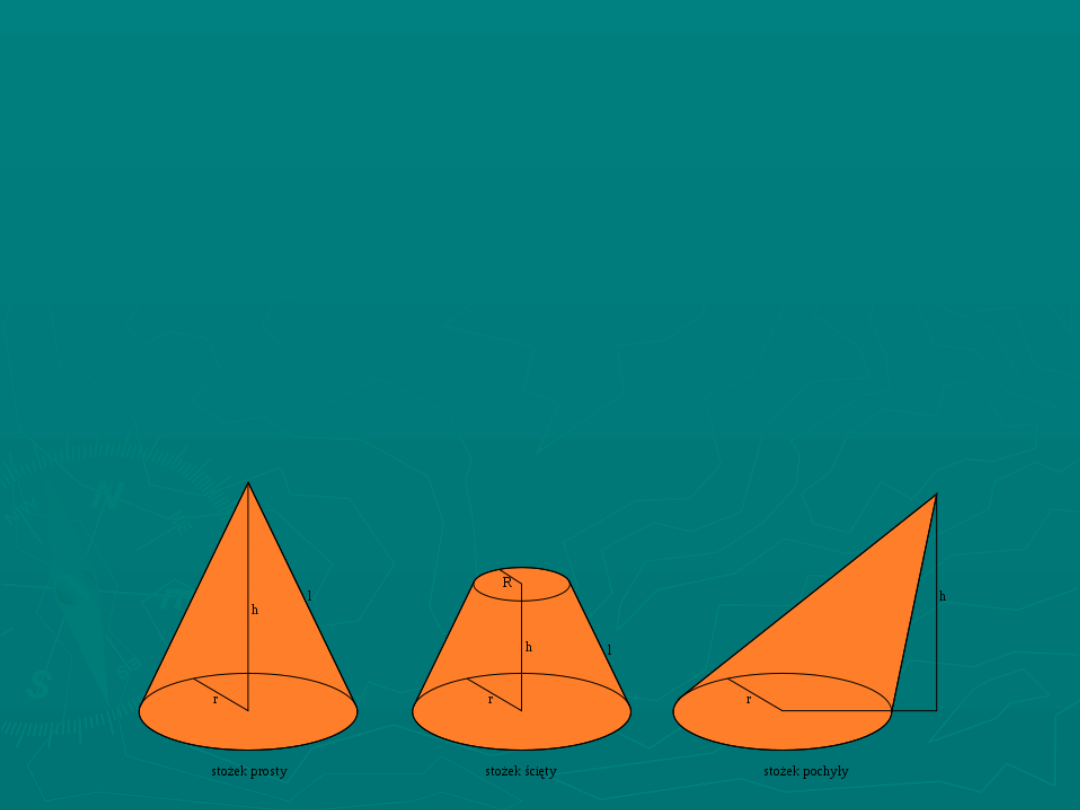
STOŻKI
STOŻKI
Stożek (dawniej
Stożek (dawniej
konus
konus
)
)
– bryła ograniczona przez
– bryła ograniczona przez
powierzchnię stożkową, której linia kierująca jest
powierzchnię stożkową, której linia kierująca jest
zamknięta, oraz przez płaszczyznę przecinającą
zamknięta, oraz przez płaszczyznę przecinającą
powierzchnię stożkową. Część płaszczyzny wycięta przez
powierzchnię stożkową. Część płaszczyzny wycięta przez
powierzchnię stożkową stanowi podstawę stożka. Może
powierzchnię stożkową stanowi podstawę stożka. Może
mieć ona kształt dowolnej figury płaskiej. Kierującą
mieć ona kształt dowolnej figury płaskiej. Kierującą
powierzchni stożkowej może być obwód podstawy.
powierzchni stożkowej może być obwód podstawy.
Wysokością stożka nazywamy odległość wierzchołka od
Wysokością stożka nazywamy odległość wierzchołka od
płaszczyzny podstawy.
płaszczyzny podstawy.
WALEC
WALEC
Walec
Walec
jest bryłą geometryczną ograniczoną powierzchnią
jest bryłą geometryczną ograniczoną powierzchnią
walcową i dwiema płaszczyznami nierównoległymi do jej
walcową i dwiema płaszczyznami nierównoległymi do jej
tworzącej. Jeżeli płaszczyzny są prostopadłe do tworzącej,
tworzącej. Jeżeli płaszczyzny są prostopadłe do tworzącej,
wówczas jest to
wówczas jest to
walec prosty
walec prosty
.
.
Walec kołowy
Walec kołowy
prosty
prosty
jest bryłą geometryczną powstałą w
jest bryłą geometryczną powstałą w
wyniku obrotu prostokąta wokół jednego z jego boków.
wyniku obrotu prostokąta wokół jednego z jego boków.
Podstawą walca oraz jego górną częścią jest koło, a jego
Podstawą walca oraz jego górną częścią jest koło, a jego
szerokość jest w każdym miejscu taka sama.
szerokość jest w każdym miejscu taka sama.
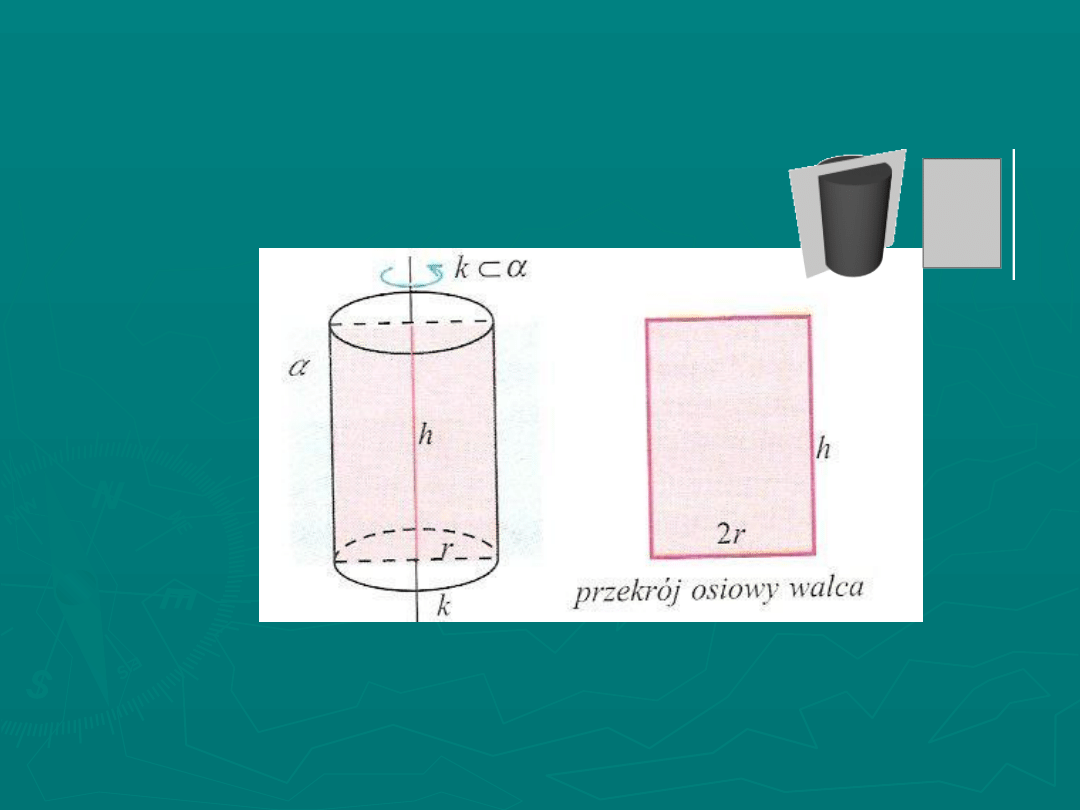
PRZEKRÓJ OSIOWY
PRZEKRÓJ OSIOWY
Przekrojem osiowym walca jest prostokąt.
Przekrojem osiowym walca jest prostokąt.
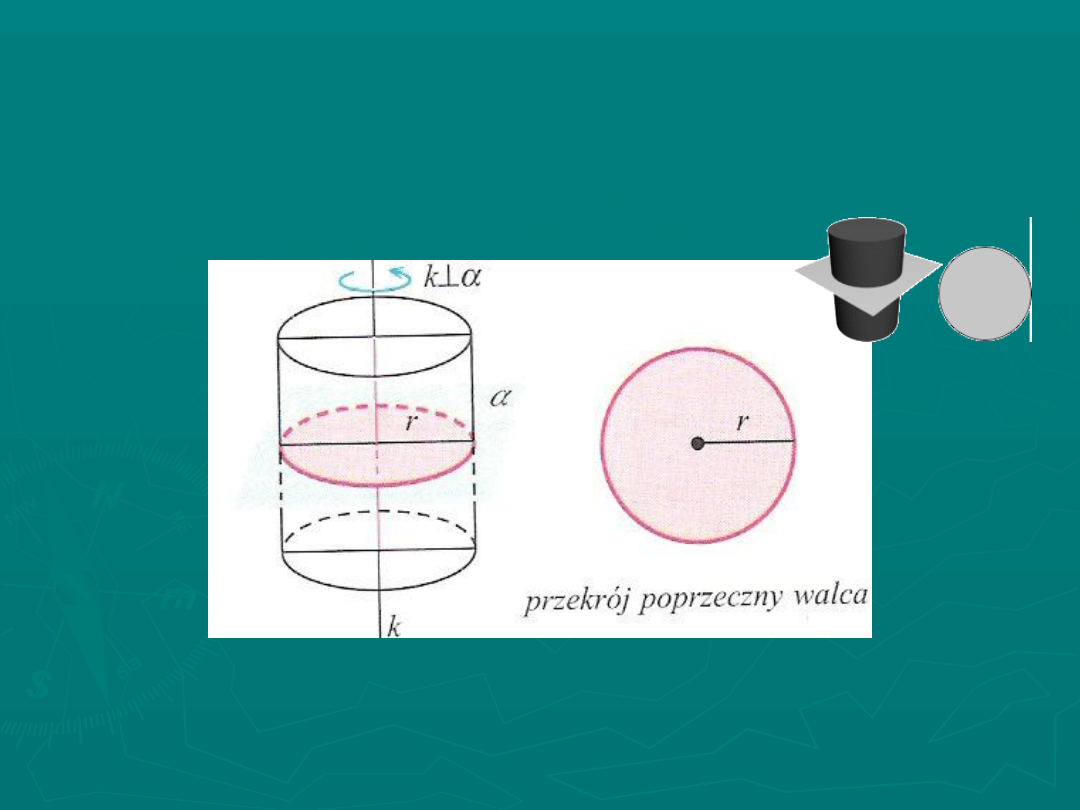
PRZEKRÓJ POPRZECZNY
PRZEKRÓJ POPRZECZNY
Przekrojem poprzecznym walca jest koło.
Przekrojem poprzecznym walca jest koło.
NA KONIEC…
NA KONIEC…
Zadanie 1
Zadanie 1
Bryły przedstawione na poniższych rysunkach to:
Bryły przedstawione na poniższych rysunkach to:
a) I - stożek, II - walec, III - ostrosłup, IV - graniastosłup
a) I - stożek, II - walec, III - ostrosłup, IV - graniastosłup
b) I - walec, II - ostrosłup, III - stożek, IV - graniastosłup
b) I - walec, II - ostrosłup, III - stożek, IV - graniastosłup
c) I - walec, II - stożek, III - graniastosłup, IV - ostrosłup
c) I - walec, II - stożek, III - graniastosłup, IV - ostrosłup
d) I - walec, II - stożek, III - ostrosłup, IV - graniastosłup
d) I - walec, II - stożek, III - ostrosłup, IV - graniastosłup
Zadanie 2
Zadanie 2
Które z poniższych zdań są fałszywe?
Które z poniższych zdań są fałszywe?
a) Ściany boczne graniastosłupów i ostrosłupów mogą być dowolnymi
a) Ściany boczne graniastosłupów i ostrosłupów mogą być dowolnymi
wielokątami.
wielokątami.
b) Ściany boczne graniastosłupów prostych są zawsze prostokątami.
b) Ściany boczne graniastosłupów prostych są zawsze prostokątami.
c) Podstawy graniastosłupów i ostrosłupów mogą być dowolnymi
c) Podstawy graniastosłupów i ostrosłupów mogą być dowolnymi
wielokątami.
wielokątami.
d) Podstawą walca i stożka jest koło.
d) Podstawą walca i stożka jest koło.
Zadanie 3
Zadanie 3
Łączna długość krawędzi prostopadłościanu o wymiarach 7cm, 2dm i 60mm wynosi:
Łączna długość krawędzi prostopadłościanu o wymiarach 7cm, 2dm i 60mm wynosi:
a) 99cm
a) 99cm
b) 33cm
b) 33cm
c) 276cm
c) 276cm
d) 132cm
d) 132cm
Zadanie 4
Zadanie 4
Na wykonanie szkieletu sześcianu zużyto 48cm drutu. Na wykonanie ścian tego sześcianu
Na wykonanie szkieletu sześcianu zużyto 48cm drutu. Na wykonanie ścian tego sześcianu
potrzebna jest tektura o łącznej powierzchni:
potrzebna jest tektura o łącznej powierzchni:
a) 16cm²
a) 16cm²
b) 288cm²
b) 288cm²
c) 96cm²
c) 96cm²
d) 48cm²
d) 48cm²
Zadanie 5
Zadanie 5
Objętość sześcianu o polu powierzchni całkowitej 150cm² wynosi:
Objętość sześcianu o polu powierzchni całkowitej 150cm² wynosi:
a) 150cm³
a) 150cm³
b) 25cm³
b) 25cm³
c) 625cm³
c) 625cm³
d) 125cm³
d) 125cm³
ODPOWIEDZI
ODPOWIEDZI
1.
1.
2.
2.
3.
3.
4.
4.
5.
5.
BIBLIOGRAFIA
BIBLIOGRAFIA
•
www.wikipedia.pl
www.wikipedia.pl
•
www.gwo.pl
www.gwo.pl
•
www.zobaczycmatematyke.krk.pl
www.zobaczycmatematyke.krk.pl
•
www.figuryprzestrzenne.pl
www.figuryprzestrzenne.pl
•
„
„
Encyklopedia matematyki” GREG
Encyklopedia matematyki” GREG
