GEODEZJA

Jedna z dziedzin nauki i techniki,

dominuje w niej wiedza o Ziemi,

wiedza o pomiarach wykonywanych w

celu zbierania informacji o kształcie i

wymiarach Ziemi, o powierzchni

Ziemi, jej szczegółach naturalnych

oraz budowlach na niej wzniesionych.

Geodezja, zajmuje się również

opracowaniem zbieranych

informacji w różnorodny sposób, a

następnie ich udostępnianiem.

Razem z rozwojem

cywilizacji zmieniały się

metody prac geodezyjnych od

prostych prac pomiarowych

wykonywanych za pomocą

pierwotnych przyrządów do
opracowań geodezyjnych

wykorzystujących obecnie

zdjęcia lotnicze, satelitarne.

Informacje geodezyjne są niezbędne do

prowadzenia jakiejkolwiek działalności

gospodarczej na powierzchni Ziemi:

 dla prac urządzeniowo-rolnych;
 do projektowania i realizowania wszelkiego

rodzaj budowli naziemnych i podziemnych;

 dla komunikacji i łączności;
 do celów poznawczych i naukowych

Podstawowe pojęcia używane w

geodezji:

powierzchnie odniesienia;
układy współrzędnych;
sieci i osnowy;
odwzorowanie.

Powierzchnie odniesienia

Podstawowym efektem prac geodezyjnych jest mapa,

czyli obraz fragmentu fizycznej powierzchni Ziemi na

płaszczyźnie. Aby formy regularne i nieregularne

Ziemi mogły odpowiadać ogólnemu kształtowi i

wymiarom bryły ziemskiej za powierzchnię przyjęto

elipsoidę obrotową.

Zidentyfikowanie powierzchni odniesienia, czyli

elipsoidy, polega na przyjęciu odpowiednich

wymiarów tej elipsoidy (długości większej i

mniejszej półosi) oraz zorientowaniu tej

elipsoidy względem bryły ziemskiej.

Jeśli informacje odniesione do elipsoidy chcemy

zobrazować na powierzchni znacznie prostszej,

jak kula lub płaszczyzna, to takie

przekształcenie nazywa się odwzorowaniem.

Przyjęcie elipsoidy odniesienia jest ściśle

związane za szczegółową znajomością geoidy.

Geoida jest powierzchnią ciągłą, jej kształt w

ogólności zbliżony do elipsoidy obrotowej

spłaszczonej na biegunach jest zależny od

rozmieszczenia mas w bryle ziemskiej i dlatego

jej zidentyfikowanie za pomocą funkcji

matematycznej jest niemożliwe. Wobec tego za

powierzchnię odniesienia przyjmuje się taką

elipsoidę obrotową, której wymiary są bardzo

zbliżone do wymiarów geoidy, a jej zorientowanie

względem geoidy pozwala na uzyskanie

minimalnych odstępów między tymi dwiema

powierzchniami.

Elipsoida obrotowa, której mała oś pokrywa się

z osią obrotu Ziemi, nazywa się elipsoidą

ziemską.

Parametry elipsoidy Karasowskiego

duża półoś a=6 378 245,000m

mała półoś b=6 356 863, 0188m

spłaszczenie p= =0,003 352 329 869

a

b

a

Układy współrzędnych

przyjmuje się w celu wyznaczania położeń

punktów na przyjętej powierzchni odniesienia.

Najczęściej stosowane są:

- układy współrzędnych geograficznych, które

dzielą się na: astronomiczne (,) i geodezyjne

(B,L)

- układ współrzędnych sferycznych biegunowych

(r, ,)

- układ współrzędnych

przestrzennych (x,y,z)

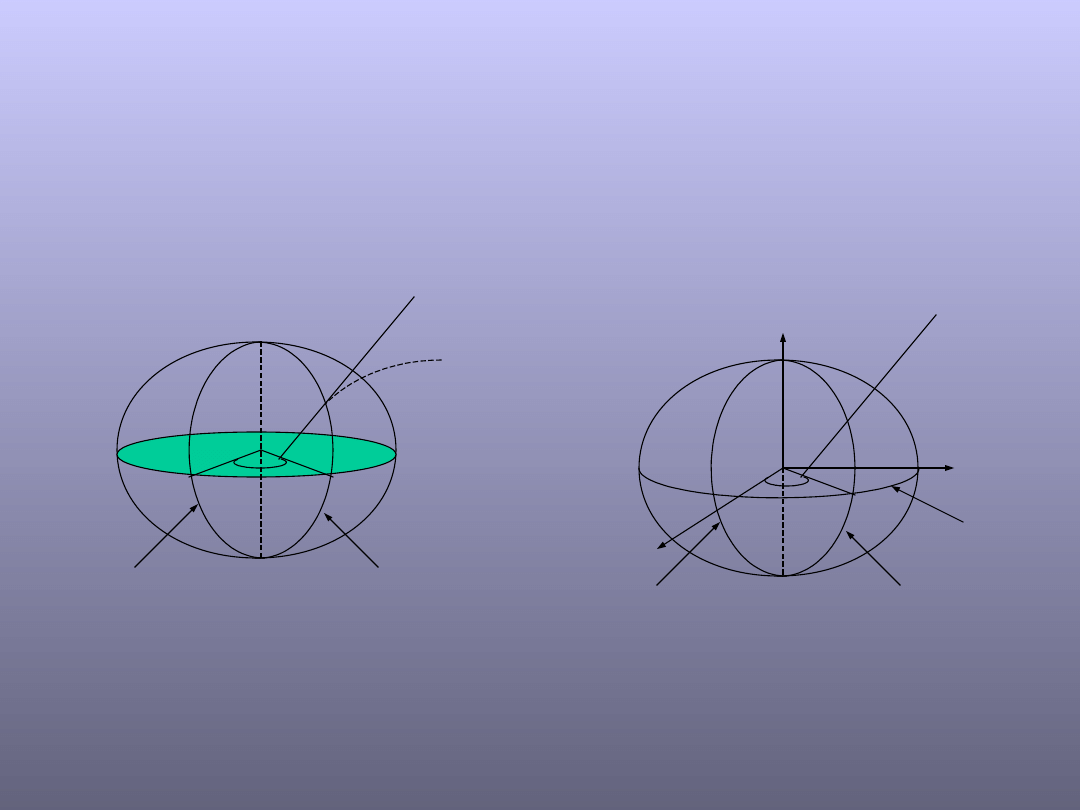
Współrzędne astronomiczne związane są z osią

obrotu Ziemi i linią pionu.

Współrzędne astronomiczne podlegają redukcji na geoidę,

redukcja ta polega na wprowadzeniu do współrzędnych

wyznaczonych z pomiarów astronomicznych poprawek ze

względu na ruchy bieguna i wpływ zakrzywienia linii pionu.

Zredukowane współrzędne przeniesione z geoidy na elipsoidę
odniesienia przez rzutowanie wzdłuż normalnych do elipsoidy

obrotowej dają w ostateczności współrzędne geograficzne

geodezyjne B,L.



południk zerowy
Greenwich

południk miejsca
obserwacji

st

yc

zn

a

do

l.

p

io

nu

l.pionu

B

B

południk zerowy
Greenwich

południk miejsca
obserwacji

no

rm

al

na

d

o

el

ip

so

id

y

równik

x

y

z

Układ współrzędnych geograficznych

astronomicznych ,

Układ współrzędnych geograficznych

geodezyjnych B,L

O

L

B

eli

ps

oi

da

ge

oi

da

Zależność pomiędzy współrzędnymi astronomicznymi

a współrzędnymi geodezyjnymi

B=-

L=-sec

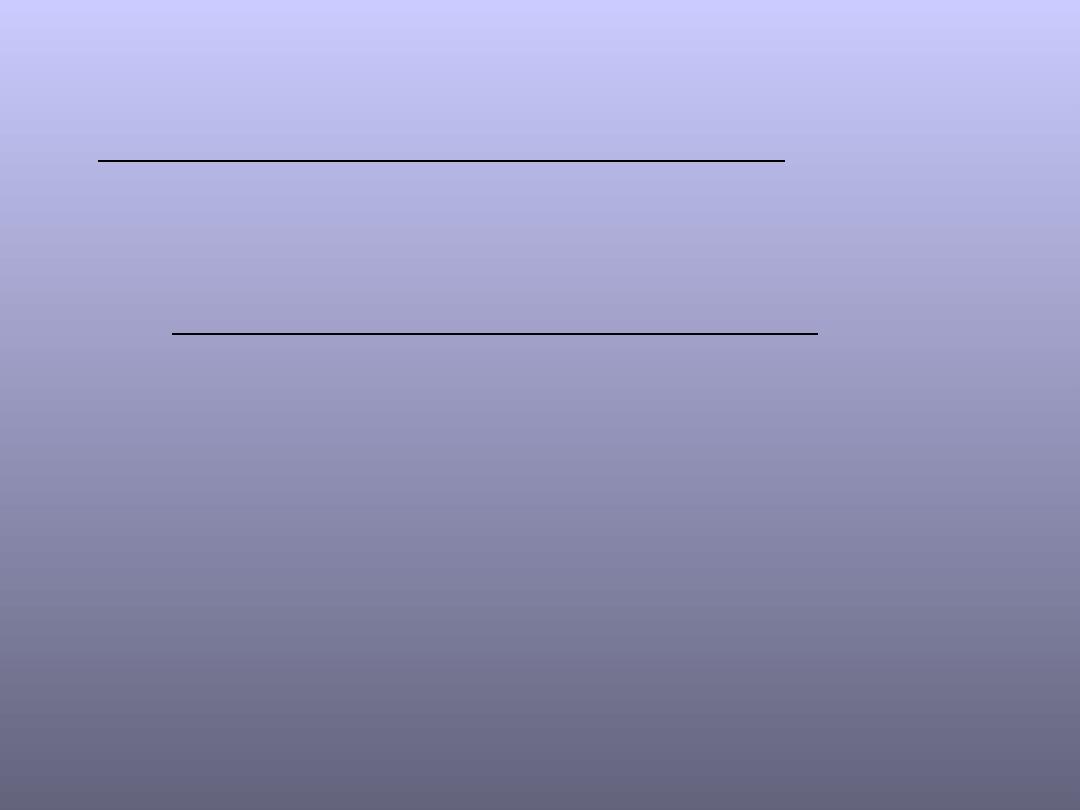
Szerokość geograficzna geodezyjna B punktu P to

kąt B, jaki tworzy normalna do elipsoidy

obrotowej (w punkcie rzutu punktu P na

powierzchnię elipsoidy) z płaszczyzną równika.

Długość geograficzna geodezyjna L to kąt

dwuścienny zawarty pomiędzy południkiem

zerowym a południkiem zawierającym punkt P.

Płaszczyzna południka geodezyjnego zawiera

normalną do elipsoidy w punkcie P i przechodzi

przez oś obrotu elipsoidy.

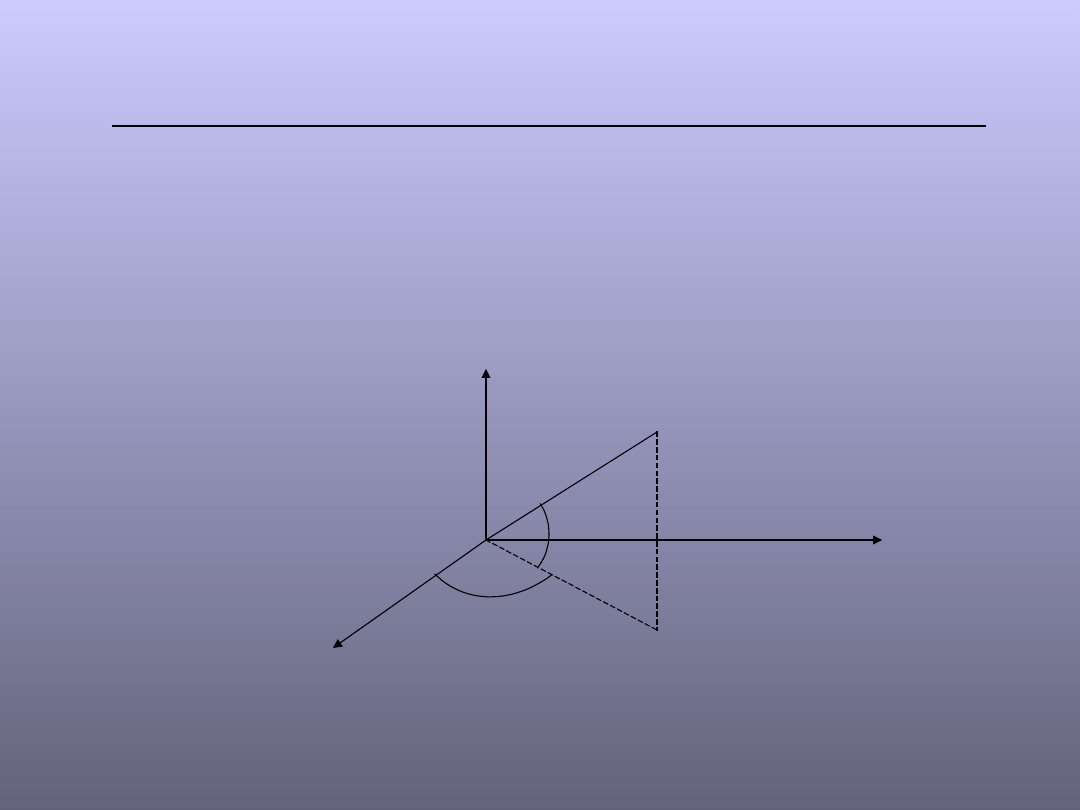
Układ współrzędnych sferycznych biegunowych

jest układem geocentrycznym. Oś z pokrywa się z

osią obrotu elipsoidy, płaszczyzna x,y jest

płaszczyzną równika, oś Ox leży w południku

przyjętym za zerowy. Kąt  jest szerokością

geocentryczną.

x

y

z

r

P

P`





Układ współrzędnych sferycznych biegunowych r, , , oraz

układ współrzędnych przestrzennych prostokątnych x,y,z.

Układ współrzędnych przestrzennych x,y,z jest

również układem geocentrycznym. Osie są

zdefiniowane tak samo, jak w układzie

współrzędnych biegunowych. Położenie punktu P

jest zdefiniowane przez podanie trzech

współrzędnych x

P

,y

P

,z

P

.

W wymienionych układach rozwiązuje się

zagadnienia związane z dużymi obszarami, na

przykład dla obszaru całego kraju lub kontynentu.

Sieci i osnowy geodezyjne

Zbiory punktów wraz z niezbędnymi o nich

informacjami tworzą sieci i osnowy

geodezyjne.

Punkty sieci i osnów geodezyjnych są jednolite

dla całego kraju. Oznaczone są w sposób

trwały na powierzchni lub niezbyt głęboko pod

powierzchnią gruntu i na podstawie pomiarów

geodezyjnych wyznacza się ich współrzędne.

Sieć pozioma lub wysokościowa jest to zbiór

punktów połączonych celowymi w konstrukcję

geodezyjną o określonej budowie geometrycznej

i określonych warunkach wyznaczania

współrzędnych x, y lub rzędnych z wszystkich

punktów. Wzdłuż celowych prowadzone są

obserwacje kątowe i liniowe, tylko kątowe lub

tylko liniowe, mogą być też wyznaczane różnice

wysokości metodą niwelacji geometrycznej lub

trygonometrycznej o określonej dokładności.

Osnowa pozioma lub wysokościowa jest to zbiór

punktów sytuacyjnych, wysokościowych lub

sytuacyjno-wysokościowych o znanych

współrzędnych x,y lub rzędnych z oraz o ustalonej

przepisami dokładności wyznaczenia punktu,

określonej dla danego typu osnowy błędami

średnimi kątów i długości albo błędami m

P

położenia

punktu w poziomie lub w pionie m

H

. Współrzędne i

rzędne x,y,z oraz błędy średnie ich wyznaczenia

uzyskuje się z wyrównania obserwacji geodezyjnych

wykonanych w sieciach charakteryzujących się

ustalonymi cechami konstrukcyjnymi i ustaloną

dokładnością obserwacji.

Odwzorowania

W związku z tym, iż nie istnieje układ

współrzędnych płaskich, w którym można

wiernie przedstawić wzajemne położenie

zbioru punktów określonych na elipsoidzie lub

na kuli powstało zagadnienie wybrania

odpowiedniego odwzorowania, czyli sposobu

przekształcenia współrzędnych punktów z

elipsoidy na współrzędne płaskie

odpowiadających im punktów na płaszczyźnie.

Odwzorowanie pozwala na przeliczenie współrzędnych z

jednego układu na inny układ oraz obliczenie poprawek

odwzorowawczych do elementów geometrycznych

określonych w pierwszym układzie, aby otrzymać

odpowiadające im elementy w drugim układzie.

Wyróżniamy następujące grupy odwzorowań kartograficznych:

-płaszczyznowe (azymutalne);

-walcowe;

-stożkowe;

-umowne (konwencjonalne, dowolne).

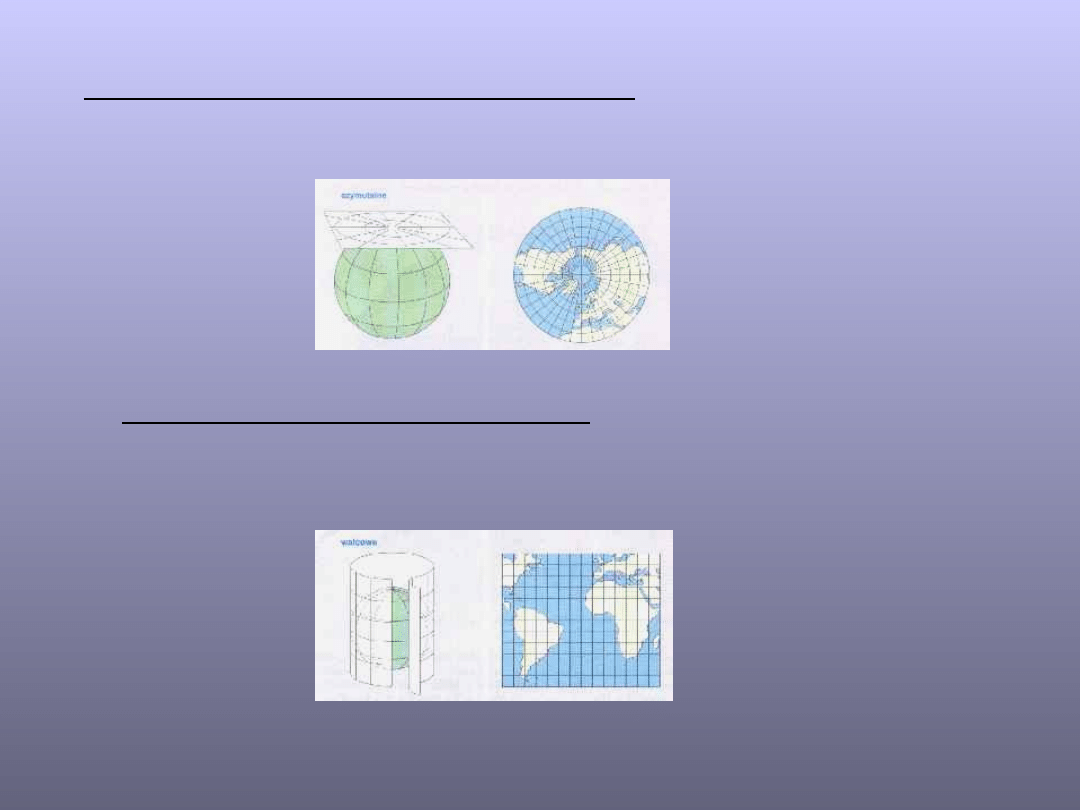
Odwzorowania płaszczyznowe powstają poprzez

bezpośrednie odtwarzanie (rzutowanie) oryginału
na przyłożonej płaszczyźnie.

W odwzorowaniu walcowym obraz oryginału
odtwarzany
jest na pobocznicy walca, którą następnie
rozwija się na płaszczyznę.

W odwzorowaniu stożkowym za powierzchnię pomocniczą,

na której odtwarza się oryginał, służy pobocznica stożka,
którą następnie rozwija się na płaszczyznę.

Odwzorowania umowne obejmują wszystkie inne powierzchnie
pomocnicze służące do odtwarzania obrazu oryginału, oprócz
trzech wcześniej wymienionych.

Do opracowania map topograficznych

terenów naszego kraju były stosowane

następujące odwzorowania kartograficzne:

-odwzorowanie wielościenne (rzut);
-odwzorowanie quasi-

stereograficzne;

-odwzorowanie Gaussa-Krugera.

Geodezja powiązana jest z dziedzinami takimi jak:
 Matematyka
 Geografia
 Fizyka
 Historia
 Ekonomia
 Biologia
 Astronomia
 Fotografia
 Budownictwo
 Inżynieria
 Informatyka