1

Właściwości

i przemiany

gazów

rzeczywistyc

h (a)

Waldemar Ufnalski

Wprowadzenie do termodynamiki

chemicznej

Wykład 9a

0,25

0,50

0,75

1,00

1,25

1,50

1,75

-1,0

-0,5

0,0

0,5

1,0

lg P/P

k

Z

1,0

1,25

1,50

2,0

4,0

0,9

0,8

0,7

2

9.1. Równania stanu

gazu

Wykład 9a

3

Model molekularny gazu

doskonałego...

• drobiny są kulami sprężystymi

poruszającymi się swobodnie

• zderzają się ze sobą i ściankami

naczynia

• objętość własna drobin jest pomijalna w

stosunku do objętości układu,

• drobiny nie oddziałują na siebie siłami

dalekie- go zasięgu.



równanie stanu gazu

doskonałego

nRT

PV 

(1
)

4

Oddziaływania van der Waalsa -
s

iły przyciągania natury

elektrostatycznej...

• trwałych dipoli cząsteczkowych (oddziaływania

orientacyjne - W. H. Keesom; 1912)



A

, 

B

- momenty dipolowe

drobin

•r - średnia odległość między
drobinami

(2
)

6

2

2

2

0

2

3

4

1

r

T

k

V

B

A

B

K























5

Oddziaływania van der Waalsa -
s

iły przyciągania natury

elektrostatycznej...

• trwałych dipoli cząsteczkowych i dipolami
wyin- dukowanymi przez nie w sąsiednich
drobinach polarnych lub niepolarnych
(oddziaływania pola- ryzacyjne - P. Deby’e;
1920)



A

, 

B

- polaryzowalność

drobin

(3
)

6

2

2

2

0

2

3

4

1

r

T

k

V

B

A

A

B

B

D





























6

Oddziaływania van der Waalsa -
s

iły przyciągania natury

elektrostatycznej...

• niepolarnych drobin w wyniku chwilowych
defor- macji sferycznej symetrii ładunków
elektrycznych (oddziaływania dyspersyjne - F.
London; 1930)

•I

A

, I

B

- pierwsza energia

jonizacji drobin

(4
)

6

2

0

2

3

4

1

r

I

I

I

I

V

B

A

B

A

B

A

L

























7

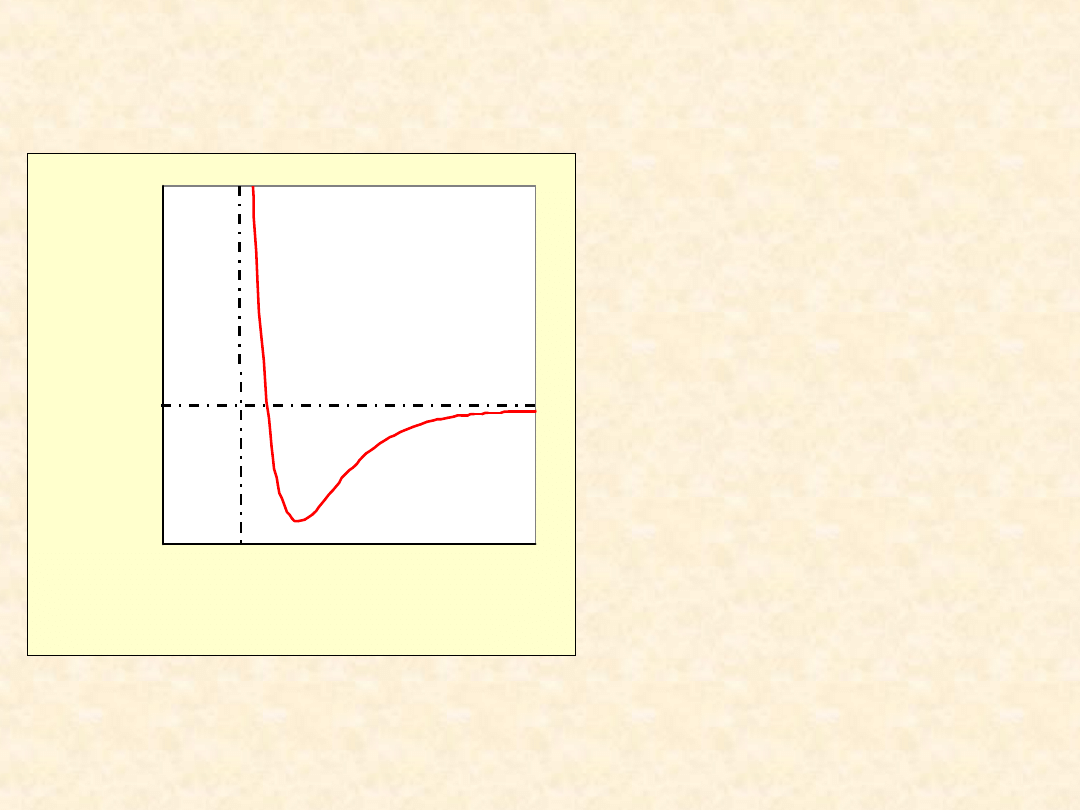
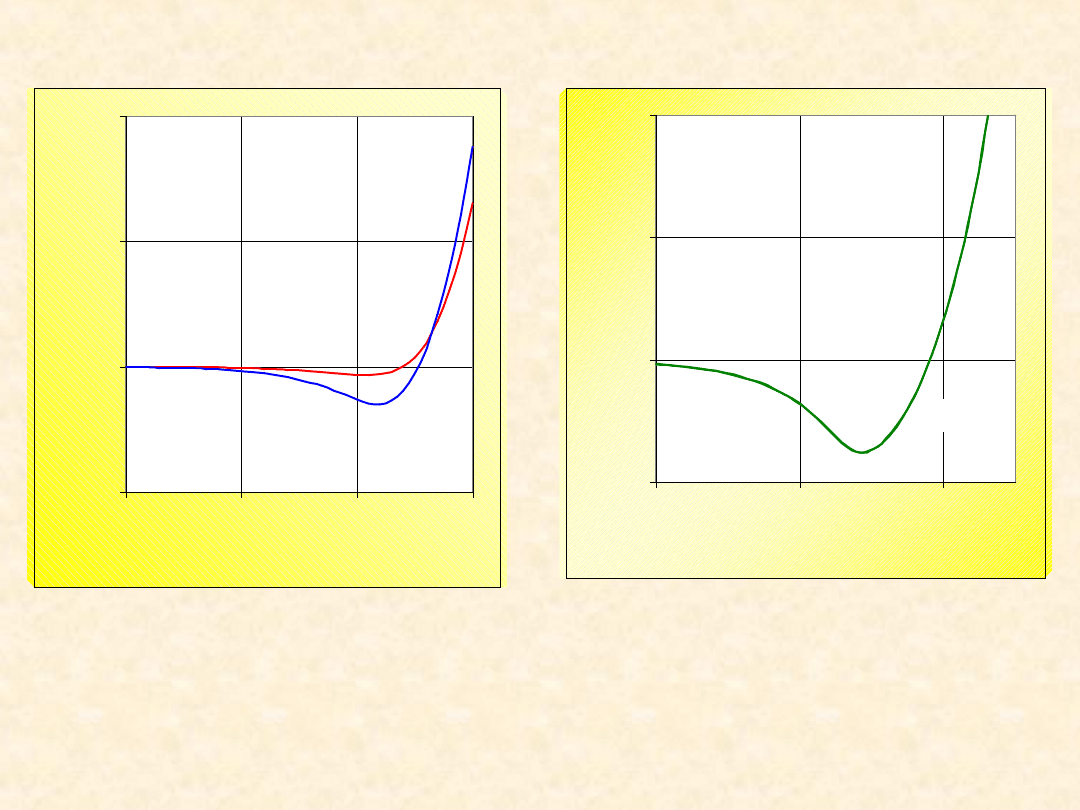
Energia potencjalna
oddziaływań

• wynik konkurencji
sił przyciągania
(van der Waalsa) i
odpychania powłok
elektronowych
(dominujących na
bar - dzo małych
odległoś - ciach)

-1200

-700

-200

300

800

1300

1800

0,25

1,25

2,25

r

V(r)

a

0

8

Równania stanu

(makroskopowa

miara odchy- leń od modelu gazu
doskonałego)...

•

Współczynnik kompresji gazu...

(5
)





RT

PV

P

T

Z

m



,

•indywidualna dla każdego gazu
funkcja tempe- ratury i ciśnienia

 

1

0







const

T

P

P

Z

lim

(6
)

9

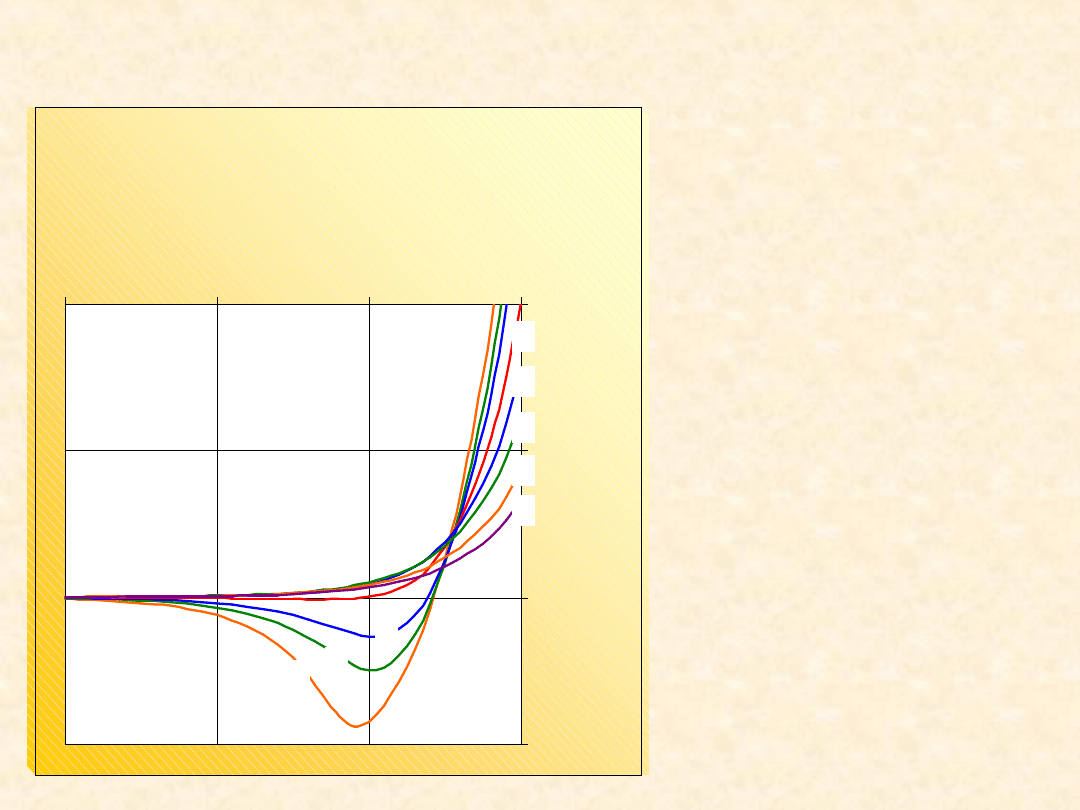
Równania
stanu ...

Współczynnik
kompresji
azotu w
temperaurze:

1 - 150 K
2 - 175 K
3 - 300 K
4 - 273,15 K
5 - 373,15 K
6 - 500 K
7 - 750 K
8 - 1000 K

0,50

1,00

1,50

2,00

5,0

6,0

7,0

8,0

lg P/Pa

Z

4

5

6

7

8

3

2

1

10

Równania
stanu...

•

Wirialne równania stanu - H. K. Onnes; 1901

(7
)

•B, B’, ... - współczynniki wirialne -
indywidual - na dla każdego gazu
funkcja temperatury

(8
)





 

 

 













3

2

1

m

m

m

V

T

D

V

T

C

V

T

B

P

T

Z ,





 

 











2

1

P

T

C

P

T

B

P

T

Z

'

'

,

11

.... wirialne równania stanu

(10
)

Współczynniki wirialne w obu
rozwinięciach łączą ze sobą
następujące zależności:

(9
)

 

 



;

'

;

'

;

'

3

2

2

2

2

3

RT

B

BC

D

D

RT

B

C

C

RT

B

B













Wirialne równanie stanu dla

umiarkowanych ciśnień





 

 

 

RT

P

T

B

P

T

B

V

T

B

RT

PV

P

T

Z

m

m















1

1

1

'

,

 

P

T

B

RT

PV

m





12

-120,0

-80,0

-40,0

0,0

0

200

400

600

T/K

B

/(

c

m

3

/m

o

l)

1

2

3

4

5

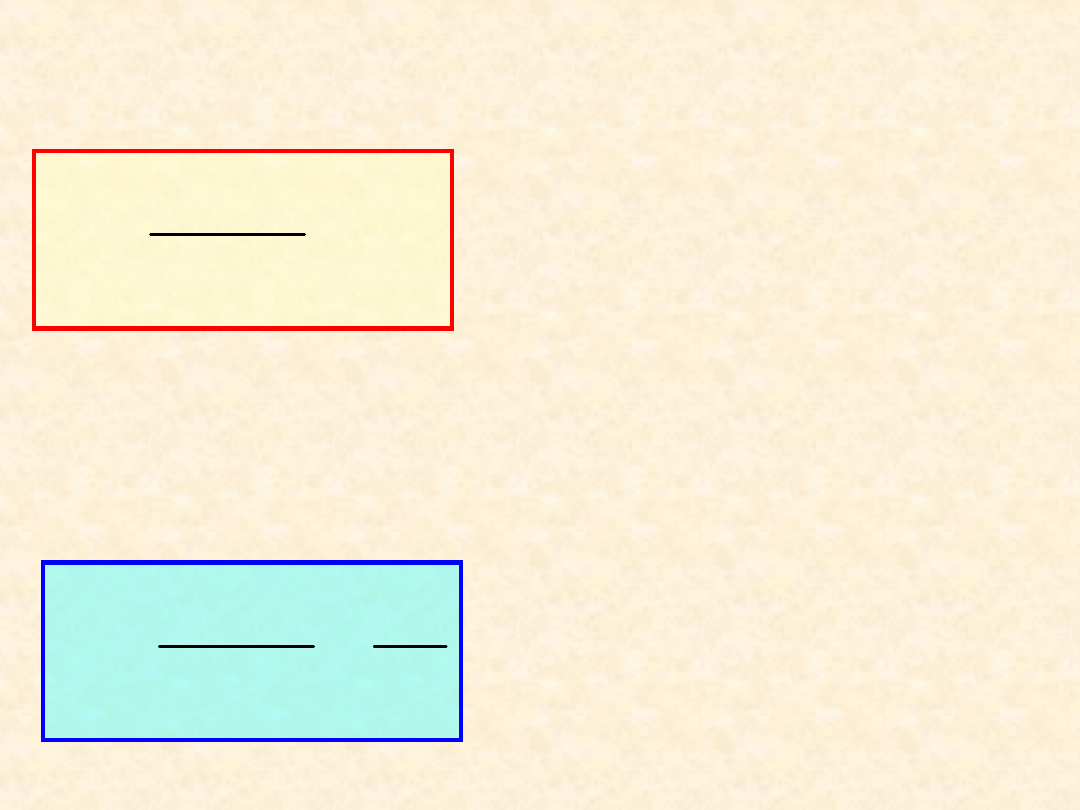
Zależność drugiego współczynnika

wirialnego od temperatury

1 - Ar
2 - CF

4

3 -
CH

4

4 - H

2

5 - N

2

Temperatura Boyle’a

B(T

B

) = 0

13

Równania
stanu...

•

J. D. van der Waals (1873) - forma ogólna:

(1
1)

b - poprawka na
objętość własną
drobin

P - ciśnienie

wewnętrzne
(poprawka na siły
przycią - gania
drobin)

(12
)

P

b

V

RT

P

m









•

J. D. van der Waals (1873) - forma szczególna:

2

m

m

V

a

b

V

RT

P







a, b - stałe
indywidualne dla
gazu

14

Równania
stanu...

•

sześcienne równania stanu - forma ogólna:

(1
3)

(14
)

• J. D. van der Waals - forma szczególna:

0

2

3















Z

Z

Z

0

2

3

















 



P

ab

V

P

a

V

P

RT

b

V

m

m

m

 

 

0

1

3

2

2

2

3























RT

abP

Z

RT

aP

Z

RT

bP

Z

15

Wybrane sześcienne równania
stanu...

(1
5)

(16
)

• van der Waals (vdW); 1873:

2

m

V

a

P 



• Berthelot (B); 1899:

2

m

TV

a

P 



• Redlich - Kwong
(RK); 1899:





b

V

V

T

a

P

m

m







2

1

(17
)

16

Wybrane sześcienne równania
stanu...

(1
8)

(19
)

• Soawe - Redlich -
Kwong (SRK); 1972:

• Lee - Erdbar -
Edminster (LEE);
1973:

 





b

V

V

T

P

m

m

SRK









 

 











b

V

b

V

T

m

V

T

P

m

m

m

LEE

















17

Wybrane sześcienne równania
stanu...

(2
0)

(21
)

• Peng - Robinson
(PR); 1976:

• Patel - Teja
(PT); 1981:

 



 



b

V

b

b

V

V

T

P

m

m

m

PR













 



 



b

V

c

b

V

V

T

P

m

m

m

PT













18

9.2. Zredukowane

równania stanu

Wykład 9a

19

V

m

P

V

k

P

k

Redukcja dwuparametrowego
równania stanu...

(22
a)

Cel: wyrażenie indywidualnych parametrów
(a,b) za pomocą parametrów krytycznych

Postępowanie:

W punkcie krytycznym
izoterma krytyczna ma
płaski punkt przegięcia:

0



















T

m

V

P

0

2

2



















T

m

V

P

(22
b)



20

Redukcja równania van der Waalsa...

(23
a)

Postępowanie:

(23
b)

2

m

m

V

a

b

V

RT

P











3

2

2

m

m

T

m

V

a

b

V

RT

V

P





























4

3

2

2

6

2

m

m

T

m

V

a

b

V

RT

V

P























(23
c)

21

Redukcja równania van der Waalsa...

(24
a)

W punkcie krytycznym (P

k

, V

k

, T

k

)

spełniony musi być układ trzech równań

(24
b)

(24
c)

2

k

k

k

k

V

a

b

V

RT

P











0

2

3

2









k

k

k

V

a

b

V

RT





0

6

2

4

3







k

k

k

V

a

b

V

RT

22

;

;

;

k

r

k

r

k

r

V

V

V

T

T

T

P

P

P







Redukcja równania van der Waalsa...

(25
)

Rozwiązanie układu równań (24a/b/c):

(2
6)

(2
7)

k

k

k

k

P

T

R

V

P

a

64

27

3

2

2

2





k

k

k

P

RT

V

b

8

3





k

k

k

T

V

P

R

3

8



Podstawienie (25) do (23a)



2

3

1

3

3

8

r

r

r

r

V

V

T

P







Zredukowane równanie
van der Waalsa

Parametry zredukowane

23

Zredukowane równanie van der
Waalsa...

Współczynnik kompresji



(2
9)

(2
8)

2

3

1

3

3

8

r

r

r

r

V

V

T

P











0

1

2

3











AB

AZ

Z

B

Z

64

27

2

r

r

T

P

A

r

r

T

P

B

8



24

Zredukowane równanie van der
Waalsa...

Krytyczny współczynnik kompresji



(3
0)

375

0

8

3

,







k

k

k

k

RT

V

P

Z

Pły n

H e

H

2

A r

N

2

O

2

Z

k

0,319 0,305 0,291 0,290 0,288

Pły n C O

2

H

2

O C H

4

C

2

H

4

C

2

H

6

Z

k

0,287 0,229 0,288 0,276 0,285

Wniosek: Równanie vdW nie opisuje ilościowo
relacji PVT w otoczeniu punktu krytycznego.

25

Zredukowane równanie Redlicha -
Kwonga...

(3
1)





b

V

V

T

a

b

V

RT

P

m

m

m









2

1





k

k

P

T

R

a

2

5

3

1

2

1

2

9

1









k

k

k

V

P

RT

b

1

2

3

1

2

3

1

3

1









k

k

k

T

V

P

R

3



(3
2)



 











1

2

1

2

1

1

2

3

3

1

2

1

3

1

3

1















r

r

r

r

r

r

V

V

T

V

T

P

(3
3)

26

Zredukowane równanie Redlicha -
Kwonga...

Współczynnik kompresji



(3
4)





0

2

3













AB

Z

B

B

A

Z

Z

 

2

5

3

1

1

2

9

1

r

r

T

P

A





r

r

T

P

B=

3

1

2

3

1



Krytyczny współczynnik kompresji



333

0

3

1

,







k

k

k

k

RT

V

P

Z

(3
5)

27

Zredukowane równanie Berthelota...

(3
6)

Krytyczny współczynnik kompresji



(3
7)

2

m

m

TV

a

b

V

RT

P







k

k

k

T

V

P

a

2

3



3

k

V

b

k

k

k

T

V

P

R

3

8



375

0

8

3

,







k

k

k

k

RT

V

P

Z

28

Zredukowane równanie Berthelota...

(3
8)

(3
9)

281

0

32

9

,





k

Z

Poprawienie dopasowania

k

k

k

T

V

P

a

2

3

16



4

k

V

b

k

k

k

T

V

P

R

9

32







r

r

r

r

r

T

V

V

T

P

9

32

4

1

3

16

2













 



































2

6

1

128

9

1

r

r

r

m

T

T

P

RT

PV

Z

Dla P

r

< 1 oraz T

r

> 1 - forma przybliżona:

29

9.3. Zasada stanów

odpowiadających sobie

Wykład 9a

30

Zasada stanów odpowiadających
sobie...

•Dwa gazy opisane zredukowanym równaniem
stanu, znajdujące się w stanach o takich
samych wartościach dwóch parametrów
zredukowanych (np. T

r

,P

r

) mają identyczną

wartość trzeciego parametru zredukowanego
(V

r

) oraz współczyn -nika kompresji

•Własności różnych gazów należy porównywać
w

stanach odpowiadających sobie

czyli

opisanych identycznymi wartościami
temperatury zreduko - wanej i ciśnienia
zredukowanego (a nie tempera - tury i
ciśnienia).

31

Zasada stanów odpowiadających
sobie...

0,5

1,0

1,5

2,0

-1,0

0,0

1,0

lg P/P

k

Z

Ar

CH

4

0,5

1,0

1,5

2,0

5,0

6,0

7,0

8,0

lg P/Pa

Z

Ar

CH

4

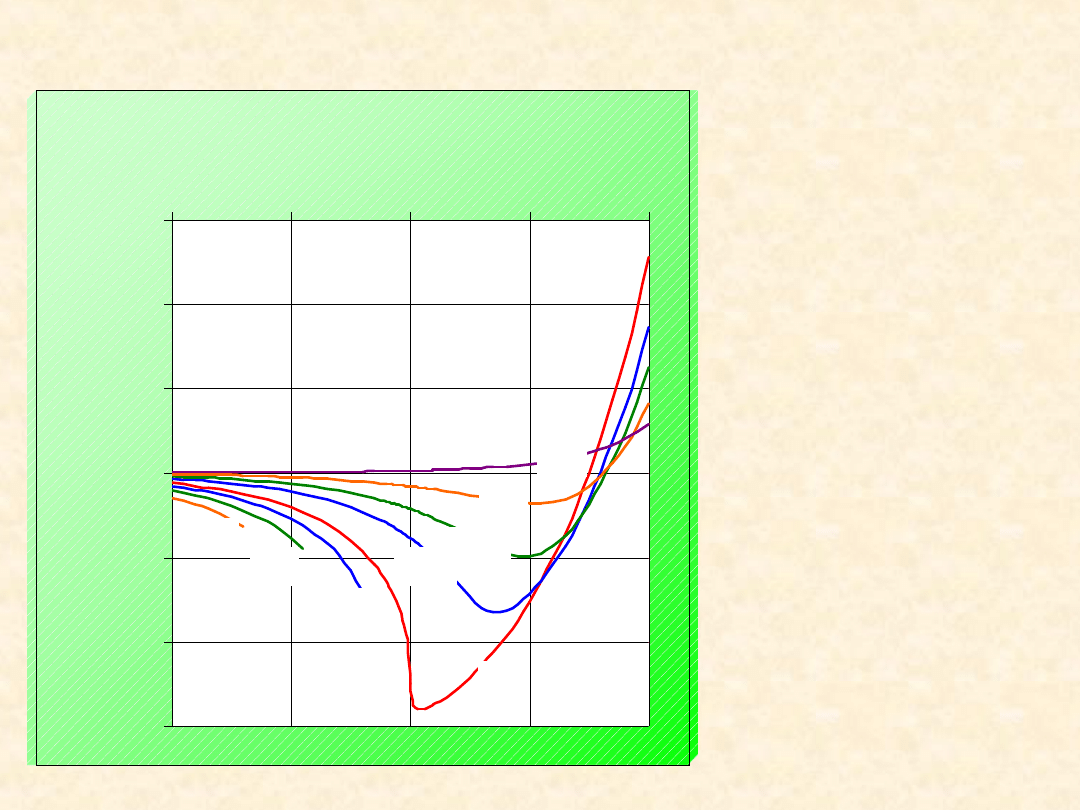
Zależność współczynnika kompresji argonu

i metanu od ciśnienia ...

w temperaturze zredukowanej T

r

=

1,25

w temperaturze T =300 K

32

Zasada stanów odpowiadających
sobie...

Uogólniony
wykres
współczynnika
kompresji gazu
van der Waalsa

Wykreślono
izotermy
zredukowane (dla
podanych wartości
T

r

)

0,25

0,50

0,75

1,00

1,25

1,50

1,75

-1,0

-0,5

0,0

0,5

1,0

lg P/P

k

Z

1,0

1,25

1,50

2,0

4,0

0,9

0,8

0,7

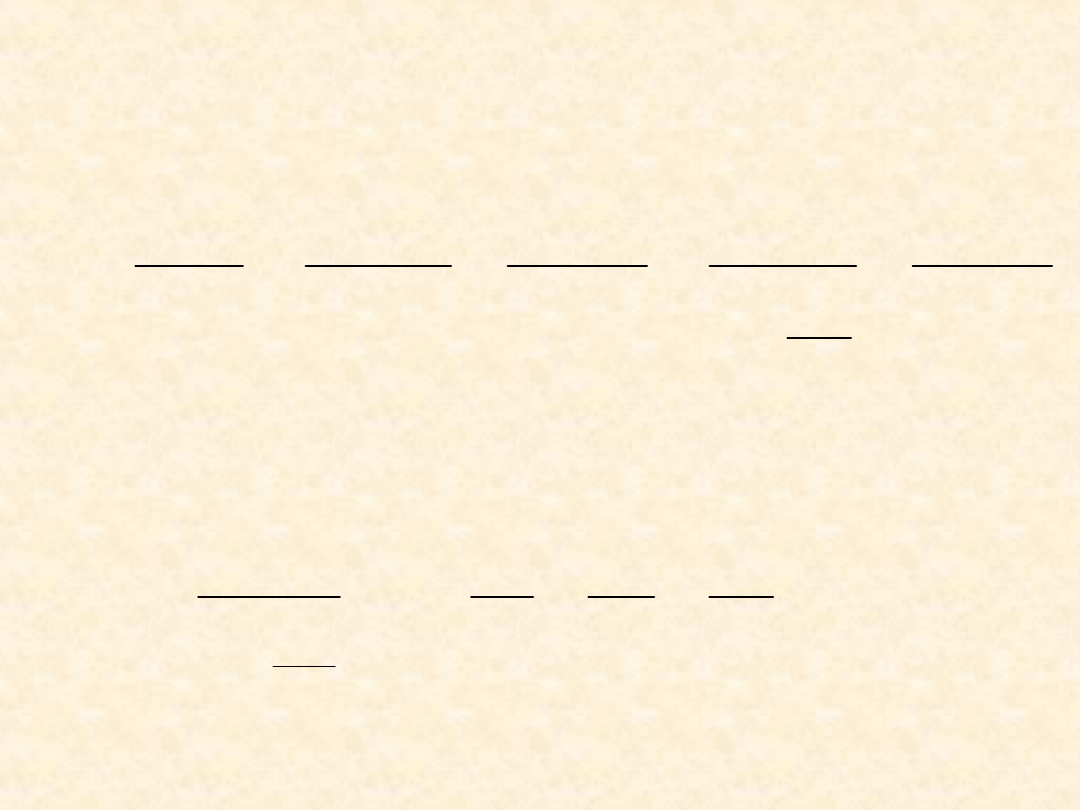
33

Zasada stanów odpowiadających
sobie...

Drugi współczynnik wirialny i temperatura
Boyle’a gazu van der Waalsa...

m

m

m

m

m

m

RTV

a

V

b

RTV

a

b

V

V

RT

PV

Z















1

1

(4
0)

Rozwinięcie w szereg Taylora

















3

3

2

2

1

1

1

m

m

m

m

V

b

V

b

V

b

V

b

(4
1)

34

Drugi współczynnik wirialny i temperatura
Boyle’a gazu van der Waalsa...

(4
2)

(4
3)

















3

3

2

2

1

m

m

m

V

b

V

b

V

RT

a

b

Z

RT

a

b

T

B





)

(

 

r

k

r

r

T

V

B

T

B

8

9

3

1







375

3

8

27

,

.







k

B

r

B

T

T

T







(4
4)

(4
5)

35

-1,00

-0,75

-0,50

-0,25

0,00

0,0

1,0

2,0

3,0

4,0

T/T

k

B

/V

k

1

2

3

4

5

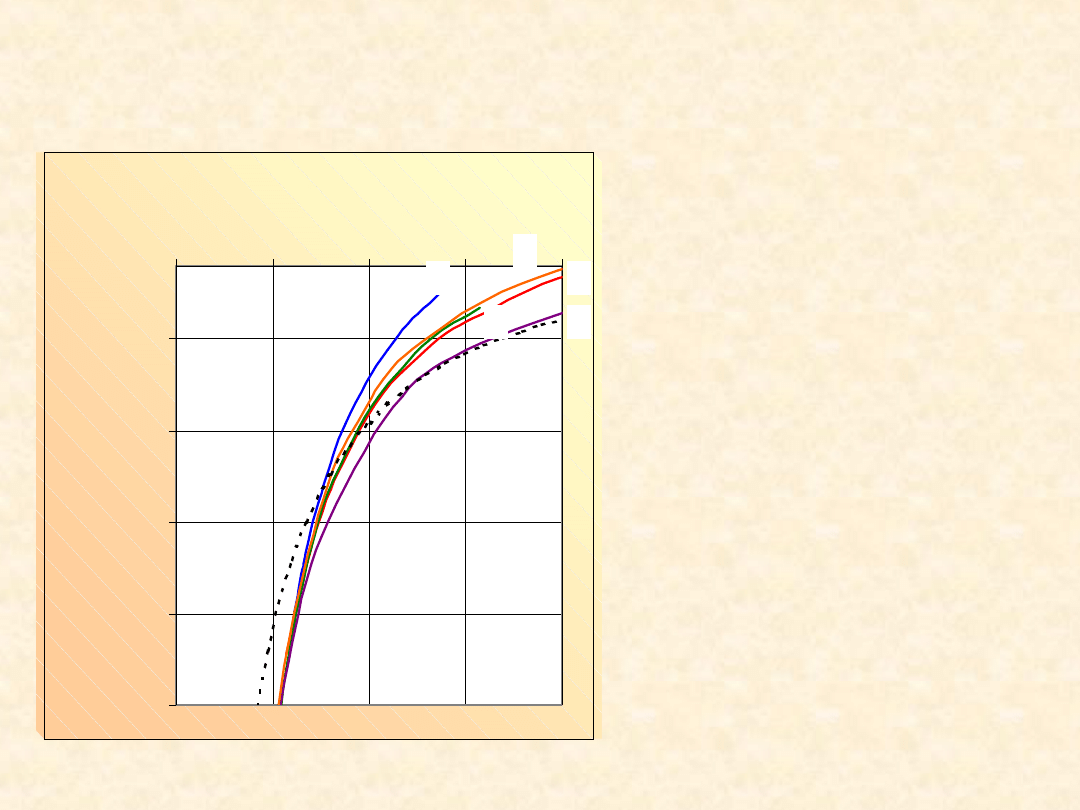
Drugi współczynnik wirialny i temperatura
Boyle’a gazu van der Waalsa...

1- Ar
2 - CF

4

3 - CH

4

4 - H

2

5 - N

2

---- - obliczona
(44)

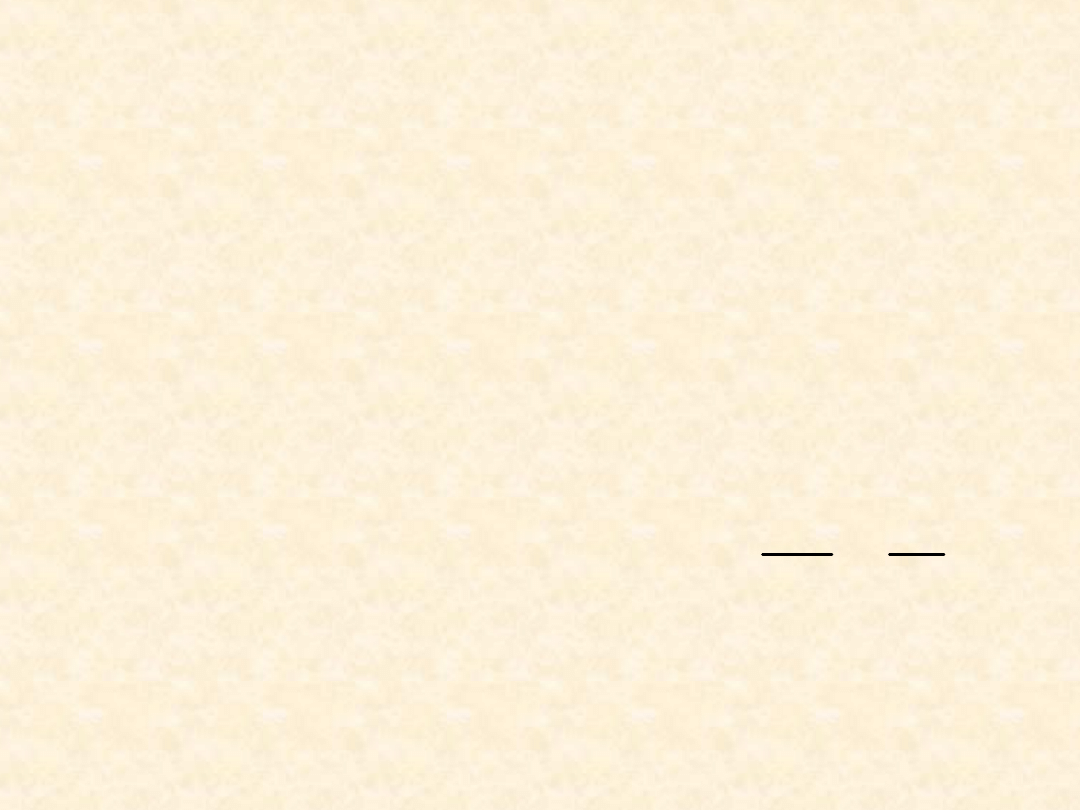
36

Zasada stanów odpowiadających
sobie...

Analiza metodami termodynamiki statystycznej...

•Energia potencjalna oddziaływania dwóch drobin
(V) musi być funkcją wyłącznie odległości środków
ich mas (r) - warunek taki mogą spełniać w
przybliżeniu drobi- ny o symetrii zbliżonej do
kulistej.
•Zależność V(r) daje się opisać wspólnym wzorem
zawierającym wyłącznie stałe indywidualne dla gazu;
np. wzorem Lennarda - Jonesa

 

6

12

r

k

r

l

r

V

i

i





•

Pomijalne są efekty kwantowe, tzn. V(r)

opisuje funkcja ciągła.

37

Zasada stanów odpowiadających
sobie...

Poprawienie „dopasowania” przez wprowadzenie
parametru będącego miarą asymetrii drobin -

czyn- nik acentryczny K. S. Pitzera

(1955)....

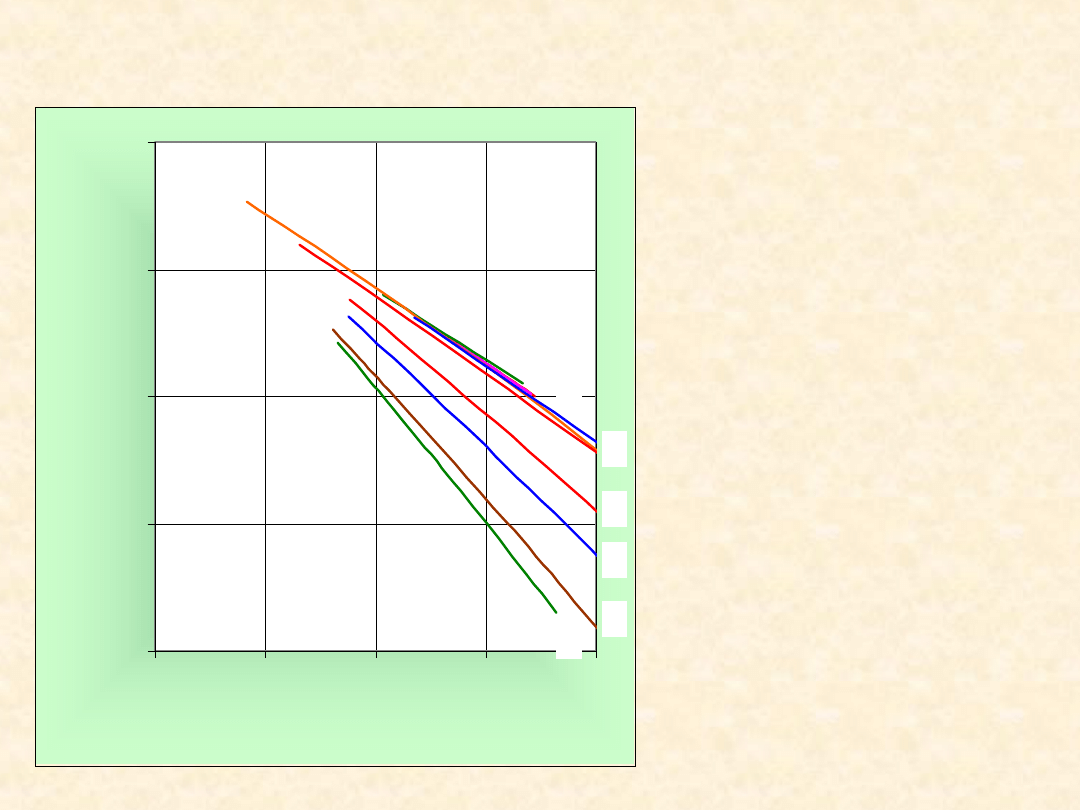
Formalna ekstrapolacja równania Clausiusa -
Clapeyrona do punktu krytycznego...

1











 





T

T

RT

H

P

P

k

k

p

k

ln

















r

r

T

a

P

1

1

ln

(46a
)

(46
b)

38

Zasada stanów odpowiadających
sobie...

0 - Ar, Ne, Kr
1 - CO, CH

4

,

N

2

2 - n - butan
3 - H

2

O

4 - metanol
5 - etanol

-4,0

-3,0

-2,0

-1,0

0,0

1,00

1,25

1,50

1,75

2,00

T

k

/T

L

g

(

P

/P

k

)

0

1

2

3

4

5

Zredukowana
prężność pary
nasyconej

39

Zasada stanów odpowiadających
sobie...

Zredukowana prężność pary nasyconej helowców...

70

0,



k

T

T

10

0,



k

P

P

0

1

70

0

,

)

,

(

lg







r

r

T

P

(47)





Czynnik acentryczny zdefiniowany jako...





00

1

70

0

,

,

lg









r

r

T

P



Pły n

A r

C H

4

C O

C O

2

H

2

O

C H

3

O H



-0,002 0,013 0,041 0,225 0,348 0,556

40

Trójparametrowa (rozszerzona)
zasada stanów odpowiadających
sobie - Pitzer (1955)

(48)

Tablice B. I. Lee oraz M. G. Keeslera
(1975) oraz równania interpolacyjne
udostępniają wartości z

(0)

oraz z

(1)























r

r

r

r

r

r

P

T

z

P

T

z

P

T

z

Z

,

,

,

)

(

)

(

)

(

2

2

1

0





41

9.4. Zredukowane

równania stanu

uwzględniające czynnik

acentryczny

Wykład 9a

42

Równanie Soave - Redlicha -
Kwonga...

(4
9)

(50
)





b

V

V

a

b

V

RT

P

m

m

m









Forma ogólna:

Skorelowane współczynniki:

c

a

a









 

 

k

k

k

k

c

P

RT

P

RT

a

2

2

42748

0

1

2

9

1

3

1

,



















2

2

1

15613

0

55171

1

48508

0

1

r

T

















,

,

,

k

k

k

k

P

RT

P

RT

b

08664

0

3

1

2

3

1

,







43

Równanie Soave - Redlicha -
Kwonga...

(51
a)

Współczynnik kompresji:





0

2

2

3













AB

Z

B

B

A

Z

Z

 

2

2

1

42748

0

2

9

1

3

1

r

r

r

r

T

P

T

P

A





,







r

r

r

r

T

P

T

P

B=

008664

0

3

1

2

3

1

,





(51
b)

(51
c)

44

Równanie Penga - Robinsona...

(5
2)

(53
)

Forma ogólna:

Skorelowane współczynniki:



 



b

V

b

b

V

V

a

b

V

RT

P

m

m

m

m













c

a

a





 

k

k

c

P

RT

a

2

45724

0,















2

2

1

26992

0

54226

1

37464

0

1

r

T

















,

,

,

k

k

P

RT

b

07780

0,



45

Równanie Penga - Robinsona...

(54
a)

Współczynnik kompresji:







 



0

2

3

1

3

2

2

2

3



















B

B

AB

Z

B

B

A

Z

B

Z

2

42572

0

r

r

T

P

A



,



r

r

T

P

B= 007780

0,

(54
b)

(54
c)

46

Dzielny nauczyciel umie innych

nauczyć nawet tego, na czym sam się

nie zna.

Tadeusz Kotarbiński, (1886 – 1981), filozof,

logik i prakseolog polski.