Podstawy sygnałów
pomiarowych i metrologii

Wyznaczanie cech
funkcyjnych sygnałów
pomiarowych

Cel

Celem ćwiczenia jest praktyczne
zapoznanie się z najczęściej
spotykanymi metodami wyznaczania
cech funkcyjnych sygnałów
pomiarowych. W ćwiczeniu
omówione zostaną: rodzaje sygnałów
pomiarowych, dziedziny ich
występowania oraz cechy funkcyjne.

Wstęp teoretyczny

Sygnałem nazywamy przebieg
dowolnej funkcji mogącej być
nośnikiem informacji.
Opis sygnału dokonywany jest za
pomocą zbioru cech punktowych i
funkcyjnych.

Sygnały mogą być opisane w trzech
dziedzinach:

czasu,
częstotliwości,
modalnej.

Sygnał może być opisany za pomocą
zbioru cech
<nazwa cechy, wartość cechy>.

Dziedzina czasu

Jest to dziedzina, w której
tradycyjnie dokonuje się opisu
sygnału. W niej także sygnały są
obserwowane. Na podstawie
obserwacji lub pomiaru można
identyfikować stany oraz zmiany
pewnych cech obserwowanego
układu, zachodzące w funkcji czasu.

Dziedzina częstotliwości

Dzięki pracom Fouriera wiadomo, że
każdy sygnał realizowany fizycznie
można przedstawić w postaci
kombinacji liniowej funkcji
harmonicznych, zwanych
składowymi tego sygnału.

Dziedzina modalna

Opis w dziedzinie modalnej jest
szczególnie dogodny w razie analizy
właściwości układów fizycznych.
Postacie drgań każdego układu
mogą być przedstawione jako sumy
drgań własnych tego układu.

Podział sygnałów
pomiarowych

Każdy sygnał może być opisany przez

model matematyczny.

Sygnały zdeterminowane:



okresowe: harmoniczne,

poliharmoniczne, nieharmoniczne



nieokresowe

Sygnały losowe

Jeśli nie można wyznaczyć wszystkich cech

danego sygnału to można go opisać za

pomocą estymatorów (własne i wzajemne).

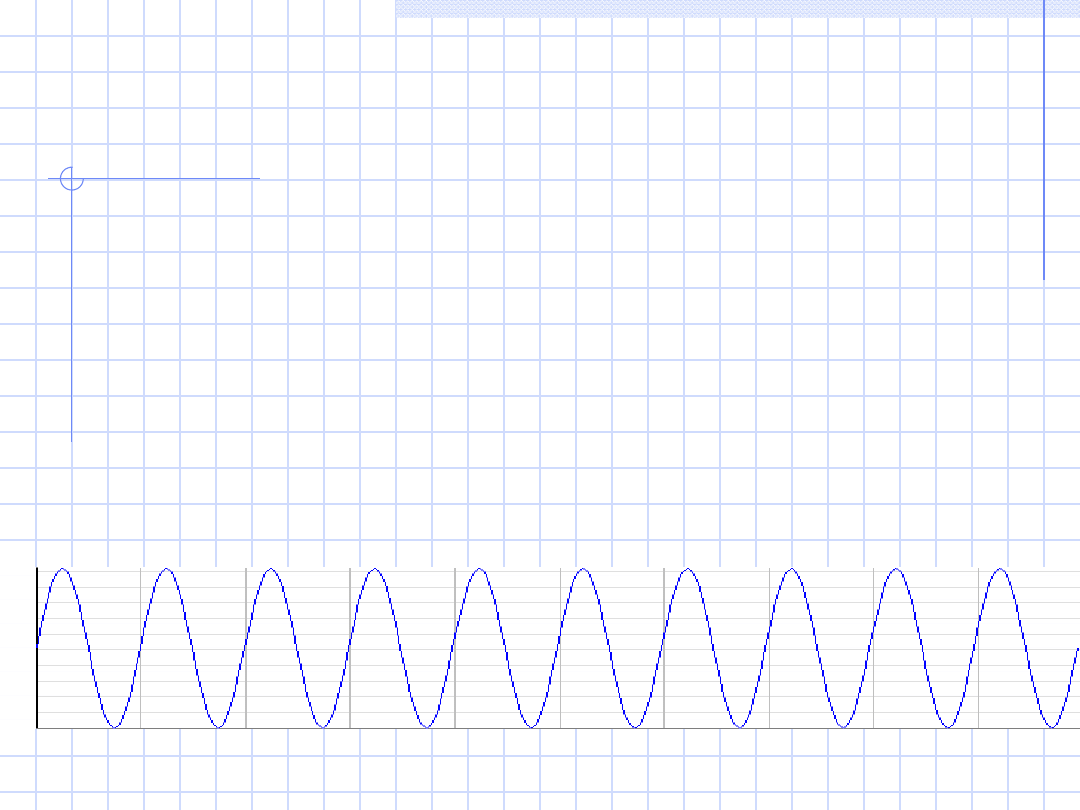
Sygnały harmoniczne

Są to sygnały okresowe, które w
dziedzinie czasu można opisać za
pomocą funkcji harmonicznej:

)

2

cos(

)

(

0











t

f

X

t

x

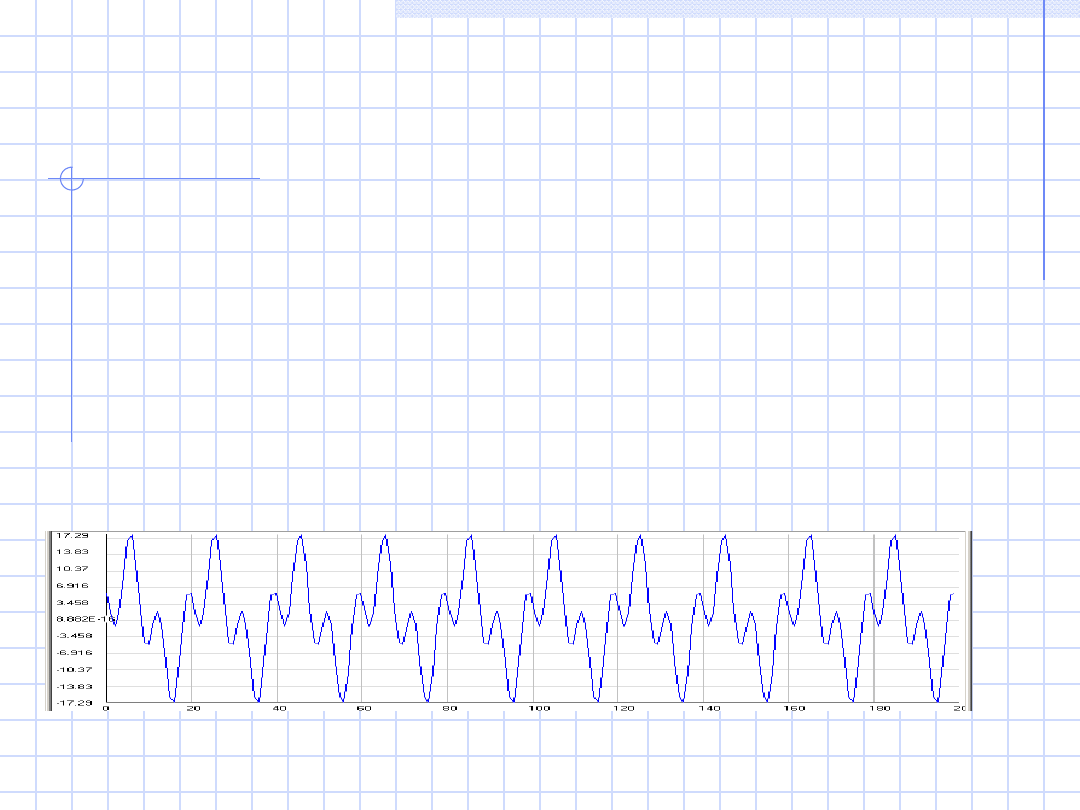
Sygnały poliharmoniczne

Sygnał poliharmoniczny można opisać w
dziedzinie czasu za pomocą kombinacji liniowej
składowych harmonicznych. Liczba tych
składowych w ogólnym wypadku być
nieskończona. Aby sygnał mógł być uznany za
poliharmoniczny, częstotliwość każdej składowej
musi być całkowitą wielokrotnością pewnej
składowej częstotliwości (podstawowej).

Sygnały okresowe
nieharmoniczne

Nie wszystkie sygnały okresowe są
sygnałami poliharmonicznymi. Np.
dystrybucja grzebieniowa lub
próbkująca, impuls Diraca.

Sygnały losowe

Sygnał losowy opisywany jest za
pomocą procesu stochastycznego,
tzn.dla sygnału losowego przyszłe
wartości pewnej wielkości fizycznej,
której przebieg jest obserwowany
podczas eksperymentu, nie mogą być
prognozowane z dokładnością zawartą
w granicach odchyłek pomiaru.

Estymatory

Estymatory własne to oceny punktowe i
funkcyjne.
Estymatory wzajemne (punktowe lub
funkcyjne) pozwalają na określenie:

podobieństwa między sygnałami
podobieństwa między źródłami sygnałów
Podobieństwa między składowymi

sygnału

Cechy sygnału

Wartości cech opisujących sygnały

można podzielić na:

punktowe, opisywane za pomocą

jednej liczby

funkcyjne,których opis realizowany

jest za pomocą funkcji.

Cechy funkcyjne

Funkcja autokorelacji
Funkcja korelacji wzajemnej
Gęstość widmowa mocy
Funkcja koherencji zwyczajnej

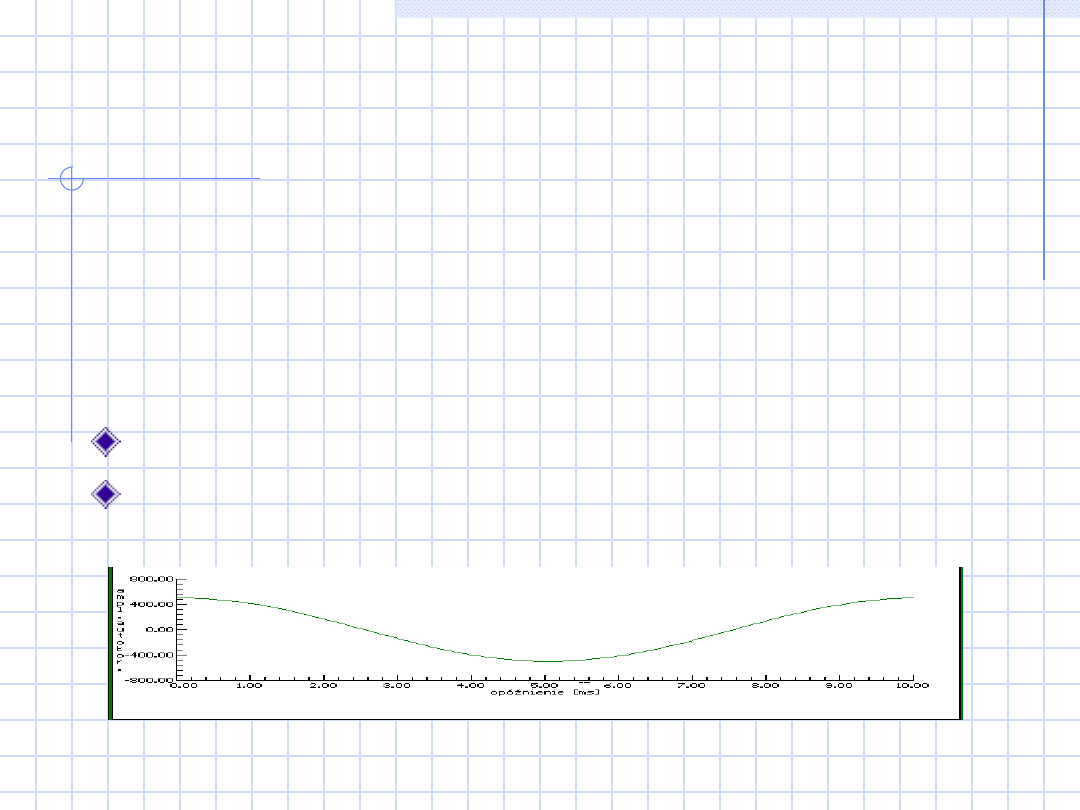
Funkcja autokorelacji

Jest to cecha sygnału losowego, umożliwiająca
identyfikację stopnia zależności wartości sygnału
w pewnej określonej chwili czasu od wartości w
chwili czasu poprzedzającej rozpatrywaną chwilę
o wartość opóźnienia. Zastosowanie:

ocena typu sygnału,
ocena występowania składowych okresowych w

sygnale ze składową szumu.

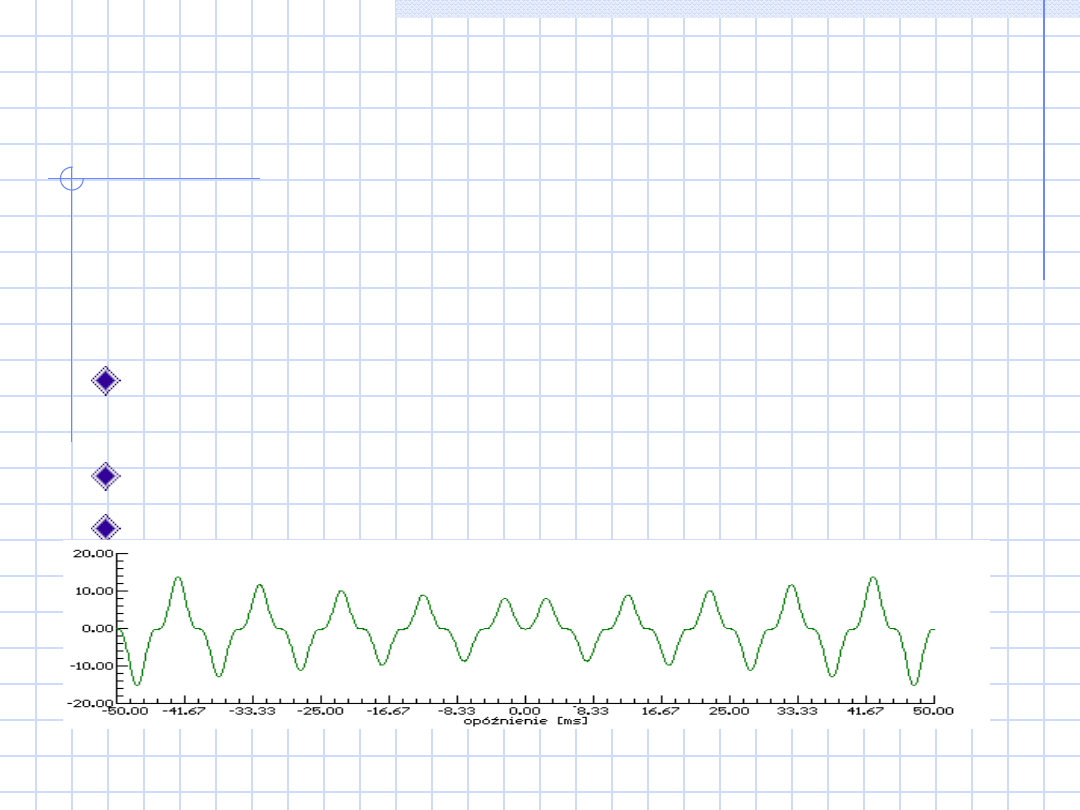
Funkcja korelacji
wzajemnej

Funkcja ta jest łączną cechą dwóch sygnałów
losowych. Charakteryzuje ona zależność wartości
jednego sygnału losowego od wartości innego
sygnału losowego.Zastosowanie:

pomiar czasu opóźnienia między dwoma

sygnałami,

identyfikacja dróg propagacji,
identyfikacja sygnału zakłóconego szumem

losowym

Gęstość widmowa mocy
i widmo mocy

Cechy funkcyjne stosowane do opisu
sygnału w dziedzinie częstotliwości.
Gęstość widmowa mocy może być
określana za pomocą :

funkcji autokorelacji,
transformaty Fouriera,
filtracji (analogowej).

Funkcja koherencji

Funkcja koherencji zwyczajnej dwóch
sygnałów określana jest za pomocą
wzajemnej gęstości widmowej.

identyfikacja własności układów

fizycznych

identyfikacja przesunięcia fazowego

pomiędzy dwoma sygnałami