Gazy

Gazy

W XIX wieku sformułowano
prawa opisujące własności
gazów na podstawie szeregu
wyników eksperymentalnych.
Są to :

Prawo Boyle’a-Mariotte’a
Prawo Gay-Lussaca
Prawo Charlesa
Hipoteza Avogadro
Prawo Daltona

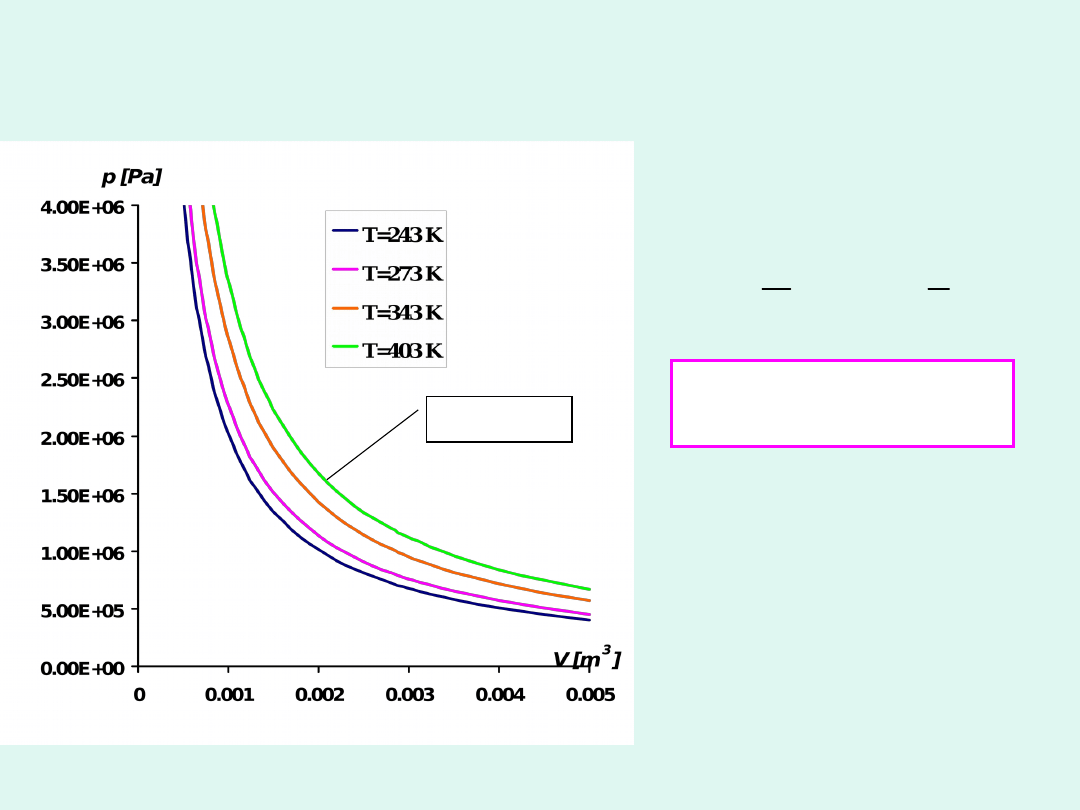
Prawo Boyle’a-Mariotte’a

p

1

V

lub

V

1

p

const

T

i

const

m

lub

const

n











const

pV

Dla pewnej stałej
ilości gazu w stałej
temperaturze
ciśnienie jest
odwrotnie
proporcjonalne do
objętości czyli iloczyn
ciśnienia i objętości
jest stały.

izoterm

a

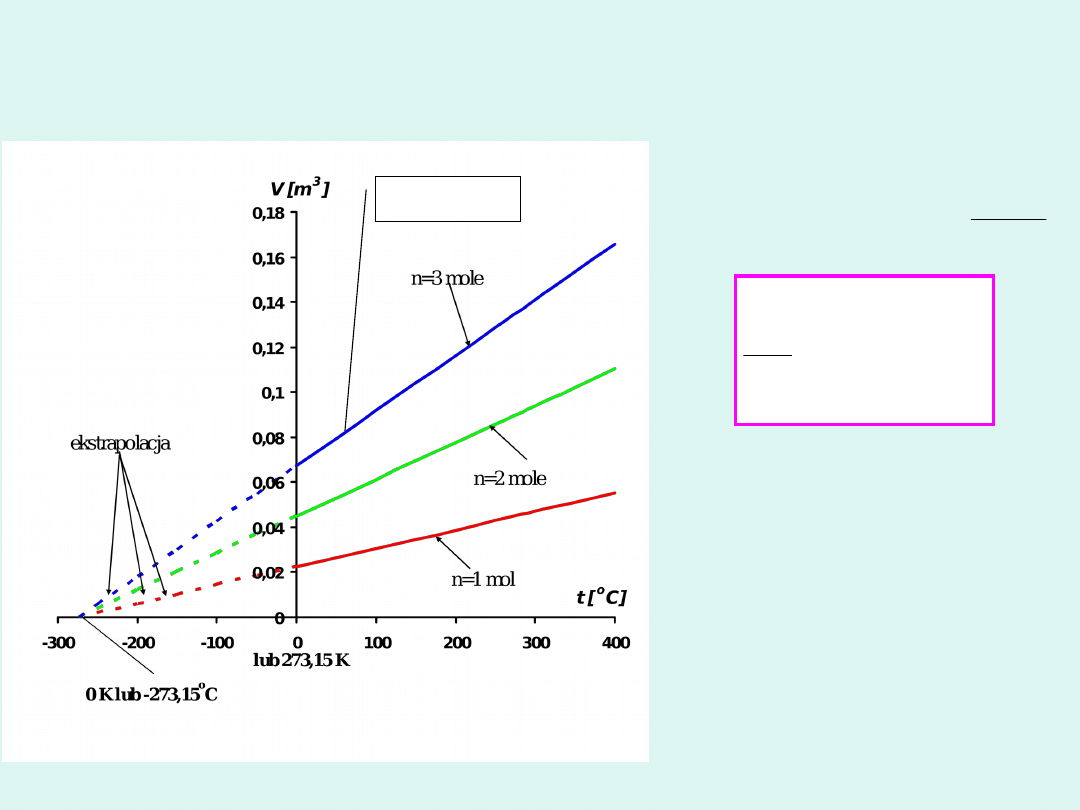
Prawo Gay-Lussaca





273,15

1

o

t

1

V

V

const

p

i

const

m

lub

const

n



















const

T

V



Dla pewnej stałej
ilości gazu pod
stałym ciśnieniem
objętość jest wprost
proporcjonalna do
temperatury.

izobara

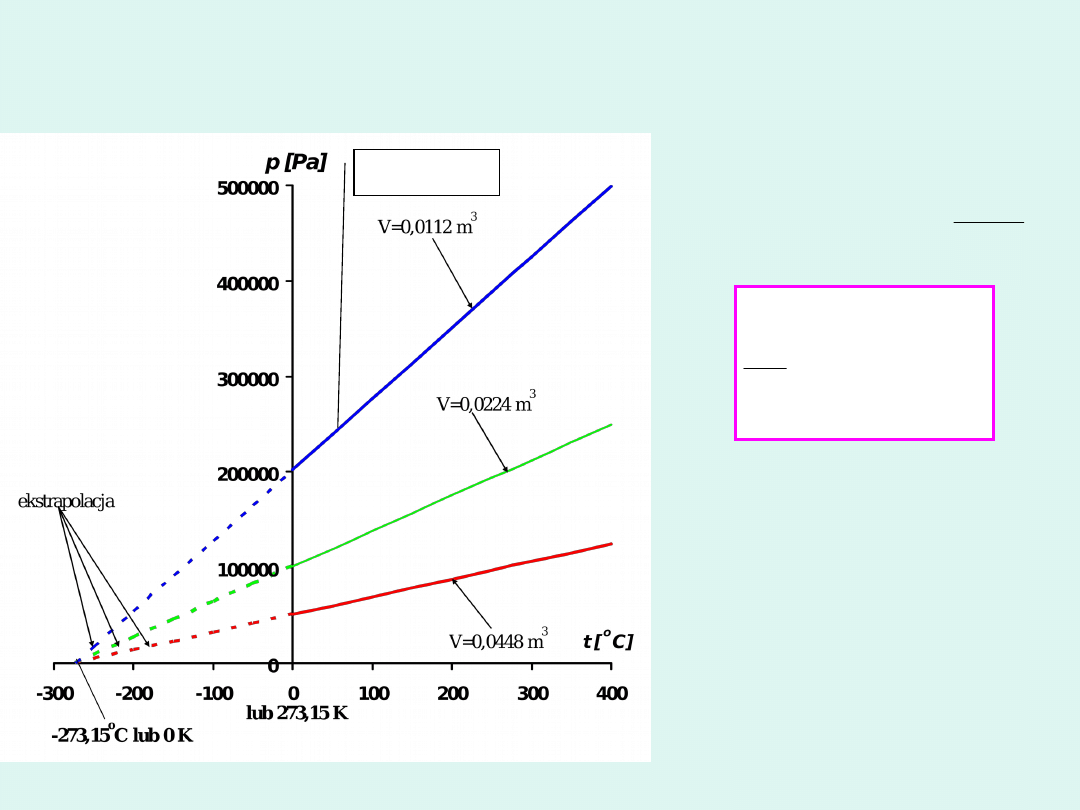
Prawo Charlesa





273,15

1

o

t

1

p

p

const

V

i

const

m

lub

const

n



















const

T

p



izochor

a

Dla pewnej stałej
ilości gazu
znajdującej się w
stałej objętości
ciśnienie jest wprost
proporcjonalne do
temperatury.

Hipoteza Avogadro

Jeśli mamy różne gazy w tej
samej objętości i temperaturze
i pod tym samym ciśnieniem, to
zawierają one te same ilości
cząsteczek.

1 mol gazu zawiera liczbę
cząsteczek wyrażającą się
liczbą Avogadro.

1

23

A

mol

10

022

6

N





 ,

Równanie stanu gazu

doskonałego (Clapeyrona)

nRT

pV

p

– ciśnienie [Pa]

V

– objetość [m

3

]

n

– liczba moli [mol]

T

- temperatura w skali

bezwzględnej [K]

R

– stała gazowa

K

mol

J

314

8

R



 ,

 

 

15

273

C

t

K

T

,







Warunki normalne

t

o

= 0°C (T = 273,15 K)

p

o

= 1,013·10

5

Pa

Objętość 1 mola gazu w tych
warunkach

V

o

= 22,4·10

-3

m

3

/mol

K

mol

J

314

8

K

15

273

mol

m

10

22,4

Pa

10

013

1

T

V

p

R

3

3

-

5

o

o

o















,

,

,

Gaz, który spełnia

równanie Clapeyrona

nazywamy doskonałym.

Wszystkie gazy, z jakimi mamy do czynienia
są,

gazami

rzeczywistymi

i

wykazują

odchylenia od równania stanu doskonałego
(nie spełniają go).

Własności gazów rzeczywistych stają się
zbliżone do własności gazu doskonałego, gdy
ich ciśnienie dąży do zera.

Inaczej mówiąc im ciśnienie gazu niższe tym
lepiej spełnia on równanie Clapeyrona.

Prawo Daltona

i

i

i

i

i

i

i

x

n

n

P

p

n

n

V

nRT

P

V

RT

n

p

p

P

















Prawo to dotyczy mieszanin
gazów.

Ciśnienie całkowite mieszaniny gazów jest sumą
ciśnień cząstkowych poszczególnych składników.
Ciśnienie cząstkowe danego składnika gazowego, to
ciśnienie jakie wywierałby, gdyby sam znajdował się
w danych warunkach.

Wniosek z prawa
Daltona

P

x

p

i

i





Teoria kinetyczno-

molekularna gazów –

model gazu doskonałego

Wymiary cząsteczek są znikomo
małe w porównaniu z
odległościami pomiędzy nimi.
Można traktować je jako punkty
materialne.
Cząsteczki są w ciągłym,
chaotycznym ruchu.
Cząsteczki nie oddziaływują na
siebie na odległość, jedynie
dochodzi do doskonale
elastycznych zderzeń.

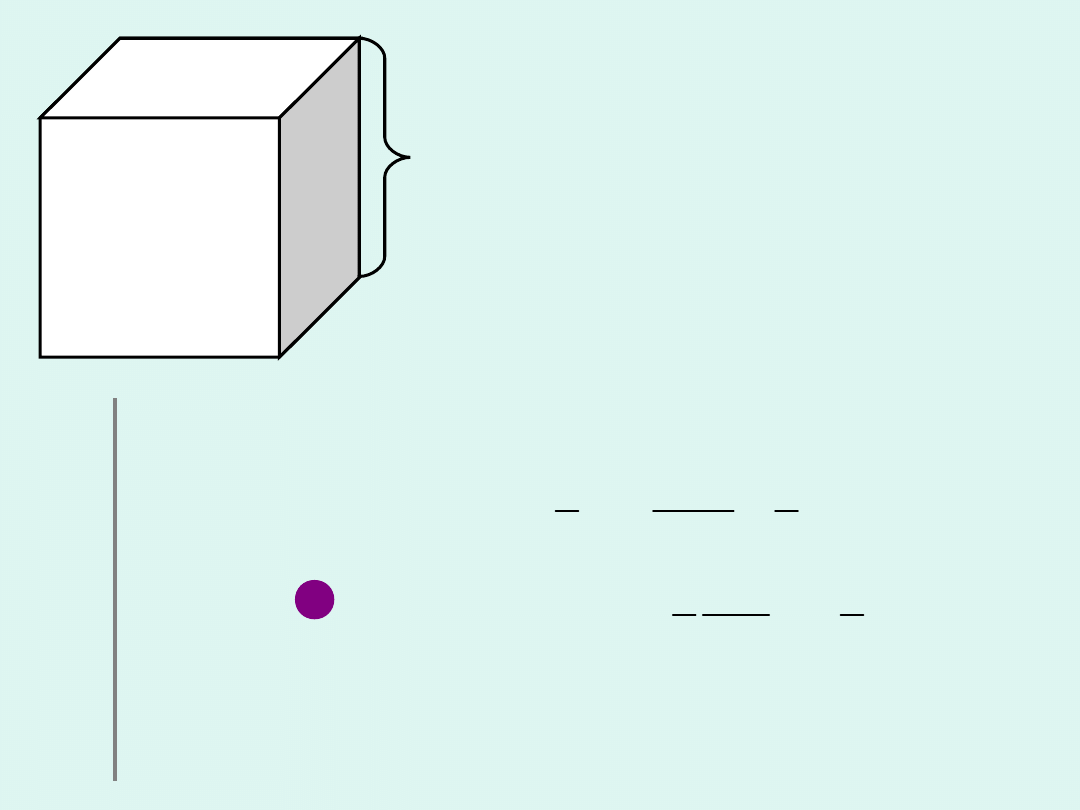
l

N

A

W sześcianie o boku

l

zamknięty jest

1 mol (N

A

)

cząsteczek, każda o masie

m

poruszająca się ze

średnią szybkością

v

.

Cząsteczki zderzając się ze
ścianami naczynia
przekazują im pęd,
wywierając na nie ciśnienie.

2

A

A kin

kin

B

A

2

mv

2

pV

N

N E

RT

3

2

3

3 R

3

E

T

k T

2N

2

=

=

=

=

=

Stała Boltzmanna

k

B

=

R/N

A

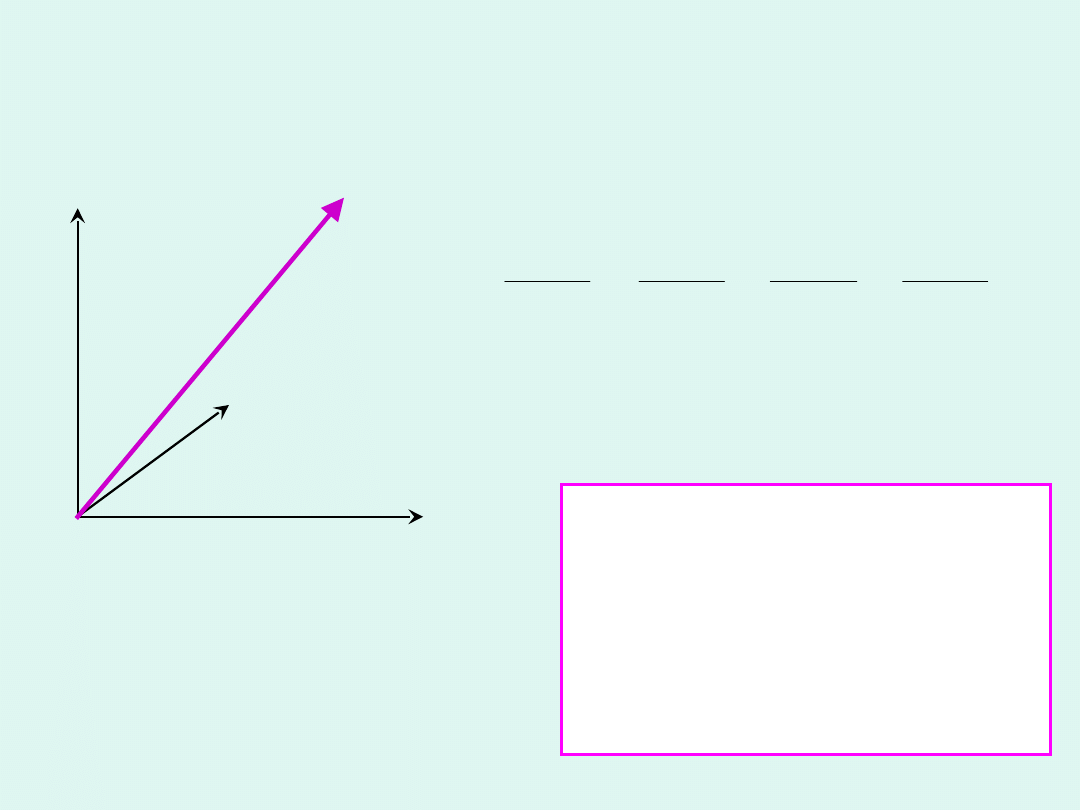
x,
v

x

z,
v

z

y,
v

y

v

Zasada ekwipartycji (równego
podziału) energii

z

,

kin

y

,

kin

x

,

kin

kin

2

z

2

y

2

x

2

z

y

x

E

E

E

E

2

mv

2

mv

2

mv

2

mv

v

v

v

v



























Na każdy stopień
swobody ruchu
cząsteczki przypada
energia wynosząca

½k

B

T

.

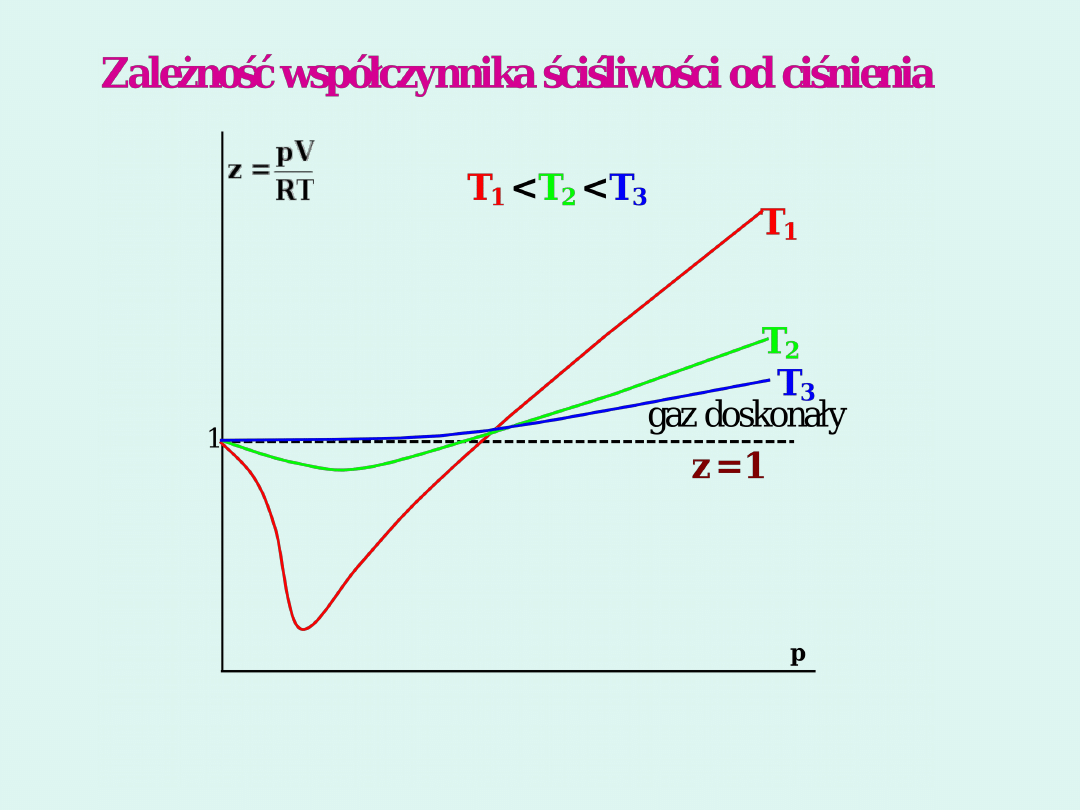
Gazy rzeczywiste

Wszystkie gazy są gazami rzeczywistymi. Nie
spełniają równania Clapeyrona.

nRT

z

pV





z

– współczynnik ściśliwości

Zależy od temperatury i ciśnienia. Dla gazu
doskonałego z = 1; dla gazu rzeczywistego
dąży do 1, gdy ciśnienie dąży do zera.

Gazy rzeczywiste

Do gazu rzeczywistego nie można zastosować modelu
opisującego gaz doskonały.

Cząsteczki gazu rzeczywistego posiadają pewną

objętość, której nie można zaniedbać.

Cząsteczki gazu rzeczywistego oddziaływają ze sobą

na odległość.

Oddziaływania międzycząsteczkowe mają charakter
odpychający i przyciągający. Gdy odległość pomiędzy
cząsteczkami jest niewielka i energia termiczna
cząsteczek jest też stosunkowo mała, zderzenia
pomiędzy nimi nie są elastyczne. Przeważają
oddziaływania przyciągające i cząsteczki „sklejają się”
z sobą, a gaz się skrapla.

Równanie

opisujące

gaz

rzeczywisty

musi

uwzględniać

objętość

własną

cząsteczek

i

oddziaływania

międzycząsteczkowe

(przyciąganie

cząsteczek).

Równanie van der Waalsa





RT

b

V

V

a

p

2















 

dla 1 mola
gazu

dla

n

moli

gazu





nRT

nb

V

V

an

p

2

2





















a,b

– stałe charakterystyczne dla danego gazu,

niezależne od temperatury

a

– stała związana z oddziaływaniami

międzycząsteczkowymi (przyciąganiem)

b

- stała związana z objętością własną

cząsteczek

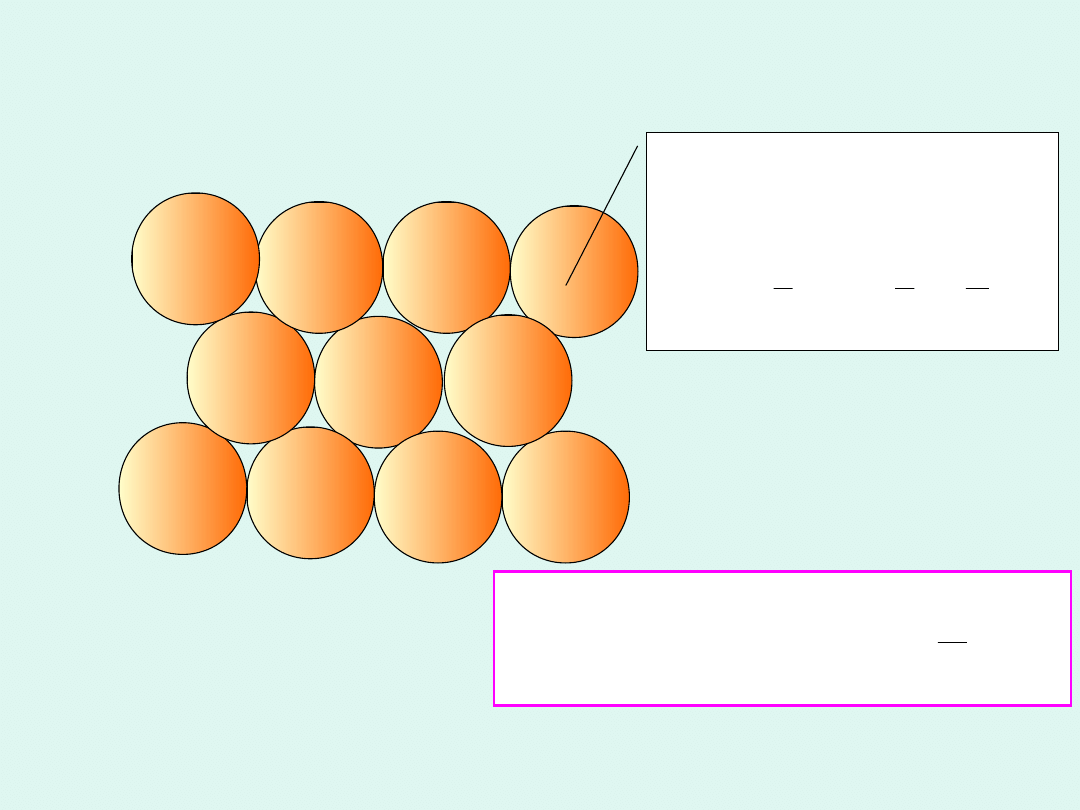
Pojedyncza

cząsteczka ma

objętość :

3

3

cz

2

3

4

r

3

4

V











 









1 mol cząsteczek
może zająć
najgęściej
upakowany,
objętość :

3

A

cz

A

r

3

4

N

4

V

N

4

b







Interpretacja stałej van der

Waalsa b

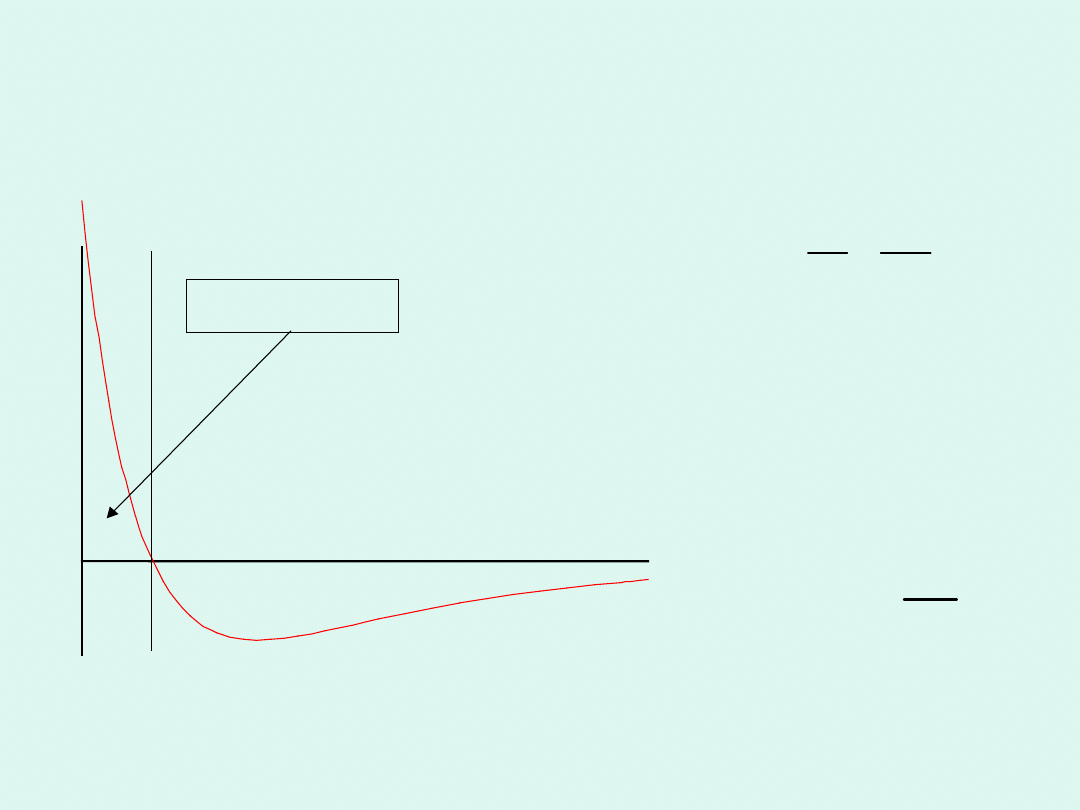
Oddziaływania pomiędzy

rzeczywistymi cząsteczkami

6

12

A

B

E

x

x

=-

+

odległość pomiędzy
cząsteczkami

E

przewaga
przyciągania

przewaga
odpychania

0

Siły odpychające są
istotne tylko dla
bardzo małych
odległości
pomiędzy
cząsteczkami,
wobec tego :

6

A

E

x

�-

Punkt krytyczny

jest to taki stan

substancji, określony przez parametry :
ciśnienie krytyczne, temperatura
krytyczna i objętość krytyczna, w którym
zanika różnica pomiędzy cieczą a parą.
Gazu nigdy nie można skroplić w
temperaturze wyższej od temperatury
krytycznej.
Powyżej temperatury krytycznej mamy do
czynienia z płynem (fazą) nadkrytyczną.
Nadkrytyczny CO

2

jest wykorzystywany do

ekstrakcji nadkrytycznej olejków
naturalnych, barwników i wielu innych
substancji z surowców naturalnych.

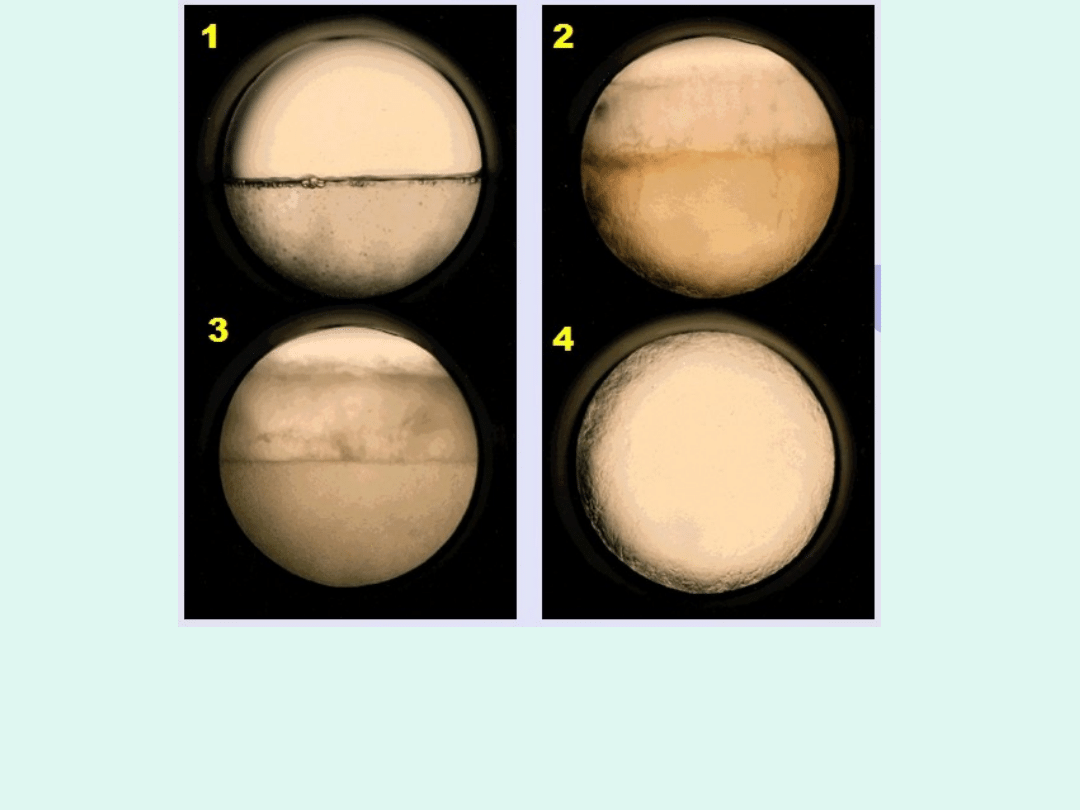
Znikanie różnicy pomiędzy gazem a

cieczą na przykładzie CO

2

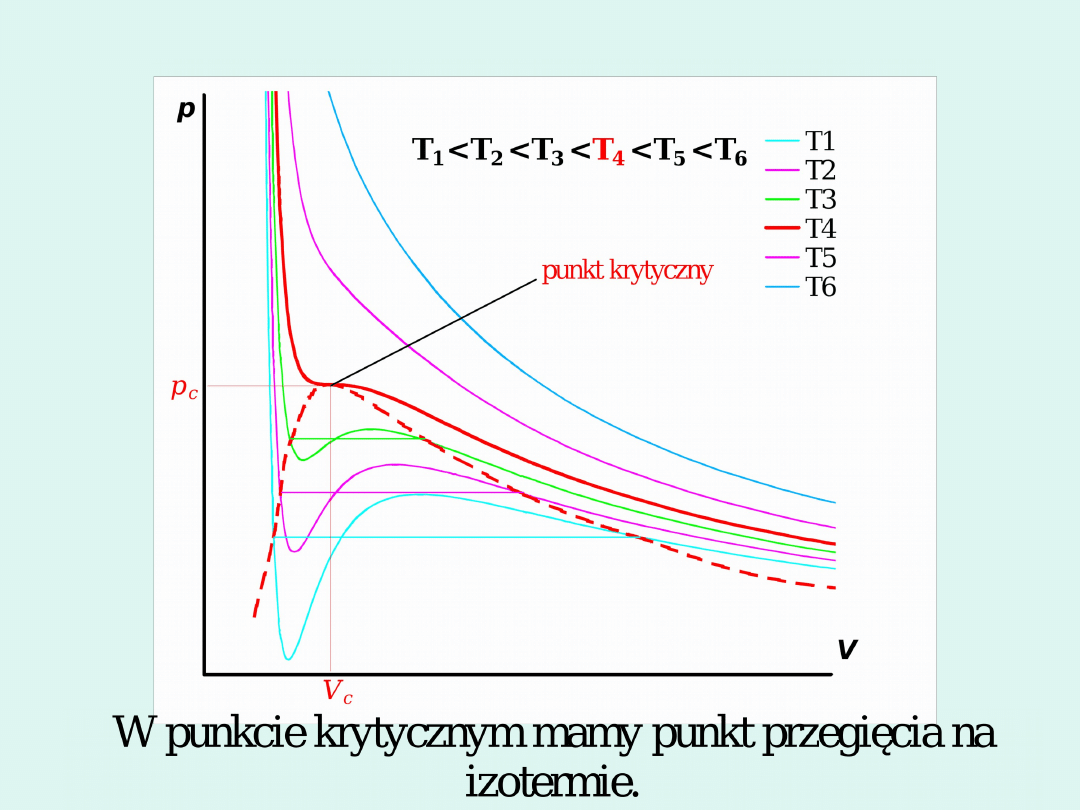
Izotermy van der Waalsa