1
I
T
P
W
ZPT
Układy cyfrowe
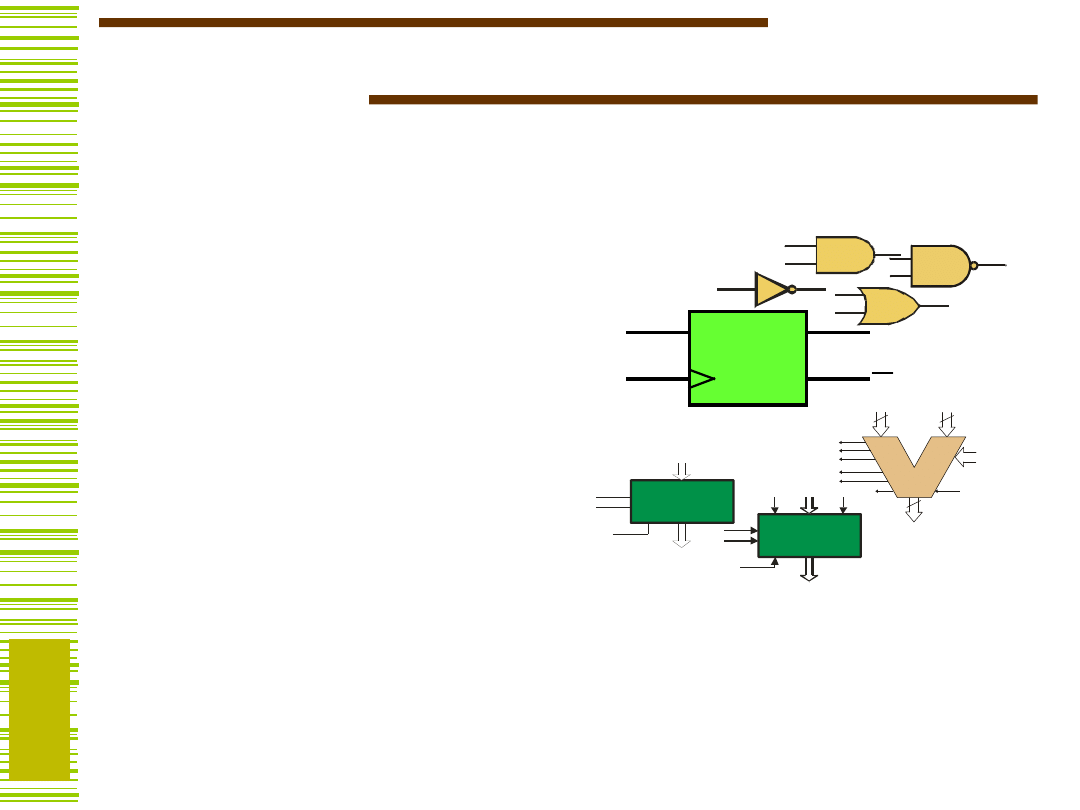
Układy logiczne (cyfrowe) konstruowane są
w różnych technologiach i na różnych
poziomach opisu.
Poziomy opisu:
1) Bramki i elementarne
układy pamięciowe
(przerzutniki)
2) Bloki funkcjonalne: układy
arytmetyczne (sumatory),
liczniki, rejestry.
Tworzą one nowe elementy konstrukcyjne, z których
buduje się złożone układy cyfrowe o różnorodnych
zastosowaniach: układy przetwarzania sygnałów,
układy sterowania, specjalizowane procesory, układy
kryptograficzne
Przerzutn
ik
typu D
D
D
Clk
Clk
Q
Q
Y
B
A
n
n
n
Y
n - 1
Z
O V R
P
G
c
n
c
0
S
A L U
R
(Q)
s
1
s
2
clock
X
Y
x
l
x
p
L
(Q)
s
1
s
2
clock
X
Y
2
I
T
P
W
ZPT
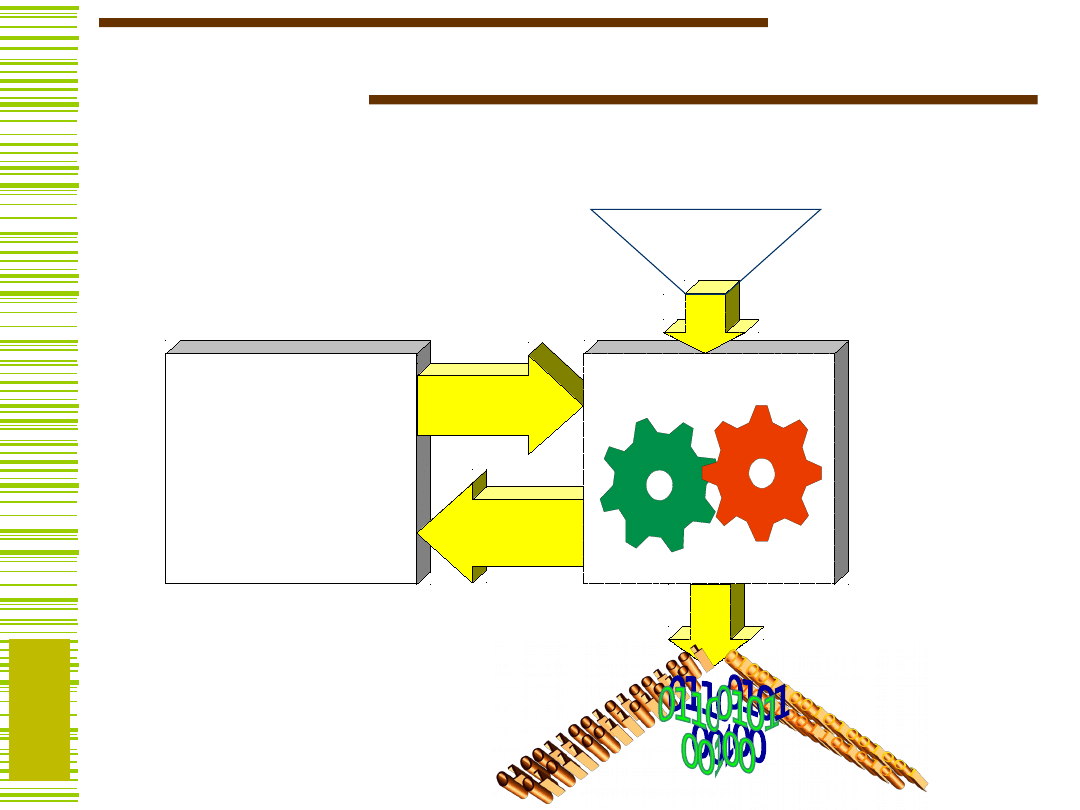
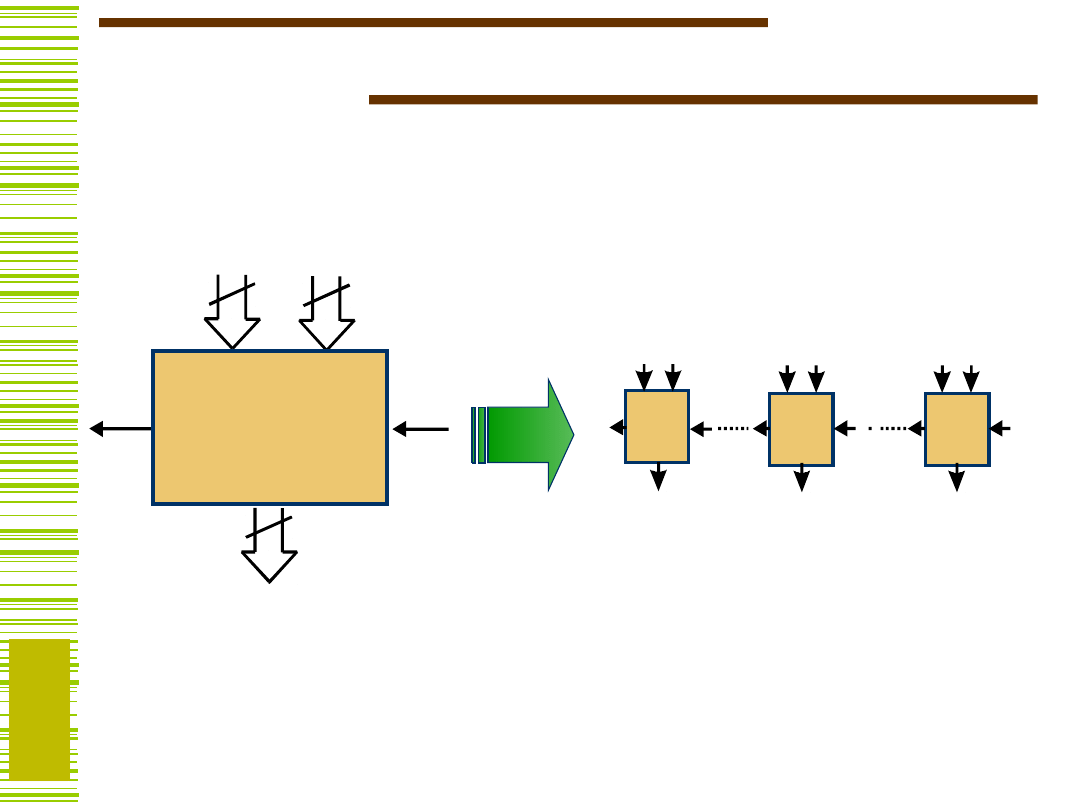
Układ
sterujący
(kontroler
)
Dane wyjściowe
Dane
wejściowe
Sygnały
sterujące
Stan części
operacyjnej
Układ operacyjny
(Datapath)
System cyfrowy
0
1
0
1
0
1
0
1
0
1
0
1
0
1
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Mikrooperacje
wywoływane przez
sygnały sterujące
3
I
T
P
W
ZPT
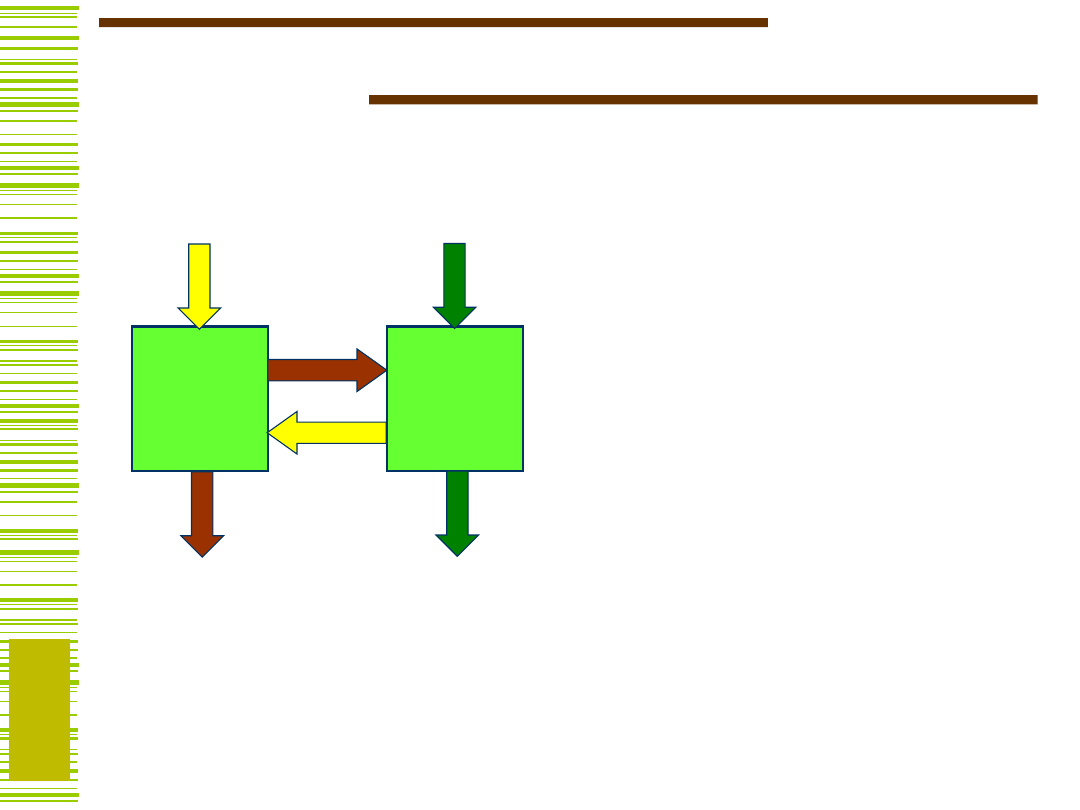
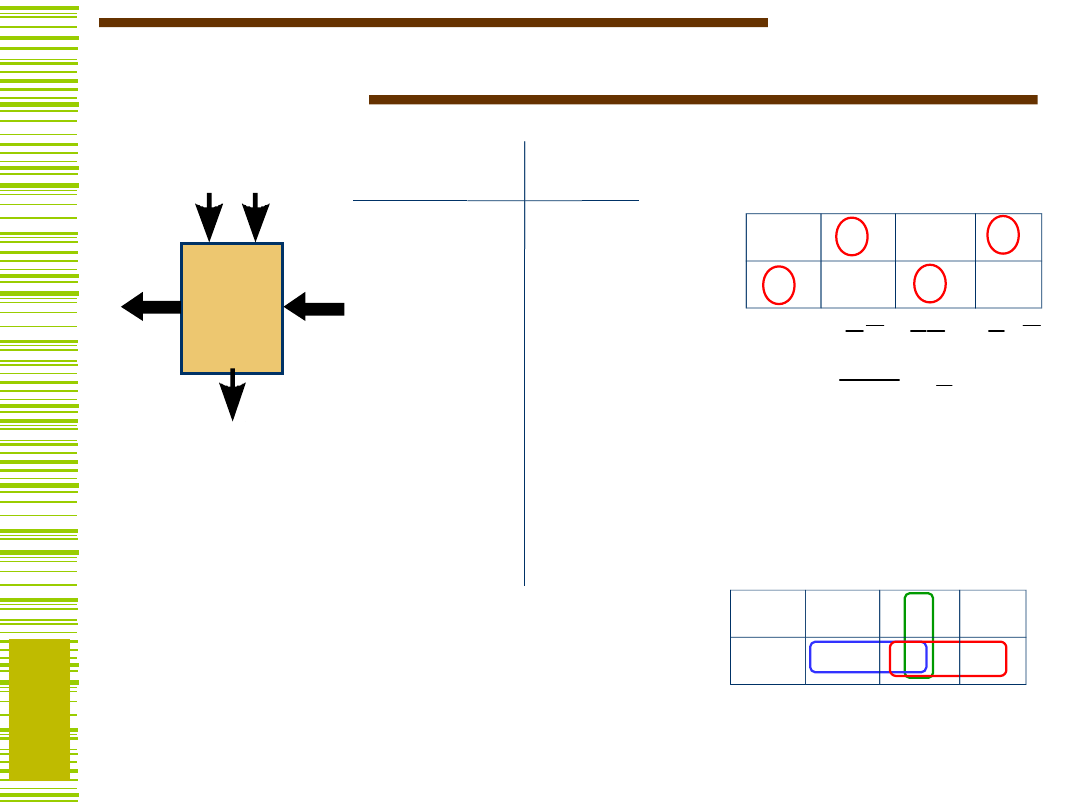
System cyfrowy…
D, F - przetwarzana
informacja (wektory
binarne),
UO - układ operacyjny
US - układ sterujący
X
Z
X
P
Z
Y
Z
D
F
X - sygnały warunków,
Z - sygnały sterujące
(mikrorozkazy)
US
UO
4
I
T
P
W
ZPT
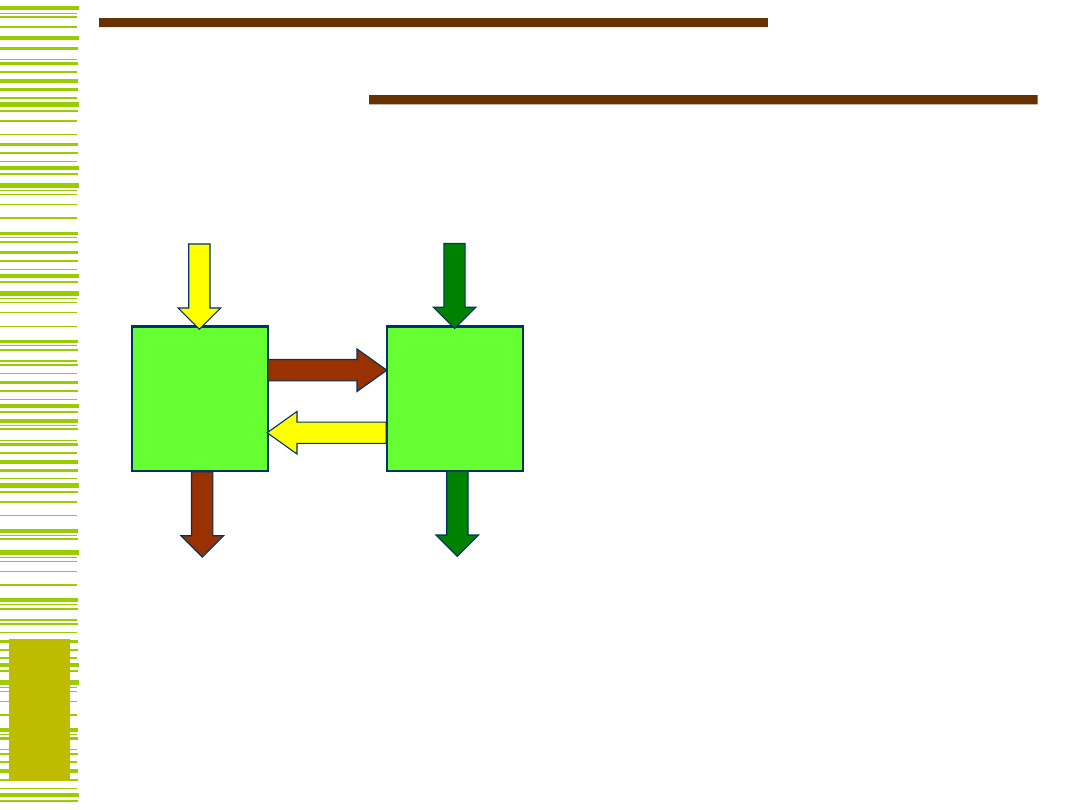
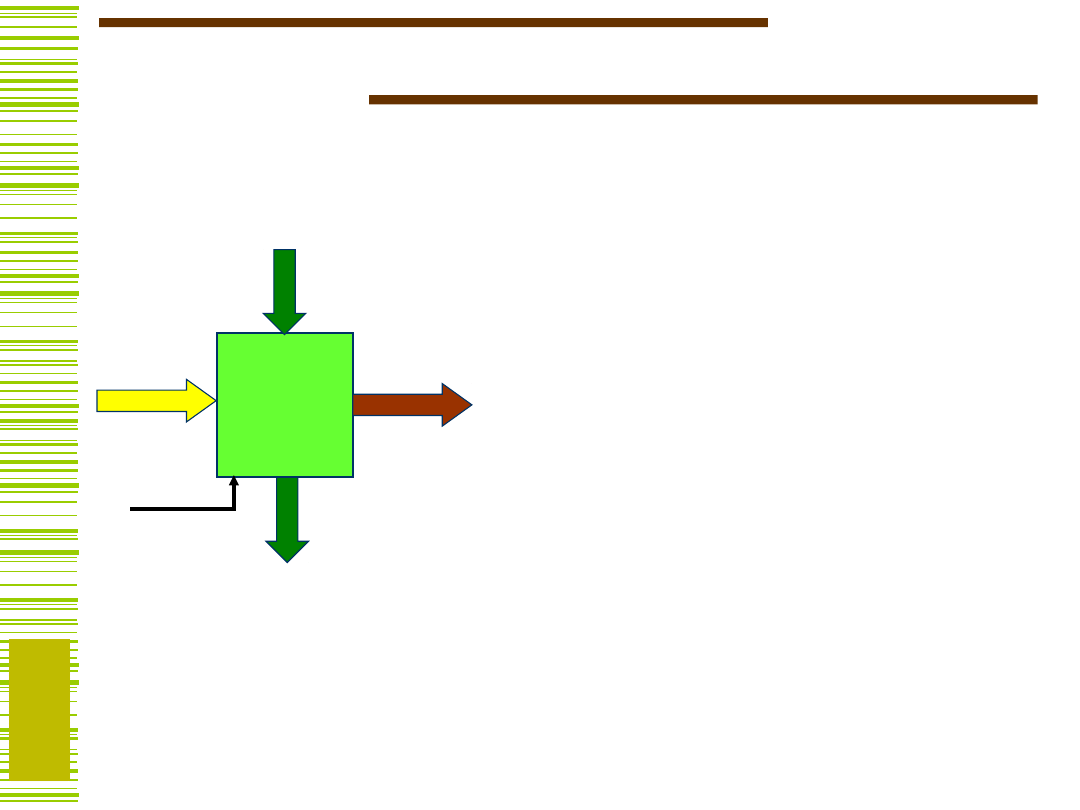
System cyfrowy - realizacja
UO – z bloków funkcjonalnych
US – automat lub układ mikroprogramowany
X
Z
X
P
Z
Y
Z
D
F
US
UO
5
I
T
P
W
ZPT
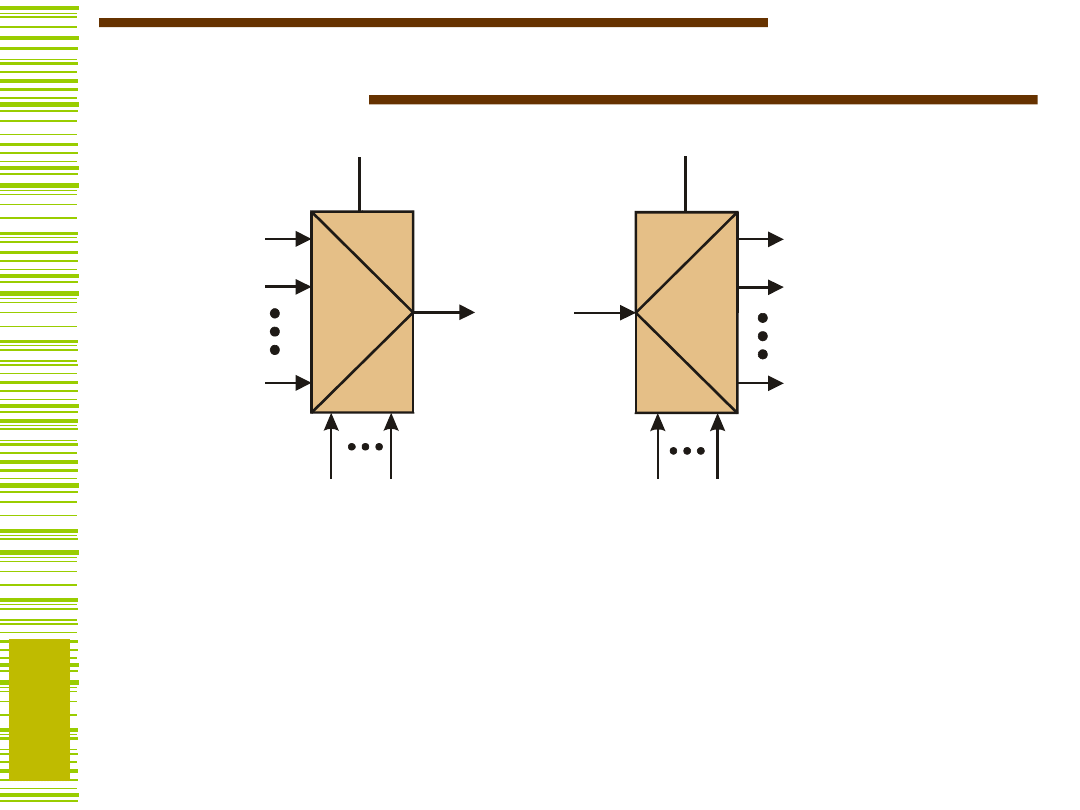
Bloki funkcjonalne
P
S
X
Y
BF
clk
X – wejścia sygnałów
reprezentujących
dane wejściowe
S – wejścia sterujące,
Y – wyjścia sygnałów
reprezentujących dane
wyjściowe,
P – wyjścia predykatowe,
sygnalizujące pewne
szczególne stany
przetwarzania danych,
clk – wejście zegarowe
6
I
T
P
W
ZPT
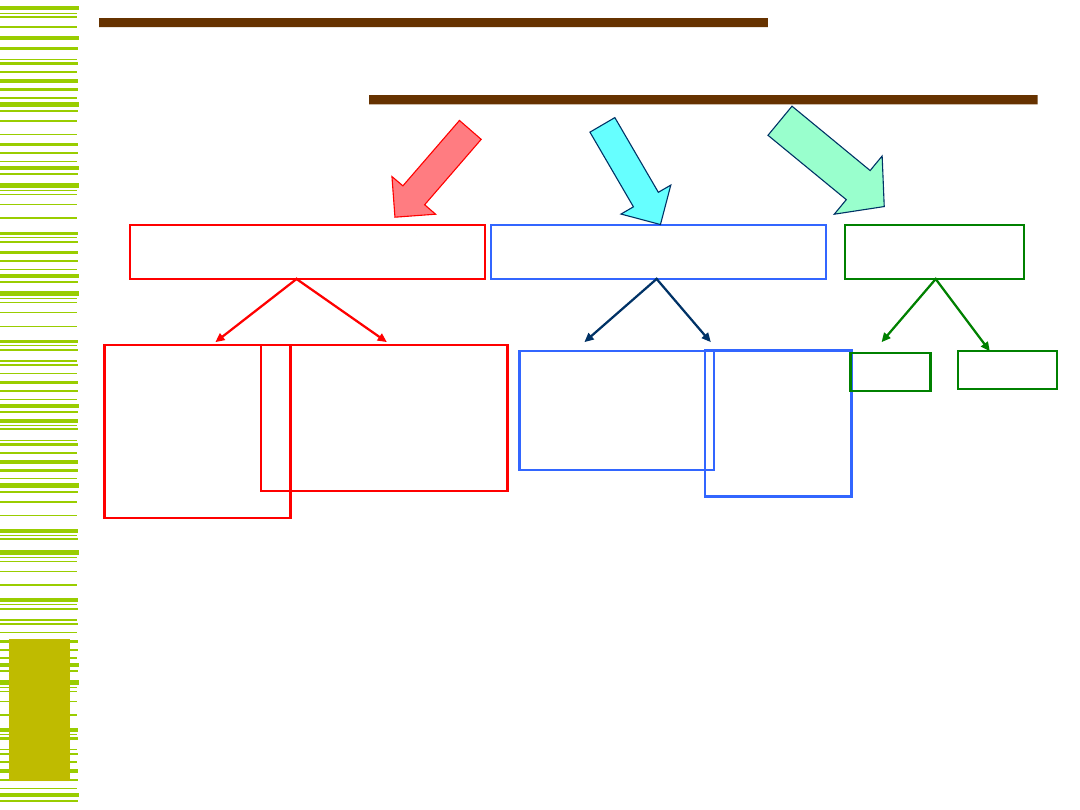
Bloki
funkcjonalne
B. kombinacyjne B. sekwencyjne Pamięci
Układy
arytmetyczne
Sumator
Układ odejmujący
Komparator
Układy
Komutacyjne
MUX
DMUX
DEC
Rejestry
Równoległe
Przesuwające
Liczniki
Zliczające
W górę
W dół
ROM
(RAM)
7
I
T
P
W
ZPT
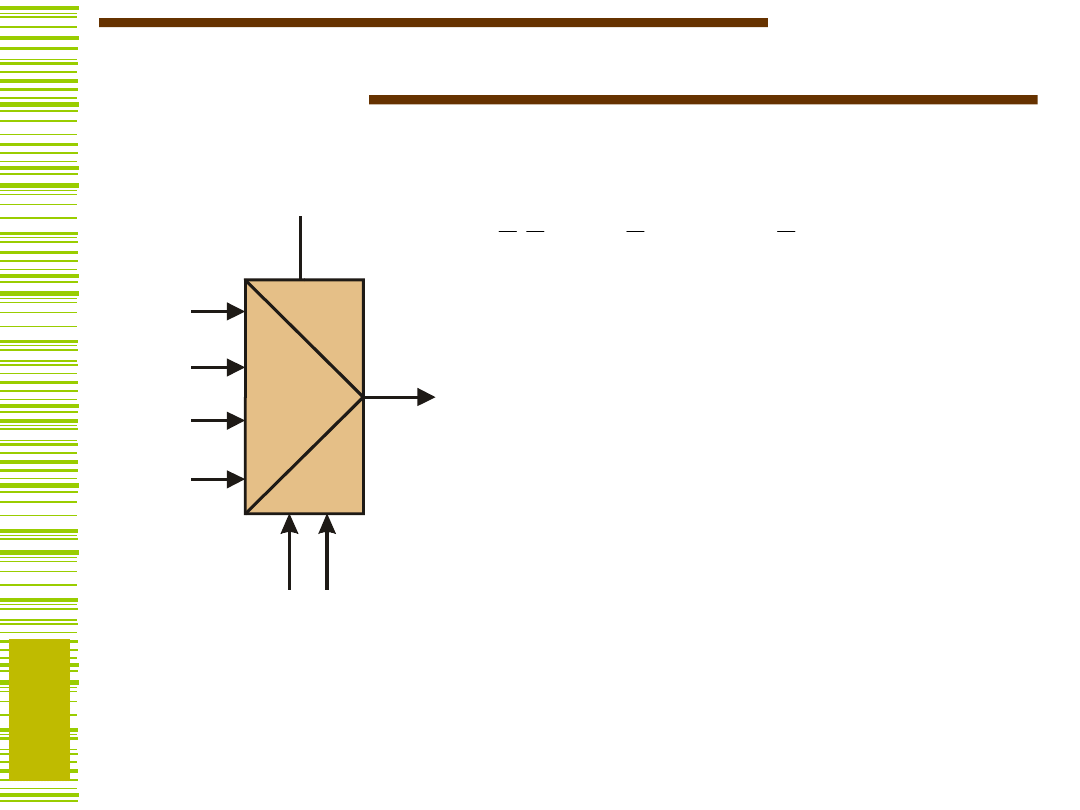
Multipleksery, demultipleksery
a
n - 1
a
0
y
e
d
d
d
0
1
N - 1
a
n - 1
a
0
e
d
y
y
y
0
1
N - 1
k = L(A),
P
k
– pełny
iloczyn
1
N
0
k
k
k
(A)d
P
e
y
MUX
DMUX
N = 2
n
(A)d
eP
y
k
k
8
I
T
P
W
ZPT
Multipleksery
1
N
0
k
k
k
(A)d
e
y
P
gdzie P
k
(A) oznacza
pełny iloczyn zmiennych
a
n–1
,...,a
0
, prostych lub
zanegowanych, zgodnie
z reprezentacją binarną
liczby k.
1
0
ad
d
a
y
3
0
1
2
0
1
1
0
1
0
0
1
d
a
a
d
a
a
d
a
a
d
a
a
y
7
0
1
2
6
0
1
2
5
0
1
2
4
0
1
2
3
0
1
2
2
0
1
2
1
0
1
2
0
0
1
2
d
a
a
a
d
a
a
a
d
a
a
a
d
a
a
a
d
a
a
a
d
a
a
a
d
a
a
a
d
a
a
a
y
Dla n = 1 (MUX 2 : 1):
dla n = 2 (MUX 4 : 1):
dla n = 3 (MUX 8 : 1):
9
I
T
P
W
ZPT
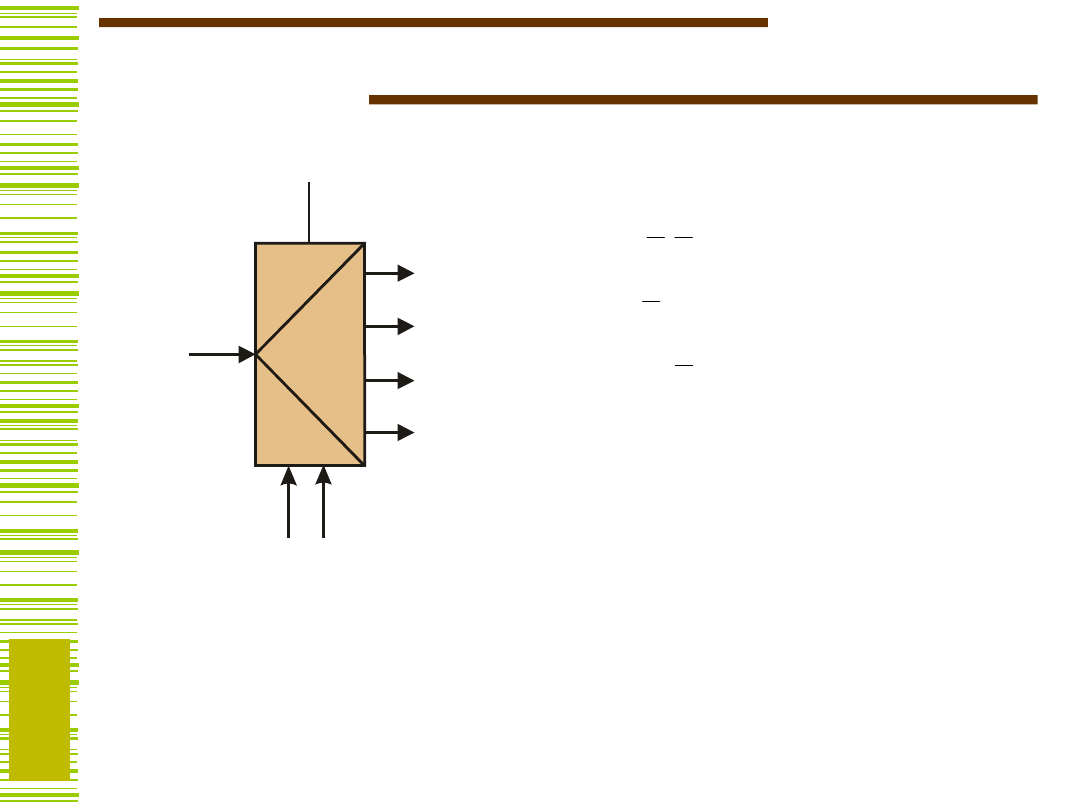
Multiplekser
e = 1
0
1
2
3
0 0
0
3
0
1
2
0
1
1
0
1
0
0
1
d
a
a
d
a
a
d
a
a
d
a
a
y
0 1
1 1
0
1
1
0
1
1
10
I
T
P
W
ZPT
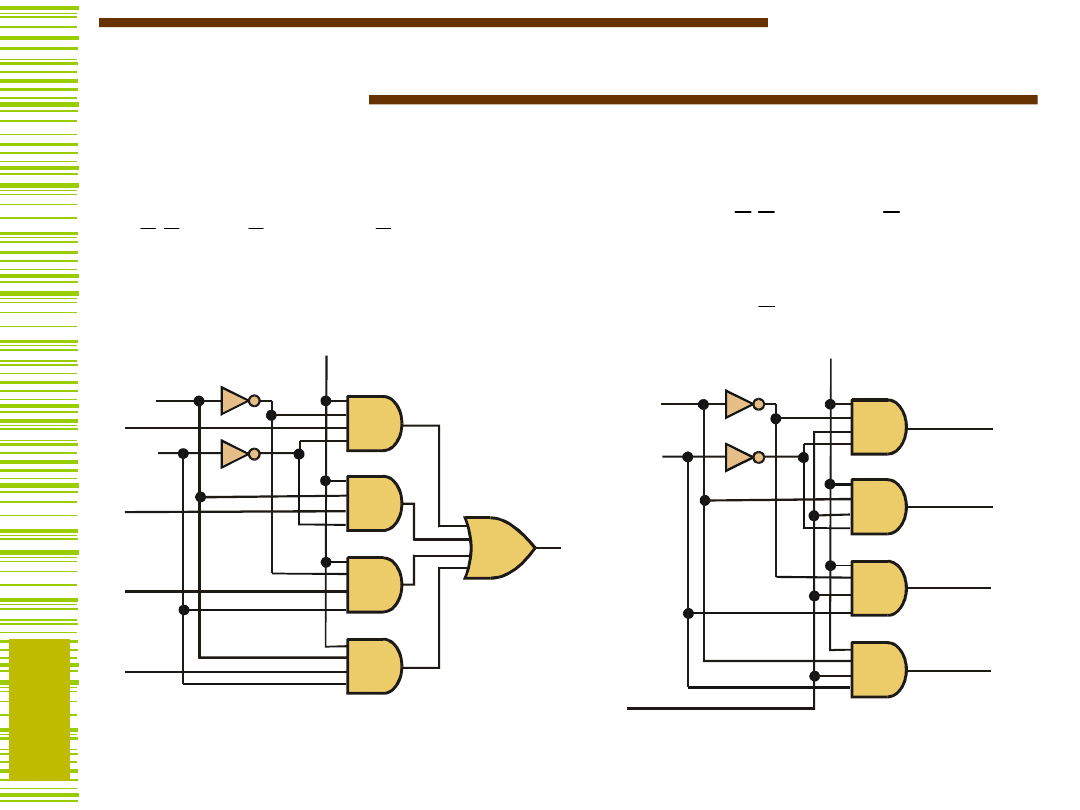
Demultiplekser
e = 1
0
1
2
3
0
0
0
d
a
a
y
d
a
a
y
d
a
a
y
d
a
a
y
0
1
3
0
1
2
0
1
1
0
1
0
0
0
0
0
0
0
0 0
0 1
1 1
1
1
1
1
11
I
T
P
W
ZPT
Multipleksery, demultipleksery
3
0
1
2
0
1
1
0
1
0
0
1
d
a
a
d
a
a
d
a
a
d
a
a
y
d
0
d
1
d
2
d
3
a
0
a
1
e
y
Multiplekse
r
a
0
a
1
e
y
0
d
y
1
y
2
y
3
d
a
a
y
d
a
a
y
d
a
a
y
d
a
a
y
0
1
3
0
1
2
0
1
1
0
1
0
Demultipleks
er
12
I
T
P
W
ZPT
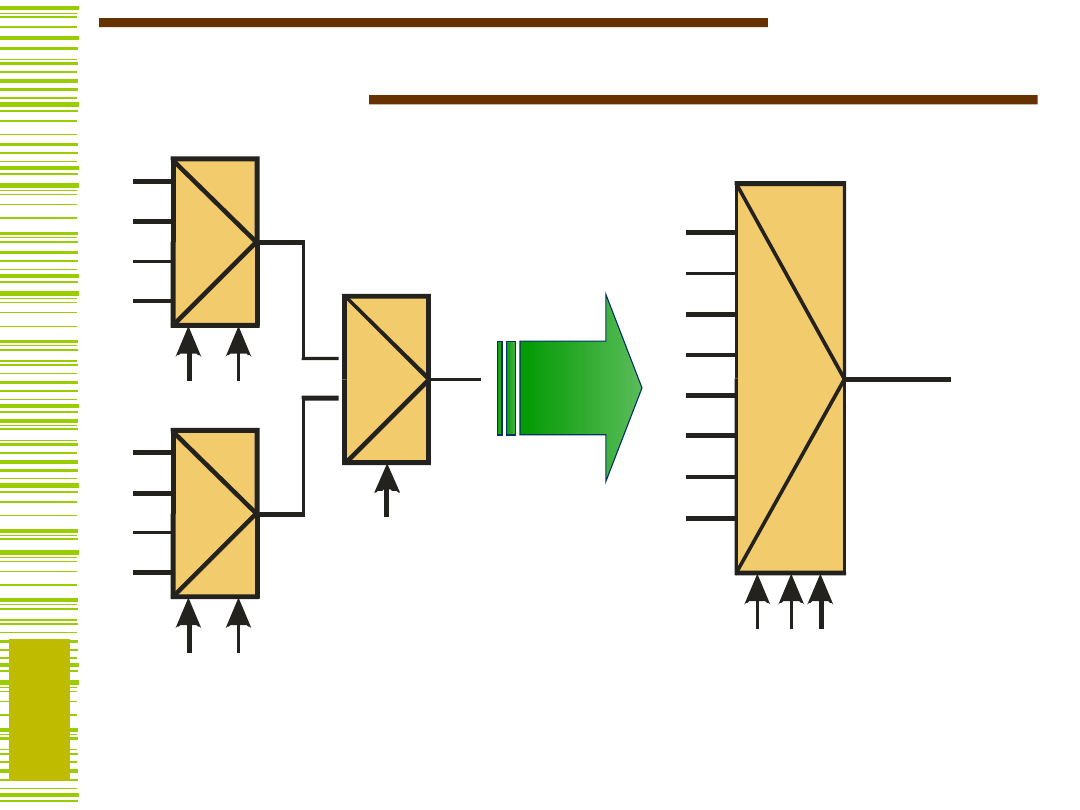
Multipleksery kaskadowe
13
I
T
P
W
ZPT
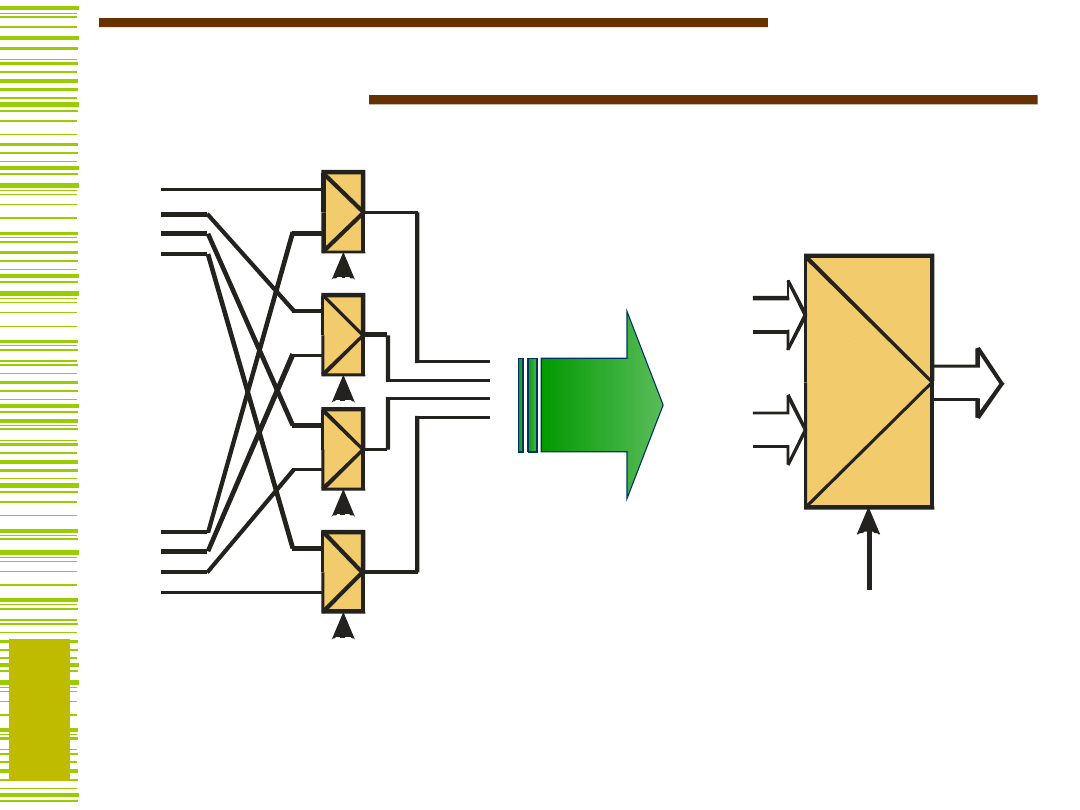
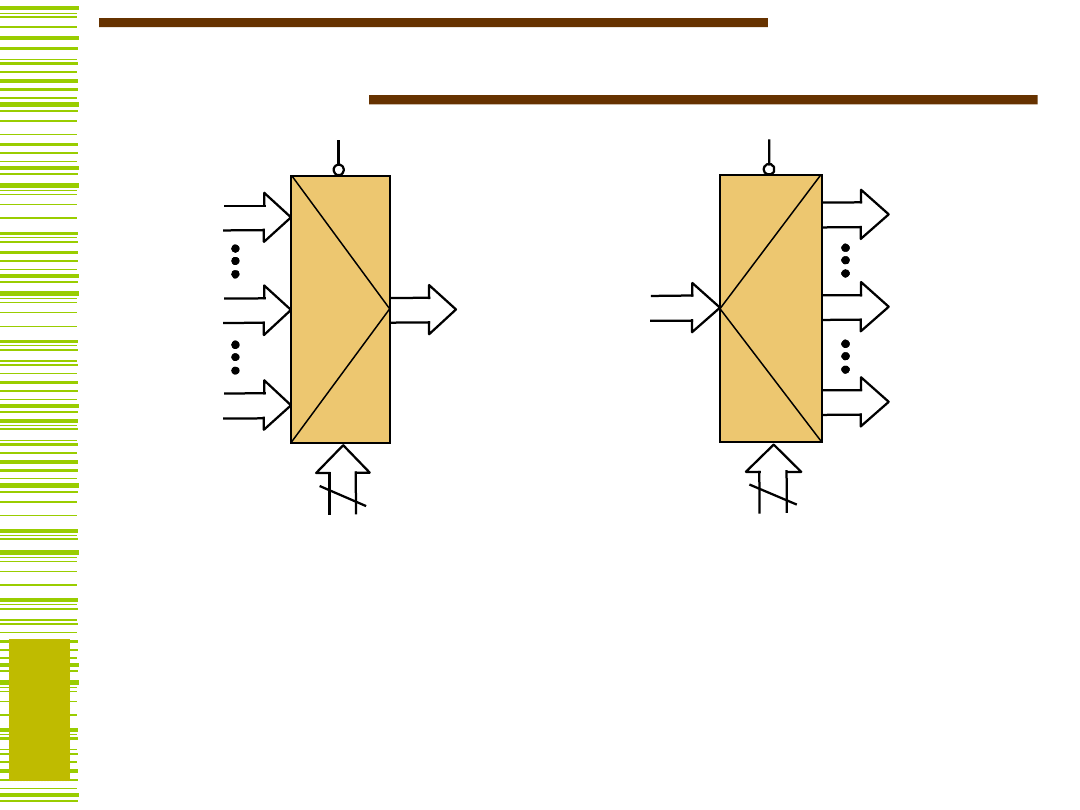
Multipleksery grupowe
A
B
A
B
14
I
T
P
W
ZPT
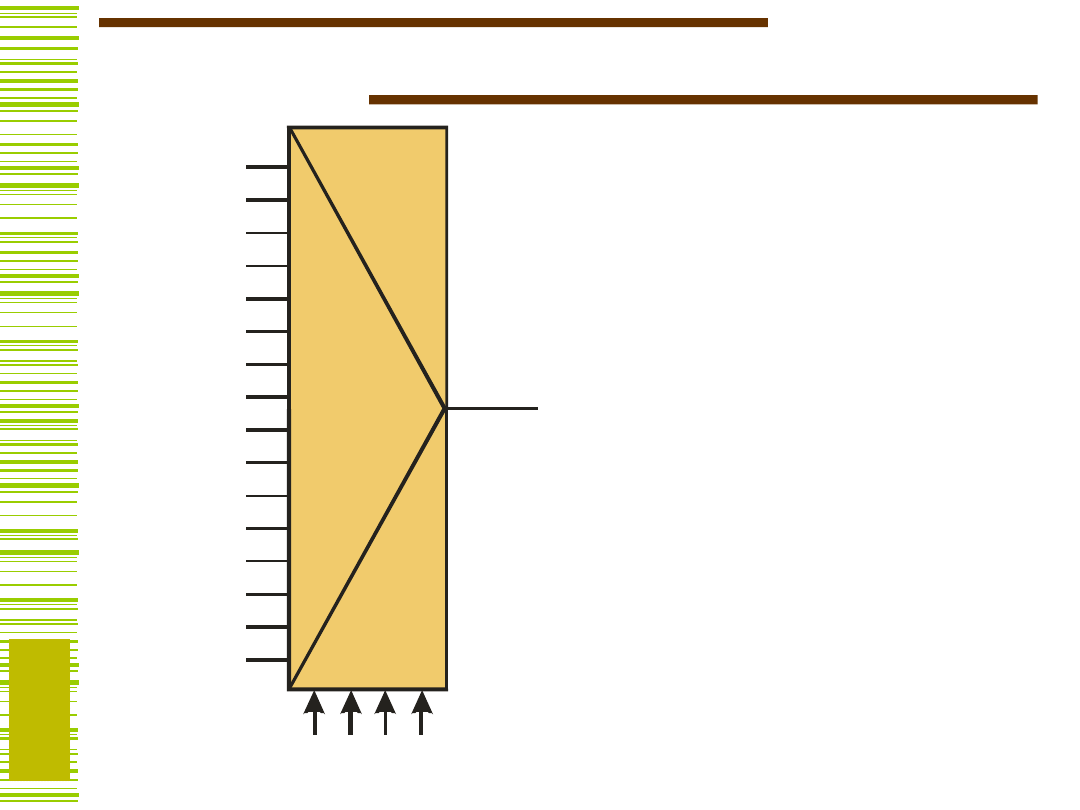
Bloki komutacyjne
Multiplekser służy do
wybierania jednego z wielu słów
wejściowych i przesyłania go na
wyjście. Na wyjściu Y pojawia
się słowo wejściowe wskazane
adresem A (wg naturalnego
kodu binarnego).
Demultiplekser służy do
przesyłania słowa X
wejściowego na jedno z
wielu wyjść; numer tego
wyjścia jest równy
aktualnej wartości adresu.
X
0
X
j
X
N-1
Y
n
A
b
Y
0
Y
j
Y
N-1
n
A
b
X
15
I
T
P
W
ZPT
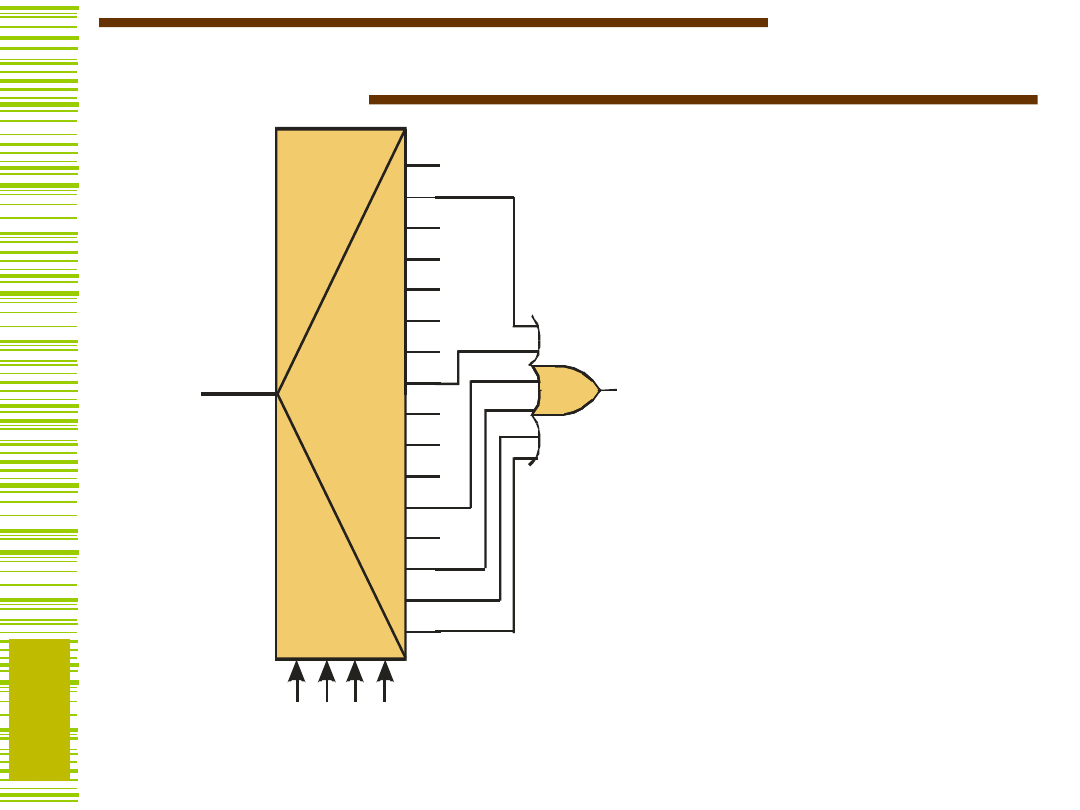
Zastosowanie MUX do realizacji funkcji
boolowskich
y =
(1,7,11,13,14,15)
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
y
0
1
0
0
0
0
0
1
0
0
0
1
0
1
1
1
x
3
x
2
x
1
x
0
16
I
T
P
W
ZPT
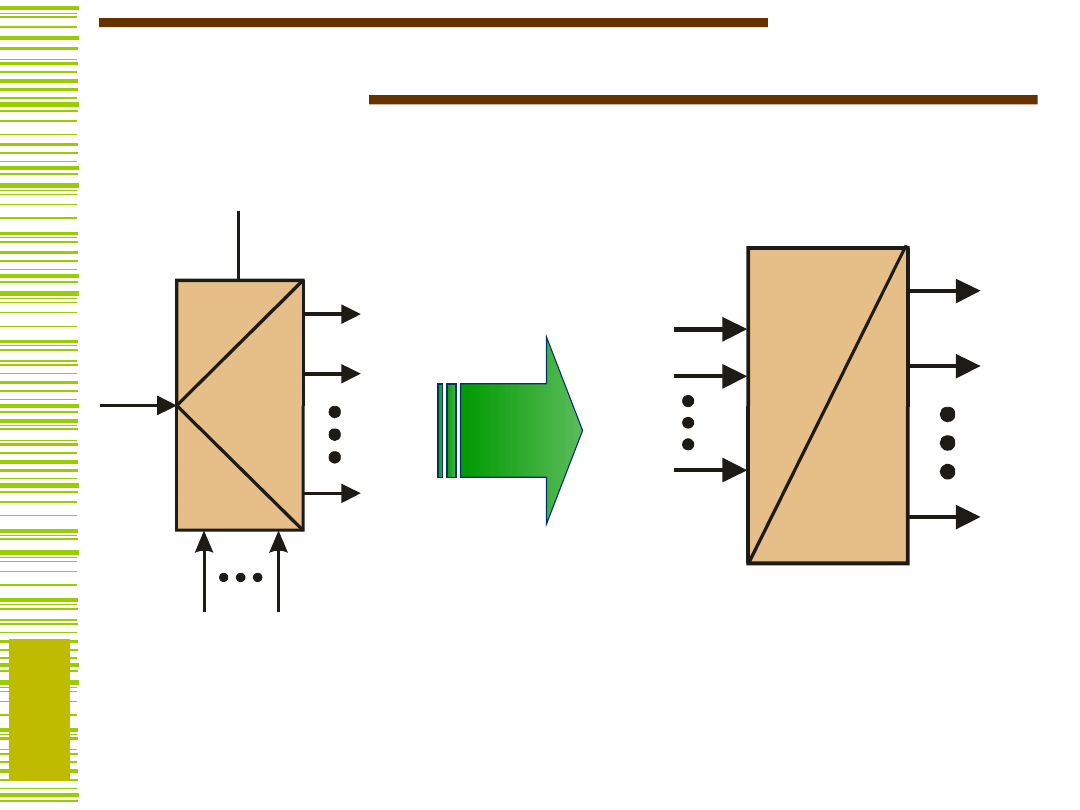
Zastosowanie MUX/DMUX do realizacji funkcji
boolowskich
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
b
y =
(1,7,11,13,14,15)
Istnieją układy FPGA, w
których komórki są
MULTIPLEKSERAMI
Ich synteza metody BDD
x
3
x
2
x
1
x
0
y
1
17
I
T
P
W
ZPT
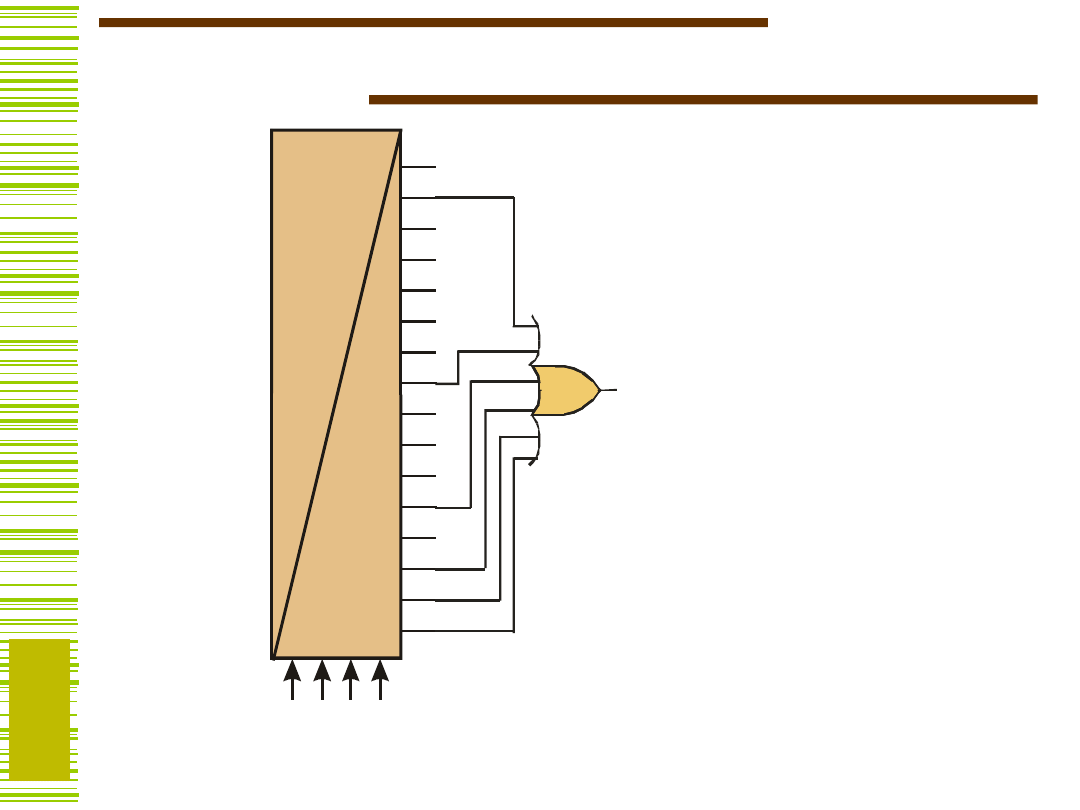
Dekoder
a
n - 1
a
0
e
d
y
y
y
0
1
N - 1
y
y
y
0
1
N - 1
a
a
a
0
1
n - 1
N =
2
n
DMU
X
DEKODER
18
I
T
P
W
ZPT
Realizacja funkcji na dekoderach
y =
(1,7,11,13,14,15)
Pojedyncza funkcja
0
1
2
3
4
5
6
7
8
9
1 0
1 1
1 2
1 3
1 4
1 5
x
3
x
2
x
1
x
0
y
19
I
T
P
W
ZPT
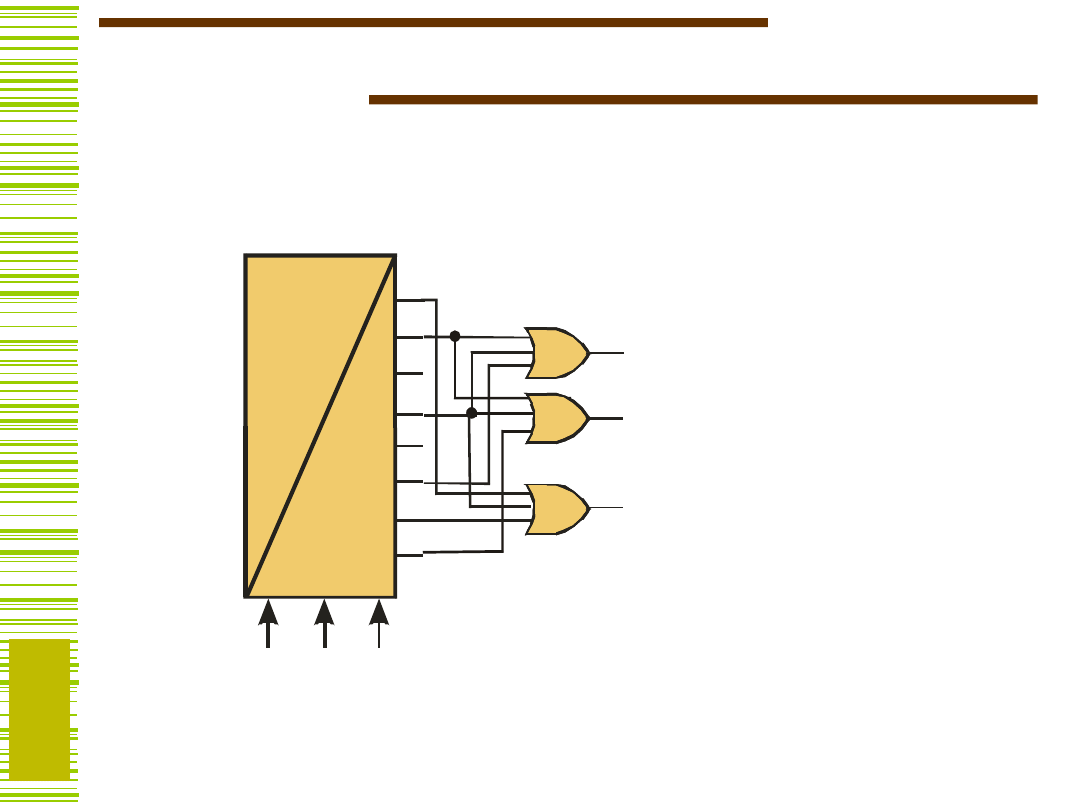
Realizacja funkcji na dekoderach
0
1
2
3
4
5
6
7
F
1
=
(1,3,5)
Zespół funkcji
F
2
=
(1,3,7)
F
3
=
(0,3,6)
F
1
F
2
F
3
x
2
x
1
x
0
20
I
T
P
W
ZPT
Układy arytmetyczne
Najprostszy sumator – ripple carry adder
a b
i
i
y
i
c
i+1
c
i
a b
0
0
y
0
c
1
c
0
a b
c
n-1
n-1
y
n-1
c
n
n-1
c
n
c
0
A
n
B
n
Y
n
1111
0
1001
0110
0
21
I
T
P
W
ZPT
Funkcje logiczne sumatora
0
0
0
1
0
1
1
1
b)
c(a
ab
b)
c(a
ab
o
c
i
c
i
b
i
a
i
y
)
b
(a
c
b
a
c
i
i
i
i
i
1
i
a
b
c
c
0
y
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
y
c
o
c
a b
ab
c
00
01
11
10
0
0
1
0
1
1
1
0
1
0
ab
c
00
01
11
10
0
0
0
1
0
1
0
1
1
1
b
a
c
y
b
a
c
b
a
c
b
a
c
b
a
c
b
a
c
cab
y
0
1
1
0
1
0
0
1
22
I
T
P
W
ZPT
Naturalny kod binarny - NKB
A
NKB
= <
a
n–1
,..., a
j
,..., a
0
>
{0,1}
1
n
0
j
j
j
NKB
D
2
a
A
L
A
23
I
T
P
W
ZPT
Kod U2
A
U2
= <a
n–1
,..., a
j
,..., a
0
>, gdzie a
j
{0,1}
Zakres: –2
n–1
≤ A
D
≤ 2
n–1
– 1
2
n
0
j
j
j
1
n
1
n
U2
D
2
a
2
a
A
L
A
Bit a
n–1
można interpretować jako bit znaku.
Jeśli a
n–1
= 0, to liczba jest dodatnia;
jeśli a
n–1
= 1 to liczba jest ujemna; pozostałe bity
stanowią uzupełnienie (różnicę) wartości liczby do
najwyższej potęgi liczby 2
<0101>│
U2
= +5│
D
; <1011>│
U2
= –
5│
D
24
I
T
P
W
ZPT
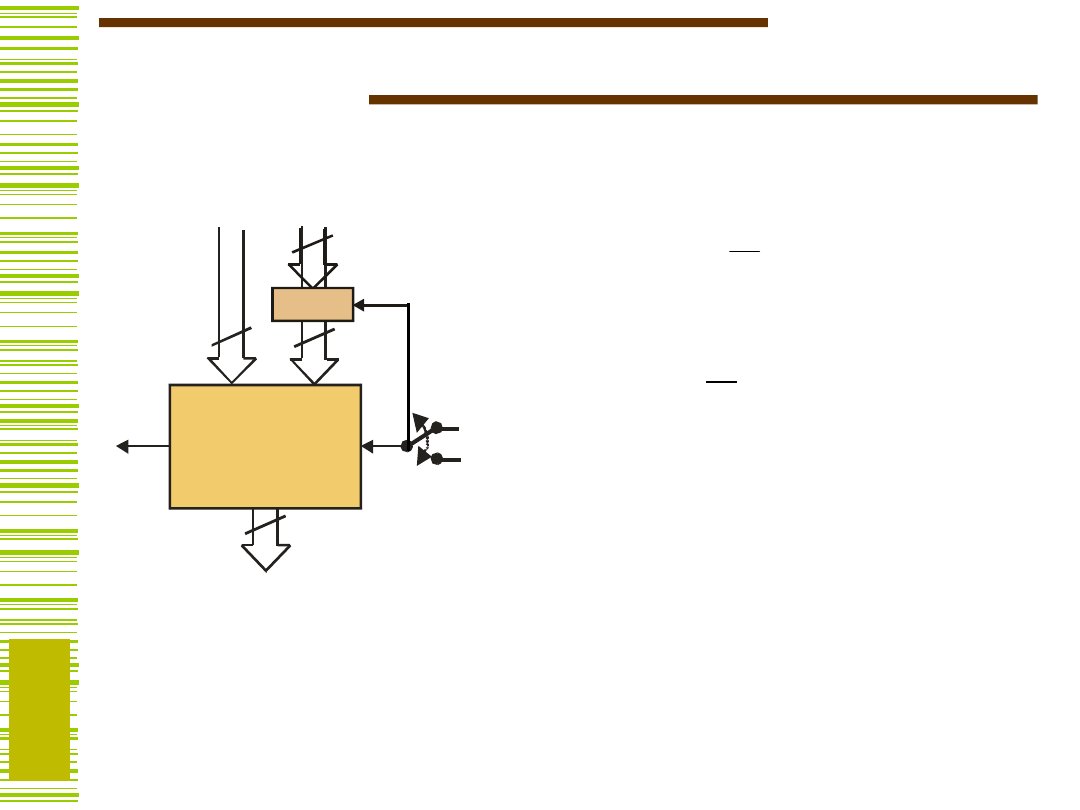
Sumator/układ odejmujący
Jak z sumatora zbudować układ odejmujący?
Y = A – B = A + (–B|
U2
)
1
Y
A
c
n
c
0
n
n
B
n
X O R
n
0
Dla c
0
= 0
Y = A + B 0 + 0 = A + B
Y = A + B c
0
+ c
0
;
c
0
{0,1}
B
–B|
U2
= +1 = B1 + 1
–B|
U2
= +1 = B1 + 1
–B|
U2
= +1 = B1 + 1
Dla c
0
= 1
Y = A + + 1 = A –
B
B
B
B
B
–
+
1
25
I
T
P
W
ZPT
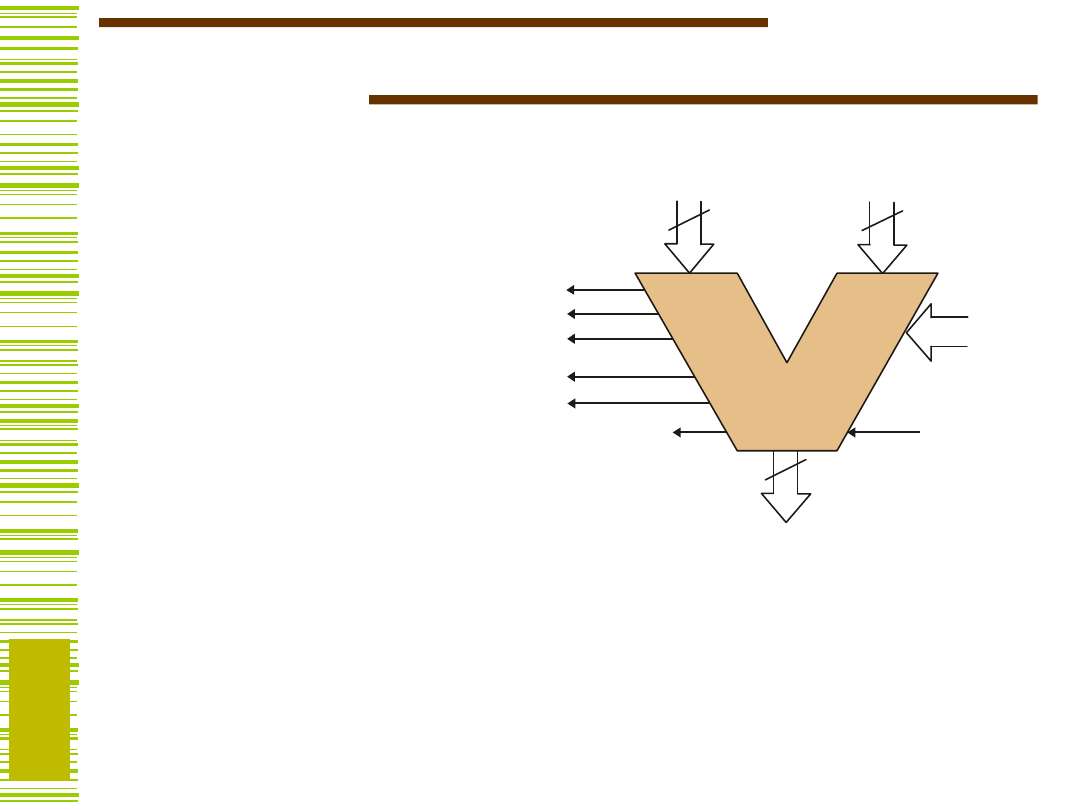
Zastosowania
Jednostka arytmetyczno-logiczna
Y
B
A
n
n
n
Y
n - 1
Z
O V R
P
G
c
n
c
0
S
A L U
Arytmometr (układ
wykonawczy:
mikrokontrolera, procesora
sygnałowego)
Inne układy
arytmetyczne:
układy mnożące
układy
kryptograficzne
...są budowane z sumatorów
26
I
T
P
W
ZPT
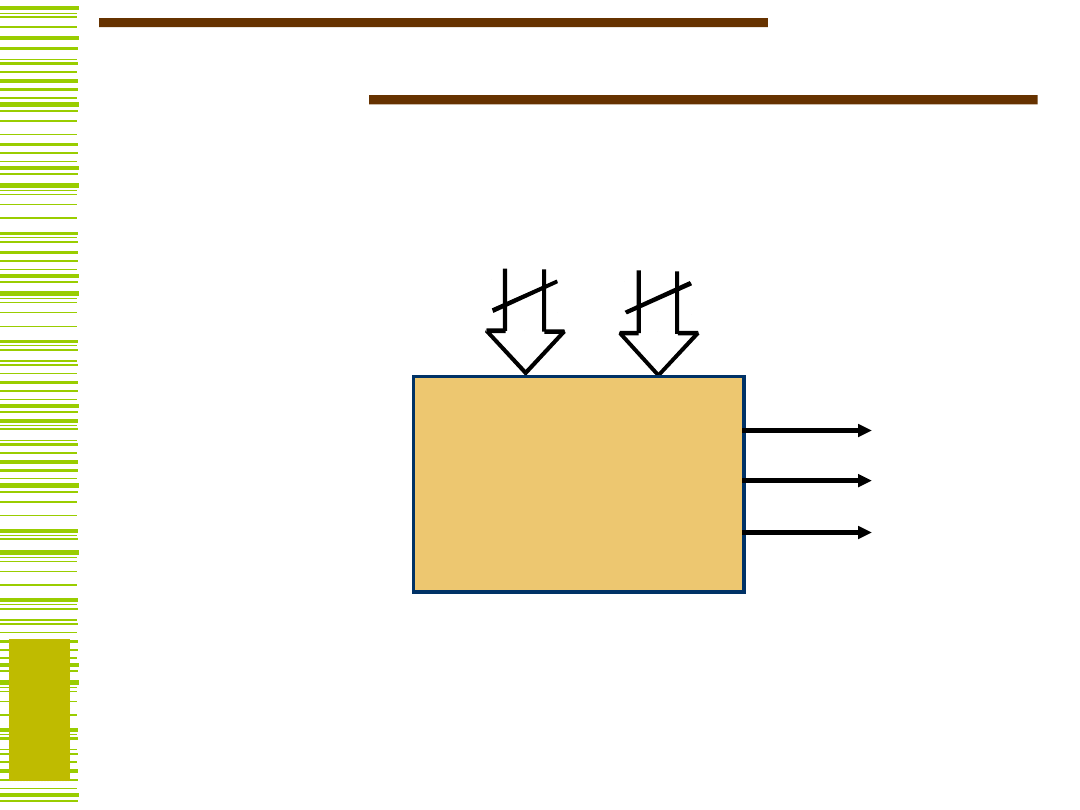
Komparator
A
n
B
n
K
„1 z 3”
A < B
A = B
A > B
27
I
T
P
W
ZPT
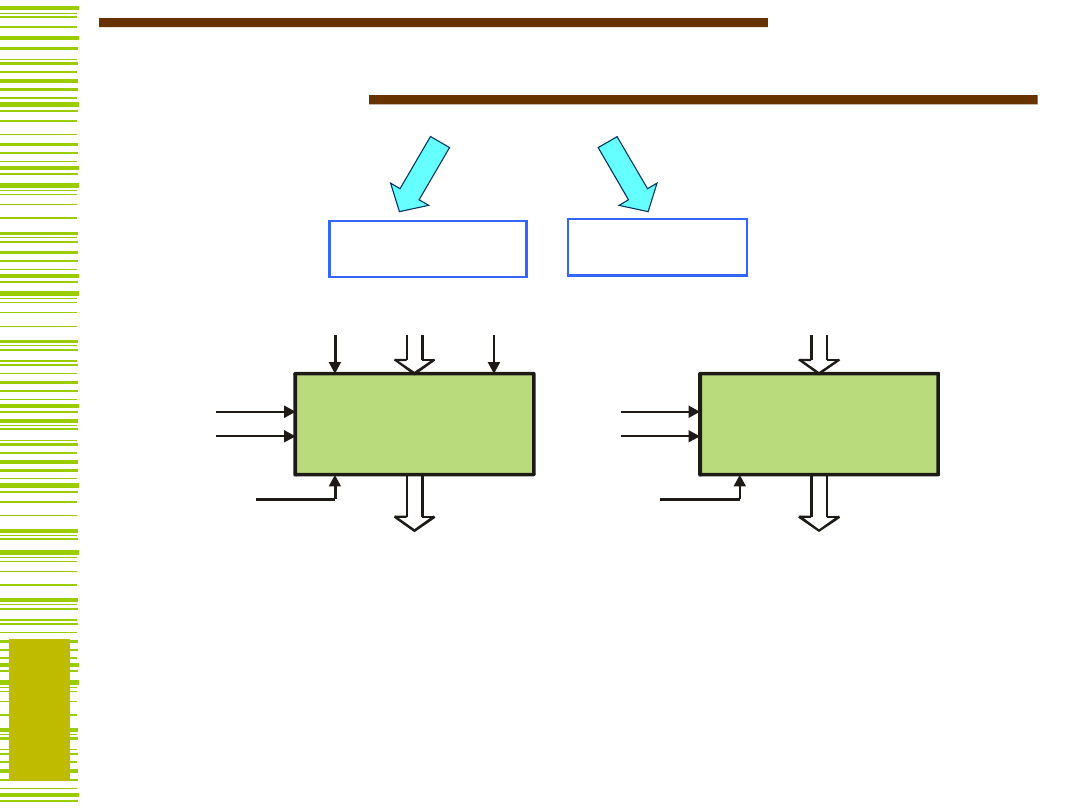
Sekwencyjne bloki funkcjonalne
Rejestry
Liczniki
L
( Q )
s
1
s
2
c lo c k
X
Y
R
( Q )
s
1
s
2
c lo c k
X
Y
x
l
x
p
Y := X LOAD
Y := Y HOLD
Y := <0...0> RESET
(CLEAR)
Y := SHR(x
p
,
Y)
Y := SHL(Y, x
l
)
Y := Y + 1 = INC(Y)
Y := Y – 1 = DEC(Y)
28
I
T
P
W
ZPT
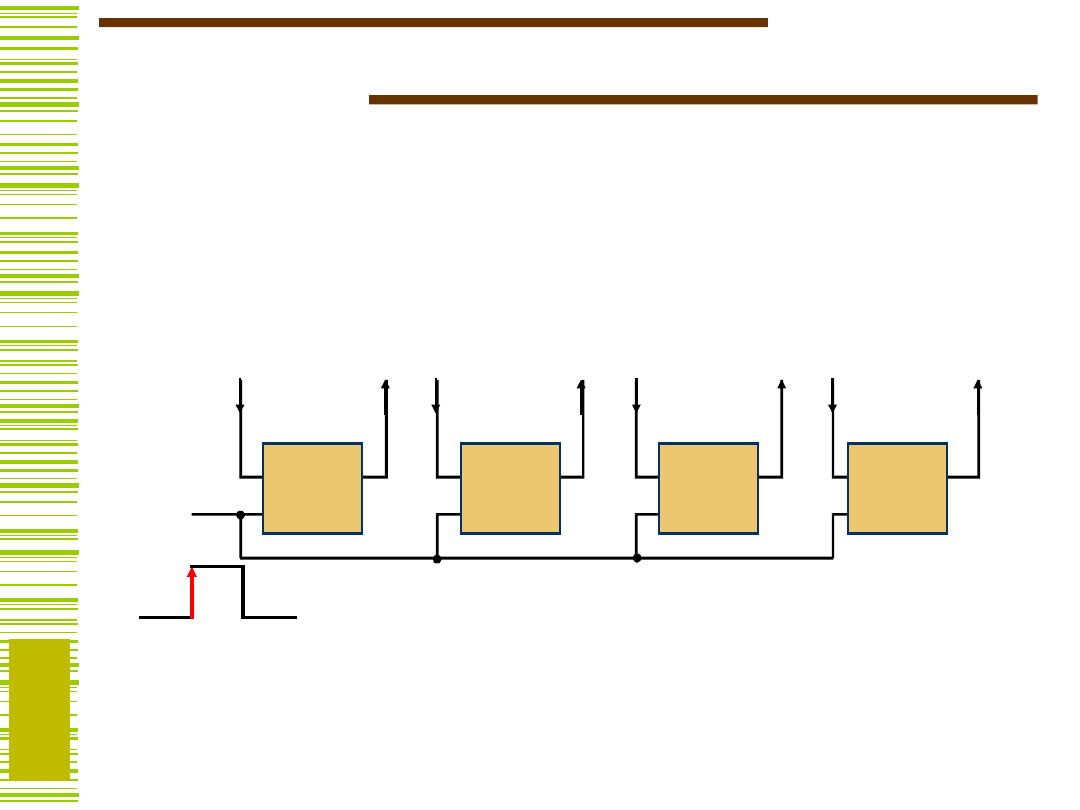
Prosty
rejestr
Rejestr zbudowany z przerzutników
– ładowanie (load) i pamiętanie
CLK
P
1
P
2
P
3
P
4
D
1
D
3
D
2
D
4
Q
1
Q
3
Q
2
Q
4
0
1
0
0
LOAD
0
1
0
0
29
I
T
P
W
ZPT
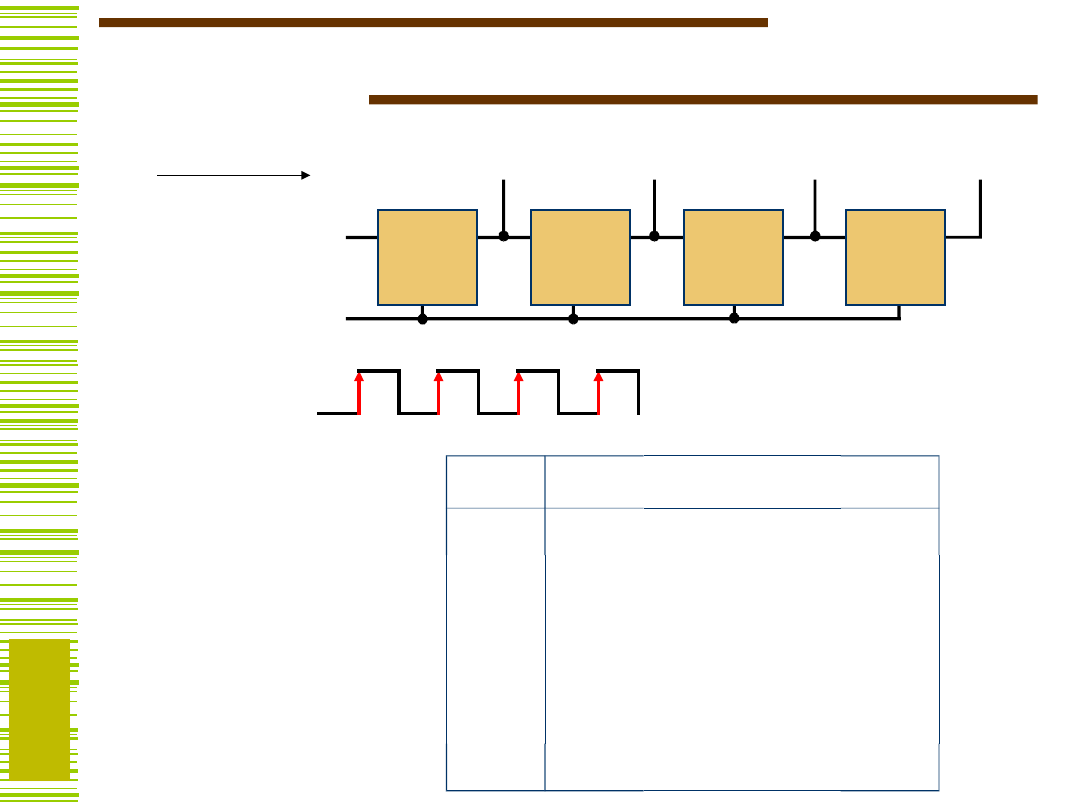
Rejestr przesuwający
WE
Q
1
Q
2
Q
3
Q
4
0
0
0
0
0
1
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
Q
1
Q
3
Q
2
Q
4
wejście
szeregowe
D
1
D
2
D
3
D
4
0
SHR
clk
0000 10
30
I
T
P
W
ZPT
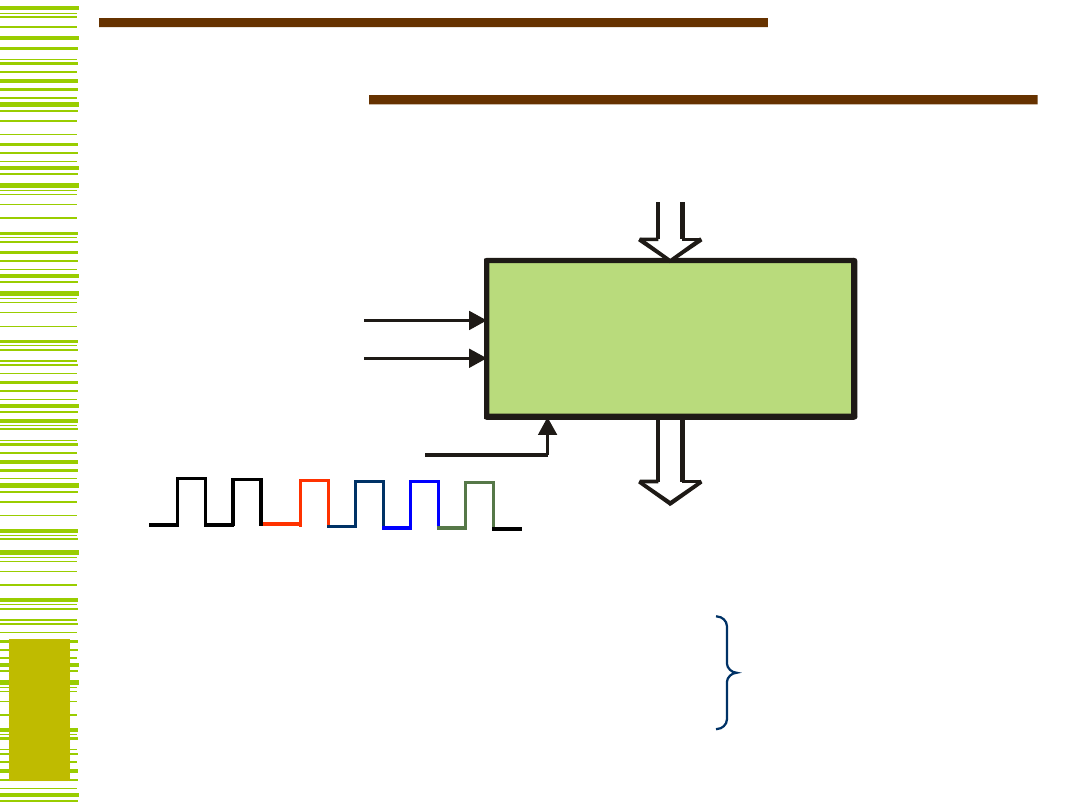
Mikrooperacje licznika
L ic z n ik
c lo c k
1100
Zliczanie
LOAD
COUNT
LOAD
HOLD
COUNT
LOAD
HOLD
0010
1101
1110
111
1
1100
31
I
T
P
W
ZPT
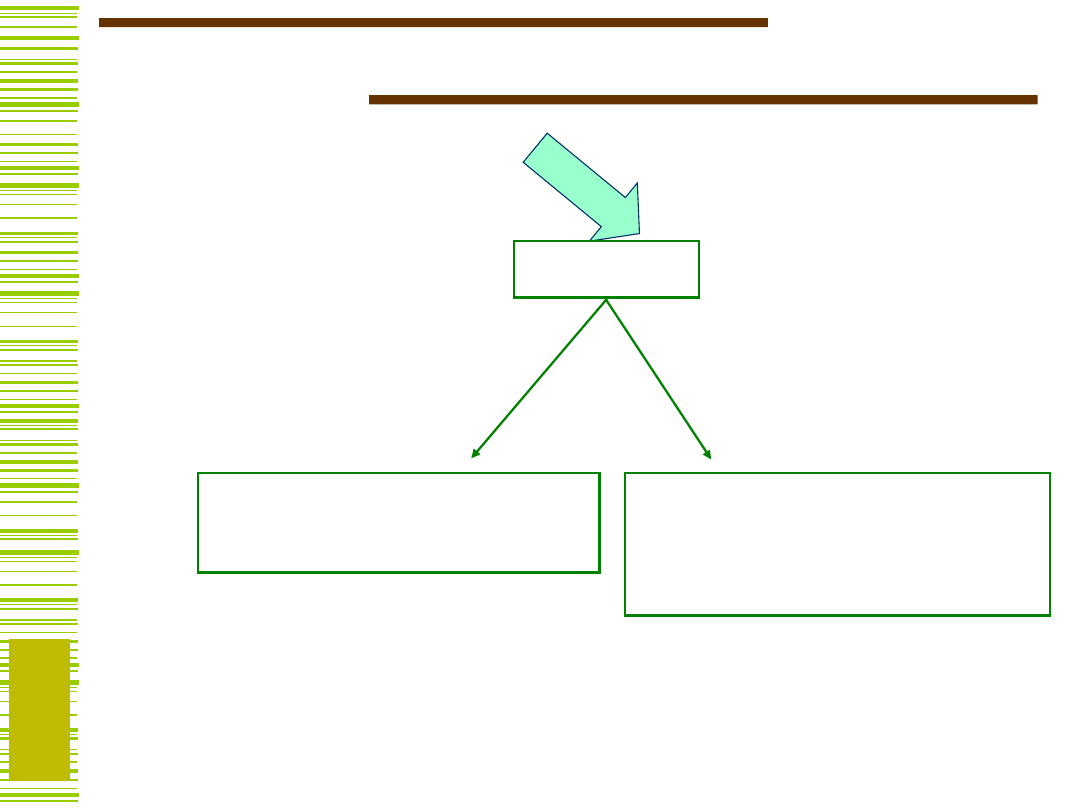
Bloki funkcjonalne
Pamięci
ROM
(Read Only Memory)
RAM
(Random Access
Memory)
32
I
T
P
W
ZPT
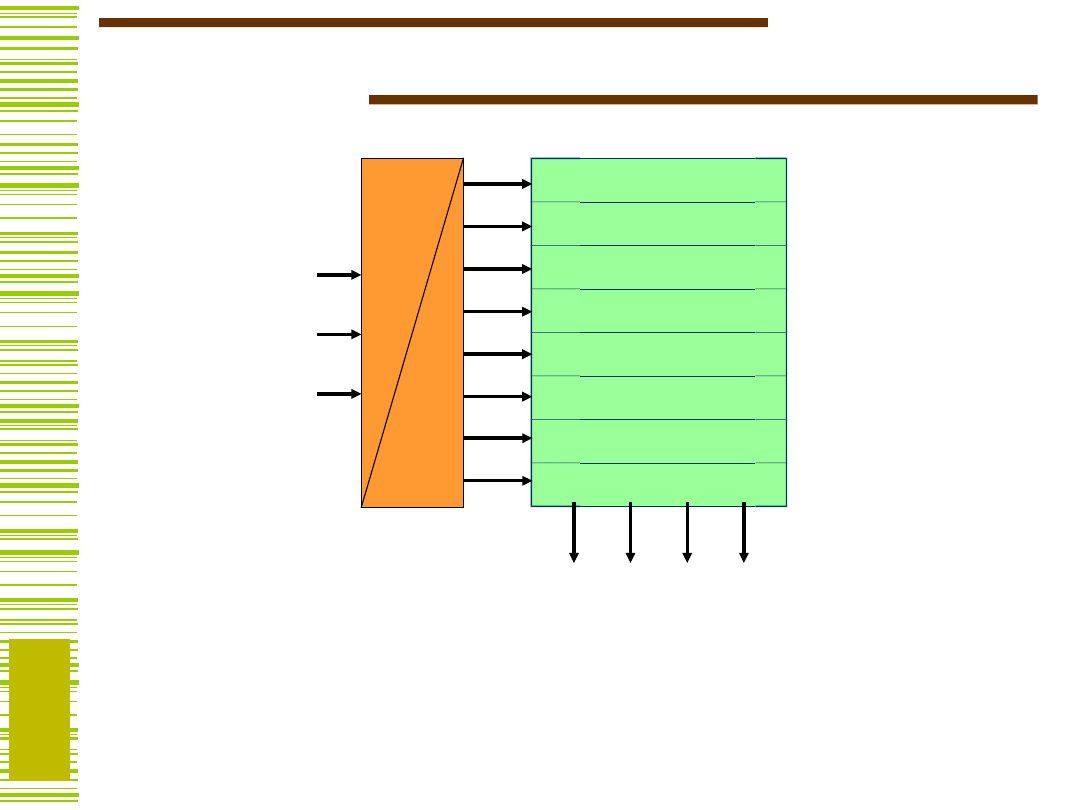
Pamięci typu ROM
ROM – uniwersalny układ kombinacyjny
A
ROM
m n
X
0
X
i
X
m-1
p
Y
n
33
I
T
P
W
ZPT
Pamięci typu ROM
Adres
ROM
8 4
0
1
2
3
4
5
6
7
0
0
0
0
0
1
1
0
1
1 1 1 1
0 1 1 0
1 1 1 0
0 1 1 0
0 1 1 0
0 1 0 1
0 0 0 0
0 1 1 0
1 1 1 0
0 1 0 1
1 1 1 1
34
I
T
P
W
ZPT
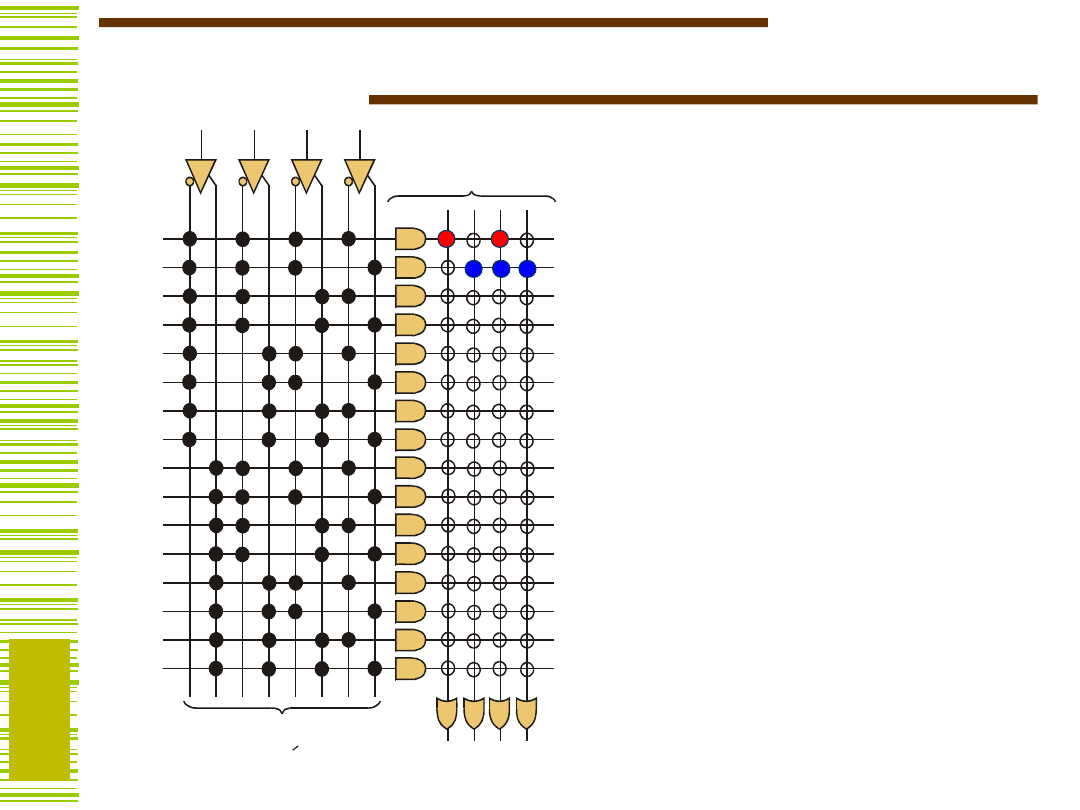
Pamięci typu ROM
(struktura)
y 3 y 2 y 1 y 0
M A T R Y C A O R
( P R O G R A M O W A L N A )
D
C
B
A
M A T R Y C A A N D
( S T A L A )
1010
0111
35
I
T
P
W
ZPT
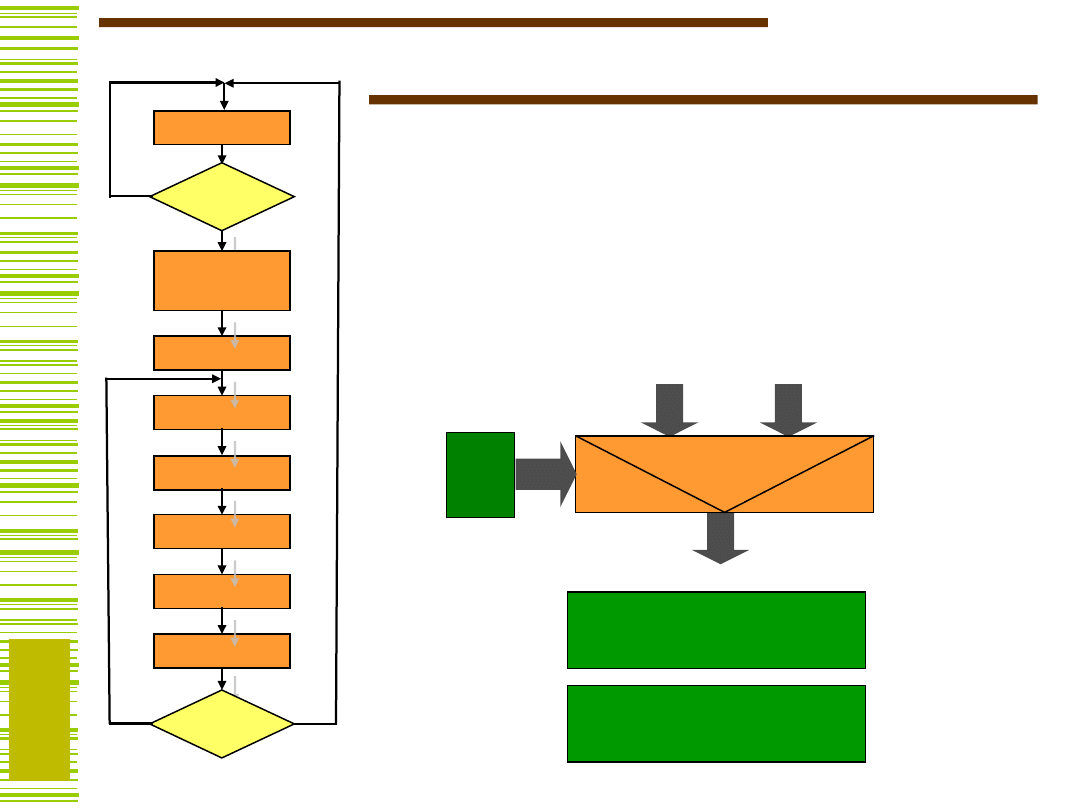
Synteza strukturalna
1. Analiza algorytmu pracy układu (sieci działań)
– zmienne, operacje
2. Dobór bloków funkcjonalnych do przechowywania
zmiennych i wykonywania operacji
3. Dobór bloków komutacyjnych
Bloki funkcjonalne są stosowane w syntezie układów
wykonawczych (operacyjnych).
36
I
T
P
W
ZPT
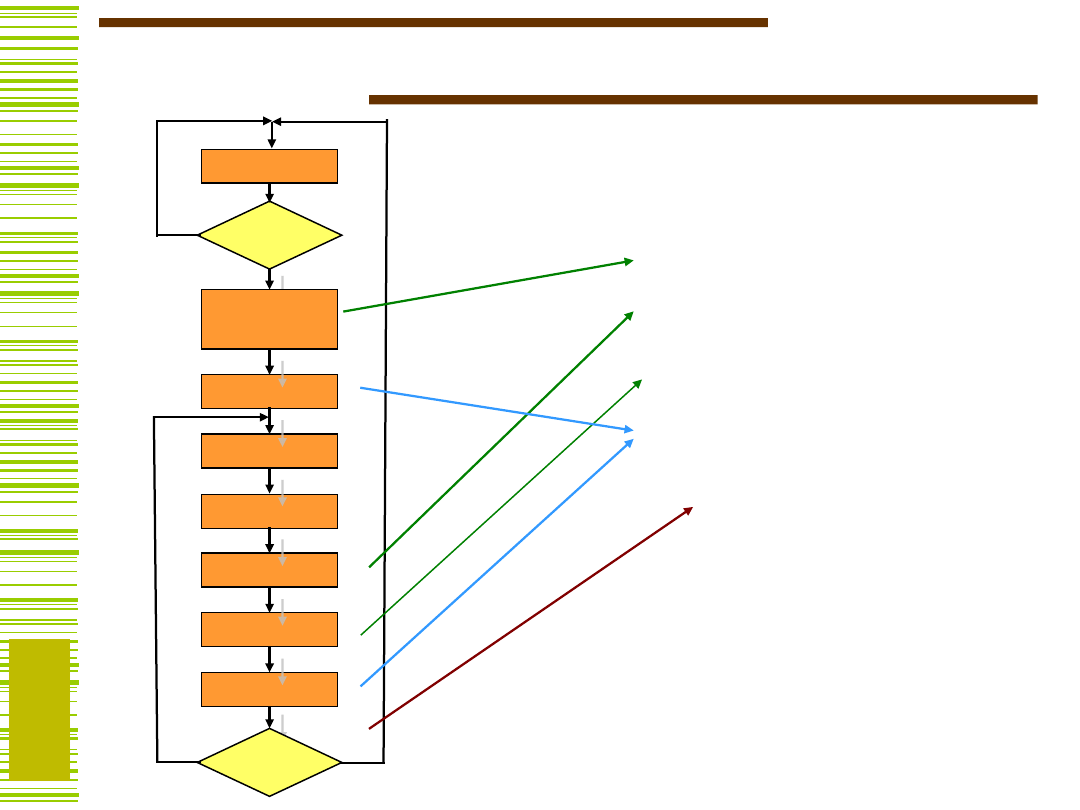
Przykład
B
D
0
D
n-1
Y
M
M(I)
I
S
B := M(I)
Y := 0
B := M(I)
Y := 0
Y = M(I)
Y = M(I)
Y := B + Y
Y := B + Y
I := I + 1
I := I + 1
B := M(I)
B := M(I)
B := B Y
B := B Y
B := B/2
B := B/2
Y := B + Y
Y := B + Y
I := 0
I := 0
NIE
0
1
TAK
Rozważmy przykład syntezy układu
cyfrowego pobierającego dane z wejść
D
0
,..., D
n–1
w celu ich przetworzenia w
rejestrach B i Y. Układ operacyjny ma
przetwarzać informację M(I ) pobieraną z
n źródeł D
0
,...,D
n–1
za pośrednictwem
multipleksera M adresowanego licznikiem
I.
37
I
T
P
W
ZPT
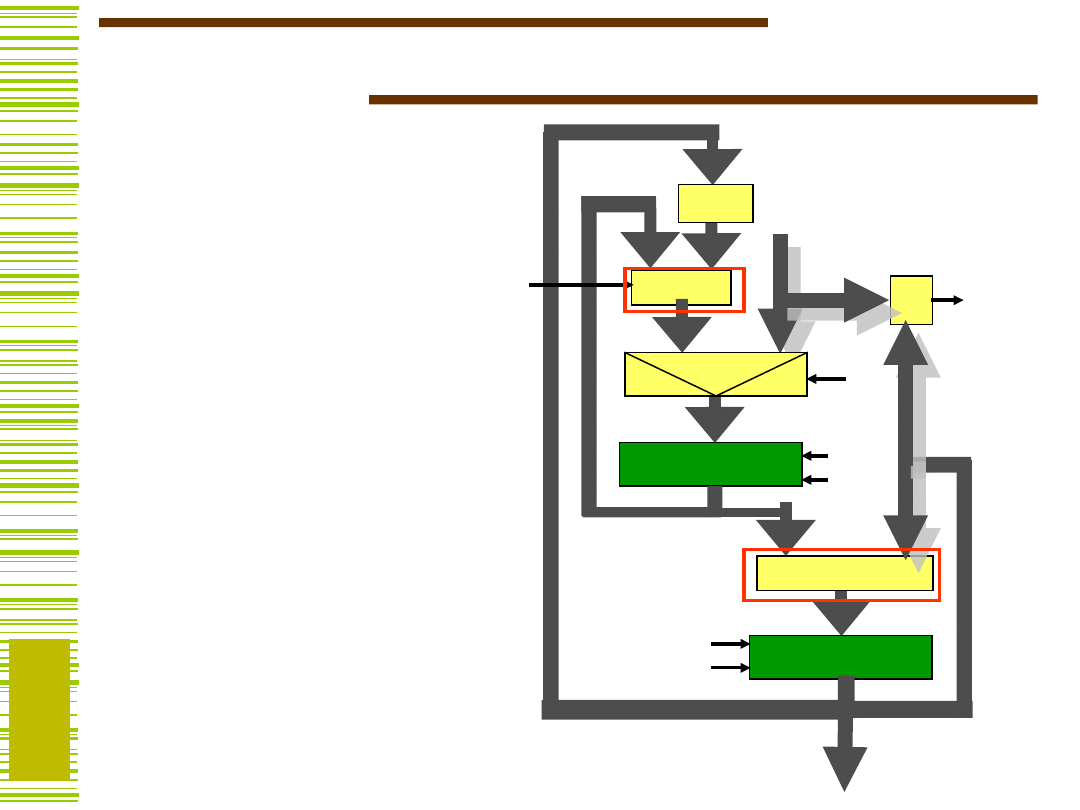
Przykład
S
B := M(I)
Y := 0
B := M(I)
Y := 0
Y = M(I)
Y = M(I)
Y := B + Y
Y := B + Y
I := I + 1
I := I + 1
B := M(I)
B := M(I)
B := B Y
B := B Y
B := B/2
B := B/2
Y := B + Y
Y := B + Y
I := 0
I := 0
NIE
0
1
TAK
B := M(I)
B := M(I)
B := B/2
B := B/2
B := B Y
B := B Y
Y := B + Y
Y := B + Y
Warunek Y = M(I)
Warunek Y = M(I)
38
I
T
P
W
ZPT
B
Y
M(I)
Y
c
0
K
do US
Y = M(I)
Y := 0
Y := B + Y
B := X
B := B/2
X
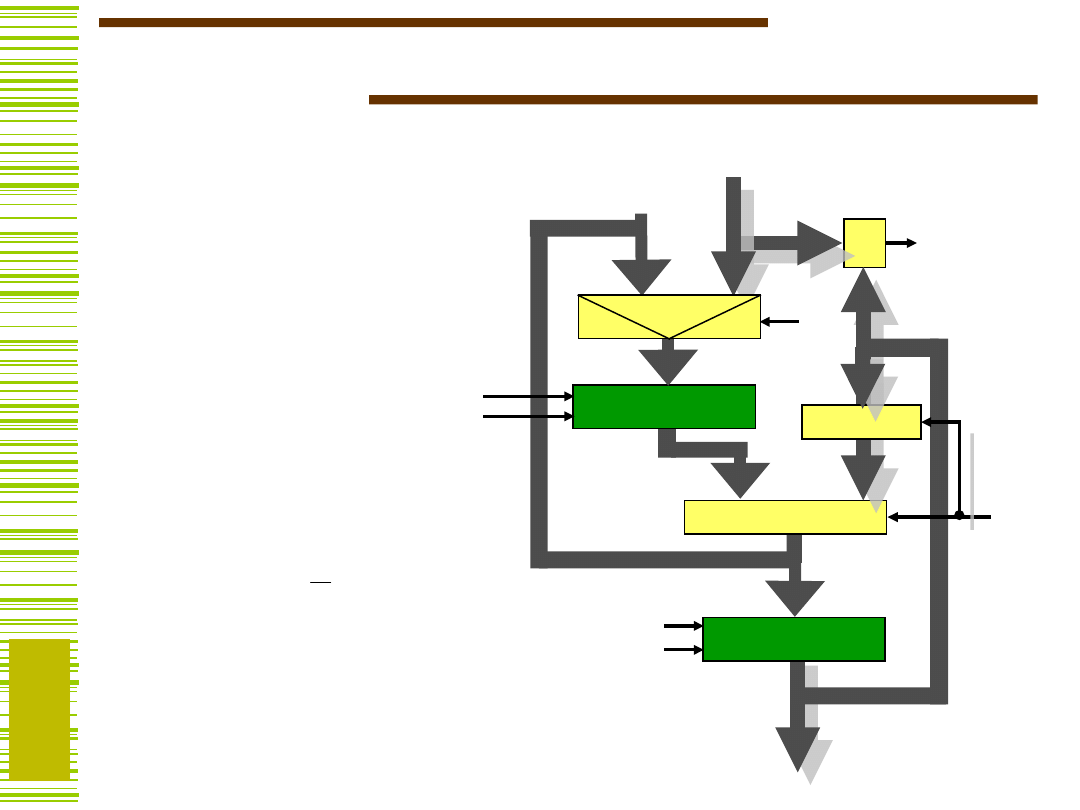
Przykład c.d.
NOT
B := M(I)
B := M(I)
B := B/2
B := B/2
B := B Y
B := B Y
Y := B + Y
Y := B + Y
Warunek Y = M(I)
Warunek Y = M(I)
(SHR(B))
B := B Y
B := B Y
Y := B + Y
Y := B + Y
39
I
T
P
W
ZPT
Y
Y
K
do US
Y = M(I)
Y := 0
Y := B + Y
X
v
M(I)
B := X
B := B/2
B
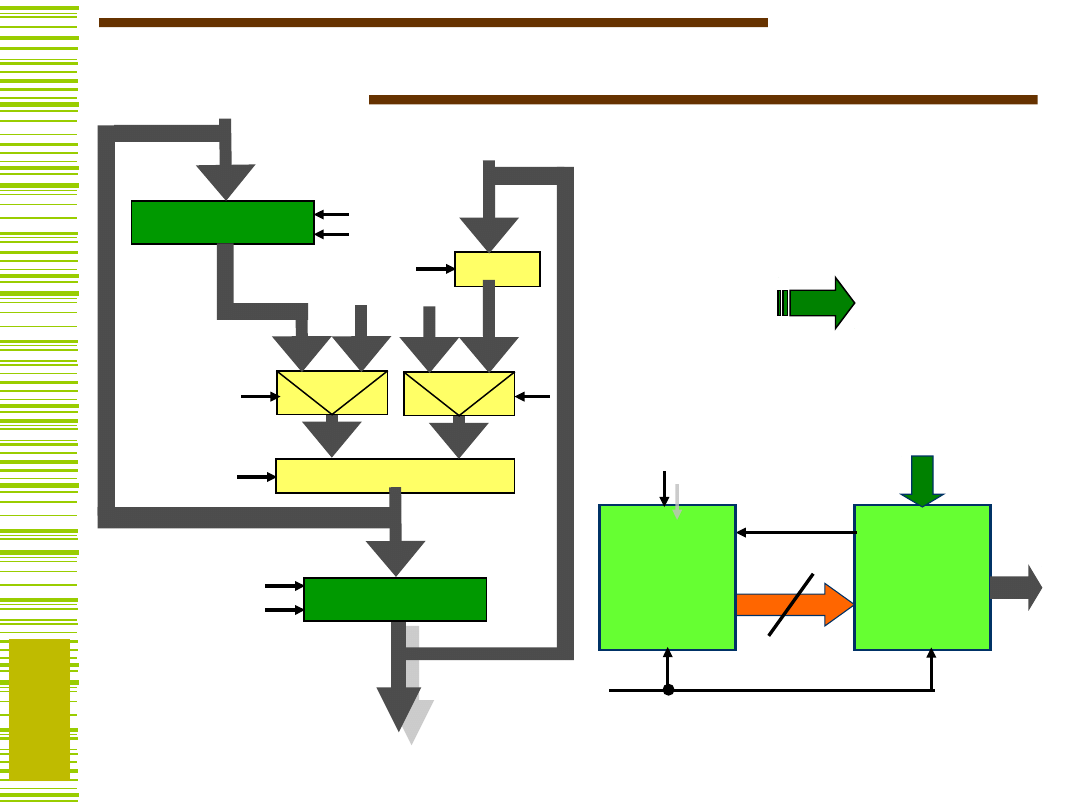
Przykład c.d.
B := B Y
B := B Y
Y := B + Y
Y := B + Y
EXOR
1
gdy V
,
Y
0
gdy V
Y,
Y
V
40
I
T
P
W
ZPT
Przykład c.d.
UO
M(I)
Y
Y = M(I)
7 (+2)
US
S
B
Y
M(I)
Y := 0
Y := B + Y
X
B := X
B := B/2
EXOR
v
c
0
Y
0
v
B Y
B Y
B + Y
B + Y
Warunek
Y = M(I)
Warunek
Y = M(I)
Warunek
F = M(I) – Y = 0
Warunek
F = M(I) – Y = 0
F
41
I
T
P
W
ZPT
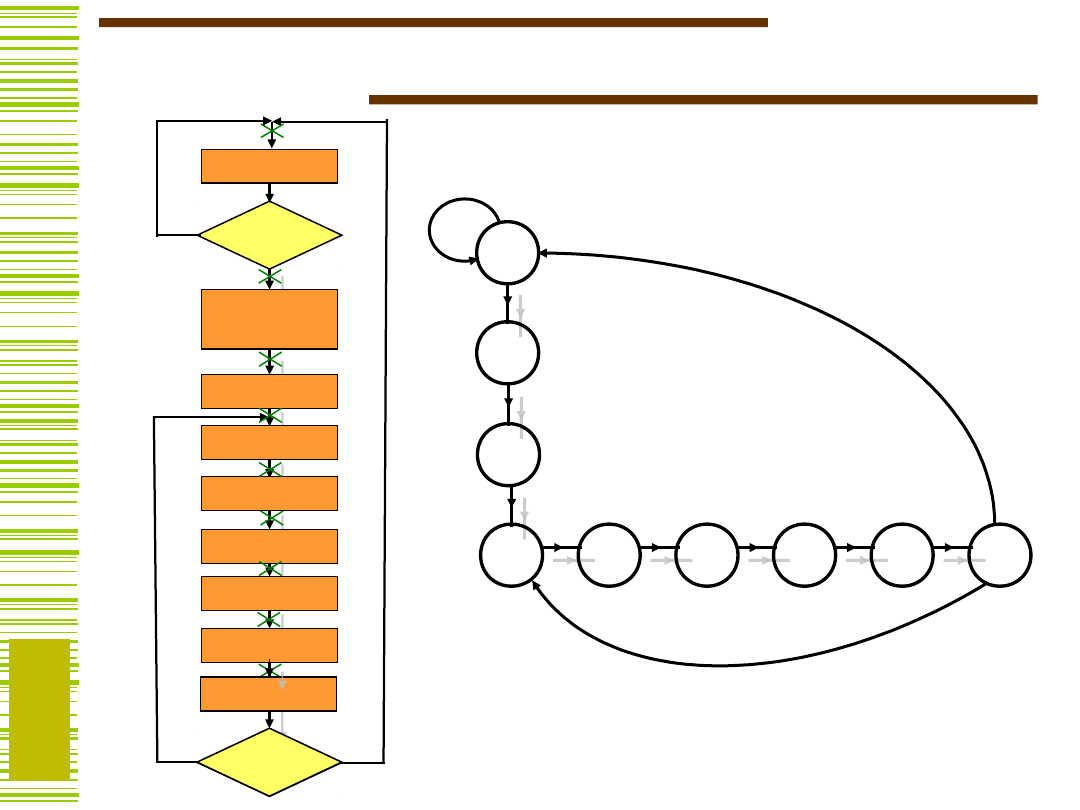
Przykład c.d.
S
B := M(I)
Y := 0
B := M(I)
Y := 0
Y := B + Y
Y := B + Y
I := I + 1
I := I + 1
B := M(I)
B := M(I)
B := B Y
B := B Y
B := B/2
B := B/2
Y := B + Y
Y := B + Y
I := 0
I := 0
NIE
0
1
TAK
A
8
A
1
Y = M(I)
Y = M(I)
A
0
A
2
A
3
A
4
A
5
A
6
A
7
F = M(I) – Y
F = M(I) – Y
F = 0
F = 0
S = x
0
S = x
0
[F = 0] = x
1
[F = 0] = x
1
- -
A
0
/Z
1
A
0
/Z
1
A
1
/Z
2
A
1
/Z
2
A
2
/Z
3
A
2
/Z
3
A
3
/Z
4
A
3
/Z
4
A
4
/Z
5
A
4
/Z
5
A
5
/Z
6
A
5
/Z
6
A
6
/Z
7
A
6
/Z
7
A
7
/Z
8
A
7
/Z
8
A
8
/Z
9
A
8
/Z
9
- -
- -
- -
- 1
- 0
- -
- -
- -
1 -
0 -
x
1
x
0
x
1
x
0
42
I
T
P
W
ZPT
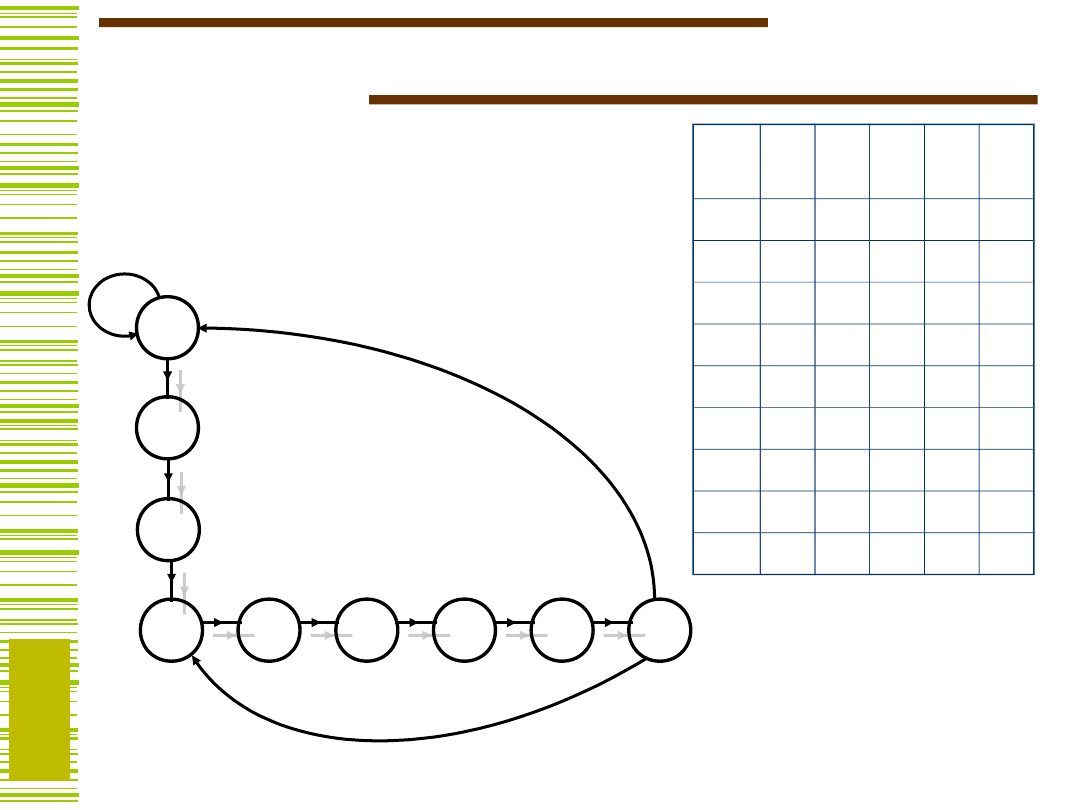
Przykład c.d.
x
1
x
0
A
00 01 11 10
Z
A
0
A
0
A
1
A
1
A
0
Z
1
A
1
A
2
A
2
A
2
A
2
Z
2
A
2
A
3
A
3
A
3
A
3
Z
3
A
3
A
4
A
4
A
4
A
4
Z
4
A
4
A
5
A
5
A
5
A
5
Z
5
A
5
A
6
A
6
A
6
A
6
Z
6
A
6
A
7
A
7
A
7
A
7
Z
7
A
7
A
8
A
8
A
8
A
8
Z
8
A
8
A
3
A
3
A
0
A
0
Z
9
- -
A
0
/Z
1
A
0
/Z
1
A
1
/Z
2
A
1
/Z
2
A
2
/Z
3
A
2
/Z
3
A
3
/Z
4
A
3
/Z
4
A
4
/Z
5
A
4
/Z
5
A
5
/Z
6
A
5
/Z
6
A
6
/Z
7
A
6
/Z
7
A
7
/Z
8
A
7
/Z
8
A
8
/Z
9
A
8
/Z
9
- -
- -
- -
- 1
- 0
- -
- -
- -
1 -
0 -
x
1
x
0
x
1
x
0
Document Outline