UŁAMKI ZWYKŁE

powtórzenie

(WŁASNOŚCI UŁAMKÓW

ZWYKŁYCH

DZIAŁANIA

WYKONYWANE NA

UŁAMKACH ZWYKŁYCH)

POKAZ ZAWIERA

INFORMACJE MIĘDZY

INNYMI O :

UŁAMKACH
WŁAŚCIWYCH

UŁAMKACH
NIEWŁAŚCIWYC
H

SKRACANIU I
ROZSZERZANIU
UŁAMKÓW

PORÓWNYWANI
U UŁAMKÓW

DODAWANIU
UŁAMKÓW

ODEJMOWANIU
UŁAMKÓW

MNOŻENIU
UŁAMKÓW

DZIELENIU
UŁAMKÓW

Ułamek składa się z

trzech elementów:

• Licznika

• Kreski ułamkowej

• Mianownika

3
2

57

LICZNIK

KRESKA UŁAMKOWA

MIANOWNIK

TO WYNIK Z DZIELENIA :

DZIELNA JEST LICZNIKIEM ,

DZIELNIK MIANOWNIKIEM ,

A KRESKA UŁAMKOWA ZASTĘPUJE ZNAK
DZIELENIA

Np.

3 : 4 =

4

3

DZIELNA

DZIELNIK

UŁAMEK JAKO WYNIK Z

DZIELENIA

ILORAZ

ILUSTRACJA UŁAMKÓW

3

2

2

1

UŁAMKI ZWYKŁE
MOŻEMY
ILUSTROWAĆ NA
RÓŻNYCH
FIGURACH

4

4

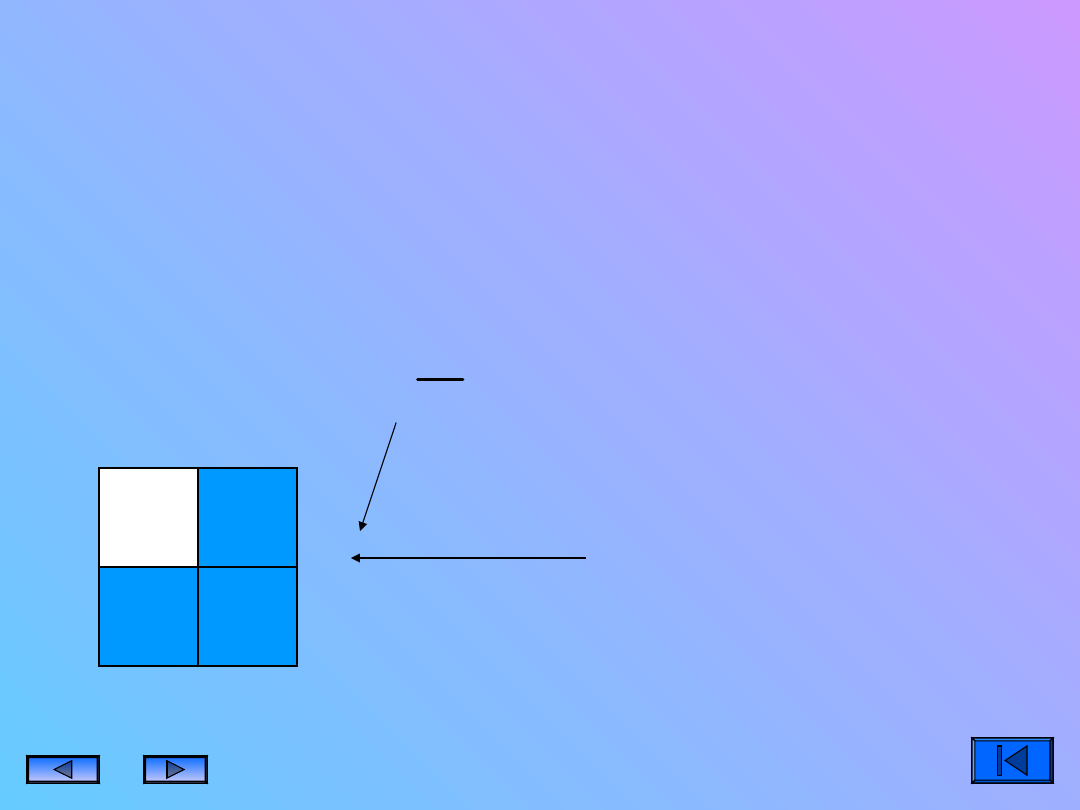
Mianownik ułamka zwykłego

mówi na ile jednakowych

części dzielimy całość, a

licznik ile tych części

bierzemy .

Np.

ułamek

4

3

Oznacza ,
że dana
figura
została
podzielon
a na
cztery
jednakow
e części i
trzy z
nich
zostały
zamalowa
ne.

Ułamki właściwe

Ułamki
właściwe to
takie , w
których
licznik jest
zawsze
mniejszy od
mianownika .

np

.

1000

1

,

229

8

,

19

7

,

58

3

,

2

1

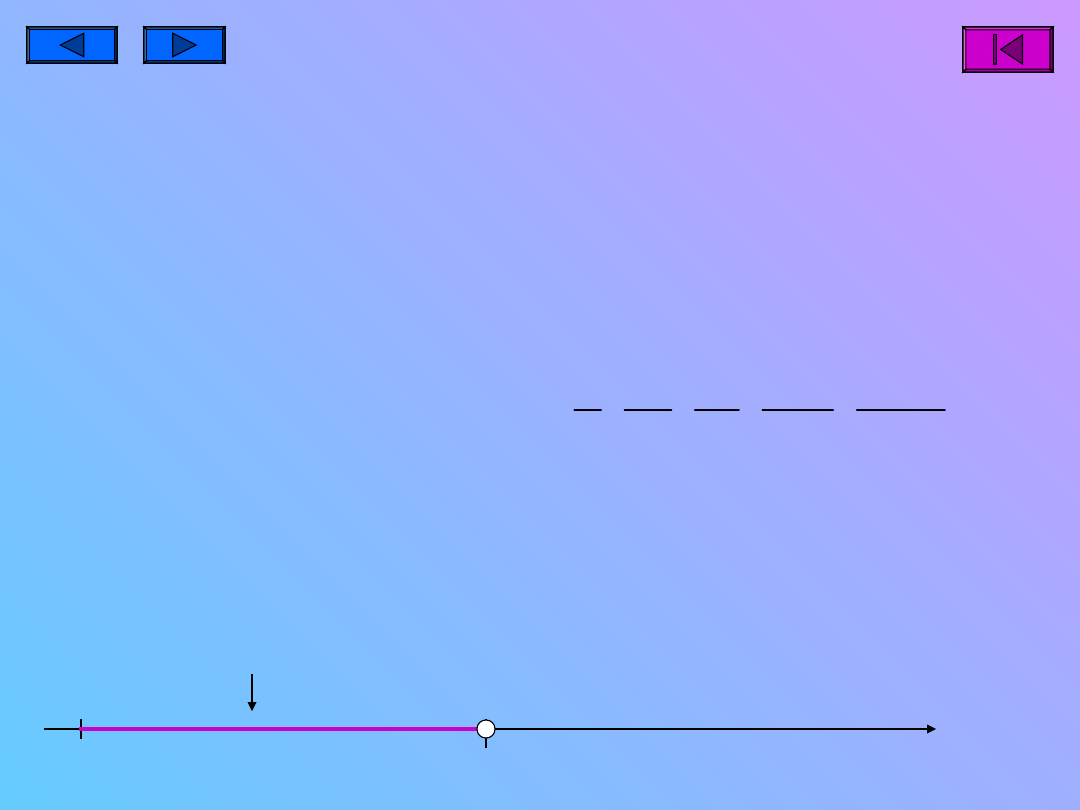
Ułamki
właściwe są
mniejsze od
jednej całości .

0

1

Ułamki
właściwe

Ułamki niewłaściwe

Ułamki niewłaściwe
to takie , w których
licznik jest zawsze
większy od
mianownika lub
równy
mianownikowi.

1000

1000

,

229

298

,

19

37

,

48

263

,

2

12

np.

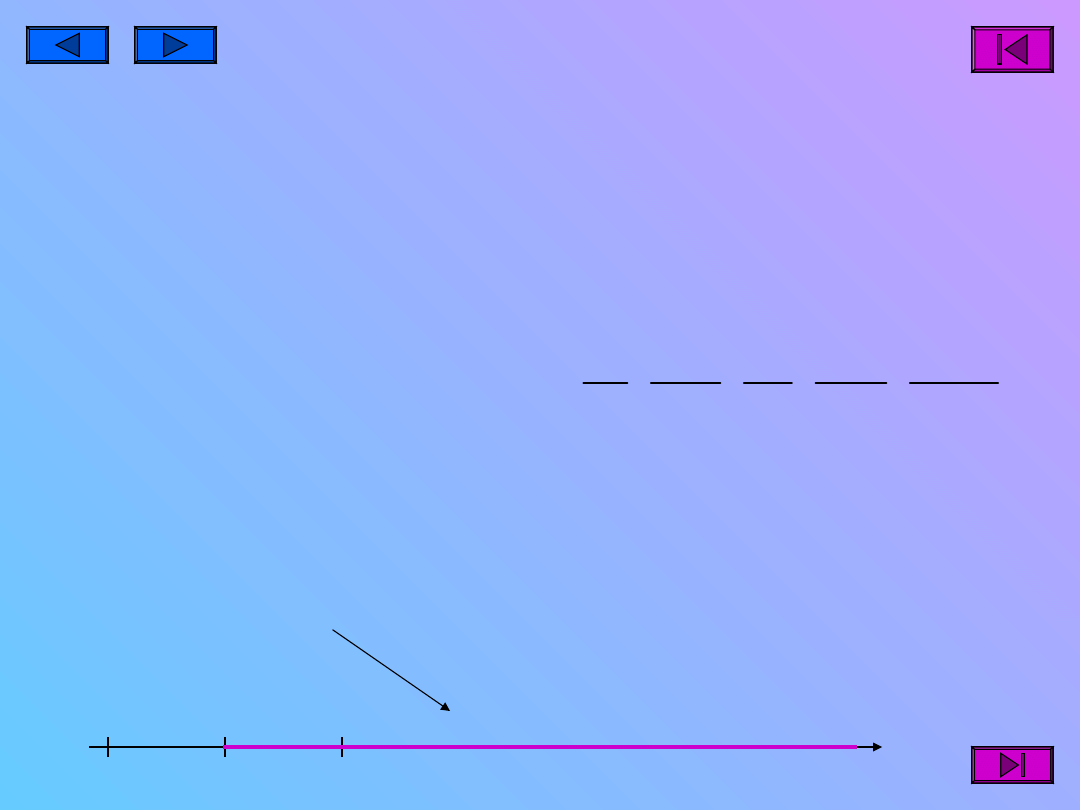
Ułamki właściwe
są większe lub
równe jednej
całości .

0

1

2

Ułamki
niewłaściwe

LICZBY MIESZANE

Z UŁAMKÓW
NIEWŁAŚCIWYCH
MOŻEMY
WYŁĄCZYĆ
CAŁOŚĆ . W TYM
CELU DZIELIMY
LICZNIK UŁAMKA
PRZEZ JEGO
MIANOWNIK :

5

2

3

5

:

17

5

17





RESZTA Z
DZIELENIA

PO WYŁĄCZENIU
CAŁOŚCI
OTRZYMUJEMY
LICZBY
MIESZANE

Przykłady
liczb
mieszanych :

8

1

3

,

45

9

550

,

19

4

98

,

7

2

8

ZAMIANA LICZB

MIESZANYCH NA UŁAMKI

NIEWŁAŚCIWE

Liczby
mieszane
można
zamienić z
powrotem na
ułamki
niewłaściwe :

7

30

7

2

4 

np.

Mnożymy
mianowni
k przez
całość

Dodaje
my
licznik

Mianowni
k
przepisuje
my bez
zmian

+

*

SKRACANIE UŁAMKÓW

ZWYKŁYCH

Ułamki
zwykłe
możemy
skracać
dzieląc
licznik i
mianownik
ułamka
przez tą
samą liczbę
różną od 0 i
1.

5

3

25

15



:

5

:

5

Ułamki zwykłe
skracamy do
momentu uzyskania
ułamków

nieskracalnych

UŁAMKI

NIESKRACALNE

Ułamki zwykłe
skracamy aż do
momentu , kiedy
otrzymamy ułamki
nieskracalne .
Ułamki nieskracalne
to takie , których nie
da się już więcej
skrócić . Licznik i
mianownik ułamka
nieskracalnego są
liczbami względnie
pierwszymi .

Wartość
ułamka
przed i po
skróceniu
jest taka
sama np.

2

1

4

2



ROZSZERZANIE

UŁAMKÓW

Ułamki zwykłe
możemy
rozszerzać
mnożąc licznik
i mianownik
ułamka przez
tą samą liczbę
różną od 0 i 1.

9

6

3

2



np.

*

3

*

3

Po
rozszerzaniu
wartość
ułamków nie
zmienia się

Porównywanie ułamków

zwykłych

Z dwóch
ułamków o
jednakowych
mianownikac
h większy jest
ten , który ma
większy
licznik. Np.

Z dwóch
ułamków o
jednakowych
licznikach
większy jest ten
, który ma
mniejszy
mianownik. Np.

8

5

8

3



8

5

11

5



Ułamki
właściwe są
zawsze
mniejsze od
ułamków
niewłaściwych
!

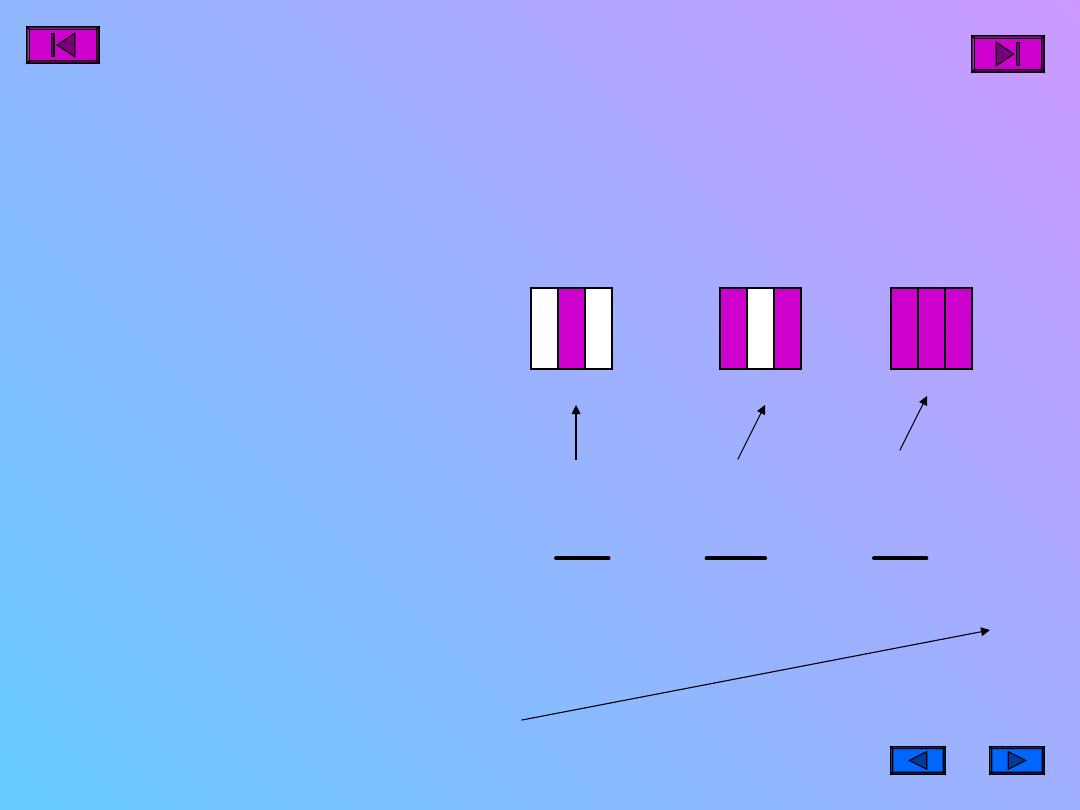
Porównywanie różnych

ułamków

ABY PORÓWNAĆ
UŁAMKI ZWYKŁE O
RÓŻNYCH
LICZNIKACH I
MIANOWNIKACH ,
NALEŻY SPROWADZIĆ
UŁAMKI DO TEGO
SAMEGO
MIANOWNIKA LUB
LICZNIKA .(Można to
zrobić poprzez
rozszerzanie lub
skracanie ułamków).

Np.

20

12

21

12

lub

35

21

35

20

5

3

...

7

4





Wstawia
my znak
mniejszo
ści

Porównujem
y

rozszerzając

DODAWANIE UŁAMKÓW

ZWYKŁYCH

UŁAMKI ZWYKŁE O
JEDNAKOWYCH
MIANOWNIKACH
DODAJEMY
NASTĘPUJĄCO :
DODAJEMY LICZNIKI ,
A MIANOWNIK
ZOSTAWIAMY BEZ
ZMIAN. JEŚLI W
WYNIKU OTRZYMAMY
UŁAMEK
NIEWŁAŚCIWY –
WYŁĄCZAMY
CAŁOŚCI .

1

3

3

3

2

3

1







ODEJMOWANIE UŁAMKÓW

ZWYKŁYCH

UŁAMKI ZWYKŁE O
JEDNAKOWYCH
MIANOWNIKACH
ODEJMUJEMY
NASTĘPUJĄCO :
ODEJMUJEMY
LICZNIKI , A
MIANOWNIK
ZOSTAWIAMY BEZ
ZMIAN.

JEŚLI NIE DA

SIĘ ODJĄĆ LICZNIKÓW
ZAMIENIAMY CAŁOŚCI
ABY OTRZYMAĆ

UŁAMEK

NIEWŁAŚCIWY.

NP.

4

3

16

12

16

7

2

16

19

2

16

7

2

16

3

3

)

11

6

2

11

7

11

13

2

11

7

11

2

3

)

7

2

7

5

7

9

7

5

7

2

1

)



























c

b

a

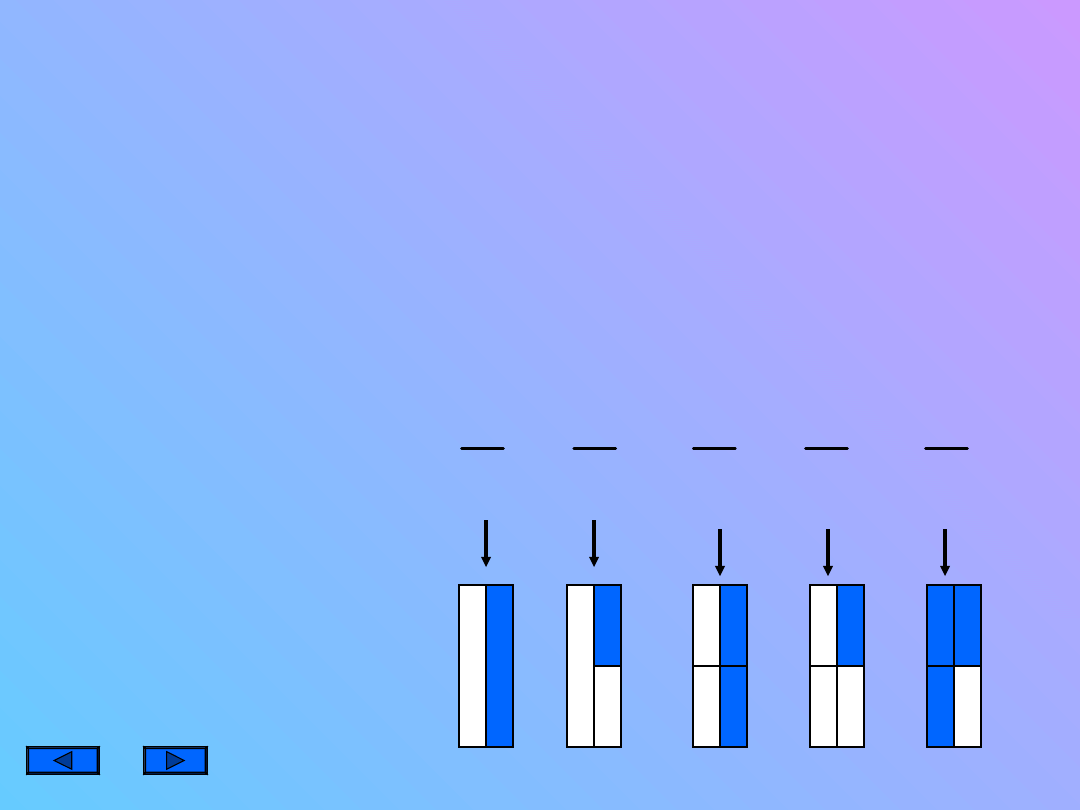
DODAWANIE I ODEJMOWANIE

UŁAMKÓW O RÓŻNYCH

MIANOWNIKACH

ABY DODAĆ LUB
ODJĄĆ UŁAMKI
O RÓŻNYCH
MIANOWNIKAC
H NALEŻY JE
NAJPIERW
SPROWADZIĆ
DO WSPÓLNEGO
MIANOWNIKA.

4

3

4

1

4

2

4

1

2

1









np.

=

+

+

=

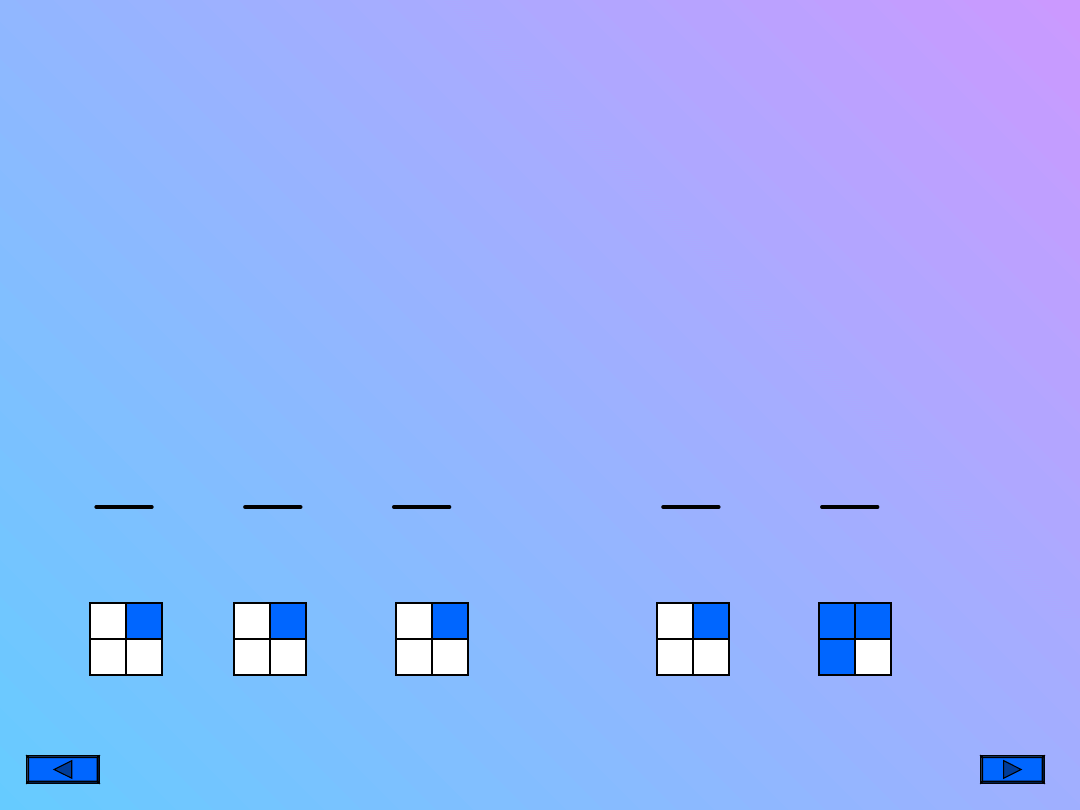
MNOŻENIE UŁAMKÓW

ZWYKŁYCH PRZEZ LICZBY

NATURALNE

Dodawanie tych samych ułamków
możemy zamienić na mnożenie
ułamków przez liczby naturalne :
np.

4

3

4

1

*

3

4

1

4

1

4

1









=

+

+

=

3 *

Aby pomnożyć ułamek zwykły

przez liczbę naturalną(lub liczbę

naturalną przez ułamek zwykły)

należy pomnożyć licznik ułamka

przez tą liczbę , a mianownik

przepisać bez zmian.

np
.

5

2

2

5

12

5

4

*

3

4

*

5

3







Przy mnożeniu
ułamków warto
pamiętać o
skracaniu !

np
.

2

1

1

1

*

2

3

2

*

4

3





Skracamy liczbę (2) z
mianownikiem( 4) przez
2 i po skreśleniu
piszemy co zostało

2

1

MNOŻENIE UŁAMKÓW

ZWYKŁYCH

PRZY MNOŻENIU
UŁAMKÓW
ZWYKŁYCH
MNOŻYMY
LICZNIK PRZEZ
LICZNIK UŁAMKA
, A MIANOWNIK
PRZEZ
MIANOWNIK

NP.

35

6

7

*

5

2

*

3

7

2

*

5

3





Przy mnożeniu
ułamki
możemy
skracać „na
krzyż”

np.

4

1

8

2

8

*

1

2

*

1

32

14

*

7

4







1

1

2

8

Należy pamiętać o tym , że nie wolno mnożyć
liczb mieszanych – zamieniamy je najpierw na
ułamki niewłaściwe!

DZIELENIE UŁAMKÓW

ZWYKŁYCH PRZEZ LICZBY

NATURALNE

Aby podzielić
ułamek zwykły
przez liczbę
naturalną
należy
pomnożyć
mianownik
ułamka przez
tą liczbę , a
licznik
przepisać bez
zmian .

: 2
=

2

1

4

1

np.

15

1

3

*

5

1

6

*

5

2

6

:

5

2







Po zamianie dzielenia na
mnożenie możemy skracać
licznik z mianownikiem

Ułamki odwrotne

W ułamku
odwrotnym do
danego licznik
staje się
mianownikiem ,
a mianownik
licznikiem

.

np. odwrotnością
ułamka :

11

6

jest

6

11

Iloczyn ułamków
(liczb) odwrotnych
jest równy 1

1

1

1

3

7

*

7

3





np
.

Aby znaleźć liczbę
odwrotną do
liczby mieszanej
(lub całości)
zamieniamy ją
najpierw na
ułamek
niewłaściwy

9

23

9

5

2

,

1

32

32





DZIELENIE LICZB

NATURALNYCH PRZEZ UŁAMKI

ZWYKŁE

ABY PODZIELIĆ LICZBĘ NATURALNĄ
PRZEZ UŁAMEK ZWYKŁY NALEŻY
POMNOŻYĆ TĄ LICZBĘ PRZEZ
ODWROTNOŚĆ UŁAMKA

16

1

16

1

4

*

4

3

4

*

12

3

4

*

12

4

3

:

12











np
.

2

1

22

2

45

2

5

*

9

2

5

*

9

5

2

:

9









4

1

Dzielenie ułamków

zwykłych

Dzielenie
ułamków
zwykłych
zamieniamy na
mnożenie
przez
odwrotność
ułamka
drugiego

21

10

3

5

*

7

2

5

3

:

7

2





np
.

Pierwszy
ułamek
przepisujemy

Drugi
odwraca
my

Po
zamianie
na
mnożenie
pamiętam
y o
skracaniu
:

8

1

2

*

4

1

*

1

10

3

*

12

5

3

10

:

12

5







np.

1

4

1

2

UŁAMKI PIĘTROWE

UŁAMKI
PIĘTROWE TO
UŁAMKI ,
KTÓRE MAJĄ
WIĘCEJ NIŻ
JEDNĄ
KRESKĘ
UŁAMKOWĄ

31

4

3

21

2

,

11

9

2

,

9

4

3

,

6

5

3

2

Przykład
y
ułamków
piętrowy
ch:

W ułamkach piętrowych
zamieniamy główną
kreskę ułamkową na
znak dzielenia :

15

14

3

7

*

5

2

7

3

:

5

2

7

3

5

2







OPRACOWANIE

Nauczyciel matematyki

Zespołu Szkół w Białce

mgr DOROTA KUDZIA