Funkcja liniowa i wprost

proporcjonalność

Definicja funkcji liniowej

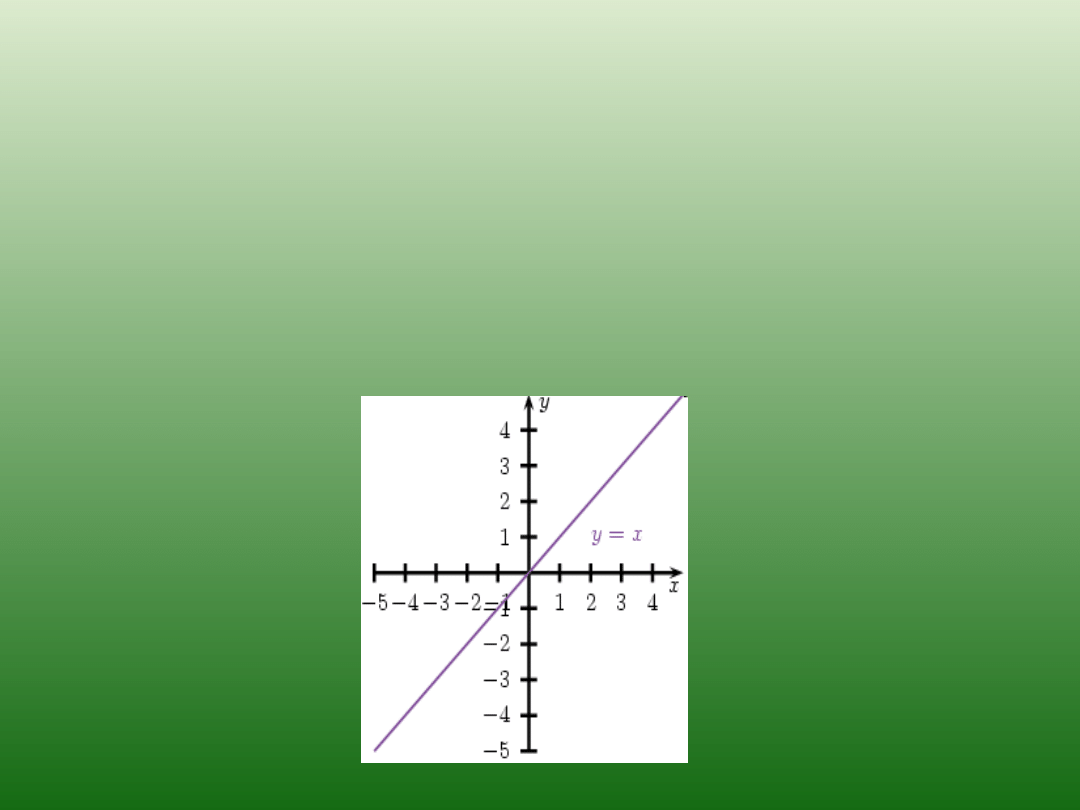
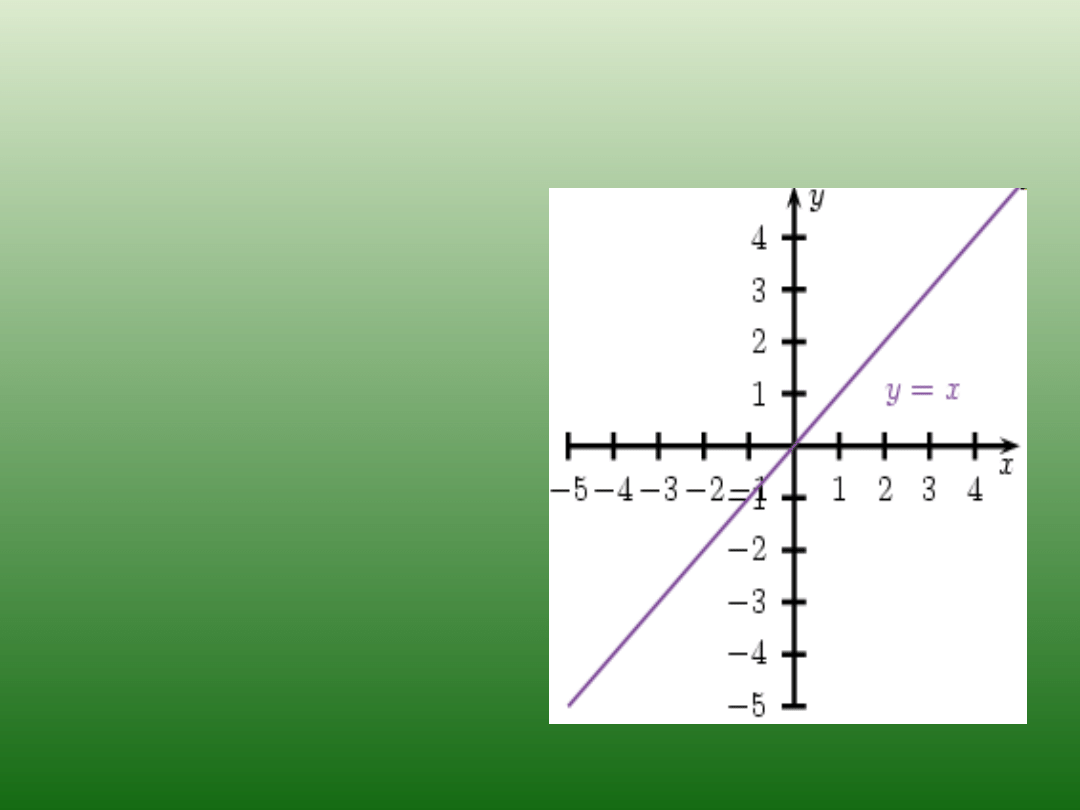
Funkcja liniowa

jest to taki rodzaj funkcji, której

wykresem jest linia prosta.

Dziedziną

funkcji liniowej jest zbiór liczb

rzeczywistych.

Wzór funkcji liniowej

Funkcje liniową opisuje się wzorem…

y = ax + b

…gdzie „a” określa kierunek funkcji, zaś „b”

miejsce przecięcia wykresu z osią Y.

Własności

Stałe

a, b

a, b mają swoje nazwy:



a

a nazywamy

współczynnikiem kierunkowym prostej

(współczynnikiem kątowym),

który decyduje o

nachyleniu wykresu do osi X,



b

b nazywamy

wyrazem wolnym (wyrazem stałym),

który wyznacza punkt przecięcia wykresu z osią Y.  

Znajdowanie punktów na osiach X

i Y

Punkt na osi Y mamy podany we wzorze funkcji, jest to

współczynnik „b”. Punktem na osi X jest tzw. Miejsce
zerowe funkcji, wyznacza się je wzorem:

x= - b/a

Funkcja różnowartościowa

To funkcja, która dla dowolnych

dwóch różnych argumentów

przyjmuje różne wartości.

Funkcja

f: X

f: X





Y

Y jest

różnowartościowa wtedy i

tylko wtedy, gdy

x

x

1

1

≠ x

≠ x

2

2

→ f (x

→ f (x

1

1

) ≠ f (x

) ≠ f (x

2

2

)

)

Monotoniczność funkcji

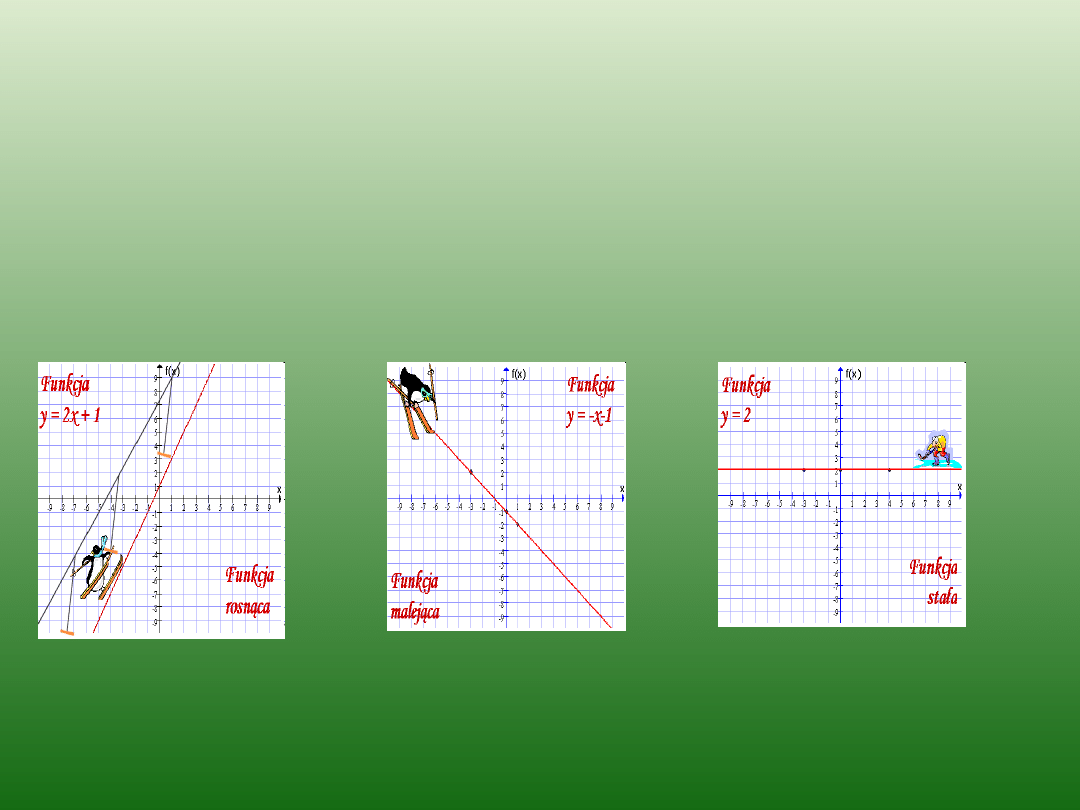
Monotoniczność

jest to badanie, czy funkcja jest

rosnąca, malejąca czy stała.

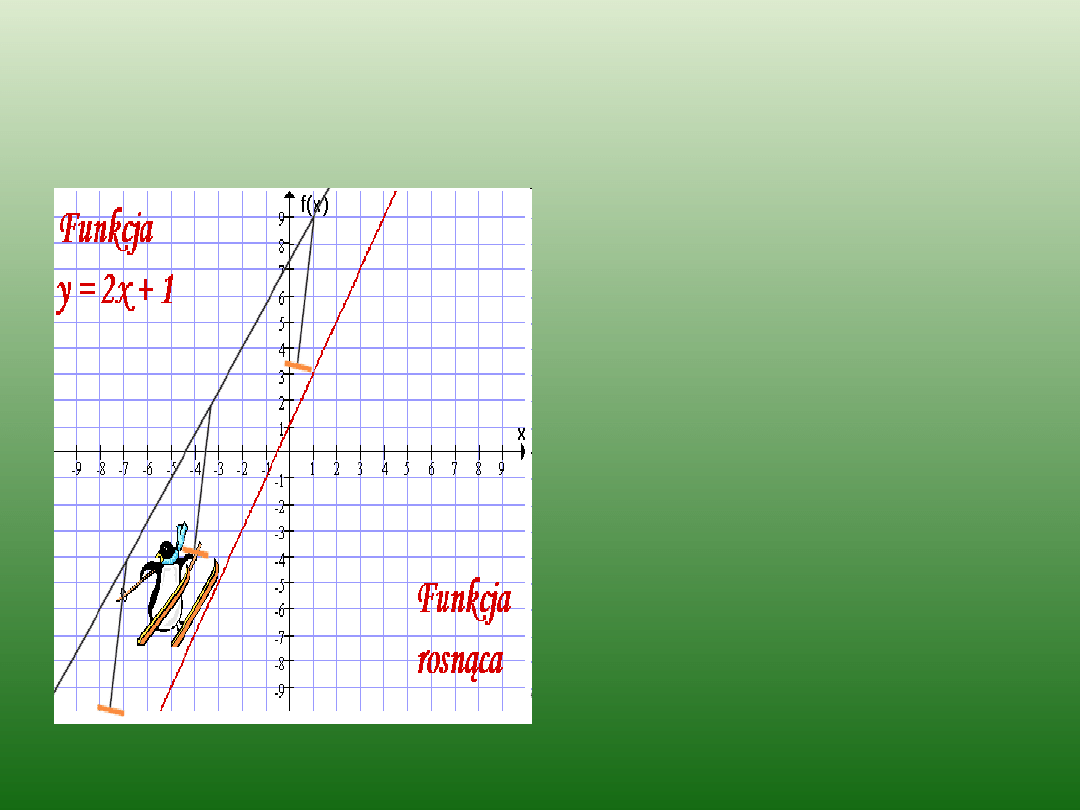
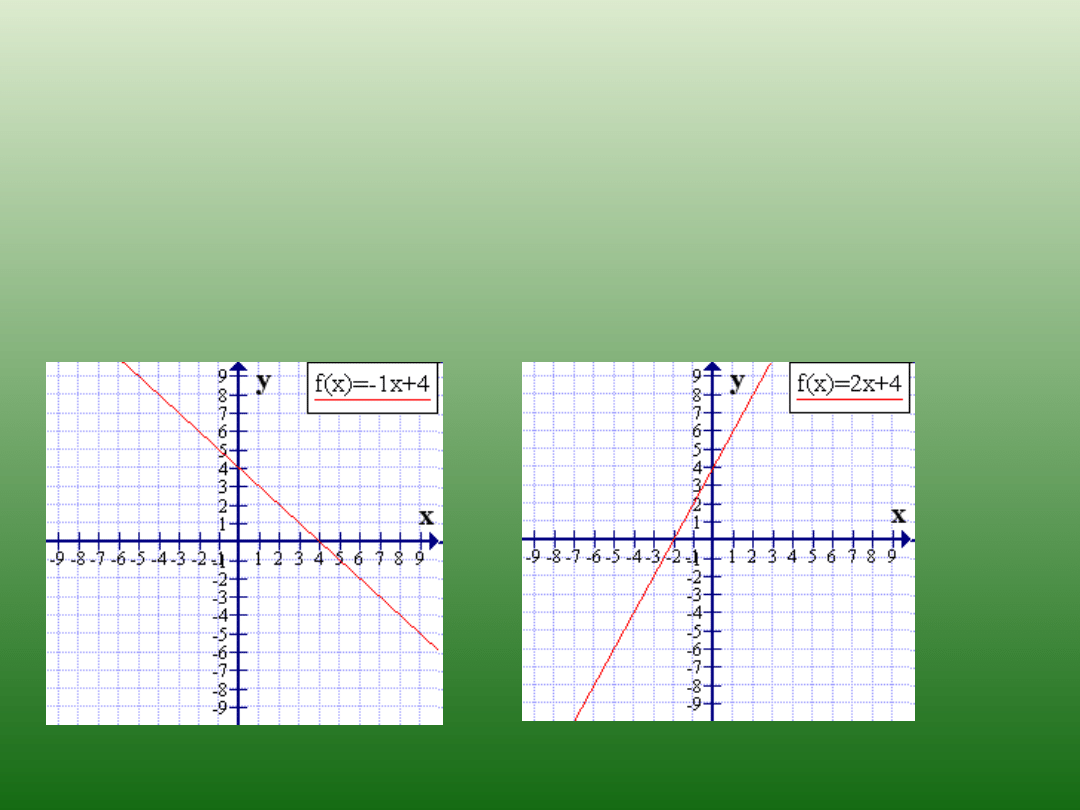
Funkcja rosnąca

Funkcję liniową nazywamy

rosnącą

, jeżeli

a > 0

a > 0 czyli

wraz ze wzrostem
argumentów rośnie
wartość funkcji.

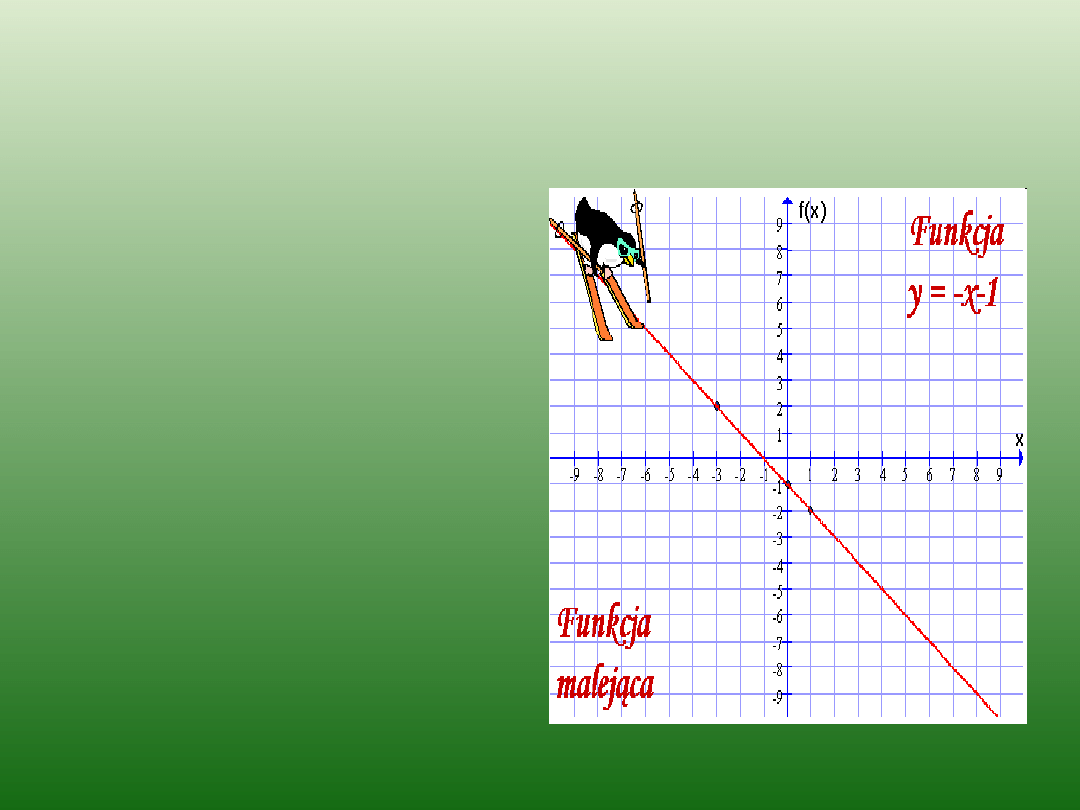
Funkcja malejąca

Funkcję liniową nazywamy

malejącą

, jeżeli

a < 0

a < 0

czyli wraz ze spadkiem
argumentów maleje
wartość funkcji.

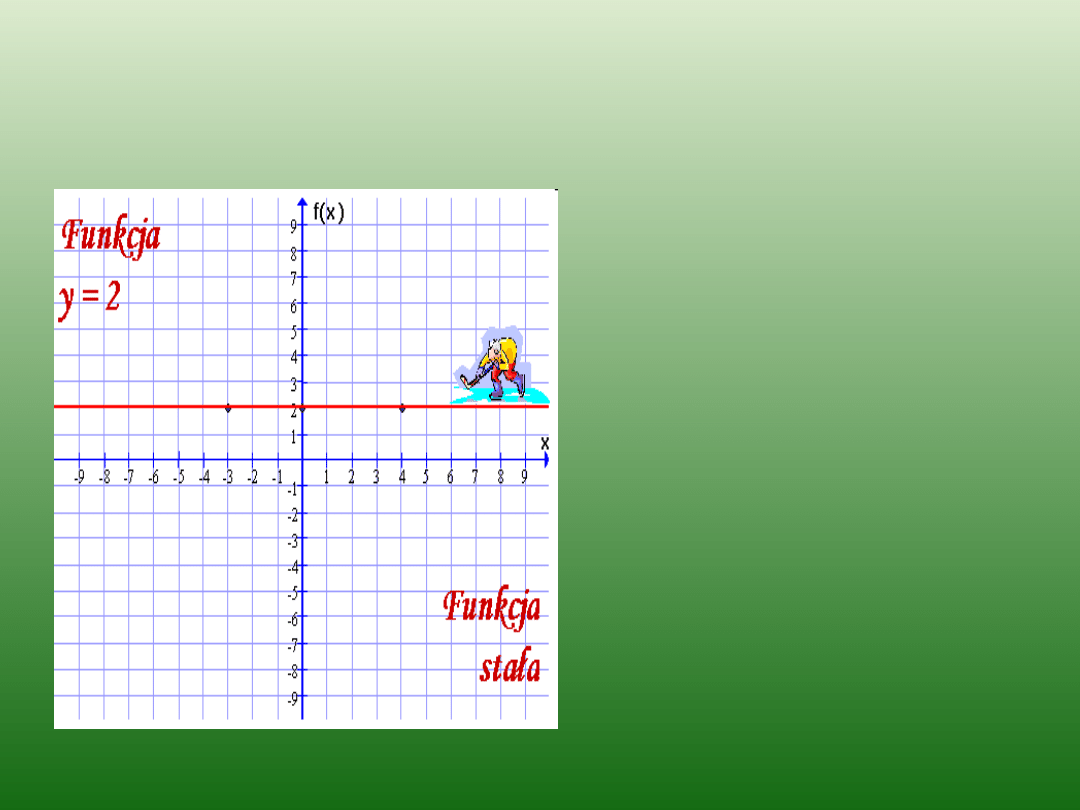
Funkcja stała

Funkcja jest

funkcją stałą

,

jeżeli

a = 0

a = 0 czyli wraz ze

wzrostem argumentów

wartość funkcji nie ulega

zmianie (jest stała). Jej

wzór przyjmuje wówczas

postać

f (x) = b

f (x) = b

Funkcja niemalejąca i

nierosnąca

• Każda funkcja rosnąca jest

niemalejąca, a funkcja
malejąca jest nierosnąca.

• Niemalejąca, gdy

a

a jest

nieujemne.

• Nierosnąca, gdy

a

a jest

niedodatnie.

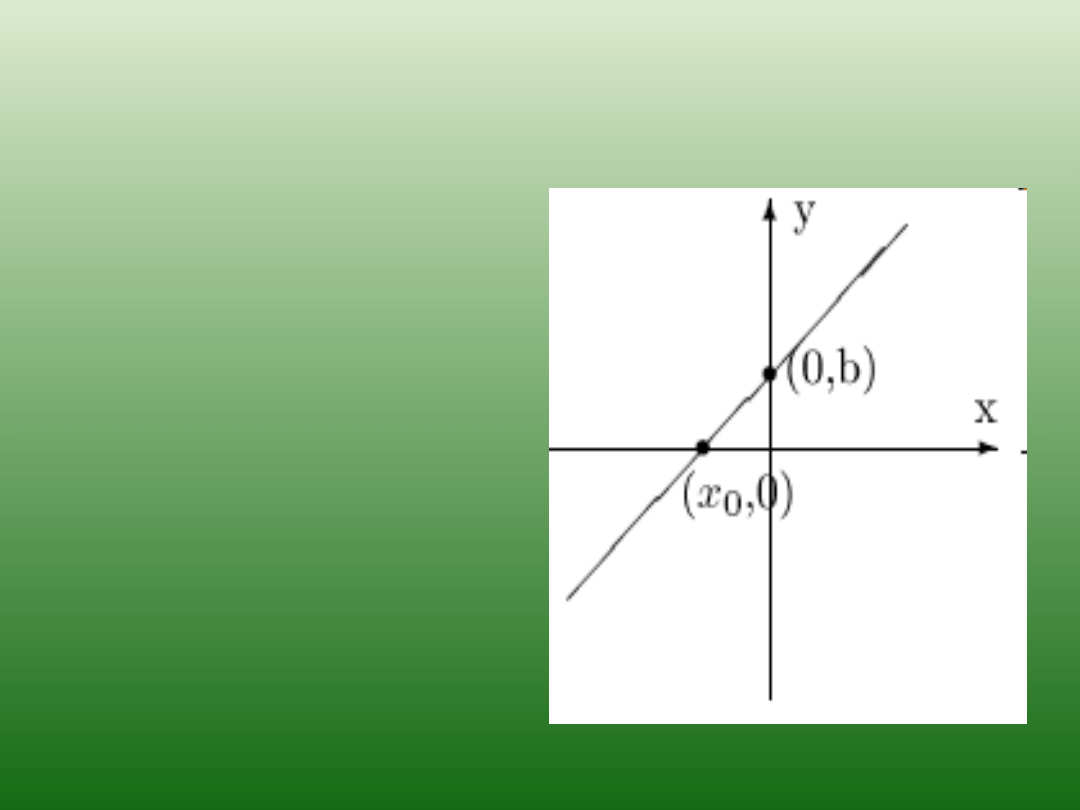
Miejsca zerowe

Jeżeli

a

a

≠ 0

≠ 0, to funkcja liniowa

jest funkcją
różnowartościową i posiada
jedno miejsce zerowe

(x

(x

0

0

, 0), gdzie x

, 0), gdzie x

0

0

= - a/b

= - a/b,

Jeżeli funkcja f jest funkcją

stałą, to albo nie posiada
miejsc zerowych (

dla b ≠ 0),

dla b ≠ 0),

albo wszystkie jej argumenty
są miejscami zerowymi

(dla b = 0).

(dla b = 0).

Zastosowanie funkcji liniowej

Jest wiele przykładów zastosowania funkcji w życiu. Jednym z nich

może być przykład dziennika lekcyjnego w szkole. Występuję
tam funkcja, gdyż każdemu uczniowi przyporządkowany jest
jeden numer z dziennika. Pomaga o nauczycielowi np.. W
szybkim odszukaniu danego ucznia w dzienniku.

Nr Imię

1

Marcin

2

Krystian

3

Rafał

4

Marek

Zastosowanie funkcji liniowej

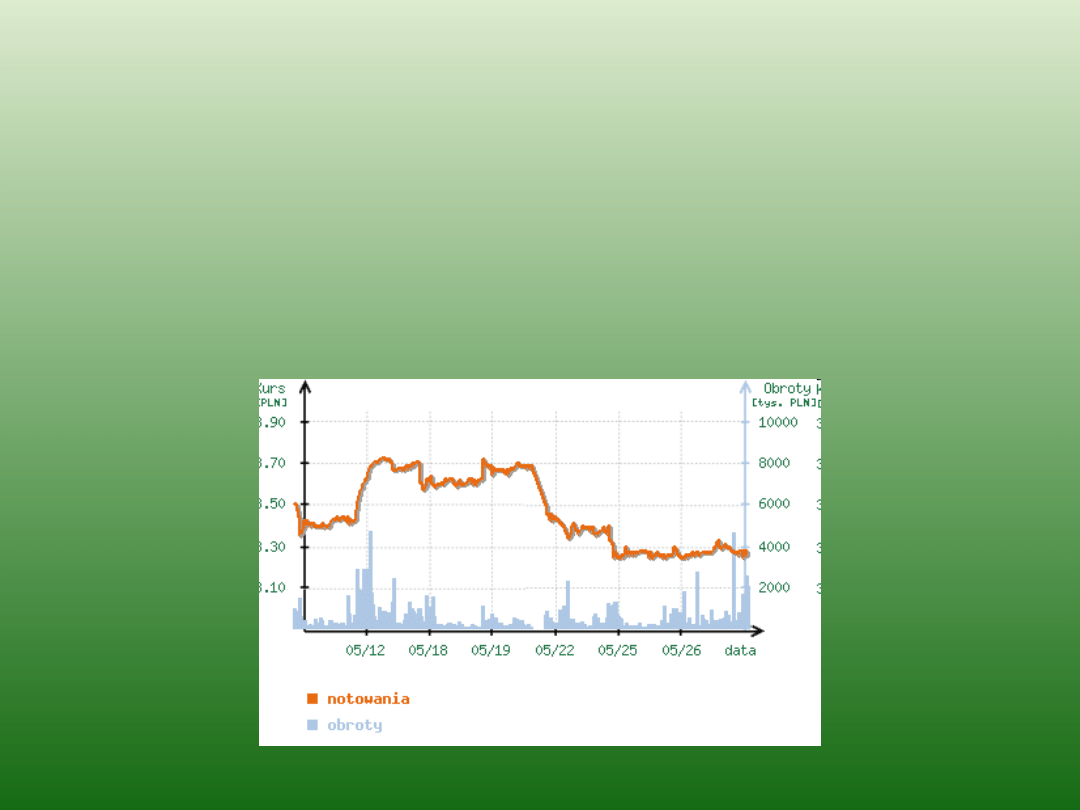
Funkcja liniowa jest też pomocna w przedstawieniu kursów na

giełdzie w postaci wykresów. Możemy np.. Odczytać z nich
jakie są kursy walut, wycenić produkty dzięki krzywym
podaży i popytu, wzrosty i upadki wartości akcji.

Proporcjonalność prosta

To taka zależność między dwiema zmiennymi wielkościami, w

której iloraz tych wielkości jest stały. Prowadzi to do wzoru:

y=kx

…pozwalającego wyliczyć jedną z nich w zależności od
drugiej. Mówimy, że obie wielkości są wprost
proporcjonalne.

Przykłady

• W ruchu ze stałą prędkością przebyta droga jest wprost

proporcjonalna do czasu jazdy.

• Cena towaru kupowanego na wagę jest wprost

proporcjonalna do tej wagi.

• W spadku swobodnym (bez oporu powietrza) prędkość

spadającego ciała jest wprost proporcjonalna do czasu
spadania.

• Przy ustalonej stawce podatku jego wartość jest wprost

proporcjonalna do kwoty, która podlega opodatkowaniu.

Autor:

Kasia Koszyczarska