Pole elektryczne – zasada

superpozycji

Jeżeli dowolnie mały ładunek q umieszczony
jest w polu elektrycznym wytwarzanym przez
więcej niż jeden ładunek działa na niego
suma sił ze strony wszystkich ładunków:

















n

F

F

F

F









2

1

E

q

E

q

E

q

E

q

n

























2

1

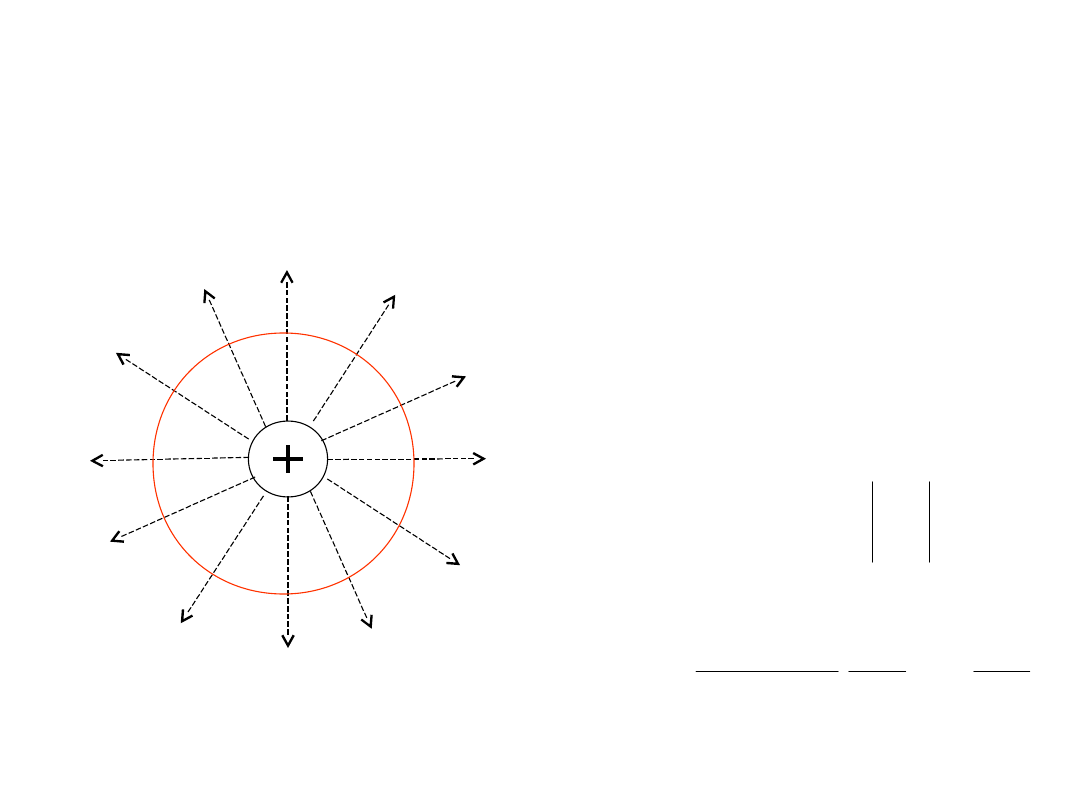
Strumień pola elektrycznego

Liczba linii sił pola elektrycznego
związanych z danym ładunkiem i
wychodzących z dowolnej geometrycznej
powierzchni zamkniętej, zawierającej
ten ładunek, zależy

tylko

od wartości

tego ładunku. Wielkość nazywamy

strumieniem pola elektrycznego

przez

zadaną powierzchnię.

E





E





Strumień pola elektrycznego

Strumień pola dla
sferycznej powierzchni
otaczającej punktowy
ładunek q :









E

r

E





2

4

0

2

0

2

4

1

4





q

r

q

r









Prawo Gaussa

S

trumień pola elektrycznego

przechodzący przez dowolna powierzchnie
zamkniętą zależy od ładunków zawartych
wewnątrz tej powierzchni:

0



q

E







Potencjał elektryczny

B

+q

Q

r

F

B

+q

C

F

C

r

0

A

Potencjał elektryczny

2

0

r

Qq

k

F

e

C



gdzie:

r

0

= AC

2

r

Qq

k

F

e

B



gdzie:

r = AB

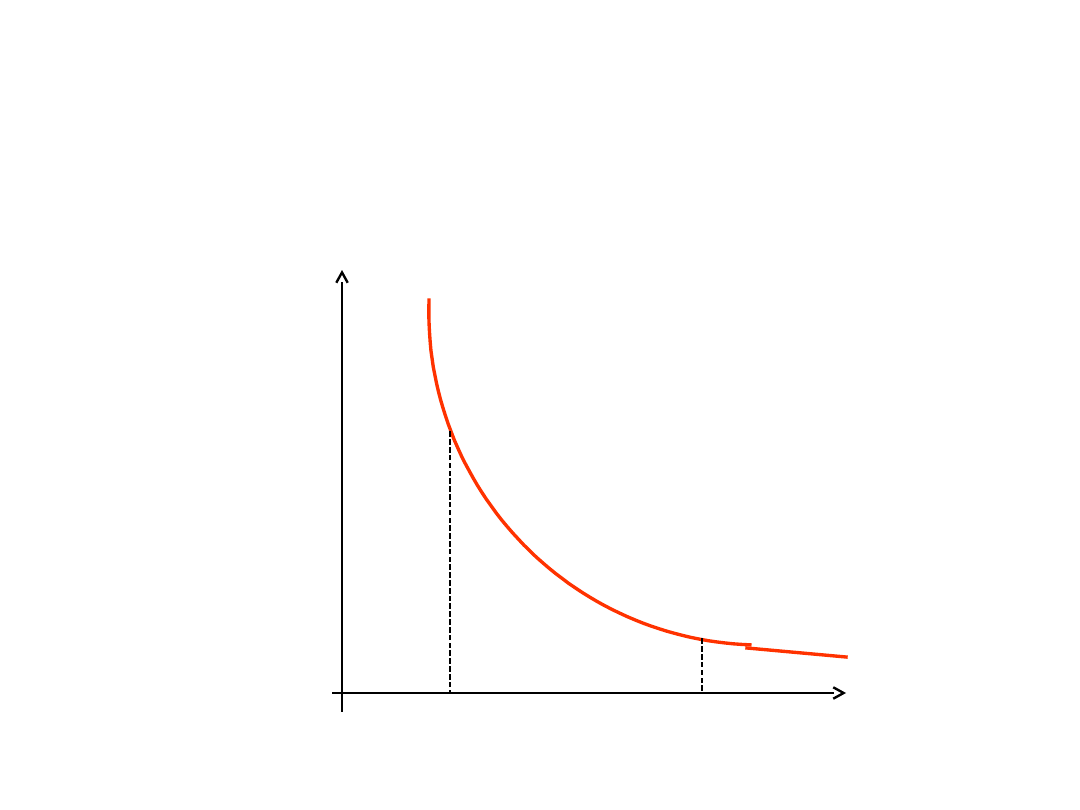
Potencjał elektryczny

F(r)

r

r

0

r

Potencjał elektryczny

r

r

Qq

k

r

Qq

k

r

Qq

k

F

F

F

e

e

e

B

C

śr

0

2

2

0







Średnia wartość siły odpychającej ładunek q
na odcinku CB jest średnią geometryczną sił
F

C

i F

B

:

Potencjał elektryczny

Czyli:

Wykonana przeciw tej sile praca przesunięcia
ładunku na drodze CB:



















0

1

1

r

r

Qq

k

A

e









r

r

r

r

Qq

k

r

r

F

A

e

śr

0

0

0













Potencjał elektryczny

Wyznaczamy energię potencjalną ładunku
przyjmując, że początkowe położenie
ładunku +q jest nieskończenie odległe od
ładunku Q wytwarzającego pole elektryczne,
czyli

0

1

,

0

0







r

r

0





p

E

Potencjał elektryczny

p

p

E

E

A







Energia potencjalna ładunku +q w p.B jest równa
pracy wykonanej przy jego przeniesieniu z
nieskończoności do p.B, czyli:

r

Qq

k

A

E

e

p







Potencjał elektryczny

Stosunek energii potencjalnej ładunku do jego
wartości q jest dla danego punktu pola
elektrycznego wielkością charakterystyczną, zwaną
potencjałem pola w tym punkcie.

q

E

V

p



czyli:

r

Q

k

qr

Qq

k

V

e

e





Potencjał elektryczny

W próżni, czyli dla:

0

4

1







e

k

r

Q

V

0

4

1







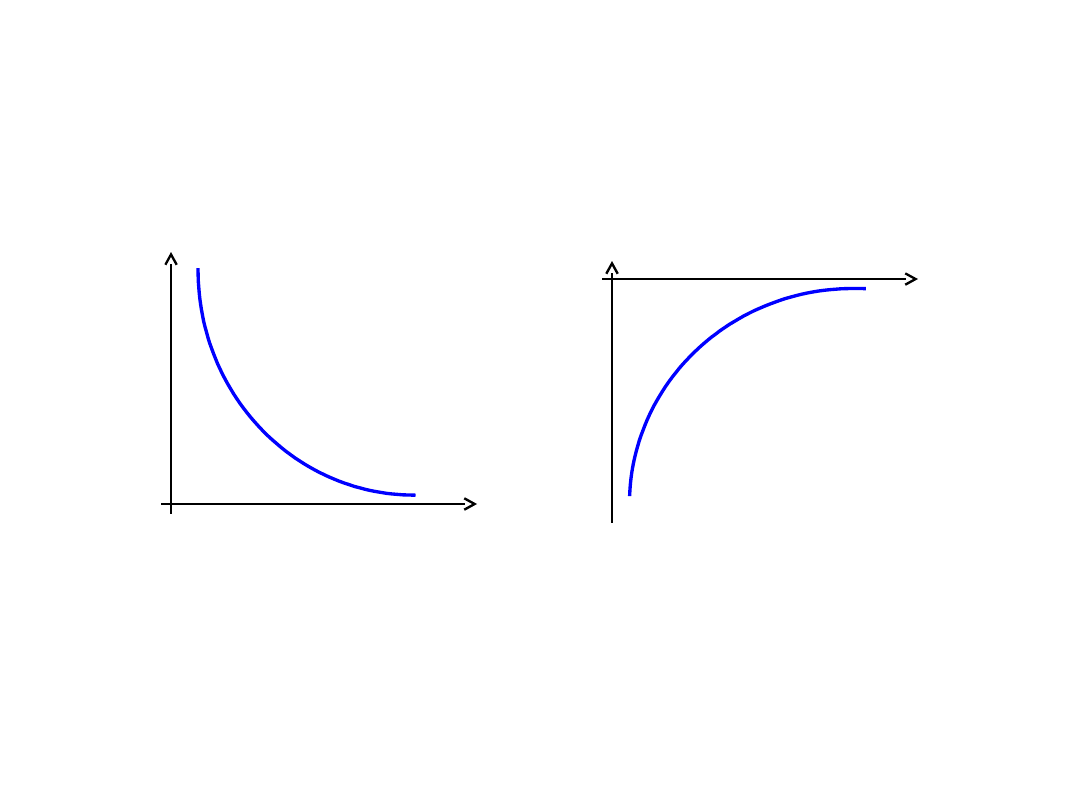
Potencjał elektryczny

V(r)

r

Potencjał pola

elektrycznego wokół

ładunku Q+

V(r)

r

Potencjał pola

elektrycznego wokół

ładunku Q-

Potencjał elektryczny

Potencjał jest wielkością skalarną
charakteryzującą określony punkt pola
elektrycznego i wyraża liczbowo wartość
pracy wykonanej przeciwko siłom pola
(w przypadku potencjału dodatniego) lub
wykonanej przez te siły (w przypadku
potencjału ujemnego) przy przeniesieniu
dodatniego ładunku jednostkowego z
nieskończoności do tego punktu.

Potencjał elektryczny

Jednostka potencjału w układzie SI:

1 wolt

- taka różnica potencjałów dwóch punktów

pola elektrycznego, która wymaga wykonania pracy

1 J przy przeniesieniu ładunku 1C.

 

 

 

3

2

2

2

1

1

1

1

1

1

1

1

As

kgm

As

s

kgm

C

J

q

E

V

p









Potencjał elektryczny

Inaczej:

Przesuwanie ładunku Q wzdłuż linii sił pola
na dowolnie małą odległość dl wymaga
wykonania pracy:

Stosunek tej pracy do ładunku nazywamy

potencjałem:

Fdl

dA

Edl

Q

Fdl

dV





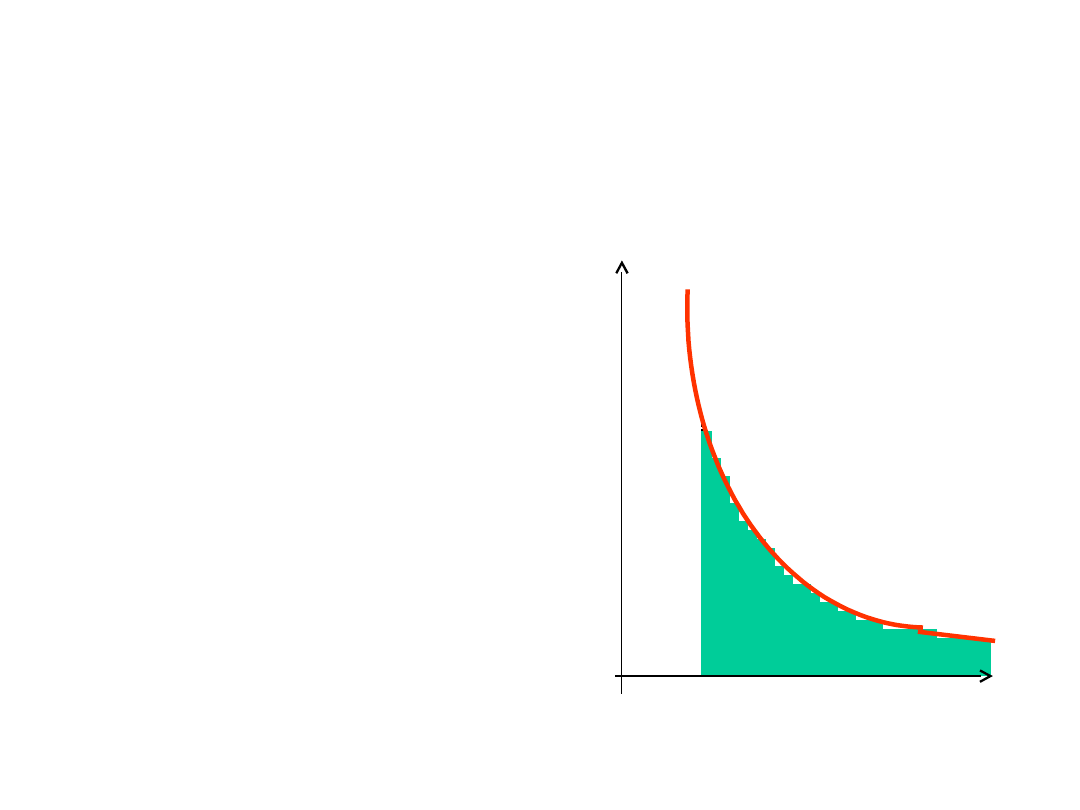
Potencjał elektryczny

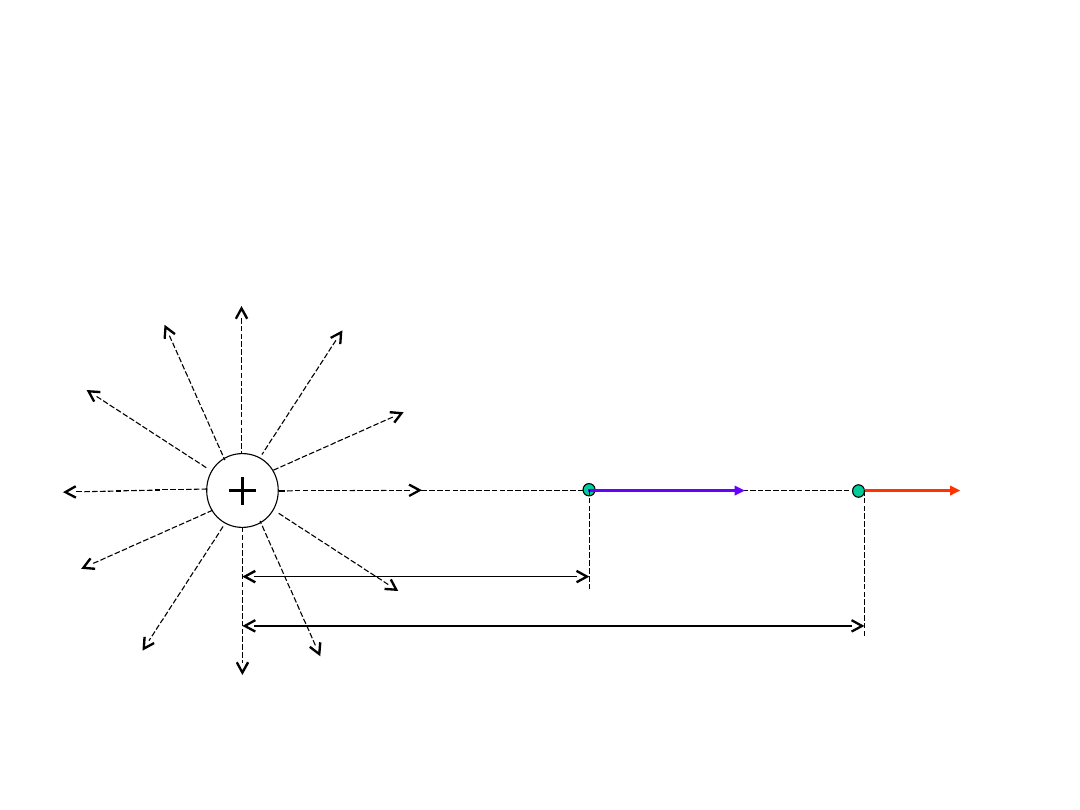
Potencjał w
dowolnym punkcie
odległym od ładunku
wytwarzającego pole
możemy określić jako
pole powierzchni pod
krzywą F(l)

F(l
)

l

Potencjał elektryczny

Potencjał w punkcie A odległym o r

A

od

ładunku jako pole powierzchni pod
krzywą F(l) przy l zmieniającym się od:

A

r

l 

do





l

czyli:







A

r

A

Edl

V

Potencjał elektryczny











dl

l

Q

V

A

r

A

2

0

4





































 







A

r

r

Q

l

Q

A

1

1

4

1

4

0

0





A

r

Q

0

4







Potencjał elektryczny

Potencjał w punkcie B:







B

r

B

Edl

V

Napięcie

Różnica potencjałów w dwóch punktach pola A i
B, odległych od ładunku o r

A

i r

B

nazywana jest

napięciem U

AB

między tymi punktami:























B

A

B

A

r

r

r

r

B

A

AB

Edl

Edl

Edl

V

V

U

Napięcie

Jednostką napięcia (tak jak i potencjału)
jest

1 wolt

A

W

s

A

s

W

C

J

V

1

1

1

1

1

1

1











Powierzchnia ekwipotencjalna

Powierzchnią ekwipotencjalną
nazywamy powierzchnię równego
potencjału, czyli zbiór punktów pola
elektrycznego, w których potencjał
jest jednakowy.

Powierzchnia ekwipotencjalna

W polu elektrycznym wytworzonym przez
pojedynczy ładunek punktowy, potencjał jest
jednakowy we wszystkich punktach
znajdujących się w jednakowej odległości r
od ładunku.

r

Q

V

0

4

1







Powierzchnie ekwipotencjalne takiego pola
mają kształt kul opisanych dookoła ładunku
wytwarzającego pole.

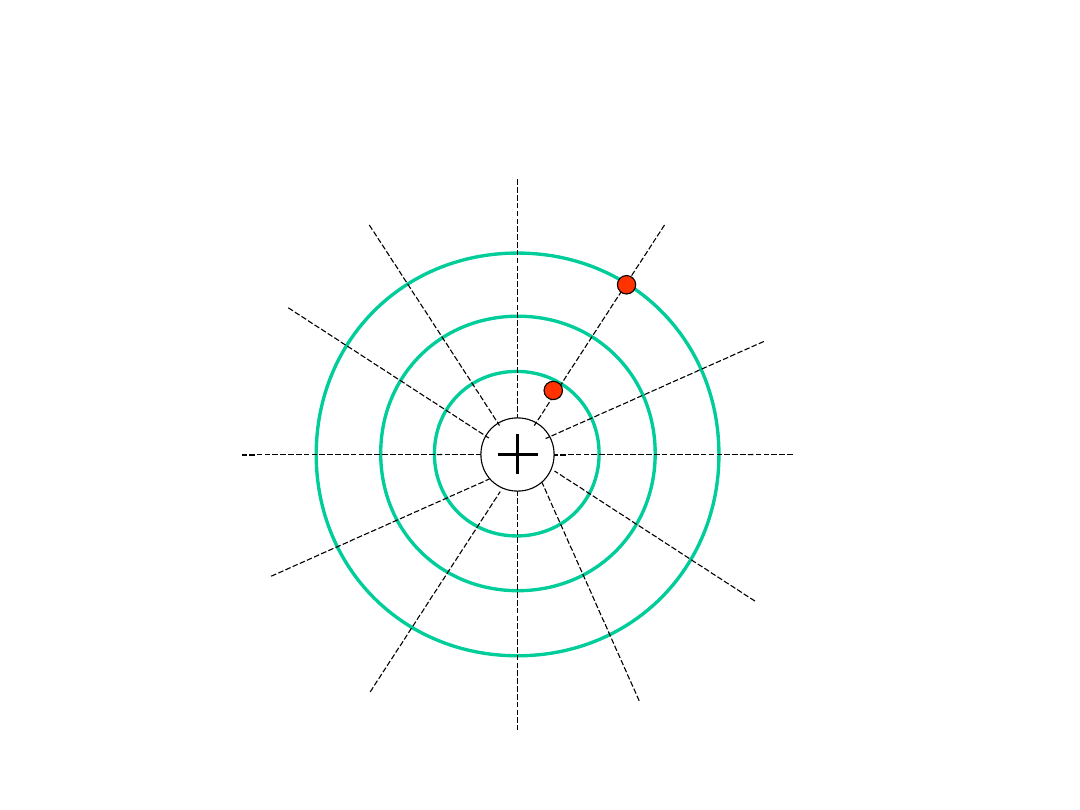
Powierzchnia ekwipotencjalna

A

B

Praca w polu elektrycznym

Energia potencjalna ładunku znajdującego
się w punkcie pola elektrycznego o
potencjale

V:

Vq

E

p



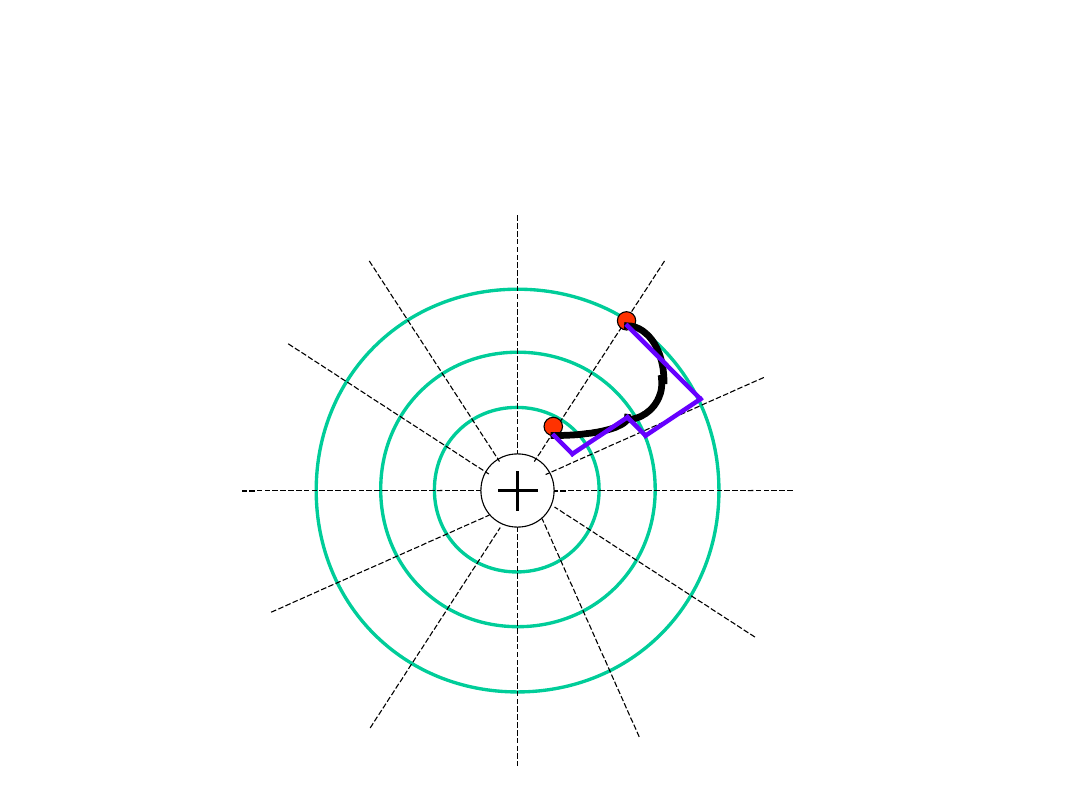
Praca w polu elektrycznym

A

B

Praca w polu elektrycznym

Przesuwanie ładunku z punktu o potencjale
V

A

do punktu o potencjale V

B

związane jest

z pracą równą różnicy energii potencjalnych
ładunku w punkcie A i w punkcie B:

pB

pA

E

E

W





Praca w polu elektrycznym















q

V

V

q

V

q

V

W

B

A

B

A

Uq



Wartość wykonanej pracy jest niezależna
od drogi, po której następuje przesunięcie.

Praca w polu elektrycznym

Niezależność pracy od kształtu drogi
oznacza, że pole elektryczne jest

polem

zachowawczym

– gdy siła w polu działa na

drodze tworzącej obwód zamknięty – suma
prac wykonanych przez siłę jest równa
zeru.

0





l

l

d

E





Natężenie pola elektrycznego

W dowolnym środowisku:

2

4

r

Q

E







gdzie
:

r







0



przenikalność elektryczna bezwzględna,
zwana przenikalnością elektryczną
środowiska w F/m

Natężenie pola elektrycznego



0

–

przenikalność elektryczna próżni



0

= 8,85•10

-12

F/m



r

–

przenikalność elektryczna względna

środowiska (wielkość bezwymiarowa)

Przenikalność elektryczna względna
wskazuje, ile razy przenikalność danego
środowiska jest większa od
przenikalności elektrycznej próżni.

Przenikalność względna

dielektryków

Rodzaj dielektryka

Przenikalno

ść

elektryczna

względna 

r

Wytrzymałoś

ć

elektryczna

w V/m

olej
transformatorowy

2  2,5

2 • 10

7

papier nasycony

3,7

2,5 • 10

8

polichlorek winylu

3,3

5 • 10

7

porcelana
izolatorowa

5,5  6,5

2 • 10

7

szkło

3,1  4,4

10

8

powietrze

~ 1

3,2 • 10

6

Natężenie pola elektrycznego

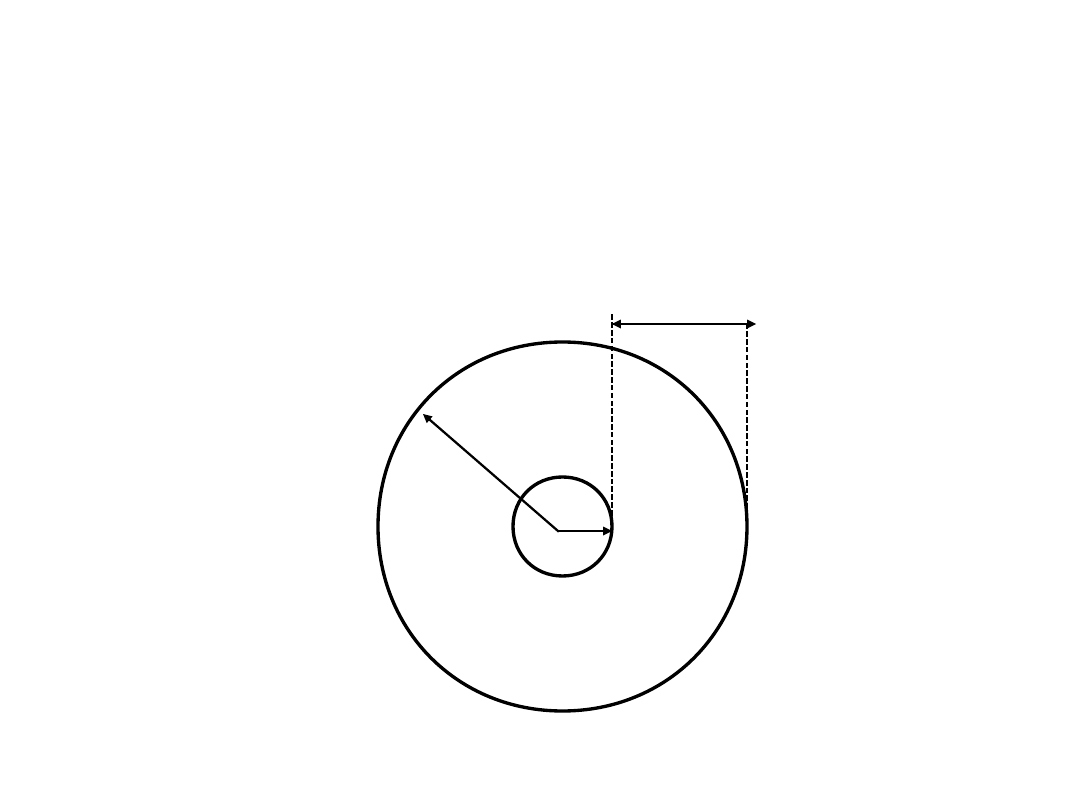
Kabel koncentryczny:

r

2

r

1

U

Natężenie pola elektrycznego

Natężenie pola elektrycznego w odległości:

r

1



r  r

2

od środka kabla opisane jest zależnością:

1

2

ln

r

r

r

U

E 

Elektryzowanie ciał

Wprowadzenie ładunku do dowolnego
ciała, czyli naelektryzowanie go:
- przez tarcie
- przez indukcję.

Elektryzowanie przez tarcie –

dielektryki.

Elektryzowanie ciał

Przewodniki mogą być
elektryzowane, jeśli są
odizolowane od innych
przewodników:
- przez tarcie
- przez indukcję

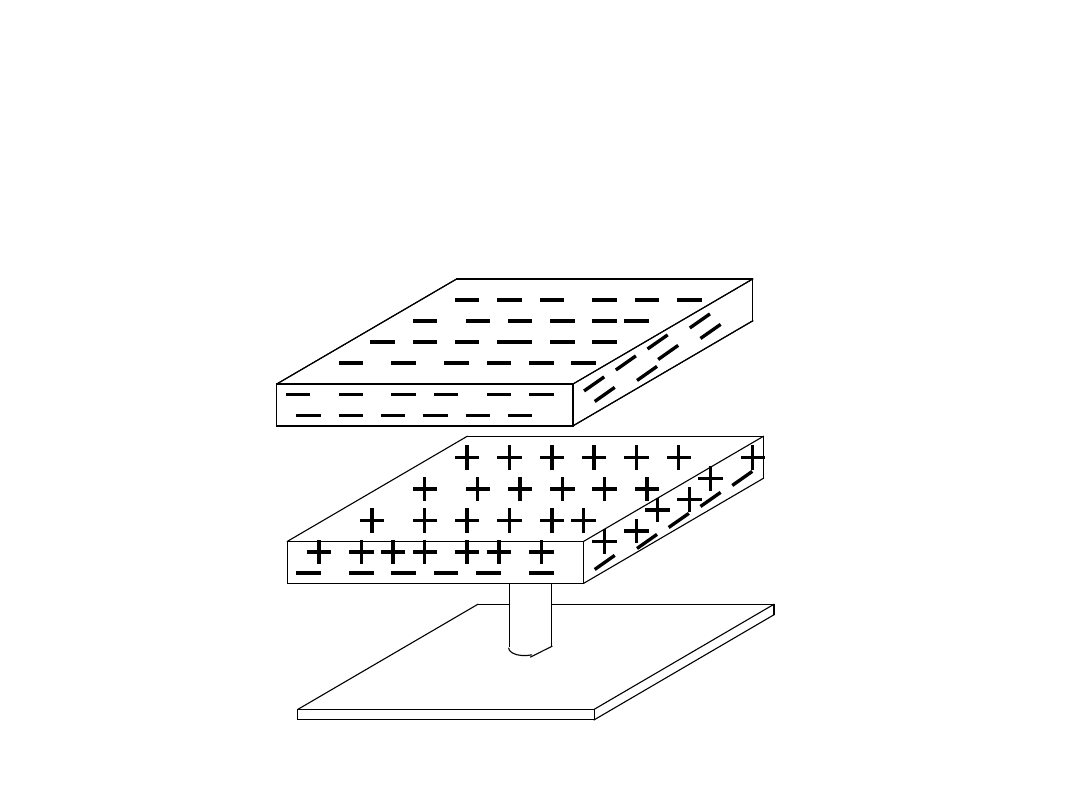
Elektryzowanie ciał

B

A

i

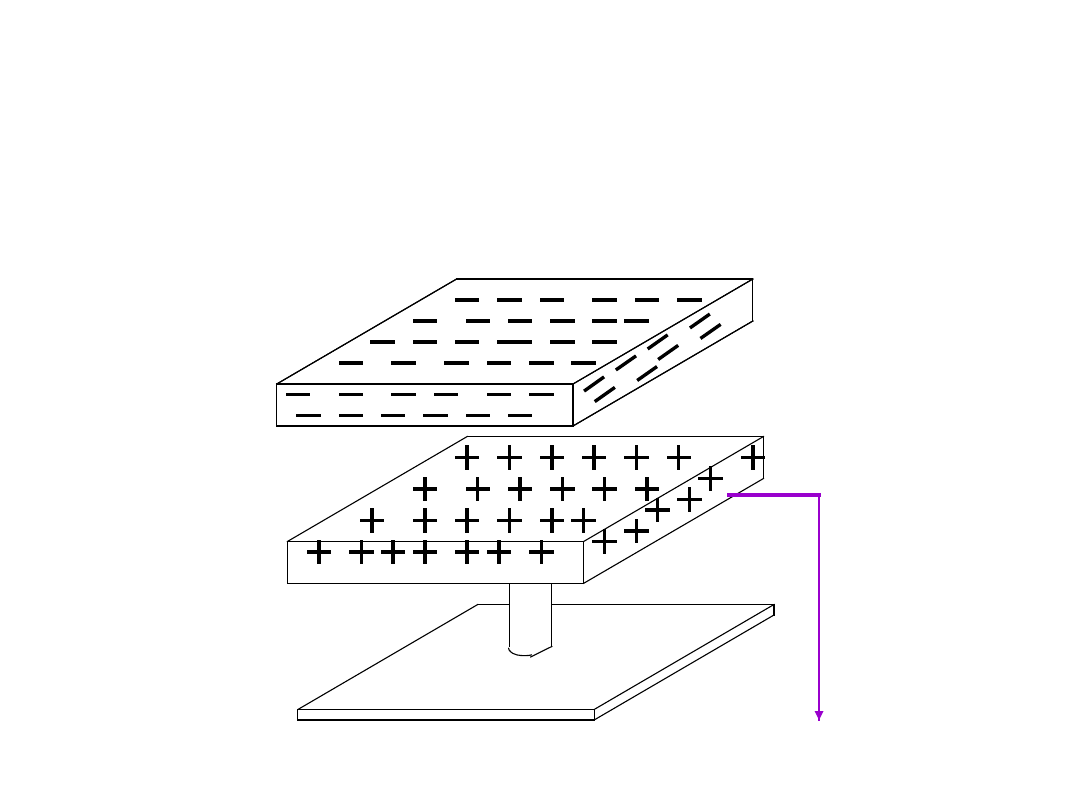
Elektryzowanie ciał

A

B

i

p

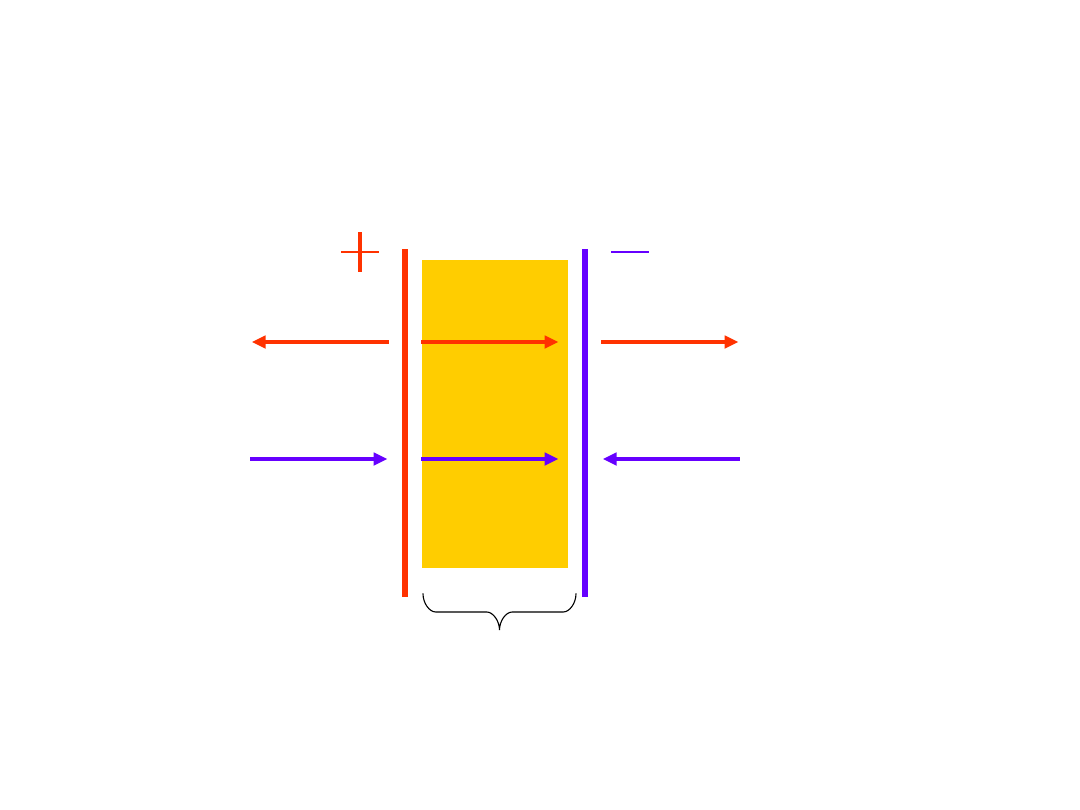
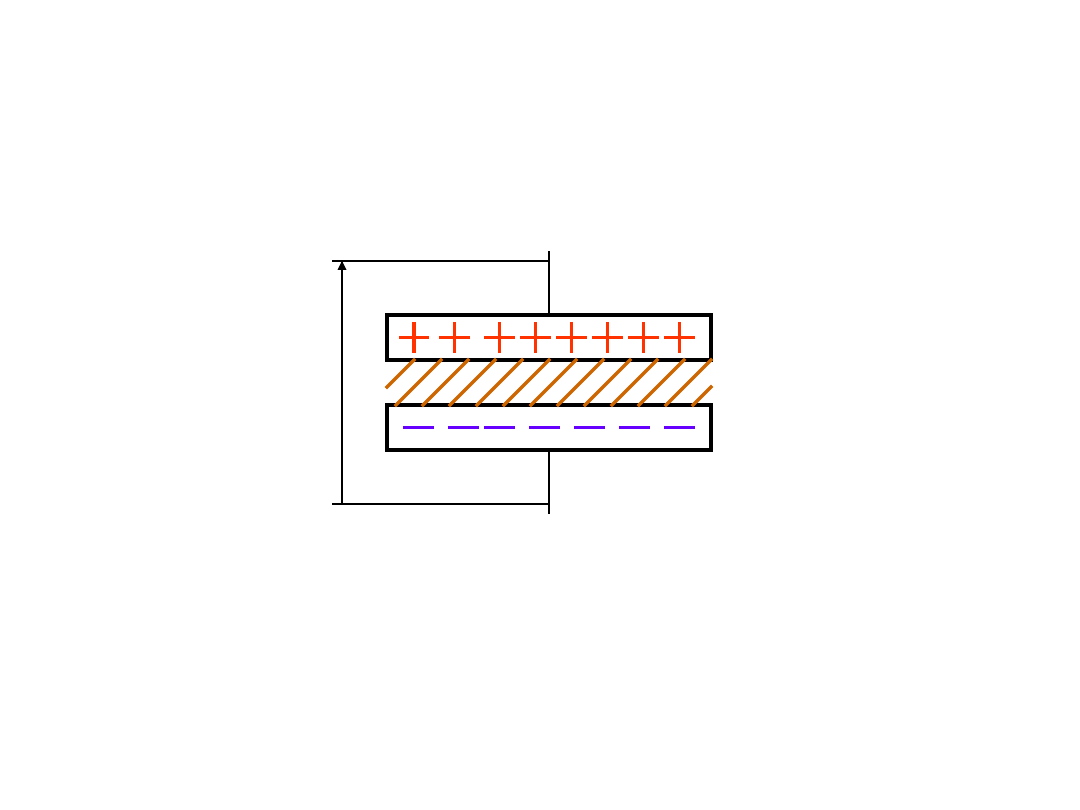
Pole elektryczne między

płaszczyznami

d

s1

s3

s2

+

-

Pole elektryczne między

płaszczyznami

Natężenie pole elektrycznego wokół
nieskończonej jednorodnie naładowanej
płaszczyzny (zgodnie z prawem Gaussa):

0

2







E

gdzie  w [C/m

2

] – gęstość

powierzchniowa ładunku.

Pole elektryczne między

płaszczyznami

Przeniesienie ładunku próbnego na drodze
od płaszczyzny naładowanej ujemnie do
naładowanej dodatnio wymaga pracy:

d

q

qEd

Fd

W

0











Pole elektryczne między

płaszczyznami

Różnica potencjałów między
płaszczyznami, czyli napięcie między
nimi wynosi:

0





d

q

W

U





Pole elektryczne między

płaszczyznami

Dla dwóch płaszczyzn o wymiarach
skończonych i polu powierzchni A

d

A

Q

d

q

W

U

0

0













Kondensatory

Ładunek Q wprowadzony do kondensatora jest

proporcjonalny do napięcia ładowania U

U

+Q

-Q

Kondensatory

CU

Q 

gdzie C – pojemność elektryczna
kondensatora

Jednostką pojemności jest farad (1F).

Kondensatory

Pojemność kondensatora jest równa 1F,
jeżeli pod wpływem napięcia 1V
występującego między elektrodami,
ładunek zgromadzony na każdej
elektrodzie jest równy 1C.

pikofarad – 1pF = 10

-12

F

nanofarad – 1nF = 10

-9

F

mikrofarad - 1F = 10

-6

F

Kondensatory

Kondensator płaski – dwie płyty przedzielone

dielektrykiem

gdzie: A – pole powierzchni elektrody
kondensatora

płaskiego [m

2

]

d – odległość elektrod [m]

d

A

C





Kondensatory

Kondensator kulisty (sferyczny) – dwie
współśrodkowe sfery.

gdzie: r

1

– promień wewnętrznej kuli [m]

r

2

– promień zewnętrznej kuli [m]

2

1

1

1

4

r

r

C









Kondensatory

Kondensator walcowy – dwa współosiowe walce
przedzielone dielektrykiem.

gdzie: l – długość kondensatora walcowego [m]
r

1

– promień wewnętrznego walca [m]

r

2

– promień zewnętrznego walca [m]

1

2

ln

2

r

r

l

C







Łączenie kondensatorów

Kondensatory mogą być
połączone:

- szeregowo
- równolegle
- szeregowo-równolegle

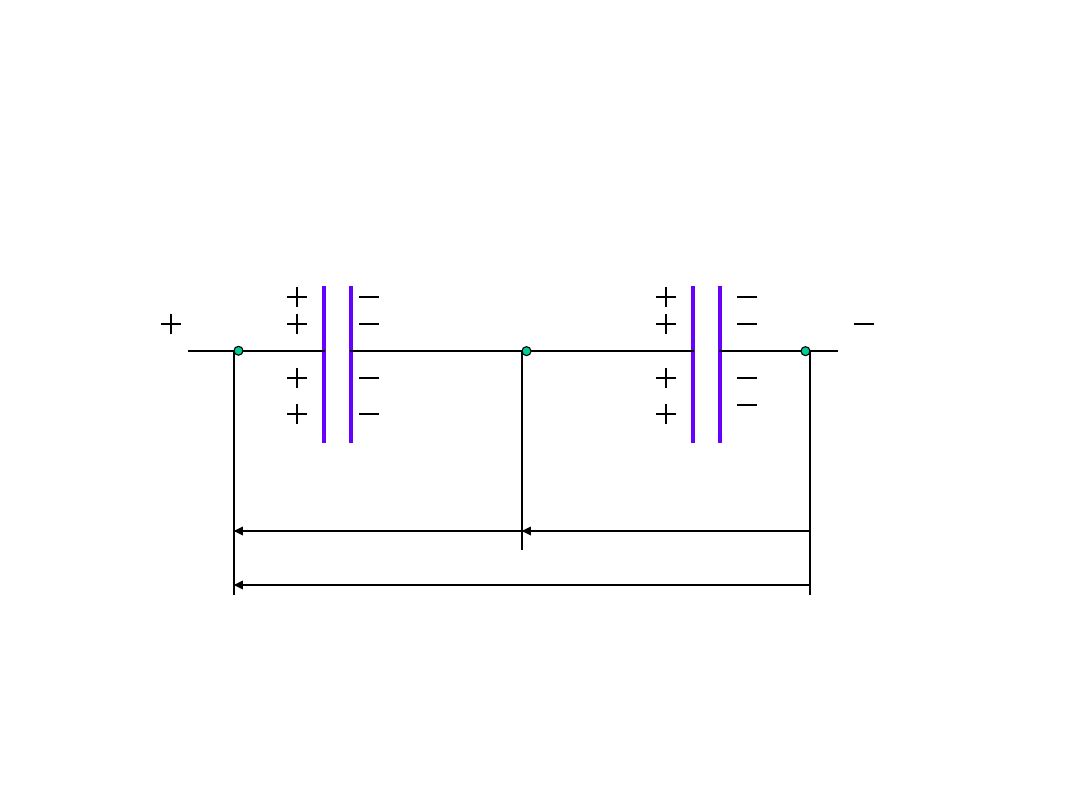
Połączenie szeregowe

kondensatorów

a

c

b

U

1

U

U

2

Q

2

Q

1

Połączenie szeregowe

kondensatorów

1

1

1

U

Q

C 

2

2

2

U

Q

C 

lub

1

1

1

C

Q

U 

2

2

2

C

Q

U 

Połączenie szeregowe

kondensatorów





















2

2

1

1

2

1

C

Q

C

Q

U

U

U

2

1

Q

Q

Q





















2

1

1

1

C

C

Q

U

Połączenie szeregowe

kondensatorów

2

1

1

1

1

C

C

C





U

Q

C 

Pojemność zastępcza układu dwóch
kondensatorów:

Połączenie szeregowe

kondensatorów







n

k

k

C

C

1

1

1

Pojemność zastępcza n kondensatorów
połączonych szeregowo:

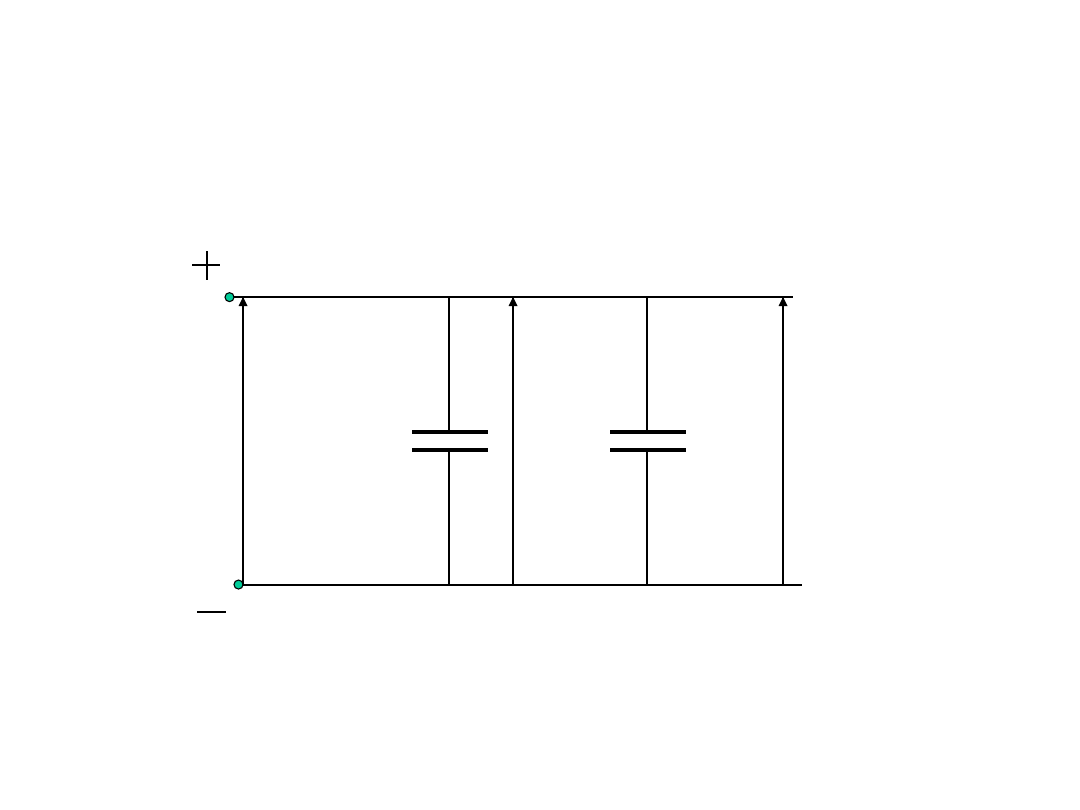
Połączenie równoległe

kondensatorów

U

U

2

U

1

Q

1

C

1

C

2

Q

2

Połączenie równoległe

kondensatorów

2

2

1

1

2

1

2

1

U

C

U

C

Q

Q

Q

U

U

U













Pojemność zastępcza dwóch kondensatorów
połączonych równolegle:

2

1

2

2

1

1

C

C

U

U

C

U

C

U

Q

C











Połączenie równoległe

kondensatorów

Pojemność zastępcza układu n
kondensatorów połączonych
równolegle:







n

k

k

C

C

1