W przypadku ruchu jednowymiarowego poruszający się ośrodek jest
nazywany strumieniem, a parametry przepływu panujące w
dowolnym przekroju  są funkcją tylko jednej współrzędnej s.

Podstawowe równania
opisujące stacjonarne
przepływy
jednowymiarowe
cieczy doskonałej:
– równanie
ciągłości,
– równanie
Bernoulliego.

,

s

m

const

3

śr

















 V

Q

.

const

2

2









z

g

p

V

V

g

p

z

V

g

p

z

1

2

1

1

2

2

2

2

2

2















.

Równanie Bernoulliego odniesione do jednostki masy zawartej w
elementarnej strudze:

,

const

2

2









p

z

g

m

V

m

energia
kinetyczna

energia potencjalna
położenia

energia potencjalna
ciśnienia

Równanie Bernoulliego odniesione do jednostki objętości:

,

const

2

2











z

p

V

ciśnienie
dynamiczne

ciśnienie
statyczne

ciśnienie
położenia
(hydrostatyczne)

Równanie Bernoulliego odniesione do jednostki ciężaru:

wysokość
prędkości

wysokość
ciśnienia

wysokość
położenia

V

g

p

z

2

2

  



const,





,

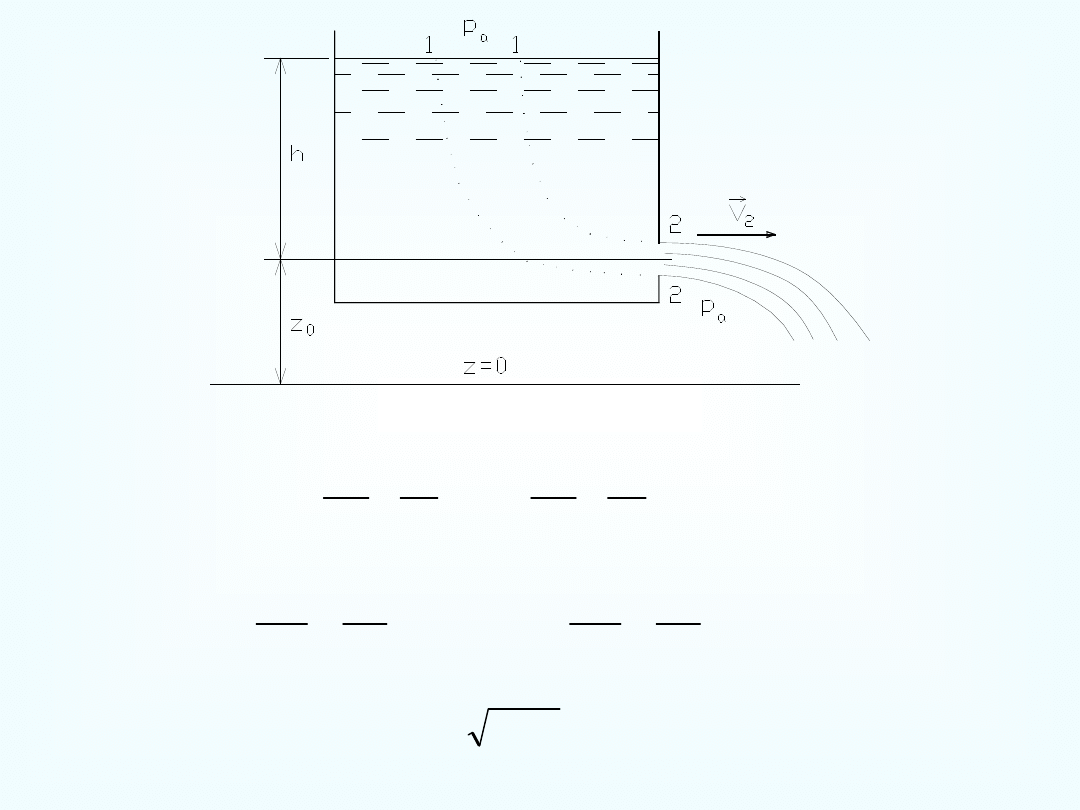
2

2

0

0

2

2

0

2

z

p

g

V

h

z

p

g

a

a

















h

g

V

2

2



,

2

2

2

2

2

2

1

1

2

1

z

p

g

V

z

p

g

V















( wzór Torriciellego )

.





,

2

2

0

2

2

2



















h

p

g

V

h

H

p

g

a

a

.

2

2

h

g

V 

,

2

2

2

2

2

2

1

1

2

1

z

p

g

V

z

p

g

V















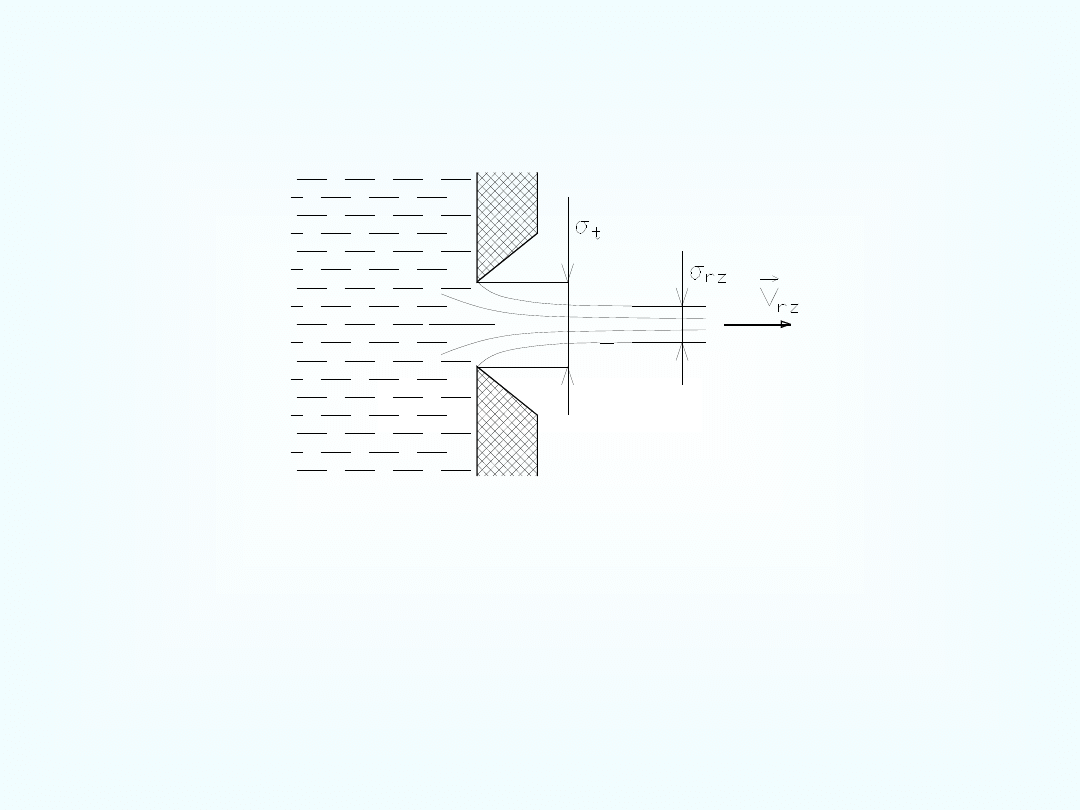
Wypływ cieczy rzeczywistej przez małe

otwory

Dokonując pomiarów wydatku cieczy wypływającej ze zbiorników
przez otwory stwierdzono, że wydatek rzeczywisty Q

rz

nie jest równy

wydatkowi teoretycznemu Q

t

.

Przyczyną tej różnicy jest zarówno mniejszy przekrój strugi σ

rz

od

powierzchni σ

t

otworu w zbiorniku, jak również mniejsze prędkości

wypływu V

rz

od prędkości obliczonej V

t

.

Zjawisko zmniejszania się przekroju strumienia w pewnej odległości
od przekroju wylotowego nazywa się kontrakcją strumienia i jest
ono charakteryzowane współczynnikiem kontrakcji, który jest
stosunkiem przekroju otworu do przekroju strugi

.

rz

t









Straty prędkości przy wypływie cieczy z małego otworu określane są
natomiast współczynnikiem prędkości

.

rz

t

V

V





Wydatek rzeczywisty

rz

rz

rz

V

Q





i następnie

.

rz

t

Q

Q







Iloczyn doświadczalnie wyznaczanych współczynników  i 

nazywany jest współczynnikiem wydatku.

,

)

(

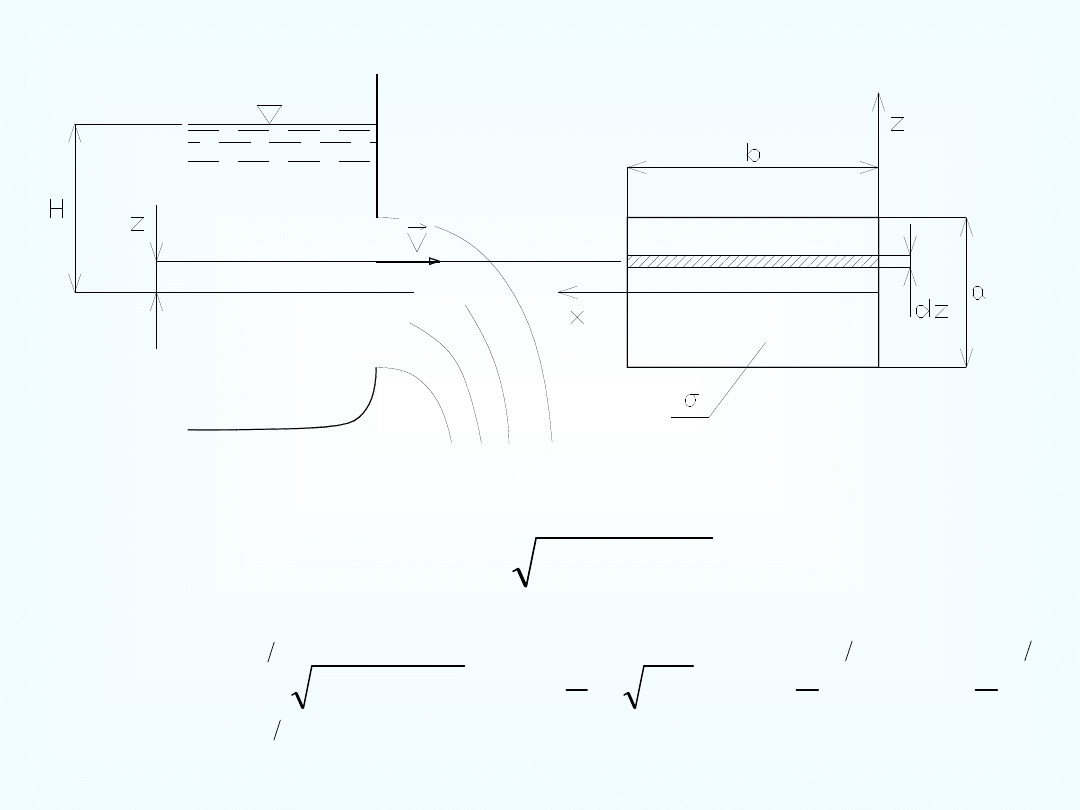
2

)

(

z

H

g

z

V





.

2

2

2

3

2

)

(

2

2

3

2

3

2

2



























 













 















a

H

a

H

g

b

z

d

b

z

H

g

d

V

Q

a

a





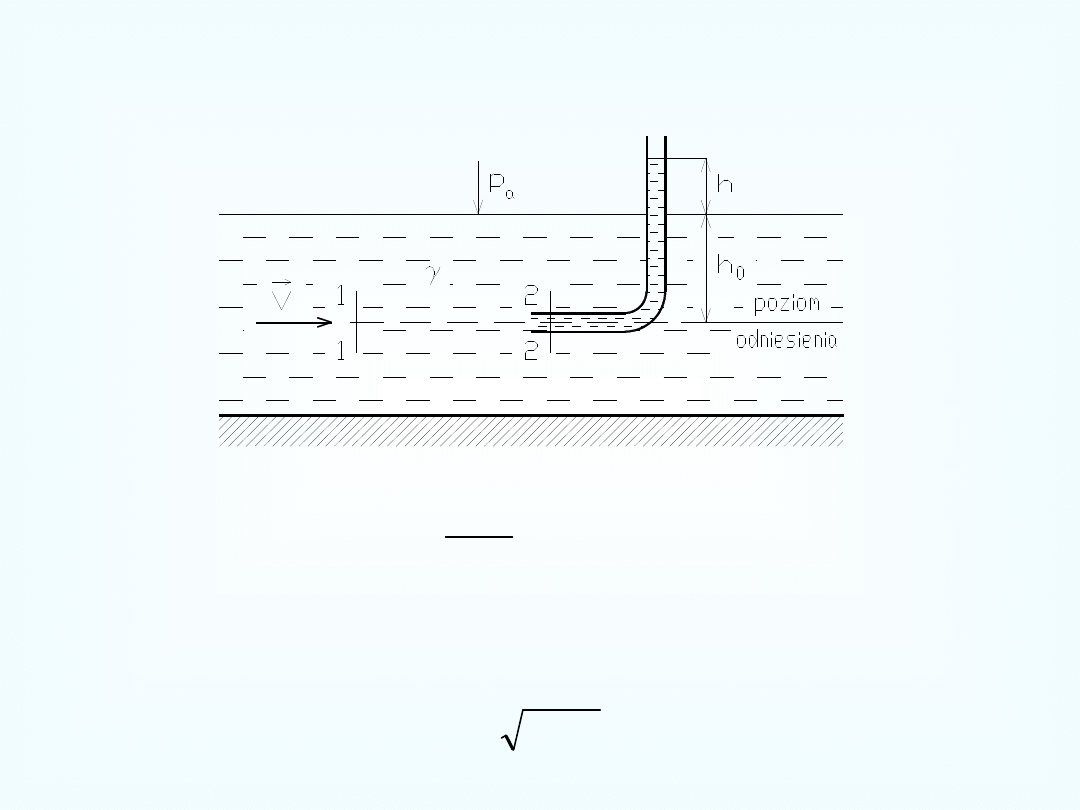
Rurka Pitota





,

,

0

0

h

h

p

p

h

p

p

a

c

a















.

2 h

g

V 

,

2

2

c

p

p

V







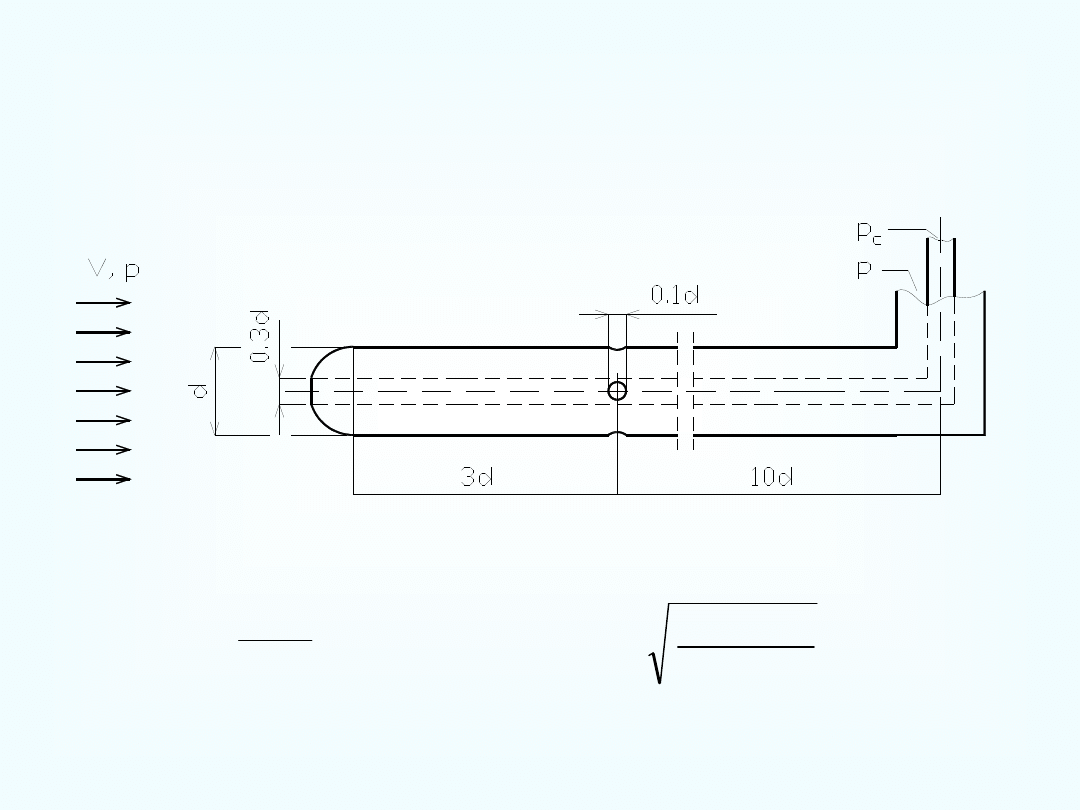
Pomiary prędkości płynu przepływającego przewodami zamkniętymi,
oprócz ciśnienia spiętrzenia musimy jeszcze mierzyć ciśnienie
statyczne.

.

)

(

2







p

p

V

c

Rurka Prandtla

,

2

2

c

p

p

V







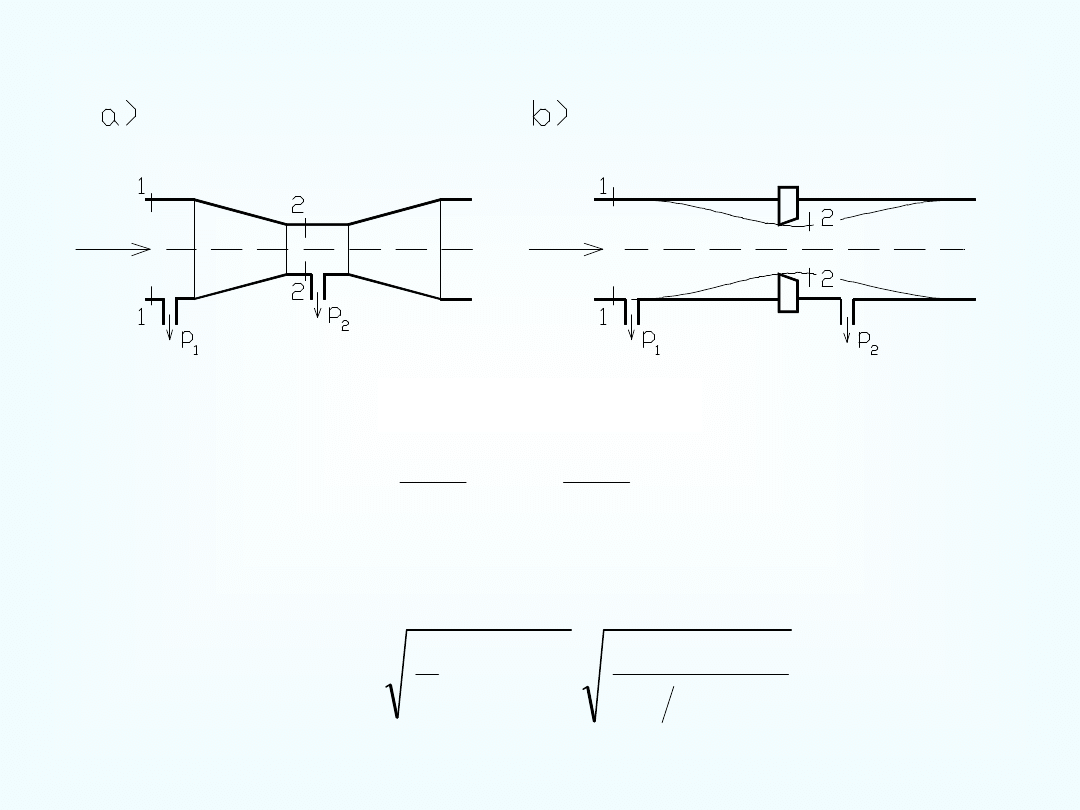
Zwężka Venturiego Kryza
pomiarowa









.

1

1

2

2

2

1

2

1

1













p

p

V

























;

,

2

2

2

2

1

1

2

2

2

1

2

1

V

V

p

V

p

V

,

const





 V

Q

.

2

2

2

1

2

2

2

2

1

1

2

1





















s

h

z

p

g

V

z

p

g

V

Wyznaczanie przepływów ustalonych i jednowymiarowych oparte
jest na dwóch podstawowych zależnościach:

Energia kinetyczna E

śr

obliczona według prędkości średniej jest na

ogół różna od energii rzeczywistej E

rz

strumienia cieczy w

rozpatrywanym przekroju:

,

2

2

2

3

śr

2

śr

2

śr

śr













V

t

d

V

t

d

Q

V

m

E

.

2

2

2

2

3

3

2

2

rz



































d

V

t

d

d

t

d

V

Q

d

t

d

V

m

d

V

E

Aby uwzględnić rzeczywistą energię kinetyczną strumienia w
przekrojach 1-1 oraz 2-2 przewodu wprowadzamy tzw.
współczynnik Coriolisa















3

śr

3

śr

rz

V

d

V

E

E

i uwzględniamy go w równaniu Bernoulliego dla przepływu
rzeczywistego

.

2

2

2

1

2

2

2

2

2

1

1

2

1

1

























s

h

z

p

g

V

z

p

g

V

Wartość współczynnika Coriolisa dla laminarnego przepływu cieczy
przez przewód
o przekroju kołowym wynosi  = 2, a w przepływie turbulentnym  =

1.026  1.08.

Straty energii mechanicznej dzielą się na straty na długości,
spowodowane tarciem cieczy lepkiej o ścianki przewodu - i na
straty lokalne, powstające w tych miejscach, gdzie ulega zmianie
wartość lub kierunek prędkości.
Straty na długości

l w przewodzie o średnicy

d

są wyznaczane za

pomocą wzoru Darcy’ego-Weisbacha

,

2

2

śr

g

V

d

l

h

s







w którym istotnym parametrem jest współczynnik strat liniowych 

,

natomiast straty lokalne - za pomocą jego postaci uproszczonej

,

2

2

śr

g

V

h

s







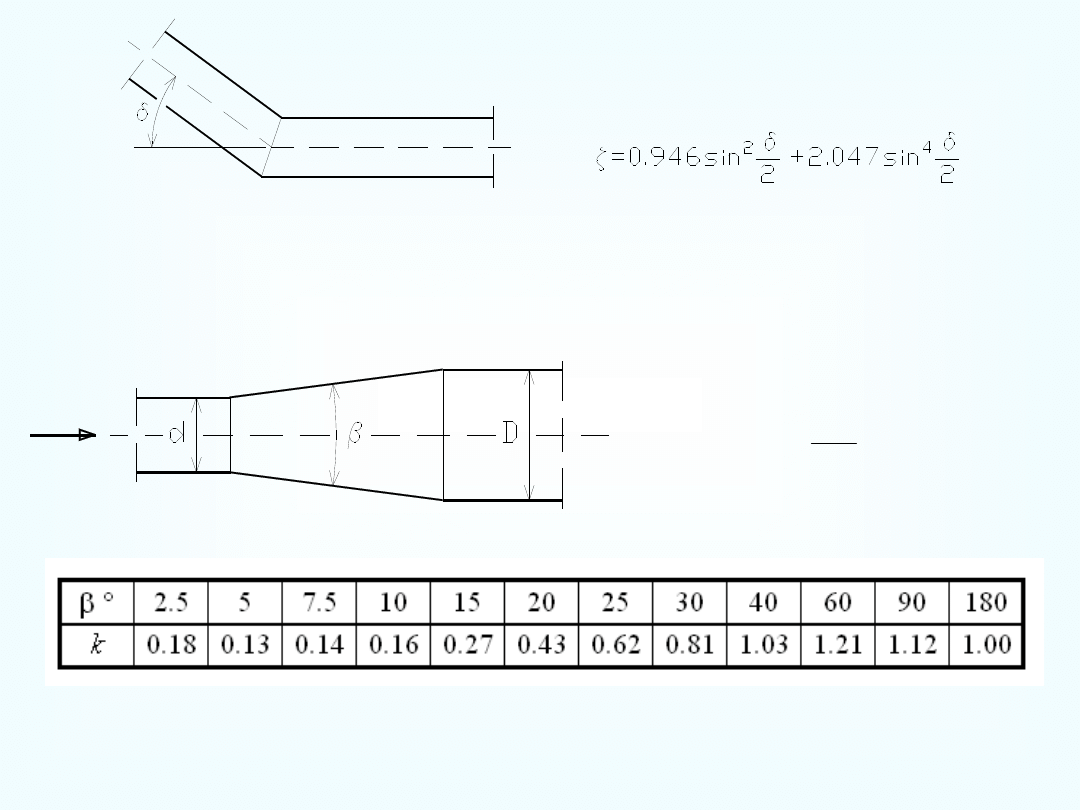
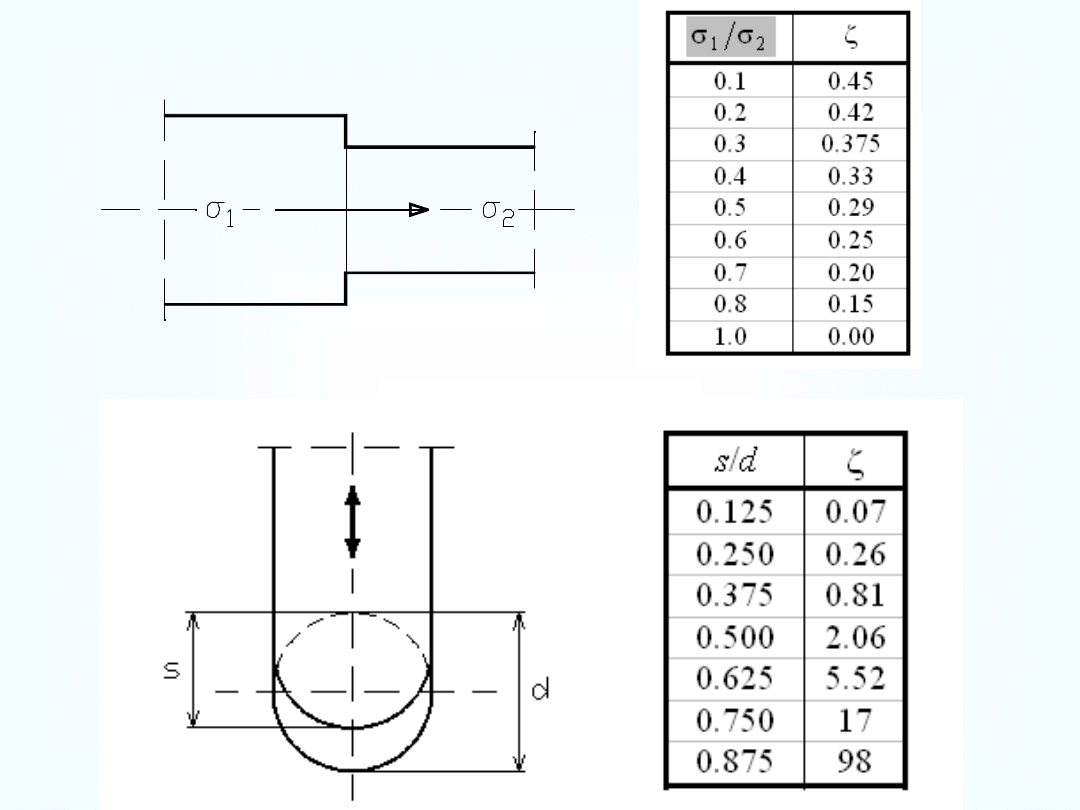
gdzie  jest współczynnikiem strat lokalnych.

,

71

.

3

Re

51

.

2

lg

2

1

























Dla przepływu laminarno-turbulentnego do obliczania współczynnika


stosowany jest półempiryczny wzór Colebrooka i White’a

  0 -

wzór Prandtla-Karmana Re   - wzór

Nikuradsego

,

d

k









,

8

.

0

Re

lg

2

1









W zakresie przepływu laminarnego, współczynnik 

można określić z

dostateczną dokładnością w sposób teoretyczny

.

Re

64





Dla przepływu turbulentnego i rury gładkiej współczynnik strat
liniowych 

określa się wzorem Blasiusa

.

Re

316

.

0

4





.

14

.

1

1

lg

2

1









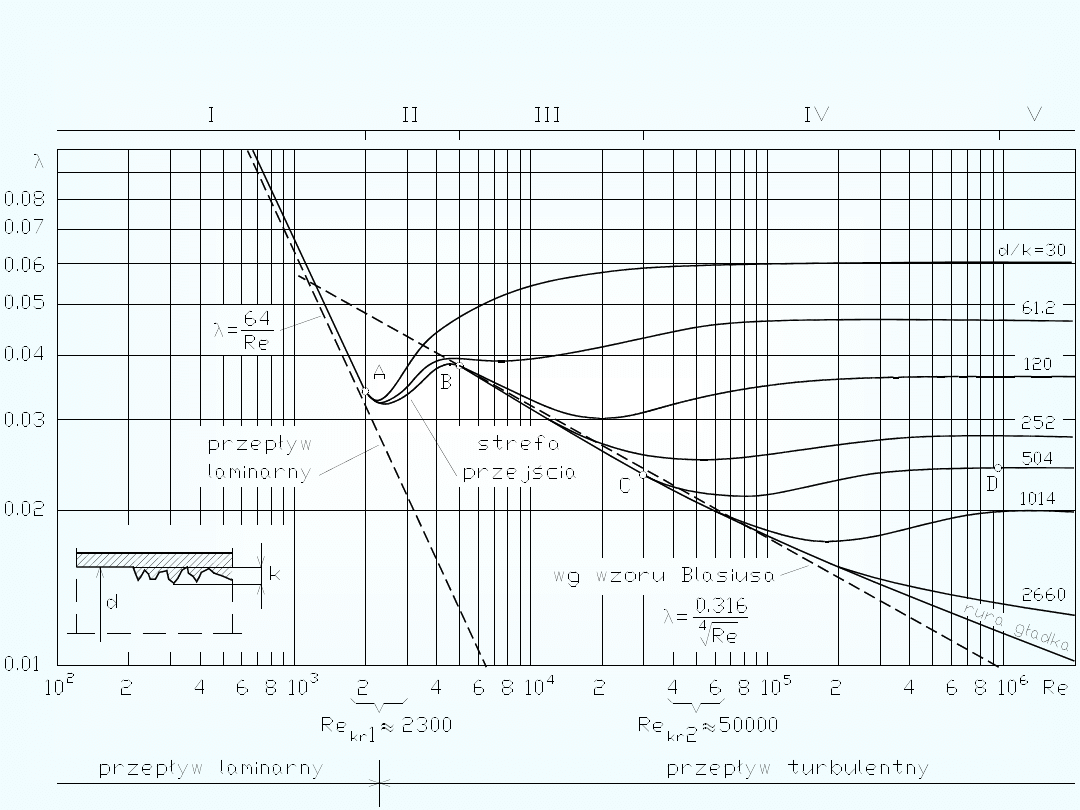
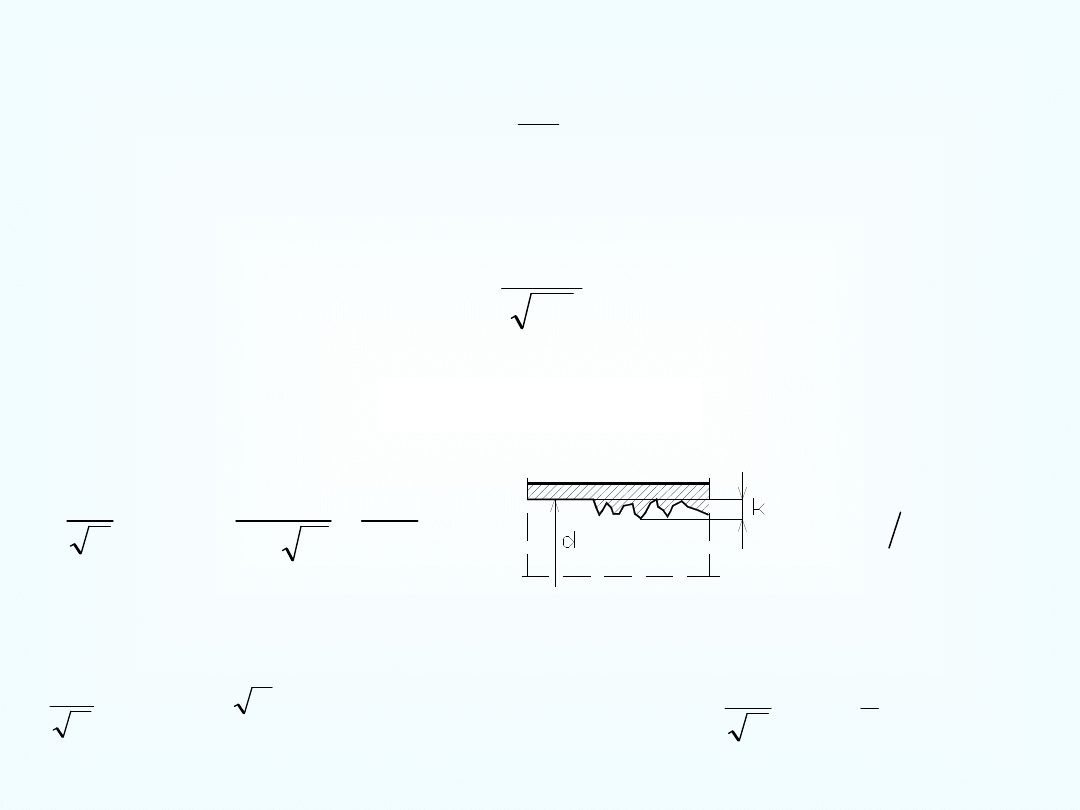
Wykres Nikuradse – określanie współczynnika strat na długości

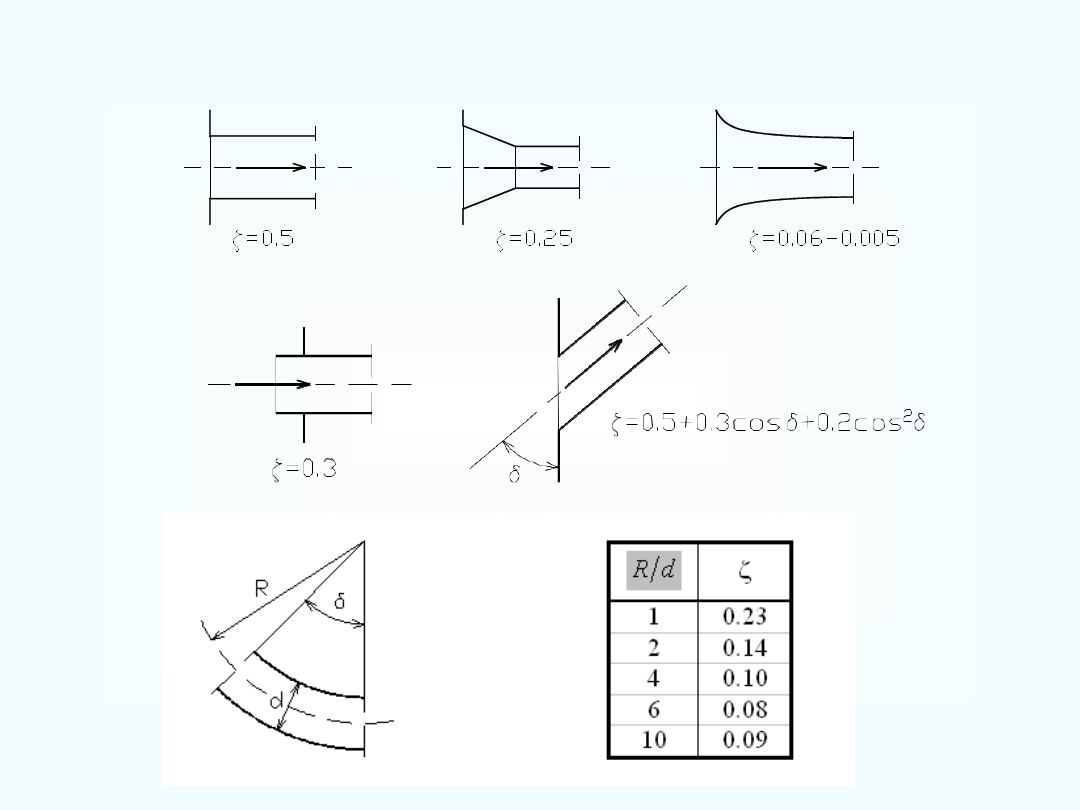
Określanie wartości współczynnika strat lokalnych

2

2

2

1











 





D

d

k

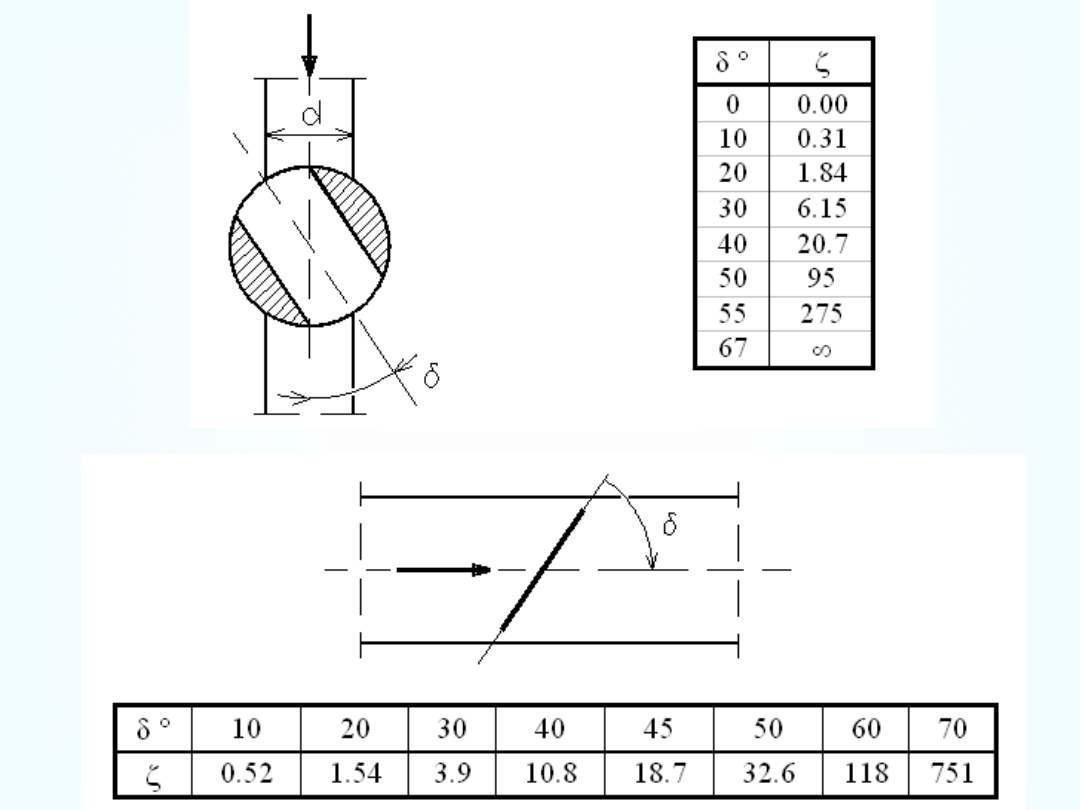
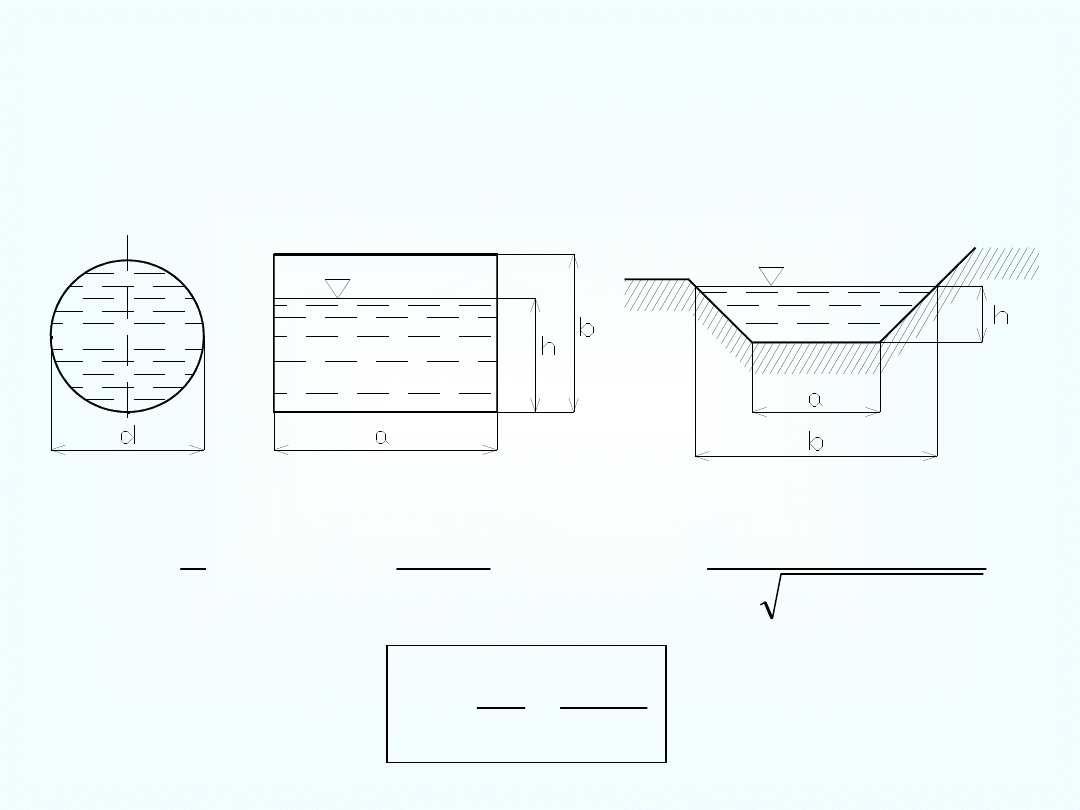
Promień hydrauliczny

Promień hydrauliczny R

h

jest stosunkiem pola przekroju zajętego

przez przepływającą ciecz do obwodu zwilżonego.

2

2

)

(

4

)

(

5

.

2

4

a

b

h

a

b

a

h

R

h

a

h

a

R

d

R

h

h

h



























h

R

V

d

V

4

Re

Do wyznaczenia reakcji strumieni swobodnych wywieranych na
przeszkody ruchome
i nieruchome oraz reakcji na ściany przewodu strumieni
zamkniętych wykorzystamy drugie prawo mechaniki:

,

P

V







t

d

d

m

m - masa
cieczy,

P



- suma sił zewnętrznych działających
na strumień.

Masę cieczy o gęstości , ulegającą zmianie pędu w czasie dt można

określić za pomocą wydatku objętościowego Q

.

t

d

Q

m 



Drugie prawo mechaniki zapisujemy więc następująco

.

P

V







 d

Q

.

)

(

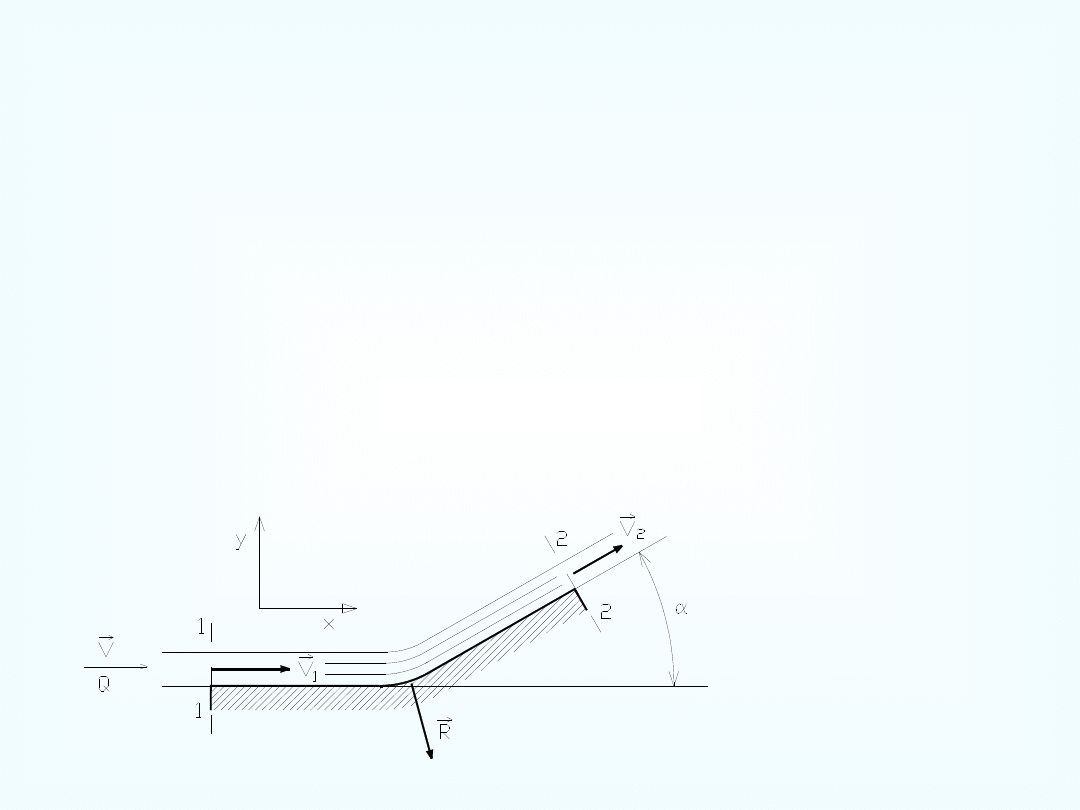
1

2

P

V

V











Q

R

e

a

k

c

j

a

R



w

y

w

i

e

r

a

n

a

p

r

z

e

z

s

w

o

b

o

d

n

y

s

t

r

u

m

i

e

ń

n

a

p

o

w

i

e

r

z

c

h

n

i

ę

c

i

a

ł

a

s

t

a

ł

e

g

o

,

p

o

z

a

n

i

e

d

b

a

n

i

u

s

t

r

a

t

t

a

r

c

i

a

i

s

i

ł

m

a

s

o

w

y

c

h

,

j

e

s

t

r

ó

w

n

a

.

P

R









Przeszkoda nieruchoma

.

)

(

2

1

V

V

R











 Q

Z

a

k

ł

a

d

a

j

ą

c

,

ż

e

w

r

o

z

w

a

ż

a

n

y

m

p

r

z

e

d

z

i

a

l

e

c

z

a

s

u

const



P



o

r

a

z

p

r

z

y

j

m

u

j

ą

c

,

ż

e

p

r

ę

d

k

o

ś

ć

z

m

i

e

n

i

a

s

i

ę

o

d

1

V



d

o

2

V



m

a

m

y

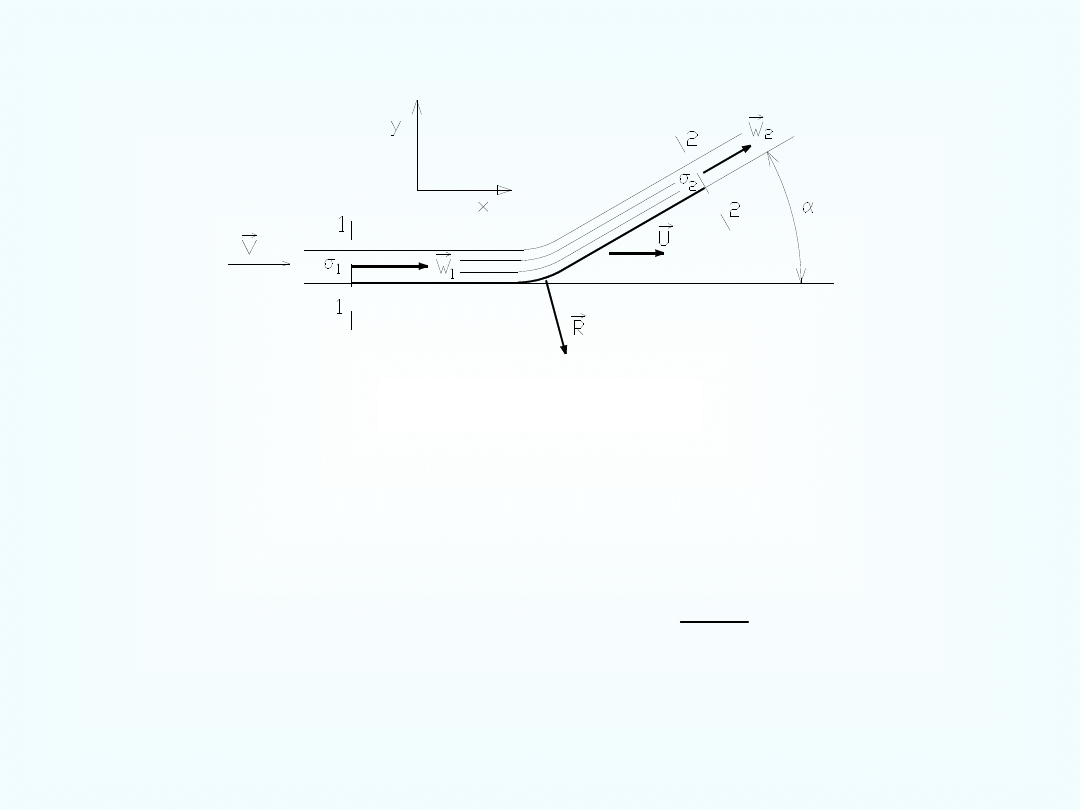
Przeszkoda ruchoma

W

p

r

z

y

p

a

d

k

u

p

r

z

e

s

z

k

o

d

y

r

u

c

h

o

m

e

j

,

p

o

r

u

s

z

a

j

ą

c

e

j

s

i

ę

z

g

o

d

n

i

e

z

k

i

e

r

u

n

k

i

e

m

s

t

r

u

m

i

e

n

i

a

w

p

ł

y

w

a

j

ą

c

e

g

o

z

e

s

t

a

ł

ą

p

r

ę

d

k

o

ś

c

i

ą

,

U



n

a

l

e

ż

y

u

w

z

g

l

ę

d

n

i

ć

p

r

ę

d

k

o

ś

c

i

w

z

g

l

ę

d

n

e

n

a

w

l

o

c

i

e

i

w

y

l

o

c

i

e

s

t

r

u

m

i

e

n

i

a

:

,

,

2

2

1

1

U

V

W

U

V

W





















co powoduje również zmiany wydatku strumienia względem
ruchomej powierzchni

.

V

U

V

Q

Q







,

1

1

W

Q 





.

)

(

2

1

W

W

R













 Q

Reakcja strumienia swobodnego na przeszkodę ruchomą jest więc
mniejsza od reakcji działającej na identyczną przeszkodę
nieruchomą i wyraża się wzorem

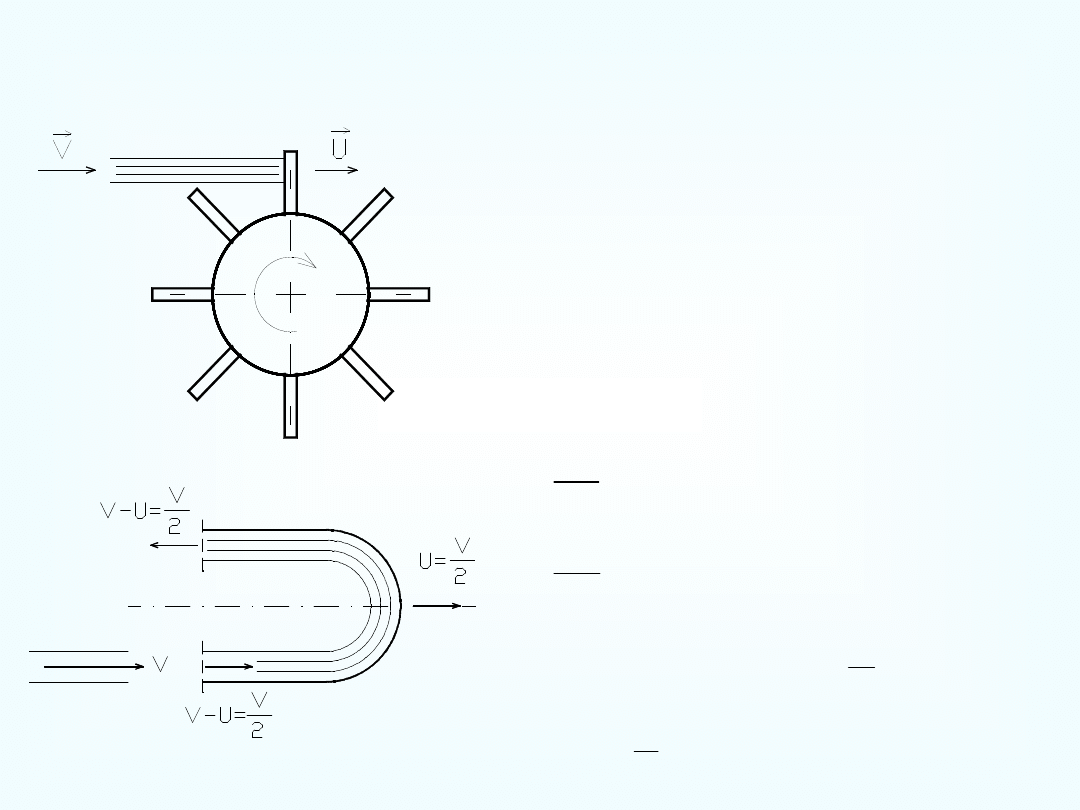
Turbiny

Moc przekazywaną przez
strumień możemy obliczyć
następująco



 



.

cos

1

U

U

V

Q

N













 U

R





 





,

,

U

V

2







 














































;

0

2

cos

1

,

0

sin

U

V

Q

U

N

U

U

V

Q

N

Maksimum mocy:

Reakcja strumienia swobodnego

.

)

(

2

1

W

W

R









 Q



,

2

1

V

U

V

W







,

1

2

W

W





.

0

2

2







U

W

V

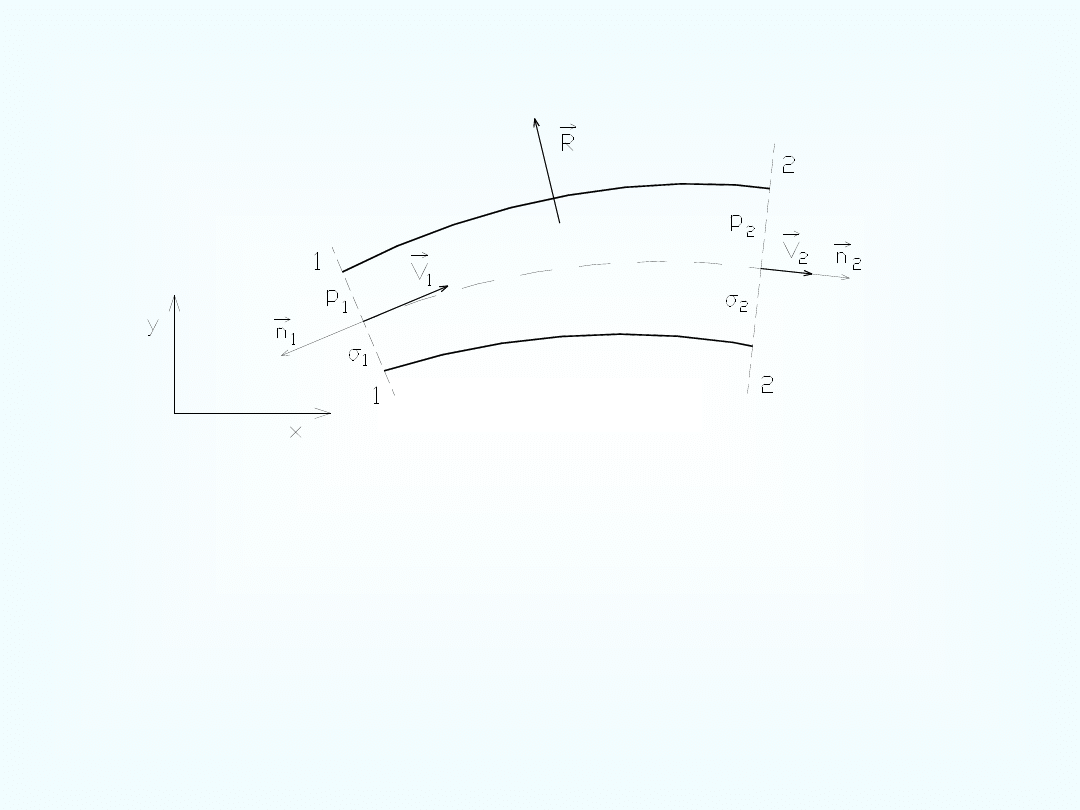
Przepływ cieczy przez przewody

B

i

o

r

ą

c

p

o

d

u

w

a

g

ę

z

a

k

r

z

y

w

i

o

n

y

o

d

c

i

n

e

k

p

r

z

e

w

o

d

u

o

z

m

i

e

n

n

y

m

p

r

z

e

k

r

o

j

u

,

o

d

d

z

i

a

ł

y

w

u

j

ą

c

y

n

a

p

ł

y

n

ą

c

ą

c

i

e

c

z

s

i

ł

ą

,

F



p

o

z

a

n

i

e

d

b

a

n

i

u

s

i

ł

m

a

s

o

w

y

c

h

m

a

m

y

,

2

2

2

1

1

1

F

n

n

P





















p

p

g

d

z

i

e

2

1

,





s

ą

p

o

l

a

m

i

p

r

z

e

k

r

o

j

ó

w

p

r

z

e

w

o

d

u

,

2

1

,

p

p

-

c

i

ś

n

i

e

n

i

a

m

i

,

2

1

,

n

n





-

n

o

r

m

a

l

n

y

m

i

z

e

w

n

ę

t

r

z

n

y

m

i

.

Z

a

t

e

m

r

e

a

k

c

j

a

,

j

a

k

ą

w

y

w

i

e

r

a

c

i

e

c

z

n

a

w

e

w

n

ę

t

r

z

n

e

ś

c

i

a

n

k

i

p

r

z

e

w

o

d

u

,

j

e

s

t

r

ó

w

n

a





.

2

2

2

1

1

1

2

1

n

n

V

V

F

R































p

p

Q

Z

a

k

ł

a

d

a

m

y

,

ż

e

c

i

a

ł

o

o

m

a

s

ie

m

p

o

r

u

s

z

a

s

ię

z

p

r

ę

d

k

o

ś

c

i

ą

,

V



a

je

g

o

p

o

ł

o

ż

e

n

i

e

je

s

t

o

k

r

e

ś

lo

n

e

w

e

k

t

o

r

e

m

.

]

,

,

[

z

y

x



r



Twierdzenie o momencie pędu (kręcie)

V

r

K







m





mówi, że jego pochodna względem czasu jest równa wypadkowej
momentów sił zewnętrznych, działających na to ciało

.

M

V

r

K















t

d

d

m

t

d

d

Rozważamy ustalony ruch cieczy o masie m i gęstości  w

płaszczyźnie Oxy, wtedy

,

)

(

x

y

z

V

y

V

x

m

K

K







Przy takich założeniach i przy wykorzystaniu zależności:

,

t

d

Q

m 







,

θ

sin

θ

cos

θ

V

r

V

V

r

V

y

V

x

x

y

x

y









otrzymujemy

.

)

(

M

V

r

d

Q







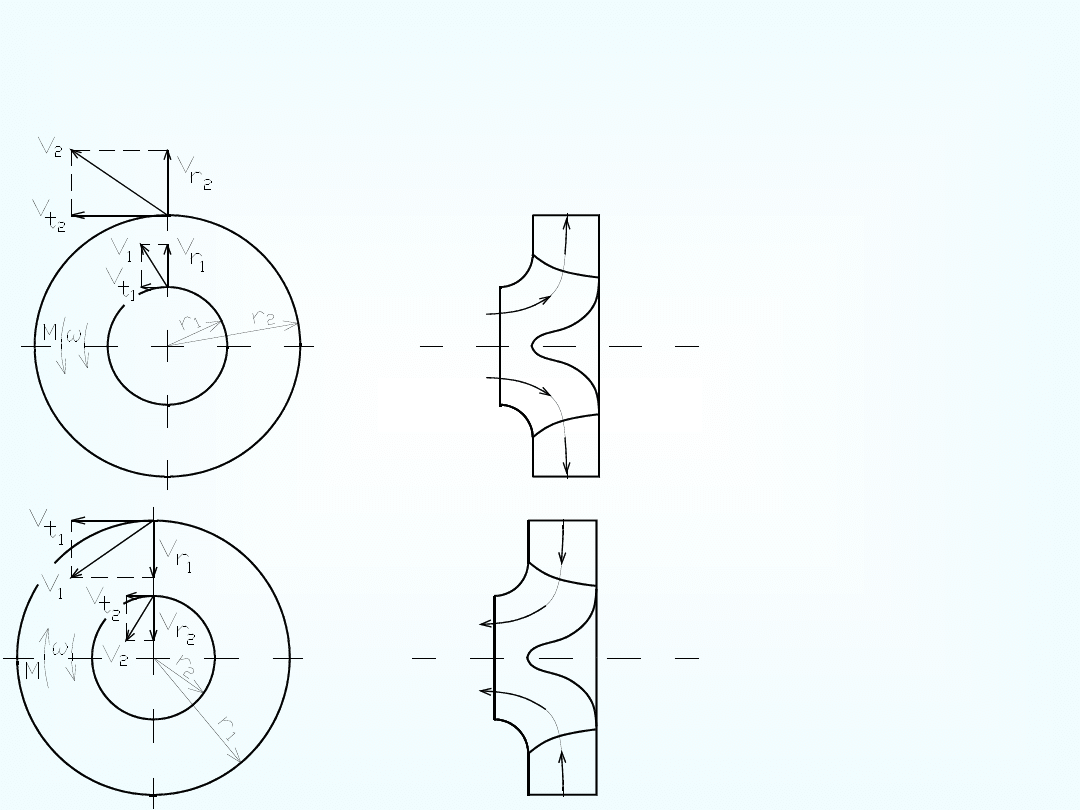
Z powyższego równania można bezpośrednio wyznaczyć moment sił
działających na wale wirnika maszyny przepływowej: takiej jak
pompa odśrodkowa, czy też turbina promieniowa





,

1

2

1

2

r

V

r

V

Q

M

t

t











.

2

1

2

1

r

V

r

V

Q

M

t

t





