„Żadne drzewo nie rośnie bez 

korzeni, podobnie i ludzie 

więdną bez rozsądku.”

Tales z Miletu

TWIERDZENIE O PROSTYCH 

PRZECINAJĄCYCH SIĘ PRZECIĘTYCH 

PROSTYMI RÓWNOLEGŁYMI. 

TWIERDZENIE ODWROTNE DO 

TWIERDZENIA TALESA.

Oba  twierdzenia  wymienione  w  temacie  tej 
lekcji  wynikają  bezpośrednio  z  twierdzenia 
Talesa.  Pierwsze  z  nich  obrazuje  trochę  inne, 
ogólniejsze podejście do twierdzenia Talesa a 
drugie, 

jak 

mówi 

sama 

nazwa, 

jest 

twierdzeniem do niego odwrotnym. 

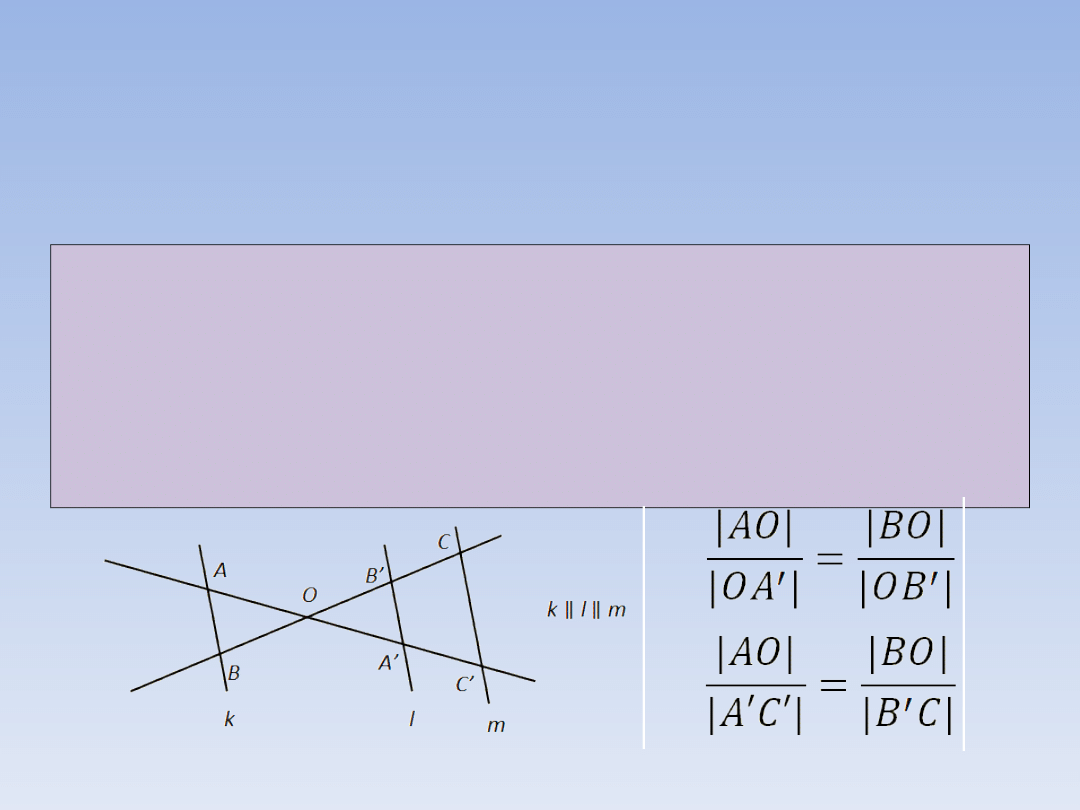
TWIERDZENIE O PROSTYCH 

PRZECINAJĄCYCH SIĘ 

PRZECIĘTYCH PROSTYMI 

RÓWNOLEGŁYMI.

Jeżeli dwie proste przecinające się przecięte 

są prostymi równoległymi, to odcinki 

wyznaczone na jednej prostej są 

proporcjonalne do odpowiednich odcinków 

na drugiej prostej.

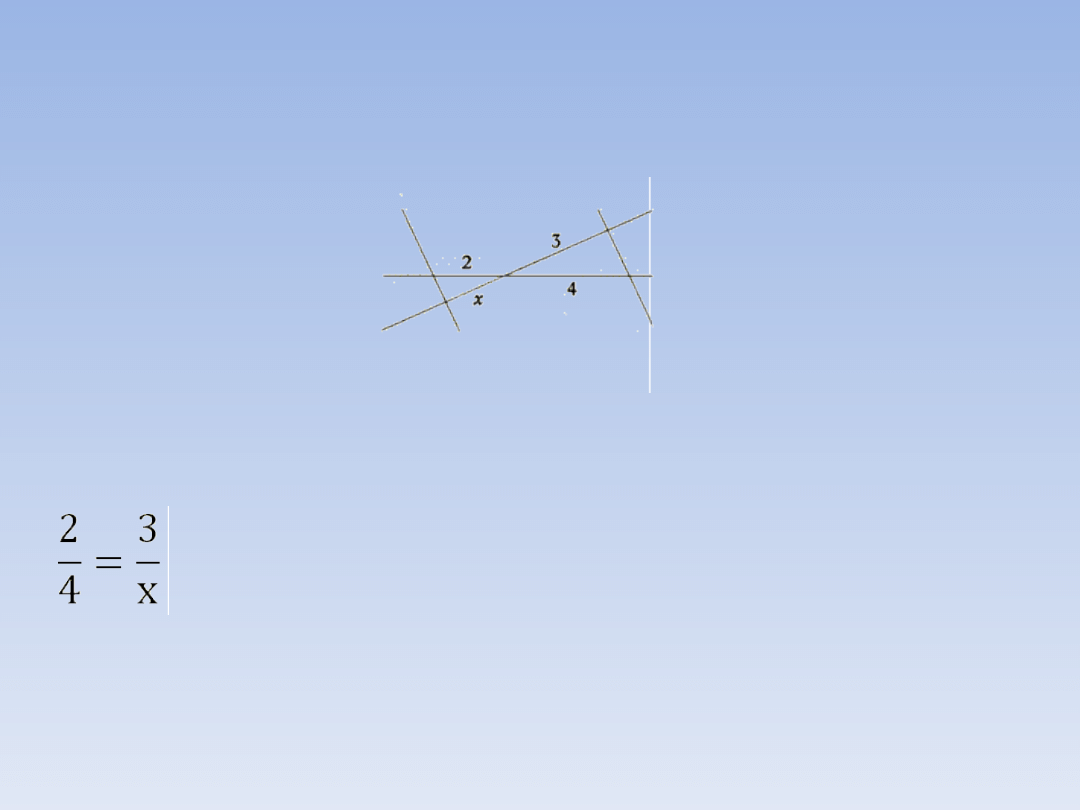
PRZYKŁADY.

PRZYKŁAD 1.
Oblicz długość odcinka oznaczoną jako x.

 

Na  podstawie  twierdzenia  o  prostych 
przecinających  się  przeciętych  prostymi 
równoległymi 

układamy 

proporcje 

i 

rozwiązujemy ją.

2 ∙ x = 3 ∙ 4
2x = 12 |: 2 
x = 6 

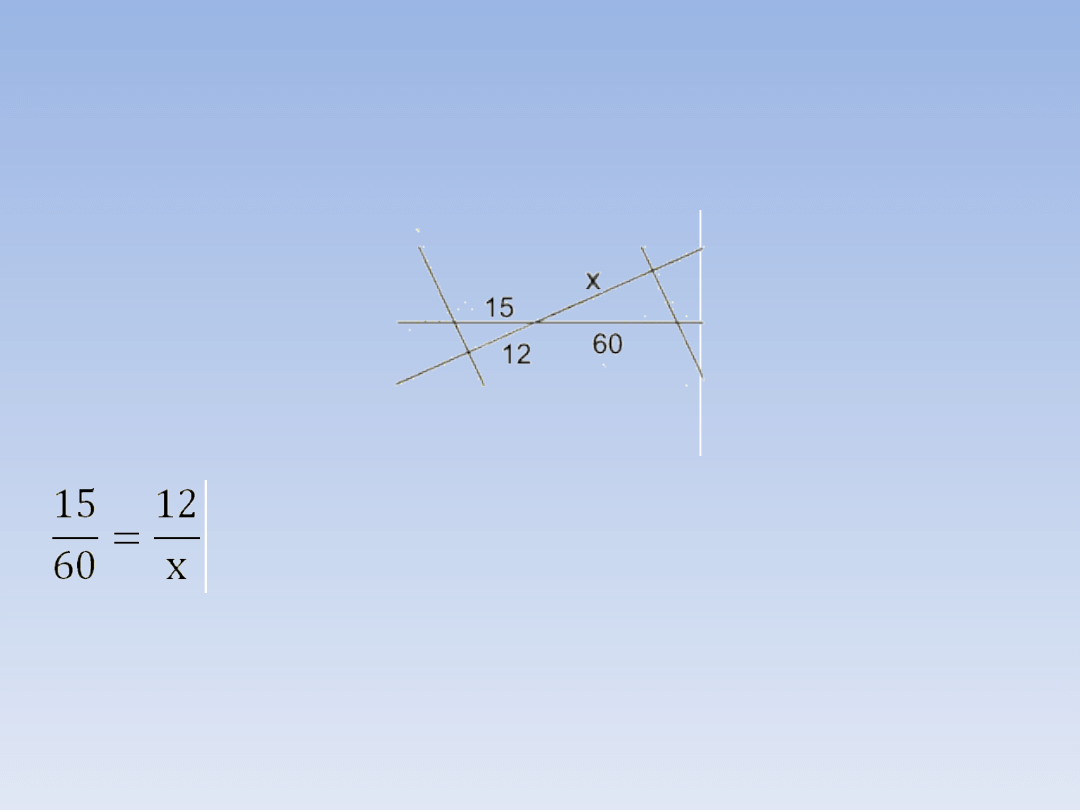
PRZYKŁADY.

PRZYKŁAD 2.
Oblicz długość odcinka oznaczoną jako x.

Układamy i rozwiązujemy odpowiednią 
proporcję:

15 ∙ x = 60 ∙ 12
15x = 720 | :15
x = 48

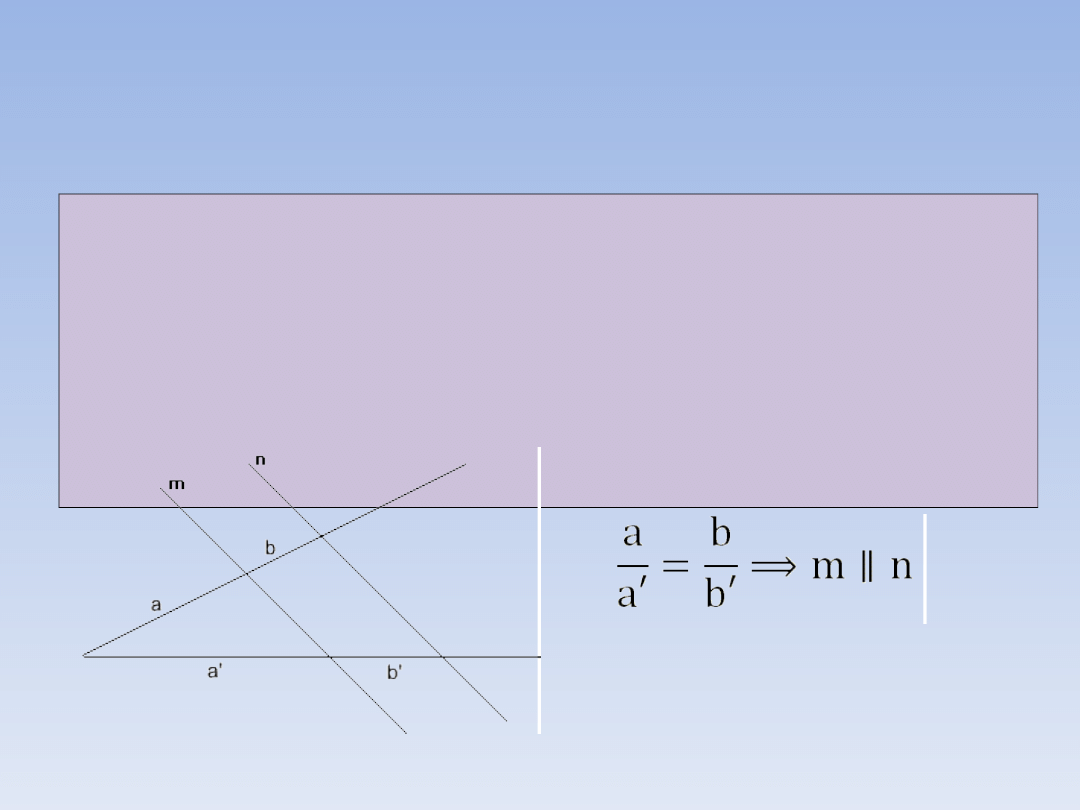
TWIERDZENIE ODWROTNE 

DO TWIERDZENIA TALESA.

Jeżeli ramiona kąta przetniemy dwiema 

prostymi i odcinki wyznaczone przez te 

proste na jednym ramieniu kąta są 

proporcjonalne do odpowiednich odcinków 

na drugim ramieniu, to proste te są 

równoległe.

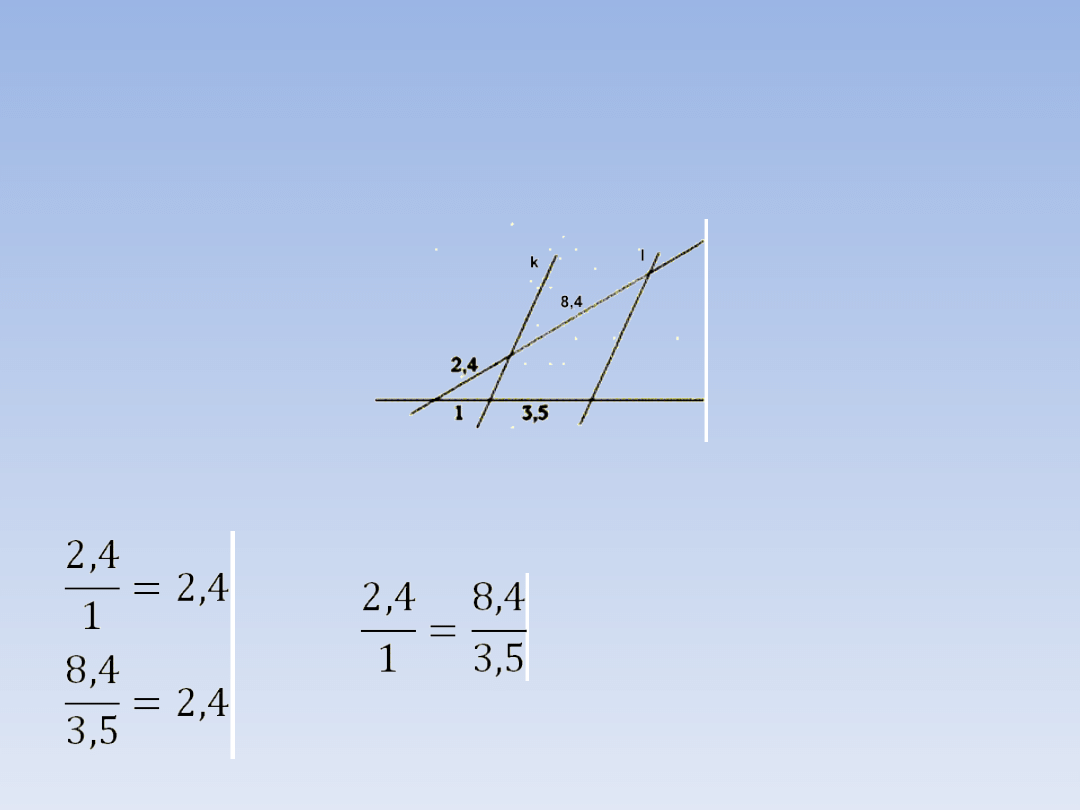
PRZYKŁADY.

PRZYKŁAD 1.
Czy proste k i l są równoległe?

Sprawdzamy  czy  odpowiednie  odcinki  są 
proporcjonalne. 

A więc proste k i l są 
równoległe.

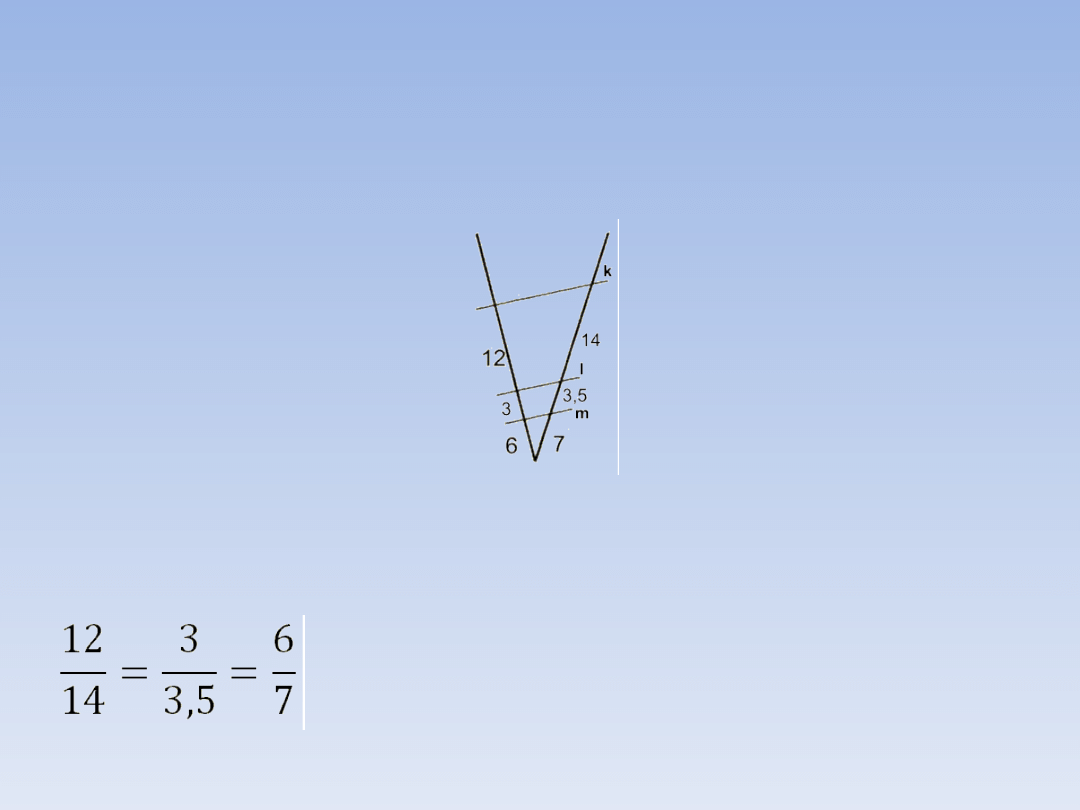
PRZYKŁADY.

PRZYKŁAD 2.
Czy proste k, l i m  są równoległe?

Sprawdzamy  czy  odpowiednie  odcinki  są 
proporcjonalne. 

Pierwszy 

ułamek 

wystarczy 

skrócić 

przez 

2 

a 

drugi 

rozszerzyć przez 2 aby otrzymać 
ostatni ułamek, a więc proste k, 
l i m są równoległe.

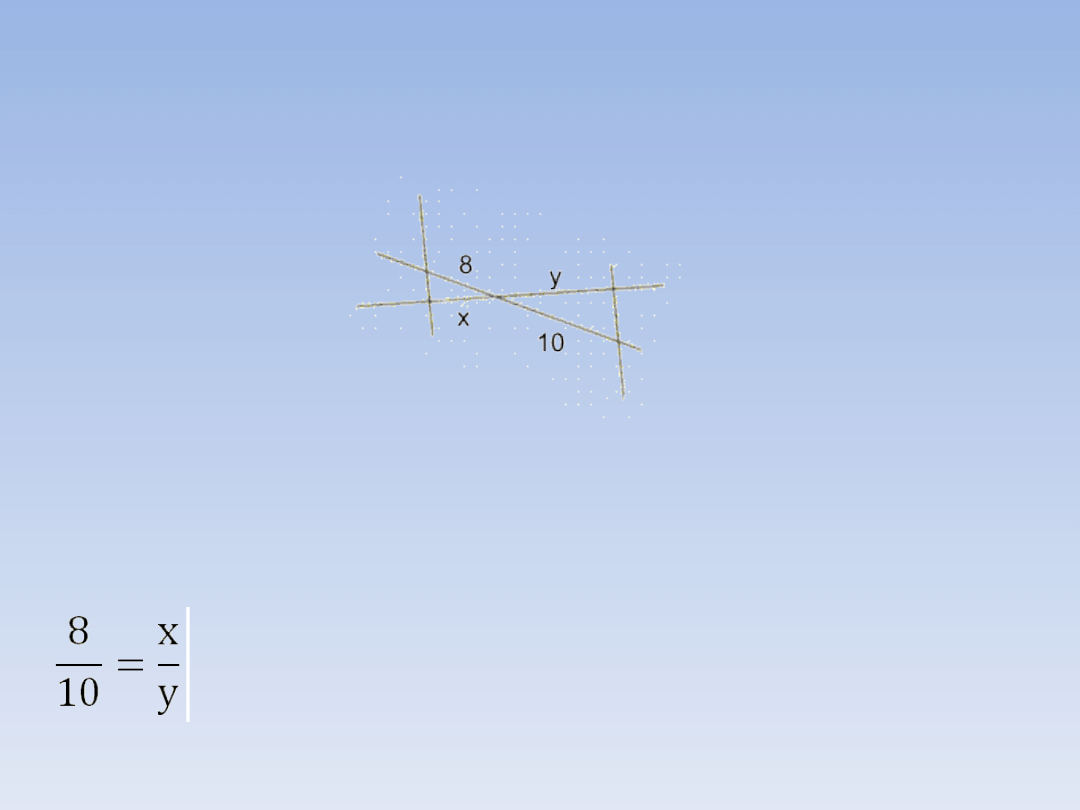
PRZYKŁADOWE ZADANIA.

ZADANIE 1.
Oblicz x i y jeżeli wiadomo, że x + y = 27.

Należy  zbudować  odpowiedni  układ  równań. 
Pierwsze równanie już mamy:
x + y = 27.
Drugie równanie otrzymamy z proporcji:

8y = 10x

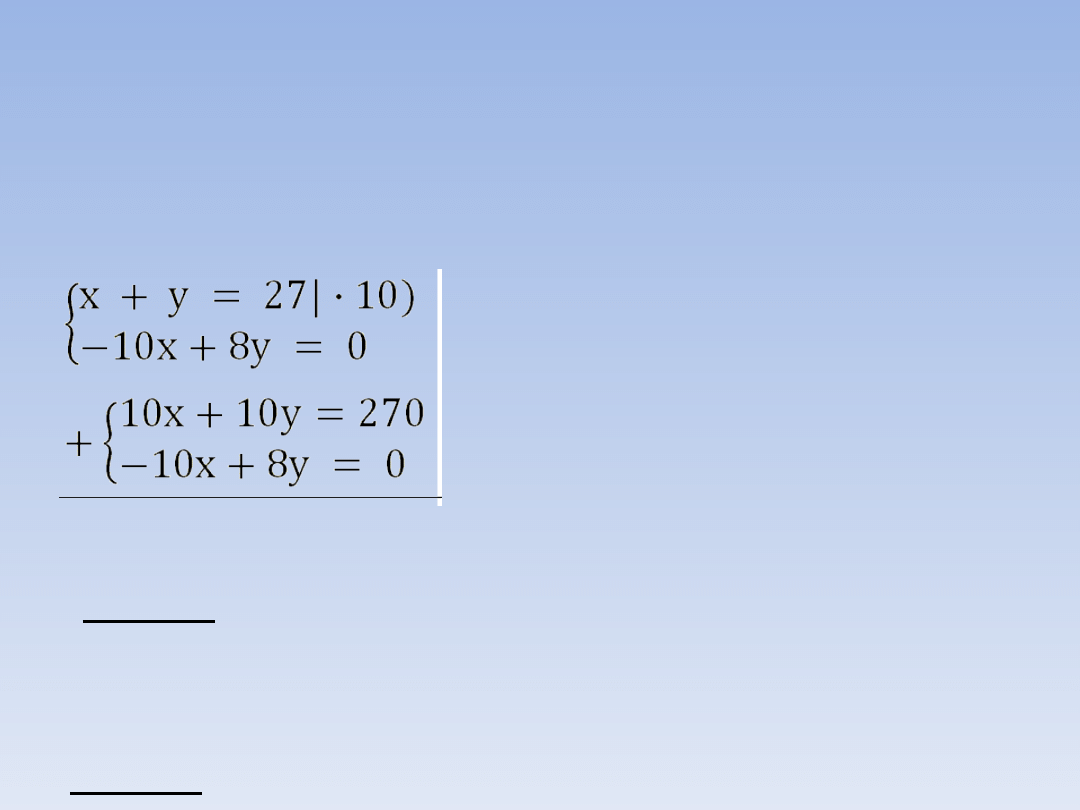
PRZYKŁADOWE ZADANIA.

ZADANIE 1 – ciąg dalszy.
Otrzymujemy 

układ 

równań, 

który 

rozwiązujemy 

metodą 

przeciwnych 

współczynników.

18y = 270 |: 18
 y = 15
x + 15 = 27
x = 27 – 15
x = 12

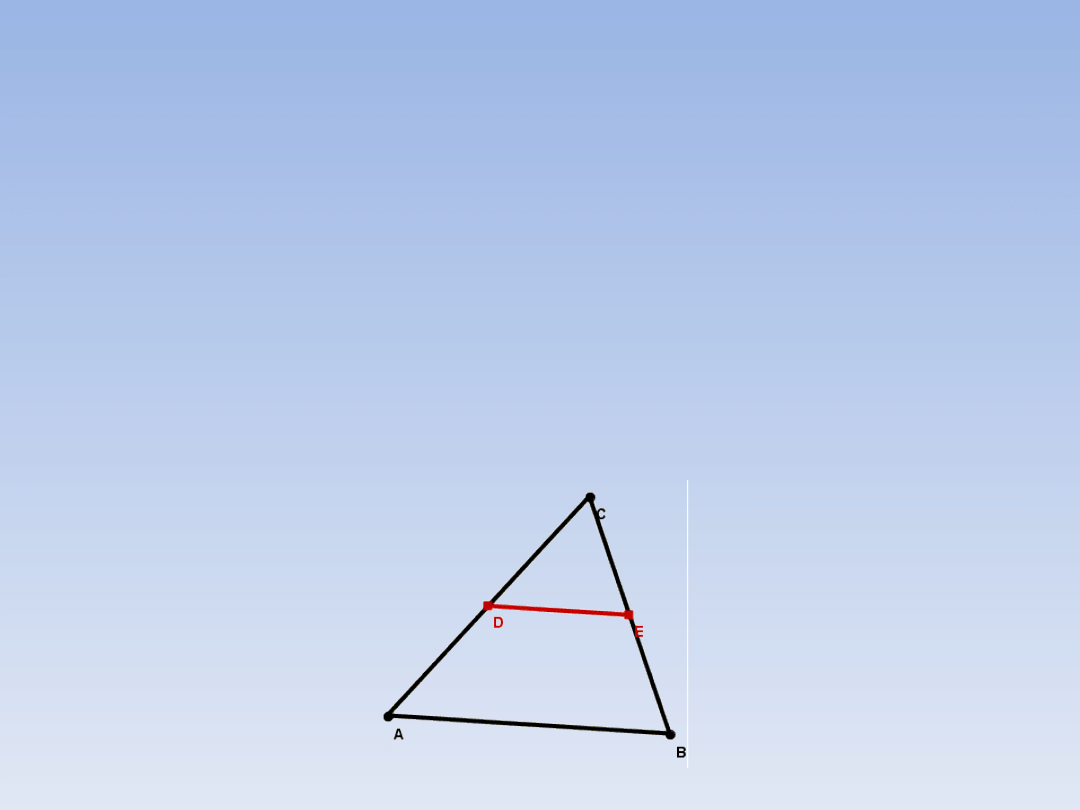
PRZYKŁADOWE ZADANIA.

ZADANIE 2.
Korzystając  z  twierdzenia  odwrotnego  do 
twierdzenia 

Talesa 

uzasadnij, 

że 

dla 

dowolnego  trójkąta  ABC  odcinek  łączący 
środki  boków  AC  i  BC  jest  równoległy  do 
boku AB. Uzasadnij, że odcinek ten jest dwa 
razy krótszy od boku AB.
Zaczniemy 

od 

wykonania 

rysunku 

przedstawiającego sytuację z zadania.

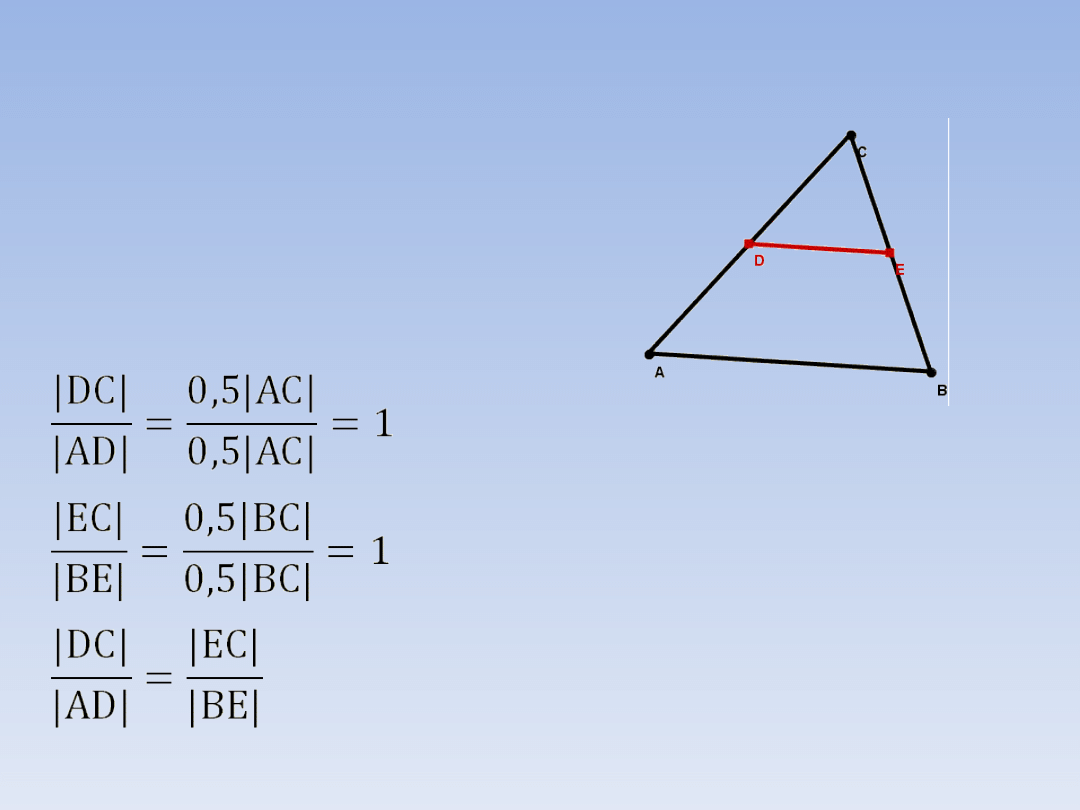
PRZYKŁADOWE ZADANIA.

ZADANIE 2 – ciąg dalszy.
Mamy: 
|AD| = |DC| = 0,5|AC|,
|BE| = |EC| = 0,5|BC|,
a więc:

                            - na mocy twierdzenia 
odwrotnego do

  twierdzenia  Talesa  odcinki  AB  i  DE  są 
równoległe.

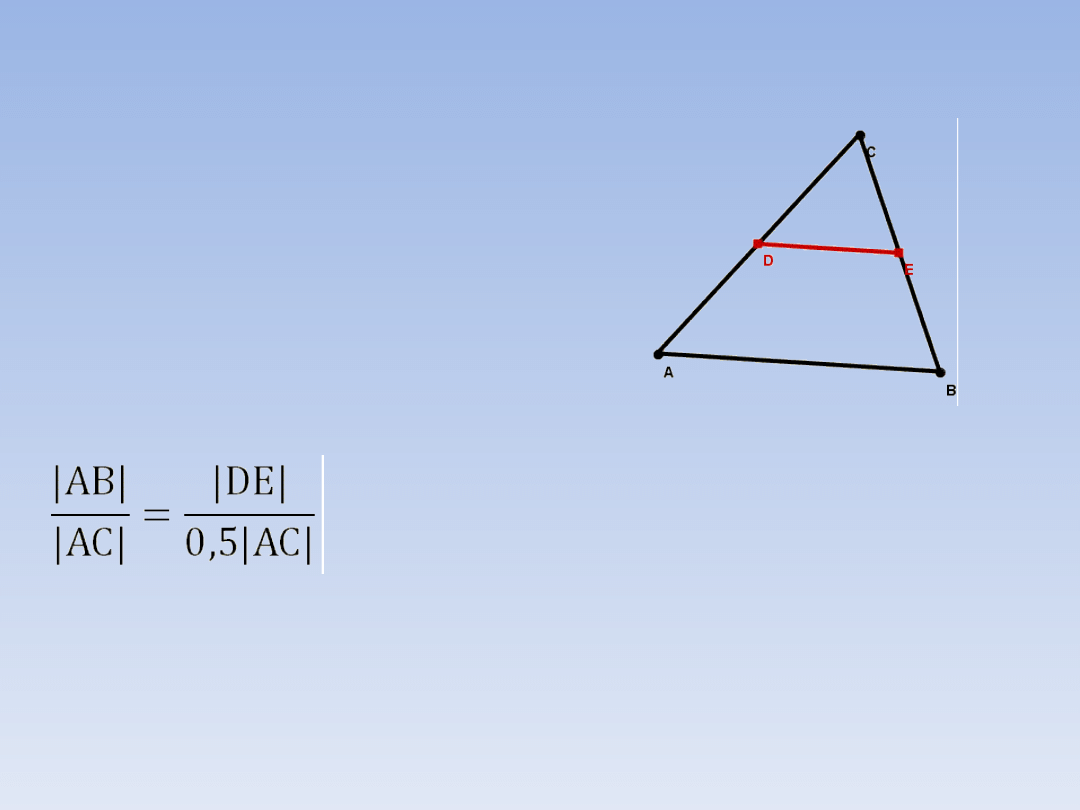
PRZYKŁADOWE ZADANIA.

ZADANIE 2 – ciąg dalszy.
Udowodniliśmy już, że odcinki DE i AB
są równoległe, możemy więc teraz
skorzystać z twierdzenia Talesa.
|DC| = 0,5|AC|
Z twierdzenia Talesa wynika proporcja:

0,5|AB||AC| = |DE||AC| /: |AC| 
0,5|AB| = |DE| - długość odcinka DE jest 
równa połowie odcinka AB. 

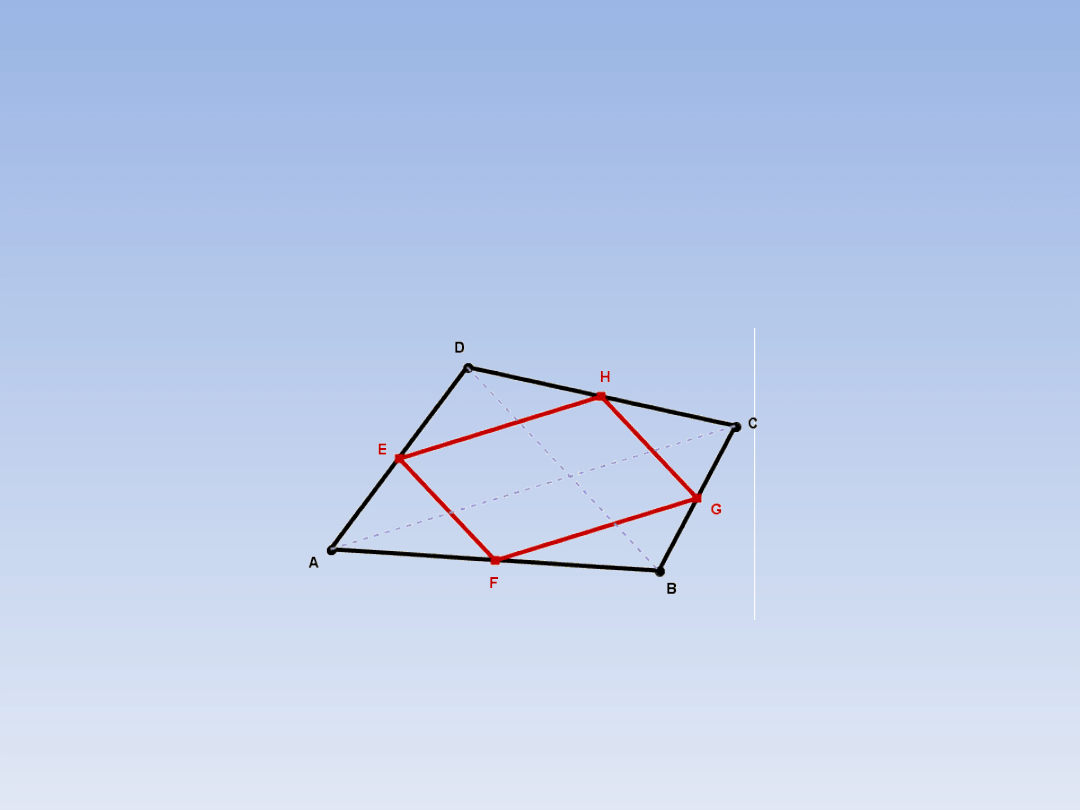
PRZYKŁADOWE ZADANIA.

ZADANIE 3.
Wykaż, że odcinki łączące środki kolejnych boków 
dowolnego czworokąta tworzą równoległobok.
Zaczynamy od rysunku:

Na  rysunku  zaznaczyliśmy  przerywanymi  liniami 
przekątne  czworokąta  ABCD.  Przyjrzyjmy  się 
trójkątom  ABD  i  BCD.  Spełniają  one  warunki 
poprzedniego  zadania  a  więc  możemy  skorzystać 
z jego wyników.

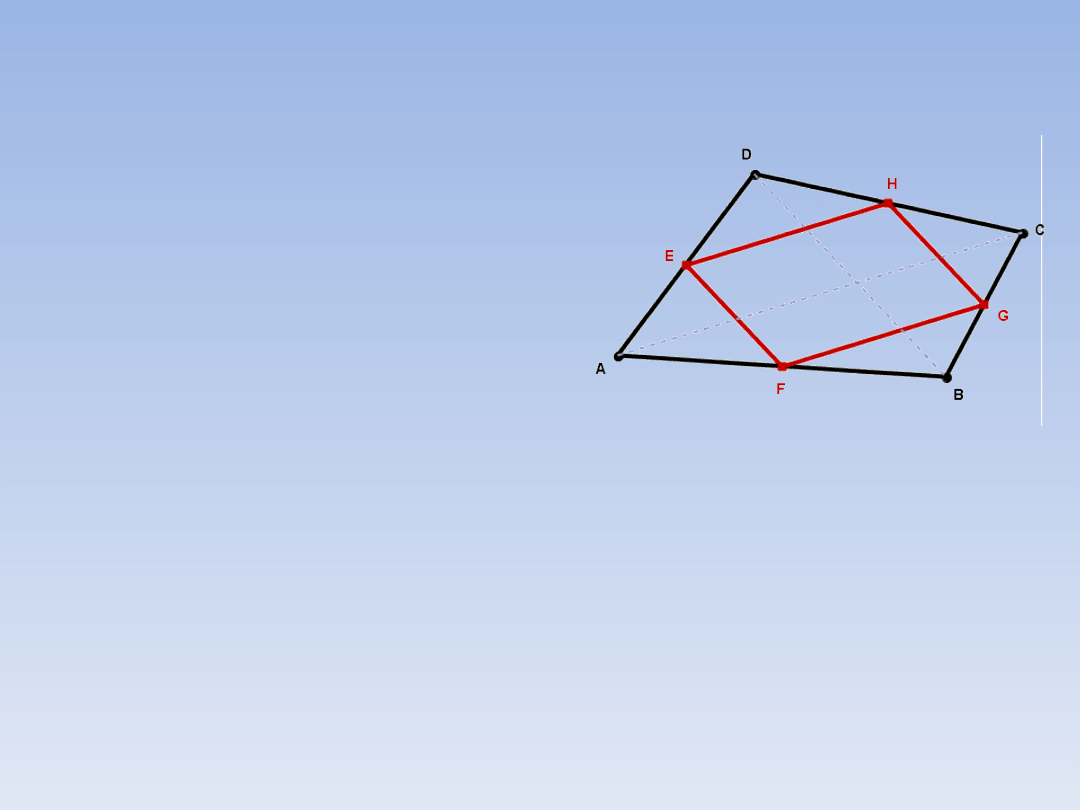
PRZYKŁADOWE ZADANIA.

ZADANIE 3 – ciąg dalszy.
W oparciu o zadanie 2 stwierdzamy,
że odcinek EF jest równoległy do
odcinka BD i ma długość 
0,5|BD|. Analogicznie odcinek
GH jest równoległy do odcinka
BD i ma długość 0,5|BD|. Skoro odcinki EF i 
GH są równoległe do tego samego odcinka 
(BD) są też równoległe do siebie, mają także 
jednakową długość (0,5 |BD|). Powtarzając 
rozumowanie dla trójkątów ABC i ACD 
udowadniamy, że czworokąt EFGH jest 
równoległobokiem. 

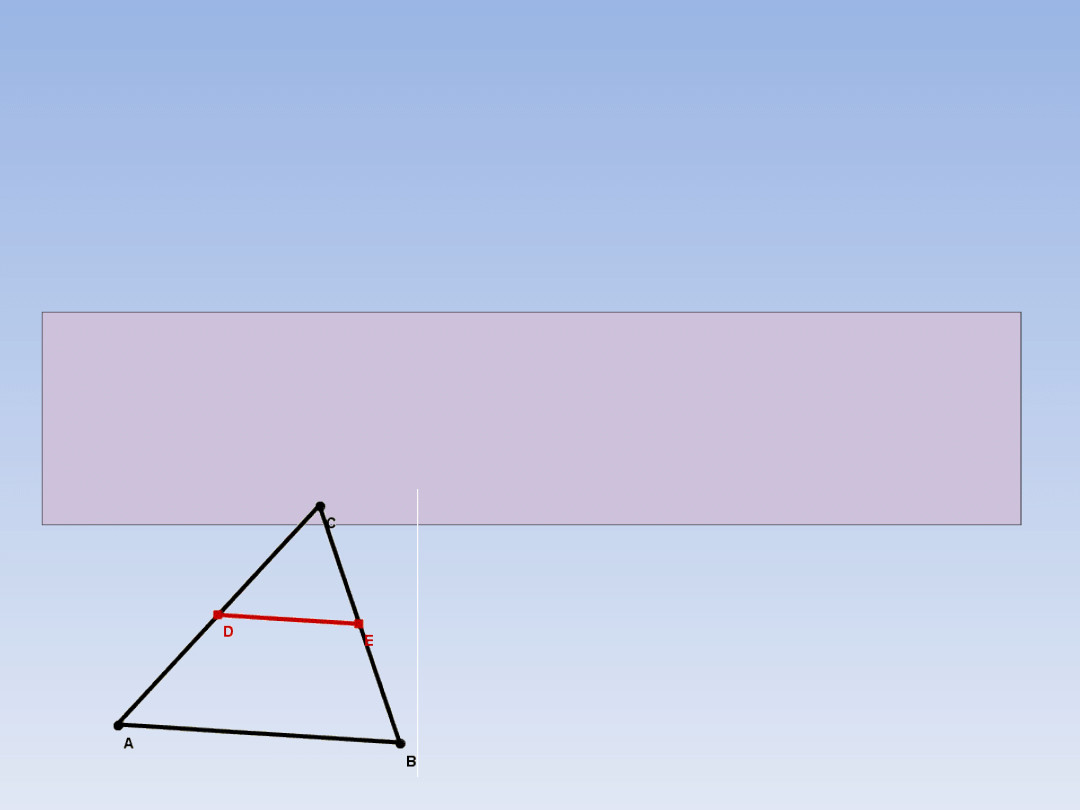
TWIERDZENIE O ODCINKU 

ŁĄCZĄCYM ŚRODKI BOKÓW 

TRÓJKĄTA.

Zadanie 2, to tak naprawdę dowód 
twierdzenia, które możemy sformułować 
następująco:  

Odcinek łączący środki dwóch boków trójkąta 

jest równoległy do trzeciego boku, a jego 

długość jest równa połowie długości tego 

boku.

|DE| = 0,5|AB|

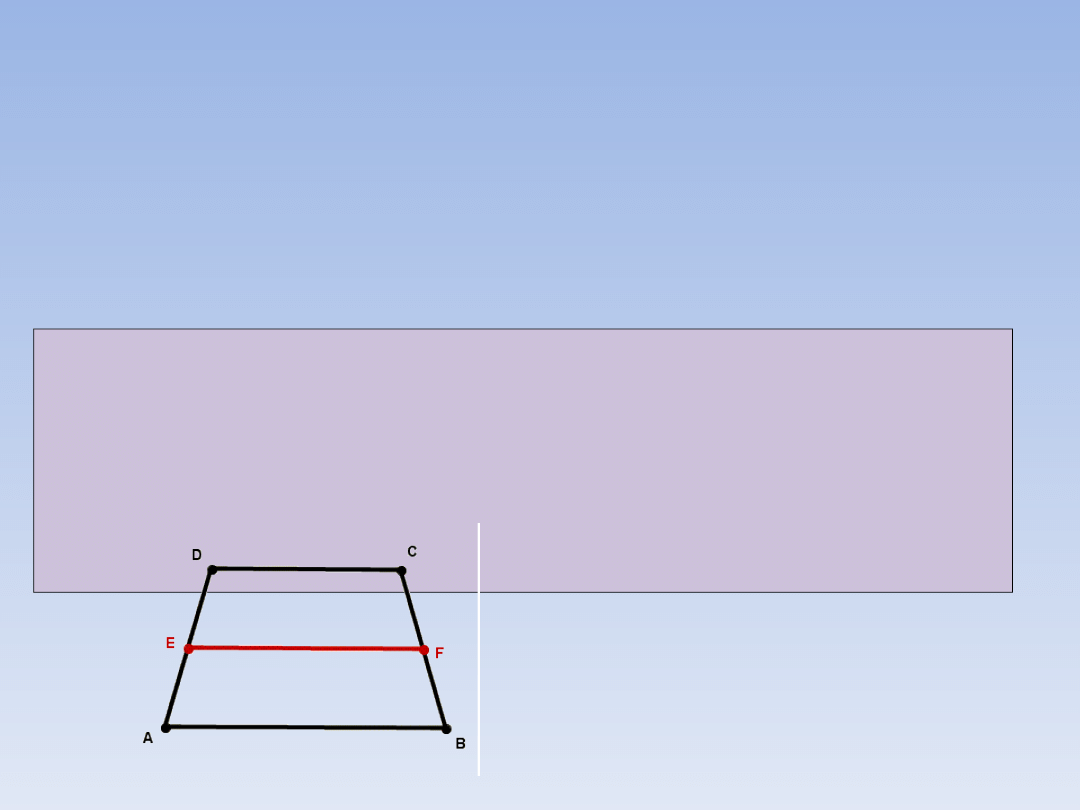
TWIERDZENIE O LINI 

ŚRODKOWEJ TRAPEZU.

Dowód  tego  twierdzenia  jest  podobny  do 
dowodu  twierdzenia  poprzedniego  -  spróbuj 
udowodnić je samodzielnie.

Odcinek łączący środki boków AD i BC 

trapezu ABCD 

(AB || CD) jest równoległy do podstaw i jego 

długość jest równa połowie sumy długości 

podstaw.

|EF| = 0,5(|AB| + |CD|)