Przykładowe

zadania

z połączeń

spawanych.

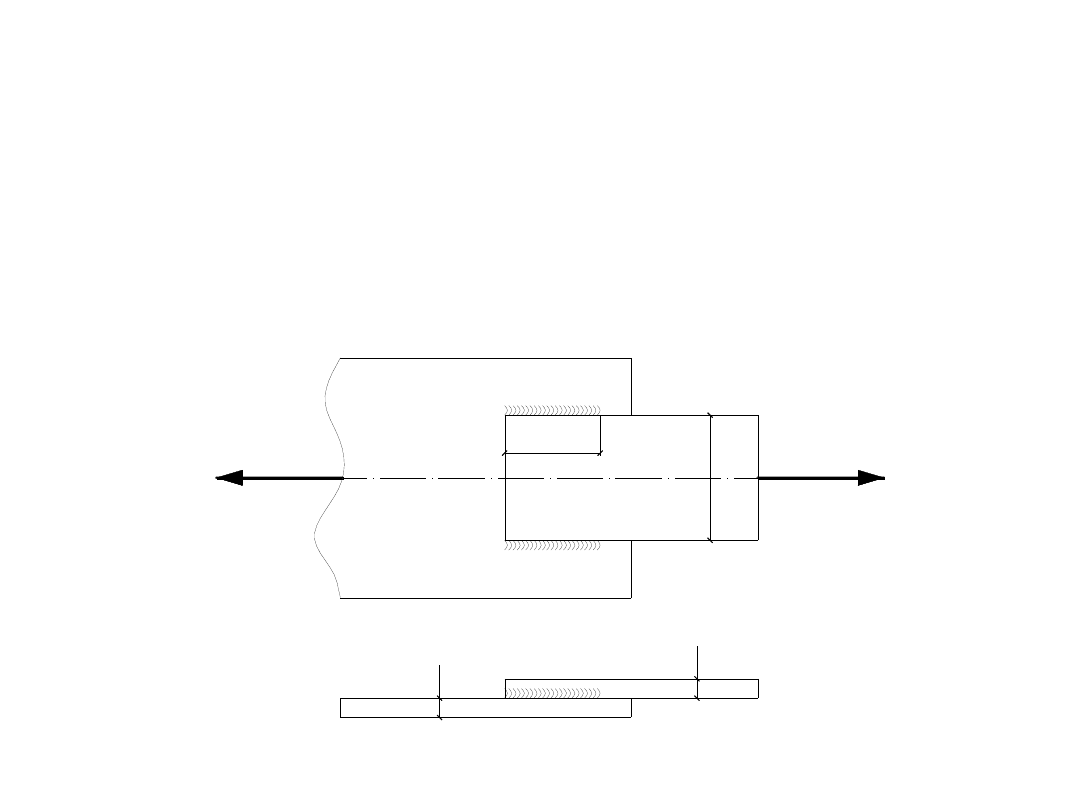
Zadanie 1.

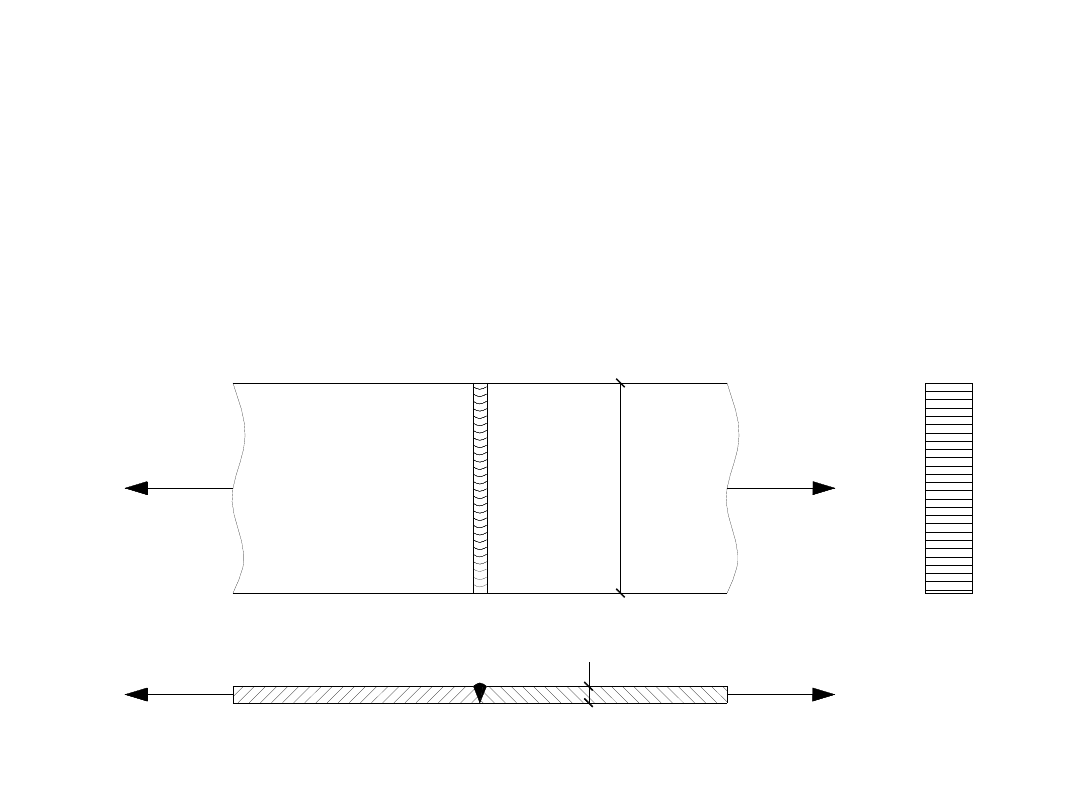
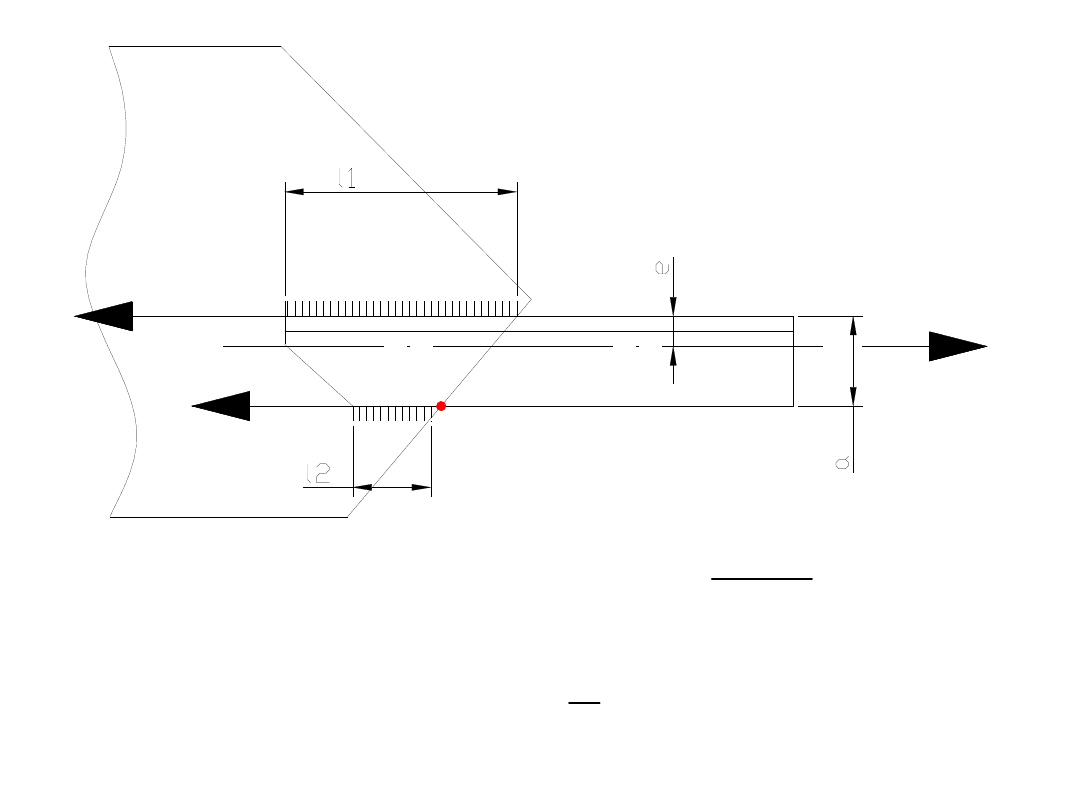
Sprawdzić nośność połączenia zakładkowego płaskownika

180 x 8 z blachą węzłową o grubości 10mm. Płaskownik rozciągany
siłą osiową P=250 kN ma być przymocowany dwiema podłużnymi
spoinami pachwinowymi o grubości a=4 mm i długości
l

1

=180 mm. Elementy wykonane są ze stali St3SX (f

d

=215 MPa;

R

e

=235 MPa)

Przyjąć, że spoina spełnia wszystkie wymagane warunki
konstrukcyjne.

l

1

b

g

1

g

2

P

P

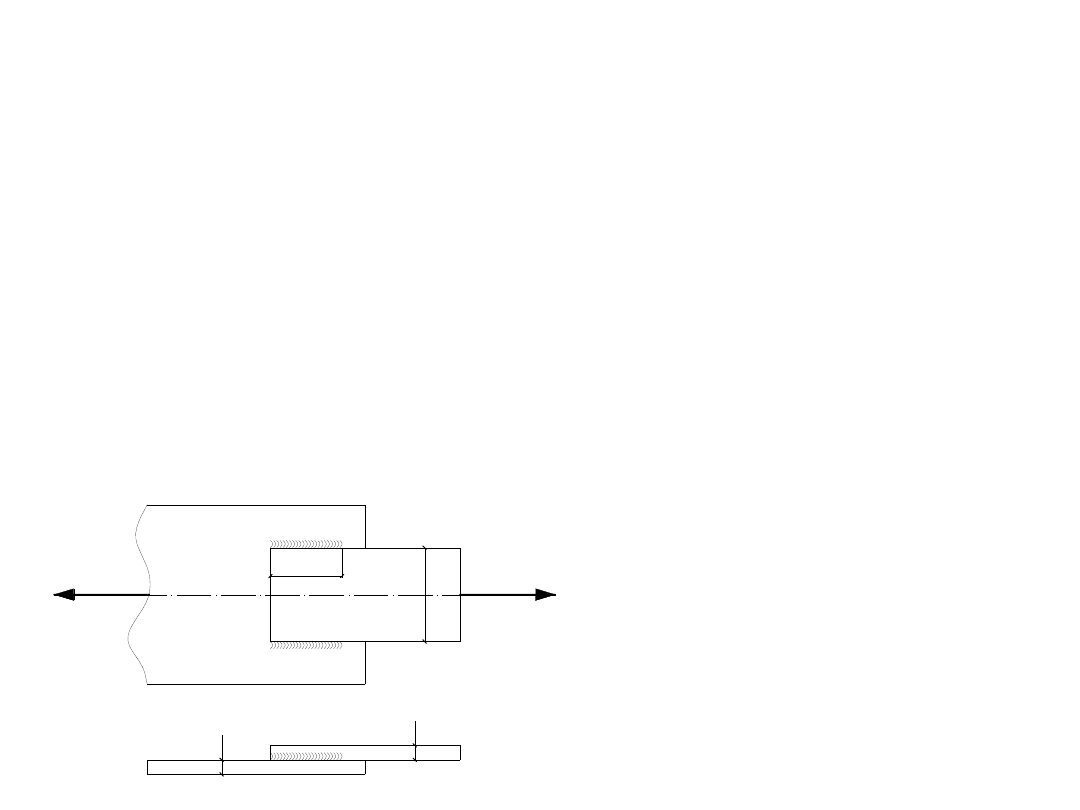
Skoro w treści podane jest, że spoina spełnia wszystkie warunki
konstrukcyjne – można odstąpić od sprawdzenia wymogów
normowych.

Gdyby w treści zadania nie było formułki, że spoina spełnia warunki
określone w normie PN 90/B-03200, wówczas należałoby sprawdzić:

l

1

≥ b (długość każdej ze spoin jest nie mniejsza niż odstęp

między nimi)

p.6.3.2.2. c

W naszym przypadku szerokość płaskownika: b = 180 mm.

Długość pojedynczej spoiny l

1

= 180 mm.

l

1

= 180 mm ≥ b = 180 mm



warunek spełniony!

b ≤ 30 g (odstęp nie przekracza 30 krotnej grubości
cieńszego elementu)

p.6.3.2.2. c

l

1

b

g

1

g

2

P

P

Cieńszy element ma grubość g

1

= 8 mm.

30 · g

1

= 30 · 8 = 240 mm

b = 180 mm ≤ 30 g = 240
mm

warunek spełniony!

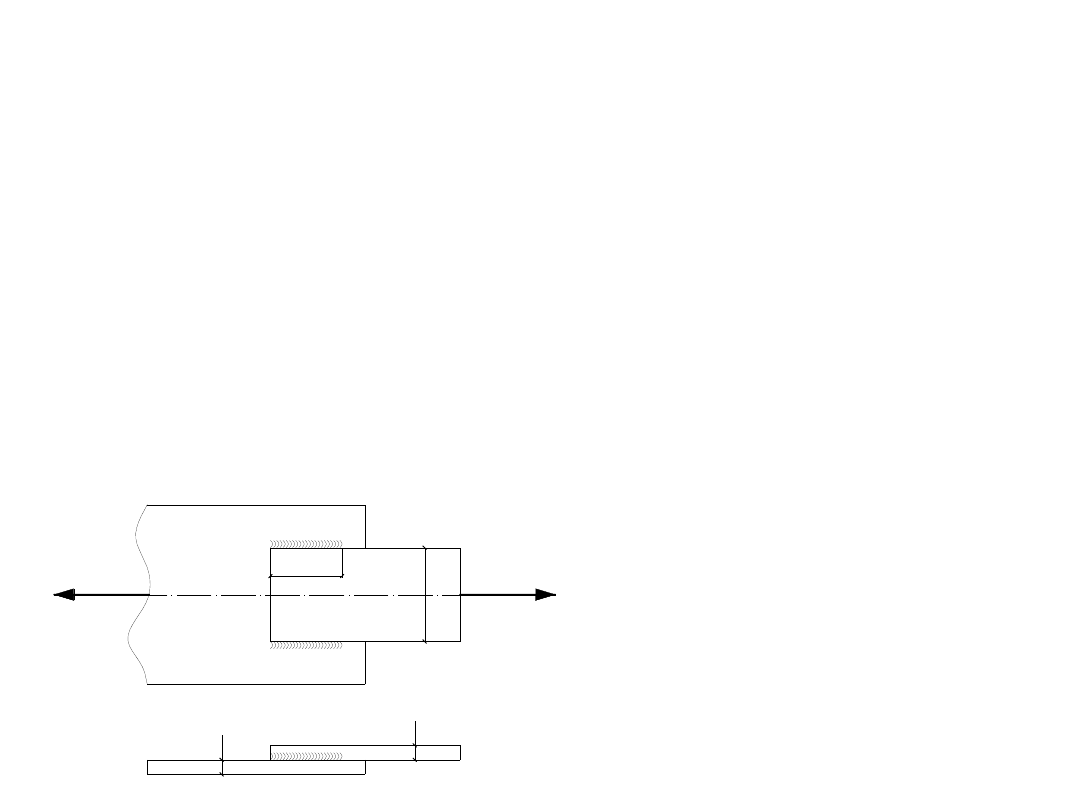
 sprawdzenie wymogów dotyczących wymiarów spoin

(p.6.3.2.2.a)

:

W treści zadania przyjęto spoinę a = 4 mm.

Warunek spełniony!

l

1

b

g

1

g

2

P

P

mm

mm

lecz

t

5

,

2

10

,

2

,

0

2







nom

a

}

{

mm

t

16

7

,

0

1



































mm

mm

mm

t

mm

a

mm

mm

mm

t

nom

16

6

,

5

8

7

,

0

7

,

0

4

5

,

2

2

10

2

,

0

2

,

0

1

2

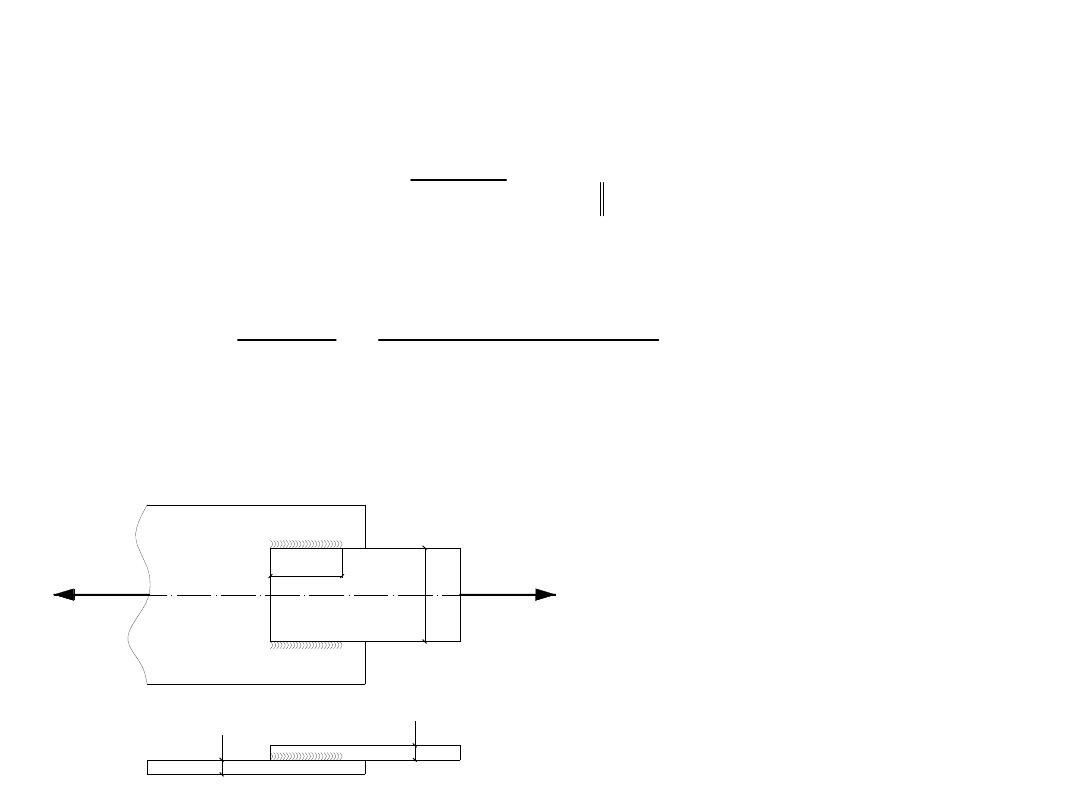
Przystępujemy do obliczeń wytrzymałościowych spoin:

Nośność połączeń zakładkowych przy obciążeniu osiowym obliczamy
z zależności:

l

1

b

g

1

g

2

P

P

Cieńszy element ma grubość g

1

= 8 mm.

30 · g

1

= 30 · 8 = 240 mm

b = 180 mm ≤ 30 g = 240
mm

warunek spełniony!

d

f

l

a

F















MPa

m

m

N

l

a

P

6

,

173

18

,

0

004

,

0

2

10

250

2

3



















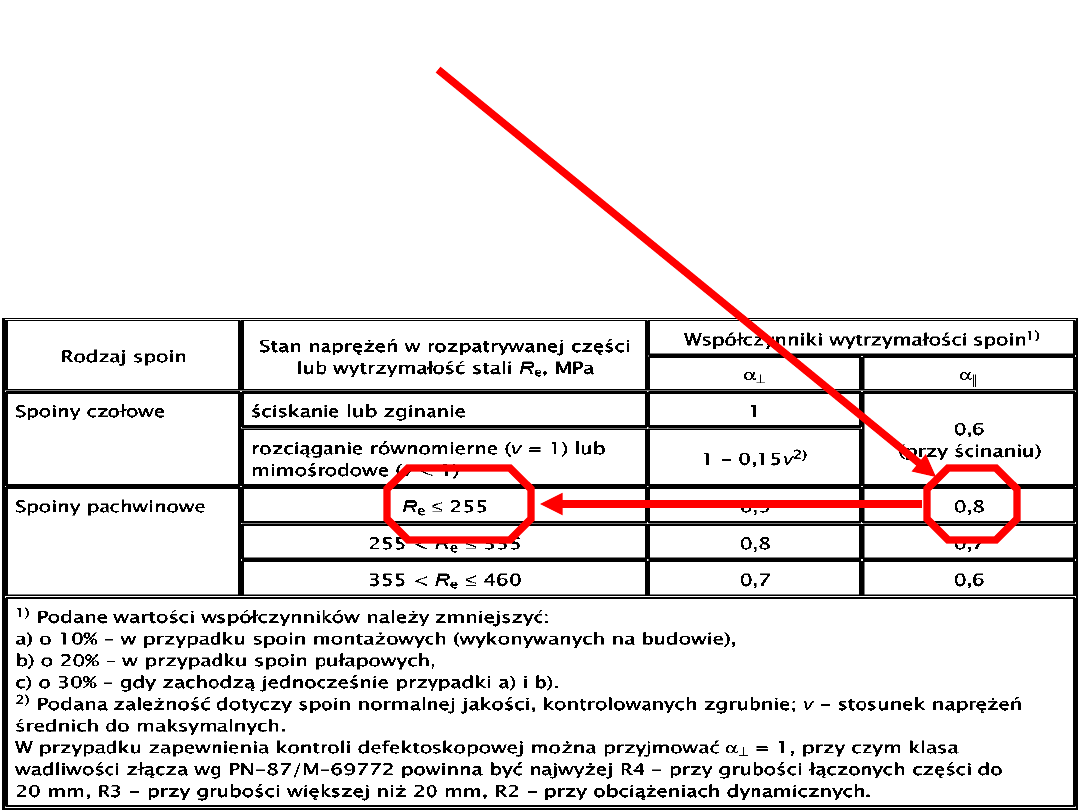
α

II

· f

d

= 0,8 · 215 MPa = 172 MPa

α

II

· f

d

= 0,8 · 215 MPa = 172 MPa

τ = 173,6 MPa > α

II

· f

d

= 172 MPa

WARUNEK NIESPEŁNIONY!!!

Maksymalna grubość wg. warunków normowych a

max

=5,6

mm – dlatego jedynym wyjściem jest zwiększenie
długości spoin.

Zwiększamy spoinę o 20 mm



l

1

= 200 mm.

MPa

m

m

N

l

a

P

156

2

,

0

004

,

0

2

10

250

2

3



















τ = 156 MPa < α

II

· f

d

= 172 MPa

WARUNEK SPEŁNIONY!!!

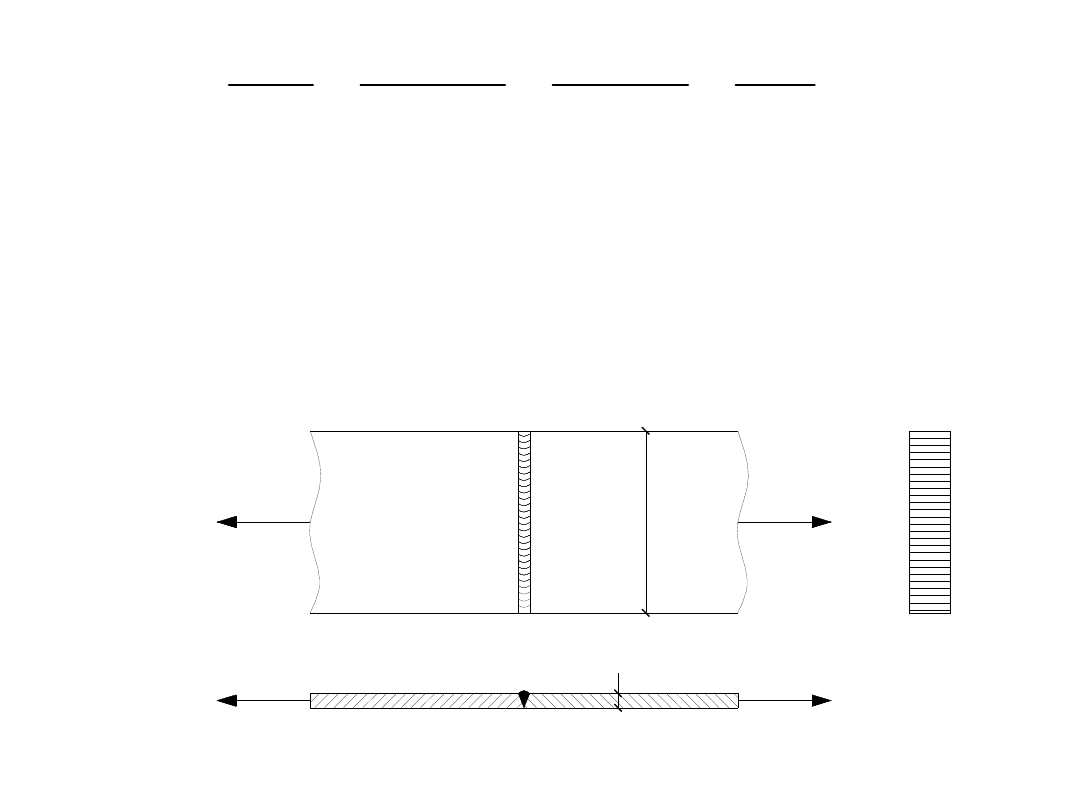
Zadanie 2.

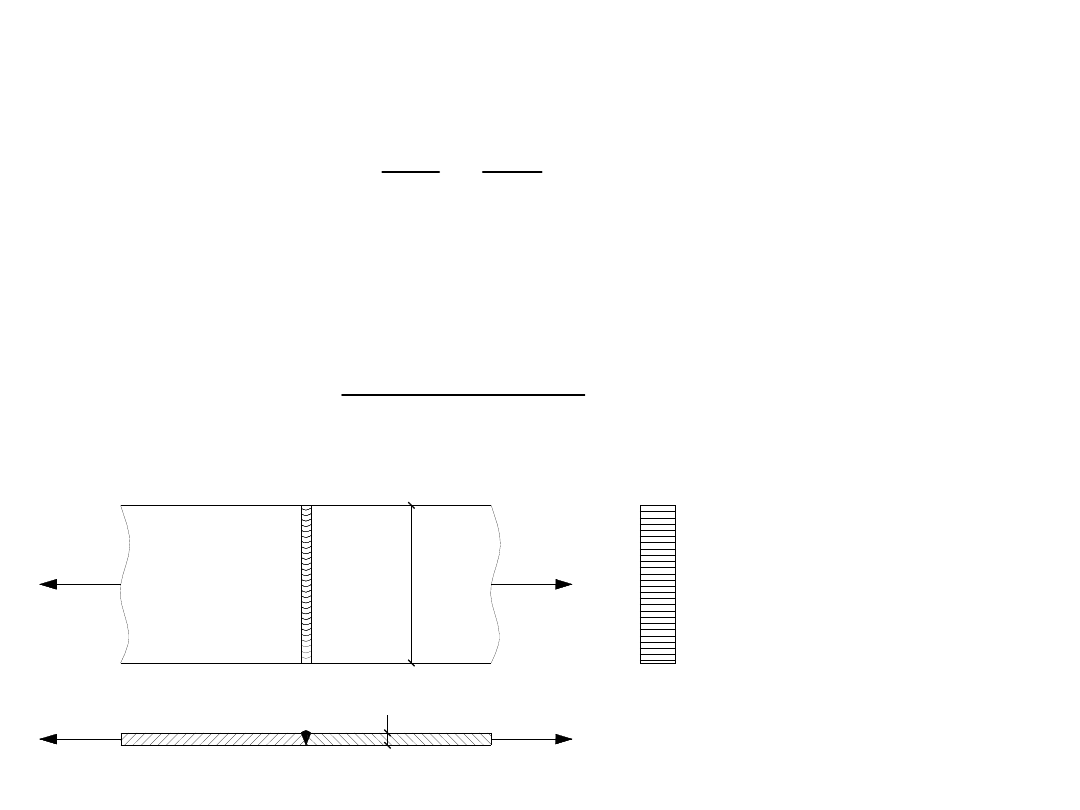
Sprawdzić nośność spoiny kontrolowanej zgrubnie w osiowo
rozciąganym styku płaskownika o przekroju 180 x 8 mm ze stali
St4 VX. Spoina jest wykonana bez kraterów końcowych (przy
użyciu płytek wybiegowych). Siła P=260 kN; wymiary spoiny:
a=8mm; l=180mm; przyjąć: f

d

=235 MPa.

P

P

P

18

0

P

8



P

P

P

18

0

P

8



Naprężenia w połączeniu tego typu (na spoinę czołową)
obliczamy wg. zależności:

d

sp

f

l

a

P

A

P

















Zgodnie z tym, co jest napisane w treści zadania a = 8
mm; l = 180 mm;

MPa

m

m

N

181

18

,

0

008

,

0

10

260

3











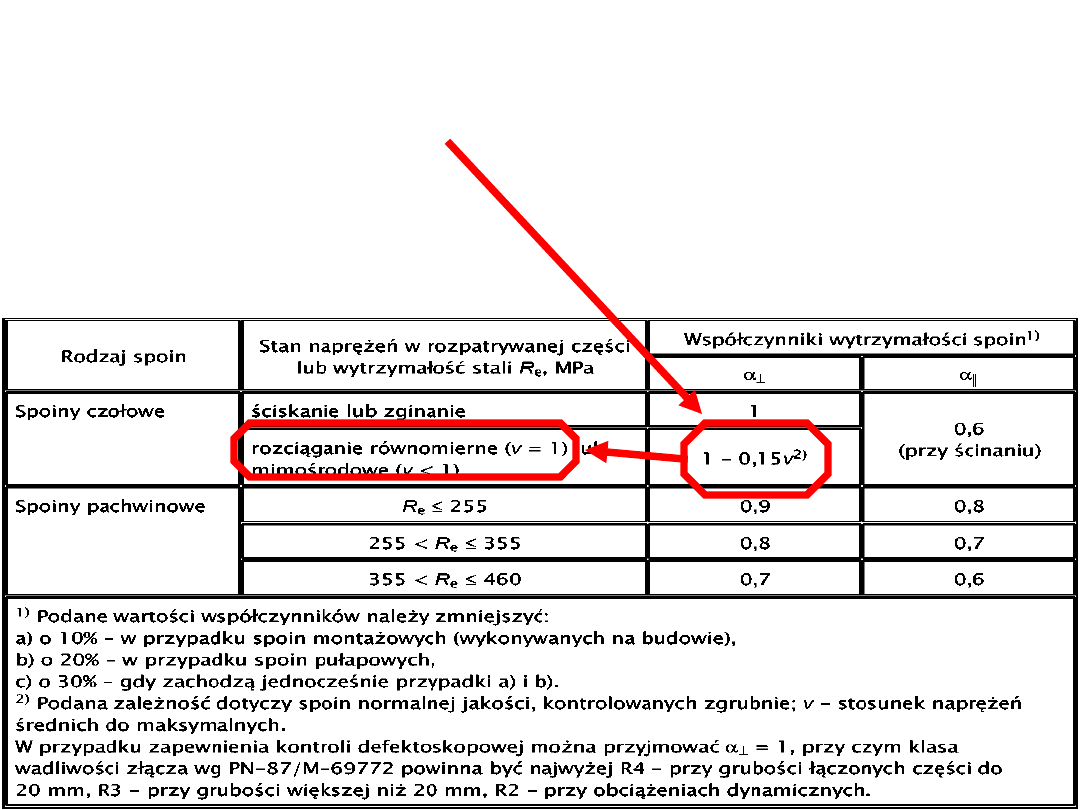
Aby nośność połączenia była zachowana, musi być
spełniony warunek:

Skoro jest to spoina czołowa, rozciągana równomiernie:

MPa

MPa

f

d

200

235

85

,

0

















σ

g

= σ

d

= σ

α

┴

= 1 – 0,15 · ν = 1 – 0,15 · 1 = 1 – 0,15 = 0,85

P

P

P

18

0

P

8



g



d

1

2

2

2

2

max













































g

d

g

śr

MPa

f

MPa

d

200

181















WARUNEK SPEŁNIONY!!!

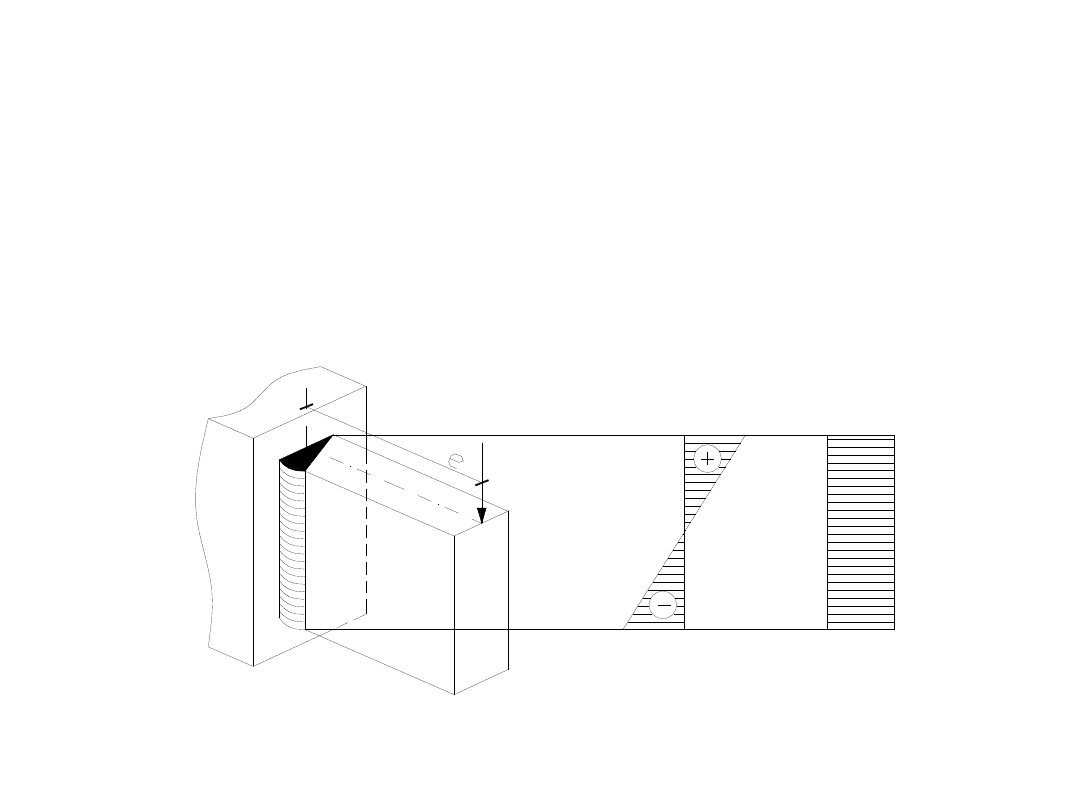
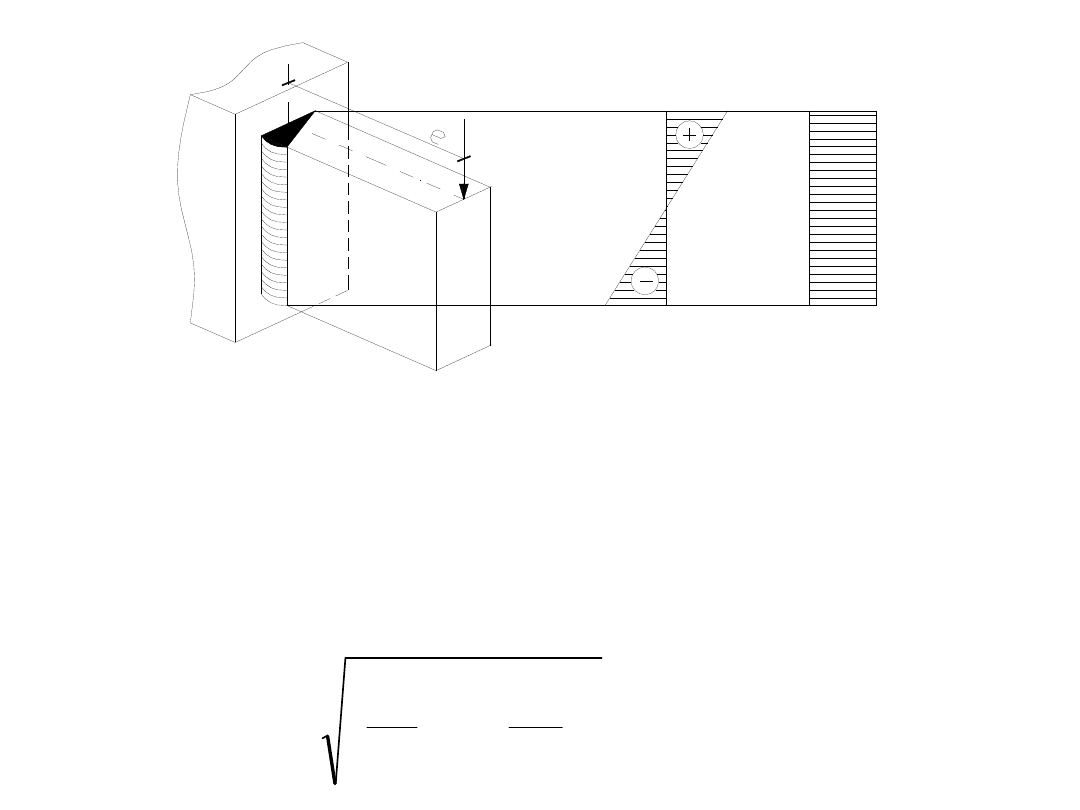
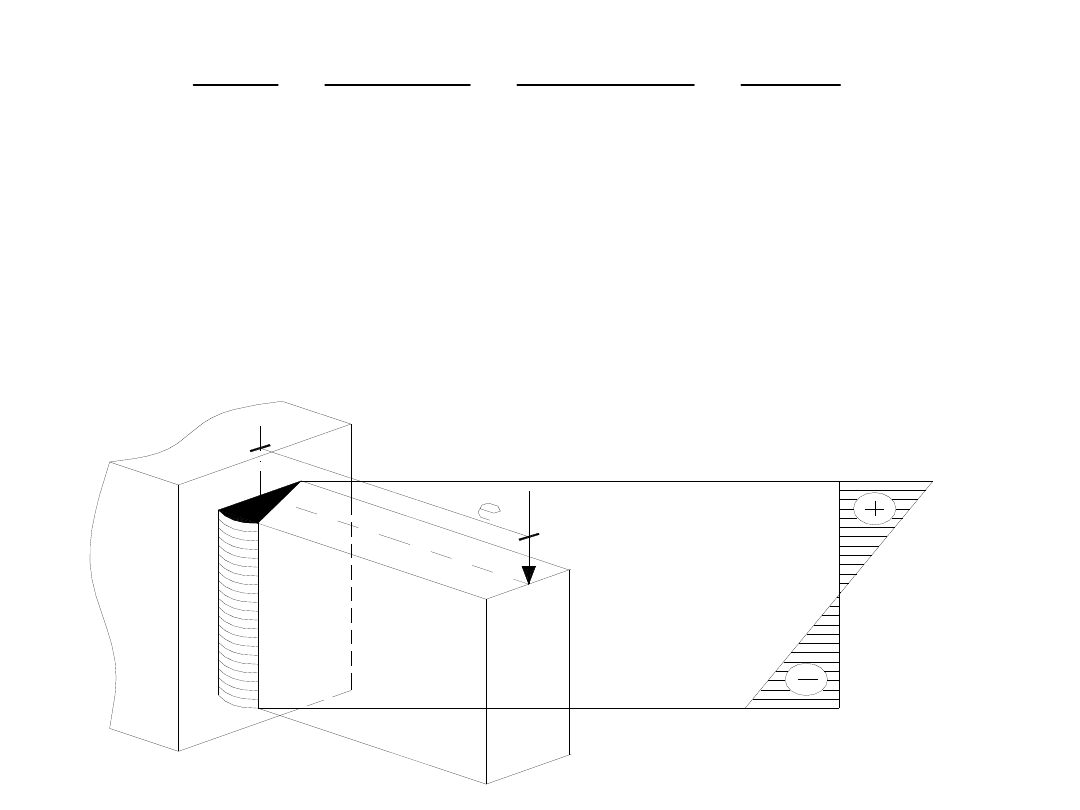
Zadanie 3.

Sprawdzić nośność spoiny czołowej kontrolowanej zgrubnie, łączącej
wspornik
ze słupem. Spoina jest wykonana bez kraterów końcowych.
Wspornik i słup są ze stali St3SY. Wspornik z blachy o grubości
g=10 mm i wysokości h=200 mm jest obciążony siłą P=80 kN w
odległości e = 160 mm od lica słupa. Wytrzymałość obliczeniowa
stali St3SY: f

d

=215 MPa.

P





P





Zgodnie z tym, co przedstawia schemat do zadania, spoina będzie
ścinana siłą P i zginana momentem M, który jest wynikiem działania
siły P na ramieniu e.

Moment M = P · e = 80kN · 0,16m = 12,8 kNm

Skoro spoina jest jednocześnie ścinana i zginana, należy obliczyć
naprężenia zastępcze według wzoru (92) PN:

fd

II































2

2









d

sp

f

W

M













d

II

sp

f

A

P











2

002

,

0

2

,

0

01

,

0

m

m

m

h

a

A

sp











3

6

2

2

10

67

,

66

6

2

,

0

01

,

0

6

m

h

a

W

sp













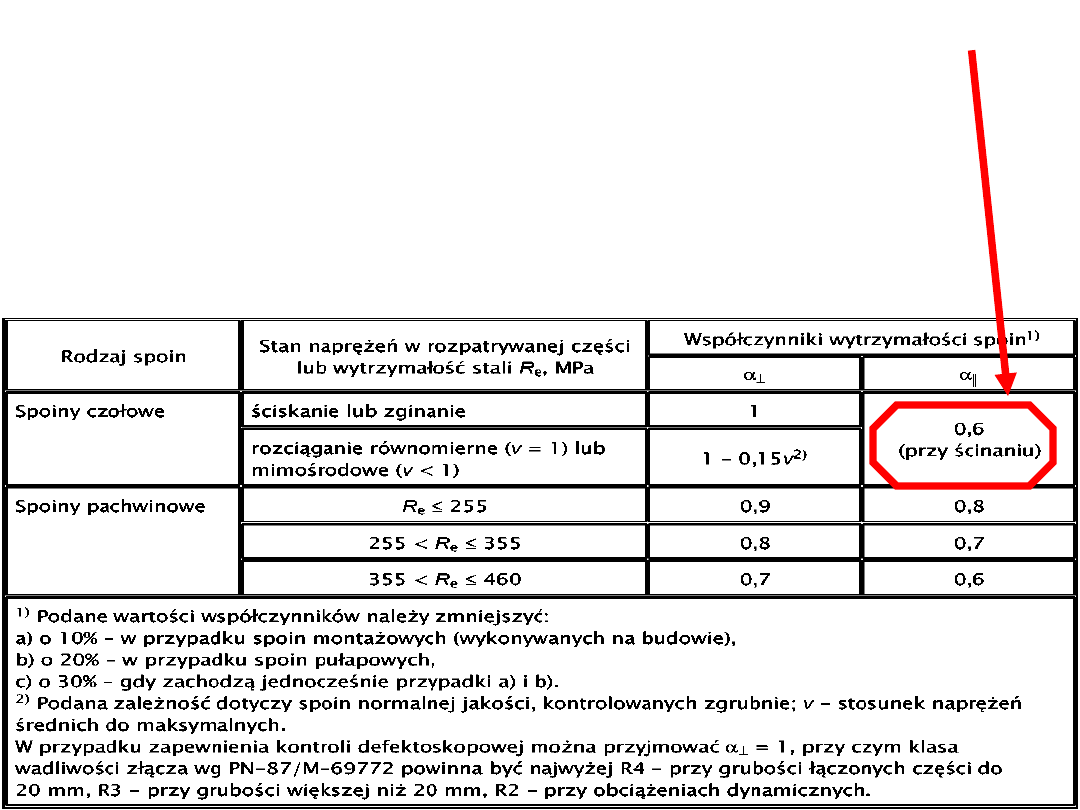
Ponieważ naprężenia styczne pochodzą od ścinania
spoiny – α

II

= 0,6 – stały współczynnik dla ścinania w

spoinach czołowych.

Naprężenia normalne w spoinie są wywołane momentem,
czyli nasza spoina jest zginana. Wg tablicy 18 PN90/B-
03200, α

┴

= 1.

σ

g

= -σ

d

α

┴

= 1 – 0,15 · ν = 1 – 0,15 · 0 = 1 – 0 = 1

0

2

0

2

2

max























g

g

d

d

g

d

g

śr





















P



g



d

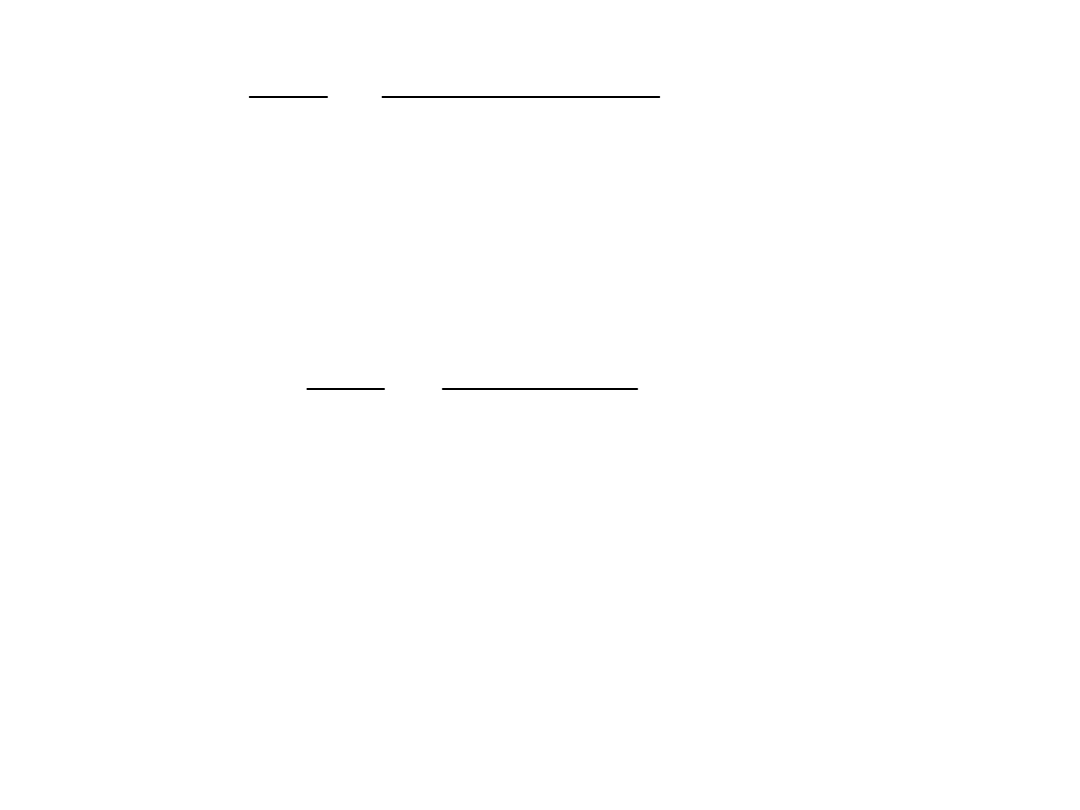
MPa

m

kNm

W

M

sp

192

10

67

,

66

8

,

12

3

6











MPa

m

kN

A

P

sp

40

002

,

0

80

2









MPa

MPa

f

MPa

d

215

215

0

,

1

192



















MPa

MPa

f

MPa

d

II

129

215

6

,

0

40

















WARUNKI SPEŁNIONE!!!

Należy jeszcze sprawdzić naprężenia zastępcze w
spoinie:

WARUNEK SPEŁNIONY!!!

Spoina czołowa łącząca wspornik ze słupem spełnia

warunek nośności.

MPa

f

MPa

d

II

215

203

6

,

0

40

0

,

1

192

2

2

2

2







































































P

5 x 200

5 x 200

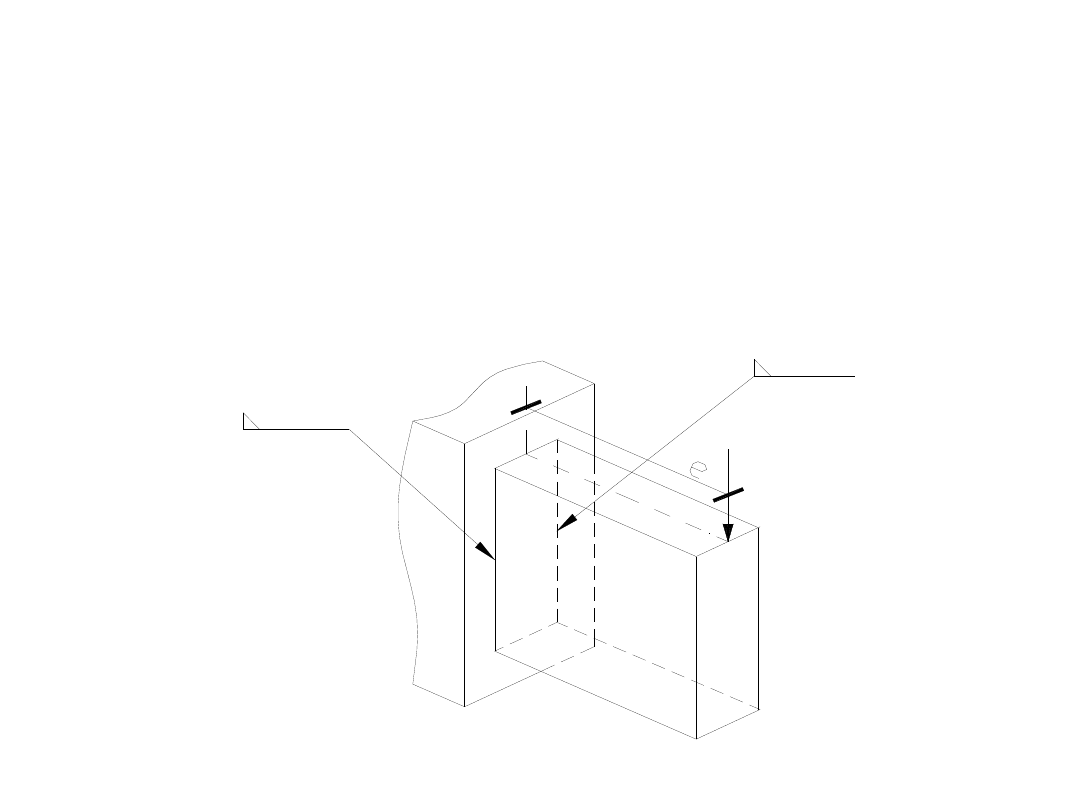
Zadanie 4.

Sprawdzić nośność teowego połączenia płaskownika ze słupe,
przyspawanego dwiema spoinami pachwinowymi o grubości a=5
mm i długości l

1

= 200mm. Materiał elementów: St3SY: f

d

=215

MPa (R

e

<255 MPa). Wspornik z blachy o grubości

g=10 mm i wysokości h=200 mm jest obciążony siłą P=80 kN w
odległości
e = 160 mm od lica słupa.

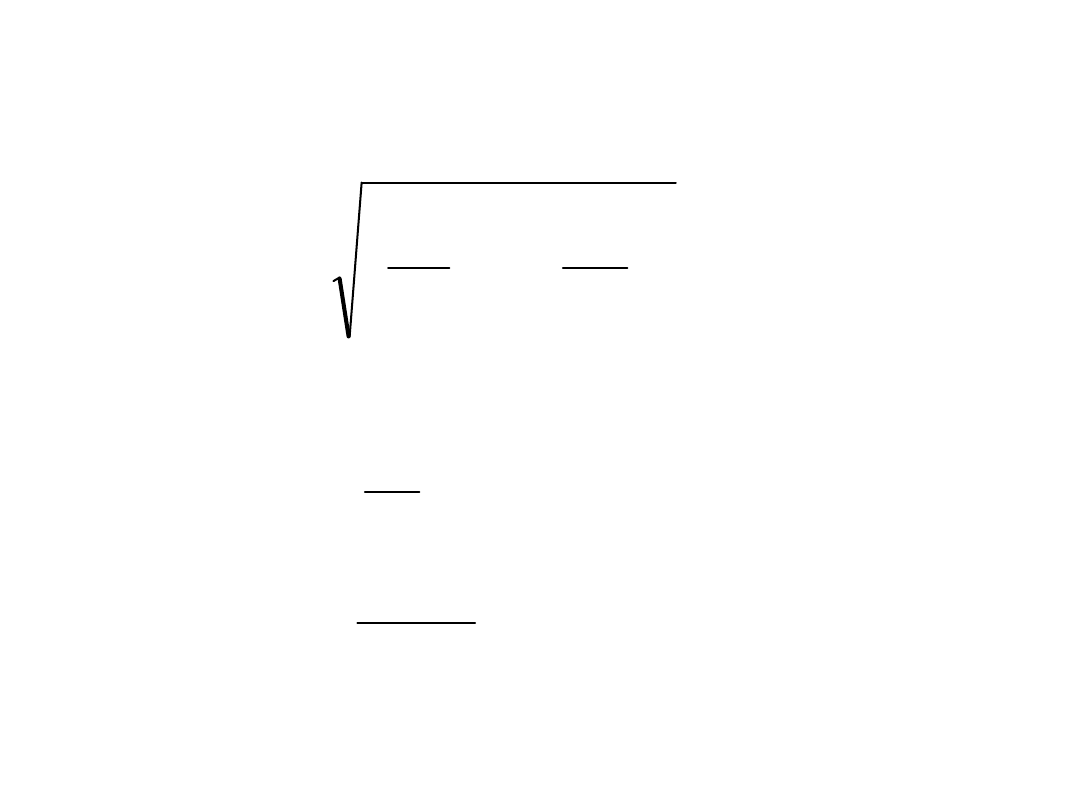
Warunek nośności spoin pachwinowych w połączeniu
teowym sprawdza się wg wzoru:

l

a

V

W

M

f

M

d

II

V

M









































2

:

gdzie

V

2

2















Obliczamy wskaźnik przekroju spoin pachwinowych:

kNm

e

P

M

m

cm

W

80

,

12

16

,

0

80

;

10

67

,

66

67

,

66

6

20

5

,

0

2

3

6

3

2

























MPa

l

a

V

MPa

W

M

M

40

20

,

0

005

,

0

2

10

80

2

192

99

,

191

10

66,67

10

12,80

3

V

6

-

3

































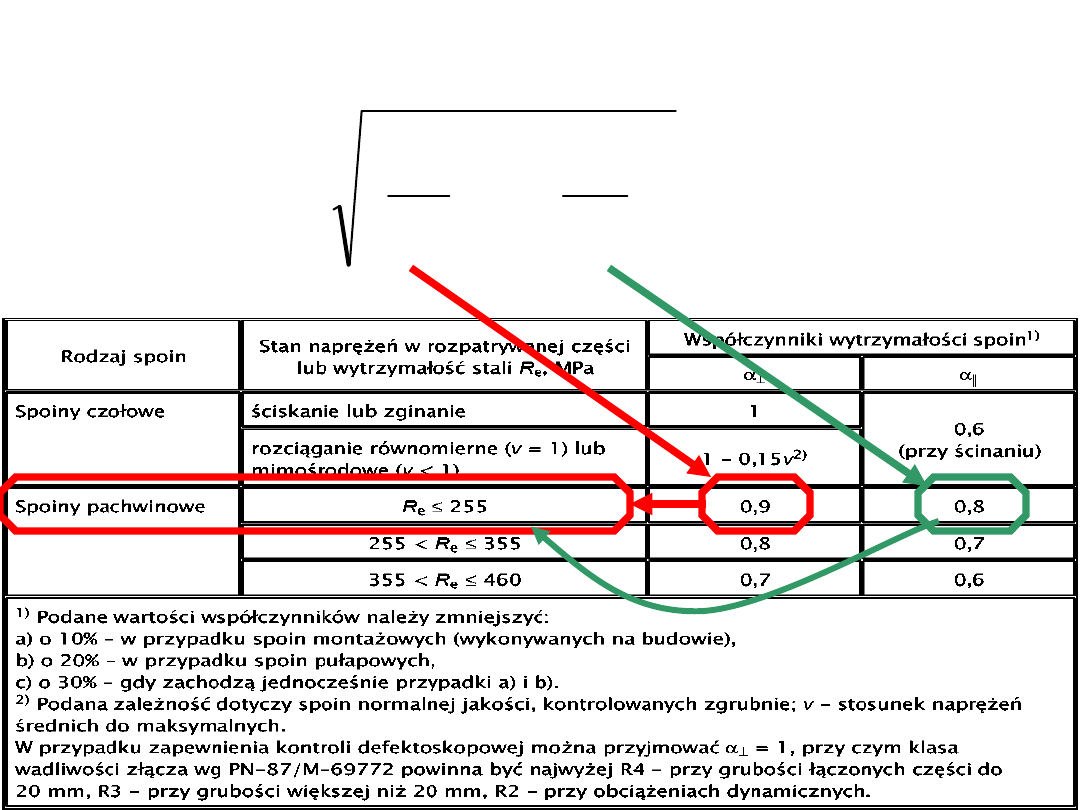
d

II

V

M

f

































2

2











W celu obliczenia naprężeń wypadkowych należy dobrać
odpowiednie współczynniki obliczeniowe wytrzymałości
spoin:

MPa

f

MPa

d

215

1

,

219

8

,

0

40

9

,

0

192

2

2





































WARUNEK NIESPEŁNIONY – NOŚNOŚĆ

PRZEKROCZONA!!!

Wobec powyższego należy zwiększyć pole przekroju
spoin. Możemy to wykonać przez zwiększenie grubości
(nie mamy możliwości wydłużenia spoiny). Zakładamy
nową grubość spoiny: a = 6 mm. Obliczamy ponownie
wskaźnik bezpieczeństwa przekroju spoiny:

;

10

0

,

80

80

6

20

6

,

0

2

3

6

3

2

m

cm

W















MPa

l

a

V

MPa

W

M

M

3

,

33

20

,

0

006

,

0

2

10

80

2

160

10

0

,

0

8

10

12,80

3

V

6

-

3































Ponownie przeliczamy naprężenia styczne cząstkowe:

MPa

f

MPa

d

215

6

,

182

8

,

0

33

9

,

0

160

2

2





































WARUNEK SPEŁNIONY – NOŚNOŚĆ ZAPEWNIONA!!!

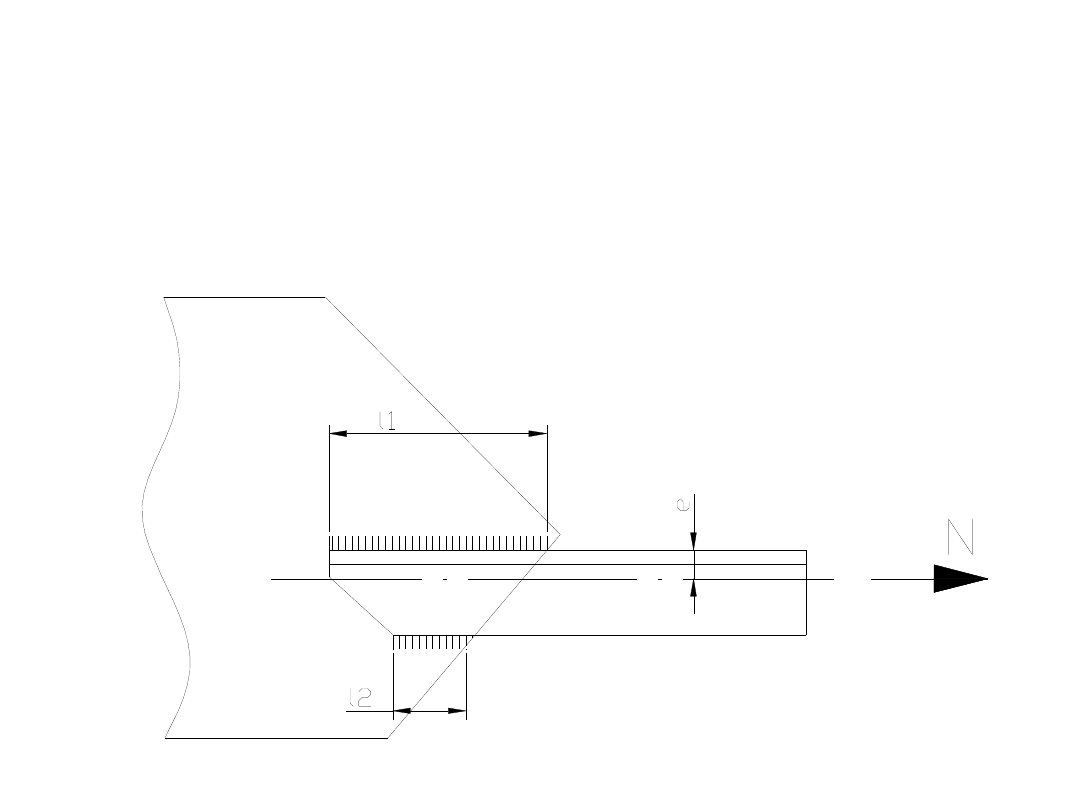
Zadanie 5.

Zaprojektować ze względu na nośność pręta
rozciąganego spawane połączenie pojedynczego
kątownika L

65 x 65 x 7 z blachą węzłową o grubości 8

mm. Przyjąć stal St3S (f

d

= 215 MPa; R

e

=235 MPa);

dla kątownika dane przyjąć z tablic.

Dane z tablicy (PN-81/H-93401):

Pole przekroju A = 8,70 cm

2

; e = 1,85 cm; g = 7 mm;

a = 65 mm;

Zgodnie z tym, co mówi PN w punkcie

4.3.1.b

.

(„Zamocowane mimośrodowo pręty pojedyncze:

(„Zamocowane mimośrodowo pręty pojedyncze:

kątowniki zamocowane jednym ramieniem, ceowniki

kątowniki zamocowane jednym ramieniem, ceowniki

zamocowane środnikiem oraz teowniki zamocowane

zamocowane środnikiem oraz teowniki zamocowane

półką można traktować jak osiowo obciążone pod

półką można traktować jak osiowo obciążone pod

warunkiem, że przyjmie się sprowadzone pole przekroju

warunkiem, że przyjmie się sprowadzone pole przekroju

A

A

ψ

ψ

wg. wzoru:”)

wg. wzoru:”)

2

2

1

1

1

3

3

A

A

A

A

A

A















2

2

1

1

1

3

3

A

A

A

A

A

A















A

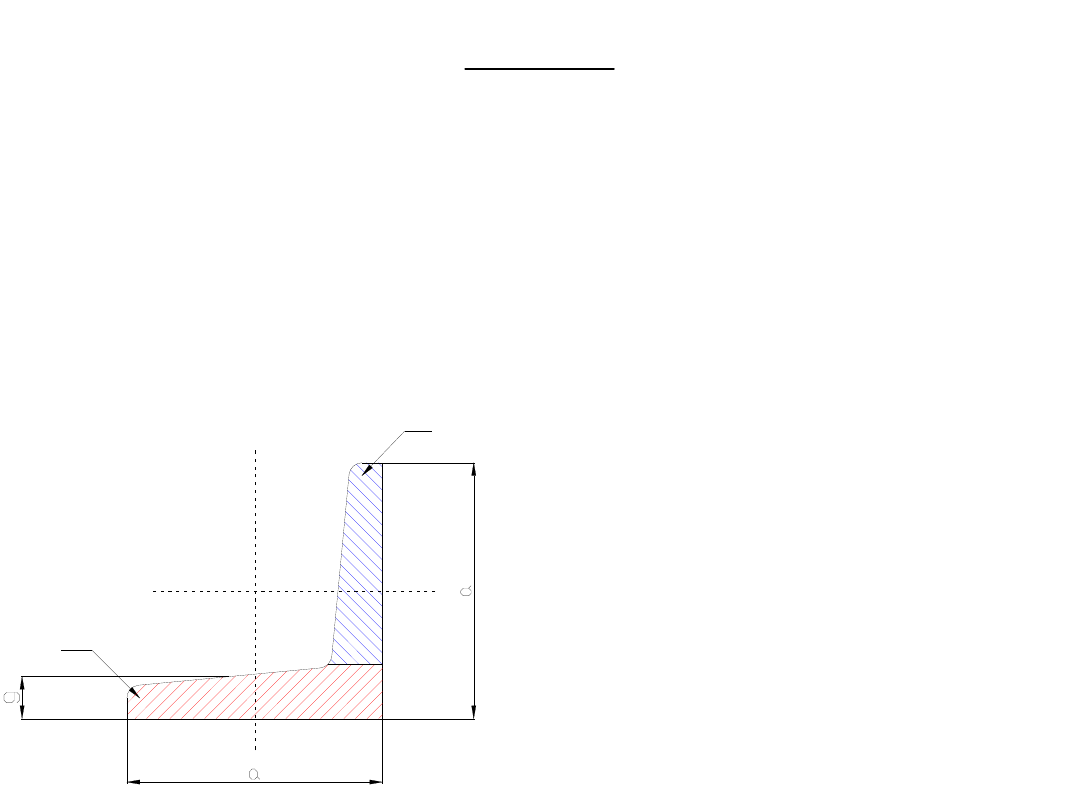
1

– pole przekroju części przylgowej kształtownika – w

naszym przypadku brutto – ponieważ stosuje się
połączenie spawane;

A

2

– pole przekroju części odstającej kształtownika

A

1

y

x

y

A

2

2

4

2

2

4

2

4

1

2

2

4

1

1

10

15

,

4

10

55

,

4

10

7

,

8

10

55

,

4

065

,

0

007

,

0

m

A

m

m

A

A

A

m

m

m

A

a

g

A





































2

4

2

2

1

1

1

10

73

,

7

15

,

4

15

,

4

55

,

4

3

55

,

4

3

55

,

4

3

3

m

A

A

A

A

A

A

A



































Mając policzone sprowadzone pole przekroju pręta –
obliczamy jego nośność na rozciąganie:

kN

kPa

m

f

A

N

d

2

,

166

10

215

10

73

,

7

3

2

4



















Następnie należy sprawdzić warunki normowe dla spoin:

Przyjęto do dalszych obliczeń a = 4 mm.

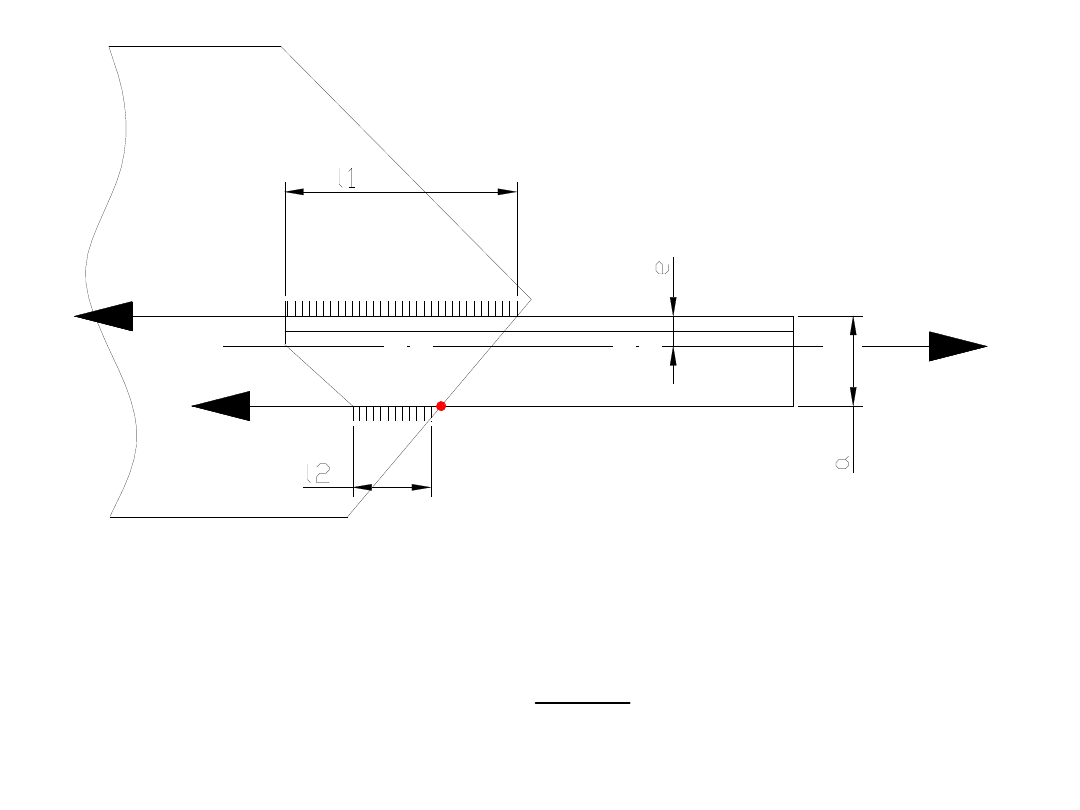
Następnie należy obliczyć obciążenie spoin. Kątownik
będzie rozciągany mimośrodowo, dlatego siły
przypadające na poszczególne spoiny będą różne.

Ich różnicę można policzyć na podstawie odczytanego z
tablic mimośrodu dla kątownika e.

Wyliczamy to z zależności:



































mm

mm

mm

t

a

mm

mm

mm

t

nom

16

9

,

4

7

7

,

0

7

,

0

5

,

2

6

,

1

8

2

,

0

2

,

0

1

2

a

e

a

N

P







1

P

1

N

P

2

A

0

)

(

0

1

















e

a

N

a

P

M

A

a

e

N

P





2

P

1

N

P

2

A

N

P

a

e

a

N

N

P

P

X





















2

2

1

0

kN

kN

a

e

a

N

P

9

,

118

65

5

,

18

65

2

,

166

1















kN

kN

a

e

N

P

3

,

47

65

5

,

18

2

,

166

2











Niezbędną, minimalną długość spoin wyliczymy
przekształcając wzór na naprężenia w połączeniu
zakładkowym:

i

d

II

i

i

d

II

a

f

P

l

f

l

a

P























a

f

P

l

a

f

P

l

d

II

d

II

















2

2

1

1

;

m

a

f

P

l

m

a

f

P

l

d

II

d

II

069

,

0

004

,

0

10

215

8

,

0

10

3

,

47

173

,

0

004

,

0

10

215

8

,

0

10

9

,

118

6

3

2

2

6

3

1

1









































Przyjęto spoiny:

-l

1

= 17,5 cm;

-l

2

= 7 cm;

Należy teraz sprawdzić warunki normowe określone

w punkcie 6.3.2.2. PN-90/B-03200























;

65

;

40

4

10

10

;

40

max

min

mm

b

mm

a

mm

l

WARUNEK SPEŁNIONY!!!

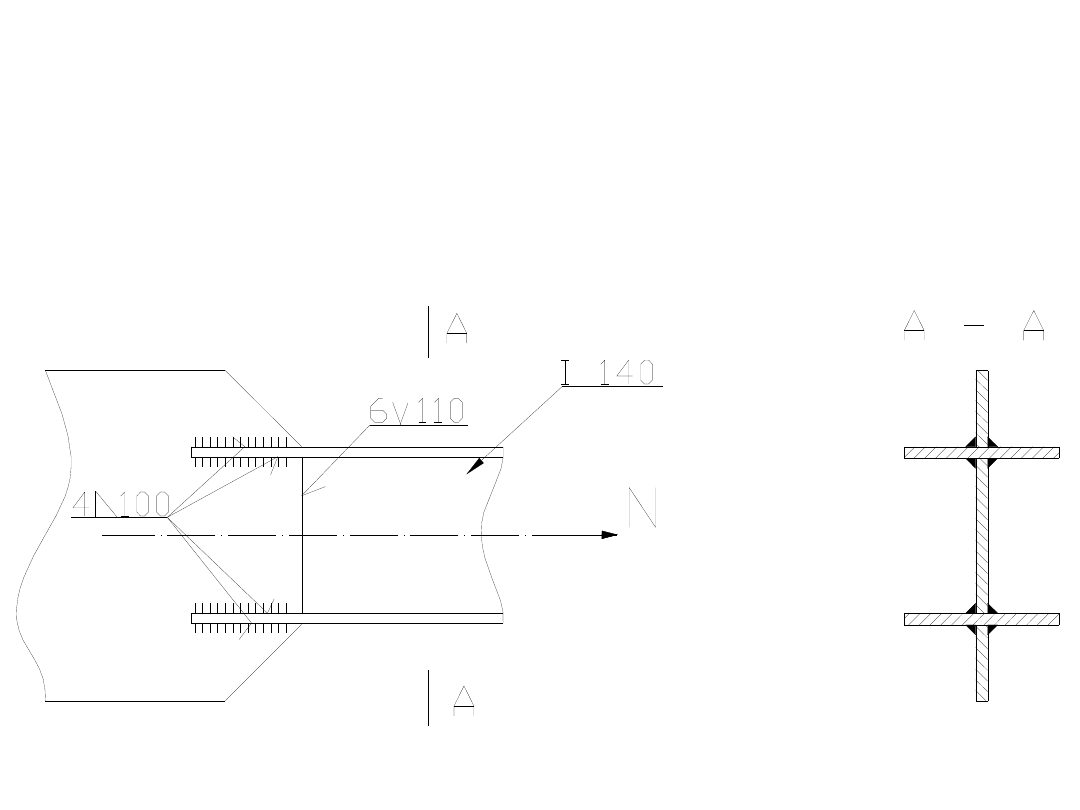
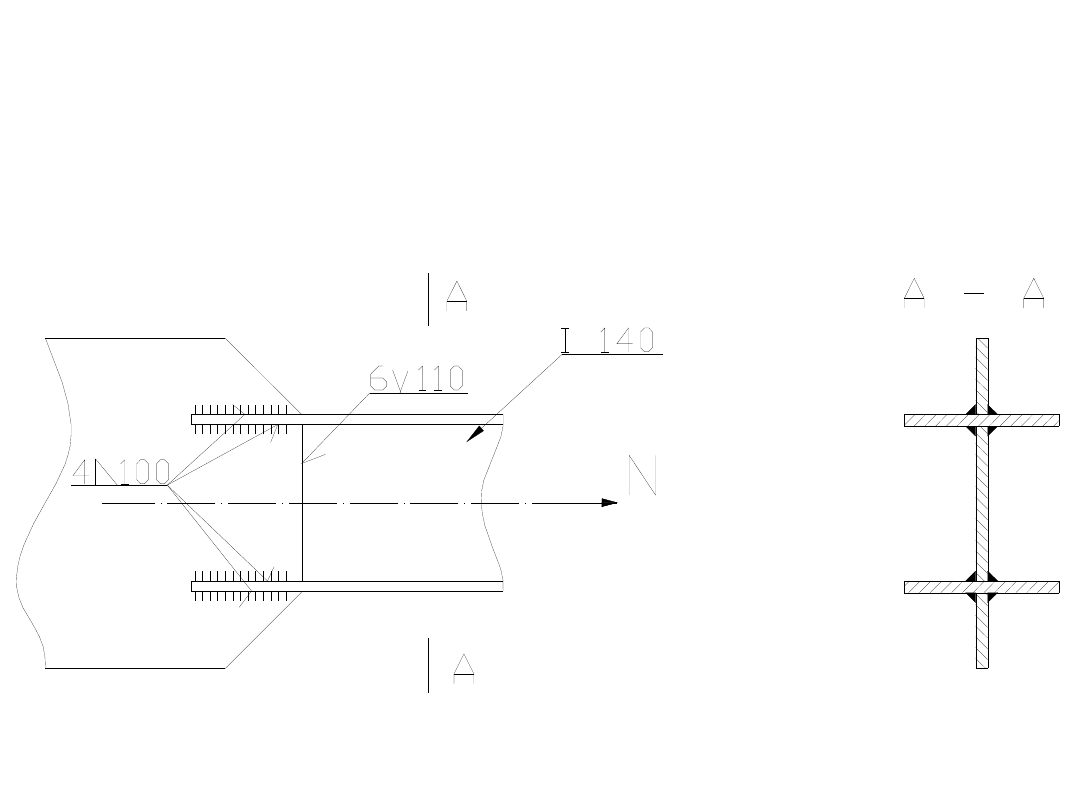
Zadanie 6.

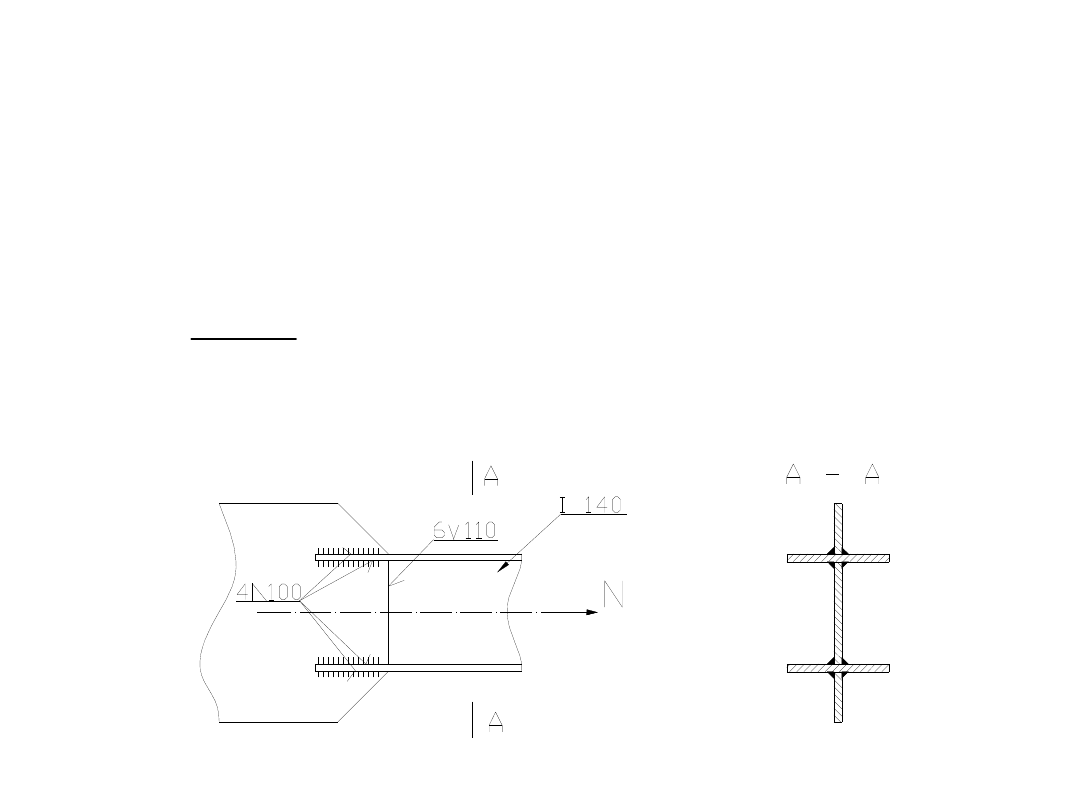
Sprawdzić nośność połączenia dwuteownika I 140 z
blachą węzłową, obciążonego siłą P= 460 kN. Stal
18G2. Spoiny kontrolowane zgrubnie. Obciążenie ma
charakter statyczny.

Dwuteownik I 140 ma grubość ścianki g=7mm, na tej
podstawie, widząc, że elementy są wykonane ze stali
18G2, z tabeli 2
PN-90/B-03200 odczytujemy wartości do obliczeń:

-f

d

= 305 MPa;

-R

e

= 355 MPa;

Powyższe wartości będą niezbędne do dalszych obliczeń i
do przyjęcia współczynnika wytrzymałości spoin.

Analizując treść zadania dowiadujemy się, że I140 jest
połączony z blachą węzłową zarówno spoiną pachwinową
jak i czołową.

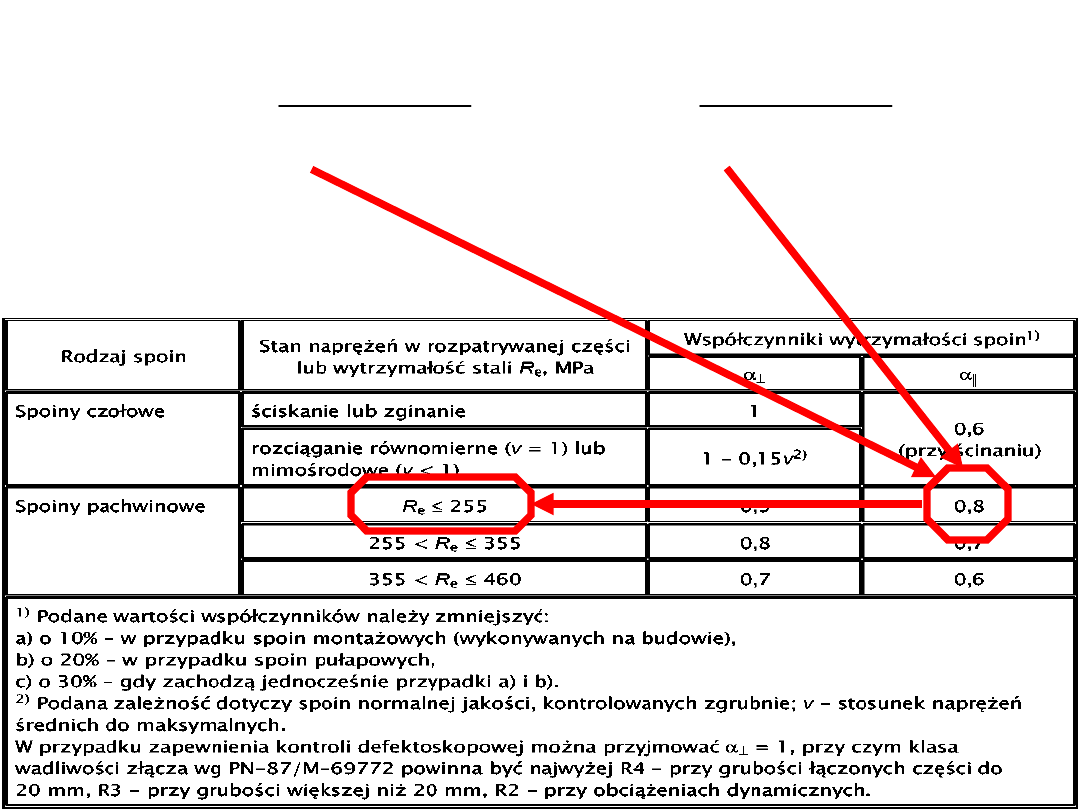
Norma stalowa PN-90/B-03200, w pkt. 6.3.3.1.b mówi,
że:

„Gdy w połączeniu występują spoiny czołowe i
pachwinowe, to w przypadku obciążeń dynamicznych nie
należy uwzględniać w obliczeniach spoin pachwinowych,
natomiast w przypadku obciążeń statycznych nośność
połączenia można ustalać jako sumę nośności spoin
czołowych i 50% nośności spoin pachwinowych.”

W naszym przypadku nośność połączenia będzie sumą
nośności spoin czołowych i połowy nośności spoin
pachwinowych.

Jeżeli oznaczymy sobie za N

1

nośność spoin czołowych, a

za N

2

nośność spoin pachwinowych, to:

N

1

+ N

2

> P – połączenie będzie spełniało I SG – warunek

nośności będzie spełniony;

N

1

+ N

2

< P – warunek nośności nie będzie spełniony;

Spoiny czołowe:

d

sp

d

sp

f

A

N

f

A

N

























1

d

sp

f

A

N











1

Pole przekroju spoiny odczytujemy z rysunku:
A = a · l = 0,006 · 0,11 = 0,00066 m

2;

kN

1

,

171

10

305

85

,

0

00066

,

0

6

1



















d

sp

f

A

N



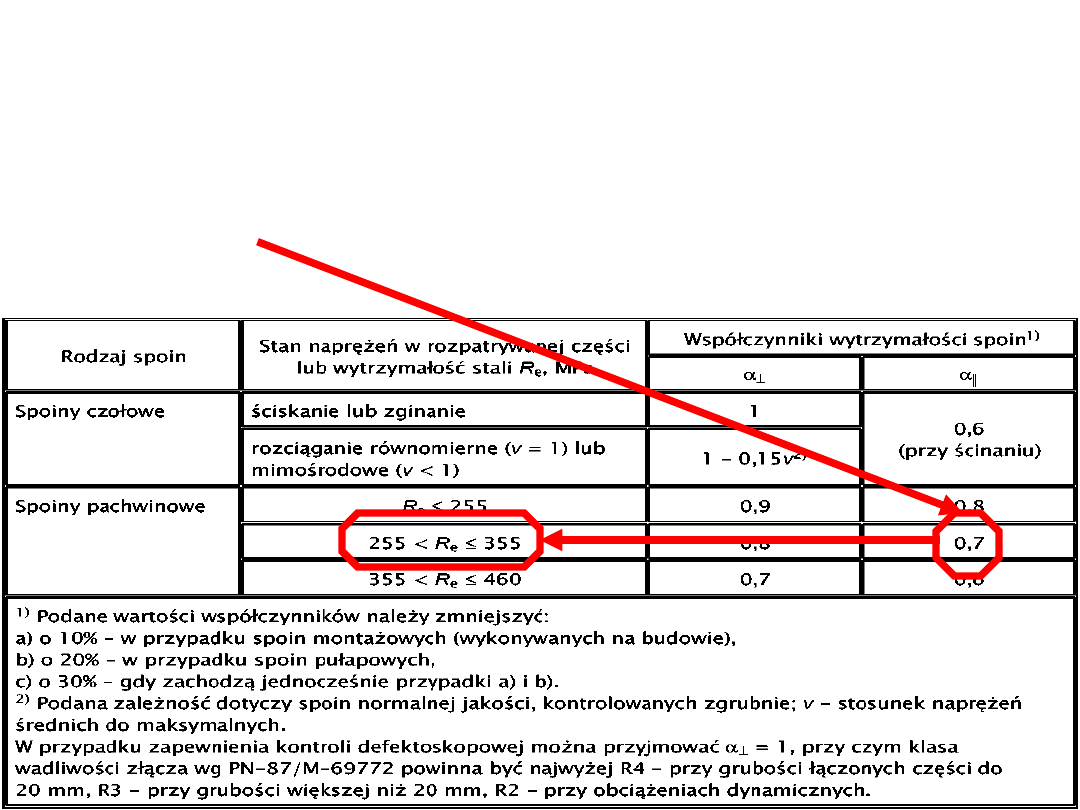
Spoina czołowa jest rozciągana równomiernie na całej
długości, zatem zgodnie z tym, co podaje norma, α

┴

= 1 –

0,15 · ν, a dla rozciągania równomiernego spoiny
czołowej ν = 1, tak więc α

┴

= 0,85.

d

II

d

II

f

l

a

N

f

l

a

N





























8

2

Spoiny pachwinowe.

Zgodnie z tym, co widać na rysunku, połączenie składa
się z ośmiu spoin pachwinowych.

Z rysunku wynika także, że są one ścinane. Tak więc:

Pole przekroju spoiny odczytujemy z rysunku:
a = 4 mm; l = 100 mm;

Współczynnik α

II

dla spoin pachwinowych:

d

II

f

l

a

N













8

2

kN

N

f

l

a

N

d

II

2

,

683

10

305

7

,

0

1

,

0

004

,

0

8

8

2

6

2



























Nośność całego połączenia:

kN

N

N

N

N

7

,

512

2

,

683

%

50

1

,

171

%

50

2

1















N = N

1

+ 50% · N

2

> P –

WARUNEK SPEŁNIONY –

NOŚNOŚĆ POŁĄCZENIA ZAPEWNIONA!!!

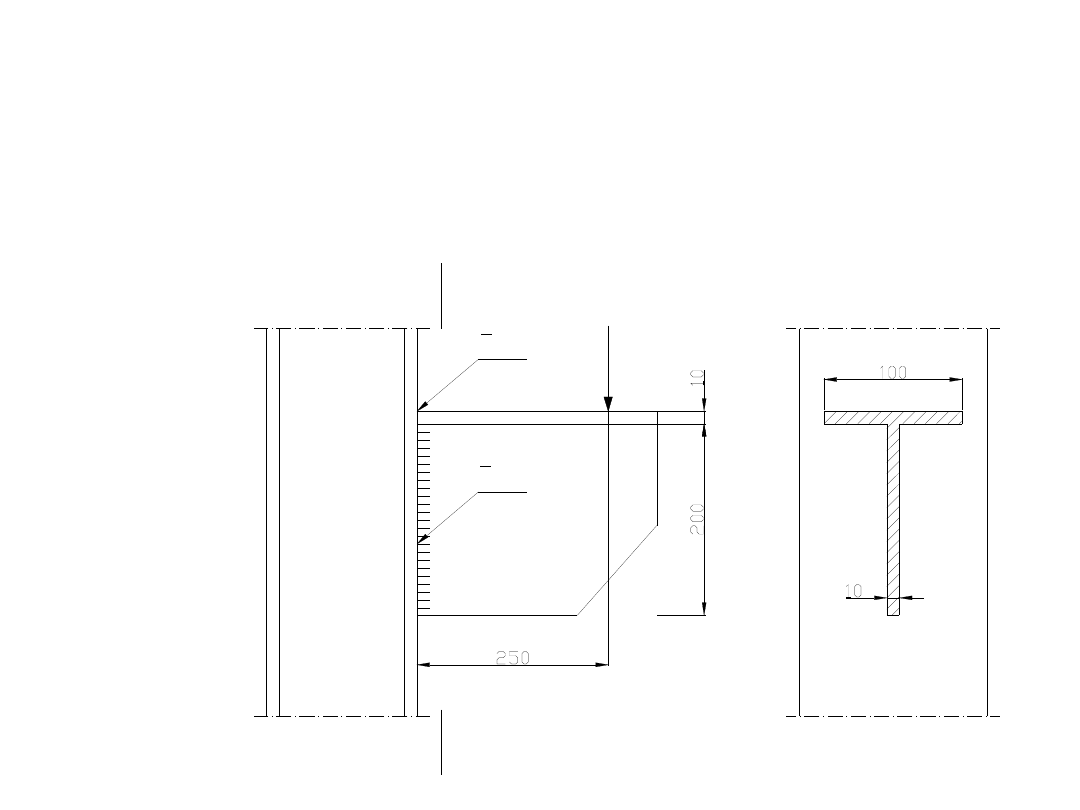
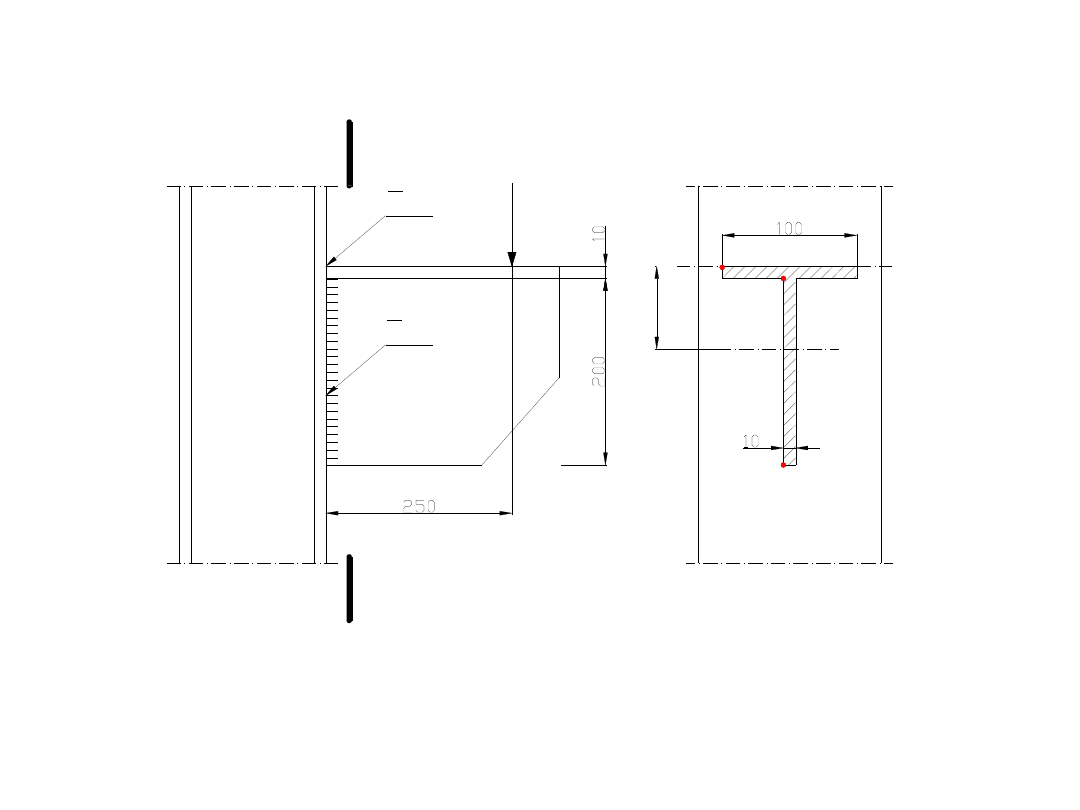
Zadanie 7.

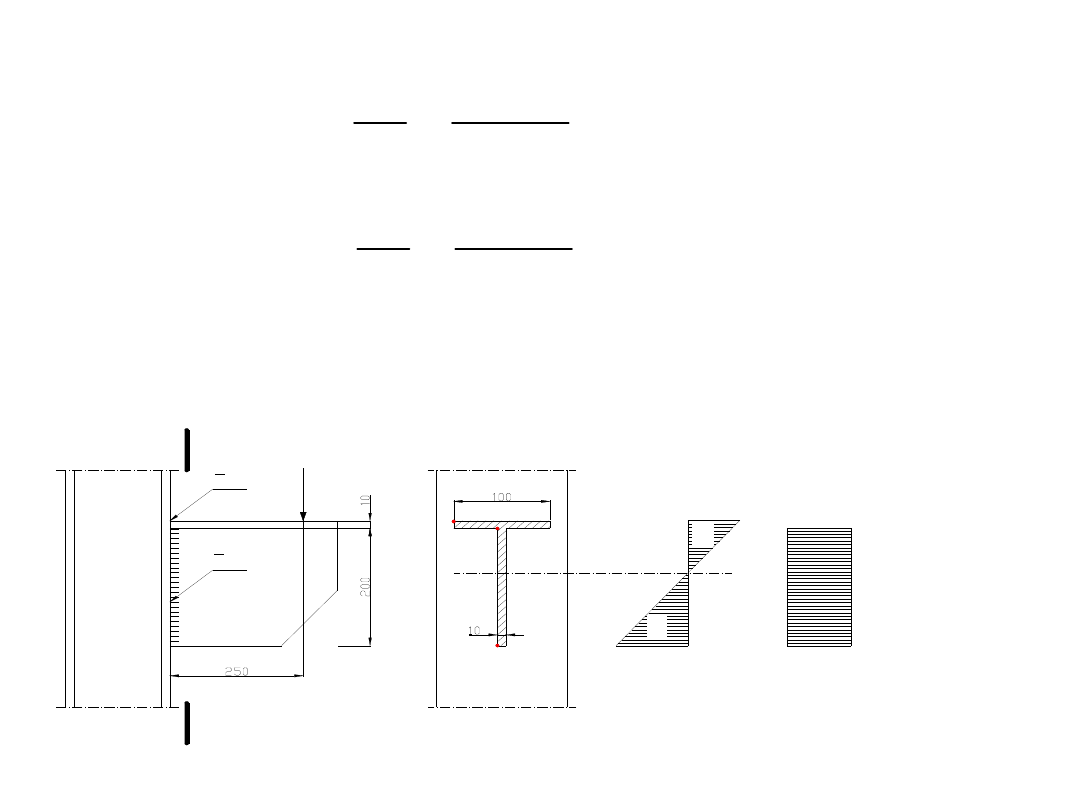
Sprawdzić naprężenia w spoinie czołowej, łączącej
wspornik ze słupem. Wspornik obciążony jest siłą F = 80
kN, ma przekrój teowy, a jego wymiary pokazano na
rysunku. Wspornik wykonano ze stali St3SY o
f

d

= 215 MPa.

A

1

2

V

1

2

V

A

F

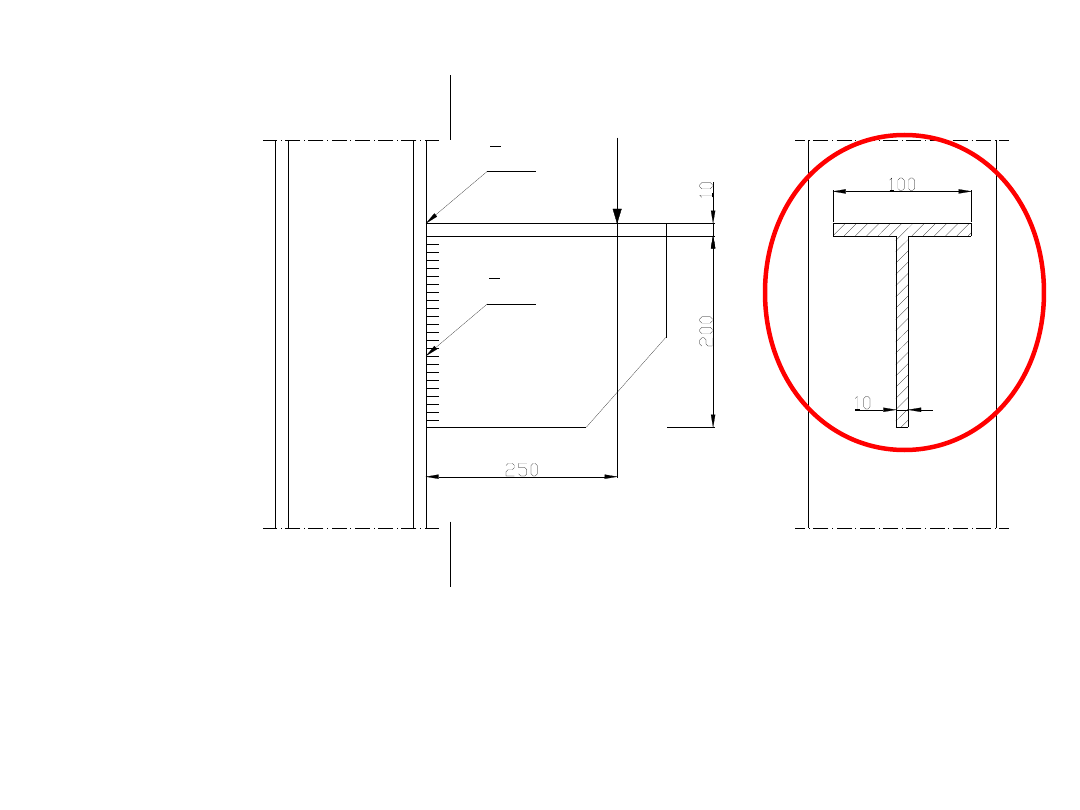
Spoiny czołowe będą miały kształt T.

A

1

2

V

1

2

V

A

F

Z rysunku wynika, że spoiny będą zginane i jednocześnie
ścinane, przy czym do naprężeń ścinających
uwzględniamy tylko spoiny pionowe.

W celu poprawnego policzenia połączenia musimy
wyznaczyć sobie kilka punktów charakterystycznych.

1 – punkt w górnych skrajnych włóknach połączenia;

2 – najniekorzystniejszy punkt przekroju – (punkt
połączenia pasa ze środnikiem);

3 – punkt położony w dolnych, skrajnych włóknach
połączenia;

Położenie środka ciężkości spoin pozwoli nam na
wyznaczenie położenia osi obojętnej oraz poznanie
rzeczywistego charakteru pracy spoin.

A

1

2

V

1

2

V

A

y

o

x

F

x

1

2

3

oś obojętna

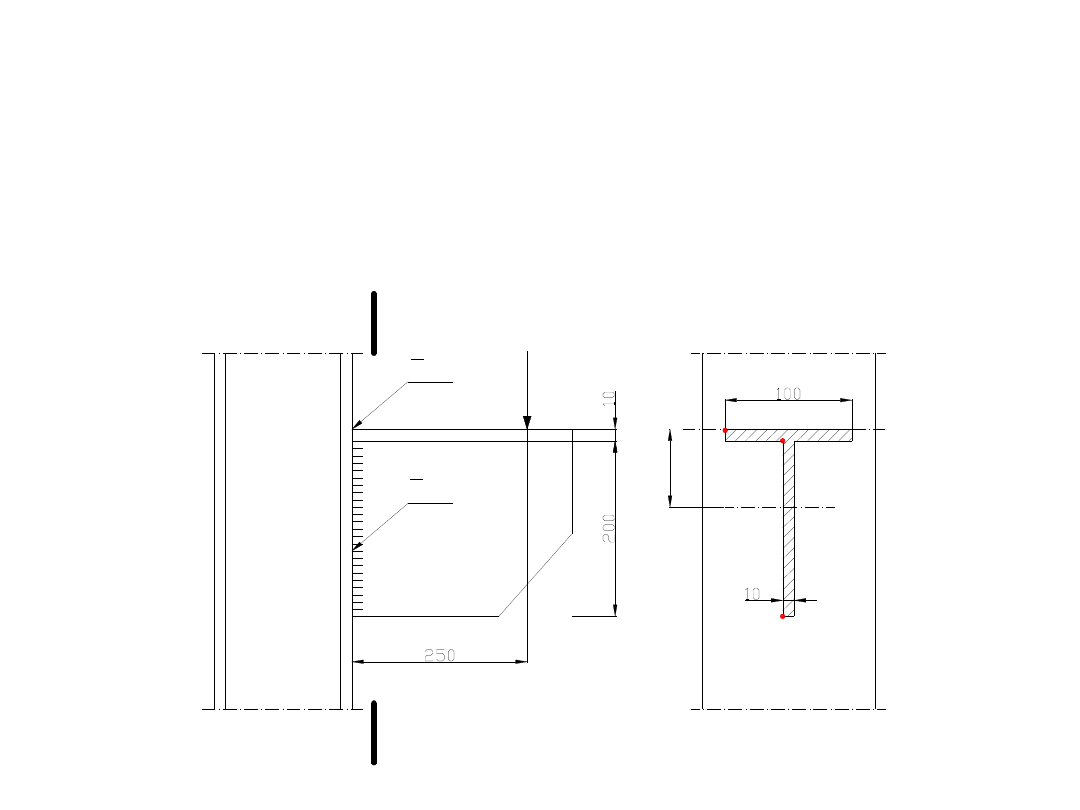
Obliczenia rozpoczniemy os wyznaczenia środka ciężkości spoin i
jednocześnie wyznaczenie położenia osi obojętnej.

Zakładamy oś x-x (przy górnej krawędzi teownika) i obliczamy
moment statyczny spoin względem osi x-x :

S

x-x

= 1,0 ·

20,0 · 11,0 + 1,0 · 10,0 · 0,5 = 225 cm

2

Pole przekroju:

A = 1,0 · 20,0 + 1,0 · 10,0 =

30,0 cm

2

A

1

2

V

1

2

V

A

y

o

x

F

x

1

2

3

oś obojętna

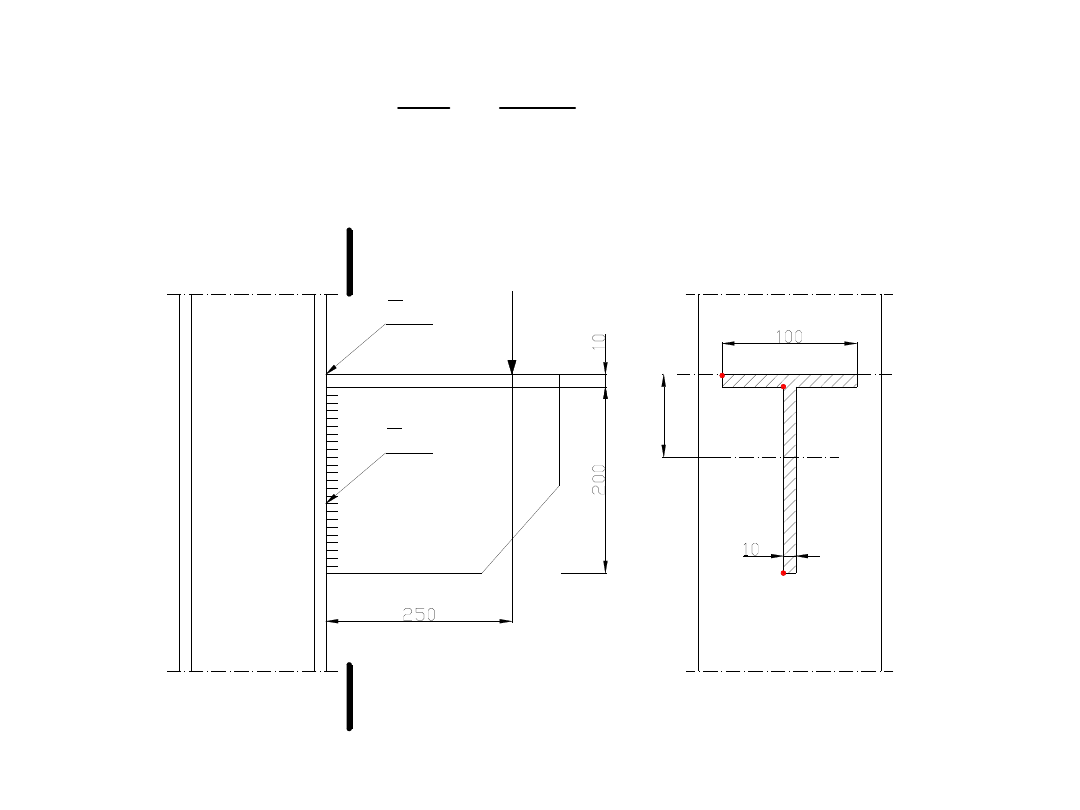
stąd:

;

5

,

7

30

225

cm

A

S

y

x

o







A

1

2

V

1

2

V

A

y

o

x

F

x

1

2

3

oś obojętna

A

1

2

V

1

2

V

A

y

o

x

F

x

1

2

3

oś obojętna

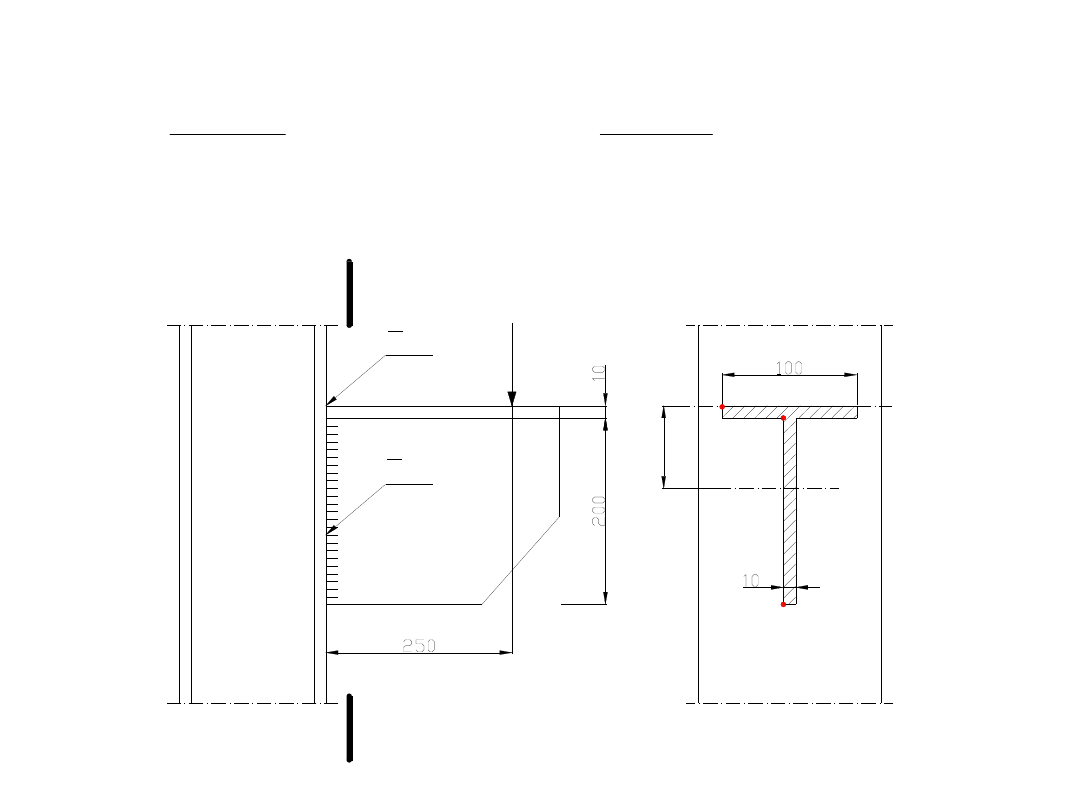
Obliczamy moment bezwładności spoin względem osi
poziomej przechodzącej przez środek ciężkości spoin:

;

50

,

1402

)

5

,

0

5

,

7

(

0

,

10

0

,

1

12

0

,

1

0

,

10

)

5

,

7

0

,

11

(

0

,

20

0

,

1

12

0

,

20

0

,

1

4

2

3

2

3

cm

I

I

xo

xo



























Obliczamy wartość wskaźnika wytrzymałości dla punku

1

i

3

.

Znając położenie osi obojętnej możemy naszkicować przybliżony wykres naprężeń
normalnych w spoinie.

3

3

3

3

1

1

89

,

103

5

,

13

5

,

1402

187

5

,

7

5

,

1402

cm

y

I

W

cm

y

I

W

xo

x

xo

x













A

1

2

V

1

2

V

A

F

1

2

3

R

S





Wiemy, że w punkcie 1 spoina
będzie rozciągana, a punkcie 2
spoina będzie ściskana.

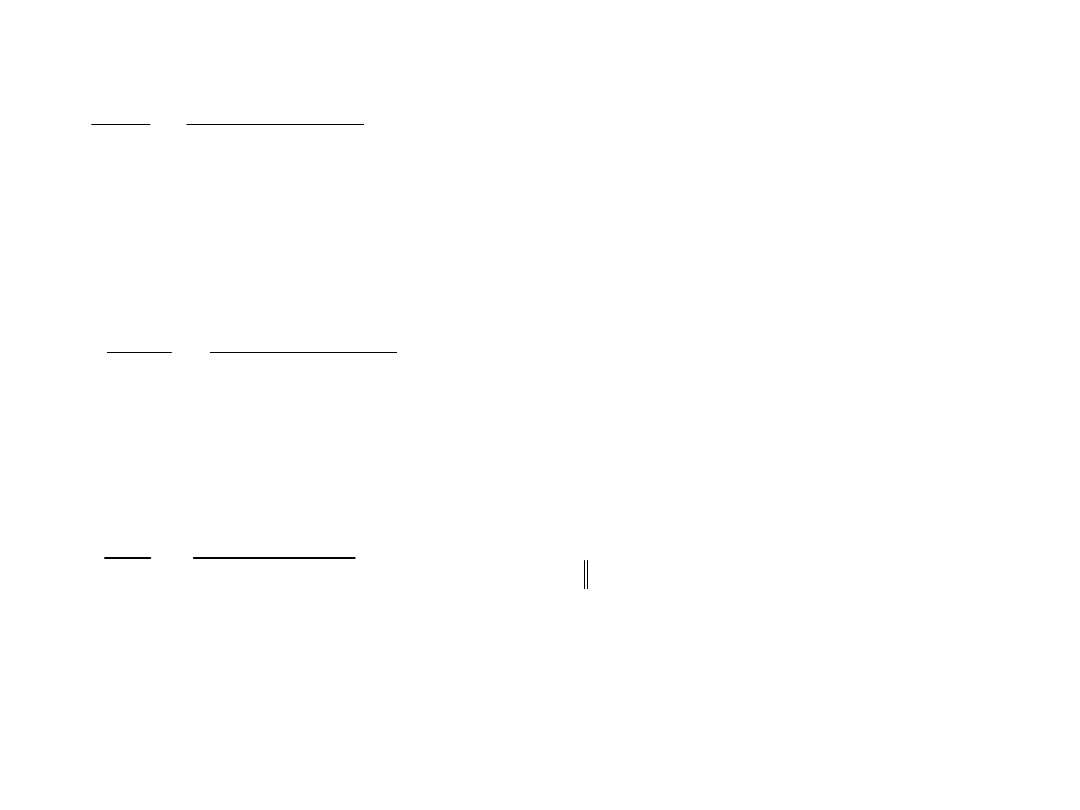
Znając charakter pracy, przystępujemy do obliczeń:

α

┴

= 0,85 (z tabeli 18 PN) – ponieważ w punkcie 1 spoina

jest rozciągana – równomiernie.

α

┴

= 1,0 (z tabeli 18 PN) – ponieważ w punkcie 3 spoina

jest ściskana.

Zakłada się, że na ścinanie pracują tylko spoiny pionowe.

α

II

=0,6 (z tabeli 18) – dla wszystkich spoin czołowych,

ścinanych, niezależnie od charakteru pracy;

MPa

f

MPa

W

M

d

X

75

,

182

215

85

,

0

96

,

106

187

25

,

0

10

80

3

1

1



























MPa

f

MPa

W

M

d

X

215

215

0

,

1

51

,

192

89

,

103

25

,

0

10

80

3

3

3



























MPa

f

MPa

A

F

d

0

,

129

215

6

,

0

40

01

,

0

20

,

0

80

























Naprężenia w punkcie 2 będą miały charakter złożony –
w punkcie połączenia pasa ze środnikiem należy obliczyć
naprężenia normalne (wywoływane zginaniem) oraz
styczne (od ścinania).

Przed podstawieniem cząstkowych wartości do wzoru na
naprężenia zastępcze w spoinie czołowej, musimy
obliczyć naprężenia średnie w spoinie. Na tej podstawie
przyjmiemy współczynnik obliczeniowy spoin dla
naprężeń normalnych.

MPa

g

I

S

F

cm

S

g

I

S

P

MPa

I

y

M

Xo

pasa

pasa

Xo

pasa

Xo

93

,

39

01

,

0

50

,

1402

0

,

70

10

80

70

)

5

,

0

5

,

7

(

0

,

1

10

69

,

92

50

,

1402

065

,

0

25

,

0

10

80

3

2

3

2

3

2

2





















































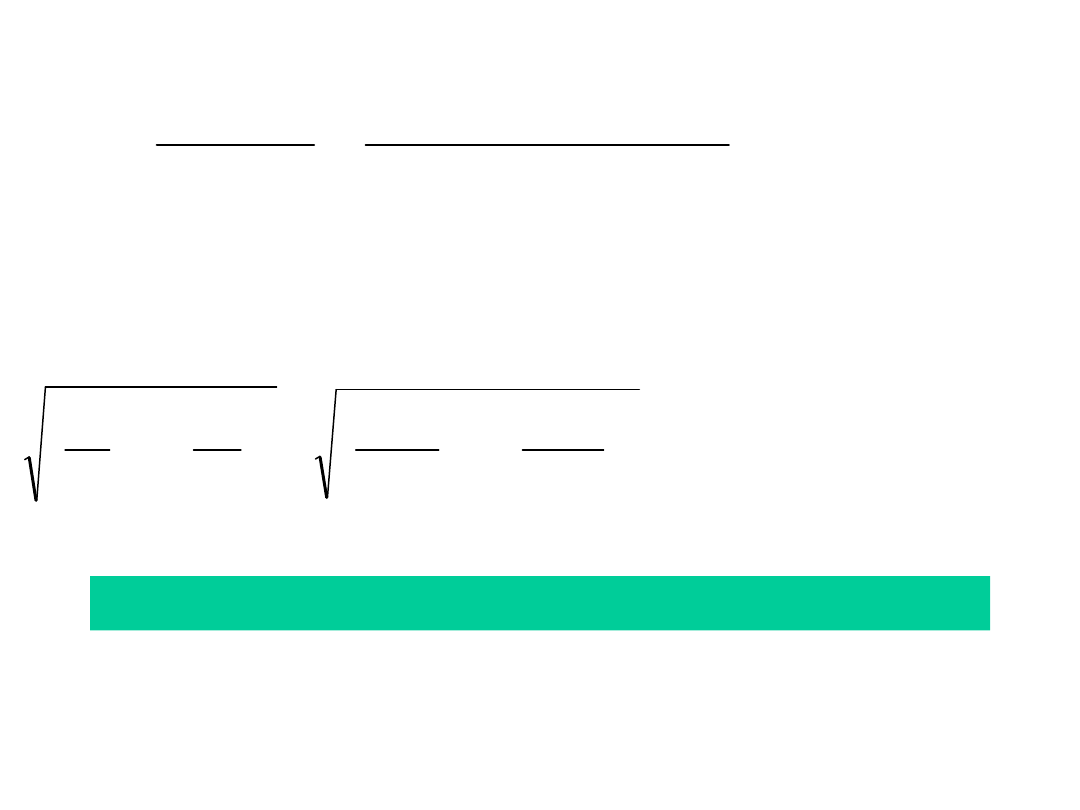
Naprężenia średnie obliczymy według zależności:

Dlatego w złożonym stanie naprężeń możemy traktować
spoinę jako ściskaną (α

┴

= 1,0).

MPa

d

g

sr

78

,

42

2

)

51

,

192

(

96

,

106

2





















MPa

f

MPa

d

II

215

05

,

114

6

,

0

93

,

39

0

,

1

62

,

92

2

2

2

2







































































NOŚNOŚĆ ZAPEWNIONA!!!

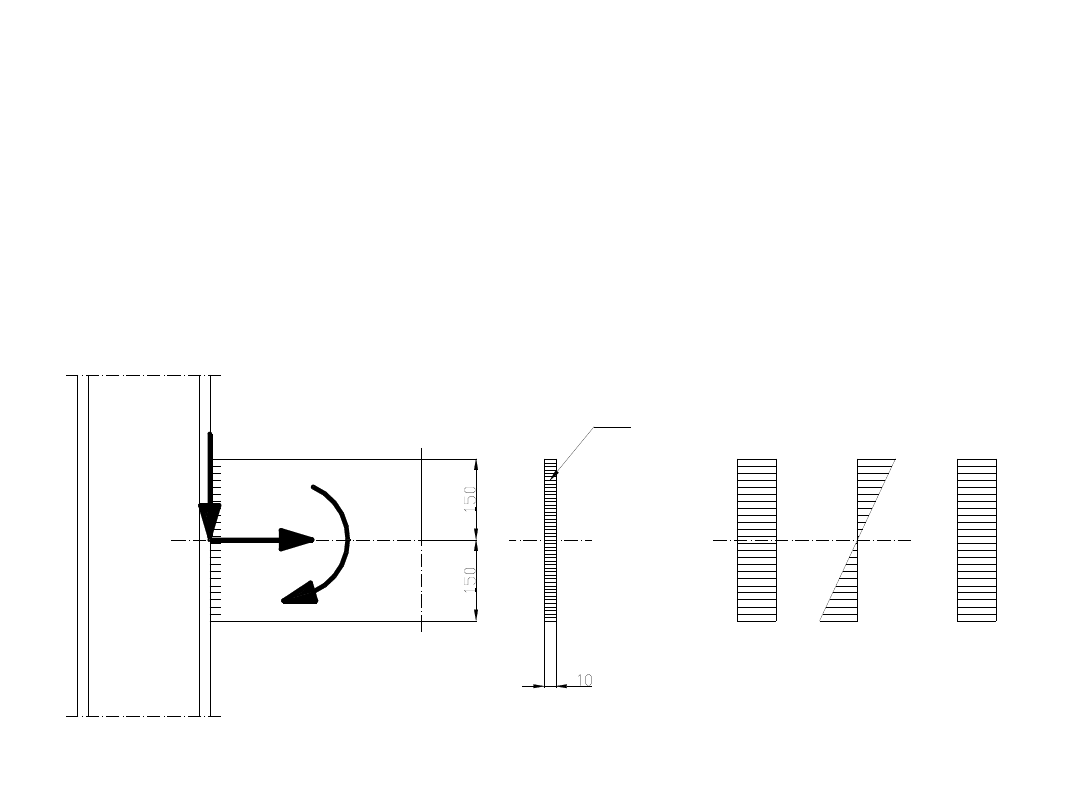
Zadanie 8.

Sprawdzić wytrzymałość spoiny czołowej łączącej blachę węzłową ze
słupem jak na rysunku. Spoina nie ma kraterów końcowych i jest
kontrolowana zgrubnie.

Elementy wykonane ze stali 18G2 (f

d

= 305 MPa);

M = 12 kNm; N = 360 kN; V = 270 kN;

A

s

N

M

V



N



M



Naprężenia normalne w połączeniu wywoła zarówno siła
N (rozciągająca) jak i moment. Naprężenia ścinające
(styczne) wywoła siła poprzeczna V.

Naprężenia normalne w tego typu połączeniu to suma
naprężeń normalnych pochodzących od siły rozciągającej
N i od naprężeń od momentu zginającego.

Charakterystyka spoiny:

Pole przekroju:

Pole przekroju czynnego przy ścinaniu (jak dla
płaskownika):

;

30

30

0

,

1

2

cm

A

s







;

27

30

9

,

0

2

cm

A

s









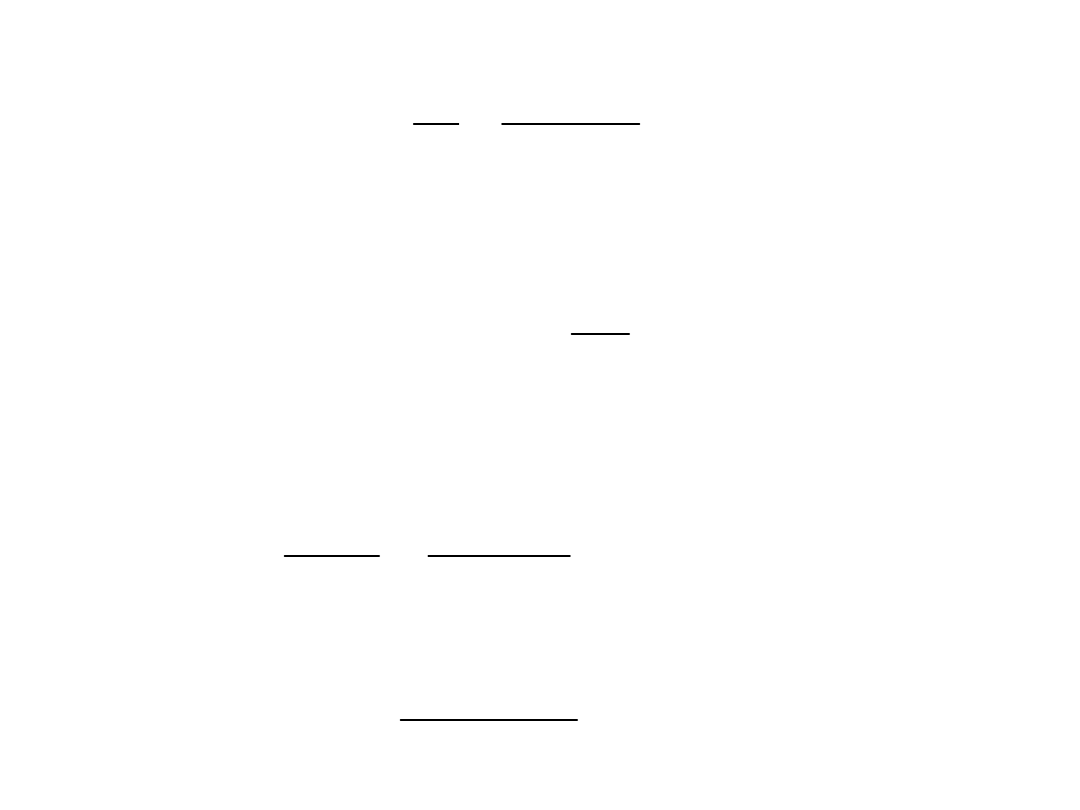
Naprężenia normalne średnie wywołane osiową siłą
rozciągającą:

Naprężenia normalne wywołane momentem zginającym:

Wskaźnik spoin:

;

120

10

30

10

360

4

3

MPa

A

N

s

N















s

M

W

M





;

10

150

6

30

0

,

1

6

3

6

2

2

m

h

b

W















;

80

10

150

10

12

6

3

MPa

M













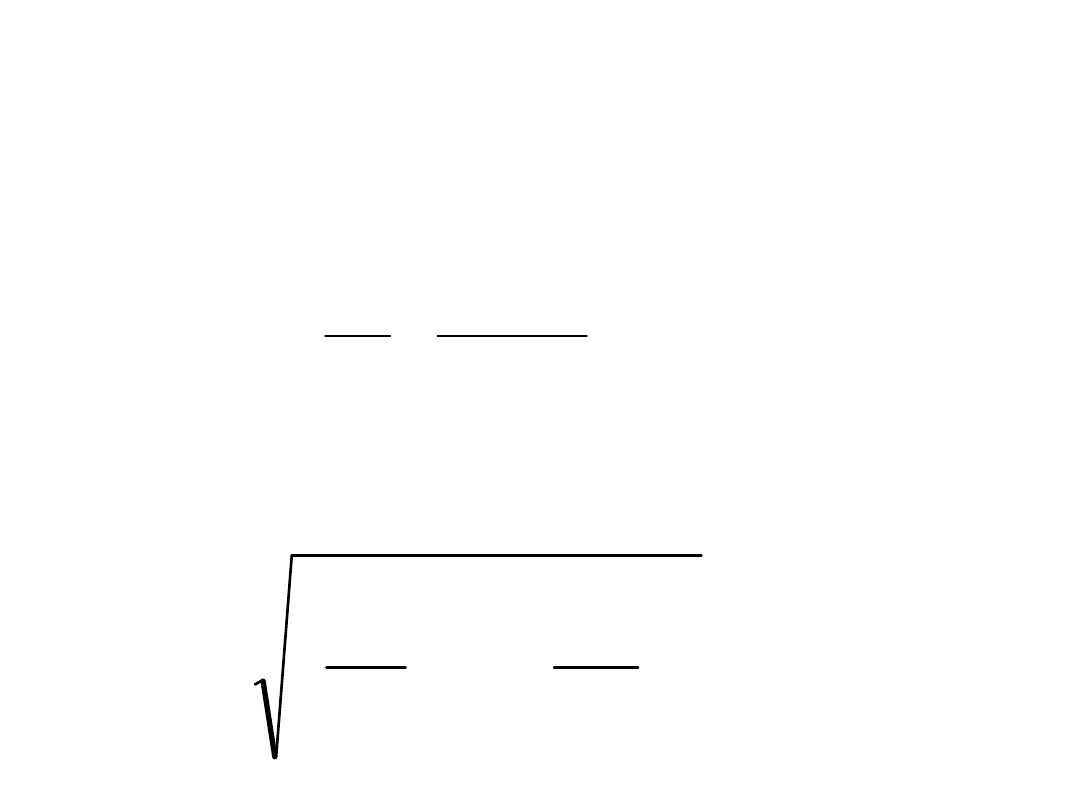
Maksymalne naprężenia normalne:

Naprężenia styczne:

Zastępczy stan naprężeń:

;

0

,

200

0

,

80

0

,

120

MPa

M

N

















;

100

10

27

10

270

4

3

MPa

A

V

s

















d

II

f































2

2









Współczynniki obliczeniowe spoiny:

-α

II

= 0,6 – spoina jest ścinana siłą V

-α

┴

=

???

Nie jesteśmy w stanie przyjąć współczynnika
bezpośrednio z tabeli 18 PN – ponieważ siła N rozciąga
nam konstrukcje, a moment powoduje zginanie. Znając
jednak charakter pracy konstrukcji wiemy, że w wyniku
zsumowania naprężeń konstrukcja podlega rozciąganiu
mimośrodowemu.

Norma w tablicy 18 definiuje współczynnik α

┴

= 1 – 0,15 ·

ν

ν – jest to stosunek naprężeń średnich do maksymalnych

α

┴

= 1 – 0,15 · 0,6 = 0,91

6

,

0

200

120







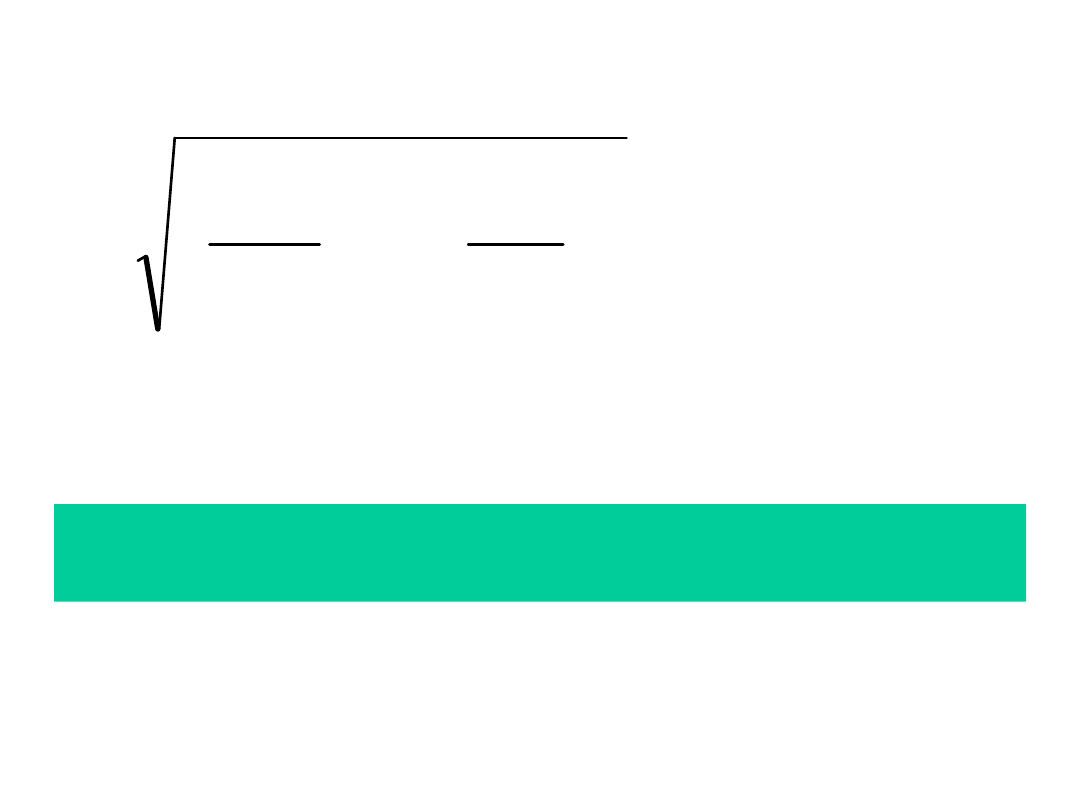
MPa

MPa

MPa

305

8

,

275

8

,

275

6

,

0

100

91

,

0

200

2

2































WARUNEK SPEŁNIONY – NOŚNOŚĆ

ZAPEWNIONA!!!

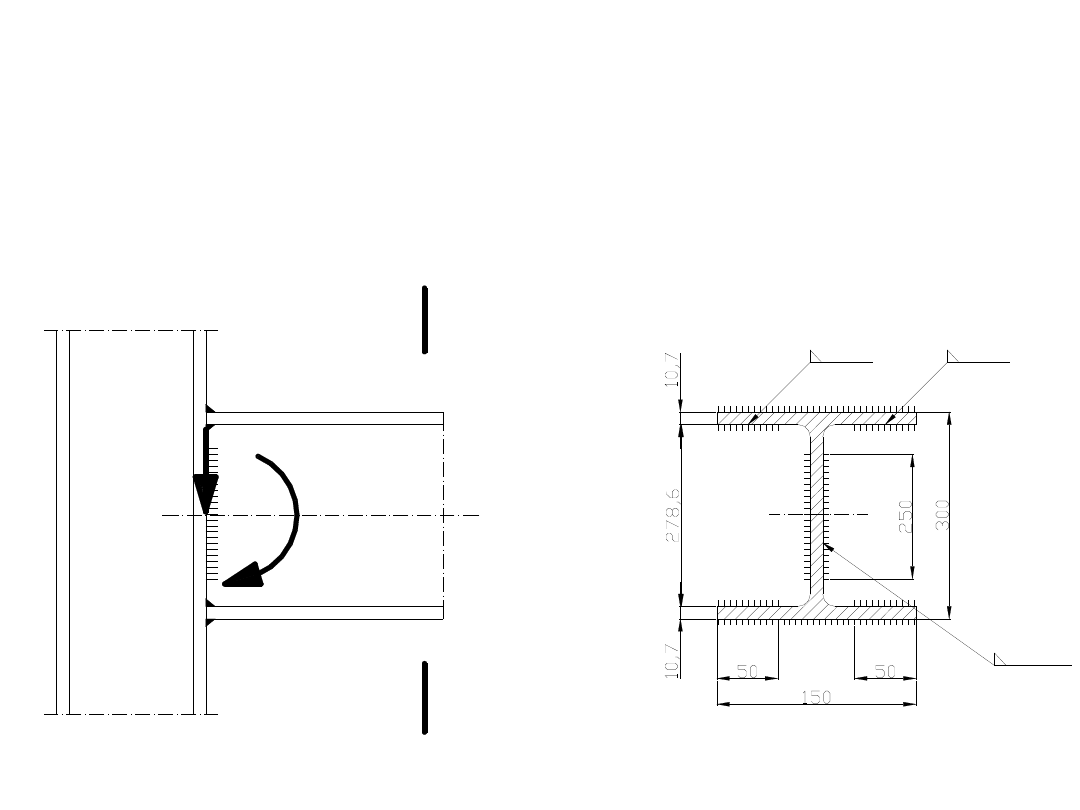
Zadanie 9.

Sprawdzić naprężenia w spoinach mocujących wspornik z
dwuteownikiem I 300 PE, wykonanego ze stali 18G2A, do słupa ze
stali 18G2A. Do obliczeń przyjąć M=100kNm; V = 55 kN;

M

V

A

A

A-A

6 x 50

6 x 50

4 x 250

x

x

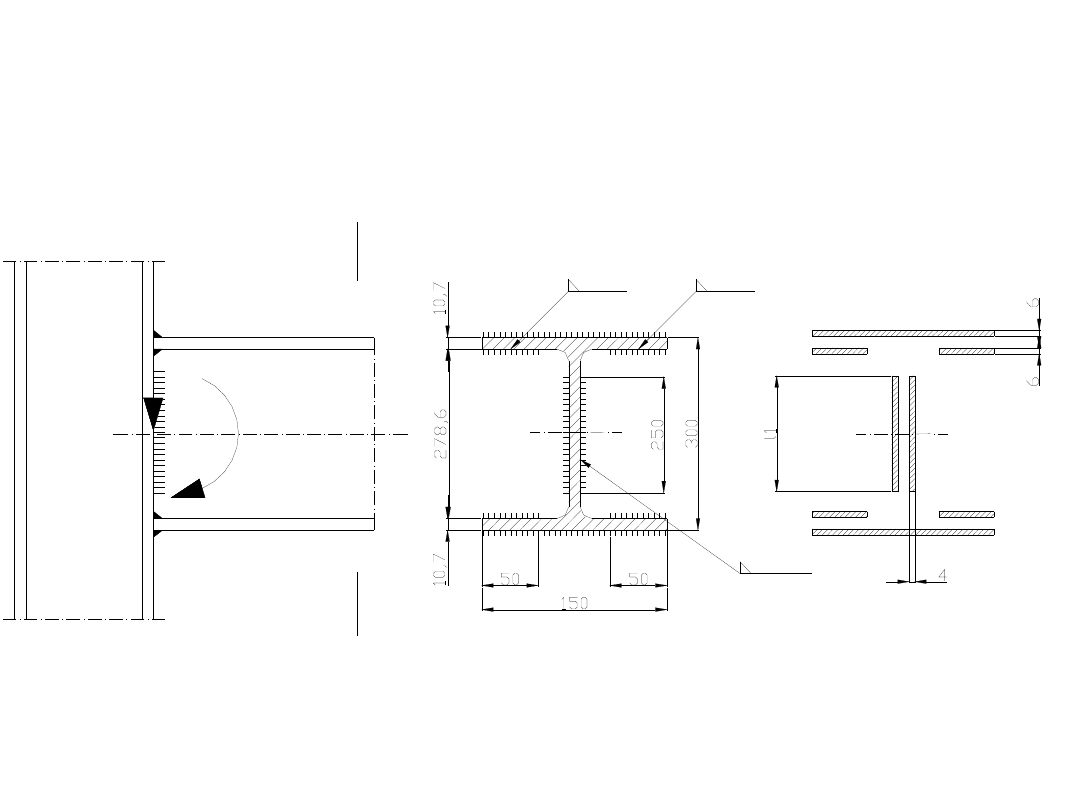
Pierwszym krokiem w tego typu zadaniach jest
wykonanie kładu spoin.

M

A

V

A

4 x 250

6 x 50

x

A-A

x

6 x 50

x

x

Kład

spoin

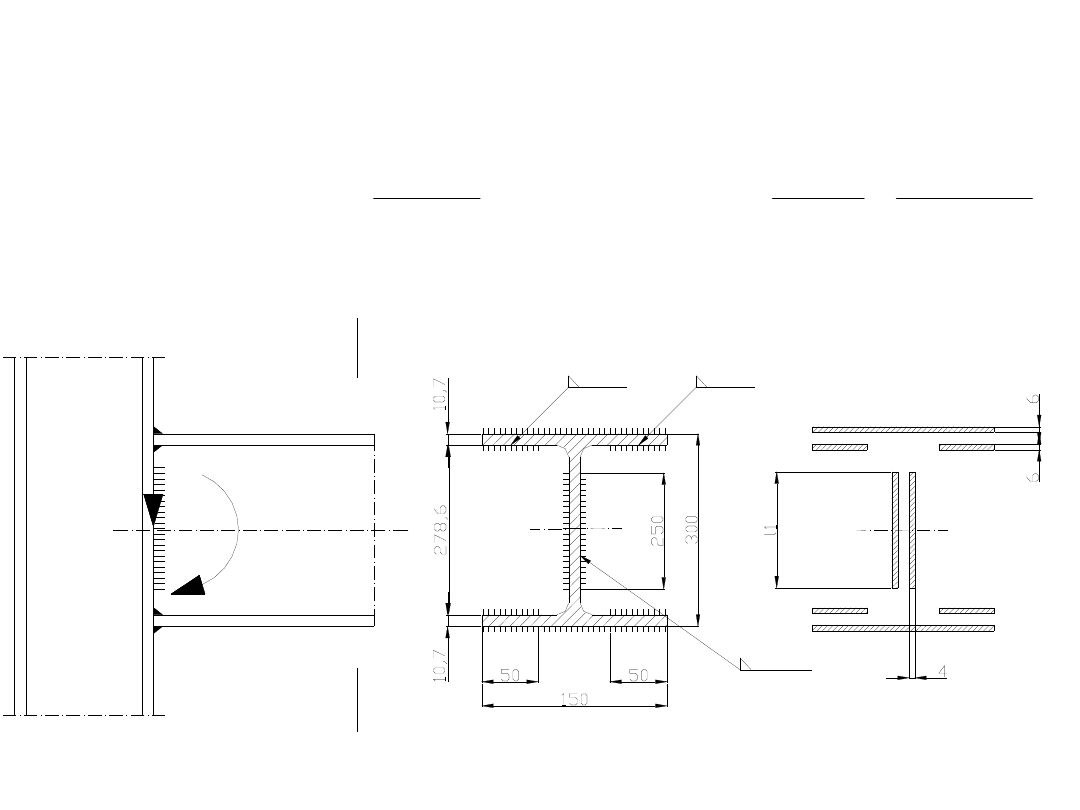
Następnie należy obliczyć wartość momentu
bezwładności kładu spoin względem osi obojętnej – w
naszym wypadku leży w połowie wysokości
kształtownika.

M

A

V

A

4 x 250

6 x 50

x

A-A

x

6 x 50

x

x

Kład

spoin

;

27

,

7849

12

0

,

25

4

,

0

12

6

,

0

5

2

7

,

14

6

,

0

5

2

12

6

,

0

15

3

,

15

0

,

6

0

,

15

2

4

3

3

2

3

2

cm

I

I

x

x













































Pole powierzchni spoin równoległych do kierunku
działania siły ścinającej:

A

sw

= 0,4 · 25,0 · 2 = 20,0 cm

2

;

Przy takim układzie spoin i obciążenia należy sprawdzić
zastępczy stan naprężeń wg wzoru:

κ – współczynnik – w naszym przypadku 0,85;

(pkt.

6.3.3.3.a PN)





d

II

f











2

2

2

3









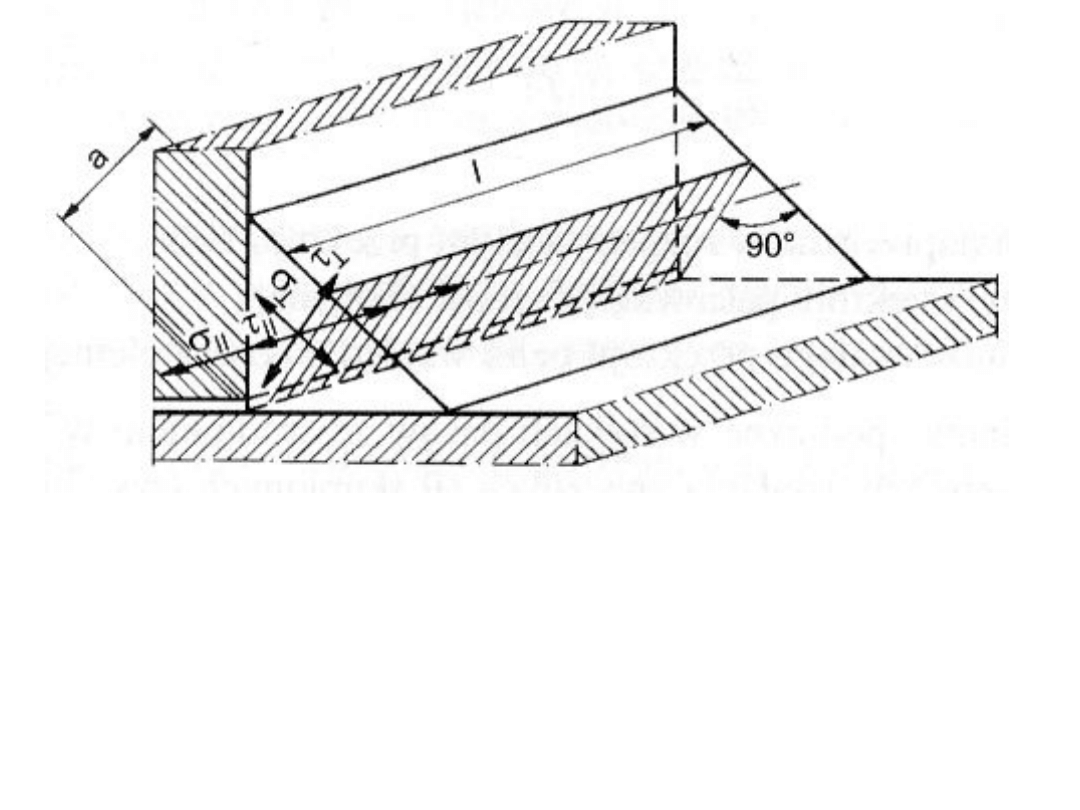
σ

┴

- naprężenia normalne w przekroju obliczeniowym

spoiny, prostopadłe do jej osi podłużnej;

τ

II

– naprężenia styczne w przekroju obliczeniowym

spoiny, równoległe do jej osi podłużnej;

τ

┴

– naprężenia styczne w przekroju obliczeniowym

spoiny, prostopadłe do jej osi podłużnej;

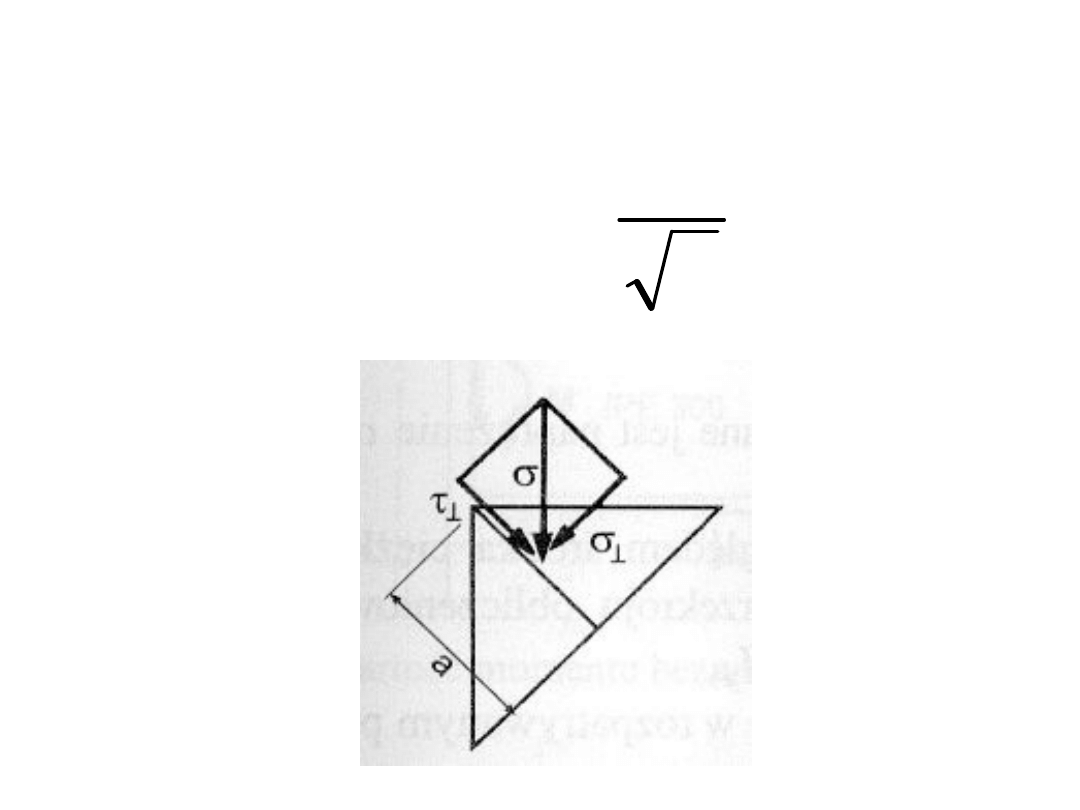
Jeżeli spoina pachwinowa ma przekrój
trójkąta prostokątnego, wówczas można
zastosować uproszczenie postaci:

2















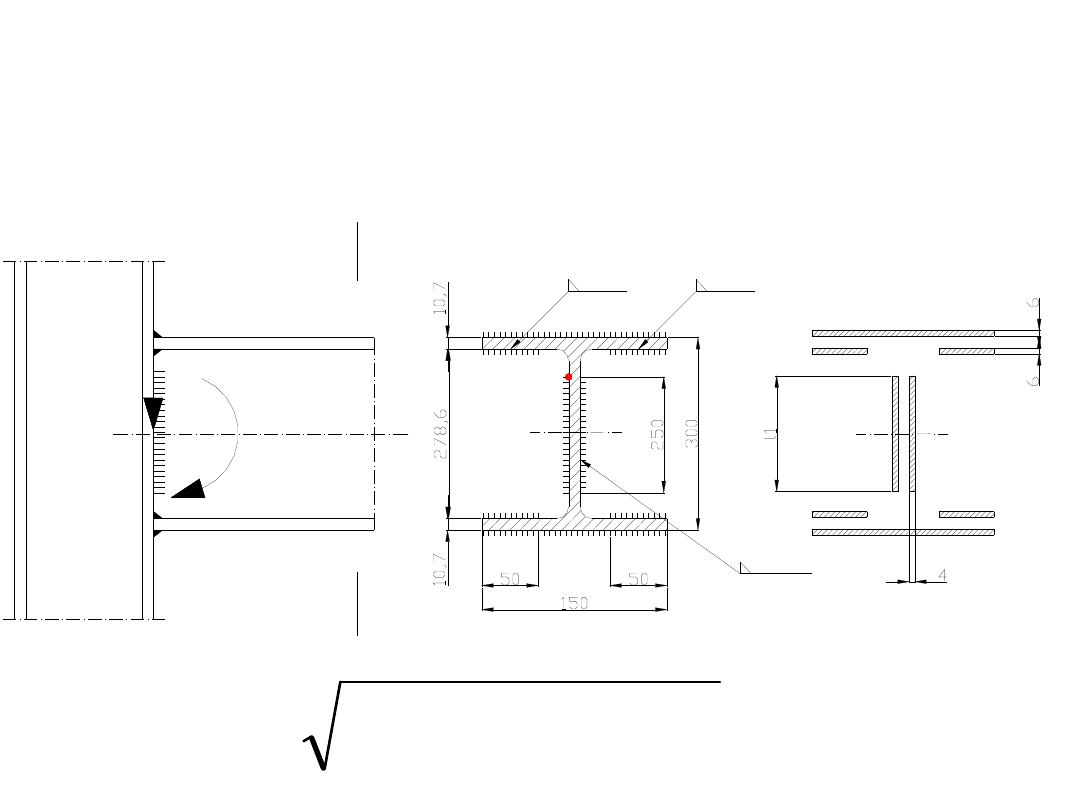
W połączeniu powinniśmy sprawdzić naprężenia w dwóch
punktach – w punkcie A, gdzie będzie występowała
koncentracja naprężeń oraz w punkcie najbardziej
oddalonym od osi obojętnej.

M

A

V

A

4 x 250

6 x 50

x

A-A

x

6 x 50

x

x

Kład

spoin

A





d

II

f











2

2

2

3









;

25

,

159

10

27

,

7849

125

,

0

100

;

50

,

27

002

,

0

55

8

MPa

I

y

M

MPa

A

V

x

a

M

sw

II



































Ponieważ nasza spoina ma przekrój trójkąta
prostokątnego, dlatego:

Mając wszystkie niezbędne cząstkowe wartości naprężeń,
możemy obliczyć naprężenia zastępcze w punkcie A:

MPa

f

MPa

d

305

61

,

112

2

25

,

159

2



























MPa

f

d

II

305

02

,

207

)

61

,

112

50

,

27

(

3

61

,

112

85

,

0

3

2

2

2

2

2

2































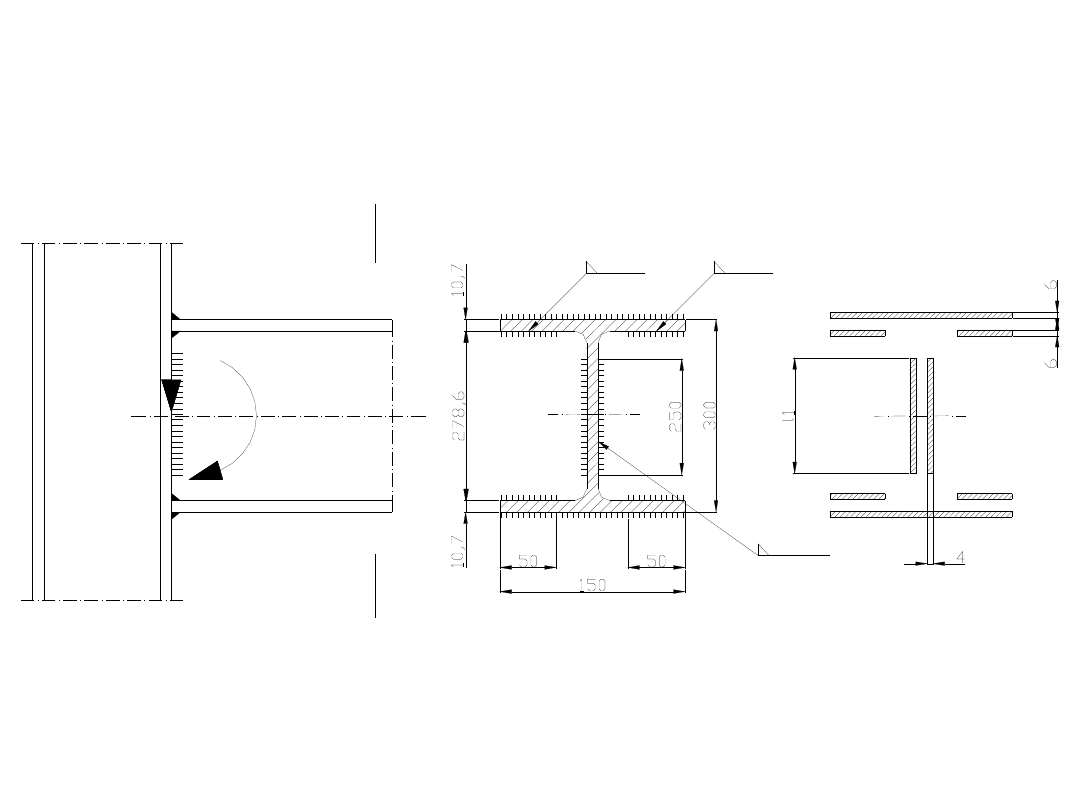
Drugim miejscem, które powinniśmy sprawdzić, jest
punkt najbardziej oddalony od osi obojętnej (w naszym
przypadku od osi x-x).

M

A

V

A

4 x 250

6 x 50

x

A-A

x

6 x 50

x

x

Kład

spoin

W miejscu najbardziej oddalonym od osi x-x także
sprawdzamy zastępczy stan naprężeń, przy czym nie
będą tu występowały naprężenia styczne τ

II

.

MPa

f

MPa

MPa

I

y

M

d

x

b

305

83

,

137

2

92

,

194

2

;

92

,

194

10

27

,

7849

153

,

0

100

8











































MPa

f

d

II

305

31

,

234

)

61

,

112

3

83

,

137

85

,

0

3

2

2

2

2

2





























W obu punktach (A i B) naprężenia w stanie zastępczym
są mniejsze od wytrzymałości stali na ściskanie /
rozciąganie –

nośność zachowana!!!