Wykład 21

Elementy

kombinatoryki.

Prawdopodobieństwo

dr Tomasz
Kowalski

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

2 /

64

Silnia

Niech n oznacza liczbę naturalną .
Iloczyn

oznaczamy symbolem n! i czytamy: n
silnia.

1 2 3

1

    



... (

)

n

n

Przyjmuje się dodatkowo, że 0! = 1.

Konwencja ta okaże się w dalszych
rozważaniach bardzo wygodna.

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

3 /

64

Wartości n! Wzór Stirlinga

n

n!

0

1

1

   

1

2

   

 2

3

    6

4

 

 24

5

120

6

        

720

7

      5

040

8

    40

320

9

  362

880

10  

3 628

800

Jak widać, gdy n rośnie,
wartości silni wzrastają
bardzo szybko.

Dla dużych n
obliczanie n! staje się
sprawą kłopotliwą.

Posługujemy się
wówczas tzw.
wzorem Stirlinga:

!

2

.

n

n

n

n n e

p

-

�

�

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

4 /

64

Przykład

Obliczyć:

16!

.

12!

!

12

!

16

12!

=

12! 13 14 15 16

� � � �

= 43
680

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

5 /

64

Przykład

Obliczyć:

100! 58!

.

98! 60!

�

�

100! 58!

98! 60!

�

�

98!

=

98! 99 100

� �

58!

�

58! 59 60

� � �

5

3

33

165

59

=

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

6 /

64

Przykład

Obliczyć:

(2 )! !

.

(2

1)! (

2)!

n n

n

n

�

+ � -

(2 )! !

(2

1)! (

2)!

n n

n

n

�

+ � -

(2 )!

n

=

(2 )! (2

1)

n

n

� +

(

2)!

n

� -

(

2)! (

1)

n

n

n

� -

� -

�

(

1)

2

1

n

n

n

- �

=

+

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

7 /

64

Symbol Newtona

Niech n, k N

0

oraz k  n. Symbolem

Newtona nazywamy

liczbę oznaczaną przez

i równą













k

n

!

.

! (

)!

n

k n k

� -

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

8 /

64

Przykład

Obliczyć:

10

.

3

� �

� �

� �

10

3

� �

� �

� �

10!

3! 7!

=

�

7! 8 9 10

2 3 7!

���

=

��

3

4

120

=

!

.

! (

)!

n

n

k

k n k

� �

=

� �

� -

� �

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

9 /

64

Własności symbolu Newtona

1.

1,

0

n

n
n

�� ��

=

=

�� ��

�� ��

2.

,

1

n

n

��

=

��

��

3.

,

n

n

k

n k

� � �

�

=

� � �

�

-

� � �

�

1

4.

.

1

1

n

n

n

k

k

k

+

� � �

� �

�

+

=

� � �

� �

�

+

+

� � �

� �

�

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

10 /

64

Trójkąt Pascala

Wartości symbolu Newtona można ustawić w
następującą tablicę zwaną trójkątem Pascala:

.......

..........

..........

..........

..........

..........

3

3

2

3

1

3

0

3

2

2

1

2

0

2

1

1

0

1

0

0

























































































































1

1

1

1

2

1

1

3

3

1

...................................

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

11 /

64

Trójkąt Pascala

Zasady tworzenia trójkąta Pascala:

w najwyższym wierszu wpisujemy
jedynkę

w drugim wierszu od góry -
dwie jedynki

w trzecim wierszu kolejno 1,
2, 1,

w każdym następnym wierszu
o jedną liczbę więcej, niż w
poprzednim; na lewym i
prawym skraju jedynki,

1

1
1

1 2 1

1

3 3

1

3
3

1 4 6 4
1

1 5 10 10
5 1

a na każdym innym miejscu -
liczbę, która jest sumą
dwóch liczb widniejących w
poprzednim wierszu
bezpośrednio nad nią

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

12 /

64

Podstawy kombinatoryki

W kombinatoryce mamy w zasadzie do
czynienia z dwoma sposobami losowań:

losowanie, w którym jest istotna kolejność
wylosowanych elementów,

losowanie, w którym nie jest istotna kolejność
wylosowanych elementów, a jedynie ich
liczebność.

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

13 /

64

Podstawy kombinatoryki

Jednocześnie możemy rozróżnić losowania, w
których:

elementy nie powtarzają się w doświadczeniu,

dopuszcza się powtarzanie elementów w
doświadczeniu.

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

14 /

64

Permutacje

Wynik losowania, w którym wykorzystujemy
wszystkie elementy, ale te nie mogą się
powtarzać i kolejność wylosowanych elementów
jest istotna, nazywamy permutacją.

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

15 /

64

Kombinacje

Wynik losowania, w którym kolejność
występujących elementów nie jest istotna, ale
też żaden z nich się nie powtarza nazywamy
kombinacją.

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

16 /

64

Wariacje bez powtórzeń

Wynik losowania, w którym kolejność
występujących elementów jest istotna, ale
żaden z nich się nie powtarza nazywamy
wariacją bez powtórzeń.

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

17 /

64

Wariacje z powtórzeniami

Wynik losowania, w którym kolejność
występujących elementów jest istotna, ale
elementy mogą się powtórzyć nazywamy
wariacją z powtórzeniami.

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

18 /

64

Permutacje

Niech V będzie n-elementowym zbiorem.
Każdy n-wyrazowy różnowartościowy
ciąg, którego wyrazami są elementy zbioru
V nazywamy permutacją (bez powtórzeń)
tego zbioru.

Inaczej: Permutacja zbioru to jakiekolwiek
uporządkowanie tego zbioru.

Jeżeli zbiór V ma n elementów, to liczba
wszystkich permutacji tego zbioru wynosi

!

n

P

n

=

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

19 /

64

Przykład

Permutacjami zbioru

A={ a, s, i }

są ciągi

3

3! 1 2 3 6.

P = = ��=

(a,s,i), (a,i,s), (s,i,a), (s,a,i), (i,a,s), (i,s,a),

a liczba permutacji zbioru 3-

elementowego wynosi

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

20 /

64

Przykład

W urnie jest 5 kul o numerach 1, 2, 3, 4,
5. Wyciągamy kolejno wszystkie kule i
notujemy ich numery według kolejności
wyciągnięcia. Ile można tym sposobem
otrzymać różnych liczb?

5

5! 1 2 3 4 5 120.

P = = ����=

Wynik doświadczenia jest ciągiem
utworzonym z pięciu liczb.

Wszystkich takich ciągów, a więc i różnych
liczb, jest zatem:

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

21 /

64

Przykład

24

40320

4! 8! 1 2 3 4 1 2 3 4 5 6 7 8 24 40320 967680.

� = �����������= �

=

14 2 43 1 4 44 2 4 4 43

Na ile sposobów można przydzielić
czterem studentkom i ośmiu studentom
dwanaście ponumerowanych miejsc tak by
studentki zajęły cztery pierwsze miejsca?

Studentki można ustawić na 4! sposobów.
Do każdego z tych sposobów można
dołączyć 8! sposobów ustawienia
studentów. Zatem będzie to ostatecznie 4!
·8! sposobów

1

2

3

4

5

6

7

8

9

10

11

12

K K K K M M M M M M M M

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

22 /

64

Kombinacje (bez powtórzeń)

Kombinacją k-elementową (bez powtórzeń)
zbioru V mającego n elementów nazywamy
każdy k-elementowy podzbiór tego zbioru.

Inaczej: Kombinacja zbioru to wynik
jakiekolwiek losowania bez zwracania
elementów tego zbioru.

Jeżeli zbiór V ma n elementów i k  n,

to liczba wszystkich k-elementowych
kombinacji tego zbioru jest równa

!

.

! (

)!

k

n

n

C

k n k

=

� -

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

23 /

64

Przykład

4

4!

2!

2

2! 2!

��

=

=

��

�

��

3 4

��

2

2! 1 2

��

6

=

4

4!

4!

4

4! 0!

��

=

=

��

�

��

1

4!

1

1

=

�

Wypisać wszystkie kombinacje utworzone z
liter x, y, w, z.

Kombinacje 1-
elementowe:

{x}, {y},
{w}, {z},

Kombinacje 2-
elementowe:

{x, y}, {x, w}, {x, z}, {y, w},
{y, z}, {w, z},

Kombinacje 3-
elementowe:

{x, y, w}, {x, y, z}, {x, w,
z}, {y, w, z},

4

4!

3!

1

1! 3!

Razem

��

=

=

��

�

��

4

1! 3!

�

�

4

=

4

4!

3!

3

3! 1!

��

=

=

��

�

��

4

3!

�

4

1!

=

�

Kombinacje 4-
elementowe: {x, y, w,

z}.

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

24 /

64

Przykład

W grze lotto losuje się 6 kul bez zwracania
spośród 49 ponumerowanych kul. Ile jest
możliwych wyników?

Wynik losowania jest kombinacją 6-
elementową ze zbioru 49-elementowego.
Wszystkich możliwych wyników losowań jest
zatem:

6

49

49

49!

43!

6

6! 43!

C

� �

=

=

=

� �

�

� �

44 45 46 47 48 49

1 2 3 4 5 6 43!

� � � � � �

������

=

44

=

22

45

�

153

46 47 48

� � �

122

49

1 2

�

� 3

� 4

� 5

� 6

�

13983816

=

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

25 /

64

Wariacje bez powtórzeń

Każdy k-elementowy ciąg różnowartościowy,
którego wyrazami są elementy n-
elementowego zbioru V nazywamy k-
wyrazową wariacją bez powtórzeń tego
zbioru.

Inaczej: Wariacje to uporządkowane
kombinacje.

Jeżeli zbiór V ma n elementów i k  n,

to liczba wszystkich k-elementowych
wariacji bez powtórzeń tego zbioru jest
równa

!

.

(

)!

k

n

n

V

n k

=

-

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

26 /

64

Przykład

Ile można wykonać różnych dwukolorowych
chorągiewek z sześciu barw?

Każdą chorągiewkę można
utożsamiać z dwuelementowym
różnowartościowym ciągiem,
którego wyrazy pochodzą ze zbioru
6-elementowego.

3

6

6!

6!

4!

(6 2)! 4!

V =

= =

-

5 6

4!

��

30

=

Liczba chorągiewek
wynosi:

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

27 /

64

Wariacje z powtórzeniami

Każdy k-elementowy ciąg, którego wyrazami
są elementy n-elementowego zbioru V
nazywamy k-wyrazową wariacją z
powtórzeniami tego zbioru.

Jeżeli zbiór V ma n elementów, to liczba
wszystkich k-elementowych wariacji z
powtórzeniami tego zbioru jest równa

.

k

k

n

W

n

=

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

28 /

64

Przykład

Ile różnych trzycyfrowych liczb można
utworzyć z cyfr: 1, 2, 3, 4, jeżeli cyfry mogą
się powtarzać?

Każdą trzycyfrową liczbę można
utożsamiać z trójelementowym ciągiem,
którego wyrazy pochodzą ze zbioru 4-
elementowego.

3

3

4

4

64

W = =

Ilość takich liczb
wynosi:

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

29 /

64

Zdarzenia elementarne. Przestrzeń

probabilistyczna

Najprostsze wyniki doświadczenia
losowego nazywamy zdarzeniami
elementarnymi i oznaczamy zwykle .

Zbiór wszystkich wyników doświadczenia
(zdarzeń elementarnych związanych z
doświadczeniem) nazywamy przestrzenią
probabilistyczną lub zdarzeniem pewnym
i oznaczamy symbolem .

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

30 /

64

Zdarzenia

Dowolny podzbiór przestrzeni
probabilistycznej nazywamy zdarzeniem.

Jeżeli zdarzenie elementarne  jest

elementem zbioru A, to mówimy, że sprzyja
ono zdarzeniu A.

Zdarzeniem niemożliwym nazywamy
podzbiór pusty przestrzeni .

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

31 /

64

Działania na zdarzeniach

Zdarzenia są zbiorami – zatem
działania na zdarzeniach i prawa
działań są takie same jak w
przypadku zbiorów.

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

32 /

64

Zawieranie się zdarzeń

Jeżeli każde zdarzenie elementarne
sprzyjające zdarzeniu A sprzyja również
zdarzeniu B, to mówimy, że A zawiera się
w B i piszemy A  B .

B

A

(

)

A B

A

B

w

w

w

�W

� �

� � �

�

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

33 /

64

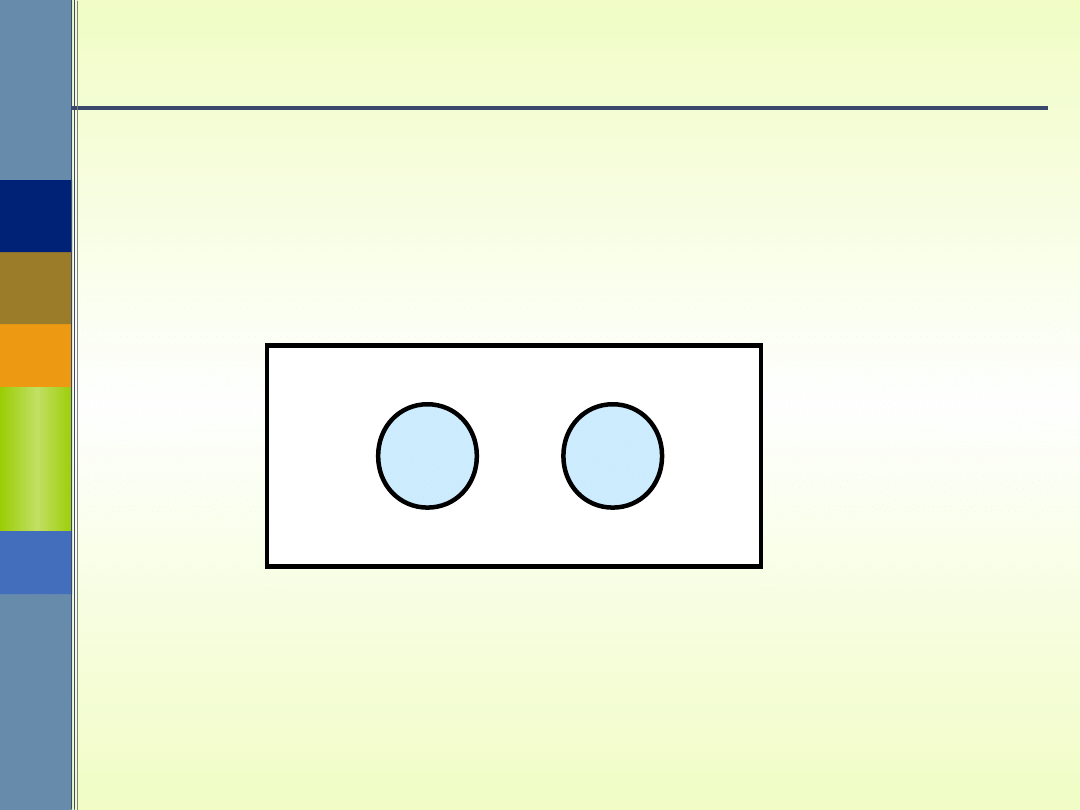
Iloczyn (koniunkcja) zdarzeń

Iloczynem (koniunkcją) zdarzeń A i B
nazywamy zdarzenie, któremu sprzyjają
zdarzenia elementarne sprzyjające
jednocześnie A i B. Zdarzenie to oznaczamy
symbolem AB .



A

B

AB

{ :

}

A B

A

B

w w

w

� =

� � �

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

34 /

64

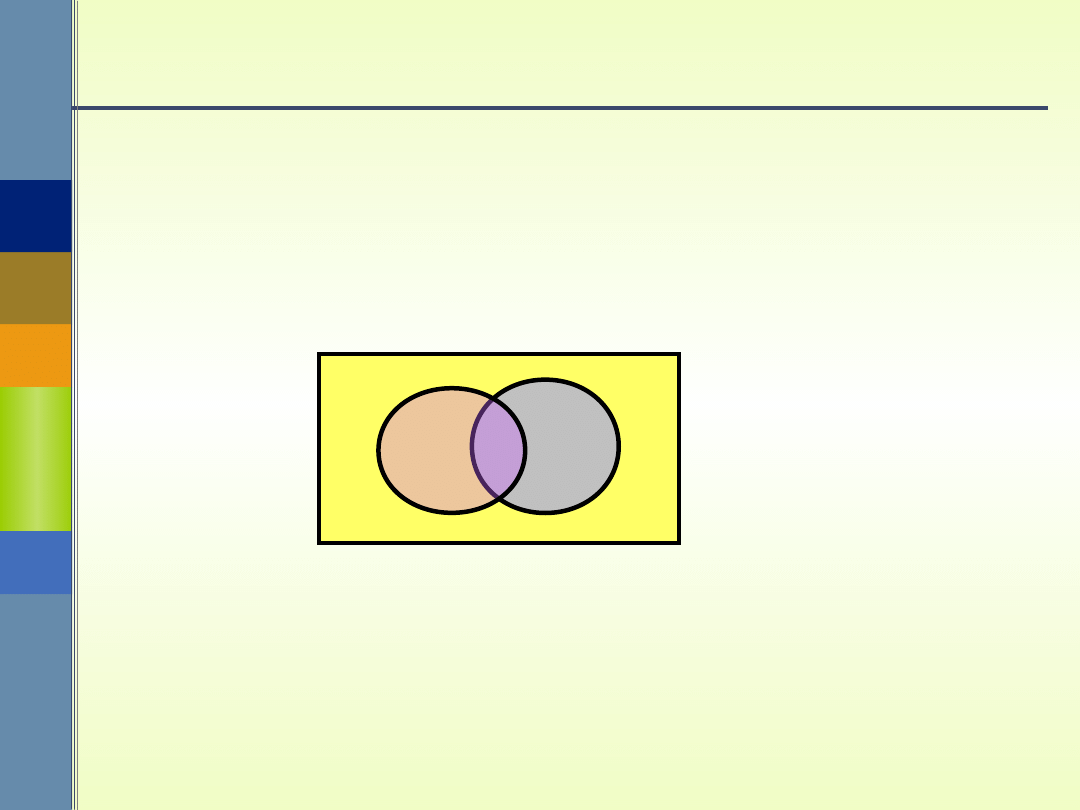
Zdarzenia wykluczające się

Zdarzenia A i B nazywamy
wykluczającymi się, jeżeli AB = 



B

A

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

35 /

64

Suma (alternatywa) zdarzeń

Sumą (alternatywą) zdarzeń A i B nazywamy
zdarzenie, któremu sprzyjają zdarzenia
elementarne sprzyjające A lub B. Zdarzenie to
oznaczamy symbolem AB .



A

B

{ :

}

A B

A

B

w w

w

� =

� � �

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

36 /

64

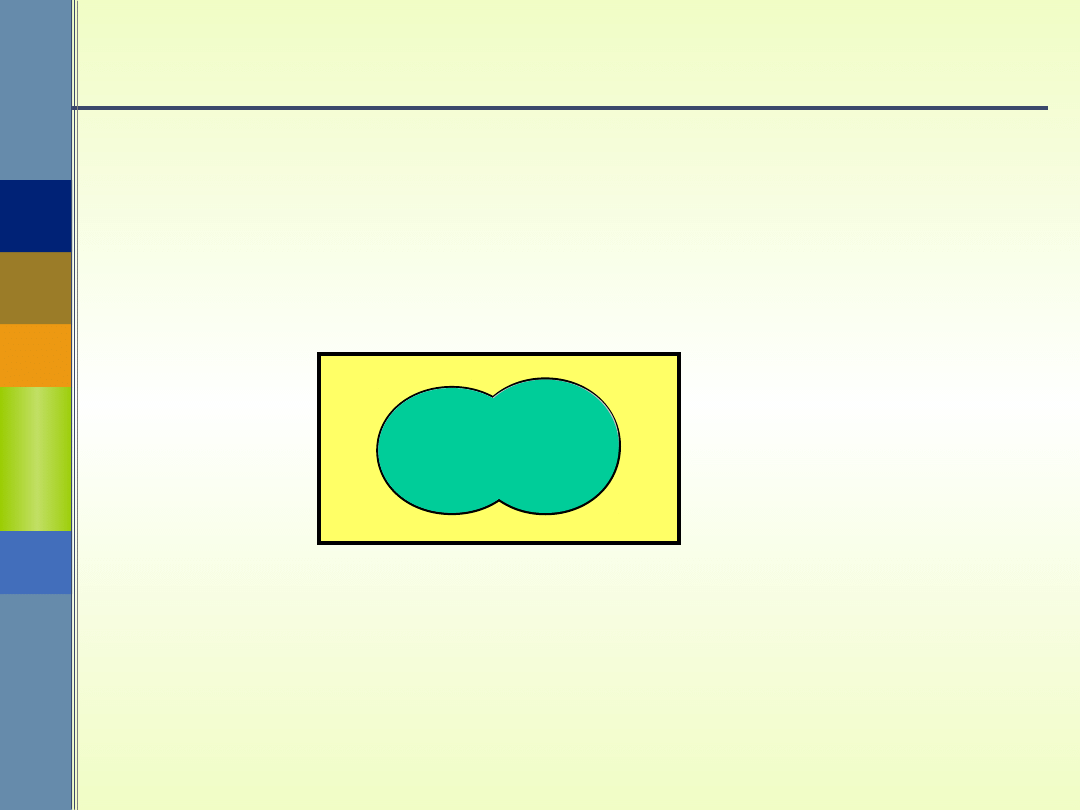
Suma (alternatywa) zdarzeń

Sumą (alternatywą) zdarzeń A i B nazywamy
zdarzenie, któremu sprzyjają zdarzenia
elementarne sprzyjające A lub B. Zdarzenie to
oznaczamy symbolem AB .



A

B

{ :

}

A B

A

B

w w

w

� =

� � �

AB

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

37 /

64

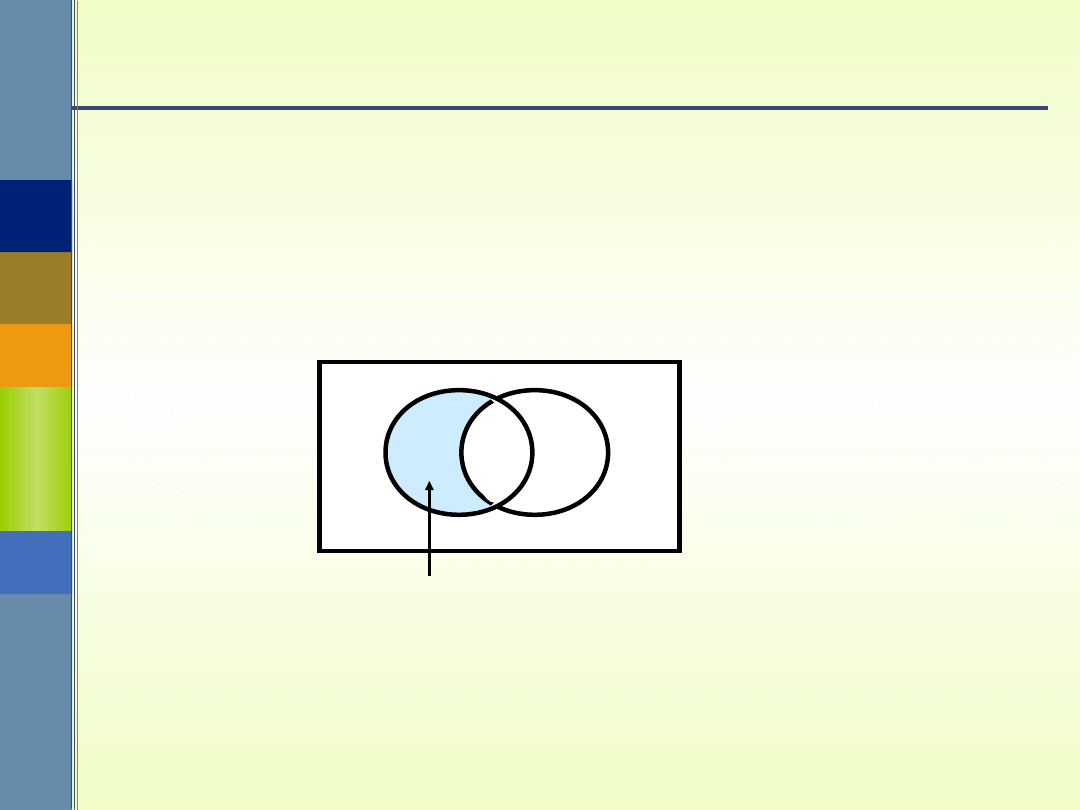
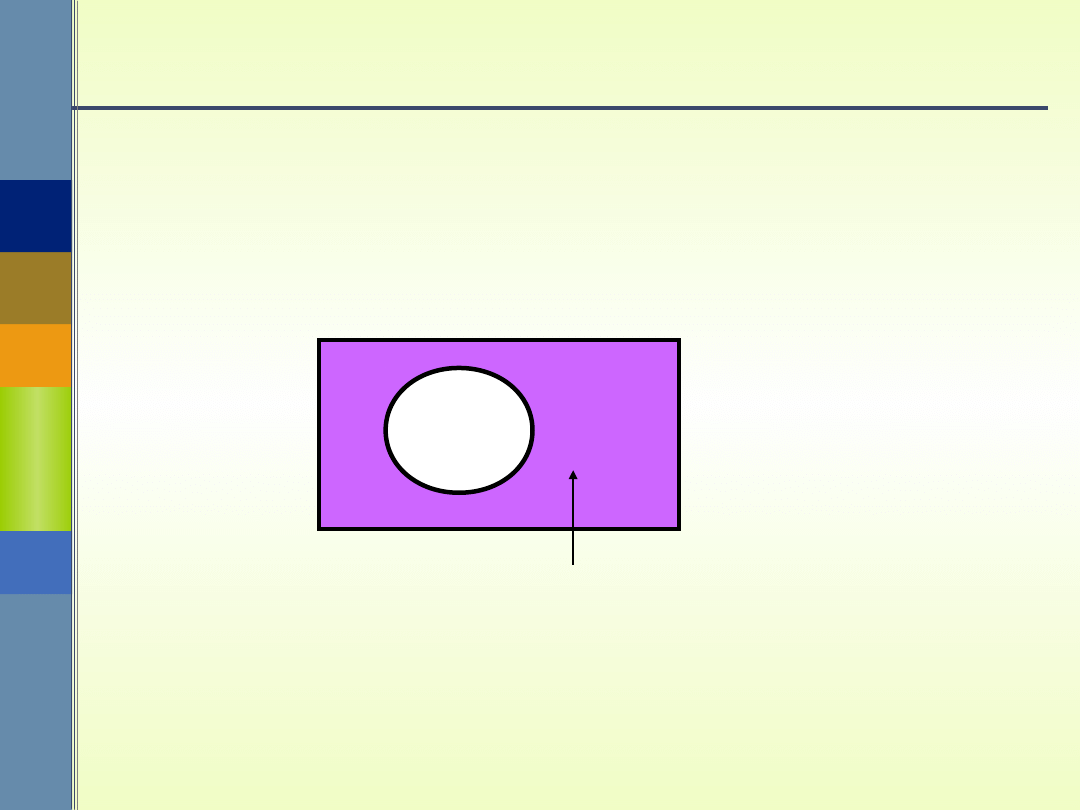
Różnica zdarzeń

Różnicą zdarzeń A i B nazywamy
zdarzenie, któremu sprzyjają zdarzenia
elementarne sprzyjające A i nie sprzyjające
B. Zdarzenie to oznaczamy symbolem A \ B
lub symbolem A - B.



A

B

\

{ :

}

A B

A

B

w w

w

=

� � �

A \ B

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

38 /

64

Zdarzenie przeciwne

Zdarzenie



\ A nazywamy zdarzeniem

przeciwnym do A i oznaczamy symbolem
A

/

.



A

/

\

{

:

}

A

A

A

w

w

=W

= �W

�

A

/

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

39 /

64

Definicja prawdopodobieństwa

Prawdopodobieństwem nazywamy funkcję
P, która każdemu zdarzeniu A  

przyporządkowuje dokładnie jedną liczbę
P(A) spełniającą warunki:

1. 0

( ) 1,

P A

�

�

2.

( ) 1,

P W =

3. Jeżeli

, to (

)

( )

( ).

A B

P A B

P A

P B

� =�

�

=

+

Liczbę p = P(A) nazywamy
prawdopodobieństwem zdarzenia A.

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

40 /

64

Inne definicje

prawdopodobieństwa

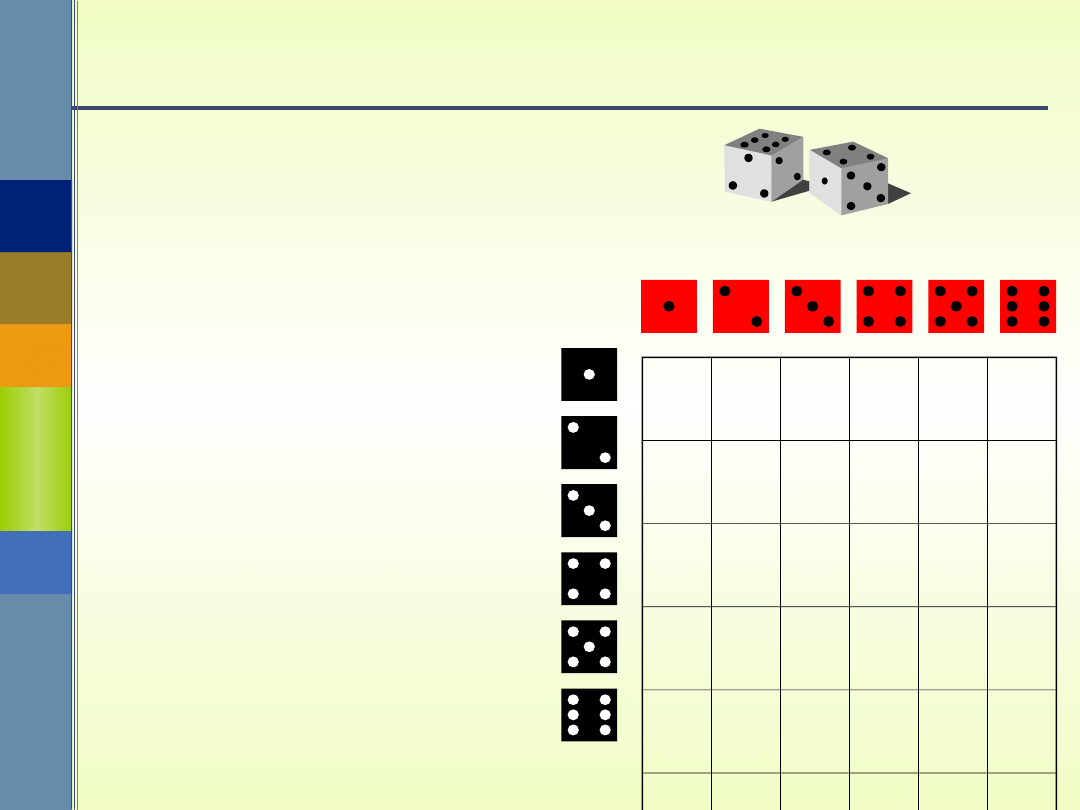
Definicja klasyczna (Laplace'a) z
roku 1812.

Jeżeli zbiór  składa się z n () zdarzeń

elementarnych jednakowo możliwych i wśród
nich dokładnie n(A) sprzyja zdarzeniu A, to

( )

( )

.

( )

n A

P A

n

=

W

Wszystkie
zdarzenia

Zdarzenia

sprzyjające A

Zdarzenia

sprzyjające A

P (A) =

4

9

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

41 /

64





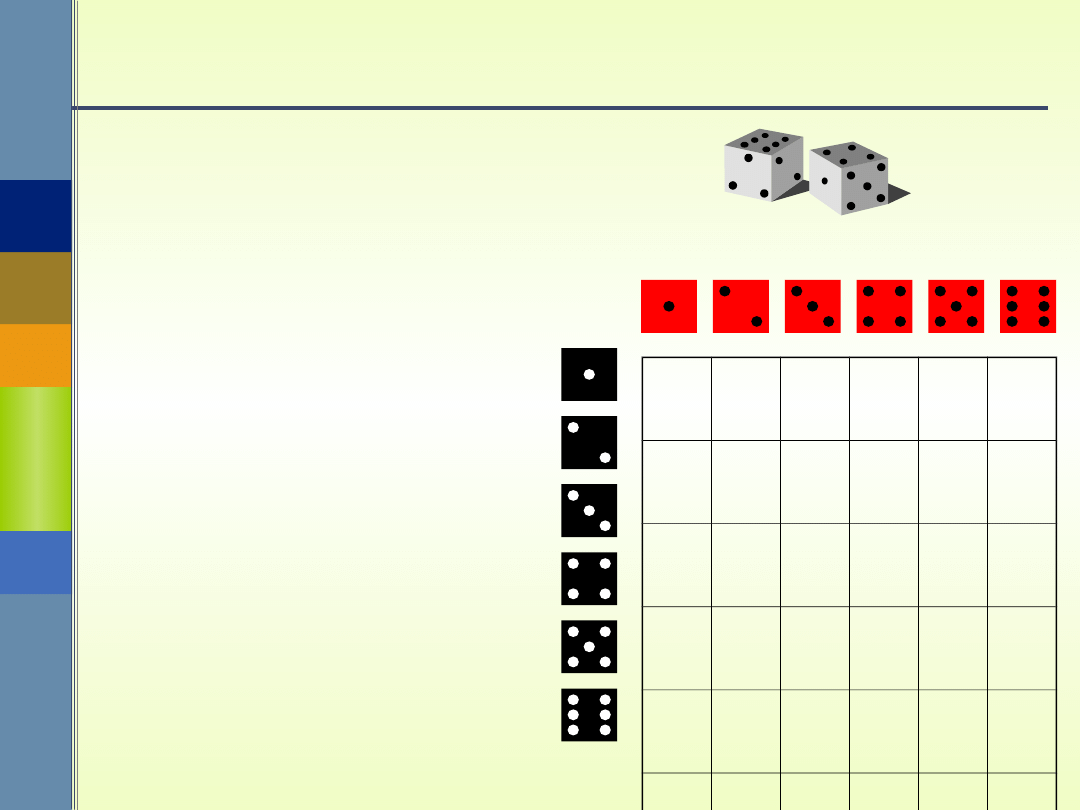
={(i,j): i,j

=1,2,3,4,5,6}

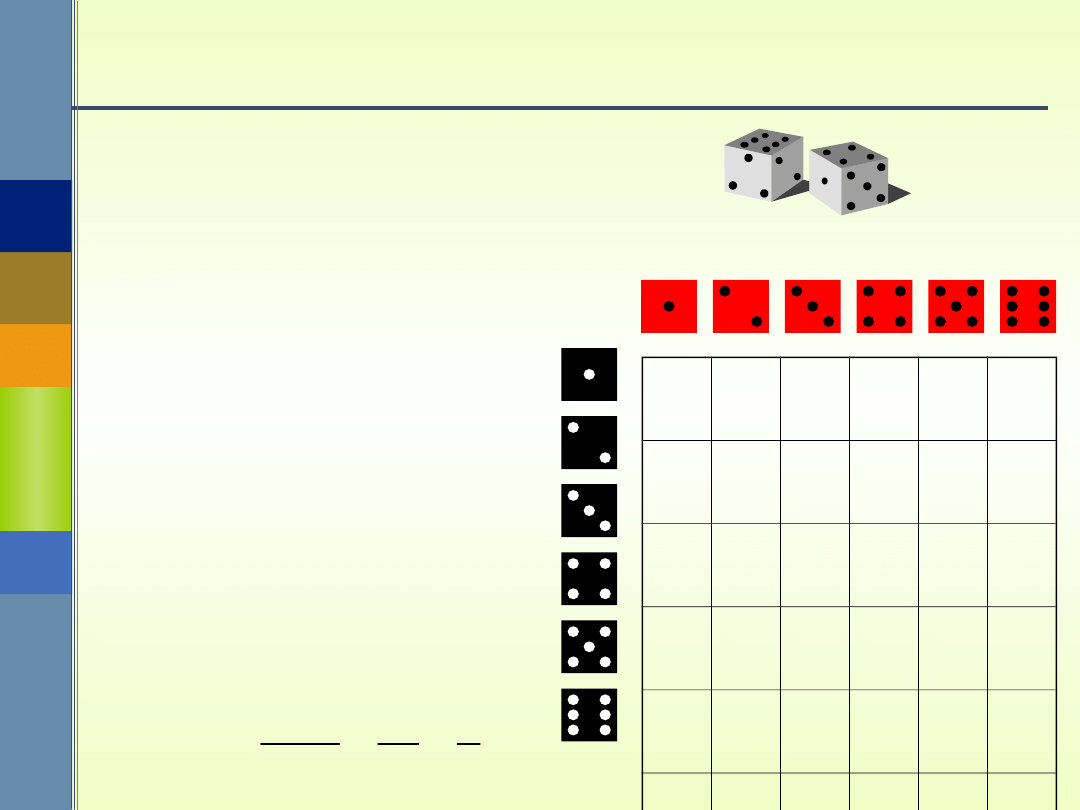
Przykład

Rzucamy dwiema kostkami do gry.
Jakie jest prawdopodobieństwo, że

suma wyrzuconych oczek:
a) wynosi dokładnie 7,
b) jest większa od 8,
c) jest podzielna przez 5?

(1,1
)

(1,2
)

(1,3
)

(1,4
)

(1,5
)

(1,6
)

(2,1
)

(2,2
)

(2,3
)

(2,4
)

(2,5
)

(2,6
)

(3,1
)

(3,2
)

(3,3
)

(3,4
)

(3,5
)

(3,6
)

(4,1
)

(4,2
)

(4,3
)

(4,4
)

(4,5
)

(4,6
)

(5,1

)

(5,2

)

(5,3

)

(5,4

)

(5,5

)

(5,6

)

(6,1
)

(6,2
)

(6,3
)

(6,4
)

(6,5
)

(6,6
)

n( ) =

36

a)

A



={(i,j): i +j =

7}

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

42 /

64





={(i,j): i,j

=1,2,3,4,5,6}

Przykład

Rzucamy dwiema kostkami do gry.
Jakie jest prawdopodobieństwo, że

suma wyrzuconych oczek:
a) wynosi dokładnie 7,
b) jest większa od 8,
c) jest podzielna przez 5?

(1,1
)

(1,2
)

(1,3
)

(1,4
)

(1,5
)

(1,
6)

(2,1
)

(2,2
)

(2,3
)

(2,4
)

(2,
5)

(2,6
)

(3,1
)

(3,2
)

(3,3
)

(3,
4)

(3,5
)

(3,6
)

(4,1
)

(4,2
)

(4,
3)

(4,4
)

(4,5
)

(4,6
)

(5,1

)

(5,
2)

(5,3

)

(5,4

)

(5,5

)

(5,6

)

(6,
1)

(6,2
)

(6,3
)

(6,4
)

(6,5
)

(6,6
)

n( ) =

36

a)

A



={(i,j): i +j =

7} n(A) = 6

( )

6

1

( )

.

( ) 36 6

n A

P A

n

=

=

=

W

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

43 /

64





={(i,j): i,j

=1,2,3,4,5,6}

Przykład

Rzucamy dwiema kostkami do gry.
Jakie jest prawdopodobieństwo, że

suma wyrzuconych oczek:
a) wynosi dokładnie 7,
b) jest większa od 8,
c) jest podzielna przez 5?

(1,1
)

(1,2
)

(1,3
)

(1,4
)

(1,5
)

(1,6
)

(2,1
)

(2,2
)

(2,3
)

(2,4
)

(2,5
)

(2,6
)

(3,1
)

(3,2
)

(3,3
)

(3,4
)

(3,5
)

(3,6
)

(4,1
)

(4,2
)

(4,3
)

(4,4
)

(4,5
)

(4,6
)

(5,1

)

(5,2

)

(5,3

)

(5,4

)

(5,5

)

(5,6

)

(6,1
)

(6,2
)

(6,3
)

(6,4
)

(6,5
)

(6,6
)

n( ) =

36

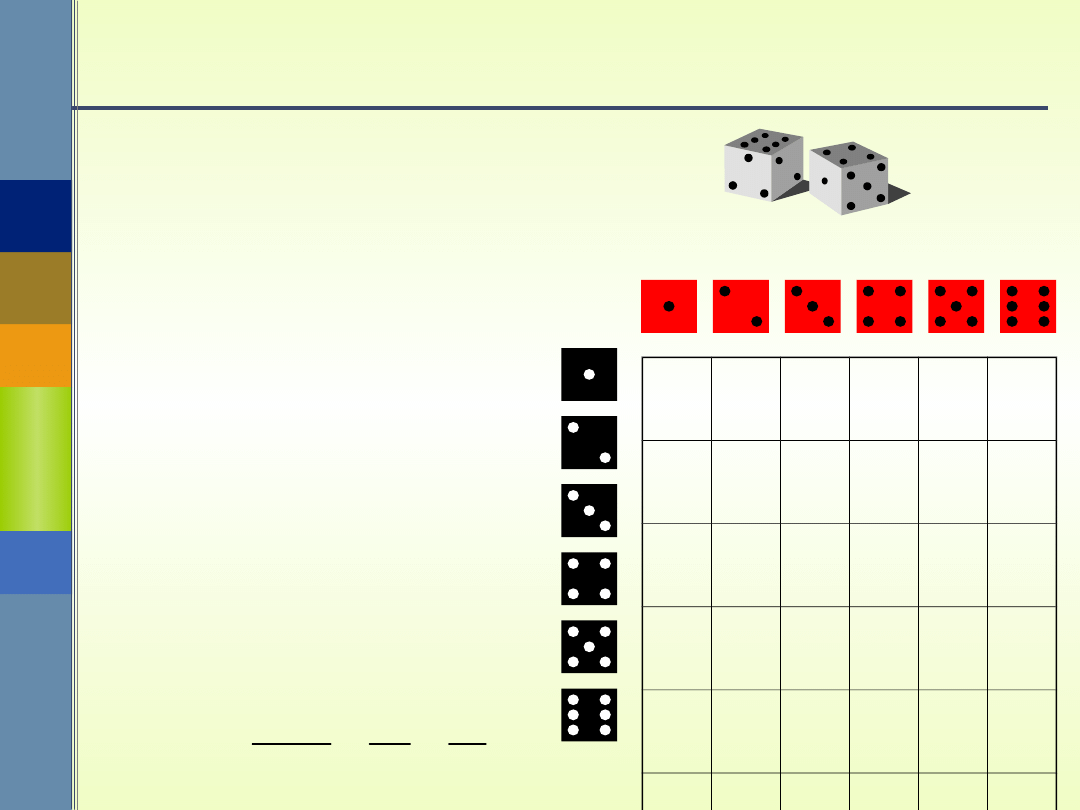
b)

B



={(i,j): i +,j >

8}

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

44 /

64





={(i,j): i,j

=1,2,3,4,5,6}

Przykład

Rzucamy dwiema kostkami do gry.
Jakie jest prawdopodobieństwo, że

suma wyrzuconych oczek:
a) wynosi dokładnie 7,
b) jest większa od 8,
c) jest podzielna przez 5?

(1,1
)

(1,2
)

(1,3
)

(1,4
)

(1,5
)

(1,6
)

(2,1
)

(2,2
)

(2,3
)

(2,4
)

(2,5
)

(2,6
)

(3,1
)

(3,2
)

(3,3
)

(3,4
)

(3,5
)

(3,
6)

(4,1
)

(4,2
)

(4,3
)

(4,4
)

(4,
5)

(4,
6)

(5,1

)

(5,2

)

(5,3

)

(5,
4)

(5,
5)

(5,
6)

(6,1
)

(6,2
)

(6,
3)

(6,
4)

(6,
5)

(6,
6)

n( ) =

36

b)

B



={(i,j): i +,j >

8} n(B) =

10

( ) 10

5

( )

.

( ) 36 18

n B

P B

n

=

=

=

W

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

45 /

64





={(i,j): i,j

=1,2,3,4,5,6}

Przykład

Rzucamy dwiema kostkami do gry.
Jakie jest prawdopodobieństwo, że

suma wyrzuconych oczek:
a) wynosi dokładnie 7,
b) jest większa od 8,
c) jest podzielna przez 5?

(1,1
)

(1,2
)

(1,3
)

(1,4
)

(1,5
)

(1,6
)

(2,1
)

(2,2
)

(2,3
)

(2,4
)

(2,5
)

(2,6
)

(3,1
)

(3,2
)

(3,3
)

(3,4
)

(3,5
)

(3,6
)

(4,1
)

(4,2
)

(4,3
)

(4,4
)

(4,5
)

(4,6
)

(5,1

)

(5,2

)

(5,3

)

(5,4

)

(5,5

)

(5,6

)

(6,1
)

(6,2
)

(6,3
)

(6,4
)

(6,5
)

(6,6
)

n( ) =

36

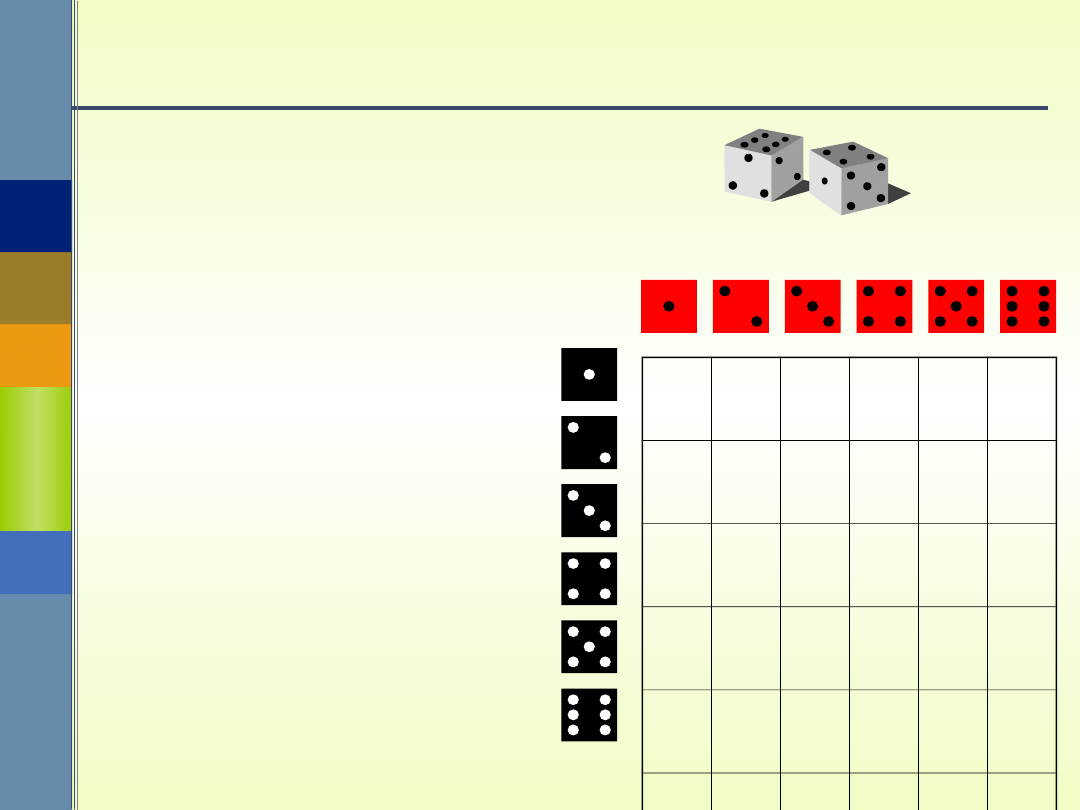
c)

C



={(i,j): 5| (i

+,j)}

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

46 /

64





={(i,j): i,j

=1,2,3,4,5,6}

Przykład

Rzucamy dwiema kostkami do gry.
Jakie jest prawdopodobieństwo, że

suma wyrzuconych oczek:
a) wynosi dokładnie 7,
b) jest większa od 8,
c) jest podzielna przez 5?

(1,1
)

(1,2
)

(1,3
)

(1,
4)

(1,5
)

(1,6
)

(2,1
)

(2,2
)

(2,
3)

(2,4
)

(2,5
)

(2,6
)

(3,1
)

(3,
2)

(3,3
)

(3,4
)

(3,5
)

(3,6
)

(4,
1)

(4,2
)

(4,3
)

(4,4
)

(4,5
)

(4,
6)

(5,1

)

(5,2

)

(5,3

)

(5,4

)

(5,
5)

(5,6

)

(6,1
)

(6,2
)

(6,3
)

(6,
4)

(6,5
)

(6,6
)

n( ) =

36

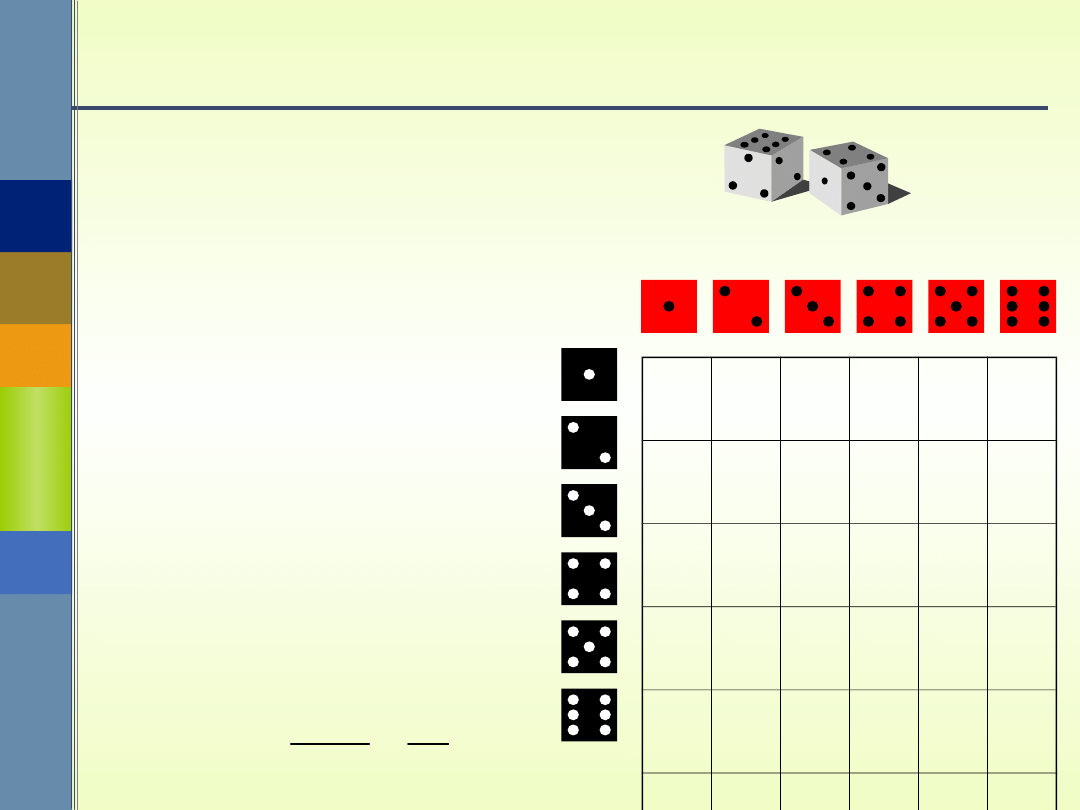
c)

C



={(i,j): 5| (i

+,j)}n(C) = 7

( )

7

( )

.

( ) 36

n C

P C

n

=

=

W

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

47 /

64

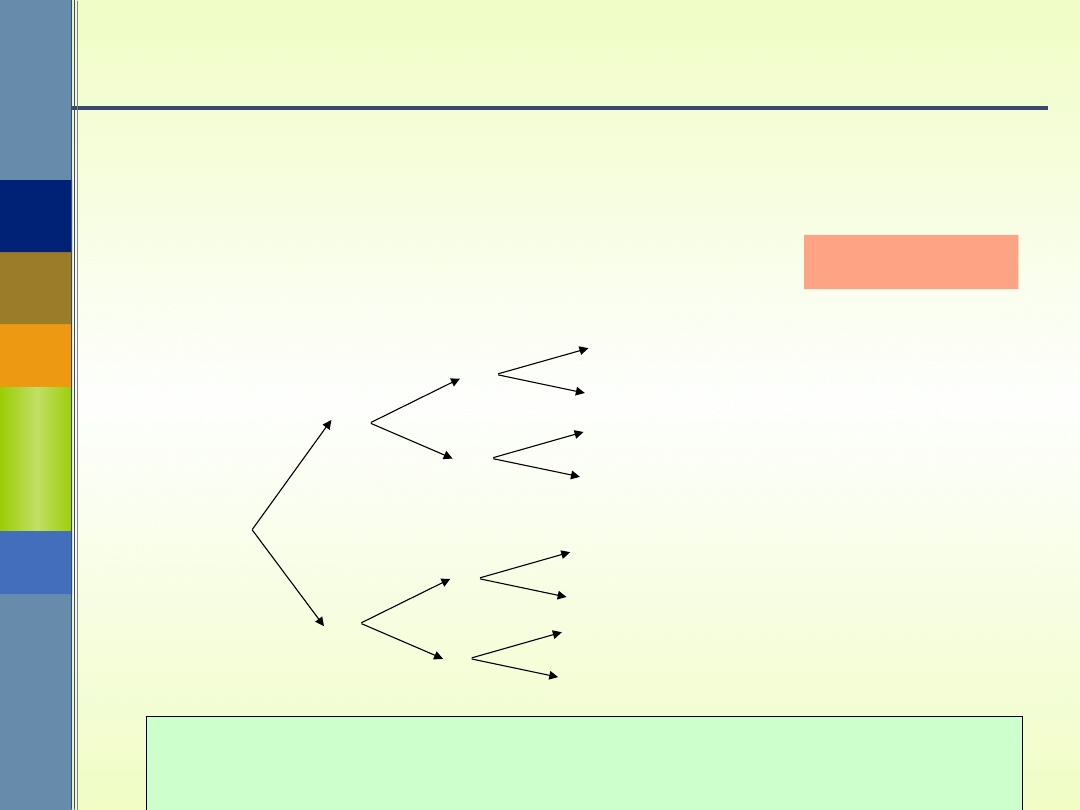
Przykład

R

O

R

O

O

R

R

R

R

R

O

O

O

O

RRR

RRO
ROR

ROO

ORR

ORO
OOR

OOO

 = {RRR, RRO, ROR, ROO, ORR, ORO, OOR,

OOO}

Rzucono trzy razy symetryczną monetą.
Obliczyć prawdopodobieństwo, że orzeł
wypadł 2 razy.

STAR
T

Wyniki pierwszego
rzutu

Wyniki dwóch
rzutów

Wyniki trzech
rzutów

n() = 8

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

48 /

64

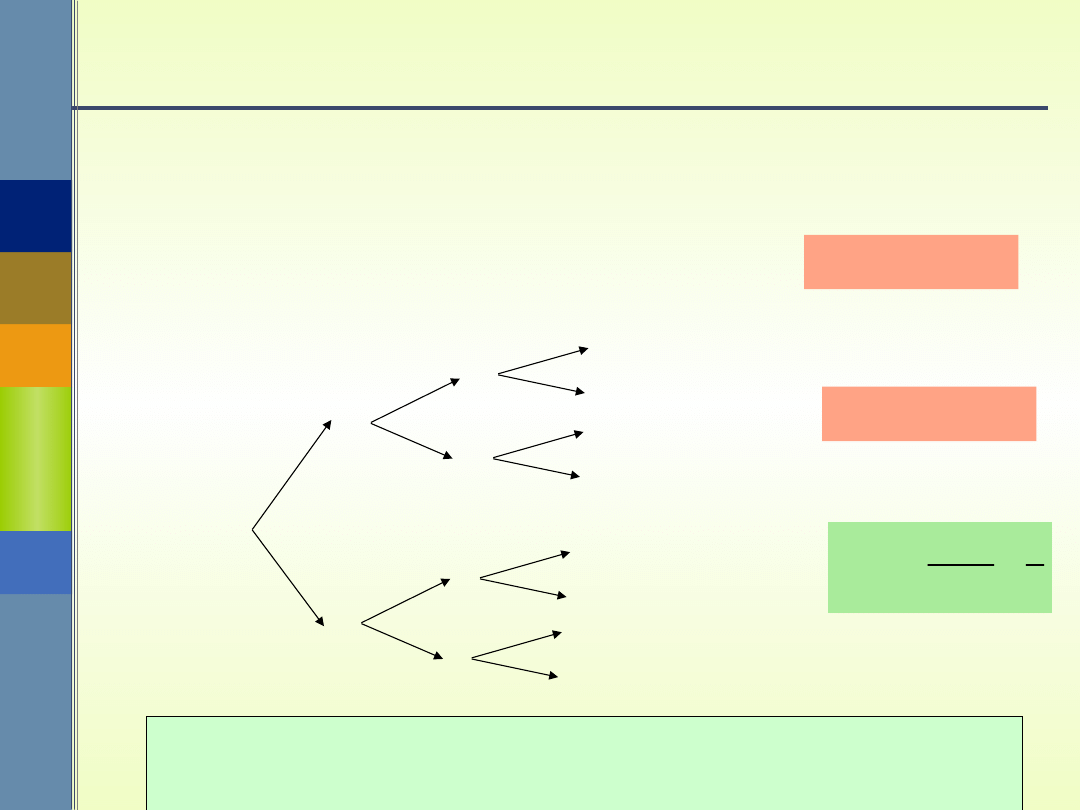
Przykład

R

O

R

O

O

R

R

R

R

R

O

O

O

O

RRR

RRO
ROR

ROO

ORR

ORO
OOR

OOO

 = {RRR, RRO, ROR, ROO, ORR, ORO, OOR,

OOO}

Rzucono trzy razy symetryczną monetą.
Obliczyć prawdopodobieństwo, że orzeł
wypadł 2 razy.

STAR
T

Wyniki pierwszego
rzutu

Wyniki dwóch
rzutów

Wyniki trzech
rzutów

n() = 8

n(A) = 3

( ) 3

( )

( ) 8

n A

P A

n

=

=

W

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

49 /

64

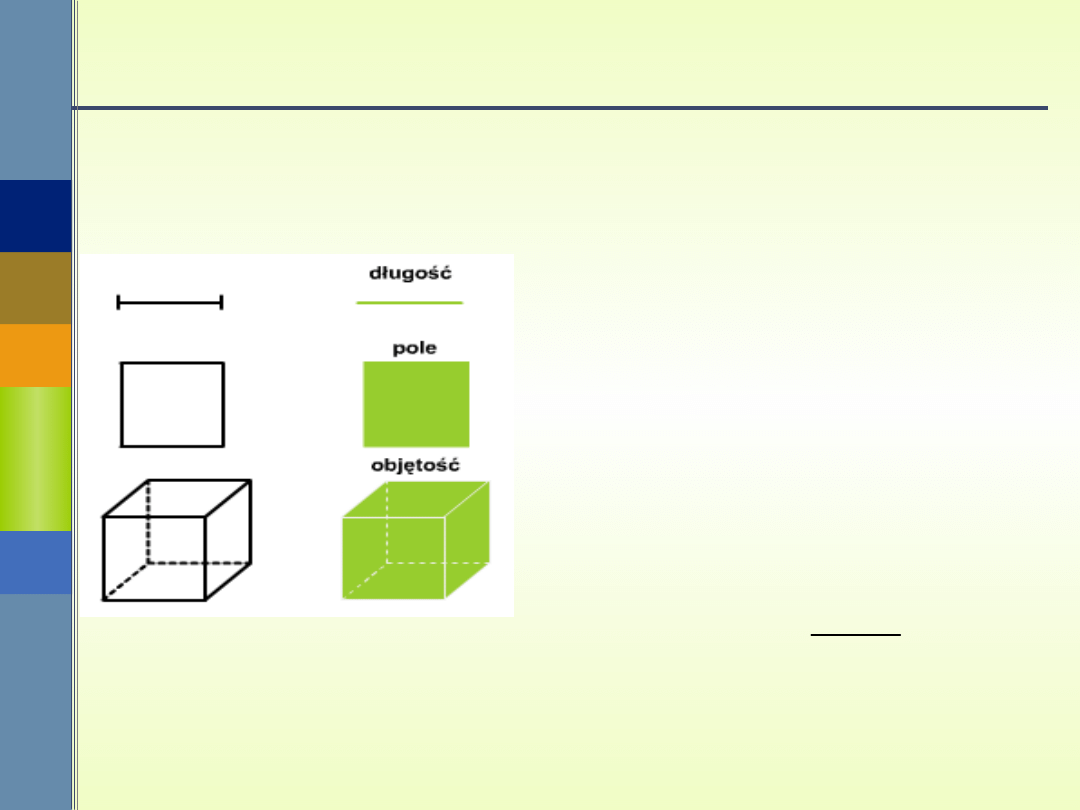
Prawdopodobieństwo geometryczne

Definicja klasyczna nie pozwala obliczać
prawdopodobieństwa w przypadku, gdy zbiory A i
Ω są nieskończone.

Jeżeli jednak zbiory te mają
interpretację
geometryczną, zamiast
liczebności zbiorów można
użyć miary geometrycznej
(długość, pole powierzchni,
objętość).

( )

( )

( )

m A

p A

m

=

W

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

50 /

64

Z przedziału  = [0,4] wybieramy losowo punkt.

Jakie jest prawdopodobieństwo, że wybrany
punkt będzie należał do przedziału A = [1,2]?

Miary odpowiednich zbiorów – tutaj długości
przedziałów – są równe odpowiednio: l() = 4 i l(A)

= 1.

Prawdopodobieństwo opisanego zdarzenia
wynosi:

( ) 1

( )

.

( ) 4

l A

P A

l

=

=

W

Przykład

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

51 /

64

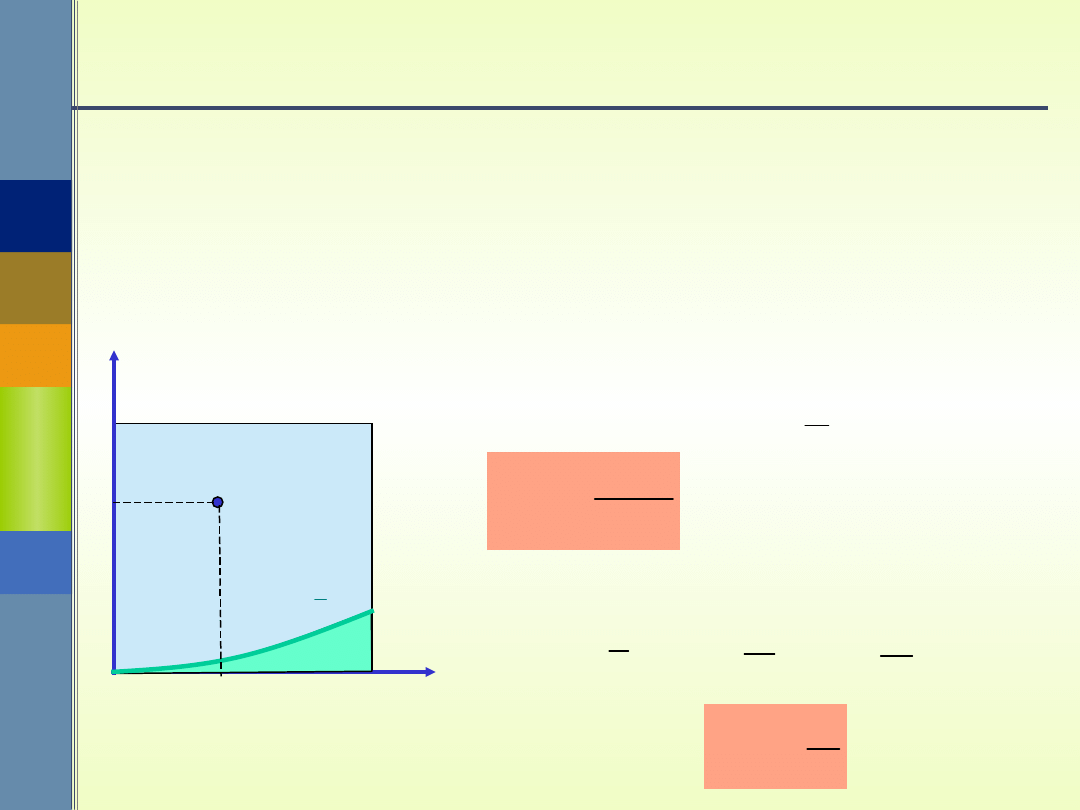
Przykład

Z odcinka [0;1] wybieramy losowo i niezależnie od
siebie dwie liczby p i q, a następnie tworzymy
równanie x

2

+ px + q = 0 . Jakie jest

prawdopodobieństwo, że mieć ono będzie
pierwiastki rzeczywiste?

 = {(p,q): 0  p  1, 0 

q  1 }

1

1

p

q



A = {(p,q): p

2

– 4q  0 }

2

1

4

q

p

�

2

1
4

q

p

=

A

( )

( )

( )

m A

P A

m

=

W

( ) 1

m W =

1

2

0

1

( )

4

m A

p dp

=

=

�

1

( )

12

P A =

1

3

0

1

12

p

�

�

�

�

�

�

1

12

=

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

52 /

64

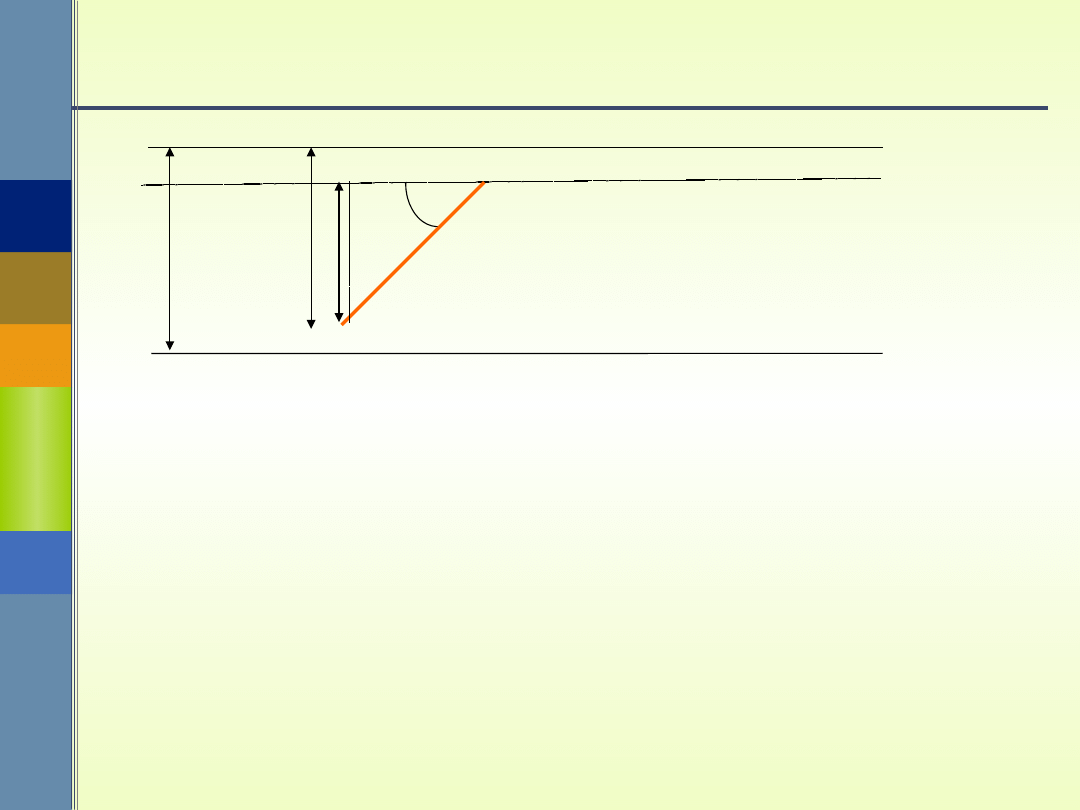
Zadanie Buffona

Płaszczyznę podzielono prostymi równoległymi
odległymi o D. Na płaszczyznę tę rzucamy w
sposób przypadkowy igłę o długości L < D. Jakie
jest prawdopodobieństwo przecięcia przez igłę
jednej z tych prostych?

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

53 /

64

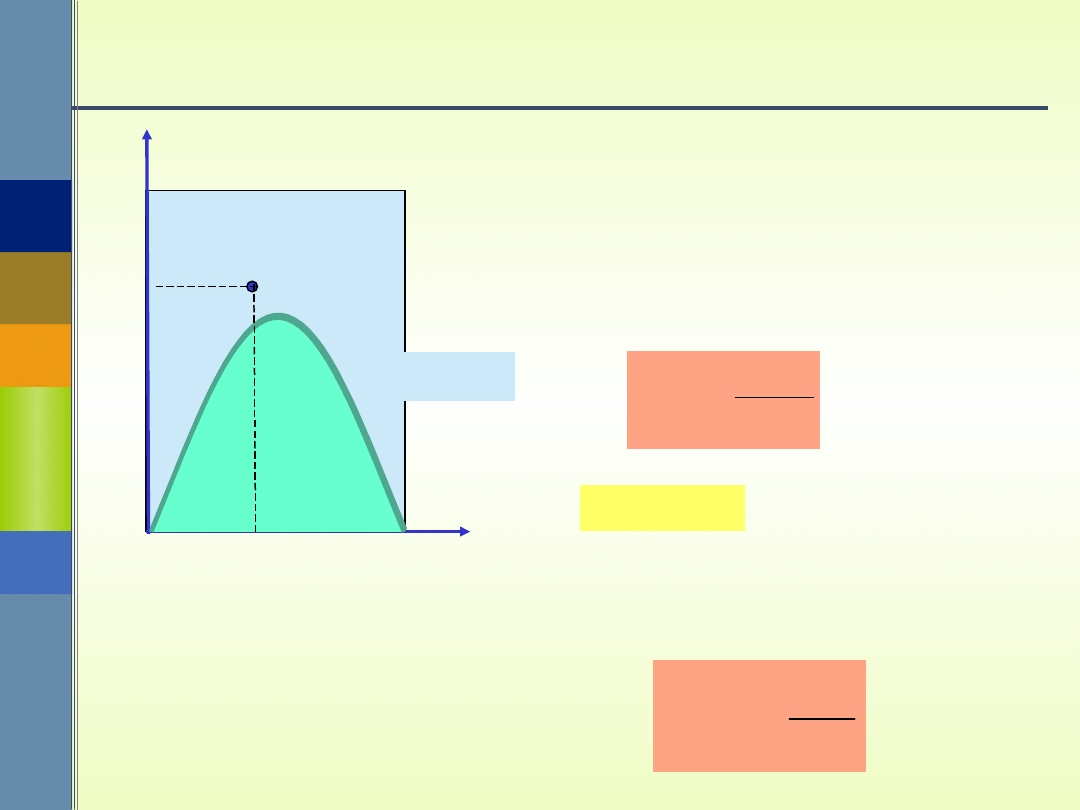
Zadanie Buffona



sin

L

d 

0

 

 

D

y 



0

Igła przetnie linię, gdy

sin .

y L

q

�



y

L

D

d

Położenie igły można opisać przy pomocy
dwóch liczb:



- kąt, jaki tworzy igła z dowolną prostą równoległą do

narysowanych,

y – odległość skrajnego końca igły do najbliższej linii
znajdującej się powyżej tego końca.

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

54 /

64



D



y



sin

y L

q

=

 = {(



, y): 0 



 , 0  y

 D }

A = {(



, y): y  L sin



}

Zadanie Buffona

A

( )

( )

( )

m A

P A

m

=

W

( )

m

D

p

W =

0

( )

sin

m A

L

d

t

q q

=

=

�

2

( )

L

P A

D

p

=

[

]

0

cos

L

p

q

-

=

cos

cos0

L

L

p +

2L

=

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

55 /

64

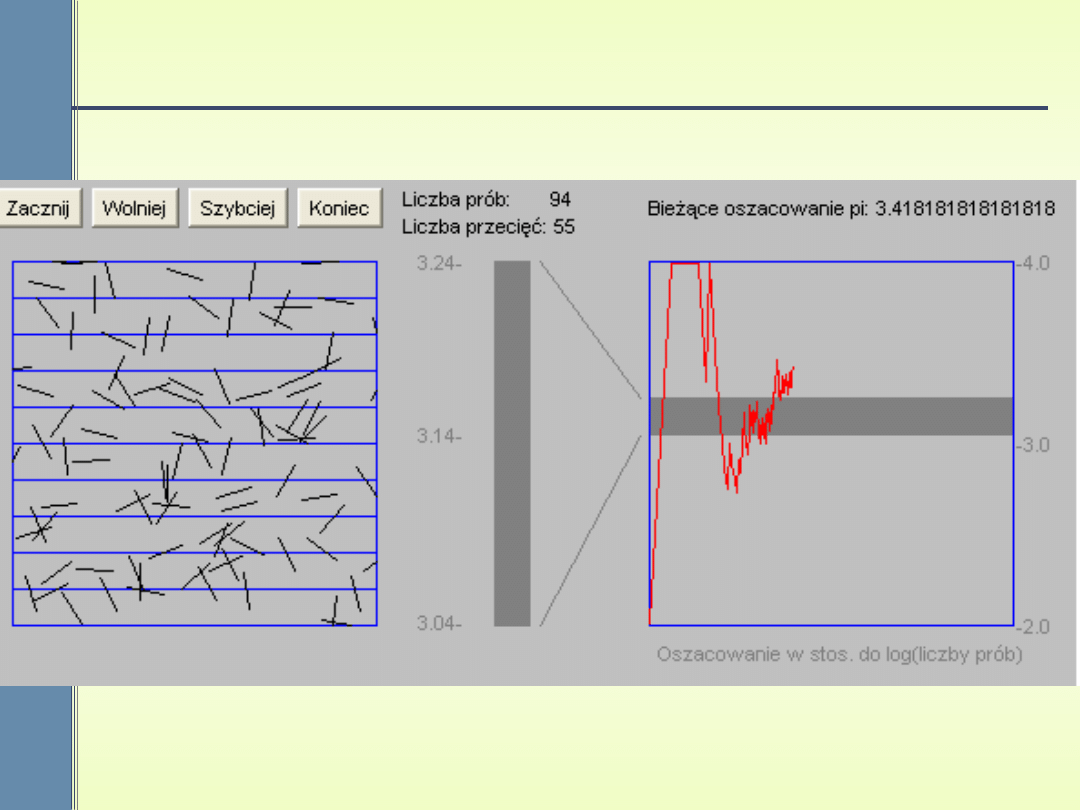
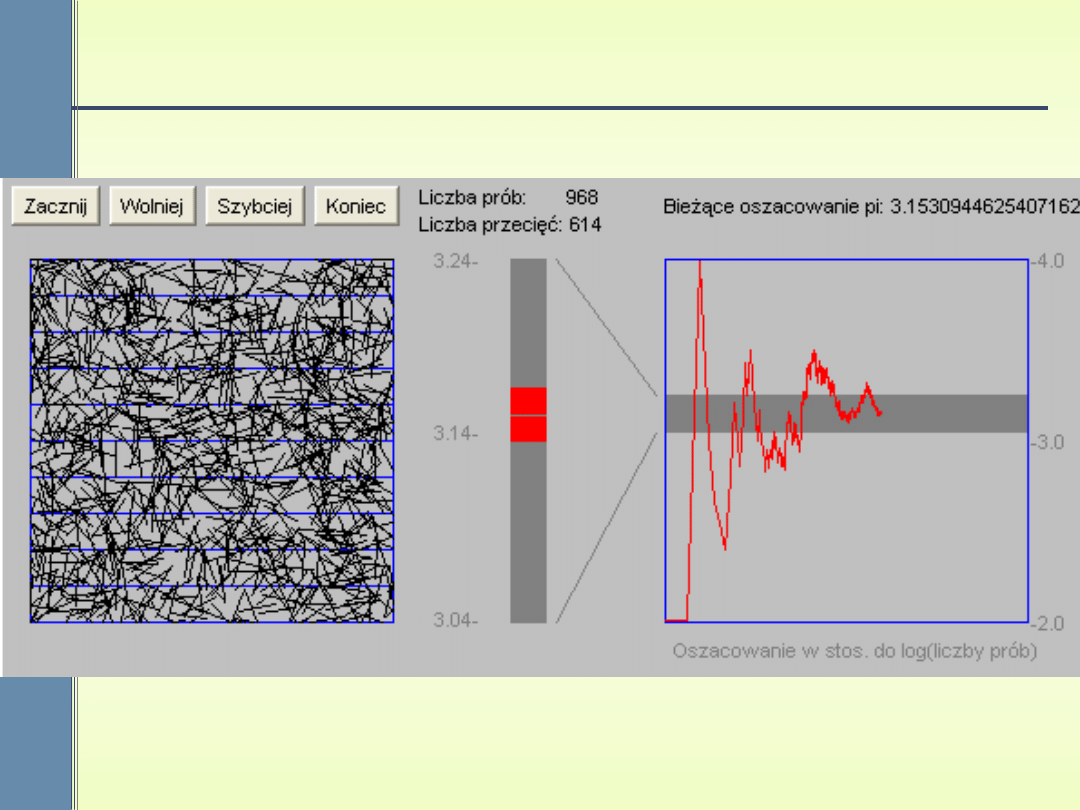
Symulacja rzutów Buffona

2

( )

.

L

P A

Dp

=

liczba igiel przecinających linię

P(przecięcia)

liczba rzuconych igiel

�

2 liczba wszystkich rzuconych igiel

liczba igiel przecinających

L

D

p � �

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

56 /

64

Symulacja rzutów Buffona

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

57 /

64

Symulacja rzutów Buffona

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

58 /

64

Symulacja rzutów Buffona

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

59 /

64

Paradoks urodzin – pytania

Na sali znajduje się n przypadkowych ludzi. Jakie
jest prawdopodobieństwo, że przynajmniej dwoje z
nich obchodzi urodziny tego samego dnia?
(Przyjąć, że rok ma 365 dni).

Jeżeli przyjmiemy, że p(n) oznacza szukane
prawdopodobieństwo, to określić n, dla którego:

a) p(n) > 50 %,

b) p(n) > 99 %,

c) p(n) > 99,99996
%,

d) p(n) = 100 %.

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

60 /

64

Paradoks urodzin – odpowiedzi

Wyznaczymy prawdopodobieństwo , że każdy
z n przypad-kowych ludzi, obchodzi urodziny
innego dnia.

( )

p n

364

363

365 (

1)

( ) 1 (

) (

) (

)

365

365

365

n

p n

-

-

= �

�

�

�

�

( ) 1

( )

p n

p n

= -

Prawdopodobieństwo, że trzeci

człowiek ma inną date

urodzenia niż dwaj pierwsi.

Dla pierwszego

człowieka to

prawdopodobieństwo

wynosi 1.

Prawdopodobieństwo, że drugi

człowiek ma inną date

urodzenia niż pierwszy.

365!

(365) (365

)!

n

n

=

-

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

61 /

64

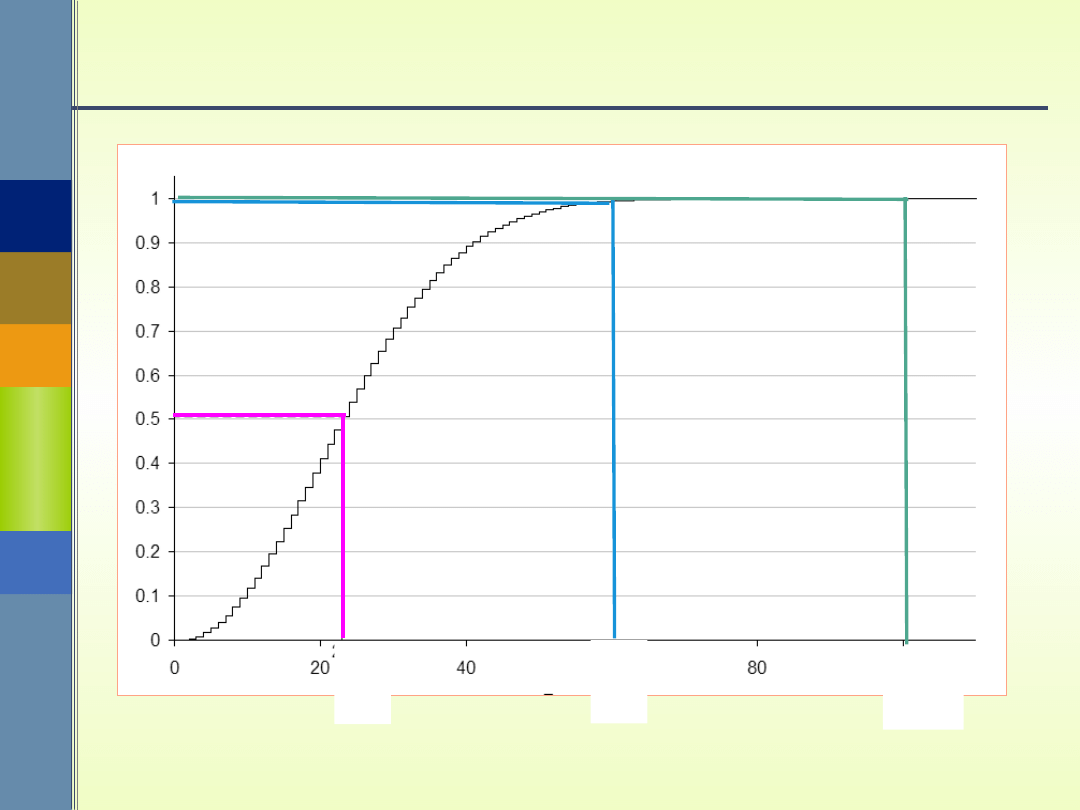
Paradoks urodzin – odpowiedzi

a) Dla 23 i więcej ludzi

–

p(n) > 50 %.

b) Dla 60 i więcej ludzi

–

p(n) > 99 %.

c) Dla 100 i więcej ludzi

–

p(n) > 99,99996

%.

d) Dla 366 i więcej ludzi

–

p(n) = 100 %.

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

62 /

64

Ilustracja graficzna paradoksu

urodzin

2
3

6
0

10
0

x - liczba przypadkowych
osób

p – prawdop. przynajmniej
jednej wspólnej daty
urodzin

Tomasz Kowalski - Matematyka. Wykład 21: Kombinatoryka.
Prawdopodobieństwo

Slajd

63 /

64