Metody Monte Carlo

Najszerzej: są to metody oparte na wykorzystaniu
liczb losowych do rozwiązania określonego problemu
obliczeniowego.

Początki: prawdopodobnie starożytność

Pierwsze udokumentowane użycie: G. Comte de
Buffon (1777) obliczenia całki przez rzucanie igły
na poziomą płaszczyznę
pokrytą równoległymi liniami prostymi.

Pierwsze zastosowanie na wielką skalę: J. von
Neumann, S. Ulam, N. Metropolis, R.P. Feynman i
in. (lata 1940-te; projekt Manhattan) obliczenia
rozpraszania i absorpcji neutronów. Nazwa
,,Monte Carlo” została wymyślona jako kryptonim
dla tego typu rachunków i odpowiednich metod
matematycznych.

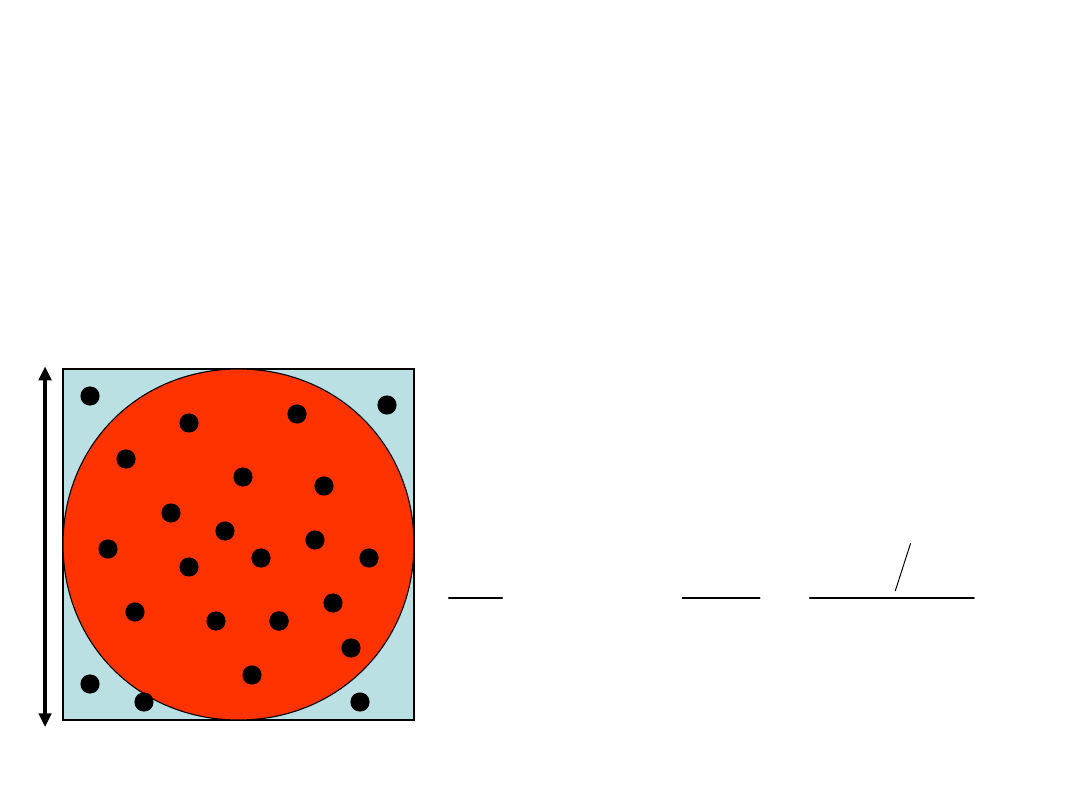
Zgrubny podział metod Monte Carlo

Metoda von Neumanna

Metoda Metropolisa (łańcuchy Markowa)

Przykład zastosowania
podejścia von Neumanna do
obliczania liczby 

1

 















1

2

1

4

2

lim

tot

N

N

n

S

S





Metoda Metropolisa (łańcuchy Markowa)

1. Bierzemy startową konfigurację układu daną współrzędnymi

(x

1

0

,y

1

0

,z

1

0

,…,x

n

0

,y

n

0

,z

n

0

); tej konfiguracji odpowiada energia E

0

.

2. Zaburzamy losowo wybraną współrzędną, np. x

i

0

or x

i

(mała

wartość).

3. Obliczamy energię nowej konfiguracji i oznaczamy ją jako E

1

.

4. Jeżeli E

1

<E

0

to nową konfigurację akceptujemy traktując jako

nową konfigurację startową i przechodzimy do punktu 1; w
przeciwnym przypadku przechodzimy do punktu 5.

5. Wykonujemy test Metropolisa:

a) Generujemy liczbę losową y z przedziału (0,1).

b) Jeżeli exp[-(E

1

-E

0

)/kT]>y, (k jest stałą Boltzmanna)

akceptujemy nową konfigurację, w przeciwnym przypadku
przechodzimy do punktu 2 ze starą konfiguracją.

Podstawowe pojęcia teorii prawdopodobieństwa:

•Zdarzenie elementarne jest to możliwy wynik
doświadczenia losowego, zwykle przypisane jest jemu
pewne prawdopodobieństwo wystąpienia.

•Prawdopodobieństwo jest to funkcja P(X), która
przyporządkowuje każdemu elementowi zbioru
zdarzeń losowych pewną nieujemną wartość
rzeczywistą.

Definicje prawdopodobieństwa:

n

A

k

A

P

n

n

)

(

lim

)

(







Definicja klasyczna (Laplace'a) w roku 1812.

Prawdopodobieństwem zajścia zdarzenia A
nazywamy iloraz liczby zdarzeń sprzyjających
zdarzeniu A do liczby wszystkich możliwych
przypadków, zakładając, że wszystkie przypadki
wzajemnie się wykluczają i są jednakowo możliwe.

Definicja częstościowa:

gdzie k

n

(A) to liczba rezultatów

sprzyjających zdarzeniu A po n
próbach.

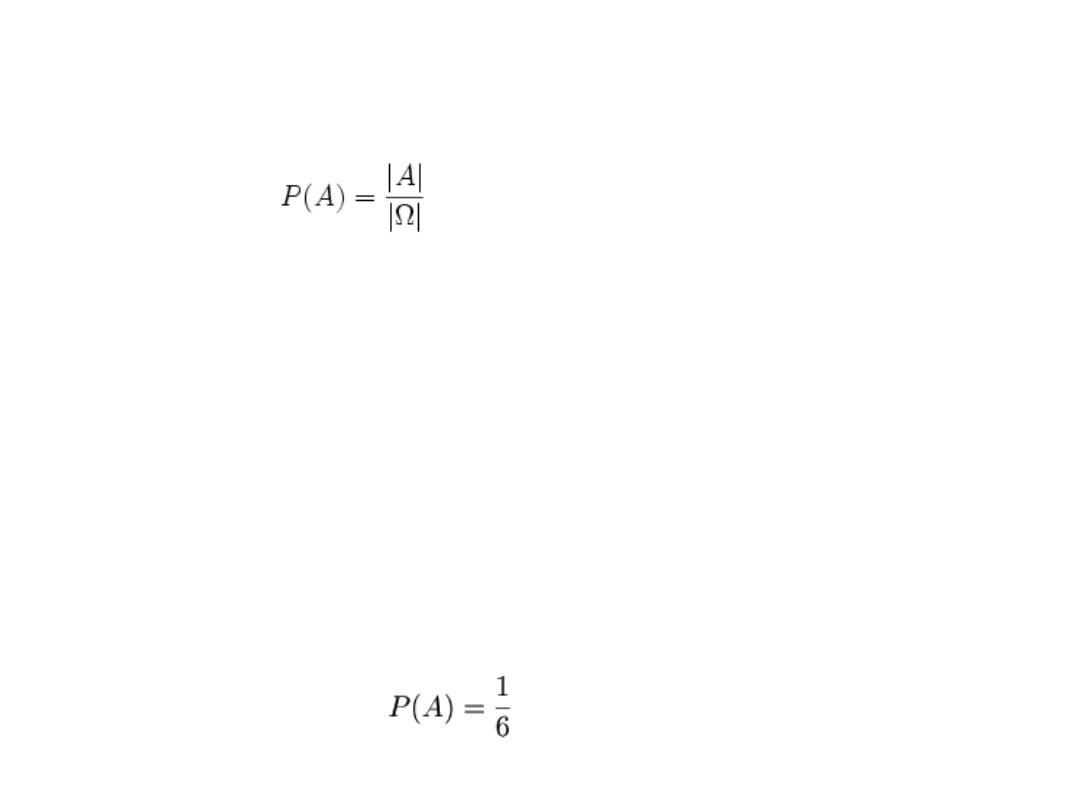
Prawdopodobieństwo zajścia zdarzenia A możemy
zapisać w postaci:

gdzie |A| oznacza liczbę elementów zbioru A, zaś |Ω|
liczbę elementów zbioru Ω.

Przykład: Rzucamy sześcienną kostką. Jakie jest
prawdopodobieństwo, że liczba oczek będzie większa
od 5?

Zbiór zdarzeń elementarnych Ω = {1, 2, 3, 4, 5, 6},
zatem liczba możliwych zdarzeń |Ω| = 6. Zbiór zdarzeń
sprzyjających A = {6}, liczba zdarzeń sprzyjających |A|
= 1. Prawdopodobieństwo zajścia zdarzenia wynosi:

Definicje prawdopodobieństwa:

Prawdopodobieństwo geometryczne
Definicja klasyczna nie pozwala obliczać prawdopodobieństwa w
przypadku, gdy zbiory A i Ω są nieskończone, jeśli jednak zbiory
te mają interpretację geometryczną, zamiast liczebności zbiorów
można użyć miary geometrycznej (długość, pole powierzchni,
objętość).
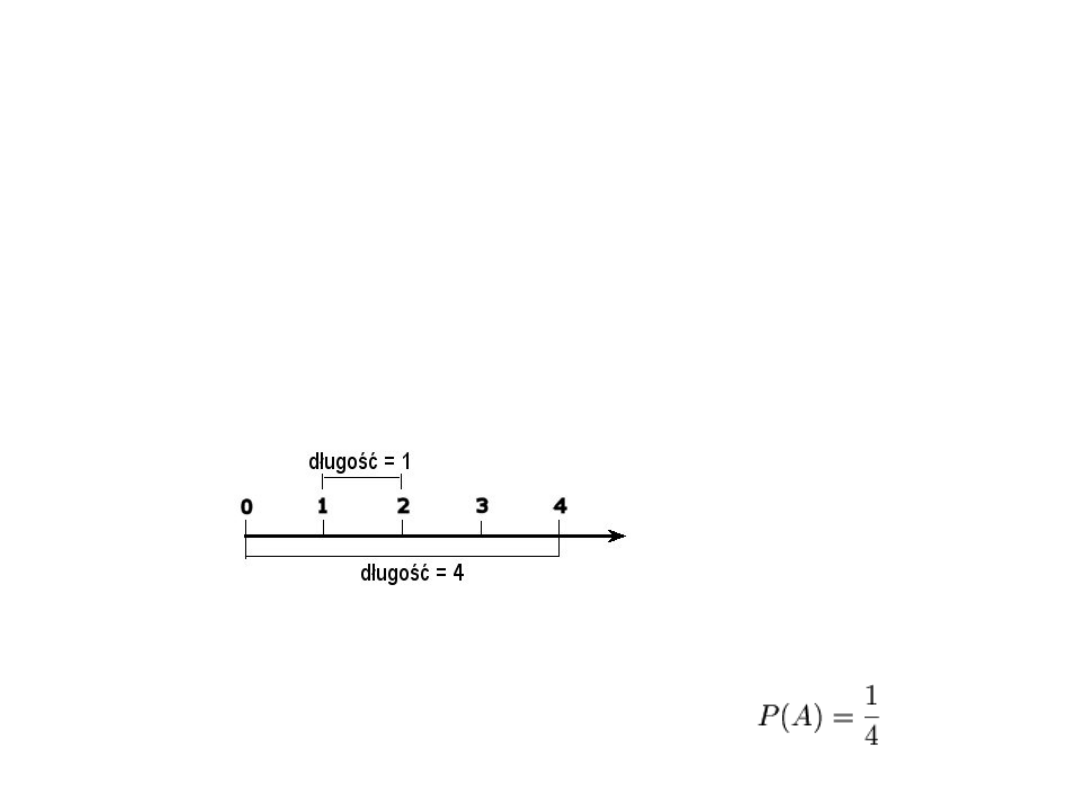
Przykład: z przedziału [0,4] wybieramy losowo punkt. Jakie jest
prawdopodobieństwo, że wybrany punkt będzie należał do
przedziału [1,2]?

Odpowiedź: Długości przedziałów wynoszą odpowiednio: |[0,4]| =
4 i |[1,2]| = 1. Zatem prawdopodobieństwo opisanego zdarzenia
wynosi:

    

Prawdopodobieństwo ma następujące własności:
P(Ω) = 1, gdzie Ω jest przestrzenią (zbiorem) zdarzeń
elementarnych
prawdopodobieństwo sumy przeliczalnego zbioru
zdarzeń parami rozłącznych jest równe sumie
prawdopodobieństw tych zdarzeń:
P(A

1



...



A

n



... ) = P(A

1

) + ... + P(A

n

) + ... Wartość

P(X) nazywa się prawdopodobieństwem zdarzenia X.
Ważniejsze własności prawdopodobieństwa:
P(A) ≥ 0
P(Ø) = 0 (UWAGA: z P(A)=0 nie wynika, że A=Ø)
A  B  P(A) ≤ P(B)

P(A) ≤ 1
A



B



P(B|A) = 1

P(A) + P(A') = 1, gdzie A′ oznacza zdarzenie losowe
przeciwne do A
P(A



B) = P(A) + P(B) - P(A



B).

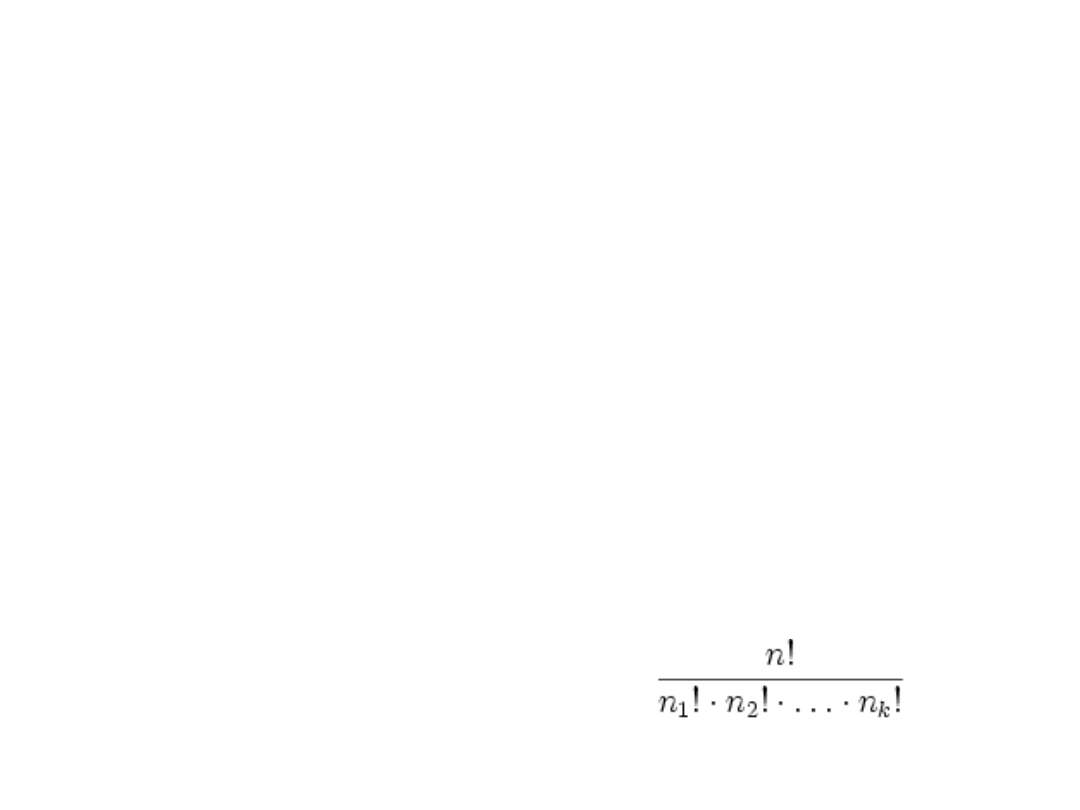
Przydatne pojęcia kombinatoryczne stosowane
przy ustalaniu liczby zdarzeń:

Permutacja jest uporządkowaniem elementów
danego zbioru – ustawieniem ich w pewnej kolejności.

Permutacja bez powtórzeń:

Permutacja z powtórzeniami:

Niech A oznacza zbiór złożony z k różnych elementów
A = {a

1

,a

2

,...,a

k

}. Permutacją n elementową z

powtórzeniami, w której elementy a

1

,a

2

,...,a

k

powtarzają się odpowiednio n

1

,n

2

,...,n

k

razy, n

1

+ n

2

+ ... + n

k

= n, jest każdy n-wyrazowy ciąg, w którym

elementy a

1

,a

2

,...,a

k

powtarzają się podaną liczbę razy.

Liczba takich permutacji z powtórzeniami wynosi:

!

n

P

n



Kombinacją k-elementową zbioru n-
elementowego A nazywa się każdy k-elementowy
podzbiór zbioru A (0≤k≤n).

Kombinacją k-elementową zbioru n-
elementowego A nazywa się każdy k-elementowy
podzbiór zbioru A (0≤k≤n) z możliwością
wystąpienia powtórzeń elementów.





)!

1

(

!

!

1









n

k

k

n

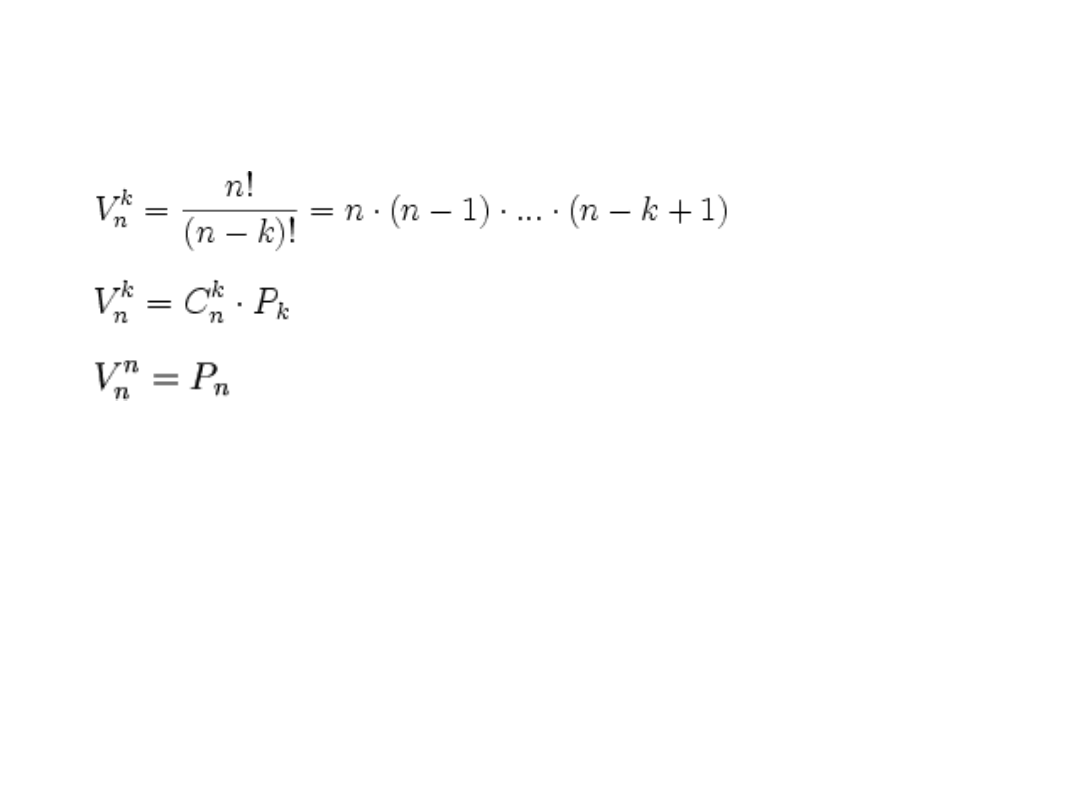
Wariacją bez powtórzeń k-wyrazową zbioru n-
elementowego A (k≤n) nazywa się każdy k-wyrazowy ciąg k
różnych elementów tego zbioru, przy czym kolejność tych
elementów ma znaczenie:

Wariacją z powtórzeniami k-wyrazową zbioru n-
elementowego A nazywa się każdy k-wyrazowy ciąg
elementów tego zbioru (dowolny element może
wystąpić wielokrotnie w ciągu).

k

k

n

n

W 

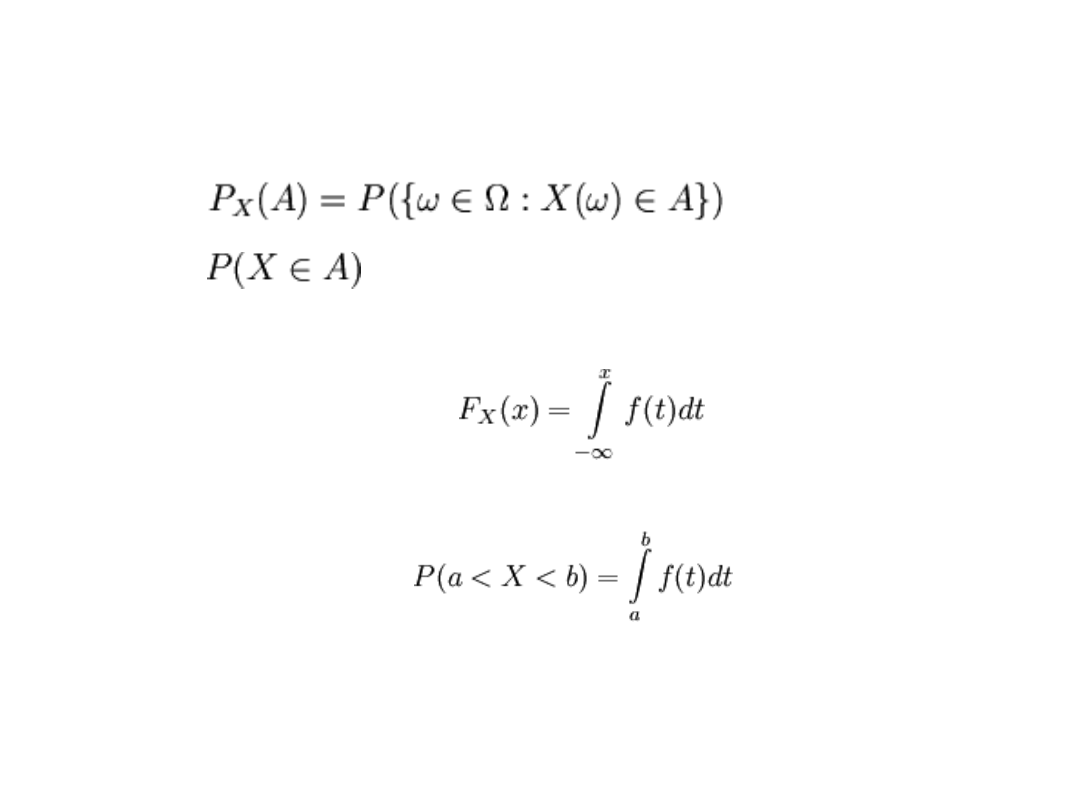
Rozkład zmiennej losowej X (o wartościach
rzeczywistych) jest to prawdopodobieństwo P

X

określone na zbiorze podzbiorów zbioru liczb
rzeczywistych R wzorem:

Funkcja gęstości rozkładu
Jeżeli istnieje funkcja f taka, że

to zmienną X nazywamy zmienną typu ciągłego. Mamy wtedy:

Funkcję f nazywamy funkcją gęstości rozkładu zmiennej X.
Funkcję P nazywamy dystrybuantą rozkładu losowego

Rozkład dwumianowy:
wielokrotna realizacja doświadczenia, w wyniku którego otrzymać
można tylko jedno z dwu wykluczających się zdarzeń –zdarzenie A
(z prawdopodobieństwem p) lub nie-A (z prawdopodobieństwem
1-p). Jako przykład można podać wielokrotnie powtarzany rzut
monetą (zdarzenie A- wyrzucenie np. reszki, p=0.5). Jeżeli wyniki
kolejnych doświadczeń oznaczymy przez x

i

(0 lub 1 w rzucaniu

monetą), to łączny rezultat n doświadczeń charakteryzuje
zmienna losowa X zdefiniowana wzorem

Niektóre rozkłady zmiennych
losowych







n

i

i

x

X

1

Rozkład dwumianowy – rozkład zależności prawdopodobieństwa
P(X=k) od wartości k w n doświadczeniach

k

n

k

p

p

k

n

k

X

P





















)

1

(

)

(

Rozkład normalny:
Mamy do czynienia z rozkładem normalnym wtedy, gdy pomiar
pewnej wielkości, mającej wartość  zakłócany jest bardzo dużą

liczbą niezależnych czynników, z których każdy z
prawdopodobieństwem ½ powoduje odchylenie o niewielką
wartość .

Gęstość prawdopodobieństwa rozkładu normalnego
niestandaryzowanego:























2

2

2

exp

2

1

)

(









x

x

f

Gęstość prawdopodobieństwa rozkładu normalnego
standaryzowanego











 



2

2

1

exp

2

1

)

(

u

u

f



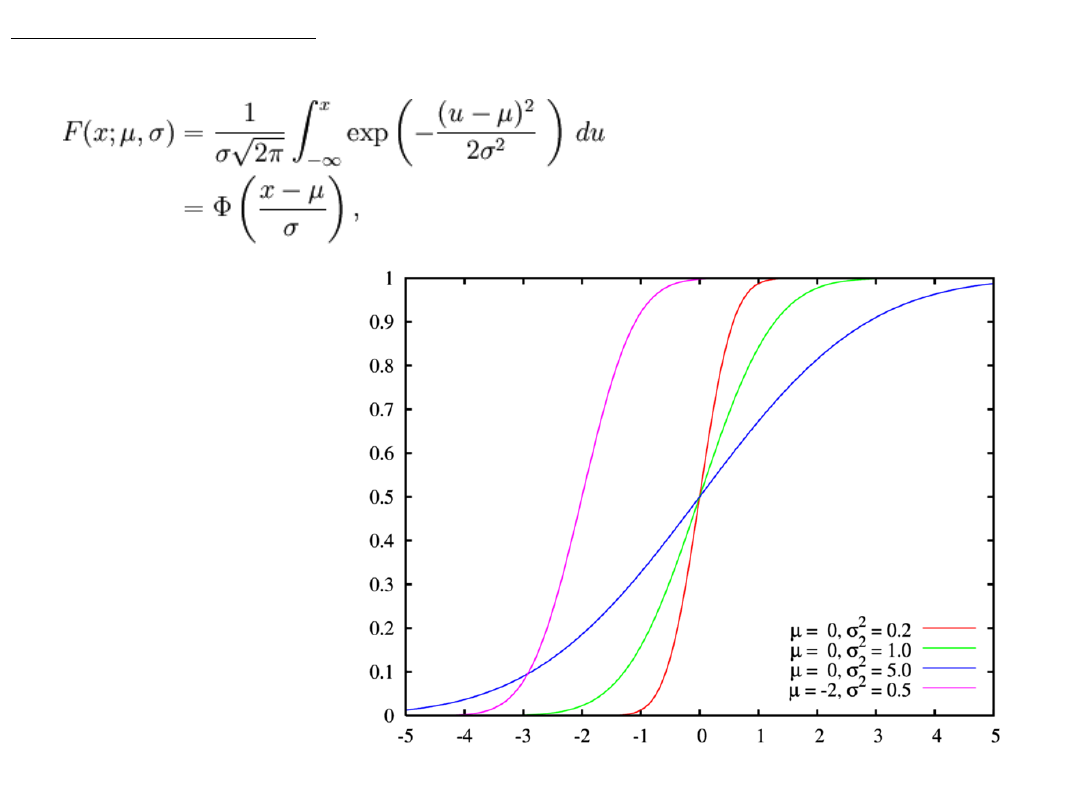
Rozkład normalny:
Dystrybuanta



(u) rozkładu niestandaryzowanego

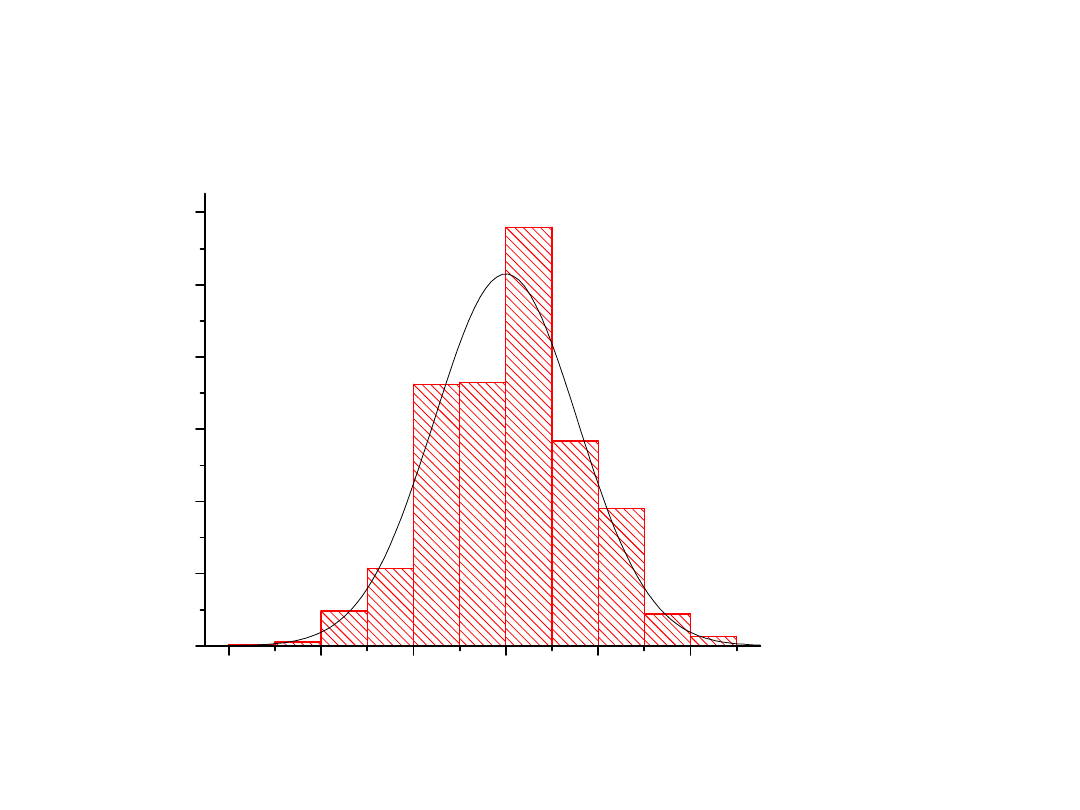
70

80

90

100

110

120

0

100

200

300

400

500

600

Teoria
klasa liczność
70-75 1.1
75-80 8.6
80-85 43.0
85-90 143.9
90-95 321.9
95-100 481.4

lic

zn

oś

ć

kl

as

y

x

Przykład wynik symulacji losowania zmiennej o rozkładzie normalnym:

Rozkład Poissona: szczególny przypadek rozkładu
dwumianowego zachodzący wtedy, gdy prawdopodobieństwo p
sukcesu jest bardzo małe, a liczba realizacji n na tyle duża, że
iloczyn np= jest wielkością stałą, dodatnią i niezbyt dużą.

























 





























e

k

n

n

k

n

k

X

P

k

k

n

k

!

1

)

(

Zastosowanie rozkładu Poissona – tam, gdzie liczba
obserwowanych przypadków n jest bardzo duża, a
prawdopodobieństwo sukcesu p bardzo małe.

Przykłady:

• rozpad promieniotwórczy: liczba jąder n duża,
prawdopodobieństwo rozpadu

konkretnego jądra bardzo

małe;

• zderzenia cząstek elementarnych, duża ilość cząstek, mała
szansa na zderzenie;

• statystyczna kontrola jakości produktów, duża ilość
sprawdzanych produktów, mała ilość produktów
wybrakowanych.

Rozkład prostokątny: Ma zastosowanie przy analizie
niepewności systematycznych. Gęstość prawdopodobieństwa
f(x) jest stała wewnątrz przedziału (a, b) i równa zero poza nim.





















b

x

i

a

x

dla

b

x

a

dla

a

b

x

f

0

1

)

(

Rozkład 

2

: Gdy X

i

są zmiennymi losowymi losowanymi z rozkładu

normalnego N(0,1), to





k

i

i

X

1

2

ma rozkład chi-kwadrat o k stopniach swobody. Gdy losowanie
odbywa się z rozkładu normalnego N(,), to zmienną losową 

2

definiujemy następująco













k

i

i

X

1

2

2

2







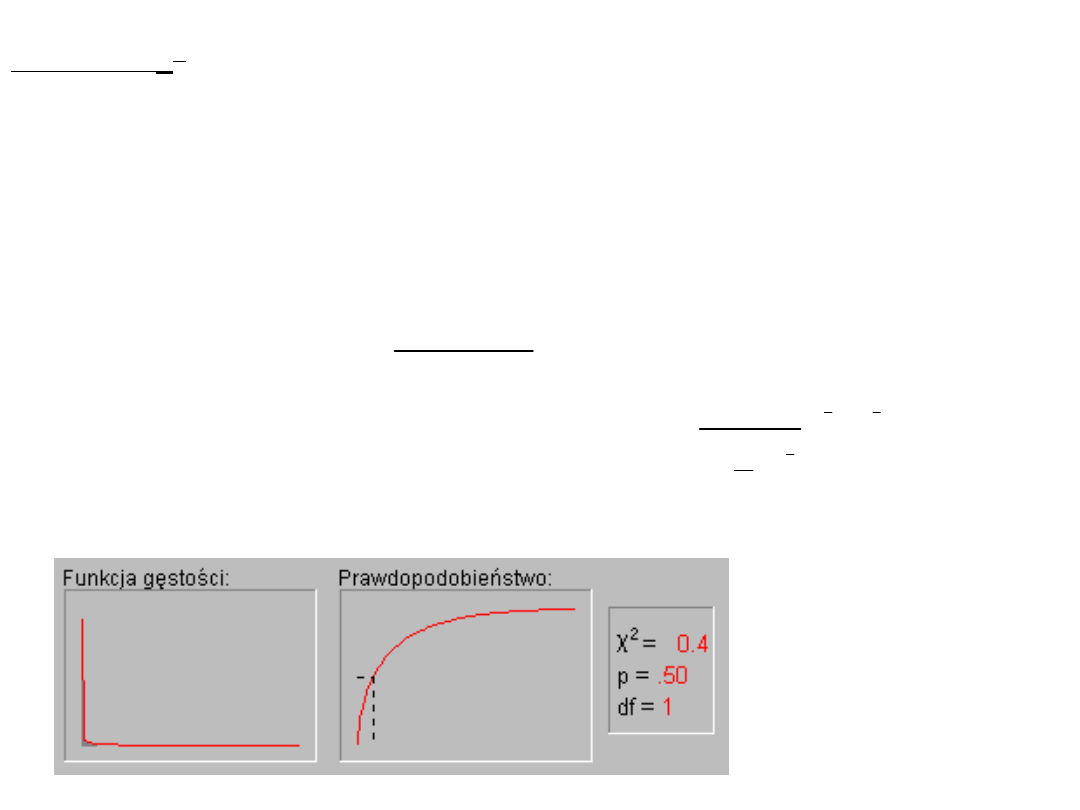
Gęstość prawdopodobieństwa rozkładu chi-kwadrat





































0

0

0

2

2

1

)

(

2

1

2

2

x

dla

x

dla

e

x

k

x

f

x

k

k

Rozkład 

2

: Gdy X

i

są zmiennymi losowymi losowanymi z rozkładu

normalnego N(0,1), to





k

i

i

X

1

2

ma rozkład chi-kwadrat o k stopniach swobody. Gdy losowanie
odbywa się z rozkładu normalnego N(,), to zmienną losową 

2

definiujemy następująco













k

i

i

X

1

2

2

2







Gęstość prawdopodobieństwa rozkładu chi-kwadrat





































0

0

0

2

2

1

)

(

2

1

2

2

x

dla

x

dla

e

x

k

x

f

x

k

k

Rozkład 

2

:

Największe znaczenie praktyczne dla rozkładu chi kwadrat mają
tablice wartości krytycznych

zmiennej losowej 

2

, dla których

2

,k





















2

,

2

k

P

 nazywa się poziomem istotności. Wielkość (1-) nazywa się poziomem ufności.