Oligopol

Model Cournot’a

Kartel

Analiza konkurencji

Model Bertranda

Monopol

Doskonała
konkurencja

Oligopo
l

Teoria
gier

MR = MC

P = MC

Dylemat

więźnia

3

Równowaga – tak
zagrają racjonalni
gracze

Efektywne
rozwiązanie

Kruszyna

I

S

Meryno

s

I

-1

,

-1

-10

,

0

S

0

,

-10

-5

,

-5

4

• Gracze:

Reynolds and Philip Morris

• Strategie: Reklamować się w telewizji (reklama), nie

reklamować się (brak)

• Wypłaty:

Zyski firm

– Każda firma zarabia 50 milionów $ ze sprzedaży
– Koszty reklamy 20 milionów $
– Reklama zabiera 30 milionów $ konkurencji

Philip Morris

brak

reklama

Reynolds

brak

50

,

50

20

,

60

reklama

60

,

20

30

,

30

Reklama papierosów

(Game Theory - Mike Shor)

5

Reklama papierosów

• Wszystkie firmy tytoniowe reklamowały

się w telewizji

• Główny lekarz ostrzegł przed skutkami

palenia papierosów

• Firmy tytoniowe bały się pozwów,

wycofały reklamy TV i obniżyły wydatki

na reklamę o 63 miliony $ - ich zyski

wzrosły o 91 milionów $

1964

1970

Model Cournota

Ujecie teoriogrowe Warunki rynkowe:

homogeniczny produkt, liniowa
funkcja popytu

• Gracze: n konkurujących

przedsiębiorstw

• Strategie: wybór wielkości produkcji

q

i

• Funkcja wypłat: zysk

)

(q

c

-

)q

q

+

...

+

p(q

=

)

(q

c

-

p(Q)q

=

i

i

i

n

1

i

i

i

i



Utarg

Koszt

Model Cournota

Przykład
Dwie firmy o identycznych funkcjach kosztów C

i

(q

i

) = 10q

i

Funkcja popytu P(q) = 100 – Q , Q = q

1

+q

2

Funkcje zysków:

2

2

2

1

2

2

2

2

1

1

2

1

2

1

1

1

10

100

10

100

q

-

))q

q

-(q

) = (

(q

- c

= p(Q)q

Π

q

-

))q

q

-(q

) = (

(q

- c

= p(Q)q

Π





Warunki maksymalizacji zysku

0

)

0

)

2

2

1

1

=

q

Π(q

=

q

Π(q









)

10

100

(

2

1

)

10

100

(

2

1

1

2

2

1









q

=

q

q

=

q

30

3

10

100

30

3

10

100

2

1









=

q

=

q

Warunki

maksymalizacji

zysku układ

równań

Równowaga

Nasha

40

900

900

2

1



p

=

Π

=

Π

Zyski/cen

a

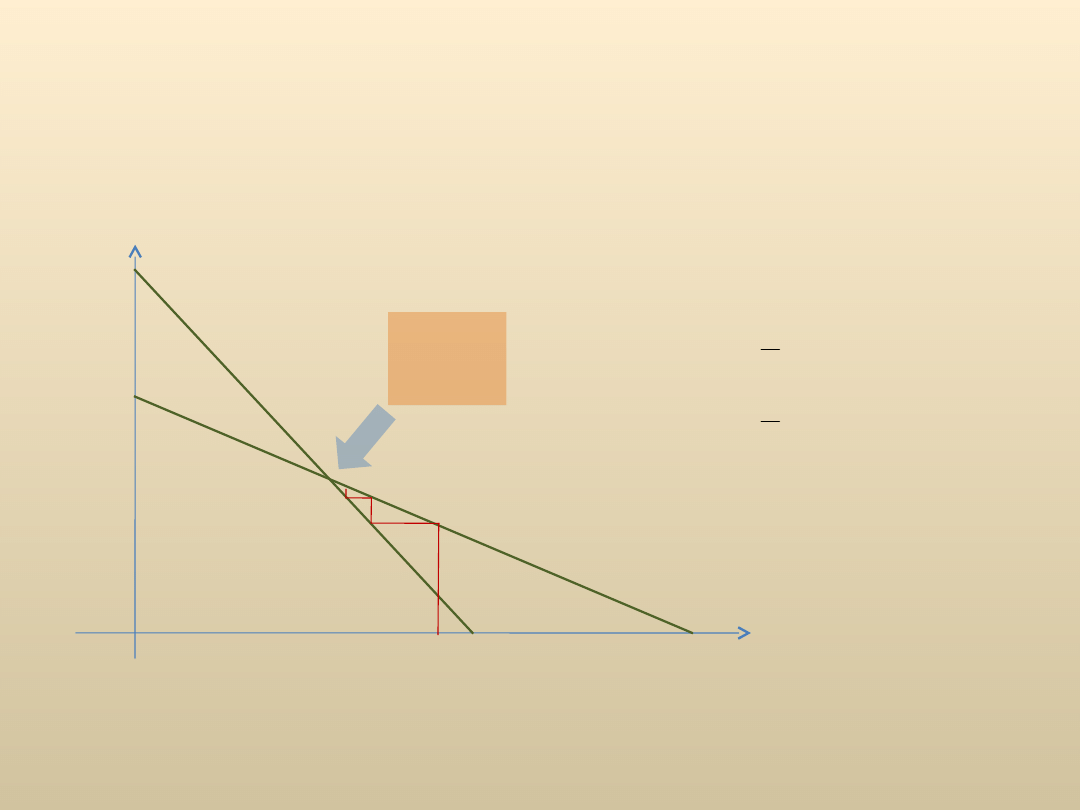
Model Cournota

Funkcja reakcji
Jak zareaguje firma 1 na działania firmy 2, aby zmaksymalizować zyski

)

10

100

(

2

1

)

(

)

10

100

(

2

1

)

(

1

1

2

2

2

1









q

=

q

R

q

=

q

R

q

1

q

2

R

2

R

1

(100-
10)/2

(100-
10)/2

(100-
10)

(100-
10)

30

30

2

1





q

q

Kartel

Firmy działają wspólnie jaka monopol

)

(q

c

= p(Q)Q -

Π

n

i

i

i

n

i

i









1

1

0

C

-

p(Q)

Q

p(Q)

i









M

Q

Warunek równowagi w kartelu

MR całej gałęzi jest równe

kosztowi krańcowemu

dla wszystkich firm

0

)

=

Q

Π(Q







MR

MC

i



Zysk

10

2

100



 Q

przykład

45



Q

55

5

,

1112

2

,

1







p

Kartel jest efektywny, ale nie jest

równowagą Nasha

(1112,11

12)

(787,

1137)

(1137,78

7)

(812,812

)

Firma 2

Firma 1

Kartel

+10

Kartel

+10

* W nawiasach zyski

Jedna z firm zwiększa produkcję
o dziesięć myśląc, że druga nie
zareaguje

Analiza konkurencji

MR = ????

R = pQ

MR= ∂R/ ∂Q

∂R = ∂Q p + ∂p Q

MR = (∂Q p + ∂p Q)/ ∂Q = p[1 + (∂p/∂Q)(Q/p)] =

= p(1 + 1/

D

)

Dla monopolu

MR = p(1 + 1/

D

) = MC

p = MC/ (1 + 1/

D

)

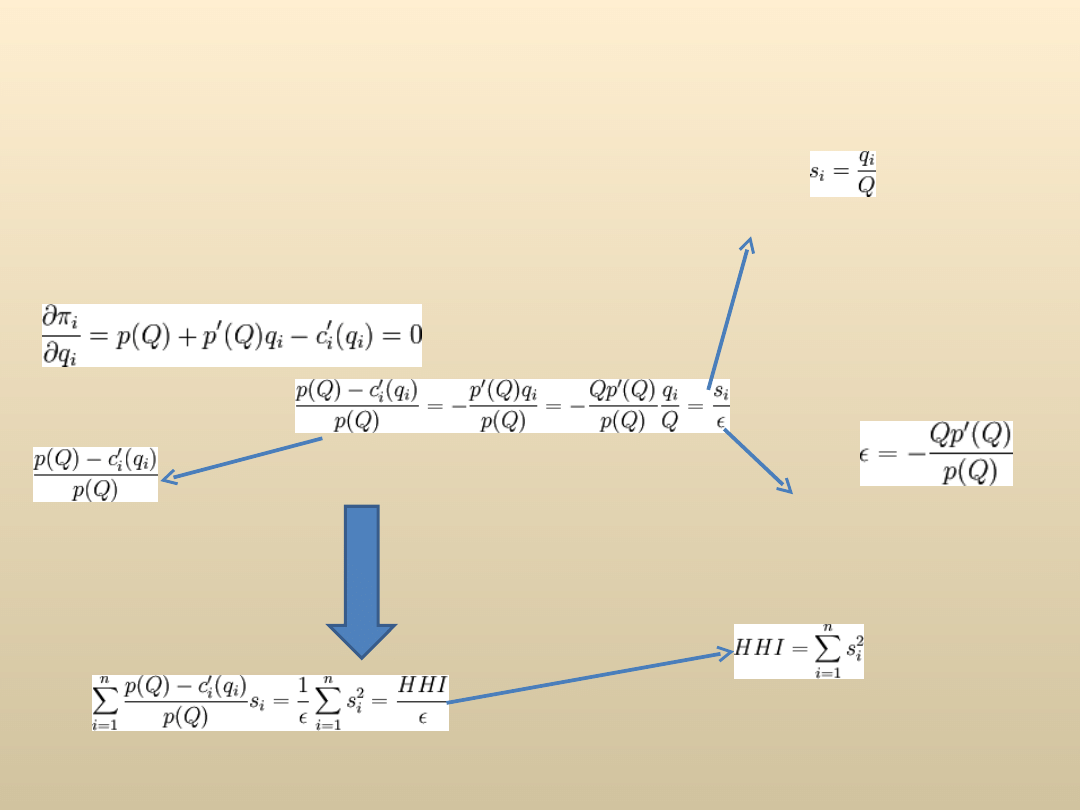
Analiza konkurencji

Zysk pojedynczej
firmy:

Po
przekształceniach:

Elastycznoś
ć

udział w rynku firmy i

)

(q

c

-

)q

q

+

...

+

p(q

=

)

(q

c

-

p(Q)q

=

i

i

i

n

1

i

i

i

i



Warunki optymalizacyjne n równań
postaci:

Podzielić przez s

i

oraz

posumować po i

indeks Herfindahla-
Hirschmana.

indeks Lernera

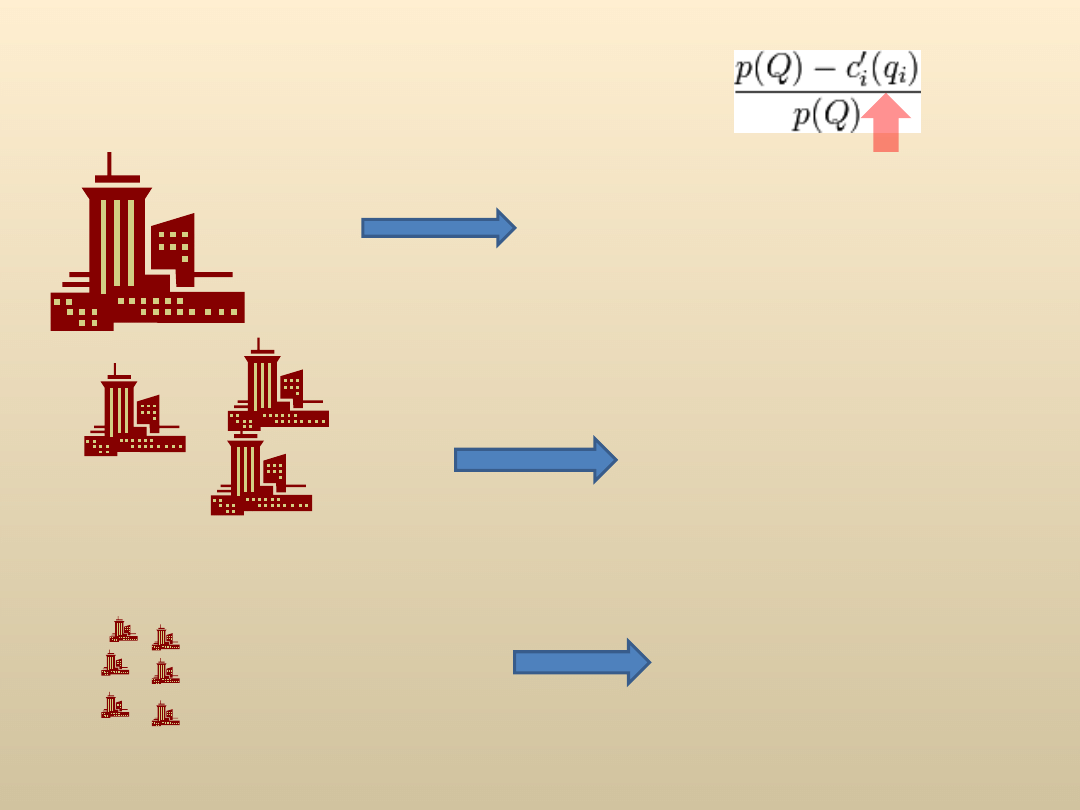
Indeks Lernera

Monop
ol

Doskonała
konkurencja

Oligopo
l

L =
1 / ε



0

L = 1 /
(n*ε)

Trzeba znać koszty
krańcowe.

Indeks Lernera

Monop
ol

Doskonała
konkurencja

Oligopo
l

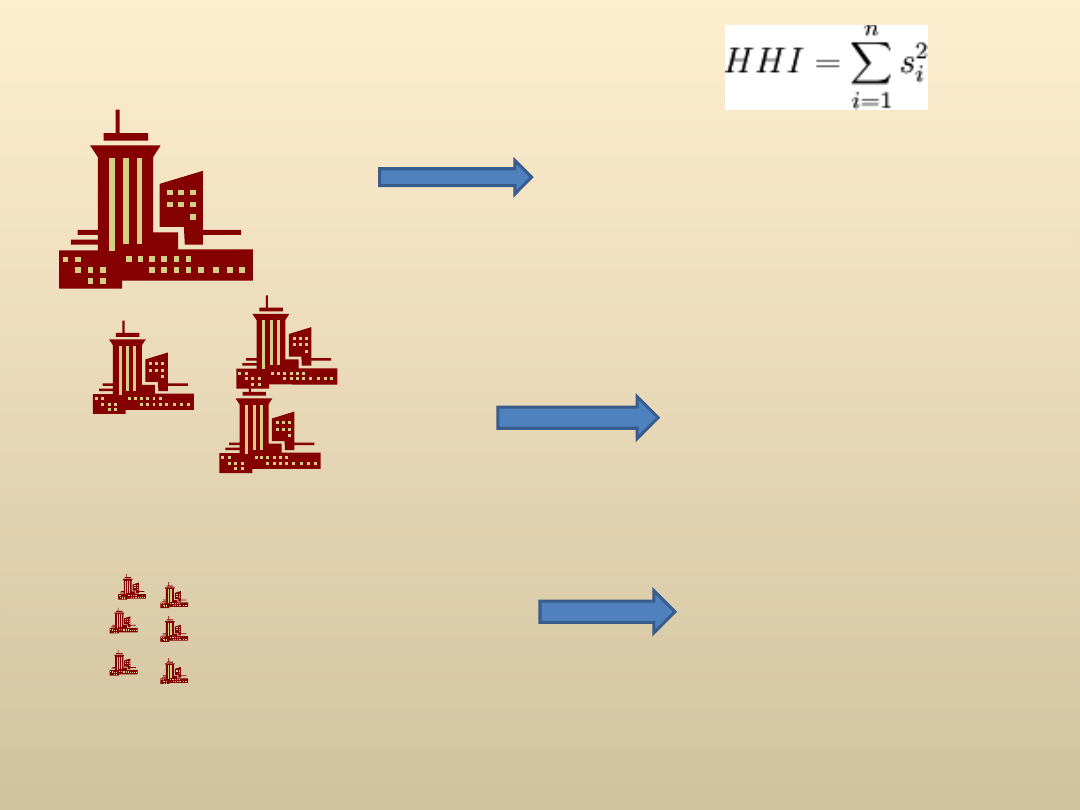
Indeks Herfindahla-Hirschmana

1

lub 10 000 ( s podane w %)

0

2 firmy
0,2
1 firma
0,6

HHI =
0,44

3 firmy
0,1
1 firma
0,7

HHI =
0,52