
1
I
T
P
W
ZPT
Espresso
. . . mankamenty
2
I
T
P
W
ZPT
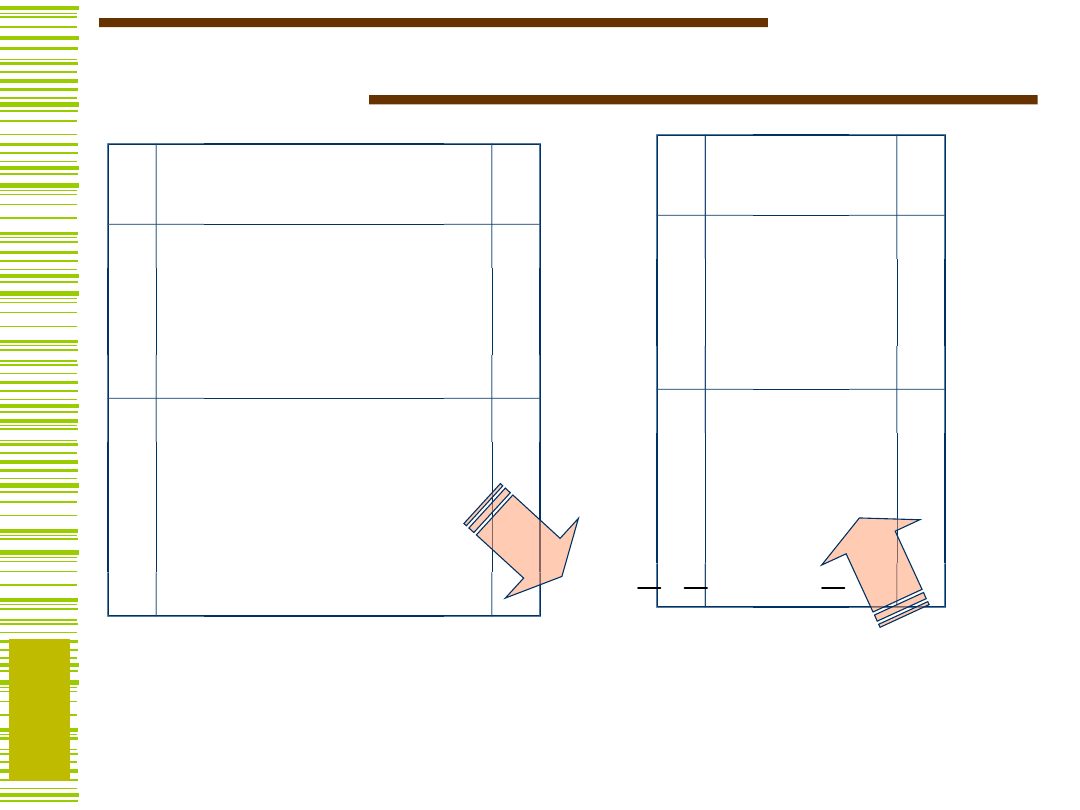
Funkcja 7 argumentów
x
1
x
2
x
3
x
4
x
5
x
6
x
7
f
1 1 0 0 0 1 0 1 0
2 1 0 1 1 1 1 0 0
3 1 1 0 1 1 1 0 0
4 1 1 1 0 1 1 1 0
5 0 1 0 0 1 0 1 1
6 1 0 0 0 1 1 0 1
7 1 0 1 0 0 0 0 1
8 1 0 1 0 1 1 0 1
9 1 1 1 0 1 0 1 1
x
2
x
4
x
6
x
7
f
1 0 0 0 1 0
2 0 1 1 0 0
3 1 1 1 0 0
4 1 0 1 1 0
5 1 0 0 1 1
6 0 0 1 0 1
7 0 0 0 0 1
8 0 0 1 0 1
9 1 0 0 1 1
Pamiętamy . . . z ekspansji
6
2
7
4
x
x
x
x
f
Czy można przewidzieć od jakich argumentów
funkcja istotnie zależy ???
3
I
T
P
W
ZPT
Przykład z Synteza układów
logicznych str 65
Funkcja
10 argumentów
Brak
x
3
.type fr
.i 10
.o 1
.p 25
0010111010 0
1010010100 0
0100011110 0
1011101011 0
1100010011 0
0100010110 0
1110100110 0
0100110000 0
0101000010 0
0111111011 1
0000010100 1
1101110011 1
0100100000 1
0100011111 1
0010000110 1
1111010001 1
1111101001 1
1111111111 1
0010000000 1
1101100111 1
0010001111 1
1111100010 1
1010111101 1
0110000110 1
0100111000 1
.e
.i 10
.o 1
.p 6
----00-1-- 1
00--0----- 1
----10-0-0 1
---1--0--1 1
------1-0- 1
-----11--1 1
.e
Espresso
10
7
6
9
7
10
7
4
10
8
6
5
5
2
1
8
6
5
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
f
- 9
argumentów

4
I
T
P
W
ZPT
.type fr
.i 10
.o 1
.p 25
0010111010 0
1010010100 0
0100011110 0
1011101011 0
1100010011 0
0100010110 0
1110100110 0
0100110000 0
0101000010 0
0111111011 1
0000010100 1
1101110011 1
0100100000 1
0100011111 1
0010000110 1
1111010001 1
1111101001 1
1111111111 1
0010000000 1
1101100111 1
0010001111 1
1111100010 1
1010111101 1
0110000110 1
0100111000 1
.e
Zagadka...
Można wykazać, że
funkcja ta jest zależna
od…
…zaledwie 7
argumentów!
Od ilu
argumentów
zależy ta
funkcja
5
I
T
P
W
ZPT
Wniosek
Espresso redukuje składniki iloczynowe
Nie redukuje
argumentów!!!

6
I
T
P
W
ZPT
PROBLEM:
Obliczania minimalnej liczby argumentów
od których funkcja istotnie zależy
...jest bardzo istotny w redukowaniu
złożoności
obliczeniowej procedur minimalizacji
funkcji boolowskich, a w konsekwencji
może się przyczynić do uzyskiwania
lepszych rezultatów.
Nowy sposób opisu funkcji: rachunek podziałów
7
I
T
P
W
ZPT
Elementy rachunku podziałów
Podziałem na zbiorze S jest system zbiorów P = {
B
i
},
którego bloki są rozłączne, czyli
B
i
B
j
=
, jeśli tylko i j
=
)
4,6
;
3,5
;
1,2
(
Podstawowe pojęcia:
Iloczyn podziałów oraz relacja .
Podzbiory nazywamy
blokami
Dla S = {1,2,3,4,5,6}, P = {{1,2}, {3,5}, {4,6} } jest
podziałem na S.
i
i
B
S
a ponadto
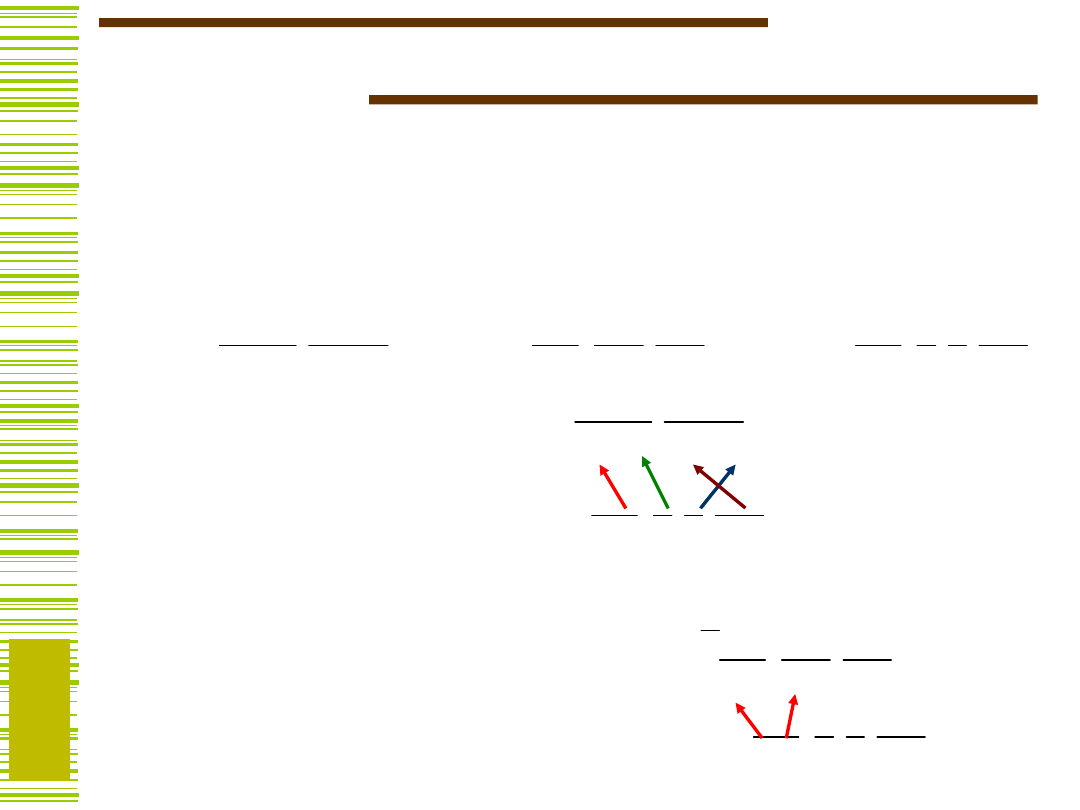
8
I
T
P
W
ZPT
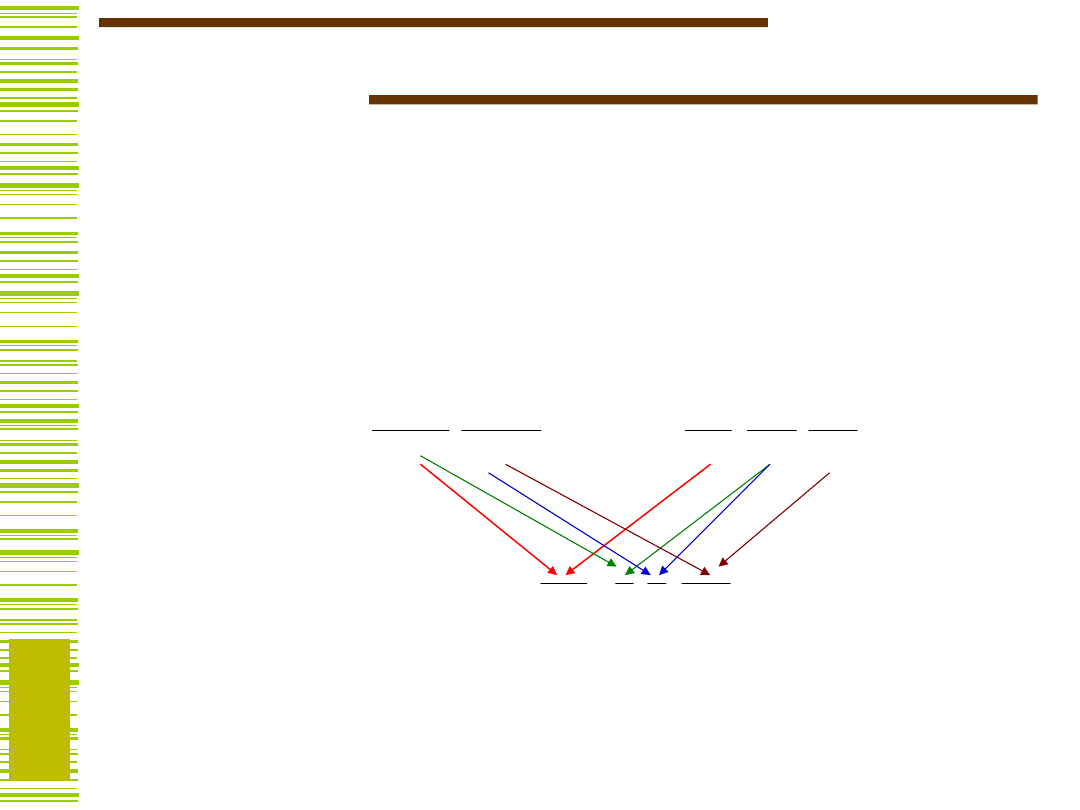
Elementy rachunku podziałów…
Powiemy, że podział P
a
jest nie większy od P
b
(co oznaczamy: P
a
P
b
), jeśli każdy blok z P
a
jest zawarty w pewnym bloku z P
b
.
b
=
)
3,5
;
2,6
;
1,4
(
)
3,5,6
;
1,2,4
(
)
3,5
;
6
;
4
;
1,2
(
a
=
c
=
c
≤
a
Tak
c
b
NIE!
(0) – podział najmniejszy
(1) – podział największy
)
3,5
;
6
;
4
;
1,2
(
c
=
)
3,5,6
;
1,2,4
(
a
=
)
3,5
;
6
;
4
;
1,2
(
c
=
b
=
)
3,5
;
2,6
;
1,4
(
9
I
T
P
W
ZPT
Elementy rachunku podziałów…
b
=
Iloczynem podziałów
a
•
b
nazywamy największy
(względem relacji ) podział, który jest nie większy od
a
oraz
b
.
)
3,5
;
2,6
;
1,4
(
)
3,5,6
;
1,2,4
(
a
=
a
•
b
=
;
1,4
(
;
2
)
3,5
;
6

10
I
T
P
W
ZPT
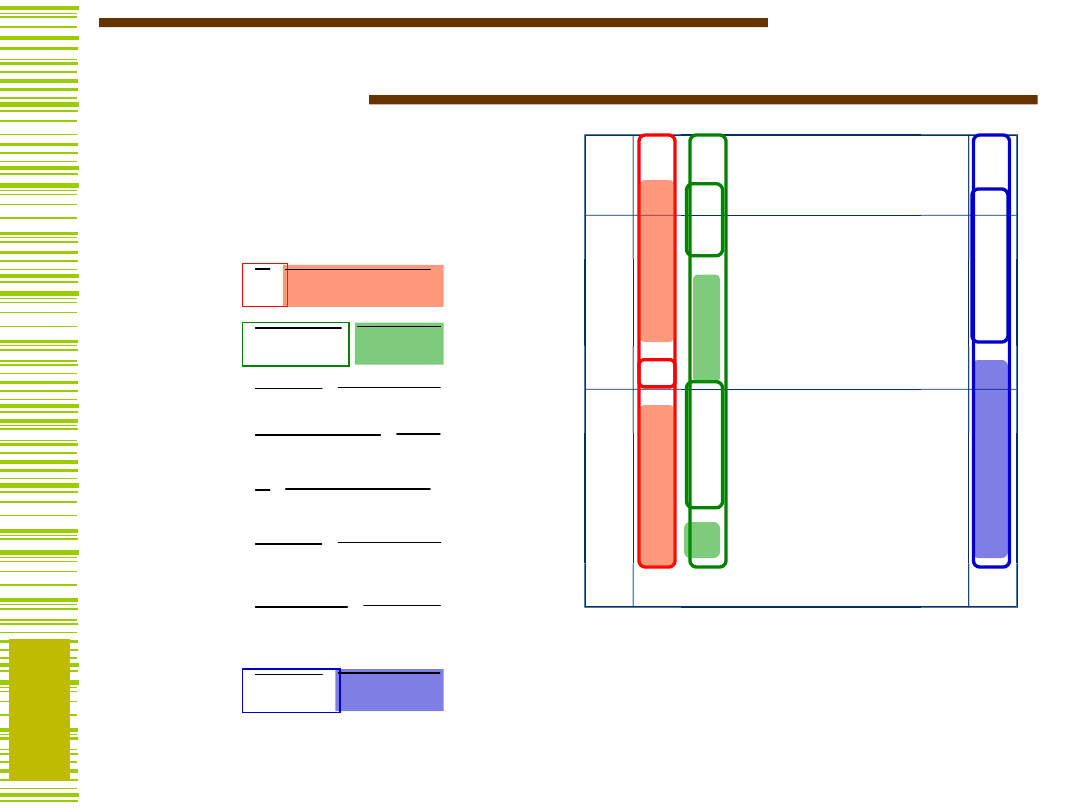
Niech P
a
i P
b
są podziałami na S oraz P
a
P
b
. Podział P
a
| P
b
jest podziałem ilorazowym P
a
i P
b
, jeżeli jego elementy są
blokami P
b
,
a bloki są blokami P
a
.
4,5
;
2,3,8
;
1,6,7
P
a
6,7
;
4,5
;
3
;
2,8
;
1
P
b
Elementy rachunku podziałów…
(4,5)
P
|
P
b
a
;
(1)(6,7)
;
(3)(2,8)
Podział ilorazowy
Na przykład:
11
I
T
P
W
ZPT
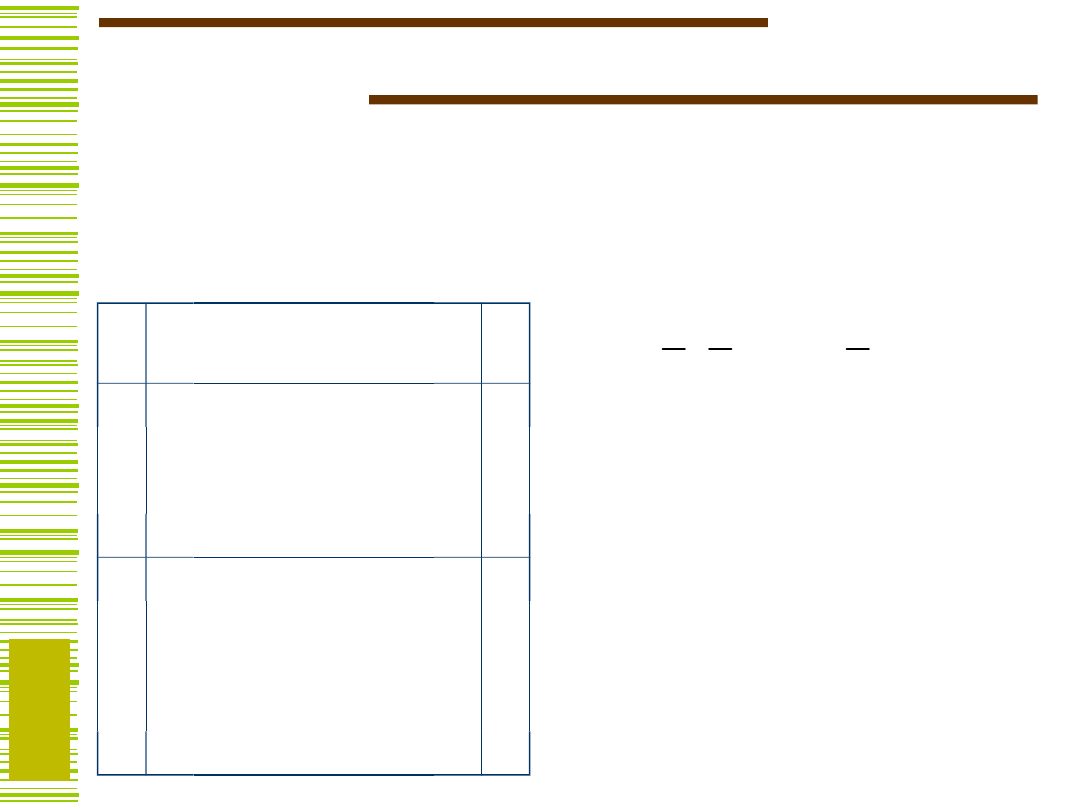
Nowy sposób opisu funkcji -
podziały
x
1
x
2
x
3
x
4
x
5
x
6
x
7
f
1 1 0 0 0 1 0 1 0
2 1 0 1 1 1 1 0 0
3 1 1 0 1 1 1 0 0
4 1 1 1 0 1 1 1 0
5 0 1 0 0 1 0 1 1
6 1 0 0 0 1 1 0 1
7 1 0 1 0 0 0 0 1
8 1 0 1 0 1 1 0 1
9 1 1 1 0 1 0 1 1
P
1
=
P
2
=
P
f
=
;
5
{
;
8
,
7
,
6
,
2
,
1
{
;
4
,
3
,
2
,
1
{
}
9
,
8
,
7
,
6
,
4
,
3
,
2
,
1
}
9
,
5
,
4
,
3
P
3
=
;
6
,
5
,
3
,
1
{
}
9
,
8
,
7
,
4
,
2
P
4
=
;
9
,
8
,
7
,
6
,
5
,
4
,
1
{
}
3
,
2
P
5
=
;
7
{
}
9
,
8
,
6
,
5
,
4
,
3
,
2
,
1
P
6
=
;
9
,
7
,
5
,
1
{
}
8
,
6
,
4
,
3
,
2
P
7
=
;
8
,
7
,
6
,
3
,
2
{
}
9
,
5
,
4
,
1
}
9
,
8
,
7
,
6
,
5
Funkcja f
12
I
T
P
W
ZPT
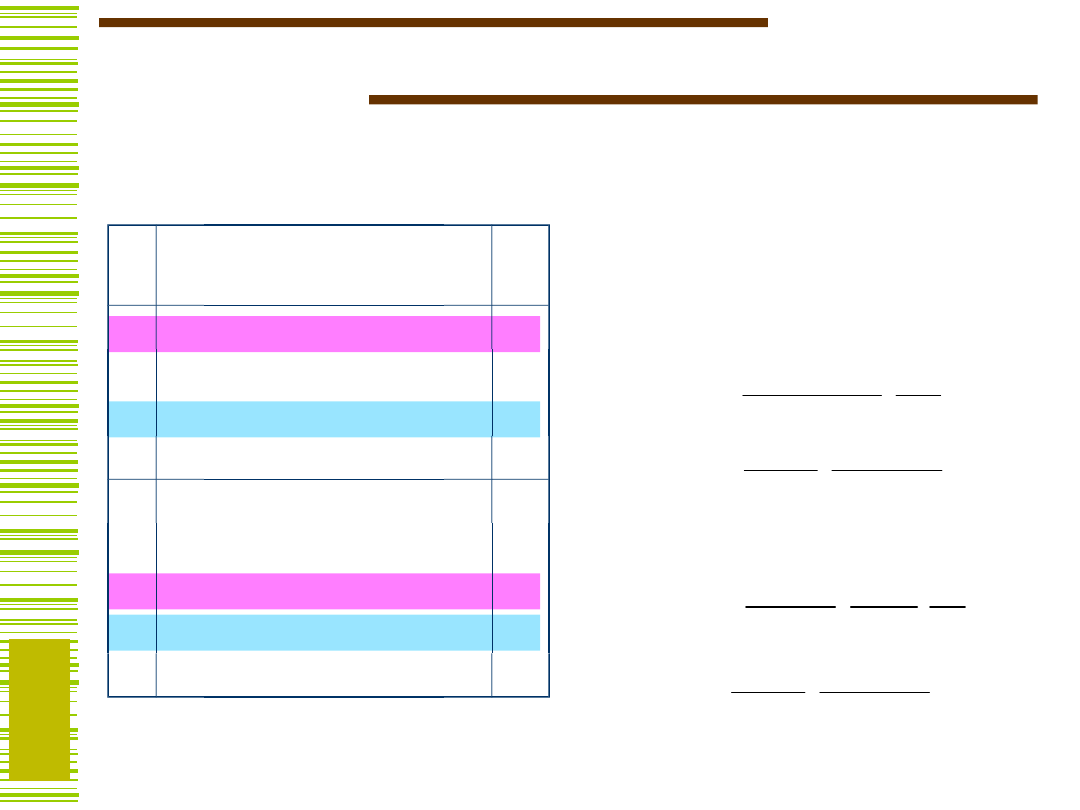
Pojęcie zmiennej niezbędnej
Jeżeli wektory
X
a
oraz X
b
: f (X
a
) f (X
b
), różnią się dokładnie
dla jednej zmiennej to zmienną taką nazywamy niezbędną
x
1
x
2
x
3
x
4
x
5
x
6
x
7
f
1 1 0 0 0 1 0 1 0
2 1 0 1 1 1 1 0 0
3 1 1 0 1 1 1 0 0
4 1 1 1 0 1 1 1 0
5 0 1 0 0 1 0 1 1
6 1 0 0 0 1 1 0 1
7 1 0 1 0 0 0 0 1
8 1 0 1 0 1 1 0 1
9 1 1 1 0 1 0 1 1
x
4
x
6
6
2
7
4
x
x
x
x
f
Zmienne niezbędne
występują w
każdym wyrażeniu
funkcji!!!
13
I
T
P
W
ZPT
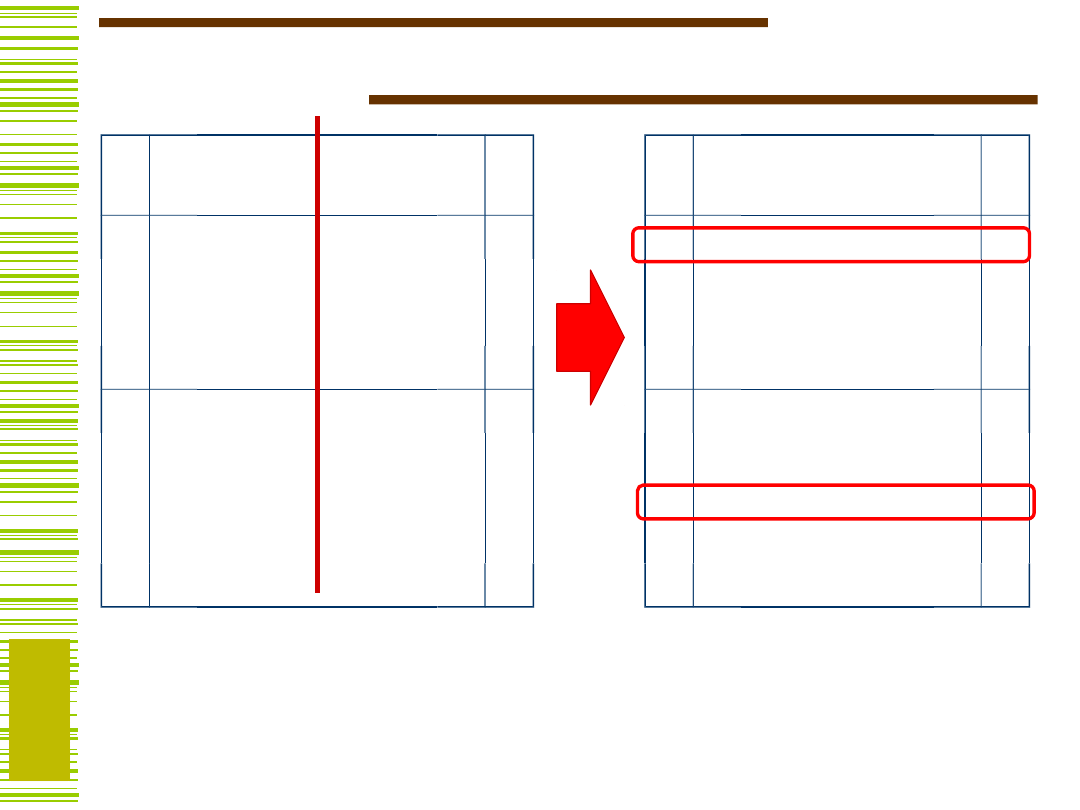
Redukcja argumentów – przykład
x
1
x
2
x
3
x
4
x
5
x
6
x
7
f
1 1 0 0 0 1 0 1
0
2 1 0 1 1 1 1 0
0
3 1 1 0 1 1 1 0
0
4 1 1 1 0 1 1 1
0
5 0 1 0 0 1 0 1
1
6 1 0 0 0 1 1 0
1
7 1 0 1 0 0 0 0
1
8 1 0 1 0 1 1 0
1
9 1 1 1 0 1 0 1
1
Funkcja f
– zmienne
niezbędne
ponieważ wiersze
2 i 8
P
6
=
}
3
,
2
;
9
,
8
,
7
,
6
,
5
,
4
,
1
{
}
8
,
6
,
4
,
3
,
2
;
9
,
7
,
5
,
1
{
Dalej liczymy iloczyn P
4
P
6
x
4
x
6
x
4
x
4
a wiersze 4 i
9
x
6
x
6
różnią się na pozycji
na
pozycji
P
4
=
P
4
•P
6
=
)
4,6,8
1,5,7,9
(
2,3
;
;
P
f
=
}
9
,
8
,
7
,
6
,
5
;
4
,
3
,
2
,
1
{
14
I
T
P
W
ZPT
Wyjaśnienie…
x
1
x
2
x
3
x
4
x
5
x
6
x
7
f
1 1 0 0 0 1 0 1 0
2 1 0 1 1 1 1 0 0
3 1 1 0 1 1 1 0 0
4 1 1 1 0 1 1 1 0
5 0 1 0 0 1 0 1 1
6 1 0 0 0 1 1 0 1
7 1 0 1 0 0 0 0 1
8 1 0 1 0 1 1 0 1
9 1 1 1 0 1 0 1 1
x
1
x
2
x
3
x
5
x
6
x
7
f
1 1 0 0 1 0 1 0
2 1 0 1 1 1 0 0
3 1 1 0 1 1 0 0
4 1 1 1 1 1 1 0
5 0 1 0 1 0 1 1
6 1 0 0 1 1 0 1
7 1 0 1 0 0 0 1
8 1 0 1 1 1 0 1
9 1 1 1 1 0 1 1
Tablica specyfikacji jest sprzeczna, ponieważ
f(101110) = 0 (wektor 2)
f(101110) = 1 (wektor 8)
Zatem
x
4
jest zmienną niezbędną

15
I
T
P
W
ZPT
Pojęcie zmiennej niezbędnej
Warto przeczytać
rozdział 3.4
Obszerniejsze wyjaśnienie i interpretacja w książce:
16
I
T
P
W
ZPT
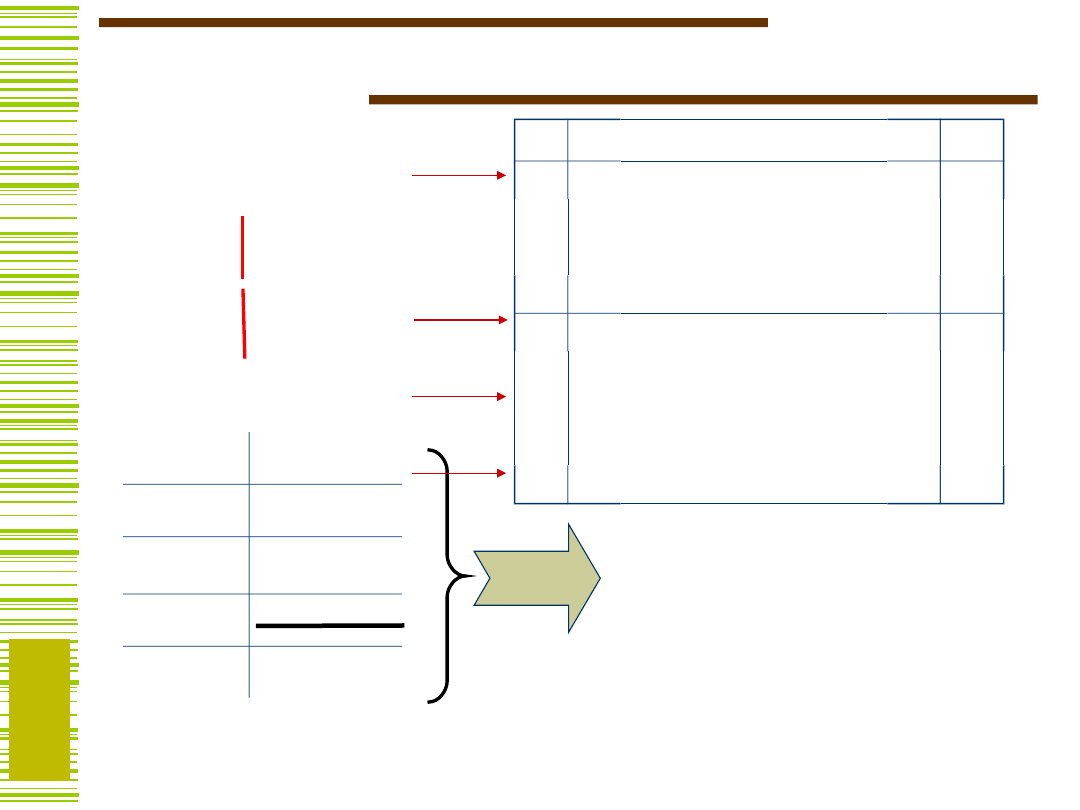
Redukcja argumentów –
przykład…
Iloczyn podziałów wyznaczonych przez zmienne
niezbędne (ozn. P
N
) ma bardzo ważną
interpretację
P
N
= P
4
•P
6
=
)
4,6,8
1,5,7,9
(
2,3
;
;
P
f
=
}
9
,
8
,
7
,
6
,
5
;
4
,
3
,
2
,
1
{
Wystarczy bowiem obliczyć,
P
N
|P
N
•P
F
=
)
(2,3)
;
(6,8)
4),
(
;
(5,7,9)
(1),
(
aby wiedzieć jakie wektory należy
rozdzielić
1, 5, 7, 9
4, 6, 8
17
I
T
P
W
ZPT
Redukcja argumentów – przykład
c.d.
1, 5, 7, 9
4, 6, 8
Tu obliczamy minimalne
pokrycie kolumnowe
1, 5
1, 7
1, 9
4, 6
4, 8
x
1
x
2
x
3
x
5
x
7
x
2
x
3
x
2
x
7
...obliczamy systematycznie...
x
1
x
2
x
3
x
4
x
5
x
6
x
7
f
1
1
0
0
0
1
0
1
0
2
1
0
1
1
1
1
0
0
3
1
1
0
1
1
1
0
0
4
1
1
1
0
1
1
1
0
5
0
1
0
0
1
0
1
1
6
1
0
0
0
1
1
0
1
7
1
0
1
0
0
0
0
1
8
1
0
1
0
1
1
0
1
9
1
1
1
0
1
0
1
1
x
1
x
2
x
3
x
5
x
7
x
2
x
3
x
7
x
2
x
3
x
2
x
7
18
I
T
P
W
ZPT
Redukcja argumentów – przykład
c.d.
(x
1
+ x
2
)
= (x
2
+x
1
)(x
2
+ x
3
)(x
2
+ x
7
)(x
3
+ x
5
+ x
7
) =
{x
2
,x
3
,x
4
,x
6
}
x
1
x
2
x
3
x
5
x
7
x
2
x
3
x
2
x
7
{x
2
,x
4
,x
5
,x
6
}
{x
2
,x
4
,x
6
,x
7
}
{x
4
,x
6
}
(x
3
+ x
5
+
x
7
)
(x
2
+
x
3
)
(x
2
+ x
7
) =
=(x
2
+x
1
x
3
x
7
)
(x
3
+ x
5
+
x
7
) =
= x
2
x
3
+ x
2
x
5
+x
2
x
7
+ x
1
x
3
x
7
+ . . .
Tylko to
było
znalezione
przez
Espresso
19
I
T
P
W
ZPT
...ale gdybyśmy wiedzieli o tym
wcześniej, że
x
1
x
2
x
3
x
4
x
5
x
6
x
7
f
1
1
0
0
0
1
0
1
0
2
1
0
1
1
1
1
0
0
3
1
1
0
1
1
1
0
0
4
1
1
1
0
1
1
1
0
5
0
1
0
0
1
0
1
1
6
1
0
0
0
1
1
0
1
7
1
0
1
0
0
0
0
1
8
1
0
1
0
1
1
0
1
9
1
1
1
0
1
0
1
1
x
2
x
4
x
6
x
7
f
1
0
0
0
1
0
2
0
1
1
0
0
3
1
1
1
0
0
4
1
0
1
1
0
5
1
0
0
1
1
6
0
0
1
0
1
7
0
0
0
0
1
8
0
0
1
0
1
9
1
0
0
1
1
A taką funkcję można
łatwo
zminimalizować
nawet
na tablicy Karnaugha
funkcja ta zależy tylko od {x
2
,x
4
,x
6
,x
7
}
20
I
T
P
W
ZPT
Wprowadzenie redukcji argumentów do
procedury ekspansji daje – w rozsądnym
czasie – wyniki lepsze niż słynne Espresso
21
I
T
P
W
ZPT
Przykład z Synteza układów logicznych
str 65
Funkcja TL27
10 argumentów
.type fr
.i 10
.o 1
.p 25
0010111010 0
1010010100 0
0100011110 0
1011101011 0
1100010011 0
0100010110 0
1110100110 0
0100110000 0
0101000010 0
0111111011 1
0000010100 1
1101110011 1
0100100000 1
0100011111 1
0010000110 1
1111010001 1
1111101001 1
1111111111 1
0010000000 1
1101100111 1
0010001111 1
1111100010 1
1010111101 1
0110000110 1
0100111000 1
.e
.i 10
.o 1
.p 6
----00-1-- 1
00--0----- 1
----10-0-01
---1--0--1 1
------1-0- 1
-----11--1 1
.e
Espresso
9 argumentów
6 termów
22
I
T
P
W
ZPT
Funkcja TL27
Funkcja TL27 przed
redukcją
.type fr
.i 10
.o 1
.p 25
0010111010 0
1010010100 0
0100011110 0
1011101011 0
1100010011 0
0100010110 0
1110100110 0
0100110000 0
0101000010 0
0111111011 1
0000010100 1
1101110011 1
0100100000 1
0100011111 1
0010000110 1
1111010001 1
1111101001 1
1111111111 1
0010000000 1
1101100111 1
0010001111 1
1111100010 1
1010111101 1
0110000110 1
0100111000 1
.e
Realizacja funkcji f1
Ilość zmiennych = 7
Ilość wektorów = 25
R3 = {1,2,4,6,7,9,10}
0001110 0
1001000 0
0101110 0
1010111 0
1101011 0
0101010 0
1100010 0
0101000 0
0110010 0
0111111 1
0001000 1
1111011 1
0100000 1
0101111 1
0000010 1
1111001 1
1110101 1
1111111 1
0000000 1
1110011 1
0000111 1
1110010 1
1001101 1
0100010 1
0101100 1
Jedno z 10
rozwiązań po
redukcji
argumentów
Pandor
23
I
T
P
W
ZPT
Przykład TL27
Funkcja 10 argumentów, 25 wektorów w TP
10
7
6
9
7
10
7
4
10
8
6
5
5
2
1
8
6
5
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
f
Wynik Pandora po RedArg – 7 argumentów, 5 termów
9
7
6
4
1
10
1
4
2
1
7
2
1
x
x
x
x
x
x
x
x
x
x
x
x
x
f
Wynik Espresso – 9 argumentów, 6 termów
24
I
T
P
W
ZPT
Funkcja KAZ
.type fr
.i 21
.o 1
.p 31
100110010110011111101 1
111011111011110111100 1
001010101000111100000 1
001001101100110110001 1
100110010011011001101 1
100101100100110110011 1
001100100111010011011 1
001101100011011011001 1
110110010011001001101 1
100110110011010010011 1
110011011011010001100 1
010001010000001100111 0
100110101011111110100 0
111001111011110011000 0
101101011100010111100 0
110110000001010100000 0
110110110111100010111 0
110000100011110010001 0
001001000101111101101 0
100100011111100110110 0
100011000110011011110 0
110101000110101100001 0
110110001101101100111 0
010000111001000000001 0
001001100101111110000 0
100100111111001110010 0
000010001110001101101 0
101000010100001110000 0
101000110101010011111 0
101010000001100011001 0
011100111110111101111 0
.end
01010 1
10110 1
00100 1
01001 1
01000 1
11010 1
10011 0
01110 0
10100 0
11000 0
11011 0
10000 0
00010 0
01111 0
00011 0
11111 0
00000 0
01101 0
00110 0
Przed redukcją
Jedno z wielu rozwiązań
po redukcji argumentów
Ile jest
takich
rozwiązań
Pandor

25
I
T
P
W
ZPT
Przykład KAZ
Silnie nieokreślona funkcja 21 argumentów,
31 wektorów w TP
Wynik Espresso – 9 argumentów, 3 termy
20
8
5
12
8
7
21
19
14
2
x
x
x
x
x
x
x
x
x
x
f
Wynik Pandora – 5 argumentów, 3 termy
20
19
2
9
4
2
19
9
4
2
x
x
x
x
x
x
x
x
x
x
f
26
I
T
P
W
ZPT
Zadanie nieco trudniejsze…
X
1
X
2
X
3
X
4
X
5
X
6
X
7
X
8
X
9
y
1
y
2
1
0
0
0
1
0
0
1
1
0
0
1
2
0
1
1
0
0
0
0
1
0
0
1
3
1
1
1
0
1
1
0
0
0
1
0
4
0
1
0
0
0
1
1
0
1
0
0
5
0
0
1
0
1
1
1
0
0
0
1
6
0
1
1
0
0
0
1
1
0
0
0
7
0
1
1
0
1
1
0
1
1
1
1
8
0
0
0
1
0
0
1
0
1
1
1
9
1
1
1
0
0
0
1
1
0
1
0
10
0
0
1
1
0
0
1
0
1
1
0
7,8
;
4,6
;
3,9,10
;
1,2,5
P
F
Jeżeli wektory
X
a
oraz X
b
: f (X
a
) f (X
b
), różnią się dokładnie
dla jednej zmiennej to zmienną taką nazywamy niezbędną

27
I
T
P
W
ZPT
Zadanie…
N =
{x
1
,x
3
,x
7
}
7,8
;
4,6
;
3,9,10
;
1,2,5
P
F
;
(1)(4)(8)
P
N
=P
1
•
P
3
•
P
7
;
(2)(7)
;
(5)(6)(10)
Zmienne niezbędne
)
(
9
;
10
6,
5,
;
3
;
2,7
;
1,4,8
P
N
;
(3)
(9)
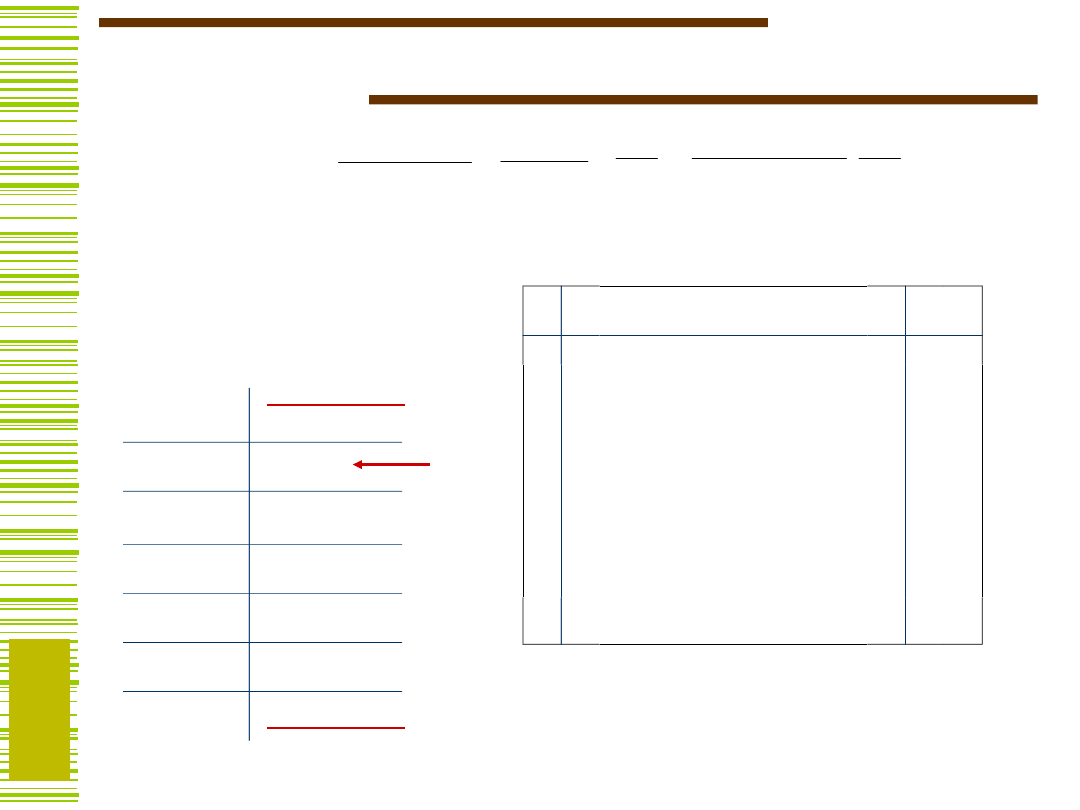
Podział ilorazowy:
P
N
|P
N
•
P
F
P
N
|
P
N
•
P
F
=
28
I
T
P
W
ZPT
Zadanie…
;
(1)(4)(8)
;
(2)(7)
;
(5)(6)(10)
F
N
P
|
P
;
(3)
(9)
2,4,6,8,
9
8,9
X
1
X
2
X
3
X
4
X
5
X
6
X
7
X
8
X
9
y
1
y
2
1
0
0
0
1
0
0
1
1
0
0
1
2
0
1
1
0
0
0
0
1
0
0
1
3
1
1
1
0
1
1
0
0
0
1
0
4
0
1
0
0
0
1
1
0
1
0
0
5
0
0
1
0
1
1
1
0
0
0
1
6
0
1
1
0
0
0
1
1
0
0
0
7
0
1
1
0
1
1
0
1
1
1
1
8
0
0
0
1
0
0
1
0
1
1
1
9
1
1
1
0
0
0
1
1
0
1
0
1
0
0
0
1
1
0
0
1
0
1
1
0
2,4,6
5,6,9
2,5,6,8
4,5,6,9
2,4,8,
9
1,4
1,
8
4,
8
2,7
5,6
6,1
0
5,1
0
v
v

29
I
T
P
W
ZPT
Zadanie…
8
6
5
2
9
6
5
6
4
2
9
8
)
8
5
(
4
6
2
)
6
5
(
8
9
Wyrażenie boolowskie według indeksów zmiennych
X
i
:
8
5
6
2
4
6
2
6
5
9
8
9
8
4
5
4
6
2
8
6
8
5
9

30
I
T
P
W
ZPT
Zadanie…
8
6
5
2
9
6
5
6
4
2
9
8
)
8
5
(
4
6
2
)
6
5
(
8
9
Wyrażenie boolowskie według indeksów zmiennych
X
i
:
8
5
6
2
4
6
2
6
5
9
8
9
8
4
5
4
6
2
8
6
8
5
9
8
6
4
8
6
5
4
8
6
8
6
2
8
5
4
8
5
4
8
6
5
8
5
2
9
8
4
9
5
4
9
6
9
2

31
I
T
P
W
ZPT
Zadanie…
Ostatecznie:
8
6
8
5
4
8
5
2
9
8
4
9
5
4
9
6
9
2
8
5
4
8
5
2
9
8
4
9
5
4
8
6
9
6
9
2
Pamiętając, że zmienne niezbędne
były:
{x
1
,x
3
,x
7
}

32
I
T
P
W
ZPT
Zadanie. . .
x
1
, x
2
, x
3
, x
7
, x
9
x
1
, x
3
, x
6
, x
7
, x
9
x
1
, x
3
, x
6
, x
7
, x
8
x
1
, x
3
, x
4
, x
5
, x
7
, x
9
x
1
, x
3
, x
4
, x
7
, x
8
, x
9
x
1
, x
2
, x
3
, x
5
, x
7
, x
8
x
1
, x
3
, x
4
, x
5
, x
7
, x
8
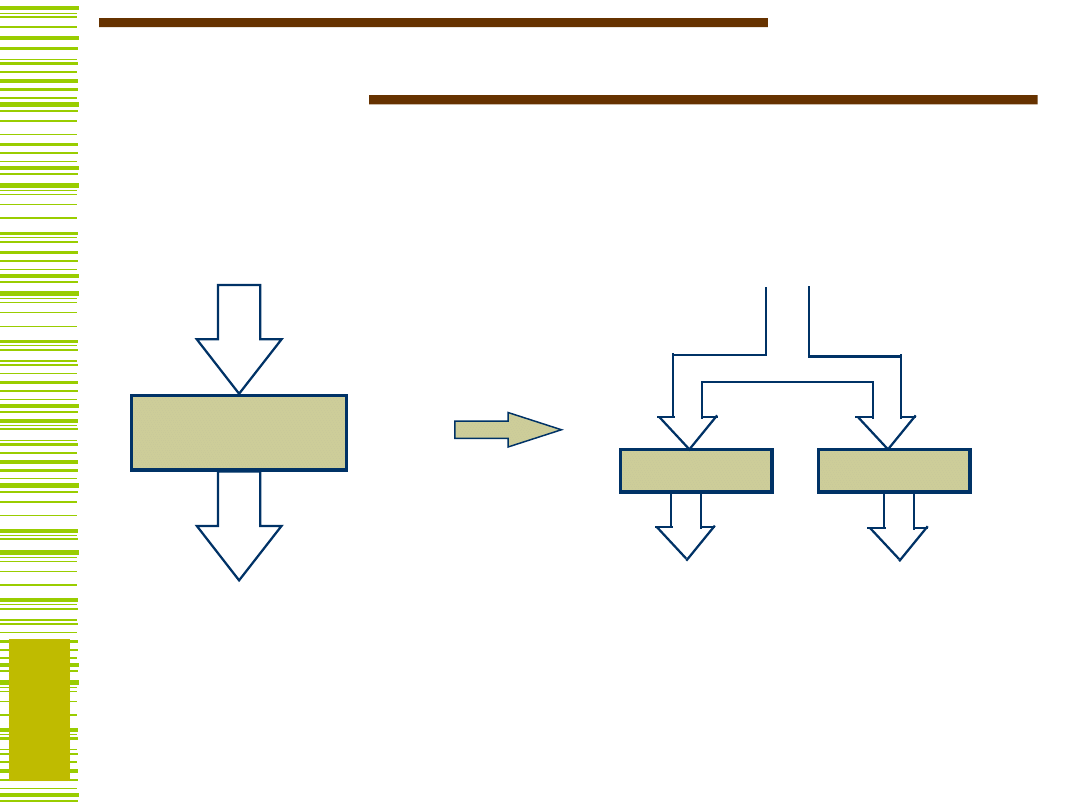
Łatwo wypisać wszystkie
minimalne rozwiązania:
8
5
4
8
5
2
9
8
4
9
5
4
8
6
9
6
9
2
{x
1
,x
3
,x
7
}
33
I
T
P
W
ZPT
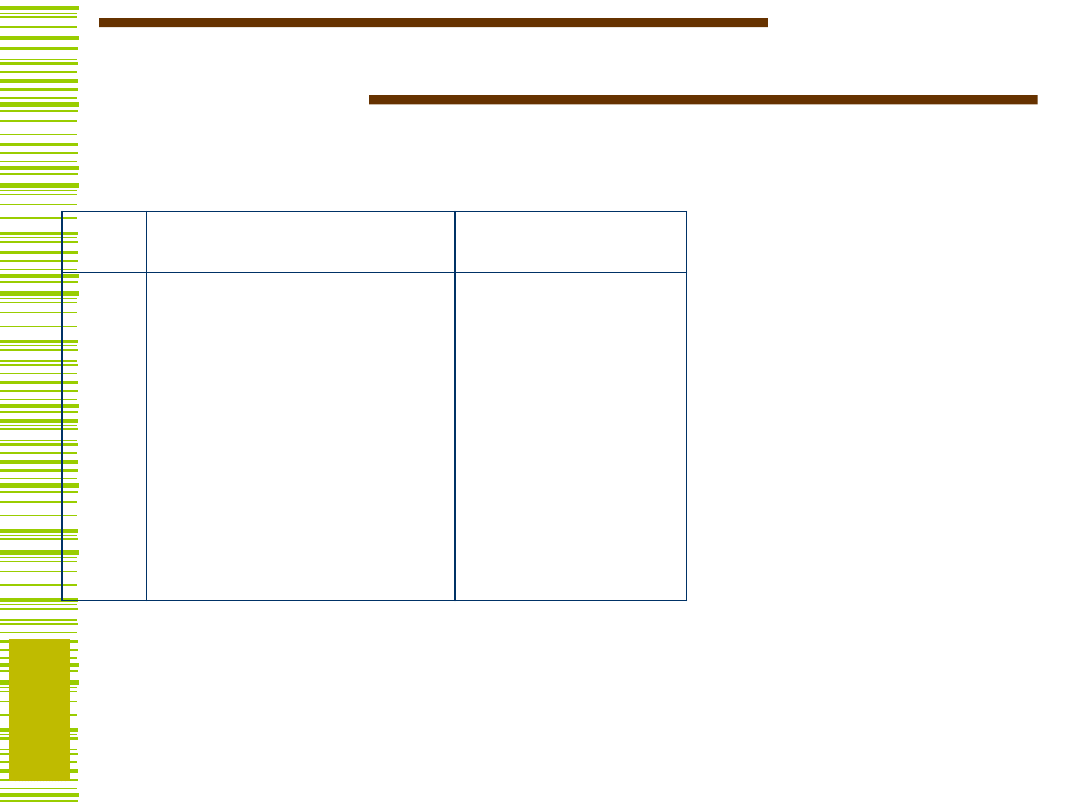
Dekompozycja równoległa…
X
Y
F
Y = Y
g
Y
h
X
h
H
X
g
Y
g
G
X
Y
h
X
X
g
X
X
h
34
I
T
P
W
ZPT
y
1
: {x
1
, x
2
, x
6
}
y
2
: {x
3
, x
4
}
y
3
: {x
1
, x
2
, x
4
, x
5
, x
8
}
{x
1
, x
2
, x
4
, x
6
, x
8
}
y
4
: {x
1
, x
2
, x
3
, x
4
, x
7
}
y
5
: {x
1
, x
2
, x
4
}
y
6
: {x
1
, x
2
, x
6
, x
8
}
0
0
0
1
–
–
1
0
0
1
1
0
0
0
11
1
–
0
1
0
0
1
0
1
1
1
0
0
0
10
1
–
1
0
1
–
0
1
1
0
1
1
0
1
9
1
–
0
0
1
1
0
0
1
0
1
1
0
1
8
0
1
0
–
0
1
0
0
0
0
0
1
1
1
7
0
0
1
0
1
1
0
0
0
1
1
1
0
0
6
1
0
–
0
0
0
0
0
0
1
0
1
0
1
5
0
1
1
1
1
0
0
0
1
0
1
1
1
1
4
1
1
0
1
1
0
0
0
0
1
1
1
0
1
3
1
0
1
–
0
0
0
0
0
0
0
1
0
1
2
0
–
0
0
0
0
0
0
1
1
1
0
0
0
1
y
6
y
5
y
4
y
3
y
2
y
1
x
8
x
7
x
6
x
5
x
4
x
3
x
2
x
1
Dekompozycja równoległa -
przykład
35
I
T
P
W
ZPT
y
1
: {x
1
, x
2
, x
6
}
y
2
: {x
3
, x
4
}
y
3
: {x
1
, x
2
, x
4
, x
5
, x
8
}
{x
1
, x
2
, x
4
, x
6
, x
8
}
y
4
: {x
1
, x
2
, x
3
, x
4
, x
7
}
y
5
: {x
1
, x
2
,
x
4
}
y
6
: {x
1
, x
2
, x
6
, x
8
}
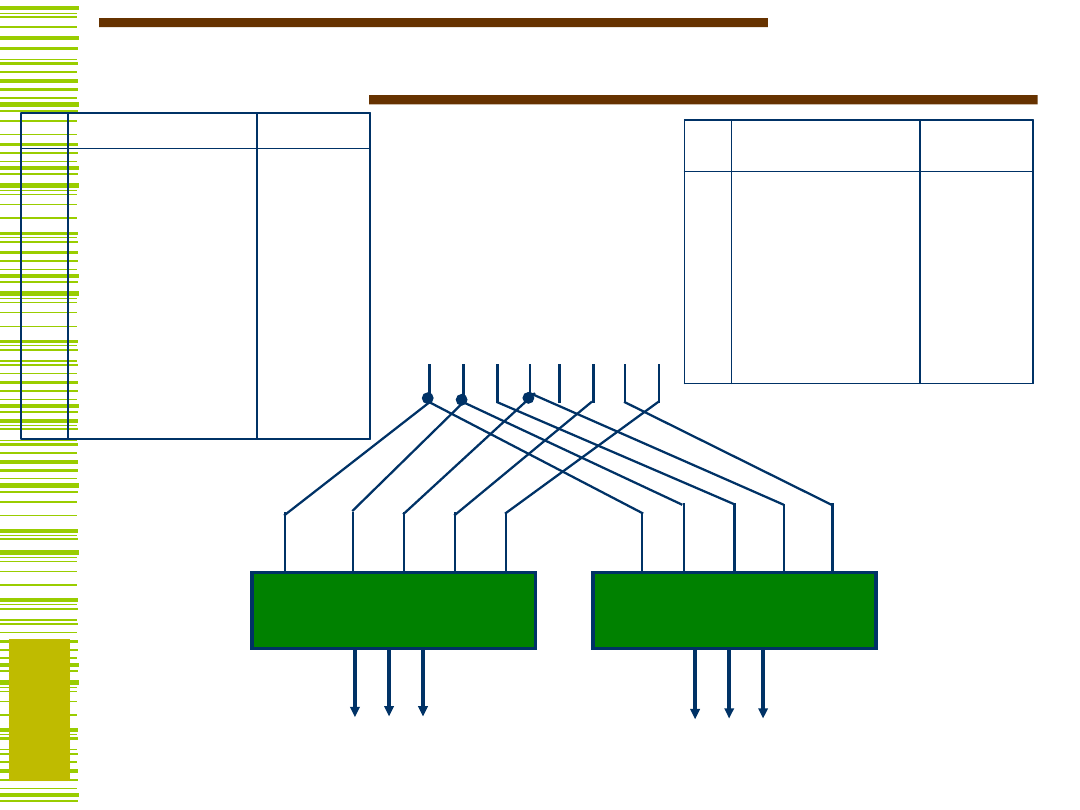
X
g
= {x
1
, x
2
, x
4
, x
6
, x
8
}
X
h
= {x
1
, x
2
, x
3
, x
4
, x
7
}
G
= {y
1
, y
3
,
y
6
}
H= {y
2
, y
4
,y
5
}
Dekompozycja równoległa -
przykład
36
I
T
P
W
ZPT
x
1
x
2
x
3
x
4
x
5
x
6
x
7
x
8
H
G
y
1
y
3
y
6
y
2
y
4
y
5
0
1
–
1
0
1
0
0
9
1
1
0
1
1
1
0
0
8
1
0
1
0
1
1
0
1
7
0
1
1
0
0
0
1
1
6
0
0
1
0
0
1
0
0
5
0
1
0
0
1
1
1
1
4
1
1
0
0
0
1
0
1
3
1
0
0
0
0
0
0
1
2
0
0
0
0
1
1
0
0
1
y
6
y
3
y
1
x
9
x
6
x
4
x
2
x
1
–
1
1
1
1
1
0
1
7
1
0
0
0
0
1
1
1
6
0
1
1
0
1
1
0
0
5
1
1
1
0
1
1
1
1
4
1
0
1
0
1
1
0
1
3
0
1
0
0
0
1
0
1
2
0
0
0
0
1
0
0
0
1
y
5
y
4
y
2
x
7
x
4
x
3
x
2
x
1
Dekompozycja równoległa -
przykład
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
Wyszukiwarka
Podobne podstrony:
W4 Proces wytwórczy oprogramowania
W4 2010
Statystyka SUM w4
w4 3
W4 2
W4 1
w4 skrócony
w4 orbitale molekularne hybrydyzacja
in w4
w4 Zazębienie ewolwentowe
TM w4
IB w4 Aud pełny
pul w9b
W4 Mitochondria i chloroplasty
Psychiatria W4 28 04 2014 Zaburzenia spowodowane substancjami psychoaktywnymi
więcej podobnych podstron