Algorytmy i struktury

danych

Temat 1

2

Algorytmy i struktury danych, temat 1

Wykład 1: Podstawowe pojęcia

algorytmów



Określenie dziedziny algorytmiki



Klasyfikacja algorytmów



Własności algorytmów



Konstrukcje algorytmiczne w językach programowania



Metody weryfikacji algorytmów



Pojęcie złożoności obliczeniowej algorytmów

3

Algorytmy i struktury danych, temat 1

Potoczne rozumienie pojęcia

„algorytm”



Algorytmika jest dziedziną wiedzy zajmującą się
badaniem algorytmów



W informatyce jest ona nieodłącznie związana z
algorytmami przetwarzania struktur danych



Potocznie algorytm jest rozumiany jako pewien przepis na
wykonanie jakiegoś zestawu czynności, prowadzących do
osiągnięcia oczekiwanego i z góry określonego celu



Mówi się również, że algorytm jest pewną ściśle określoną
procedurą obliczeniową, która dla zestawu właściwych
danych wejściowych „produkuje” żądane dane wyjściowe



Przykładami algorytmów mogą być: przepisy kulinarne,
procedury postępowania w organizacjach, procedury
rozwiązywania poszczególnych rodzajów zadań
obliczeniowych, procedury prowadzenia badań
naukowych itp..

4

Algorytmy i struktury danych, temat 1

P

ochodzenie słowa „algorytm”



Słowo „algorytm” pochodzi od



łacińskiego „algorism”, co w średniowieczu było
rozumiane jako sztuka rachowania na liczbach w
systemie decymalnym

Słowo „algorism” zostało utworzone od nazwiska

perskiego matematyka z 9-tego wieku n.e., tj.
Muhameda ibu-Musy al-Choresmi, twórcy systemu
dziesiętnego



Dzisiejsze, uogólnione znaczenie słowa algorytm
zastoso-wano w zasadzie dopiero w 20-stym stuleciu,
kiedy to algorytm zaczął być rozumiany jako:

zbiór reguł postępowania umożliwiających rozwiązanie

określonego zadania w skończonej liczbie kroków i w
skończonym czasie

5

Algorytmy i struktury danych, temat 1

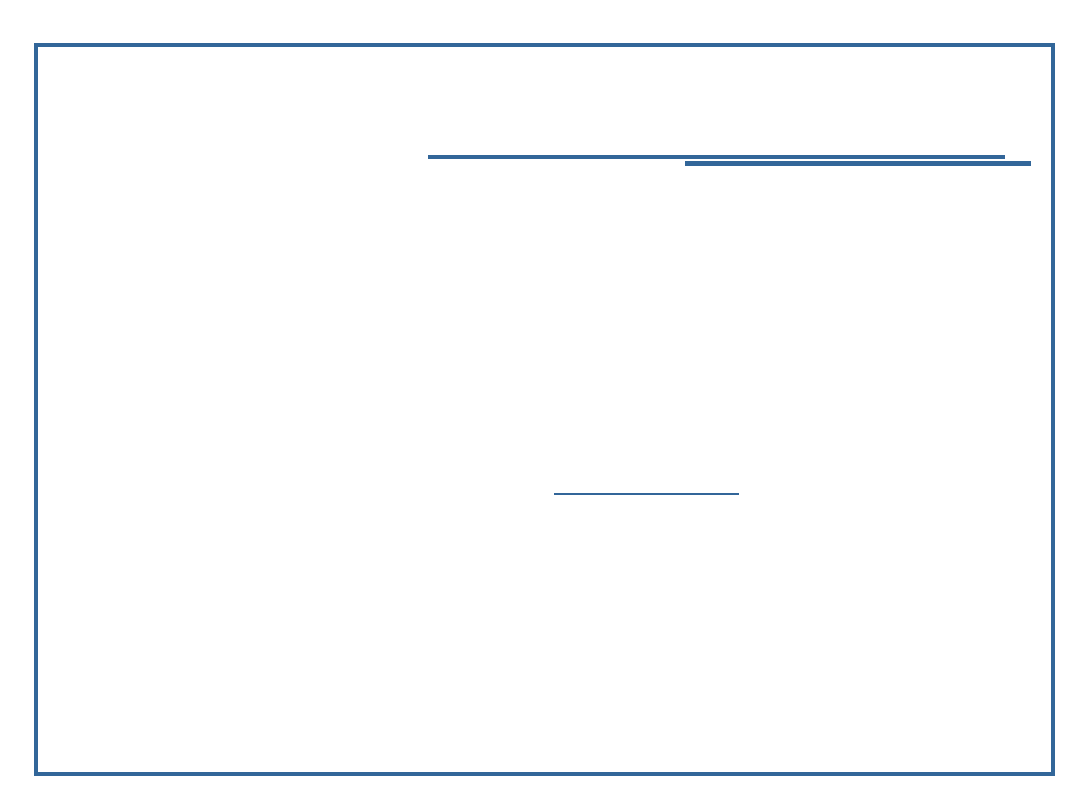
Pojęciowy model algorytmu

Def.1.: Niech:

We - oznacza zestaw danych wejściowych
Wy - zestaw danych wyjściowych
Algorytm jest rozumiany jako odwzorowanie „A”, które
dla określonego zestawu „We” generuje zestaw „Wy”:
A: We Wy,
gdzie liczności zbiorów We i Wy mogą być różne

Dane

wejściowe, We

Zestaw

czynności

Dane

wyjściowe, Wy

6

Algorytmy i struktury danych, temat 1

Przykłady zastosowań algorytmów

w informatyce



Programowanie matematyczne:



algorytmy rozwiązywania zadań liniowych (programowanie liniowe)



programowanie dynamiczne, ....



Sztuczna inteligencja, wspomaganie podejmowania decyzji



sieci nueronowe



algorytmy genetyczne



metody symulacyjne



Przetwarzanie danych:



wstawianie, wyszukiwanie i usuwanie elementów ze struktur
danych



sortowanie struktur danych



reorganizacja struktur danych, ....



Systemy operacyjne:



równoważenie obciążenia w dostępie do zasobów w systemach
rozproszonych i nierozproszonych



synchronizacja procesów współbieżnych



usuwanie nieużytków z pamięci operacyjnej.... itp., itd.

7

Algorytmy i struktury danych, temat 1

Pojęcie

dziedziny algorytmicznej



Każdy algorytm działa na zbiorze obiektów (np. liczb)
wraz z operacjami pierwotnymi, które można wykonywać
na tym zbiorze obiektów



Układ obiektów wraz z operacjami będących podstawą dla
określenia algorytmu nazywamy dziedziną algorytmiczną



Przykłady dziedzin algorytmicznych:



dziedzina algorytmiczna liczb całkowitych:



(Z, +, -, *, div, mod, :=, abs)



dziedzina algorytmiczna liczb rzeczywistych:



(R, +, -, *, /, sqrt, ln exp, sin, cos, abs, :=)



dziedzina algorytmiczna rachunku logicznego:



(B, not, and, or, xor, =>, <=>, =, >, <, <=, >=)



dziedzina algorytmiczna dla języków programowania:



zbiór symboli alfanumerycznych, reguł syntaktycznych i
semantycznych języka programowania

8

Algorytmy i struktury danych, temat 1

S

posoby zapisu algorytmów



Algorytm powinien precyzyjnie przedstawiać kolejne
jego kroki. Do opisu tych kroków mogą być stosowane
następujące sposoby:



zapisy werbalne,



zapisy formalne, np.:



zapisy graficzne (schematy blokowe),



formalne specyfikacje programów (VDM, CSP)



zapisy w postaci pseudokodów („paraprogramów”)



implementacje programów w dowolnym języku
programowania

9

Algorytmy i struktury danych, temat 1

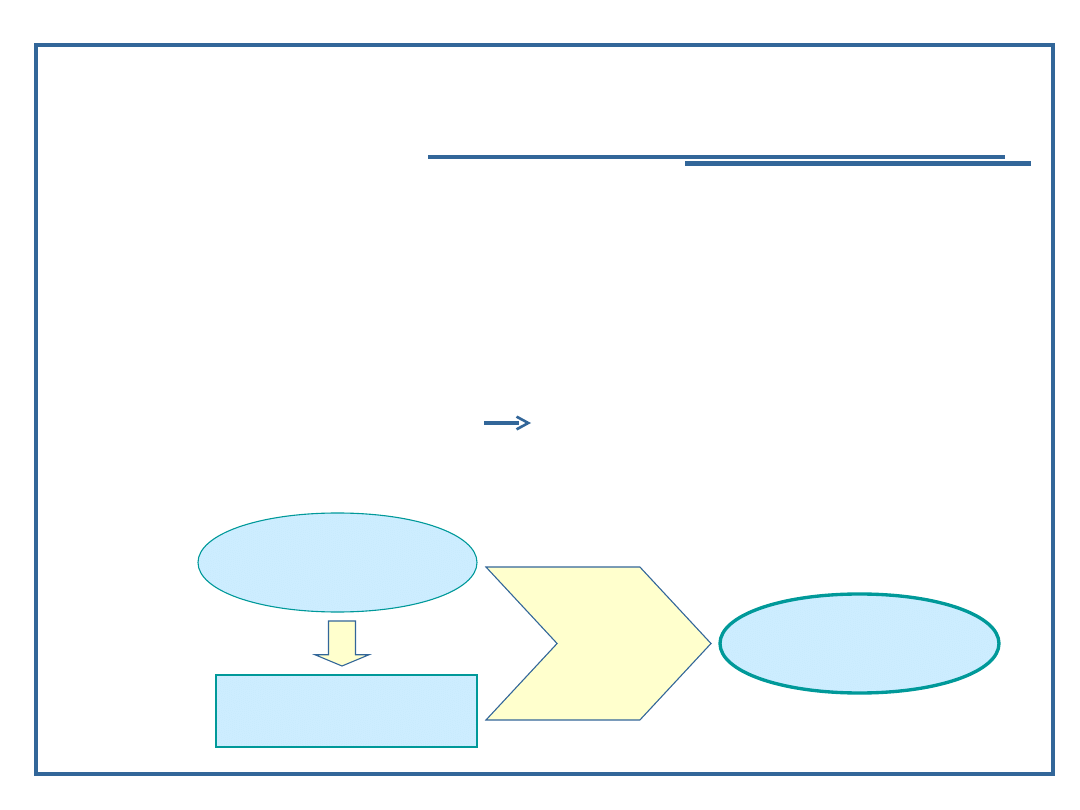
Język programowania



Język programowania jest środkiem umożliwiającym
zapis algorytmów w postaci zrozumiałej dla człowieka,
a równocześnie przetwarzanej do postaci zrozumiałej
dla komputera (maszyny algorytmicznej)

Kod źródłowy programu
(w języku programowania)

Kod wynikowy programu
(w języku maszynowym)

Przetworzenie

programu

źródłowego

w kod

maszynowy

10

Algorytmy i struktury danych, temat 1

Semiotyka języka

programowania

(syntaktyka, semantyka)



Semiotyka zajmuje się badaniem symboli, znaków. W
jej skład wchodzą:



syntaktyka, zajmująca się określaniem
przynależności danego słowa do zestawu słownika
określonego języka programowania



semantyka, zajmująca się określeniem znaczenia
programu, zapisanego w określonym języku
programowania



Zapis algorytmu w języku programowania jest
traktowany jako zapis formalny. Program komputerowy
jest uznawany za jeden z rodzajów modeli
matematycznych. Jest to algorytmiczny model zadania
czy też rzeczywistości, którą modelujemy.

11

Algorytmy i struktury danych, temat 1

Syntaktyka języka programowania



Syntaktyka jest częścią ogólnej teorii znaków (semiotyki) i
zajmuje się strukturą i formą wyrażeń, a także
dopuszczalnymi zmianami ich formy, zwanymi
„przekształceniami”.



Wyróżnia się dwa rodzaje reguł składniowych:



reguły formowania, określające zbiór wyrażeń poprawnie
zbudowanych na określonym alfabecie języka



reguły przekształcania, określające zbiór możliwych
przekształceń na bazie słów z zadanego zestawu
słownika



W dziedzinie algorytmiki, jak również logiki matematycznej
mają zastosowanie wyłącznie reguły inferencyjne, tzn. takie
przekształcenia, które są prawdziwe w sensie logiki
matematycznej

12

Algorytmy i struktury danych, temat 1

Syntaktyka języka programowania



Najczęściej przyjmuje się, że mamy do czynienia z
dwoma podzbiorami dziedziny nazywanej syntaktyką:



syntaktyka formalna, która jest rozumiana jako
ogólne badania formalne, dotyczące języków logiki i
matematyki, jak również języków naturalnych,



syntaktyka logiczna, która zajmuje się badaniem
języków logiki i matematyki (np. rachunek
predykatów, rachunek zdań)



Językami programowania, badaniem ich
algorytmiczności zajmuje się syntaktyka języków
programowania, która jest jednym z rodzajów
syntaktyk formalnych

13

Algorytmy i struktury danych, temat 1

Zapis definicji syntaktyki języka

programowania



Najczęściej stosuje się dwa sposoby opisu syntaktyki
języka programowania. Są to:



zapis Backusa-Naura BNF (Backus-Naur Form). Został
on po raz pierwszy zastosowany do opisu języka
Algol60. Przykład definicji słownika w zapisie BNF:



<operator arytmetyczny> ::= + | - | * | / | ^ | DIV | MOD;



<operator logiczny> ::= AND | OR | NOT | XOR | = ;



<nawias> ::= [ | ] | ( | ) | { | } | ‘ | begin | end.



Diagramy syntaktyczne Wirth’a (SD). Zestaw symboli
jest zapisywany w BNF, zaś reguły generowania
wyrażeń są zapisywane w specjalnej notacji graficznej.



Przykłady zapisu reguł generowania wyrażeń w BNF i
diagramach syntaktycznych SD będą przedstawione w
dalszej części wykładu

14

Algorytmy i struktury danych, temat 1

Semantyka języka programowania



Semantyka zajmuje się interpretacją formuł zapisanych
zgodnie z określonymi regułami syntaktycznymi języka



Tarski (1936r.) zaproponował używanie pojęcia
semantyka naukowa dla określenia semantyki
zajmującej się formalnym badaniem prawdziwości
formuł w zakresie znaczeniowym definiowanego języka.



Od lat 70-tych 20 wieku rozwija się tzw, semantyka
wartości logicznych (SWL), inaczej nazywana
semantyką prawdziwo-ściową. Bazuje ona na pojęciu
prawdy logicznej, na wyrażeniach zwanych
tautologiami.



Podstawą wnioskowania w SWL o prawdziwości reguły
logicznej jest dowiedzenie poprawności zdania
logicznego wyprowadzanego na podstawie kombinacji
innych, prawdziwych zdań logicznych

15

Algorytmy i struktury danych, temat 1

Klasyfikacja algorytmów,



Dla naszych rozważań posłużymy się następującą
klasyfikacją algorytmów:



algorytmy równoległe - algorytmy sekwencyjne (kroki
algorytmu wykonywane kolejno w sekwencji lub
równolegle),



algorytmy numeryczne - algorytmy nienumeryczne
(wykonywanie obliczeń lub przetwarzanie danych)



algorytmy rekurencyjne - algorytmy iteracyjne
(algorytm w kolejnych krokach wywołuje sam siebie
dla nowych wartości parametrów wykonania lub
wykonuje obliczenia w pętli dla zmieniającej się
wartości jej niezmiennika)

16

Algorytmy i struktury danych, temat 1

Klasyfikacja algorytmów,

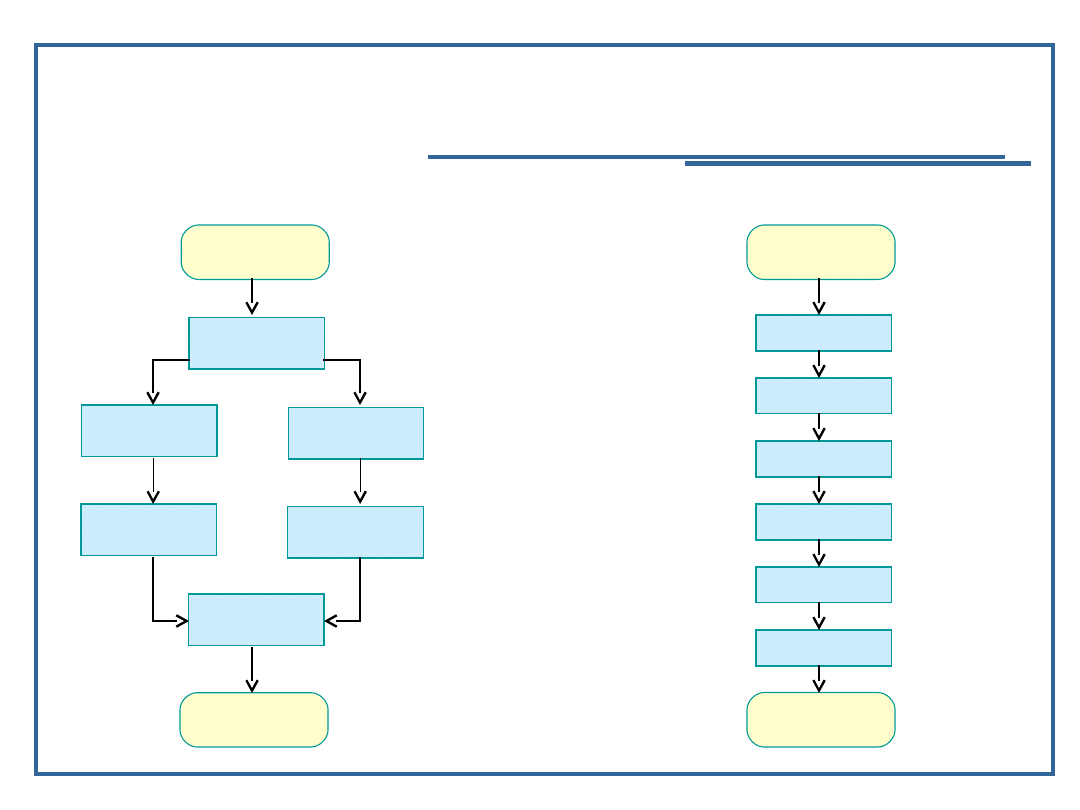
algorytmy równoległe, algorytmy sekwencynne

Algorytm równoległy: Algorytm sekwencyjny:

START

STOP

Krok_1

Krok_2

Krok_4

Krok_6

Krok_3

Krok_5

START

STOP

Krok_1

Krok_2

Krok_3

Krok_4

Krok_5

Krok_6

17

Algorytmy i struktury danych, temat 1

Przykład - pierwiastki równania

kwadratowego

START

STOP

=b

2

-4ac

x

1

=(-b-sqrt())/2a

x

2

=(-b+sqrt())/2a

Wypisz x

1

, x

2

START

STOP

=b

2

-4ac

x

1

=(-b-sqrt())/2a

x

2

=(-b+sqrt())/2a

Wypisz x

1

, x

2

Algorytm równoległy: Algorytm sekwencyjny:

18

Algorytmy i struktury danych, temat 1

Rodzaje równoległości



Równoległóść procesowa - zbiór współpracujących
elementów, z których każdy jest dość złożony i działa
w sposób zbliżony, ale niekoniecznie identyczny z
innymi.

Przykłady:



działanie supermarketu, banku, poczty - wiele kas
(okienek),



budowa - wielu murarzy , malarzy, tynkarzy, itp.



Obok równoległości procesowej wyróżnia się także
równoległość tablicową (np. musztra, aerobik) oraz
równoległość potokową (np. taśma produkcyjna).

19

Algorytmy i struktury danych, temat 1

Programowanie współbieżne



Programowanie współbieżne - zbiór technik i notacji
programistycznych służących do wyrażania potencjalnej
równoległości oraz do rozwiązywania zagadnień związanych z
powstającymi przy tym problemami synchronizacji i
komunikacji poszczególnych składowych algorytmu.



Programowanie współbieżne pozwala rozważać równoległość
algorytmu obliczeniowego bez wdawania się w szczegóły
implementacyjne (liczba procesorów, model procesu, model
pamięci, implementacja obiektów synchronizacji, algorytm
wznawiania procesów, mechanizmy komunikacji, itp.).

20

Algorytmy i struktury danych, temat 1

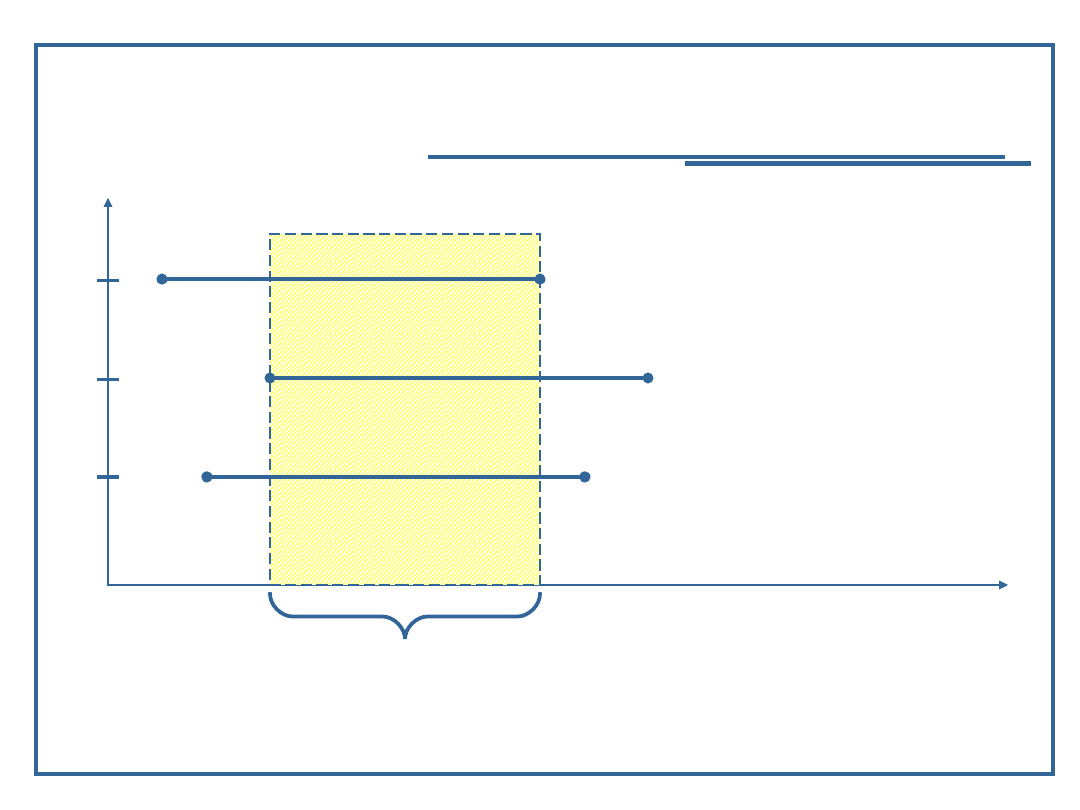
Kiedy może wystąpić współbieżność

?

t

procesy

A1

A2

A3

Potencjalna współbieżność

składowych algorytmu: A1, A2, A3

21

Algorytmy i struktury danych, temat 1

Rodzaje algorytmów współbieżnych

Algorytmy współbieżne

Klasyczne

algorytmy współbieżne

(ze współdzielonymi zasobami

fizycznymi maszyny

obliczeniowej – np. komputera)

Współbieżność rozproszona

(bez zasobów współdzielonych

-składowe algorytmu współpracują

jedynie w sensie obliczeniowym,

tzn. wypracowują na swoją rzecz

wyłącznie jakieś wartości i

komunikują się na tę okoliczność)

22

Algorytmy i struktury danych, temat 1

Różnice z zasadach implementacji

algorytmów współbieżnych



Klasyczne programowanie współbieżne - polega na
dekompozycji problemu na wiele elementów
oprogramowania, które są wykonywane przez pewną
liczbę procesorów z pamięcią współdzieloną. Są to tzw.
systemy ściśle powiązane.



Współbieżność rozproszona - polega na
dekompozycji problemu na wiele elementów
oprogramowania, które są wykonywane przez pewną
liczbę niezależnych procesorów (własny zegar taktujący
i pamięć operacyjna) komunikujących się poprzez sieć
połączeń (np. siec lokalna). Są to tzw. systemy luźno
powiązane.

23

Algorytmy i struktury danych, temat 1

Języki i środowiska programowania współbieżnego

Z konstrukcjami programowania

współbieżnego -

Concurrent Pascal, Concurrent C, CSP, Ada,

Modula 2, MODSIM II, Java, Linda, Occam, Orca

Umożliwiające programowanie

współbieżne (C/C++, Delphi Pascal).

Język programowania nie zawiera

mechanizmów synchronizacji procesów lecz

pozwala wykorzystywać obiekty

synchronizacji dostarczane przez system

operacyjny.

24

Algorytmy i struktury danych, temat 1

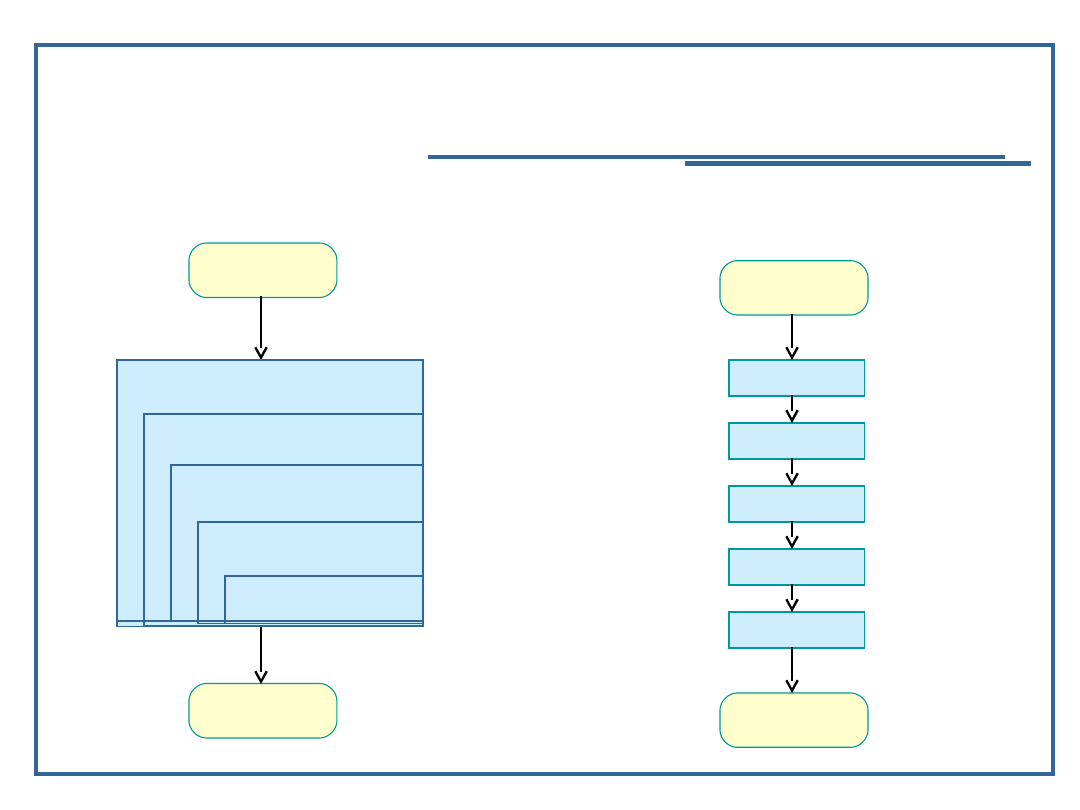
Klasyfikacja algorytmów, cd.

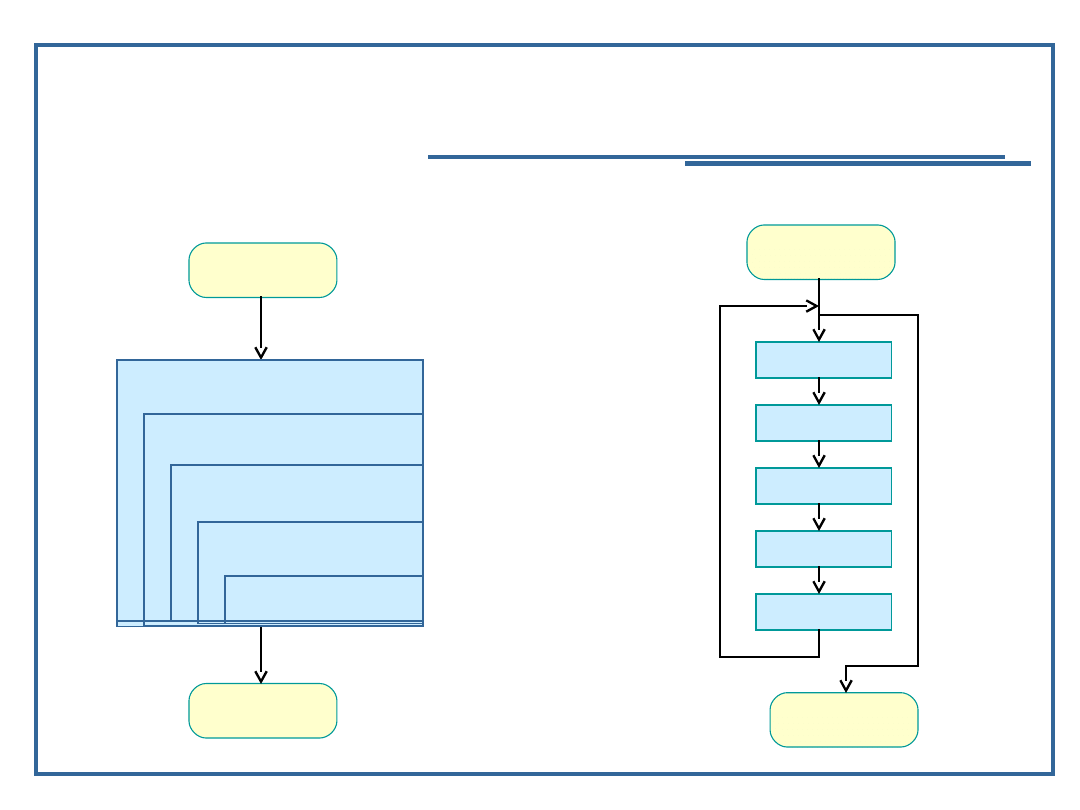
algorytmy rekurencyjne, algorytmy iteracyjne

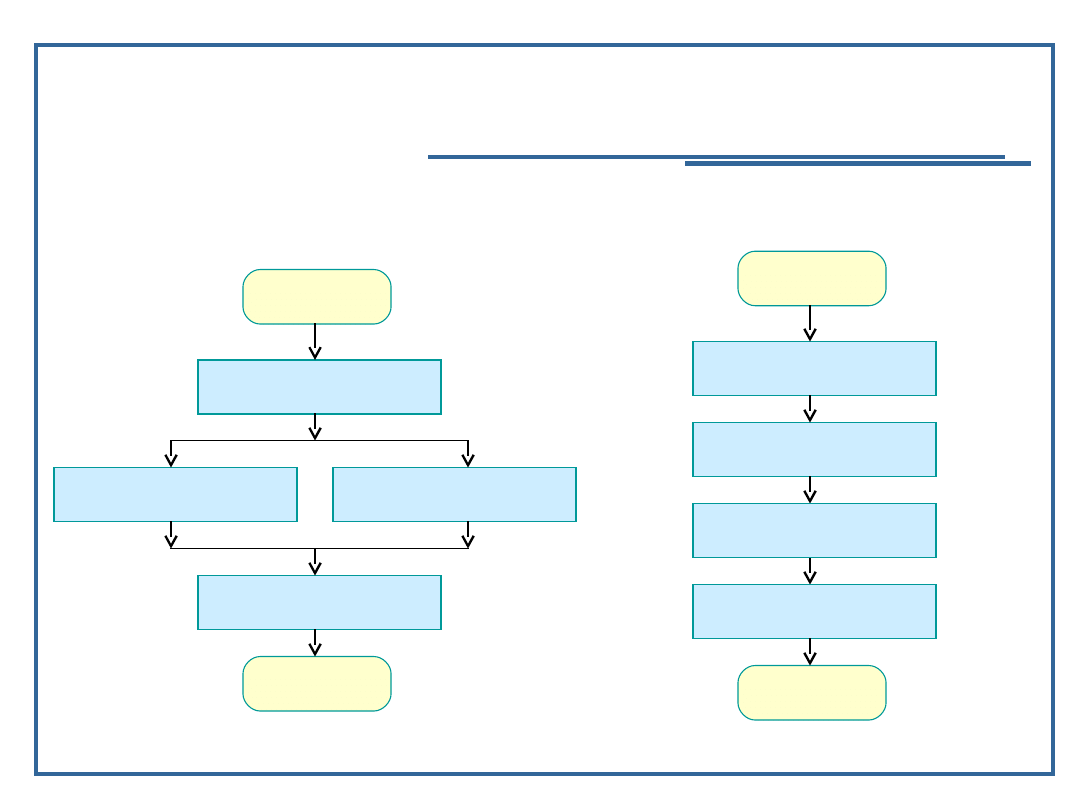
Algorytm rekurencyjny: Algorytm iteracyjny:

START

STOP

Krok_1

Krok_2

Krok_3

Krok_4

Krok_5

START

STOP

Krok_1

Krok_2

Krok_3

Krok_4

Krok_5

25

Algorytmy i struktury danych, temat 1

Przykład obliczania silni dla n=5,

Algorytm rekurencyjny: Algorytm sekwencyjny

(podobna zasada obowiązuje dla iteracji):

START

STOP

= 1

= 1* 2

= 2 * 3

= 6 * 4

= 24 * 5

START

STOP

= 5 * 4!

= 4 * 3!

3 * 2!

2 * 1!

1

= 4 * 3!

= 3 * 2!

= 2 * 1!

= 1

26

Algorytmy i struktury danych, temat 1

Wywołanie funkcji rekurencyjnej



Rekurencja oznacza wywołanie funkcji (procedury)
przez tę samą funkcję



Ważne jest, aby kolejne wywołania funkcji (procedury)
rekurencyjnej były realizowane dla kolejnych wartości
parametrów formalnych w taki sposób, aby nie doszło
do zjawiska „nieskończonej pętli rekurencyjnych
wywołań funkcji”

27

Algorytmy i struktury danych, temat 1

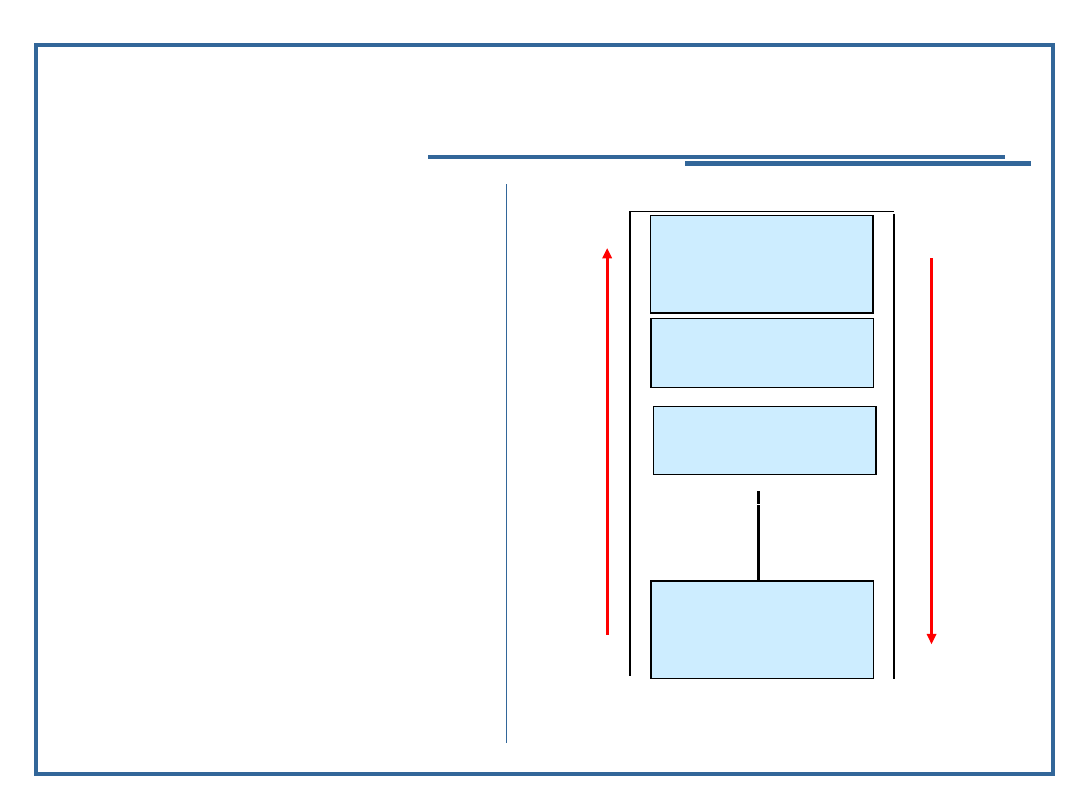
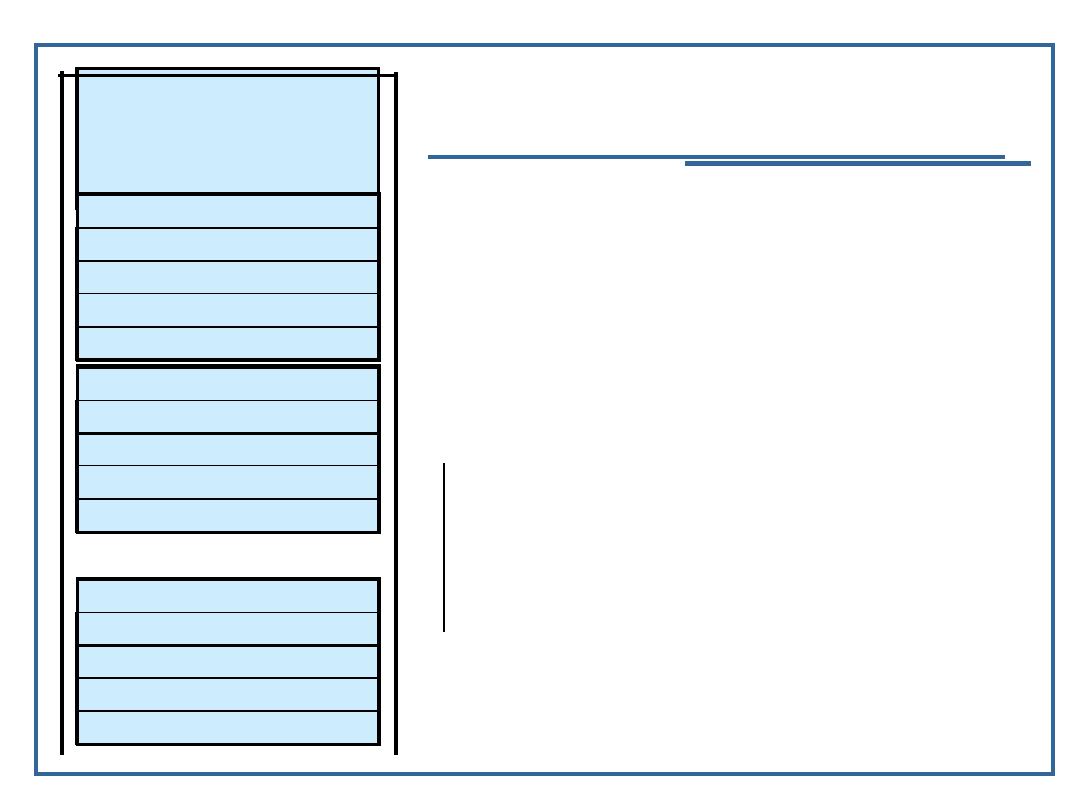
Wywołanie funkcji rekurencyjnej



Kolejne wywołania
funkcji rekurencyjnej są
związane z odkładaniem
na stosie programu
kolejnych rekordów
aktywacji procedury



W wyniku kończenia
działania
poszczególnych funkcji
na kolejnych poziomach
rekurencji kolejne
rekordy aktywacji są
zdejmowane ze stosu

Pierwszy

poziom

rekurencji

Drugi poziom

rekurencji

Trzeci poziom

rekurencji

Ostatni

poziom

rekurencji

Dno stosu

programu

Wierzchołek

stosu

k

o

le

jn

e

w

yw

o

ła

n

ia

r

e

k

u

re

n

c

yj

n

e

zw

a

ln

ia

n

ie

s

to

su

i

z

w

ro

t

p

a

ra

m

e

tr

ó

w

p

o

m

ię

d

zy

k

o

le

jn

ym

i

p

o

zi

o

m

a

m

i

re

k

u

re

n

c

ji

28

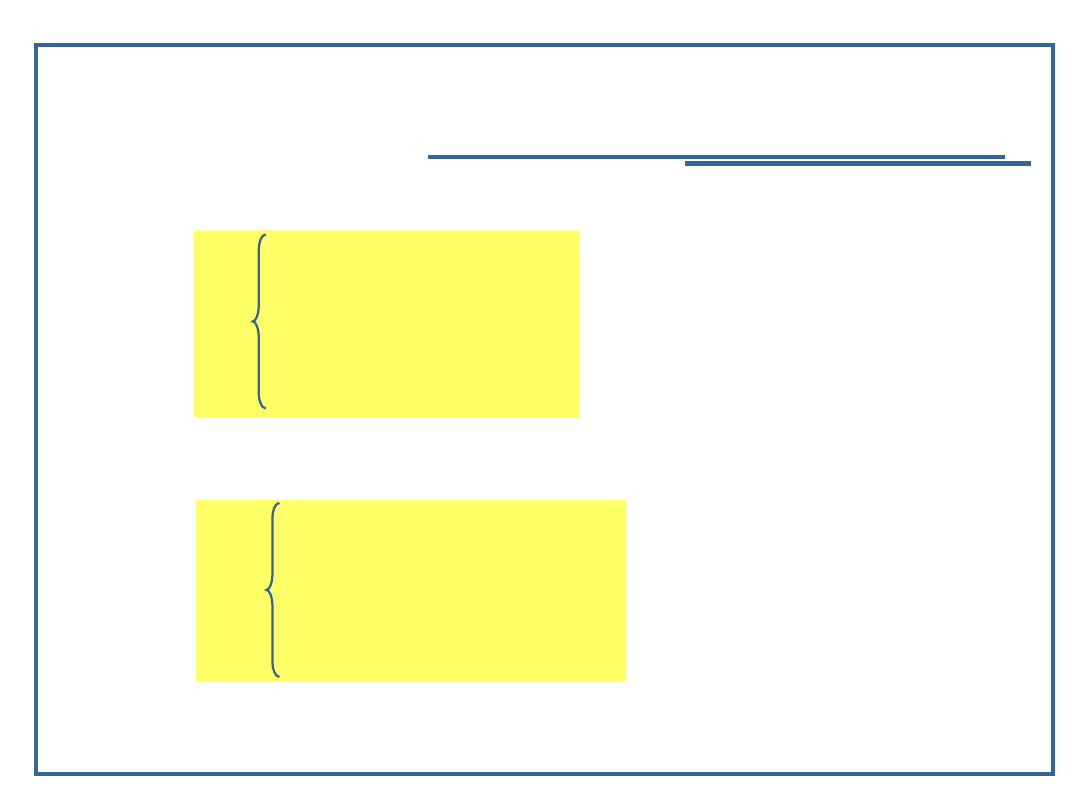
Algorytmy i struktury danych, temat 1

Stos programu w

wywołaniach

rekurencyjnych –

przykład C/C++

Adres powrotu do

systemu

operacyjnego

Dno stosu programu

Adres powrotu z funkcji

Zwracana wartość

Parametry przez adres

Parametry przez wartość

Zmienne lokalne

Adres powrotu z funkcji

Zwracana wartość

Parametry przez adres

Parametry przez wartość

Zmienne lokalne

Adres powrotu z funkcji

Zwracana wartość

Parametry przez adres

Parametry przez wartość

Zmienne lokalne

funkcja main()

funkcja f1

funkcja f2

funkcja fN

• Stos programu w

wywołaniach

rekurencyjnych jest

bardziej eksploatowany

niż wtedy, gdy

wywołania nie są

rekurencyjne
Kolejne poziomy

rekurencji wymagają

odkładania na stosie

programu kolejnych

rekordów aktywacji

funkcji
W przypadku procedur

mechanizm obsługi

stosu jest analogiczny.

Różnica polega na tym,

że nie adres do

zwracanej wartości jest

„void”

29

Algorytmy i struktury danych, temat 1

Przykłady funkcji rekurencyjnych



Znana już funkcja „silnia”:

1,

dla n=0

(warunek zakończenia rekurencji)

n!=

n*(n-1)!

dla n>0



Definicja ciągu liczb wymiernych:

1,

dla n=0

(warunek brzegowy, zakończenia)

f(n)=

f(n-1) + (1/f(n-1)), dla n>0,

określa ciąg o wartościach:

1, 2, 5/2, 29/10, 941/290, 969581/272890,.................

30

Algorytmy i struktury danych, temat 1

Funkcja rekurencyjna – ciąg liczb

Fibonacciego



Ciąg liczb Fibonacciego jest wyliczany wg formuły:

n,

dla n<2

Fib(n)=

Fib(n-2) + Fib(n-1) dla n>=2



Rekurencyjna implementacja w języku C:

long intFib (int n)

{

if (n<2)

return n;

else

return Fib(n-2) + Fib (n-1);

}

Czy na pewno stos

programu

„wytrzyma” taką

realizację funkcji

rekurencyjnej Fib?

31

Algorytmy i struktury danych, temat 1

Efektywność rekurencyjnego

wykonania funkcji Fibonacciego

n

Fib(n+1)

Liczba

dodawań

Liczba

wywołań

6

13

12

25

10

89

88

177

15

987

986

1 973

20

10 946

10 945

21 891

25

121 393

121 392

242 785

30

1 346 269

1 346 268

2 692 537

32

Algorytmy i struktury danych, temat 1

Efektywność rekurencyjnego

wykonania funkcji Fibonacciego, cd.



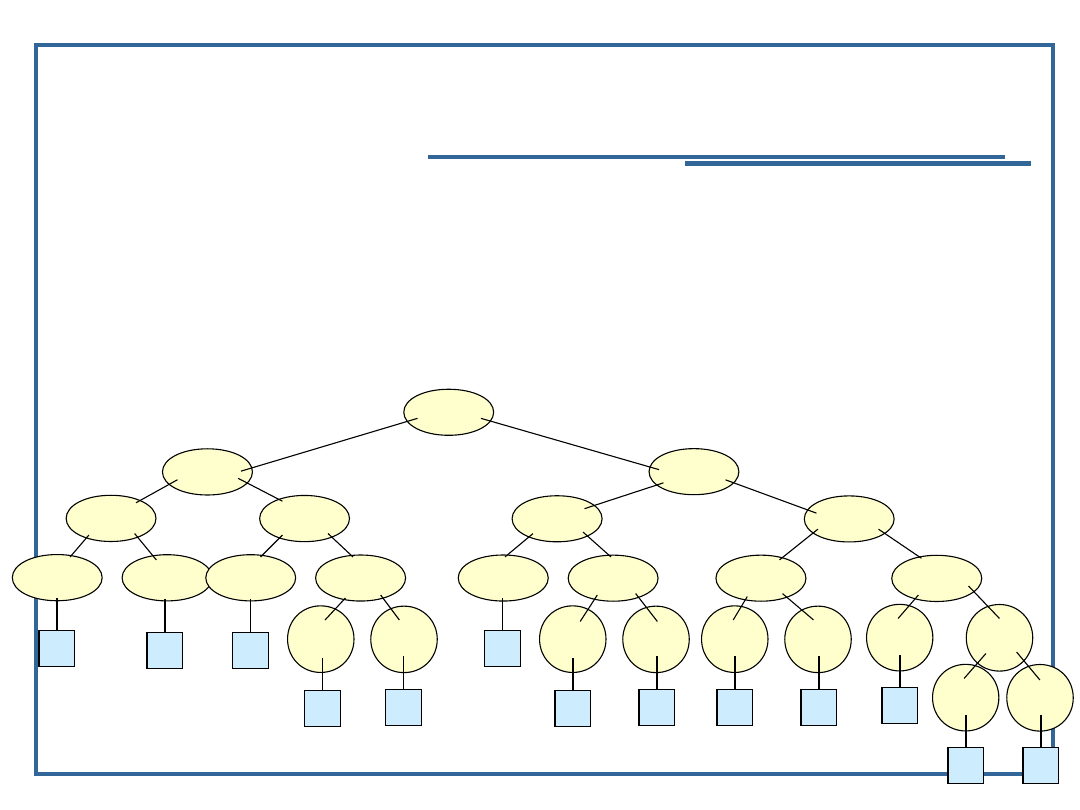
Okazuje się więc, że rekurencyjna implementacja funkcji Fibonacciego
jest niezwykle nieefektywna. Stos programu nie jest praktycznie w
stanie zrealizować tego algorytmu już dla liczb większych od 9.
Oznacza to, że program ma zbyt dużą „złożoność pamięciową”.



Przykład: drzewo wywołań dla F(6):

F(6)

F(5)

F(4)

F(2)

F(0)

F(1)

F(3)

F(1)

F(2)

F(3)

F(1)

F(2)

F(4)

F(2)

F(3)

F(
0)

F(
1)

F(
0)

F(
1)

F(
0)

F(
1)

F(
1)

F(
2)

F(
0)

F(
1)

0

1

0

1

1

0

1

0

1

0

1

1

1

33

Algorytmy i struktury danych, temat 1

Iteracyjne wykonanie rekurencyjnej

funkcji Fibonacciego



Bardziej efektywna jest iteracyjna implementacja funkcji Fibonacciego. Nie przepełniamy wtedy stosu programu i wykonujemy mniejszą liczbę przypisań wartości niż w
implementacji rekurencyjnej, dla której liczba dodawań wynosi Fib(n+1)-1, natomiast liczba przypisań jest równa: 2*Fib(n+1)-1.



Przykład implementacji metodą iteracyjną funkcji Fibonacciego:

long int IteracyjnyFib(int n)
{ register int i=2, last=0, tmp; long int current =1;
if (n<2)
return n;
else {
for ( ; i<=n; ++i) {
tmp = current;
current += last;
last = tmp;
}
return current;
}
}

34

Algorytmy i struktury danych, temat 1

Efektywność iteracyjnego

wykonania rekurencyjnej funkcji

Fibonacciego

n

Liczba przypisań

dla algorytmu

iteracyjnego

Liczba przypisań

(wywołań) dla

algorytmu

rekurencyjnego

6

15

25

10

27

177

15

42

1 973

20

57

21 891

25

72

242 785

30

87

2 692 537

35

Algorytmy i struktury danych, temat 1

Własności algorytmów



adekwatność (semantyczna poprawność) - czy
algorytm realizuje obliczenia (przetwarzanie) zgodnie z
przyjętym celem realizacji obliczeń (przetwarzania)



własność stopu - zostały zdefiniowane kryteria
zatrzymania wykonywania algorytmu w warunkach
poprawnego i niepoprawnego zakończenia obliczeń



jednoznaczność - algorytm jest zapisany w sposób na
tyle precyzyjny, że jego wykonanie jest prawie
automatycznym powtarzaniem kolejnych kroków



powtarzalność - każde wykonanie algorytmu
przebiega według takiego samego schematu działania i
prowadzi do rej samej klasy rozwiązań



złożoność obliczeniowa - nakład czasu lub zasobów
maszyny realizującej algorytm, niezbędny dla jego
prawidłowego wykonania

36

Algorytmy i struktury danych, temat 1

Konstrukcje algorytmiczne w

językach programowania



Poruszamy się w kręgu języków programowania z rodziny

Algol’60. Przedstawicielami tej rodziny są między innymi

takie języki programowania, jak:



Pascal (Niklaus Wirth),



Modula2 (Niklaus Wirth),



MODSIM II – symulacyjny język programowania (CACI),



C (Dennis Ritchie)



C++ (obiektowe rozszerzenie języka C)



Visual Basic (Microsoft)



Ada (na zamówienie Pentagonu)



Java (pochodna jezyka C++)



Omówione na kolejnych slajdach schematy konstrukcji

programowych są wzorowane na ich logice pochodzącej z

języka C/C++. W większości przypadków jest to logika

wspólna dla wszystkich powyżej wymienionych języków

programowania

37

Algorytmy i struktury danych, temat 1

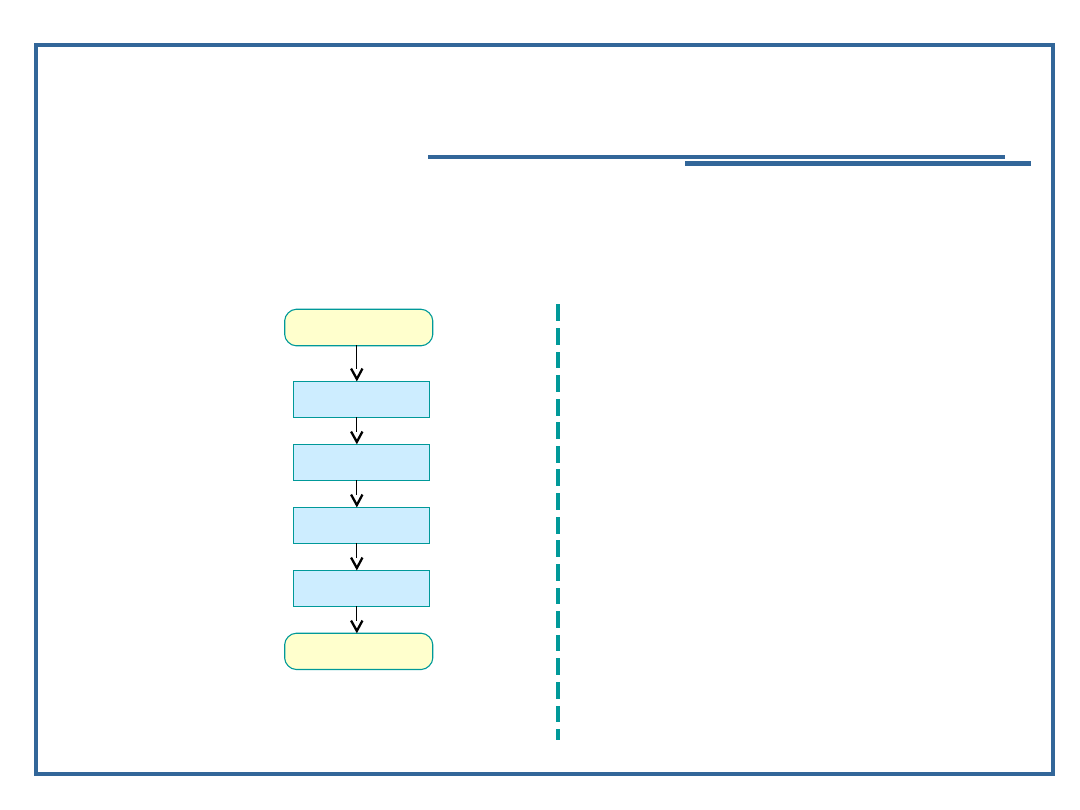
Schemat

sekwencji instrukcji



Semantyka: wykonywanie kolejnych kroków algorytmu
zgodnie z zadaną sekwencją,



Syntaktyka:

START

STOP

Krok_1

Krok_2

Krok_3

Krok_4

Schemat blokowy
sekwencji instrukcji

begin

krok_1;

krok_2;

krok_3;

krok_4;

end;

38

Algorytmy i struktury danych, temat 1

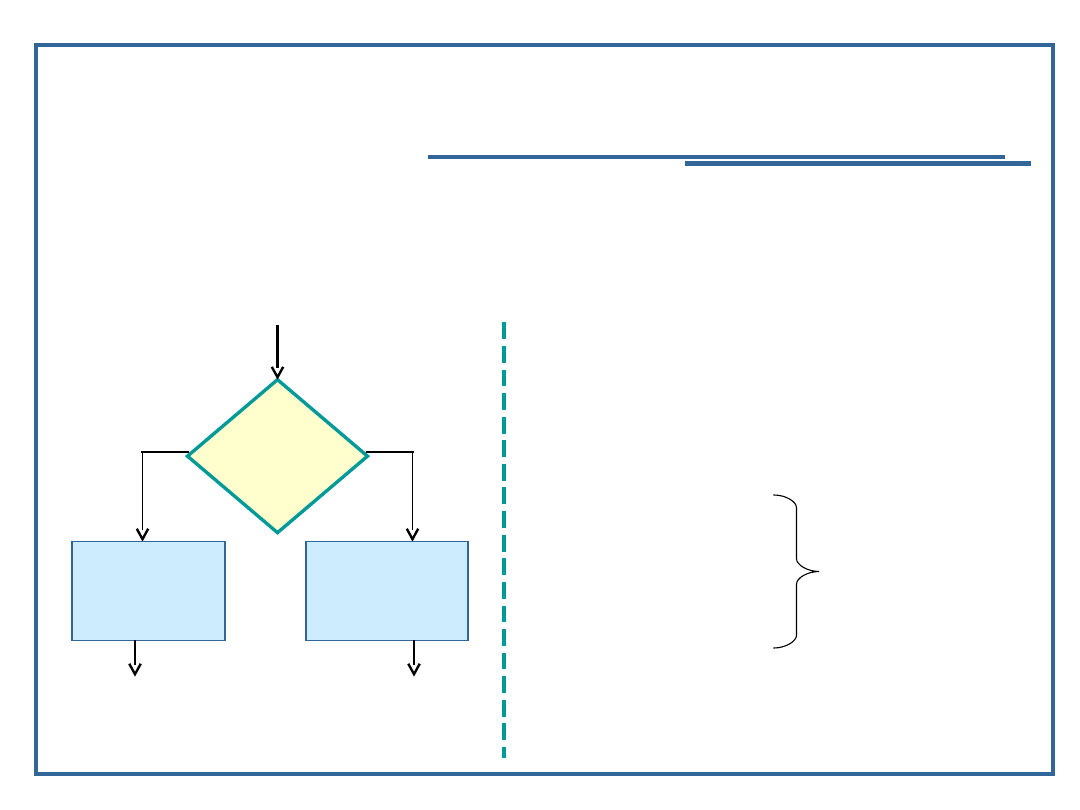
Schemat

instrukcji alternatywy



Semantyka: wybór jednego z dwóch torów przetwarzania
po sprawdzeniu prawdziwości zdania logicznego,



Syntaktyka:

if logic_assertion_is true then

action_if_true;

else

action_if_false;

end if;

Sekcja „else”
jest opcjonalna

warunek

T

N

akcja

jeśli „TAK”

akcja

jeśli „NIE”

Schemat blokowy
instrukcji „if”

39

Algorytmy i struktury danych, temat 1

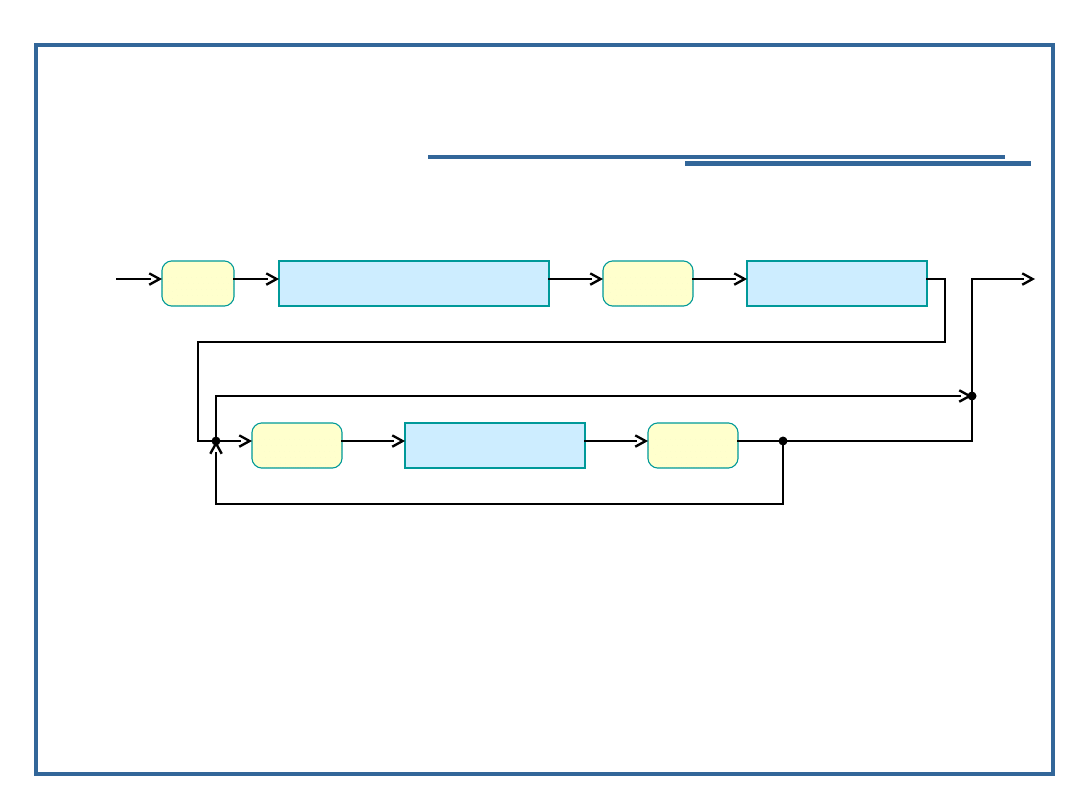
Zapis syntaktyki instrukcji warunkowej



Definicja syntaktyki instrukcji warunkowej „if-then-else” w
postaci diagramów syntaktycznych Niklausa Wirtha:

if

logic_assertion_is_true

then

action_if_true

else

action_if_false

end if



Definicja syntaktyki instrukcji warunkowej „if-then-else”
w zapisie BNF

<if_instruction> :: =

if <logic_assertion_is_true> then

<action_if_true> else <action_if_false> end if;
if <logic_assertion_is_true> then

<action_if_true> end if;

40

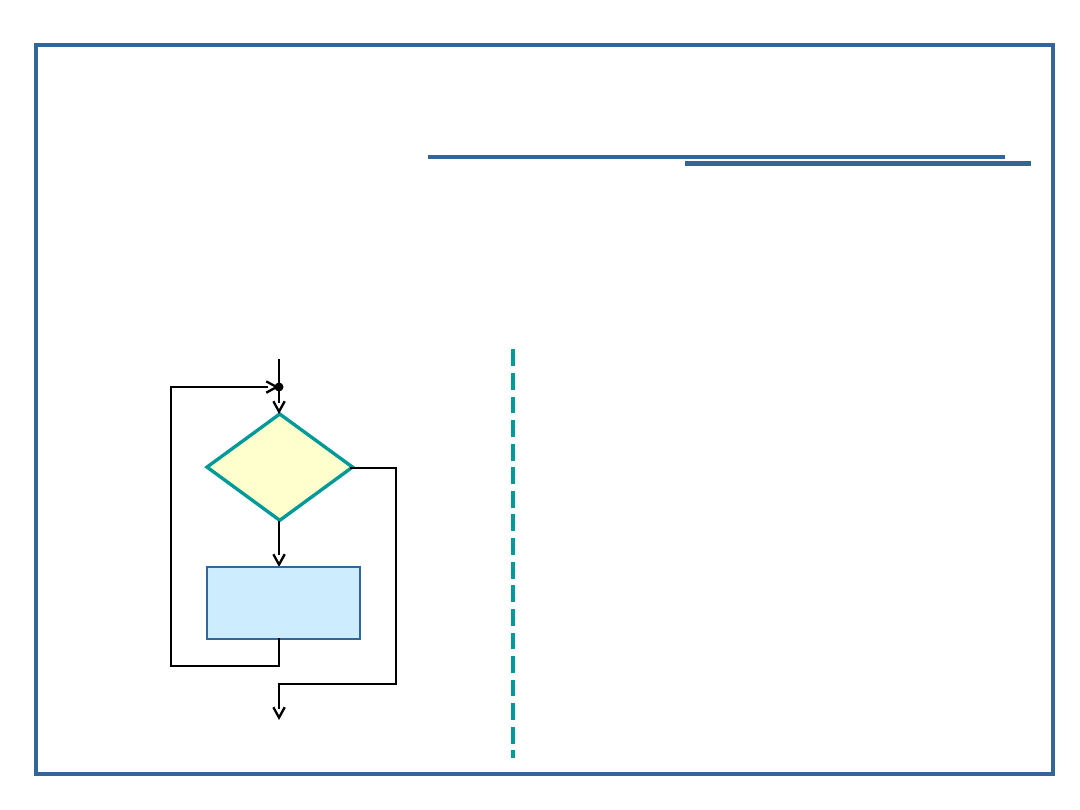
Algorytmy i struktury danych, temat 1

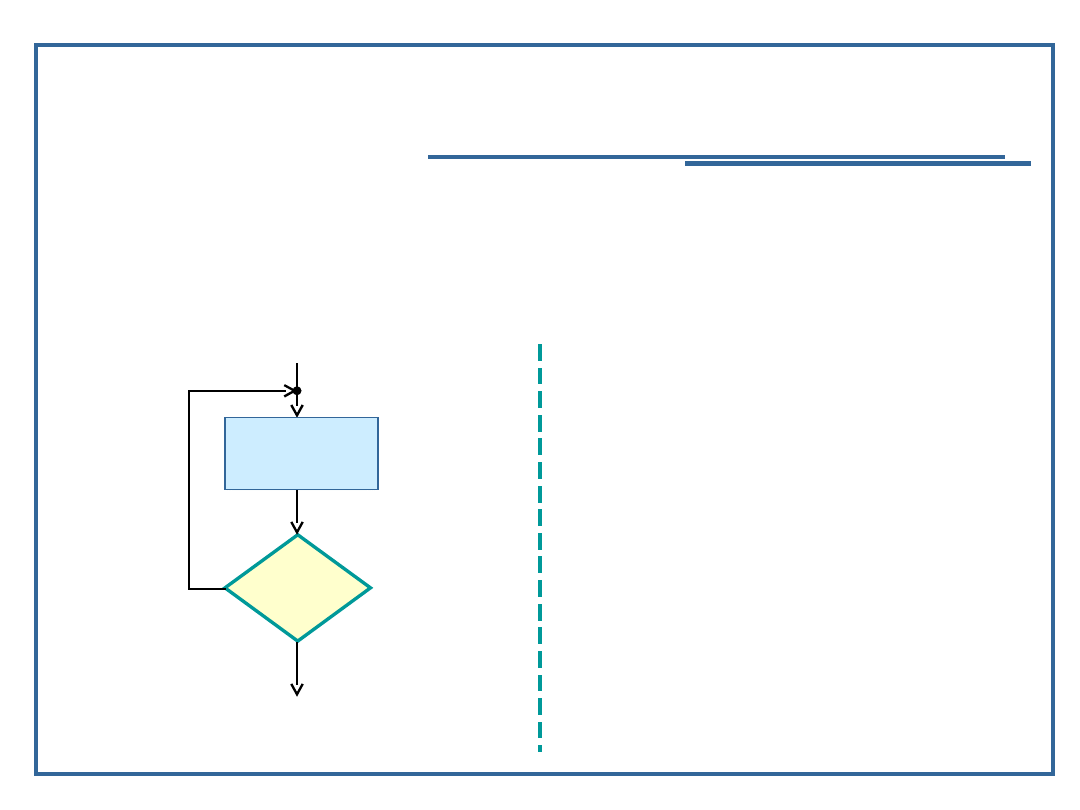
Schemat pętli iteracyjnej „podczas

gdy”



Semantyka: powtarzanie tych samych czynności
podczas zachodzenia warunku logicznego,
zdefiniowanego na wejściu do każdego kroku pętli



Syntaktyka:

warunek

T

N

powtarzane

kroki

Schemat blokowy pętli
„while-do”

while logic_assertion_is true
do

action_in_while-do_loop;

end while;

41

Algorytmy i struktury danych, temat 1

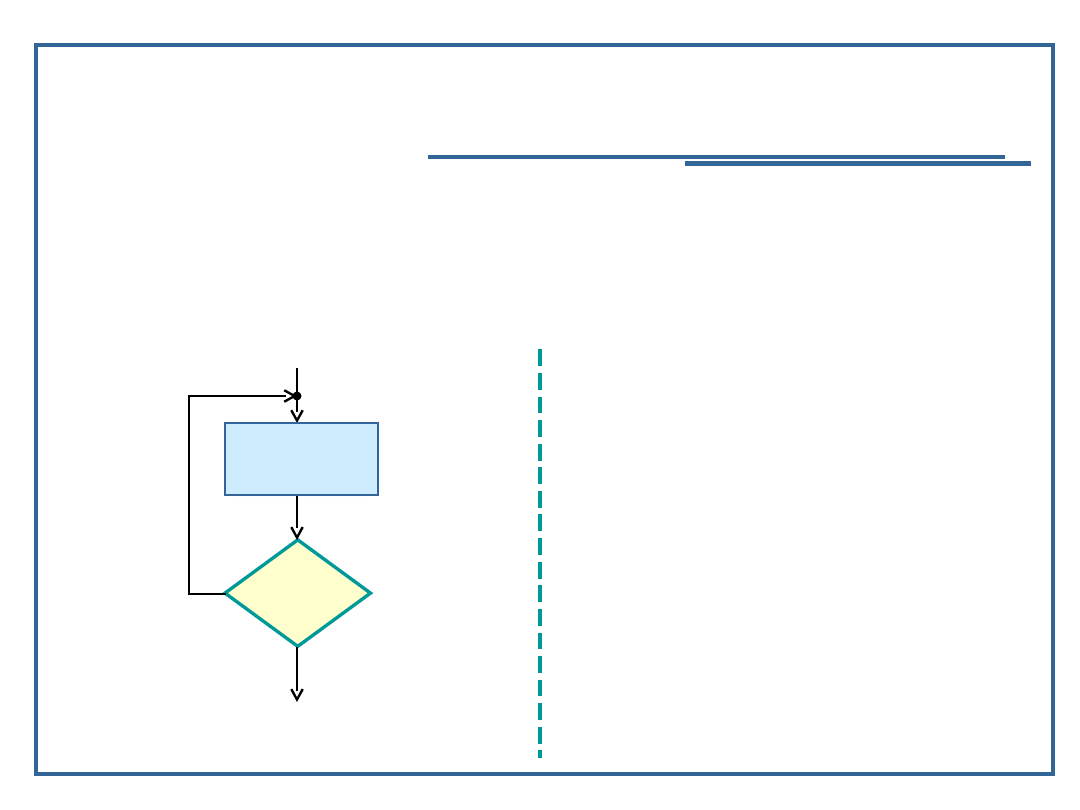
Schemat

pętli iteracyjnej „do-

while”



Semantyka: powtarzanie tych samych czynności przy
sprawdzaniu warunku logicznego, zdefiniowanego na
końcu do każdego kroku pętli



Syntaktyka:

Schemat blokowy pętli
„do-while”

warunek

T

N

powtarzane

kroki

do

action_in_do-while_loop;

while logic_assertion_is
true;

42

Algorytmy i struktury danych, temat 1

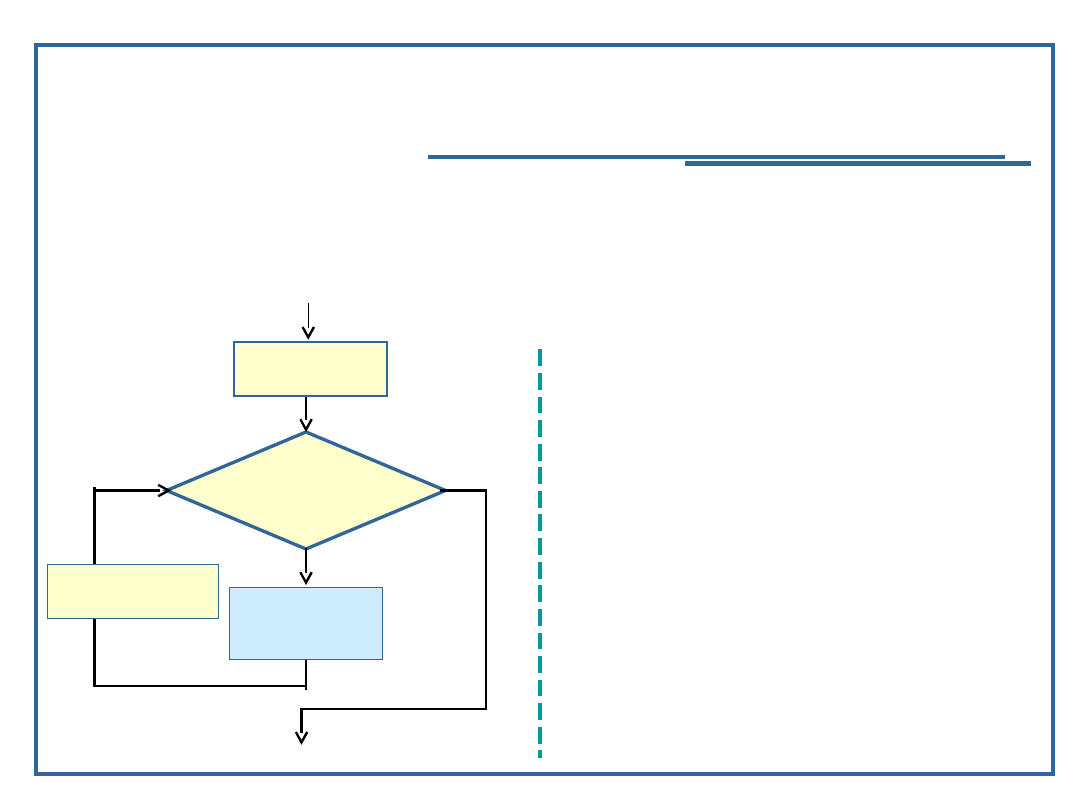
Schemat

pętli iteracyjnej „aż-do”



Semantyka: powtarzanie tych samych czynności przy
braku zachodzenia warunku logicznego, sprawdzanego
na końcu każdego kroku pętli



Syntaktyka:

Schemat blokowy pętli
„repeat-until”

warunek

N

T

powtarzane

kroki

repeat

action_in_repeat_loop;

until logic_assertion_is
false;

43

Algorytmy i struktury danych, temat 1

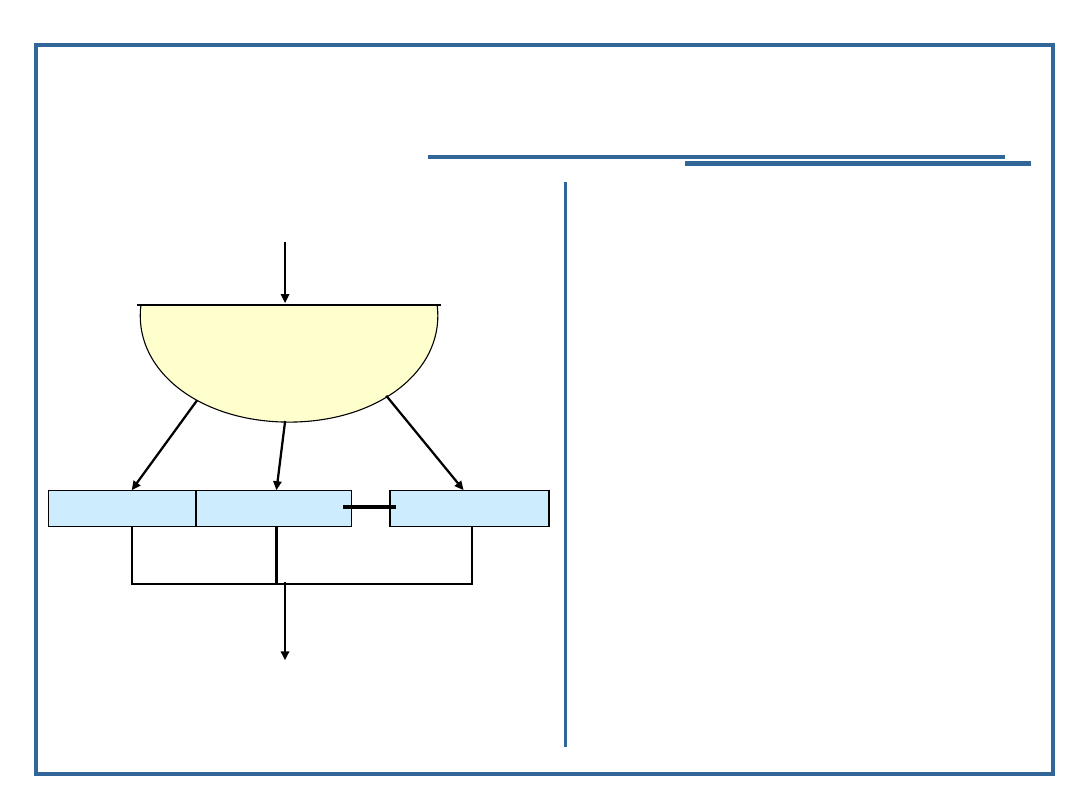
Schemat

pętli iteracyjnej „for”

(w

wersji z języka C/C++)



Semantyka: powtarzanie tych samych czynności ilość
razy określoną wartością startu, przyrostu i
niezmiennika pętli



Syntaktyka:

for

(n=start; for_invariant;

change_n_rule)

{

action_in_for_loop;

}

for_invariant_rule

T

N

powtarzane

kroki

Schemat blokowy pętli „for”

n = start

change_n_rule

44

Algorytmy i struktury danych, temat 1

Instrukcja wyboru

wielowariantowego „switch-case”

(w

wersji z języka C/C++)

switch(zmienna){

case stała1:

Instrukcje1;
Break;

case stała2:

Instrukcje1;
Break;

…………
default:

InstrukcjeD;
Break;

}

zmienna

instrukcje1 instrukcje1

instrukcjeD

stała1

stała2

default

45

Algorytmy i struktury danych, temat 1

Metody weryfikacji algorytmów

-

black box – metoda syntetyczna



Metoda czarnej skrzynki, (ang. Black box method) - polega
na weryfikacji poprawności algorytmu poprzez analizę
uzyskanych wyników jego wykonania po zadaniu
określonego zestawu danych wejściowych. W tej metodzie
nie analizuje się wewnętrznej budowy algorytmu -
analizuje się go jako jedną, zamkniętą całość.

Algorytm

Wejście

Wyniki

46

Algorytmy i struktury danych, temat 1

Metody weryfikacji algorytmów

glass (white) box – metoda analityczna



Metoda szklanej (białej) skrzynki, (ang. glass, white box) -
polega na śledzeniu poprawności algorytmu „od jego
wnetrza”. Uwzględnia się wtedy wewnętrzną logikę algorytmu.
Przykładami zastosowania metod białej skrzynki mogą być:



mapy śledzenia algorytmów - umożliwiają analizę poprawności
wykonywania się algorytmów poprzez analizę wartości zmiennych
(parametrów) w poszczególnych krokach jego wykonywania się,
podobną rolę pełnią tzw. „debuggery” będące składowymi
współczesnych środowisk programistycznych



formalne specyfikacje programów - na przykład Vienna
Development Method (VDM). Umożliwia zapis algorytm w postaci
pewnego języka formalnego. W ramach metody określona jest
semantyka i syntaktyka tego języka, jak również tzw. reguły
dowodzenia poprawności specyfikacji algorytmów (programów)



logika algorytmiczna - badanie poprawności wykonywania się
algorytmu poprzez stwierdzanie prawdziwości pewnych asercji
logicznych zdefiniowanych dla weryfikacji kolejnych kroków jego
wykonania

47

Algorytmy i struktury danych, temat 1

Złożoność obliczeniowa algorytmów

-

analiza algorytmów



Analiza algorytmów - złożoność obliczeniowa jest
podstawową własnością określaną dla algorytmów.
Zadaniem analizy algorytmu jest określenie tej
złożoności, a co za tym idzie realizowalności algorytmu.



Algorytmy realizowalne mają złożoność aproksymowaną
funkcją:



liniową (wielomianem)



logarytmiczną.

Mówi się, że takie algorytmy określają zadania ze

zbioru zadań rozwiązywalnych (a co za tym idzie
implemento-walnych). Najszybsze są algorytmy o
złożoności logarytmicznej.



Nie potrafimy skutecznie implementować algorytmów o
złożoności wykładniczej.

48

Algorytmy i struktury danych, temat 1

Rodzaje złożoności algorytmów



Złożoność zasobowa (pamięciowa) - wyrażana w skali
zajętości zasobów (PAO, pamięci zewnętrznych itp.)
niezbędnych dla realizacji algorytmu



Złożoność czasowa - wyrażana w skali czasy
wykonania algorytmu (liczba kroków, aproksymowany
czas rzeczywisty)



Przykłady szacowania wartości złożoności algorytmów
będziemy realizować przy okazji konkretnych
przykładów na kolejnych wykładach



De’facto wszystko przenosi się w konsekwencji na
koszty eksploatacji oprogramowania, realizującego
analizowany algorytm

49

Algorytmy i struktury danych, temat 1

Czynniki wpływające na złożoność

algorytmów



Rozmiar zadania - rozmiar danych niezbędnych dla
realizacji algorytmu. Bierze się pod uwagę:



rozmiar danych wejściowych



rozmiar danych roboczych



rozmiar danych wyjściowych



Czas działania algorytmu - liczba kroków przekładająca
się na czas faktycznej pracy maszyny realizującej
algorytm. Istotne znaczenie mają w tym przypadku:



złożoność rozwiązywanego zadania



sposób konstrukcji algorytmu



wydajność maszyny realizującej obliczenia

50

Algorytmy i struktury danych, temat 1

Funkcja kosztu algorytmu



Funkcja kosztu zasobowego algorytmu stanowi odwzorowanie
rozmiaru zadania w umowne jednostki kosztu algorytmu (np.
rozmiar zasobów, jednostki monetarne (złotówki, dolary itp.)):



FKz : RZ -> WKz,

gdzie:

FKz - funkcja kosztu zasobowego,

RZ - rozmiar zadania,
WKz - wartość kosztu zasobowego,



Dla potrzeb wykładu pozostaniemy jedynie przy kosztach
zasobowych algorytmów.



Jednak nie tylko koszty zasobowe są brane pod uwagę. Często
analizuje się inne koszty realizacji algorytmów (np. pieniądze).



Przejrzyj ponownie slajdy z analizą efektywności algrytmu Fibonacciego. Co
możesz powiedzieć na temat jego złożoności obliczeniowej?

51

Algorytmy i struktury danych, temat 1

Podsumowanie:



Poznaliśmy podstawowe pojęcia algorytmiki



Jest to wiedza podstawowa na naszym przedmiocie



Następny wykład:



poznamy na nim między innymi definicję struktury danych

i przykłady różnych struktur danych

dziękuję za uwagę