FALE

Ruch falowy
Fala –zaburzenie pewnej wielkości fizycznej
charakteryzującej stan ośrodka rozprzestrzeniające
się w przestrzeni.

Powierzchnia łączącą wszystkie punkty ośrodka, do
której dociera w danej chwili zaburzenie –
powierzchnia falowa lub czoło fali. Powierzchnie
falowe mogą mieć różne kształty, np. fale kuliste lub
fale płaskie. Kierunek ruchu fali wyznaczają
promienie fali.

Fale podłużne i fale poprzeczne
Fala podłużna – kierunek drgań cząstek ośrodka
jest równoległy do kierunku rozchodzenia się fali.
Przykład: fala dźwiękowa.

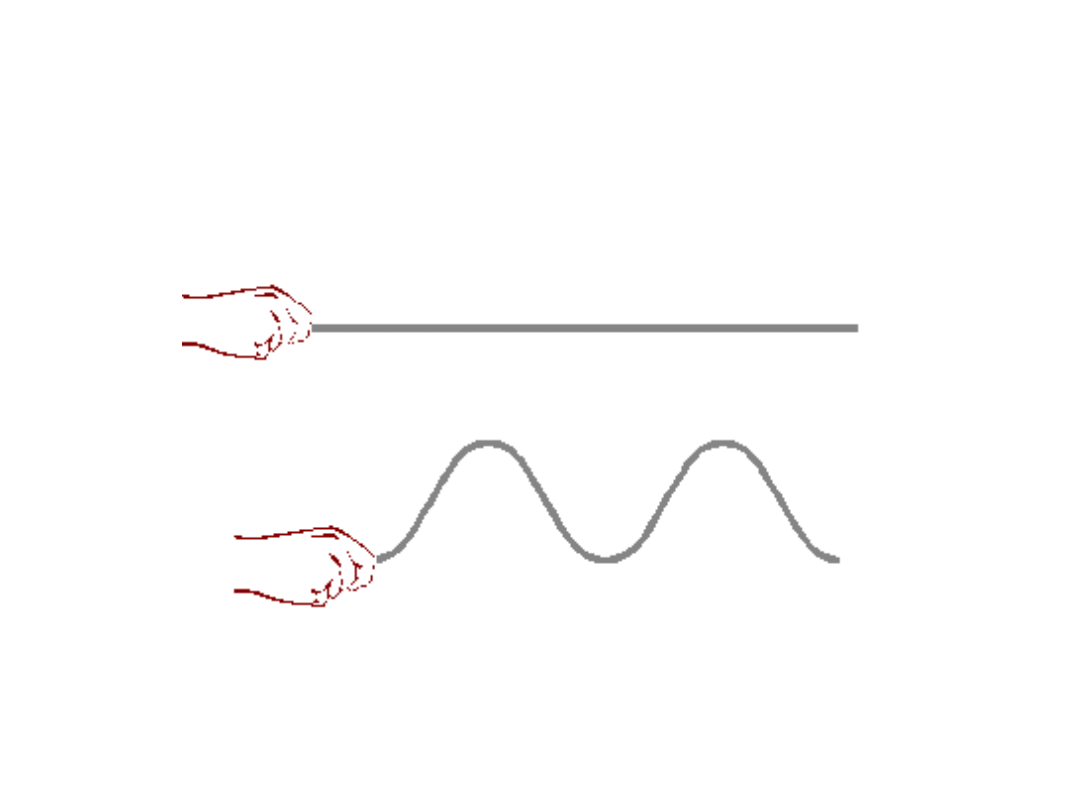
Fala poprzeczna – kierunek drgań cząstek ośrodka jest
prostopadły do kierunku rozchodzenia się fali.
Przykład: fale elektromagnetyczne, w szczególności
światło, które mogą rozchodzić się także w próżni.

W ciałach stałych mogą się rozchodzić fale
mechaniczne podłużne i fale poprzeczne, w cieczach
i gazach – tylko fale podłużne.

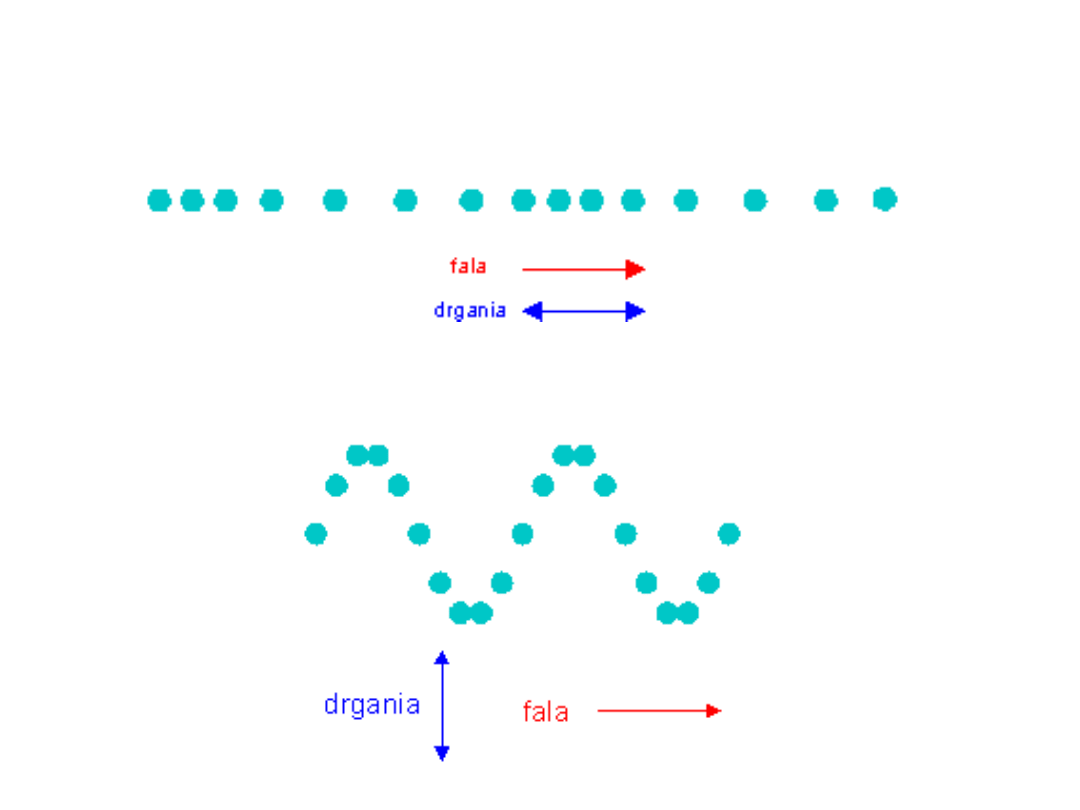
Fala podłużna

Fala poprzeczna











t

A

u



cos

v

x

v

x



















0

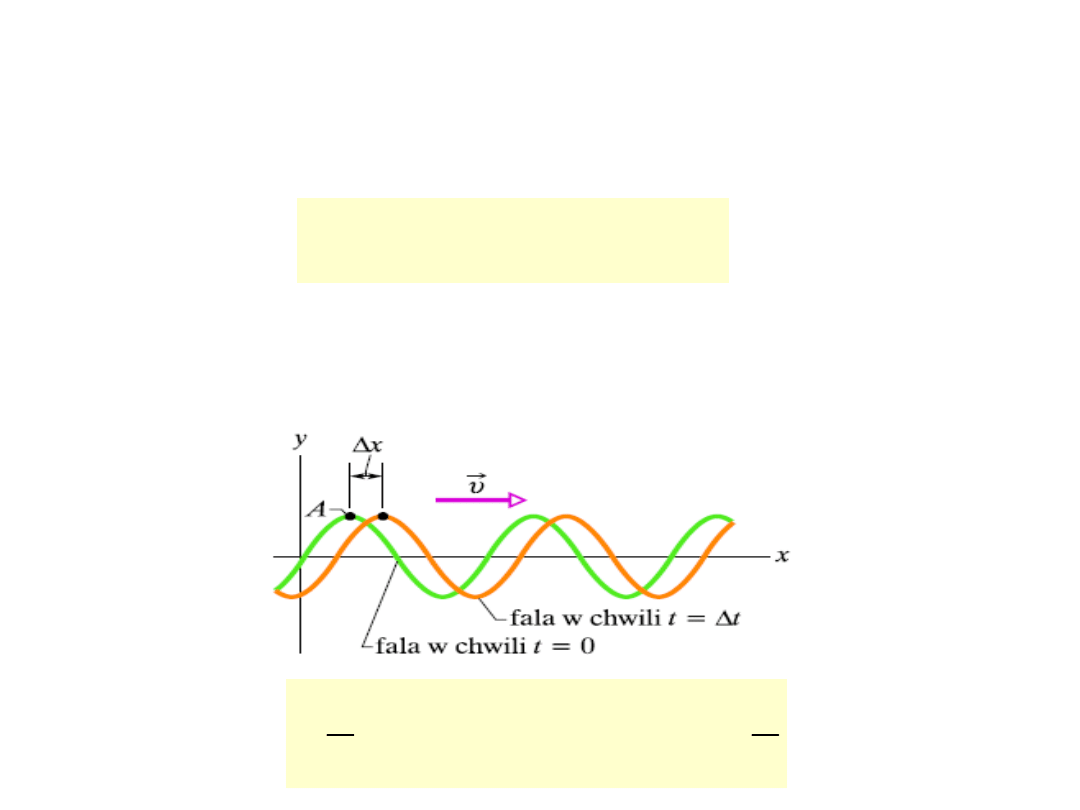
Fala harmoniczna płaska

: rozchodzenie się w

pewnym kierunku drgań harmonicznych. Równanie fali
określa wychylenie u danego punktu o współrzędnej x w
funkcji czasu t .

Załóżmy, że faza początkowa w chwili t = 0 w
punkcie x = 0 wynosi = 0 . Tę samą fazę będzie

miał punkt o współrzędnej x w późniejszej chwili
czasu t= x/v.

Równanie fali harmonicznej płaskiej

 





kx

t

A

t

x

u







cos

,

vT

v

k

k























2

2

2

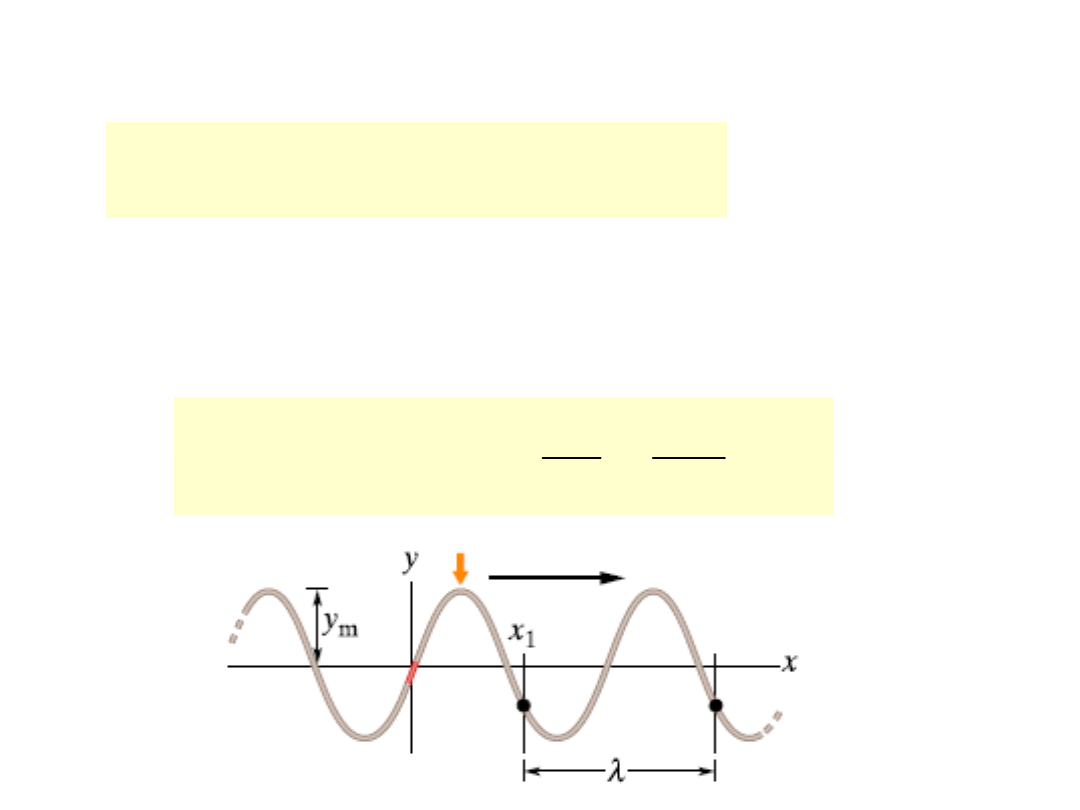
Długość fali – najmniejszą odległość dwóch punktów,
których fazy różnią się o 2 (czyli które drgają tak

samo)

k= ω/ν liczba falowa

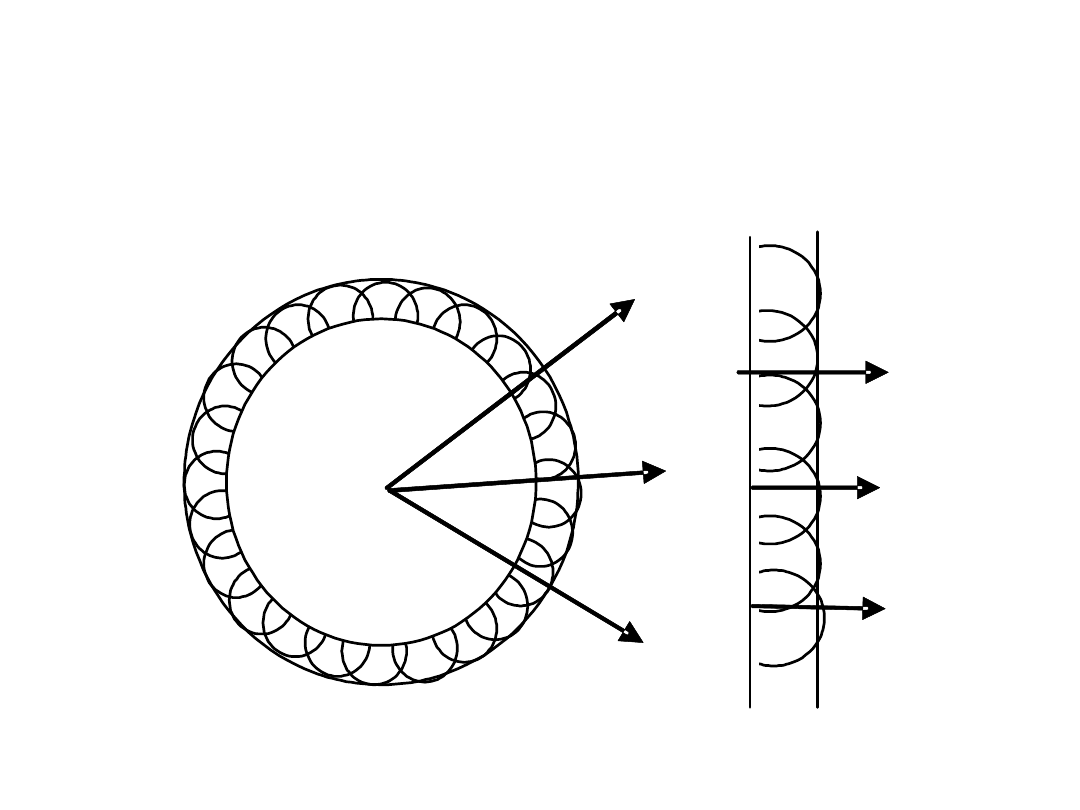
Każdy punkt ośrodka, do którego dociera czoło fali źródłem elementarnej fali

kulistej.

Zasada Huygensa , ugięcie (dyfrakcja) fal

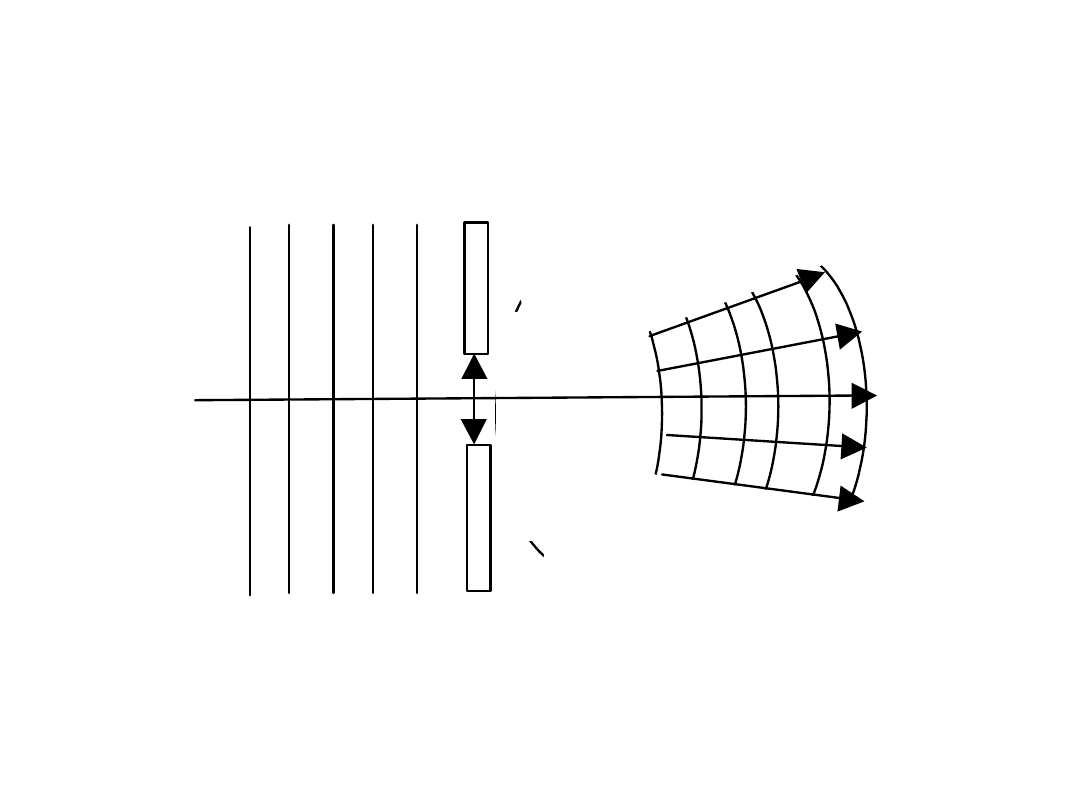
Gdy fala napotyka na przeszkodę z otworem to powierzchnia falowa ulega

zniekształceniu.

a



5



a



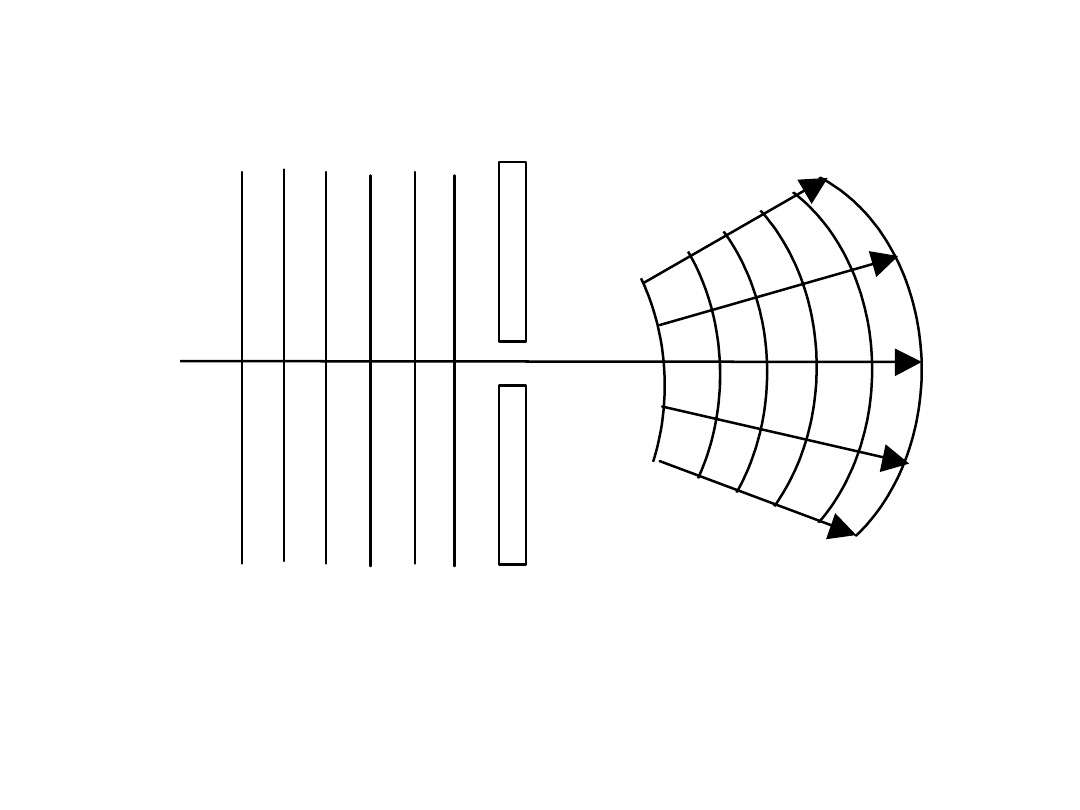
3



a





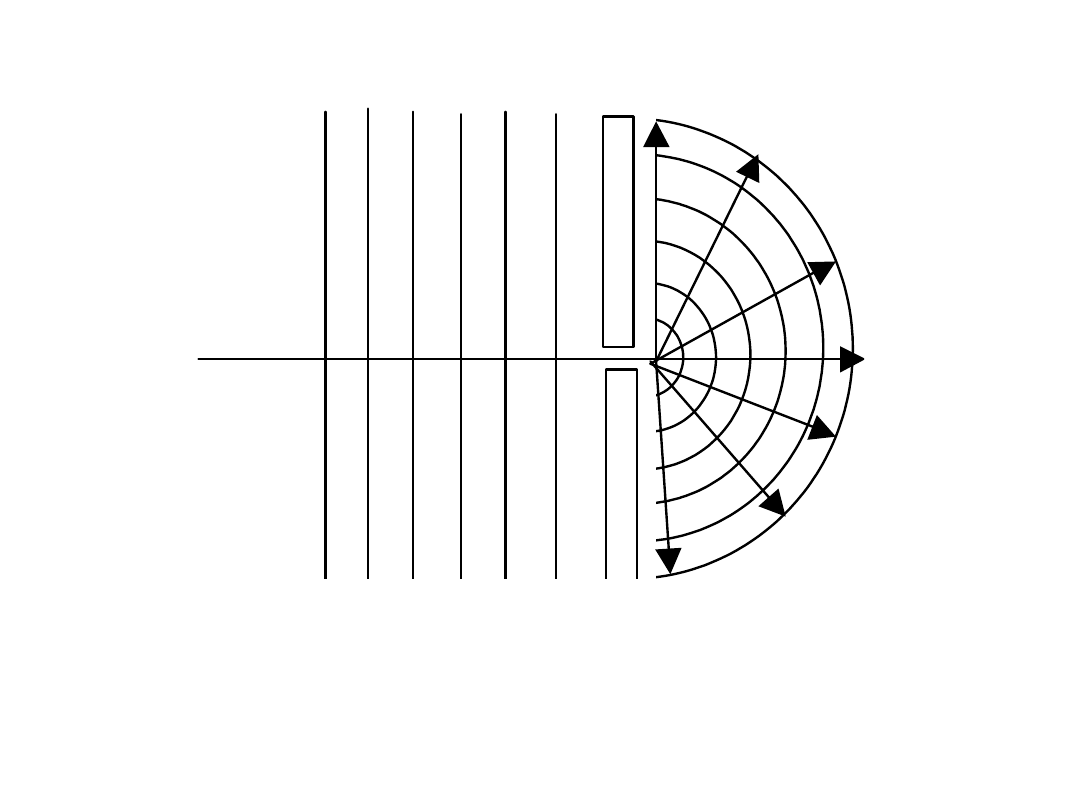
a

 





t

kx

A

t

x

u





 cos

,

1































t

kx

t

kx

A

u

u

u





cos

cos

2

1

 













t

kx

A

t

x

u



cos

,

2

Wypadkowa fala w punkcie o współrzednej x opisana jest wzorem:





























 



2

cos

2

cos

2

t

kx

A

u













 

2

cos

2A

Wyrażenie

 





t

kx

A

t

x

u





 cos

,

1

 





t

kx

A

t

x

u





 cos

,

2

   

t

kx

A

u

u

u



cos

cos

2

2

1







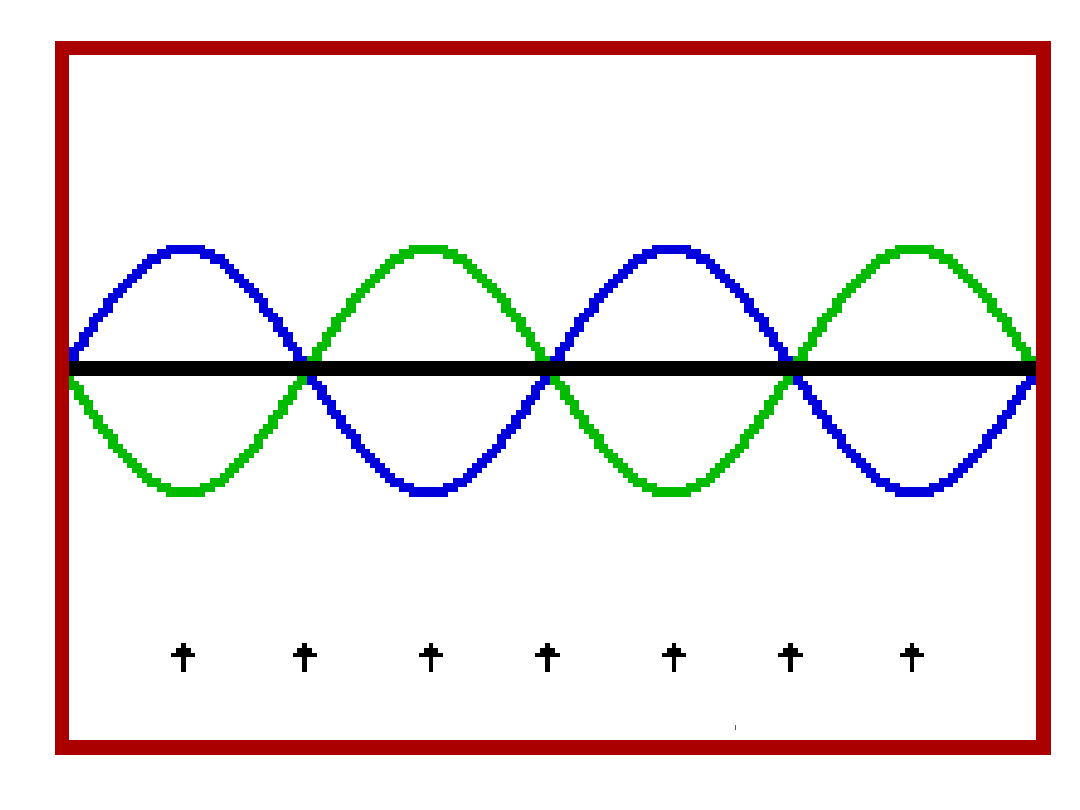
Każdy punkt drga ruchem harmonicznym z częstością
kołową , amplituda dla różnych punktów jest różna. W

punktach, dla których





n

kx





2

amplituda jest równa zeru. Punkty te nazywamy węzłami.

n – liczba całkowita

W punktach, dla których



n

kx

amplituda ma wartość maksymalną równą 2A. Punkty
te nazywamy strzałkami.
Położenie strzałek i węzłów jest niezmienne w czasie i
dlatego taką falę nazywamy falą stojącą.

Sąsiednie strzałki (węzły) spełniają równania dla n
różniących się o 1. Ponieważ k  



, odległość

między sąsiednimi węzłami (strzałkami) wynosi /2 .

n – liczba całkowita

W

W

W

W

S

S

S

Zjawisko Dopplera

Gdy źródło dźwięku porusza się w kierunku nieruchomego obserwatora

słyszy on dźwięk o wyższej częstości niż wtedy gdy źródło jest w spoczynku,

natomiast gdy źródło dźwięku oddala się od obserwatora słyszy on dźwięk o

niższej częstości. Można to wyrazić wzorem:

z

v

v

v

f

f





'

gdzie znak plus odnosi się do ruchu w kierunku od obserwatora, a znak minus do

ruchu w kierunku obserwatora, v jest to prędkość dźwięku, v

z

jest to prędkość

źródła.

Podobne rezultaty otrzymujemy wtedy gdy obserwator jest w ruchu do lub od

spoczywającego źródła dźwięku. wtedy obserwator odbiera dźwięki o częstości:

v

v

v

f

f

0

'





gdzie znak plus odnosi się do ruchu w kierunku źródła, a znak minus do ruchu od

źródła, v jest to prędkość dźwięku, v

0

jest to prędkość obserwatora.

Jeżeli zarówno źródło jak i obserwator poruszają się to obserwator słyszy częstość:

z

v

v

v

v

f

f







0

'

gdzie znak plus w liczniku i minus w mianowniku odnoszą się do sytuacji gdy

obserwator i źródło poruszają się do siebie, a znak minus w liczniku i plus w

mianowniku odnoszą się do sytuacji gdy obserwator i źródło poruszają się od siebie