Digital Image

Processing

Lecture 2:

Operacje arytmetyczne

Professor

Valery Starovoitov

2

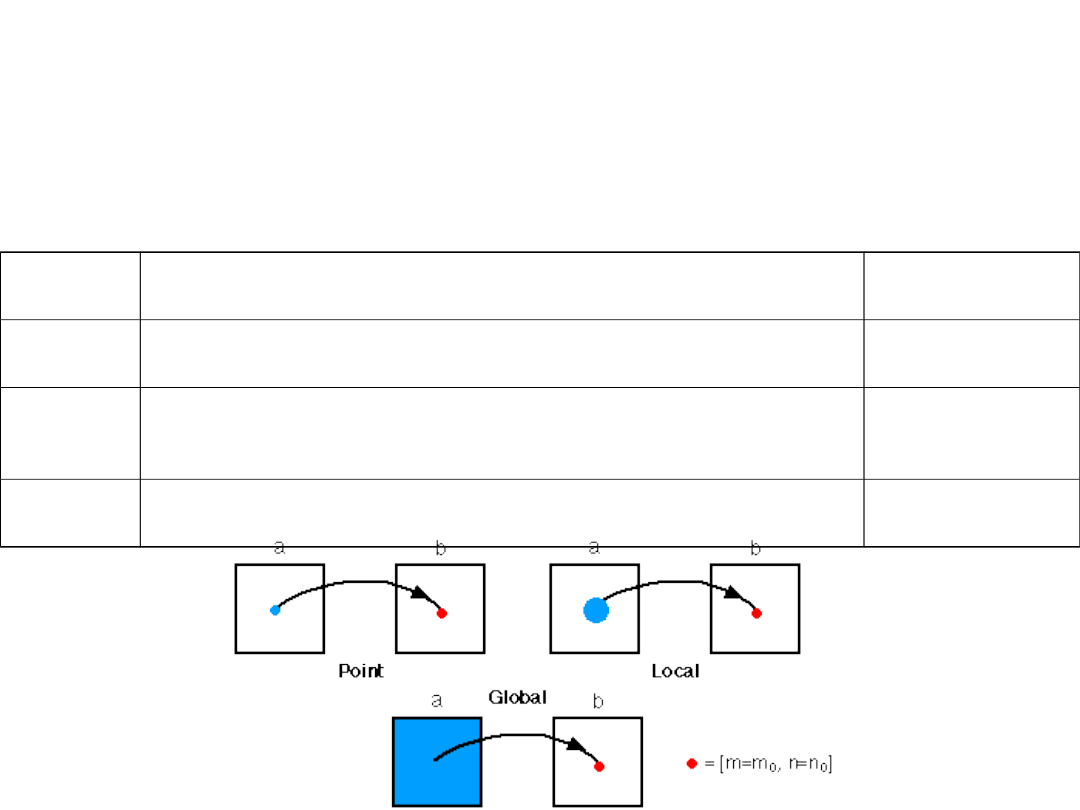
Characteristics of Image Operations

Types of operations (Image size = N x N; neighborhood size = P x

P. Note that the complexity is specified in operations per pixel.)

Operatio

n

Characterization

Complexity/Pixe

l

Point

- the output value at a specific coordinate is dependent

only on the input value at that same coordinate.

constant

Local

- the output value at a specific coordinate is dependent on

the input values in the neighborhood of that same

coordinate.

P*P

Global

- the output value at a specific coordinate is dependent on

all the values in the input image.

N*N

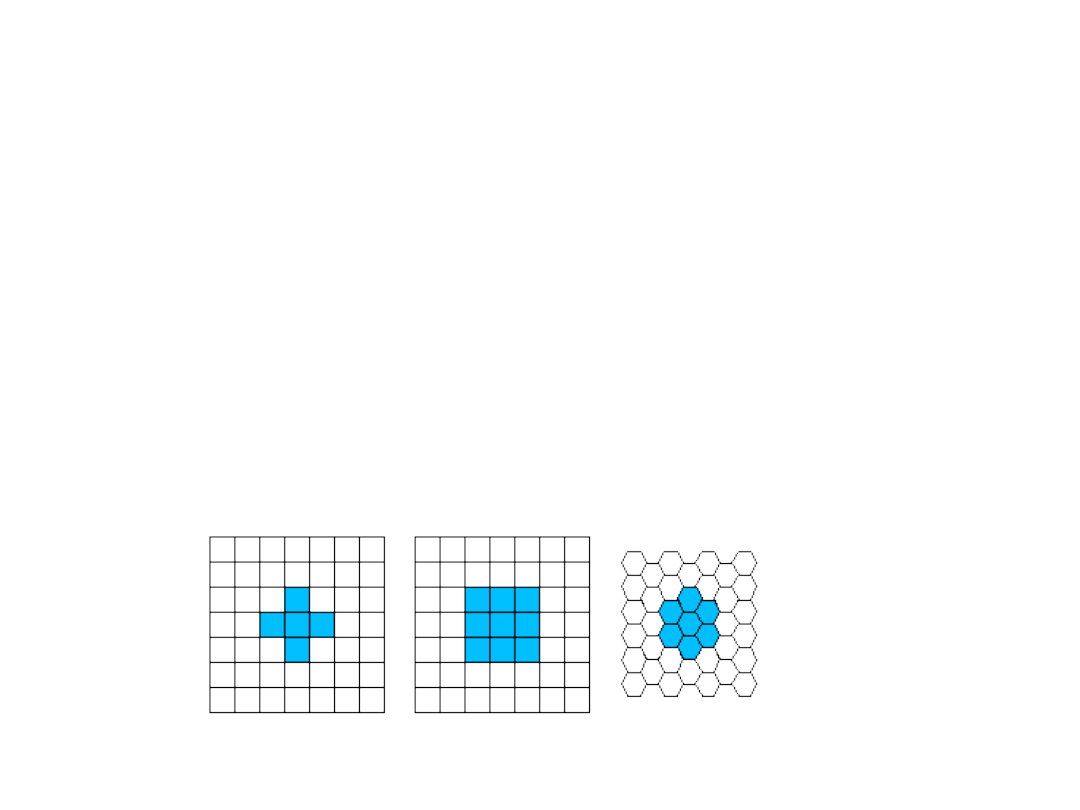
3

Types of neighborhoods

Neighborhood operations play a key role in digital image processing.

Rectangular sampling - In most cases, images are sampled by laying a rectangular grid

over an image.

Hexagonal sampling - An alternative sampling scheme is termed hexagonal sampling.

We will restrict our attention to only rectangular sampling as it remains, due to hardware

and software considerations, the method of choice.

Some of the most common neighborhoods are the 4-connected neighborhood and the 8-

connected neighborhood in the case of rectangular sampling and the 6-connected

neighborhood in the case of hexagonal sampling.

•

Rectangular sampling, hexagonal

sampling;
4-connected 8-connected 6-

connected

4

Image Statistics

In image processing it is common to use simple statistics of images.
The notion of a statistic is connected to the concept of a probability

distribution of signal amplitudes. For a given region or image we

can define the probability distribution function of the brightnesses

in that region and the probability density function of the

brightnesses in that region. We assume that we are dealing with a

digitized image A=a[m,n].

• Probability distribution function of the brightnesses,

P(a),

is the probability that a brightness chosen from the region is

less than or equal to a given brightness value a.

• Probability density function of the brightnesses

The probability that a brightness in a region falls between a

and
a+da, given the probability distribution function P(a), can be

expressed as p(a) a where p(a) is the probability density

function:

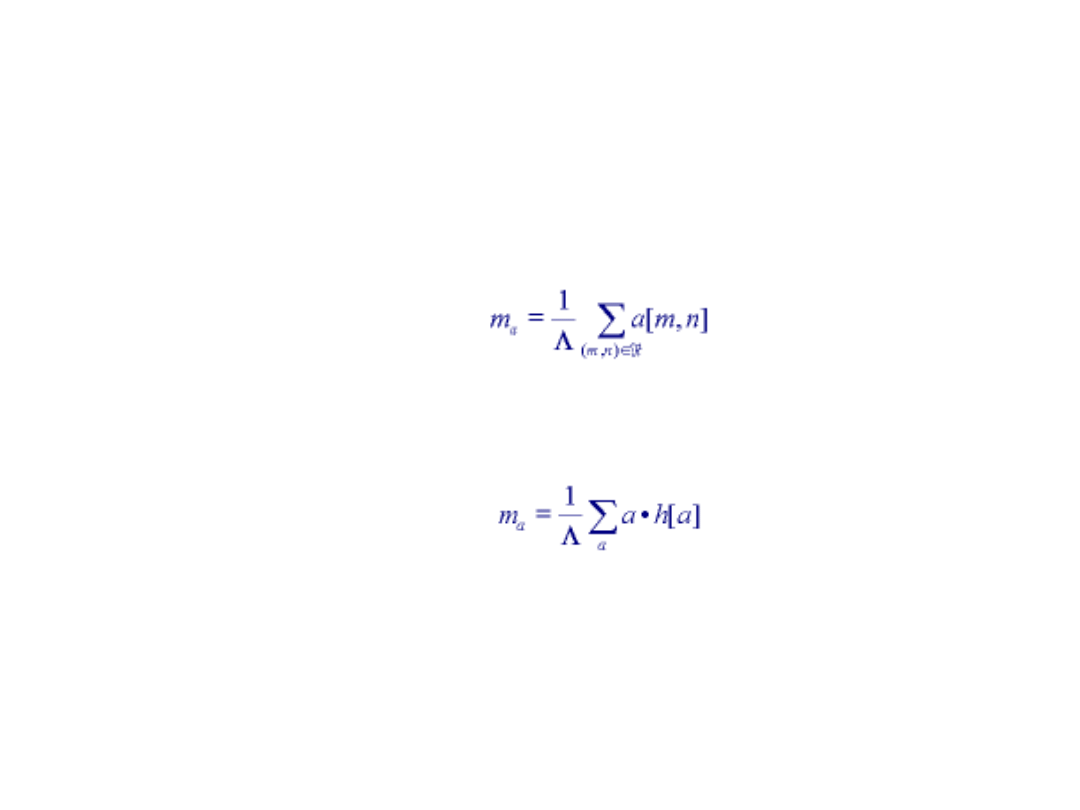
5

Average

• The average brightness of a region is defined as the

sample mean of the pixel brightnesses within that

region. The average, ma, of the brightnesses over

the pixels within a region ( ) is given by:

• Alternatively, we can use a formulation based upon

the (unnormalized) brightness histogram, h(a) =

*p(a), with discrete brightness values a. This gives:

• The average brightness, ma, is an estimate of the

mean brightness, ua, of the underlying brightness

probability distribution.

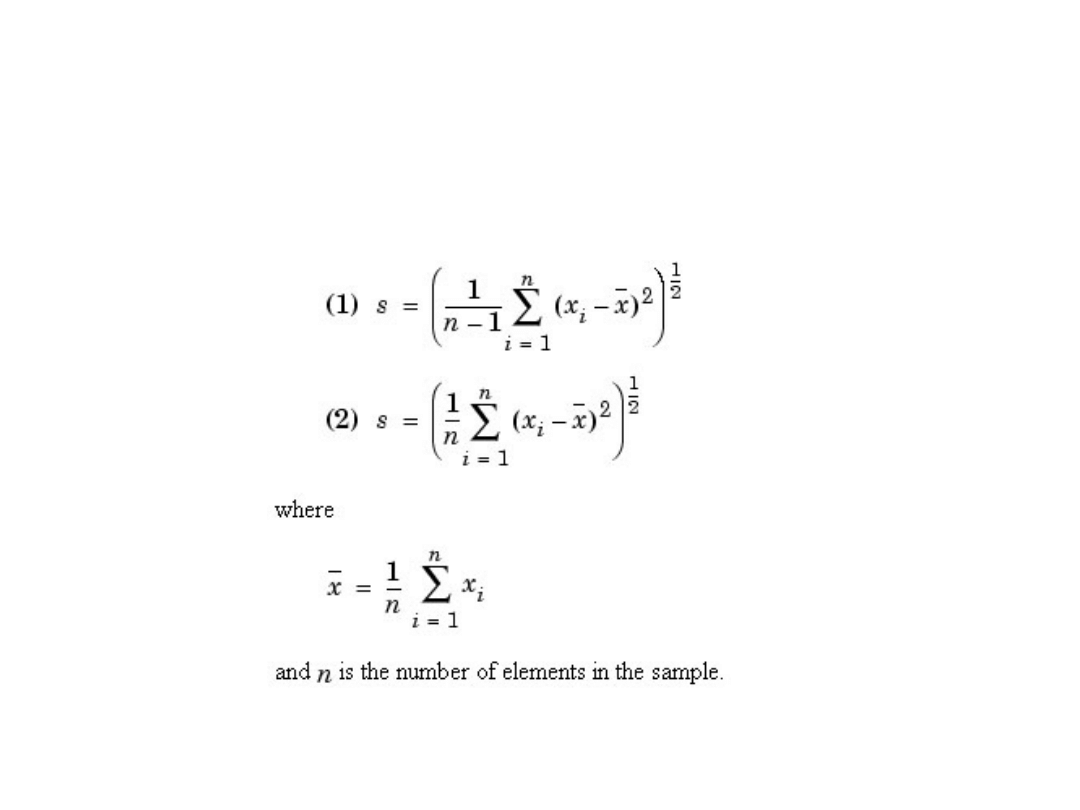
6

Standard

deviation

A digital image X=[xi].

7

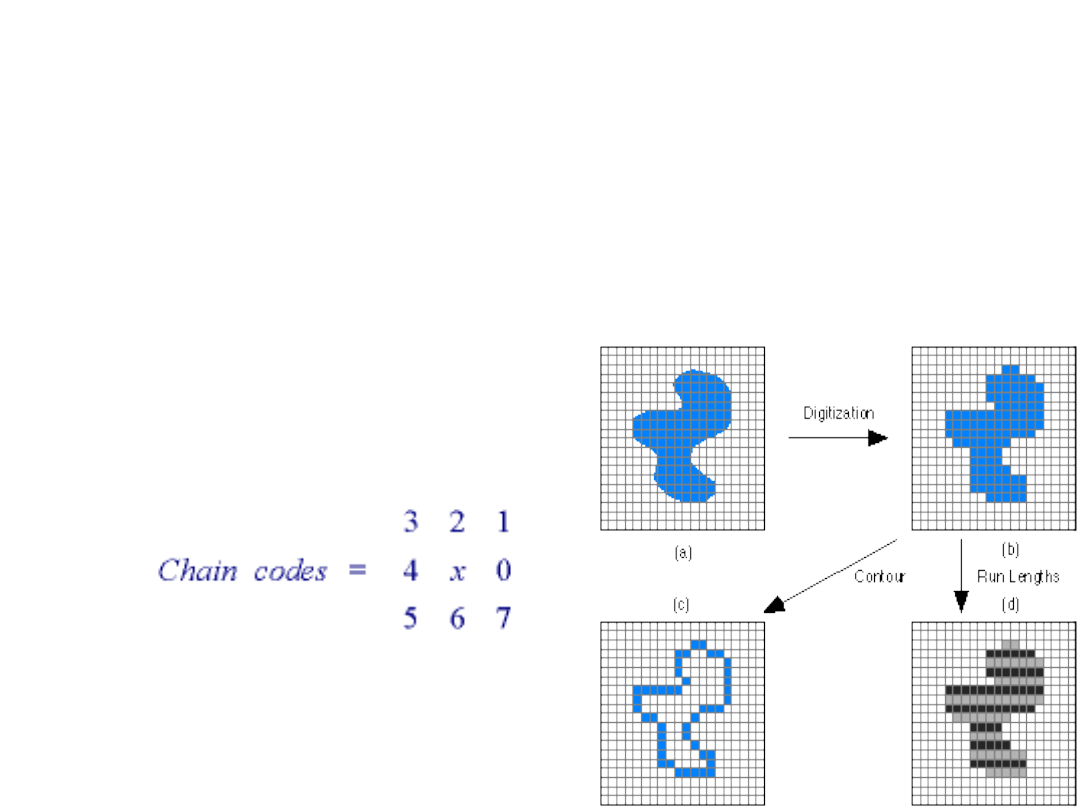
Contour Representations

We follow the contour in a clockwise

manner and keep track of the directions as
we go from one contour pixel to the next.
For the standard implementation of the
chain code we consider a contour pixel to
be an object pixel that has a background
(non-object) pixel as one or more of its 4-
connected neighbors. The codes associated
with eight possible directions are the chain
codes and, with x as the current contour
pixel position, the codes are generally
defined as:

Several techniques exist to represent the region or object by describing its contour
•

Chain code

(Freeman)

•

Run-length

code

8

Algorithms

Algorithms can be divided into four categories:

1) operations based on simple logic & mathematics,
2) on the image histogram,
3) on convolution,
4) on mathematical morphology.

Further, these operations can also be described in

terms of their implementation as a point operation,
a local operation, or a global operation

9

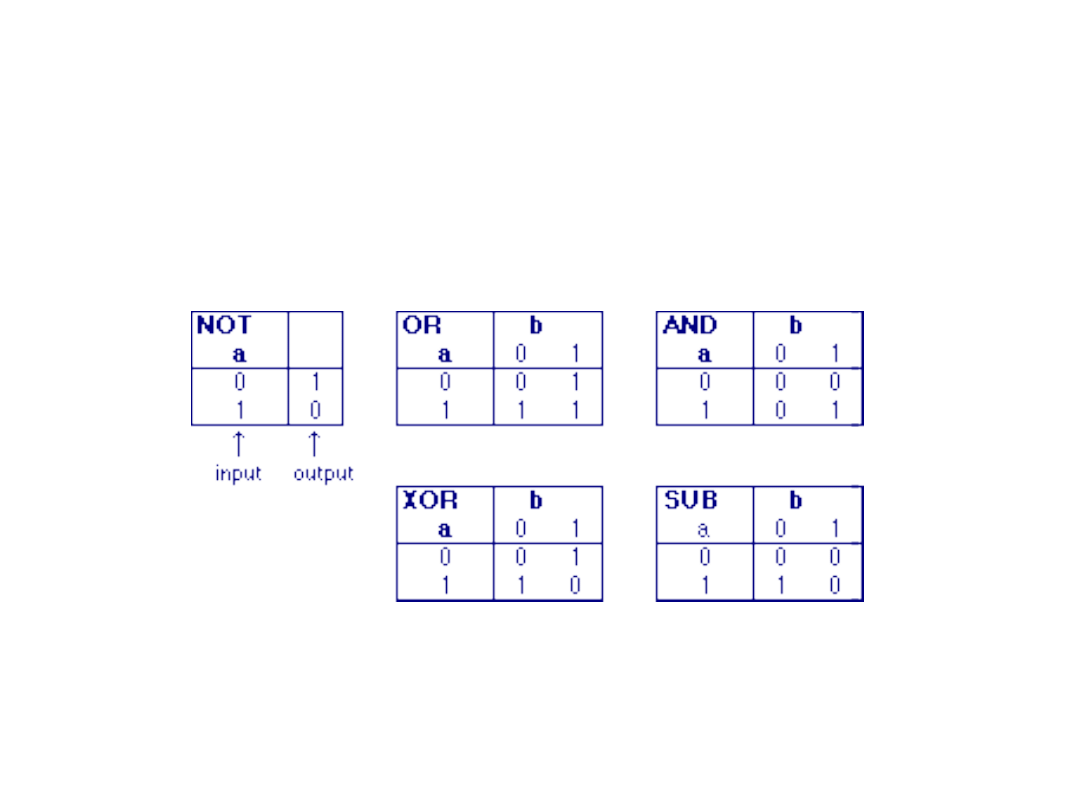
Logic Operations

• Logic operation performs on gray-level

images, the pixel values are processed as
binary numbers

• light represents a binary 1, and dark

represents a binary 0

• NOT operation = negative transformation

10

11

12

Example of AND Operation

original image AND image

mask

result of AND

operation

13

Example of OR Operation

original image

OR image

mask

result of OR

operation

14

1) Operacje arytmetyczne

• Dodanie/odjęcie do obrazu J stałej b przesuwa cały obraz

w kierunku jaśniejszej lub ciemniejszej tonacji, co często
pozwala zauważyć obiekty uprzednio niedostrzegalne. Taka
operacja prowadzi do zwiększenia/zmniejszenia jasności
obrazu. Jasność wynikową Jw w punkcie (x,y) możemy
wyrazić wzorem

• Jw(x,y) = J(x,y)  b. (2.1)

• Należy jednak pamiętać, aby nie przekroczyć zakresu

minimalnej i maksymalnej wartości jasności, tzn. 0 i 255.
Jeżeli za stałą b przyjmiemy maksymalną wartość jasności, to
odjęcie od niej obrazu spowoduje otrzymanie negatywu

• Jw(x,y) = 255 – J(x,y).

(2.2)

15

Negative image

16

• Mnożenie i dzielenie obrazu wykorzystywane jest

bardzo często dla polepszenia jakości obrazu.

Operacja mnożenia obrazu przez stałą a wyraża się

wzorem

• Jw(x,y) = a J(x,y).

(2.3)

• Przekształcenie to dla a>1 zwiększa, zaś dla 0<a<1

zmniejsza zróżnicowanie stopni szarości obrazu czyli

kontrast. Zbyt duże zwiększenie zróżnicowania

szarości zwykle pociąga za sobą utratę części

informacji w następstwie niezbędnej normalizacji.

• Opisane wyżej operacje na obrazie należą do grupy

operacji liniowych, ponieważ można je opisać wzorem

• Jw(x,y) = a J(x,y) + b. (2.4)

17

• Dodawanie obrazów odbywa się na zasadzie sumowania

wartości poszczególnych odpowiadających sobie pikseli w

obrazach (analogicznie jakbyśmy potraktowali obrazy

jako macierze liczb i je dodali do siebie otrzymując

macierz sumaryczną). Tak więc piksel obrazu wynikowego

Jw będący sumą jasności pikseli obrazów J1 i J2 wyraża

się wzorem

• Jw(x,y) = J1(x,y) + J2(x,y) (2.5)

• Problem, jaki możemy napotkać przy dodawaniu obrazów,

to przekroczenie dopuszczalnego zakresu jasności lub

koloru dla danej palety barw. Na przykład, jeżeli dodamy

do siebie dwa jasne piksele tak, iż przekroczona zostanie

wartość maksymalna, to nastąpi przepełnienie i w

rezultacie możemy otrzymać piksel ciemny.

18

• Odejmowanie obrazów przebiega analogicznie do

dodawania i wyraża się wzorem

• Jw(x,y) = J1(x,y) – J2(x,y). (2.6)

• Tak jak przy dodawaniu tutaj pojawiają się podobne

problemy związane ze skalowaniem jasności.

19

•

Pewnym uogólnieniem operacji (2.5) jest mieszanie obrazów –

ważenie obrazów. Mieszanie liniowe dwu obrazów A i B polega na

zsumowaniu ich jasności odpowiednio z wagami  i (1‑):

•

Jw(x,y) =  *J1(x,y) + (1 - ) *J2(x,y) (2.7)   [0,1]

•

W procesie mieszania liniowego nie musimy się martwić

o normalizację albo obcinanie na końcach zakresów jasności. Teraz

mamy pewność, iż jasności generowane przez przekształcenie (2.7)

zawsze mieszczą się pomiędzy dopuszczalną wartością minimalną

i maksymalną. Zmieniając płynnie w powyższym wzorze parametr 

od 0 do 1 możemy uzyskać efekt przechodzenia jednego obrazu w

drugi.

•

Ogólnie w przypadku N obrazów możemy zastosować mieszanie

wagowe. Wtedy poszczególne obrazy mnożymy przez wagi i

reprezentujące udział i‑tego obrazu (i = 1,2,...,N) w obrazie

wynikowym. Podejście to możemy wyrazić wzorem

•

Jw(x,y) =



1 *J1(x,y) +



2 *J2(x,y) + ... +



N *JN(x,y) (2.8)

•

Podobnie jak przy mieszaniu dwóch obrazów nie występuje tu

problem normalizacji, ponieważ sumowanie odbywa się z wagami



i.







N

i

i

1

1



20

Operacje nieliniowe

Operacje nieliniowe

• Operację potęgowania wykonywaną na poszczególnych

pikselach możemy zapisać następująco:

• (2.9)

• gdzie  - wykładnik,  > 0.
• Aby wzór (2.9) zastosować do transformacji jasności należy go

odpowiednio przygotować: przeprowadzić normalizację

jasności obrazu, a potem ją przeskalować do pełnego zakresu.

Przy założeniu, że Jmin=0 końcowa postać wzoru (2.9) będzie

następująca:

•
• gdzie Jmax  255.

Potęgowanie

)

,

(

)

,

(

y

x

J

y

x

J

w





















max

)

,

(

225

)

,

(

J

y

x

J

y

x

J

w



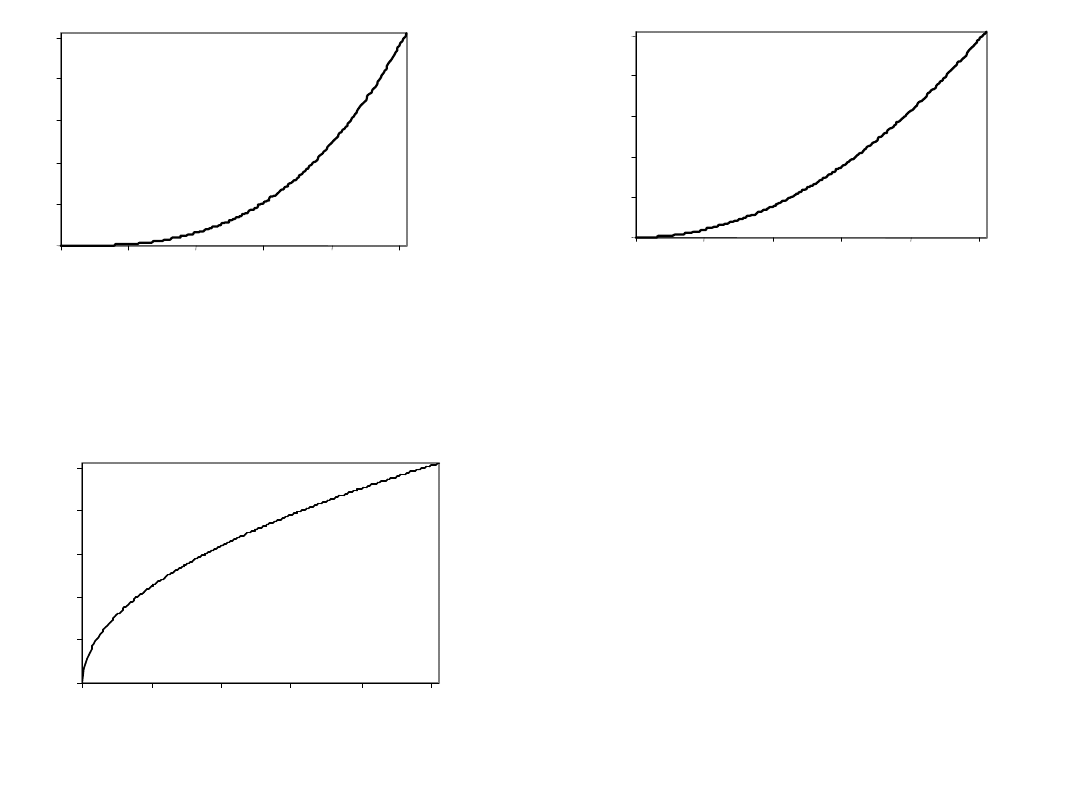
21

Wykres funkcji transformacji (dla wartości z przedziału 0-

255): a) kwadratowej, b) sześciennej

0

50

100

150

200

250

0

50

100

150

200

250



= 2

0

50

100

150

200

250

0

50

100

150

200

250



= 3

0

50

100

150

200

250

0

50

100

150

200

250

Wykres funkcji
pierwiastka
kwadratowego

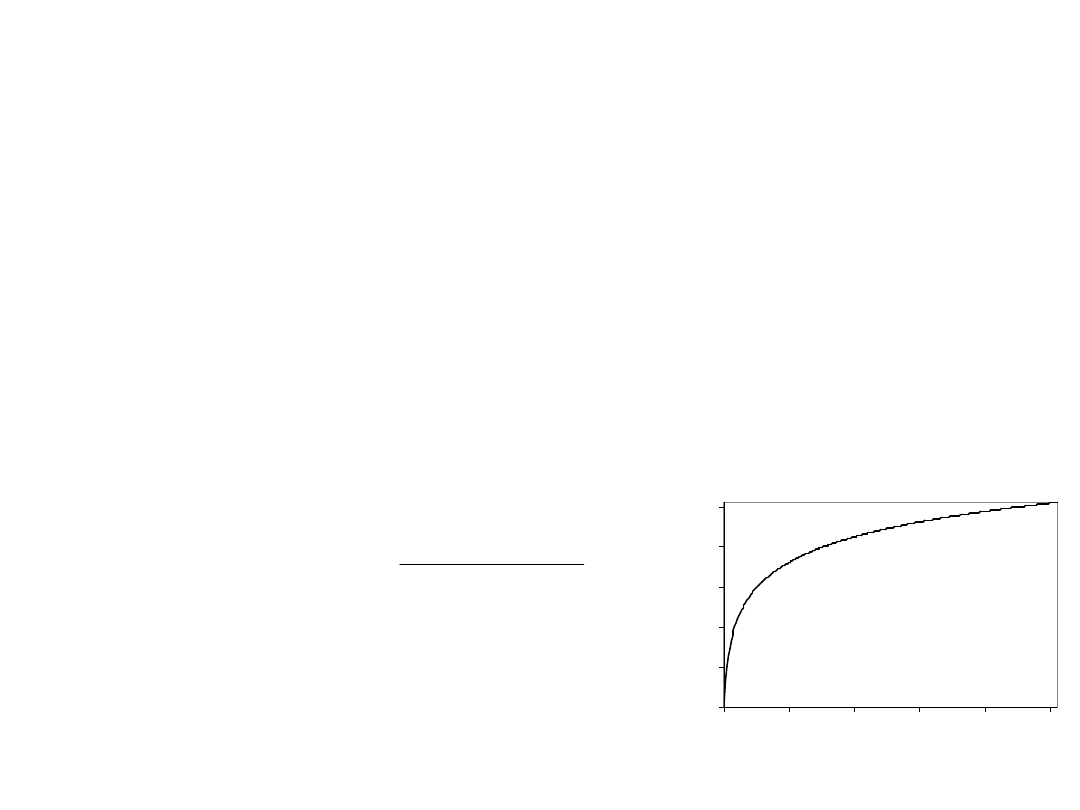
22

Logarytmowanie obrazu

• Wzór funkcji logarytmicznej używanej w przetwarzaniu obrazów jest

następujący:

• Jw(x,y) = 255*log(1 + J(x,y)/255)

(2.10)

• Po przeprowadzeniu analogicznych operacji, jak dla wzoru (2.9) wzór

(2.10) przyjmie postać:









max

1

log

)

,

(

1

log

255

)

,

(

J

y

x

J

y

x

J

w









0

50

100

150

200

250

0

50

100

150

200

250

23

Conclusion:

Principle

Objective of Enhancement

• Process an image so that the result will

be more suitable than the original image
for a specific application.

• The suitableness is up to each

application.

• A method which is quite useful for

enhancing an image may not necessarily
be the best approach for enhancing
another images

24

Good images

• For human visual

– The visual evaluation of image quality is a highly

subjective process.

– It is hard to standardize the definition of a good

image.

• For machine perception

– The evaluation task is easier.
– A good image is one which gives the best machine

recognition results.

• A certain amount of trial and error usually is

required before a particular image

enhancement approach is selected.