Podstawowe operacje arytmetyczne
i logiczne w systemie dwójkowym
mgr inż. Bartosz BRZOZOWSKI
konsultacje: wtorek 15-17
pokój/budynek: 126/36
brzozowski.studentlive.pl
tel.: 261 839 851
Podstawowe operacje arytmetyczne
i logiczne w systemie dwójkowym
mgr inż. Bartosz BRZOZOWSKI
konsultacje: wtorek 15-17
pokój/budynek: 126/36
brzozowski.studentlive.pl
tel.: 261 839 851
Podstawowe operacje arytmetyczne i logiczne
w systemie dwójkowym
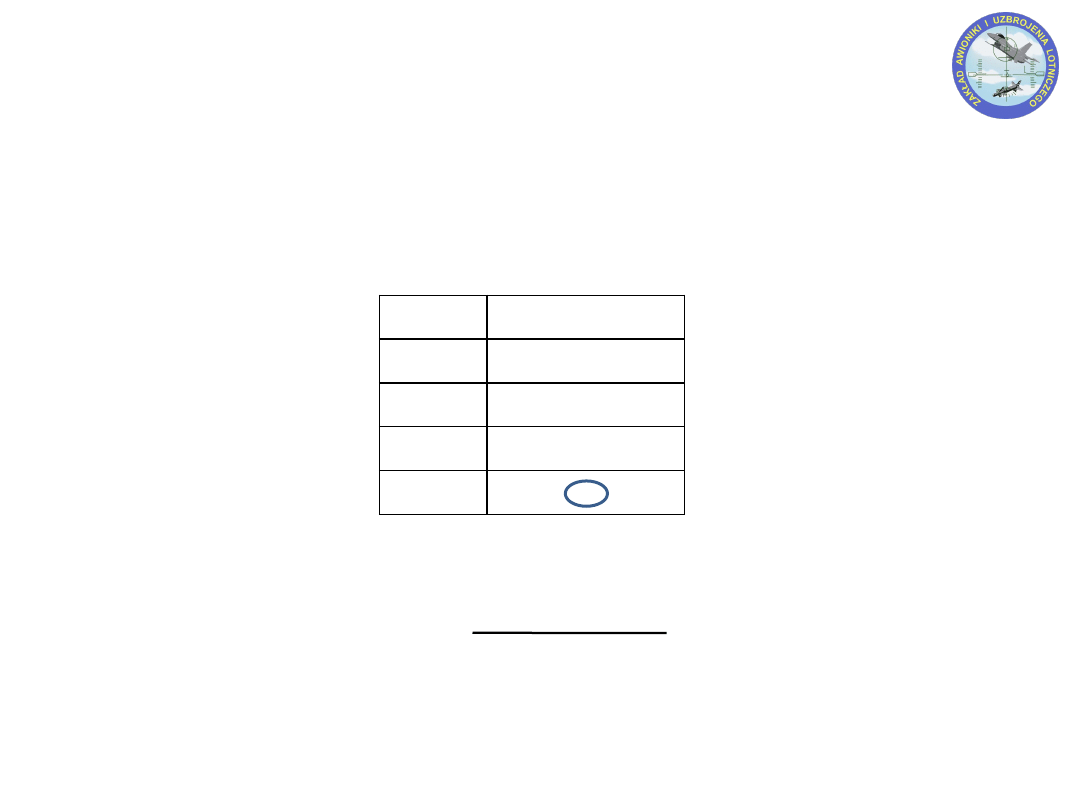
Dodawanie
a b
a + b
0 0
0
0 1
1
1 0
1
1 1
10
+ 1 1 1 0 1 1 0 0
1 1 0 1 0 1 0 1
0 1
0
1
0
1
0
1
0
1
1
1
1
1
1
WAT 2015
mgr inż. Bartosz Brzozowski
2
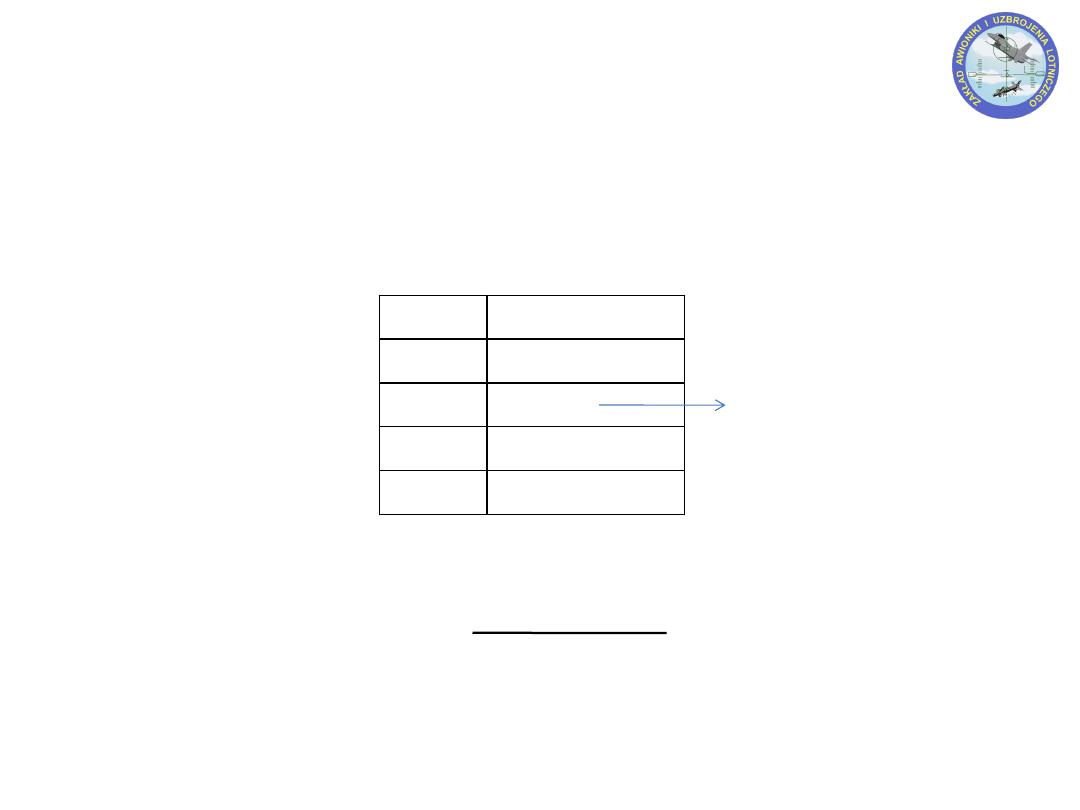
Odejmowanie
a b
a - b
0 0
0
0 1
1
1 0
1
1 1
0
- 0 1 1 0 1 1 0 0
1 1 0 1 0 1 0 1
0 0 1
1
pożyczka do
następnej pozycji
1
0
1
1
1
1
0
Podstawowe operacje arytmetyczne i logiczne
w systemie dwójkowym
WAT 2015
mgr inż. Bartosz Brzozowski
3
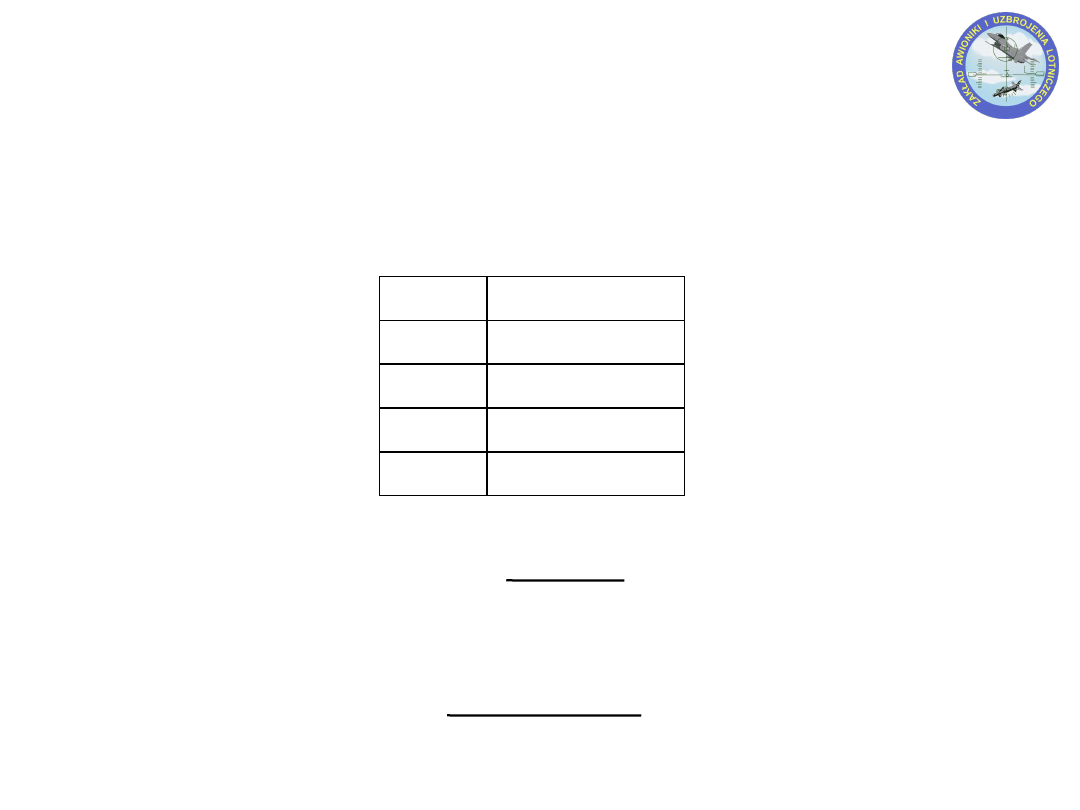
Mnożenie
a b
a · b
0 0
0
0 1
0
1 0
0
1 1
1
· 1 0 1 1
1 1 0 1
1 1 0 1
1 1 0 1
0 0 0 0
1 1 0 1
+
1 0 0 0 1 1 1 1
Podstawowe operacje arytmetyczne i logiczne
w systemie dwójkowym
WAT 2015
mgr inż. Bartosz Brzozowski
4
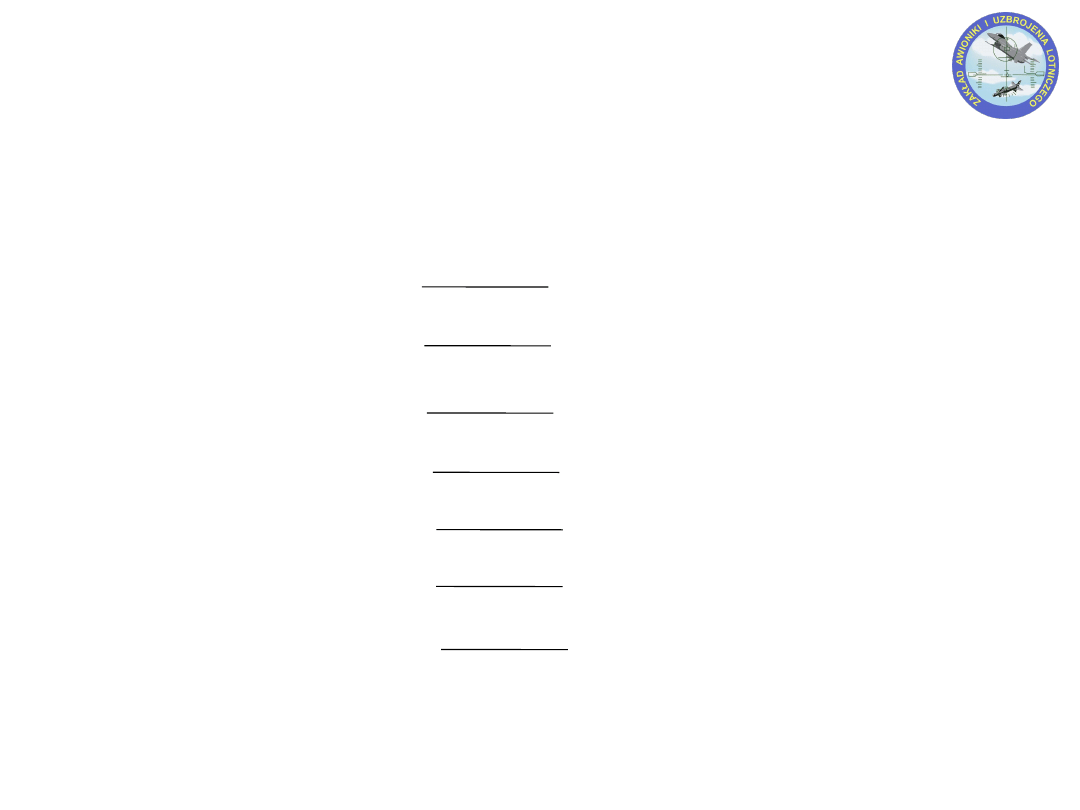
110
Dzielenie
110101101 : 111
01101
1
-111
1101
1
101
-111
100101
1
-111
1001
1
-111
1001
0
-111
10
1
-111
Podstawowe operacje arytmetyczne i logiczne
w systemie dwójkowym
WAT 2015
mgr inż. Bartosz Brzozowski
5
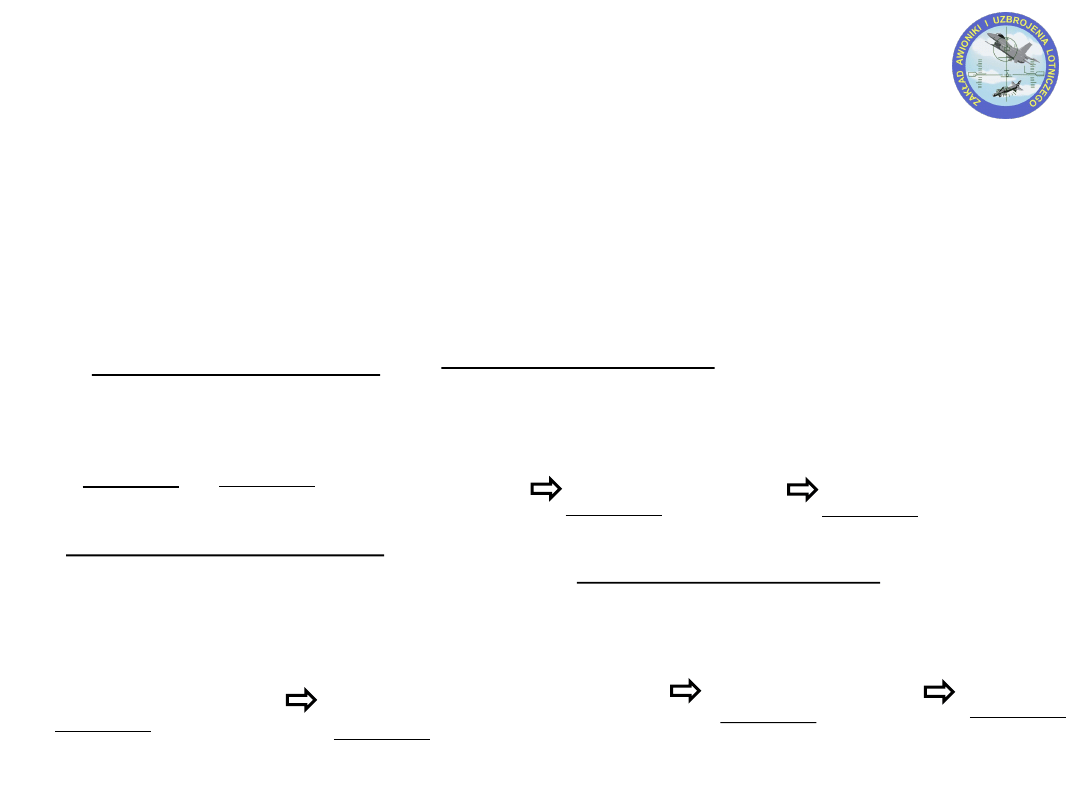
KOD ZNAK-MODUŁ (ZM)
Najstarszy bit określa znak – 0 „+”; 1 „-”
Liczby kodowane w naturalnym kodzie binarnym
-4
(10)
=1100
(2)
4
(10)
=0100
(2)
-1
(10)
=1001
(2)
1
(10)
=0001
(2)
Przykłady dla liczb kodowanych na 4 bitach
Dodawanie - ten sam znak
Znak pozostaje bez zmian
1100
(2)
+1001
(2)
1101
(2)
0001
(2)
+0100
(2)
0101
(2)
Dodawanie – różne znaki
Odejmujemy od większego modułu mniejszy
Znak większego modułu
1100
(2)
+0001
(2)
1001
(2)
+0100
(2)
1100
(2)
- 0001
(2)
1011
(2)
0100
(2)
-1001
(2)
0011
(2)
Odejmowanie - ten sam znak
Odejmujemy od większego modułu mniejszy
Ten sam znak jeżeli odjemna jest większa
Przeciwny gdy odjemna jest mniejsza
1100
(2)
- 1001
(2)
1011
(2)
0001
(2)
- 0100
(2)
0100
(2)
- 0001
(2)
1011
(2)
Odejmowanie – różne znaki
Dodawanie modułów
Znak odjemnej
1100
(2)
- 0001
(2)
1100
(2)
+0001
(2)
1101
(2)
0001
(2)
- 1100
(2)
0001
(2)
+1100
(2)
0101
(2)
Podstawowe operacje arytmetyczne i logiczne
w systemie dwójkowym
6
WAT 2015
mgr inż. Bartosz Brzozowski
KOD UZUPEŁNIEŃ DO JEDNOŚCI (U1)
Liczby dodatnie kodowane w naturalnym kodzie binarnym, najstarszy bit musi być 0
Liczby ujemne kodowane jako bitowa negacja danej liczby, najstarszy bit staje się 1
4
(10)
=0100
(2)
-4
(10)
=1011
(2)
1
(10)
=0001
(2)
-1
(10)
=1110
(2)
Przykłady dla liczb kodowanych na 4 bitach
Dwie reprezentacje 0
(10)
: -0 = 1111; +0=0000
Dodawanie
Przeniesienie poza najstarszy bit należy dodać
1011
(2)
+1110
(2)
11001
(2)
1001
(2)
+0001
(2)
1010
(2)
0100
(2)
+1110
(2)
10010
(2)
0010
(2)
+0001
(2)
0011
(2)
Odejmowanie
Należy zanegować bity drugiej liczby i tak powstałe liczby dodać
1011
(2)
- 1110
(2)
1011
(2)
+0001
(2)
1100
(2)
0100
(2)
- 1110
(2)
0100
(2)
+0001
(2)
0101
(2)
0100
(2)
- 0001
(2)
0100
(2)
+1110
(2)
10010
(2)
0010
(2)
+0001
(2)
0011
(2)
Podstawowe operacje arytmetyczne i logiczne
w systemie dwójkowym
WAT 2015
mgr inż. Bartosz Brzozowski
7
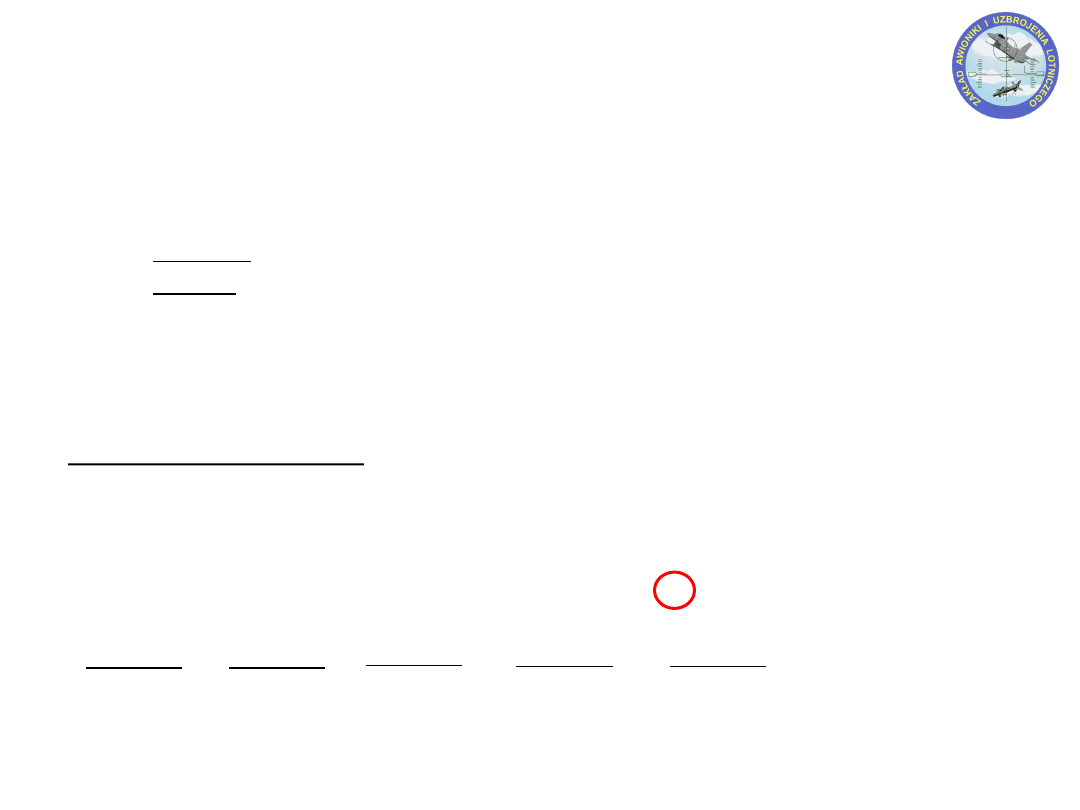
KOD UZUPEŁNIEŃ DO DWÓCH (U2)
Liczby dodatnie kodowane w naturalnym kodzie binarnym, najstarszy bit musi być 0
Liczby ujemne kodowane jako bitowa negacja danej liczby zwiększona o 1.
(zmiana z ujemnej na dodatnią tak samo)
Najczęstsza metoda reprezentacji INTEGER
4
(10)
=0100
(2)
-4
(10)
=1100
(2)
1
(10)
=0001
(2)
-1
(10)
=1111
(2)
Przykłady dla liczb kodowanych na 4 bitach
Dodawanie i Odejmowanie
Jak w naturalnym binarnym
Sprawdzenie przepełnienia – XOR dwóch ostatnich przeniesień/pożyczek
1100
(2)
+1111
(2)
1011
(2)
1100
(2)
+0001
(2)
1101
(2)
1100
(2)
- 1111
(2)
1101
(2)
0001
(2)
- 1100
(2)
0101
(2)
1 1 0 0
0 0 0 0
1 1 1 1
1 1 0 0
0100
(2)
- 1100
(2)
1000
(2)
1 0 0 0
OVERFLOW
Podstawowe operacje arytmetyczne i logiczne
w systemie dwójkowym
WAT 2015
mgr inż. Bartosz Brzozowski
8