Nieparametryczne metody

statystyczne

Biometria i

Biostatystyka

Metody nieparametryczne



Z założenia test t dla dwóch próbek

wymaga, by obie populacje, z których

pochodzą próbki miały rozkład normalny o

takich samych wariancjach (test

aproksymacyjny t, gdy wariancje są różne).



Wiele innych powszechnie stosowanych

procedur ma w swoim założeniu

normalność rozkładów. Na szczęście

większość z nich jest odporna na drobne

odstępstwa od normalności rozkładów.

Metody nieparametryczne



Jednakże jest cała grupa procedur
wnioskowania statystycznego,
które nie wymagają oceny
wariancji czy wartości średniej w
populacji, a hipotezy nie dotyczą
jawnie parametrów rozkładów.



Takie procedury nazywane są

testami nieparametrycznymi

.

Termin „metody nieparametryczne” był po raz pierwszy użyty przez
J.Wolfowitza w 1942

Metody nieparametryczne



Metody te zazwyczaj nie formułują
założeń co do rozkładu analizowanej
zmiennej losowej (np. nie wymagają
normalności rozkładu), aczkolwiek
mogą pojawiać się założenia, iż
porównywane populacje mają taką
samą zmienność albo kształt funkcji
gęstości prawdopodobieństwa.

Metody nieparametryczne



Testy nieparametryczne mogą być
używane zarówno w sytuacjach, w
których stosuje się testy parametryczne,
np. test t dla dwóch próbek, jak i tam,
gdzie tych metod zastosować nie można.



Będziemy tych metod używać do analizy
zmiennych rangowych a niektóre z nich
także do analizy atrybutów.

Metody nieparametryczne



Jednakże, jeśli można zastosować test
parametryczny i nieparametryczny,
wówczas zawsze test parametryczny
będzie miał moc co najmniej taką jak
test nieparametryczny (tzn. metoda
nieparametryczna ma większe
prawdopodobieństwo popełnienia
błędu typu II).

Metody nieparametryczne



Często jednak różnice mocy testu
parametrycznego i jego
odpowiednika nieparametrycznego
nie są tak duże i ulegają
zmniejszeniu wraz ze wzrostem
liczności próbki.

Pojedyncza próbka. Test
znaków.



Załóżmy, że jesteśmy zainteresowani
testowaniem hipotezy o którejś ze
statystyk opisowych położenia i nie
wiemy niczego więcej o rozkładzie
zmiennej losowej poza tym, iż jest ciągła.



Wygodnie jest wykorzystać medianę m
jako statystykę położenia, gdyż ma
własność:

2

1

)

m

X

(

P

)

m

X

(

P









Pojedyncza próbka. Test
znaków.



Hipoteza zerowa ma zatem postać:
H

0

: m=m

0

i jeśli jest prawdziwa, spodziewamy
się mniej więcej takiej samej liczby
obserwacji powyżej jak i poniżej m

0

a jeśli próbka odbiega zbyt mocno
od tego, odrzucamy H

0

.

Pojedyncza próbka. Test
znaków.



Test opisywany jest najczęściej jako
przypisywanie każdej z obserwacji znaku
plus (jeśli wartość jest większa od mediany
m

0

) albo minus jeśli jest poniżej m

0

(założenie o ciągłości teoretycznie
wyklucza przypadki, dla których
obserwacja jest dokładnie równa m

0

, jeśli

jednak mamy taki przypadek to
przypisujemy mu zero).

Pojedyncza próbka. Test
znaków.



Oznaczmy zatem przez N

+

liczbę znaków

plus: N

+

=#{k: X

k

>m

0

}.



Załóżmy, że hipoteza alternatywna jest
dwustronna i ma postać H

A

: m≠m

0

.



Odrzucamy zatem H

0

jeśli N

+

jest albo

zbyt duża albo zbyt mała, a powstały w
ten sposób test nazywany jest testem
znaków.

Pojedyncza próbka. Test
znaków.



Załóżmy iż X

1

, ..., X

n

są realizacjami

ciągłej zmiennej losowej o
medianie m i stawiamy hipotezę
zerową H

0

: m=m

0

versus H

A

: m≠m

0.



Odrzucamy H

0

jeśli N

+

≤ k lub N

+

≥

n−k na poziomie istotności:



















k

j

n

j

n

0

2

1

2

1



Pojedyncza próbka. Test
znaków.



Dowód: Zakładając słuszność H

0

,

N

+

bin(n,½), co oznacza, że

zmienna losowa n−N

+

(liczba

minusów) ma również rozkład
dwumianowy bin(n,½) oraz:































k

j

n

j

n

k

n

N

P

k

N

P

0

2

1

2

1

)

(

)

(

Pojedyncza próbka. Test
znaków.



Zatem poziom istotności może być
bezpośrednio wyrażony z wykorzystaniem
dystrybuanty rozkładu dwumianowego bin(n,½),
co jest łatwym obliczeniowo zadaniem.



Ponieważ zmienna losowa N

+

jest z natury

swojej zmienną dyskretną, więc nie zawsze uda
się określić k, dla którego poziom istotności jest
równy dokładnie założonemu, przyjmujemy
zatem najbliższy mniejszy niż α.

Przykład 1



Szczury laboratoryjne przechodzą labirynt i
mierzony jest czas przejścia. Szczur albo
bezproblemowo radzi sobie z zadaniem i
dociera do wyjścia w miarę szybko, albo też
gubi się i znajduje wyjście po długim czasie.
Oznacza to, że rzadko pojawiać się będą
czasy pośrednie.



Dystrybucja czasu przejścia może być
jednak uznana za symetryczną.

Przykład 1



Uznano, że średni czas przejścia
wynosi więcej niż 100 sekund.



Zebrano następujące dane i należy
zweryfikować tę hipotezę na
poziomie α 5%:

26,31,43,163,171,181,193,199,206,
210

Przykład 1



Ponieważ dystrybucja jest symetryczna
wartość średnia µ i mediana m są sobie
równe.



Formułujemy hipotezy H

0

: µ=100 versus

H

A

: µ>100, i odrzucamy H

0

jeśli N

+

≥n−k

gdzie n=10 a k spełnia

Otrzymujemy k=2.



















k

0

j

10

05

.

0

j

10

2

1

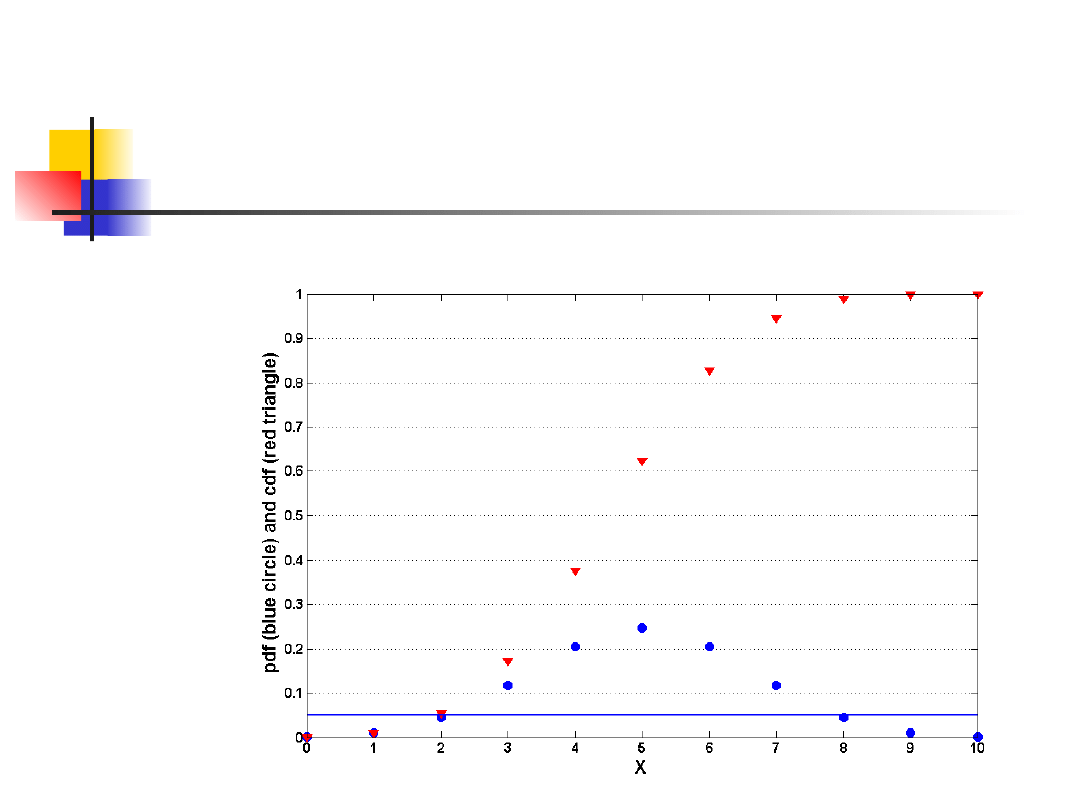
Przykład 1

Przykład 1



Zatem odrzucamy jeśli N

+

≥8.



Dla naszych danych
26,31,43,

163

,

171,181,193,199,206,210

obserwowana wartość N

+

=7, więc nie

mamy podstaw do odrzucenia H

0

na

poziomie α=0.05.

Pojedyncza próbka.
Test Wilcoxona.



Jeśli rozkład zmiennej losowej jest
symetryczny, wartość średnia i mediana
są sobie równe to formułujemy hipotezę w
dziedzinie średniej µ zamiast mediany m.



Załóżmy, że chcemy zweryfikować
hipotezę H

0

: µ=µ

0

na podstawie obserwacji

X

1

, ..., X

n

, realizacji ciągłej zmiennej

losowej o symetrycznym rozkładzie.

Pojedyncza próbka.
Test Wilcoxona.



Rozważmy wartości absolutne
odchyłek od µ

0

|X

1

−µ

0

|, ..., |X

n

−µ

0

|, i

uporządkujmy je od najmniejszej do
największej.



Przyporządkujmy każdej wartości X

k

jej rangę R

k

, tak, że R

k

=j jeśli X

k

ma

j-tą najmniejszą absolutną odchyłkę
od µ

0

.

Pojedyncza próbka.
Test Wilcoxona.



Trzeba równocześnie pamiętać dla
każdej obserwacji X

k

po której

stronie µ

0

się znajdowała, poprzez

przypisanie wartości wskaźnika I

k











przypadku

przeciwnym

w

0

X

1

I

0

k

k



Pojedyncza próbka.
Test Wilcoxona.



Ostatecznie, dla każdej obserwacji X

k

otrzymujemy parę (R

k

,I

k

), rangę oraz

wskaźnik położenia względem µ

0

.



Użyjemy następującej statystyki testowej

która jest po prostu sumą rang wszystkich
obserwacji powyżej µ

0

.







n

1

k

k

k

I

R

W

Pojedyncza próbka.
Test Wilcoxona.



Zmienna losowa W przyjmuje wartości
od 0 (wszystkie obserwacje poniżej µ

0

)

do n(n+1)/2 (wszystkie obserwacje
powyżej µ

0

).



Jeśli H

0

jest prawdziwa, dystrybucja W

jest symetryczna o średniej n(n+1)/4, i
odrzucimy H

0

jeśli obliczone W odstaje

zbyt mocno od swojej wartości średniej.

Pojedyncza próbka.
Test Wilcoxona.



Jak zwykle musimy sprecyzować
pojęcie „zbyt mocno odstaje” co
wymaga znajomości dystrybucji
zmiennej losowej W.



Wymaga to znajomości własności
funkcji tworzących
prawdopodobieństwa.

Pojedyncza próbka.
Test Wilcoxona.



Ogólnie, rozkład
prawdopodobieństwa W ma
postać:

gdzie α(r) jest współczynnikiem
składnika s

r

w rozwinięciu

2

)

1

n

(

n

,...,

1

,

0

r

,

2

)

r

(

)

r

W

(

P

n

















n

1

k

k

)

s

1

(

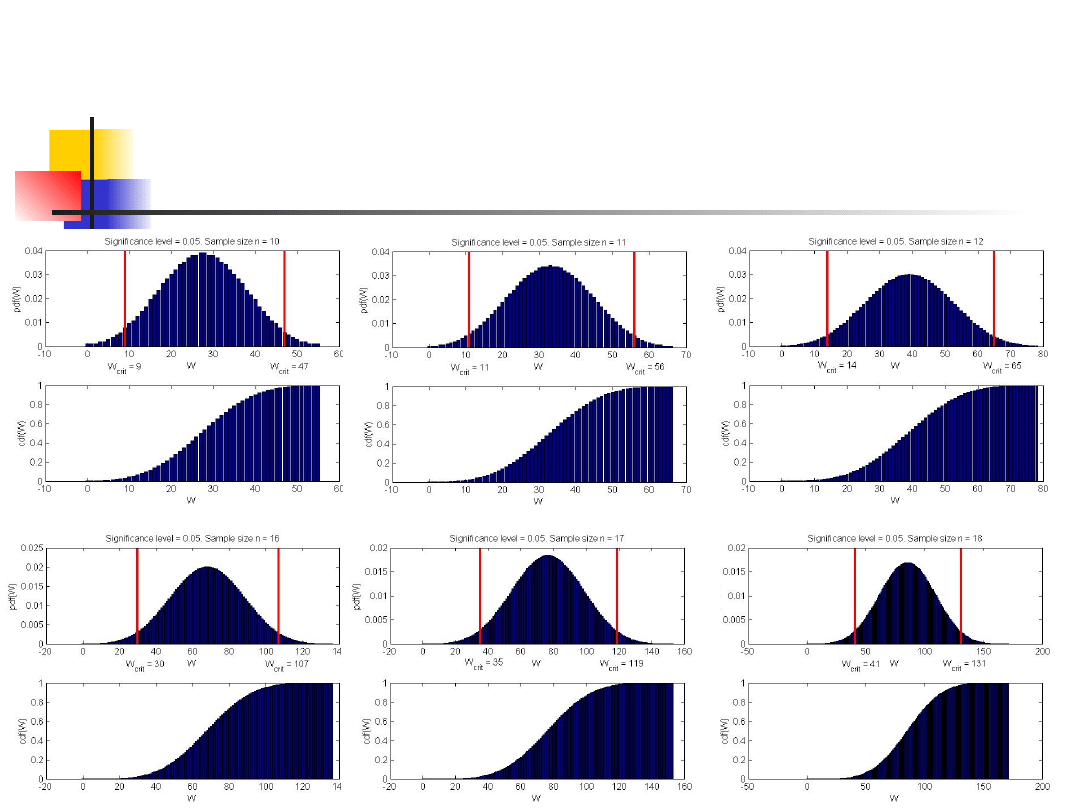
Dystrybucja statystyki W

Pojedyncza próbka.
Test Wilcoxona.



Jeśli H

0

jest prawdziwa a liczność

próbki jest duża, możemy
wykorzystać następujące
przybliżenie rozkładu W rozkładem
normalnym o parametrach:

24

)

1

n

2

)(

1

n

(

n

]

W

[

Var

4

)

1

n

(

n

]

W

[

E











Pojedyncza próbka.
Test Wilcoxona.



Definiujemy zatem dla próbek o
dużej liczności statystykę

)

1

,

0

(

N

24

/

)

1

n

2

)(

1

n

(

n

4

/

)

1

n

(

n

W

T













Przykład 2



Podaje się najczęściej, iż gęstość Ziemi wynosi
5.52g/cm

3

. W swoim słynnym doświadczeniu w

1798, Henry Cavendish przeprowadził serię
eksperymentów pomiaru gęstości.



Uzyskał następujące wyniki przy 29 powtórzeniach:
4.07,4.88,5.10,5.26,5.27,5.29,5.29,5.30,5.34,5.34,
5.36,5.395.42,5.44,5.46,5.47,5.50,5.53,5.55,5.57,5
.58,5.61,5.62,5.635.65,5.75,5.79,5.85,5.86
a średnia z próbki wyniosła 5.42.

Przykład 2



Niech µ oznacza rzeczywistą, nieznaną
wartość średnią i zweryfikujmy hipotezę
H

0

: µ=5.52 versus H

A

: µ≠5.52 na

poziomie 5%.



Wykorzystamy w tym celu statystykę T i
normalne przybliżenie rozkładu W. Dla
α=0.05, odrzucimy H

0

jeśli |T|≥1.96,

n=29.

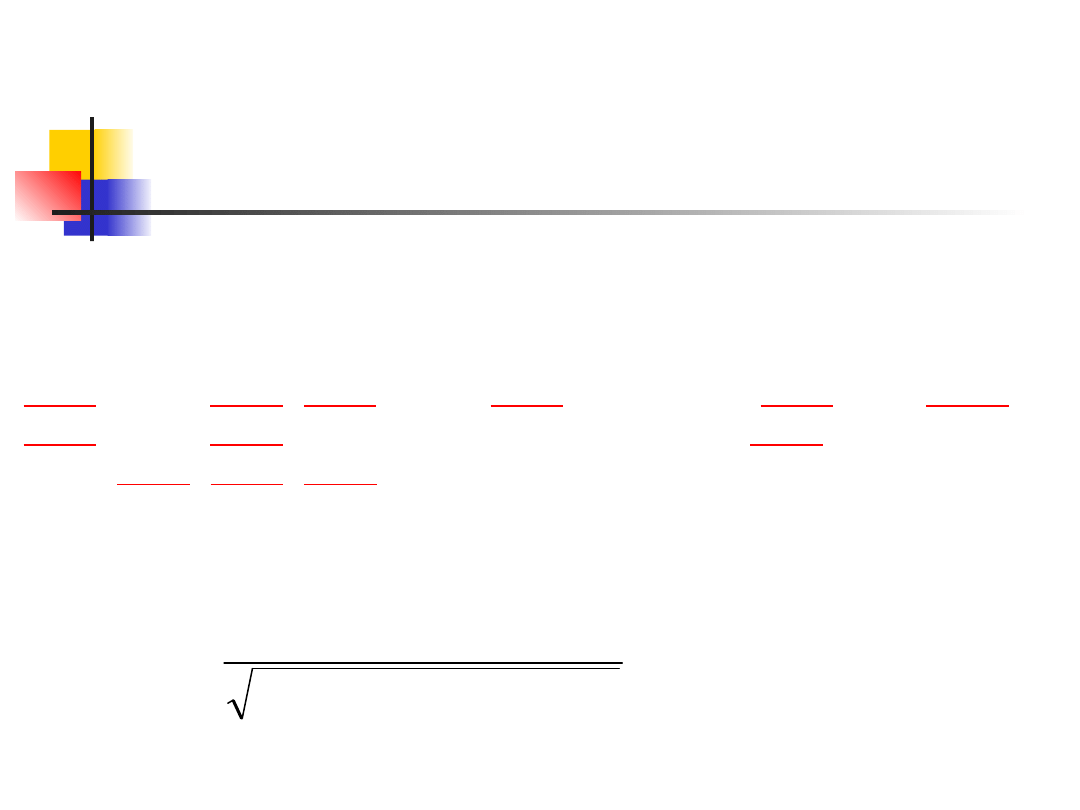
Przykład 2

Wartości absolutne odchyłek |X

k

−5.52|, k=1, ..., 29,

uporządkowane według wartości, z dodatnimi odchyłkami
zaznaczonymi podkreśleniem, są następujące:

0.01

, 0.02,

0.03

,

0.05

, 0.05,

0.06

, 0.06, 0.08,

0.09

,0.10,

0.10

,

0.11

, 0.13,

0.13

, 0.16, 0.18, 0.18, 0.22,0.23,

0.23

, 0.23, 0.25,

0.26,

0.27

,

0.33

,

0.34

, 0.42, 0.64,1.45

Wartość statystyki
W=1+3+4.5+6.5+9+10.5+12+13.5+20+24+25+ 26 = 155
oraz

i |T|=1.35. Nie mamy zatem podstaw do odrzucenia H

0

.

35

.

1

24

/

)

1

29

2

(

30

29

4

/

30

29

155

T

















Testy rangowe dla dwóch
próbek.



Pomimo tego, że zaproponowano wiele
metod nieparametrycznych testowania
różnic pomiędzy dyspersją czy, w
ogólnym przypadku, zmiennością
dwóch populacji, żadna z nich nie
zyskała powszechnej akceptacji.



Najczęściej stosowany test to
nieparametryczny odpowiednik testu t
dla dwóch próbek.

Testy rangowe dla dwóch
próbek.



Test został zaproponowany, dla
przypadku próbek o takiej samej
liczności, przez Wilcoxona (1945) a
następnie zmodyfikowany dla
przypadku próbek o różnej liczności
przez Manna i Whitneya (1947).



Test jest zatem oficjalnie zwany testem
Wilcoxona-Manna-Whitneya, albo,
częściej, testem U Mann-Whitneya.

Test U Mann-Whitneya



W tym teście, jak w wielu testach
nieparametrycznych, bezpośrednie
wartości pomiarów nie są
wykorzystywane a jedynie ich
rangi.

Rangi



Pomiary mogą mieć przypisane rangi albo w
porządku malejącym (od największego do
najmniejszego) albo rosnącym (od
najmniejszego do największego).



Jeśli przypisujemy rangi pomiarom od
największego do najmniejszego to pomiar o
największej wartości będzie miał rangę 1,
następny rangę 2 itd., a najmniejszy rangę
N, gdzie N = n

1

+n

2

(suma liczności obu

próbek).

Przykład 3 - Wzrost

Wzrost

mężczyzn

[cm]

Wzrost kobiet

[cm]

Rangi

wzrostu

mężczyzn

Rangi

wzrostu

kobiet

193

175

1

7

188

173

2

8

185

168

3

10

183

165

4

11

180

163

5

12

178

6

170

9

n

1

=7

n

2

=5

Rangi



Kiedy dwie lub więcej obserwacji ma
dokładnie taką samą wartość
mówimy, iż są

związane

(ang.

tied)

.



Ranga przypisana takim
obserwacjom jest średnią rang, które
byłyby przypisane tym obserwacjom,
gdyby nie były one związane.

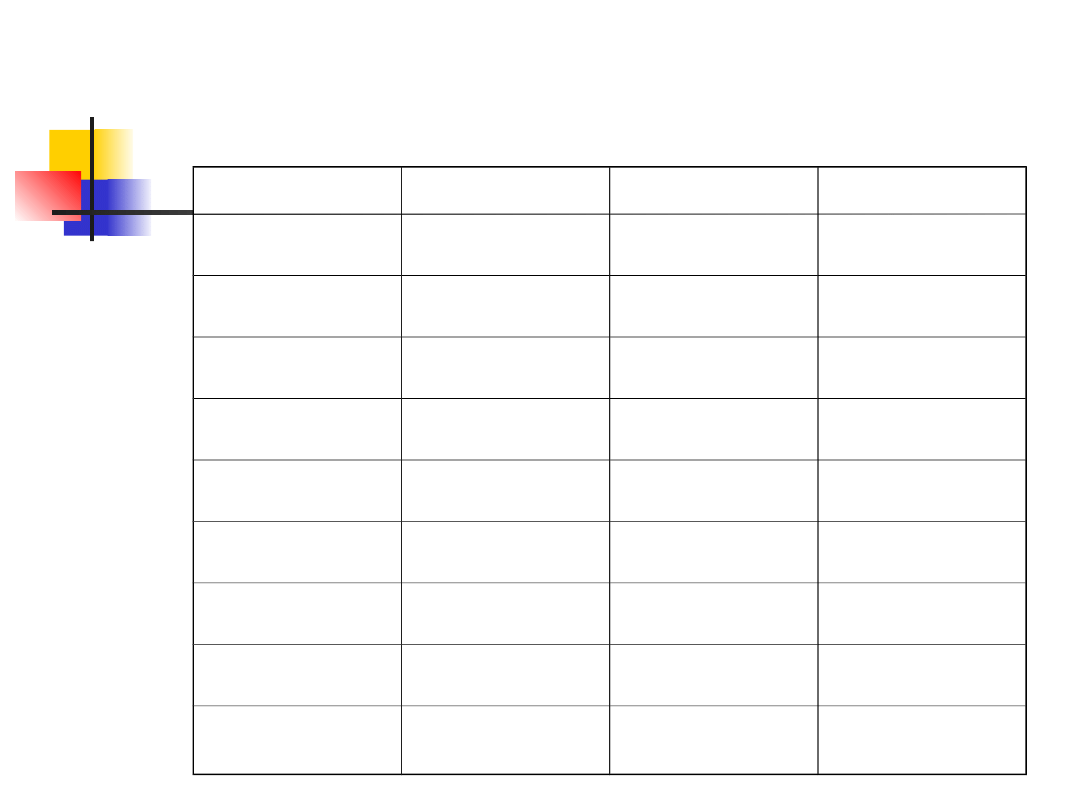
Przykład 4 –
Prędkość maszynopisania

Po kursie

Rangi

Bez kursu

Rangi

44

32

?

48

40

36

44

32

?

44

51

34

45

30

2

54

26

1

56

n

1

=8

n

2

=7

Rangi



Na przykład, kodując zbiór danych w

systemie od najmniejszej do największej

wartości, trzecia i czwarta wartość są

związane i wynoszą 32 słowa na minutę,

dlatego każdej z nich przypisujemy

rangę (3+4)/2=3.5



Ósma, dziewiąta i dziesiąta obserwacja

są również związane i wynoszą 44 słowa

na minutę, więc każda z nich otrzymuje

rangę (8+9+10)/3=9

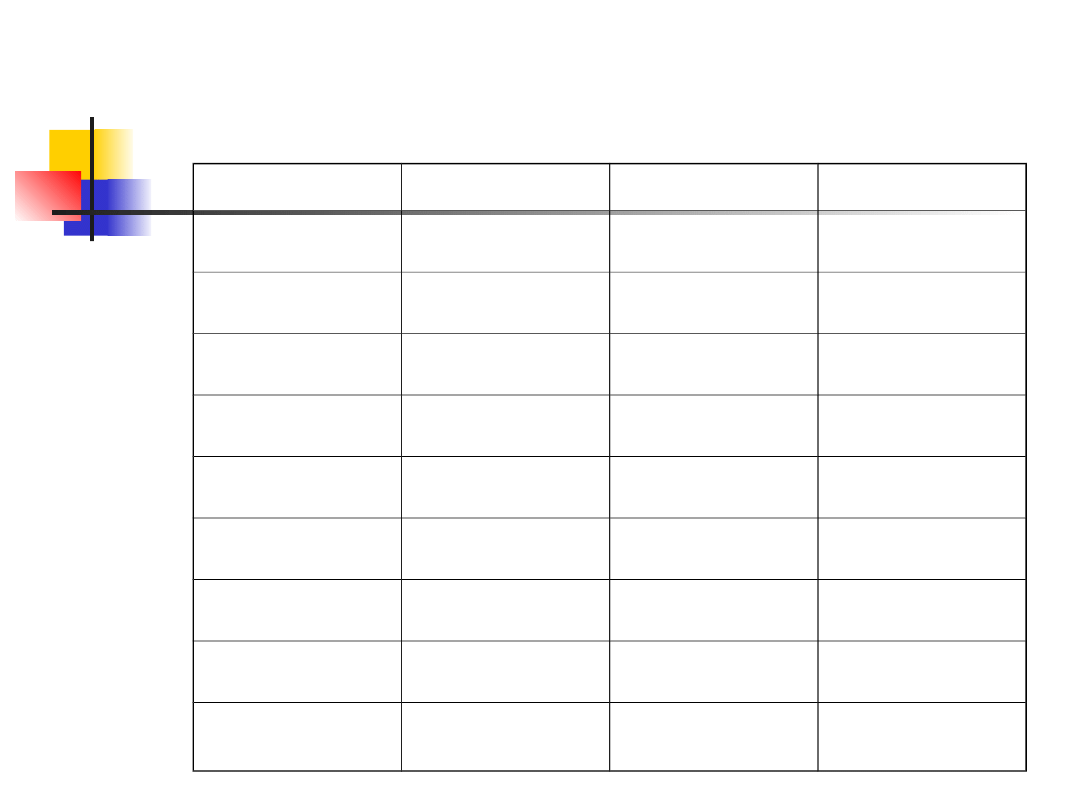
Przykład 4 –
Prędkość maszynopisania

Po kursie

Rangi

Bez kursu

Rangi

44

9

32

3.5

48

12

40

7

36

6

44

9

32

3.5

44

9

51

13

34

5

45

11

30

2

54

14

26

1

56

15

n

1

=8

n

2

=7

Test U Mann-Whitneya



Mając przypisane wszystkie rangi,

obliczamy statystykę Mann-

Whitneya

gdzie n

1

oraz n

2

są liczbami

obserwacji w każdej z próbek,

natomiast R

1

jest sumą rang

obserwacji z próbki pierwszej.

1

1

1

2

1

R

2

)

1

n

(

n

n

n

U









Test U Mann-Whitneya



Dla testu dwustronnego, obliczona
wartość U jest porównywana z
wartością graniczną U

,n1,n2

zamieszczoną w odpowiednich
tabelach statystycznych.



W tabelach zakłada się najczęściej
że n

1

<n

2

. Jeśli n

1

>n

2

należy użyć

U

,n2,n1

jako wartości krytycznej testu.

Test U Mann-Whitneya



Statystyka Mann-Whitneya może
być także obliczona jako:

(gdzie R

2

jest sumą rang

obserwacji z drugiej próbki), gdyż
etykietowanie próbek jako 1 czy 2
jest zupełnie arbitralne.

2

2

2

1

2

'

R

2

)

1

n

(

n

n

n

U









Test U Mann-Whitneya



Przeprowadzając test dwustronny
musimy obliczyć obie wartości U i
U

’

, a większa z nich porównywana

jest z wartością krytyczną.

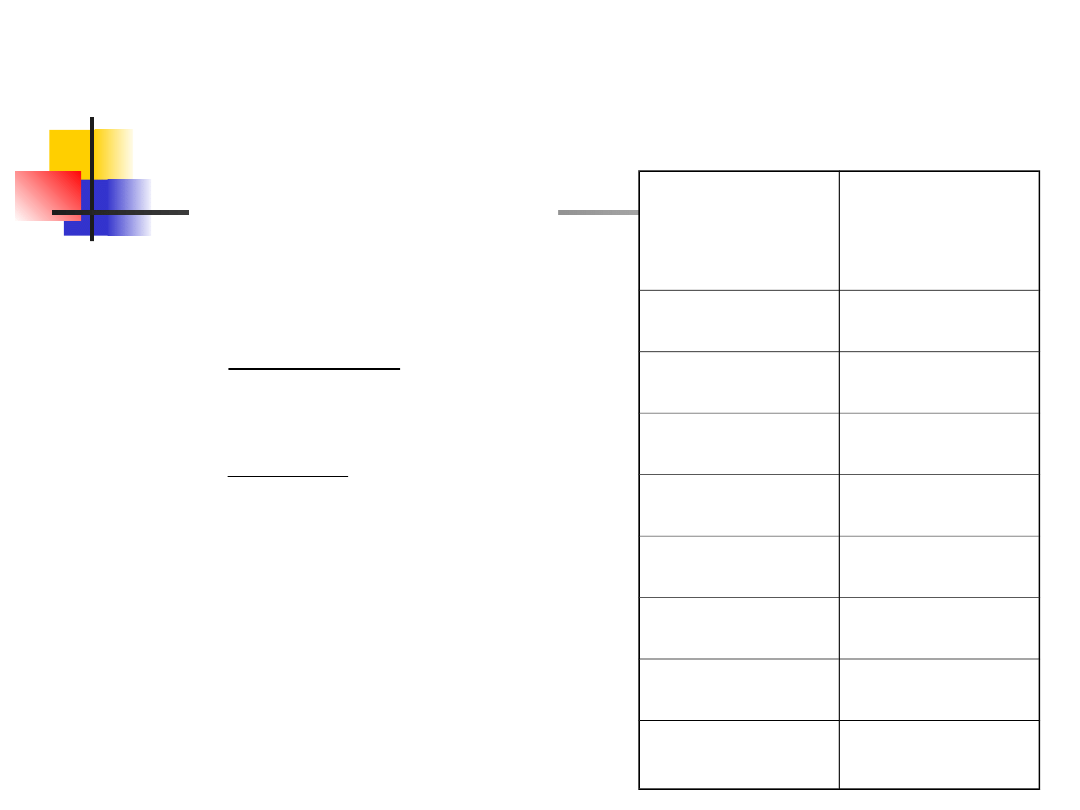
Przykład 3

Rangi

wzrostu

mężczyzn

Rangi

wzrostu

kobiet

1

7

2

8

3

10

4

11

5

12

6
9

R

1

=30

R

2

=48

odrzucona

zostaje

H

5

33

poniewa

ż

5

U

U

2

U

33

30

2

)

8

)(

7

(

)

5

)(

7

(

R

2

)

1

n

(

n

n

n

U

0

7

,

5

,

05

.

0

5

,

7

,

05

.

0

'

1

1

1

2

1



























H

0

: Studenci są

takiego samego
wzrostu,
niezależnie od płci.

H

1

: Wzrost zależny

jest od płci.

Test U Mann-Whitneya



Można zauważyć, że



U (lub U

’

) jest również równa liczbie pomiarów,

które są większe od obserwacji w drugiej próbie.



Dla grupy kobiet, każda z rang 7 i 8 jest większa

od 6 rang z grupy mężczyzn, a każda z rang 10, 11

i 12 each przekracza wszystkich 7 rang mężczyzn,

sumując otrzymujemy 6+6+7+7+7=33=U. W

grupie mężczyzn, tylko ranga 9 przewyższa 2 rangi

z grupy kobiet, co daje 2=U

’

.

U

n

n

U

2

1

'





Test U Mann-Whitneya



Test U Mann-Whitneya jest testem o

największej mocy wśród testów

nieparametrycznych; jeśli zastosujemy do

analizy porównawczej rozkładów normalnych

oba – test t dla dwóch próbek i test U Mann-

Whitneya – ten drugi będzie miał moc około

95% testu parametrycznego.



Jeśli natomiast istnieją silne odchyłki od

założeń testu t, test Mann-Whitneya będzie

miał większą moc.

Inne rozwiązania



Alternatywą dla testów
nieparametrycznych jest
zastosowanie testu t dla dwóch
próbek po obliczeniu rang
(nazywane jest to często
transformacją rangową danych).



Taka procedura ma moc taką samą
jak test Mann-Whitneya.

Jednostronny test U Mann-
Whitneya.



W przypadku testu jednostronnego
konieczne jest określenie, która
część dystrybucji statystyki Mann-
Whitney nas interesuje.



Determinuje to, czy w teście
wykorzystywana będzie wartość U
czy U

’

.

Jednostronny test U Mann-
Whitneya.

H

0

: Grupa 1  Grupa

2

H

1

: Grupa 1 < Grupa

2

H

0

: Grupa 1  Grupa

2

H

1

: Grupa 1 > Grupa

2

Rangowanie z dołu

do góry

U

U’

Rangowanie z góry

do dołu

U’

U

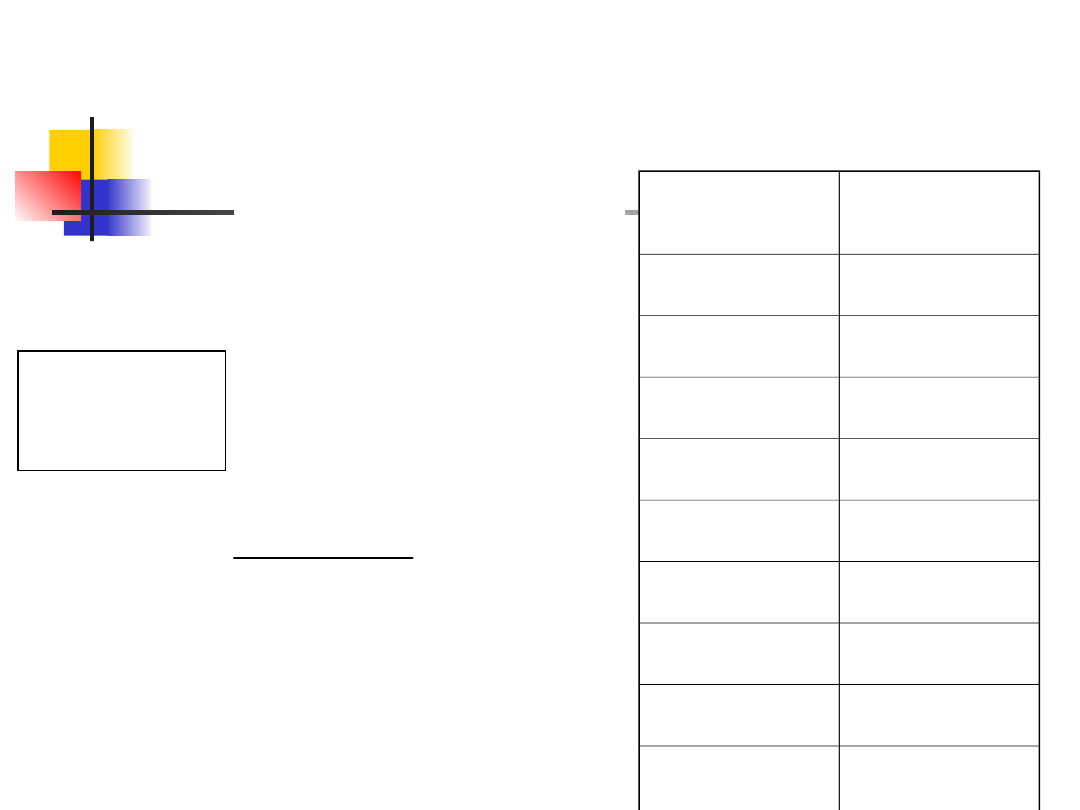
Przykład 4

Grupa 1

po kursie

Grupa 2

bez kursu

9

3.5

12

7

6

9

3.5

9

13

5

11

2

14

1

15

R

1

=83.5 R

2

=36.5

odrzucamy

H

10

5

.

47

poniewa

ż

10

U

U

5

.

47

R

2

)

1

n

(

n

n

n

'

U

0

8

,

7

],

1

[

05

.

0

7

,

8

],

1

[

05

.

0

2

2

2

1

2

















H

0

: Prędkość

maszynopisania nie
jest większa wśród
osób, które
ukończyły kurs w
porównaniu do osób
bez szkolenia.

H

1

: Prędkość

maszynopisania jest
większa w grupie
osób po kursie

Rangowanie
:

z dołu do

góry

Normalna aproksymacja
testu U Mann-Whitneya



Tablice z wartościami krytycznymi
testu Mann-Whitney są określone
tylko dla małych liczności próbek.



Rozkład zmiennej losowej U
zmierza do normalnego wraz ze
wzrostem liczebności.

Normalna aproksymacja
testu U Mann-Whitneya



Dla dużych n

1

i n

2

wykorzystujemy

fakt, że U ma wartość średnią

i odchylenie standardowe

2

n

n

2

1

U





12

)

1

N

(

n

n

2

1

U







Normalna aproksymacja
testu U Mann-Whitneya



Zatem, jeśli obliczymy U albo U’ a
liczność n

1

bądź n

2

jest większa od tych

zamieszczonych w tablicach, poziom
istotności może być obliczony poprzez



lub, uwzględniając poprawkę ze
względu na nieciągłość

U

U

U

Z









.

5

.

0

|

U

|

Z

U

U

C











Normalna aproksymacja
testu U Mann-Whitneya



Pamiętając, iż rozkład t dla = jest

identyczny z rozkładem normalnym,
możemy wartość krytyczną Z



określić jako

równą wartości krytycznej t

,

.



Gdy korzystamy w normalnej aproksymacji
dla testu dwustronnego, wystarczy
obliczyć tylko jedną z wartości U albo U’.



Można również sformułować test
jednostronny.

Przykład 5



Jednostronny test Mann-Whitney
został użyty do zbadania hipotezy,
czy zwierzęta, którym podawano
dodatkowo witaminy i
mikroelementy przybrały więcej na
wadze w porównaniu do zwierząt
bez dodatków.

Przykład 5



W trakcie eksperymentu, 22 zwierzęta (grupa
1) hodowano podając równocześnie witaminy i
mikroelementy, a 46 zwierząt hodowano
metodami tradycyjnymi, nie podając żadnych
dodatkowych witamin (grupa 2).



Masie ciała zwierząt przypisano rangi od 1 (dla
najmniejszej wagi) to 68 (dla wagi
największej), oraz obliczono U otrzymując 282.

Przykład 5

H

0

: Masa ciała zwierząt karmionych

witaminami nie jest większa niż
masa ciała zwierząt karmionych
standardowo.

H

1

: Masa zwierząt karmionych

witaminami jest wyższa od masy
zwierząt hodowanych bez witamin.

Przykład 5

Dla testu
jednostronnego
 = 0.05
t

0.05[1],

= 1.6449

Ponieważ Z = 2.94 >
1.6449, odrzucamy H

0

(p=0.0016)

94

.

2

28

.

76

224

'

U

Z

28

.

76

12

)

1

N

(

n

n

506

2

n

n

730

282

46

22

'

U

n

n

'

U

282

U

68

N

,

46

n

,

22

n

U

U

2

1

U

2

1

U

2

1

2

1















































Test U Mann-Whitneya dla
zmiennych w skali
porządkowej



Test U Mann-Whitneya może być również stosowany
do analizy danych przedstawionych w skali
porządkowej.



Przykład 6 pokazuje tę procedurę. Dwadzieścioro
pięcioro studentów wybrało kurs z zoologii.
Studentów podzielono losowo do dwóch grup
prowadzonych przez innych nauczycieli. Na
podstawie wyników końcowych zweryfikować
hipotezę zerową, że studenci z uzyskują takie same
wyniki niezależnie od prowadzącego ćwiczenia.

Example 4

Asystent A

Asystent B

Ocena

Ranga

Ocena

Ranga

A

3

A

3

A

3

A

3

A

3

B+

7.5

A-

6

B+

7.5

B

10

B

10

B

10

B-

12

C+

13.5

C

16.5

C_

13.5

C

16.5

C

16.5

C-

19.5

C

16.5

D

22.5

C-

19.5

D

22.5

D

22.5

D

22.5

D-

25

R

1

=114.5

R

2

=210.5

Przykład 6

H

odrzucenia

do

podstaw

ma

nie

114

5

.

105

poniewa

ż

114

U

5

.

48

U

n

n

'

U

5

.

105

R

2

)

1

n

(

n

n

n

U

0

14

,

11

],

2

[

05

.

0

2

1

1

1

1

2

1





















Testowanie różnic
pomiędzy medianami.



Można wyobrazić sobie sytuację, w której
interesować nas będzie odpowiedź na pytanie,
czy dwie próbki pochodzą z populacji o takich
samych medianach – jest to tzw.

test

medianowy

(Mood, 1950).



Procedura wymaga obliczenia tzw. globalnej
mediany oraz konstrukcji odpowiedniej tablicy
kontyngencyjnej o wymiarze 2x2.



Tak powstała tablica kontyngencyjna może być
analizowana z wykorzystaniem np. testu 

2

.

Przykład 7

H

0

: Dwie próbki pochodzą z populacji

o takiej samej medianie (tzn.

mediana ocen jest taka sama w

obu populacjach, niezależnie od

nauczyciela).

H

1

: Mediany obu populacji są różne.

=0.05

Przykład 7

Mediana dla wszystkich N pomiarów

wynosi (N=25):
X

(N+1)/2

=X

13

=grade C+

Powstaje zatem następująca tablica

kontyngencyjna.

Przykład 7 7

Asystent

A

Asystent

B

Suma R

i

Powyżej

mediany

6

6

12

Nie więcej

niż

mediana

5

8

13

Całkowite

C

i

11

14

25

Przykład 7



Możemy obliczyć statystykę





0

2

1

,

05

.

0

2

1

2

1

2

2

N

21

12

22

11

2

C

H

hipotezy

odrzucenia

do

podstaw

mamy

nie

zatem

841

.

3

X

031

.

0

R

R

C

C

|

f

f

f

f

|

N













Test porównawczy dla dwóch
próbek wyrażonych w skali
nominalnej (atrybutów)



Możemy porównać dwie próbki
danych w skali nominalnej poprzez
odpowiednio skonstruowaną
tablicę kontyngencyjną 2xC oraz
test niezależności 

2

.

Tablice kontyngencyjne



Hipoteza zerowa stanowi, że
częstości obserwacji umieszczone
w wierszach macierzy są
niezależne od częstości w
kolumnach (częstości „kolumnowe”
są niezależne od „wierszowych”).

Przykład 8

Płeć

Kolor włosów

Ogółe

m

Czarne

Brązowe

Blond

Rude

Mężczyź

ni

32

43

16

9

100

Kobiety

55

65

64

16

200

Ogółe

m

87

108

80

25

300

Schematy próbkowania

Trzeba sobie uświadomić, że są trzy schematy

eksperymentu zebrania danych z przykładu
8:

1. Można losowo wybrać 100 mężczyzn i

zapytać ich o kolor włosów oraz losowo
wybrać 200 kobiet i również zapytać je o
kolor włosów.
Oznacza to, że ustalono liczności danych w
wierszach tablicy kontyngencyjnej (100 oraz
200).

Schematy próbkowania

2. Albo, możemy zdecydować iż pytamy

o płeć losowo wybrane 87 osoby o
czarnych włosach, 108 osób o włosach
brązowych, 80 osób o włosach w
kolorze blond oraz 25 osób rudych.
Tak przeprowadzony eksperyment
odpowiada schematowi o ustalonych
wcześniej licznościach w kolumnach.

Schematy próbkowania

3. Albo, pytamy losowo wybrane 300

osób o kolor włosów i płeć.
Taki eksperyment wymaga jedynie
określenia całkowitej liczności
próby.

Schematy próbkowania

Niezależnie od schematu

eksperymentu, analizę danych
można przeprowadzić w taki sam
sposób.

Test niezależności 

2

W analizie 

2

tablic

kontyngencyjnych korzystamy ze
standardowej formuły na
statystykę 

2

:

Ogółem, liczność oczekiwana dla

każdej z komórek tabeli wynosi:









.

fˆ

)

fˆ

f

(

ij

2

ij

ij

2

N

C

R

N

N

C

N

R

fˆ

j

i

j

i

ij





























Test niezależności 

2

Mając obliczoną wartość statystyki



2

, jej znamienność statystyczna

może być wyznaczona poprzez
porównanie wartości z rozkładem


2

o (r-1)(c-1) liczbie stopni

swobody.

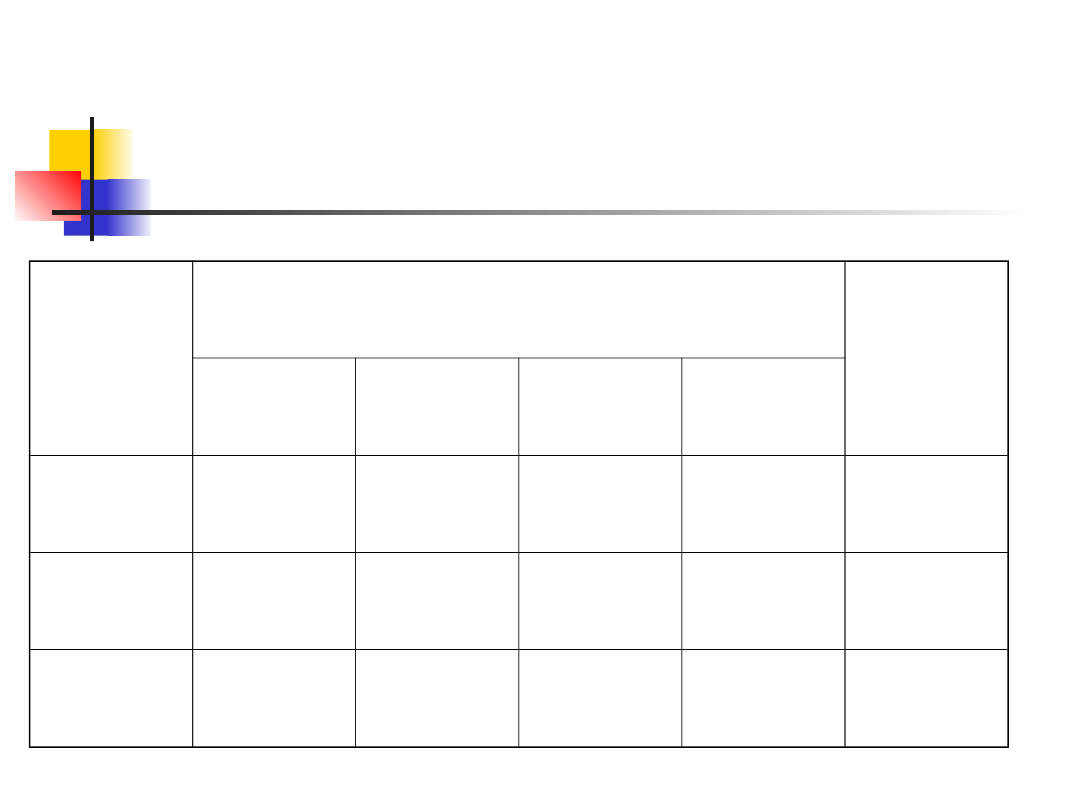
Przykład 8 – oczekiwane
liczności

Płeć

Kolor włosów

Ogółe

m

Czarne

Brązowe

Blond

Rude

Mężczyź

ni

29.00 36.00 26.67

8.33

100

Kobiety

58.00 72.00 53.33 16.67

200

Ogółe

m

87

108

80

25

300

Przykład 8

.

H

odrzucamy

zatem

815

.

7

;

3

)

1

c

)(

1

r

(

987

.

8

67

.

16

)

67

.

16

16

(

33

.

53

)

33

.

53

64

(

72

)

72

65

(

58

)

58

55

(

33

.

8

)

33

.

8

9

(

67

.

26

)

67

.

26

16

(

36

)

36

43

(

29

)

29

32

(

fˆ

)

fˆ

f

(

0

2

3

,

05

.

0

2

2

2

2

2

2

2

2

ij

2

ij

ij

2

























































