1

Metody statystyczne w badaniach

i poprawie jakości

2

Arkusze zliczeniowe

Najprostszą formą ilościowej oceny przebiegu

procesu są arkusze zliczeniowe. Za pomocą arkuszy
zbierane są podstawowe dane liczbowe charakteryzujące
aktualna sytuację. Zwykle są one pierwszym narzędziem
używanym w początkowej fazie określania problemów z
zakresu sterowania jakością lub procesem. Zebrane dane
stanowią podstawę dla dalszej analizy i są przetwarzane
w inne formy potrzebne dla stosowania bardziej
zaawansowanych metod, jak np. tablice rozkładów
częstości, statystyki opisowe lub wykresy Pareto.

3

• wybranie i uzgodnienie zjawiska, które jest badane

(wskazanie istotnych cech),

• ustalenie okresu czasu, przez który dane będą

zbierane,

• zaprojektowanie czytelnej formy arkusza - łatwej w

interpretacji i wygodnej w użyciu,

• zbieranie danych i wypełnianie arkusza (stosowanie

jednolitej techniki zliczania),

• wypełnienie dodatkowych kolumn arkusza, które

zawierają podsumowania i wyniki zagregowane,
opracowane na podstawie rubryk podstawowych,

Etapy wprowadzania i stosowania arkusza:

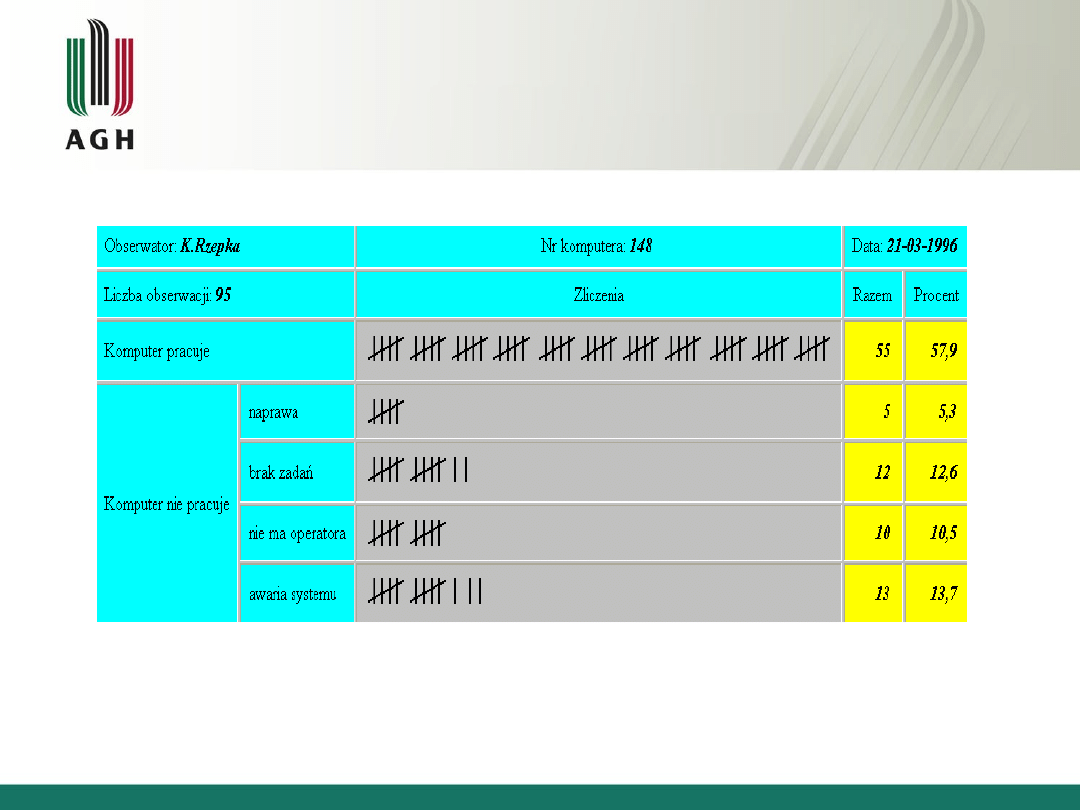
4

Przykład wypełnionego arkusza

Przykład wypełnionego arkusza

5

Poza ilościowym opisem zmienności

analizowana jest także struktura (rozkład) danych.
Chodzi głównie o to, aby stworzyć dla obserwowanej
zmienności pewien model. Mając przed sobą wszystkie
zebrane wyniki obserwacji zazwyczaj trudno jest
wskazać model ich zamienności. Pomocnym zabiegiem
jest uporządkowanie i posegregowanie danych
liczbowych w celu uzyskania rozkładu częstości.
Pierwszym krokiem jest podzielenie całego zakresu
zmienności na podprzedziały. Następnie zliczane są
wartości, które zawarte są w poszczególnych
podprzedziałach. Tablica częstości pokazuje, ile
wartości z analizowanego zbioru mieści się w każdym z

podprzedziałów.

6

Etapy wyznaczania rozkładu:

• określenie liczności próbki,
• wyznaczenie zakresu zmienności danych czyli

rozstępu w próbce,

• podzielenie zakresu zmienności na pewną liczbę

przedziałów w zależności od liczby pomiarów
pierwotnych (zwykle na 6 do 12 przedziałów),

• określenie szerokości przedziału - najlepiej

jednakowej dla wszystkich,

• wyznaczenie granic dla przedziałów (zapewnienie

jednoznaczności przypisania pomiaru do przedziału),

• wyznaczenie liczb pomiarów w poszczególnych

przedziałach - opracowanie tablicy rozkładu

Rozkład częstości

Rozkład częstości

opracowywany jest dla oceny

opracowywany jest dla oceny

zmienności wyników uzyskanych w próbce

zmienności wyników uzyskanych w próbce

losowej

losowej

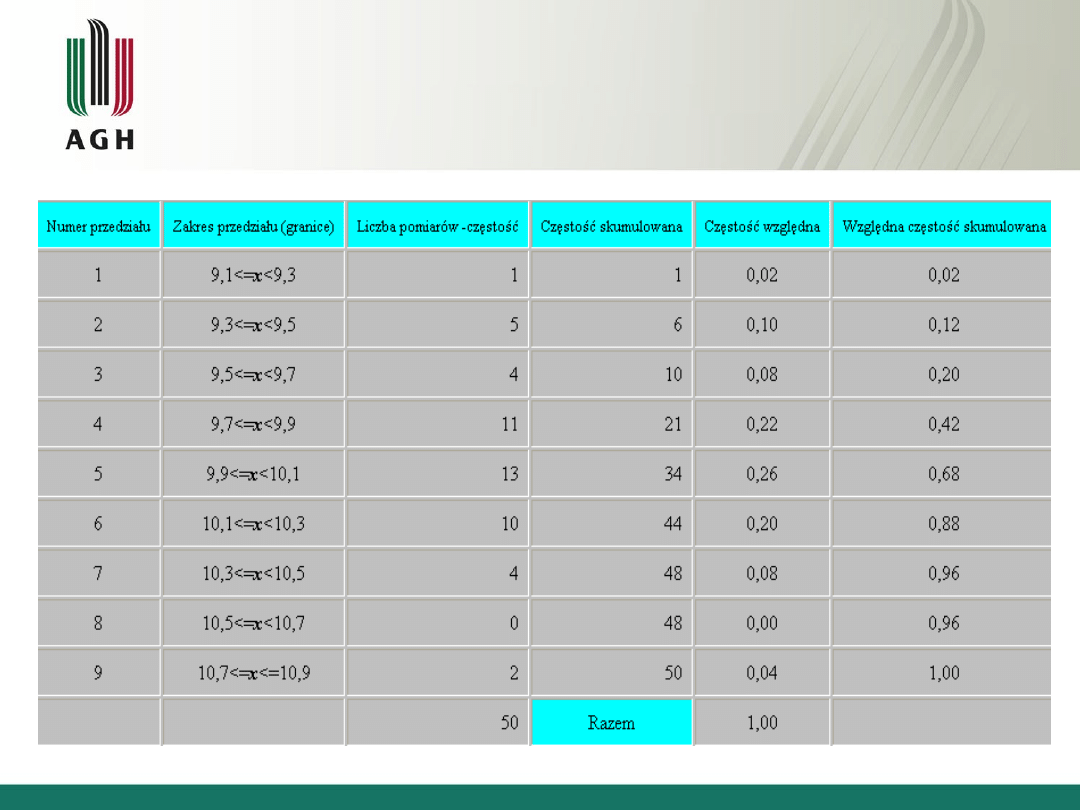
7

Przykład

Przykład tablicy rozkładu

częstości

częstości

8

Tablica rozkładu częstości może być bardzo

pomocna przy wstępnej analizie problemów z zakresu

zarządzania jakością.

Przy tworzeniu tablicy rozkładu częstości należy:

– określić liczbę przedziałów na które dzielimy zakres

zmienności,

– określić ich granice

Te dwa parametry są ze sobą związane. Zwykle są

określane metodą prób i błędów lub na podstawie

doświadczenia i analogii.

9

Podczas opracowywania tablicy rozkładu częstości
należy przestrzegać następujących zasad:

•

Liczba podprzedziałów powinna wynosić od 4 do 20,

•

Szerokość przedziału powinna być w zasadzie stała,

•

Dolna granica pierwszego podprzedziału powinna być

nieco mniejsza od najmniejszej wartości w zbiorze

danych,

•

Granice przedziałów powinny być tak oznaczone, aby

nie było wątpliwości do którego przedziału należy

zaliczyć wartość pomiaru równą jednej z nich

10

Histogram

Histogram j

est graficznym przedstawieniem

est graficznym przedstawieniem

rozkładu częstości za pomocą wykresu słupkowego.

rozkładu częstości za pomocą wykresu słupkowego.

Pozwala ocenić kształt rozkładu częstości i zdecydować,

Pozwala ocenić kształt rozkładu częstości i zdecydować,

czy sygnalizuje on nieprawidłowości w przebiegu procesu.

czy sygnalizuje on nieprawidłowości w przebiegu procesu.

Histogram jest często podstawowym narzędziem oceny

Histogram jest często podstawowym narzędziem oceny

jakości materiałów i surowców zaopatrzeniowych. W takim

jakości materiałów i surowców zaopatrzeniowych. W takim

przypadku dodatkowo zaznaczone są na nim granice

przypadku dodatkowo zaznaczone są na nim granice

tolerancji, które mogą wynikać z ustaleń technologicznych

tolerancji, które mogą wynikać z ustaleń technologicznych

lub warunków kontaktu z dostawcą.

lub warunków kontaktu z dostawcą.

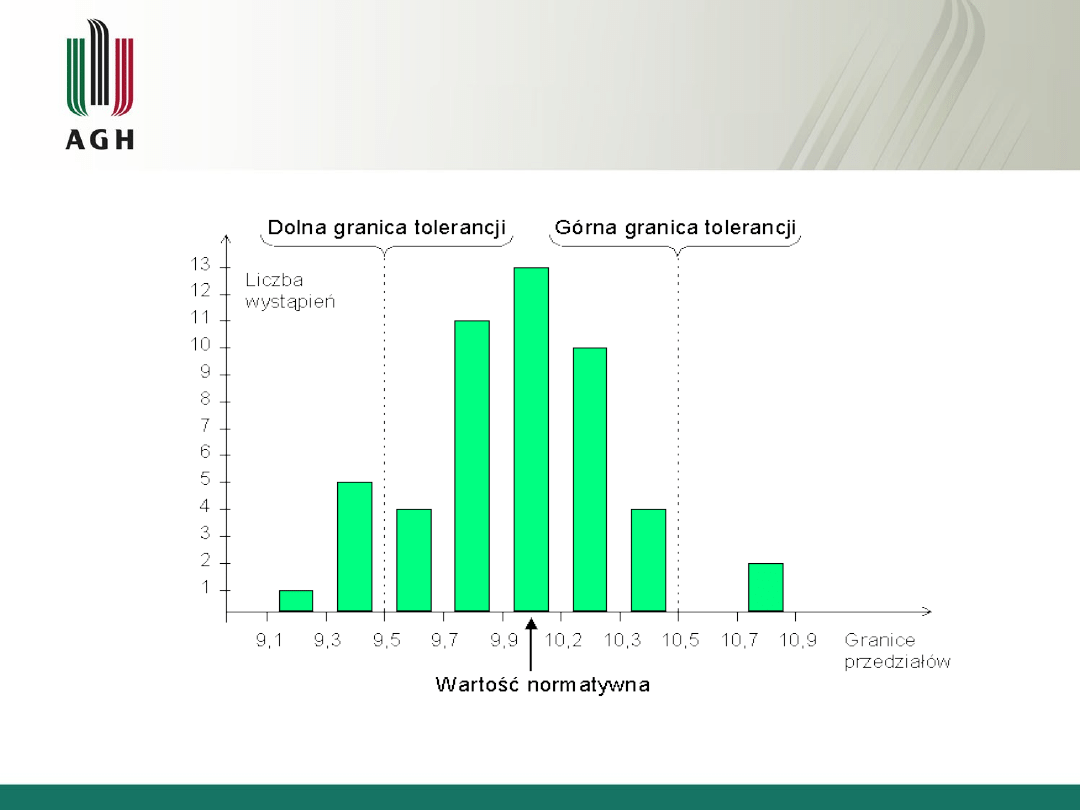
11

Histogram - wykres słupkowy przedstawiający

rozkład częstości

12

Histogramy, ze względu na swoją poglądowość i

umożliwienie szybkiej oceny rozkładu, są szeroko
stosowane w kontroli zaopatrzenia. Dla zdolności
procesu duże znaczenie mają surowce wejściowe. Ich
jakość przenosi się na otrzymywane produkty końcowe.
Zapewnienie dostaw odpowiedniej jakości jest
niezbędnym elementem zarządzania jakością w całym
procesie

13

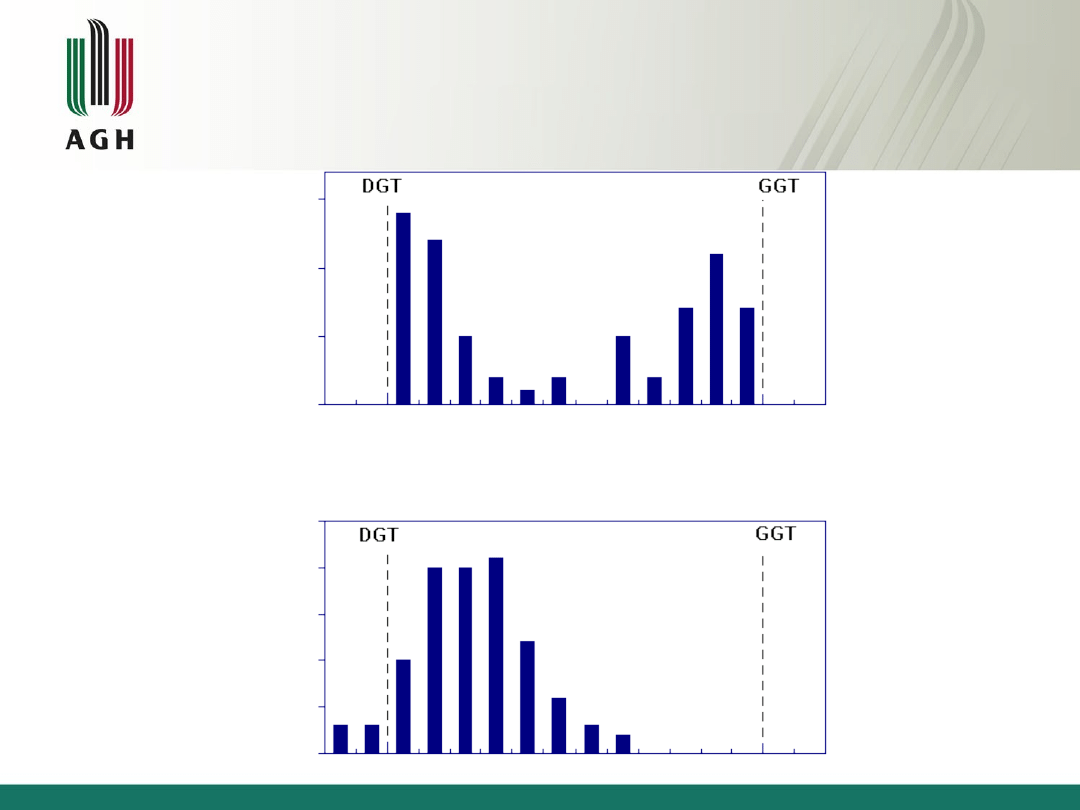
Charakterystyczne histogramy z zakresu

wstępnej kontroli jakości materiałów

zaopatrzeniowych



DGT oznacza dolną granicę tolerancji

• GGT oznacza górną granicę tolerancji
• przyjęto, że wartość normatywna położona jest pośrodku

przedziału tolerancji

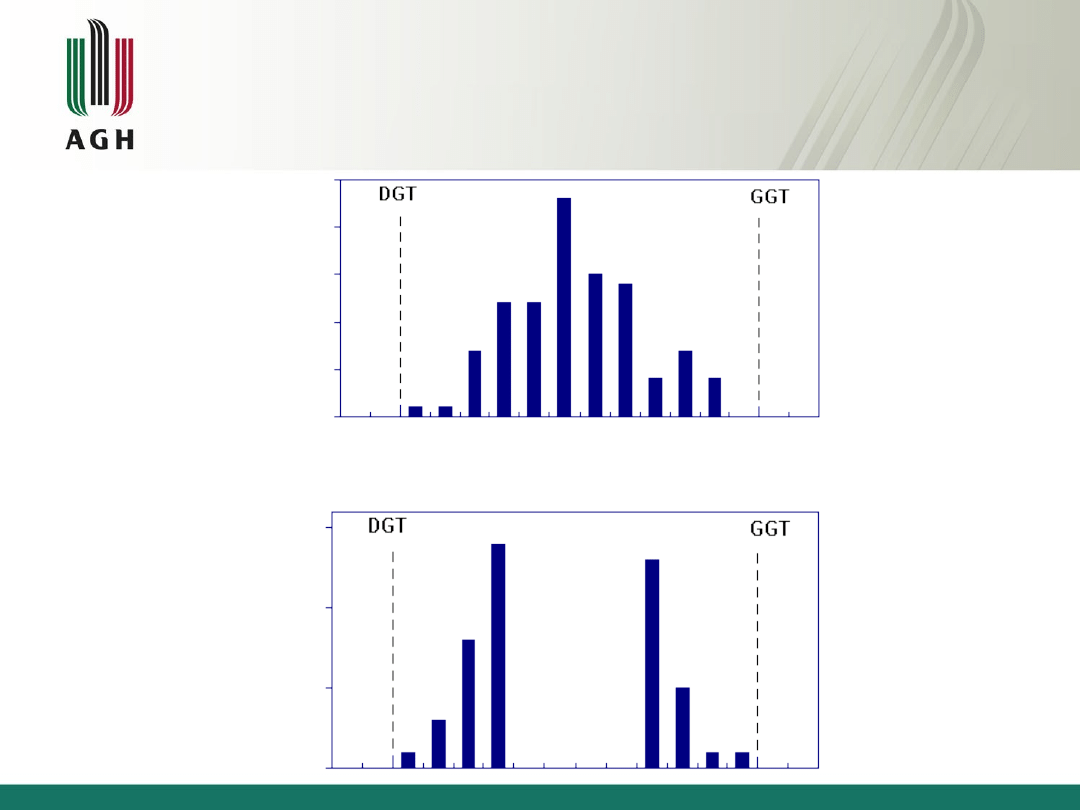
14

Histogram "normalny"

Wycięty histogram "normalny"

Wycięty histogram "normalny"

15

Nałożone i obcięte dwa histogramy "normalne"

Przesunięty histogram "normalny"

16

Statystyki opisowe

B

B

ardzo często w analizie praktycznych problemów

ardzo często w analizie praktycznych problemów

z dziedziny zarządzania jakością wykorzystuje się proste

z dziedziny zarządzania jakością wykorzystuje się proste

charakterystyki jakościowe do opisu większych zbiorów

charakterystyki jakościowe do opisu większych zbiorów

danych.

danych.

S

S

tatystykami opisowymi nazywane są takie

tatystykami opisowymi nazywane są takie

charakterystyki liczbowe, które opisują zbiory danych

charakterystyki liczbowe, które opisują zbiory danych

interpretowane jako zbiory wartości pewnej zmiennej

interpretowane jako zbiory wartości pewnej zmiennej

losowej, uzyskane na drodze eksperymentów losowych

losowej, uzyskane na drodze eksperymentów losowych

(próbkowania populacji).

(próbkowania populacji).

17

Podstawowe statystyki opisowe służą do ilościowej
oceny zasadniczych cech zbioru wartości liczbowych,
do których należą:

 wartość przeciętna
• stopień zmienności (bezwzględnej lub odniesionej do

wartości przeciętnej)

• kształt rozkładu wartości ( symetria i spłaszczenie)

18





wykrycie związku przyczynowo-skutkowego pomiędzy

dwoma mierzalnymi cechami procesu lub produktu
(korelacja pozytywna, negatywna lub jej brak)

 wykrycie par danych (x

i

, y

i

) , które odbiegają od

korelacji wykazywanej przez większość pozostałych par

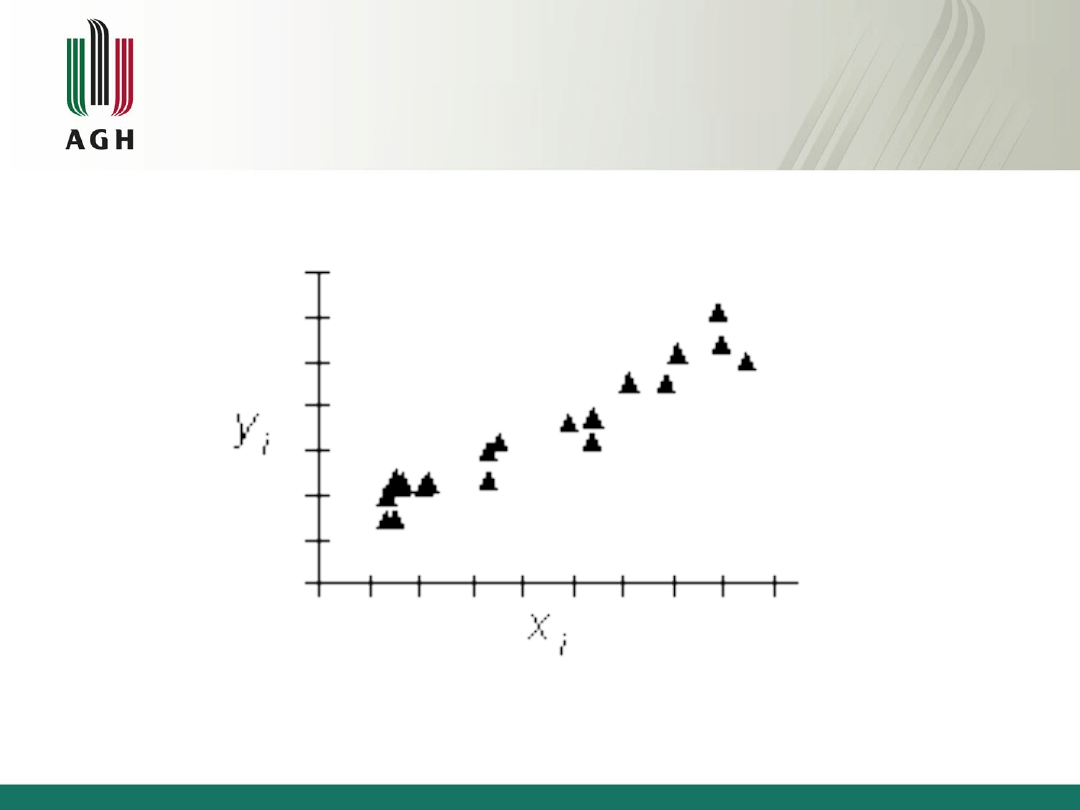
Wykres rozproszony

Wykres rozproszony

służy do prostej analizy

korelacji pomiędzy dwoma seriami danych x

1

, x

2

,…,x

n

i

y

1

, y

2

,…,y

n

19

Korelacja pozytywna - oznacza, że rosnącym

wartościom jednej zmiennej odpowiadają

rosnące wartości drugiej

20

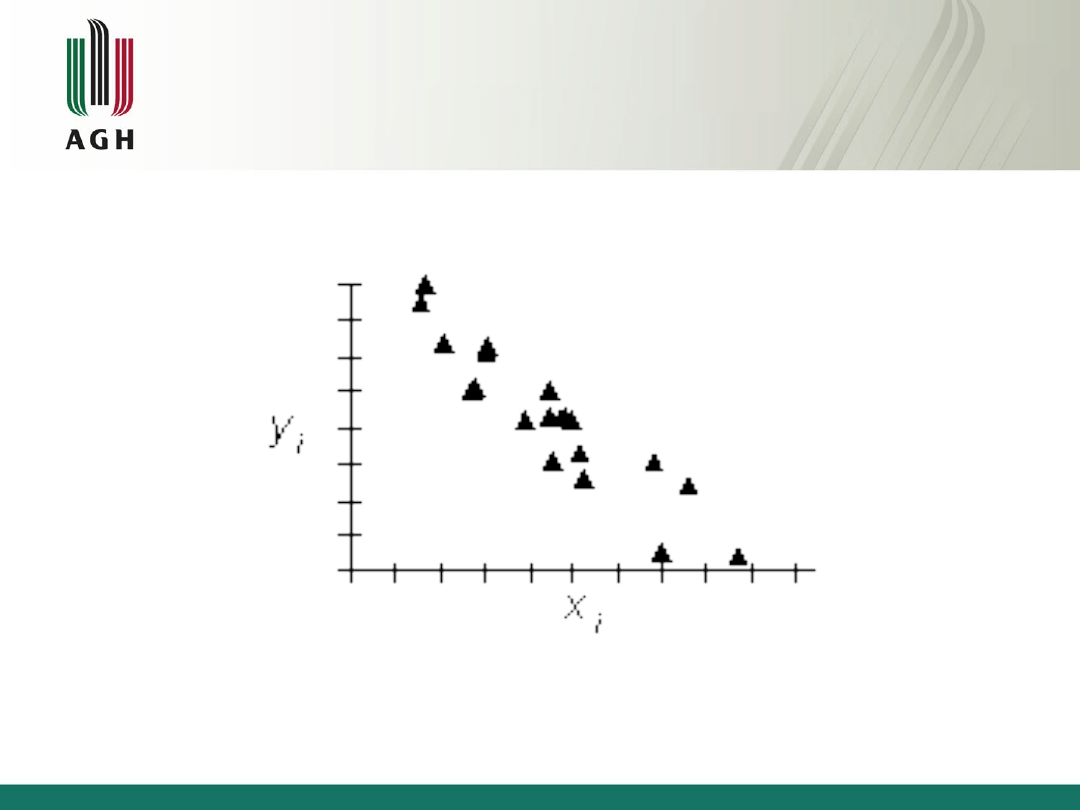
Korelacja negatywna– oznacza, że wzrostowi

wartości jednej zmiennej odpowiada

zmniejszanie się wartości drugiej

21

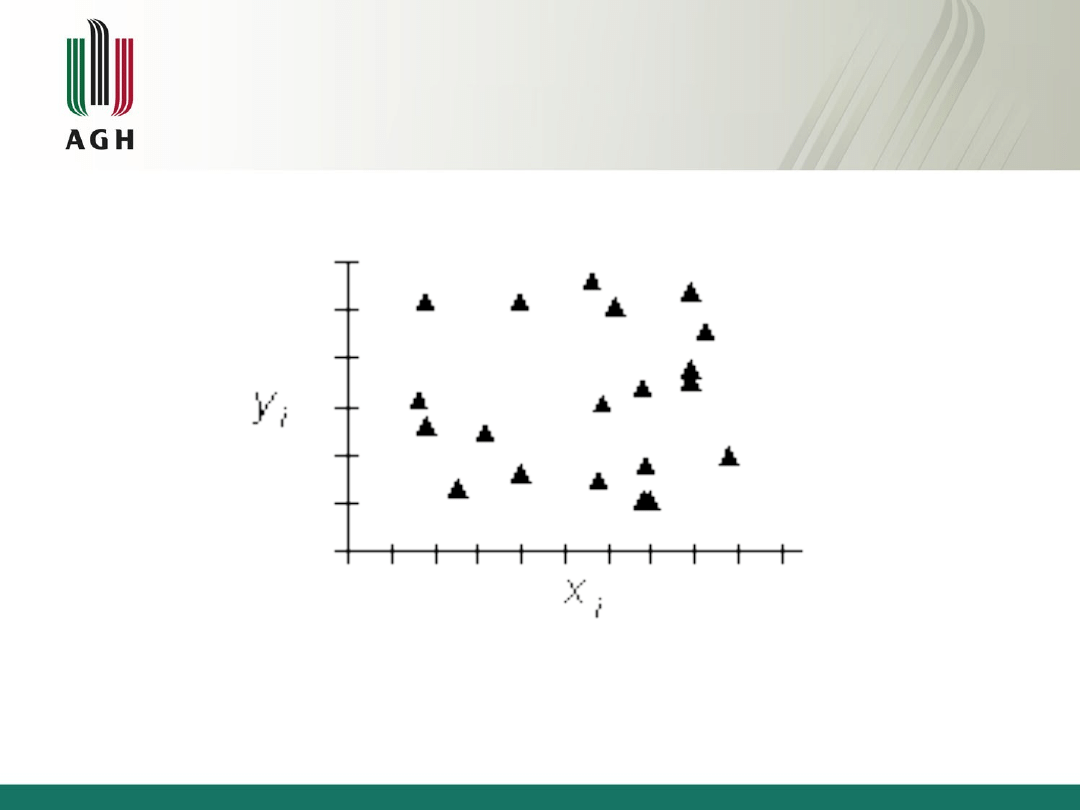
Brak korelacji- to stan, w którym nie można

uchwycić wyraźnej zależności pomiędzy

wartościami zmiennych

22

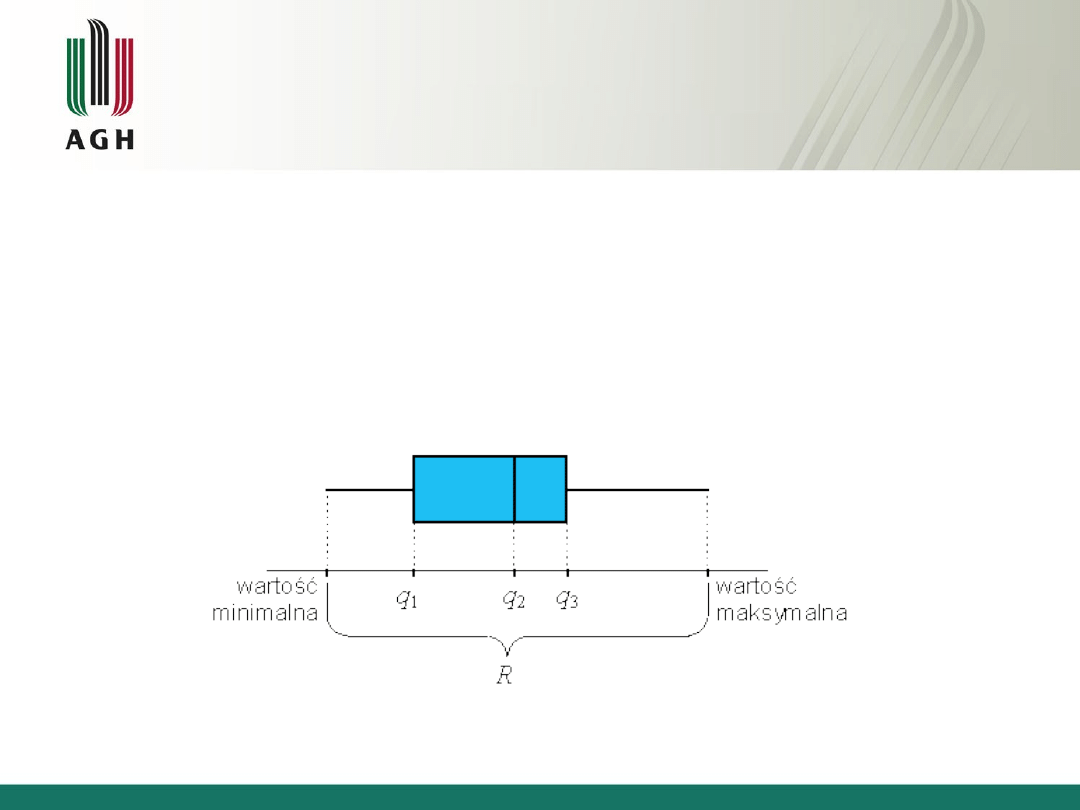
Wykres skrzynkowy

Wykres skrzynkowy może obrazować zmiany

rozkładu w kolejnych próbkach, jeśli dla każdej z nich
wyznaczono kwartyle (w tym medianę) i rozstęp

.

.

Schemat "skrzynki" pokazującej relację pomiędzy
charakterystykami empirycznymi wyznaczonymi dla
pojedynczej próbki:

23

Wykres skrzynkowy jest szczególnie przydatny do

oceny ewolucji rozkładów danych w czasie lub do
analizy przebiegu procesu podczas zmian parametrów
sterujących. Za jego pomocą można szybko wskazać
zmiany zachodzące w kolejnych próbkach, z których
każda przedstawiona jest w postaci pojedynczego
wykresu skrzynkowego. Wykres skrzynkowy jest
efektywnym narzędziem obserwacji procesów również
dlatego, że wyznaczenie wszystkich wartości
potrzebnych do jego zrobienia jest łatwe i szybkie.

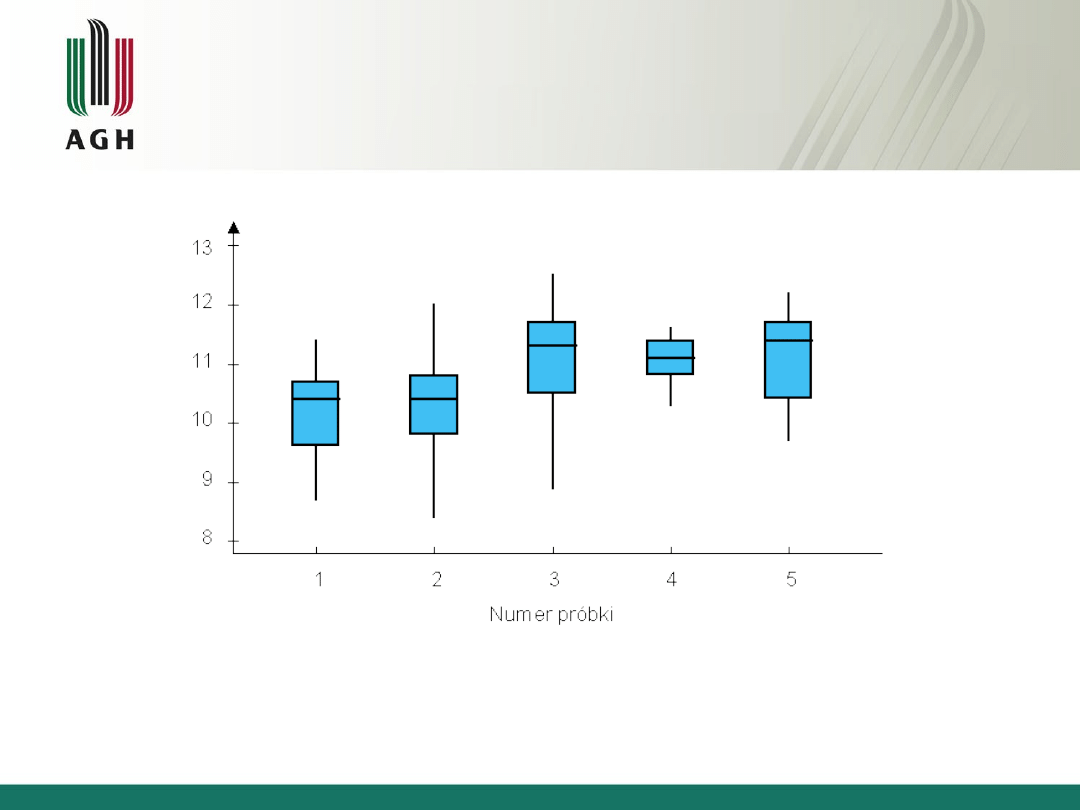
24

Przykład wykresu skrzynkowego

25

Wykresy Pareto

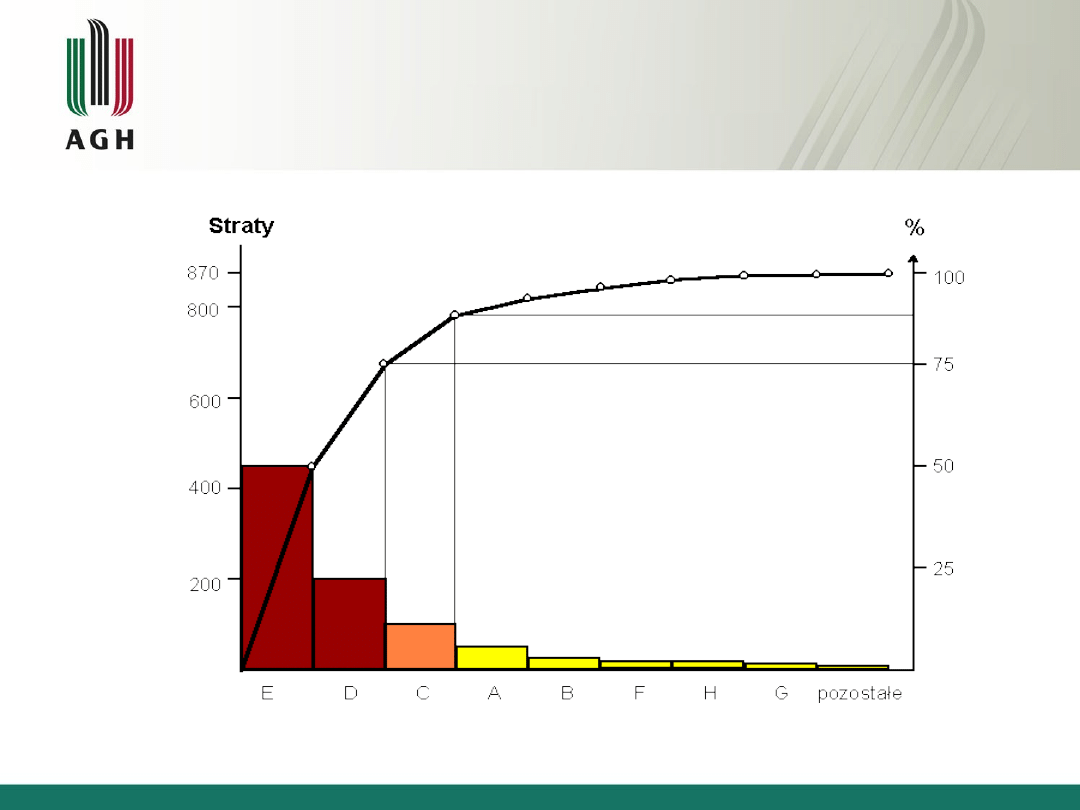
Wykres Pareto-Lorentza wspomaga weryfikację hipotezy
Pareto - 20% przyczyn decyduje o powstawaniu 80% błędów.
Te krytyczne przyczyny powinny zostać wyróżnione, aby
zasoby przeznaczone na poprawę jakości mogły zostać
właściwie skoncentrowane w celu ich usunięcia. Nie zawsze
cechy procesy potwierdzają regułę Pareto i dlatego można ją
traktować jako hipotezę, która jest potwierdzana (lub nie)
poprzez analizę związków przyczynowo-skutkowych

26

Wykresem Pareto nazywany jest wykres słupkowy

oparty na uporządkowanych malejąco wartościach
liczbowych, związanych z poszczególnymi kategoriami.
Jest on często uzupełniany tzw. krzywą Lorentza, która
pokazuje wzrost skumulowanego udziału procentowego
wyróżnionych kategorii. Krzywa udziału procentowego
ma swoją oddzielną skalę, umieszczoną na osi po
prawej stronie wykresu. Wykres Pareto może być
konstruowany w oparciu o tablicę rozkładu częstości,
która opisuje występowanie analizowanego skutku w
różnych obszarach lub z różnych przyczyn. Zatem jest
on rodzajem uporządkowanego malejąco histogramu.

27

Wykres Pareto

28

K

K

arty kontrolne przeznaczone są do badania zmienności

arty kontrolne przeznaczone są do badania zmienności

w ramach operacyjnego zarządzania procesem

w ramach operacyjnego zarządzania procesem

produkcyjnym. Na tę zmienność mają wpływ dwa rodzaje

produkcyjnym. Na tę zmienność mają wpływ dwa rodzaje

przyczyn. Pewien zakres zmienności w procesie wynika z

przyczyn. Pewien zakres zmienności w procesie wynika z

wielu stale obecnych przyczyn normalnych i jest

wielu stale obecnych przyczyn normalnych i jest

nieunikniony. Musi on być kontrolowany, ale bez

nieunikniony. Musi on być kontrolowany, ale bez

zasadniczych zmian w procesie nie można go zmienić- jest

zasadniczych zmian w procesie nie można go zmienić- jest

jego naturalną cechą. Podczas przebiegu procesu zdarzają

jego naturalną cechą. Podczas przebiegu procesu zdarzają

się także znaczne odchylenia od wartości nominalnej, które

się także znaczne odchylenia od wartości nominalnej, które

są wynikiem pojawienia się przyczyn szczególnych. Można

są wynikiem pojawienia się przyczyn szczególnych. Można

podjąć działania zapobiegawcze, które ograniczą bądź

podjąć działania zapobiegawcze, które ograniczą bądź

wyeliminują ich wpływ. Zatem w każdym procesie mamy do

wyeliminują ich wpływ. Zatem w każdym procesie mamy do

czynienia z dwoma rodzajami zmienności naturalną i

czynienia z dwoma rodzajami zmienności naturalną i

nadzwyczajną, przy czym każda z nich ma inne cechy.

nadzwyczajną, przy czym każda z nich ma inne cechy.

Podstawowe karty kontrolne

29





Ma wiele małych

Ma wiele małych

składowych

składowych



Nie można wskazać

Nie można wskazać

pojedynczych przyczyn

pojedynczych przyczyn



Pozostaje na stałym

Pozostaje na stałym

poziomie

poziomie



Ma przewidywalny wpływ

Ma przewidywalny wpływ

na rezultaty

na rezultaty



Zmniejszenie wymaga

Zmniejszenie wymaga

dokonania zasadniczych

dokonania zasadniczych

zmian w procesie

zmian w procesie



Określenie poziomu jest

Określenie poziomu jest

podstawą dla wykrywania

podstawą dla wykrywania

przyczyn szczególnych

przyczyn szczególnych

Nadzwyczajna zmienność
procesu

:

:



Ma kilka głównych

Ma kilka głównych

składowych

składowych



Zwykle można określić

Zwykle można określić

związek

związek

pomiędzy przyczyną i

pomiędzy przyczyną i

skutkiem

skutkiem



Pojawia się nieregularnie

Pojawia się nieregularnie



Często trudno przewidzieć

Często trudno przewidzieć

skutki

skutki



Usuwana poprzez działania

Usuwana poprzez działania

wąsko ukierunkowane

wąsko ukierunkowane



Wskazywana poprzez

Wskazywana poprzez

interpretację kart

interpretację kart

kontrolnych

kontrolnych

Naturalna

Naturalna

zmienność procesu:

zmienność procesu:

30

Przykłady normalnych

przyczyn zmienności:

• Wibracja urządzeń

• Wpływ operatora

• Zmienna temperatura i

wilgotność

• Niejednorodne surowce

• Zmienne wymiary

elementów składowych

• Nieprecyzyjne instrukcje

i procedury

• Hałaśliwe otoczenie

• Zmienne proporcje

mieszanin i roztworów

Przykłady szczególnych
przyczyn zmienności:



Wadliwe surowce i półprodukty

 Zużyte narzędzia

 Zatrzymanie procesu

 Błąd obsługi

 Awaria zasilania lub przepięcie

 Błędne przygotowanie
składników

 Brak nadzoru

 Niewykonanie czynności

 Przegrzanie lub niedogrzanie

31

Karta kontrolna służy do:

• rozróżniania kiedy mamy do czynienia z

naturalnym, a kiedy z nadzwyczajnym rozkładem
wyników w próbce

• wykrywania kiedy na kontrolowany proces miały

wpływ normalne, a kiedy szczególne przyczyny
zmienności

• oceny czy proces jest wyregulowany (pod kontrolą

statystyczną)

32

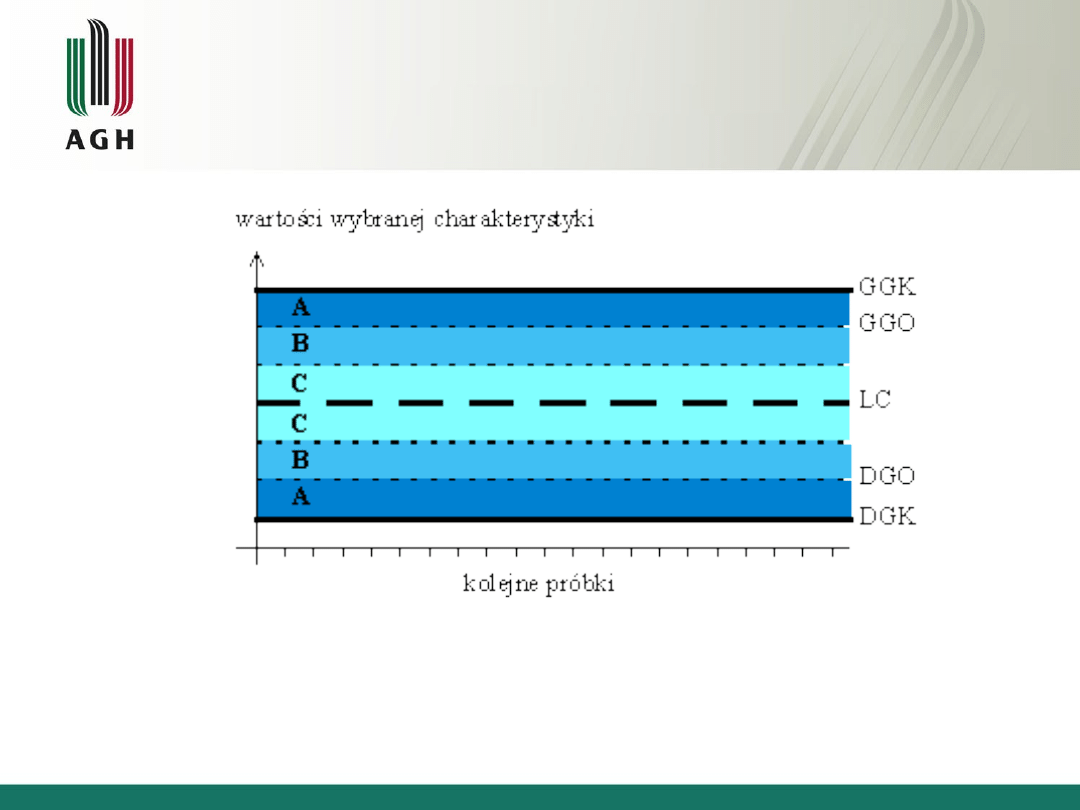
Ogólny schemat karty kontrolnej

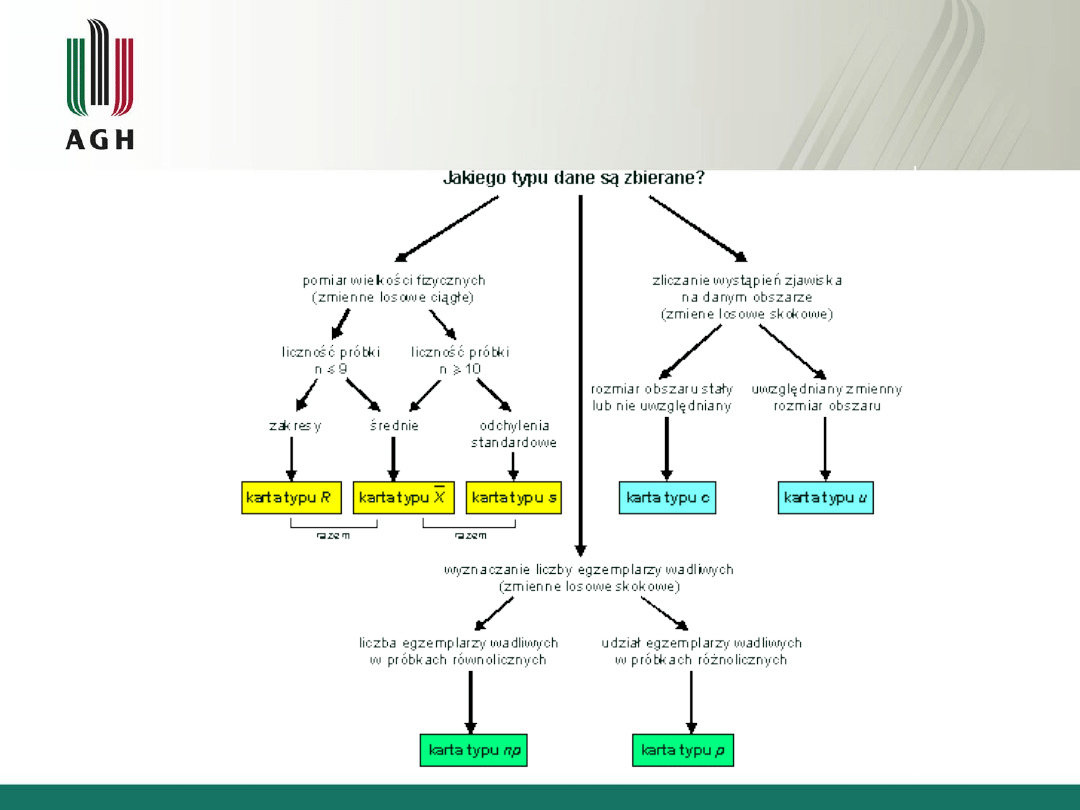
33

Podstawowe karty kontrolne Shewharta

Podstawowe karty kontrolne Shewharta

dobierane są w zależności od rodzaju

dobierane są w zależności od rodzaju

gromadzonych danych

gromadzonych danych

34

Wyznaczanie linii centralnej i granic kontrolnych

Linia centralna wskazuje wartość przeciętną dla

badanej statystyki a granice kontrolne wyznaczają

obszar odrzucania wartości dla testowanej hipotezy.

Wyznaczane są one z odpowiednich wzorów na

podstawie:

• Liczebności próbki

• Średniego udziału wadliwych egzemplarzy w próbce

• Średniej liczby wystąpień zjawiska na stałym

obszarze

• Średniej liczbie wystąpień zjawiska w jednostce

obszaru

• Średniej ze średniej wartości w próbkach

• Średniego zakresu pomiarów w próbkach

• Średniego odchylenia standardowego pomiarów w

próbkach

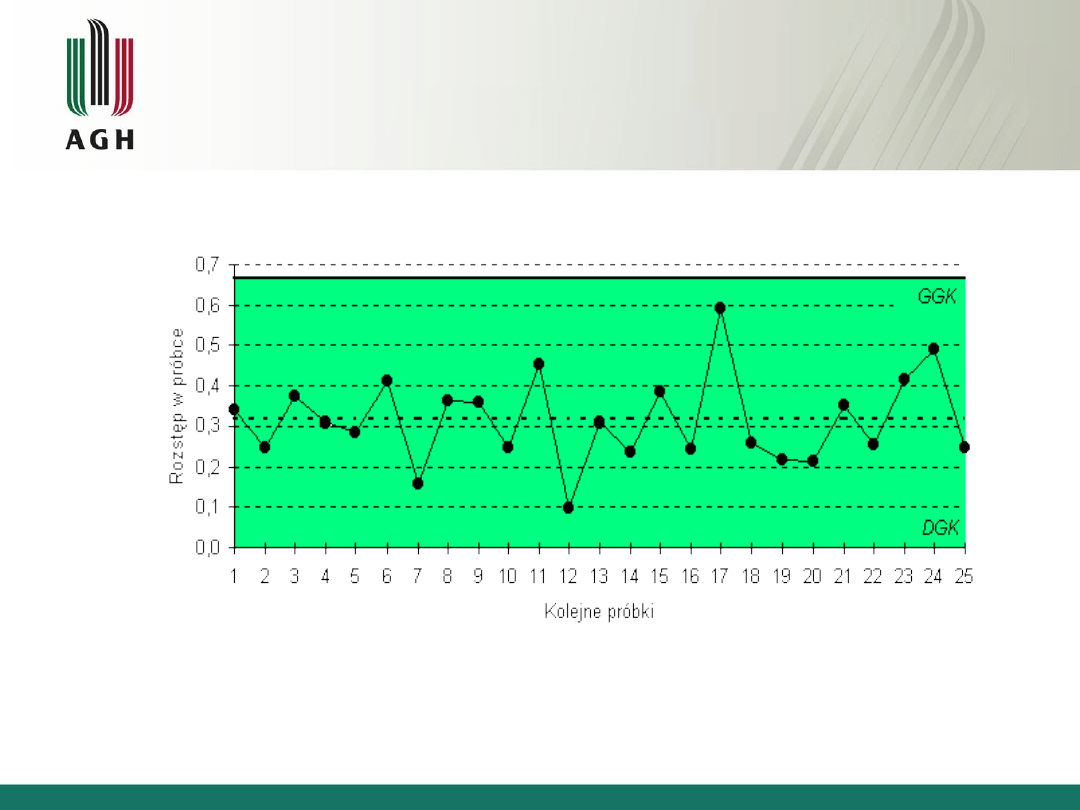
35

Karta dla rozstępu w próbce - karta typu R

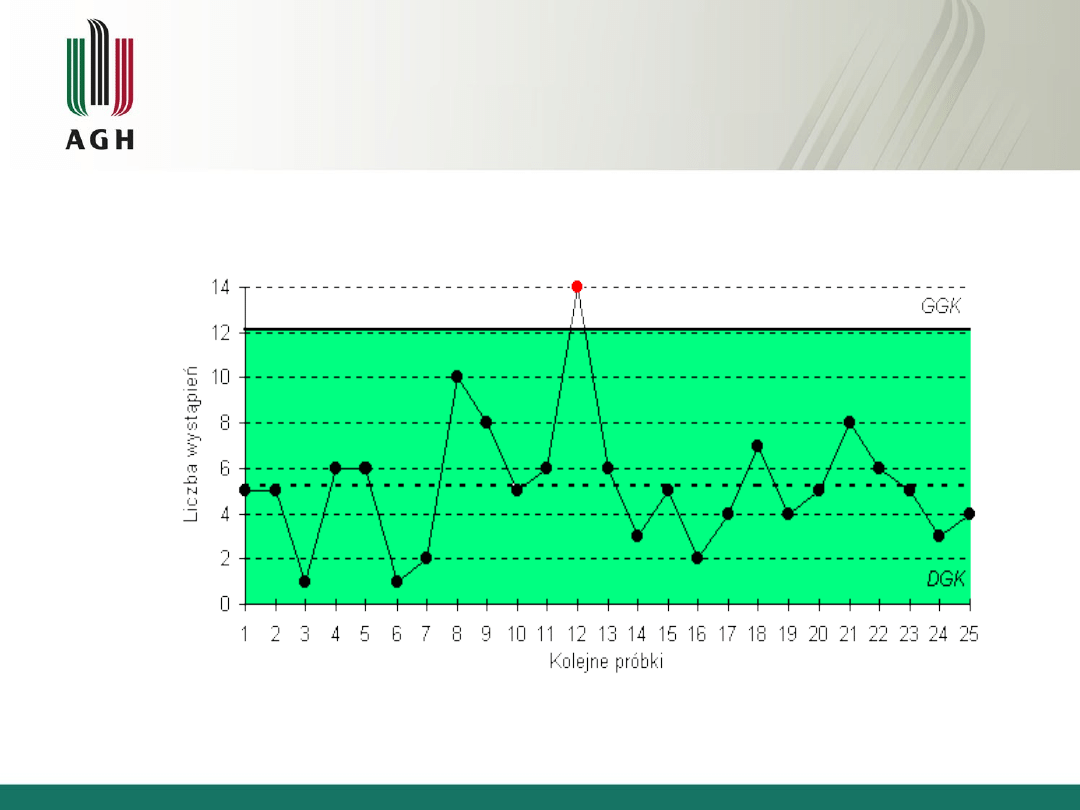
36

Karta dla liczby wad na wybranym obszarze -

karta typu C

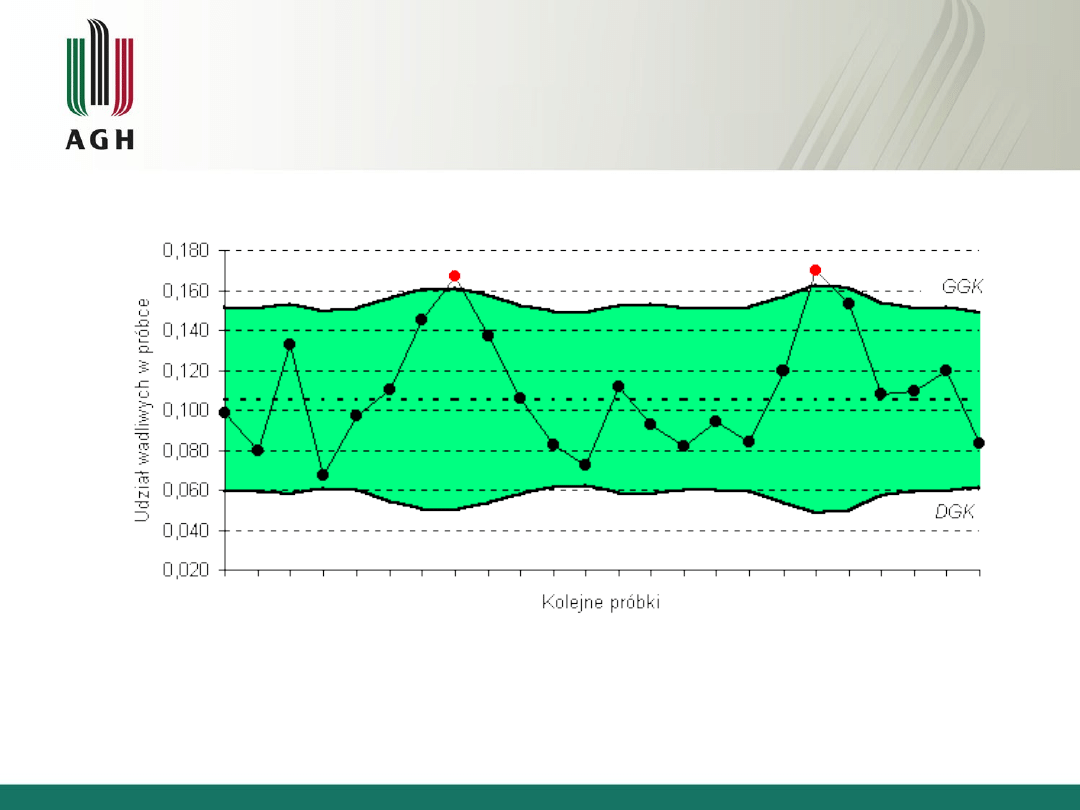
37

Karta dla udziału wadliwych egzemplarzy w

próbce - karta typu p

38

Literatura:

1. J. Sikorski „Statystyczne metody sterowania jakością”