Co to jest NMR

 Spektroskopia NMR -

Spektroskopia

Magnetycznego Rezonansu Jądrowego
(ang. Nuclear Magnetic Resonance)
 Potocznie w języku polskim: rezonans
magnetyczny.
 Jedna z najczęściej stosowanych obecnie
technik spektroskopowych w chemii i
medycynie.

Historia NMR

Teoretycy przewidzieli zjawisko NMR już dość wcześnie, bo tuż po I
Wojnie Światowej. Ze względu jednak na kłopoty techniczne
doświadczalnego potwierdzenia tych przewidywań dokonano dopiero
tuż po II Wojnie Światowej. Uczyniły to w 1945 r. równocześnie dwie
grupy uczonych: z Uniwersytetu Stanfort i z Uniwersytetu Harvard.
Rezonansem początkowo zajmowali się głównie fizycy, jednak z
momentem odkrycia przesunięcia chemicznego - rok 1950 -
stał on się domeną chemików.

W roku 1953 amerykańska firma

VARIAN

wyprodukowała pierwsze

komercyjne urządzenie służące do wykonywania widm tzw.
rezonansu magnetycznego o wysokiej zdolności rozdzielczej zwane
spektrometrem NMR. Rok 1966 to data przełomowa dla NMR -
profesor

Ernst

ulepsza metodę detekcji sygnału NMR wykorzystując

matematyczną operację zwaną transformacją Fouriera (dostał za to
Nagrodę Nobla w 1991 r.).

Nobel 1952 (Fizyka)

"for their development of new methods for

nuclear magnetic precision measurements and

discoveries in connection therewith"

Felix Bloch

Stanford University

Edward Mills Purcell

Harvard University

Charakter metody

• NMR to metoda:

– spektroskopowa

h

1

E

1

E

2

h

2

absorpcj
a

źródło
promieniowania

obserwacja

Spektroskopia NMR polega na wzbudzaniu spinów
jądrowych znajdujących się w zewnętrznym polu
magnetycznym poprzez wiązkę fal elektromagnetycznych,
a następnie rejestrację promieniowania
elektromagnetycznego powstającego na skutek zjawisk
relaksacji, gdzie przez relaksację rozumiemy powrót układu
spinów jądrowych do stanu równowagi termodynamicznej.
NMR jest zatem jedną ze spektroskopii absorpcyjnych.

Warunkiem obserwacji

oddziaływania

materii

z

promieniowaniem

elektromagnetycznym

jest

absorpcja energii

Aby nastąpiła absorpcja energii

...

• Konieczne jest zróżnicowanie stanów energetycznych

(tj. cząsteczki muszą mieć możliwość przebywania w
stanach o niższej i wyższej energii)

• Konieczne jest istnienie cząsteczek w stanie zdolnym

przyjąć energię (tj. niewzbudzonych)

• Kwant promieniowania elektromagnetycznego

niosącego tę energię musi być taki sam jak różnica
energii pomiędzy stanem przed i po wzbudzeniu

Przejście pomiędzy jakimi

poziomami energetycznymi
cząsteczki można uzyskać
napromieniowując ją
promieniowaniem o

częstości

fal radiowych

?

Nie ma takich poziomów

Jądro atomowe posiada spin

spin

• spin może przyjmować różne wartości dla różnych jąder (dla jądra danego

nuklidu jest zawsze taki sam)

• ze spinem związana jest

jądrowa kwantowa liczba spinowa I

, która przyjmuje

wartości całkowite lub połówkowe t.j. 0, 1, 2, … lub 1/2, 3/2, 5/2, …

• ze spinem związany jest

moment magnetyczny μ

• wielkość momentu magnetycznego jest kwantowana (przyjmuje tylko

niektóre, dyskretnie zadane wartości)

magnetyczną liczbą spinową m

I

= I, I-1,

I-2,…, -I

• jądrowy moment magnetyczny oddziałuje z zewnętrznym polem

magnetycznym

• energia tego oddziaływania jest proporcjonalna do wielkości momentu

magnetycznego

• w polu magnetycznym następuje zróżnicowanie energii stanów jądra

(zniesienie degeneracji) ze względu na m

I

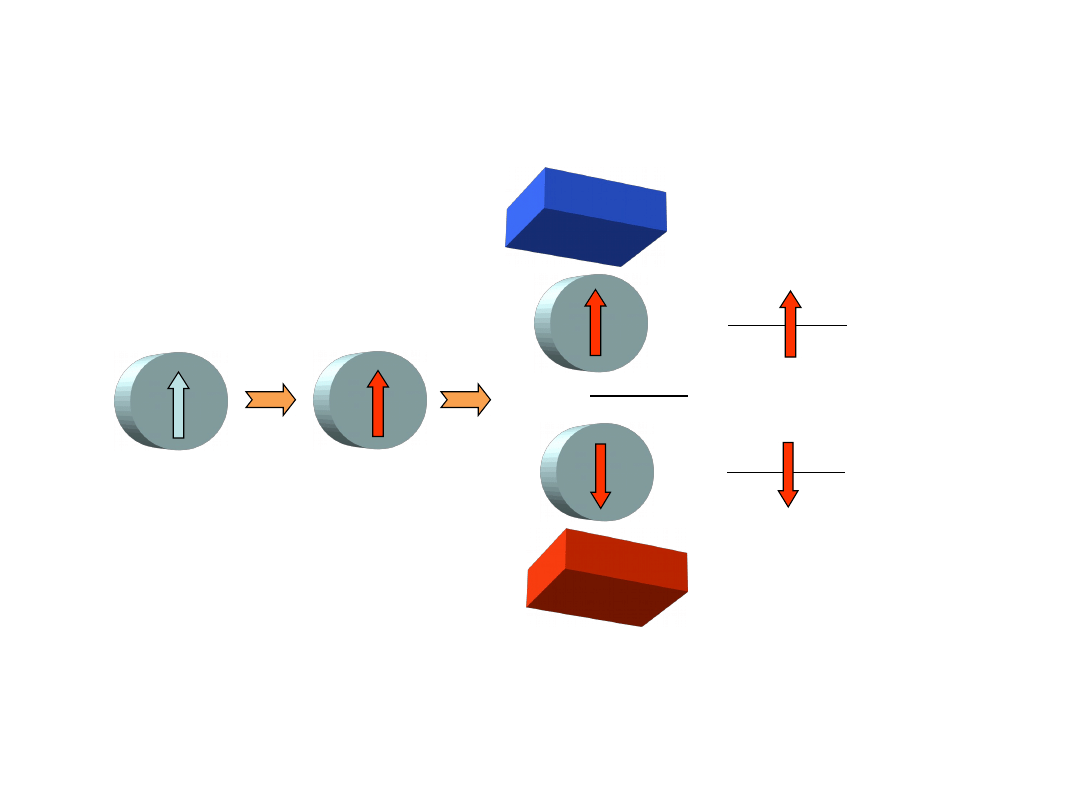
Jądro atomowe posiada spin

spin

SPIN

I

ħ

MOMENT

MAGNETYCZNY



ħ

I

S

N



ħ

I

B

-



ħ

I

B

ZRÓŻNICOWANIE

ENERGII

POLE

MAGNETYCZNE

O INDUKCJI B

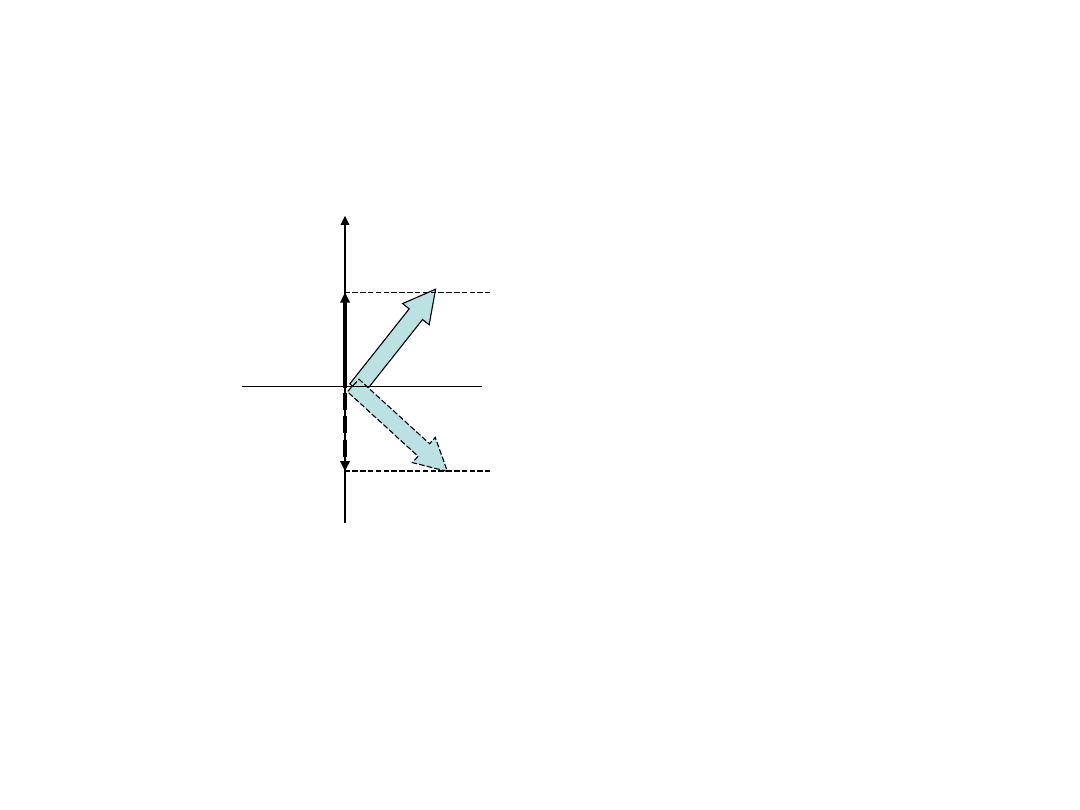
JĄDRO ATOMOWE W POLU

MAGNETYCZNYM

μ

B

o

μ

z

m

I

= -

½

m

I

= ½

E = - μ

z

B

0

E = μ

z

B

0

Degeneracja stanów spinowych jądra
została zniesiona przez pole
magnetyczne.

Różnica energii

E = 2 μ

z

B

0

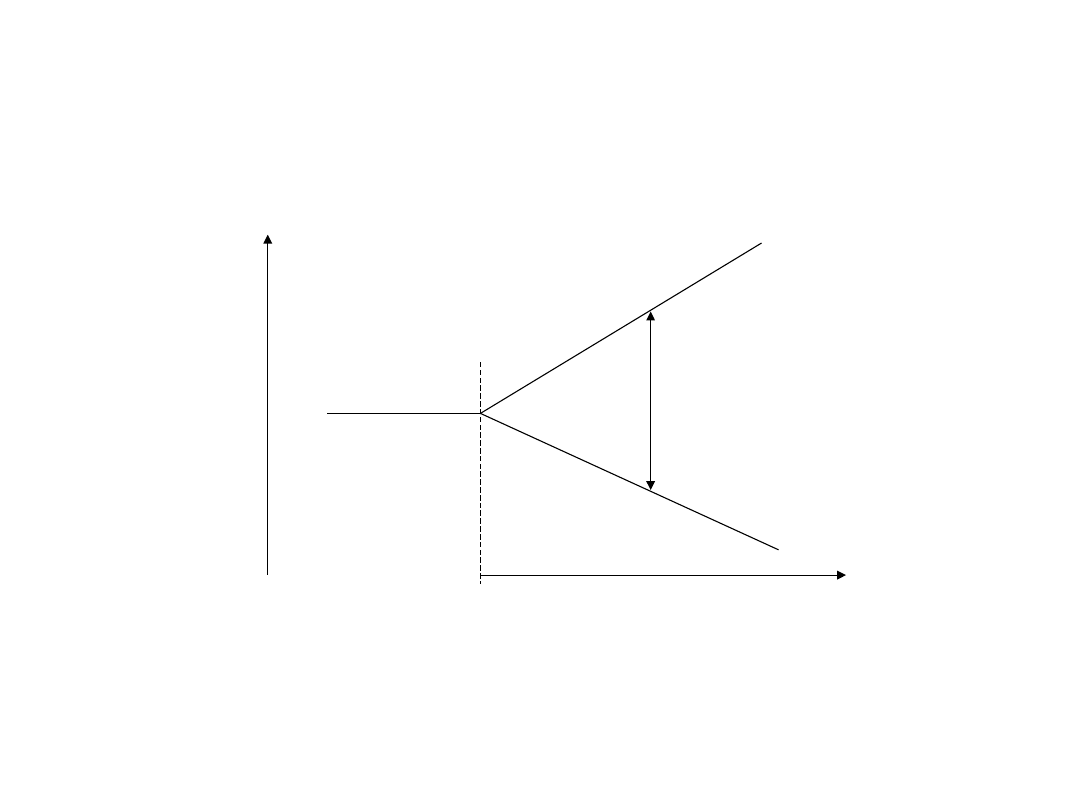
JĄDRO ATOMOWE W POLU

MAGNETYCZNYM

E

B

0

= 0

B

0

> 0

E

m

I

= -

½

m

I

= ½

(degeneracja)

(zniesienie
degeneracji)

Rezonans

• Absorpcja energii niesionej przez promieniowanie

elektromagnetyczne może zaistnieć dzięki energetycznemu
zróżnicowaniu jądrowych stanów spinowych wywołanemu
przez zewnętrzne pole magnetyczne.

• Promieniowanie elektromagnetyczne o częstości  niesie

energię kwantu h.

• Aby nastąpiła absorpcja musi być spełniony warunek E =

h

• W przypadku jądra atomowego w polu magnetycznym B

0

:

h

0

= 2μ

z

B

0

=



ħB

0

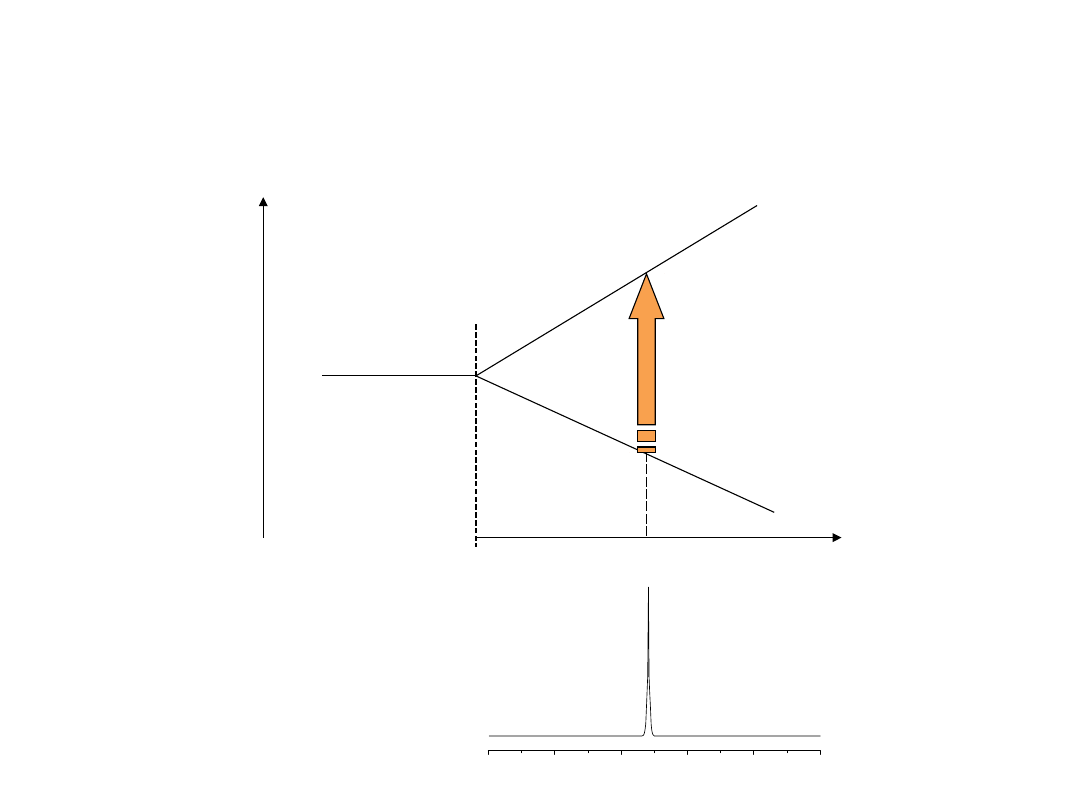
Warunek rezonansu

E

B

0

m

I

= -

½

m

I

= ½

E =

ħB

0

=

h

0

h

0

0

1

2

3

4

5

B

Niektóre jądra w polu magnetycznym ustawiają się zarówno
równolegle do linii pola (co nas nie dziwi - bo tak właśnie zachowuje się
igła magnetyczna w kompasie) jak i antyrównolegle. Oba ustawienia
różnią się tylko nieznacznie energią i dlatego tylko niewiele więcej
jąder jest ustawionych równolegle, niż antyrównolegle do linii pola
magnetycznego.

Stosunek ilości jąder ustawionych równolegle do ustawionych
antyrownolegle do linii pola zależy od rodzaju jądra (bardzo), natężenia
pola magnetycznego (tez bardzo) i od temperatury (niewiele).

W temperaturze 25

o

C i w polu o indukcji jednej tesli (1T) na każde 20

000 000 jąder wodoru ustawionych równolegle do linii pola przypadają
19 999 932 jąder ustawionych antyrownolegle.

To wyjaśnia dlaczego doświadczalnego potwierdzenia zjawiska
rezonansu dokonano dopiero w 25 lat po jego teoretycznym odkryciu -
po prostu potrzeba do tego aparatury o niewyobrażalnej wręcz
czułości.

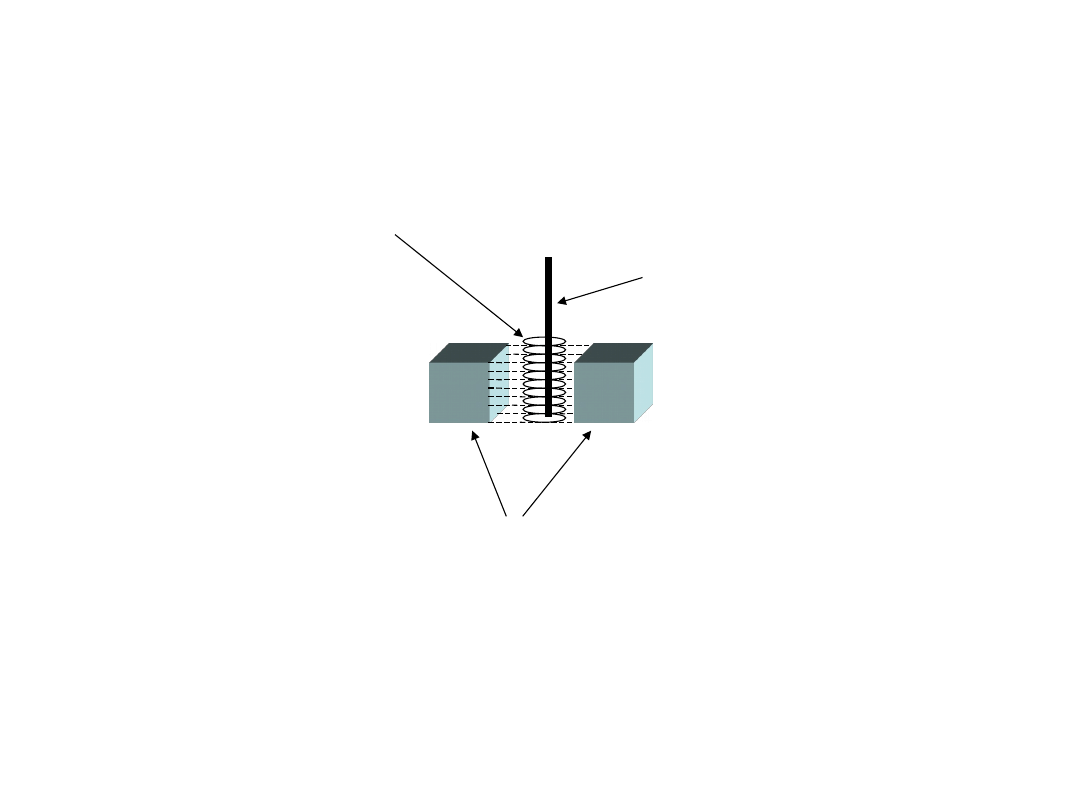
Schemat ideowy spektrometru

NMR

N

S

probówka

pomiarowa

układ cewek nadawczo-
odbiorczych

magnes

B

o



0

Choć do warunku rezonansu można dochodzić zarówno przez zmianę
częstości dla próbki w stałym polu magnetycznym jak i przez zmianę pola
przy stałej częstości, to we współczesnych spektrometrach stosowany jest
praktycznie tylko pierwszy z tych sposobów.

Do 1966r. spektrometry NMR rejestrowały widma tzw. metodą

metodą

fali ciągłej

fali ciągłej

. W stabilnym polu magnetycznym generowanym

przez dwa magnesy sztabkowe umieszczano próbkę.
Następnie generowano promieniowanie elektromagnetyczne o
liniowo zmieniającej się częstotliwości i obserwowano kiedy
zajdzie absorpcja.

Metoda ta miała jednak wiele wad.

Po pierwsze, średni czas rejestracji podstawowego widma
protonowego (jest to najprostszy do obserwacji i najczęściej
stosowany rezonans) wynosił nawet pół godziny lub dłużej. Po
drugie metody tej nie dało się zastosować do innych jąder
dających słabszy sygnał, bądź o mniejszym
rozpowszechnieniu w przyrodzie.

Pierwszym krokiem do zwiększenia czułości metody było
generowanie silniejszego pola magnetycznego - zastosowano
elektromagnesy. Zwiększenie pola powoduje, że różnica liczby
spinów ustawionych równolegle do pola i antyrównolegle
zwiększa się (jest to praktycznie zależność liniowa), a wiec
liczba jąder dających sygnał również zwiększa się. Metoda ta
jednak była mało skuteczna. Mocy magnesów nie dało się
zwiększyć aż tak znacznie, aby była możliwa obserwacja jąder
mało czułych izotopów. Węgiel 13C tak potrzebny chemikom
organikom był ciągle poza zasięgiem NMR-u.

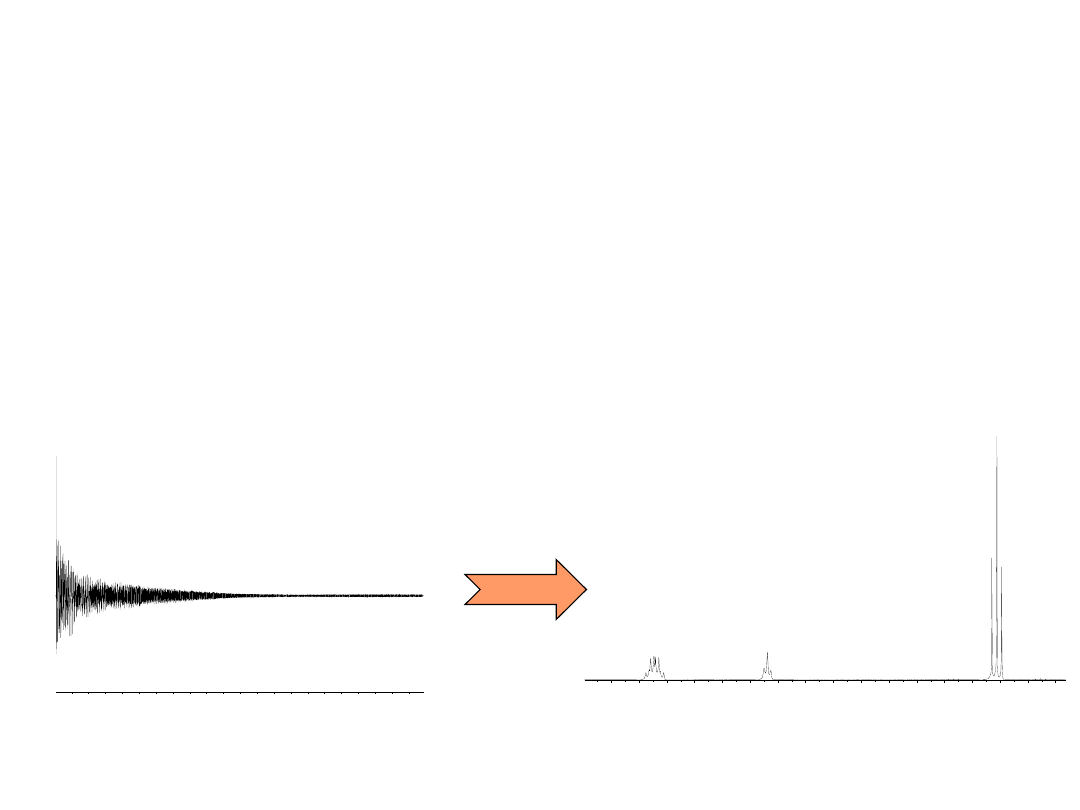
Prawdziwy przełom spowodowało odkrycie profesora Ernsta w
1966r. Wpadł on na pomysł tzw. impulsowej metody rejestracji
widm. Polega ona na tym, że próbkę umieszczoną w
jednorodnym polu magnetycznym naświetlamy na raz całym
zakresem częstotliwości, a potem w ciągu kilku sekund
zbieramy widmo. Widmo takie nie jest niestety dla nas
zrozumiale w postaci "surowej". Zebrane informacje musimy
poddać pewnym matematycznym przekształceniom (zwanym
transformacja Fouriera) aby otrzymać widmo takie jak przy
rejestracji metodą fali ciągłej.

(sec)

0.10

0.20

0.30

0.40

0.50

0.60

0.70

0.80

0.90

1.00

(ppm)

0.8

1.0

1.2

1.4

1.6

1.8

2.0

2.2

2.4

2.6

2.8

3.0

3.2

3.4

3.6

3.8

4.0

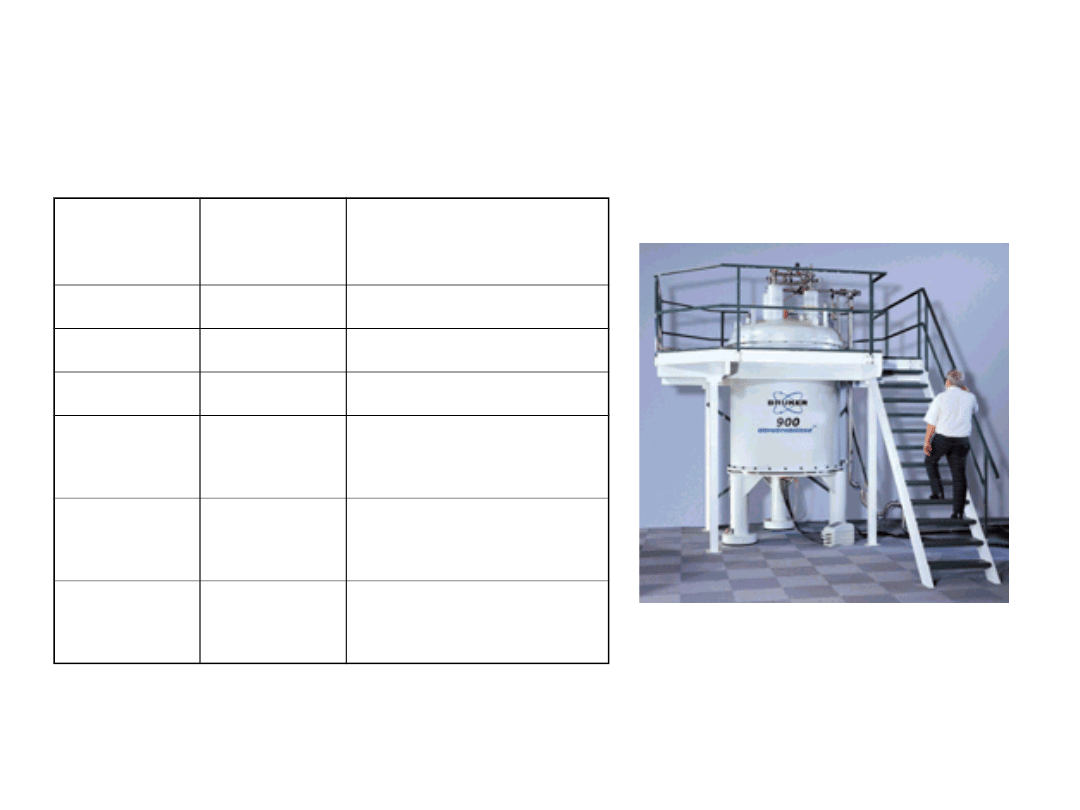
Kolejnym krokiem w NMR było wynalezienie magnesów
nadprzewodzących, pozwalających generować pola
magnetyczne nawet dziesięciokrotnie silniejsze niż pola
pochodzące z elektromagnesów. Sam w sobie taki magnes jest
cudem techniki. Solenoid z kilku kilometrów drutu miedzianego z
wtopionymi nadprzewodzącymi żyłkami zanurzony w ciekłym
helu (temp. wrzenia -269

o

C) zamknięty w płaszczu próżniowym

otoczonym ciekłym azotem i następnym płaszczem próżniowym
generuje w całej objętości próbki prawie idealnie jednorodne
pole o natężeniu ponad 20T. Magnes taki wygląda jak beczka o
wysokości 2m, średnicy około 120cm i wadze dochodzącej do
600kg.

Drugim co do ważności elementem konstrukcyjnym tego
urządzenia jest tzw. sonda. Jest to element umieszczany w
środku magnesu i służący do generowania fali
elektromagnetycznej oraz do "zbierania" sygnału.

Stosowane magnesy

B

o

[T]



o

(H)

[MHz]

typ

1.4

60

elektromagnes

2.3

100

elektromagnes

7

300

nadprzewodzący

11

500

nadprzewodzący

14

600

nadprzewodzący

21

900

nadprzewodzący

Warunek stosowalności metody

• Aby nastąpiło zróżnicowanie energetyczne

stanów spinowych musi być tych stanów
więcej niż jeden.

• Zróżnicowanie stanów jest możliwe tylko

dla spinu jądrowego różnego od zera, czyli
dla jąder atomowych tylko tych nuklidów,
dla których spinowa liczba kwantowa

I > 0

Jądra atomowe o niezerowym spinie
nazywa się

jądrami magnetycznymi.

Skład jądra atomowego a spin

jądrowy

• Dla parzystych Z i A

I

= 0

• Dla nieparzystej Z i parzystej A

I

jest liczbą

całkowitą

• Dla nieparzystych Z i A oraz parzystej Z i

nieparzystej A

I

jest całkowitą wielokrotnością ½

E

A

Z

Nuklid

Naturalna
zawartość [%]

Spin I
[ħ]

Częstość
rezonansowa 

o

[MHz]

przy indukcji 2.35 T

Względna
czułość

Elektryczny moment
kwadrupolowy [e 10

-

26

cm

2

]

1

H

99.98

1/2

100

1.00

-

2

H

0.016

1

15.35

0.01

0.277

10

B

18.82

3

9.305

0.02

11.1

11

B

81.17

3/2

31.17

0.165

3.55

13

C

1.108

1/2

25.19

0.016

-

14

N

99.63

1

7.22

0.001

2.0

15

N

0.37

1/2

10.13

0.001

-

17

O

0.037

5/2

13.56

0.03

–0.4

19

F

100

1/2

94.08

0.83

-

27

Al

100

5/2

26.06

0.21

14.9

29

Si

4.67

1/2

19.86

0.08

-

31

P

100

1/2

40.48

0.07

-

33

S

0.74

3/2

7.67

0.0023

–6.4

35

Cl

75.5

3/2

9.80

0.0047

–8.0

37

Cl

24.5

3/2

8.15

0.0027

–6.2

117

Sn

7.62

1/2

35.62

0.045

-

119

Sn

8.68

1/2

37.27

0.052

-

195

Pt

33.7

1/2

21.50

0.01

-

199

Hg

16.9

1/2

17.88

0.0057

-

203

Tl

29.5

1/2

57.14

0.19

-

205

Tl

70.5

1/2

57.71

0.19

-

207

Pb

21.11

1/2

20.90

0.01

-

Charakter metody

• NMR to metoda:

– Spektroskopowa
– Rezonansowa

– Analityczna

Z warunku rezonansu można wywieść, że jądra
atomowe

różnych

nuklidów o niezerowym spinie

będą absorbować kwant energii promieniowania o
danej częstości



0

przy

różnej

wartości indukcji

magnetycznej

B

0

oraz jądra atomowe

różnych

nuklidów o niezerowym spinie przy danej wartości
indukcji magnetycznej

B

0

będą absorbować kwanty

energii promieniowania o

różnej

częstości



0

(tzw.

częstości podstawowej jądra

).

E =



ħB

0

=

h

0

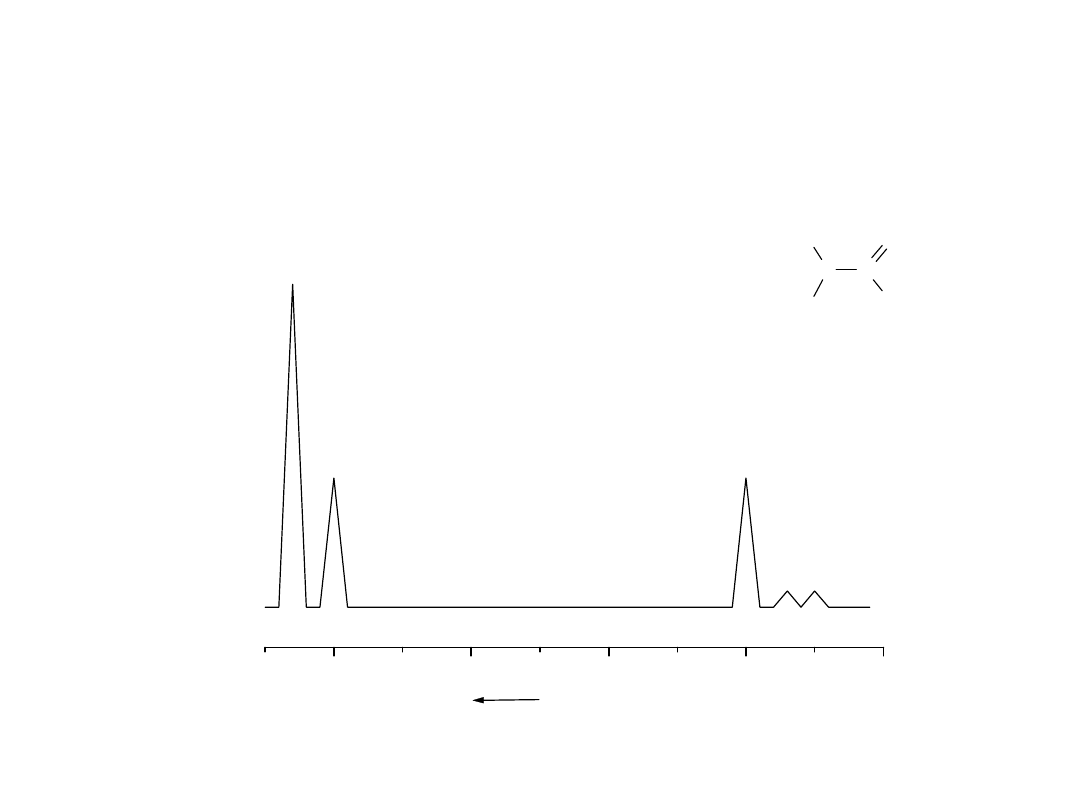
(Bardzo) Hipotetyczne widmo

multijądrowe

40

30

20

10

0

B

o

= 1 T

15

N

17

O

13

C

19

F

1

H



[MHz]

N C

O

CF

3

H

3

C

H

3

C

Spektroskopia NMR wysokiej

rozdzielczości

• Eksperymenty NMR wykonuje się dla danego typu jądra

(np.

1

H,

13

C,

31

P)

• Warunek rezonansu jest dla danego typu jądra spełniony

przy częstościach w pobliżu



0

,

a nie dokładnie przy tej

wartości

• Dla jądra danego typu rezonans może następować przy

różnych częstościach



zależnie od związku, w którym się

to jądro znajduje

• W danym związku chemicznym częstości rezonansowe

jąder tego samego typu mogą być różne (jądra mogą być

magnetycznie nierównoważne

)

Źródło zróżnicowania częstości

rezonansowych jąder danego

typu

• Jądro atomowe umieszczone w związku

chemicznym jest fragmentem złożonego

układu innych jąder i

chmur elektronowych

,

które znajdują się pomiędzy danym jądrem i

zewnętrznym polem magnetycznym.

• Zewnętrzne pole magnetyczne B

0

indukuje w

chmurze elektronowej prąd kołowy, z którym

związane jest pole magnetyczne skierowane

przeciwnie

do B

0

. Lokalne natężenie pola

magnetycznego wokół jądra jest zatem

zmniejszone o wartość proporcjonalną do B

0

.

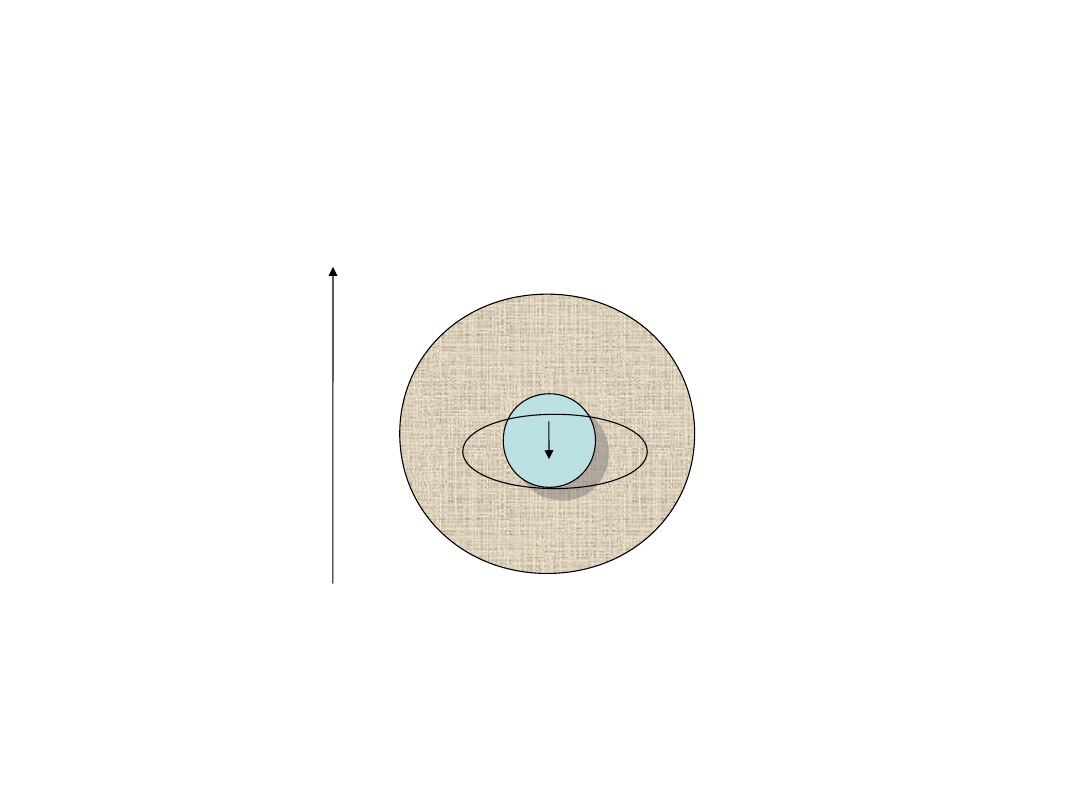
Elektrony wokół jądra

modyfikują pole magnetyczne

B

0

B

0

B

lok

= B

0

(1 - )

 - stała ekranowania (przesłaniania)

Warunek rezonansu

• W wyniku przesłaniania jądra do spełnienia

warunku rezonansu konieczne jest albo większe
natężenie pola (przy danej częstości) albo mniejsza
częstotliwość (przy danym polu) niż by to wynikało
z warunku rezonansu obliczonego dla B

o

i 

o

danego

jądra.

• Modyfikacja pola magnetycznego w punkcie jądra

zależy od wielkości

gęstości elektronowej

w

otoczeniu jądra czyli w danym atomie cząsteczki.

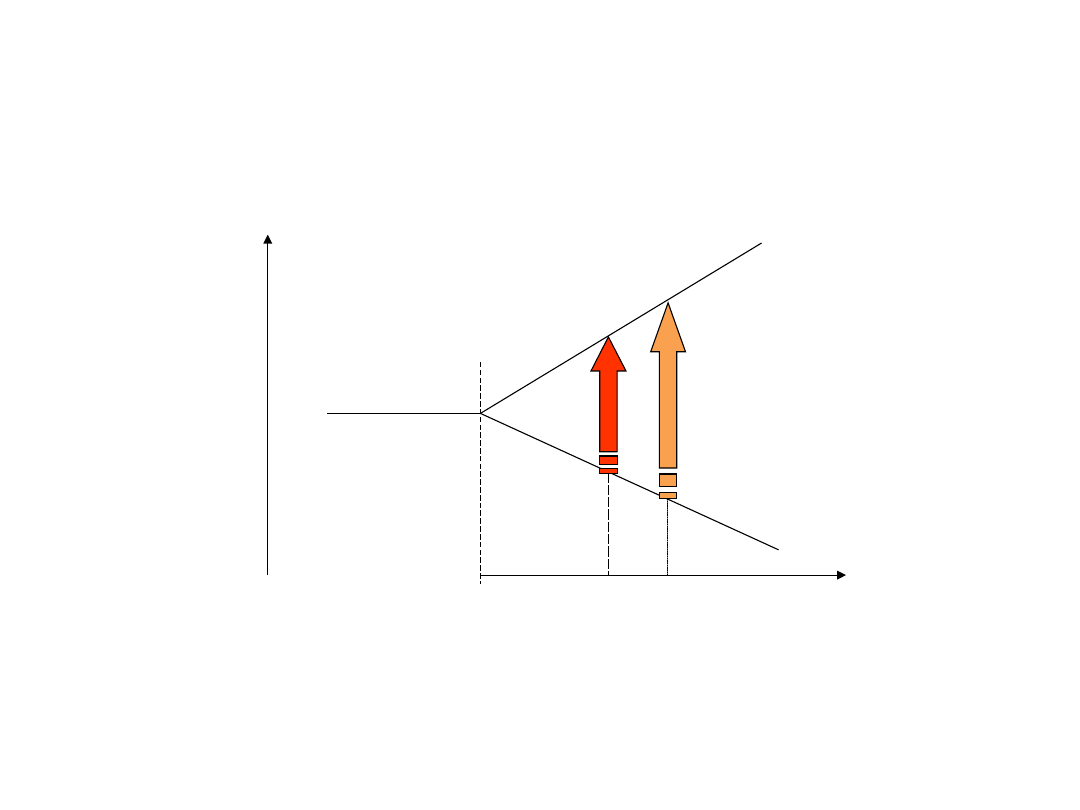
Warunek rezonansu

- przesunięcie chemiczne -

E

B

lok

B

0

m

I

= -

½

m

I

= ½

E

1

=

ħB

0

= h

0

E

2

=

ħB

lok

= h

h

0

h

Przesunięcie chemiczne

• Różnica pomiędzy częstością

rezonansową jądra w konkretnym
otoczeniu a częstością podstawową 

o

dla jądra tego typu nazywa się

przesunięciem chemicznym.

• Zakres przesunięć chemicznych dla

jąder danego typu jest rzędu 0.1-10 kHz

Widmo NMR

•Wykres zależności intensywności absorpcji od
częstości rezonansowej nazywa się widmem
NMR.

•Dla substancji zawierającej różne jądra
magnetyczne można otrzymać różne widma
NMR zależnie od rodzaju pobudzanego jądra,
czyli zastosowanej częstości podstawowej 

o

przy danym natężeniu pola magnetycznego B

0

np.:

B

0

= 7 T 

o

= 300 MHz dla

1

H

i 75 MHz dla

13

C

B

0

= 11 T 

o

= 500 MHz dla

1

H

i 126 MHz dla

13

C

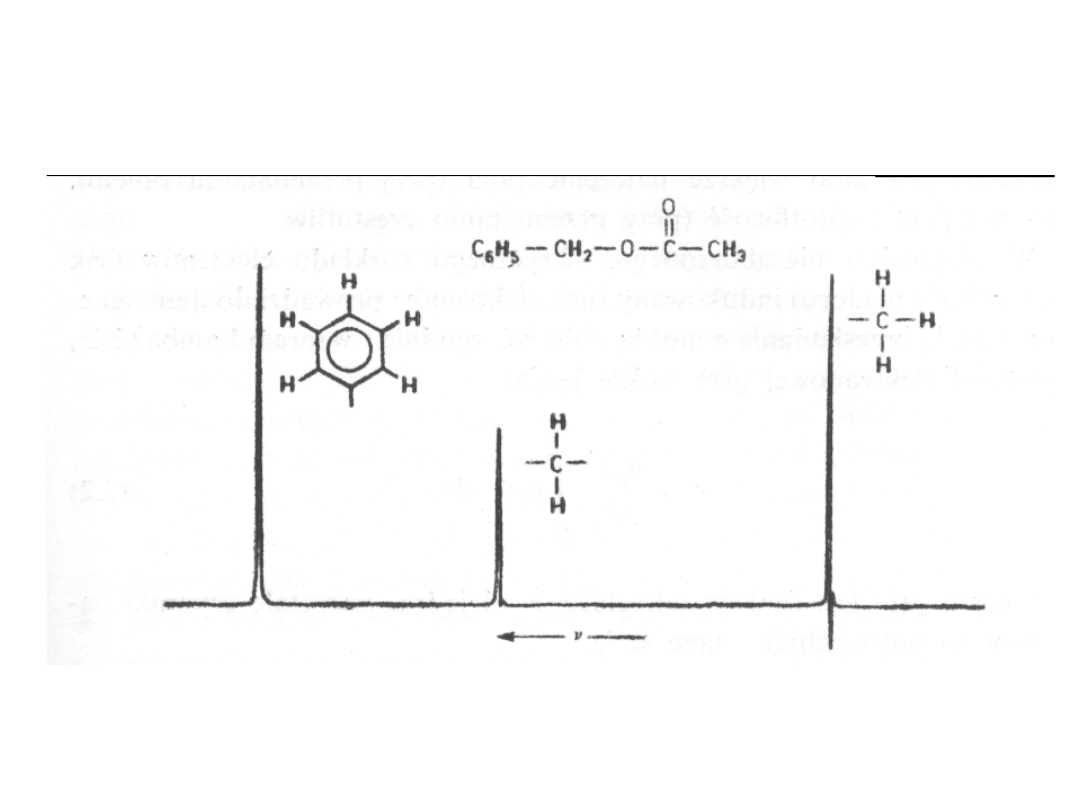
Typowe widmo

1

H NMR

116 Hz

193 Hz

965 Hz

300 Hz

500 Hz

2500 Hz

433 Hz

721 Hz

3605 Hz

1.4 T

1.4 T

2.3 T

2.3 T

11.1 T

11.1 T

B

B

0

0

Przesunięcie chemiczne

Ze względu na różne wartości stosowanej indukcji

magnetycznej B w różnych spektrometrach oraz

trudności w precyzyjnym wyznaczaniu częstości

rezonansowych skala przesunięć chemicznych

określana jest według częstości rezonansowej wzorca i

normalizowana do wartości bezwymiarowej



:

„Jednostką” tak zdefiniowanej skali przesunięć jest

ppm

(części na milion –

p

arts

p

er

m

illion)

0

wz

ν

ν

ν

δ





10

Hz

Hz

6

-





8

2

10

10

δ]

[

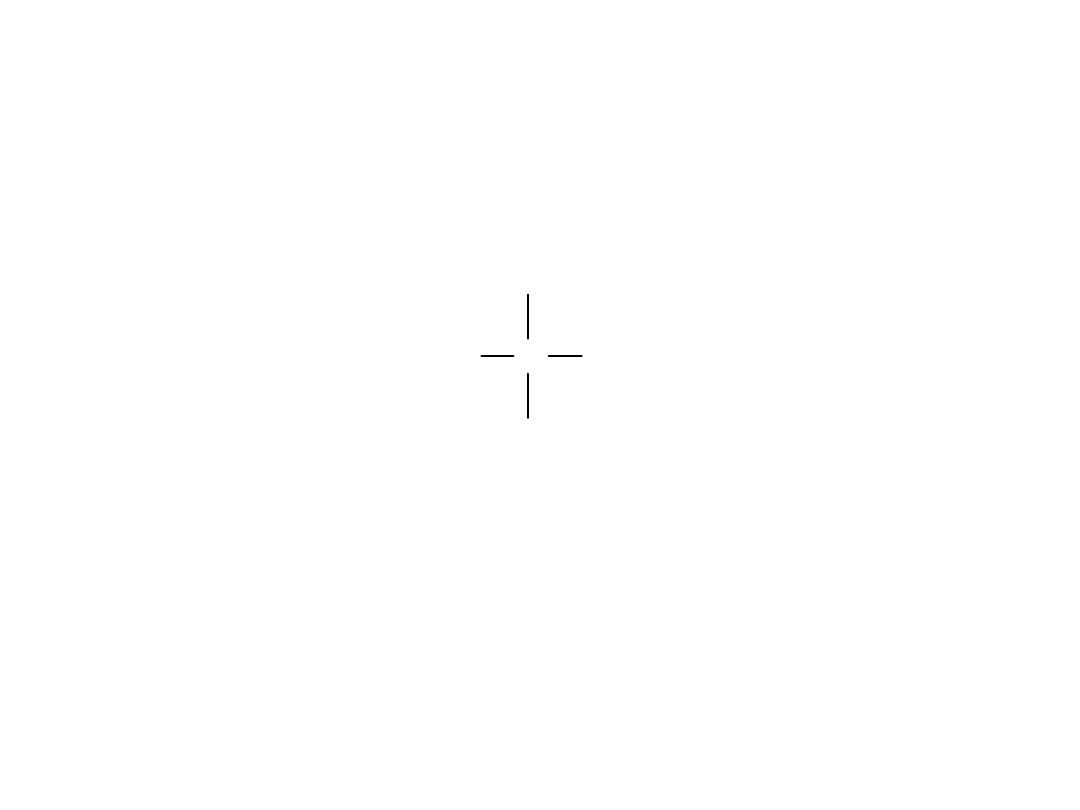
Wzorzec przesunięcia

chemicznego dla

1

H i

13

C

CH

3

Si

CH

3

CH

3

H

3

C

Tetrametylosilan

TMS

 ≡ 0

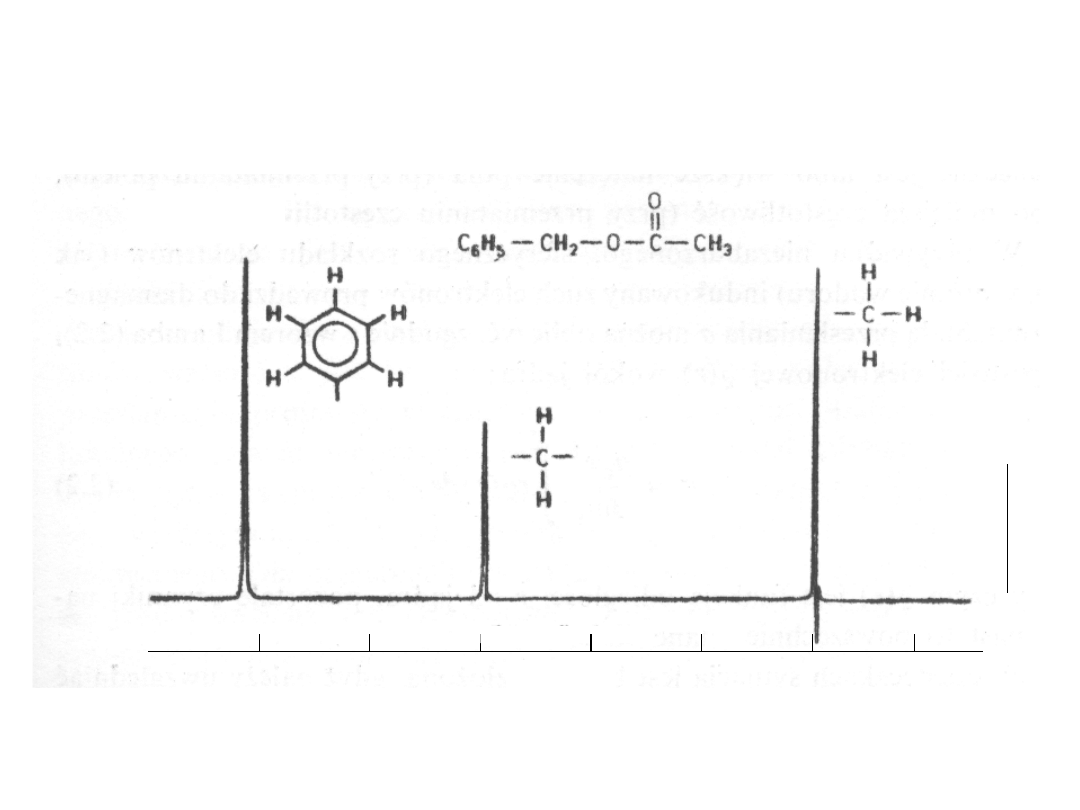
Typowe widmo

1

H NMR

7 6 5 4 3 2
1



Si(CH

3

)

4

(TMS)

 = 0

Wartości przesunięć chemicznych



dla danego związku

nie zależą

od

natężenia zastosowanego pola magnetycznego B

0

Przesunięcie chemiczne

• Wartość przesunięcia chemicznego



jest bardzo

silnie zdeterminowana przez otoczenie i

jednoznacznie określa pozycję jądra w związku.

• Wartość przesunięcia chemicznego jądra w danym

otoczeniu chemicznym zawiera się w granicach

charakterystycznych dla tego otoczenia.

• Jądra atomowe danego typu, należące do danej

grupy chemicznej (np. węglowodorowej,

karbonylowej, hydroksylowej, karboksylowej),

rezonują w typowych dla tych grup zakresach

przesunięć chemicznych, więc ich przesunięcia

chemiczne



w różnych związkach będą podobne i

mogą stanowić kryterium analityczne.

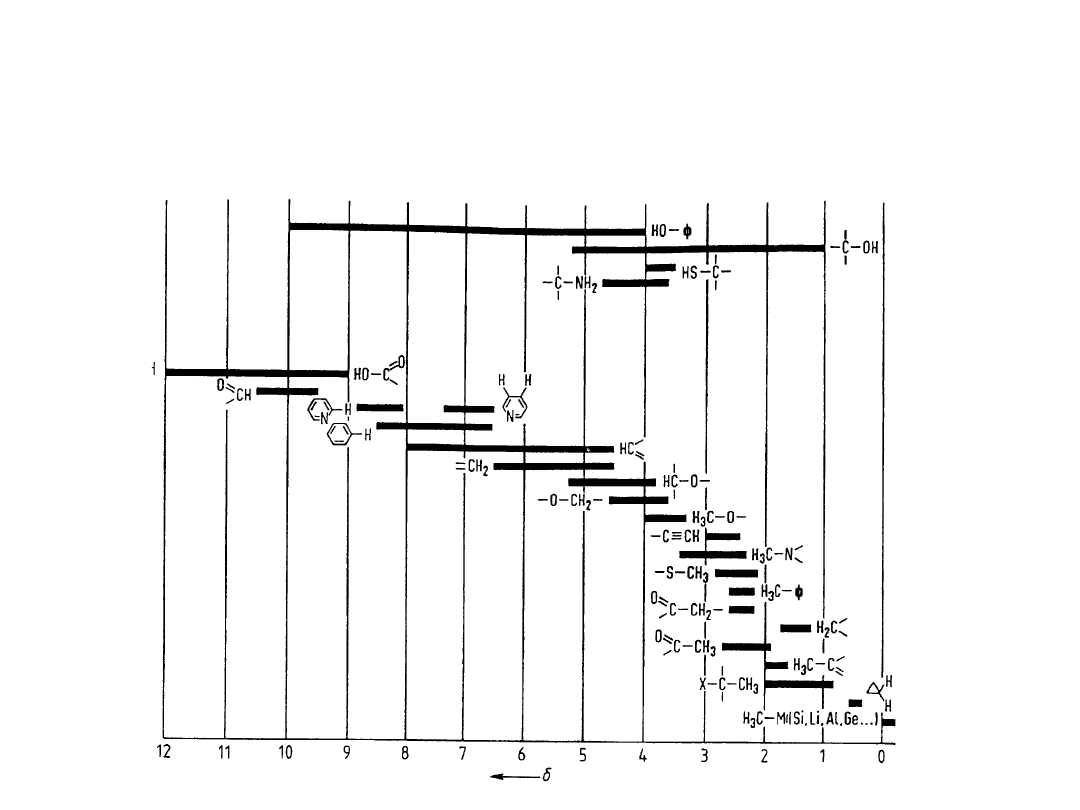
Zakresy przesunięć

chemicznych

1

H dla różnych

grup organicznych

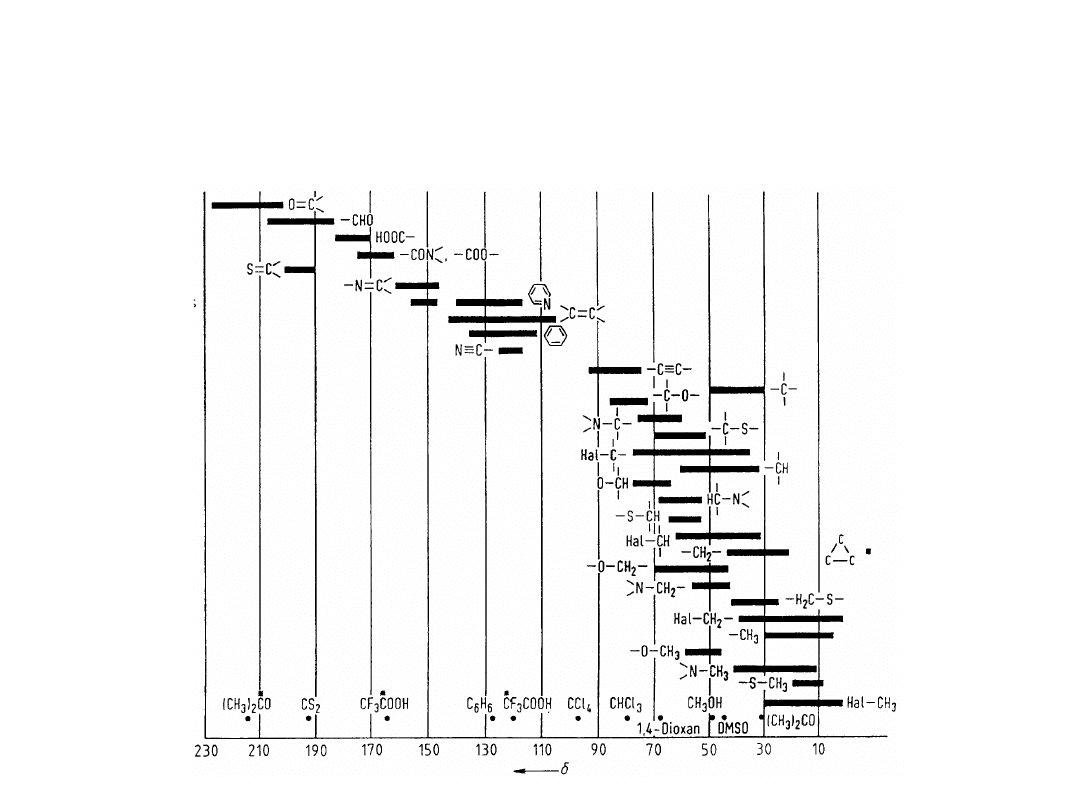
Zakresy przesunięć

chemicznych

13

C dla różnych

grup organicznych

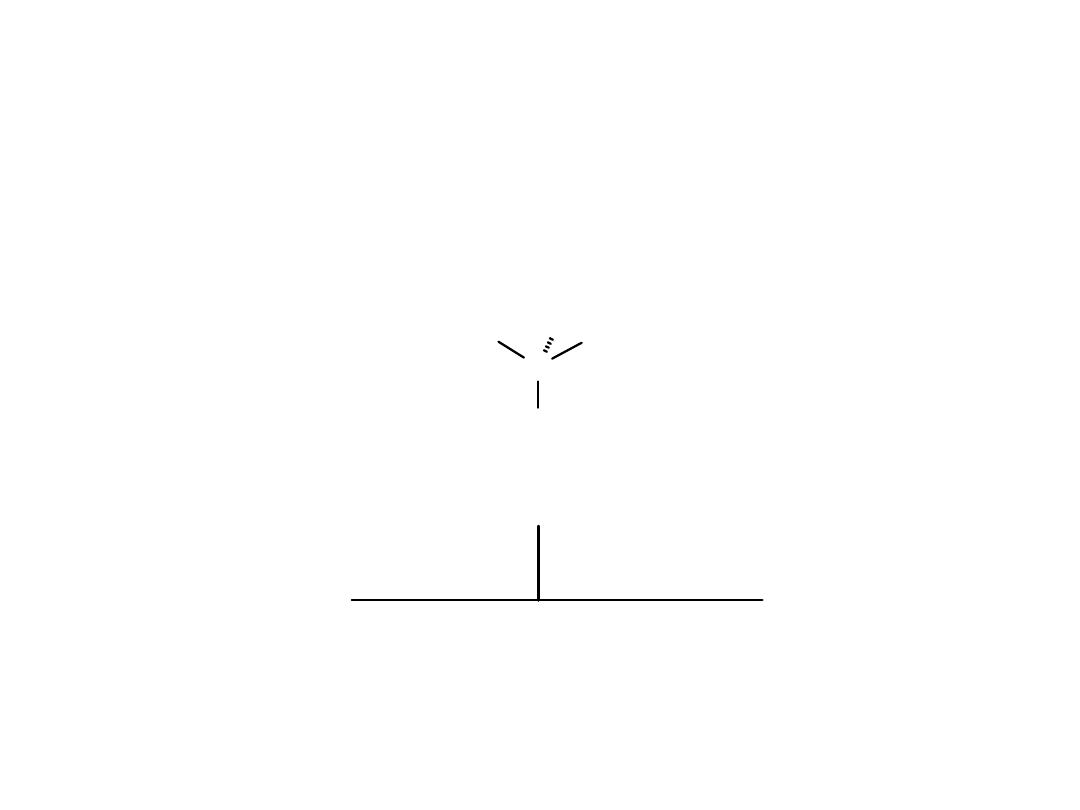
Przesunięcie chemiczne

protony w grupie metylowej CH

3

są zawsze równocenne

C

H

H

H

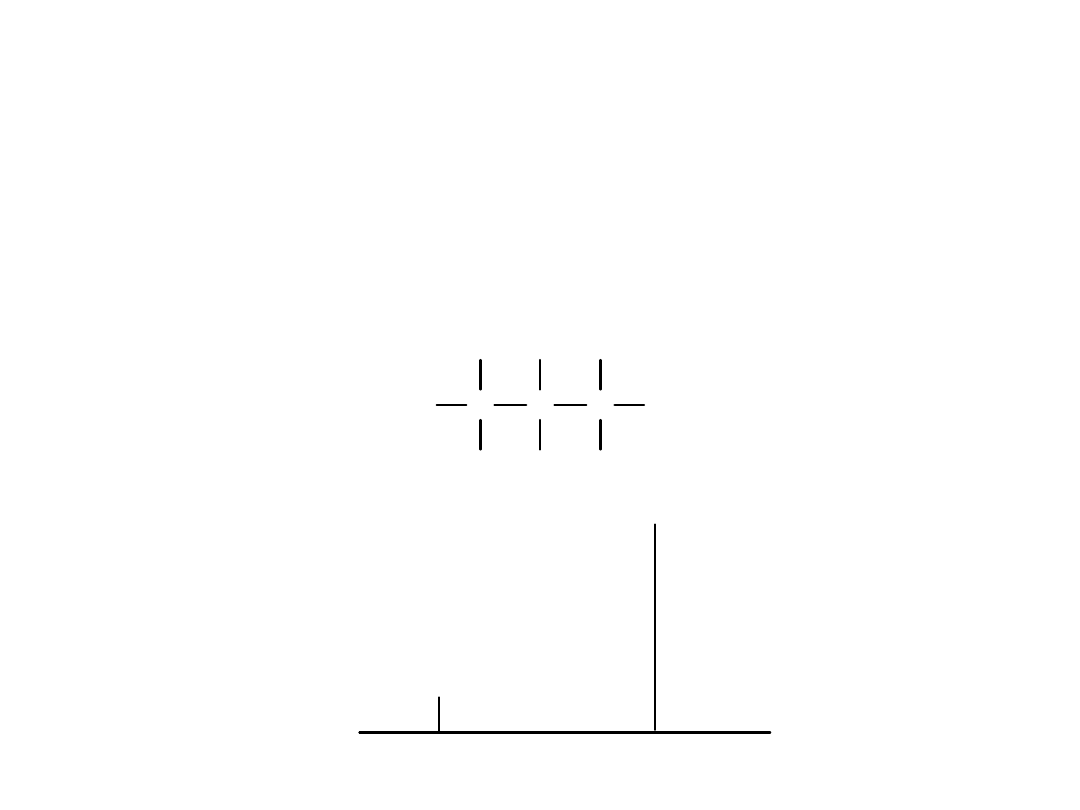
Przesunięcie chemiczne

protony i węgle w różnych grupach CH

3

połączonych z tym samym

atomem są równocenne ...

C C C

Cl

H

H

H

H

H

H

H

CH

3

CHCl

Przesunięcie chemiczne

protony i węgle w różnych grupach CH

3

połączonych z tym samym

atomem są równocenne, o ile są związane elementem symetrii

C C

Cl

H

CH

3

CH

3

CH

3

(trans)

CH

3

(cis)

Zahamowana

rotacja

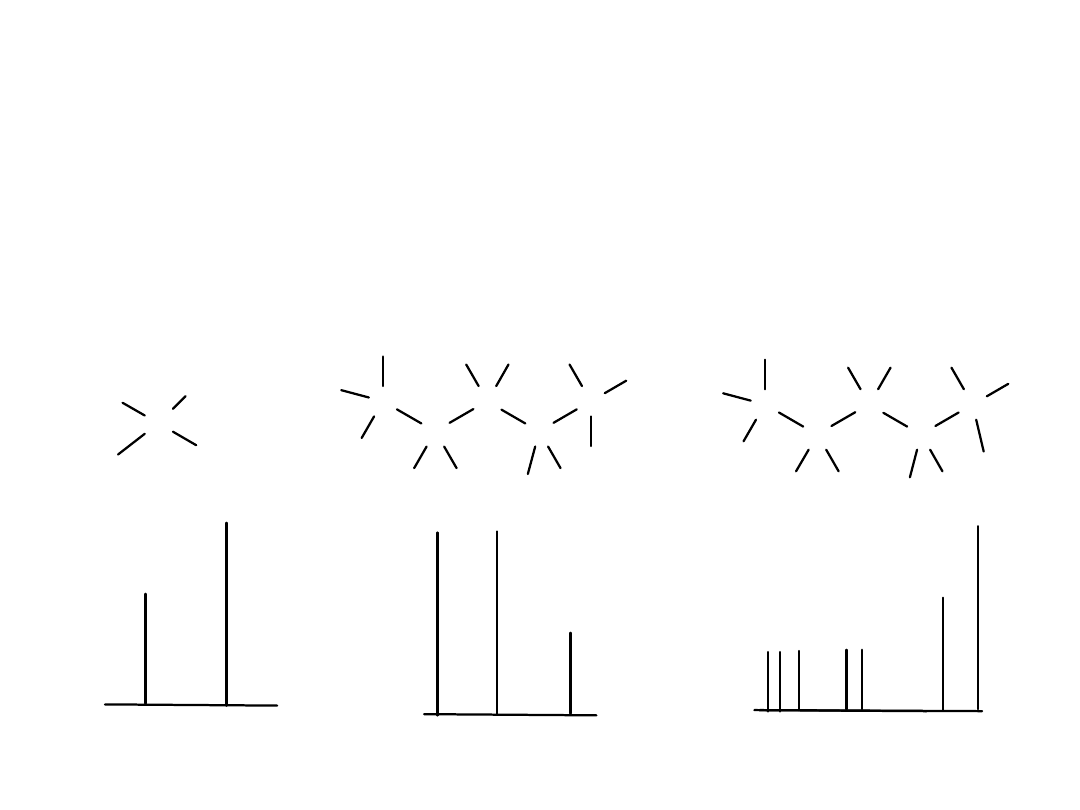
Przesunięcie chemiczne

protony grupy metylenowej -CH

2

- są równocenne, o ile nie

sąsiadują z centrum asymetrii (centrum chiralnym) …

Cl

C

CH

3

H

H

CClH

2

CH

3

CH

2

równocenne

1,5

2,4

3

C

C

C

C

C

Cl

Cl

H

H

H

H

H H H H

H H

1

2

3

4

5

C

C

C

C

C

Cl

H

H

H

H

H

H Cl H H

H H

1

2

3

4

5

1a,b 2 3a,b

4

5

CH

2

nierównocenne

2-C – węgiel

asymetryczny

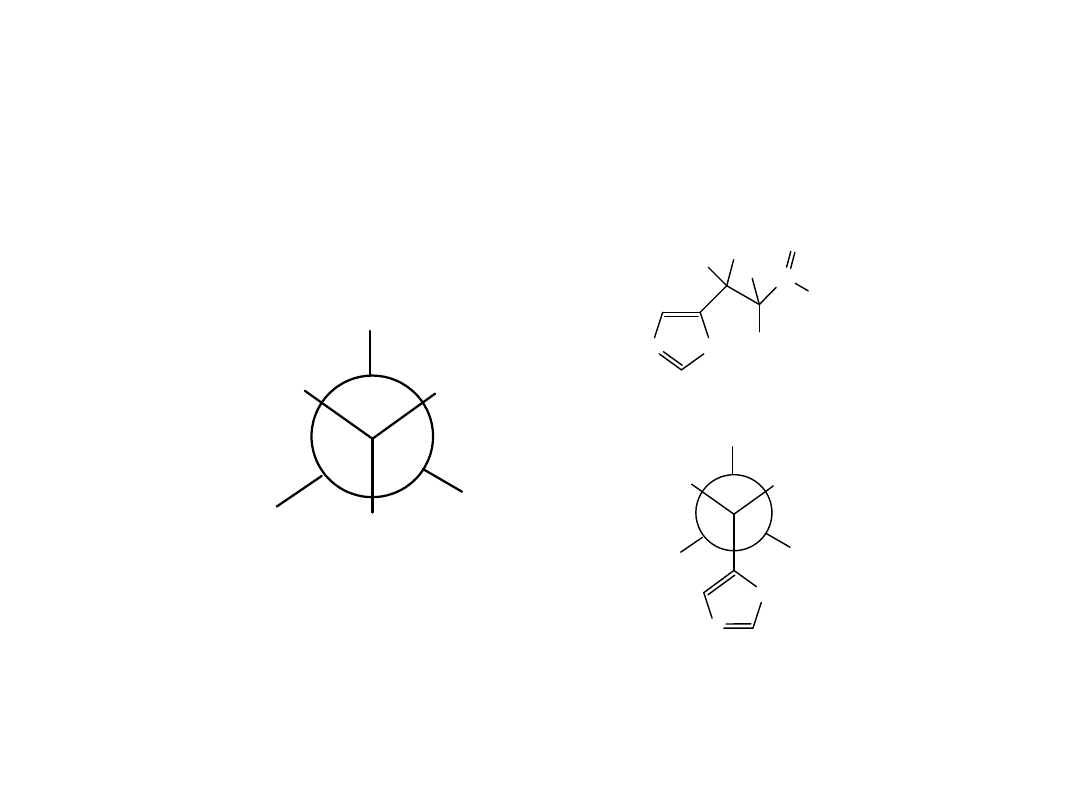
Przesunięcie chemiczne

protony grupy metylenowej -CH

2

- są równocenne, o ile nie

sąsiadują z centrum asymetrii (centrum chiralnym) …

R

1

R

3

R

2

H

a

H

b

X

Protony H

a

i H

b

są

diastereotopowe

, t.j. nie ma elementu

symetrii, który by je łączył; są nierównocenne (magnetycznie

nierównoważne) i wykazują różne przesunięcia chemiczne

C

O

OH

NH

2

H

H H

N

NH

H

a

H

b

N

NH

COOH

NH

2

H

Przesunięcie chemiczne

• Liczba zróżnicowanych sygnałów

rezonansowych (pochodzących od grup
nierównocennych jąder) w widmie NMR
pozwala określić symetrię cząsteczki.

• Analiza liczby sygnałów w widmie NMR

pozwala rozróżnić izomery.

• Widma NMR enancjomerów są identyczne.

Intensywność sygnału

• Intensywność integralna

linii

rezonansowych (pole powierzchni pod

krzywą) jest wprost proporcjonalna do

liczby rezonujących jąder o danym

przesunięciu chemicznym.

• Względna intensywność integralna linii

widmowych pozwala określić liczbę jąder

równoważnych w grupach funkcyjnych

cząsteczki.

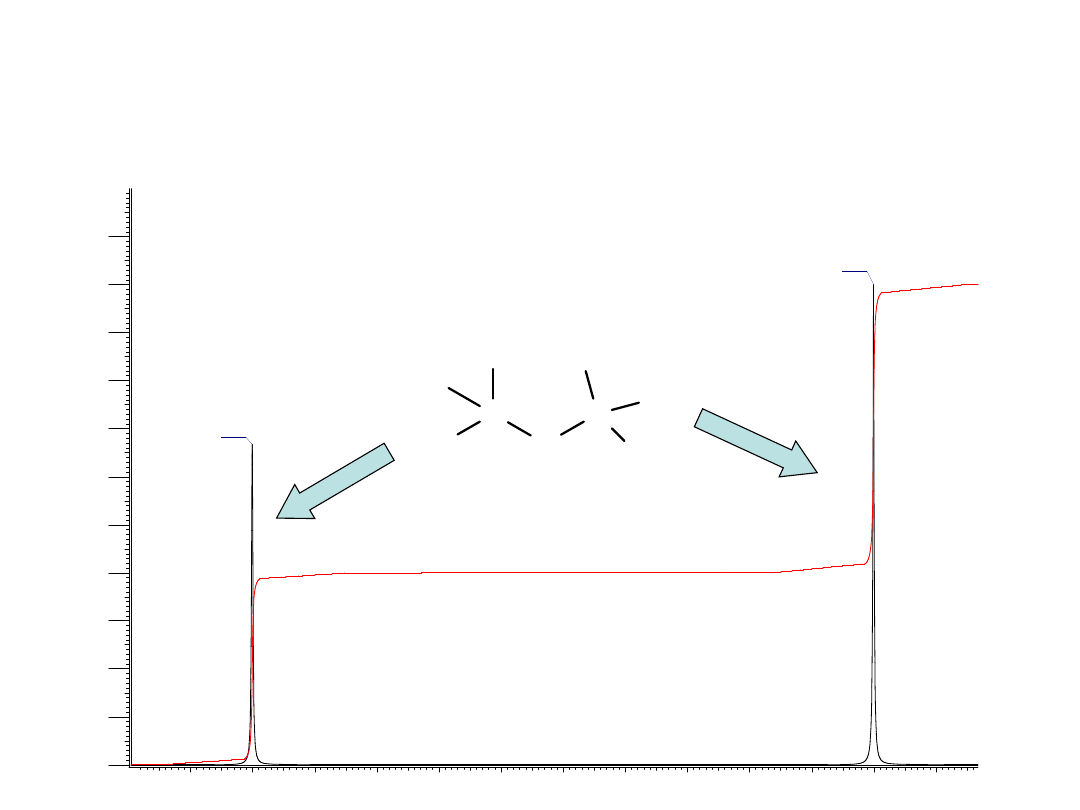
Intensywność sygnału

4.10

4.00

3.90

3.80

3.70

3.60

3.50

3.40

3.30

3.20

3.10

3.00

2.90

0.0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

4.0

4.5

5.0

5.5

1.91

1.27

C

O

C

H

H

H

H

H

Cl

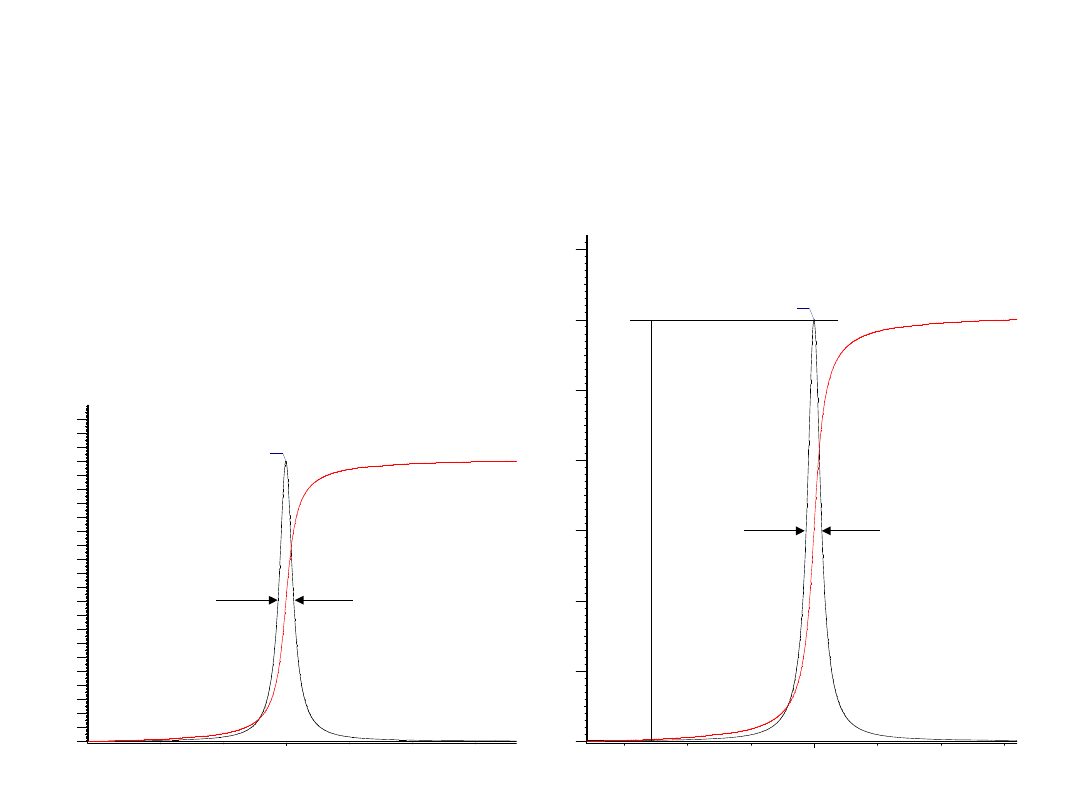
Intensywność sygnału

4.00

0.00

0.10

0.20

0.30

0.40

0.50

0.60

0.70

0.80

0.90

1.00

1.10

1.20

1.30

1.40

1.50

1.60

1.70

1.80

1.90

2.00

2.10

2.20

2.30

2.40

1.27

3.00

0.0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

1.91

CH

2

CH

3

h

max

h

½

Γ

½

Γ

½

S ~ h

max

x

Γ

½

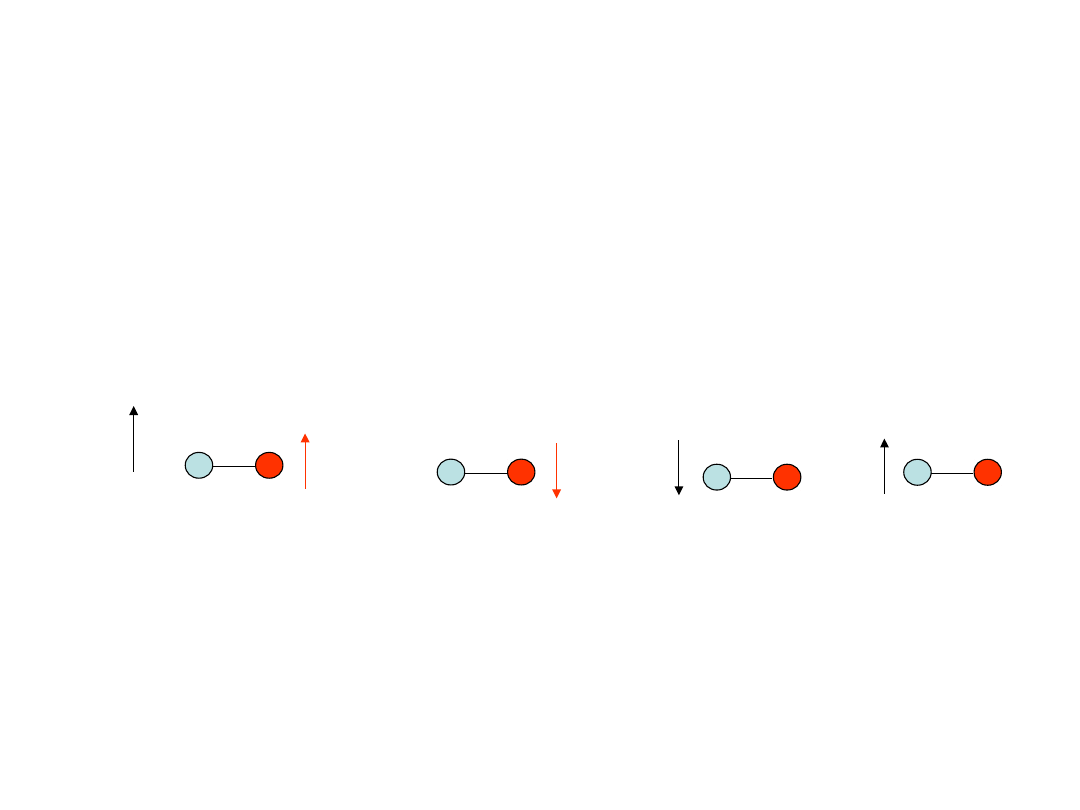
Oddziaływanie międzyjądrowe.

Sprzężenie spin-spin

• W polu magnetycznym stan energetyczny

magnetycznego jądra A zależy od stanu

energetycznego sąsiedniego magnetycznego

jądra X i na odwrót.

• Indukcja magnetyczna w punkcie jądra A

zależy od tego, czy jądro X ma spin skierowany

zgodnie, czy przeciwnie do kierunku B

o

A

X

A

X

A

X

A

X

B

o

Oddziaływanie międzyjądrowe.

Sprzężenie spin-spin

• Załóżmy, że jądro A mające I = ½ oddziałuje z jądrem X I = ½

• Dla jądra A nastąpi modyfikacja stanu podstawowego i

wzbudzonego. Oba te stany ulegną rozszczepieniu na dwa
poziomy, tak że w sumie będą cztery poziomy zamiast dwóch.

• Wielkość rozszczepienia poziomów energetycznych na skutek

oddziaływania międzyjądrowego E

SS

jest proporcjonalna do

wielkości

stałej sprzężenia J

i magnetycznych spinowych liczb

kwantowych oddziałujących jąder:

E

SS

= Jm

1

m

2

h,

np. dla I = ½: E

SS

=  ¼Jh

Oddziaływanie międzyjądrowe.

Sprzężenie spin-spin

• Na skutek bliskości innych jąder

magnetycznych w cząsteczce związku
chemicznego energia jądrowego stanu
spinowego zostaje zmodyfikowana.

• Jądra magnetyczne w atomach połączonych

wiązaniami chemicznymi wzajemnie
rozszczepiają swoje spinowe poziomy
energetyczne.

• Rozszczepieniu ulega zarówno poziom stanu

podstawowego jak i poziom stanu wzbudzonego.

• Wielkość rozszczepienia

nie zależy

od natężenia

pola magnetycznego.

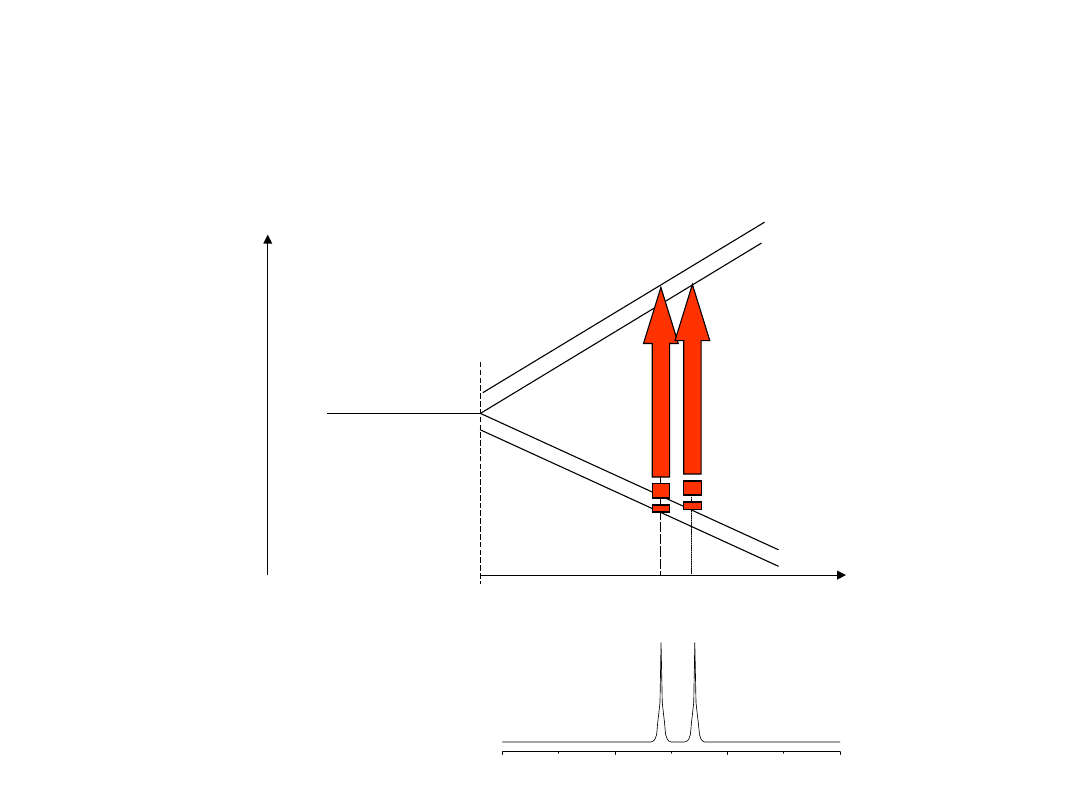
Warunek rezonansu

- sprzężenie spin-spin -

E

B

1

B

2

ħB

1

=

h

ħB

2

=

h

h

2 jądra o spinie

½

1

2

3

4

B

m

I

= ½ ,

-½

m

I

= ½ ,

½

m

I

= -½ , ½

m

I

= -½ , -½

Reguła wyboru:

Dozwolone są przejścia
między stanami, dla których |
m

T

| = 1





i

I

i

m

m

)

(

T

m

T

0

1

0

-1

AX

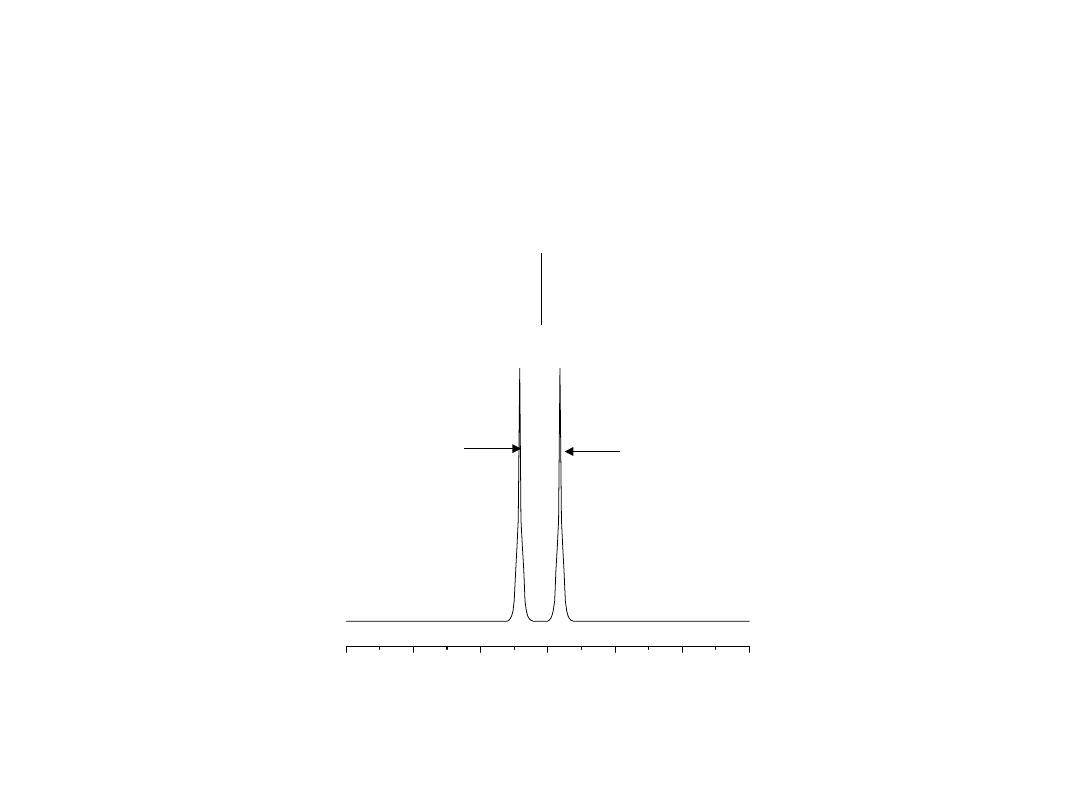
Oddziaływanie międzyjądrowe.

Sprzężenie spin-spin

4.0

3.5

3.0

2.5

2.0

1.5

1.0



[Hz]



1



2

J

AX



A



A

= 

1

– ½ J

AX



A

= 

2

+ ½ J

AX

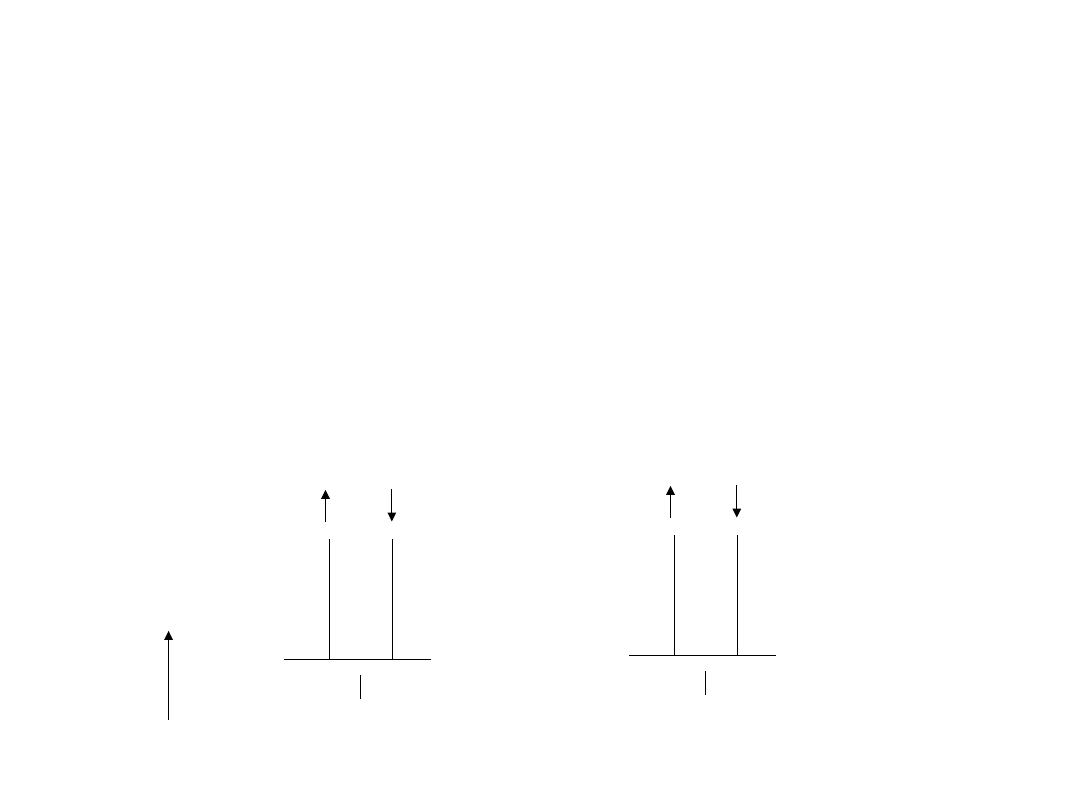
Oddziaływanie międzyjądrowe.

Sprzężenie spin-spin

Układy spinowe

AX np. CH

A

-CH

X

Proton H

A

oddziałuje z protonem H

X

. Spiny jąder H

A

i H

X

mogą

przyjmować różne orientacje względem pola:

J

AX



X

1 : 1

orientacj

e spinów

X

orientacj

e spinów

A

J

AX



A

1 : 1

B

o

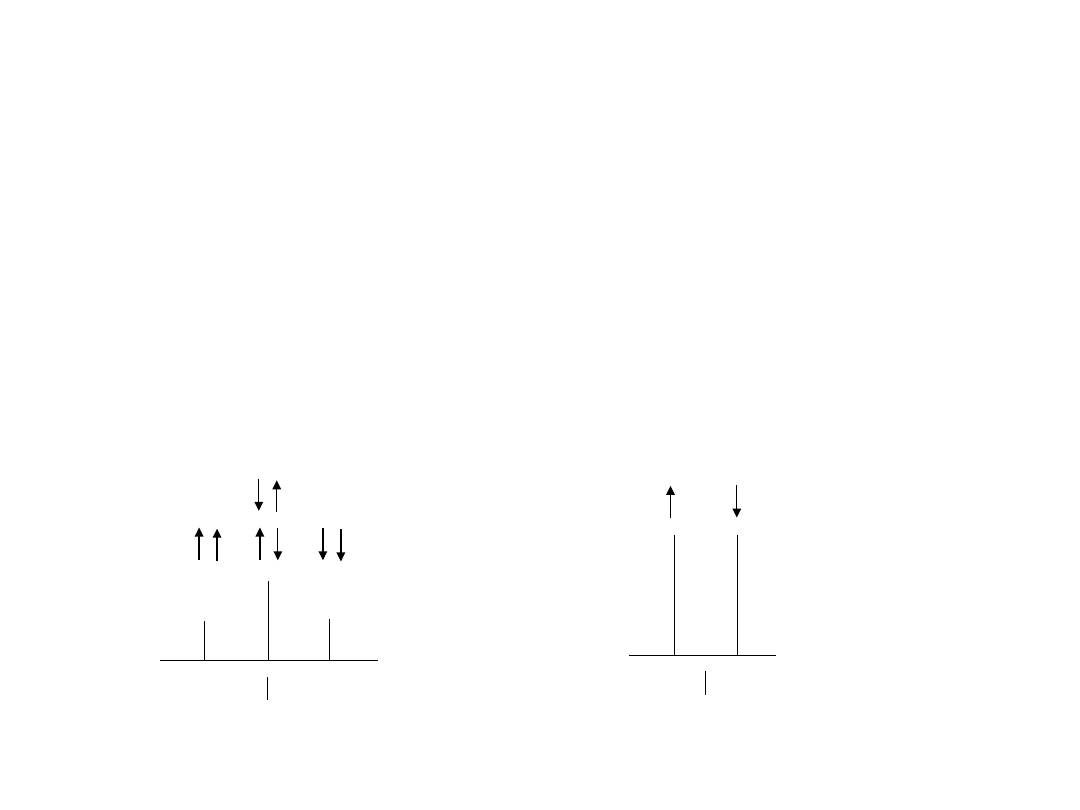
Oddziaływanie międzyjądrowe.

Sprzężenie spin-spin

Układy spinowe

AX

2

np. CH

A

-

CH

2

X

Proton H

A

oddziałuje z dwoma równocennymi protonami H

X

. Spiny

jąder H

X

mogą przyjmować różne orientacje względem pola i

względem siebie:

J

AX

J

AX

J

AX



A



X

1 : 2 :

1

1 : 1

orientacj

e spinów

X

orientacj

e spinów

A

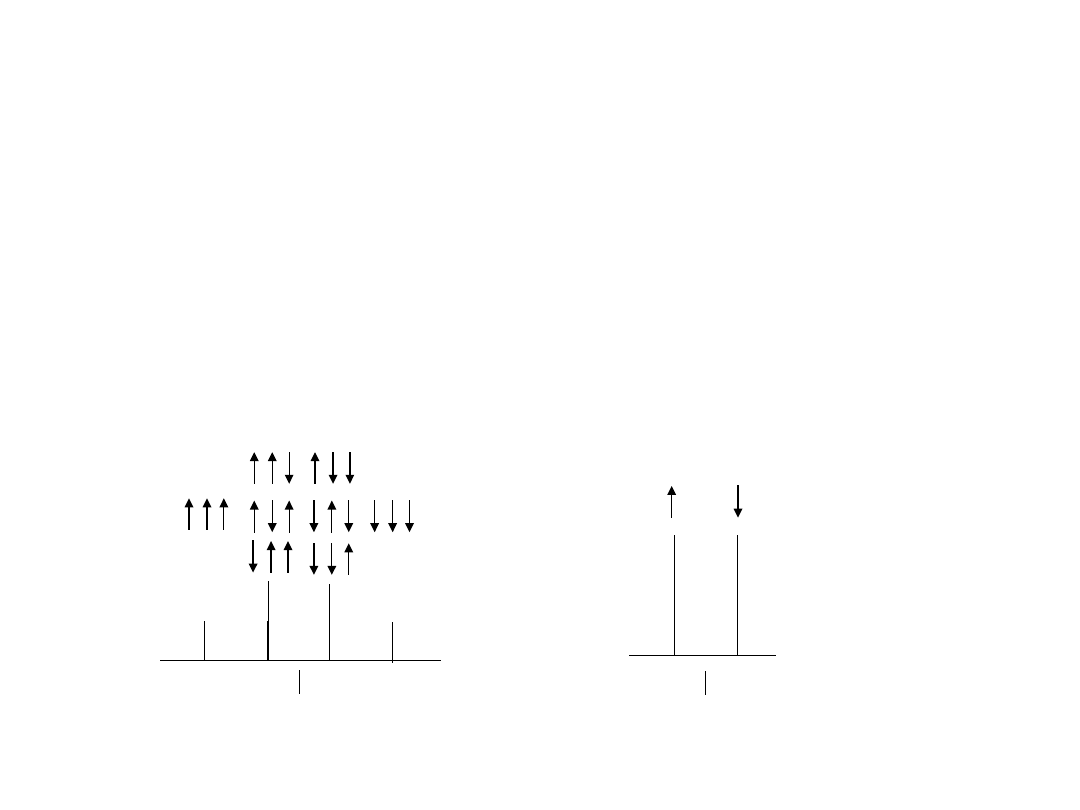
Oddziaływanie międzyjądrowe.

Sprzężenie spin-spin

Układy spinowe

AX

3

np. CH

A

-

CH

3

X

Proton H

A

oddziałuje z trzema równocennymi protonami H

X

. Spiny jąder

H

X

mogą przyjmować różne orientacje względem pola i względem

siebie:

J

AX

J

AX

J

AX



A



X

1 : 1

J

AX

orientacj

e spinów

X

orientacj

e spinów

A

1 : 3 : 3 :

1

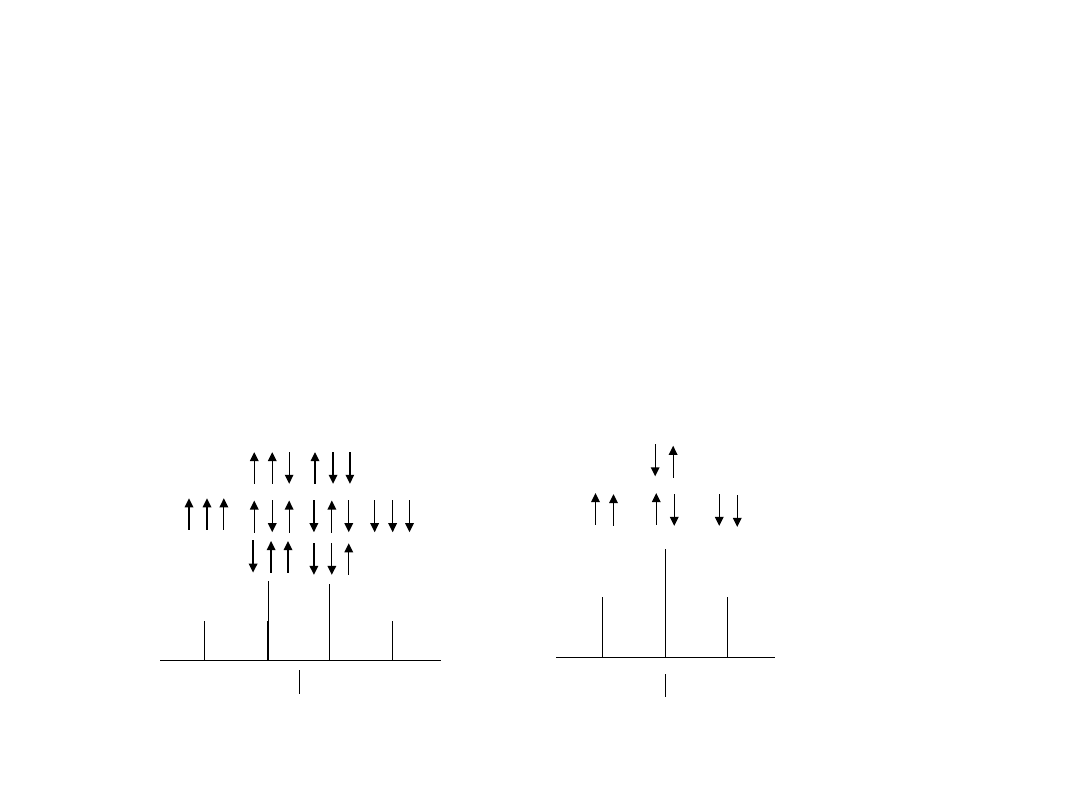
Oddziaływanie międzyjądrowe.

Sprzężenie spin-spin

Układy spinowe

A

2

X

3

np. CH

2

A

-CH

3

X

Protony H

A

oddziałują z trzema równocennymi protonami H

X

. Jądra H

X

oddziałują z dwoma równocennymi jądrami H

A

. Spiny obu grup jąder

mogą przyjmować różne orientacje względem pola i względem siebie
w obrębie grupy:

J

AX

J

AX



A

1 : 3 : 3 :

1

J

AX

orientacj

e spinów

X

orientacj

e spinów

A

J

AX

J

AX



X

1 : 2 :

1

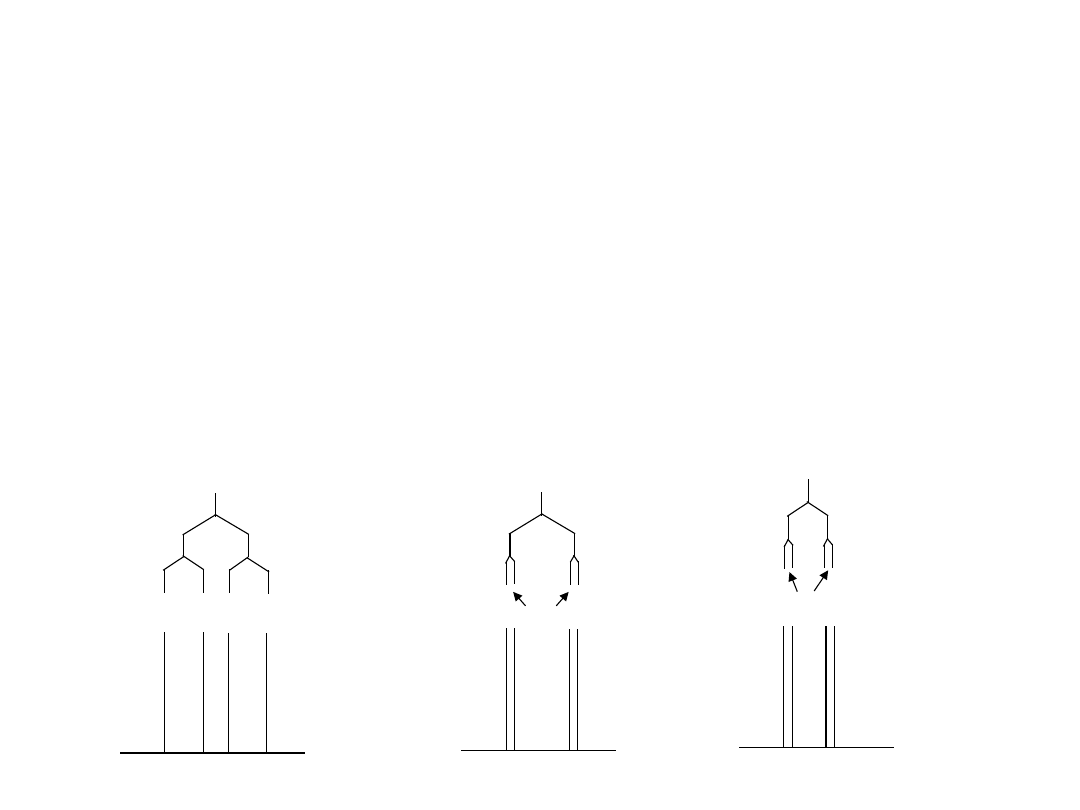
Oddziaływanie międzyjądrowe.

Sprzężenie spin-spin

Układy spinowe

AMX np.

-CH

A

=CH

M

H

X

W trójspinowym układzie AMX trzy nierównocenne jądra sprzęgają się
niezależnie każde z każdym. Dla każdej pary sprzęgających się jąder
wielkość stałej sprzężenia J może być inna.



M

J

AX



A



X

J

AX

J

AM

J

AM

J

MX

J

AX

J

MX

Sprzężenie spin-spin.

Warunki występowania

rozszczepienia

• Aby na widmie NMR ujawniła się struktura subtelna

spowodowana oddziaływaniem między dwoma jądrami,
konieczne jest by były one

magnetycznie nierównoważne

(różniły się przesunięciem chemicznym ).

• W układzie spinowym A

n

obserwuje się singlet (sygnał bez

struktury subtelnej).

• Aby na widmie NMR ujawniła się struktura subtelna

spowodowana oddziaływaniem między dwoma jądrami,
konieczne jest by wielkość stałej sprzężenia między tymi
jądrami J była większa niż szerokość linii rezonansowej .

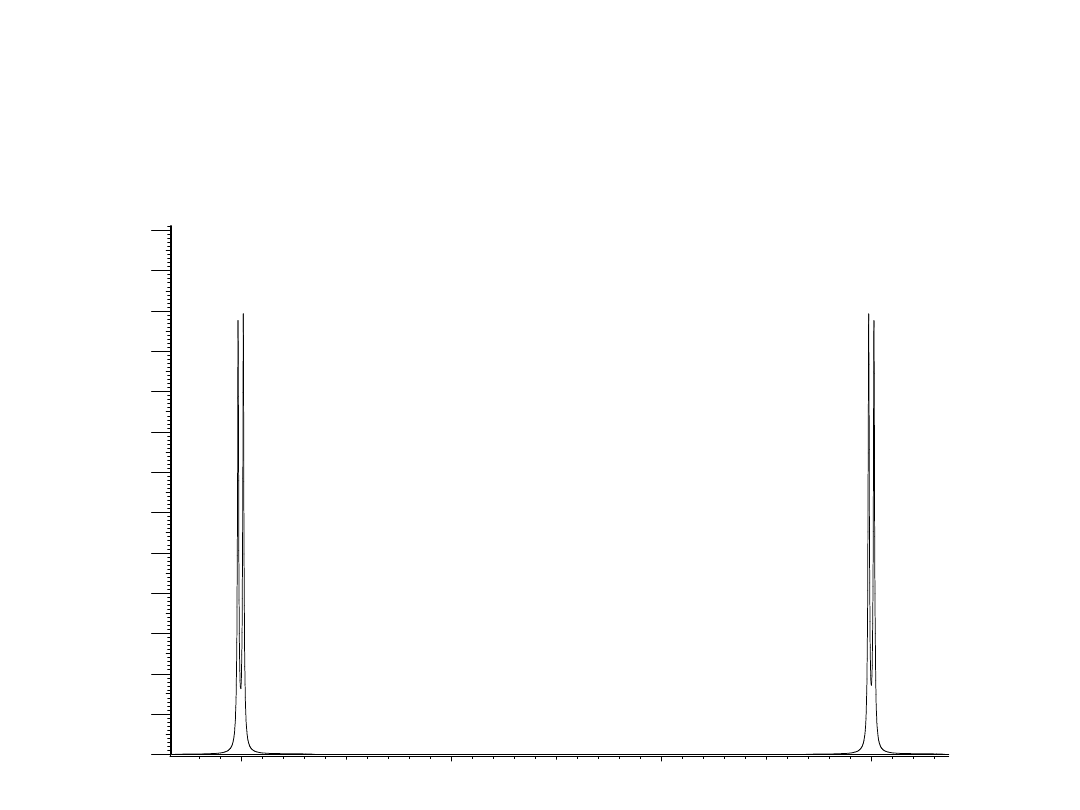
Sprzężenie spin-spin.

Warunki występowania

rozszczepienia

1.30

1.20

1.10

1.00

0.00

0.10

0.20

0.30

0.40

0.50

0.60

0.70

0.80

0.90

1.00

1.10

1.20

1.30

I = ½ , J = 1 Hz,  = 0.3

Hz

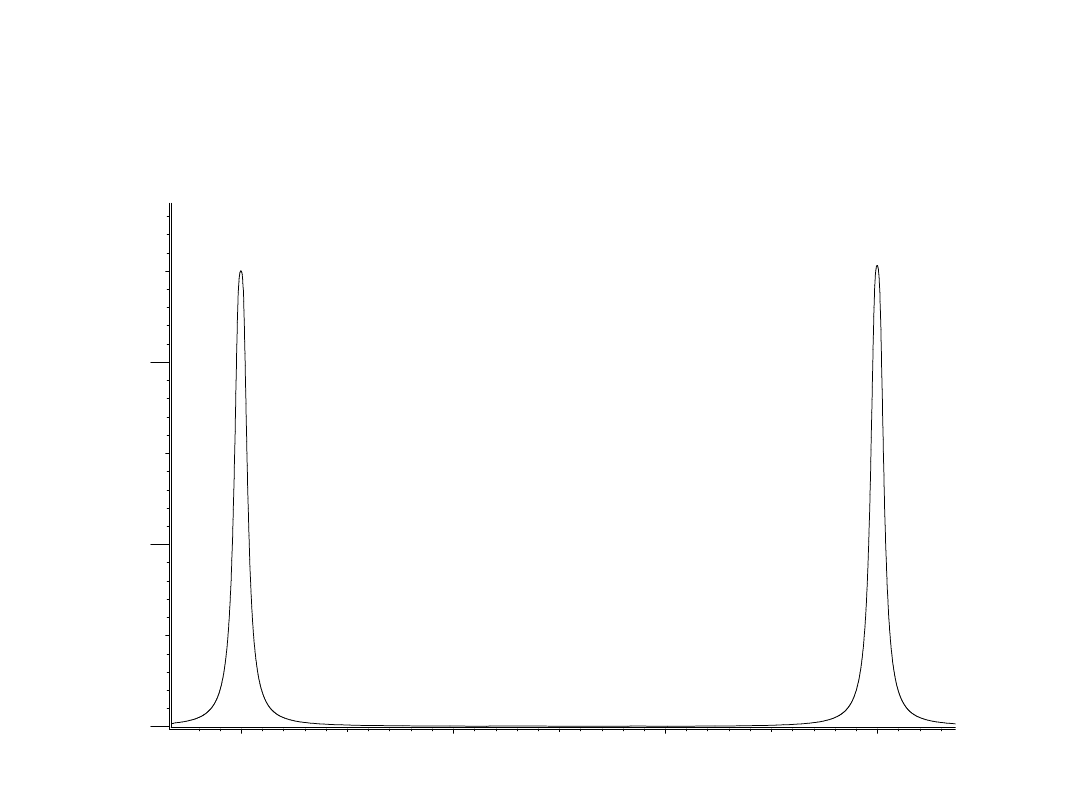
Sprzężenie spin-spin.

Warunki występowania

rozszczepienia

1.30

1.20

1.10

1.00

0.00

0.10

0.20

I = ½ , J = 1 Hz,  = 2 Hz

Oddziaływanie międzyjądrowe.

Sprzężenie spin-spin

• Dla sprzężeń proton-proton (

1

H -

1

H)

zakres wielkości stałych sprzężeń J
wynosi 0.1-20 Hz.

• W tzw. widmach protonowych (

1

H

NMR) uwidaczniają się zazwyczaj
sprzężenia dla jąder wodoru
„odległych” od siebie w cząsteczce o
co najwyżej 3 wiązania.

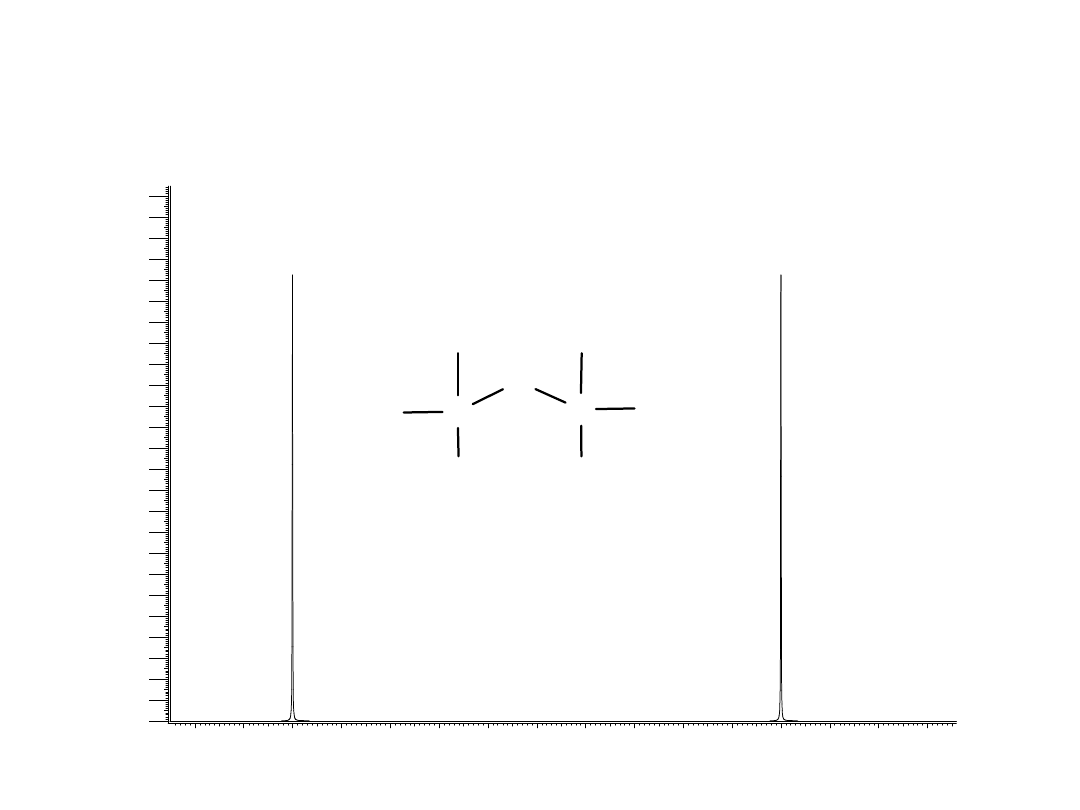
Dwa jądra nie oddziałujące

I = ½, J = 0 Hz

3.20

3.10

3.00

2.90

2.80

2.70

2.60

2.50

2.40

2.30

2.20

2.10

2.00

1.90

1.80

1.70

0.00

0.10

0.20

0.30

0.40

0.50

0.60

0.70

0.80

0.90

1.00

1.10

1.20

1.30

1.40

1.50

1.60

1.70

1.80

1.90

2.00

2.10

2.20

2.30

2.40

2.50

Cl C

CCl

3

H

O

C

CCl

3

CCl

3

H

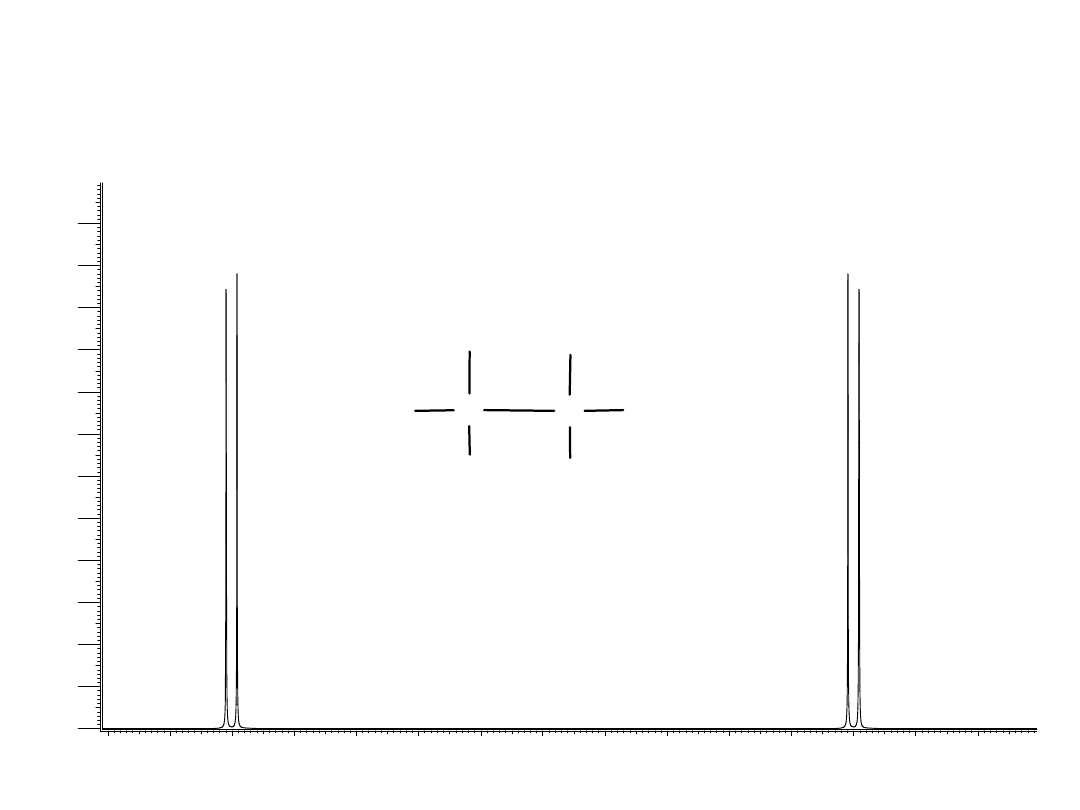
Dwa jądra oddziałujące

I = ½, J = 7 Hz

3.20

3.10

3.00

2.90

2.80

2.70

2.60

2.50

2.40

2.30

2.20

2.10

2.00

1.90

1.80

0.00

0.10

0.20

0.30

0.40

0.50

0.60

0.70

0.80

0.90

1.00

1.10

1.20

Cl C

CCl

3

H

H

CCl

3

CCl

3

C

Oddziaływanie międzyjądrowe.

Sprzężenie spin-spin

• Siła sprzężenia spin-spin wyrażona wielkością

stałej sprzężenia J nie zależy od zewnętrznego

pola magnetycznego. Zatem bez względu na

wielkość indukcji magnetycznej B

o

J będzie

miało tę samą wartość dla danego układu

sprzęgających się jąder.

• Wartość J odczytywana z widma NMR jako

odległość pomiędzy kolejnymi składowymi

multipletu

musi

być podawana jako różnica

częstości

tych składowych w hercach.

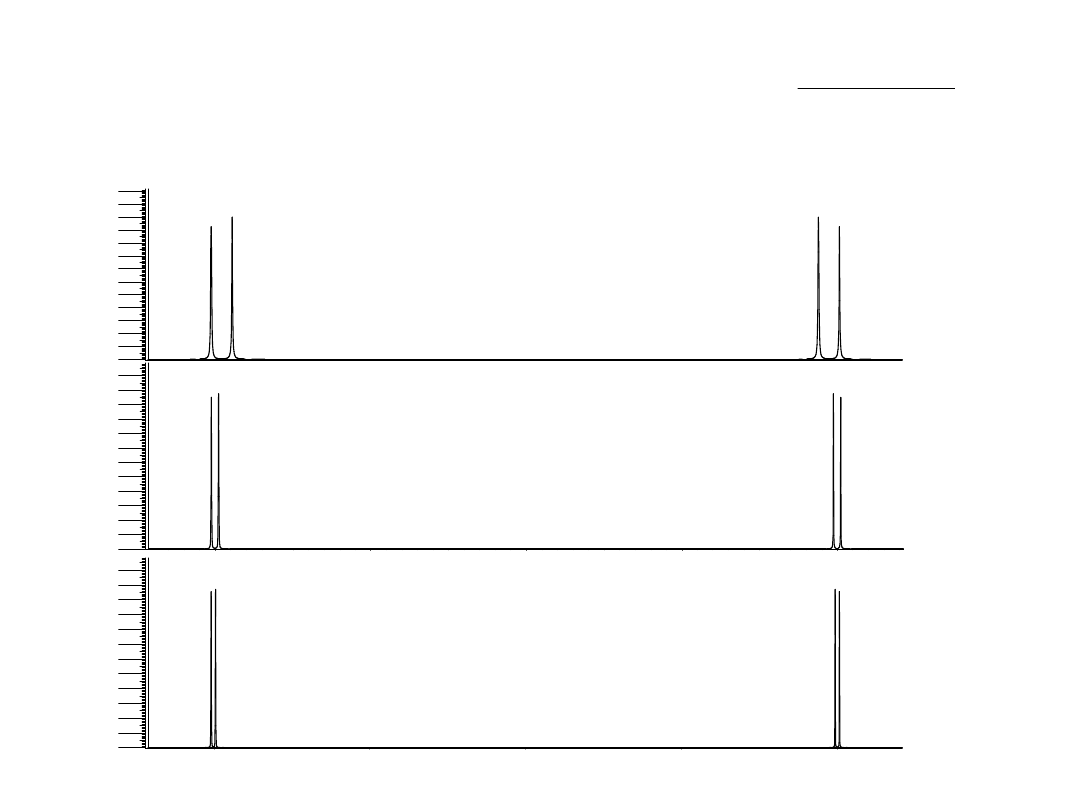
Dwa jądra

oddziałujące

I = ½, J = 7 Hz

3 .0

2 .5

2.0

1 .5

1.0

0 .0 0

0 .1 0

0 .2 0

0 .3 0

0 .4 0

0 .5 0

0 .6 0

0 .7 0

0 .8 0

0 .9 0

1 .0 0

1 .1 0

1 .2 0

1 .3 0

3.0

2.5

2 .0

1. 5

1 .0

0.0 0

0.1 0

0.2 0

0.3 0

0.4 0

0.5 0

0.6 0

0.7 0

0.8 0

0.9 0

1.0 0

1.1 0

1.2 0

3. 0

2.5

2.0

1 .5

1. 0

0 .0 0

0 .1 0

0 .2 0

0 .3 0

0 .4 0

0 .5 0

0 .6 0

0 .7 0

0 .8 0

0 .9 0

1 .0 0

1 .1 0

1 .2 0

[ppm]

100 MHz

300 MHz

500 MHz



o

















wz

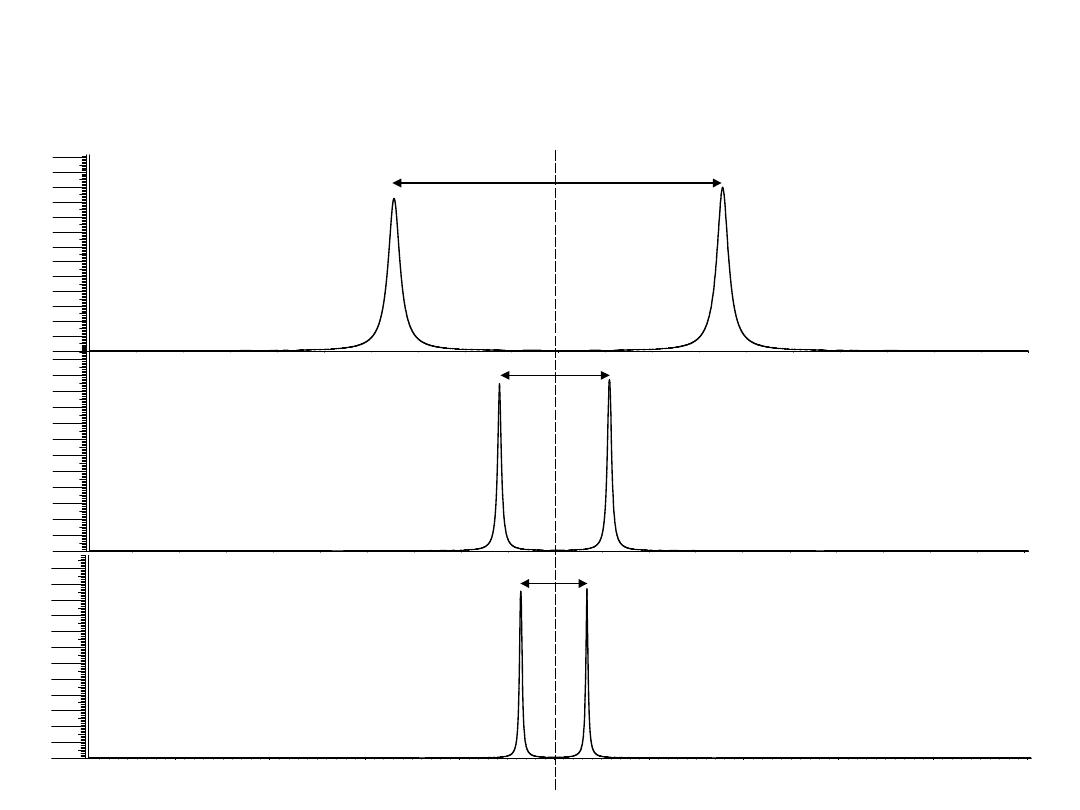
Dwa jądra oddziałujące

I = ½, J = 7 Hz

1540

1530

1520

1510

1500

1490

1480

1470

1460

1450

0. 00

0. 10

0. 20

0. 30

0. 40

0. 50

0. 60

0. 70

0. 80

0. 90

1. 00

1. 10

1. 20

3. 00

2.90

0.00

0.10

0.20

0.30

0.40

0.50

0.60

0.70

0.80

0.90

1.00

1.10

1.20

3.00

2. 90

0.00

0.10

0.20

0.30

0.40

0.50

0.60

0.70

0.80

0.90

1.00

1.10

1.20

1.30

100 MHz

300 MHz

500 MHz



o

[ppm]

7 Hz

7 Hz

7 Hz

Sprzężenie spin-spin.

Multipletowość

•

Liczba składowych struktury subtelnej

M

(

multipletowość

) linii

rezonansowej przy danym przesunięciu chemicznym 

1

zależy od:

a)

kwantowej liczby spinowej

I

jądra, z którym sprzęga się jądro o

przesunięciu 

1

b)

liczby

N

równoważnych magnetycznie jąder, z którymi sprzęga się

jądro o przesunięciu 

1

M = 2NI + 1

•

Dla I = ½ M = N + 1 (np. dla

1

H,

19

F,

13

C,

31

P)

•

Częstość rezonansowa (przesunięcie chemiczne) sygnału
wykazującego strukturę subtelną wyznaczona jest przez centrum
multipletu, tj. centralną składową multipletu przy nieparzystej
liczbie składowych lub punkt leżący w środku pomiędzy najbardziej
wewnętrznymi składowymi multipletu przy parzystej liczbie
składowych.

Multipletowość

• Grupa etylowa –CH

2

–CH

3

Każdy z protonów grupy –CH

2

– sprzęga

się z trzema protonami grupy metylowej,
N = 3
Dla

1

H I = ½

M = 2NI+1 = 2 x 3 x ½ + 1= 4

Sygnał grupy metylenowej ulegnie

rozszczepieniu na cztery składowe

(będzie kwartetem)

Multipletowość

• Grupa etylowa –CH

2

–CH

3

Każdy z protonów grupy –CH

3

sprzęga się

z dwoma protonami grupy metylenowej,
N = 2
Dla

1

H I = ½

M = 2NI+1 = 2 x 2 x ½ + 1= 3

Sygnał grupy metylowej ulegnie

rozszczepieniu na trzy składowe (będzie

trypletem)

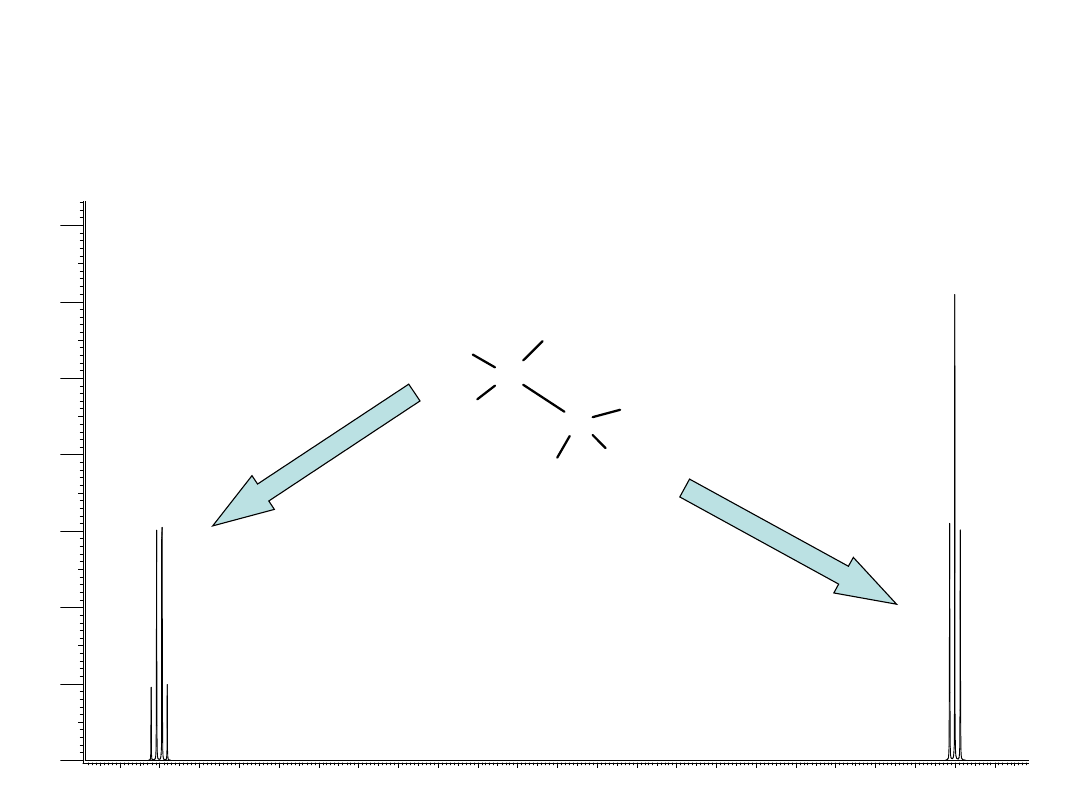
Oddziaływanie międzyjądrowe.

Sprzężenie spin-spin

3.10

3.00

2.90

2.80

2.70

2.60

2.50

2.40

2.30

2.20

2.10

2.00

1.90

1.80

1.70

1.60

1.50

1.40

1.30

1.20

1.10

1.00

0.90

0.0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

H

C

C

H

I

H

H

H

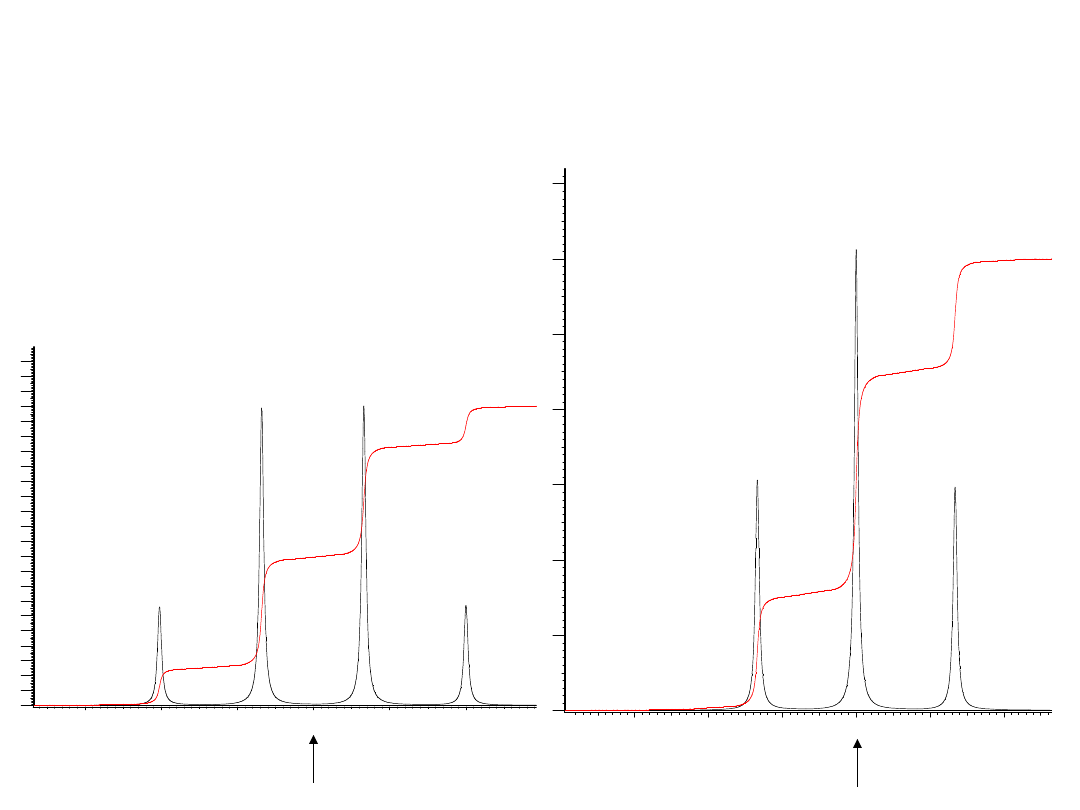
Względna intensywność składowych

multipletów grupy etylowej

1515

1510

1505

1500

1495

1490

0.00

0.10

0.20

0.30

0.40

0.50

0.60

0.70

0.80

0.90

1.00

1.10

1.20

1.30

1.40

1.50

1.60

1.70

1.80

1.90

2.00

2.10

2.20

2.30

2.40

515

510

505

500

495

490

0.0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

CH

2

CH

3

1

3

3

1

1

1

2

W obu multipletach odległości (w
hercach) pomiędzy kolejnymi
składowymi są identyczne i wynoszą
J.



(CH

2

)



(CH

3

)

Multipletowość

• Grupa izopropylowa CH

3

–CH–CH

3

Każdy z protonów grup –CH

3

sprzęga się

z 1 protonem,
N = 1
Dla

1

H I = ½

M = 2NI+1 = 2 x 1 x ½ + 1= 2
Sygnał grup metylowych ulegnie

rozszczepieniu na dwie składowe (będzie

dubletem)

Multipletowość

• Grupa izopropylowa CH

3

–CH–CH

3

Proton grupy –CH– sprzęga się z 6
protonami,
N = 6
Dla

1

H I = ½

M = 2NI+1 = 2 x 6 x ½ + 1= 7
Sygnał grupy –CH– ulegnie rozszczepieniu
na siedem składowych (będzie septetem)

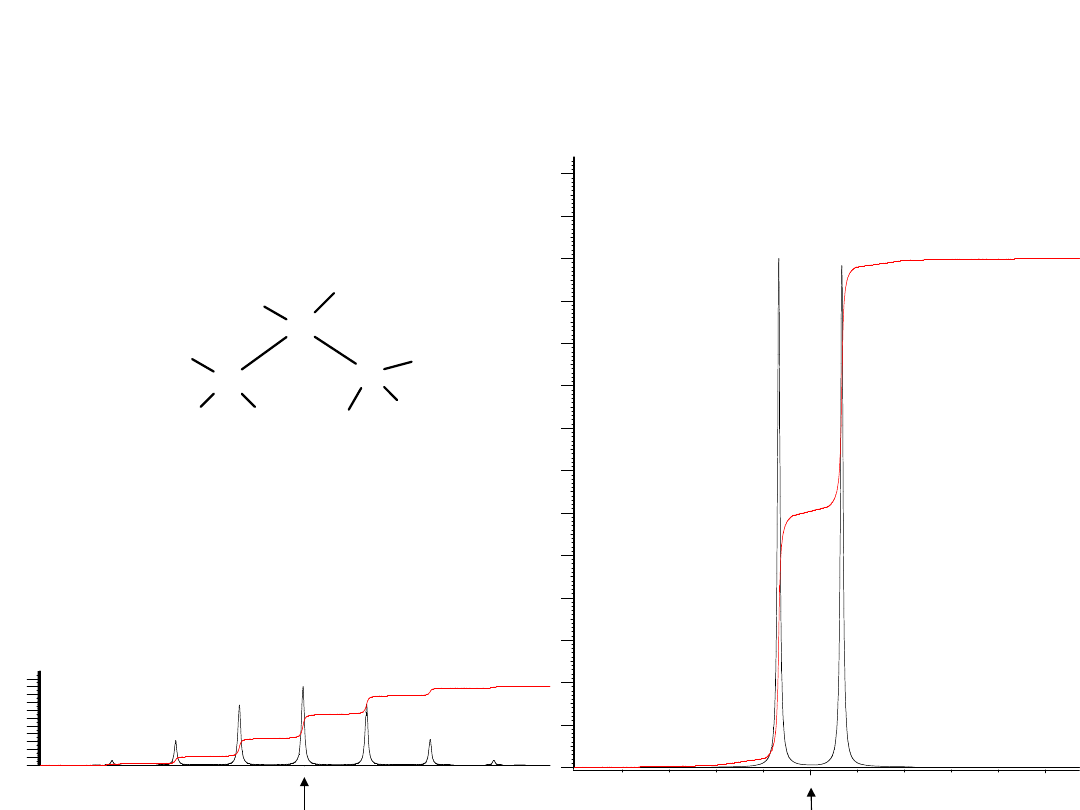
Względna intensywność składowych

multipletów grupy izopropylowej

3. 0 0

0 . 00

0 . 10

0 . 20

0 . 30

0 . 40

0 . 50

0 . 60

0 . 70

0 . 80

0 . 90

1 . 00

1 . 10

1 . 20

1.00

0.0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

4.0

4.5

5.0

5.5

6.0

6.5

7.0

1

1

1

6

6

15

15

20

1

CH

2 x CH

3

C

C

C

H

I

H

H

H

H

H

H

 (CH)



(CH

3

)

Względna intensywność składowych

multipletów dla sprzężenia z jądrami o

I = ½

• Przy sprzężeniu z N jądrami o wartości spinowej liczby kwantowej

I = ½ względne intensywności składowych multipletu mają się do
siebie jak współczynniki rozwinięcia dwumianu (a + b)

N

.

N
0

1

1

1

1

2

1

2

1

3

1

3

3

1

4

1

4

6

4

1

5

1

5

10 10 5

1

6

1

6 15 20 15

6

1

Trójkąt Pascala

Zastosowanie spektroskopii

NMR w analizie jakościowej.

Podsumowanie

1) Liczba linii rezonansowych –

symetria

cząsteczki.

2) Analiza przesunięć chemicznych –

grupy

funkcyjne.

3) Względna intensywność linii –

skład

związku chemicznego.

4) Analiza sprzężeń spin-spin –

sekwencja

grup funkcyjnych.

Zastosowanie NMR w medycynie

 w szeroko pojętej tomografii komputerowej wykorzystującej źródło
pola magnetycznego (rezonans magnetyczny) w diagnostyce
mózgu, klatki piersiowej

 mammografii

 układów naczyniowych

 ośrodkowego układu nerwowego

 jamy brzusznej

 przestrzeni zaotrzewnowej

 miednicy

Zakres badań diagnostycznych

wykorzystujących spektroskopię NMR

 diagnostyka metodą MR-I, pozwalająca na tworzenie dokładnych
obrazów narządów i okolic ciała w przekrojach w dowolnej
płaszczyźnie (w szczególności struktury wewnątrzczaszkowe i
wewnątrzkręgowe). Wysoką jakość uzyskiwanych w badaniu obrazów
zapewnia wykorzystanie magnesu nadprzewodnikowego o natężeniu
2T oraz specjalistycznych cewek narządowych (np. kolanowa,
głowowa, sutkowa). Badania rekomendowane są szczególnie do
oceny centralnego układu nerwowego i układu kostno-mięśniowo-
stawowego. Nieinwazyjność metody pozwala na bezpieczne
wykrywanie chorób oraz monitorowanie leczenia w przypadkach
zmian nowotworowych, zapalnych, urazowych i zwyrodnieniowych

Przewaga NMR nad zdjęciami rentgenowskimi jest dwojaka.

Po pierwsze ani pole magnetyczne, ani fale radiowe (bo przeważnie
takich używa się w rezonansie) nie są tak szkodliwe jak promienie X, a
po drugie NMR daje możliwość wykonania dowolnego przekroju, a nie
tylko rzutu na klisze jak w przypadku tradycyjnego prześwietlenia.
Stosując NMR możemy także praktycznie bez ograniczeń powiększać
sobie dowolny interesujący nas fragment obserwowanego
przedmiotu. Zarówno wiec lekarzom jak i biologom NMR daje do ręki
potężne narzędzie badawcze.

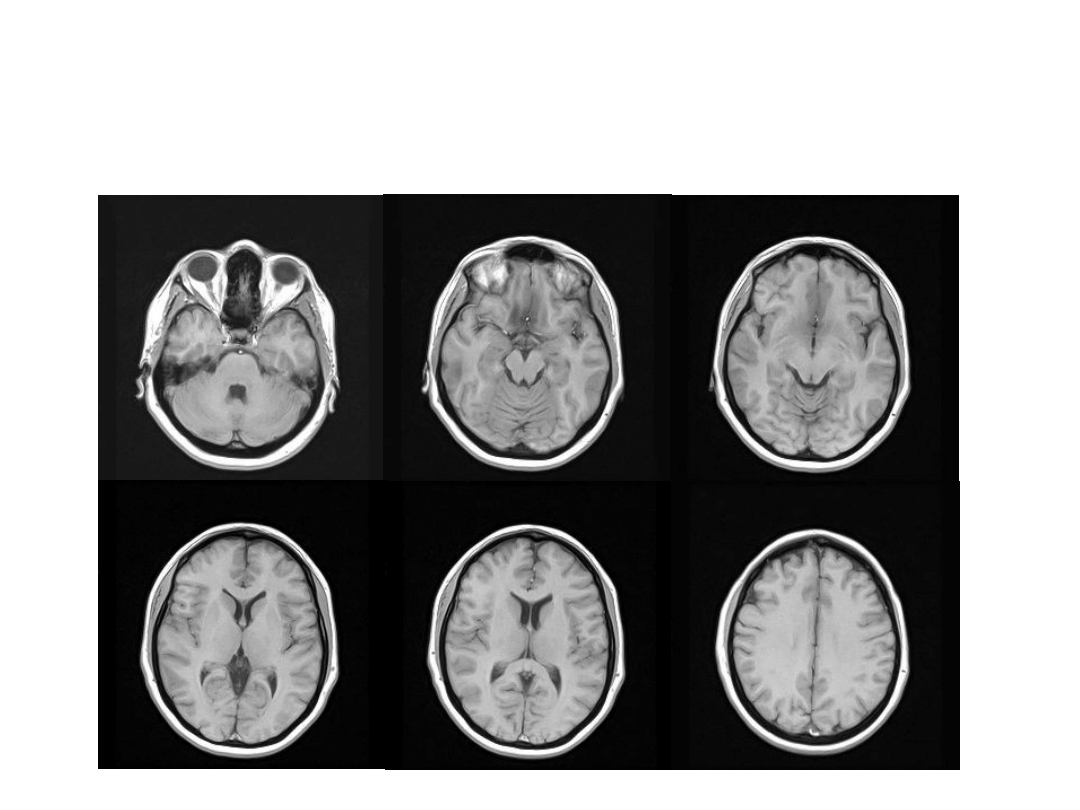
MRI – obrazowanie magnetycznym rezonansem

jądrowym

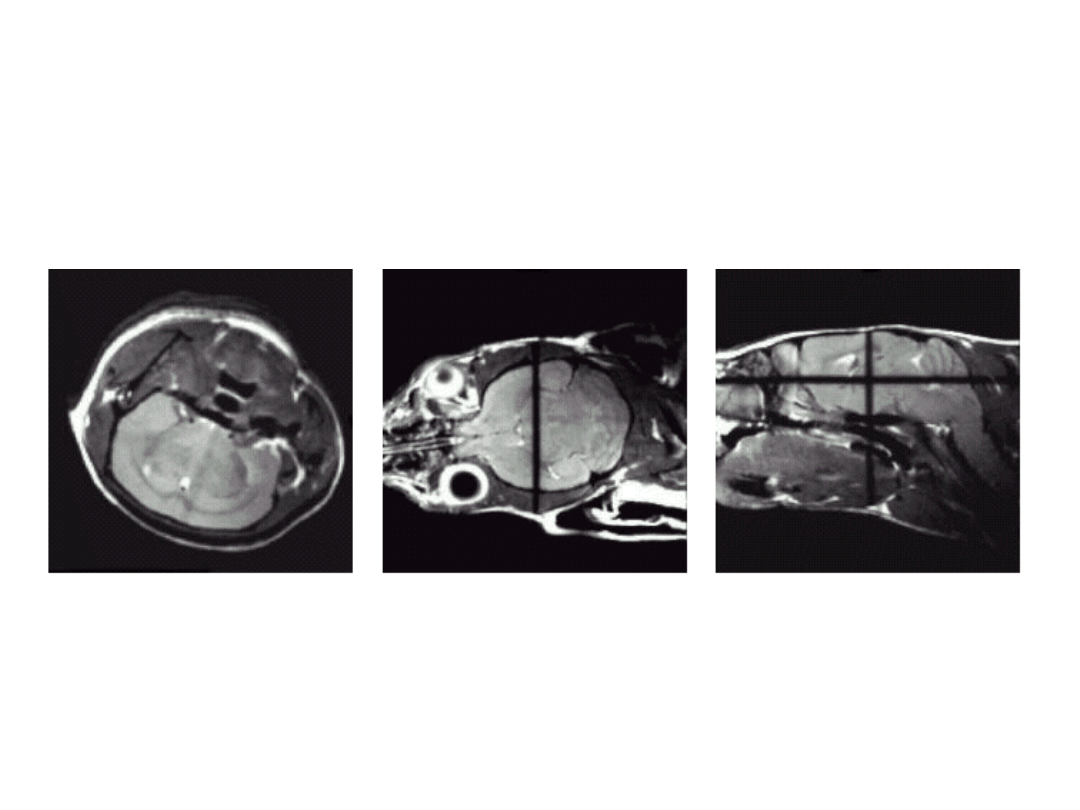
Mózg myszy, model działający

Obrazowanie rezonansem

magnetycznym in vivo

Paul C. Lauterbur

Department of Chemistry
University of Illinois

Sir Peter Mansfield

School of Physics and
Astronomy
University of Nottingham

Nobel 2003 (Medycyna i fizjologia)

za pionierskie badania nad MRI

EPR

Electron Paramagnetic Resonance

The science of electron paramagnetic

resonance (EPR) spectroscopy is very similar
to the more familiar NMR. Both deal with the
interaction of electromagnetic radiation with
magnetic moments; in case of EPR, the
magnetic moments arise from electron rather
than nuclei.

Each electron possesses an intristic

magnetic-dipole moment that arises from its
spin. In most systems electrons occur in pairs
such that the net moment is zero. Hence only
species that contains one or more unpaired
electrons possess the net spin moment
necessary for interaction with an
electromagnetic field.

EPR technique

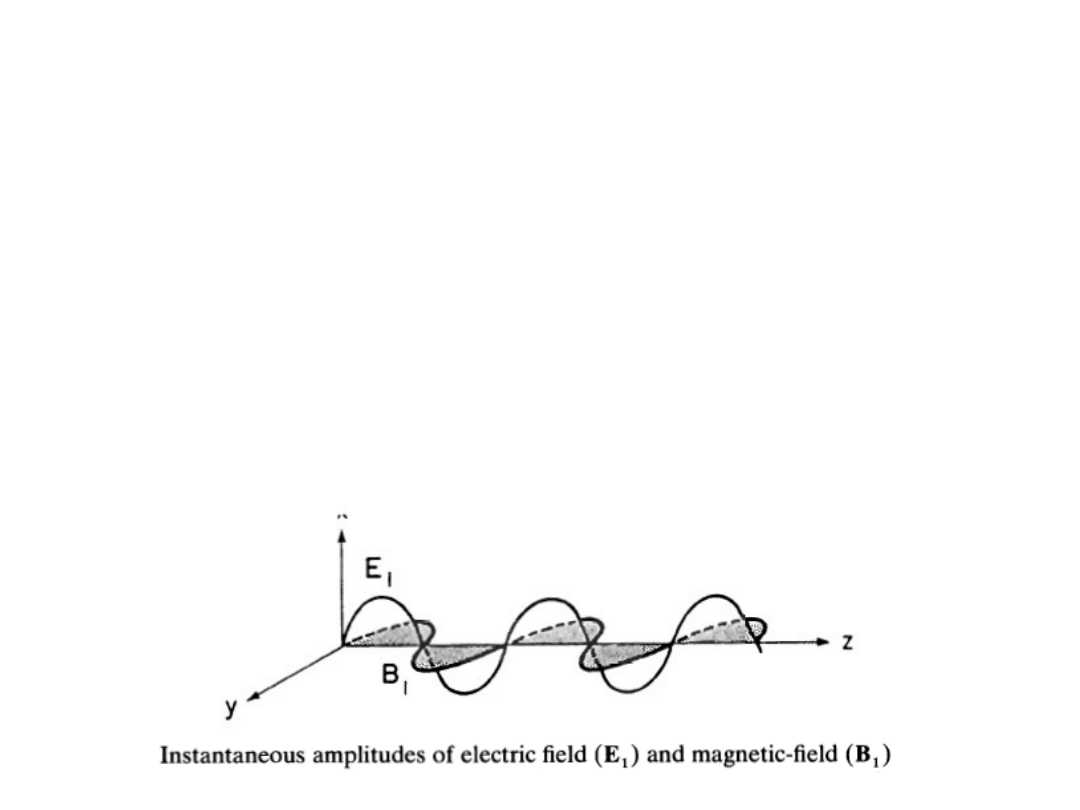
Electromagnetic radiation may be regarded

classically as coupled electric (E) and magnetic (B)
fields perpendicular to the direction of propagation
, both oscilating at some frequency ().

The energy of any given photon is given by

the quantity h, where h is the famous Planck

constant

For EPR, the commonly used frequency

range is 10

9

-10

11

s

-1

(1-100 GHz)

Electromagnetic resonance

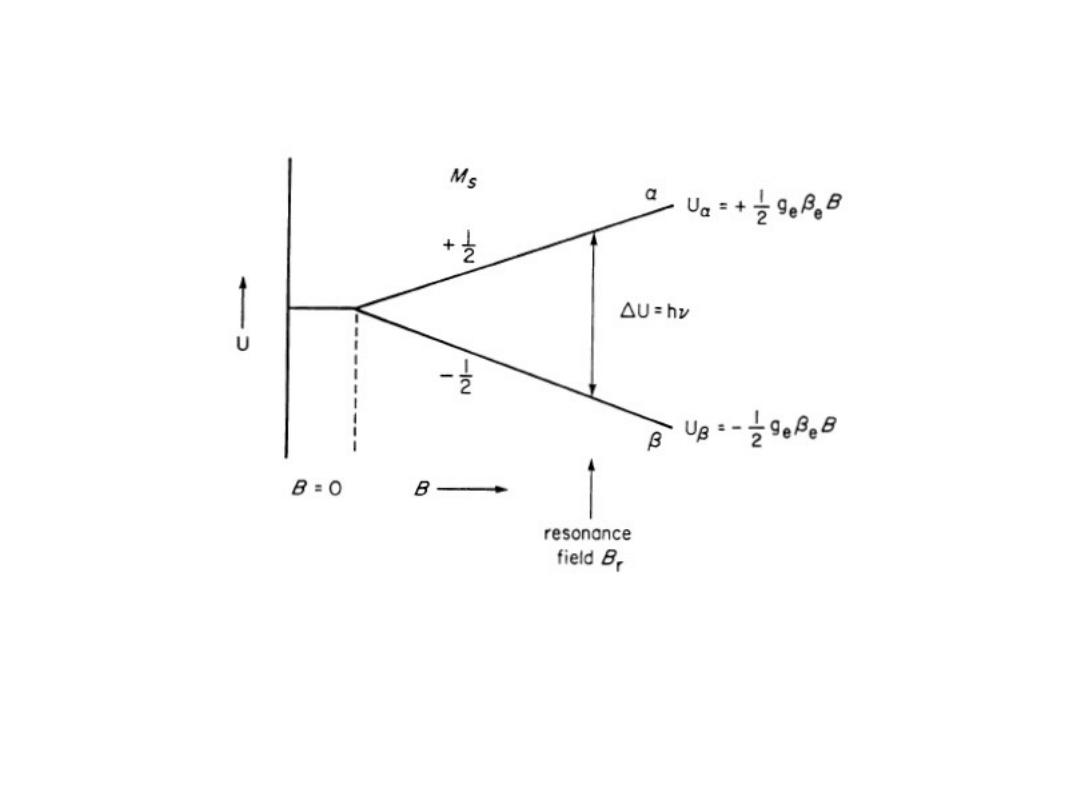
Energy-level scheme for the simplest system

(free electron) as a function of applied magnetic
field B. U



and U



represents the energies of the Ms

= +1/2 and –1/2.

Resonance condition

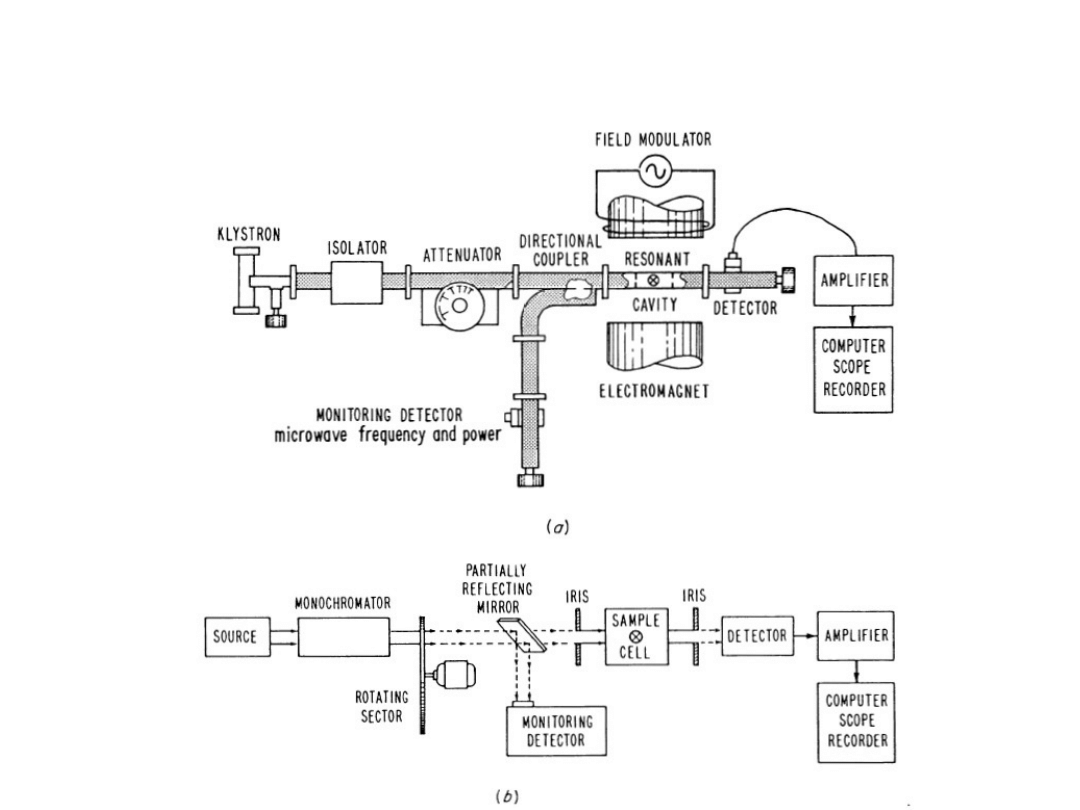
EPR spectrometer scheme

Source – usually a klystron, a vacuum tube wuth
low noise characteristics. The field is genetared by
oscillations within its own cavity. For commonly
used X-band specrometers the frequency is about
9,5 GHz (wavelenght of ~32 mm).

Resonator – most commonly used is resonant
cavity. The one wishes to operate in resonant
mode that maximalizes B in the location of the
sample – at resonance, the energy density in
resonator may be thousands of times that in the
waveguide. As alternative recently developed
loop-gap resonator may be used for energy
dissipative samples. Transmision cavities, with
separate input and output irises are rarelly used.
In practice, a reflection cavity, in which single iris
fulfills both functions, is commonly used.

EPR spectrometer

Magnetic field - for NMR and EPR the static
magnetic field is necessary and must be very stable
and uniform over sample volume, as in other case
observed spectral line is broadened. Simple
electromagnet of well defined characteristic is
used.

Detector – numerous types of solid-state diodes are
sensitive to micowave energy. Absorption of
photons by the sample is indicated by change in the
detector current. A direct detection of the
absorption signal is avoided due to noise. Signal-to-
noise ratio is improved by signal modulation at
preselected frequency. Typically, the resulting
signal is rectified and resembles the first derivative
of an absorption line.

EPR spectrometer

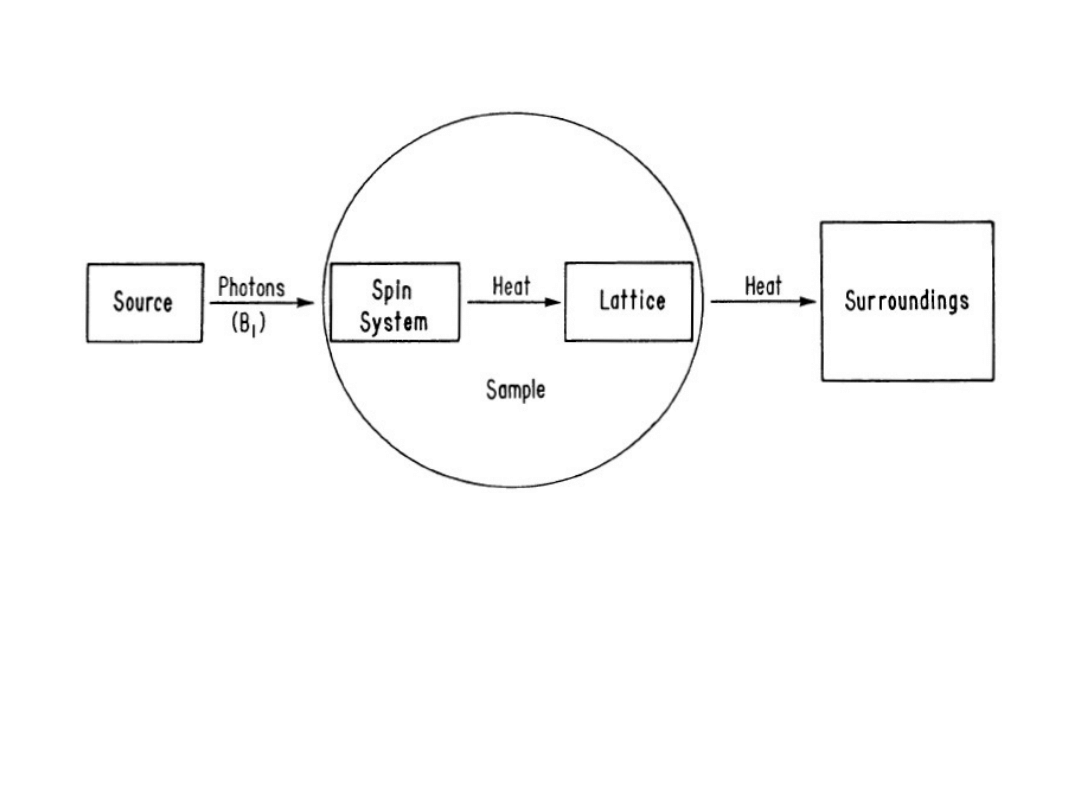
Energy flow in magnetic-resonance

experiment

Other possible way is to transfer energy to

another paramagnetic species, such as oxygen on
metal ion from transition group. This has
implications in power-saturation experiments
(described later)

- free radicals in the solid, liquid and gasseous
phases

- transition ions

- various point defects (localised inperfections) in
solids, as a F center – electron trapped in crystals
and glasses

- systems with conducting electrons, e.g.
semiconductors

- REDOX centers in biological systems

EPR in science and technology

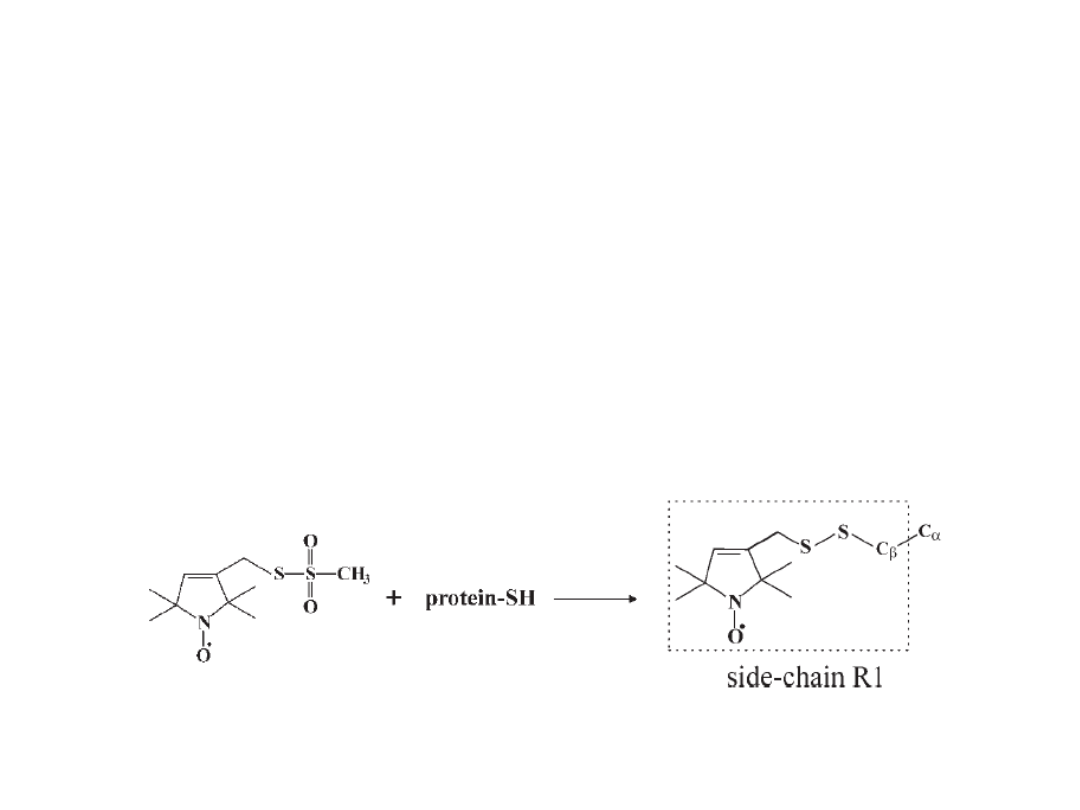
EPR and proteins

As proteins usually do not have unpaired

electrons it is necessary to introduce label to get
resonance signal. Commonly used one is MTSL [(1-
oxyl-2,2,5,5-tetramethylpyrroline-3-methyl)-
methanethiosulfonate]. MTSL react with –SH group
of cystein. The procedure is called site-directed spin
labeling (SDSL) and usually requires only one cystein
residue to be avaible for reaction.

SDSL – tool for monitoring the

structure and dynamics

From the EPR spectrum of R1, one can obtain
parameters as:

- solvent accessibility () – from the collision

frequency of the nitroxide with paramagnetic
reagents such as O2 and NiEDDA (Ni(II)
ethylenediaminediacetic acid) in solution — collision
of R1 with these reagents results in a decrease in the
spin-lattice relaxation time of the spin label

- mobility (Ms) of the R1 side chain

- the distance between R1 and another
paramagnetic center in the protein, which can be
either a second nitroxide or a metal ion

The mobility and distances are deduced from the EPR
spectral lineshape.

Advantages and disadvantages of SDSL
with EPR

+ use relatively small amounds of protein

+ sample can be prepared in conditions as close to
natural as preparation methods allow

+ spectra is simple and relatively easy to analyse

+ virtually the best approach to investigate large
membrane proteins

- need to introduce label, usually relatively small,
but still can alter protein structure/function

- not very usefull for proteins with much native
cystein residues

- getting global information about protein structure
usually means very much work

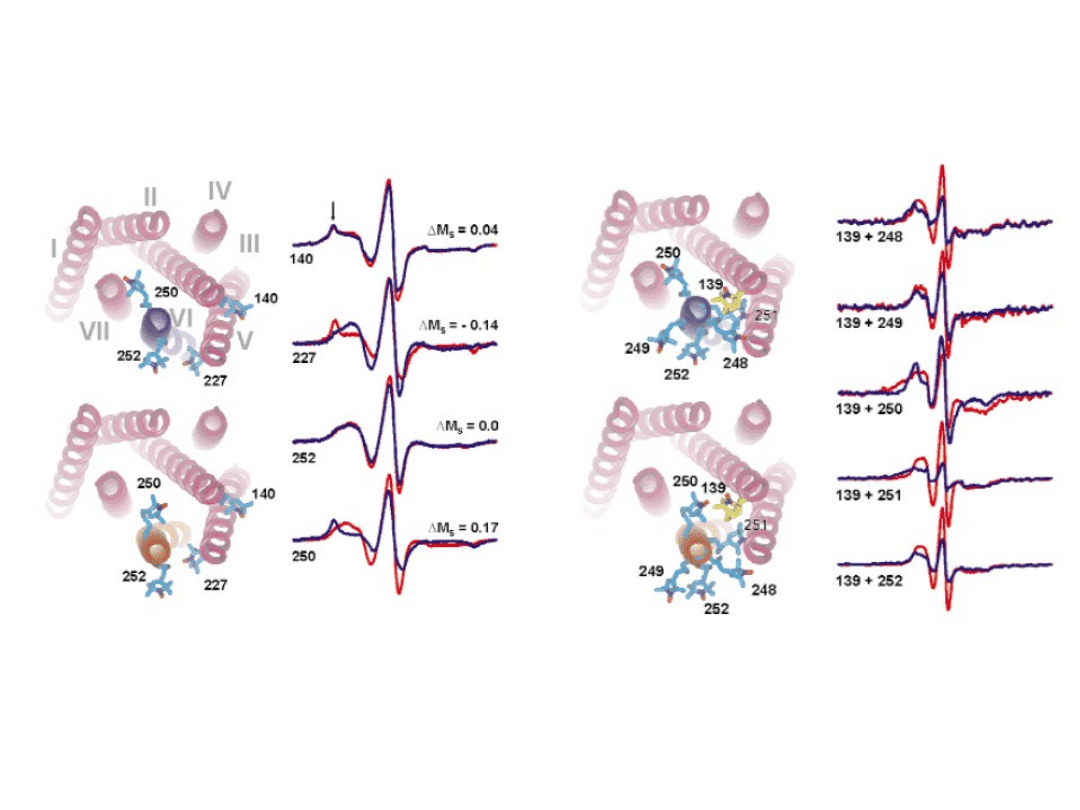
Example on rhodopsin

Mobility change in the
resting (blue helix)34
and activated (red
helix) states

Distance
measurement

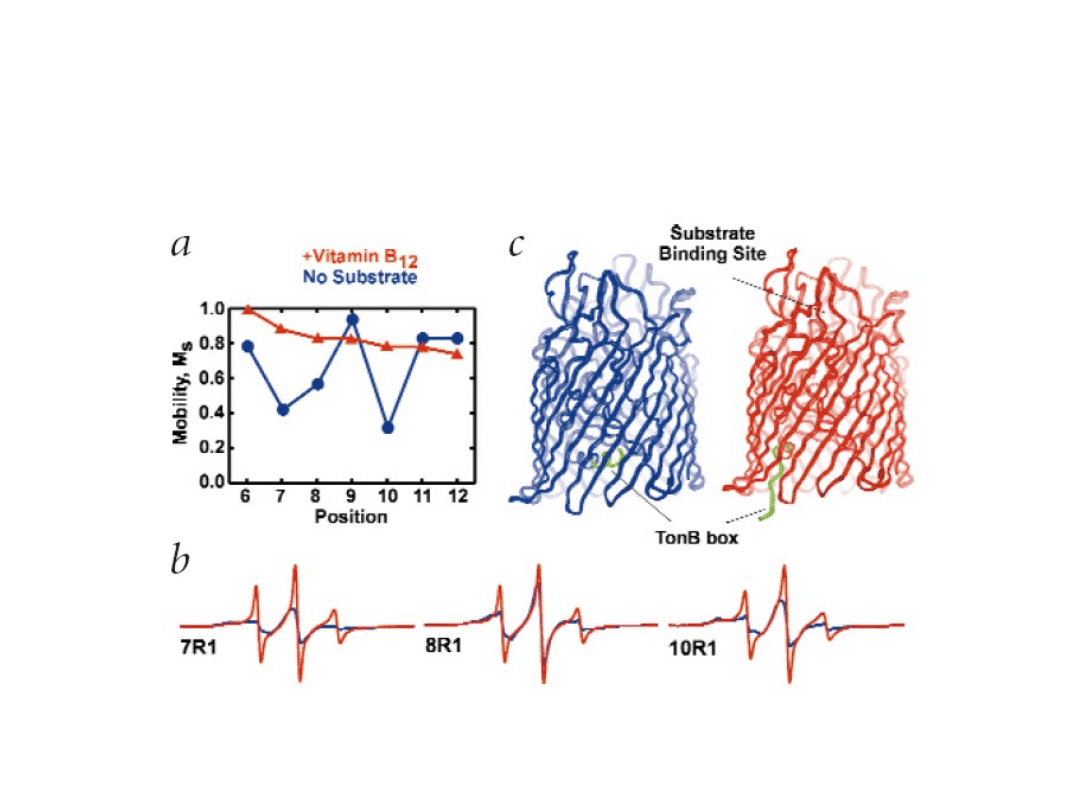
Ton-box in BtuB unfolds in response to substrate

binding becoming avaible for TonB