Podstawy prognozowania

Prognoza

jest sądem

bezwarunkowym (oznajmującym) o
kształtowaniu się zjawiska w ściśle
określonym momencie w przyszłości,
przy czym prawdziwość tego sądu nie
jest znana w momencie jego
formułowania.

Prognoza jest wynikiem procesu

nazywanego

prognozowaniem

(predykcją)

.

2

GK (WEiP(3) - 2011)

Wprowadzenie

Prognozowanie

jest oparte na prawidłowościach

charakteryzujących prognozowane zjawisko lub
występujących między tym zjawiskiem a innymi zjawiskami.
Mogą to być prawidłowości występujące:

•w rozwoju prognozowanego zjawiska

– częstość

występowania, tendencja rozwojowa, wahania sezonowe,
wahania okresowe itp.,

•pomiędzy zjawiskiem prognozowanym a innymi zjawiskami

– zależności przyczynowo-skutkowe, zależności
symptomatyczne (współistnienia), podobieństwo zmian itp.
Możliwe jest zatem wnioskowanie o tym, że:

•zdarzenie nastąpi, ponieważ występowało w przeszłości

–

np. przewiduje się, że pokonanie tej samej drogi zajmie tyle
samo czasu, co przeciętnie zajmowało dotychczas,

•zdarzenie nastąpi, ponieważ wskazuje na to częstość jego
występowania

– np. przewidywanie liczby błędów w tekście,

•zdarzenie nastąpi, ponieważ wskazuje na to jego silne
powiązanie z innymi zdarzeniami (zdarzeniem), które
nastąpiło

– np. przewidywanie liczby zachorowań na grypę w

zależności od temperatury otoczenia.

3

GK (WEiP(3) - 2011)

Wprowadzenie

Okres, dla którego jest tworzona prognoza, nosi nazwę

okresu prognozy

, natomiast liczba okresów objętych prognozą

–

horyzontu prognozy

.

Prognoza dotyczy wystąpienia określonego zdarzenia

w przyszłości, opisywanego pewną zmienną, która nosi nazwę

zmiennej prognozowanej

.

W zależności od typu tej zmiennej

(ilościowy, jakościowy) wyróżnia się prognozowanie

ilościowe

i

jakościowe

. Prognoza

ilościowa

może być prognozą

punktową

(określona wartość przyjmowana przez zmienną

prognozowaną) lub

przedziałową

(przedział, w którym zawiera

się wartość przyjmowana przez zmienna prognozowaną).
Prognoza

jakościowa

jest budowana w przypadku, gdy

zdarzeniem jest stan prognozowanej zmiennej jakościowej lub
słownie opisana sytuacja dotycząca tej zmiennej.

Prognozy mogą być

krótko-, średnio- i długookresowe

.

Prognoza krótkookresowa

jest budowana na okres, w którym

w prognozowanym zjawisku zachodzą tylko zmiany ilościowe.
Prognoza krótkookresowa zwykle polega na ekstrapolacji
dotychczas występujących prawidłowości zmiennej
prognozowanej.

Prognoza średniookresowa

jest budowana na

okres, w którym w prognozowanym zjawisku zachodzą przede
wszystkim zmiany ilościowe i niewielkie, ale zauważalne –
zmiany jakościowe.

Prognoza długookresowa

dotyczy okresu,

w którym w prognozowanym zjawisku mogą zajść istotne
zmiany jakościowe.

4

GK (WEiP(3) - 2011)

Wprowadzenie

Metoda

jest to sposób zastosowany ze świadomością

możliwości jego zastosowania w przypadkach takiego typu,
jakiego egzemplarz w danym przypadku rozpatruje osoba
działająca [T. Kotarbiński].

Metoda prognozowania

obejmuje sposób

przetworzenia danych o przeszłości oraz sposób przejścia od
danych przetworzonych do prognozy [M. Cieślak].

Diagnozowanie przeszłości odbywa się przez budowę

modelu formalnego (ekonometrycznego czy trendu) lub
myślowego (np. w umyśle eksperta).

Sposób przejścia od danych przetworzonych o

przeszłości do prognozy nazywa się

regułą prognozowania

.

5

GK (WEiP(3) - 2011)

Wprowadzenie

Reguły prognozowania

Wyróżnia się następujące reguły prognozowania:

•podstawową,

•według największego prawdopodobieństwa,

•według mediany,

•minimalizującą oczekiwaną stratę.

Reguła podstawowa (reguła prognozowania według

wartości oczekiwanej

)

– najpowszechniej stosowana.

Prognozą jest stan zmiennej prognozowanej w okresie

T

,

otrzymany z modelu tej zmiennej przy

założeniu stałości

relacji

opisujących zależności pomiędzy tą zmienną a

innymi zmiennymi ją opisującymi (zmiennymi
objaśniającymi), tj. przy założeniu, że model będzie
aktualny w okresie prognozowania

T

. Przyjęcie tej reguły

oznacza w praktyce, że prognozę otrzymuje się drogą

ekstrapolacji modelu

poza próbę. Omawiana reguła

charakteryzuje się dwoma istotnymi własnościami: w
przypadku klasycznego (standardowego) modelu regresji
liniowej (ekonometrycznego) daje prognozy nieobciążone
oraz jest łatwa do stosowania.

6

GK (WEiP(3) - 2011)

Predyktorem w tej regule jest

warunkowa wartość

oczekiwana

,

tj. regresja zmiennej objaśnianej względem

zmiennych objaśniających, która wyraża się następującą
zależnością:

Prognozy

uzyskiwane wg tej reguły będą się różniły (jak każda
prognoza) od przyszłej realizacji zmiennej prognozowanej
(objaśnianej), ale przy wielokrotnym powtarzaniu
prognozowania w tych samych warunkach przebiegu
zjawiska opisywanego zmiennymi objaśniającymi, należy
oczekiwać, że średni błąd ciągu tak otrzymanych prognoz
będzie równy zeru.

Omawiana reguła daje prognozy minimalizujące

funkcję strat

Str

,

która jest równa błędowi

średniokwadratowemu:













n

1

t

2

t

t

y

ˆ

y

n

1

Str

(

)

t

t

1t

2t

kt

ˆy

E y x ,x ,...,x , t 1,2,...,n

=

=

p

T

T

ˆ

y

y

=

7

GK (WEiP(3) - 2011)

Reguły prognozowania

Jedną z częściej stosowanych odmian reguły

podstawowej jest tzw.

reguła podstawowa z poprawką

która jest

wykorzystywana w przypadku, gdy występują uzasadnione
przypuszczenia co do tego, że ostatnio obserwowane
odchylenia danych empirycznych od teoretycznych
(uzyskanych na podstawie modelu) zostaną zachowane również
w przyszłości. W takim przypadku reguła przyjmuje postać:

Sposób szacowania poprawki

popr

zależy od liczby

zaobserwowanych odchyleń od modelu. Jeżeli zmiana, o której
sądzi się, że będzie stała, wystąpiła w ostatniej chwili

(

t = n

),

dla której istnieją obserwacje, to:

Jeżeli zmiana wystąpiła w

m

ostatnich chwilach, poprawkę

szacuje się z zależności:

(

)

n

t

t

t n m 1

1

ˆ

popr

y

y .

m

= - +

=

-

�

(

)

p

T

T

T

1T

2T

kT

t 1,2,...,n

ˆ

y

y

popr E y x ,x ,...,x

popr,

=

=

+

=

+

n

n

ˆ

popr y

y .

=

-

8

GK (WEiP(3) - 2011)

Reguły prognozowania

9

GK (WEiP(3) - 2011)

Reguły prognozowania

Reguła prognozowania według

największego

prawdopodobieństwa

–

stosowana ze względu na to, że w wielu

sytuacjach nie jest możliwe wielokrotne powtarzanie
prognozowania zjawiska z zachowaniem tych samych
warunków zatem prognoza, szczególnie ekonometryczna, ma
charakter incydentalny, jednorazowy w danych warunkach. W
takim przypadku zasadne jest dążenie do uzyskania prognozy
charakteryzującej się najwyższym prawdopodobieństwem
realizacji, tj. prognozy na poziomie

dominanty

rozkładu

prognoz, co można zapisać w następujący sposób:

gdzie jest prawdopodobieństwem, z jakim zmienna
prognozowana (objaśniana) przyjmie wartość
Omawiana reguła daje prognozy maksymalizujące
prawdopodobieństwo „trafienia” w przyszłą realizację
zmiennej prognozowanej. W tym przypadku funkcja strat

Str

:

osiąga minimum, gdy prognoza przyjmie wartość dominanty
rozkładu.

( )

( )

{

}

D

D

p

t

t

t

T

ˆ

ˆ

ˆ

y

y : P y

P y , t 1,2,...,n

=

�

=

( )

p

T

P y

p

T

y .

{

}

p

D

T

T

ε 0

ˆ

Str max P y

yε

+

�

=

-

<

D

T

ˆy

10

GK (WEiP(3) - 2011)

Reguły prognozowania

Reguła prognozowania według

mediany

–

stosowana w szczególnych przypadkach prognozowania
opartego na modelach wielorównaniowych. W omawianym
przypadku zasadne jest dążenie do uzyskania prognozy
zbliżonej do

mediany

rozkładu prognoz, tj. w ogólnym

przypadku rozkładu:

a w przypadku rozkładu dyskretnego z małą liczbą
wartości zmiennej prognozowanej (objaśnianej):

gdzie jest wartością zmiennej prognozowanej, różną
od mediany zmiennej

y

t

.

Omawiana reguła daje prognozy minimalizujące funkcję
strat

Str

, która jest równa błędowi bezwzględnemu:

(

)

(

)

{

}

M

M

p

M

p

t

t

t

T

t

T

ˆ

ˆ

ˆ

ˆ

y

y : P y

y

0,5 P y

y

0,5, t 1,2,...,n

==ٳ=�=

(

)

(

)

{

}

M

M

p

M

p

t

t

t

T

t

T

ˆ

ˆ

ˆ

ˆ

y

y : P y

y

0,5 P y

y

0,5, t 1,2,...,n

=�ٳ=�=

p

T

y

.

ˆ









n

1

t

t

t

y

y

n

1

Str

Reguła prognozowania

minimalizującego oczekiwaną stratę

– stosowana w przypadkach, gdy błędowi prognozy można
przypisać określoną stratę:

gdzie oznacza stratę przypisaną
Za prognozę przyjmuje się tę przewidywaną wartość
zmiennej prognozowanej, która minimalizuje stratę.

( )

( )

{

}

S

S

p

t

t

t

T

ˆ

ˆ

ˆ

y

y :W y

W y , t 1,2,...,n

=

�

=

 

S

t

y

W ˆ

.

ˆ

S

t

y

11

GK (WEiP(3) - 2011)

Reguły prognozowania

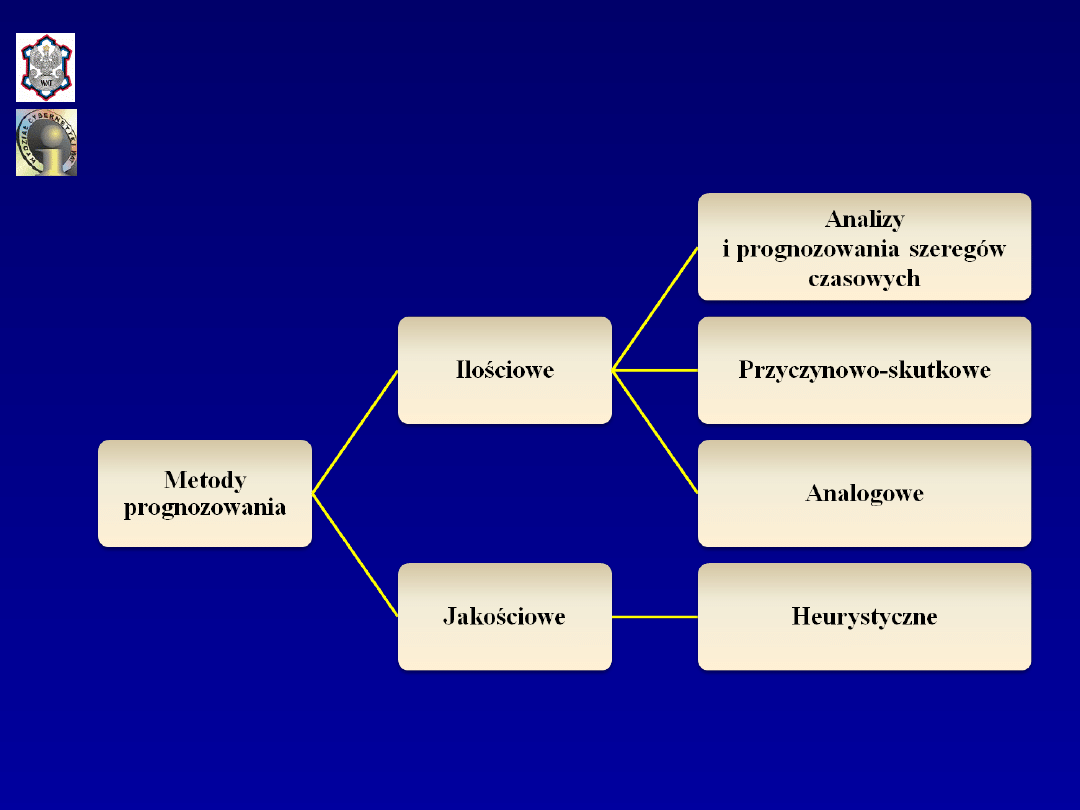
Klasyfikacja metod
prognozowania (jedna z
możliwych)

12

GK (WEiP(3) - 2011)

Metody prognozowania

Metody analizy i prognozowania szeregów czasowych

charakteryzują się tym, że korzystają w analizie
(diagnozowaniu) przeszłości prognozowanego zjawiska z
danych o dotychczasowym kształtowaniu się zmiennej
(zmiennych) prognozowanej. Dane te zwykle mają postać
jedno- lub wielowymiarowego szeregu czasowego.

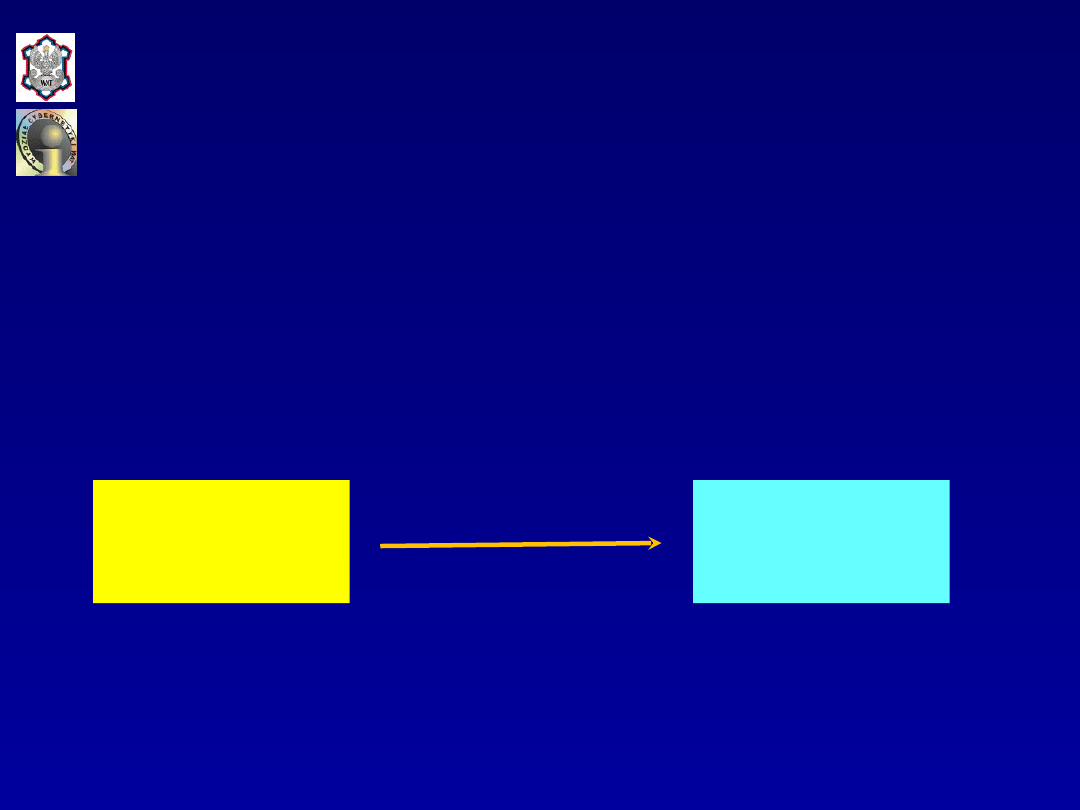
Schemat prognozowania na podstawie

jednowymiarowego szeregu czasowego [M. Cieślak]

Model

Reguła

prognozowania

p

p

p

n

n 1

T

y ,y ,...,y

+

1

2

n

y ,y ,...,y

13

GK (WEiP(3) - 2011)

Metody prognozowania

W szeregach czasowych czas i przeszłe wartości zmiennej
prognozowanej reprezentują wszystkie czynniki wpływające
na zachowanie tej zmiennej w przyszłości. Metody analizy i
prognozowania szeregów czasowych są wykorzystywane
głównie do budowania prognoz krótkookresowych.

Omawiana klasa metod prognozowania opiera się na

modelach szeregów czasowych, z których do najczęściej
wykorzystywanych należy zaliczyć:

•modele tzw. tradycyjne, oparte na średniej ruchomej,
modele wygładzania wykładniczego oraz analityczne i
adaptacyjne modele tendencji rozwojowej także z
uwzględnieniem wahań periodycznych,

•modele oparte na teorii procesów stochastycznych: modele
procesów stacjonarnych (modele procesów autoregresji
AR(p), średniej ruchomej MA(q), autoregresji i średniej
ruchomej ARMA(p,q)), modele procesów niestacjonarnych
(np. model procesu zintegrowanego ARIMA(p,d,q)).

14

GK (WEiP(3) - 2011)

Metody prognozowania

Istotą

metod prognozowania przyczynowo-

skutkowego

jest budowanie prognoz na podstawie modelu

objaśniającego zachowanie (zmiany) zmiennej (zmiennych)
prognozowanej przez zmiany zmiennych objaśniających. W
praktyce najczęściej są wykorzystywane

modele

ekonometryczne

, a w przypadkach, gdy teoria nie wskazuje

na istnienie relacji pomiędzy zmienną prognozowaną a
zmiennymi objaśniającymi, natomiast w praktyce takie
relacje są stwierdzane – prognozowanie opiera się na

modelach symptomatycznych

.

Wymienione modele mogą być wykorzystywane do

prognozowania jedynie w warunkach, gdy znane są wartości
zmiennych objaśnianych w okresie prognozowania. Zatem
prognozowanie za pomocą tych modeli ma charakter
pośredni: najpierw wyznaczane są wartości zmiennych
objaśniających w okresie prognozowania, a następnie
prognoza wartości zmiennej prognozowanej.

15

GK (WEiP(3) - 2011)

Metody prognozowania

Model

Reguła

prognozowani

a

1

2

n

y ,y ,...,y

p

p

p

n

n 1

T

y ,y ,...,y

+

11

1k

21

2k

n1

nk

x

... x

x

... x

...

... ...

x

... x

*

*

11

1k

*

*

21

2k

*

*

n1

nk

x

... x

x

... x

...

... ...

x

... x

PRZESZŁOŚĆ

PRZYSZŁOŚĆ

Prognozy lub

decyzje

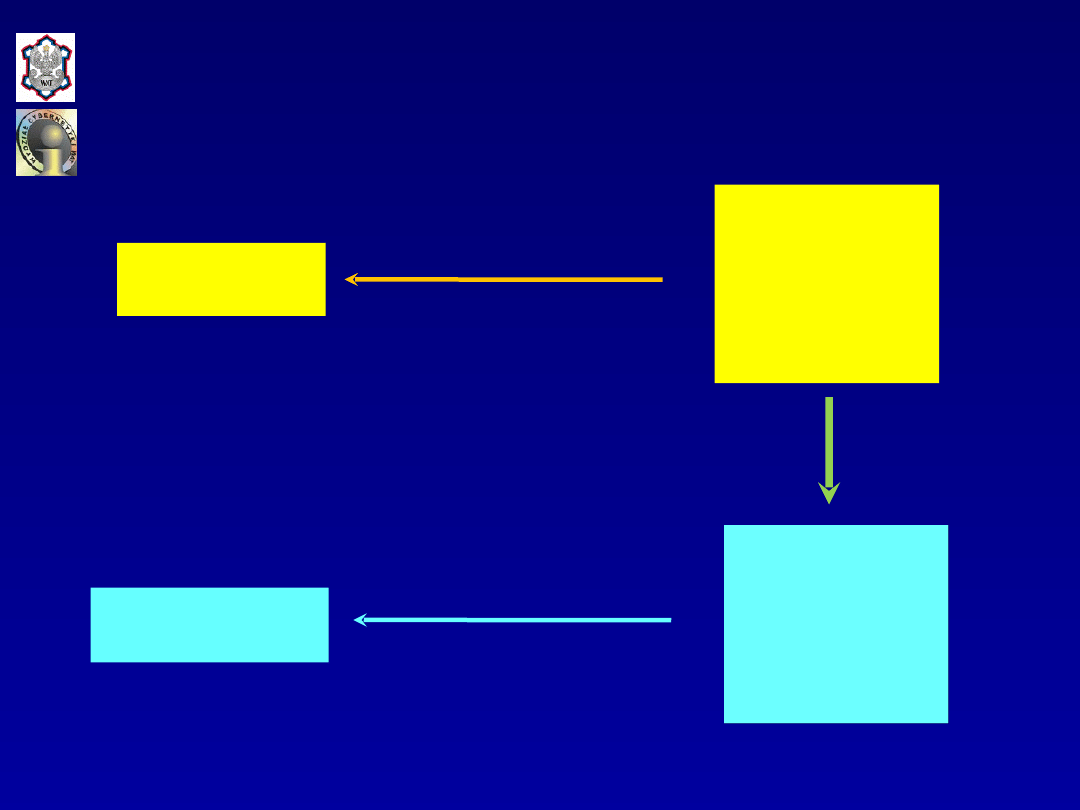
Schemat prognozowania jednej
zmiennej
z

k

zmiennymi objaśniającymi [M.

Cieślak]

16

GK (WEiP(3) - 2011)

Metody prognozowania

Metody

analogowe są wykorzystywane do

prognozowania zmiennych na podstawie danych o innych
zmiennych podobnych, których związku przyczynowego ze
zmienna prognozowaną nie można dowieść.

Istota zmiennych uwzględnianych w metodzie

analogowej może być taka sama jak zmiennej
prognozowanej (np. liczba gospodarstw domowych
użytkujących zmywarki do naczyń w Polsce i w krajach z
nami sąsiadujących), bądź inna (np. sprzedaż książek i
sprzedaż telewizorów).

Metody analogowe nie opierają na ekstrapolacji

prawidłowości charakteryzujących zmiany zmiennej
prognozowanej, odkrytych na podstawie diagnozowania jej
przeszłości, ale na założeniu o wspólnych drogach rozwoju
zmiennej prognozowanej i zmiennych do niej podobnych.

Omawiana klas metod jest wykorzystywana do

budowania prognoz średnio- i długookresowych.

17

GK (WEiP(3) - 2011)

Metody prognozowania

Podobieństwo

zmiennych

Regu

ła

prog

nozo

wan

i

a

1

2

n

y ,y ,...,y

p

p

p

n

n 1

T

y ,y ,...,y

+

1

1

1

s

2

2

1

s

r

r

1

s

y

... y

y

... y

... ... ...

y

... y

PRZESZŁOŚĆ

PRZYSZŁOŚĆ

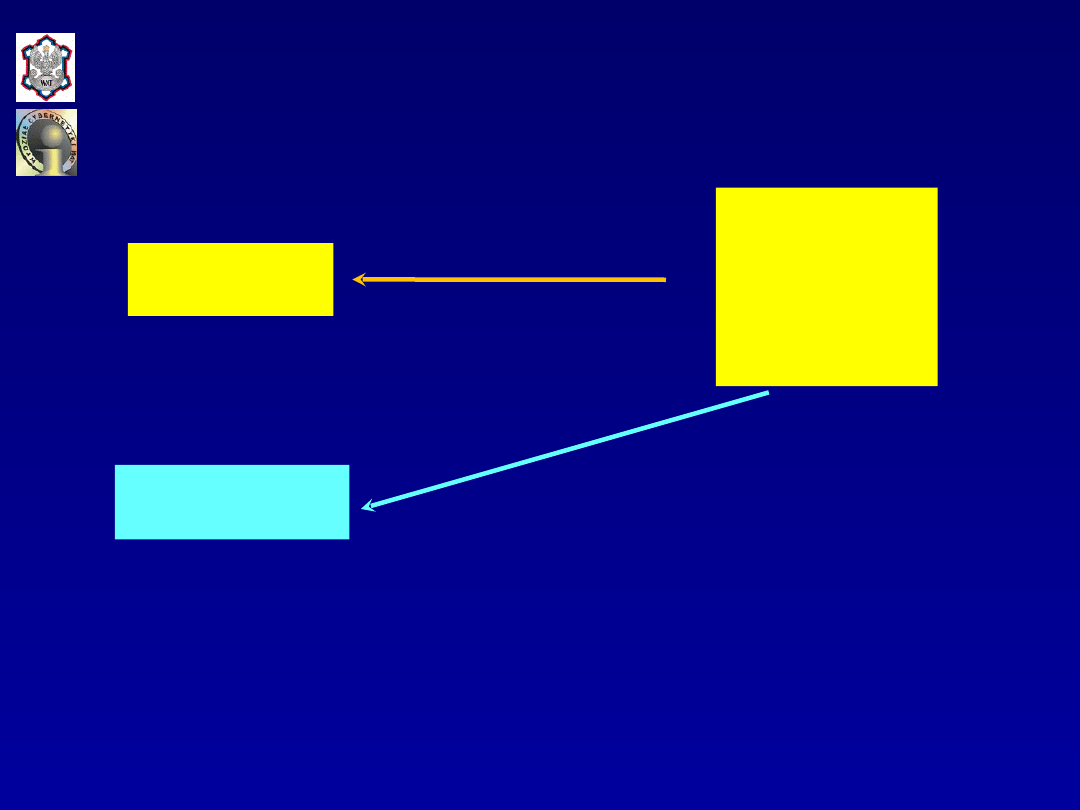
Schemat prognozowania analogowego
[M. Cieślak]

18

GK (WEiP(3) - 2011)

Metody prognozowania

Metody heurystyczne

polegają na korzystaniu z opinii

ekspertów. Istotą tych metod jest dążenie do połączenia
myślenia racjonalnego i intuicji. Ekspert buduje w myślach
model prognozowanego zjawiska, uwzględniając w nim fakty
znane i intuicyjnie przeczuwane, zarówno ilościowe, jak i
jakościowe. W procesie prognozowania udział bierze od kilku
do kilkudziesięciu ekspertów, którzy mogą swoje opinie
dotyczące prognozowanego zjawiska wypowiadać w jednej,
bądź w kilku kolejnych sesjach. W przypadku omawianych
metod istotne jest uzyskanie opinii ekspertów, zgodnych
według przyjętego kryterium oceny zgodności.

W ramach omawianej klasy metod najczęściej są

wykorzystywane: burza mózgów, metoda delficka i metoda
wpływów krzyżowych.

Opinie

ekspertów

o

prognozowanym

zjawisku

Prognoza

Model myślowy

Reguła

prognozowania

19

GK (WEiP(3) - 2011)

Metody prognozowania

Ponieważ

prognozowanie

jest przewidywaniem

przyszłych zdarzeń, zatem

prognozy

mogą być

nietrafne

zatem są

niepewne

. Miarą

stopnia niepewności

prognozy

jest

błąd prognozy

.

Prognoza

,

której stopień niepewności

(błąd) jest akceptowalny przez jej odbiorcę nosi nazwę

prognozy dopuszczalnej

.

W procesie prognozowania mogą być przyjmowane

różne założenia dotyczące relacji pomiędzy przeszłością a
przyszłością, które decydują o jakości prognozy. Skrajne
założenia, to:

•związki występujące między zjawiskiem prognozowanym a
innymi oddziałującymi na nie zjawiskami mają charakter
stały,

•związki występujące między zjawiskiem prognozowanym a
innymi oddziałującymi na nie zjawiskami w przeszłości
mogą podlegać mniejszym lub większym zmianom w
przyszłości.

20

GK (WEiP(3) - 2011)

Jakość prognoz

Błąd prognozy

określa się jako różnicę pomiędzy

rzeczywistą wartością zmiennej prognozowanej w okresie
prognozowania

T

(

T>n

) a prognozą tej zmiennej w tym samym

okresie prognozowania:

Błąd prognozy może być wyznaczany zarówno po upływie

okresu prognozowania, tzn. gdy

jest już znana

realizacja

zmiennej prognozowanej w okresie prognozowania, jak i przed
upływem okresu prognozowania, tzn. gdy realizacja zmiennej
prognozowanej

nie jest jeszcze znana

w okresie prognozowania.

W pierwszym przypadku mówi się o błędzie

ex post

, czyli o

trafności

prognozy, a w drugim o błędzie

ex ante

, czyli o

dokładności

prognozy.

W przypadku, gdy

znana jest rzeczywista wartość

zmiennej prognozowanej w okresie

prognozowania wyznaczany

błąd prognozy

ex post

jest

liczbą

równą różnicy między prognozą

a tą rzeczywistą wartością zmiennej prognozowanej. Błąd
prognozy

ex post

jest miarą

trafności

prognozy.

W przypadku, gdy w procesie prognozowania

nie jest

znana rzeczywista wartość zmiennej prognozowanej w okresie
prognozowania

, różnica między prognozą a nieznaną rzeczywistą

wartością zmiennej prognozowanej jest traktowana jako

zmienna

losowa

, której estymator odchylenia standardowego jest średnim

błędem prognozy

ex ante

.

Błąd prognozy

ex ante

jest miarą

dopuszczalności

prognozy.

*

p

T

T

Θ y

y .

=

-

21

GK (WEiP(3) - 2011)

Jakość prognoz

Niech

i=1,2,…,m

oznacza numer wykonanej prognozy

(numer okresu prognozowania), a oraz odpowiednio
prognozę i wartość rzeczywistą zmiennej prognozowanej w

i-

tym

okresie prognozowania. Najczęściej wykorzystywanymi

miarami są następujące:



bezwzględny błąd predykcji ex post w okresie prognozy i

(i=1,2,…,m):



względny błąd predykcji ex post w okresie prognozy i (i=1,2,

…,m):



średni błąd predykcji ex post (average error, AE lub mean

error, ME):

p

i

y

*

i

y

*

p

i

i

i

y

y

J = -

*

p

i

i

i

*
i

y

y

y

y

-

=













m

1

i

p

i

*

i

y

y

m

1

ME

22

GK (WEiP(3) - 2011)

Błędy prognozy ex post



średni błąd procentowy (average percentage error, APE lub
mean percentage error, MPE):

Wadą omówionych miar jest to, że dodatnie i ujemne błędy

prognozy znoszą się. Tego błędu nie mają następujące
miary absolutne:



średni błąd absolutny (average absolute error, AAE lub
mean absolute error, MAE)



średni absolutny błąd procentowy (average absolute
percentage error, AAPE lub mean absolute percentage
error, MAPE)

100

y

y

y

MAPE

100

y

y

y

m

1

MAPE

m

1

i

*

i

m

1

i

p

i

*

i

m

1

i

*

i

p

i

*

i

lub

































m

1

i

p

i

*

i

y

y

m

1

MAE









100

y

y

y

MPE

100

y

y

y

m

1

MPE

m

1

i

*

i

m

1

i

p

i

*

i

m

1

i

*

i

p

i

*

i

lub

























23

GK (WEiP(3) - 2011)

Błędy prognozy ex post

Porównanie

ME

i

MAE (MPE

i

MAPE)

dostarcza

informacji o popełnianych ewentualnych systematycznych
błędach zaniżania lub zawyżania prognoz w stosunku do
wartości zaobserwowanych. W przypadku, gdy prognozy są
systematycznie niższe lub wyższe od wartości
zaobserwowanych

ME

i

MAE

oraz

MPE

i

MAPE

są co do

wartości absolutnej równe sobie, natomiast, gdy prognozy są
różnokierunkowe (raz niższe, a raz wyższe) w stosunku do
wartości zaobserwowanych miary

ME

i

MPE

są znacznie niższe

odpowiednio od

MAE

i

MAPE

. Ponadto miary

MPE

i

MAPE

pozwalają na porównywanie różnych modeli wykorzystywanych
do prognozowania wartości tej samej zmiennej objaśnianej.

24

GK (WEiP(3) - 2011)

Błędy prognozy ex post

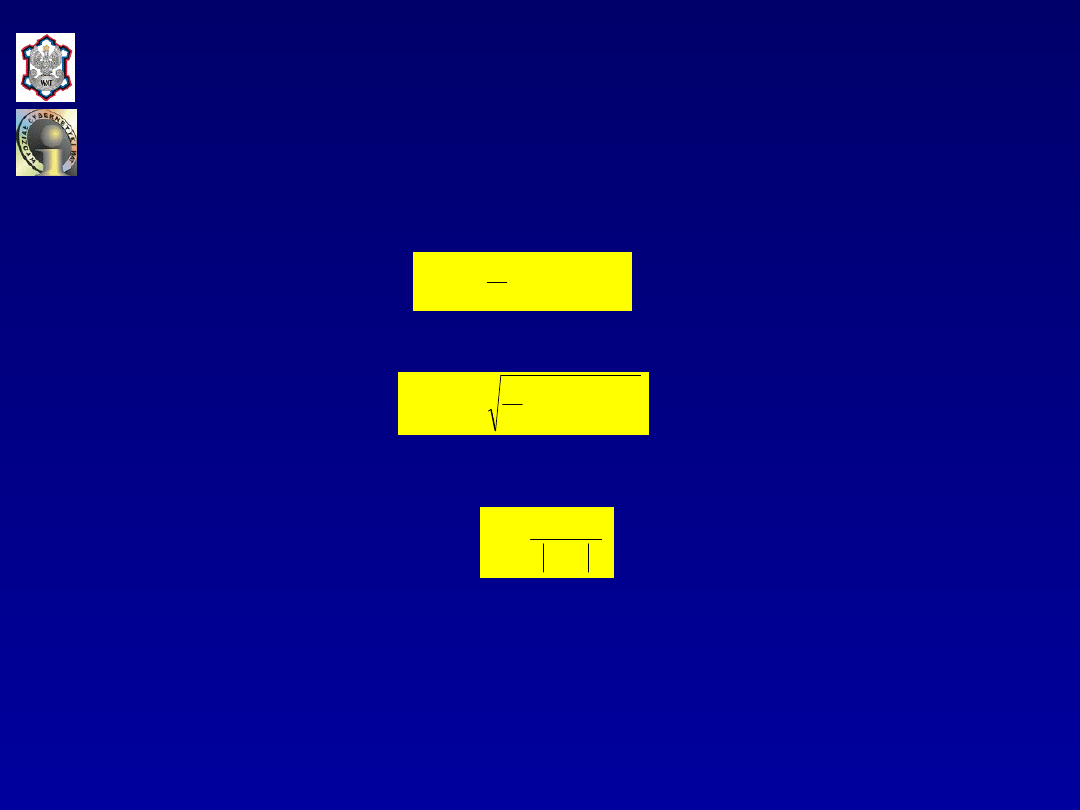
Szczególnie niepożądane w prognozowaniu są błędy
nietypowo duże. Obecność tych błędów może wykazać
następująca miara:



błąd średniokwadratowy (mean square error, MSE):



pierwiastek błędu średniokwadratowego (root mean square

error, RMSE):



względny błąd prognozy ex post:

Istotne różnice

MAE

i

RMSE wskazują na występowanie w

prognozach bardzo dużych błędów.

Podobne do przedstawionych wyżej miar są

wykorzystywane również miary, które zostały skonstruowane
na podstawie

średniego błędu procentowego (MPE)

.













m

1

i

2

p

i

i

y

y

m

1

RMSE

*













m

1

i

2

p

i

*

i

y

y

m

1

MSE

p

RMSE

v

.

ME

=

25

GK (WEiP(3) - 2011)

Błędy prognozy ex post

Do oceny dokładności prognozowania są wykorzystywane
następujące współczynniki:



współczynnik rozbieżności (equality coeffic

ient):

Niskie wartości wskaźnika

U

wskazują na dużą dokładność

prognoz.



współczynnik Theila:





 

 

 

 

 

0,1

U

,

y

m

1

y

m

1

RMSE

y

m

1

y

m

1

y

y

m

1

U

m

1

i

2

p

i

m

1

i

2

*

i

m

1

i

2

p

i

m

1

i

2

*

i

m

1

i

2

p

i

*

i

































 













m

1

i

2

*

i

m

1

i

2

p

i

*

i

2

y

y

y

I

26

GK (WEiP(3) - 2011)

Błędy prognozy ex post

Wartość

I

informuje o popełnionym przeciętnym błędzie

prognozy w rozpatrywanych

m

okresach prognozowania.

Współczynnik Theila można przedstawić w postaci
następującej sumy:

gdzie:



składnik jest miarą obciążoności prognozy, tj.

niewłaściwego określenia wartości oczekiwanej prognozy i
wyraża się zależnością:

przy czym: oraz ,

2

3

2

2

2

1

2

I

I

I

I







2

1

I





 









m

1

i

2

*

i

2

p

*

2

1

y

y

y

I







m

1

i

*

i

*

y

m

1

y







m

1

i

p

i

p

y

m

1

y

27

GK (WEiP(3) - 2011)

Błędy prognozy ex post



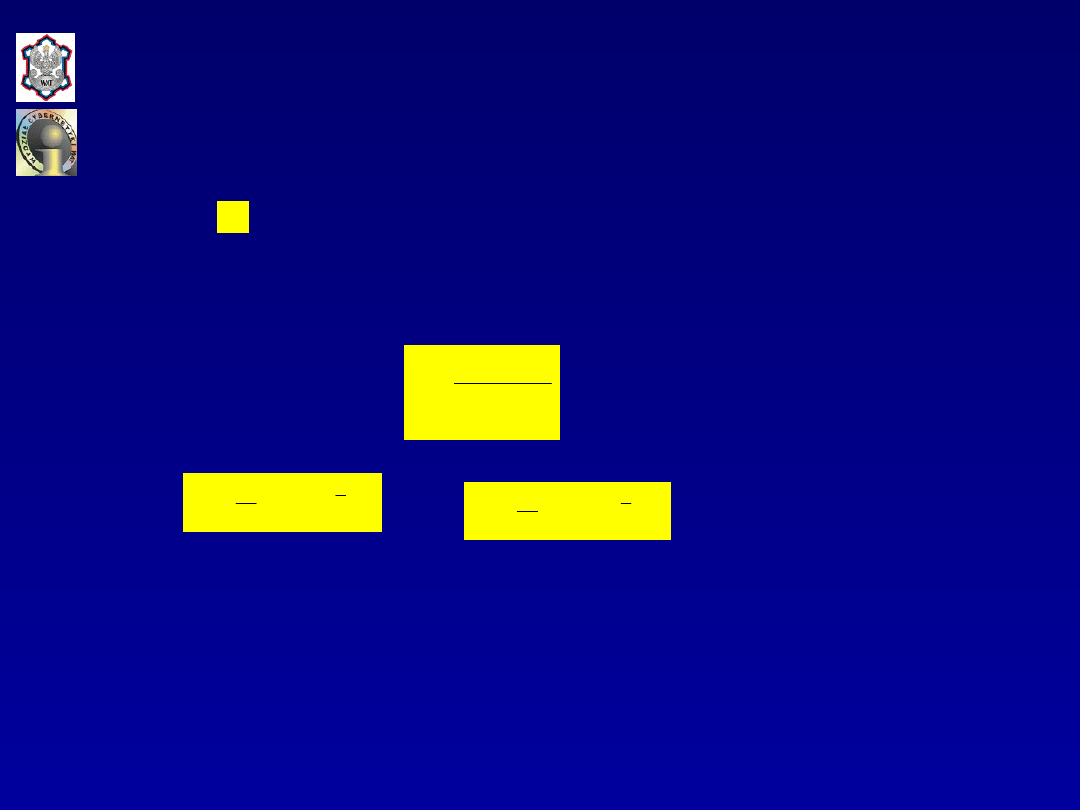
składnik jest miarą braku elastyczności modelu, tj.
stopnia dopasowania zmienności prognozy do rzeczywistych
wahań prognozowanej zmiennej objaśnianej (stopień
odwzorowania przez model wariancji zmiennej objaśnianej)
i wyraża się zależnością:

gdzie: oraz ,

2

2

I





 









m

1

i

2

*

i

2

p

*

2

2

y

S

S

I













m

1

i

2

*

*

i

2

*

y

y

m

1

S













m

1

i

2

p

p

i

2

p

y

y

m

1

S

28

GK (WEiP(3) - 2011)

Błędy prognozy ex post



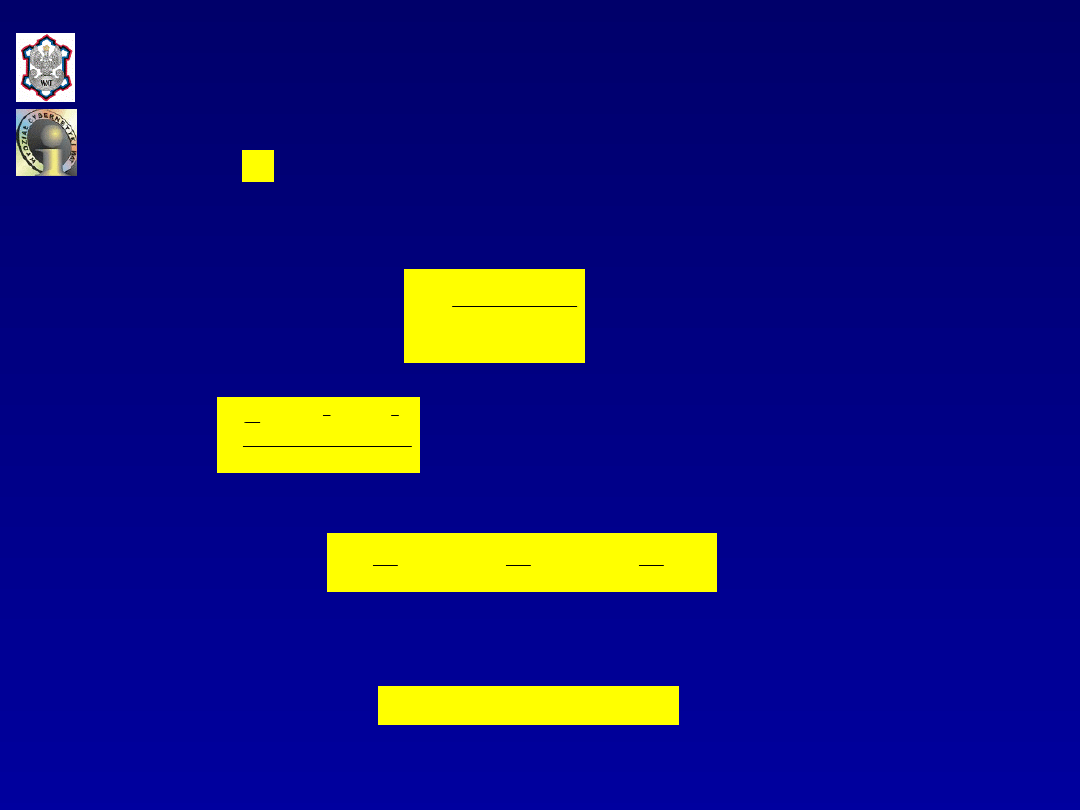
składnik jest miarą błędu niesystematycznego,
pozostałego po wyeliminowaniu obciążenia prognozy i
błędu wynikającego z braku elastyczności modelu (błędu
wariancji) i wyraża się zależnością:

gdzie:

Łatwiejsze w zastosowaniu są wskaźniki procentowe postaci:

W praktyce dąży się do tego, aby dla modelu

wykorzystywanego do predykcji spełnione były
następujące zależności:

.





 









m

1

i

2

*

i

2

p

*

2

3

y

r

1

S

2S

I

2

3

I



 



.

p

*

m

1

i

*

*

i

p

p

i

S

S

y

y

y

y

m

1

r













.

ˆ

ˆ

ˆ

100

I

I

I

100,

I

I

I

100,

I

I

I

2

2

3

2

3

2

2

2

2

2

2

2

1

2

1













.

ˆ

ˆ

ˆ

100

I

0

I

I

2

3

2

2

2

1

oraz







29

GK (WEiP(3) - 2011)

Błędy prognozy ex post

Błąd prognozy (predykcji) ex ante

może być tylko

szacowany, ponieważ w chwili wyznaczania prognozy nie jest
znana rzeczywista wartość zmiennej prognozowanej w
horyzoncie prognozowania. Sposób dokonywania oszacowania
tego błędu zależy od przyjętej metody prognozowania.

Dalej będzie rozważane szacowanie błędu

ex ante

dla

przypadku stosowania

metody prognozowania przyczynowo-

skutkowego i podstawowej reguły prognozowania w przypadku
jednorównaniowego liniowego modelu ekonometrycznego

.

Zgodnie z przyjętymi wcześniej założeniami błąd

prognozy

ex ante

będący różnicą między nieznaną wartością

zmiennej prognozowanej w okresie prognozowania a
wyznaczoną dla tego okresu prognozą, jest zmienną losową.
Powszechnie stosowaną charakterystyką rozproszenia
możliwych prognoz wokół możliwych realizacji zmiennej
prognozowanej w okresie prognozowania

T>n

jest

wariancja

prognozy (predykcji)

:

(

)

2

2

*

p

p

T

T

T n.

S

E y

y

,

>

=

-

30

GK (WEiP(3) - 2011)

Błędy prognozy ex ante

Wyznaczenie wariancji prognozy uzyskanej według reguły
podstawowej dla jednorównaniowego liniowego modelu
ekonometrycznego.

Wektor oszacowań parametrów strukturalnych modelu

uzyskany za
pomocą KMNK jest postaci

i stąd wartości teoretyczne zmiennej prognozowanej
(objaśnianej)

Ponieważ

więc





,

y

X

X

X

a

T

1

T





.

Xa

y

ˆ

e

y

y



ˆ





.

ˆ

y

X

X

X

X

y

Xa

y

y

y

e

T

1

T















31

GK (WEiP(3) - 2011)

Błędy prognozy ex ante

Macierz wariancji i kowariancji estymatorów parametrów
strukturalnych modelu jest postaci:

przy czym nieobciążonym estymatorem wariancji resztowej



e

2

jest

(

k - liczba estymowanych parametrów strukturalnych

modelu ekonometrycznego

):

Przy założeniu znajomości wartości zmiennych
objaśniających w okresie prognozy oraz stałości wariancji
składnika losowego modelu, prognoza otrzymana na
podstawie rozpatrywanego modelu ekonometrycznego jest
równa:

gdzie

x

*

oznacza kolumnowy wektor wartości zmiennych

objaśniających w okresie prognozowania, a



*

- składnik

losowy w okresie prognozowania, przy czym zgodnie z
założeniami KMNK

 





,

X

X

σ

a

D

1

T

2

e

2





.

k

n

e

e

S

T

2

e





 





 

,

α

x

ε

E

α

x

ε

α

x

E

y

E

y

T

*

*

T

*

*

T

*













*

( )

*

Eε

0.

=

32

GK (WEiP(3) - 2011)

Błędy prognozy ex ante

Ponieważ nie są znane prawdziwe wartości parametrów
strukturalnych modelu w praktyce korzysta się z ich
oszacowania, co powoduje, że prognoza przyjmie postać:

Należy zauważyć, że

oraz

gdzie



*

2

oznacza wariancję składnika losowego w

okresie prognozowania.

.

a

x

y

T

*

p



   

 

.

α

x

a

E

x

a

x

E

y

E

T

*

T

*

T

*

p







  



































,

x

X

X

x

σ

x

α

a

α

a

E

x

x

α

a

α

a

x

E

α

a

x

E

α

x

a

x

E

y

D

*

1

T

T

*

2

*

*

T

T

*

*

T

T

*

2

T

*

2

T

*

T

*

p

2



























33

GK (WEiP(3) - 2011)

Błędy prognozy ex ante

34

GK (WEiP(3) - 2011)

Błędy prognozy ex ante

Wariancja prognozy w rozpatrywanym przypadku jest

wariancją zmiennej losowej określającej różnicę pomiędzy
rzeczywistą wartością zmiennej prognozowanej (objaśnianej)
a wartością prognozy w okresie prognozowania, tj.:

Zgodnie z założeniami predykcji prostej, przyjmuje się, że
wartość oczekiwana te zmiennej losowej jest równa zeru, tj.:

przy czym

oraz

Uwzględniając przyjęte założenia dotyczące predykcji

prostej oraz wcześniejsze obliczenia, wariancję predykcji
można wyznaczyć z następującej zależności:













.

*

*

*

*

*

*

*

p

*

p

ε

α

a

x

ε

α

x

a

x

ε

α

x

y

y

y

































,

*

*

*

p

ε

α

a

x

E

y

y

E









 

α

a

E



 

.

0

ε

E

*















 





 

 

 

 





.

x

X

X

x

1

σ

σ

a

x

D

ε

D

α

x

D

a

x

D

ε

α

x

D

a

x

D

ε

α

x

a

x

D

y

y

D

T

*

1

T

*

2

*

2

*

*

2

*

2

*

2

*

2

*

*

2

*

2

*

*

*

2

*

p

2











 































35

GK (WEiP(3) - 2011)

Błędy prognozy ex ante

Wariancja predykcji może być także wyznaczona z zależności
równoważnej postaci:

gdzie oznacza wariancję estymatora

a

i

parametru

strukturalnego



i

oraz oznacza kowariancję estymatorów

a

i

i

a

j

parametrów strukturalnych



i

i



j

odpowiednio.

Ponieważ wariancja



*

2

składnika losowego modelu w okresie

prognozowania nie jest znana, zatem korzysta się z wartości
jej estymatora

S

e

2

, a oszacowanie błędu prognozy

ex ante

wyznacza się z zależności:

Pierwiastek kwadratowy z powyższej zależności, tj.

S

p

nosi

nazwę

średniego błędu predykcji (prognozy) ex ante

(bezwzględnego błędu prognozy ex ante)

.





 

 

 

,

,a

a

cov

x

x

2

a

var

x

σ

y

y

D

1

k

0

i

k

i

j

j

i

*

j

*

i

k

0

i

i

2

*

i

2

*

*

p

2





















 

i

a

var





j

i

,a

a

cov









.

x

X

X

x

1

S

S

T

*

1

T

*

2

e

2
p







36

GK (WEiP(3) - 2011)

Błędy prognozy ex ante

Do

ceny dopuszczalności prognozy stosuje się

względny błąd

predykcji (prognozy) ex ante

:

Kryterium dopuszczalności predykcji punktowej formułuje się
często w postaci następującego warunku nakładanego na

względny błąd

predykcji (prognozy) ex ante

:

.

poszukuje się

takiego rozwiązania, dla którego spełniona byłaby
Nierówność

v

p

 

, w której



jest z góry zadaną liczbą, zależną

od konkretnych warunków i potrzeb wymaganych w zakresie
dokładności prognozowania. W praktyce przyjmuje się
najczęściej

 = 0,05

lub

 = 0,1

.

W przypadku prognoz

jakościowych

(ale także

ilościowych) formułuje
Się kryterium dopuszczalności prognozy postaci

przy czym liczby

 > 0

oraz

0 <

 < 1

(wiarygodność prognozy)

są dobierane z uwzględnieniem wymagań praktycznych.





,

γ

ε

y

y

P

p

*







p

p

p

S

v

.

y

=

W przypadku

predykcji przedziałowej

analizuje się

najczęściej trzy następujące

błędy prognozy ex ante

:



prawdopodobieństwo spełnienia się prognozy (wiarygodność

predykcji) – ze z góry arbitralnie przyjętym poziomem ufności

1-



prognozy przedziałowej (

1-



oznacza procent trafnych

prognoz przedziałowych w długim ciągu prognozowania),



precyzja prognozy (predykcji)

d

p

- połowa przedziału

prognozy (określa maksymalny błąd prognozy przedziałowej),



względna precyzja predykcji

v

p

:

p

p

p

d

v

.

y

=

37

GK (WEiP(3) - 2011)

Błędy prognozy ex ante

Błędy prognoz ex post

mogą być wykorzystywane do

oceny

dopuszczalności

prognozy pod następującymi warunkami:

•nie uległy dezaktualizacji przesłanki przyjęte do wyznaczenia
prognoz poprzednich i rozpatrywanej,

•do wyznaczenia rozpatrywanej prognozy stosuje się tę samą
metodę i regułę co przy wyznaczaniu prognoz poprzednich,

•przedział weryfikacji poprzednich prognoz jest taki sam jak
horyzont prognozy rozpatrywanej.
Jeżeli prognoza jest wyznaczana na jeden okres, to wykorzystuje
się z zasady miarę w postaci

bezwzględnego

lub

względnego

błędu prognozy ex post w okresie prognozy t

. W pozostałych

przypadkach można posługiwać się

średnim absolutnym błędem

procentowym (MAPE)

lub

błędem średniokwadratowym (MSE)

–

preferowany ze względu na porównywalność z

bezwzględnym

błędem prognozy ex ante

. Jako kryterium dopuszczalności

prognozy przyjmuje się arbitralnie (na ogół) krytyczną wartość
wybranego błędu prognozy

ex post

.

W praktyce często dopuszczalności prognozy określa się

na podstawie

błędów prognoz wygasłych

, wyznaczanych z

wykorzystaniem tej samej metody co do wyznaczenia prognozy
rozpatrywanej.

Prognoza wygasła

– prognoza wyznaczona na taki okres

prognozowania, dla którego jest znana prawdziwa wartość
zmiennej prognozowanej, tzn. na okres

t



n

. Błędy prognoz

wygasłych oblicza się tak samo jak błędy prognoz

ex post

.

38

GK (WEiP(3) - 2011)

Błędy ex post i dopuszczalność

prognozy

Do badania dopuszczalności prognozy może być stosowany

także

współczynnik Janusowy

(oparty na prognozach wygasłych)

postaci:

w którego liczniku znajduje się błąd średniokwadratowy prognozy

ex post

, a w mianowniku – wariancja resztowa modelu,

wykorzystywanego do prognozowania.

Współczynnik

J

2

umożliwia ocenę dopuszczalności

prognozy poprzez ocenę aktualności modelu użytego do jej
utworzenia. Jeżeli

J

2



1

, to model wykorzystywany w procesie

prognozowania jest nadal aktualny, a prognozy tworzone na jego
podstawie – dopuszczalne.
Jeżeli odbiorca prognozy nie poda własnych kryteriów
dopuszczalności prognozy, to w praktyce opiera się ją – w
zależności od możliwości obliczenia - na

względnym błędzie

prognozy (predykcji) ex post

lub

ex ante

. I tak przyjmuje się, że:

•

v

p



0,03

– prognoza jest bardzo dobra,

•

0,03 <

v

p



0,05

– prognoza jest dobra,

•

0,05 <

v

p



0,1

– prognoza dopuszczalna,

•

0,1 <

v

p

– prognoza niedopuszczalna.

(

)

(

)

m

2

p

i

i

2

i 1

n

2

t

t

t 1

1

y

y

m

J

,

1

ˆ

y

y

n

=

=

-

=

-

�

�

39

GK (WEiP(3) - 2011)

Błędy ex post i dopuszczalność

prognozy

1. Sformułowanie zadania prognostycznego –

określenie zjawiska (zmiennej), którego
kształtowanie się będzie przedmiotem
prognozowania, zmiennych charakteryzujących to
zjawisko oraz zasięgu prognozy (okresu
prognozowania).

2. Określenie przesłanek prognostycznych –

sformułowanie hipotez dotyczących powiązań
pomiędzy zmienną prognozowaną a zmiennymi ją
charakteryzującymi.

3. Zebranie danych empirycznych.
4. Określenie metody (metod) prognozowania.
5. Wyznaczenie prognozy.
6. Oszacowanie trafności prognozy.
7. Wykorzystanie i monitorowanie prognozy.

40

GK (WEiP(3) - 2011)

Etapy procesu prognozowania

41

GK (WEiP(3) - 2011)