Jednorównaniowy

liniowy model

ekonometryczny

Literatura

1.

A. D. Aczel:

Statystyka w zarządzaniu

. PWN, Warszawa, 2000.

2.

J. Dziechciarz:

Ekonometria. Metody, przykłady, zadania

. AE,

Wrocław, 2003.

3.

D. Fiłatowa, M. Grzywaczewski:

Wstęp do ekonometrii

teoretycznej

. Wyd.

Politechniki Radomskiej, Radom, 2004.

4.

J.B. Gajda:

Ekonometria praktyczna

. Absolwent, Łódź, 2002.

5.

J.B. Gajda

:

Ekonometria. Wykład i łatwe obliczenia w programie

komputerowym

. Wyd. C.H. BECK, Warszawa, 2004.

6.

A.S. Goldberger:

Teoria ekonometrii

. PWE, Warszawa, 1972.

7.

A. Goryl, Z. Jędrzejczak, K. Kukuła, J. Osiewalski, A. Walkosz:

Wprowadzenie do ekonometrii w przykładach i zadaniach

. PWN,

Warszawa, 2003.

8.

M. Gruszczyński, M. Podgórska:

Ekonometria

. SGH, Warszawa,

2003.

9.

B. Guzik, W. Jurek:

Podstawowe metody ekonometrii

. AE, Poznań,

2003.

10. T. Kufel: Ekonometria. Rozwiązywanie problemów z

wykorzystaniem programu GRETL. PWN, Warszawa, 2007.

2

GK (WEiP(01) - 2011)

Literatura (cd)

12.

G.S. Maddala:

Ekonometria

(tłum. z jęz. ang. „Introduction to

Economectrics”, Wiley, Chichester England, 2001). PWN, Warszawa,

2006.

13.

E. Nowak:

Zarys metod ekonometrii.

Zbiór zadań. PWN, Warszawa,

2006.

14.

W. Ostasiewicz:

Metody ilościowe w ekonomii.

AE, Wrocław, 1999.

15.

A. Snarska:

Statystyka. Ekonometria. Prognozowanie. Ćwiczenia z

Excelem.

Placet, Warszawa, 2005.

16.

J. Sołtysiak:

Podstawy ekonometrii. Ekonomia – Statystyka –

Matematyka.

Wydawnictwo Gdańskiej Szkoły Humanistycznej,

Gdańsk, 2007.

17.

D. Strahl, E. Sobczak, M. Markowska, B. Bal-Domańska:

Modelowanie ekonometryczne z EXCELEM. Materiały pomocnicze

do laboratoriów z ekonometrii.

AE, Wrocław, 2002.

18.

H. Theil:

Zasady ekonometria praktyczna.

PWN, Warszawa, 1979.

19.

A. Welfe:

Ekonometria.

PWE, Warszawa, 2003.

20.

A. Welfe:

Ekonometria. Zbiór zadań.

PWE, Warszawa, 2003.

21.

J.W. Wiśniewski, Z. Zieliński:

Elementy ekonometrii.

UMK, Toruń,

1998.

22.

A. Zeliaś:

Teoria prognozy.

PWE, Warszawa, 1979.

23.

A. Zeliaś:

Prognozowanie ekonomiczne. Teoria, przykłady, zadania.

PWN, Warszawa, 2004.

3

GK (WEiP(01) - 2011)

Badanie zależności między

zjawiskami

Prowadzenie jakiejkolwiek działalności, szczególnie

gospodarczej wymaga umiejętności przewidywania zachowania
się (zmian) badanej wielkości, reprezentującej interesujące nas
zjawisko w zależności od zmian innych zjawisk, których wpływ
na zjawisko badane uważamy za istotny. Takie przewidywanie
nosi nazwę

prognozowania

.

Zależności występujące między zjawiskami mogą być

ustalane w sposób intuicyjny lub z wykorzystaniem metod
formalnych. W pierwszym przypadku mówi się o

modelowaniu

intuicyjnym

, a w drugim – o

modelowaniu ekonometrycznym

.

Modelowanie i prognozowanie intuicyjne

polega na

nieformalnej, intuicyjnej ocenie charakteru zmian badanego
zjawiska w zależności od zmian innych zjawisk i wyciągnięciu na
tej podstawie wniosku (prognozy), co do przyszłego zachowania
badanego zjawiska, gdy zjawiska wpływające na jego zachowanie
osiągną pewien stan. Stosuje się metody ekspertów oraz
analogii.

Modelowanie i prognozowanie ekonometryczne

można

traktować jako formalne ujęcie intuicyjnie określonych
zależności pomiędzy zjawiskiem badanym a zjawiskami na nie
wpływającymi. Ta formalizacja jest zwykle dokonywana z
wykorzystaniem metod z zakresu statystyki matematycznej.
Modelowanie ekonometryczne obiektywizuje proces
prognozowania.

4

GK (WEiP(01) - 2011)

Między badanymi zjawiskami ekonomicznymi mogą

zachodzić następujące wiążące je zależności:

•zależność przyczynowa

– wynika ze związku przyczynowego,

którego istnienie można wyjaśnić na gruncie wiedzy
teoretycznej (np. wpływ wzrostu dochodów na wzrost
wydatków),

•zależność symptomatyczna

– wynika z istnienia przyczyny

kształtującej zależność, chociaż nie ma wyjaśniającej jej teorii,

•zależność korelacyjna

– stwierdzona na podstawie obserwacji

o podobnym zachowaniu zjawisk, chociaż nie ma teorii
potwierdzającej istnienie związku przyczynowego i nie
wiadomo, czy taka teoria w ogóle istnieje,

•zależność pozorna

– występuje wtedy, gdy nie można znaleźć

przyczyn, powodujących podobne zachowanie badanych zjawisk
(np. korelacja pomiędzy liczbą bocianów a liczbą urodzin),

•niezależność pozorna

– występuje wtedy, gdy w wyniku badań

nie udaje się potwierdzić powiązania między zjawiskami w
rzeczywistości od siebie zależnymi. Taki przypadek może
zachodzić w procesie modelowania ekonometrycznego i jest
spowodowany niedostateczną precyzją prowadzonych badań
(np. zbyt mała próba, błędny dobór narzędzi badawczych).

5

GK (WEiP(01) - 2011)

Badanie zależności między

zjawiskami

O dwóch zjawiskach mówi się, że są skorelowane

(statystycznie zależne), jeżeli zmianie wartości jednego z nich
towarzyszy

skłonność

drugiego z nich do zmiany swojej

wartości. Zatem, zależność statystyczna nie oznacza, iż zmiana
wartości jednego ze zjawisk jest przyczyną zmiany wartości
drugiego z nich, chociaż tego nie można wykluczyć.

Zależność statystyczną można badać na dwa sposoby:

korzystając z

analizy korelacji

oraz korzystając z

analizy

regresji

. Pierwsze podejście pozwala tylko na określenie siły i

kierunku zależności pomiędzy badanymi zjawiskami
(nieprzydatne do prognozowania), natomiast drugie podejście
pozwala na określenie formalnej postaci wyrażenia
opisującego zależności pomiędzy badanymi zjawiskami, które
może być wykorzystane w procesie prognozowania.

Ekonometria posługuje się drugim z wymienionych podejść.

Podstawą

modelowania ekonometrycznego

jest zjawisko

zależności statystycznej

,

inaczej

korelacji

.

6

GK (WEiP(01) - 2011)

Badanie zależności między

zjawiskami

Co to jest ekonometria?

Ekonometria

- nauka

o metodach badania ilościowych

zależności występujących między zjawiskami ekonomicznymi za
pomocą wyspecjalizowanego aparatu statystyczno-matematycznego.

Ekonometria koncentruje się głównie na:
•ilościowej ocenie relacji między zjawiskami ekonomicznymi,
•konfrontacji teorii ekonomii z praktyką ekonomiczną,
•prognozowaniu wyników działalności gospodarczej.

Problemy ekonometryczne:
•weryfikowanie ogólnych praw i twierdzeń z zakresu ekonomii przy
wykorzystaniu danych empirycznych,
•testowanie hipotez ekonomicznych,
•prognozowanie zjawisk ekonomicznych.

Wspólną cechą wymienionych grup problemów badawczych jest to, że ich
merytoryczna weryfikacja jest oparta na danych empirycznych.

7

GK (WEiP(01) - 2011)

Model ekonometryczny

Model ekonometryczny

jest

kwantyfikowaną relacją zadaną w postaci
jednego równania matematycznego lub
układu takich równań, łączącą w sposób
zgodny z teorią ekonomii dane
empiryczne dotyczące zjawisk
gospodarczych. Parametry tej relacji są
przedmiotem estymacji.

8

GK (WEiP(01) - 2011)

Ze względu na rolę, jaką odgrywają zjawiska

ekonomiczne uwzględniane w modelu, można je podzielić na
dwa rodzaje: zjawiska ekonomiczne wyjaśniane przez model,
nazywane

zmiennymi objaśnianymi (endogenicznymi)

, oraz

zjawiska ekonomiczne, które oddziałują na zmienne
objaśniane, nazywane

zmiennymi objaśniającymi

(egzogenicznymi)

.

Ogólnie model ekonometryczny jest przedstawiany w

następującej postaci formalnej:

gdzie:

X=(X

1

,X

2

,…,X

k

)

- wektor wartości zmiennych

objaśniających uznanych, jako istotnie oddziałujące na
zmienną objaśnianą

y

,



- wektor parametrów strukturalnych

modelu, charakteryzujących wpływ poszczególnych zmiennych
objaśniających na kształtowanie się zmiennej objaśnianej,

ε

-

błąd modelu spowodowany czynnikami losowymi (tzw. składnik
losowy lub odchylenie losowe modelu),

f

– analityczna postać

funkcji zmiennych objaśniających i parametrów
strukturalnych, ustalana w trakcie budowy modelu.





ε

X,

f

y

,





9

GK (WEiP(01) - 2011)

Model ekonometryczny

Modele ekonometryczne można klasyfikować według różnych
kryteriów, np.:

•

liczby zmiennych objaśniających

- modele z

jedną

i

wieloma

zmiennymi objaśniającymi,

•

postaci analitycznej

- modele

liniowe

i

nieliniowe

,

•

liczby zmiennych objaśnianych (równań) w modelu

- modele

jedno-

i

wielorównaniowe

. W modelu jednorównaniowym

występuje tylko jedna zmienna objaśniana,

•

interpretacji zmiennych objaśniających

– modele

przyczynowo-skutkowe

(wszystkie zmienne objaśniające są

traktowane jako przyczyny kształtowania się zmiennej
objaśnianej), modele

symptomatyczne

(zmienne objaśniające

są wybierane a priori i są traktowane jako symptomy pewnych
zjawisk kształtujących zmienną objaśnianą),

•

roli czynnika czasu w modelu

- modele z

statyczne

i

dynamiczne

, a wśród tych ostatnich - modele

autoregresyjne

i

modele

tendencji rozwojowej

.

10

GK (WEiP(01) - 2011)

Model ekonometryczny

Etapy modelowania
ekonometrycznego

1. Sformułowanie modelu

ekonometrycznego.

2. Zgromadzenie odpowiednich danych

empirycznych.

3. Dobór zmiennych modelu.
4. Estymacja parametrów modelu.
5. Weryfikacja merytoryczna i

statystyczna modelu.

6. Interpretacja ekonomiczna

uzyskanych wyników.

11

GK (WEiP(01) - 2011)

Dalej będzie rozpatrywany

jednorównaniowy liniowy

względem parametrów strukturalnych statyczny model
ekonometryczny z wieloma zmiennymi objaśniającymi.

Statycznym modelem ekonometrycznym jest model,

który zawiera tylko zmienne egzogeniczne przypisane do tej
samej chwili czasu co zmienna endogeniczna

. Postać

analityczna (zapis macierzowy) takiego modelu jest

równaniem algebraicznym

postaci:

gdzie:

y

- zmienna objaśniana (zmienna losowa),

X

i

- zmienne

objaśniające (zmienne nielosowe),

α

i

- parametry strukturalne

modelu (skalary),



- składnik losowy (zmienna losowa).

0

1

1

2

2

k

k

yα α X

α X

... α X

ε X a e

= +

+

+ +

+ =

+

12

GK (WEiP(01) - 2011)

Liniowy model ekonometryczny

W rozpatrywanym modelu ekonometrycznym

występują wielkości znane (

y

oraz

X

i

)

i nieznane, tzw.

parametry. Wyróżnia się

parametry strukturalne

(

α

i

) oraz

parametry struktury stochastycznej

modelu (dotyczą

probabilistycznych własności składnika losowego



).

Praktyczna użyteczność modelu wymaga oszacowania
wartości (estymacji) tych parametrów na podstawie zebranych
danych empirycznych znanych wielkości występujących w
modelu, tj.

y

oraz

X

i

i przyjętych założeń (zostaną

przedstawione dalej).

Często jest stosowany inny równoważny (szczegółowy)

zapis rozpatrywanego modelu:

gdzie:

y

t

- obserwacja zmiennej objaśnianej,

x

it

- obserwacja i-tej

zmiennej objaśniającej,

α

i

- i-ty parametr strukturalny

modelu,



t

- wartość składnika losowego w obserwowanej

zmiennej objaśnianej,

t

– numer kolejnej obserwacji.

,n)

1,2,

(t

t

kt

k

2t

2

1t

1

0

t

ε

x

α

x

α

x

α

α

y

...

,

...















13

GK (WEiP(01) - 2011)

Liniowy model ekonometryczny









































































































































kn

2n

1n

k2

22

12

k1

21

11

k

2

1

k

1

0

n

2

1

in

i2

i1

i

n

2

1

x

x

x

1

x

x

x

1

x

x

x

1

X

X

X

X

α

α

α

α

,

ε

ε

ε

ε

,

x

x

x

X

,

y

y

y

y

...

...

...

...

...

...

...

...

,

...

,

,

,

,

...

...

...

...

1

Powiązanie modelu w postaci ogólnej i szczegółowej:

14

GK (WEiP(01) - 2011)

Liniowy model ekonometryczny

Interpretacja parametrów strukturalnych modelu
ekonometrycznego.

Warunkowa wartość oczekiwana zmiennej objaśnianej przy
znanych wartościach zmiennych objaśniających jest równa:

a jej pochodna cząstkowa po

x

it

:

Stąd wynika, że parametr strukturalny



i

mierzy oczekiwaną

zmianę zmiennej objaśnianej

y

t

jako efekt zmiany

i-tej

zmiennej objaśniającej

x

it

o jedną jednostkę,

gdy wartości

innych zmiennych objaśniających modelu pozostają
niezmienione

(warunek

ceteris paribus

).





,n

1,2,

t

,

x

α

x

α

x

α

α

x

y

E

kt

k

2t

2

1t

1

0

T

t

t

...

...













 

.

i

it

T

t

t

α

x

x

y

E







15

GK (WEiP(01) - 2011)

Liniowy model ekonometryczny

Składnik losowy

(



) w modelu ekonometrycznym jest

uwzględniany z następujących powodów:

•w modelu nie mogą być ujęte wszystkie zmienne
objaśniające,

•postać modelu może być nieadekwatna do rzeczywistych
zależności pomiędzy zmiennymi,

•zachowanie podmiotów ekonomicznych jest trudno
przewidywalne,

•dane statystyczne reprezentujące poszczególne zmienne
ujęte w modelu mogą być obarczone błędami,

•zmienność próby, tj. zmienność oszacowania parametrów
strukturalnych modelu w zależności od danych empirycznych.

16

GK (WEiP(01) - 2011)

Liniowy model ekonometryczny

Estymacja (szacowanie wartości parametrów

strukturalnych, wyznaczanie ocen parametrów strukturalnych)
liniowego modelu ekonometrycznego jest dokonywana na
podstawie danych empirycznych, opisujących kształtowanie się
zmiennej objaśnianej oraz zmiennych objaśniających.
Procedurę estymacji można sprowadzić do procedury w
wyniku, której zostaną przypisane wartości liczbowe
parametrom strukturalnym modelu, zapewniające jego
najlepsze dopasowanie do zebranych danych empirycznych.

Najpowszechniejszą metodą szacowania (estymacji)

parametrów strukturalnych rozpatrywanego liniowego modelu
ekonometrycznego jest procedura aproksymacyjna nazywana

klasyczną metodą najmniejszych kwadratów (KMNK

). Idea tej

metody sprowadza się do takiego wyznaczenia ocen
parametrów

α

0

, α

1

, α

2

,

, α

k

, aby

suma kwadratów odchyleń

zaobserwowanych wartości zmiennej objaśnianej (dane
empiryczne) od jej wartości obliczonych z modelu (tzw.
wartości teoretyczne) była najmniejsza

.

Estymacja modelu liniowego

17

GK (WEiP(01) - 2011)

Zadanie estymacji parametrów strukturalnych

α

0

, α

1

,

α

2

,

, α

k

jest równoważne zadaniu estymacji wartości

oczekiwanej zmiennej objaśnianej na podstawie danych
empirycznych (próby statystycznej). Ponieważ przyjęto, że w
rozpatrywanym modelu wartość ta wyraża się równaniem
linii (hiperpłaszczyzny), więc poprzez odpowiedni dobór
(estymację) wartości parametrów strukturalnych

α

0

, α

1

,

α

2

,

, α

k

poszukiwana jest linia najlepiej „dopasowana” do

zebranych danych empirycznych. Za najlepiej „dopasowaną”
linię w metodzie KMNK uważa się taką, która minimalizuje
sumę kwadratów reszt

e

tj. różnic które traktuje się jako realizacje składnika
losowego



t

.

Oszacowania (oceny) parametrów strukturalnych

(wartości liczbowe tych parametrów), oznaczane dalej przez

a

0

, a

1

, a

2

,

, a

k

różnią się od nieznanych ich rzeczywistych

wartości

α

0

, α

1

, α

2

,

, α

k

i mogą być różne dla różnych

zbiorów danych empirycznych tej samej zmiennej
objaśnianej i tych samy zmiennych objaśniających.

t

t

t

ˆ

e

y

y ,

= -

18

GK (WEiP(01) - 2011)

Estymacja modelu liniowego

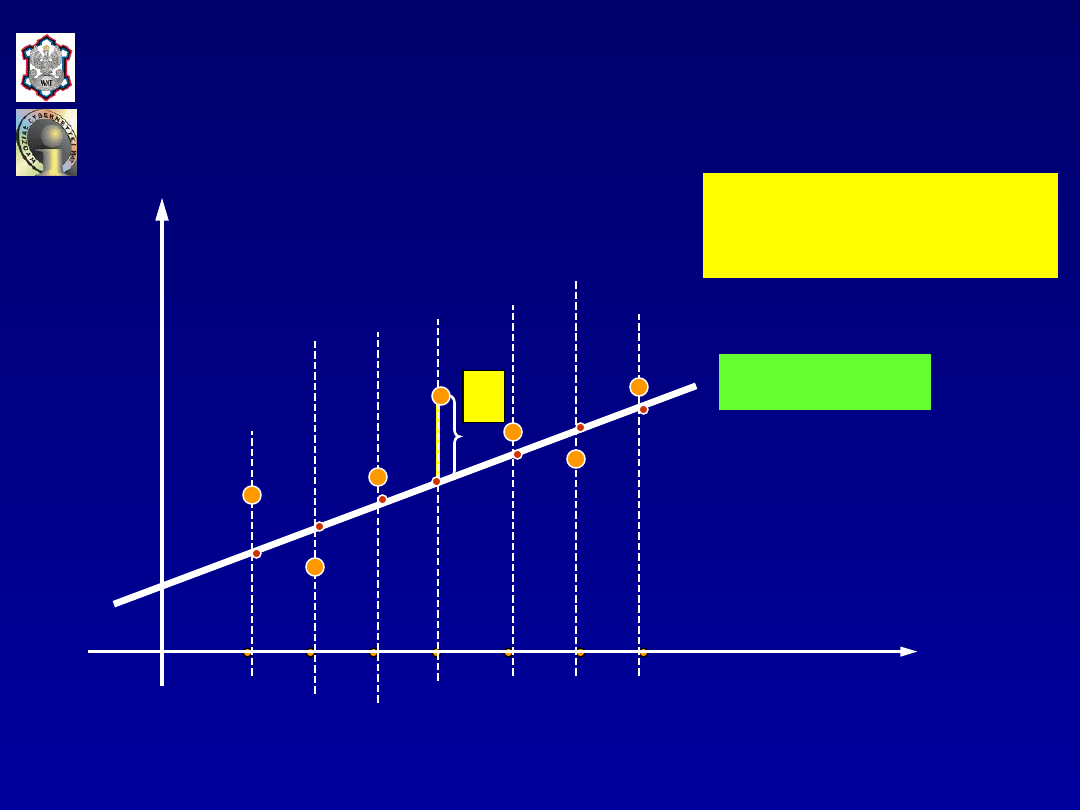
Ideę KMNK można zapisać formalnie w sposób następujący:

gdzie:

przy czym

są oszacowaniami (wartościami) parametrów strukturalnych
modelu, uzyskanymi za pomocą KMNK.

 





a

a

ψ

min

yˆ

y

e

n

1

t

2

t

t

n

1

t

2

t

















,n)

1,2,

(t

,

x

a

x

a

x

a

a

y

kt

k

2t

2

1t

1

0

t

...

...

ˆ













k

1

0

a

,...,

a

,

a

19

GK (WEiP(01) - 2011)

Estymacja modelu liniowego

Dalej zostanie rozpatrzony przypadek, gdy zmienna

objaśniana jest kształtowana tylko przez jedną zmienną
objaśniającą, liniowy model ekonometryczny przyjmuje postać

równania linii prostej

w przestrzeni dwuwymiarowej, w której

osią rzędnych jest oś wartości przyjmowanych przez zmienną
objaśnianą, a osią odciętych – oś wartości przyjmowanych
przez zmienną objaśniającą:

Obserwacje (dane empiryczne) zmiennej objaśnianej i

zmiennej objaśniającej można traktować jako punkty w
przestrzeni, których układ graficzny sugeruje liniową
zależność między zmienną objaśnianą a objaśniającą.

Przy założeniu, że powyższy model spełnia

założenia

Gaussa-Markowa

,

równanie postaci

:

wyznacza linię regresji populacji generalnej (regresja typu I),
co oznacza, że przechodzi ona przez punkty, będące
wartościami średnimi wielu niezależnych doświadczeń,
których jedną realizację reprezentuje próba

y

1

, y

2

,

, y

n

.

,n)

1,2,

(t

,

x

α

α

y

t

1

0

t

...











t

1

0

t

x

α

α

)

E(y





20

GK (WEiP(01) - 2011)

Estymacja modelu liniowego

Zbiór

y

1

, y

2

,

, y

n

jest zbiorem niezależnych zmiennych

losowych o rozkładzie normalnym o tej samej wariancji, ale o
różnych wartościach oczekiwanych, tj.:

Parametry

α

0

i

α

1

nie są znane, ale mogą zostać oszacowane

na podstawie próby statystycznej, tzn. wartości
zaobserwowanych zmiennej objaśnianej

y

i objaśniającej

x

. Na

podstawie próby otrzymuje się równanie linii regresji II
rodzaju (w próbie) postaci:

gdzie:
- wartość teoretyczna zmiennej objaśnianej

y

odpowiadającej

t

-

tej obserwacji,

- estymatory parametrów strukturalnych modelu,
odpowiednio:

α

0

, α

1

.

Ponieważ estymatory parametrów strukturalnych modelu są
zmiennymi losowymi, więc w praktyce są stosowane ich
realizacje w próbie, które noszą nazwę

ocen

lub

oszacowań

parametrów strukturalnych

i są oznaczane przez

a

0

, a

1

odpowiednio. Zatem wartości teoretyczne zmiennej
objaśnianej będą wyznaczane z zależności:





.

,σ

x

α

α

N

:

y

t

1

0

t



)

...

ˆ

ˆ

y

ˆ

t

,n

1,2,

(t

,

x

α

α

t

1

0







t

yˆ

1

0

ˆ

,

ˆ





.

...

ˆ

,n)

1,2,

(t

,

x

a

a

y

t

1

0

t







21

GK (WEiP(01) - 2011)

Estymacja modelu liniowego

Ponieważ reszty

są obliczane jako

różnice pomiędzy wartościami empirycznymi

zmiennej objaśnianej a jej wartościami teoretycznymi

, więc

każda wartość empiryczna zmiennej objaśnianej może być
traktowana jako suma wartości teoretycznej, obliczonej z
wyestymowanego modelu ekonometrycznego i odpowiedniej
reszty, tj.:

Występują zatem cztery następujące funkcje:
• linia regresji populacji generalnej:
• linia regresji próby (wartości teoretyczne):
• wartości empiryczne w populacji generalnej:
• wartości empiryczne w próbie:

t

t

t

yˆ

y

e





t

t

t

0

1 t

t

(t 1,2,...,n)

ˆ

y

y e a a x e ,

.

=

= + = +

+

,

t

1

0

t

x

α

α

)

E(y





,

ˆ

t

1

0

t

x

a

a

y





,

t

t

1

0

t

x

y













.

t

t

1

0

t

e

x

a

a

y







22

GK (WEiP(01) - 2011)

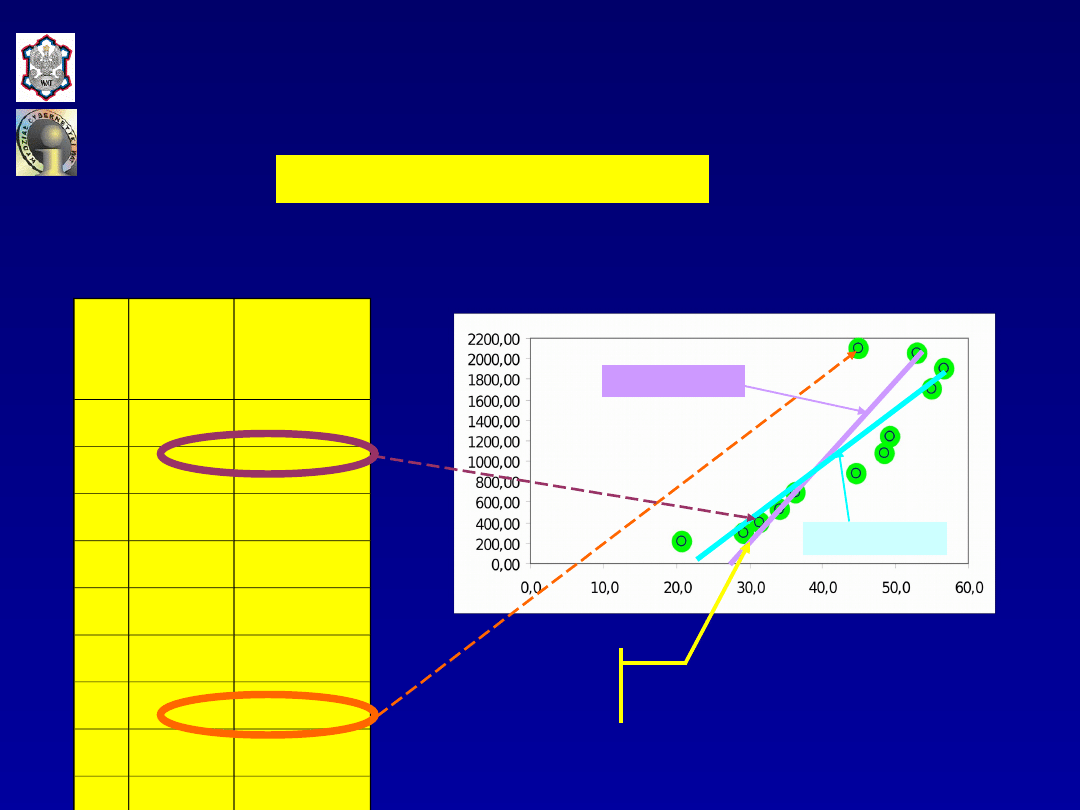
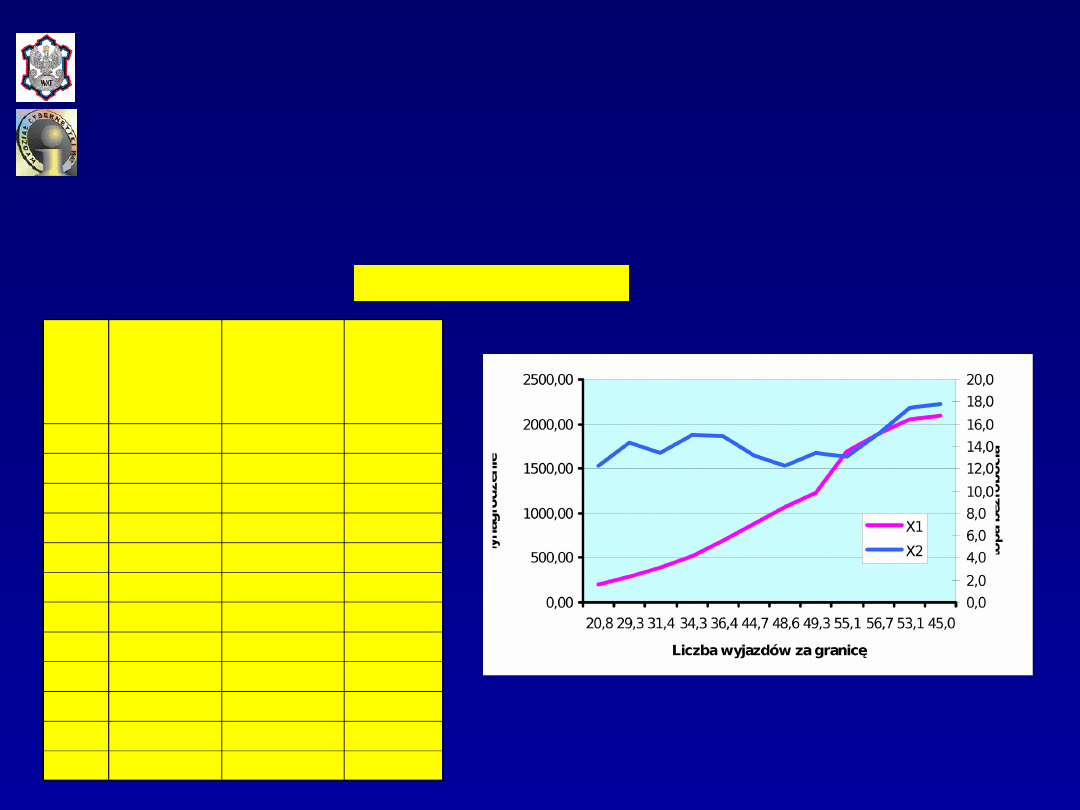
Estymacja modelu liniowego

Rok

Liczba

wyjazdów

za

granicę

[mln]

Przeciętne

wynagrodzen

ie brutto [zł]

199

1

20,8

205,63

199

2

29,3

289,73

199

3

31,4

390,43

199

4

34,3

525,02

199

5

36,4

690,92

199

6

44,7

874,30

199

7

48,6

1065,76

199

8

49,3

1232,69

199

9

55,1

1697,12

200

0

56,7

1893,74

200

1

53,1

2045,11

200

2

45,0

2097,83

Dane empiryczne

Graficzna prezentacja danych
empirycznych

,12)

1,2,

(t

t

t

1

0

t

ε

x

α

α

y

...

,









Linie
regresji

 

 

x

a

a

y

1

1

1

0





 

 

x

a

a

y

2

1

2

0





23

GK (WEiP(01) - 2011)

Estymacja modelu liniowego

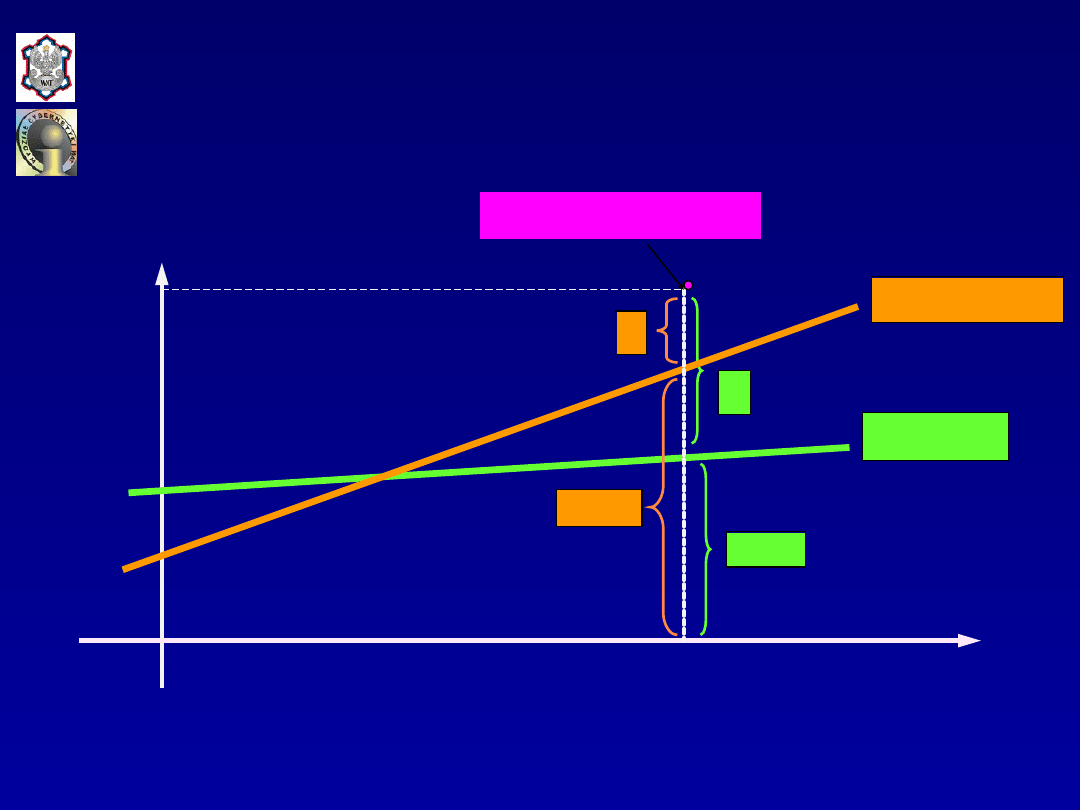
y

x

x

a

a

yˆ

1

0





t

e

t

1

0

x

a

a 

x

α

α

)

y

E(

1

0





t

ε

t

1

0

x

α

α 

x

t

t

t

1

0

t

ε

x

α

α

y







y

t

24

GK (WEiP(01) - 2011)

Estymacja modelu liniowego

 

min

a

n

1

t

2

t

e

a

ψ









x

1

x

2

x

3

x

4

x

5

x

6

x

7

x

4

e

x

a

a

y

ˆ

1

0





y

25

GK (WEiP(01) - 2011)

Estymacja modelu liniowego

Funkcja

jest dodatnio określoną formą kwadratową parametrów

a

0

i

a

1

,

zatem

warunkiem koniecznym

istnienia jej minimum jest

zerowanie się pierwszych pochodnych cząstkowych względem
ocen parametrów strukturalnych, tj. zachodzenie równości:

a

warunkiem wystarczającym

– dodatniość drugich czystych

pochodnych, tj.:

oraz dodatnio określony

hesjan

, tj.

H(a

0

,a

1

) > 0

, tj.



















n

1

t

t

e

ψ(a)

2

0

a

ψ(a)

0,

a

ψ(a)

1

0













0

a

ψ(a)

0,

a

ψ(a)

2

1

2

2

0

2













0

a

a

ψ(a)

a

a

ψ(a)

a

ψ(a)

a

ψ(a)

0

1

2

1

0

2

2

1

2

2

0

2





























26

GK (WEiP(01) - 2011)

Estymacja modelu liniowego

Po wykonaniu różniczkowania funkcji

(a)

względem

a

0

otrzymuje się:

stąd ostatecznie

Oznacza to, że

suma reszt modelu jest równa zeru

.

0

)

x

a

a

(y

2

a

)

x

a

a

(y

a

ψ(a)

t

1

0

n

1

t

t

0

2

t

1

0

n

1

t

t

0





















































.

ˆ

0

e

y

y

x

a

a

y

n

1

t

t

n

1

t

t

t

n

1

t

t

1

0

t

























27

GK (WEiP(01) - 2011)

Estymacja modelu liniowego

Po zróżniczkowaniu funkcji

(a)

względem

a

1

otrzymuje się:

stąd ostatecznie

Oznacza to, że

reszty modelu nie są skorelowane ze zmienną

objaśniającą

.

0

)

x

a

a

(y

x

2

a

)

x

a

a

(y

a

ψ(a)

t

1

0

n

1

t

t

t

1

2

t

1

0

n

1

t

t

1





















































.

ˆ

0

e

x

y

y

x

x

a

a

y

x

n

1

t

t

t

n

1

t

t

t

t

n

1

t

t

1

0

t

t

























28

GK (WEiP(01) - 2011)

Estymacja modelu liniowego

Warunkiem wystarczającym

istnienia minimum funkcji

(a)

jest dodatnio określony hesjan tej funkcji postaci:

Jak łatwo zauważyć warunek istnienia minimum funkcji

(a)

jest spełniony, bowiem hesjan

H(a

0

,a

1

) > 0

.

.













































n

1

t

2

j

i

n

1

t

2

t

n

1

t

t

n

1

t

t

2

1

2

0

1

2

1

0

2

2

0

2

1

0

)

x

(x

4

x

2

x

2

x

2

2n

a

ψ(a)

a

a

ψ(a)

a

a

ψ(a)

a

ψ(a)

)

,a

H(a

29

GK (WEiP(01) - 2011)

Estymacja modelu liniowego

Minimum funkcji

(a)

istnieje w punkcie, w którym

są spełnione warunki konieczne istnienia ekstremum, tj. w
punkcie, w którym pochodne cząstkowe funkcji

(a)

po

ocenach

a

0

i

a

1

parametrów strukturalnych



0

i



1

przyjmują

wartości równe zeru (0). Zatem punkt ten wyznacza
następujący układ równań, nazywany

układem równań

normalnych

:

Układ ten może być rozwiązany względem

a

0

oraz

a

1

za pomocą dowolnej znanej metody rozwiązywania układu
równań algebraicznych.













































0

)

x

a

a

(y

x

a

ψ(a)

0

)

x

a

a

(y

a

ψ(a)

t

1

0

n

1

t

t

t

1

t

1

0

n

1

t

t

0

30

GK (WEiP(01) - 2011)

Estymacja modelu liniowego

Po rozwinięciu, układ równań normalnych przyjmuje postać:

Rozwiązując powyższy układ otrzymuje się następujące
zależności do wyznaczania ocen

a

0

i

a

1

parametrów

strukturalnych



0

i



1

modelu:













































































1

0

n

1

t

t

n

1

t

t

t

1

n

1

t

t

0

n

1

t

t

a

a

x

y

x

a

x

na

y

n

1

t

2

t

x

x

a

y

a

1

0





2

n

1

t

t

t

n

1

t

t

n

1

t

2

2

t

n

1

t

t

t

1

)

x

(x

/

)

y

)(y

x

(x

x

n

x

/

y

x

n

y

x

a





































































31

GK (WEiP(01) - 2011)

Estymacja modelu liniowego

Oszacowania (estymatory) parametrów strukturalnych
modelu liniowego otrzymane za pomocą metody KMNK
mają następujące własności:

•liniowość

– estymator jest sumą zmiennych losowych,

•nieobciążoność

– wartość oczekiwana estymatora jest

równa wartości szacowanego parametru, tj.

•efektywność

– ma minimalną wariancję,

•zgodność

– estymator jest stochastycznie zbieżny do

szacowanego parametru, tj.

0,1)

(i

,

α

)

E(a

i

i





.

1,

}

α

a

P{

lim

0,1)

(i

i

i

n















32

GK (WEiP(01) - 2011)

Estymacja modelu liniowego

KMNK – model z wieloma

zmiennymi

Wszystkie dotychczasowe rozważania dotyczące

modelu z jedną zmienną objaśniającą można łatwo rozszerzyć
na przypadek liniowego modelu ekonometrycznego z

wieloma

zmiennymi objaśniającymi

.

Postać analityczna (zapis macierzowy) takiego modelu

jest następująca:

gdzie:

y

- zmienna objaśniana (zmienna losowa),

X

i

- zmienne

objaśniające (zmienne nielosowe),

α

i

- parametry strukturalne

modelu (skalary),



- składnik losowy (zmienna losowa).

Przyjmuje się, że powyższy model spełnia wszystkie

założenia Gaussa-Markowa, umożliwiające zastosowanie
KMNK do estymacji jego parametrów strukturalnych.





















X

ε

X

α

X

α

X

α

α

y

k

k

2

2

1

1

0

...

33

GK (WEiP(01) - 2011)

Kryterium

KMNK

dla modelu z wieloma zmiennymi

objaśniającymi jest takie samo jak dla modelu z jedną
zmienna objaśniającą:

Warunkiem koniecznym

istnienia minimum funkcji

(a)

jest:

a

warunkiem wystarczającym

- dodatnia określoność

hesjanu

H(a

0

,a

1

)

tej funkcji.

0

a

ψ(a)

,

0,

a

ψ(a)

0,

a

ψ(a)

k

1

0



















...

 





min

n

1

t

2

t

t

n

1

t

2

t

yˆ

y

e

a

a

ψ

















34

GK (WEiP(01) - 2011)

KMNK – model z wieloma

zmiennymi

Stąd układ równań normalnych przyjmuje postać:

a hesjan:

k)

,

...

0,1,2,

(i

...

...





























































0,

)

x

a

x

a

x

a

a

(y

x

2

a

)

x

a

x

a

x

a

a

(y

a

ψ(a)

tk

k

t2

2

t1

1

0

n

1

t

t

ti

i

2

tk

k

t2

2

t1

1

0

n

1

t

t

i

.

...

...

...

...

...

...

...

...

2

k

2

1

k

2

0

k

2

k

0

2

2

1

2

0

1

2

k

0

2

1

0

2

2

0

2

k

1

0

a

ψ(a)

a

a

ψ(a)

a

a

ψ(a)

a

a

ψ(a)

a

ψ(a)

a

a

ψ(a)

a

a

ψ(a)

a

a

ψ(a)

a

ψ(a)

)

,a

,

,a

H(a



















































35

GK (WEiP(01) - 2011)

KMNK – model z wieloma

zmiennymi

W praktyce wygodniej jest posługiwać się zapisem
macierzowym modelu ekonometrycznego, tj.:

oraz

W zapisie macierzowym wektor reszt modelu wyrazi się
zależnością:

Zatem w celu uzyskania oceny parametrów strukturalnych,
zgodnie z ideą KMNK minimalizacji będzie podlegać funkcja
postaci:







X

y

.

e

Xa

y





.

Xa

y

e





min

e

e

ψ(a)

a

T





36

GK (WEiP(01) - 2011)

KMNK – model z wieloma

zmiennymi

W zapisie wektorowym

warunek konieczny

(układ równań

normalnych) istnienia minimum funkcji

(a)

przyjmie

postać:

Stąd otrzymuje się równanie

po rozwiązaniu, którego uzyskuje się następujący wektor
oszacowań parametrów strukturalnych modelu:

.

y

X

X)

(X

a

T

1

T







 















.

0

Xa

2X

y

2X

Xa

X

a

y

X

2a

y

y

a

Xa

X

a

y

X

a

Xa

y

y

y

a

Xa

y

Xa

y

a

a

e

e

a

ψ(a)

T

T

T

T

T

T

T

T

T

T

T

T

T

T

T





















































y

X

Xa

X

T

T



37

GK (WEiP(01) - 2011)

KMNK – model z wieloma

zmiennymi

Analizując zależność

warto zwrócić uwagę na to, że występująca w niej macierz

tzw. macierz momentów może być przedstawiona w postaci:

y

X

X)

(X

a

T

1

T





X

X

T

.

...

...

...

...

...

...

...

...

...



















































































































n

1

t

2

kt

n

1

t

2t

kt

n

1

t

1t

kt

n

1

t

kt

n

1

t

kt

2t

n

1

t

2

2t

n

1

t

1t

2t

n

1

t

2t

n

1

t

kt

1t

n

1

t

2t

1t

n

1

t

2

1t

n

1

t

1t

n

1

t

kt

n

1

t

2t

n

1

t

1t

T

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

n

X

X

38

GK (WEiP(01) - 2011)

KMNK – model z wieloma

zmiennymi

Na podstawie uzyskanych oszacowań parametrów
strukturalnych modelu i danych empirycznych wyznacza
się:

•oszacowanie wariancji składnika losowego (wariancja
reszt)

•oszacowanie macierzy wariancji i kowariancji ocen
parametrów strukturalnych modelu

•standardowe błędy oszacowania parametrów
strukturalnych modelu

gdzie

d

ii

, (i=0,1,…,k)

jest elementem z głównej przekątnej

macierzy

D

2

(a)

,

•przedziały ufności dla oszacowań parametrów
strukturalnych modelu

1

k

n

e

1

k

n

e

e

S

n

1

t

2

t

T

2

e

















.

X)

(X

S

(a)

D

1

T

2

e

2





39

GK (WEiP(01) - 2011)

KMNK – model z wieloma

zmiennymi

ii

i

d

)

S(a 





.

...,k)

0,1,2,

(i

,

γ

1

)

S(a

t

a

α

)

S(a

t

a

P

i

1)

(k

γ,n

i

i

i

1)

(k

γ,n

i























Należy mieć na względzie to, że

średni

błąd oszacowania każdego parametru
strukturalnego

modelu zależy zarówno od

siły

wewnętrznej korelacji

zmiennej

objaśniającej związanej z parametrem
strukturalnym z pozostałymi zmiennymi
objaśniającymi, jak i od siły

korelacji

zewnętrznej

, tj. między zmienną objaśnianą,

a wszystkimi zmiennymi objaśniającymi.

40

GK (WEiP(01) - 2011)

KMNK – model z wieloma

zmiennymi

Własności wektora

a

oszacowań parametrów

strukturalnych modelu liniowego wyznaczonego metodą
KMNK:









y

n

0

y

n

e

y

n

e

y

n

y

y

y

aX

y

y

0

e

X

a

e

(Xa)

e

y

0

Xa

X

y

X

Xa)

(y

X

e

X

0

y

1

y

1

e

1

,1

1,1,

1

Xa

y

e,

Xa

y

n

1

t

t

n

1

t

t

n

1

t

t

n

1

t

t

t

n

1

t

t

T

T

T

T

T

T

T

T

T

T

T

T

T

T

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

...

ˆ





































































41

GK (WEiP(01) - 2011)

KMNK – model z wieloma

zmiennymi

KMNK może być stosowana w przypadkach, gdy spełnione są
następujące założenia (Gaussa-Markowa):

Założenie 1.

Model jest niezmienniczy ze względu na

obserwacje

Założenie 2.

Model jest liniowy względem parametrów

strukturalnych lub jest sprowadzalny do takiej postaci:

Założenie 3.

Relacje występujące między zmiennymi w modelu

są stabilne.

Założenie 4.

Zmienne objaśniające są nielosowe.

n)

1,...,

(t

...

...

y

t









),

,ε

,x

,

,x

f(x

)

,ε

,x

,

,x

(x

f

t

kt

2t

1t

t

kt

2t

1t

t

ε

Xα

ε

X

α

X

α

X

α

α

y

k

k

2

2

1

1

0

















...

42

GK (WEiP(01) - 2011)

KMNK – założenia

Założenie 5.

Elementy macierzy

X

(wartości zmiennych

objaśniających) są nielosowe i są ustalone w powtarzalnych
próbach –

warunek identyfikacji

. Przyjęcie tego założenia

powoduje, że rozkład zmiennej objaśnianej nie jest
rozkładem warunkowym względem zmiennych
objaśniających, tzn. spełnione są:

Założenie 6.

Zmienne objaśniające są wolne od

współliniowości, tzn., że żadna ze zmiennych objaśniających
nie może być kombinacją liniową pozostałych. Formalnie
oznacza to, iż macierz wartości zmiennych objaśniających

X

ma pełny rząd kolumnowy, tj.:

r(X) = k+1

(w konsekwencji

także

r(X

T

X) = k+1

).

Założenie 7.

Liczba obserwacji (danych empirycznych) musi

spełniać nierówność:

n > k+1

.

.

...

,

...

)

(y

D

)

,x

,

,x

|x

(y

D

)

E(y

)

,x

,

,x

|x

E(y

t

2

kt

2t

1t

t

2

t

kt

2t

1t

t





43

GK (WEiP(01) - 2011)

KMNK – założenia

Założenie 8.

Składnik losowy



ma

n-wymiarowy

rozkład

normalny:

Założenie 9

. Występujące zakłócenia, które reprezentuje

składnik losowy mają tendencję do wzajemnej redukcji, co
oznacza, że wartość oczekiwana tego składnika jest równa
zeru:

Założenie 10

.

Składnik losowy jest sferyczny, co oznacza, że:

a. nie występuje

autokorelacja

składnika losowego

:

b. składnik losowy jest

homoskedastyczny

, (ma skończoną i

stałą w czasie wariancję):

   





.

:

ε

,D

ε

E

N

2



 

.

0

ε

E



,

0

τ

0,

)

,ε

Cov(ε

τ

t

t







 

.

I

σ

ε

D

2

2



44

GK (WEiP(01) - 2011)

KMNK – założenia

Założenie 11.

Składnik losowy nie jest skorelowany z żadną

zmienną objaśniającą.

Założenie 12.

Informacje zawarte w próbie są jedynymi

informacjami, na podstawie których dokonuje się estymacji
parametrów liniowego modelu ekonometrycznego.

Podane założenia definiują tzw.

standardowy model

liniowy

45

GK (WEiP(01) - 2011)

KMNK – założenia

Przykład

Oszacować parametry strukturalne liniowego modelu
ekonometrycznego , opisującego relację pomiędzy liczbą
wyjazdów zagranicznych Polaków (

y

) z przeciętnym

wynagrodzeniem (

X

1

) oraz wielkością stopy bezrobocia (

X

2

)

w Polsce latach 1991-2002. Postać modelu:

Rok

Liczba

wyjazdów

za granicę

[mln] y

Przeciętne

wynagrodz

enie brutto

[zł]

X

1

Stopa

bezroboc

ia [%]

X

2

1991

20,8

205,63

12,2

1992

29,3

289,73

14,3

1993

31,4

390,43

13,4

1994

34,3

525,02

15,0

1995

36,4

690,92

14,9

1996

44,7

874,30

13,2

1997

48,6

1065,76

12,3

1998

49,3

1232,69

13,4

1999

55,1

1697,12

13,1

2000

56,7

1893,74

15,1

2001

53,1

2045,11

17,5

2002

45,0

2097,83

17,8

.

ε

X

α

X

α

α

y

2

2

1

1

0









46

GK (WEiP(01) - 2011)

Rozwiązanie.

Oszacowanie

a

0

,

a

1

i

a

2

parametrów strukturalnych



0

,



1

i



2

modelu otrzymuje się z następującego wyrażenia

(macierzowego):

Macierz

X

:

Wektor

y

:

.

y

X

X)

(X

a

T

1

T

























































17,8

2097,83

1

17,5

2045,11

1

15,1

1893,74

1

13,1

1679,12

1

13,4

1232,69

1

12,3

1065,76

1

13,2

874,30

1

14,9

690,92

1

15,0

525,02

1

13,4

390,43

1

14,3

289,73

1

12,2

205,63

1













































































45,0

53,1

56,7

55,1

49,3

48,6

44,7

36,4

34,3

31,4

29,3

20,8

47

GK (WEiP(01) - 2011)

Przykład

Obliczenie oszacowań (ocen) parametrów strukturalnych
modelu:

















2507,7

195179,794

172,2

195179,794

1

19501281,8

13008,28

172,2

13008,28

12

X

X

T

.

y

X

X)

(X

T

1

T

















































2,4186

0,018

57,2451

a

a

a

2

1

0































17482

0,04307411

93600

0,00006788

32967

0,54451985

93600

0,00006788

21859

0,00000029

59729

0,00065747

32967

0,54451985

59729

0,00065747

23694

7,18447393

1

T

X

X

48

GK (WEiP(01) - 2011)

Przykład

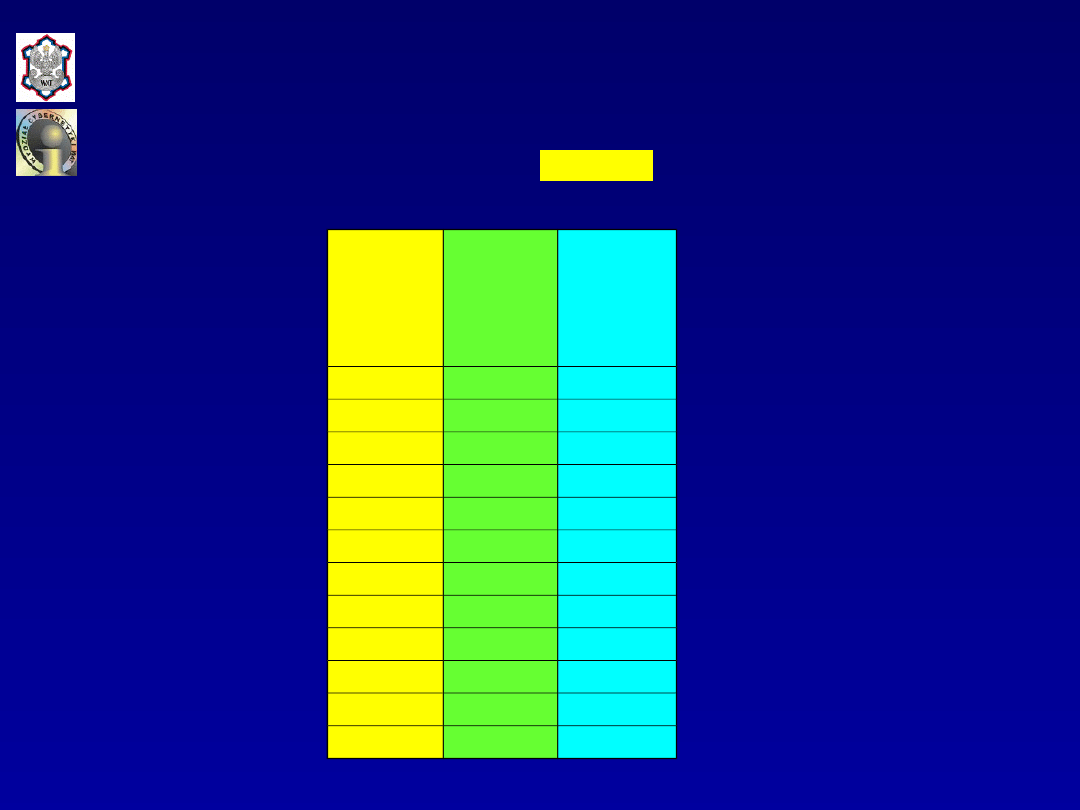
Obliczenie reszt modelu z zależności:

.

ˆ

t

t

t

y

y

e





Liczba

wyjazdów

za granicę

[mln] y

(dane

empiryczne)

Liczba

wyjazdów

za granicę

[mln] y^

(dane

teoretyczne

)

Reszty

modelu

e

20,8

31,448

-10,648

29,3

27,883

1,417

31,4

31,872

-0,472

34,3

30,425

3,875

36,4

33,653

2,747

44,7

41,065

3,635

48,6

46,688

1,912

49,3

47,032

2,268

55,1

56,117

-1,017

56,7

54,818

1,882

53,1

51,738

1,362

45,0

51,962

-6,962

49

GK (WEiP(01) - 2011)

Przykład

Obliczenie wariancji składnika losowego (wariancja reszt),
macierzy wariancji i kowariancji reszt oraz standardowych
błędów oszacowania parametrów strukturalnych modelu:

• wariancja reszt

• macierz wariancji i kowariancji

• standardowe błędy oszacowania parametrów strukturalnych
modelu

23,8984

1

2

12

215,0857

1

k

n

e

1

k

n

e

e

S

n

1

t

2

t

T

2

e



























































1,029402

0,00162

13,0132

0,00162

0,000007

0,015713

13,0132

0,015713

171,6974

1

T

2

e

2

X)

(X

S

(a)

D

.

,

,

1,0146

1,029402

d

)

S(a

0,0026

0,000007

d

)

S(a

13,1033

171,6974

d

)

S(a

22

2

11

1

00

0



















50

GK (WEiP(01) - 2011)

Przykład

Wyznaczenie przedziałów ufności dla oszacowań
parametrów strukturalnych modelu na poziomie ufności

0,95

:







 









 









 



0,1234

4,7138;

1,0146

2,262157

2,4186

1,0146;

2,262157

2,4186

0,0239

0,0121;

0,0026

2,262157

0,018

0,0026;

2,262157

0,018

86,8958

27,6124;

13,1033

2,262157

57,2541

13,1033;

2,262157

57,2541

)

S(a

t

a

);

S(a

t

a

)

S(a

t

a

);

S(a

t

a

)

S(a

t

a

);

S(a

t

a

2

1)

(2

0,05;12

2

2

1)

(2

0,05;12

2

1

1)

(2

0,05;12

1

1

1)

(2

0,05;12

1

0

1)

(2

0,05;12

0

0

1)

(2

0,05;12

0





























































































51

GK (WEiP(01) - 2011)

Przykład

52

GK (WEiP(01) - 2011)