



d

r

in

ż.

P

io

tr

C

za

rn

y

w

o

jt

e

k

d

r

in

ż.

P

io

tr

C

za

rn

y

w

o

jt

e

k

Wykład nr 5

Elektrotechnika - Teoria

Obwodów

AiR NS, sem. 2.





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

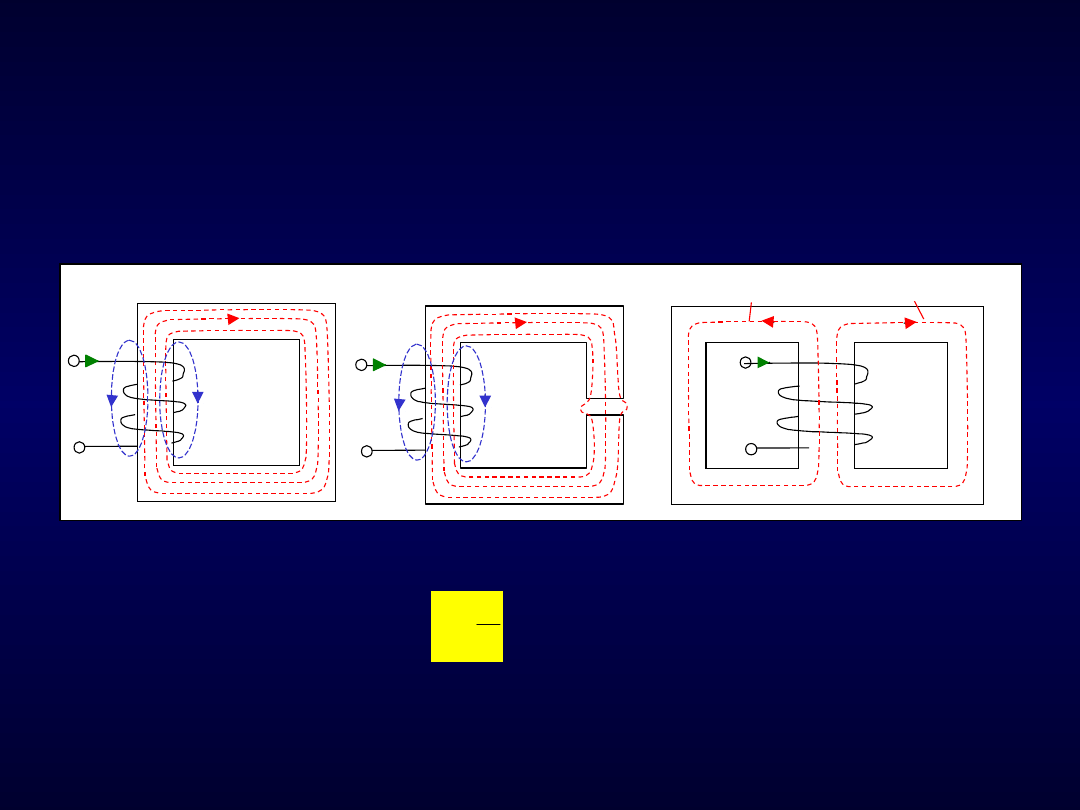
Obwody magnetyczne

Obwodem magnetycznym nazywa się zamkniętą drogę dla przepływu
skupionego strumienia magnetycznego.
W wielu urządzeniach elektrycznych np. transformatorach, maszynach
elektrycznych itp. zachodzi potrzeba koncentracji strumienia magnetycznego w
pewnych ich częściach oraz odpowiedniego jego ukształtowania. Osiąga się to
przez zastosowanie materiałów ferromagnetycznych odznaczających się dużą
przenikalnością magnetyczną.

Rys. 92. Przykłady obwodów magnetycznych

Nazwa obwód magnetyczny powstała przez analogię do obwodów elektrycznych.
Analogia jest czysto formalna – procesy w obwodzie magnetycznym mają
zupełnie inny charakter fizyczny niż procesy przepływu prądu elektrycznego w
obwodzie.

Współczynnik
rozproszenia:

(148)







r





z





r



r



 




I

I

I





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

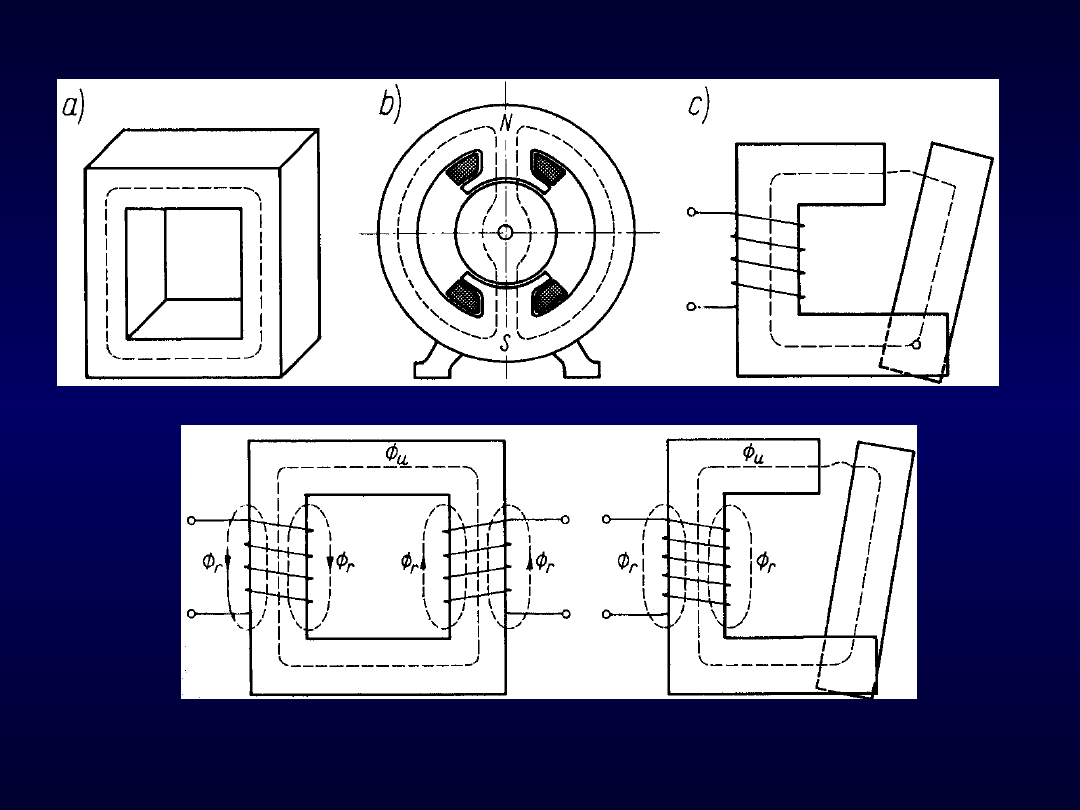
Obwody magnetyczne

Rys. 93. Przykłady rzeczywistych obwodów magnetycznych i rozkład

strumienia magnetycznego

d)

e)





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

cd. Obwody magnetyczne

Utrzymywanie w przestrzeni stałego strumienia magnetycznego nie wymaga
dostarczania energii (natomiast prąd elektryczny wymaga podtrzymywania -
dostarczania energii).

W obwodach magnetycznych strumień magnetyczny płynie nie tylko przez
elementy obwodu, ale również przez przestrzeń otaczającą, tworząc tzw.
strumień rozproszenia 

r

(bezużyteczny – kilka do kilkunastu % strumienia

użytecznego ). W obwodach elektrycznych prąd zamyka się tylko poprzez

elementy obwodu.

W przybliżonych obliczeniach obwodów magnetycznych pomija się strumień
rozproszenia.
Podstawowe prawa obwodów magnetycznych opierają się na ciągłości
strumienia magnetycznego i na prawie przepływu.

Można stwierdzić, że w obwodzie magnetycznym nierozgałęzionym, strumień
użyteczny jest na całej długości obwodu jednakowy.

W obwodzie magnetycznym rozgałęzionym suma strumieni schodzących się w
miejscu rozgałęzienia (węźle) jest równa zeru, czyli suma strumieni
dochodzących do miejsca rozgałęzienia jest równa sumie strumieni
odchodzących (

I prawo Kirchhoffa dla obwodów magnetycznych

):

(149)



0







d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

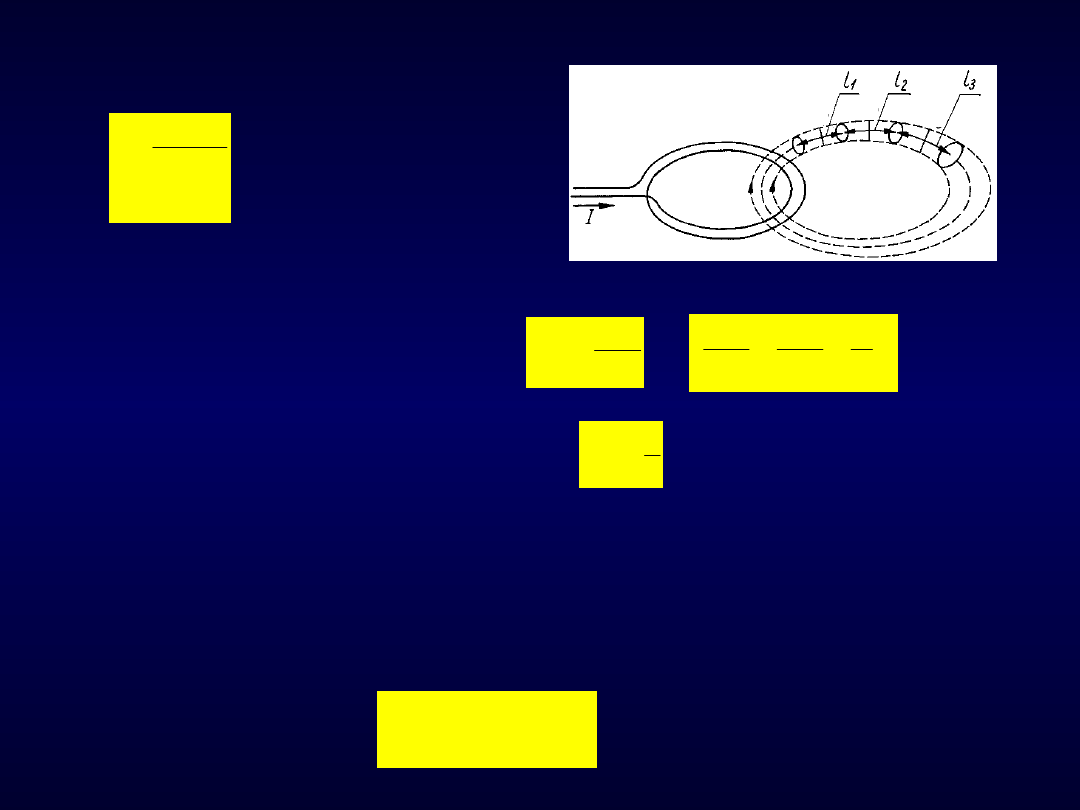
cd. Obwody magnetyczne

Prawo Ohma dla obwodu magnetycznego:

(1)







n

1

i

mi

R

NI



gdzie: NI – przepływ równy sile
magnetomotorycznej (odpowiednik siły
elektromotorycznej E),

 - strumień

(odpowiednik prądu I), R

m

– reluktancja

(opór magnetyczny) – odpowiada
rezystancji R, l – średnia droga
strumienia magnetycznego.

S

R

m







l

(11)

S

B

śr





(12)



















H

1

s

1

s

V

A

(w przybliżeniu)

gdzie: B

śr

– indukcja magnetyczna – odpowiada gęstości prądu J (jako gęstość

strumienia magnetycznego).

II prawo Kirhchoffa dla obwodów magnetycznych

– w oczku obwodu

magnetycznego suma spadków napięć magnetycznych jest równa sumie sił
magnetomotorycznych:

(13)















n

1

i

i

i

n

1

i

mi

l

H

R



Rys. 94. Prawo Ohma dla

OM

S

1

S

2

S

3





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

cd. Obwody magnetyczne

Tabela 5. Analogie między wielkościami magnetycznymi i elektrycznymi

Nazwa

Pole magnetyczne Pole elektryczne

Przepływ – siła elektromotoryczna

NI (Hl, )

E

Napięcie magnetyczne – napięcie

elektryczne

R

m

U

Strumień magnetyczny – prąd

elektryczny



I

Indukcja magnetyczna - gęstość prądu

B

J

Reluktancja - rezystancja

R

m

R

W obwodach, których są części z materiałów ferromagnetycznych –
przenikalność magnetyczna zależy od natężenia pola magnetycznego co nie
pozwala bezpośrednio korzystać z prawa Ohma i praw Kirhchoffa.
Gdy obliczenia dotyczą części liniowej charakterystyki magnesowania można
przyjmować, że przenikalność magnetyczna i reluktancja są niezależne od pola
magnetycznego i prowadzić obliczenia na podstawie prawa Ohma i praw
Kirhchoffa.

Obliczanie obwodów magnetycznych





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

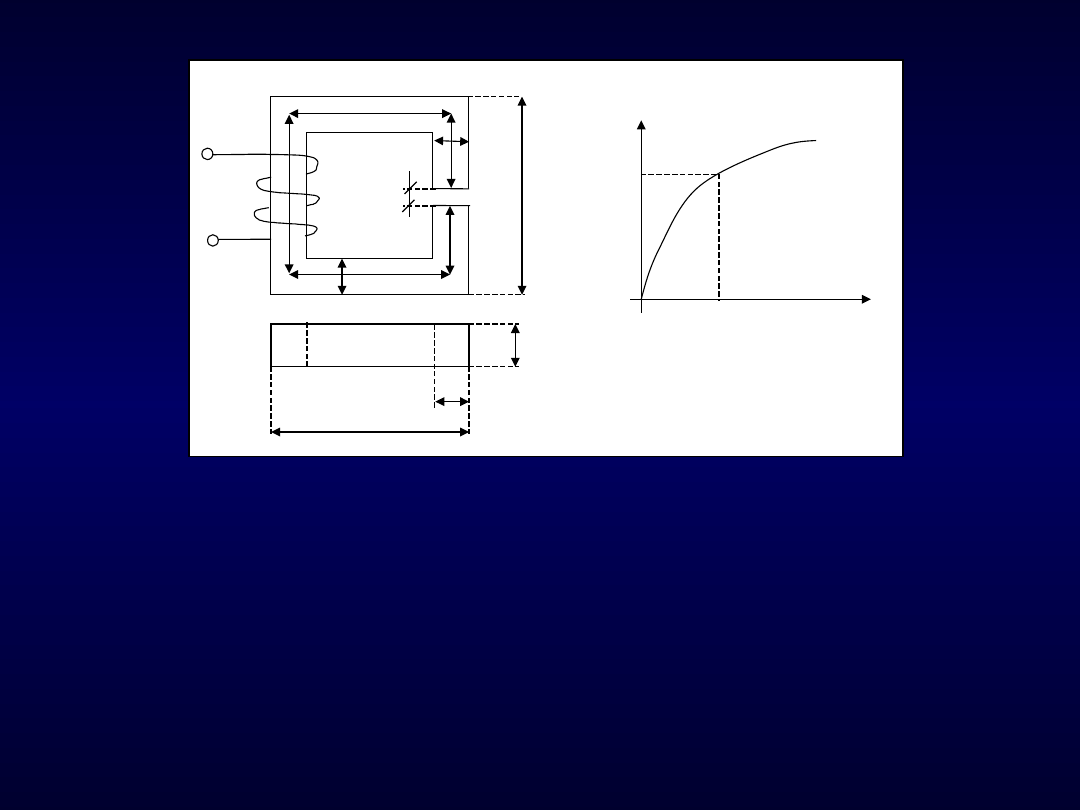
cd. Obliczanie obwodów magnetycznych

Dane są wymiary obwodu i szczeliny powietrznej oraz indukcja magnetyczna w
szczelinie B

p

i



r

(niezależna od natężenia pola przy danej B).

Należy obliczyć przepływ NI.

Rys. 95. Sposób określania wymiarów obwodu magnetycznego

e

l

1

l

2

l

3

l

4

l

5

a

d

b

l

p

c

g

H

B

0

H

1

B

1

Kolejność rozwiązywania:

A – obwody w których przenikalność i reluktancja są niezależne od pola

magnetycznego:

1. Obwód magnetyczny dzieli się na części i oblicza średnią długość drogi

strumienia magnetycznego w tych częściach – l

1

... l

n

dla S

1

... S

n

;





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

cd. Obliczanie obwodów magnetycznych

2. Oblicza się reluktancję poszczególnych części obwodu magnetycznego;

3. Dodaje się wyznaczone reluktancje;

4. Przepływ oblicza się z prawa Ohma dla obwodu magnetycznego (strumień

magnetyczny obliczany jest z zależności od indukcji magnetycznej w
szczelinie

powietrznej

 = B

p

S

p

) – przyjęliśmy, że strumień magnetyczny we wszystkich częściach

obwodu jest taki sam - brak strumienia rozproszenia.

n

r

0

mn

S

R











n

l

p

0

mp

S

R







p

l

p

p

S

B





















m

p

p

m

n

1

i

mi

R

S

B

R

NI

R

NI





(14)

(1)





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

cd. Obliczanie obwodów magnetycznych

B – obwody w których przenikalność i reluktancja są zależne od pola

magnetycznego (korzystamy z prawa przepływu)

1. Jak poprzednio;
2. Strumień w obwodzie:
3. Obliczamy średnie indukcje w poszczególnych częściach obwodu

magnetycznego:

4. Z charakterystyki magnesowania B = f(H) wyznacza się natężenie pola

magnetycznego odpowiadające wartościom tych indukcji, dla B

n

- H

n

;

. Oblicza się spadki napięć magnetycznych na poszczególnych odcinkach

obwodu magnetycznego: H

n

l

n

;

6. Oblicza się spadek napięcia magnetycznego w szczelinie powietrznej;

7. Ostatecznie przepływ oblicza się z prawa przepływu.

p

0

p

p

p

l

B

l

H













n

1

i

i

i

NI

l

H



(18)

(19)

p

p

S

B





n

n

S

B





(16)

(17)





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

Indukcja elektromagnetyczna

Zjawisko odkryte w 1831 r przez M. Faradaya.
Istotą zjawiska jest powstawanie siły elektromotorycznej w dowolnym obwodzie
elektrycznym przy zmianie strumienia magnetycznego skojarzonego z tym
obwodem.
Siła elektromotoryczna (SEM) powstaje niezależnie od tego, czy strumień
magnetyczny zmienia się w czasie (SEM transformacji), czy też jest powodowana
ruchem pola względem obwodu lub obwodu względem pola (SEM rotacji).

Prawo Faradaya (zjawisko indukcji elektromagnetycznej):

Siła elektromotoryczna

jest proporcjonalna do zmian w czasie strumienia skojarzonego z obwodem:

(16)

dt

d

e







Strumień skojarzony w przypadku obwodu jednozwojowego jest strumieniem
objętym tym zwojem

 = .

Dla obwodu wielozwojowego jest równy sumie strumieni skojarzonych z każdym
zwojem:
 = 

1

+



2

+...+



n

.

Przy obliczaniu SEM indukowanej należy uwzględnić całkowity strumień
skojarzony z uzwojeniem (zarówno zewnętrzny jak i powstający w wyniku
przepływu prądu w rozważanym uzwojeniu).





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

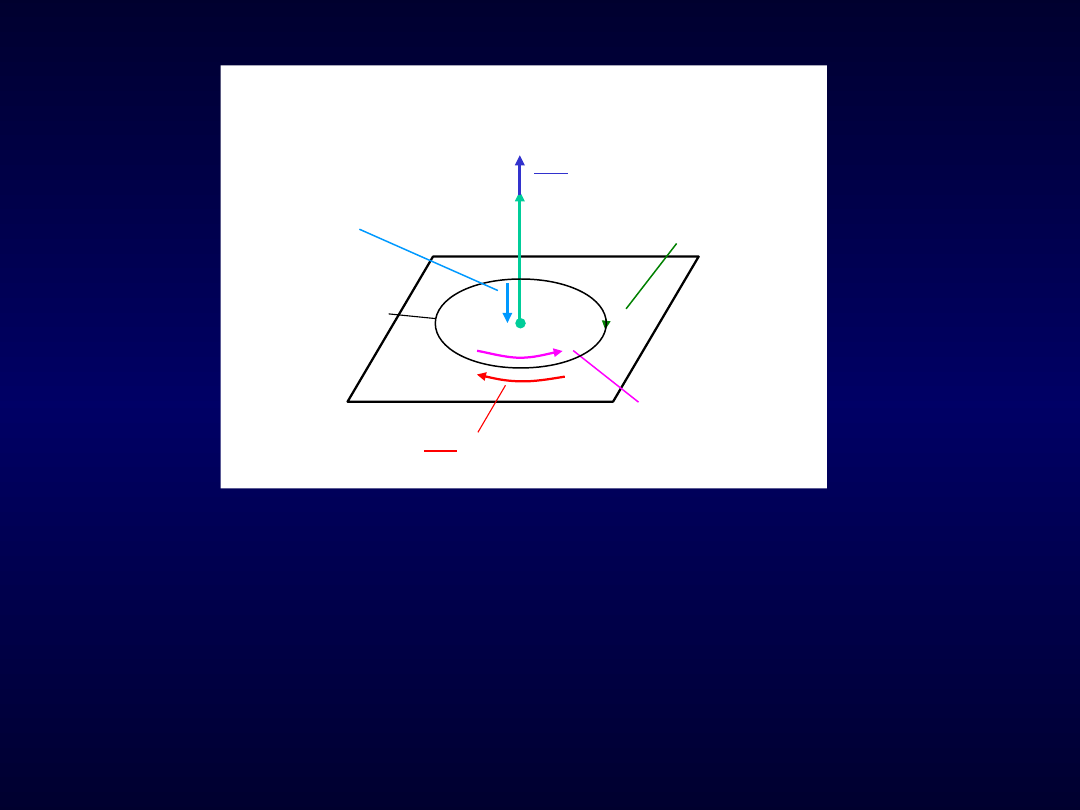
cd. Indukcja elektromagnetyczna

Rys. 96. Zjawisko indukcji elektromagnetycznej – wzajemna zależność

zwrotów SEM, prądów i strumieni magnetycznych

Znak „-” w prawie Faradaya wynika z umownego przyjęcia za dodatnią SEM,
która wywołuje prąd będący źródłem strumienia magnetycznego o umownym
zwrocie dodatnim.

Zwrot SEM indukowanej np. przy wzroście strumienia magnetycznego
dodatniego (d

 > 0) musi być zgodnie z

regułą Lenza

– taki, że prąd przez nią

wywołany wytworzy strumień magnetyczny o umownym zwrocie ujemnym,
przeciwdziałający wzrostowi strumienia dodatniego.



D

o

d

a

tn

i

zw

ro

t

st

ru

m

ie

n

ia

d
dt >0

-e

d



dt >0

Rzeczywisty zwrot
SEM indukowanej
przy

e

Zwrot SEM
indukowanej przyjęty
za dodatni (dodatni
zwrot prądu i)

i

Rzeczywisty zwrot
prądu zgodny z
kierunkiem SEM
indukowanej

obwó
d



i

Strumień
wywołany prądem
i





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

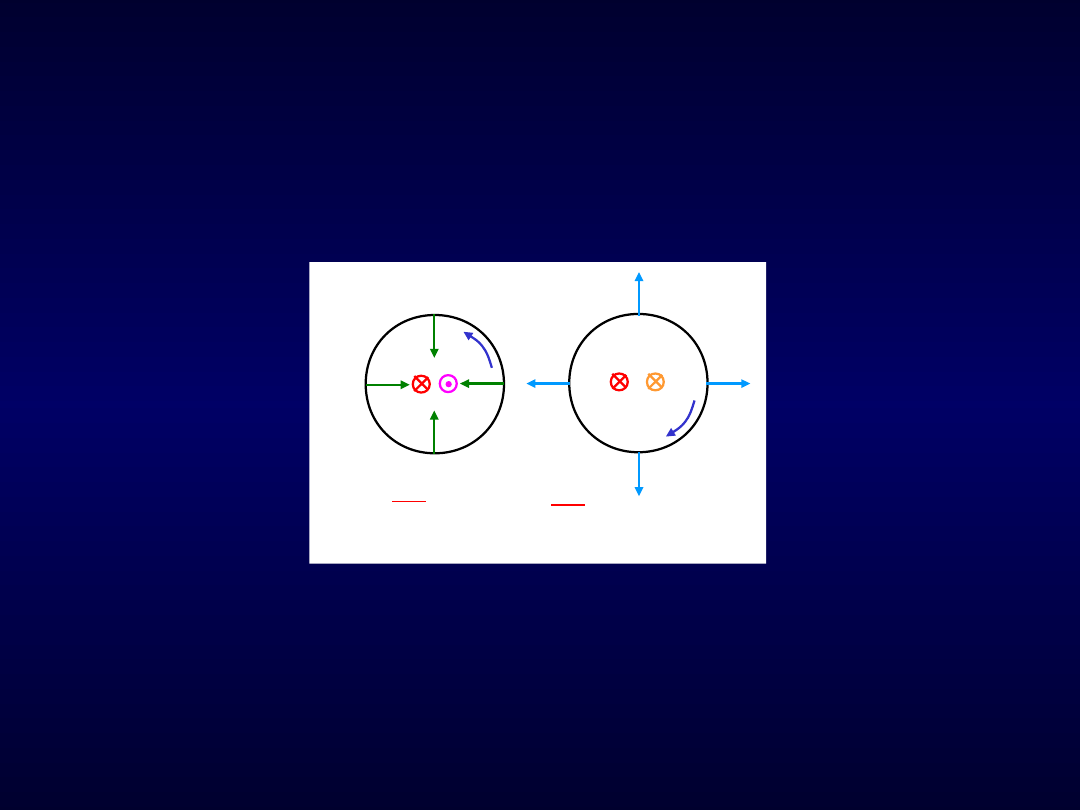
cd. Indukcja elektromagnetyczna

Rys. 97. Wyjaśnienie reguły Lenza

SEM wywołująca prąd elektryczny wzbudzający strumień magnetyczny o zwrocie
ujemnym jest ujemna.

Reguła Lenza (prawo bezwładności elektromagnetycznej):

Jakiekolwiek zmiany

strumienia magnetycznego skojarzonego z przewodzącym obwodem
zamkniętym powodują powstawanie sił elektromotorycznych i sił
mechanicznych, przeciwdziałających zmianom skojarzonego strumienia
magnetycznego.

Zwiększeniu się strumienia

 towarzyszy powstanie prądu I wywołującego

strumień magnetyczny



1

o zwrocie przeciwnym do

, który przeciwdziała

zmianom zachodzącym w obwodzie.

F

F

F

F

F

F

F

F







1



1

E, I

E, I

a)

b)

d



dt >

0

d



dt <

0

Przy zmniejszaniu

 zwrot prądu I jest taki, że wywołuje strumień magnetyczny



1

o zwrocie zgodnym z

, przeciwdziałający zmianom zachodzącym w

obwodzie.





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

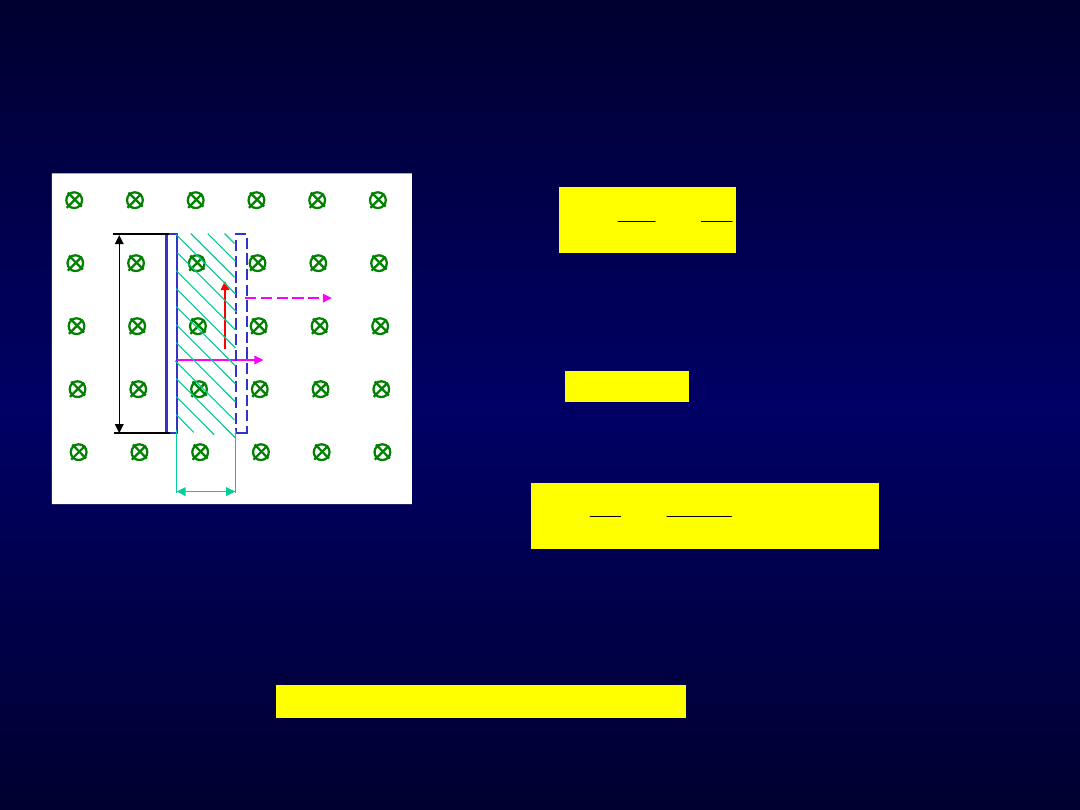
cd. Indukcja elektromagnetyczna

Rys. 98. Indukowanie się siły

elektromotorycznej przy poruszaniu

się przewodu w stałym polu

magnetycznym

W elektrotechnice częstym przypadkiem jest ruch przewodu prostoliniowego o
długości l w równomiernym polu magnetycznym o indukcji B. Ruch odbywa się z
prędkością

 (kierunki B i  są do siebie prostopadłe).

(161)

dt

d

dt

d

e













d

 przecinany w czasie dt przez poruszający

się przewód o długości l ma wartość:

(162)

dt

B

d





l



Zatem SEM:

(163)

 

V

B

dt

dt

B

dt

d

e







l

l













Jeżeli B i

 nie są do siebie prostopadła, a kąt między nimi wynosi , to:

(164)











sin

B

e

sin

dt

B

d

l

l









Zwrot SEM indukowanej w przewodzie wyznaczamy korzystając z

reguły prawej

dłoni

.

B

l

v

v

E

vdt





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

cd. Indukcja elektromagnetyczna

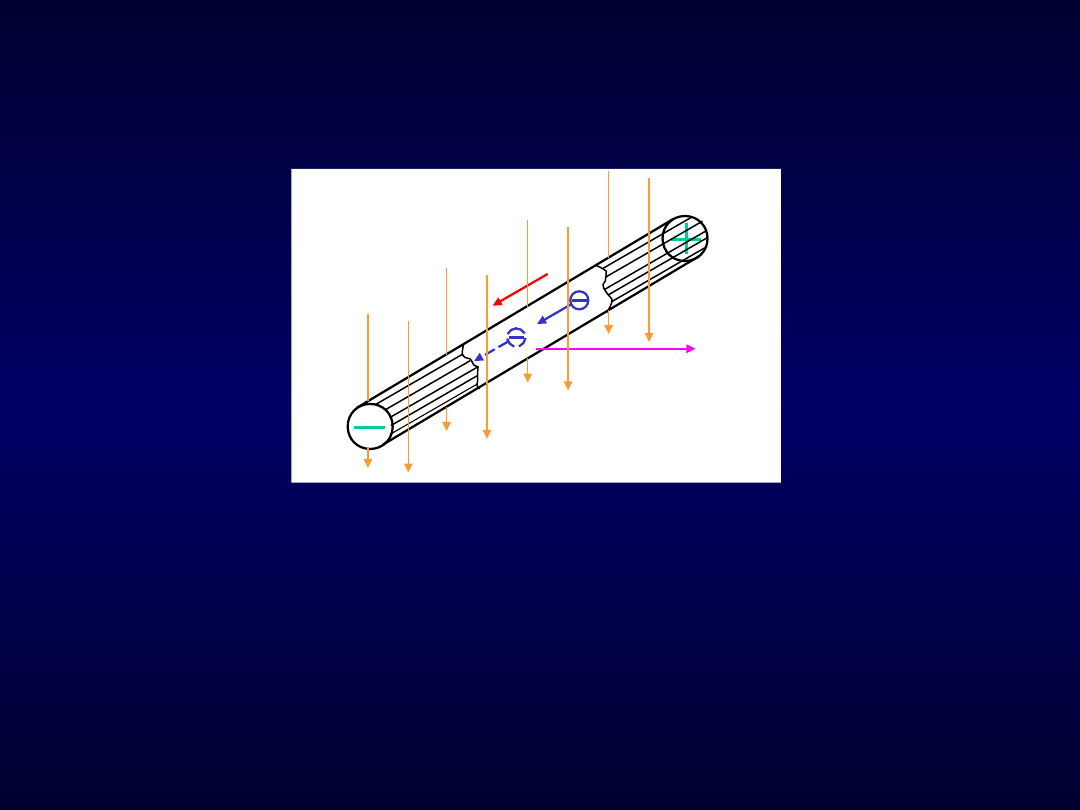
Rys. 99. Wyjaśnienie zjawiska powstawania SEM (rzeczywisty zwrot) przy ruchu

przewodu w równomiernym polu magnetycznym

Jeżeli wektor indukcji magnetycznej wchodzi do wyprostowanej prawej dłoni, a
kierunek ruchu przewodu wskazuje odciągnięty kciuk (w płaszczyźnie dłoni), to
wyciągnięte palce wskazują zwrot SEM indukowanej.

Jeżeli przewód porusza się w polu magnetycznym to na elektrony swobodne
poruszające się wraz z przewodem w polu magnetycznym działają siły
powodujące przesuwanie elektronów w kierunku końca 1 przewodu.
W wyniku ruchu elektronów koniec 2 przewodu ładuje się dodatnio (odpływają z
niego elektrony swobodne, a jony dodatnie pozostają, nie mając swobody
ruchu), natomiast koniec 1 ładuje się ujemnie i powstaje różnica potencjałów
elektrycznych, która określa SEM indukowaną.

1

2

v

E

e

F

e

F

B





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

Siła elektromotoryczna indukcji własnej

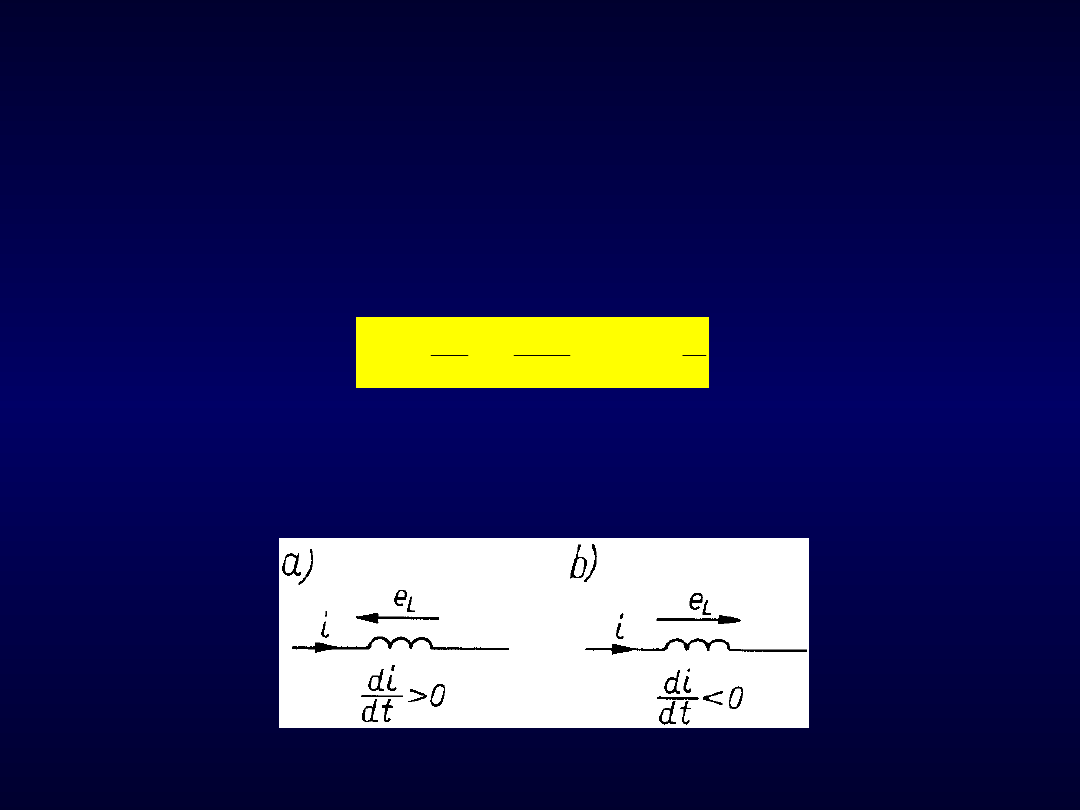
Rys. 100. Powstawanie SEM indukcji własnej a) ujemnej, b) dodatniej

Jeżeli w dowolnym obwodzie elektrycznym płynie prąd, to jest on źródłem pola i
strumienia magnetycznego skojarzonego z tym obwodem.

Przy zmieniającym się w czasie prądzie strumień magnetyczny wywoływany
przez ten prąd, a skojarzony z obwodem, będzie się zmieniał co spowoduje
powstanie SEM – nazywanej

SEM indukcji własnej

, albo

samoindukcji

(proces

powstawania – zjawisko samoindukcji).

„-” przyrost dodatni prądu powoduje powstawanie ujemnej SEM indukcji
własnej, która wywołuje ujemny prąd przeciwdziałający wzrostowi prądu
dodatniego (reg. Lenza).

 

dt

di

L

dt

Li

d

dt

d

e

const

L

L

















(16)





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

Siła elektromotoryczna indukcji wzajemnej

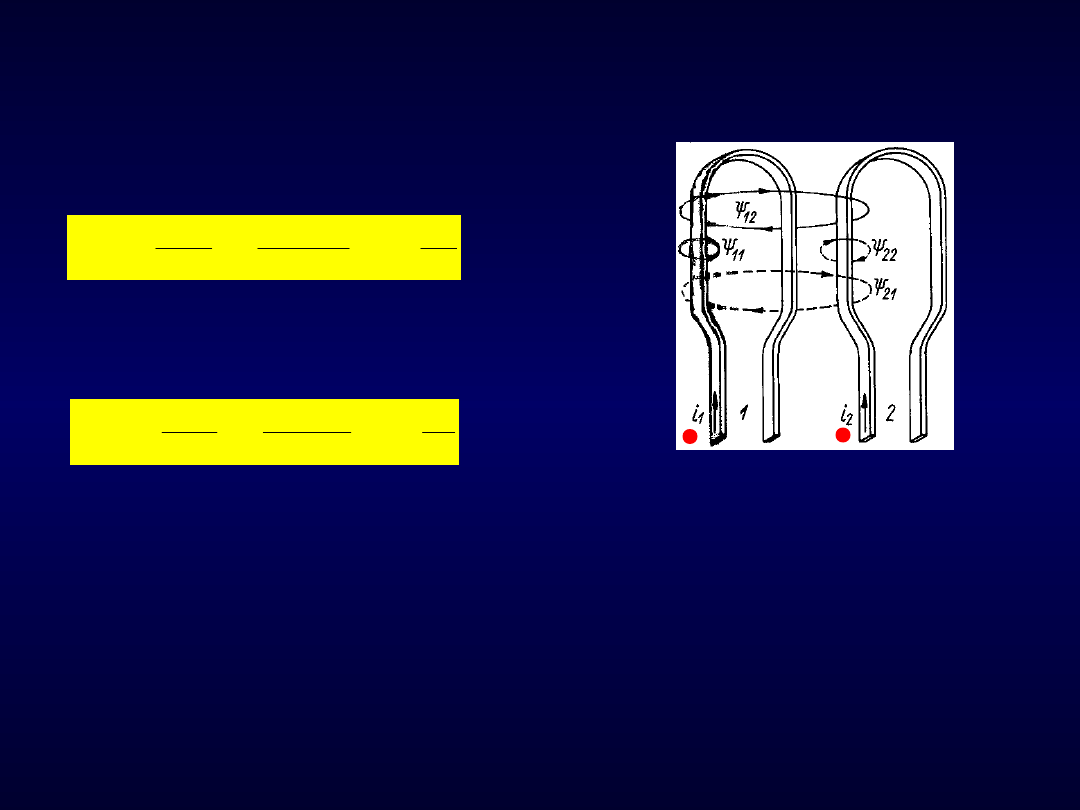
Rys. 101. Powstawanie SEM indukcji

wzajemnej

Jeżeli w sąsiedztwie rozpatrywanej cewki znajduje się druga cewka z nią
sprzężona, to zmienny strumień magnetyczny cewki pierwszej wyindukuje w niej

SEM indukcji wzajemnej

o wartości:

w obwodzie 1:

w obwodzie 2:

W celu ustalenia znaku przy „M” wprowadza się pojęcie zacisków
jednakoimiennych.
W zależności bowiem od zwrotów prądów w obu cewkach i sposobu nawinięcia ich
uzwojeń, strumienie mogą być zgodne lub przeciwne.

Sprzężenie magnetyczne dodatnie – zgodne zwroty



12

i



21

„+” przy M.

Sprzężenie magnetyczne ujemne – przeciwne zwroty



12

i



21

„-” przy M.

(166)





dt

di

M

dt

i

M

d

dt

d

e

2

2

21

1

M





















dt

di

M

dt

i

M

d

dt

d

e

1

1

12

2

M

















(167)





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

cd. Siła elektromotoryczna indukcji wzajemnej

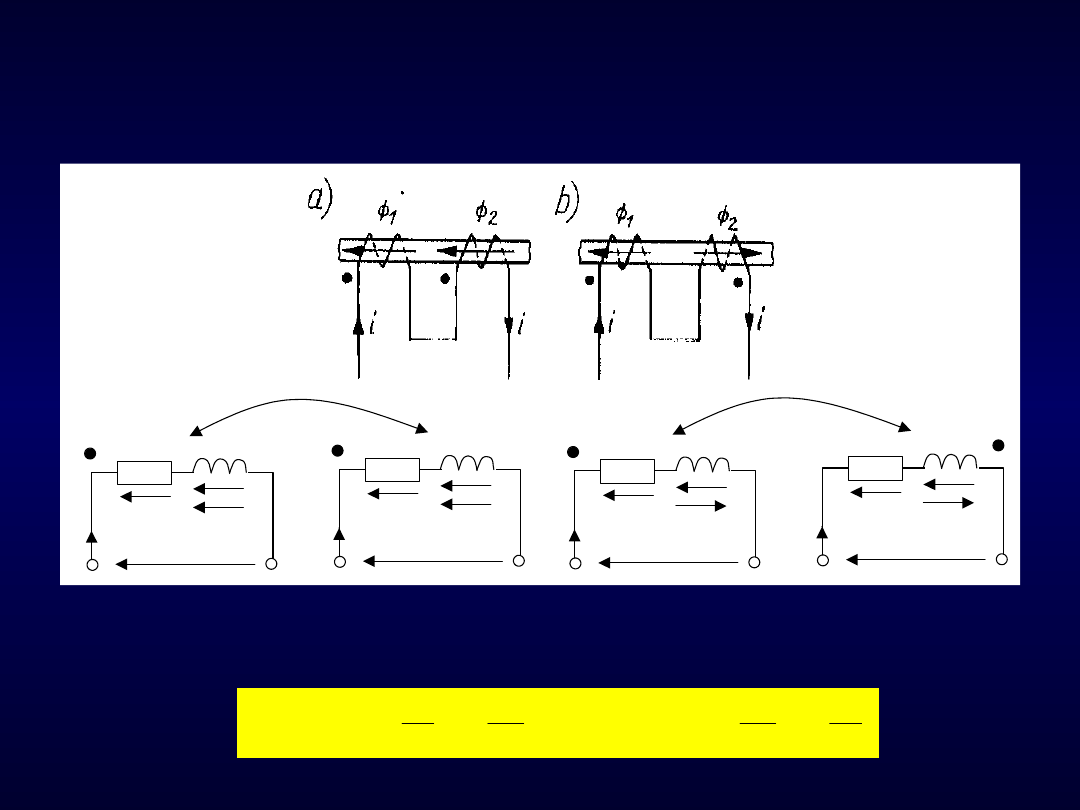
Rys. 102. Ilustracja pojęcia zacisków jednakoimiennych

oraz sprzężenie magnetyczne dodatnie (a) i ujemne (b)

Te zaciski, do których dopływają prądy i

1

oraz i

2

przy zgodności strumieni

magnetycznych tworzą parę tzw. zacisków jednakoimiennych (+M gdy i lub i

1

oraz i

2

mają jednakowe zwroty względem zacisków jednakoimiennych).

u

1

i

1

R

L1

L

1

u

2

i

2

R

L2

L

2

M

u

1

i

1

R

L1

L

1

u

2

i

2

R

L2

L

2

M

+

-

(168)





































dt

di

M

dt

di

L

i

R

u

dt

di

M

dt

di

L

i

R

u

1

2

2

2

2

2

2

1

1

1

1

1





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

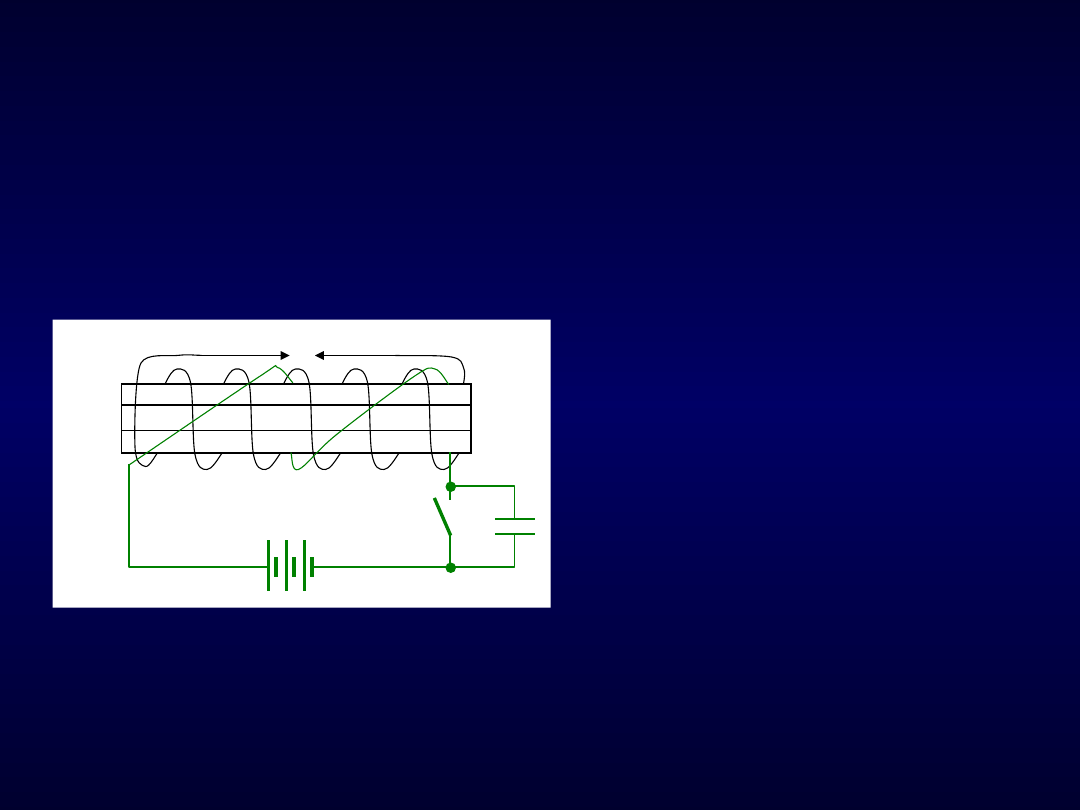
Zjawisko indukcji wzajemnej

Rys. 103. Działanie cewki zapłonowej

Zjawisko indukcji wzajemnej jest wykorzystywane w praktyce w wielu
urządzeniach np.:

transformatorach

przeznaczonych do przekształcania

zmiennej energii elektrycznej o jednym poziomie napięcia na energię
elektryczną o innym poziomie napięcia; w

piecach indukcyjnych

służących do

nagrzewania i topienia metali; w

urządzeniach zapłonowych silników

benzynowych

(cewka zapłonowa – dwa uzwojenia: pierwotne o małej liczbie

zwojów, zasilane poprzez przerywacz z akumulatora (6 – 12 V) oraz uzwojenie
wtórne o kilkaset razy większej liczbie zwojów, łączone poprzez rozdzielacz
kolejno ze świecami zapłonowymi każdego z cylindrów).

Podczas przerywania prądu w
uzwojeniu pierwotnym indukuje się
w uzwojeniu wtórnym wysokie
napięcie powodujące przeskok iskry.
Kondensator

C

przyłączany

równolegle do przerywacza P, ma
na celu zapobieżenie paleniu się
łuku między stykami przerywacza
podczas ich rozdzielania (szybsze
przerwanie obwodu)

P

C

Indukcja elektromagnetyczna może być zjawiskiem niepożądanym np. w
urządzeniach

radiotechnicznych, gdzie

powstają

zakłócenia wywołane

indukowanymi SEM, w niektórych obwodach tych urządzeń na skutek sprzężeń
magnetycznych z obwodami peryferyjnymi.





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

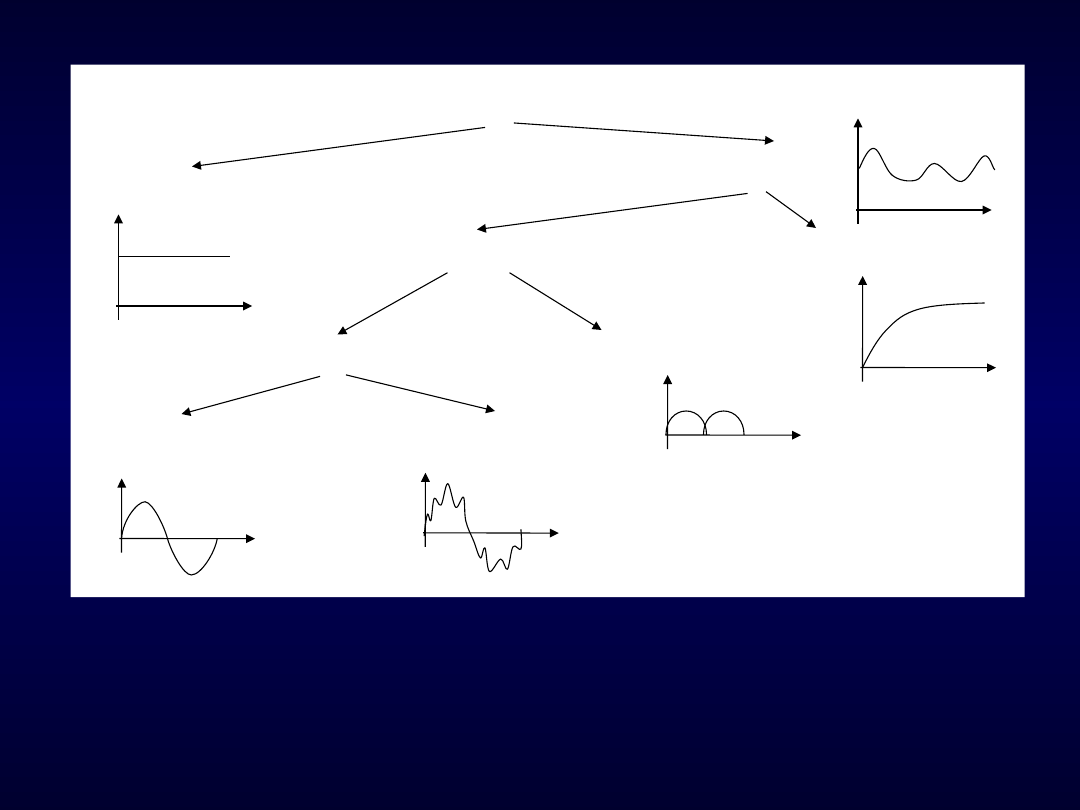
Obwód elektryczny jednofazowy prądu sinusoidalnego

Rys. 104. Podział prądów (napięć) ze względu na zależność od czasu

Prąd okresowo zmienny – opisany funkcją spełniającą zależność:

f(t +T) = f(t)

T – okres – najmniejszy przedział czasu, po którym powtarza się wartość funkcji
f(t).

Prąd elektryczny

Prąd stały

i

t

Prąd zmienny

i

t

Prąd okresowo

zmienny

Prąd bezokresowy

i

t

Prąd przemienny

Prąd tętniący

i

t

Prąd sinusoidalny

i

t

Prąd odkształcony

i

t





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

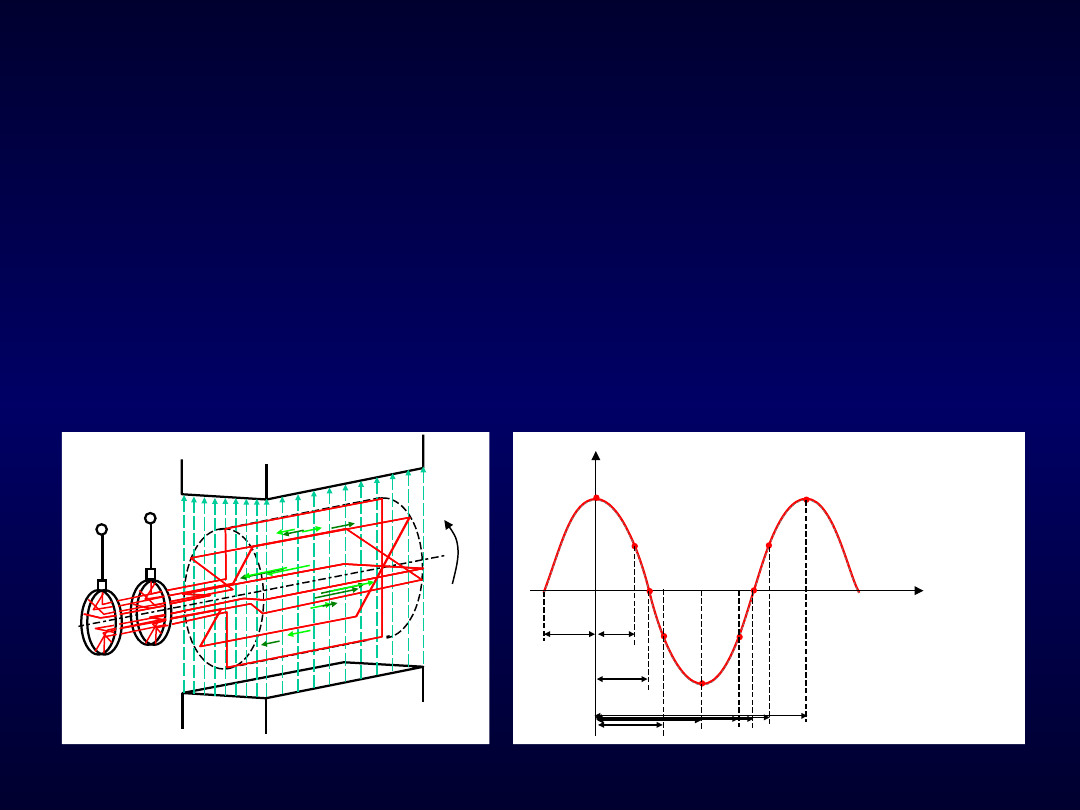
cd. Obwód elektryczny jednofazowy prądu sinusoidalnego

Rys. 105. Pojedyncza ramka jako model prądnicy i SEM indukowana w ramce

Prądy przemienne – wartość średnia w okresie jest równa zero, prądy tętniące –
wartość średnia w okresie różna od zera – można przedstawiać jako sumę
składowej stałej równej wartości średniej za okres oraz składowej przemiennej,
której wartość średnia za okres równa jest zero.
Prąd przemienny o innym kształcie niż sinusoidalny można na ogół przedstawić
jako sumę prądów sinusoidalnych o różnych częstotliwościach.

Powstawanie prądu sinusoidalnie zmiennego

Aby w obwodzie mającym rezystancję R popłynął prąd sinusoidalnie zmienny
należy podłączyć go do źródła napięcia sinusoidalnie zmiennego.
Takim źródłem jest prądnica prądu sinusoidalnie zmiennego (najprostszy model
rys. 1).

B

t

e



e

e























d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

cd. Obwód elektryczny jednofazowy prądu sinusoidalnego

Prostokątna ramka z przewodnika wiruje z prędkością kątową  w równomiernym

polu magnetycznym o indukcji magnetycznej B.

Załóżmy, że pierwotnie ramka była w położeniu takim, że jej płaszczyzna była
prostopadła do linii pola magnetycznego, wtedy strumień magnetyczny
przenikający ramkę był największy, równy amplitudzie strumienia:

Przy obracaniu ramki strumień  przenikający ramkę będzie się zmieniał:

(169)

S

B

m







(17)







cos

m





 - kąt o jaki obróci się ramka od położenia początkowego. Przy stałej prędkości

obrotowej ramki kąt obrotu  jest proporcjonalny do czasu:

(171)

t



 

 - prędkość kątowa ramki, wtedy:

(172)

t

cos

m















d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

cd. Obwód elektryczny jednofazowy prądu sinusoidalnego

Zgodnie z prawem indukcji – SEM indukowana w ramce jest równa:

(173)





t

sin

E

t

sin

dt

t

cos

d

dt

d

dt

d

e

m

m

m

































m

m

E





-

amplituda siły elektromotorycznej

.

T [s] – czas pełnego obrotu ramki –

okres

obrotu o pełen kąt - 2 radiana.

Prędkość kątowa ramki wynosi –

pulsacja przebiegu sinusoidalnego

:

(174)

 

s

rad

T

2



 

Częstotliwość przebiegu sinusoidalnego

:

(17)





s

1

Hz

2

T

1

f















d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

cd. Obwód elektryczny jednofazowy prądu sinusoidalnego

W Europie w tym w Polsce f =  Hz – częstotliwość sieciowa, przemysłowa,
znamionowa, techniczna, elektromagnetyczna.

W USA i Kanadzie f = 6 Hz.









 t

(176)







 





t

sin

U

u

m

Wartość chwilowa napięcia

(chwili t):

(177)

 - faza przebiegu sinusoidalnego;

 -

faza początkowa

przebiegu (w chwili t = ).

Przy analizie przebiegów sinusoidalnych przyjmuje się zasadę mierzenia czasu t
od momentu, w którym przebieg zaczynamy obserwować, czyli t = .

Ponieważ ramka w chwili t =  może się znajdować w dowolnym położeniu
obrócona o kąt  w stosunku do położenia pierwotnego, a obraca się ze stałą

prędkością kątową , to po czasie t ramka obróci się o kąt:





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

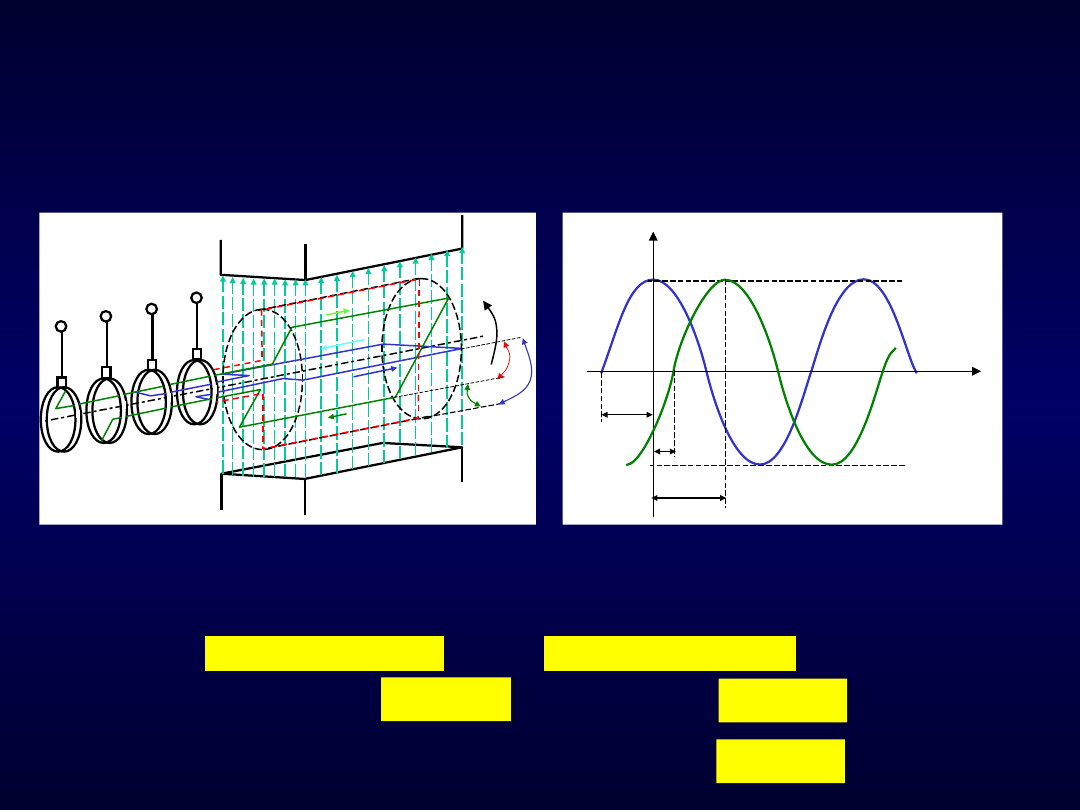
cd. Obwód elektryczny jednofazowy prądu sinusoidalnego

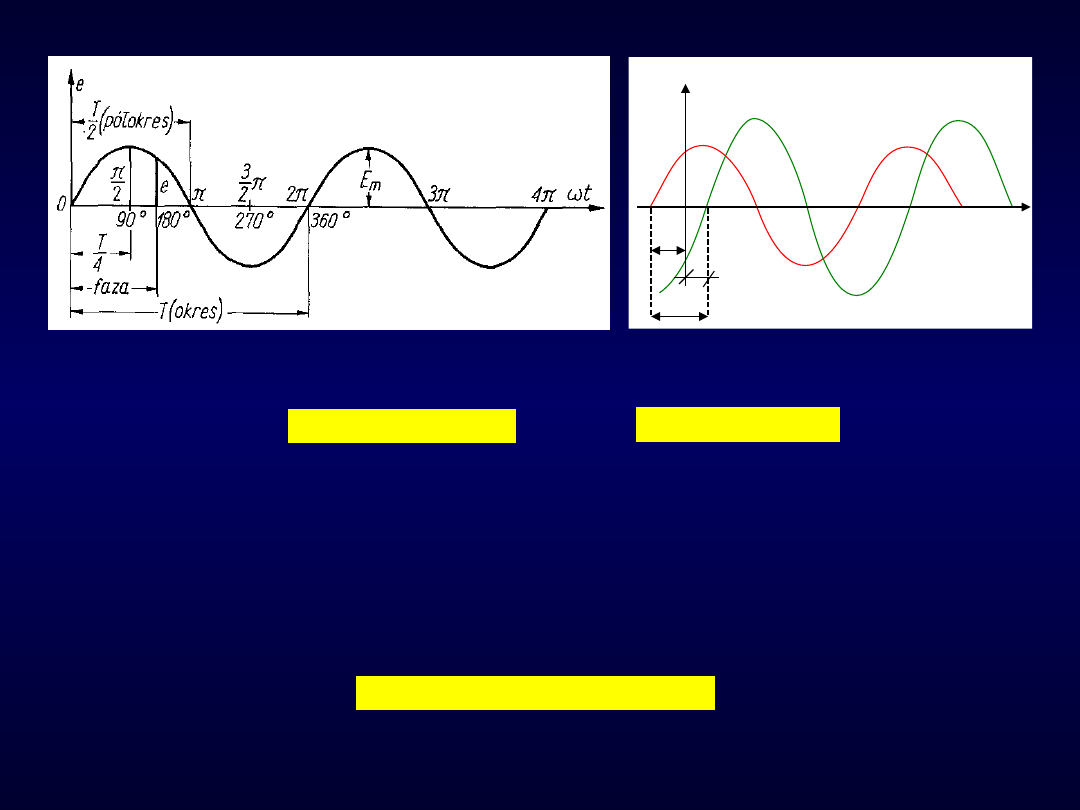
Rys. 106. Dwie ramki przesunięte względem siebie i przebiegi indukowanych w

nich napięć

Rozpatrzmy model prądnicy z dwiema wzajemnie przesuniętymi ramkami.

Chwilę dla jakiej zaczynamy obserwację układu odzwierciedlają, na wykresie,
wartości faz początkowych napięć indukowanych w ramkach.

U

m1

, U

m2

– amplitudy napięć (wartości maksymalne);



1

, 

2

- fazy początkowe przebiegów (w chwili t = ).





1

1

m

1

t

sin

U

u



 





Wartość chwilowa napięć:

(178)





2

2

m

2

t

sin

U

u



 





B

t

u



1



u

1

U

m1

U

m2



2

u

2







1



2



1

=

+9

o



2

= -3

o

 = 12

o





d

r

in

ż.

P

io

tr

d

r

in

ż.

P

io

tr

C

za

rn

yw

o

jt

e

k

C

za

rn

yw

o

jt

e

k

cd. Obwód elektryczny jednofazowy prądu sinusoidalnego



u

- faza początkowa napięcia (opóźniona względem chwili t =  – ze znakiem

„-”);


i

- faza początkowa prądu (wyprzedza chwilę t =  – ze znakiem „+”);

Rys. 107. Przebieg wartości chwilowej napięcia sinusoidalnego (SEM) oraz

przebiegi przesunięte w fazie

t

u

i



i



u







u

m

t

sin

U

u



 





(179)





i

m

t

sin

I

i



 







 



i

u

i

u

t

t



























(18)

Sinusoidalnie zmienne napięcia i prądy występujące w obwodach
elektromagnetycznych mają zwykle jednakową częstotliwość, a różnią się
amplitudą i fazą początkową – są synchroniczne (w synchronizmie).
Przesunięcie w fazie między napięciem i prądem równe jest różnicy faz
początkowych:

Przebiegi w fazie: ta sama faza początkowa, przejście przez zero, maksima i
minima występują jednocześnie.