Konstrukcje stalowe
Zagadnienia
Model materiału sprężysto-idealnie
plastycznego
Fazy wytężenia bisymetrycznego przekroju
zginanego
Moment zginający w przekroju częściowo
uplastycznionym
Nośność obliczeniowa przekrojów krępych
Przykład obliczeniowy (plastyczna rezerwa
nośności przekroju)
Plastyczna rezerwa konstrukcji
Nośność obliczeniowa przekrojów krępych
Konstrukcje stalowe
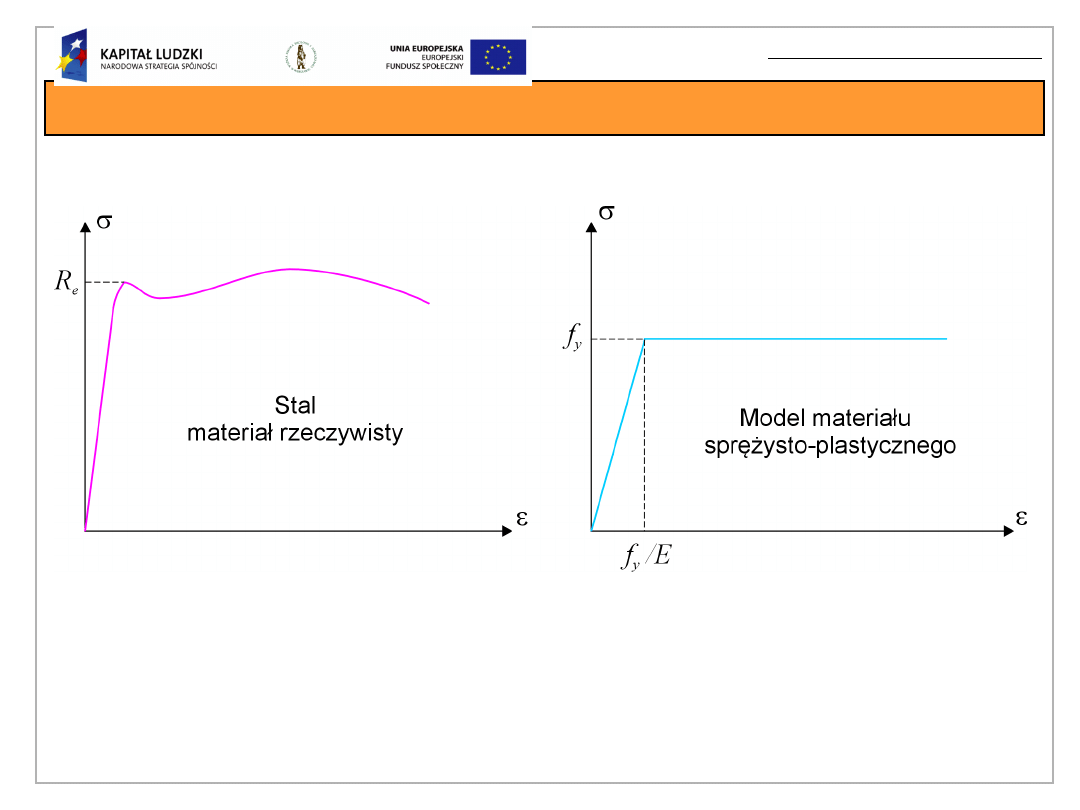
Model materiału sprężysto-idealnie plastycznego
R
e
– granica plastyczności,
f
y
– nominalna wartość granicy
plastyczności,
E – moduł Younga.
Konstrukcje stalowe
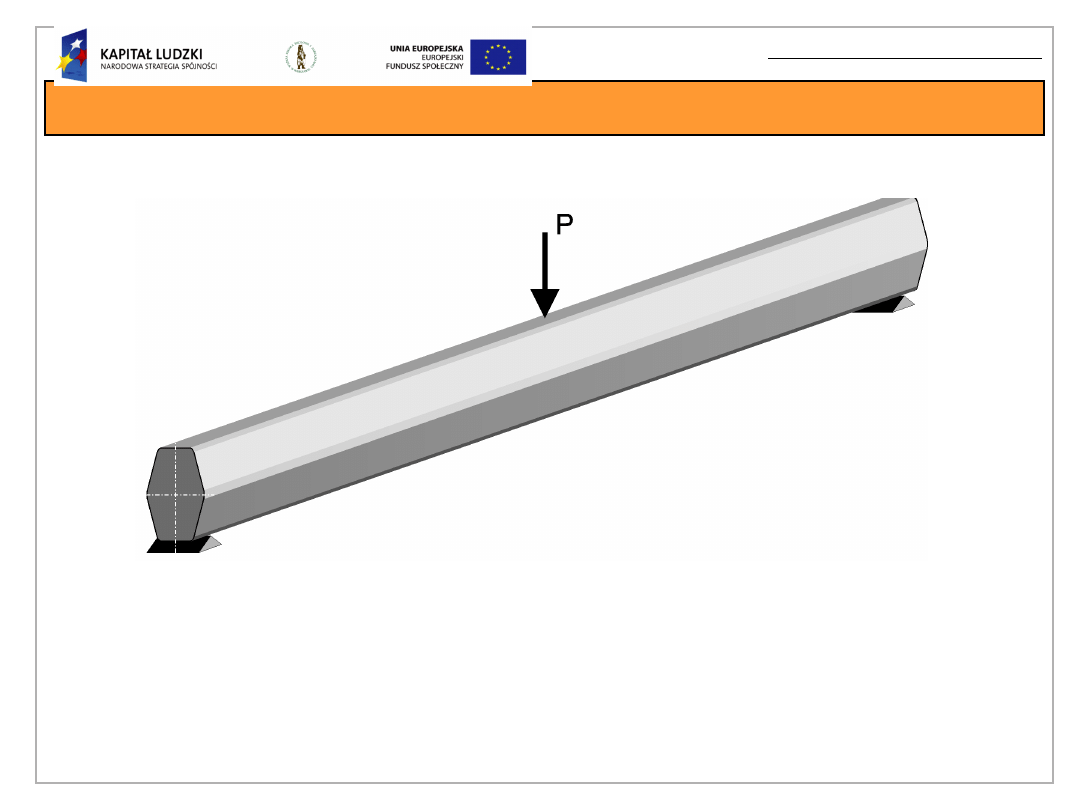
Fazy wytężenia bisymetrycznego przekroju
zginanego
Belka o krępym przekroju
bisymetrycznym, wykonana
z materiału sprężysto-idealnie
plastycznego
Konstrukcje stalowe
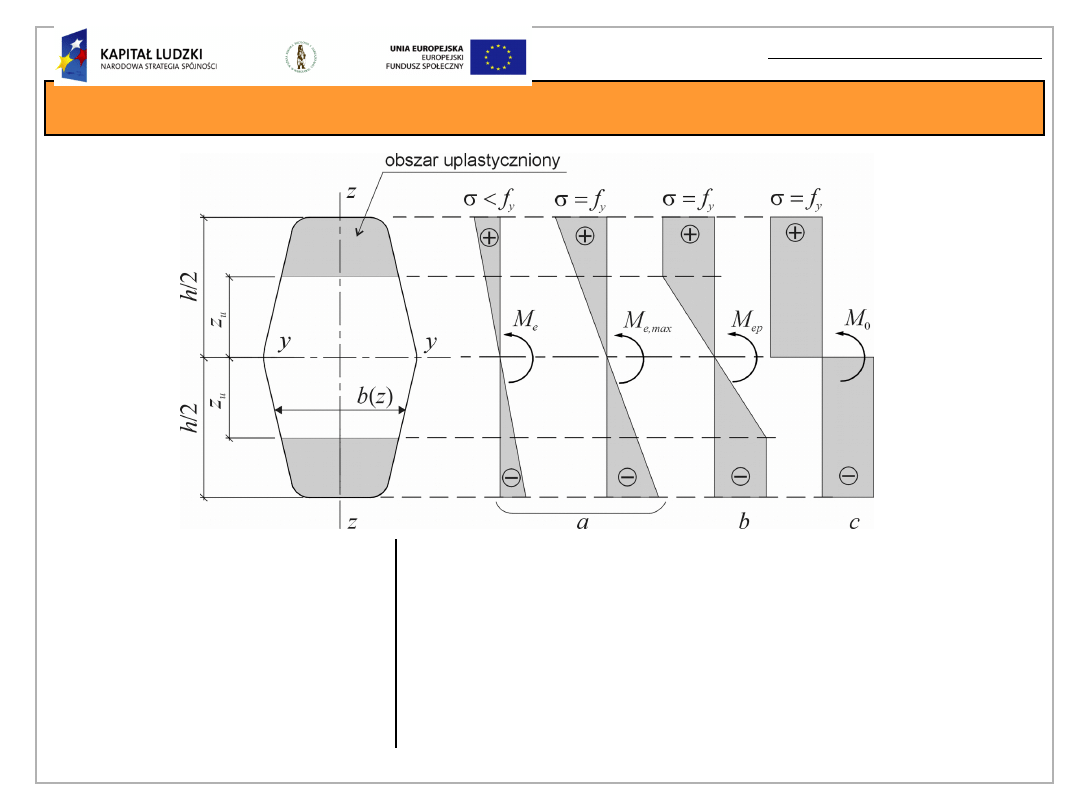
Fazy wytężenia bisymetrycznego przekroju
zginanego
e,max
M
M
a
)
0
)
M
M
M
b
e,max
0
)
M
M
c
– maksymalna wartość momentu
zginającego w zakresie
odkształceń sprężystych
e,max
M
0
M
– moment graniczny
Konstrukcje stalowe
Moment zginający w przekroju częściowo
uplastycznionym
z
z
f
z
z
u
y
u
z
f
h/
z
z
y
u
sign
2
Funkcje rozkładu
naprężenia
– obszar sprężysty rdzeń
sprężysty
– obszar
uplastyczniony
Moment zginający przy odkształceniach sprężysto-
plastycznych
y
p
y
e
y
h
z
z
u
y
h
ep
f
S
W
z
z
z
b
z
z
z
b
z
f
z
z
z
b
M
u
u
)
2
(
d
)
(
2
d
)
(
2
d
)
(
2
2
/
0
2
2
/
0
Konstrukcje stalowe
Nośność obliczeniowa przekrojów krępych
y
el
W
,
– wskaźnik
wytrzymałości całego
przekroju
y
S
– moment statyczny
połowy przekroju
2
/
h
z
u
Maksymalny moment sprężysty
znajdziemy zakładając
y
p
y
e
y
ep
f
S
W
M
)
2
(
y
y
el
e,max
f
W
M
,
0
u
z
Moment graniczny
otrzymujemy dla
y
y
f
S
M
2
0
e
y
W
– wskaźnik wytrzymałości rdzenia
sprężystego
p
y
S
– moment statyczny jednej części obszaru
uplastycznionego
Konstrukcje stalowe
Nośność obliczeniowa przekrojów krępych
Nośność obliczeniowa przekrojów klasy 1 i 2 (EN 1993-1-
1:2005+AC:2006)
0
,
,
/
M
y
y
pl
Rd
pl
f
W
M
y
y
pl
S
W
2
,
– plastyczny wskaźnik
wytrzymałości przekroju
(wskaźnik oporu plastycznego)
Nośność obliczeniowa
przekrojów klasy 3
0
,
,
/
M
y
y
el
Rd
el
f
W
M
Konstrukcje stalowe
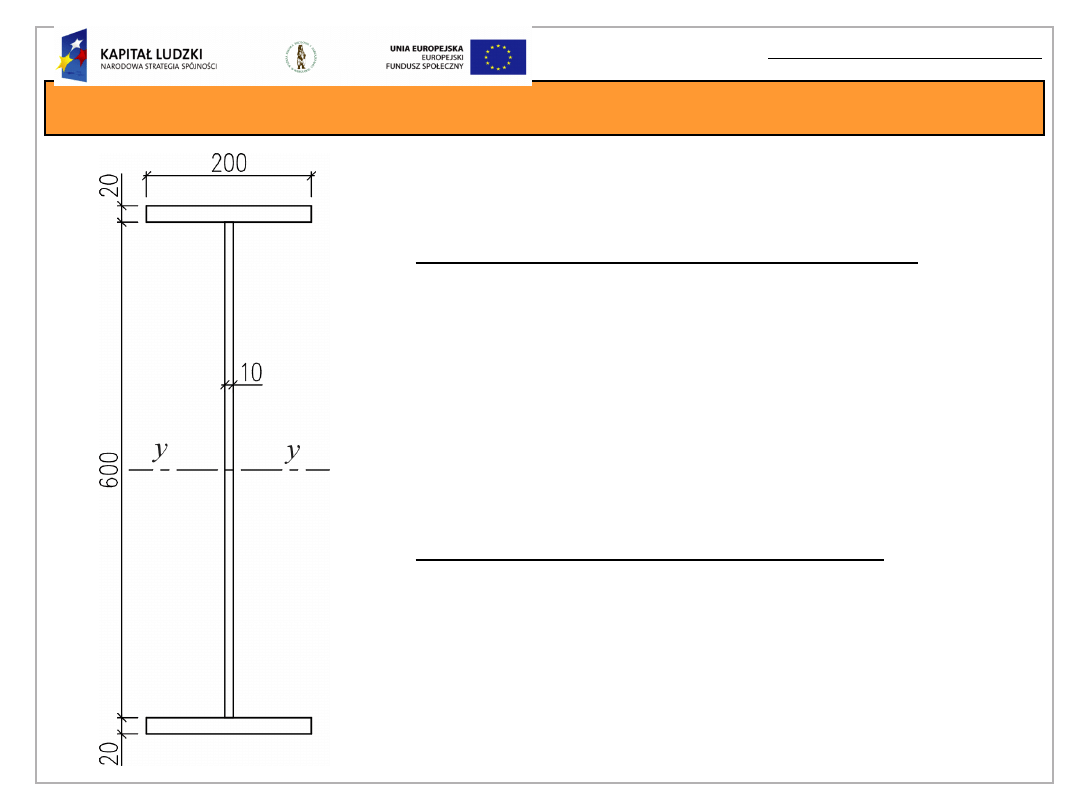
Przykład obliczeniowy
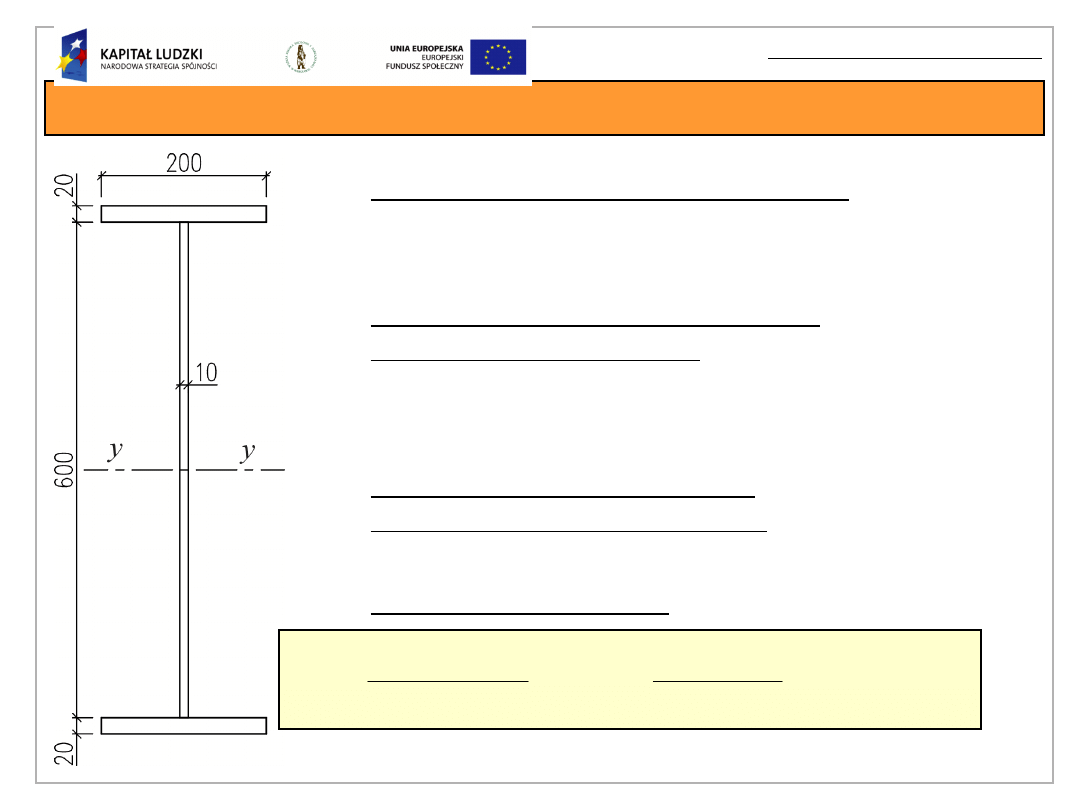
Cechy geometryczne przekroju
szerokość pasów
b
f
=
200 mm,
grubość pasów
t
f
= 20 mm,
grubość środnika
t
w
=
10 mm,
wysokość środnika
r =
600 mm.
Dla belki wykonanej ze stali S235 i o
przekroju jak na rysunku określić:
maksymalny moment sprężysty,
moment sprężysto-plastyczny przy
założeniu pełnego uplastycznienia
pasów przekroju,
moment graniczny.
Konstrukcje stalowe
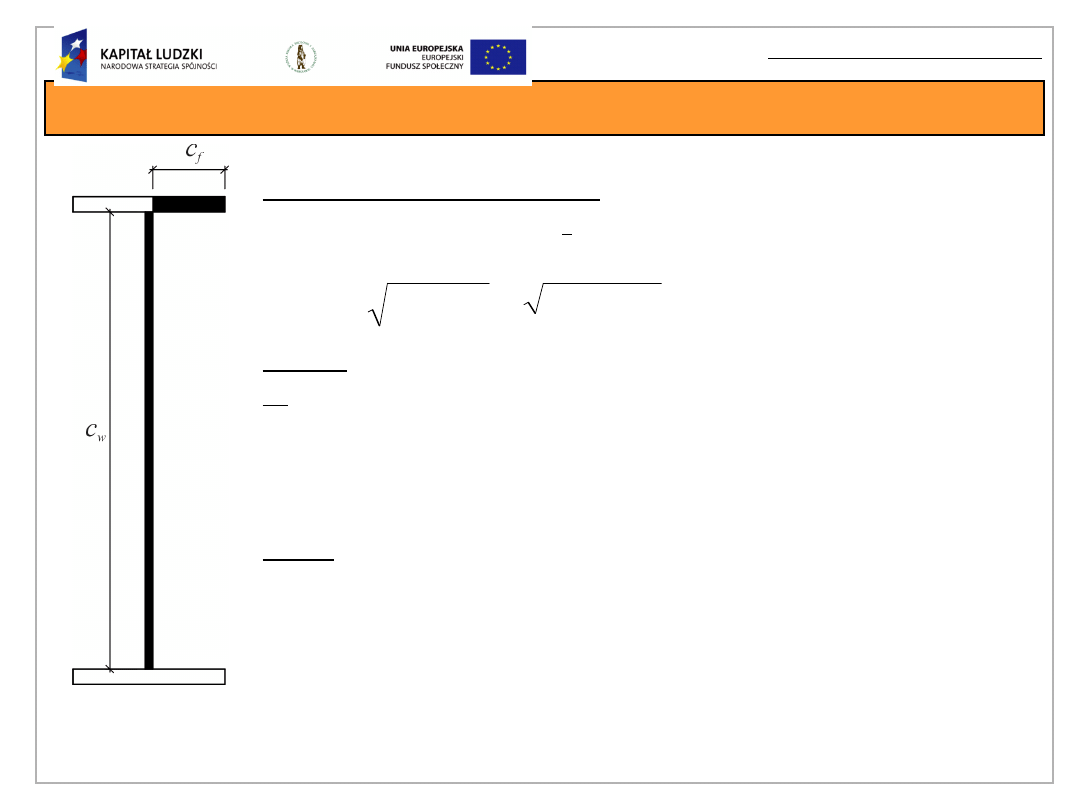
Przykład obliczeniowy
Klasyfikacja przekroju (tablica 5.2 w EN 1993-
1-1:2005+AC:2006)
środn
ik
mm
600
w
w
h
c
0
,
72
0
,
1
72
72
0
,
60
10
/
600
/
w
w
t
c
mm
0
,
95
)
10
200
(
5
,
0
)
(
5
,
0
w
f
f
t
b
c
0
,
9
0
,
1
9
9
75
,
4
20
/
95
/
f
f
t
c
pasy
– klasa
1.
– klasa
1.
Przekrój niewrażliwy na miejscową utratę stateczności,
posiada rezerwę plastycznej nośności.
Parametr
mechaniczny
0
,
1
235
/
235
/
235
y
f
Konstrukcje stalowe
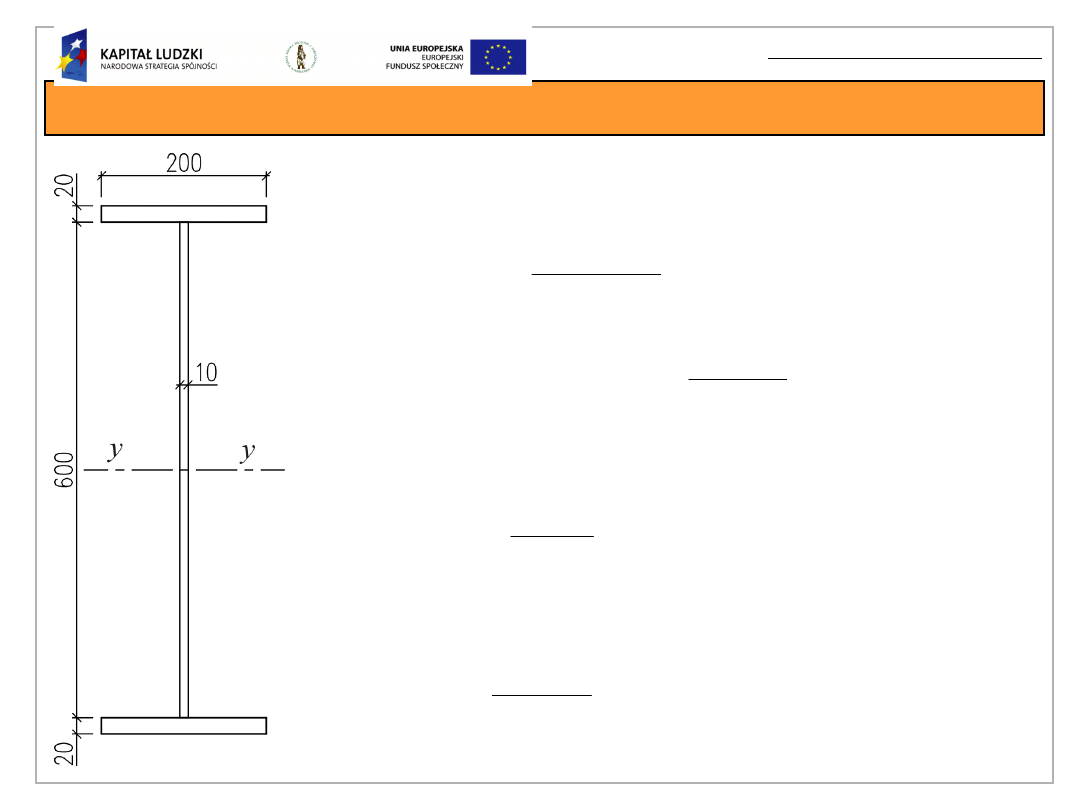
Przykład obliczeniowy
Moment bezwładności przekroju
względem osi y-y
4
3
2
3
cm
94907
12
60
0
,
1
0
,
31
0
,
2
0
,
20
12
0
,
2
0
,
20
2
y
J
Wskaźnik wytrzymałości przekroju
względem osi y-y
3
,
cm
2966
32
94907
y
el
W
Wskaźnik wytrzymałości środnika
(rdzeń sprężysty)
3
2
cm
00
6
6
60
0
,
1
e
y
W
Konstrukcje stalowe
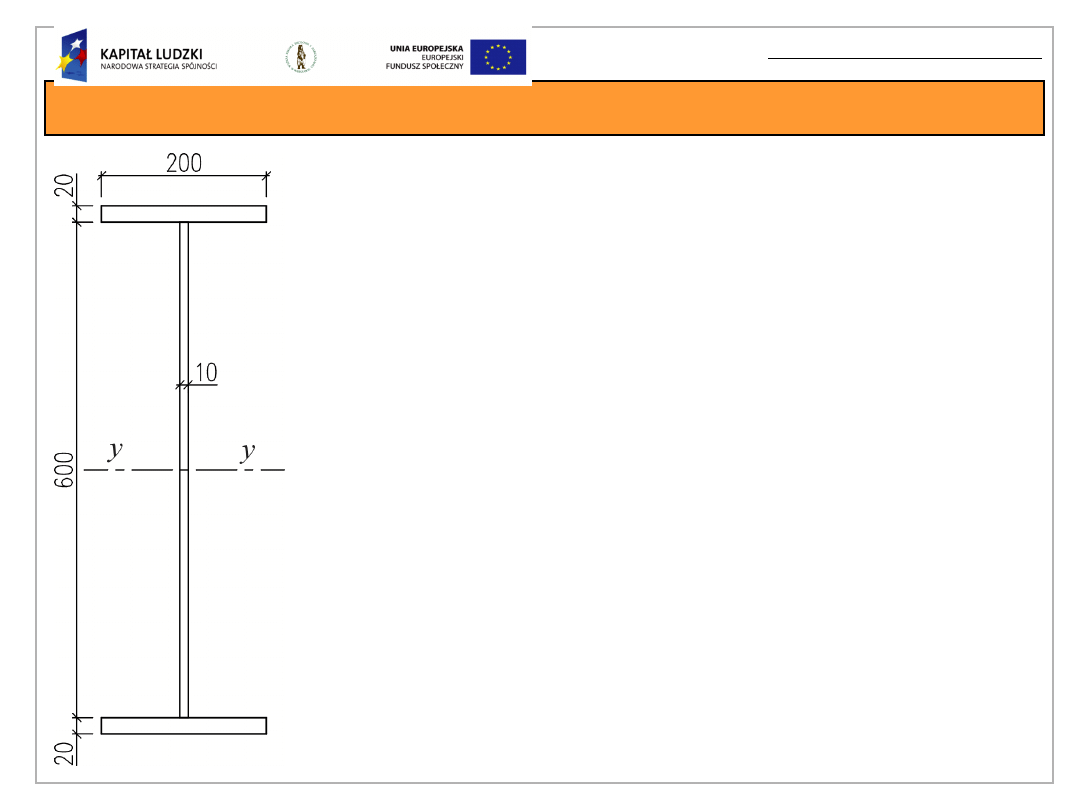
Przykład obliczeniowy
Moment statyczny pasa (część
uplastyczniona)
3
cm
1240
0
,
31
0
,
20
0
,
2
p
y
S
Moment statyczny połowy przekroju
3
cm
690
1
0
.
15
0
,
30
0
,
1
0
,
31
0
,
20
0
,
2
y
S
Wskaźnik oporu plastycznego
3
,
cm
3380
1690
2
2
y
y
pl
S
W
Konstrukcje stalowe
Przykład obliczeniowy
Maksymalny moment sprężysty
kNm
697
kNcm
69701
5
,
23
2966
,
y
y
el
e,max
f
W
M
Moment sprężysto-plastyczny
(uplastycznione pasy)
Moment graniczny (pełne
uplastycznienie przekroju)
kNm
724
kNcm
72380
5
,
23
)
1240
2
600
(
)
2
(
y
p
y
e
y
ep
f
S
W
M
kNm
794
kNcm
79430
5
,
23
3380
,
0
y
y
pl
f
W
M
Rezerwa plastyczna
%
14
%
100
697
697
794
%
100
0
e,max
e,max
pl
M
M
M
R
Konstrukcje stalowe
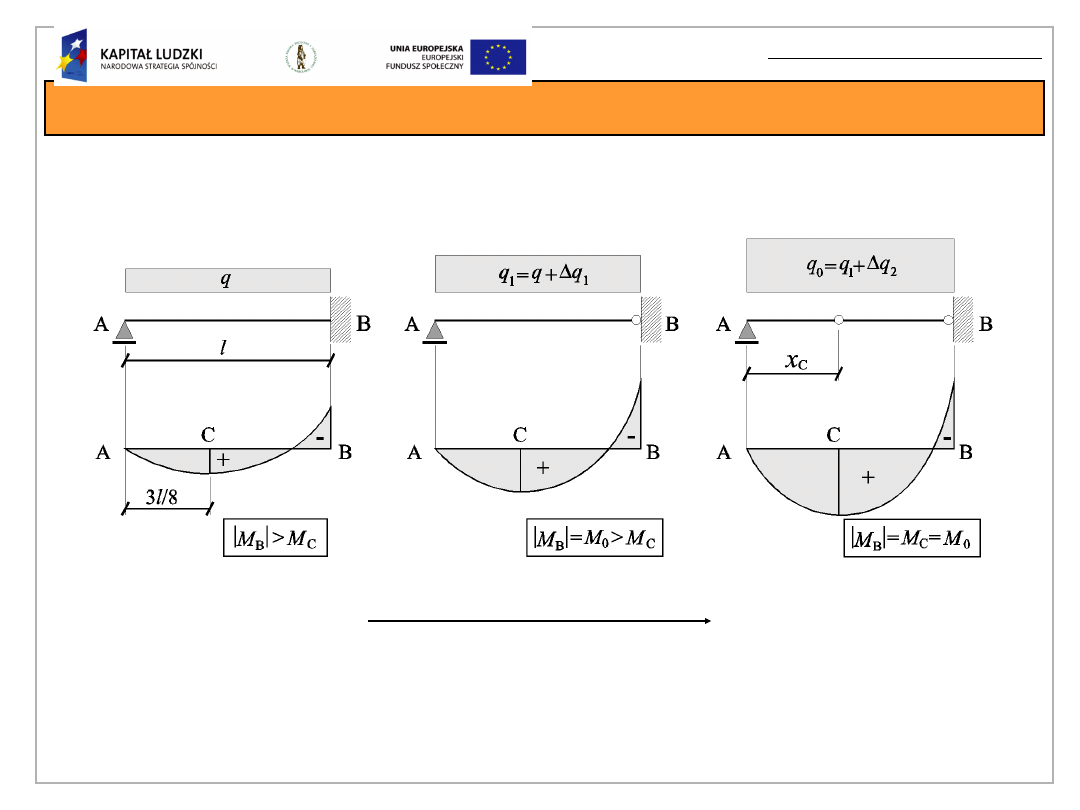
Plastyczna rezerwa konstrukcji
Plastyczna redystrybucja momentów
zginających
Konstrukcje stalowe
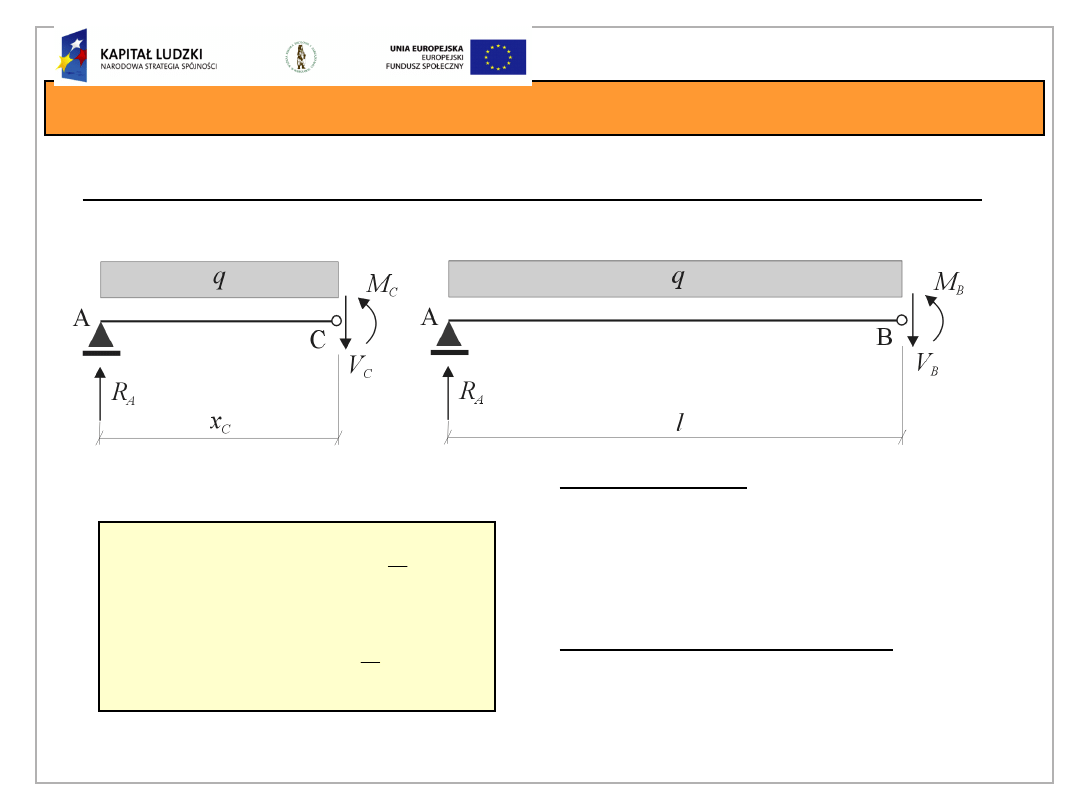
Obciążenie graniczne belki
Warunki równowagi momentów w przegubach plastycznych
.
2
1
:
,
2
1
:
2
2
ql
l
R
M
B
qx
x
R
M
C
A
B
c
C
A
C
Warunki plastyczności
0
0
,
M
M
M
M
B
C
Równanie sił
0)
(
0
C
C
A
C
A
C
V
qx
R
V
R
qx
Konstrukcje stalowe
Obciążenie graniczne belki
Podstawiając reakcję i warunki plastyczności do pierwszego
równania momentów, otrzymujemy
2
0
2
0
2
2
1
C
C
x
M
q
qx
M
Po wykorzystaniu tego wyniku w drugim równaniu momentów
będzie:
0
2
1
2
1
2
2
ql
l
qx
qx
C
C
Jest to równanie kwadratowe, z którego wyznaczamy
pierwiastek leżący w obszarze belki. Ostatecznie obciążenie
graniczne wynosi
l
x
C
)
1
2
(
2
0
2
0
2
0
)
2
2
3
(
2
)
1
2
(
2
l
M
l
M
q
Konstrukcje stalowe
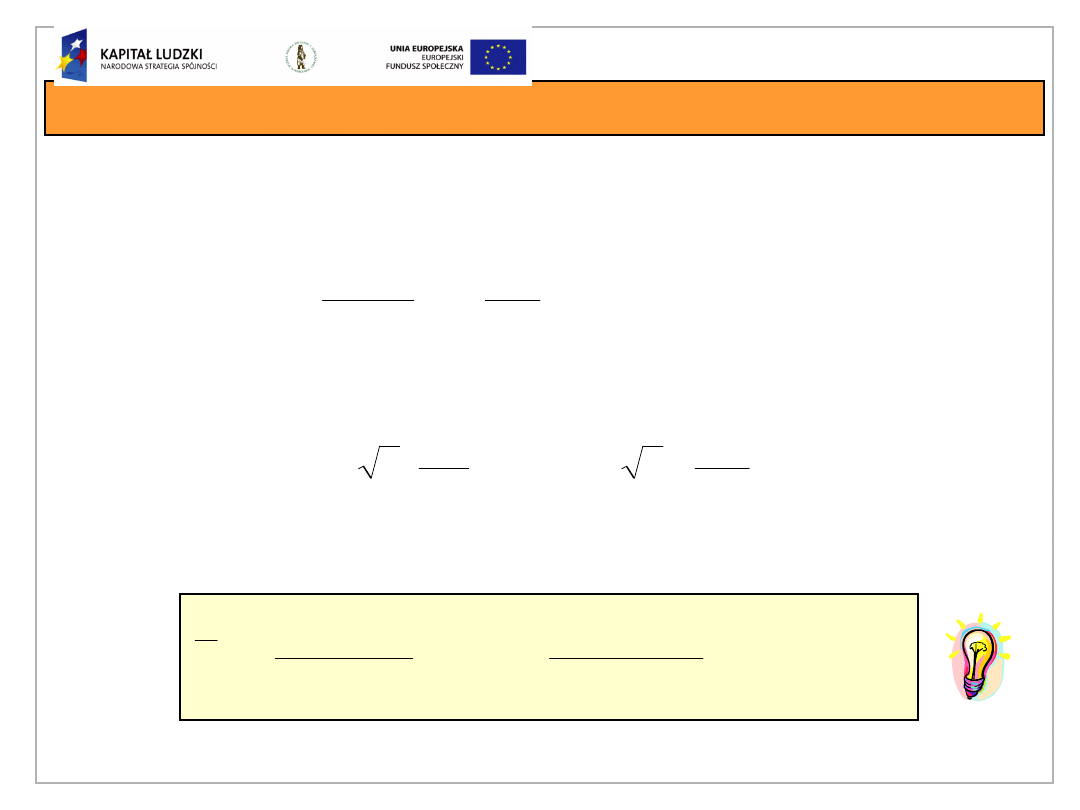
Obciążenie graniczne belki
Dla danych z poprzedniego przykładu obliczymy
nośność sprężystą belki
o rozpiętości 10 m.
kN/m
8
,
55
10
697
8
8
2
2
,
,
l
M
q
max
e
max
e
Nośność graniczna
kN/m
6
,
92
10
794
)
2
2
3
(
2
)
2
2
3
(
2
2
2
0
0
l
M
q
Rezerwa plastyczna konstrukcji
%
66
%
100
8
,
55
8
,
55
6
,
92
%
100
0
e,max
e,max
pl
q
q
q
R
Konstrukcje stalowe
W wykładzie omówiono następujące zagadnienia
Model materiału sprężysto-idealnie
plastycznego
Fazy wytężenia bisymetrycznego przekroju
zginanego
Moment zginający w przekroju częściowo
uplastycznionym
Nośność obliczeniowa przekrojów krępych
Przykład obliczeniowy (plastyczna rezerwa
nośności przekroju)
Plastyczna rezerwa konstrukcji
Koniec