Wektorem

nazywa się odcinek skierowany , w którym

punkt A uważa się za początek wektora, a punkt B za koniec
wektora

AB

A

B

a

Wektory równoległe do jednej prostej nazywa się kolinearnymi,
wektory równoległe do jednej płaszczyzny – komplanarnymi.

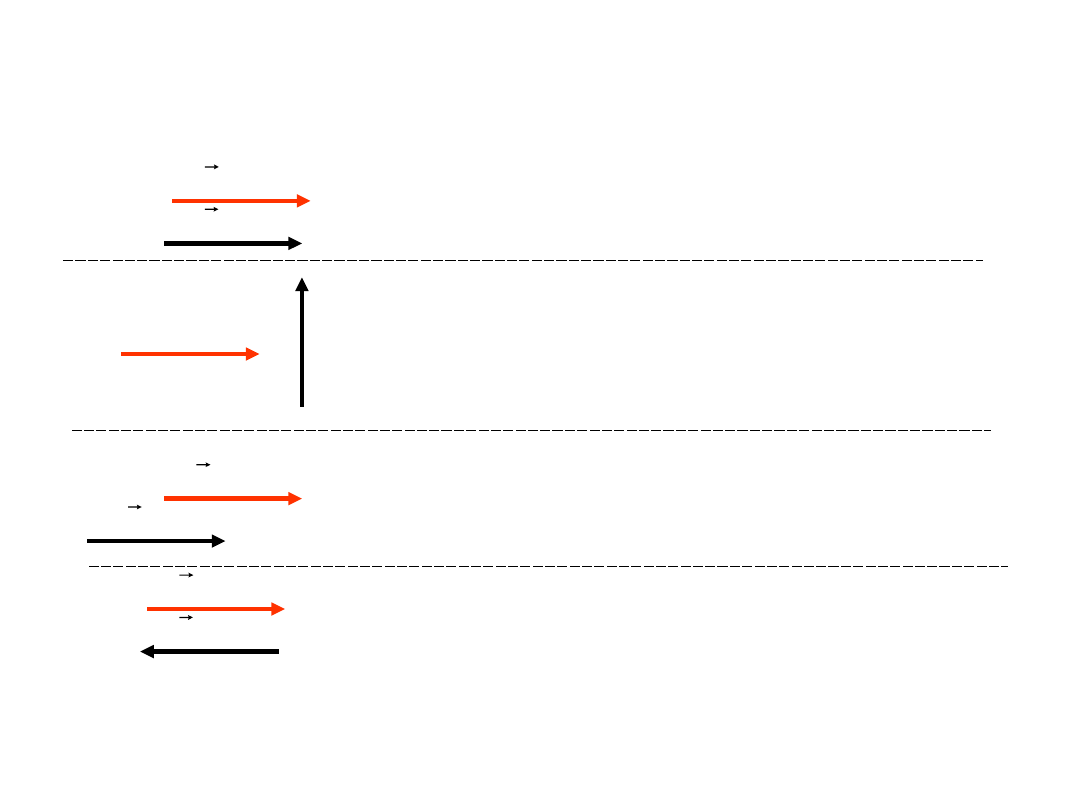
Jeżeli mamy dwa wektory to możemy określić ich wzajemne położenie.
Mogą one być wzajemnie:

- równoległe -

jeżeli proste zawierające
kierunki obu wektorów są
równoległe do siebie

                                 
                                 

       

- prostopadłe -

jeżeli proste zawierające
kierunki obu wektorów są
prostopadłe do siebie

                                 
                                 

                               

- równe -

jeżeli wszystkie swoje
cechy (długość, kierunek,
zwrot) mają takie same

                                 
                                 

                      

- przeciwne -

jeżeli mają ten sam
kierunek, taką samą
długość lecz przeciwne
zwroty

                                 
                                 

               

v

u

v

u

v

u

Współrzędne wektora względem osi

Niech wektor a z osią Ox, wtedy współrzędną wektora tej osi
opisuje wzór

a

x

= wsp

x

a = |a| cos 

Współrzędna sumy wektorów względem osi jest równa sumie
współrzędnych wektorów składowych względem osi

wsp

x

(a+b) = wsp

x

a + wsp

x

b

a

wsp

x

a

x

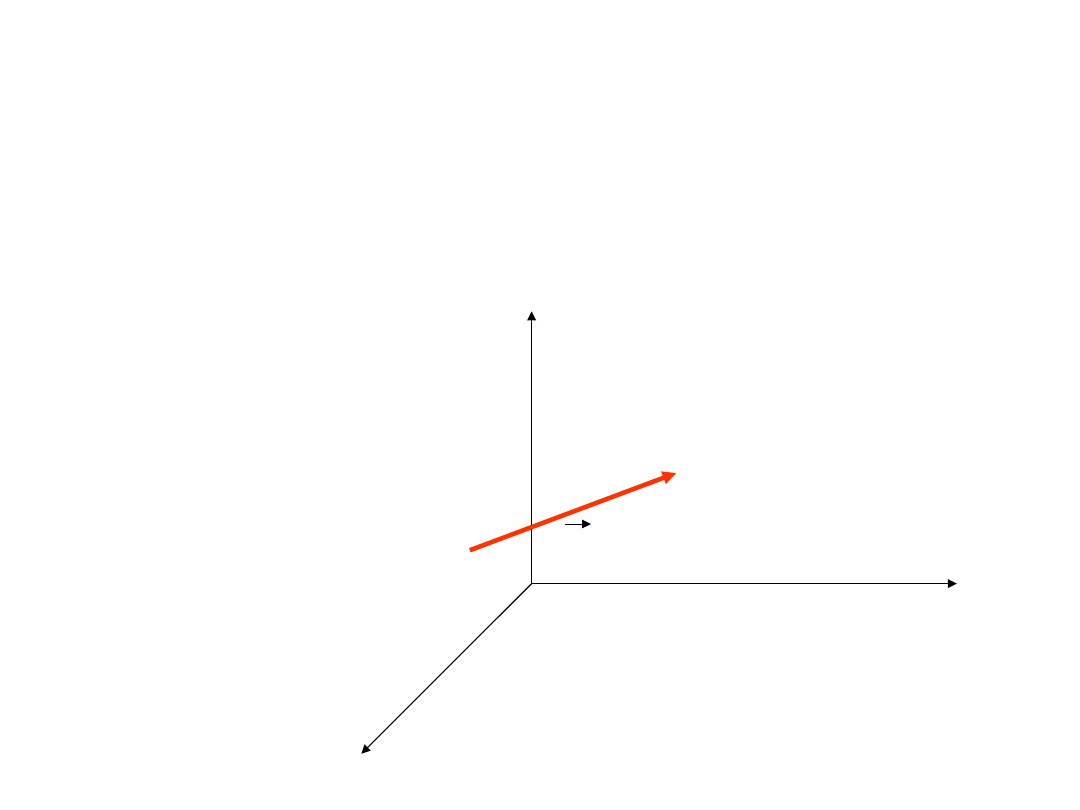
Wektory w układzie współrzędnych

Jeżeli mamy dany dwa punkty A(x

1

, y

1

, z

1

), B(x

2

, y

2

, z

2

),

to zbiór trzech uporządkowanych liczb (x

2

-x

1

,y

2

-y

1

,z

2

-z

1

)

nazywamy współrzędnymi wektora o początku w punkcie
A i końcu w punkcie B.         

Z

X

Y

O

B(x

2

, y

2

, z

2

)

A(x

1

, y

1

, z

1

)

c(x

2

-x

1

,y

2

-y

1

,z

2

-z

1

)

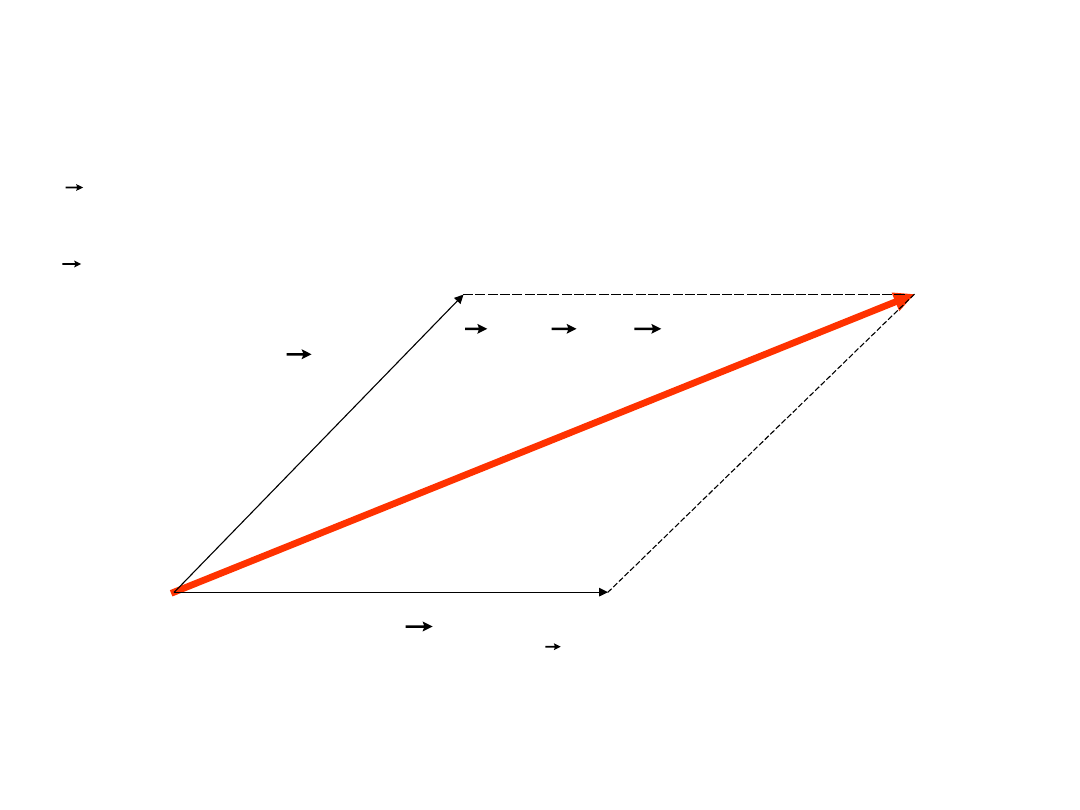
Suma wektorów

– metoda równoległoboku

a

b

b

a

c









z

y

x

a

,

a

,

a

a 





z

y

x

b

,

b

,

b

b





z

z

y

y

x

x

b

a

,

b

a

,

b

a

c









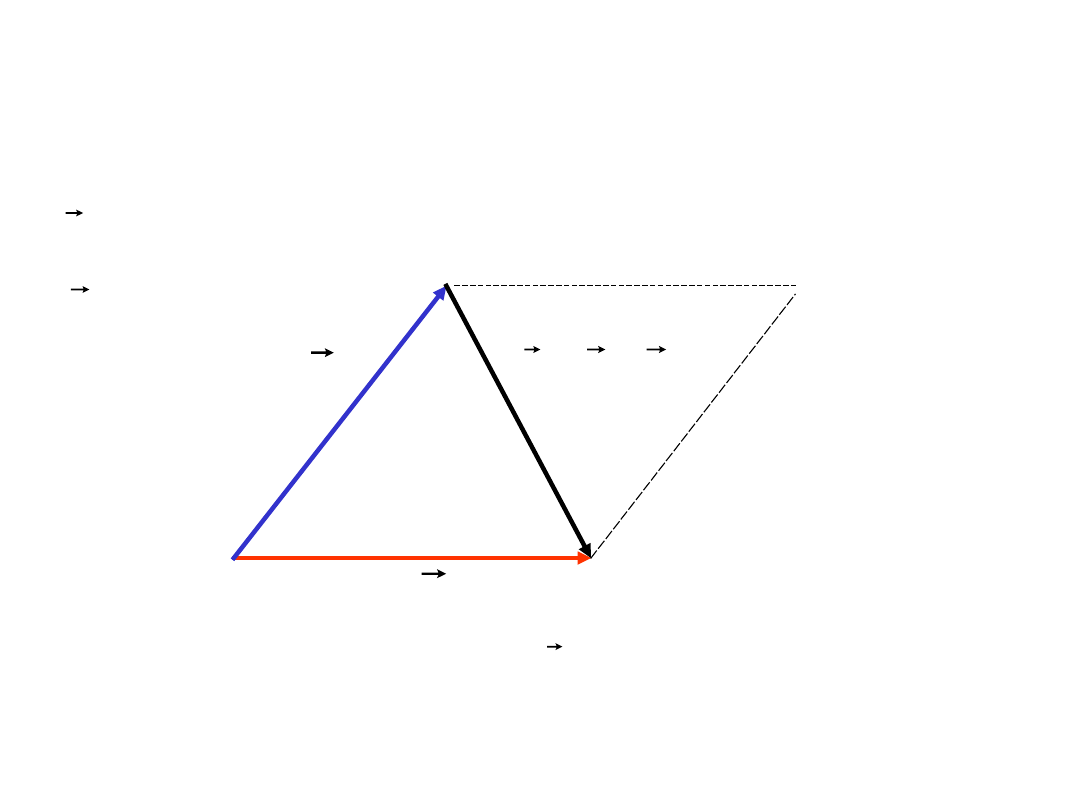
Metoda równoległoboku – można stworzyć równoległobok dla sumy
wektorów a i b, a rozwiązaniem będzie druga z przekątnych

b

b

a

c





a

Różnica wektorów





z

y

x

a

,

a

,

a

a 





z

y

x

b

,

b

,

b

b





z

z

y

y

x

x

b

a

,

b

a

,

b

a

c









Iloczynem wektora przez skalar

nazywamy nowy

wektor mający długość a · |m| i skierowany zgodnie z wektorem
a gdy m > 0 i przeciwnie do wektora a gdy m < 0

a

m

a

b





)

m

(

a

b







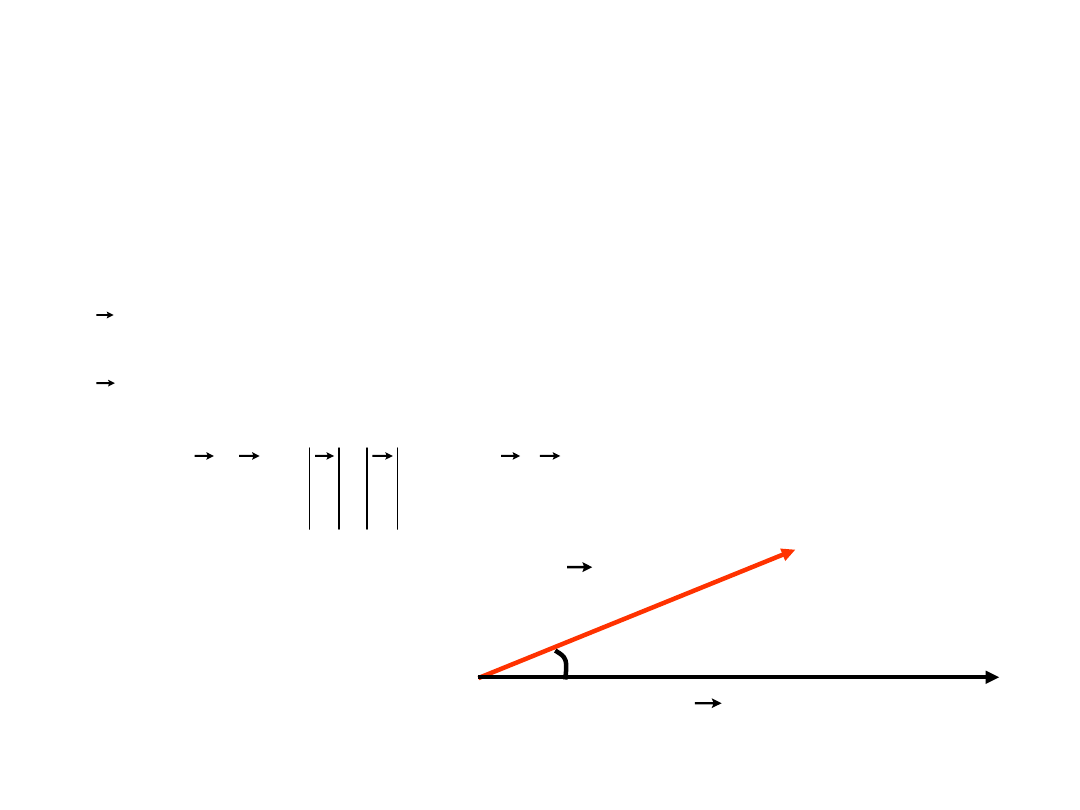
Iloczyn skalarny wektorów

Iloczynem skalarnym dwóch wektorów jest liczba równa iloczynowi
długości tych wektorów i cosinusa kąta zawartego między nimi:

 

Należy pamiętać, że iloczyn skalarny jest liczbą (skalarem),
a nie wektorem.

 

                   

z

z

y

y

x

x

b

a

b

a

b

a

)

b

,

a

cos(

b

a

b

a

c

















a

b





z

y

x

a

,

a

,

a

a 





z

y

x

b

,

b

,

b

b

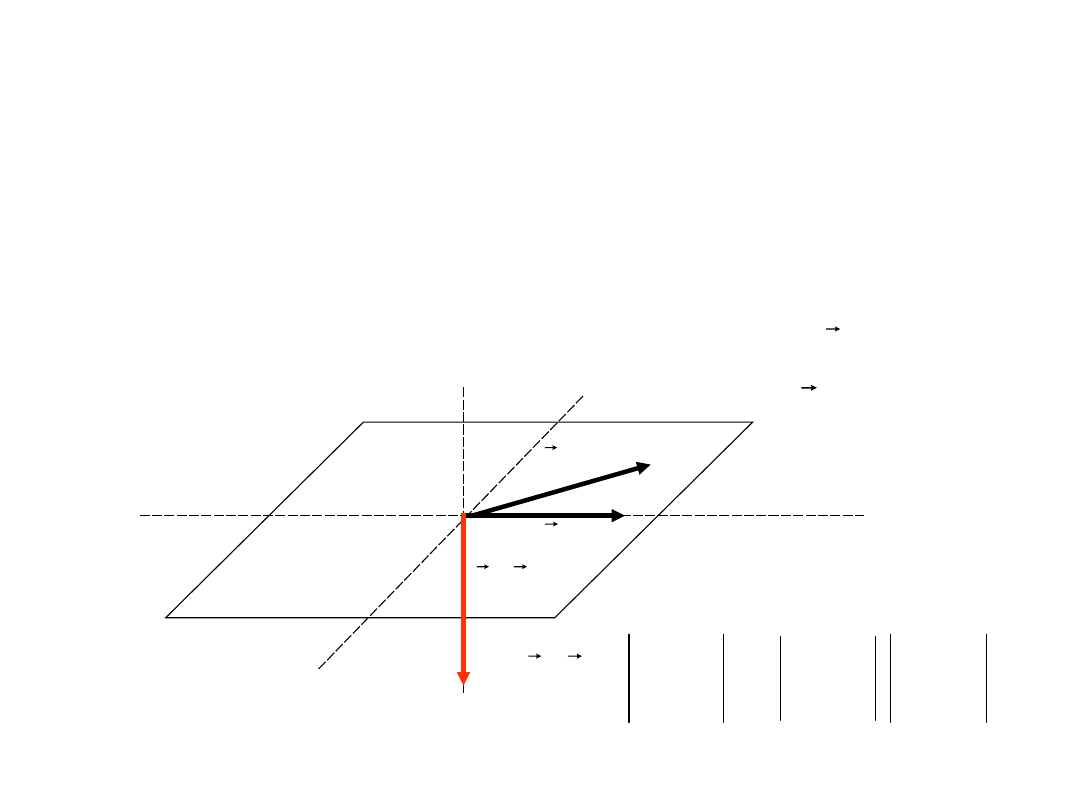
Iloczyn wektorowy

Iloczynem wektorowym dwóch wektorów u i v,
nazywamy
wektor w:

•który jest prostopadły do płaszczyzny rozpiętej na
wektorach u i v  

•punkt przyłożenia wektora w pokrywa się z
początkami
wektorów u i v  

•którego długość jest równa polu równoległoboku
rozpiętego
na tych wektorach u i v
Którego zwrot jest określony regułą śruby
prawoskrętnej

b

a

b

a

























y

x

y

x

z

x

z

x

z

y

z

y

b

b

a

a

,

b

b

a

a

1

,

b

b

a

a

b

a





z

y

x

a

,

a

,

a

a 





z

y

x

b

,

b

,

b

b

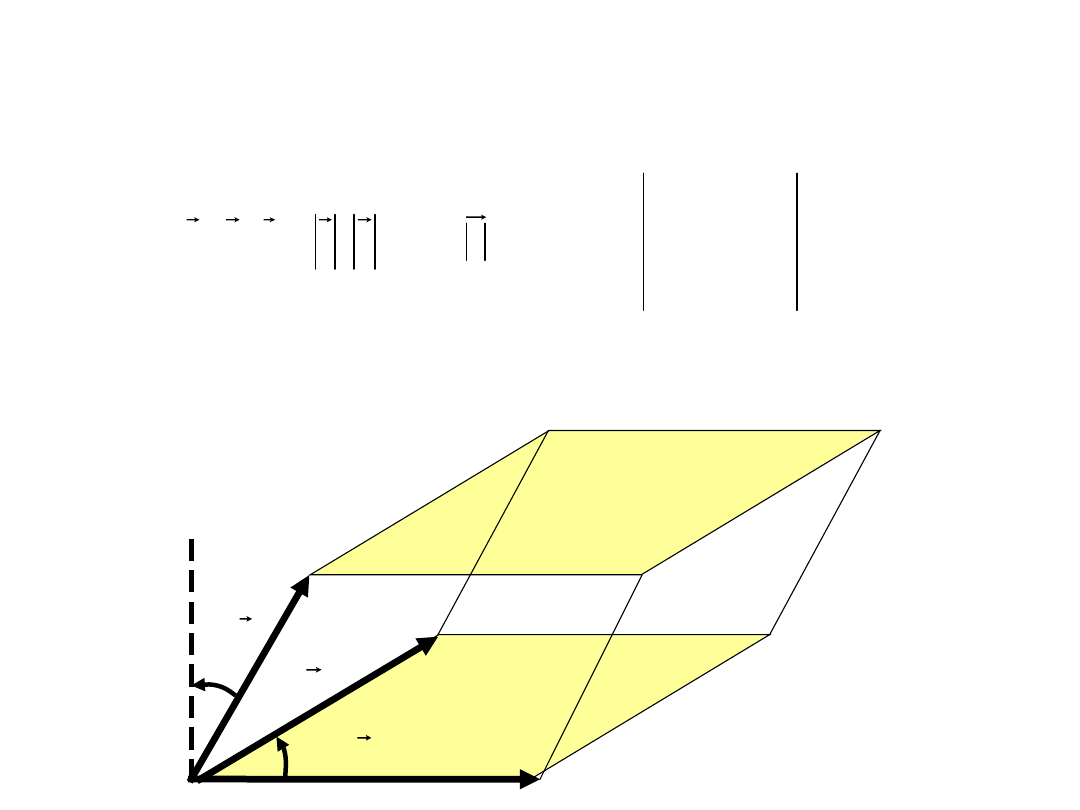
ILOCZYN MIESZANY TRÓJKI WEKTORÓW

Jeżeli wektory a, b, c są wyrażone przez współrzędne to:

 



 



z

y

x

z

y

x

z

y

x

c

c

c

b

b

b

a

a

a

det

cos

c

sin

b

a

c

b

a



















Jeżeli dwa spośród trzech danych wektorów są równe lub
równoległe to ich iloczyn mieszany jest równy 0

c

b

a













z

y

x

z

y

x

b

,

b

,

b

b

;

a

,

a

,

a

a





Warunkiem koniecznym i dostatecznym prostopadłości
dwóch wektorów niezerowych

jest, by ich iloczyn skalarny był równy zeru.

0

b

a

b

a

b

a

b

a

z

z

y

y

x

x











Równoległość wektorów

Warunkiem koniecznym i wystarczającym

równoległości dwóch wektorów niezerowych









z

y

x

z

y

x

b

,

b

,

b

b

;

a

,

a

,

a

a





jest, aby wyacznik

z

z

y

y

x

x

b

a

b

a

b

a





0

b

b

b

a

a

a

1

1

1

z

y

x

z

y

x





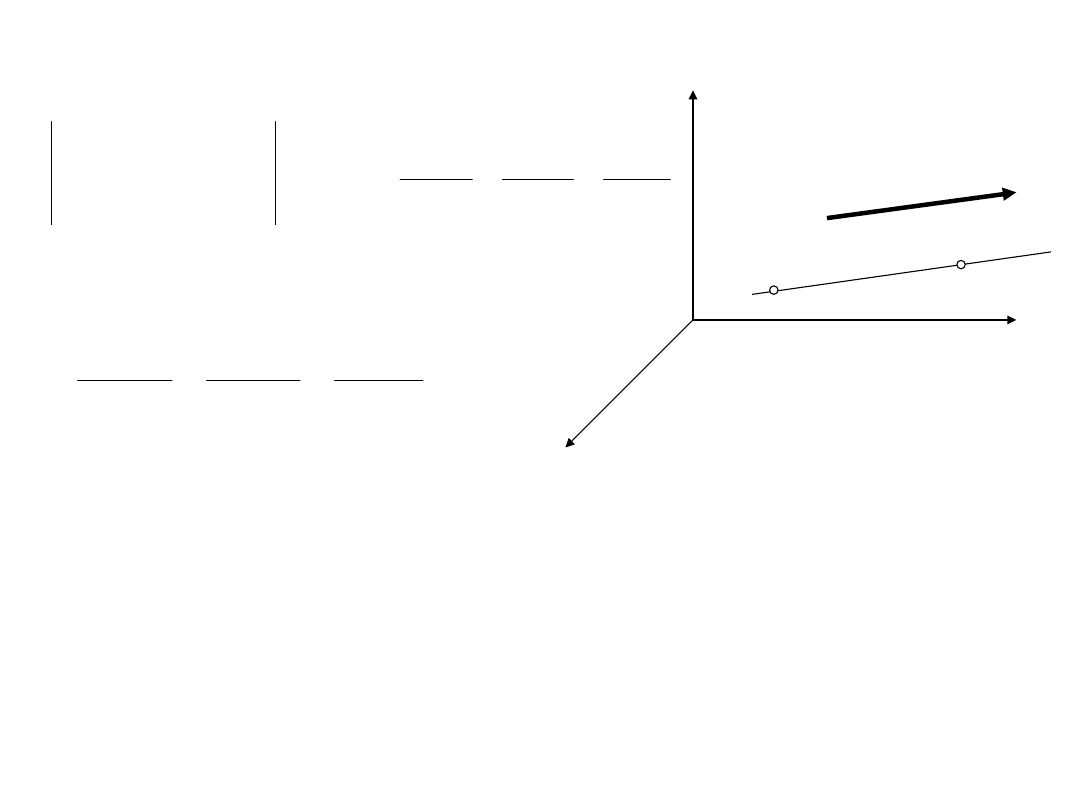
RÓWNANIE PROSTEJ W PRZESTRZENI

V=[a;b;c]

M

0

(x

0

,y

0

,z

0

)

M(x,y,z)

0

x

y

z

Równanie parametryczne prostej























ct

z

z

bt

y

y

at

x

x

1

1

1

Równanie prostej przechodzącej przez dwa różne punkty

1

2

1

1

2

1

1

2

1

z

z

z

z

y

y

y

y

x

x

x

x

















0

c

b

a

z

z

y

y

x

x

k

j

i

o

o

o











b

z

z

b

y

y

a

x

x

o

o

o











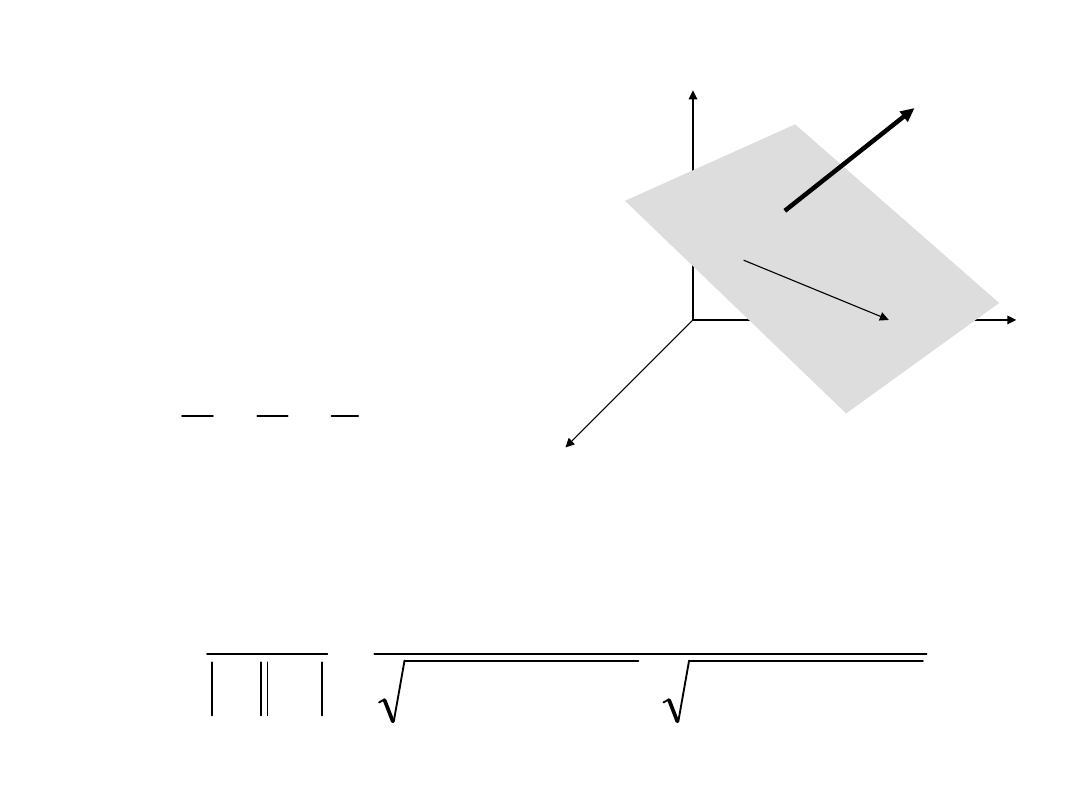
PŁASZCZYZNA

Ogólne równanie płaszczyzny

A(x-x

o

) + B(y-y

o

) + C(z-z

o

) = 0

Odcinkowe równanie płaszczyzny

1

c

z

b

y

a

x







Kąt zawarty między płaszczyznami

V=[A;B;C]

M

0

(x

0

,y

0

,z

0

)

M(x,y,z)

0

x

y

z

2
2

2
2

2
2

2
2

2
2

2
2

2

1

2

1

2

1

2

1

2

1

C

B

A

C

B

A

C

C

B

B

A

A

V

V

V

V

cos

























Ax + By + Cz+D = 0

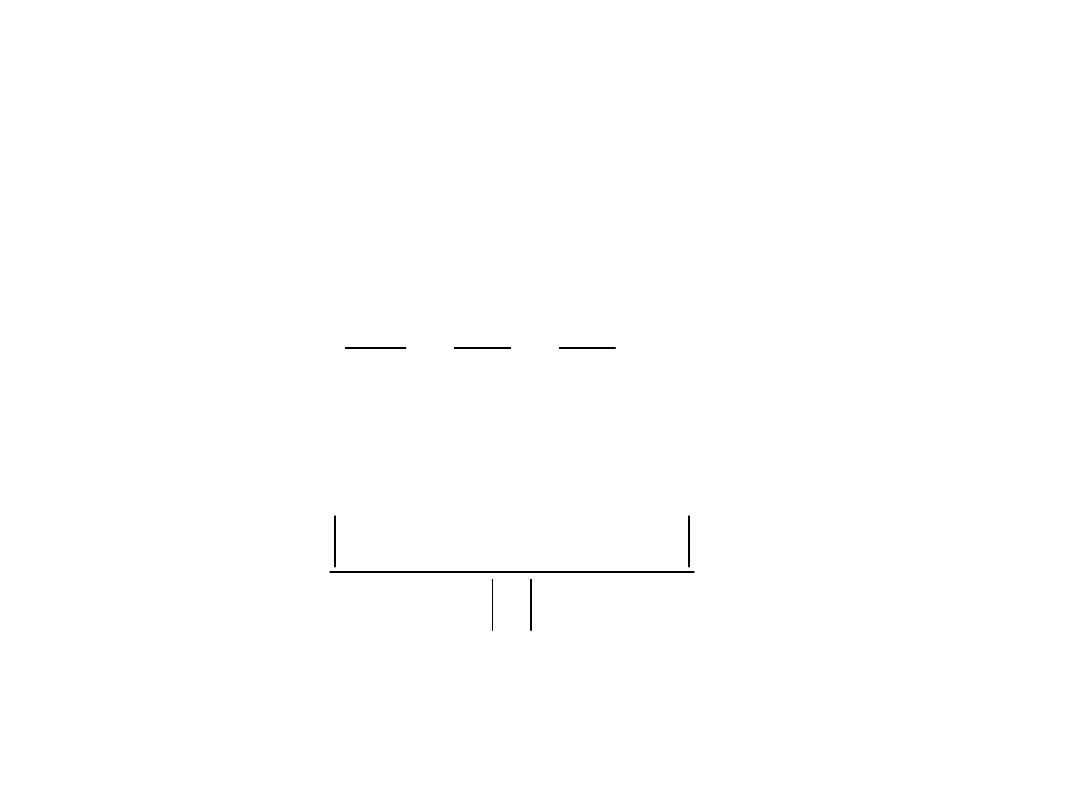
Warunek prostopadłości płaszczyzn

0

C

C

B

B

A

A

1

2

2

1

2

1







Warunek równoległości płaszczyzn

2

1

2

1

2

1

C

C

B

B

A

A





Odległość punktu M

0

(x

0

,y

0

,z

0

) od płaszczyzny Ax+By+Cz+D=0

V

D

Cz

By

Ax

d

0

0

0









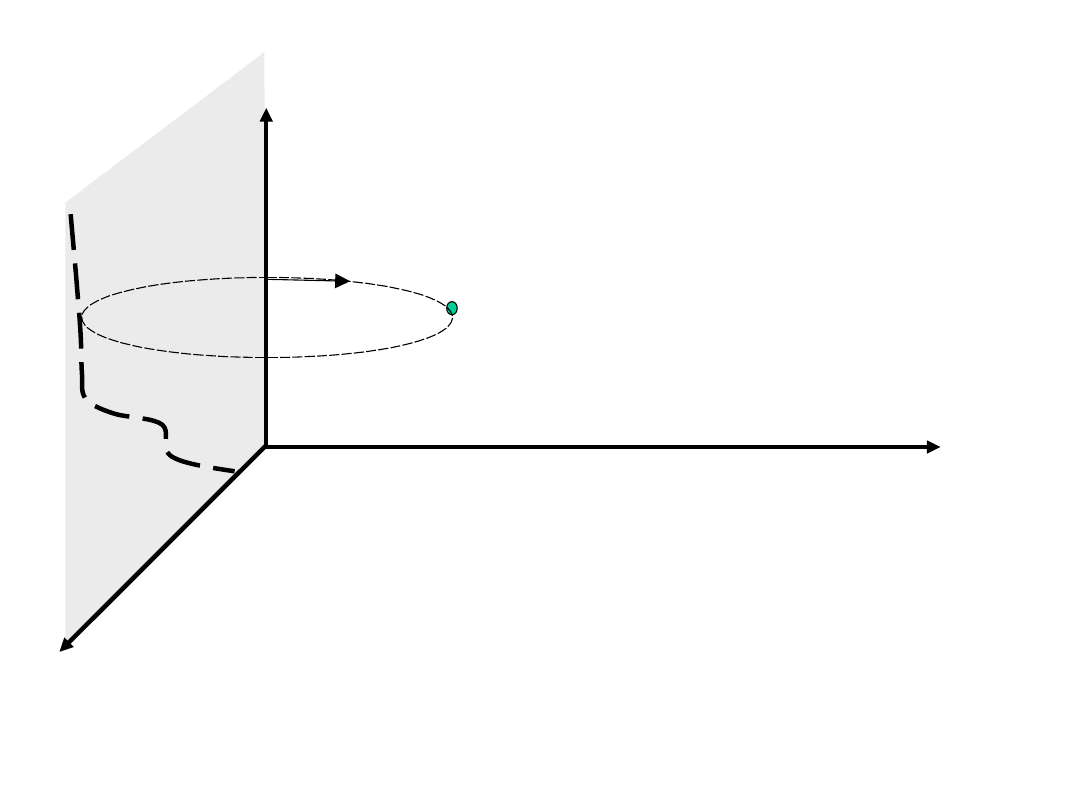
Powierzchnie stopnia drugiego

x=f(z)

z

x

y

y=0

P

0

Obracamy krzywą x=f(z) dookoła osi Oz. Każdy punkt P

0

nie leżący na osi z zatoczy okrąg:

2

0

2

2

))

z

(

f

(

y

x





W związku z tym równanie powierzchni przyjmie postać:

)

z

(

f

y

x

2

2

2





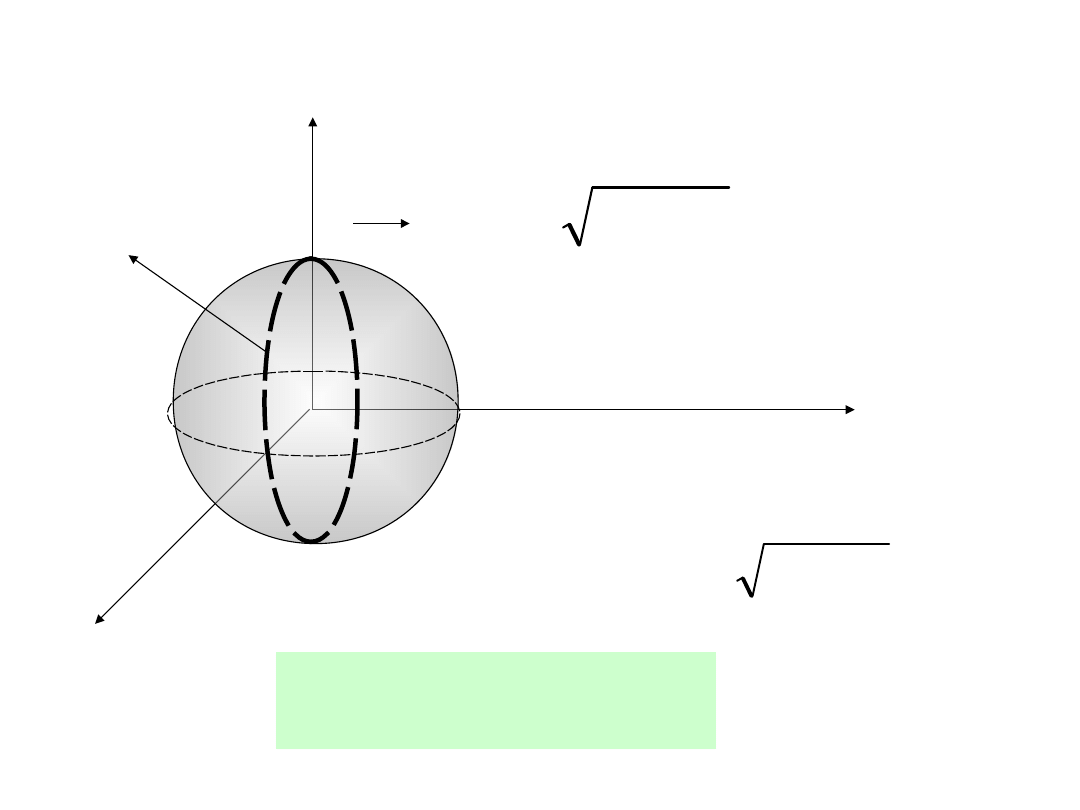
Kula

2

2

2

r

z

x





2

2

z

r

x





)

z

(

f

y

x

2

2

2





2

2

2

2

z

r

y

x







2

2

2

2

r

z

y

x







z

x

y

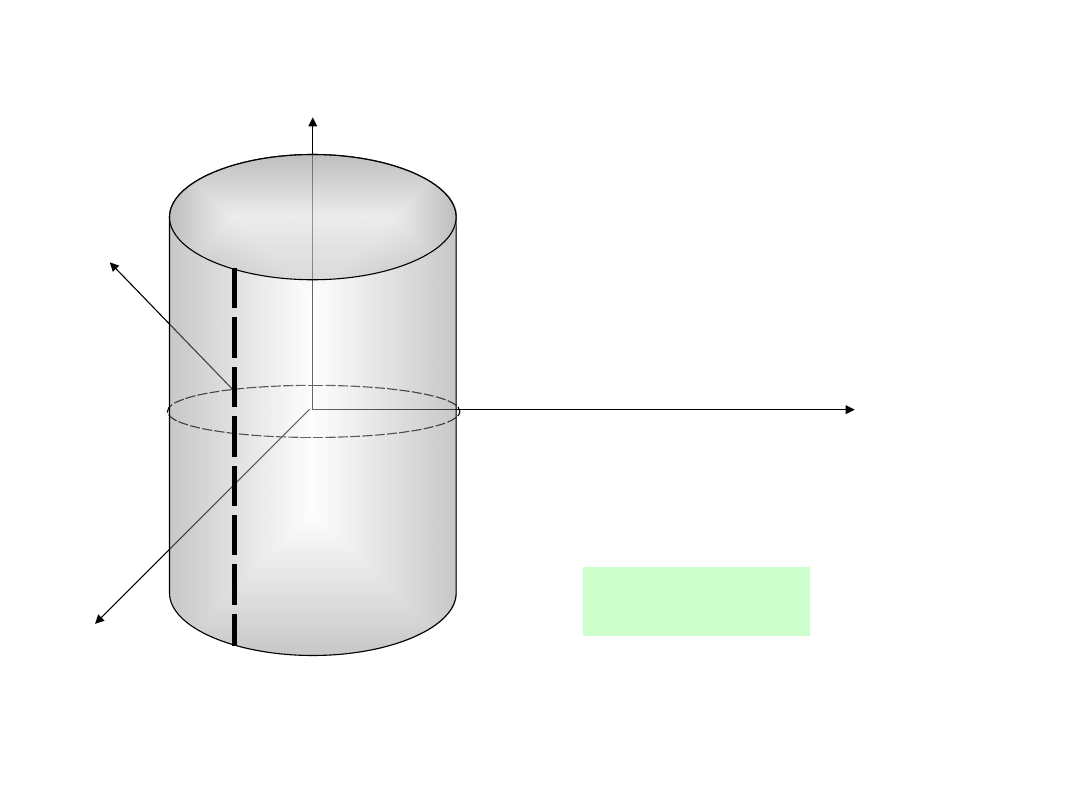
Walec

r

x 

)

z

(

f

y

x

2

2

2





2

2

2

r

y

x





z

x

y

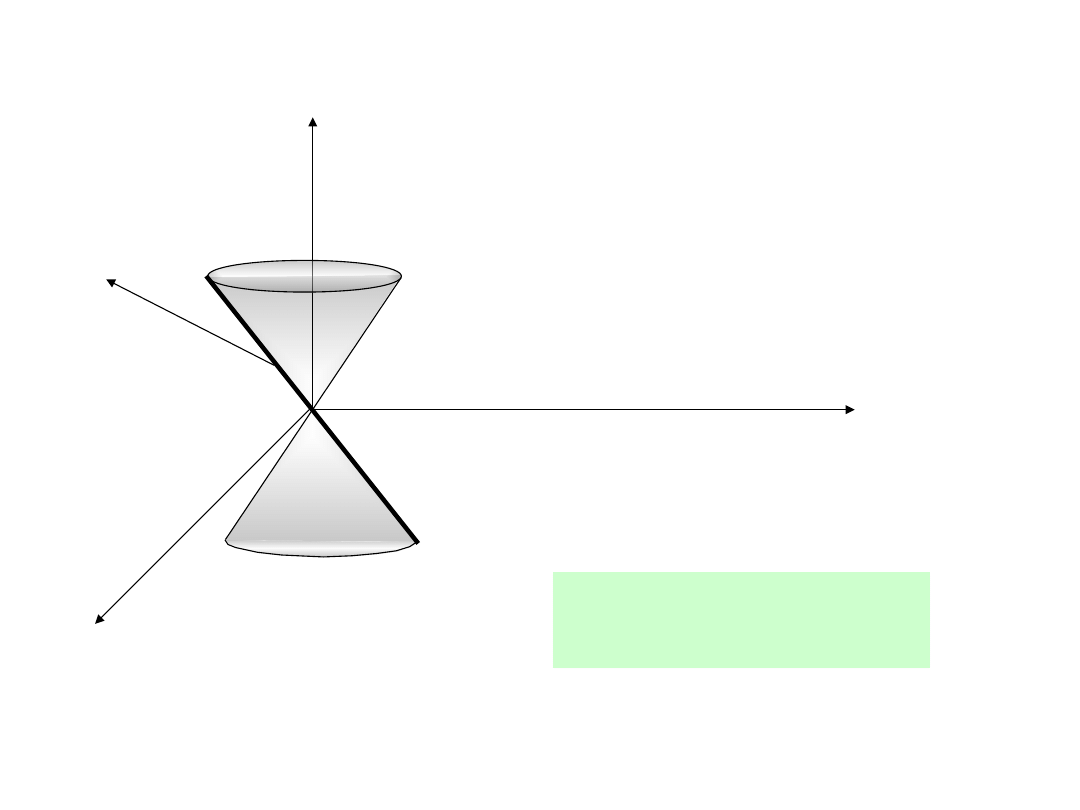
Stożek kołowy

az

x 

)

z

(

f

y

x

2

2

2





2

2

2

2

z

a

y

x





z

x

y

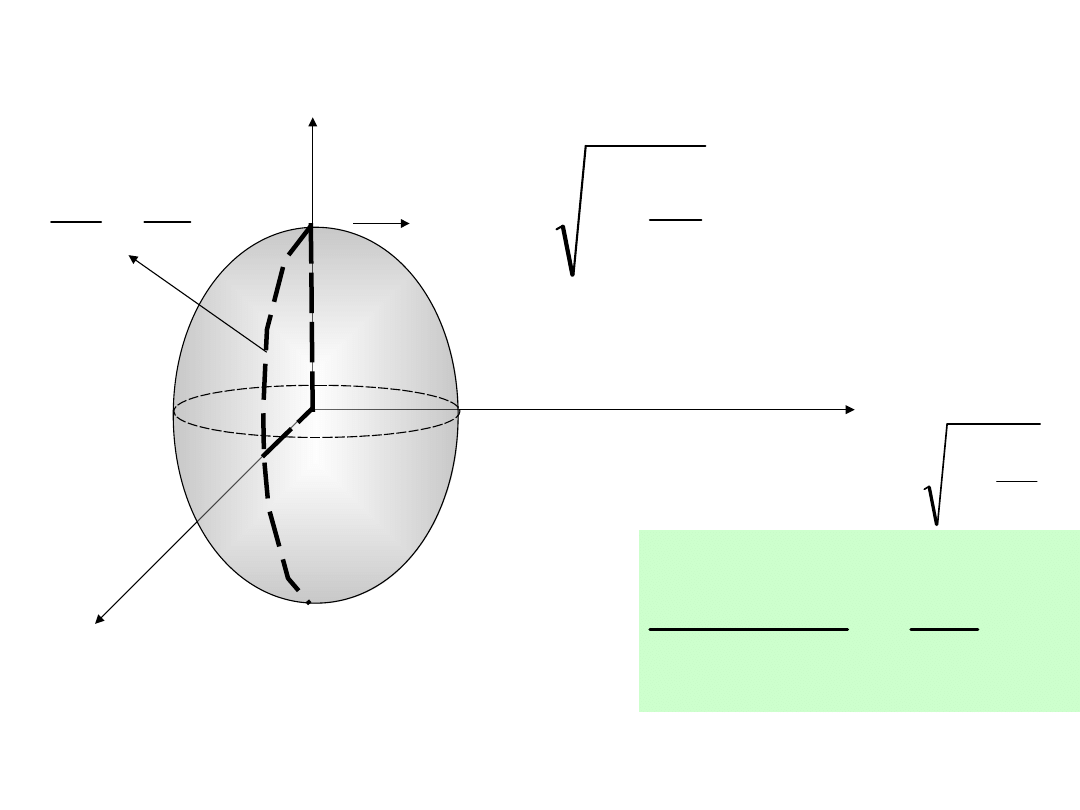
Elipsoida

1

c

z

a

x

2

2

2

2





2

2

c

z

1

a

x





)

z

(

f

y

x

2

2

2





2

2

2

2

2

c

z

1

a

y

x





















1

c

z

a

y

x

2

2

2

2

2







z

x

y

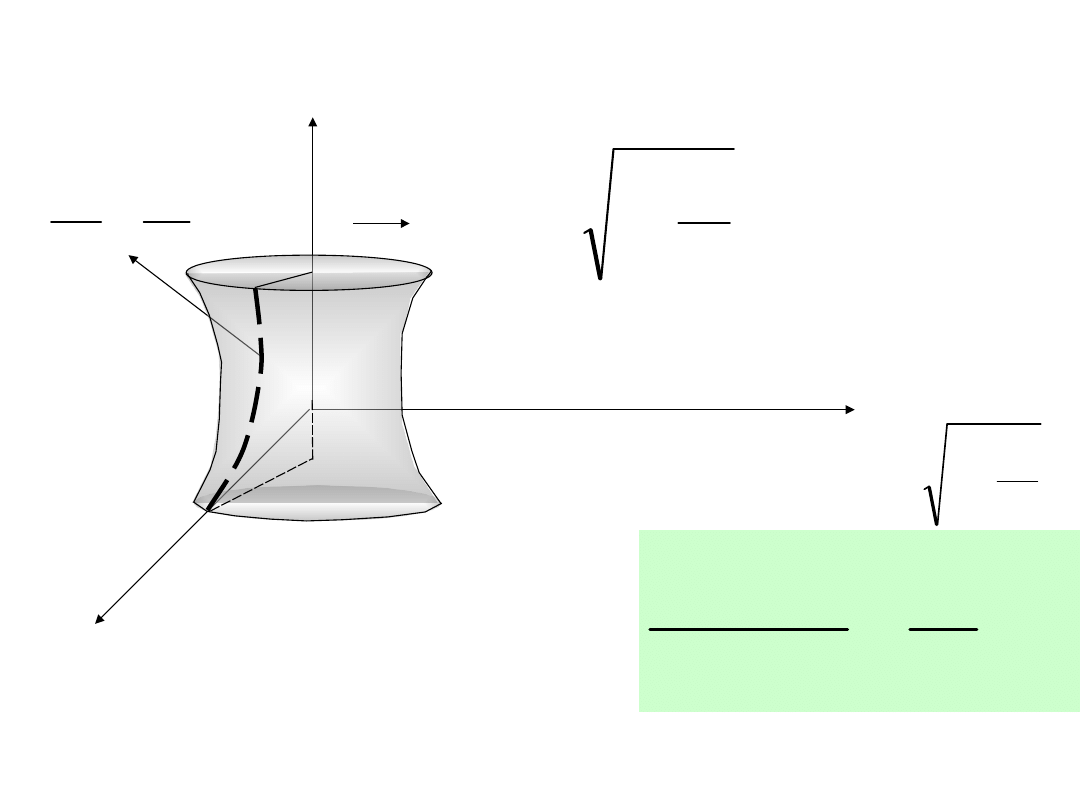
Hiperboloida

1

c

z

a

x

2

2

2

2





2

2

c

z

1

a

x





z

x

y

)

z

(

f

y

x

2

2

2





2

2

2

2

2

c

z

1

a

y

x





















1

c

z

a

y

x

2

2

2

2

2







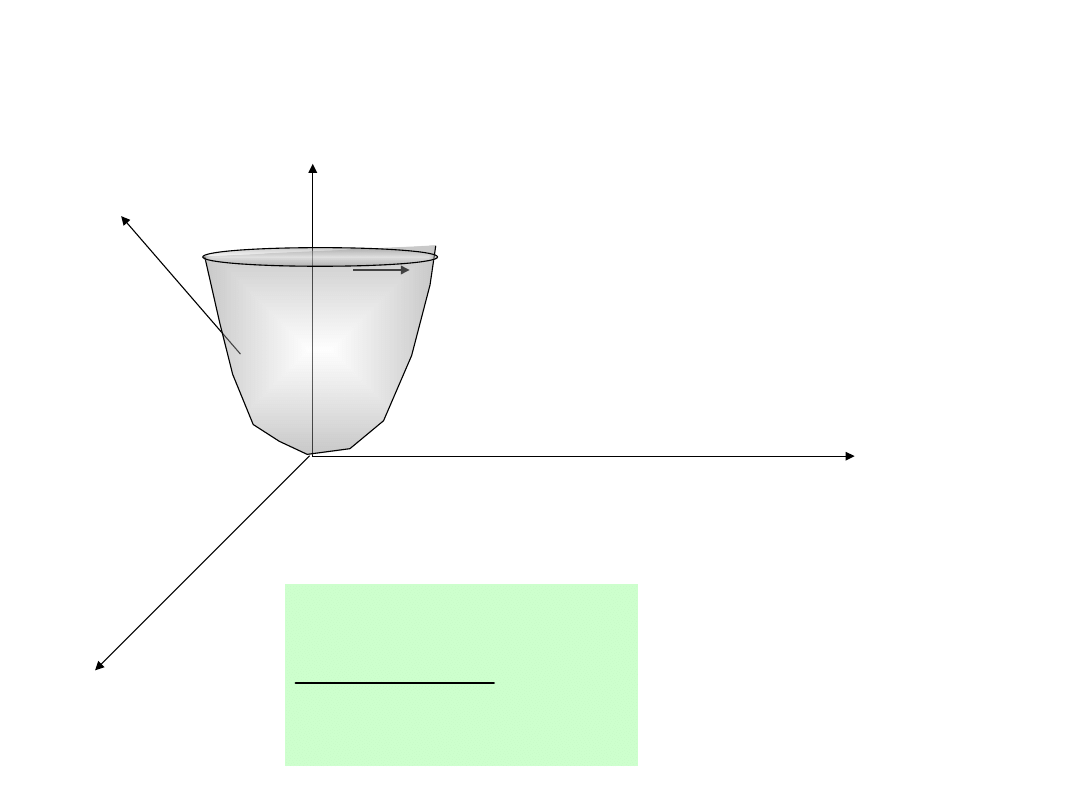
Paraboloida

az

2

x

2



)

z

(

f

y

x

2

2

2





az

2

y

x

2

2





z

2

a

y

x

2

2





z

x

y