Metody zagęszczania
osnowy szczegółowej -
wcięcia
Wcięcia wyznaczające jednoznacznie
położenie punktów (bez kontroli pomiaru i
wyrównania):
-
pojedynczych punktów (liniowe, w przód, w
bok, kombinowane, wstecz)
-
par punktów (zadanie Hansena, Mareka)
-
wielopunktowe (złożone)
Wcięcia z obserwacjami nadliczbowymi
(możliwością wyrównania)
-
wcięcia dwustronne,
-
wolne stanowisko (free station)
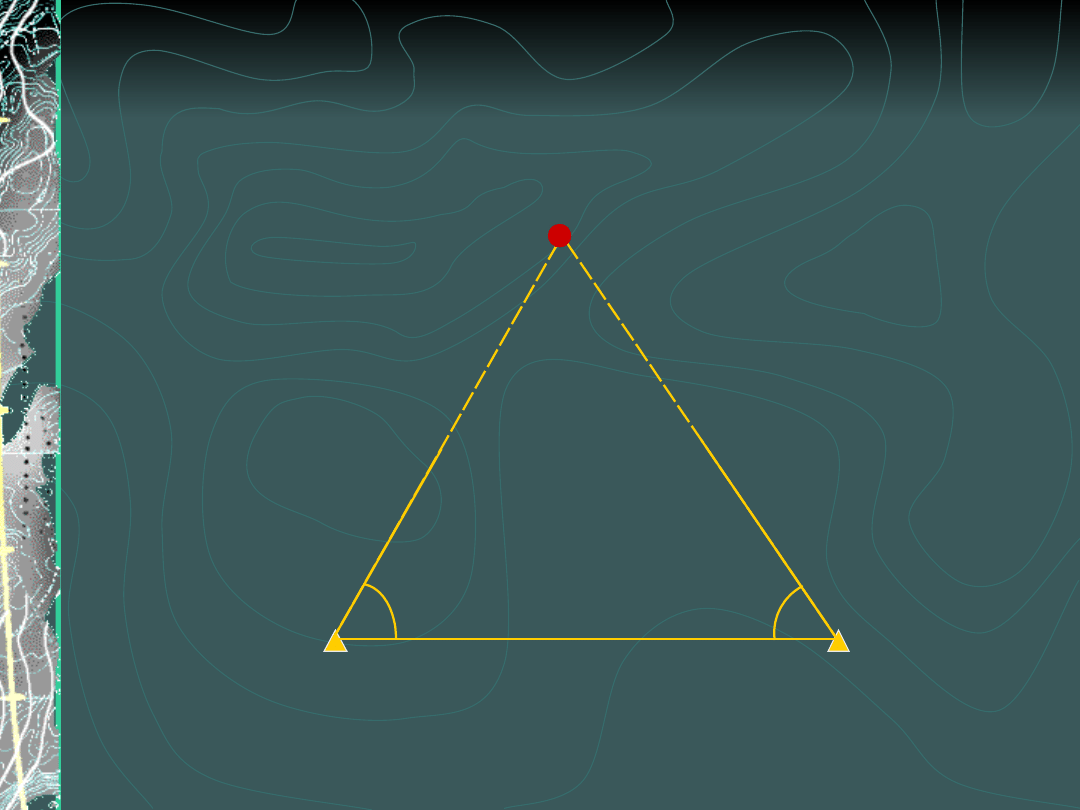
Wcięcia pojedynczych
punktów
W przód (kątowe)
A
P
B
β
α
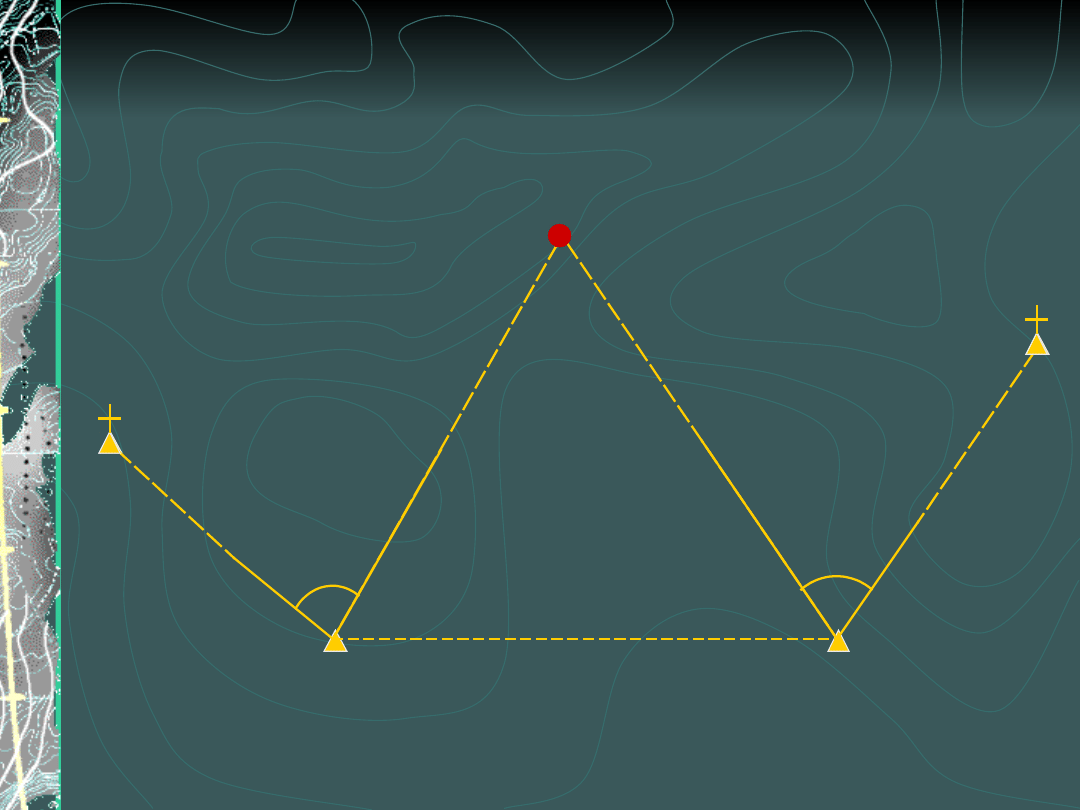
Ogólny przypadek wcięcia
w przód (wcięcie
azymutalne)
A
P
B
β
α
C
D
brak
celowej
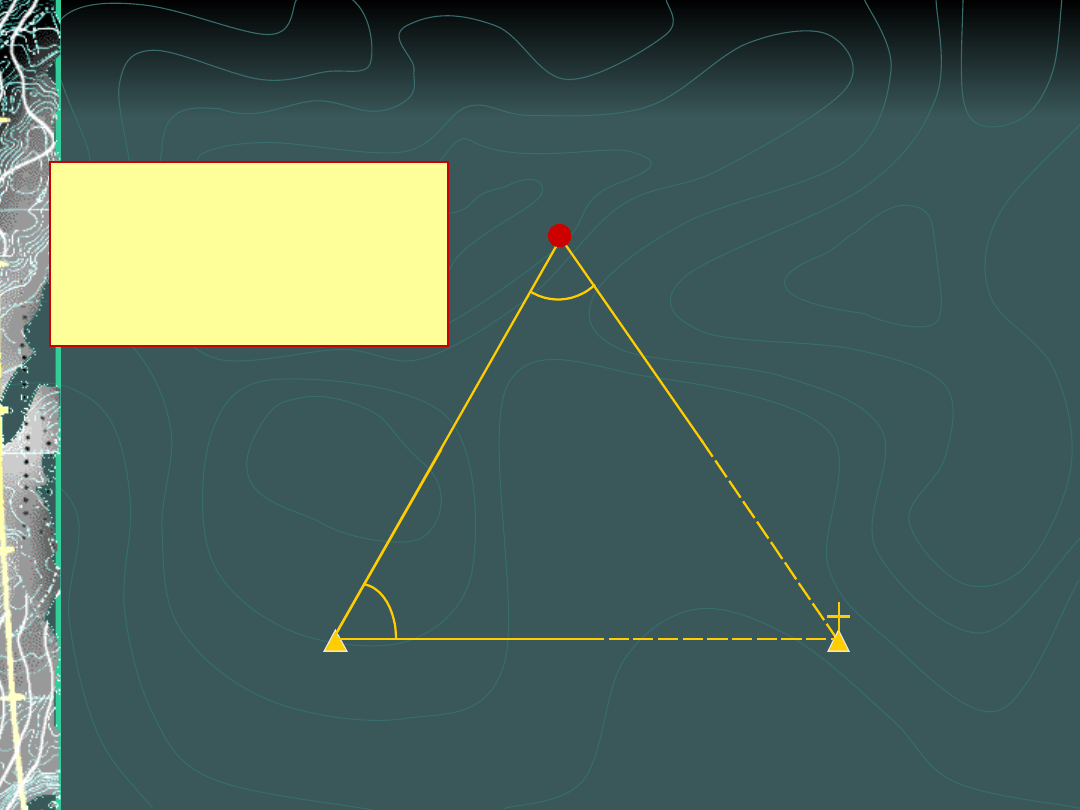
Wcięcie w bok
A
P
B
γ
α
Modyfikacja wcięcia w przód
Wcięcie to ma inną
charakterystykę
dokładnościową
niż wcięcie w przód !
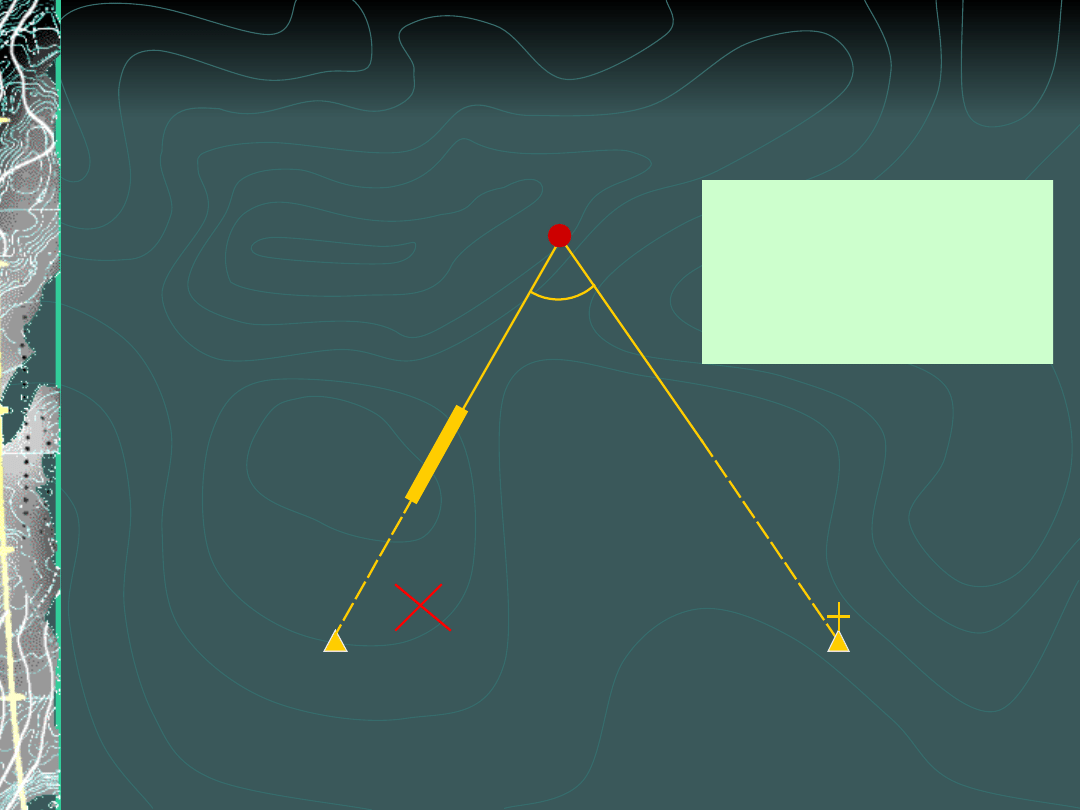
Wcięcie kątowo-liniowe
A
P
B
γ
α
Modyfikacja wcięcia w bok – wcięcie kątowo-
liniowe (kombinowane) – różne nazwy w
podręcznikach
Zamiast kąta
γ mierzymy
długość AP
(d)
Zaleta:
obserwacje
są
wykonywane
na punkcie
wyznaczany
m
d
Zalecane do
zagęszczania
osnowy
pomiarowej
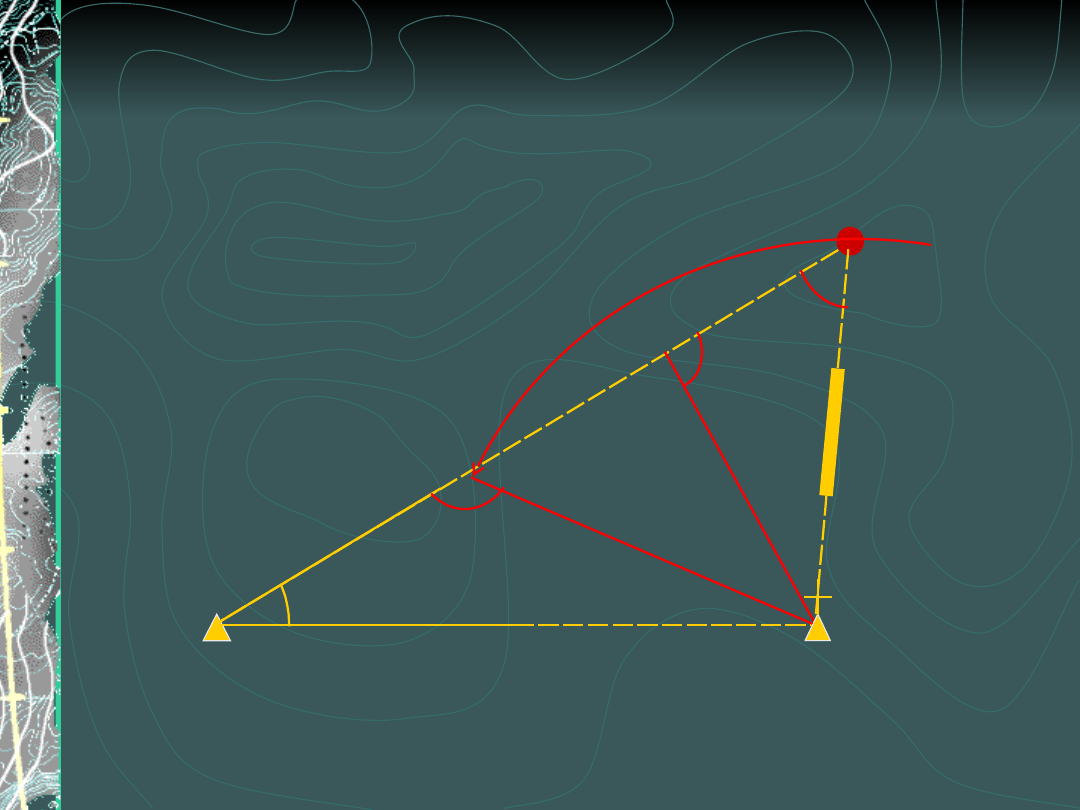
Inne wcięcie kombinowane
(zadanie ma dwa rozwiązania !)
B
sin (γ) = sin (200 – γ)
Zamiast kąta
γ mierzymy
długość PB
(d)
A
P’
α
d
P
.
200
g
-γ
γ
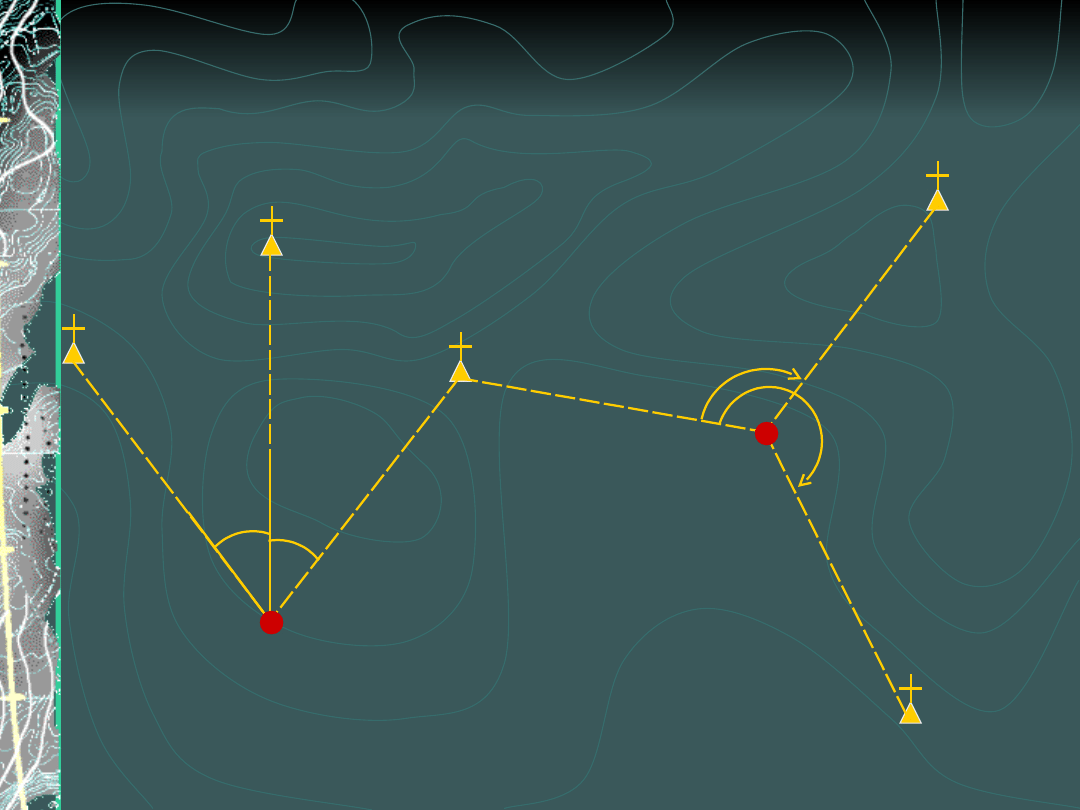
Wcięcie wstecz (zadanie
Pothenota)
Pomiar na punkcie wyznaczanym
do punktów niedostępnych
C
P
B
β
α
α
β
A
E
D
P
W zależności od metody
obliczeń przyjmuje się kąty lub
kierunki
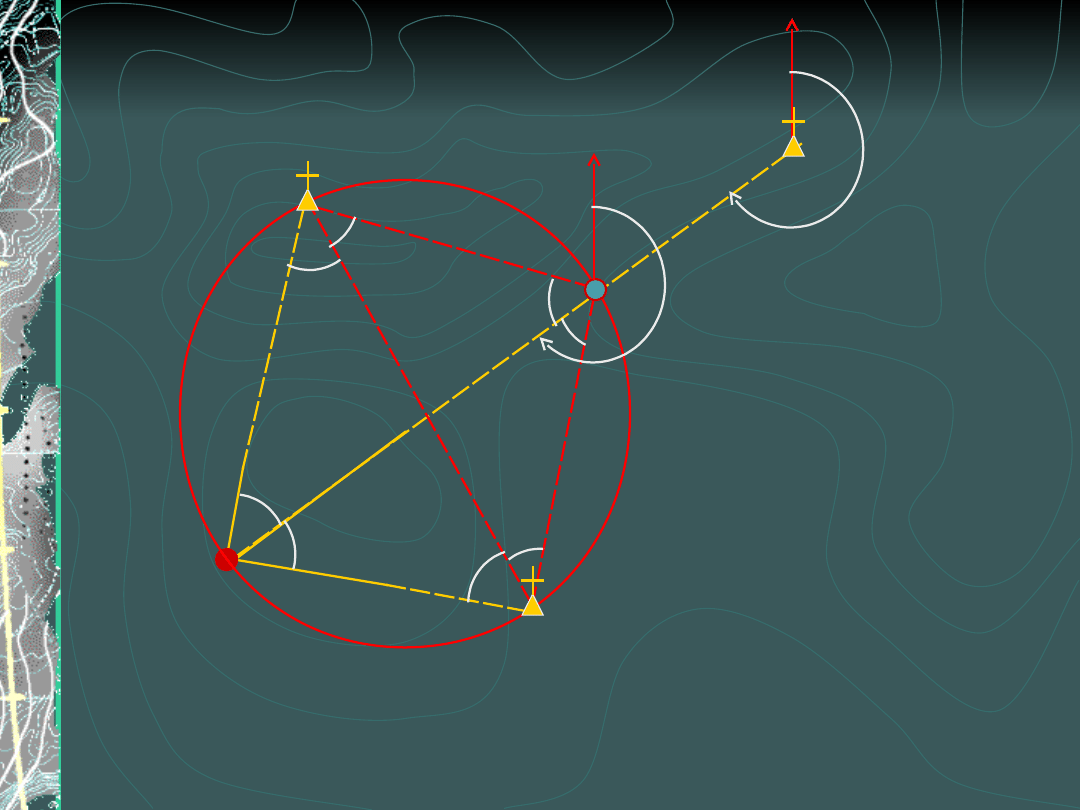
Metoda Collinsa
1. Obliczyć współrzędne
punktu Collinsa Q
wcięciem w przód w
oparciu o kąty
α i β
2. Obliczyć kąty γ i δ z
różnicy azymutów
3. Obliczyć współrzędne
punktu P wcięciem w
przód w oparciu o kąty γ
i δ
C
A
B
β
α
P
α
β
Q
δ
γ
δ
γ
A
QP
= A
BQ
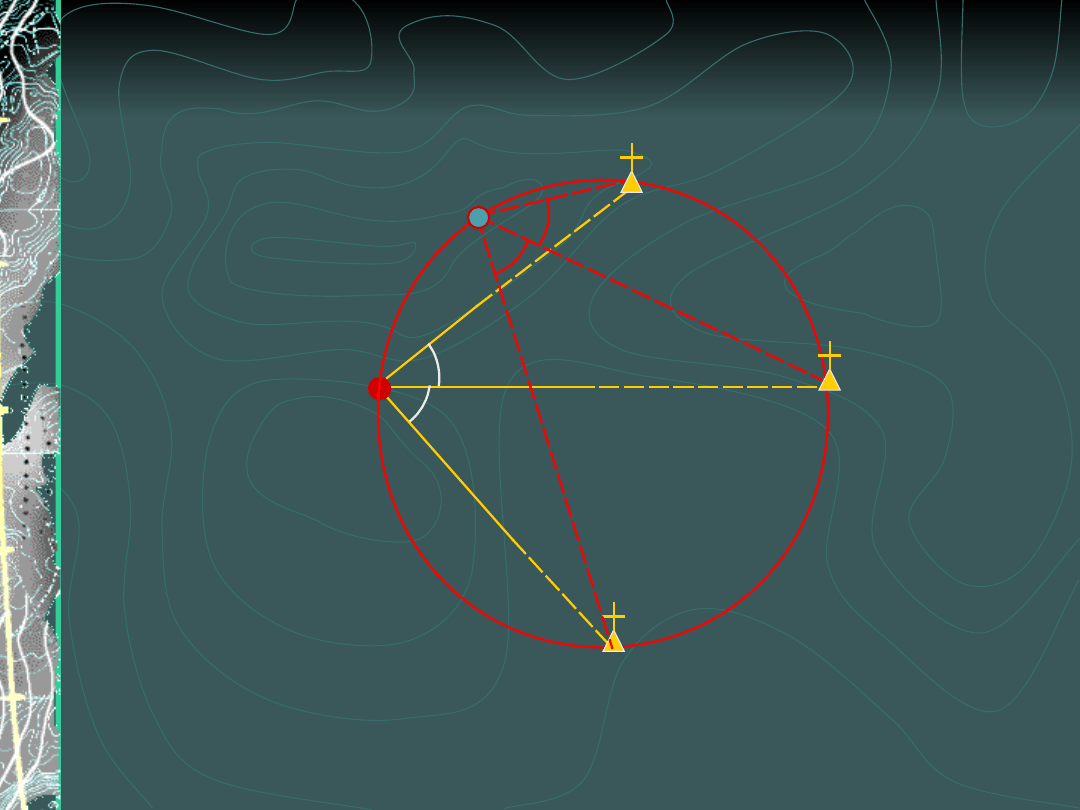
Wcięcie wstecz -
wyznaczalność
A
Wcięcie niewyznaczalne
wszystkie punkty na jednym
okręgu
C
B
β
α
P
α
β
P
Wcięcia wielopunktowe
Par punktów:
•
zadanie Hansena
•
zadanie Mareka
Złożone
Liczba obserwacji n powinna być
równa liczbie niewiadomych u
u = 2 p
gdzie: p – liczba punktów
wyznaczanych
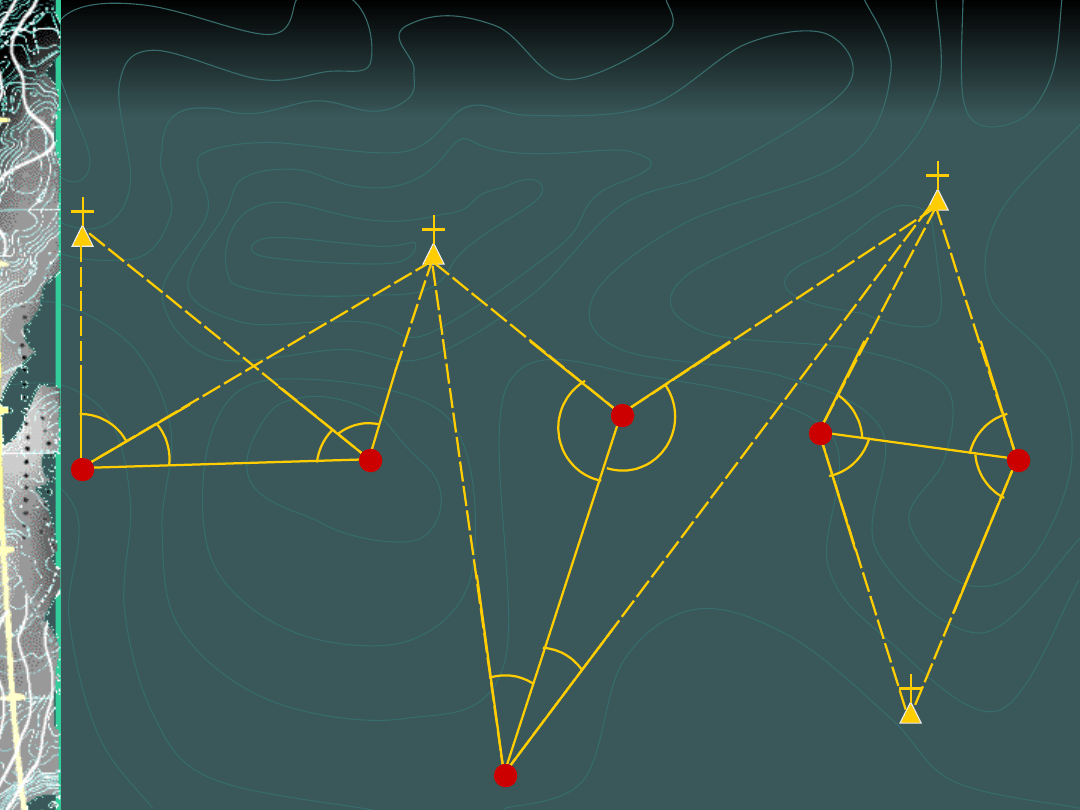
Wcięcie wstecz na dwa punkty
(zadanie Hansena)
Pomiar na punktach
wyznaczanych
3 wersje
C
P
B
β
α
α
β
A
D
P
P
Q
Q
Q
β
α
γ
δ
γ
γ
δ
δ
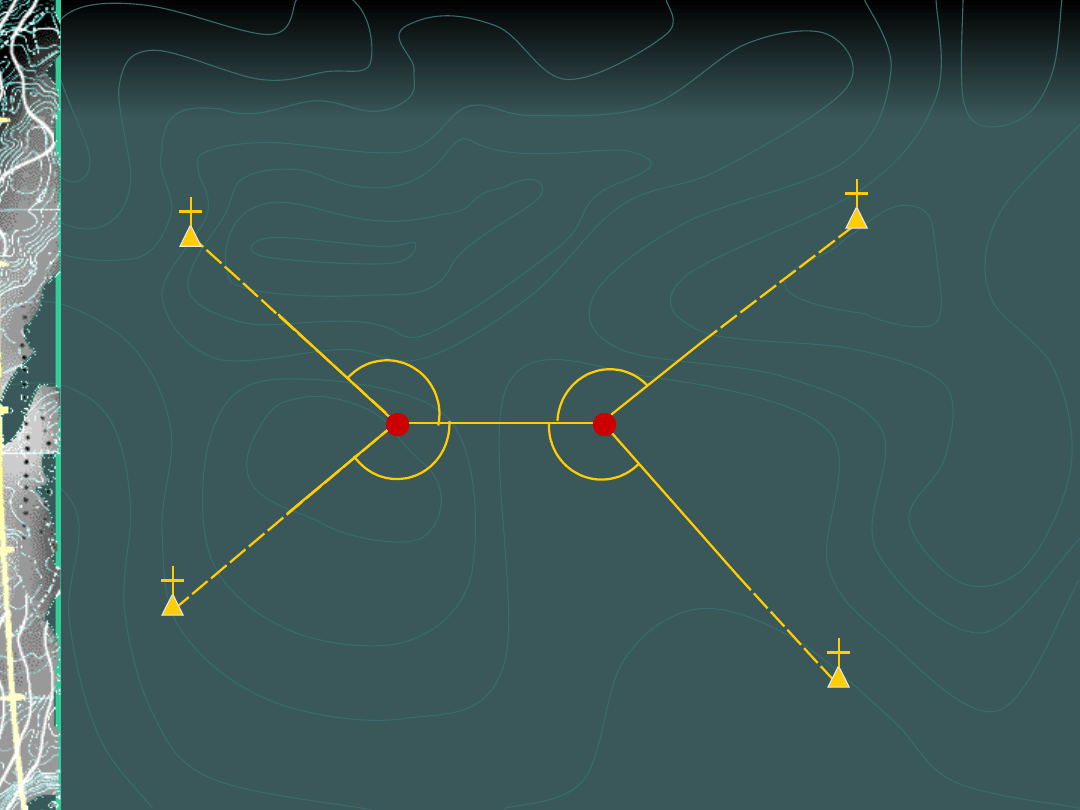
Wcięcie wstecz na cztery punkty
(zadanie Mareka)
Pomiar na punktach
wyznaczanych
C
P
B
A
D
β
α
γ
δ
R
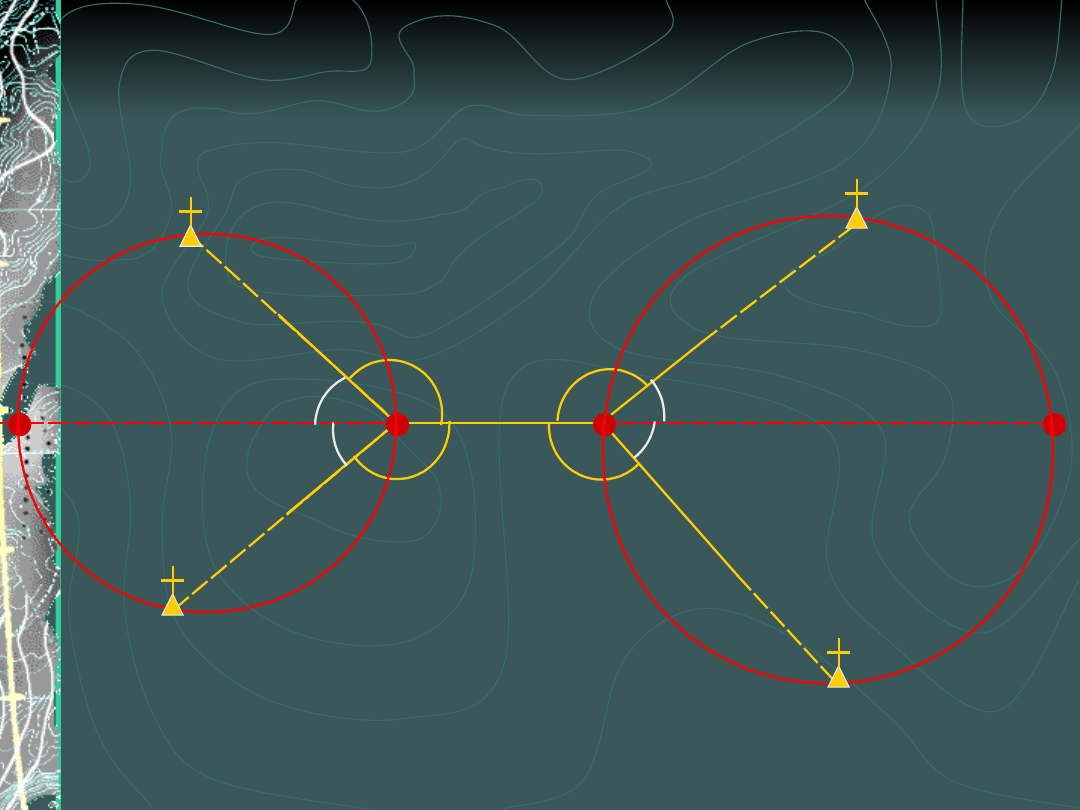
Wcięcie wstecz na cztery punkty
(zadanie Mareka)
Widoczny sposób rozwiązania
metoda Collinsa
C
P
B
A
D
Q
1
β
α
γ
δ
R
Q
2
200
g
-
α
β
200
g
-
β
200
g
-
γ
200
g
-
δ
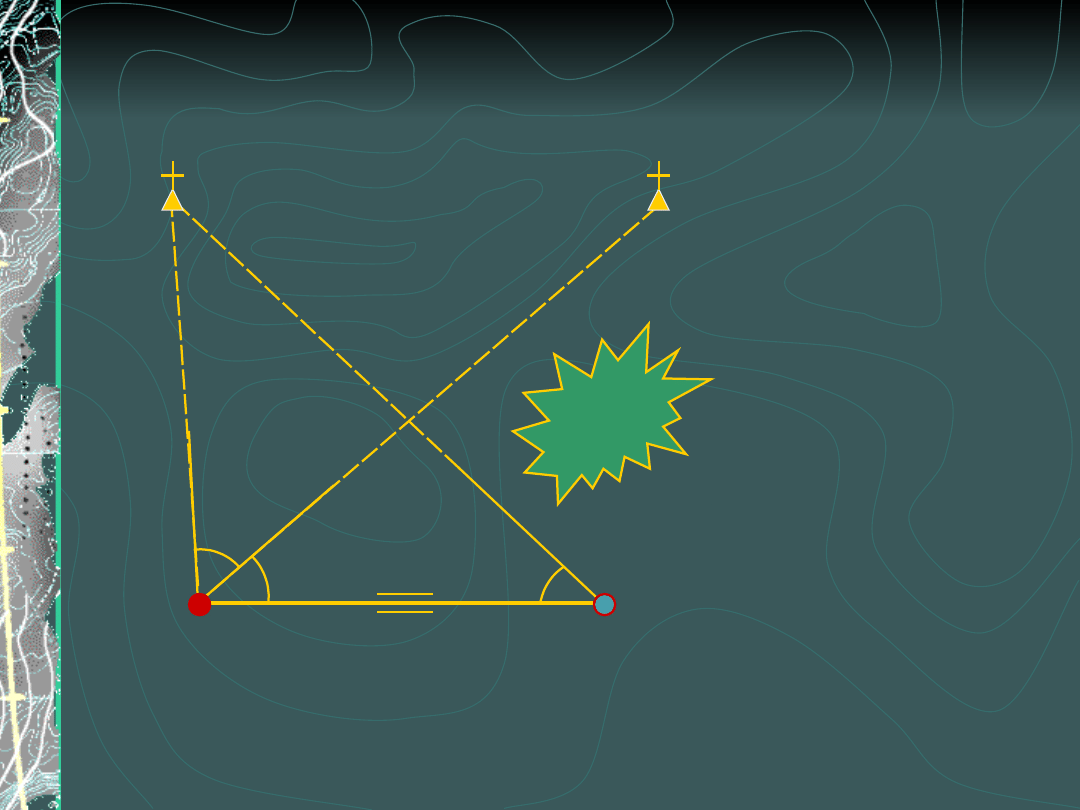
Wcięcie wstecz na dwa punkty w
celu
wyznaczenia pojedynczego
punktu
P – punkt wyznaczany
R – punkt pomocniczy
P
B
A
β
α
γ
R
Mierzymy:
α, β, γ, d
d
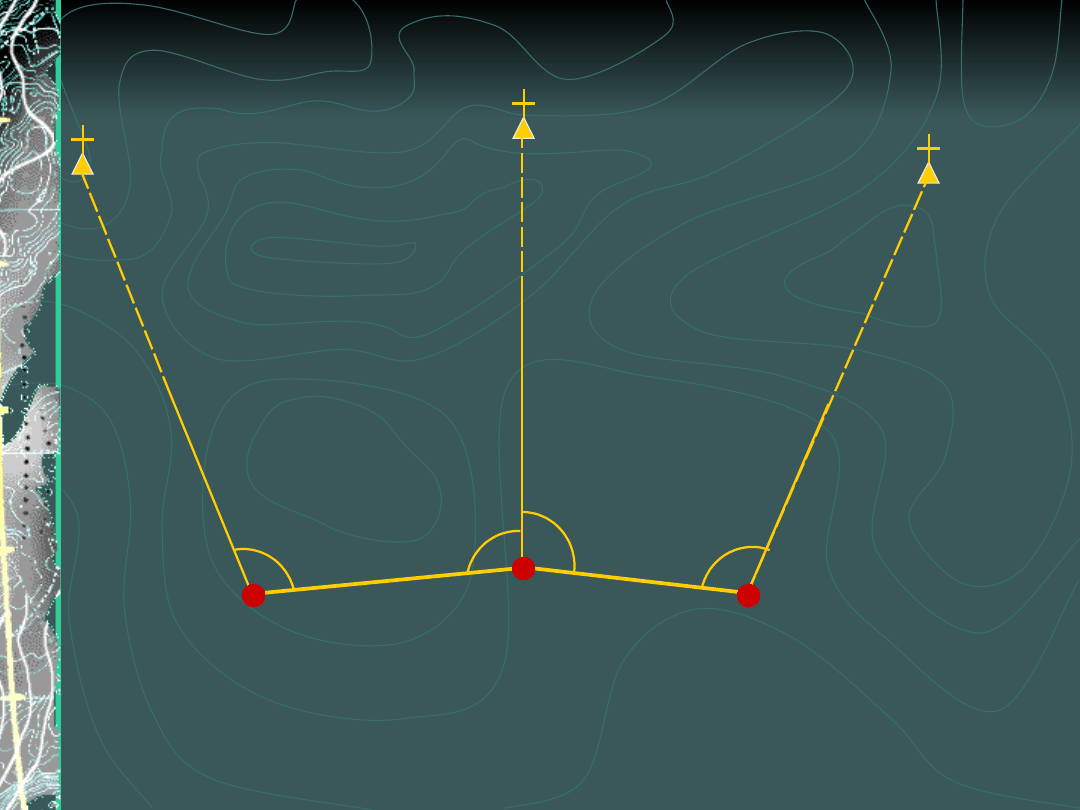
Wcięcie złożone z pomiarem długości
(przykład1)
Pomiar na punktach
wyznaczanych
C
P
B
β
A
R
Q
γ
δ
Mierzymy:
α, β, γ, δ , a,
b
α
a
b
n=n
d
+n
kt
=2+
4=6
u=2p=2x3=6
n=u
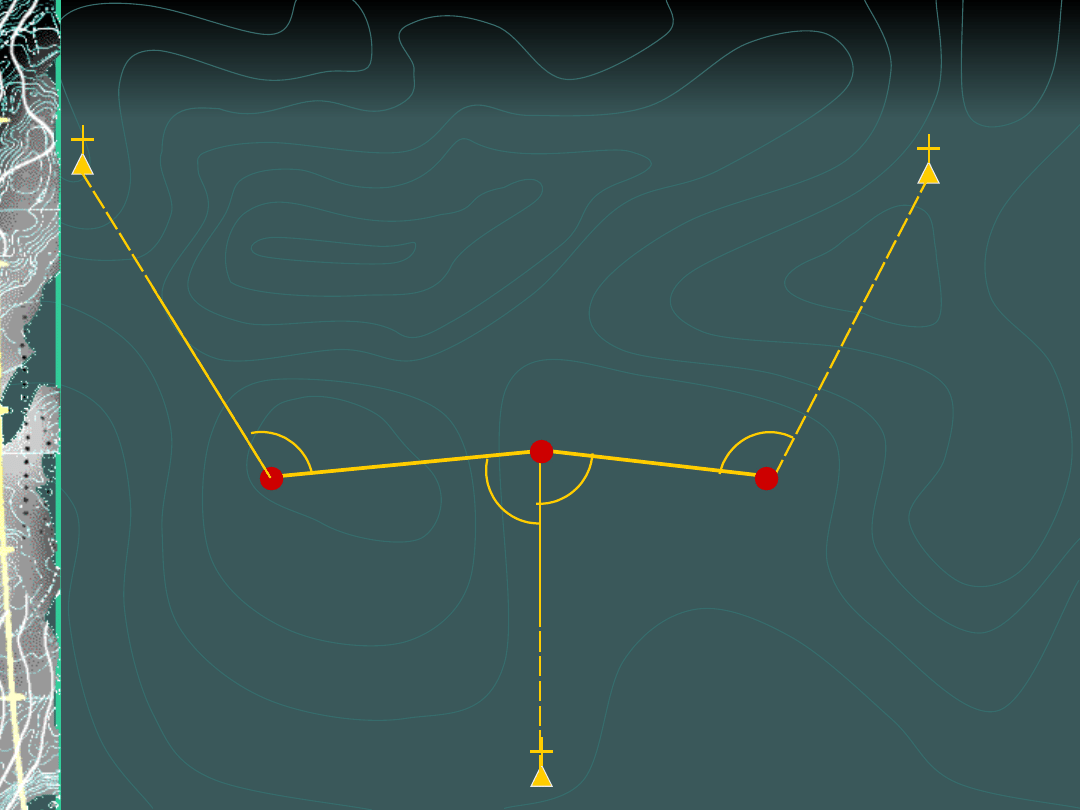
Wcięcie złożone z pomiarem długości
(przykład2)
Pomiar na punktach
wyznaczanych
C
B
A
Mierzymy:
α, β, γ, δ , a,
b
P
β
R
Q
γ
δ
α
a
b
n=n
d
+n
kt
=2+
4=6
u=2p=2x3=6
n=u
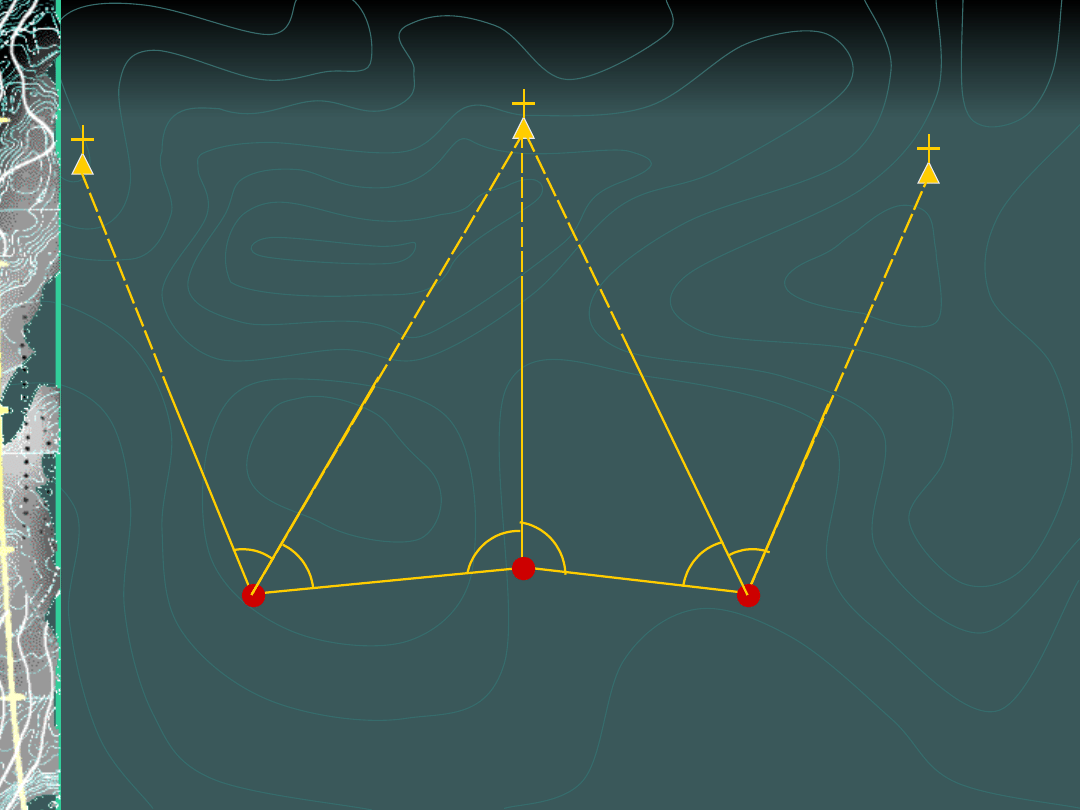
Wcięcie złożone kątowe (przykład)
Pomiar na punktach
wyznaczanych
C
P
B
β
A
R
Q
γ
δ
Mierzymy:
α, β, γ, δ , ε,
η
α
n=n
kt
=6
u=2p=2x3=6
n=u
ε
η
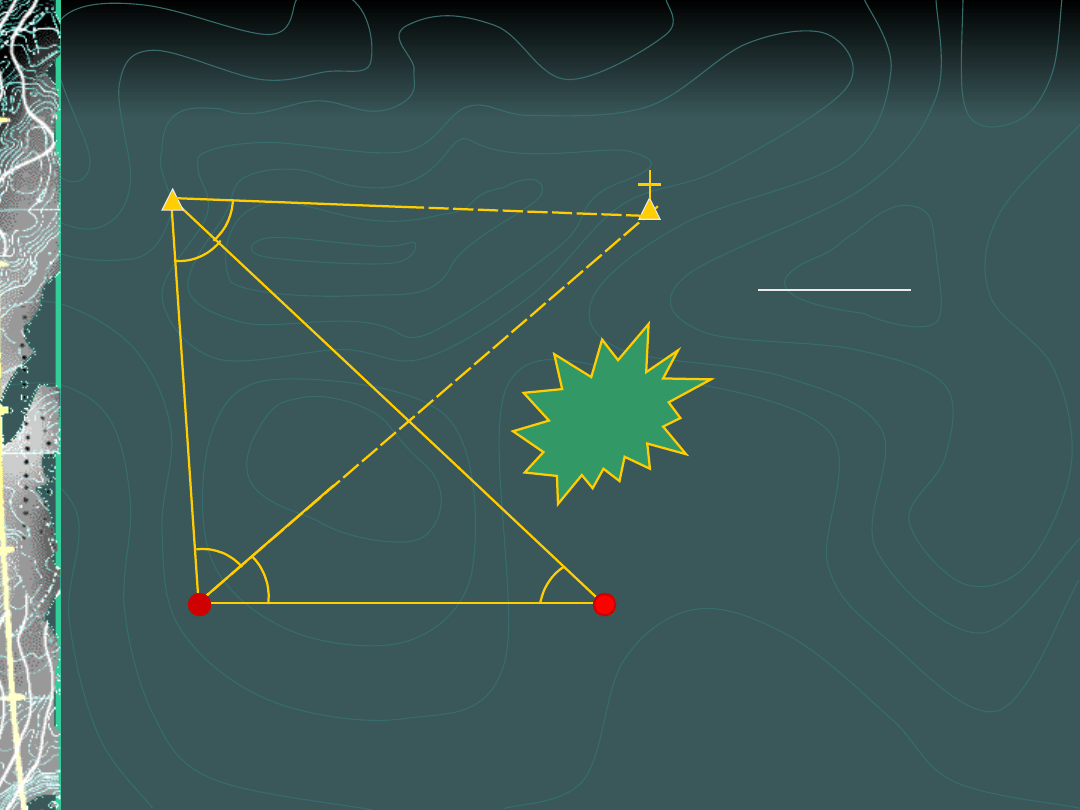
Wcięcie obustronne
(przykład)
P, R – punkty wyznaczane
P
B
A
β
α
γ
R
Mierzymy:
α, β, γ, δ, ε
n = 5
u = 2 x 2 = 4
n>u –
obserwacja
nadliczbowa
daje możliwość
wyrównania
δ
ε
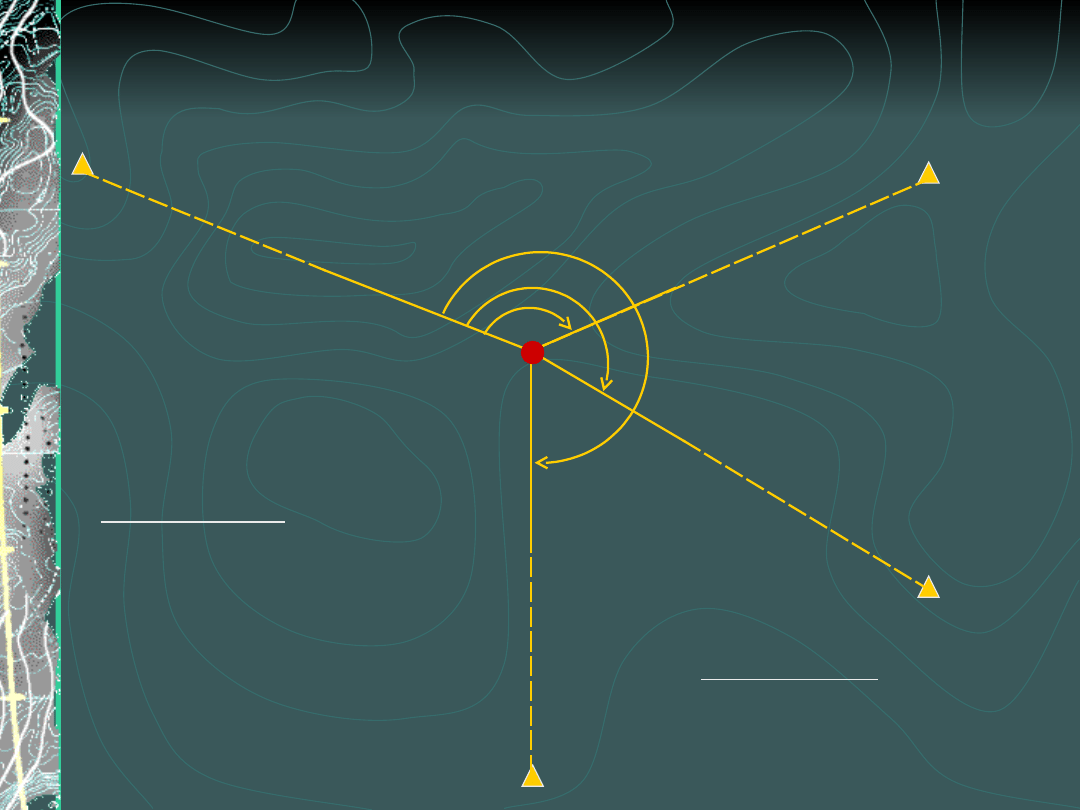
Swobodne stanowisko
(pełne)
Obliczenie:
- metoda
transformacji
- wyrównanie ścisłe
C
B
A
Mierzymy:
kierunki i
długości
P
k
2
, d
2
k
3
, d
3
γ
k
1
=0,
d
1
k
n
, d
n
n=n
d
+n
kt
=4+
3=7
u=2p=2x1=2
n>u
N
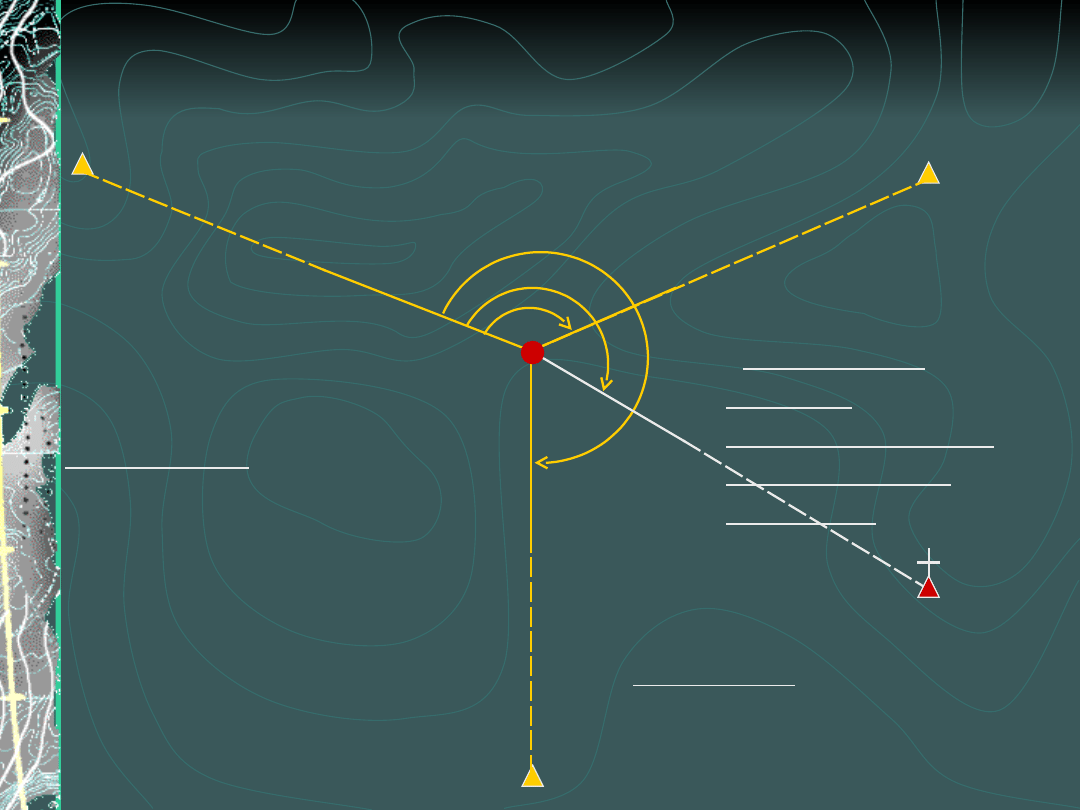
Swobodne stanowisko
(niepełne)
Obliczenie:
wyrównanie ścisłe (zadanie
zaprogramowane w TC 407)
C
B
A
Mierzymy:
kierunki
i dostępne długości
P
k
2
, d
2
k
3
γ
k
1
=0,
d
1
k
n
, d
n
n=n
d
+n
kt
=3+
3=6
u=2p=2x1=2
n>u
N
celowa do
punktu
niedostępnego
bez pomiaru
długości