1

Rozpoznawanie 

obrazów

2

Proces przetwarzania w systemie 

wizyjnym może być podzielony na trzy 

części:

•Uzyskanie cyfrowej reprezentacji obrazu 

(recepcja, akwizycja);

•Przetworzenie obrazu cyfrowego z 

wykorzystaniem technik komputerowych;

•Analiza i przetworzenie rezultatów w celu 

sterowania robotami, kontroli automatycznych 
procesów, kontroli jakości, itp. 

3

Główne funkcje systemu wizyjnego to:

 

•Kontrola (określenie pozycji i ewentualne 

wygenerowanie komend do robota w celu 
wykonania pewnych czynności. Np. wybranie 
obszaru do malowania przez robota, kontrola 
elementów, itp. );

•Badanie (określenie parametrów elementów, np. 

kształtu, jakości powierzchni, ilości otworów );

•Wprowadzanie danych (informacje o jakości 

produktów, materiałów mogą być umieszczone w 
bazie danych. W tym czasie te dane mogą być 
sprawdzone w procesie inspekcji.).

4

Zestawienie obrazujące możliwości 

człowieka i cyfrowego systemu 

wizyjnego:

Cecha

Człowiek

Komputer 

Zdolności

adaptacyjne 

Duże zdolności adaptacyjne, 

związane zarówno z celem jak 

i typem wejścia.

System sztywny w sensie 

postawionego celu 

rozpoznania oraz w sensie 

typu wejścia (wymaga obrazu 

dyskretnego - piksele). 

Sposób

rozpoznawa

nia 

Zdolności dokonywania 

względnie dokładnych 

oszacowań badanych 

obiektów, np. wykrywanie 

zepsutych owoców na 

podstawie koloru, tekstury 

(faktury), kształtu, zapachu. 

Zdolność dokonywania 

pomiarów przestrzennych na 

zdeterminowanym obrazie 

wejściowym, np.: długość i 

powierzchnia – zliczanie 

pikeseli.

Kolor 

Subiektywna interpretacja.

Pomiar parametrów R,G, B. 

Czułość 

Ograniczona zdolność 

identyfikacji poziomów 

szarości (~7 - 10). 

Zależna od rodzaju układu 

pozyskiwania obrazu. 

5

Cecha

Człowiek

Komputer 

Czas reakcji 

~0,1 s 

Zależnie od realizacji 

sprzętowej i oprogramowania 

systemu komputerowego 

~1/1000s lub mniejszy. 

Działanie w 

przestrzeni 2D 

i 3D 

Łatwa lokalizacja i 

rozpoznanie obiektów. 

Łatwiejsza lokalizacja i 

rozpoznanie obiektów w 

przestrzeni 2D niże 3D. 

Percepcja 

Percepcja jasności w 

skali logarytmicznej. 

Wpływ otaczającego 

obszaru (tła) na sposób 

percepcji 

Możliwość percepcji zarówno 

w skali liniowej jak i 

logarytmicznej. 

Zakres fal 

380 - 780 nm 

~10nm – promieniowanie X

do ~10

3

 m (podczerwień). 

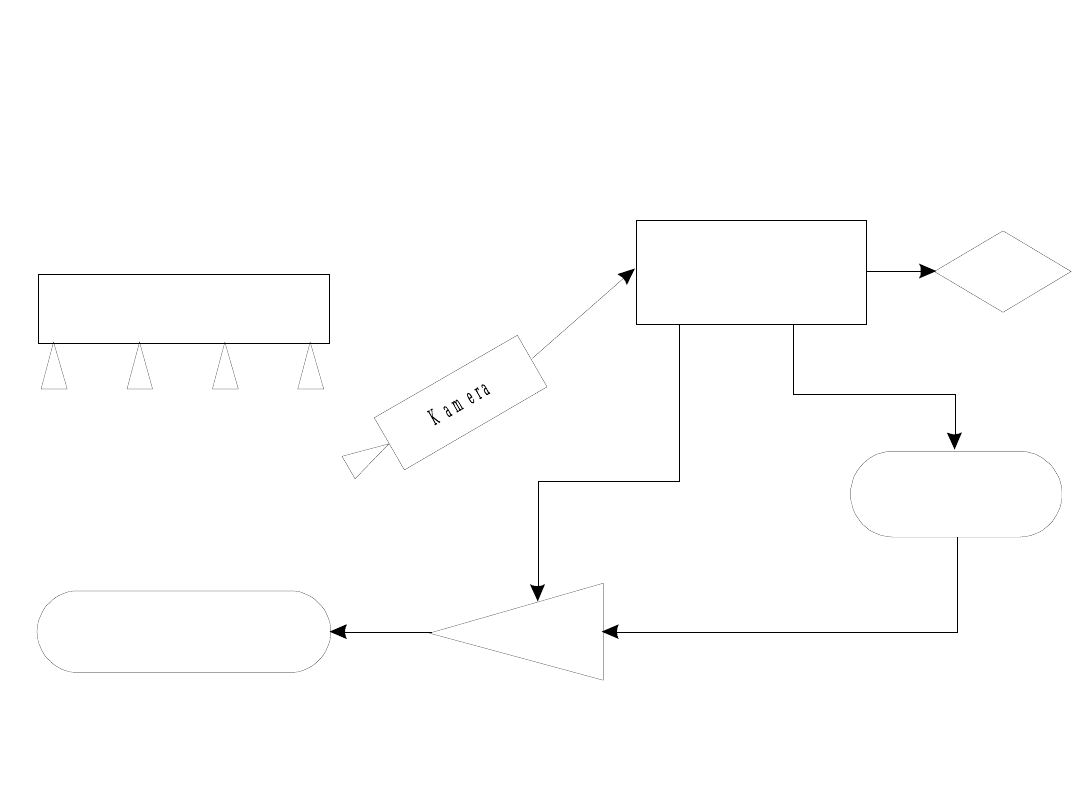
6

Przykładowy schemat blokowy 

cyfrowego systemu wizyjnego:

P r o c e s

p r o d u k c y j n y

O ś w i e tl e n i e

P r o c e s

k o n t r o l n y

C y f ro w y   s y s t e m

w i z y j n y

Z a rz ą d z a n i e

A l a r m

7

W literaturze stosunkowo często spotyka się 
propozycje różnych parametrów, które mogą być 
wykorzystane do opisu kształtu obiektów 
widocznych na obrazie. 

Wybierając współczynniki decydujemy się albo na 
dokładniejsze odwzorowanie kształtu obiektu, 
albo na szybsze działanie algorytmu. 

Kryteria rozpoznawania i klasyfikacji 

obiektów cyfrowych 

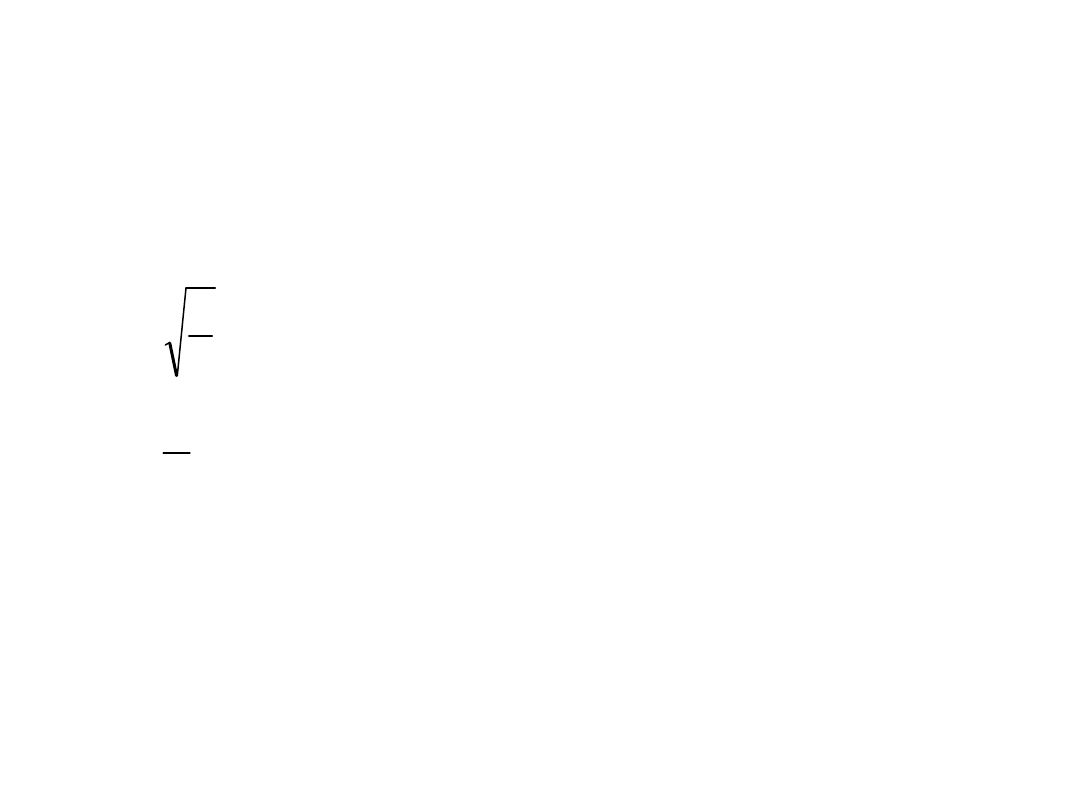
8





S

2

1

W





L

2

W

Współczynniki kształtu

Współczynniki cyrkularności: 

W1 (wyznacza średnicę koła, którego 
pole jest równe polu danego obiektu)

W2 (Wyznacza średnicę koła o 
obwodzie równym obwodowi 
analizowanego obiektu) 

gdzie:

L – obwód rzutu obiektu
S – pole rzutu obiektu

Powyższe współczynniki powinny być 
normalizowane.

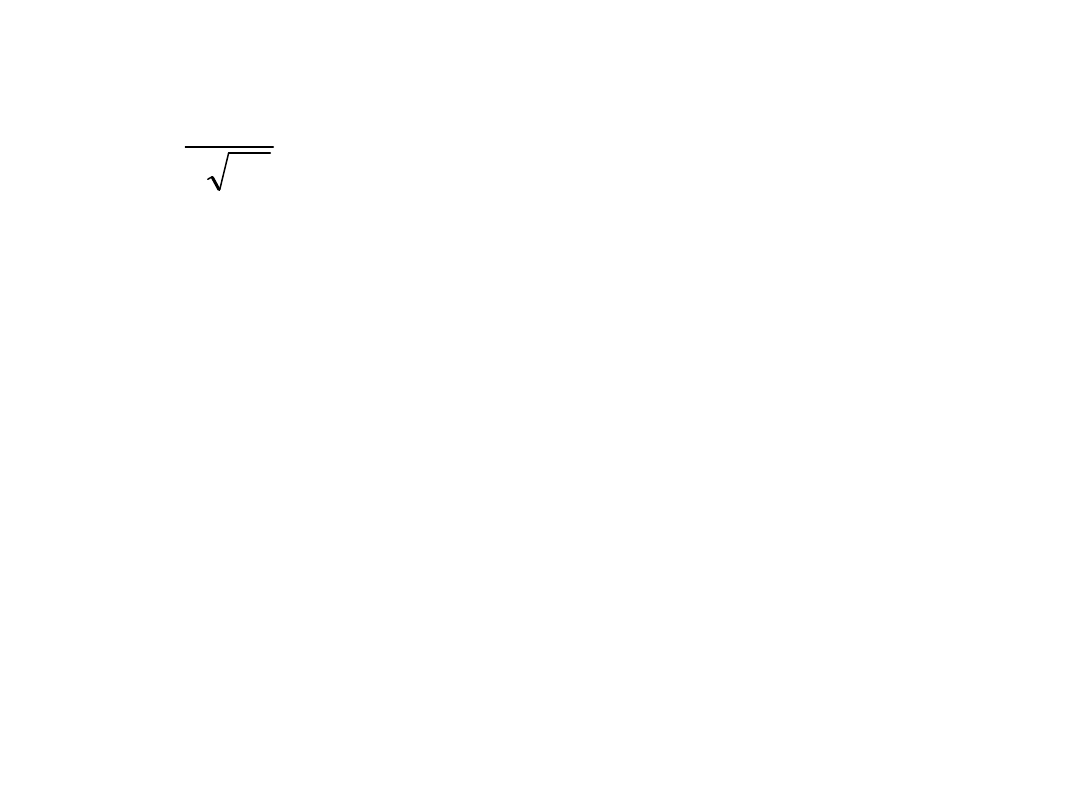
9

współczynnik Malinowskiej 

Można go jeszcze bardziej 
uprościć otrzymując w 
rezultacie współczynnik 
nazwany Mz (W9). 

1

S

2

L

3

W







Współczynniki W1, W2, W3 mają prostą postać 
i są szybkie do obliczenia. 

10

współczynnik Blaira-
Blissa (większa 
wrażliwość na zmiany 
kształtu)

współczynnik 
Danielssona







i

2

i

r

2

S

4

W

gdzie:

i – numer piksela obiektu
r

i

 – odległość piksela obiektu od środka 

ciężkości obiektu
l

i

 – minimalna odległość piksela od konturu 

obiektu

2

i

i

3

l

S

5

W

















11

współczynnik Harlicka

gdzie:

i – numer piksela obiektu
d

i

 – odległość pikseli konturu obiektu od jego 

środka ciężkości
n – liczba punktów konturu





















i

2

i

2

i

i

1

d

n

d

6

W

Współczynniki W4, W5, W6 wolniejsze w 
obliczaniu niż W1, W2, W3. 

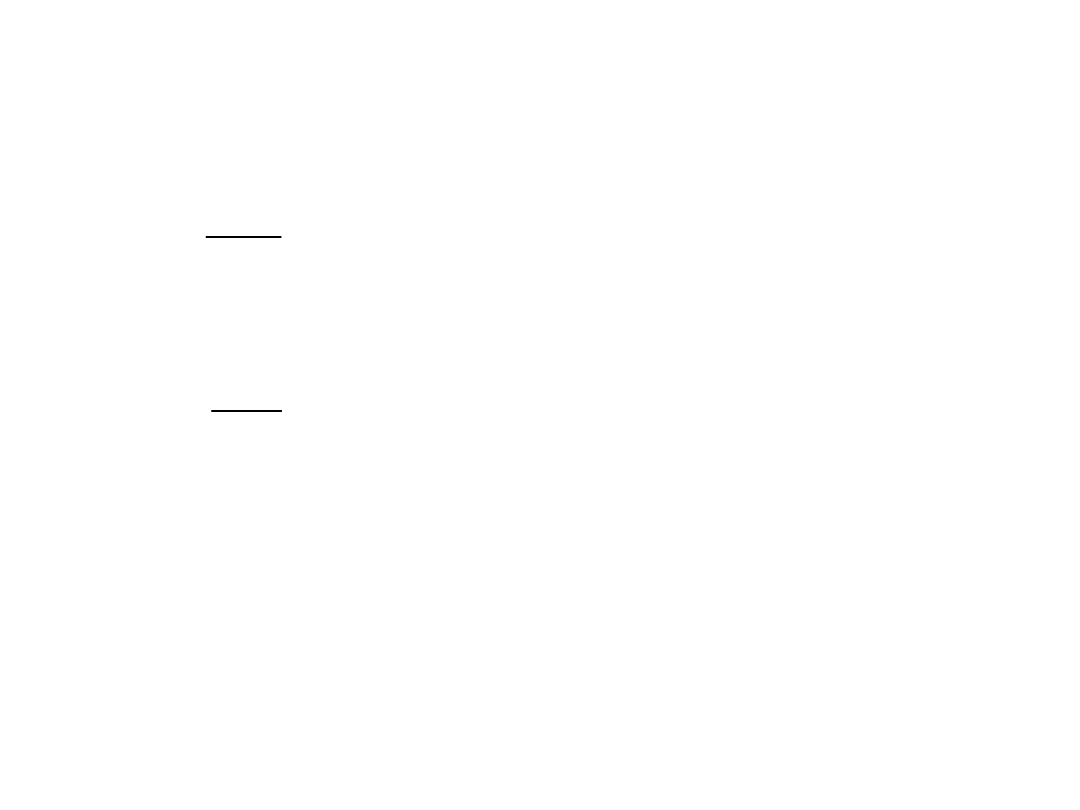
12

Czasami są przydatne cechy pośrednie, które 
określają np. współczynniki:

W7 (nazywany Lp1), badający 
zmienność minimalnej i 
maksymalnej odległości środka 
ciężkości od konturu obiektu 

W8 (nazywany Lp2) podający 
stosunek maksymalnego 
gabarytu do obwodu obiektu.

max

min

R

r

7

W 

L

L

8

W

max



gdzie:

r

min

 – minimalna odległość konturu od środka 

ciężkości
R

max

 – maksymalna  odległość konturu od środka 

ciężkości
L

max

 – maksymalny gabaryt obiektu

L – obwód rzutu obiektu

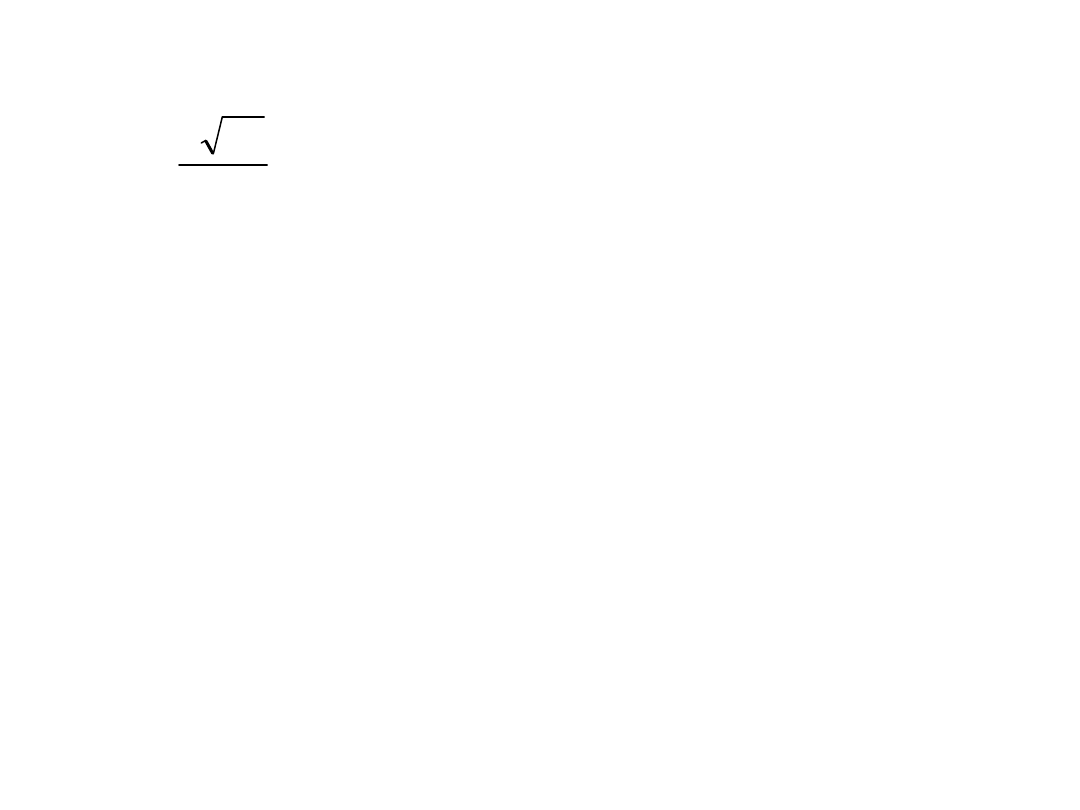
13

L

S

2

9

W





W9 nazwany współczynnikiem Mz 

(uproszczony współczynnik 
Malinowskiej)

gdzie:

L – obwód rzutu obiektu
S – pole rzutu obiektu

14

Podstawowe parametry:

 

 

















przypadku

pozostalym

w

0

obiekt

gdy

1

j

,

i

p

j

,

i

p

S

n

1

i

m

1

j

 

 

















przypadku

pozostalym

w

0

kontur

gdy

1

j

,

i

p

j

,

i

p

L

n

1

i

m

1

j

pole 
obiektu:

obwód 
obiektu:

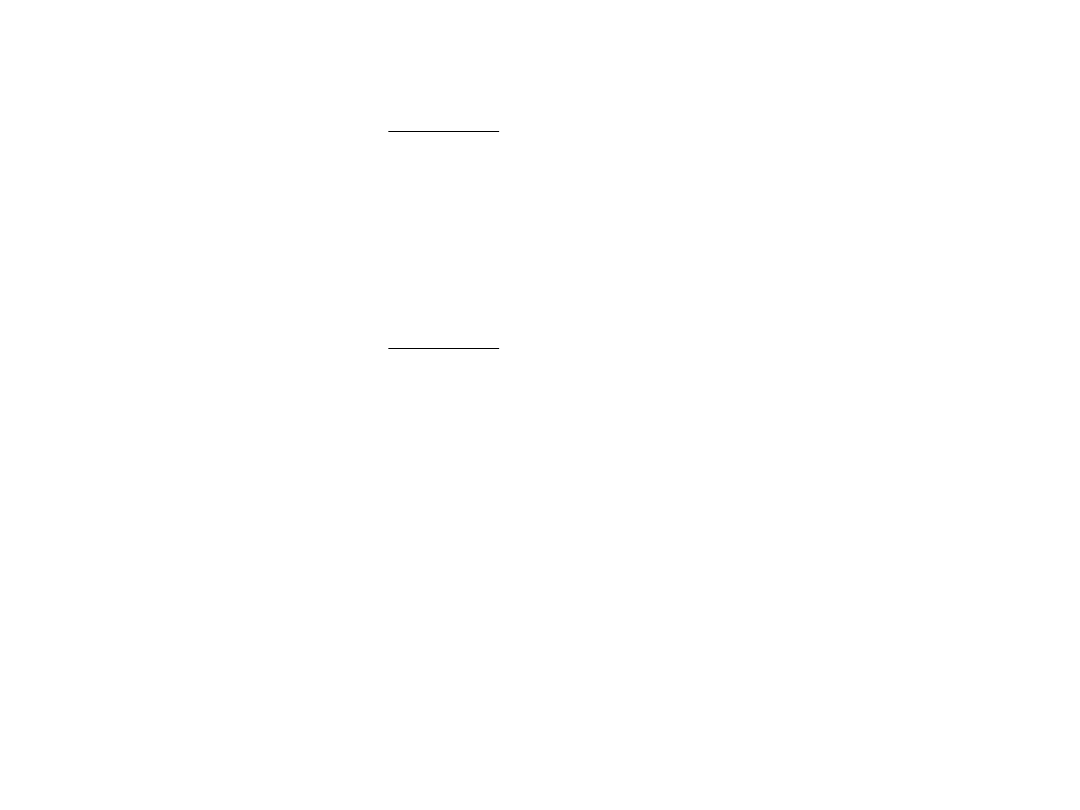
15

































przypadku

pozostalym

w

0

obiekt

gdy

j

k

S

k

y

~

przypadku

pozostalym

w

0

obiekt

gdy

i

k

S

k

x

~

n

1

i

m

1

j

n

1

i

m

1

j

gdzie:

S – pole obiektu
L – obwód obiektu
n x m – rozmiar obiektu
     – współrzędna x środka ciężkości
     – współrzędna y środka ciężkości

x

~

y

~

środek 
ciężkości:

16

Przykładowe figury: 

17

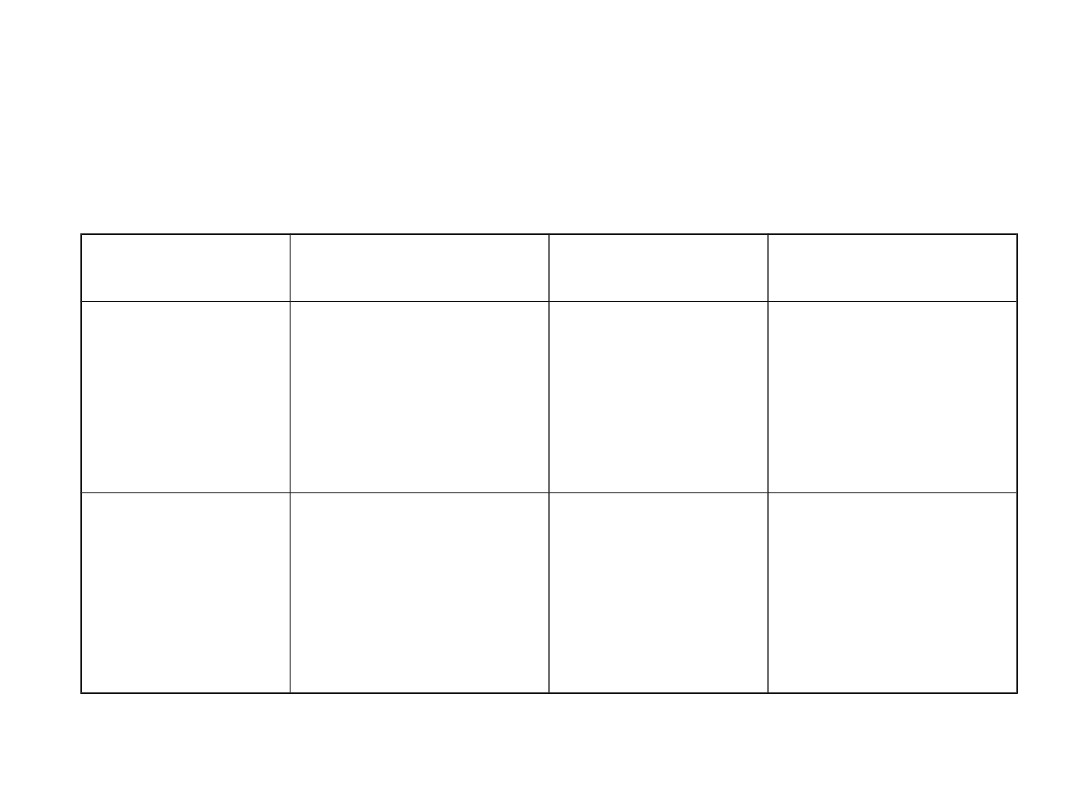
Formuła 

Crofton’a:



































135

45

90

0

N

N

2

a

N

N

a

4

L



gdzie:

N

0

  N

90

  N

45

  N

135

 – rzuty figury dla 

wybranych 

kierunków rzutowania,

a – odległość punktów siatki.

18

Przykładowe elementy strukturalne do wyznaczania 
długości rzutów figury: 

kąt

otoczenie 

kąt

otoczenie 

0

o

90

o

45

o

135

o





















X

X

X

1

0

X

X

X

X





















X

X

X

X

0

X

1

X

X





















X

X

X

X

0

X

X

1

X





















X

X

X

X

0

X

X

X

1

19

Momenty geometryczne:

 

















dxdy

y

,

x

f

y

x

m

q

p

pq

Dwuwymiarowy moment rzędu (p+q) dla funkcji 
f(x,y) : 









n

i

m

j

ij

q

p

pq

x

j

i

m

1

1

20



 

 























dxdy

y

,

x

f

y

~

y

x

~

x

M

q

p

pq

00

10

m

m

x

~

00

01

m

m

y

~

Moment centralny

   

f(x,y):

gdzi
e:

  















n

i

m

j

ij

q

p

pq

x

j

j

i

i

M

1

1

~

~

00

10

m

m

i

~



00

01

m

m

j

~



21

Momenty centralne można przedstawić za 
pomocą momentów zwykłych: 

00

00

m

M 

0

m

m

m

m

M

00

00

01

01

01



















0

m

m

m

m

M

00

00

10

10

10



















00

01

10

11

11

m

m

m

m

M





00

2

10

20

20

m

m

m

M





00

2

01

02

02

m

m

m

M





22

2

01

20

11

21

21

i

m

2

j

m

i

m

2

m

M

~

~

~









2

10

02

11

12

12

j

m

2

i

m

j

m

2

m

M

~

~

~









2

10

20

30

30

i

m

2

i

m

3

m

M

~

~





2

01

02

03

03

j

m

2

j

m

3

m

M

~

~





23

Z powyższych zależności możemy 

wyznaczyć niezmienniki momentowe: 

2
oo

02

20

m

M

M

1

M









4
oo

2

11

2

02

20

m

M

4

M

M

2

M









 



5
oo

2

03

21

2

12

30

m

M

M

3

M

3

M

3

M











 



5
oo

2

03

21

2

12

30

m

M

M

M

M

4

M









24



 

 













7
oo

03

21

12

30

11

2

03

21

2

12

30

02

20

m

M

M

M

M

M

4

M

M

M

M

M

M

6

M



















4
oo

2

11

02

20

m

M

M

M

7

M









 















 

 







10

00

2

03

21

2

12

30

03

21

03

21

2

03

21

2

12

30

12

30

12

30

m

M

M

M

M

3

M

M

M

M

3

M

M

3

M

M

M

M

M

3

M

5

M



























25













7
oo

12

21

03

30

11

2
21

12

03

02

2

12

03

21

20

m

M

M

M

M

M

M

M

M

M

M

M

M

M

9

M

























10

oo

12

21

03

2
21

12

30

2

21

12

03

30

m

M

M

M

M

M

M

4

M

M

M

M

10

M











5
oo

2
21

2

12

03

21

12

30

m

M

M

M

M

M

M

8

M









Wszystkie powyższe momenty teoretycznie powinny 
być inwariantne (niezmienne) ze względu na obrót, 
translację i zmianę skali obiektu.

26

W celu ujednolicenia obrazów o 

różnych rozmiarach wykorzystuje się 

znormalizowany moment centralny:





 

1

2

q

p

00

pq

1

2

q

p

00

pq

pq

m

M

M

M

N













Znormalizowane momenty centralne nie zapewniają 
niezmienniczości ze względu na obrót.

Dlatego wprowadzono niezmienniki momentowe, 
które maja te własność.

27

02

20

N

N

1

M









2

11

2

02

20

N

4

N

N

2

M









 



2

03

21

2

12

30

3

3

3

N

N

N

N

M









Z powyższych zależności możemy 

wyznaczyć niezmienniki momentowe:



 



2

03

21

2

12

30

4

N

N

N

N

M









28





 















 

 







2

03

21

2

12

30

03

21

03

21

2

03

21

2

12

30

12

30

12

30

N

N

N

N

3

N

N

N

N

3

N

N

3

N

N

N

N

N

3

N

5

M





























 

 













03

21

12

30

11

2

03

21

2

12

30

02

20

N

N

N

N

N

4

N

N

N

N

N

N

6

M



















2

11

02

20

N

N

N

7

M





29

2

21

2

12

03

21

12

30

N

N

N

N

N

N

8

M





















12

21

03

30

11

2

21

12

30

02

2

12

03

21

20

9

N

N

N

N

N

N

N

N

N

N

N

N

N

M



























12

21

03

2

21

12

30

2

21

12

03

30

N

N

N

N

N

N

4

N

N

N

N

10

M













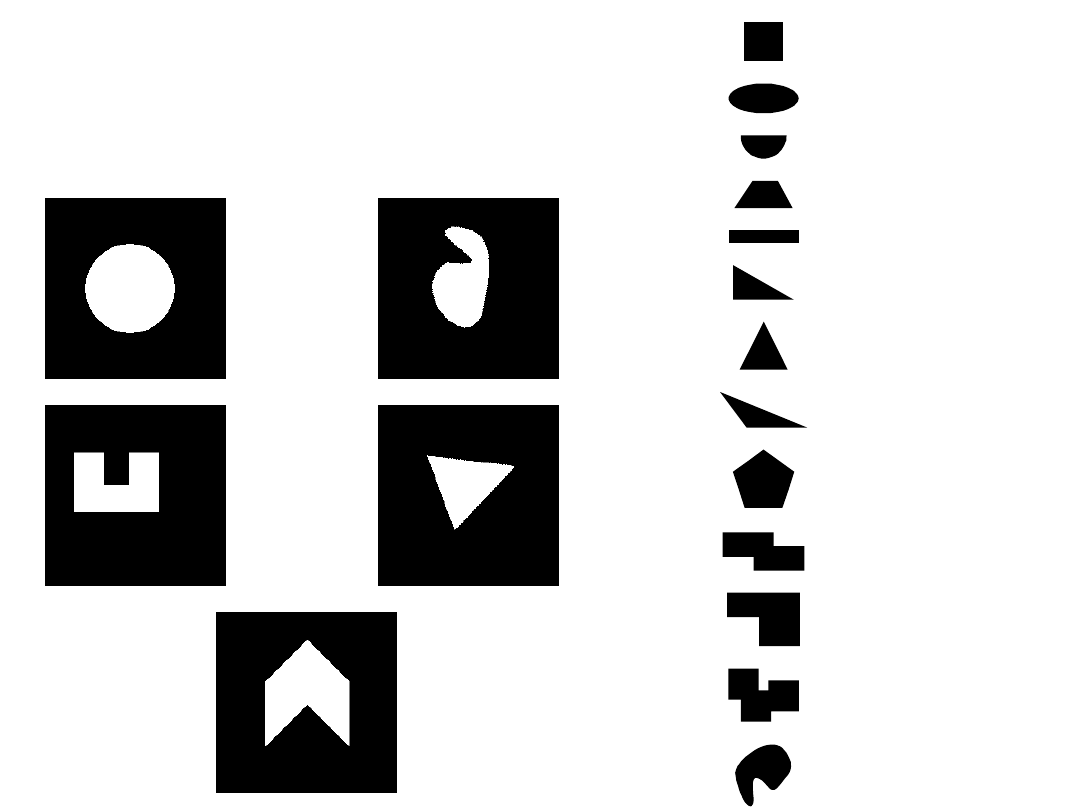
30

Przykłady klas 

rozpoznawanych 

obiektów:

k w a d r a t

e l i p s a

p ó ł k o l e

tr a p e z

p r o s t o k ą t

tr ó j k ą t   p r o s t o k ą t n y

tr ó j k ą t   r ó w n o r a m i e n n y

tr ó j k ą t   r o z w a r t o k ą tn y

p i ę c i o k ą t

k s z t a ł t   1

k s z t a ł t   2

k s z t a ł   3

k s z t a ł t   4

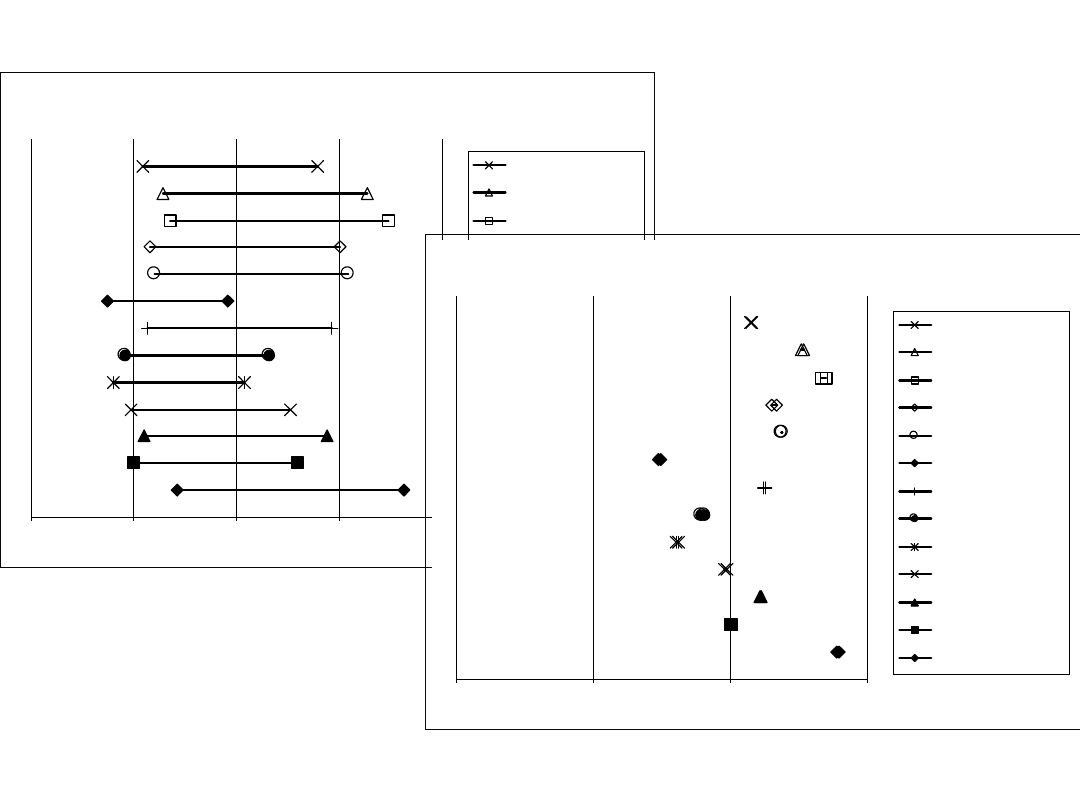
31

Współczynnik W1

Zakres zmienności współczynnika W1

0

50

100

150

200

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

Zakres zmienności współczynnika W1

0

50

100

150

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

Bez zmiany skali

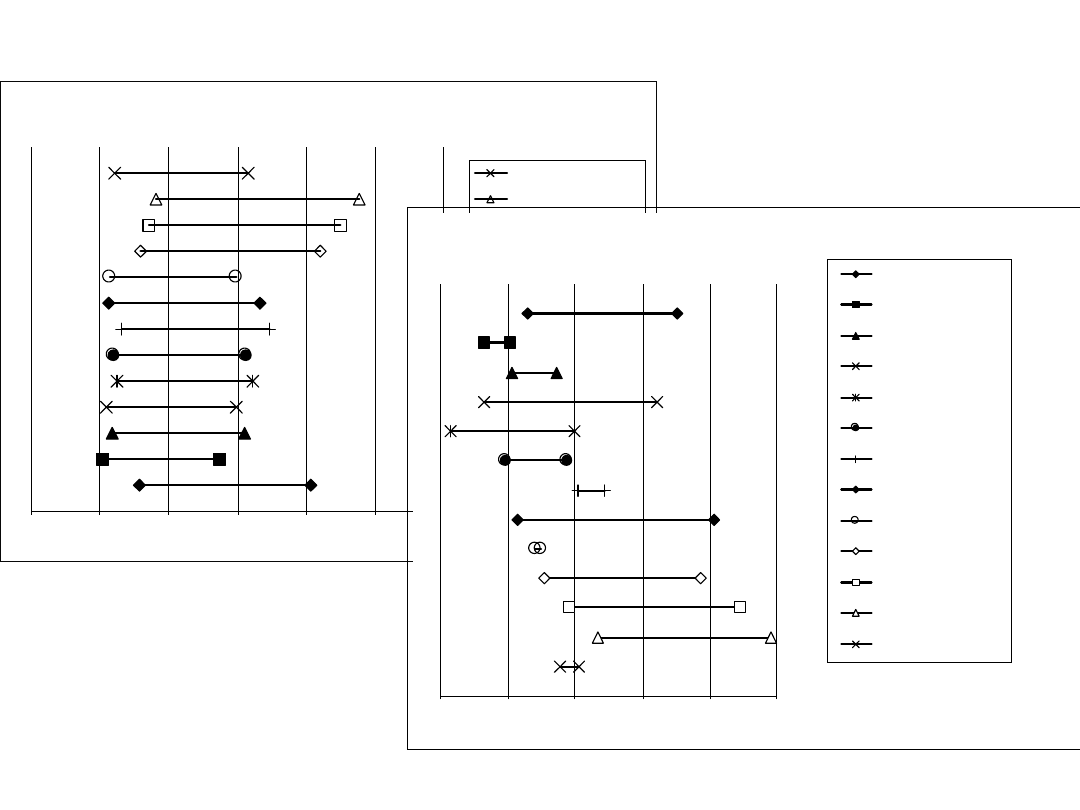
32

Współczynnik W2

Zakres zmienności współczynnika W2

0

50

100

150

200

250

300

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

Zakres zmienności współczynnika W2

85

105

125

145

165

185

Kwadrat

Elipsa

Półkole

Trapez

Prostokąt

Trójkąt prostokątny

Trójkąt równoramienny

Trójkąt rozwartokątny

Pięciokąt

Kształt 1

Kształt 2

Kształt 3

Kształt 4

Bez zmiany skali

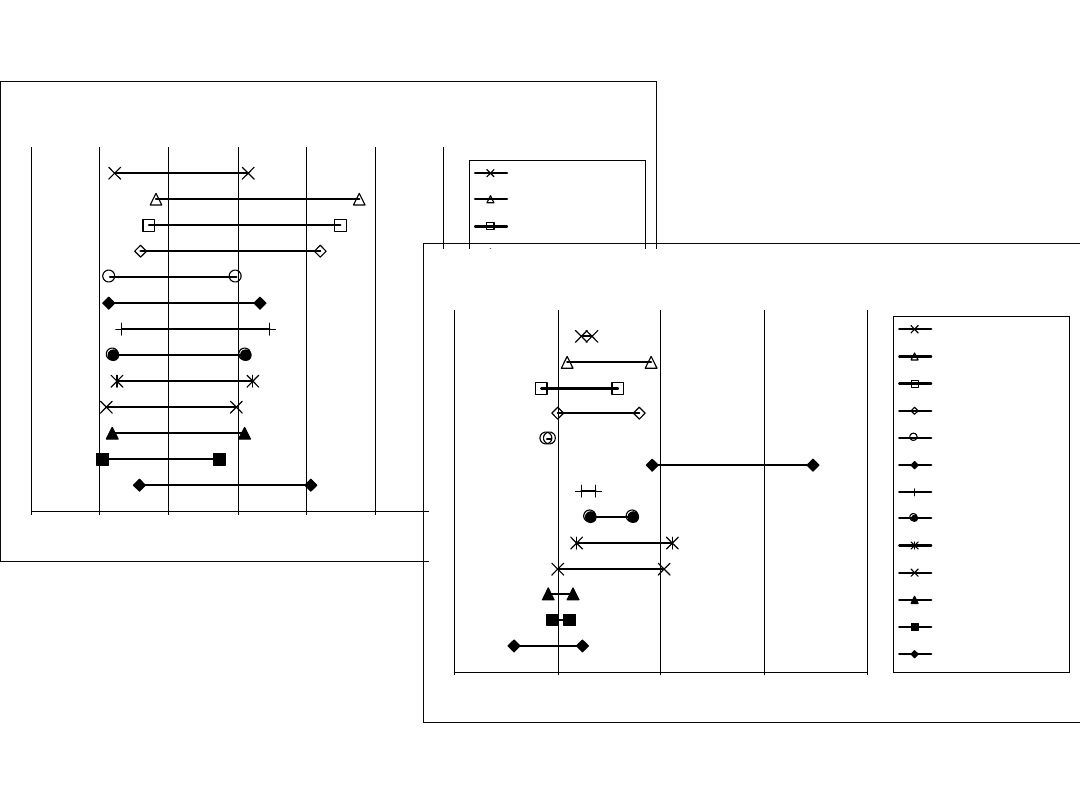
33

Współczynniki W2 i W3

Zakres zmienności współczynnika W2

0

50

100

150

200

250

300

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

Zakres zmienności współczynnika W3

-0,5

0

0,5

1

1,5

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

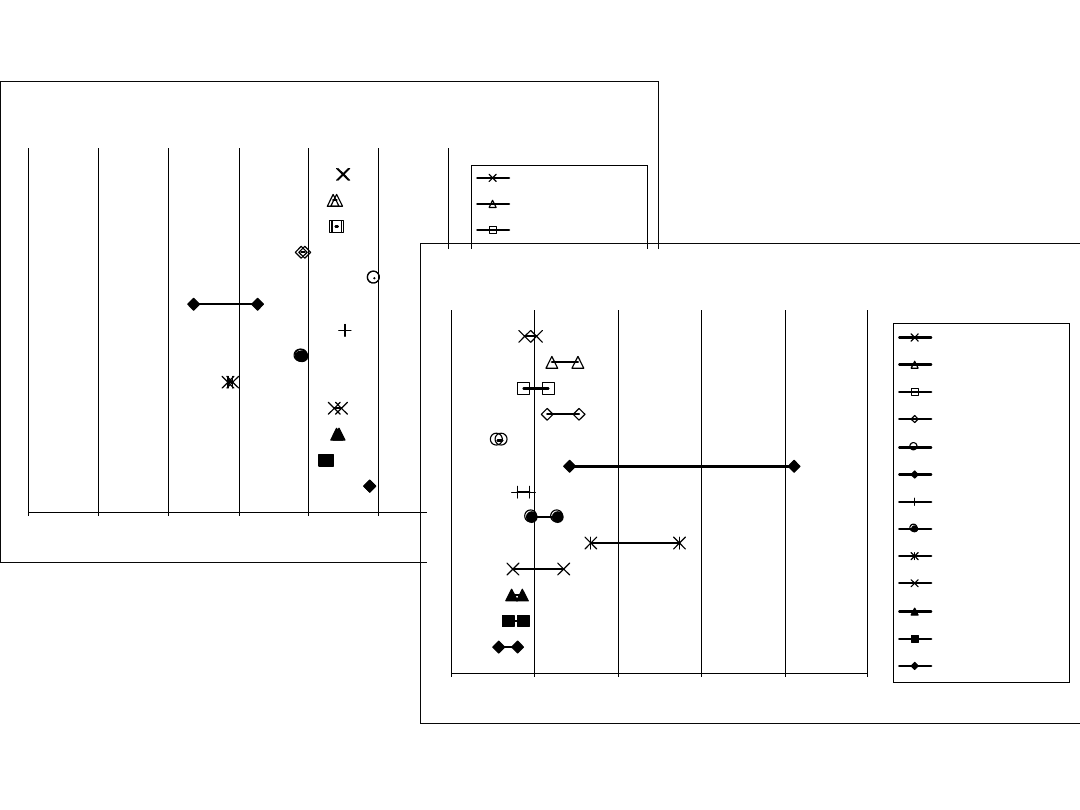
34

Współczynniki W4 i W5

Zakres zmienności współczynnika W4

0

0,2

0,4

0,6

0,8

1

1,2

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

Zakres zmienności współczynnika W5

0

50

100

150

200

250

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

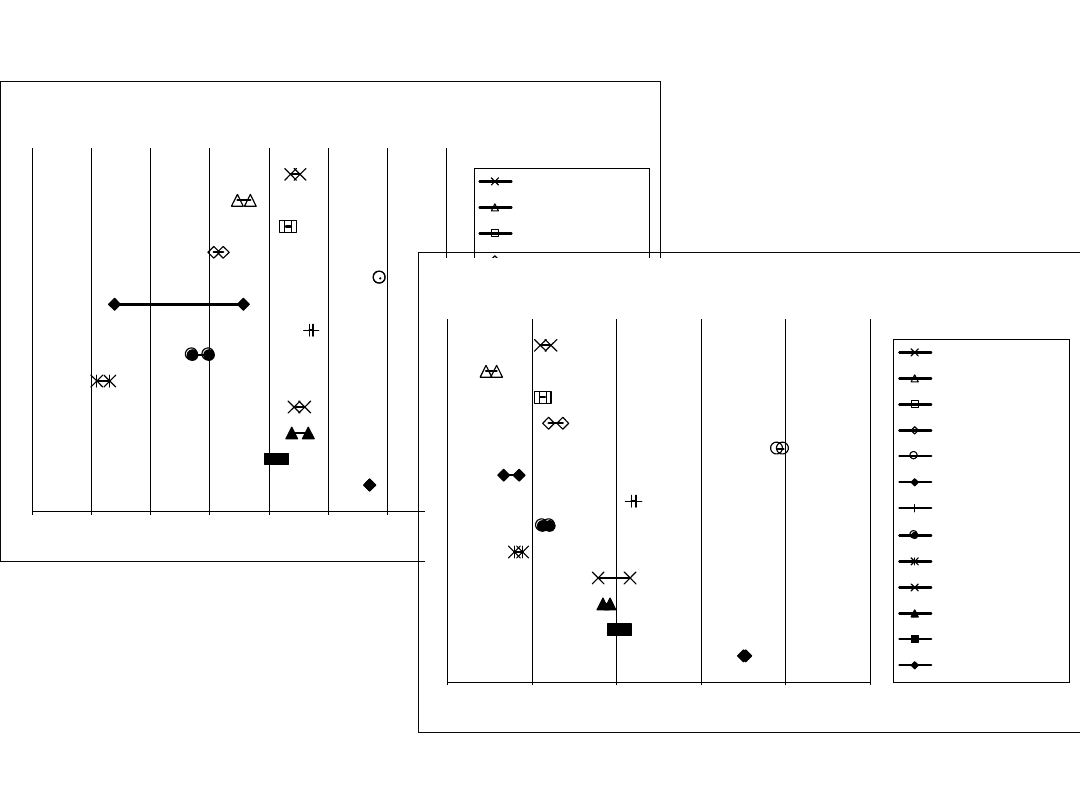
35

Współczynniki W6 i W7

Zakres zmienności współczynnika W6

0,88

0,9

0,92

0,94

0,96

0,98

1

1,02

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

Zakres zmienności współczynnika W7

0

0,2

0,4

0,6

0,8

1

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

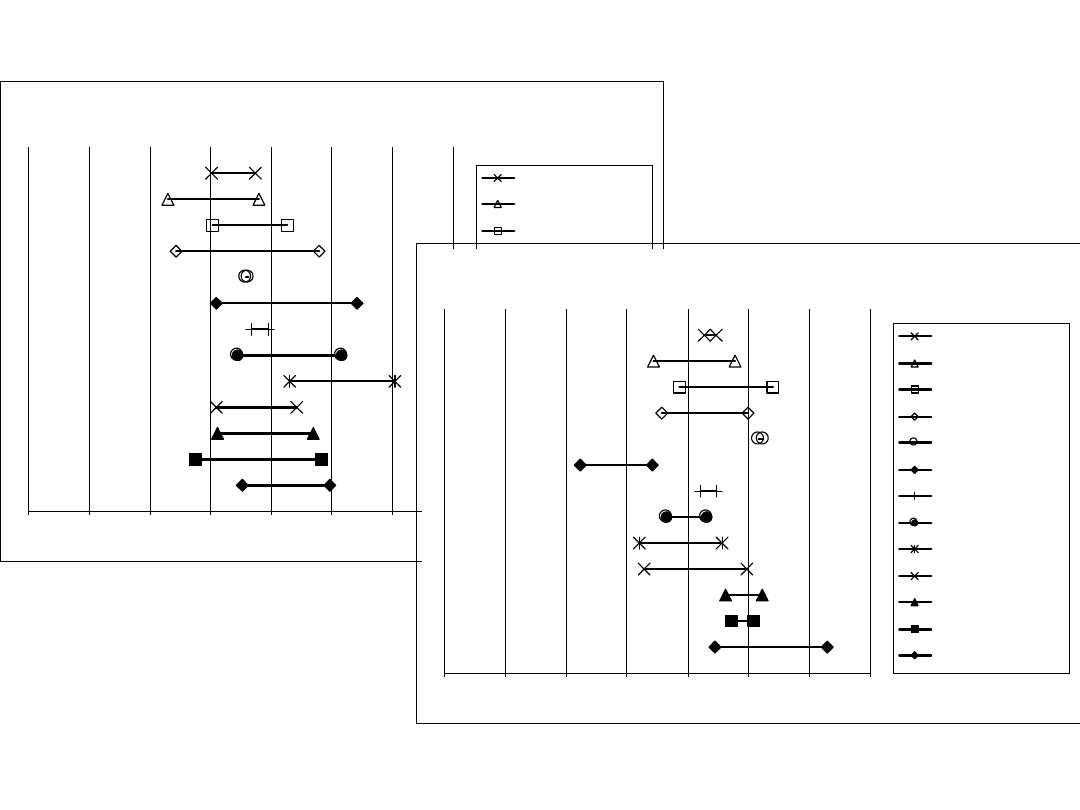
36

Współczynniki W8 i W9

Zakres zmienności współczynnika W8

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

Zakres zmienności współczynnika W9

0

0,2

0,4

0,6

0,8

1

1,2

1,4

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

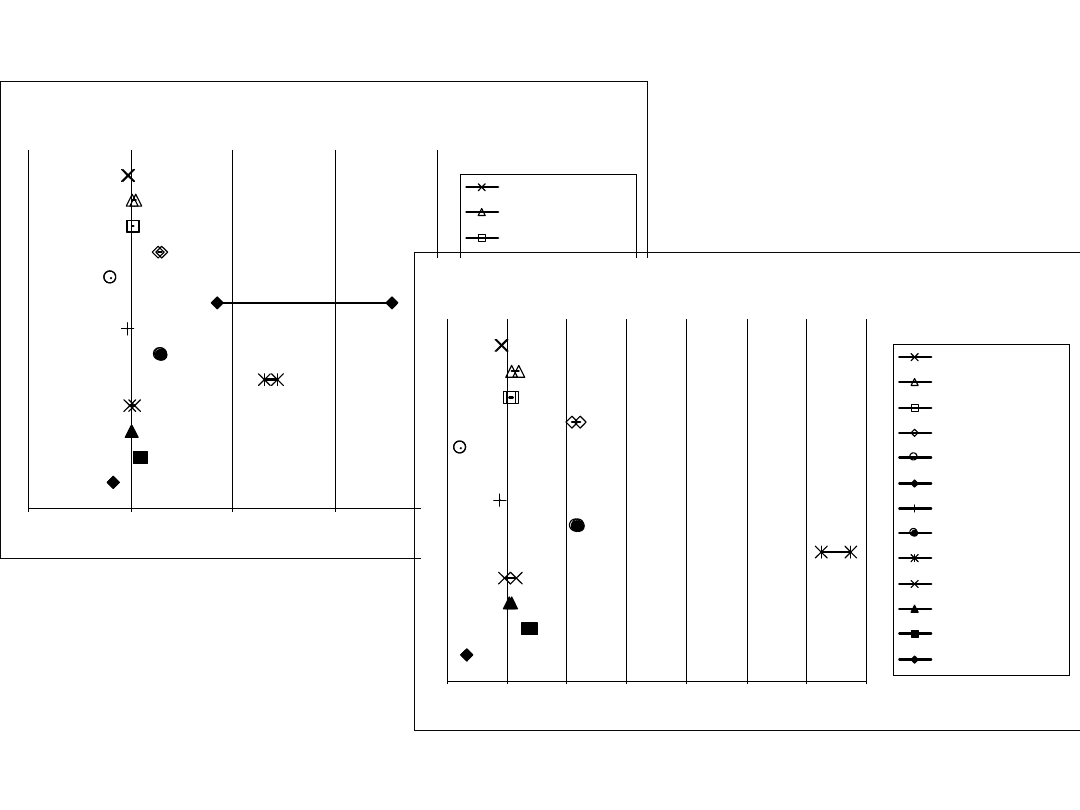
37

Moment M1

Zakres zmienności współczynnika M1

0

0,2

0,4

0,6

0,8

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

Zakres zmienności współczynnika M1

0,15

0,2

0,25

0,3

0,35

0,4

0,45

0,5

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

Po usunięciu 
trójkąta 
rozwartokątnego

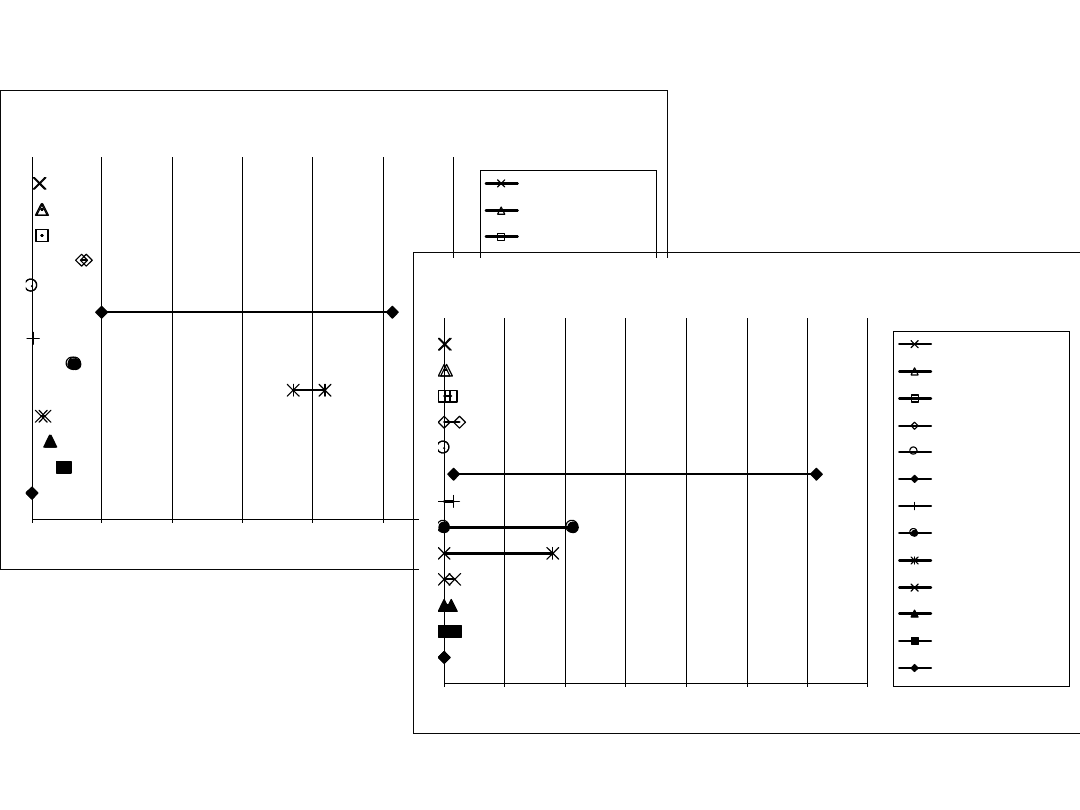
38

Momenty M2 i M3

Zakres zmienności współczynnika M2

0

0,05

0,1

0,15

0,2

0,25

0,3

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

Zakres zmienności współczynnika M3

0

50

100

150

200

250

300

350

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

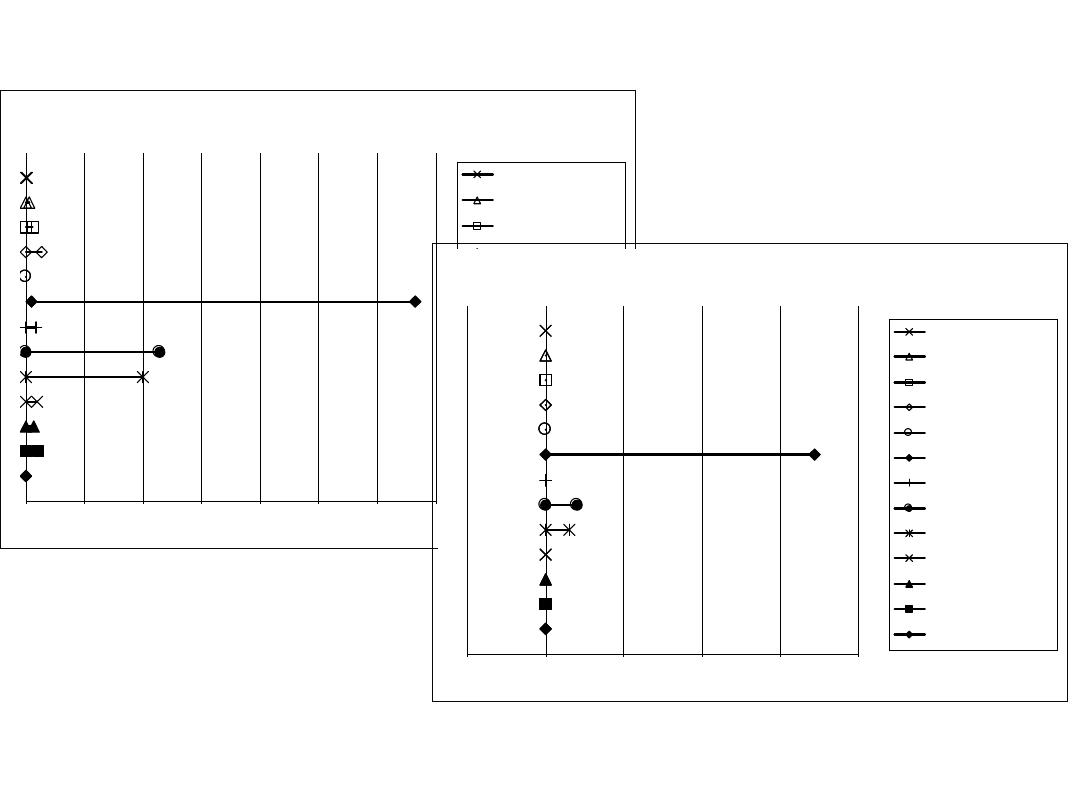
39

Momenty M4 i M5

Zakres zmienności współczynnika M4

0

5

10

15

20

25

30

35

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

Zakres zmienności współczynnika M5

-1000

0

1000

2000

3000

4000

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

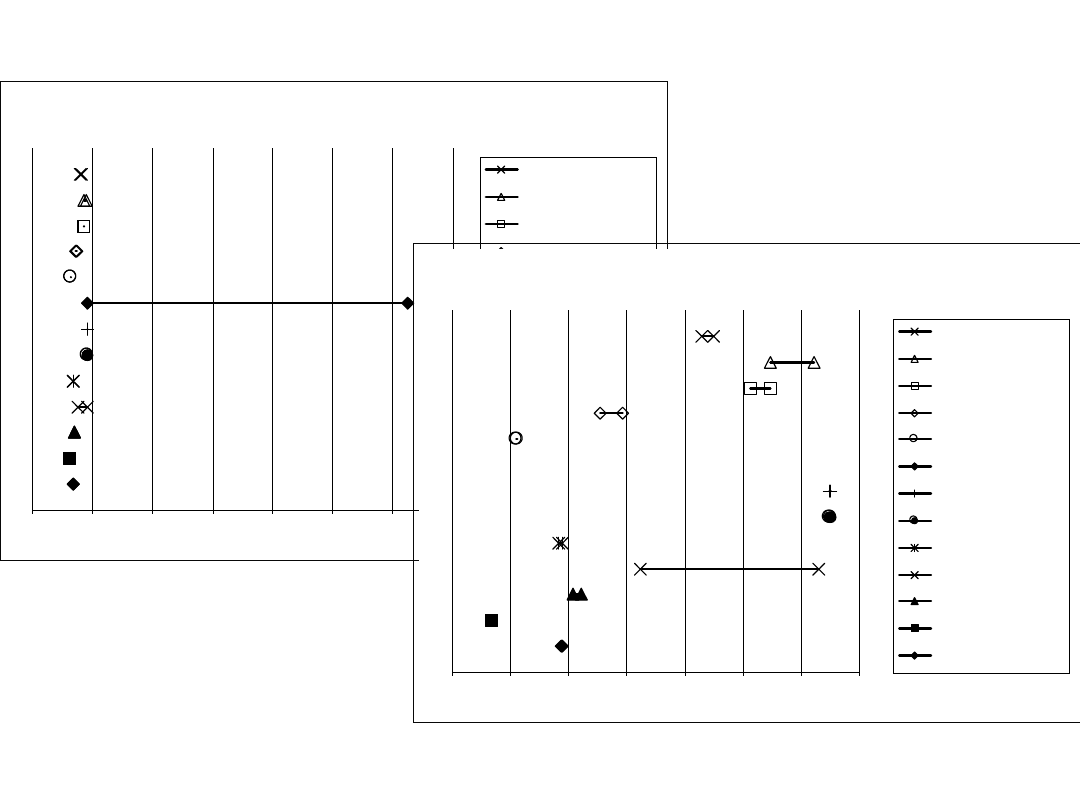
40

Moment M7

Zakres zmienności współczynnika M7

0

0,01

0,02

0,03

0,04

0,05

0,06

0,07

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

Zakres zmienności współczynnika M7

0,006

0,0065

0,007

0,0075

0,008

0,0085

0,009

0,0095

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

Po usunięciu 
trójkąta 
rozwartokątnego

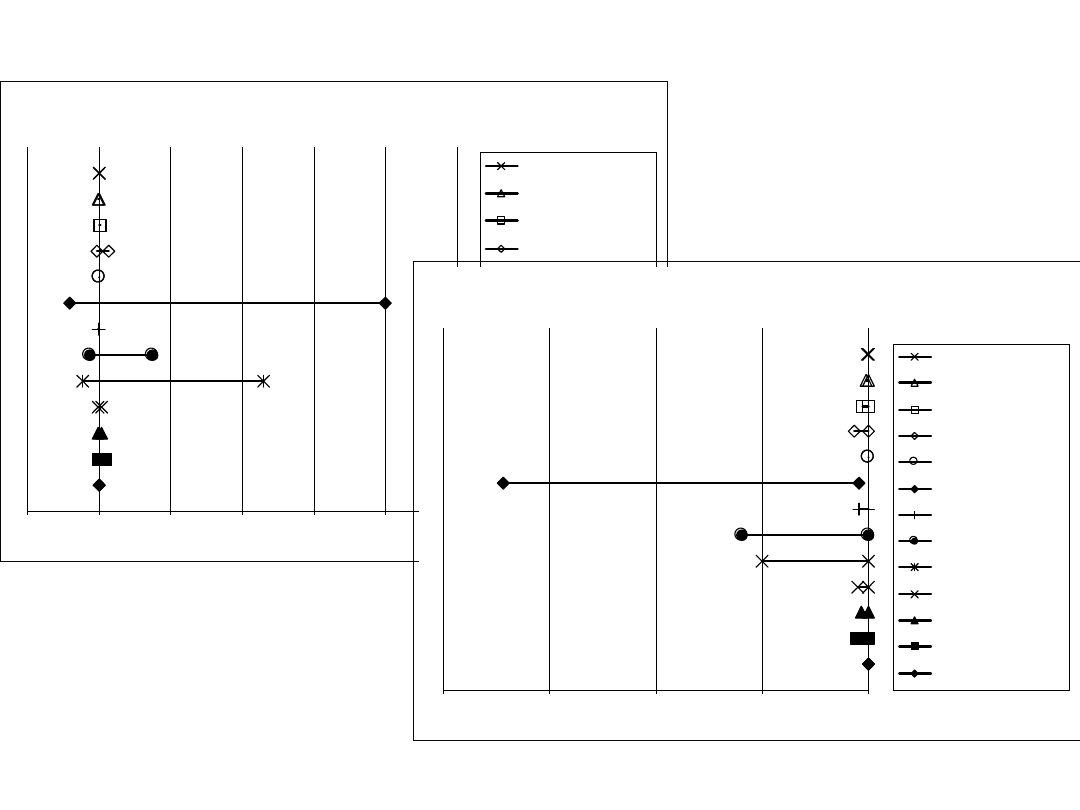
41

Momenty M6 i M8

Zakres zmienności współczynnika M6

-2

0

2

4

6

8

10

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

Zakres zmienności współczynnika M8

-40

-30

-20

-10

0

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

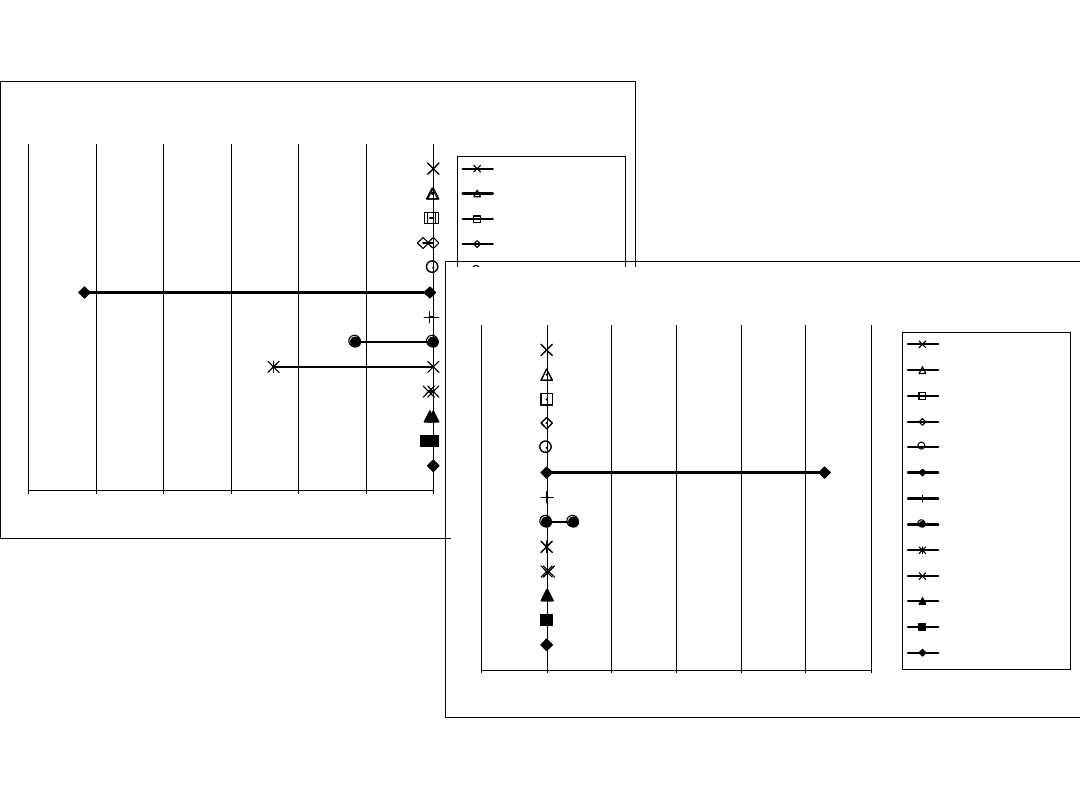
42

Momenty M9 i M10

Zakres zmienności współczynnika M9

-12

-10

-8

-6

-4

-2

0

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

Zakres zmienności współczynnika M10

-0,005

0

0,005

0,01

0,015

0,02

0,025

Kształt 4

Kształt 3

Kształt 2

Kształt 1

Pięciokąt

Trójkąt rozwartokątny

Trójkąt równoramienny

Trójkąt prostokątny

Prostokąt

Trapez

Półkole

Elipsa

Kwadrat

43

Porównanie setek takich 

rysunków i związanych z 

nimi tabel wartości pozwala 

na wyselekcjonowanie 

najlepszych cech i na ocenę 

ich jakości.

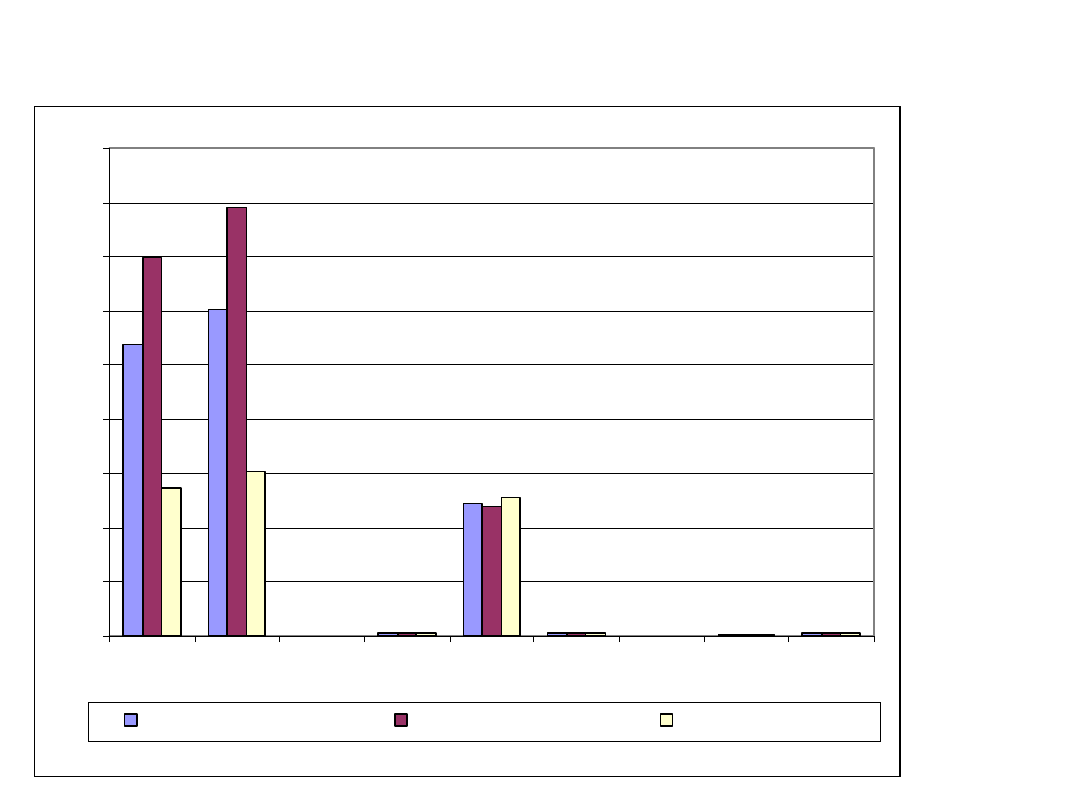
44

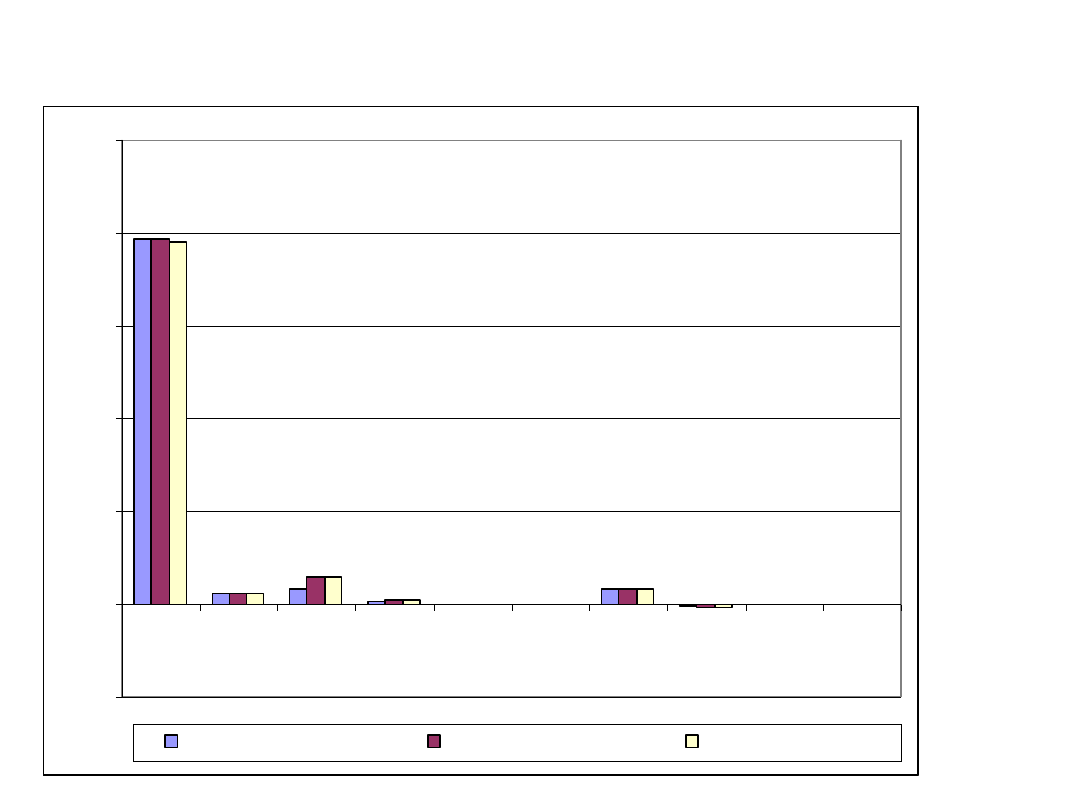
Wrażliwość współczynników kształtu na 

zmianę skali: 

0

20

40

60

80

100

120

140

160

180

W1

W2

W3

W4

W5

W6

W7

W8

W9

kształt 4 - podstawowy

kształt 4 - 130 procent

kształt 4 - 50 procent

45

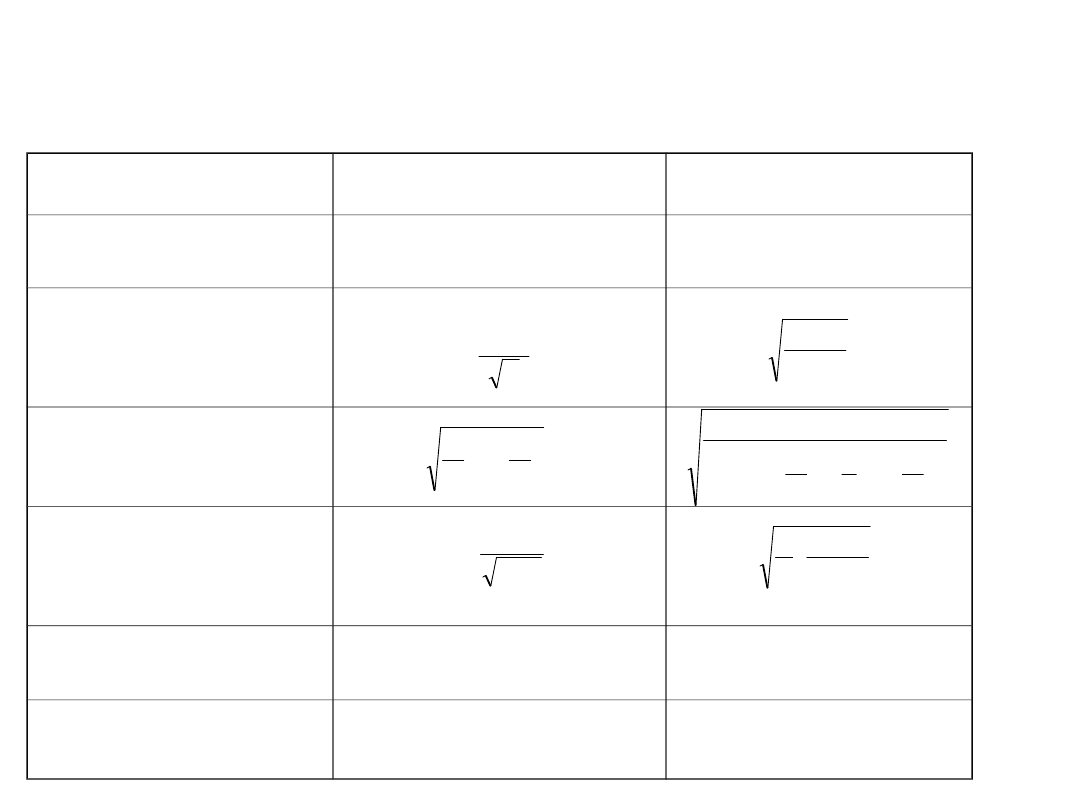
Niewrażliwość momentów na zmianę 

skali: 

-0,05

0

0,05

0,1

0,15

0,2

0,25

M1

M2

M3

M4

M5

M6

M7

M8

M9

M10

kształt 4 - podstawowy

kształt 4 - 130 procent

kształt 4 - 50 procent

46

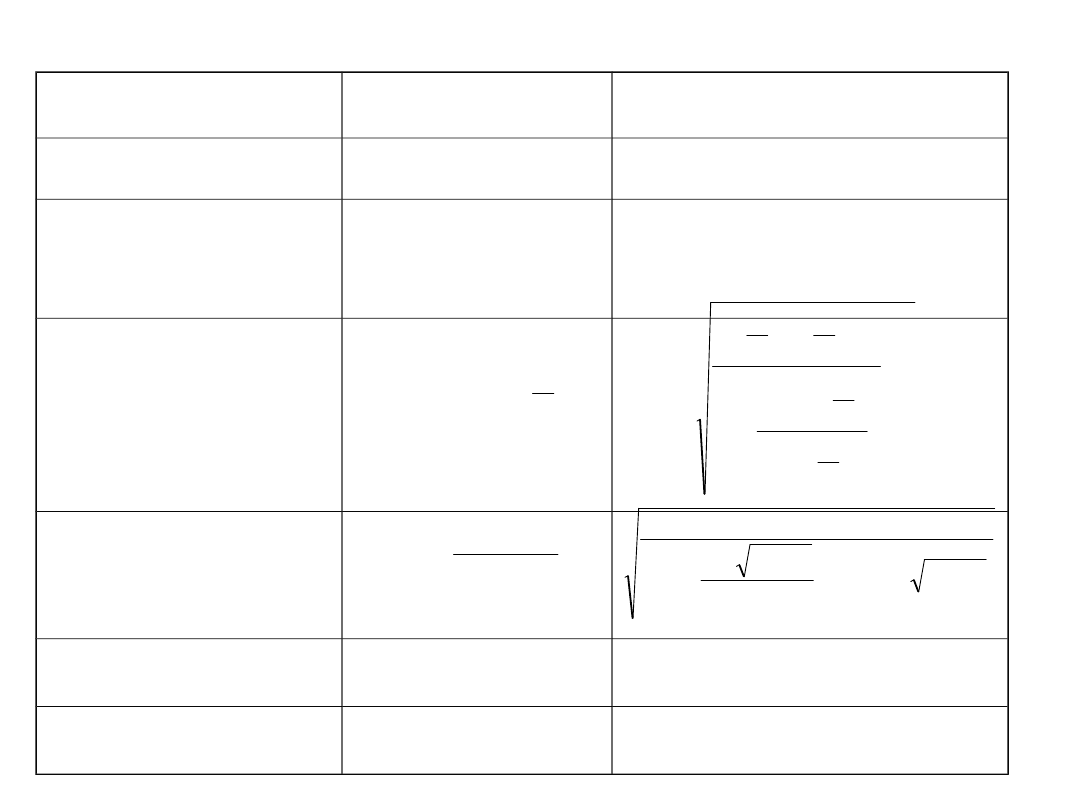
Porównanie teoretycznych wartości kilku 

przykładowych współczynników dla 

wybranych figur geometrycznych:

W3

W4

Koło

Elipsa o 
mimośrodzie 

wynoszącym g

Wielokąt o m 
bokach

Prostokąt o 
stosunku boków 
wynoszącym g

Kwadrat

Odcinek

5

,

1

g

g

1

75

,

0





1

m

tg

m





















g

g

1







128

,

0





0

1

2

g

1

g

2















































m

tg

3

1

m

ctg

m







0

977

,

0



2

g

1

g

6







47

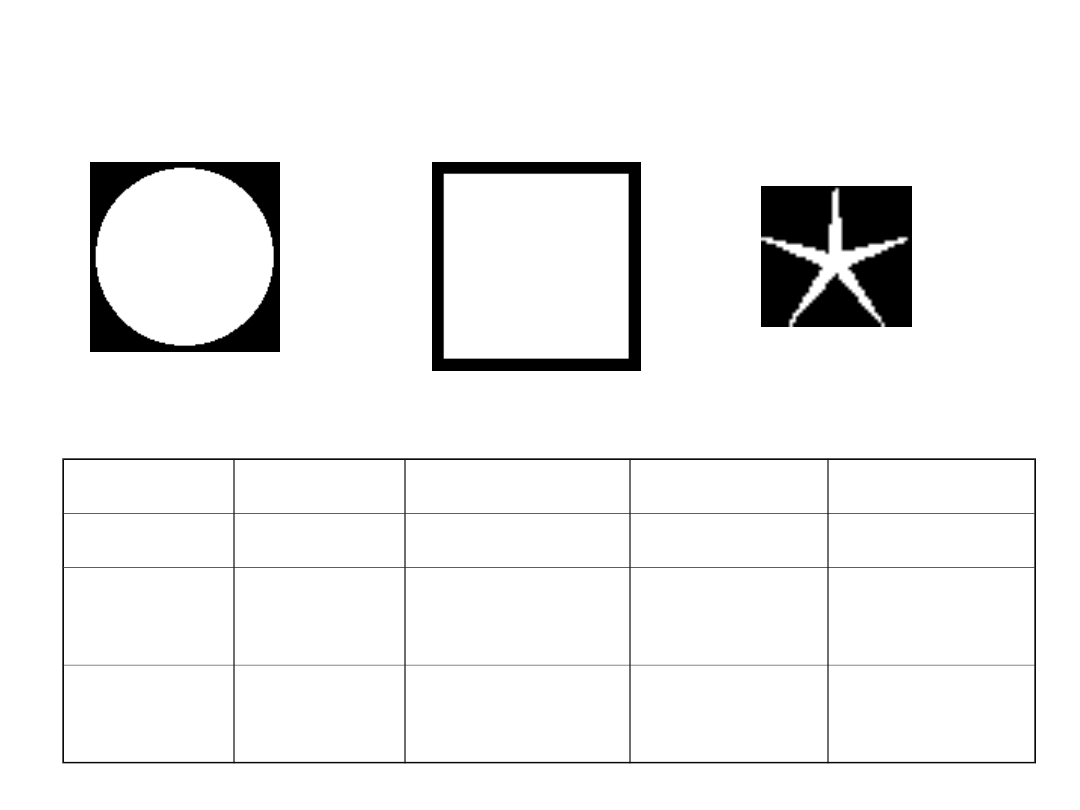
cd:

W5

W6

Koło

Elipsa o 

mimośrodzie 
wynoszącym g

Wielokąt o m 

bokach

Prostokąt o 
stosunku boków 
wynoszącym g

Kwadrat

Odcinek

274

,

28





?

?

0

36

105

,

0

















m

tg

m

9







2

3

g

g

144





1

m

cos

m

sin

1

ln

m

tg

m

2















































































2

2

g

1

g

ln

g

g

1

1

ln

g

g































48

Parametry przykładowych obiektów:

pole

pole2(cm

2

)

obw

obw2(cm)

koło

10936

13,6101

370,84

13,083

kwadra

t

15129

18,8284

465,33

16,416

gwiazd

ka

324

0,4032

198,83

7,014

49

Parametry przykładowych obiektów-2:

pole

pole2(cm

2

)

obw

obw2(cm

)

koło2cm-

100

19504

12,5832

498,10

12,652

koło2cm-

200

77818

12,5513

988,61

12,555

koło2cm-

300

175044

12,5479

1482,27

12,550

50

Parametry przykładowych obiektów-3:

pole

pole2(cm

2

)

obw

obw2(cm

)

kwadrat5cm-

100

38811

25,0393

748,64

19,015

kwadrat5cm-

200

155233 25,0375

1491,9

2

18,947

kwadrat5cm-

300

349278 25,0378

2238,9

9

18,957

51

Parametry przykładowych obiektów-4:

pole

pole2(cm

2

)

obw

obw2(cm

)

trójkąt5cm-

100

19404

12,5187

634,43

16,114

trójkąt5cm-

200

77619

12,5192

1274,2

2

16,183

trójkąt5cm-

300

174640 12,5190

1909,7

6

16,169

52

Parametry przykładowych obiektów-5:

W1

W2

W3

W4

W8

W9

koło2cm-100 157,585

7

158,549

5

0,0061

1,0000

0,3151

99

0,9939

koło2cm-200 314,771

3

314,684

8

-0,0003

1,0000

0,3166

06

1,0003

koło2cm-300 472,094

2

471,820

1

-0,0006

1,0000

0,3177

57

1,0006

kwadrat5cm-
100

222,296

4

238,300

0

0,0720 0,9772 0,2631

43

0,9328

kwadrat5cm-

200

444,577

1

474,893

0

0,0682 0,9772 0,2634

19

0,9362

kwadrat5cm-
300

666,869

2

712,693

0

0,0687 0,9772 0,2635

12

0,9357

trójkąt5cm-
100

157,181

2

201,944

7

0,2848 0,7217 0,3074 0,7783

trójkąt5cm-
200

314,368

5

405,596

5

0,2902 0,7237 0,3084 0,7751

trójkąt5cm-
300

471,549

1

607,894

8

0,2891 0,7217 0,3084 0,7757

53

Parametry przykładowych obiektów-6:

M1

M2

M3

M4

M5

M6

koło2cm-100 0,15915

6

0,0253

31

1,53E-

11

3,56E-

12

-3,23E-

27

2,95E-

26

koło2cm-200 0,15915

5

0,0253

31

5,37E-

11

8,89E-

13

1,18E-

31

-3,83E-

26

koło2cm-300 0,15915

5

0,0253

30

2,08E-

11

2,11E-

12

-1,32E-

29

-2,07E-

21

kwadrat5cm-
100

0,16667

1

0,0277

79

1,66E-

10

1,84E-

11

-1,02E-

21

-1,22E-

20

kwadrat5cm-

200

0,16666

2

0,0277

76

2,54E-

11

2,87E-

12

-6,67E-

24

-5,17E-

18

kwadrat5cm-
300

0,16666

5

0,0277

77

5,06E-

12

5,67E-

13

-2,64E-

25

-4,65E-

19

trójkąt5cm-
100

0,19443

4

0,0378

05

6,85E-

04

2,76E-

05

9,86E-

09

7,67E-

07

trójkąt5cm-
200

0,19444

8

0,0378

10

6,86E-

04

2,74E-

05

9,79E-

09

7,62E-

07

trójkąt5cm-
300

0,19444

3

0,0378

08

6,86E-

04

2,75E-

05

9,79E-

09

7,63E-

07

54

Parametry przykładowych obiektów-7:

M7

M8

M9

M10

ci

cj

koło2cm-100 0,00633

3

-2,14E-

12

-1,93E-

13

-3,69E-

24

118,5

0

118,5

0

koło2cm-200 0,00633

3

-2,56E-

11

-9,01E-

13

-1,14E-

23

236,5

2

236,5

0

koło2cm-300 0,00633

3

-7,28E-

12

-2,28E-

13

-7,69E-

24

354,5

1

354,4

9

kwadrat5cm-
100

0,00694

5

-1,84E-

11

-1,54E-

12

3,51E-

26

158,0

0

157,9

9

kwadrat5cm-
200

0,00694

4

-2,84E-

12

-2,36E-

13

3,68E-

25

315,5

0

315,5

0

kwadrat5cm-

300

0,00694

4

-5,64E-

13

-4,68E-

14

1,91E-

26

473,0

0

473,0

0

trójkąt5cm-
100

0,00925

8

-5,76E-

04

-2,74E-

05

1,11E-

13

170,8

3

137,9

9

trójkąt5cm-
200

0,00926

0

-5,76E-

04

-2,74E-

05

7,28E-

15

341,1

7

276,0

0

trójkąt5cm-
300

0,00925

9

-5,76E-

04

-2,74E-

05

1,39E-

15

512,5

0

414,0

0

00

10

m

m

x

~

00

01

m

m

y

~

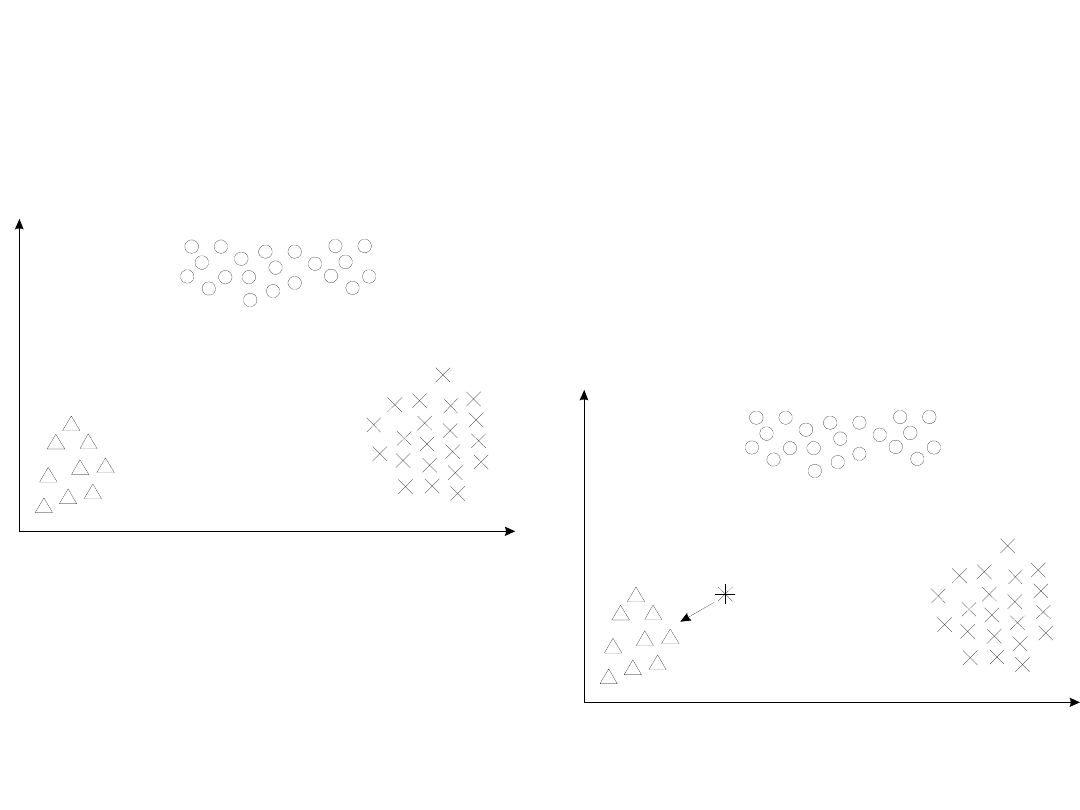
55

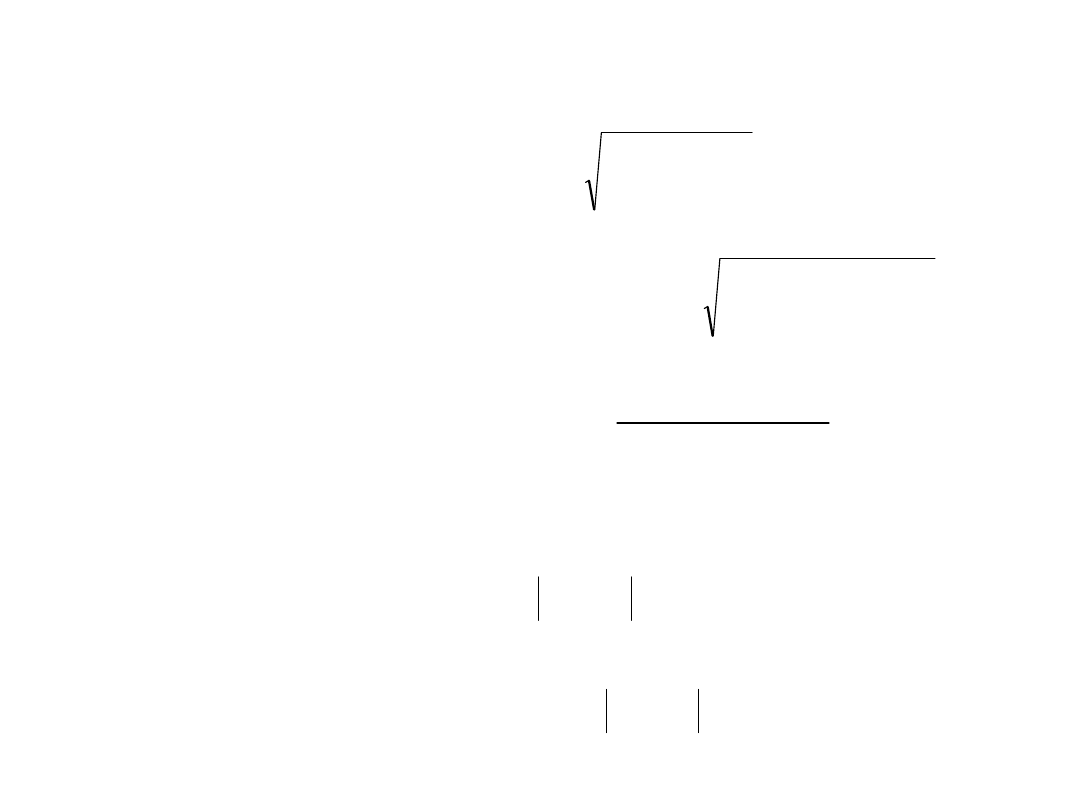
Metody minimalnoodległościowe

x

2

x

1

x

2

x

1

Dwuwymiarowa przestrzeń 
cech: 

Podejmowanie decyzji 
w metodzie NN: 

56

Stosowane metryki (normy):

- metryka 
euklidesowa:

- metryka euklidesowa z 
wagą:

- metryka uliczna:

- metryka 
Czebyszewa:













n

1

2

1

x

x

)

x

,

x

(







































n

1

2

2

x

x

)

x

,

x

(





























n

1

3

x

x

)

x

,

x

(



































x

x

max

)

x

,

x

(

1

5









gdzie wagi określane 
np. na przedziale 
zmienności:

 

 









x

min

x

max

1

U

x

U

x









57

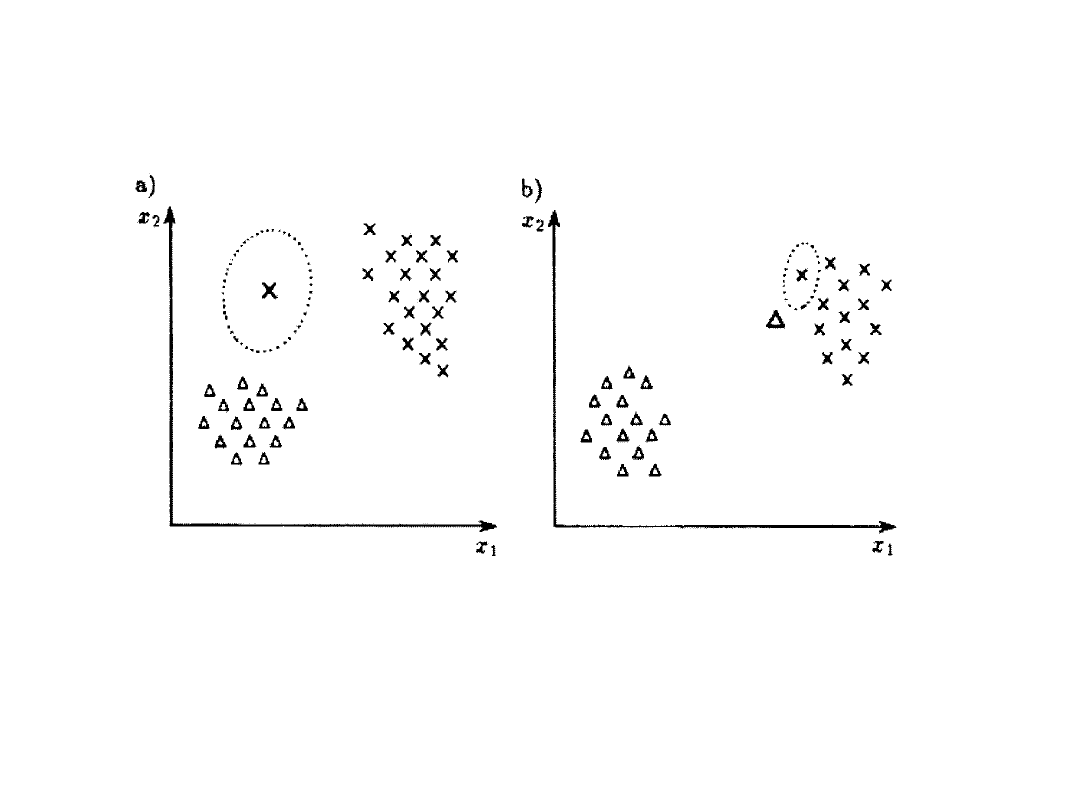
W przypadku gdy położenie (a) lub sklasyfikowanie 
(b) chociaż jednego obiektu ciągu uczącego jest 
błędne.

Podejmowanie błędnych decyzji:

58

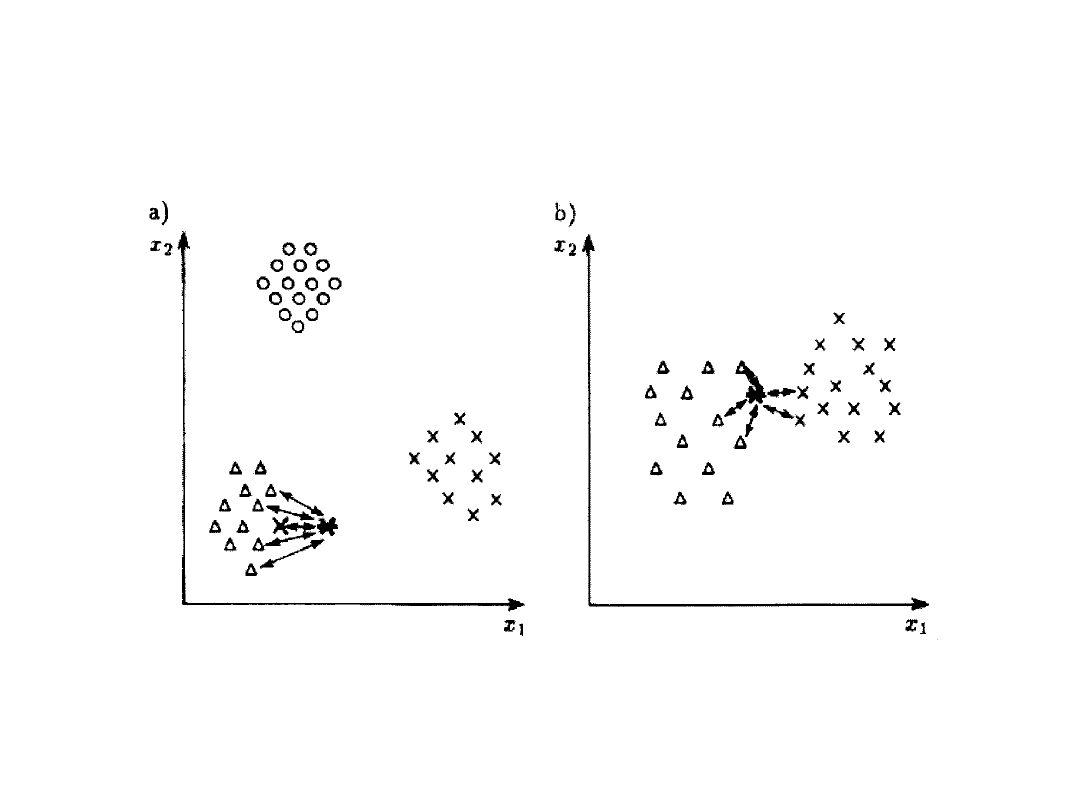
Zapobiega błędom wynikającym z pomyłek w ciągu 
uczącym (a), ale ogranicza czułość metody (b).:

Metoda αNN:

Parametr α jest wybierany tak 
aby:   

W praktyce α jest małą liczbą 
całkowitą.

i

I

i

N

min







59

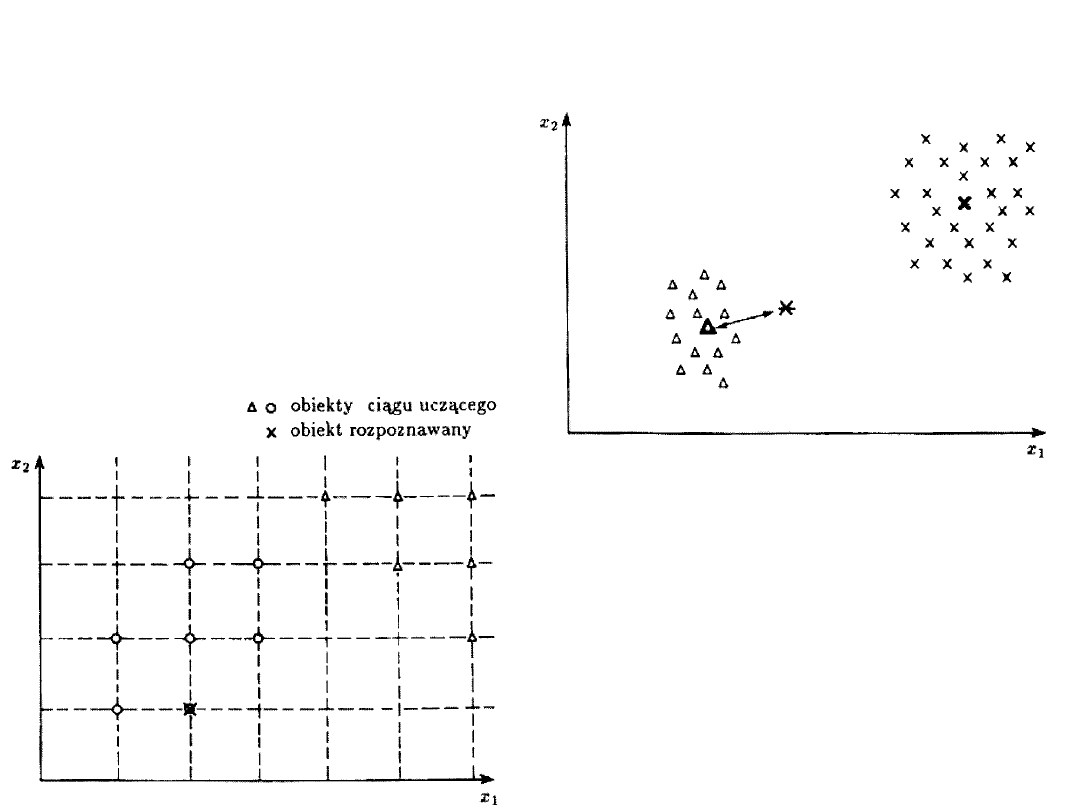
Metody wzorców:

Ilustracja pojęcia wzorca:

Przy dyskretnych cechach 
prawdopodobieństwo rozpoznania 
metodą pokrycia punktów jest 
bardzo duże

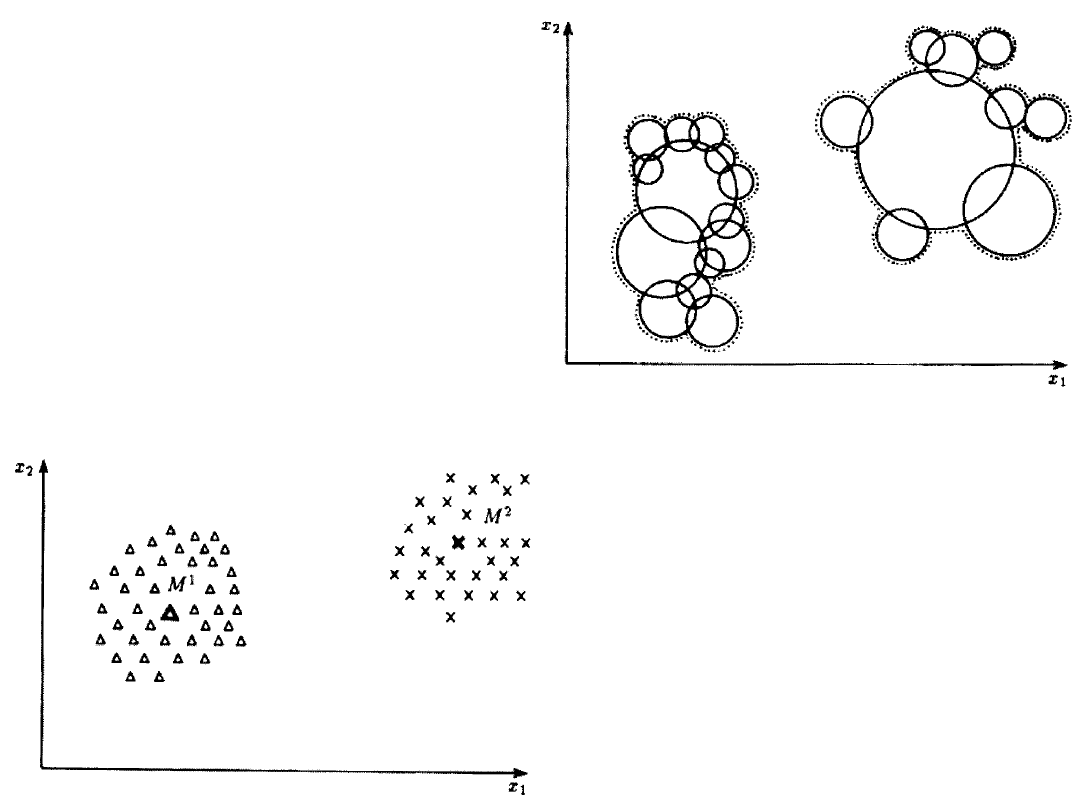
60

Otoczenia kuliste o różnych 
promieniach pozwalają 
bardzo dokładnie 
odwzorować kształty 
obszarów o różnej 
topografii.

Metoda NM (najbliższej 
mody):

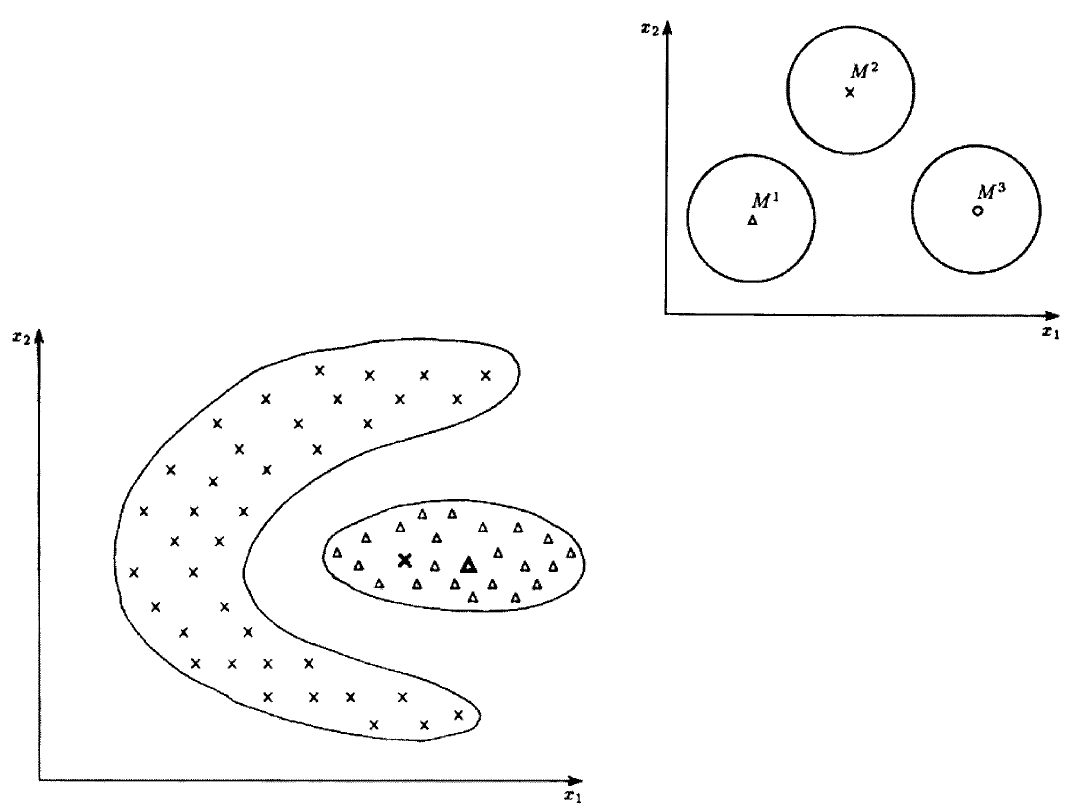
61

Przykłady klas, dla 
których średnia nie jest 
dobrym wzorcem dla 
całej klasy.

Przyjęcie mody M jako 

środka ciężkości obiektów 

rozważanych klas bywa 

bardzo dobrym rozwiązaniem 

w przypadku klas o 

regularnych i stosunkowo 

prostych kształtach:

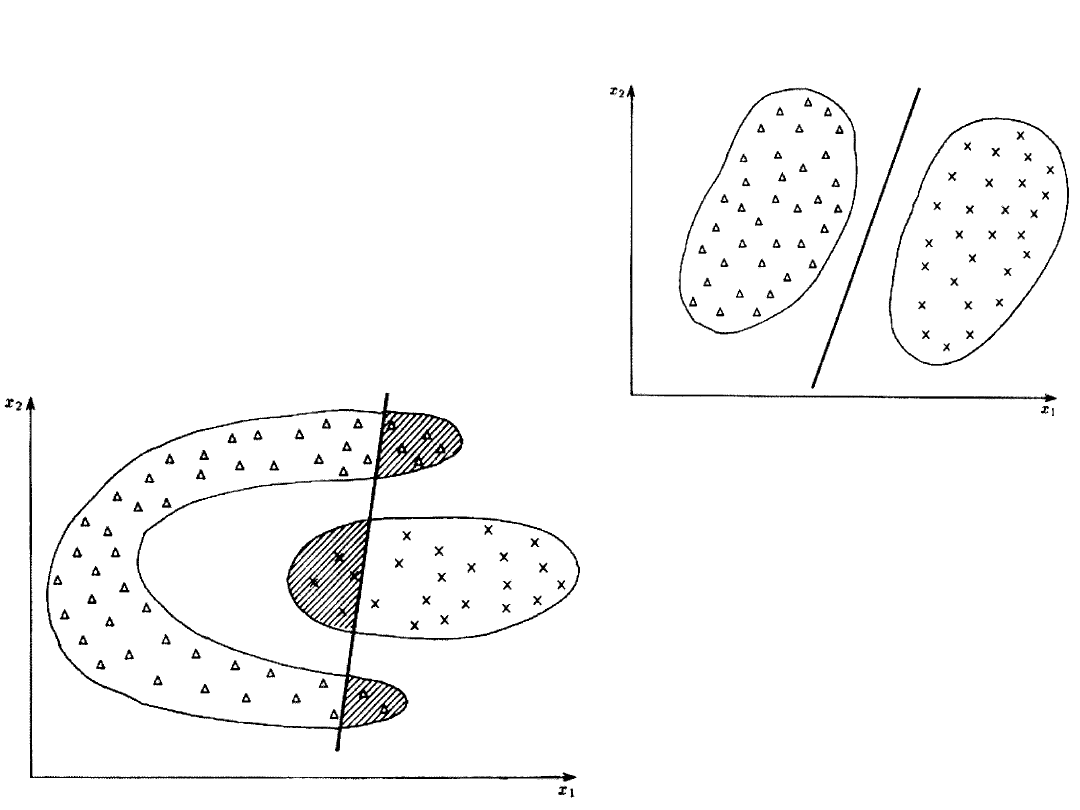
62

Metody aproksymacyjne:

Przykład liniowej 
separowalności klas:

Przykład zadania, 
które nie jest liniowo 
separowalne:

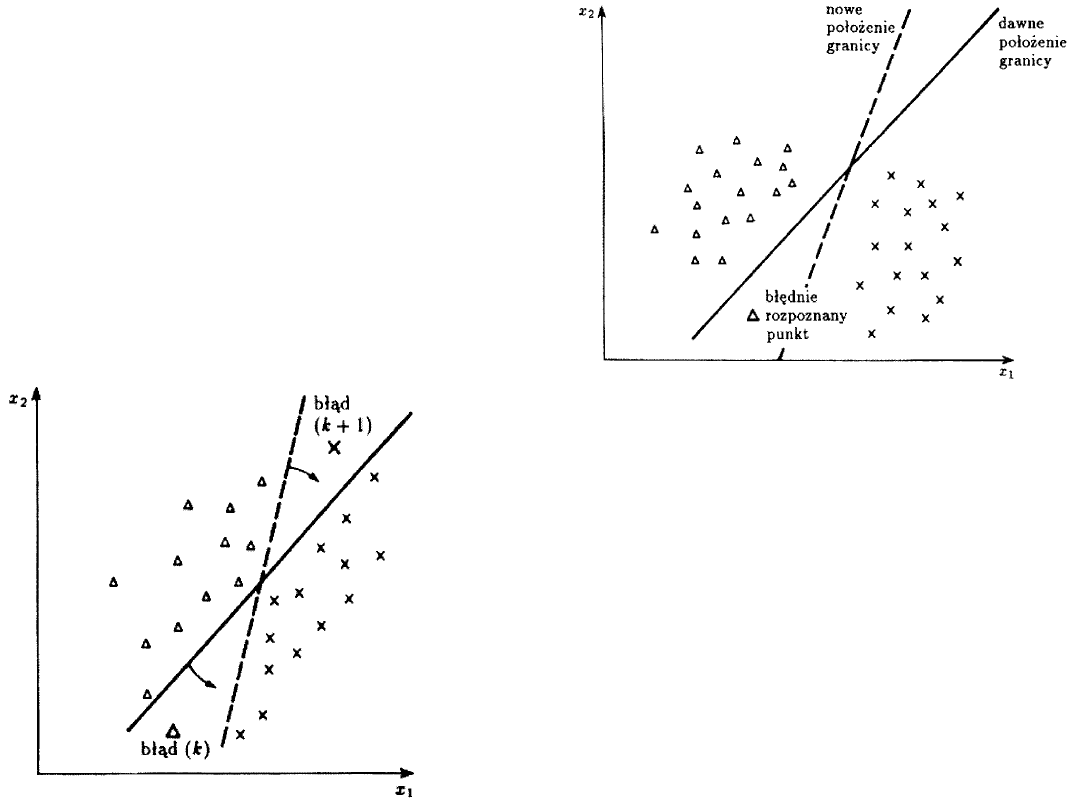
63

Proces uczenia 
polegający na 
przemieszczaniu 
granicznej 
płaszczyzny:

Poprawka położenia 
linii granicznej 
spowodowana przez 
jeden błędnie 
sklasyfikowany punkt: