RÓWNANIA

RÓWNANIA

RÓŻNICZKOWE

RÓŻNICZKOWE

WYKŁAD 12

2

Szeregi Fouriera

Szeregi Fouriera

3

Szeregi Fouriera

Szeregi Fouriera

4

Szeregi Fouriera

Szeregi Fouriera

5

Szeregi Fouriera

Szeregi Fouriera

6

Szeregi Fouriera

Szeregi Fouriera

7

Szeregi Fouriera

Szeregi Fouriera

8

Szeregi Fouriera

Szeregi Fouriera

9

Szeregi Fouriera

Szeregi Fouriera

x

O

f
(x)



-



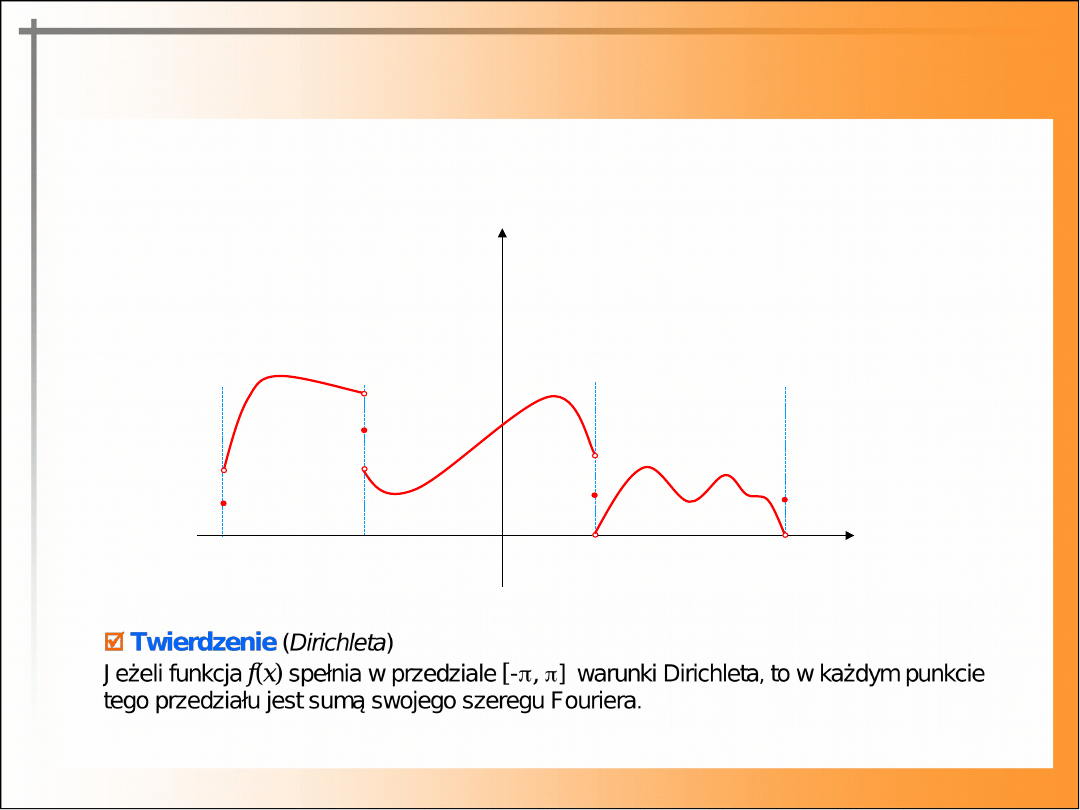
Przykład

Wykres funkcji spełniającej warunki Dirichleta

10

Szeregi Fouriera

Szeregi Fouriera

Szeregi Fouriera

Szeregi Fouriera

k

kx

x

S

n

n

k

n

sin

)

1

(

2

)

(

1

1











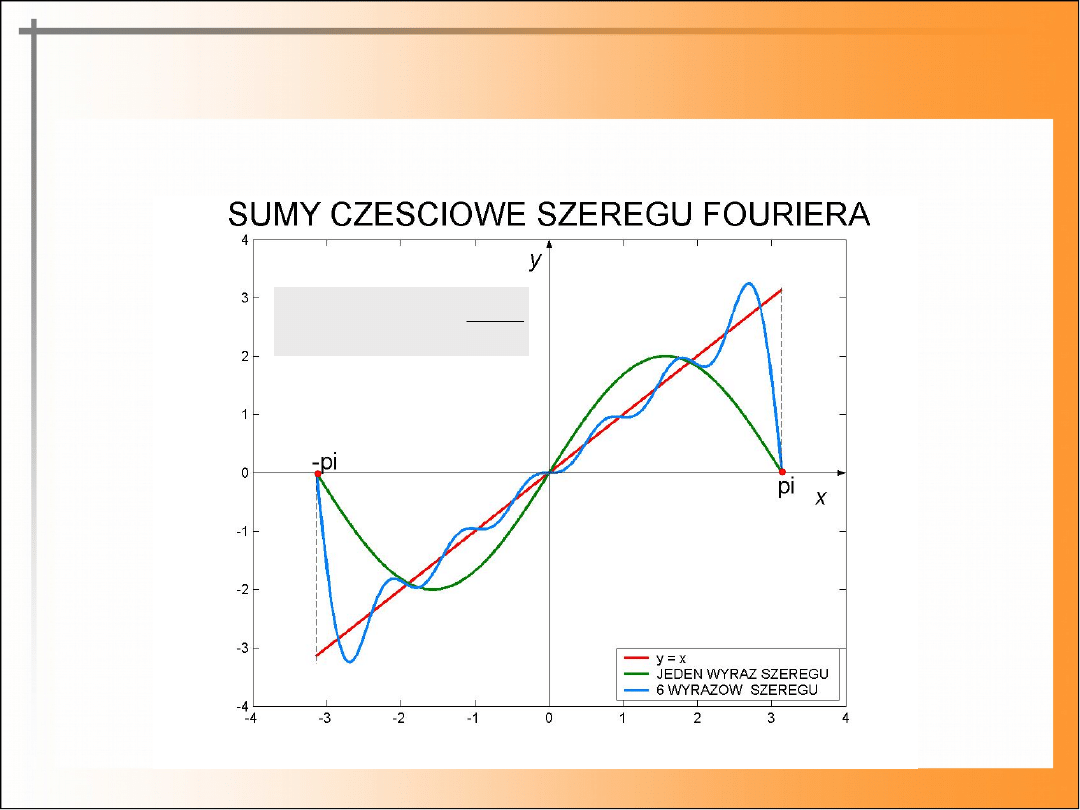
Przykład (c.
d.)

Szeregi Fouriera

Szeregi Fouriera

k

kx

x

S

n

n

k

n

sin

)

1

(

2

)

(

1

1











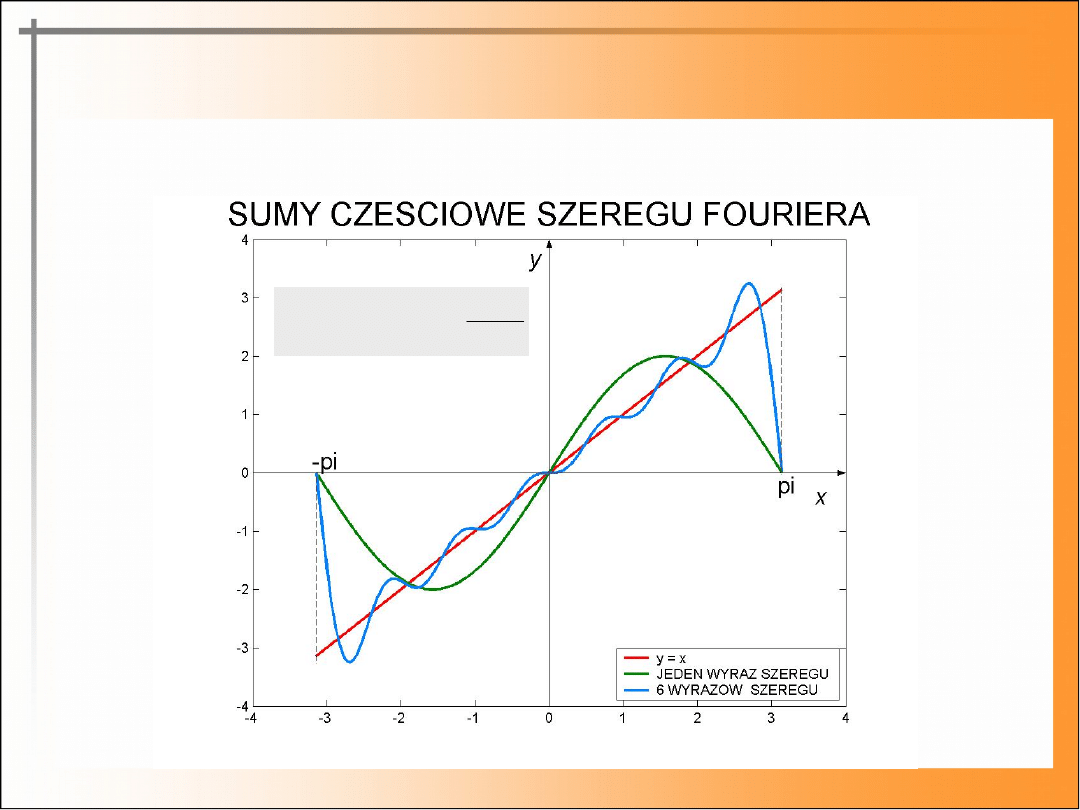
Przykład (c.
d.)

Szeregi Fouriera

Szeregi Fouriera

k

kx

x

S

n

k

sin

)

1

(

2

)

(

1

50

1

50











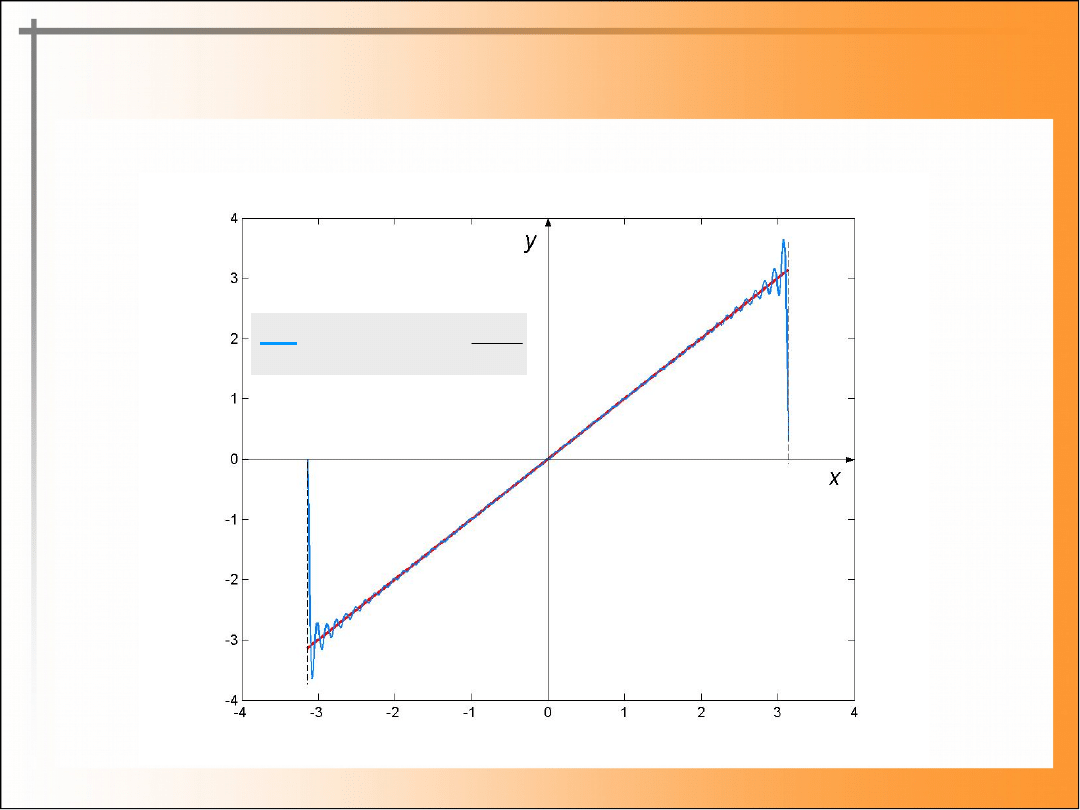
Przykład (c.
d.)

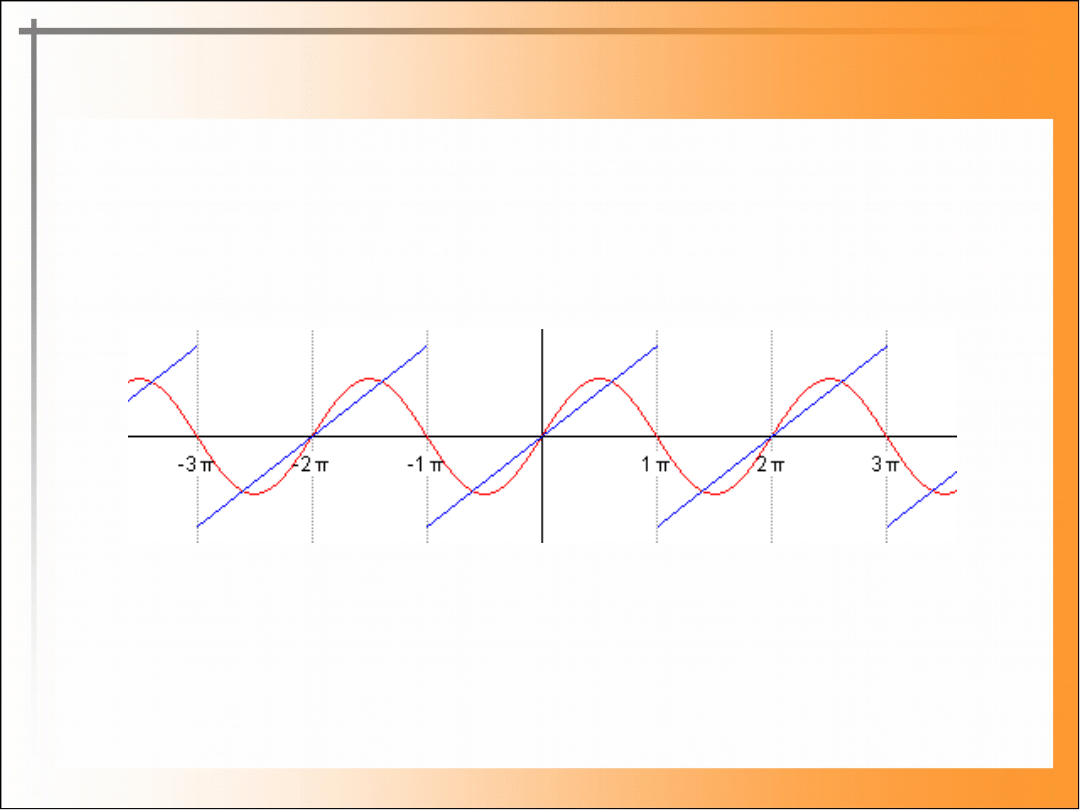
Szeregi Fouriera

Szeregi Fouriera

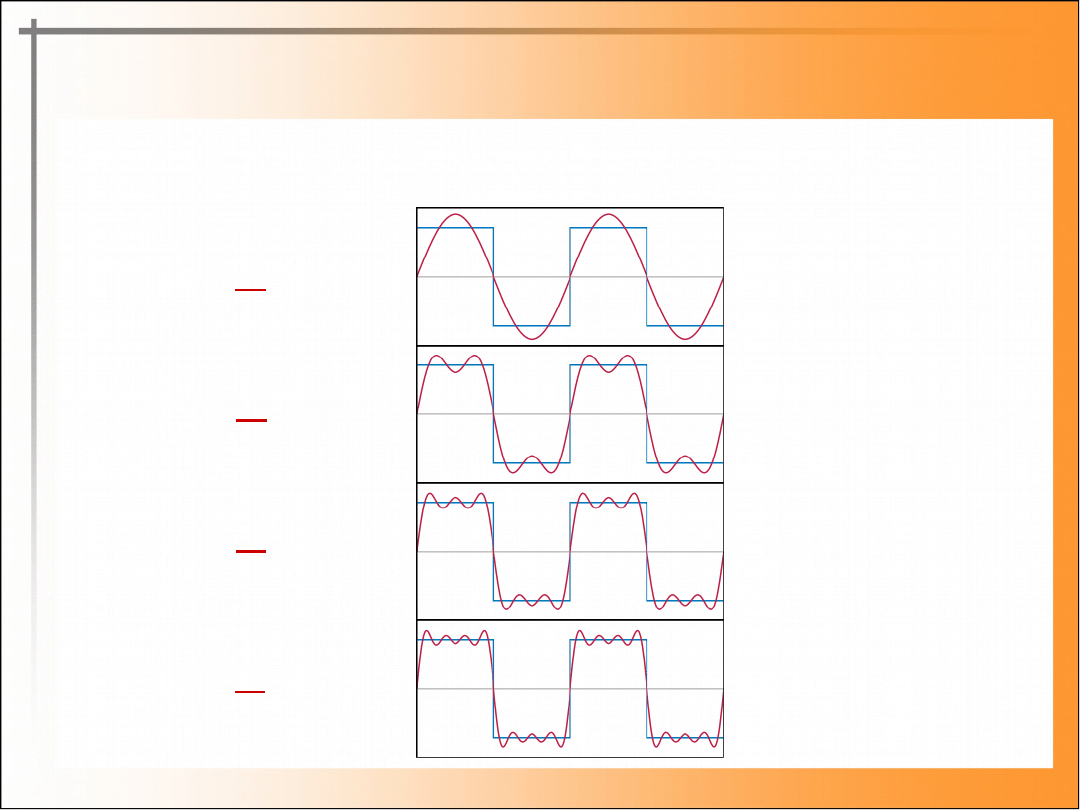
Szeregi Fouriera

Szeregi Fouriera

n =
1

n =
2

n =
4

n =
3

Przykład

Aproksymacja „sygnału prostokątnego” za pomocą pierwszych 4 wyrazów
szeregu Fouriera

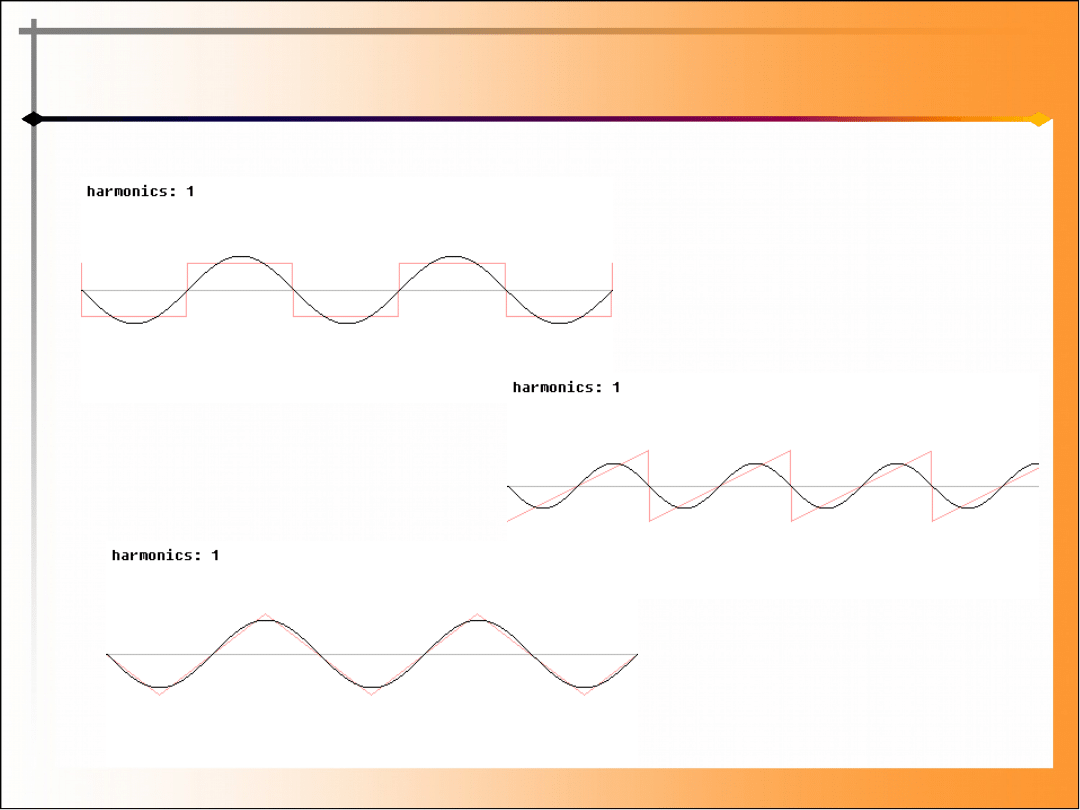
Trygonometryczny szereg Fouriera - animacja

Szeregi Fouriera

Szeregi Fouriera

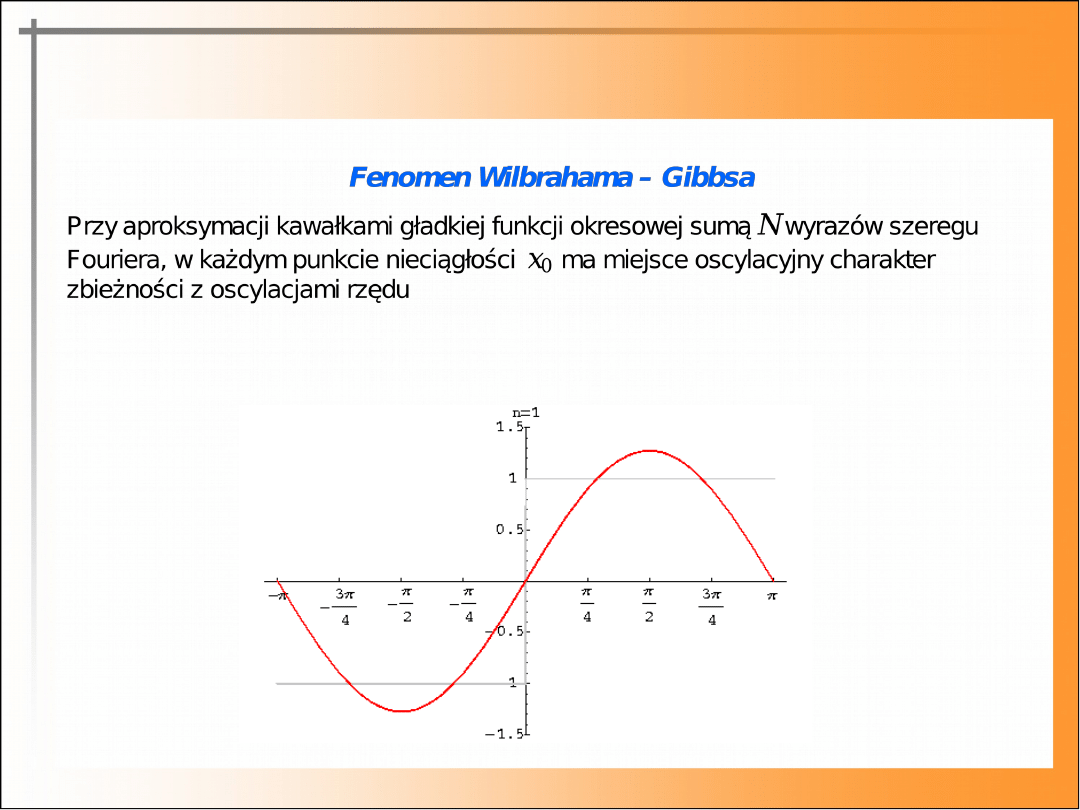
17

Szeregi Fouriera

Szeregi Fouriera

18

Szeregi Fouriera

Szeregi Fouriera

Szeregi Fouriera

Szeregi Fouriera

0

cos

)

(

1















nxdx

t

f

a

n

(nieparzysta)

×

(parzysta)

| |

(nieparzysta)

0

)

(

1

0















dx

x

f

a





















0

sin

)

(

2

sin

)

(

1

nxdx

x

f

nxdx

x

f

b

n

| |

(parzysta)

(nieparzysta)

×

(nieparzysta)

(nieparzysta)





)

(x

f

x



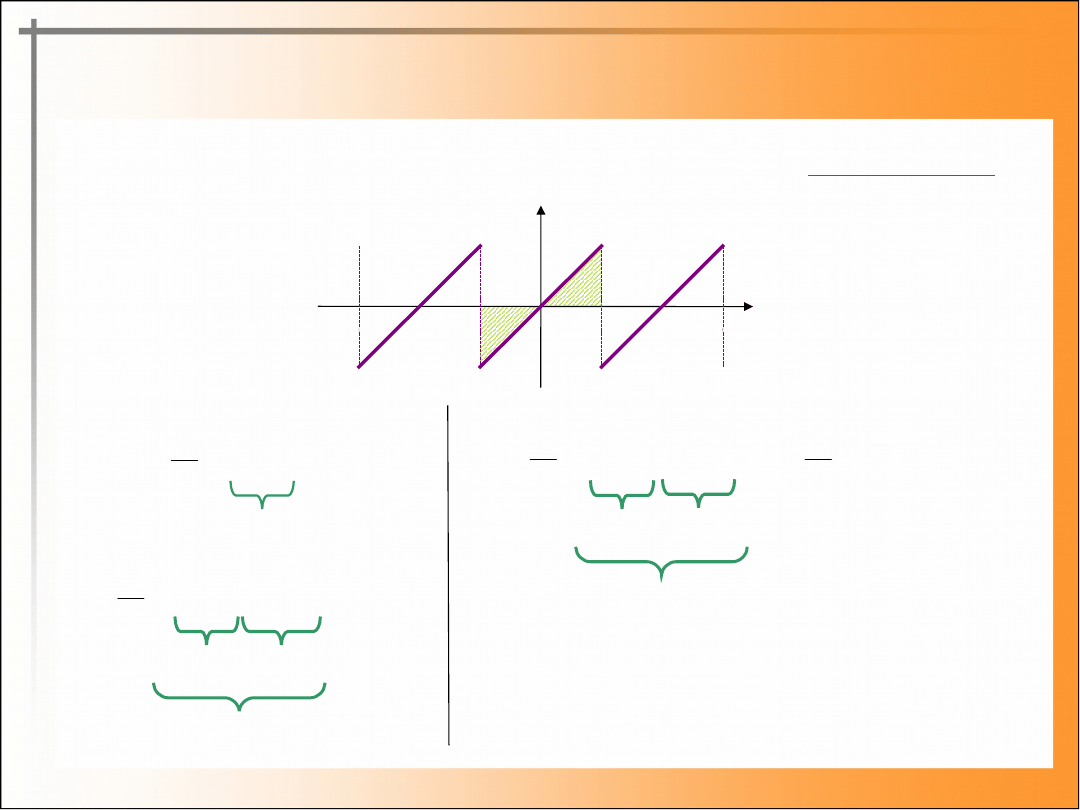
Wyznaczanie współczynników Fouriera funkcji nieparzystej

Szeregi Fouriera

Szeregi Fouriera







)

(x

f

x

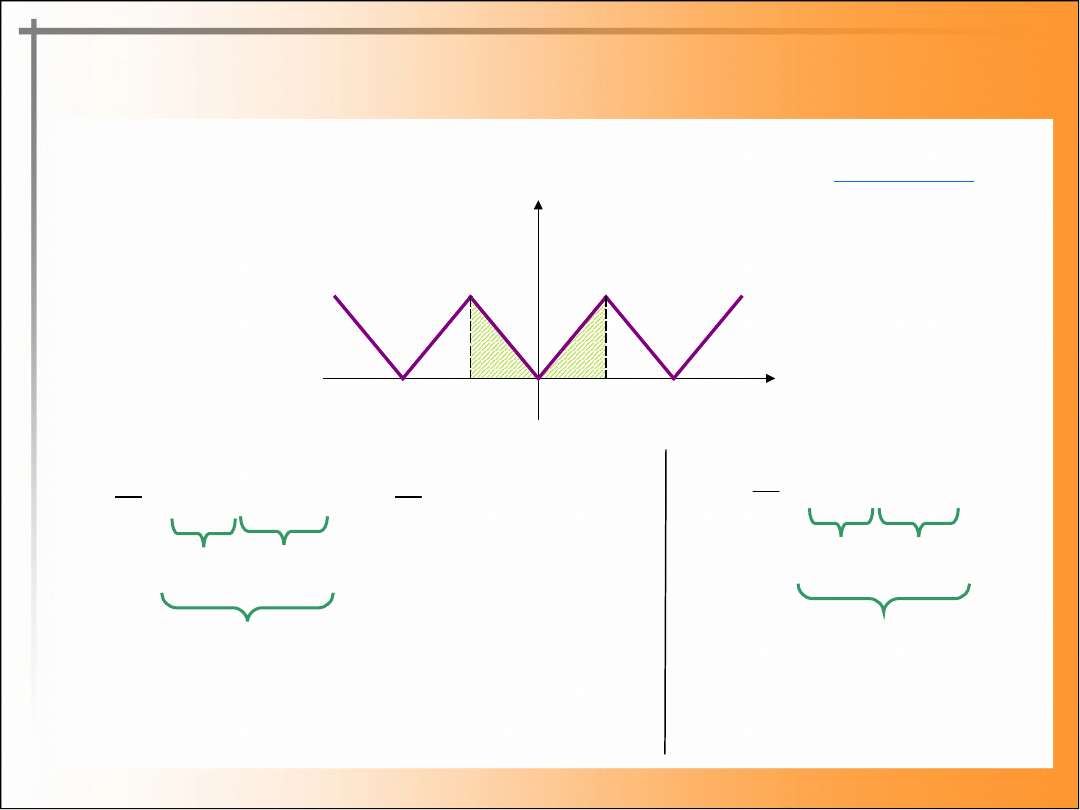
Wyznaczanie współczynników Fouriera funkcji parzystej





















0

cos

)

(

2

cos

)

(

1

nxdx

x

f

nxdx

x

f

a

n

| |

(parzysta)

0

sin

)

(

2















nxdx

x

f

b

n

(parzysta)

×

(nieparzysta)

| |

(nieparzysta)

(parzysta)

×

(parzysta)

Przykłady rozwijania funkcji w szeregi Fouriera w załączonym pliku:

Szereg_Fouriera_przyklady

Szeregi Fouriera

Szeregi Fouriera

22

Szeregi Fouriera

Szeregi Fouriera

23

Szeregi Fouriera

Szeregi Fouriera

DZIĘKUJĘ ZA

DZIĘKUJĘ ZA

UWAGĘ

UWAGĘ