Przetworniki

Przetworniki

Cyfra/Analog i

Cyfra/Analog i

Analog/Cyfra

Analog/Cyfra

Technika cyfrowa

Technika cyfrowa

Ernest Jamro, Agnieszka Dąbrowska

Ernest Jamro, Agnieszka Dąbrowska

Katedra Elektroniki, AGH

Katedra Elektroniki, AGH

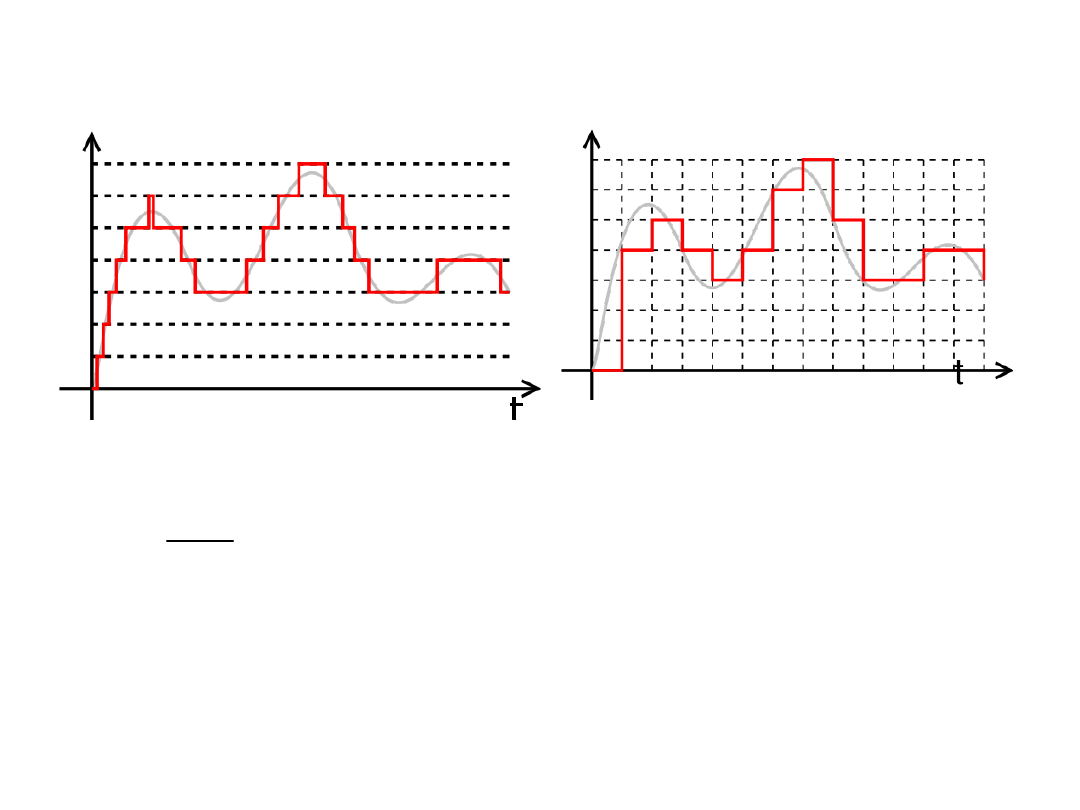
Kwantowanie

Sygnał kwantowany

Sygnał cyfrowy

N

ref

V

q

2



q – kwant – waga napięciowa
najmniej znaczącego bitu
przetwarzania

V

ref

– napięcie referencyjne (lub

zakres pomiarowy: V

max

-V

min

)

N- liczba bitów przetwornika

Przykład:

V

ref

=1V,

N=10,

q=
1/10241mV

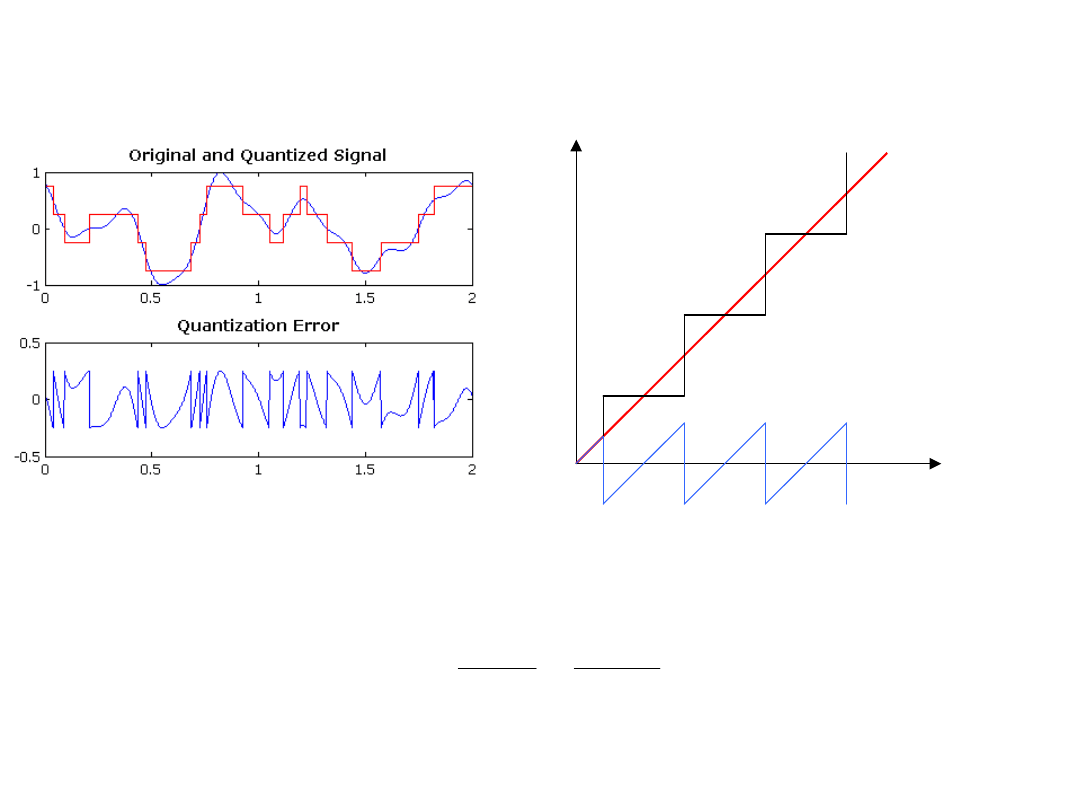
Błąd kwantyzacji

SNR – Signal-to-Noise Ratio – stosunek sygnału do
szumu

2

2

noise

signal

noise

signal

U

U

P

P

SNR





Analog

Q(x)-po
kwantyzacji

x

Q

err

(x)-bład kwantyzacji

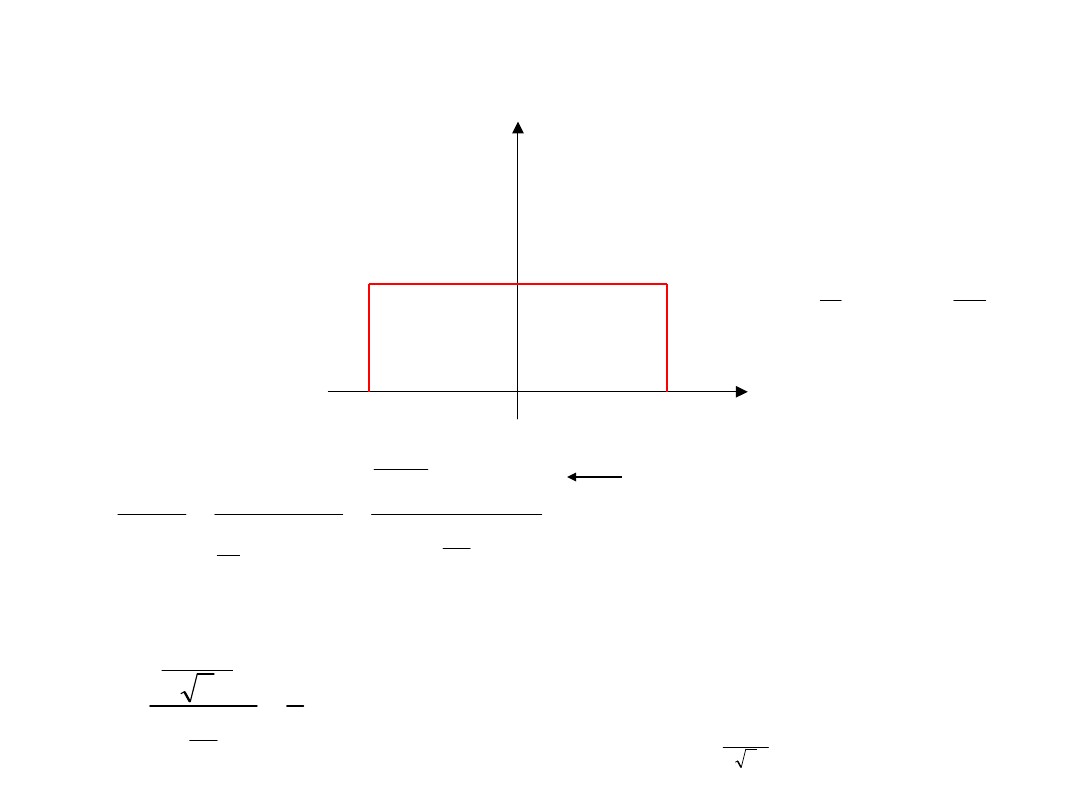
Błąd kwantyzacji – c.d.

P

err

(x)

-Q/2

Q/2

1/Q

12

1

2

2

/

2

/

2

2

Q

de

e

Q

err

Q

Q











]

/

[

2

12

2

1

1

)

(

2

2

/

2

2

/

2

2

2

/

2

/

2

2

2

V

V

Q

du

u

Q

du

u

Q

dt

t

f

U

U

SNR

N

Q

Q

N

Q

Q

noise

Signal

N

N



























Dla przebiegu trójkątnego w pełnym
zakresie pomiarowym

równomierny rozkład

błędu kwantyzacji

]

[

02

.

6

)

2

log(

20

)

2

log(

10

)

log(

10

2

dB

N

N

SNR

SNR

N

dB





















]

[

761

.

1

02

.

6

sin

dB

N

SNR

dB







Sinusoida – pełny zakres pomiarowy:
wartość skuteczna równa się

N

N

Q

Q

SNR

2

2

1

sin

2

2

3

12

)

2

2

(







2

2

1

Q

N

Próbkowanie

Próbkowanie

Katedra Elektroniki AGH

Katedra Elektroniki AGH

Przebieg wejściowy

Impulsy próbkujące

Dyskretny przebieg wejściowy

Dyskretny przebieg wejściowy

z pamiętaniem stanów

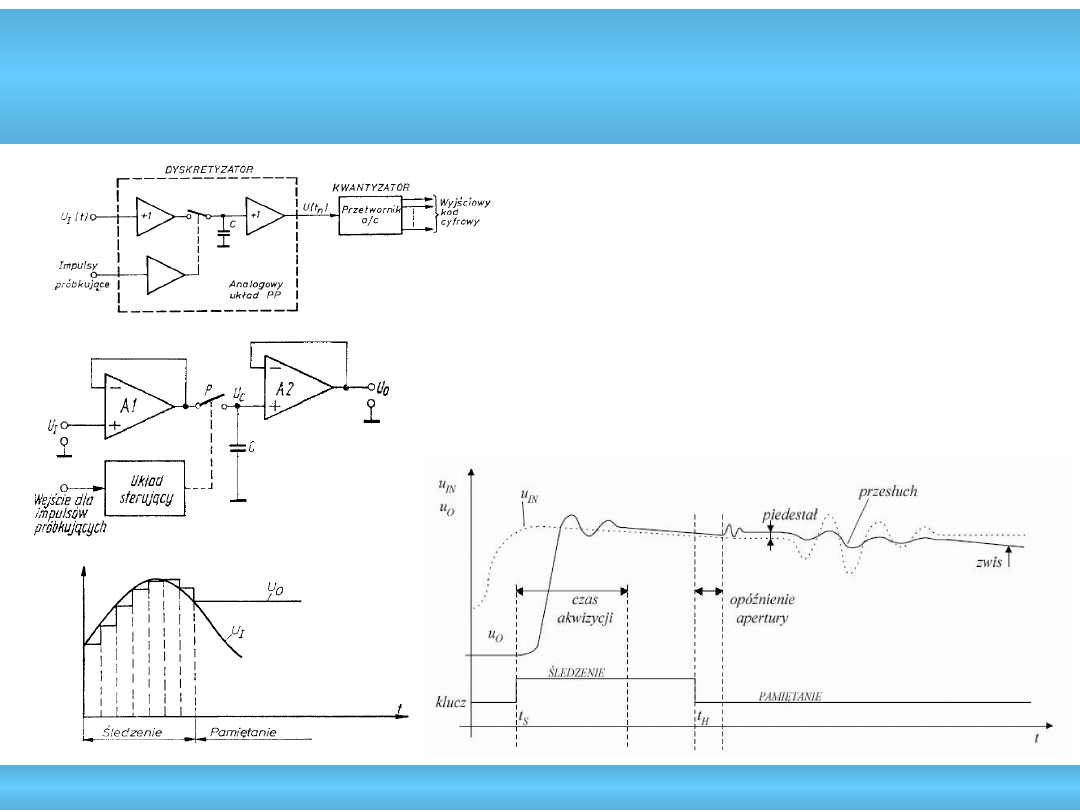
Układy próbkująco-pamiętające

Układy próbkująco-pamiętające

Katedra Elektroniki AGH

Katedra Elektroniki AGH

• czas akwizycji – czas pomiędzy

zamknięciem klucza a ustaleniem
wartości napięcia wyjściowego
równej wartości napięcia wejściowego
z zadaną dokładnością (0,2s – 25ns)

• dokładność: 8 – 12 bitów

• maksymalna szybkość narastania:

(0,5-900 V/s)

• zwis (spadek napięcia na kondensatorze

pamiętającym w fazie pamiętania):
1mV/s – 1kV/s

Zakres pomiarowy (ang. Full

Scale)

y

00

01

10

11

brak

x

Zakres

Zakres pomiarowy = 2

N

Q

Największa reprezentowana wartość: (2

N

-1)

Q

Przykład:

N=8, V

ref

=1V, V

max

=255/256=0.996V

Uwag na reprezentację liczb: z przesunięciem –
najczęstsza reprezentacja liczb w przetwornikach
AC i CA

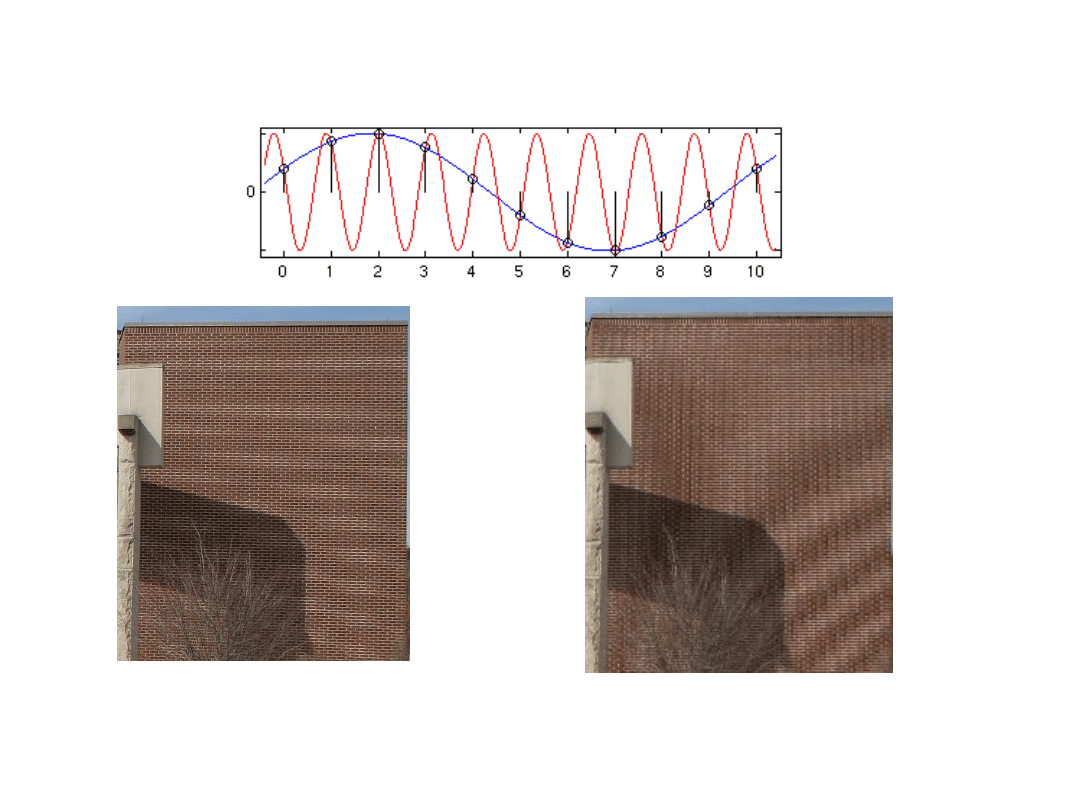
Aliasing

Właściwy obraz

Aliasing

Potrzeba stosowania filtru dolnoprzepustowego na
wejściu przetwornika

Parametry statyczne

Parametry statyczne

przetworników

przetworników

Katedra Elektroniki AGH

Katedra Elektroniki AGH

• Rozdzielczość – stosunek przedziału kwantyzacji Q do pełnego zakresu prze-

twornika FS, jest równa odwrotności liczby poziomów kwan-
tyzacji, najczęściej określana liczbą bitów N słowa cyfrowego

• Dokładność przetwornika (bezwzględna lub względna) – największa różnica

między rzeczywistą a przewidywaną wartością sygnału ana-
logowego dla danego słowa cyfrowego

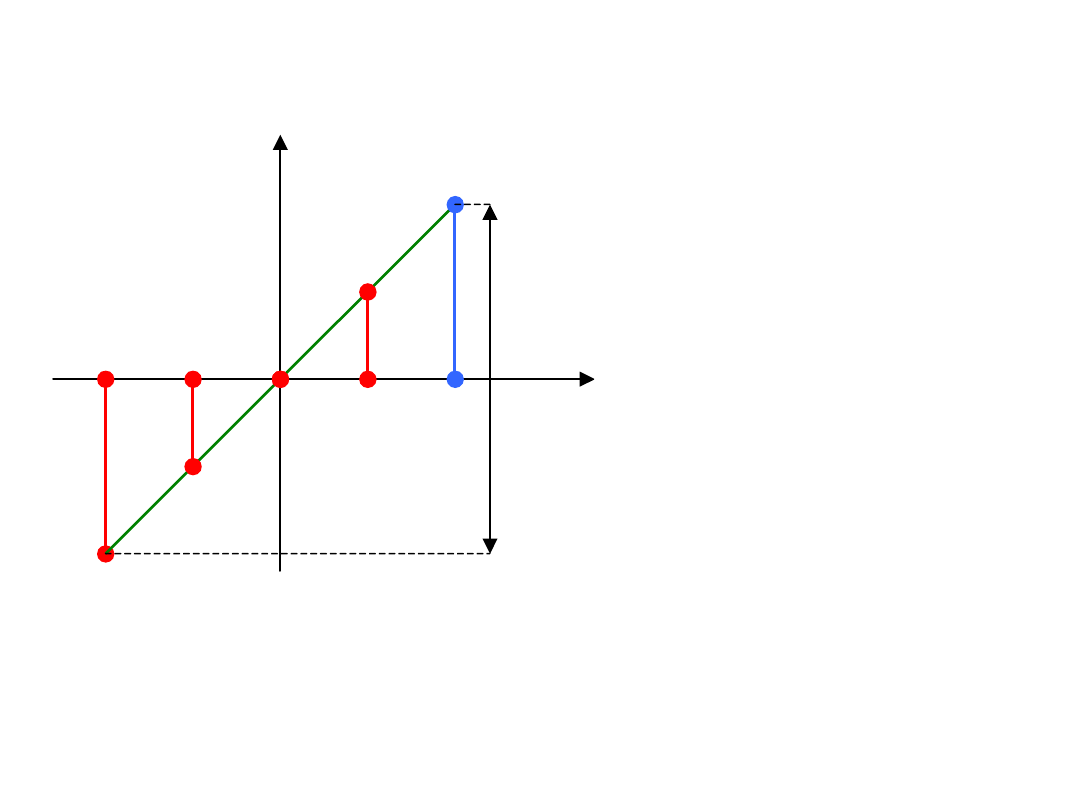
• Błąd przesunięcia (bezwzględny lub względny) –

różnica między rzeczywistą
a idealną wartością sy-
gnału analogowego dla mini-
malnej wartości cyfrowej

Parametry statyczne

Parametry statyczne

przetworników

przetworników

Katedra Elektroniki AGH

Katedra Elektroniki AGH

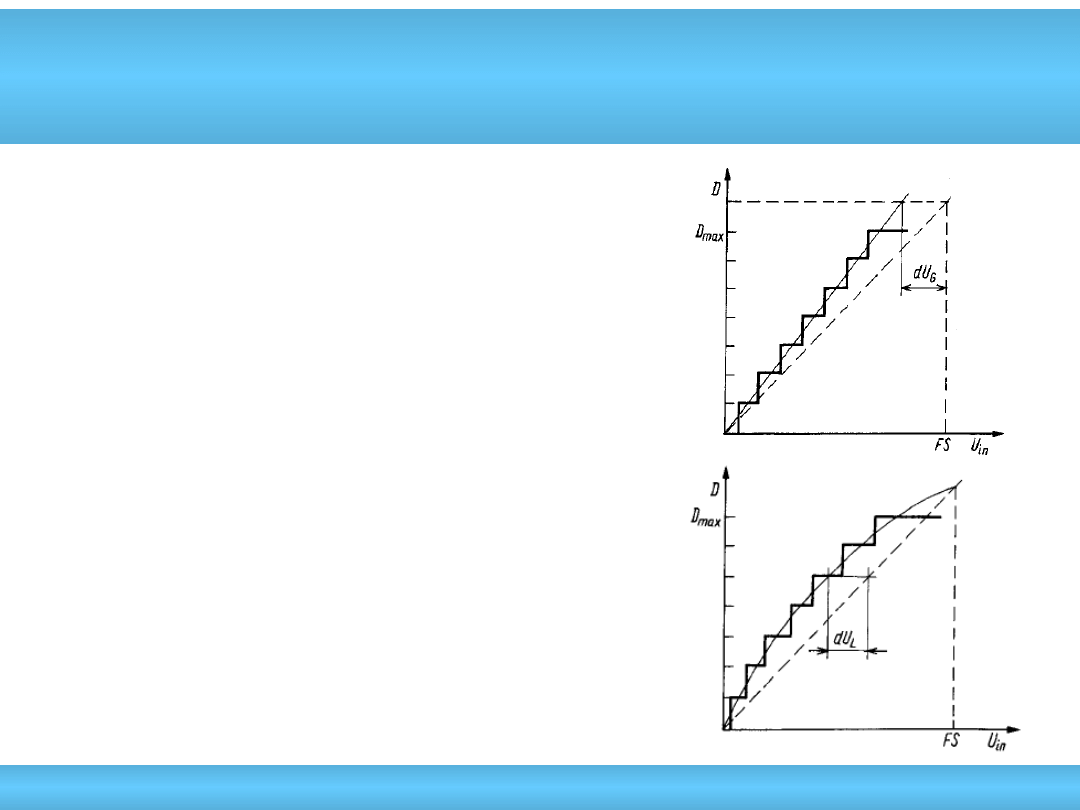
• Błąd skalowania (wzmocnienia ang.
gain error) –
różnica między przewidywaną i
ekstrapolowaną wartością rzeczywistą
sygnału analogowego

dla pełnego

zakresu przetwornika

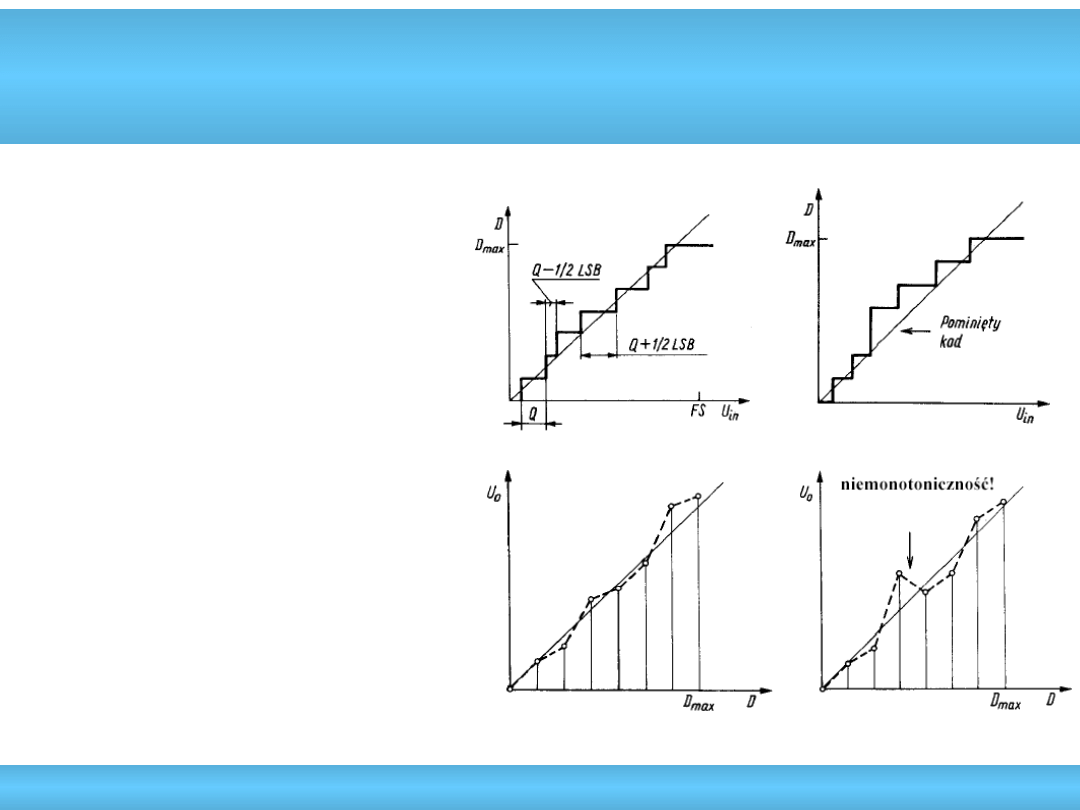
• Nieliniowość całkowa (ang. Integral
Nonlinearity - INL) – największe
odchylenie rzeczywistej charakterystyki
przetwarzania od linii prostej

Parametry statyczne

Parametry statyczne

przetworników

przetworników

Katedra Elektroniki AGH

Katedra Elektroniki AGH

• Nieliniowość
różniczkowa
(ang. Differencial
Nonlinearity – DNL ) –
charakteryzuje lokalne
odchylenia charakterystyki
od linii prostej

|DNR | < 1 LSB
błąd pominiętych kodów
(ang. No-missing codes) dla
A/C lub przetwornik
monotoniczny dla C/A

|DNR

|

> 1 LSB

przyrost liczby wejściowej D
powoduje zmniejszanie
sygnału wyjściowego
(niemonotoniczność)

A/C

C/A

Parametry dynamiczne

Parametry dynamiczne

przetworników C/A

przetworników C/A

Katedra Elektroniki AGH

Katedra Elektroniki AGH

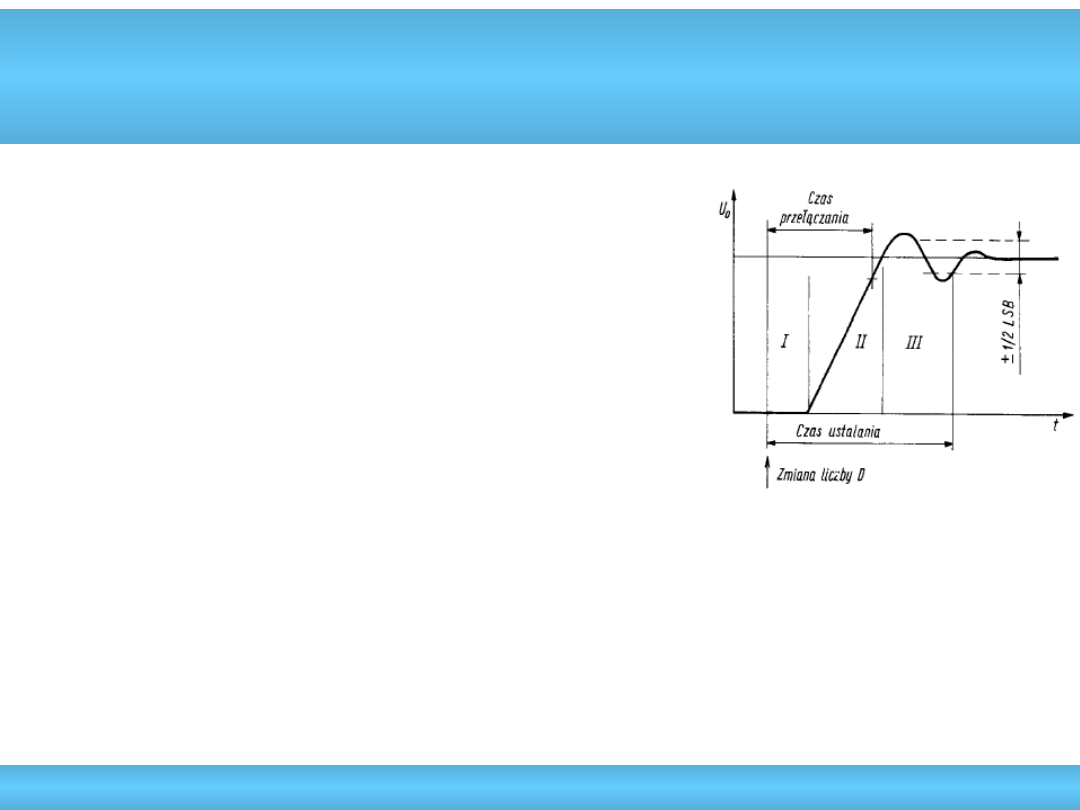
• Czas ustalania (konwersji) – czas, po
którym

sygnał wyjściowy ustali się z

dokładnością

lepszą niż 0,5LSB dla

najgorszego przypadku

zmiany liczby

wejściowej (0FS)

• Czas przełączania – czas zmiany napięcia
wyjściowe-

go przetwornika od wartości

początkowej do

90% zakresu zmiany

napięcia wyjściowego

• Maksymalna częstotliwość przetwarzania – maksymalna liczba konwersji na

sekundę, częstotliwość graniczna = 1/czas konwersji

• Szpilki napięcia (ang. glitch) – szpilki związane z przenikaniem przez pojemności

pasożytnicze cyfrowych sygnałów przełączających klucze analogowe

Parametry dynamiczne

Parametry dynamiczne

przetworników A/C

przetworników A/C

Katedra Elektroniki AGH

Katedra Elektroniki AGH

• Czas konwersji – czas potrzebny do jednego całkowitego przetworzenia sygnału

analogowego na wartość cyfrową z pełną specyfikowaną dokładnością

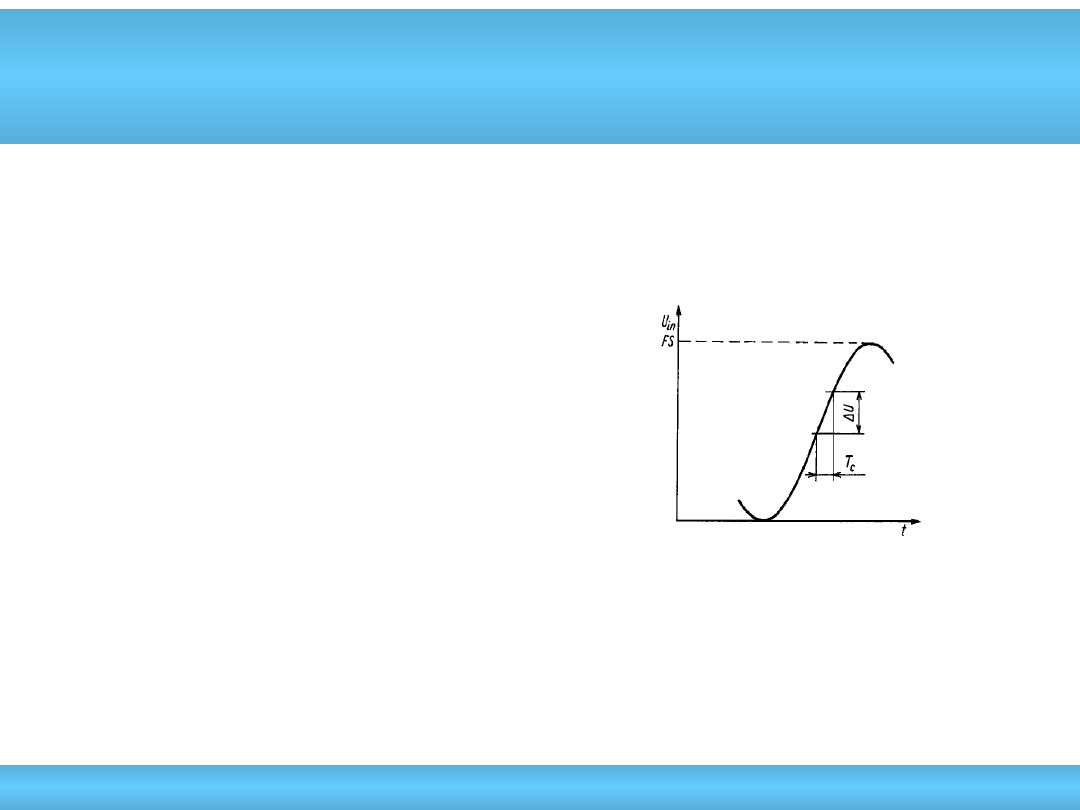
• Błąd dynamiczny przetwarzania A/C – równy
zmianie wartości sygnału wejściowego
następującej w czasie wykonywania
konwersji przez przetwornik A/C

U=2f•A•T

c

U<FS/2

N

w czasie konwersji T

c

f

max

=(2

N+1

 T

c

)

-1

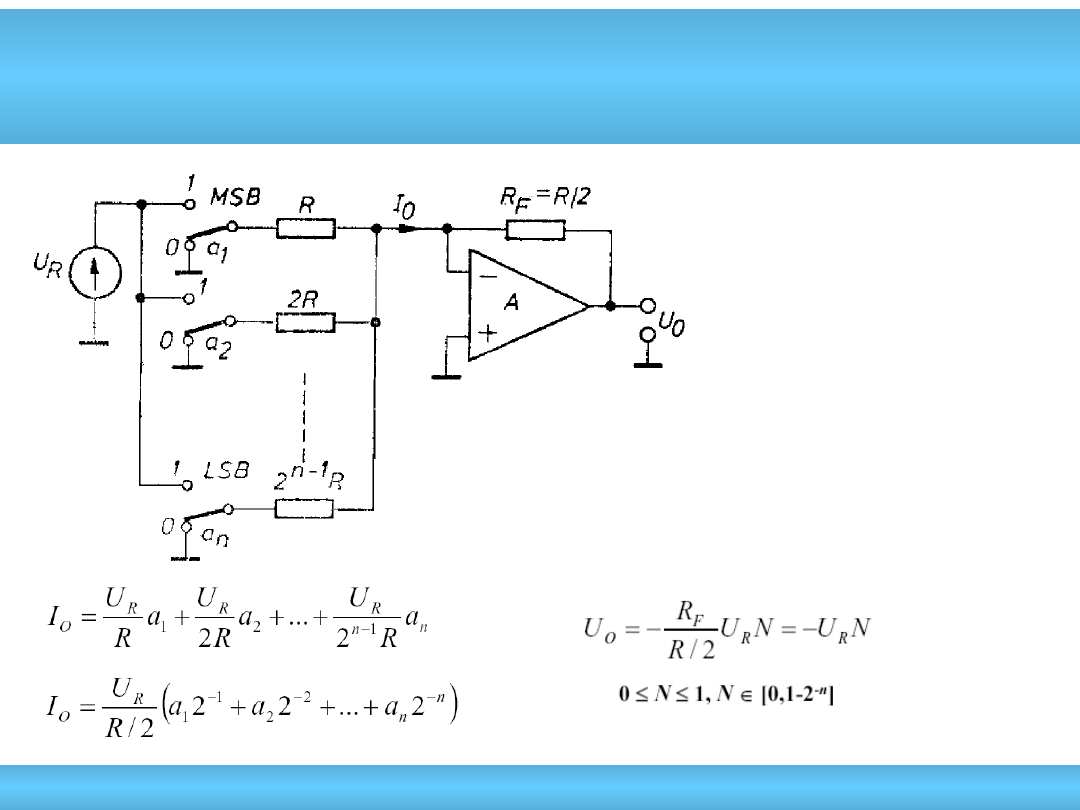
Przetwornik z siecią wagową

Przetwornik z siecią wagową

Katedra Elektroniki AGH

Katedra Elektroniki AGH

• wolny (przez
zastosowanie
wzmacniacza
operacyjnego)

• wymagane duże i
bardzo dokładne
rezystancje

• klucze analogowe
przełączają duże
napięcia

• Duże błędy DNL
Nie stosowany w
praktyce

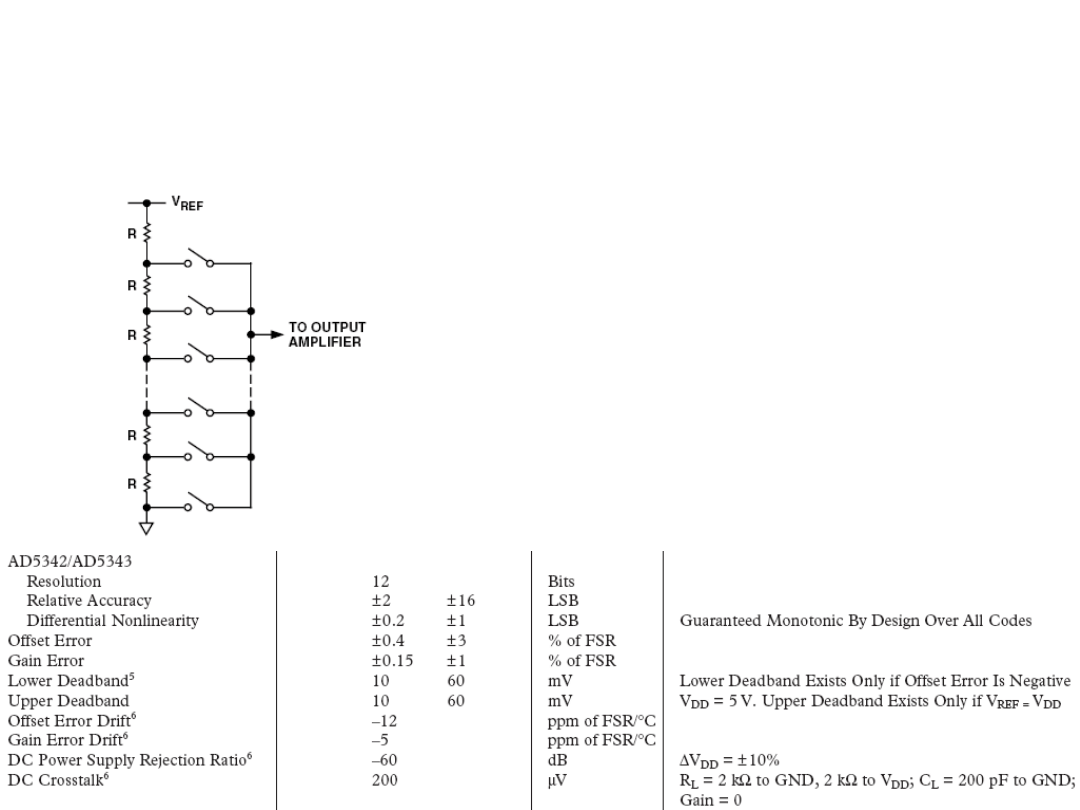
Przetwornik C/A z

łańcuchem rezystorów

(ang. Resistor String)

Zalety:

•Wymaga takich samych rezystorów

•Rezystory nie musza być bardzo dokładne

•Małe błędy statyczne

Wady:

Duża liczba użytych elementów 2

N

, dlatego N=8-

12bitów

Przykład: AD5332: Dual 8-Bit DAC

AD5343: Dual 12-Bit DAC

Typ Max

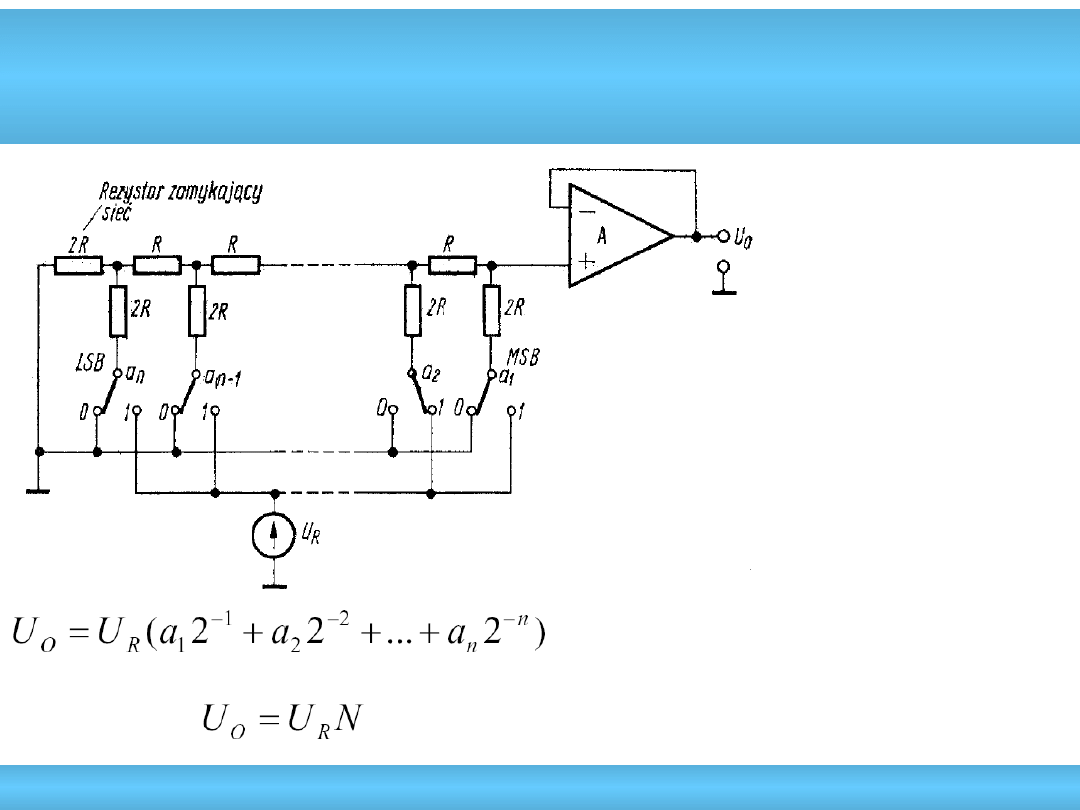
Przetwornik z drabinką R-2R

Przetwornik z drabinką R-2R

Katedra Elektroniki AGH

Katedra Elektroniki AGH

• wskazane użycie jak największych

rezystancji – kompromis
między szybkością działania
a dokładnością przetwornika

• napięcie na kluczach jest małe

• minimalny wpływ nieliniowości

kluczy na dokładność
przetwornika

• wzmacniacz operacyjny ogranicza

szybkość działania

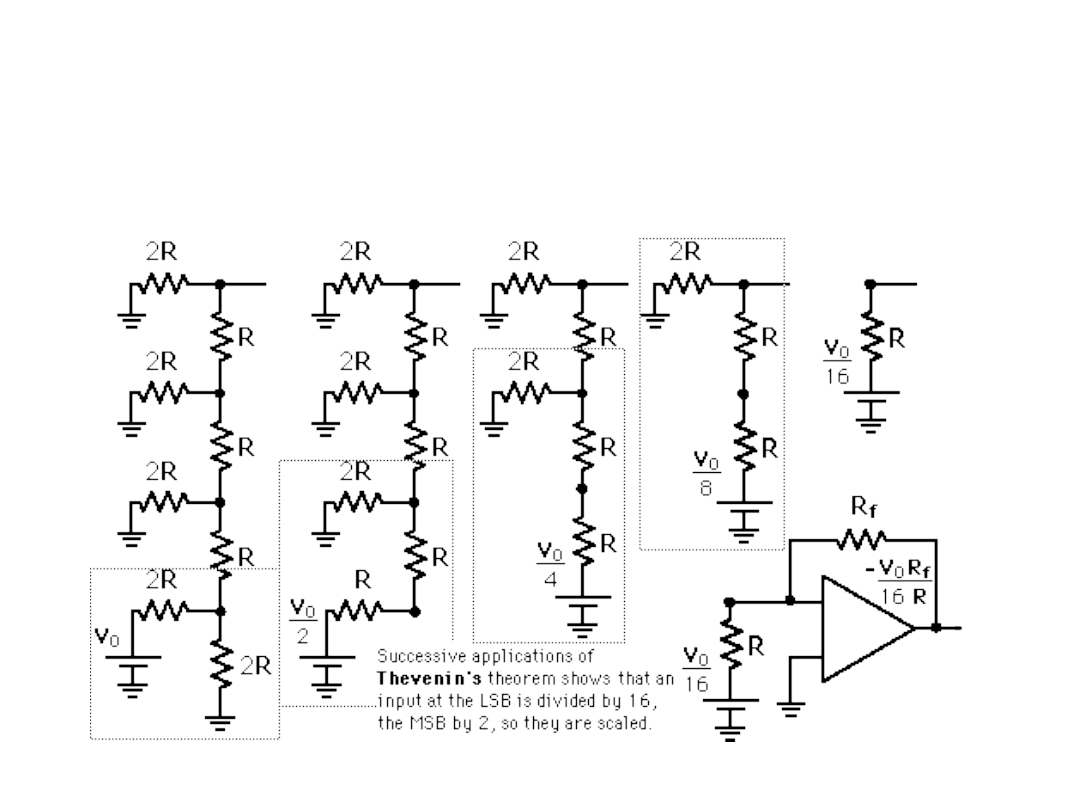
Przetwornik z drabinką R-

Przetwornik z drabinką R-

2R –

2R –

Wytłumaczenie działania

Wytłumaczenie działania

Impuls Napięcia

(ang. Glitch Impulse:

[Vps])

Impuls powstaje głównie przy zmianie najstarszego bitu,
jego przyczyną różna szybkość włączania i wyłączania się
kluczy np. w przetworniku z drabinką R-2R

0111...11

1000...00

t

ON

<t

OFF

t

ON

>t

OFF

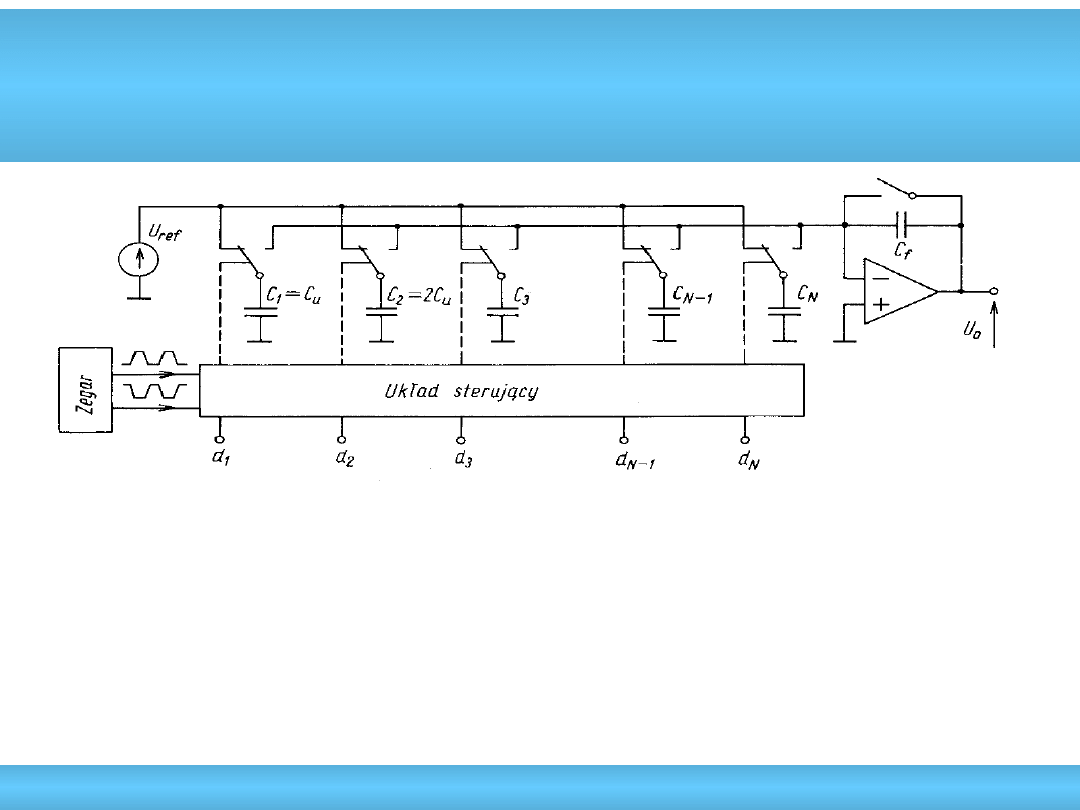
Przetwornik C/A z pojemnościami

Przetwornik C/A z pojemnościami

wagowymi

wagowymi

Katedra Elektroniki AGH

Katedra Elektroniki AGH

• dwie fazy działania przetwornika: I – ładowanie pojemności do napięcia U

ref

II – odpowiednie kondensatory łączone do wejścia wzmacniacza
operacyjnego

• szybszy niż przetwornik z siecią wagową, ograniczenie tylko szybkością

działania kluczy oraz czasem ładowania pojemności

• wada: duży zakres wartości pojemności

• pojemności pasożytnicze – rozdzielczość przetwornika 7 – 8 bitów

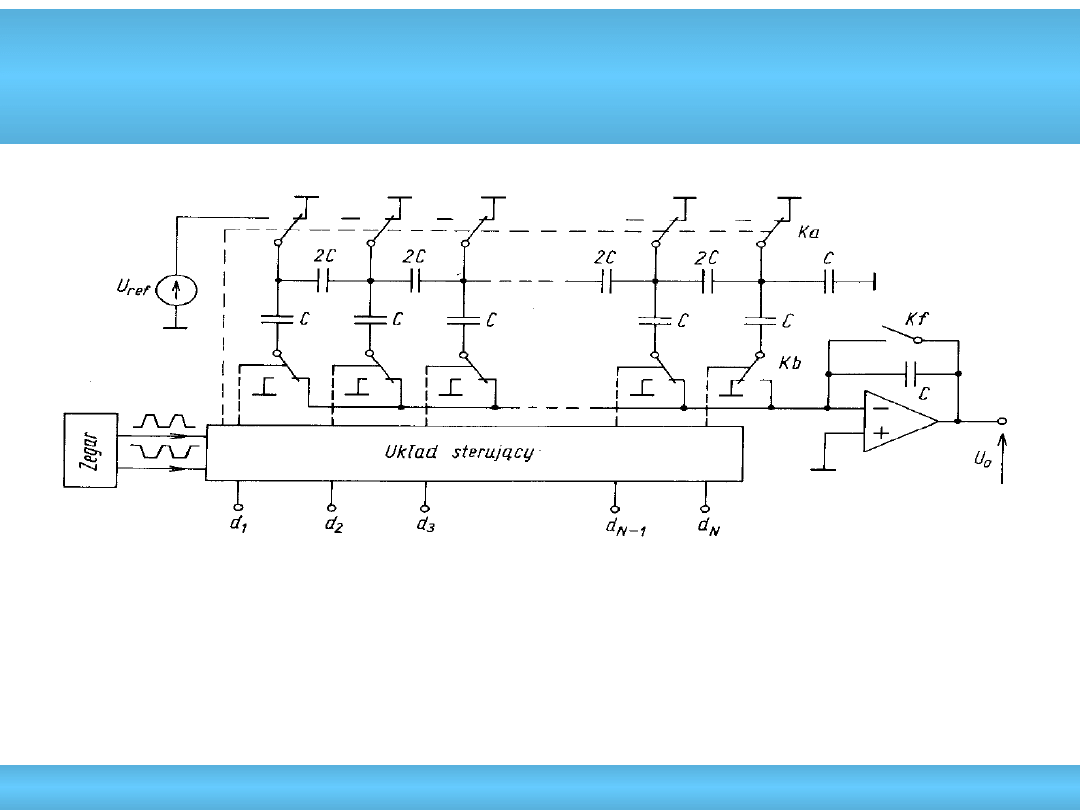
Przetwornik C/A z siecią C-2C

Przetwornik C/A z siecią C-2C

Katedra Elektroniki AGH

Katedra Elektroniki AGH

• dwie fazy działania: I – ładowanie kondensatorów (U

ref

, U

ref

/2, U

ref

/4, ...)

II – Kf zamknięty (rozładowuje C), Ka – złączenie górnych węzłów
do masy, Kb – dołączenie odpowiednich kondensatorów do WO

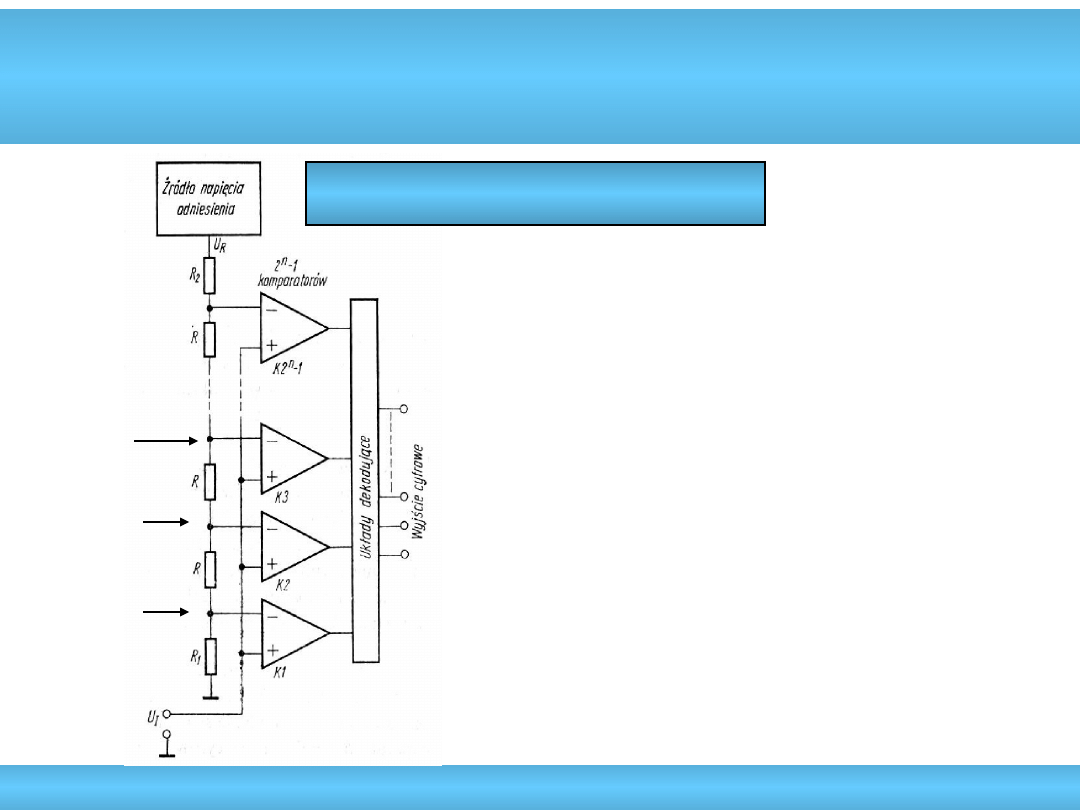
A/C bezpośredniego porównania

A/C bezpośredniego porównania

Katedra Elektroniki AGH

Katedra Elektroniki AGH

Równoległe (flash)

Równoległe (flash)

• najszybsze przetworniki A/C
• ograniczona rozdzielczość (max. 12 bit)
• czas konwersji <1ns dla układów z

tranzystorami MESFET

• częstotliwość: 20-500MHz
• komparatory ograniczają szybkość

i dokładność przetwarzania

• wzrost poboru mocy (0,25-7,5W)
• skomplikowany dekoder
• trudności w doborze dzielnika

R

1

= R/2

(zero=
1/2LSB

2.5 LSB

1.5 LSB

0.5 LSB

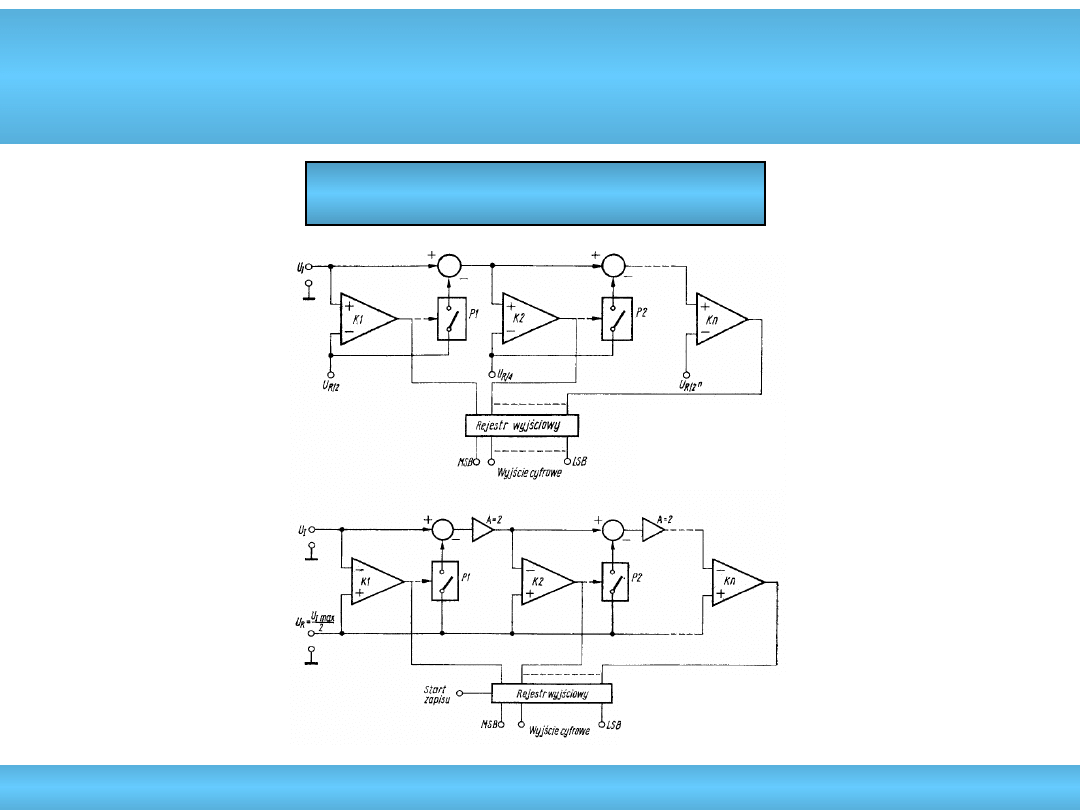
A/C bezpośredniego porównania

A/C bezpośredniego porównania

Katedra Elektroniki AGH

Katedra Elektroniki AGH

Szeregowe

Szeregowe

wagowy

z podwajaniem

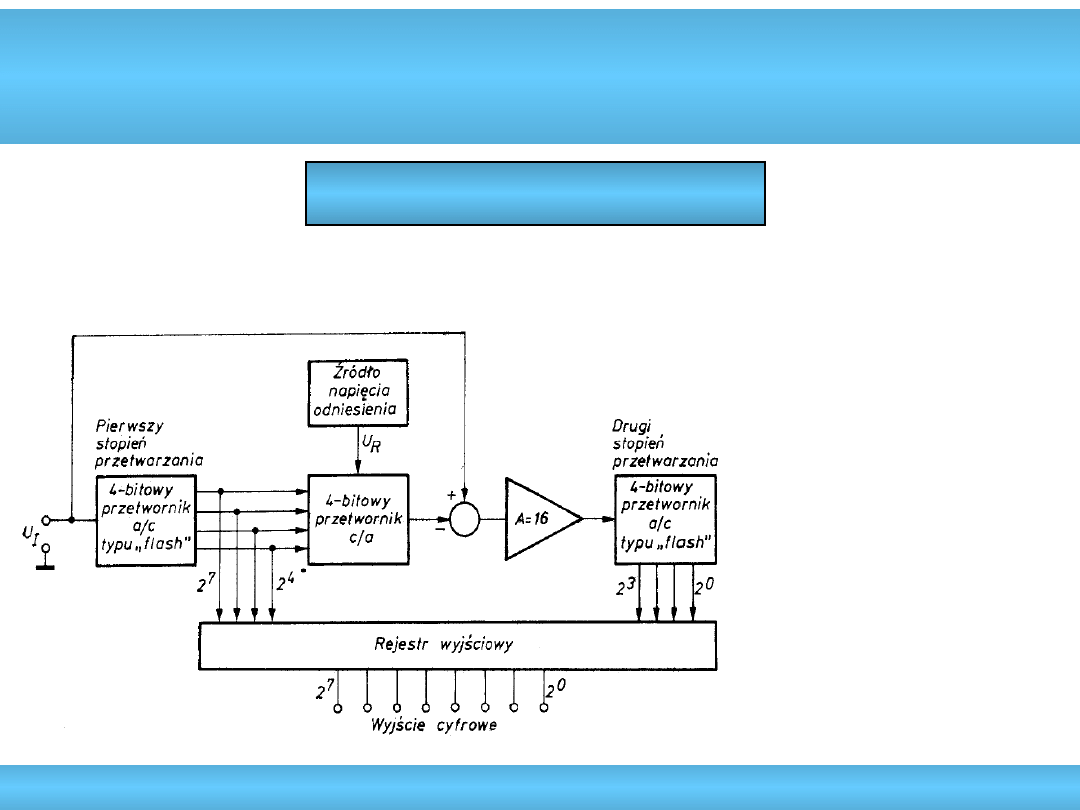
A/C bezpośredniego porównania

A/C bezpośredniego porównania

Katedra Elektroniki AGH

Katedra Elektroniki AGH

Szeregowo-równoległe

Szeregowo-równoległe

• 8-16 bitów
• częstotliwość: 0,2-40MHz
• moc strat: 0,04-20W

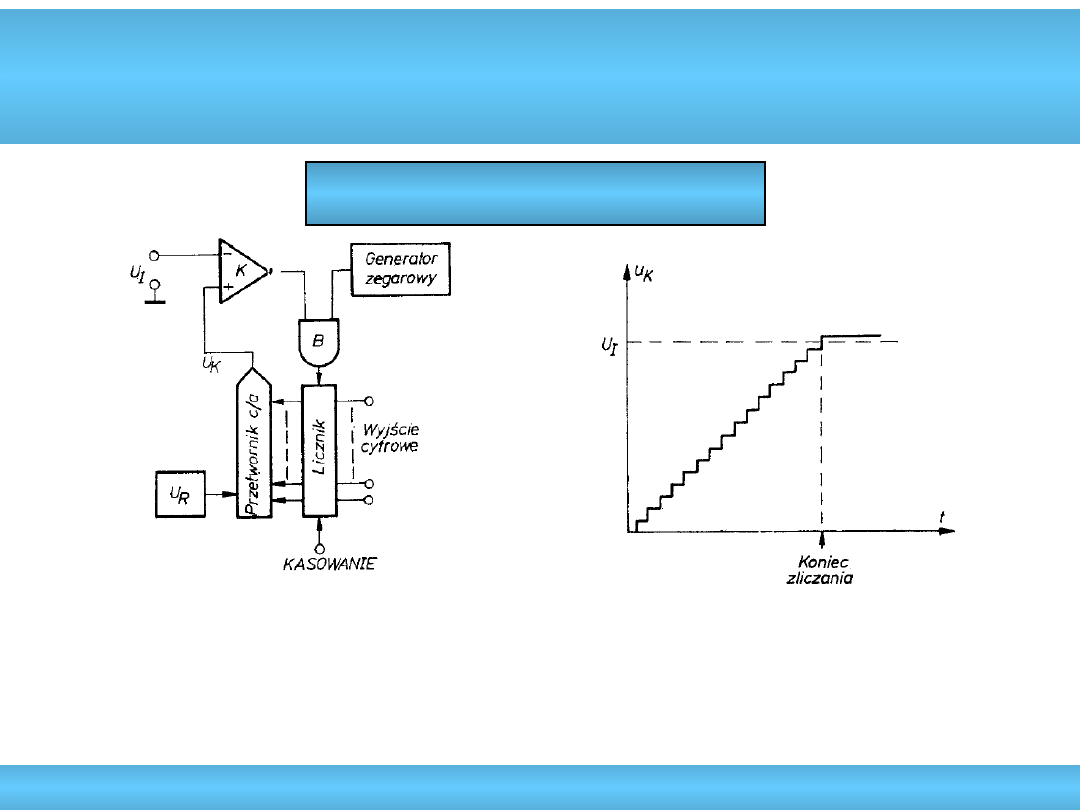
Kompensacyjne przetworniki A/C

Kompensacyjne przetworniki A/C

Katedra Elektroniki AGH

Katedra Elektroniki AGH

Kompensacja równomierna

Kompensacja równomierna

• oparty na zasadzie zliczania impulsów zegara
• długi czas przetwarzania (max. 2

n

t

c

)

• rzadko stosowany

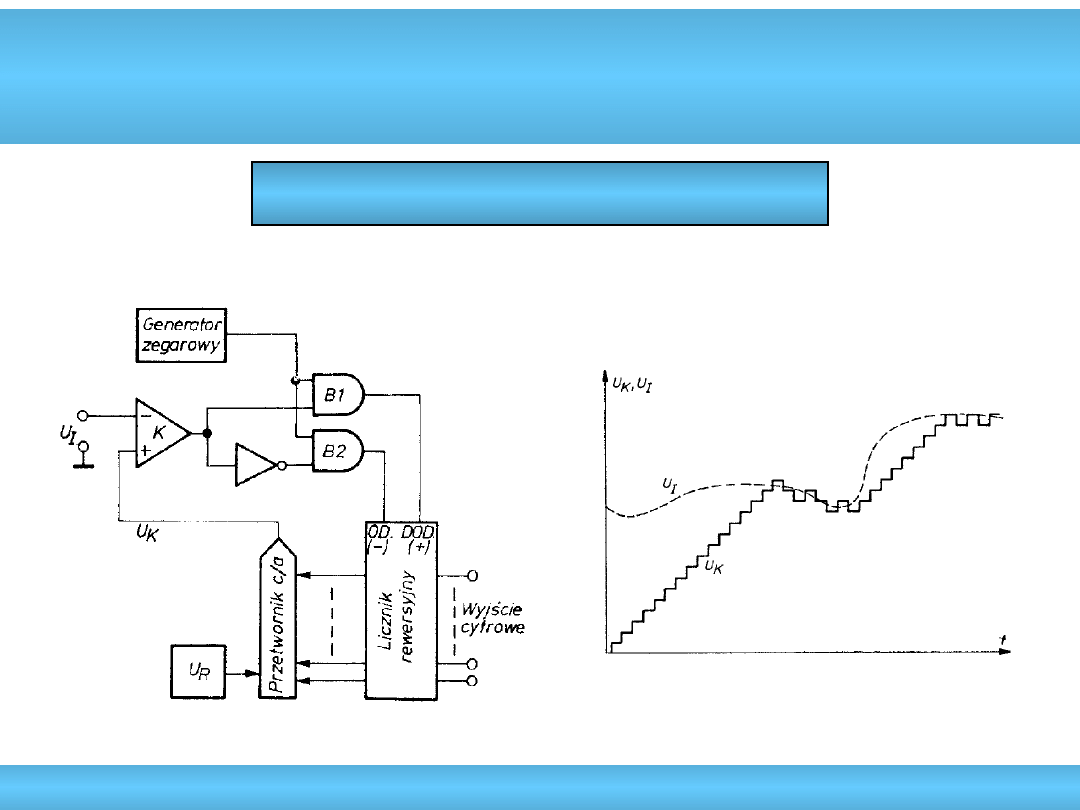
Kompensacyjne przetworniki A/C

Kompensacyjne przetworniki A/C

Katedra Elektroniki AGH

Katedra Elektroniki AGH

Kompensacja równomierna - nadążny

Kompensacja równomierna - nadążny

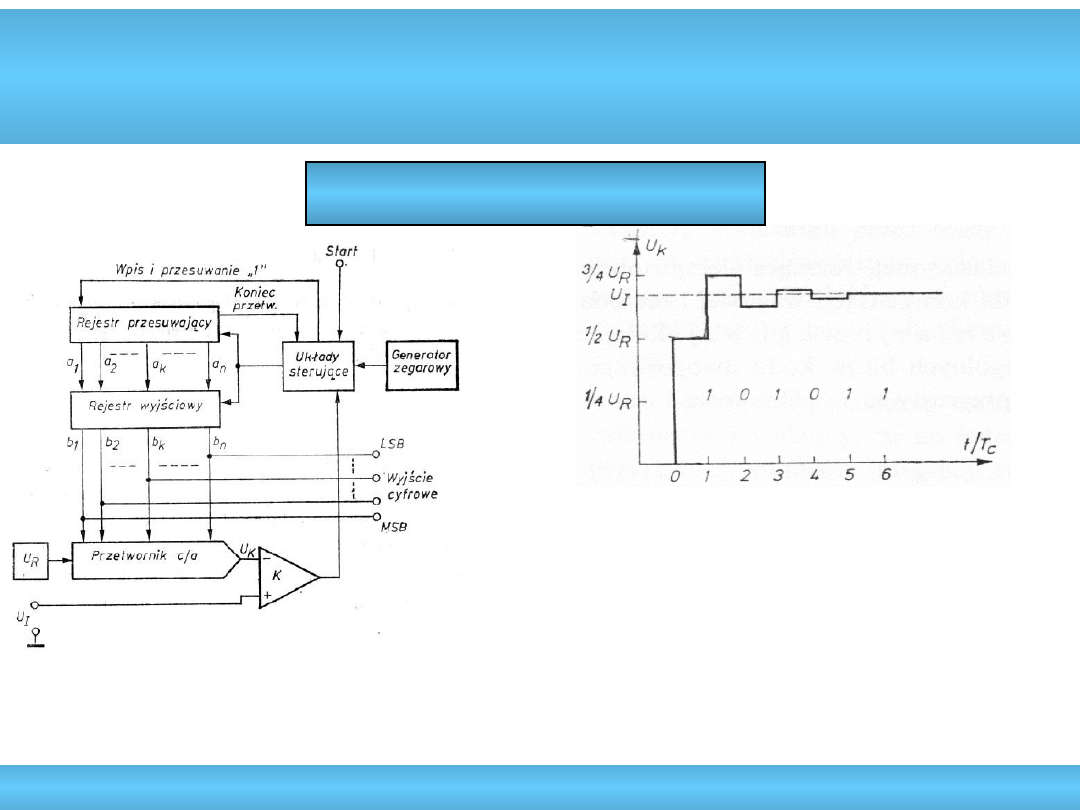
Kompensacyjne przetworniki A/C

Kompensacyjne przetworniki A/C

Katedra Elektroniki AGH

Katedra Elektroniki AGH

Kompensacja wagowa

Kompensacja wagowa

• krótki czas przetwarzania (nt

c

)

• duża nieliniowość różniczkowa C/A

• łatwy do realizacji w układach monolitycznych

• rozdzielczość 8-16 bitów

• przetwornik C/A z drabinką R-2R

• 5-10MSPS przy rozdzielczości 10-12bitów

• moc strat: 15mW-1W

Metody Czasowo-

Częstotliwościowe

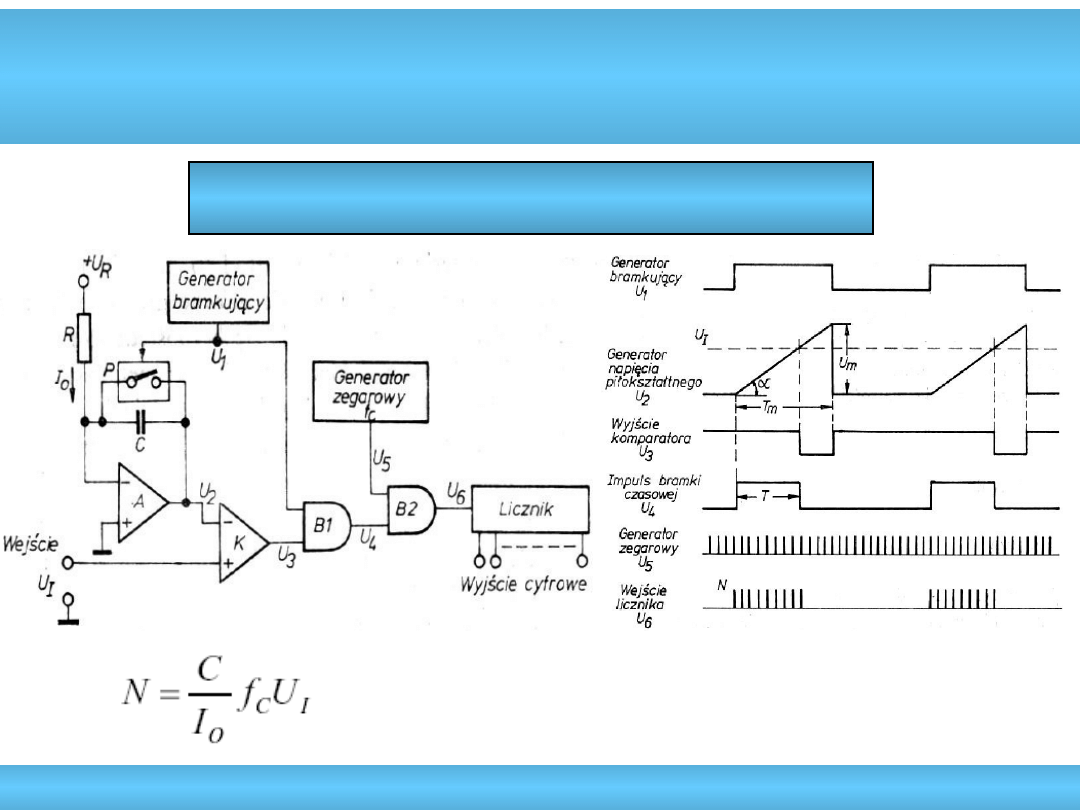
Metoda czasowa A/C

Metoda czasowa A/C

Katedra Elektroniki AGH

Katedra Elektroniki AGH

Czasowa prosta = Całkowanie pojedyncze

Czasowa prosta = Całkowanie pojedyncze

• niska dokładność (0,1%)

Metoda czasowa A/C

Metoda czasowa A/C

Katedra Elektroniki AGH

Katedra Elektroniki AGH

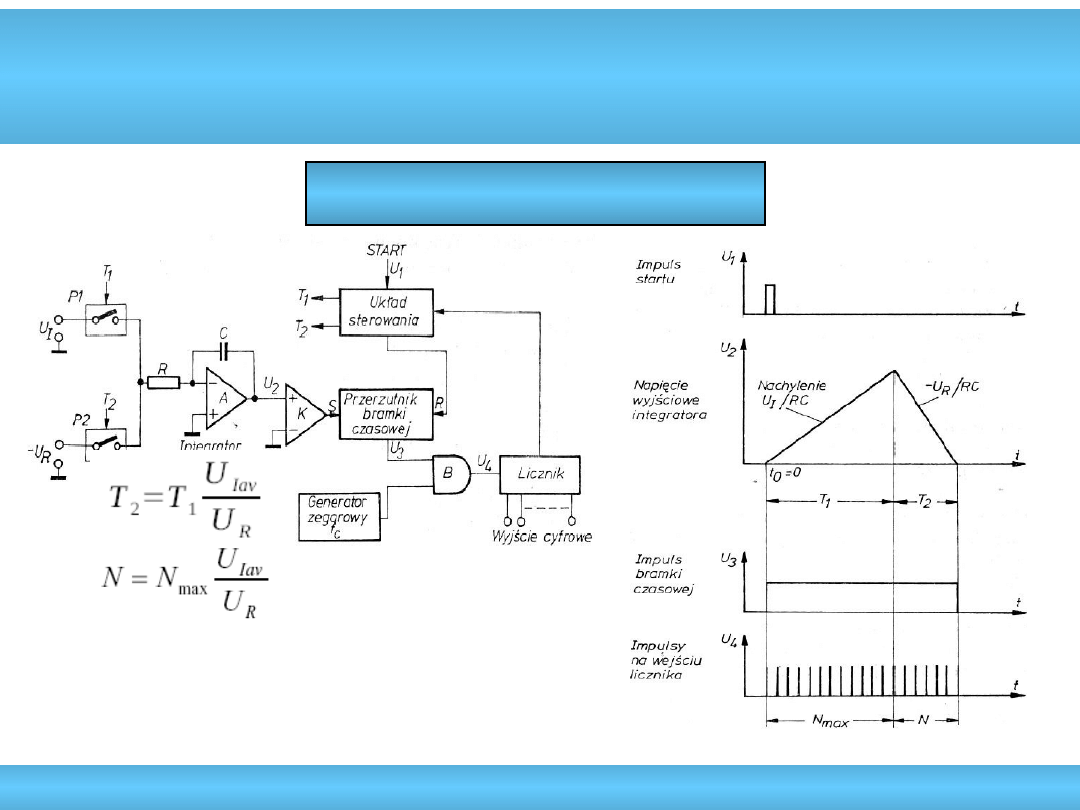
Podwójne całkowanie

Podwójne całkowanie

• duża rozdzielczość: 12-26 bitów

• duża dokładność (0,01%)
• duży czas przetwarzania: 20ms-1s (T

1

wielokrotność 20ms)

• mała moc strat: 0,6-450mW

Metoda częstotliwościowa

Metoda częstotliwościowa

Katedra Elektroniki AGH

Katedra Elektroniki AGH

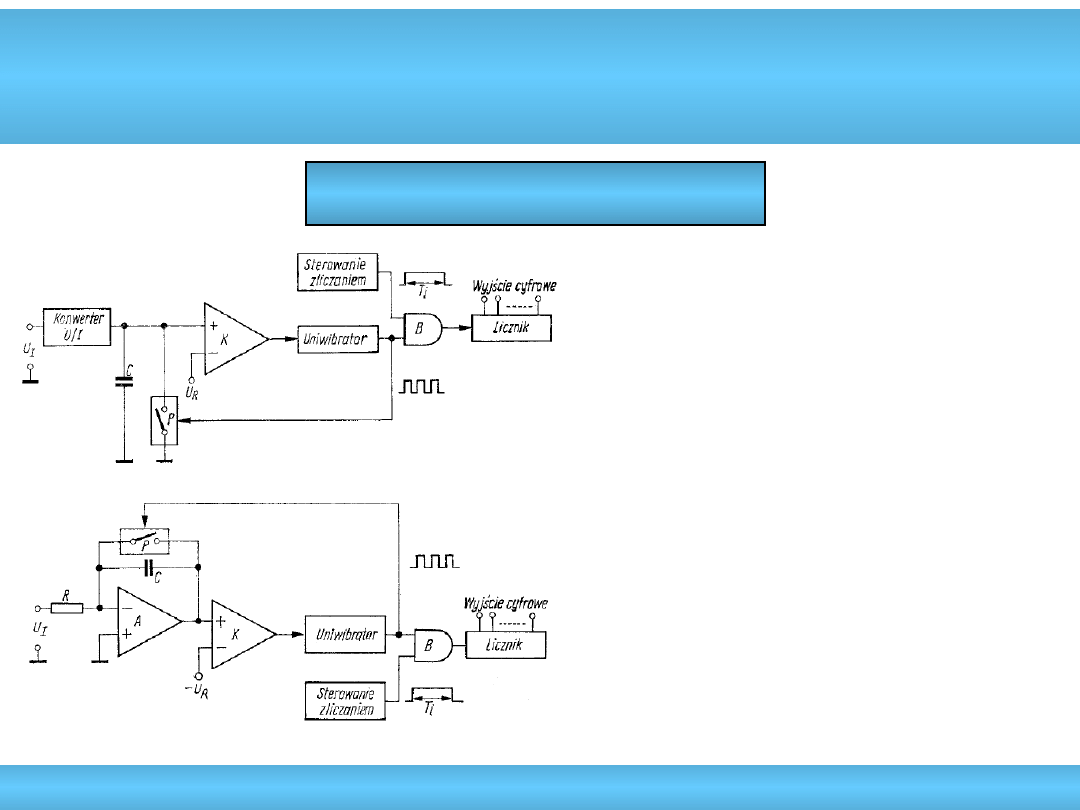
Prosta

Prosta

• napięcie wejściowe zmieniane

na impulsy o częstotliwości
proporcjonalnej do wartości
tego napięcia

• mała dokładność (ok.1%)
• rzadko stosowane

C/A Modulacja Szerokości Impulsu

C/A Modulacja Szerokości Impulsu

(ang. Pulse-Width Modulation -

(ang. Pulse-Width Modulation -

PWM)

PWM)

Katedra Elektroniki AGH

Katedra Elektroniki AGH

•

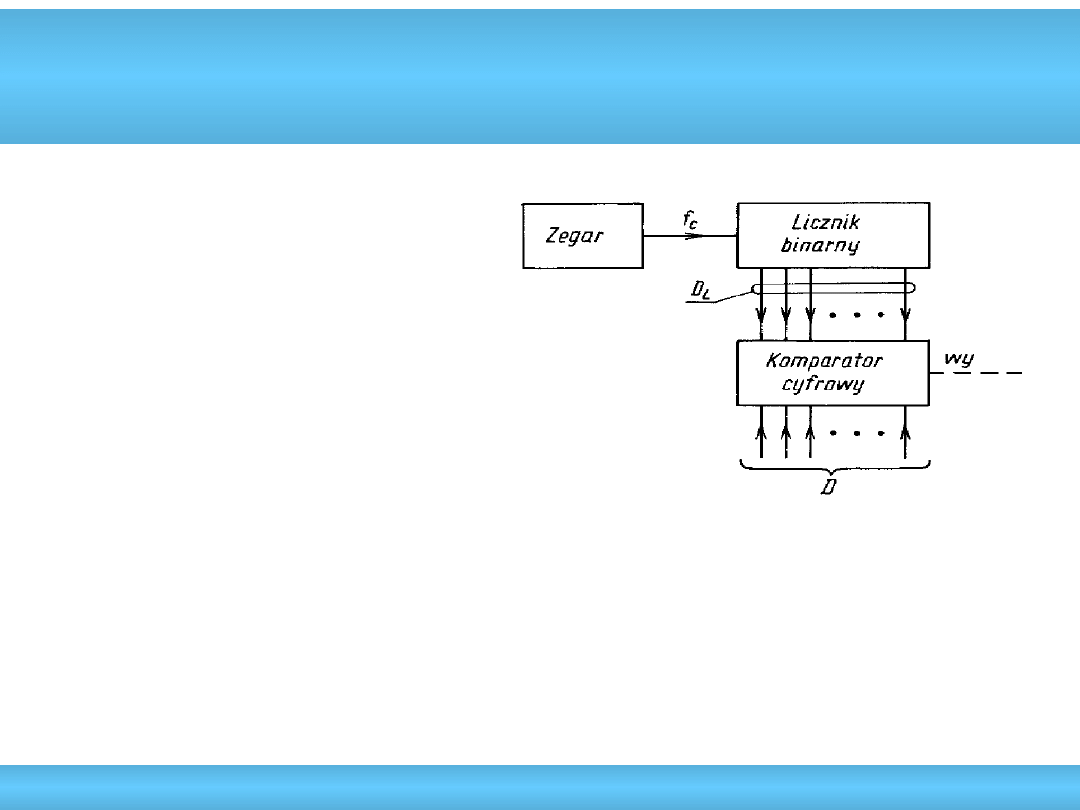
wielkość cyfrowa

przetwarzana na ciąg
impulsów o stałej amplitudzie
i o współczynniku wypełnienia
proporcjonalnym do słowa cyfrowego

• relatywnie długi czas konwersji 2

N

/f

clk

• możliwość uzyskania bardzo dużej rozdzielczości

• monotoniczne

• niewielka nieliniowość różniczkowa

•konieczność stosowania dobrego filtru dolnoprzepustowego na
wyjściu – dlatego przetwornik ten ma głównie znaczenie teoretyczne
lub też tam gdzie nie trzeba stosować filtru, np. do sterowania
jasnością diód LED

U

o

= U

ref

D/2

N

Przykład:
Częstotliwość przetwornika f

ADC

=100kHz, N=16, f

clk

= 65MHz

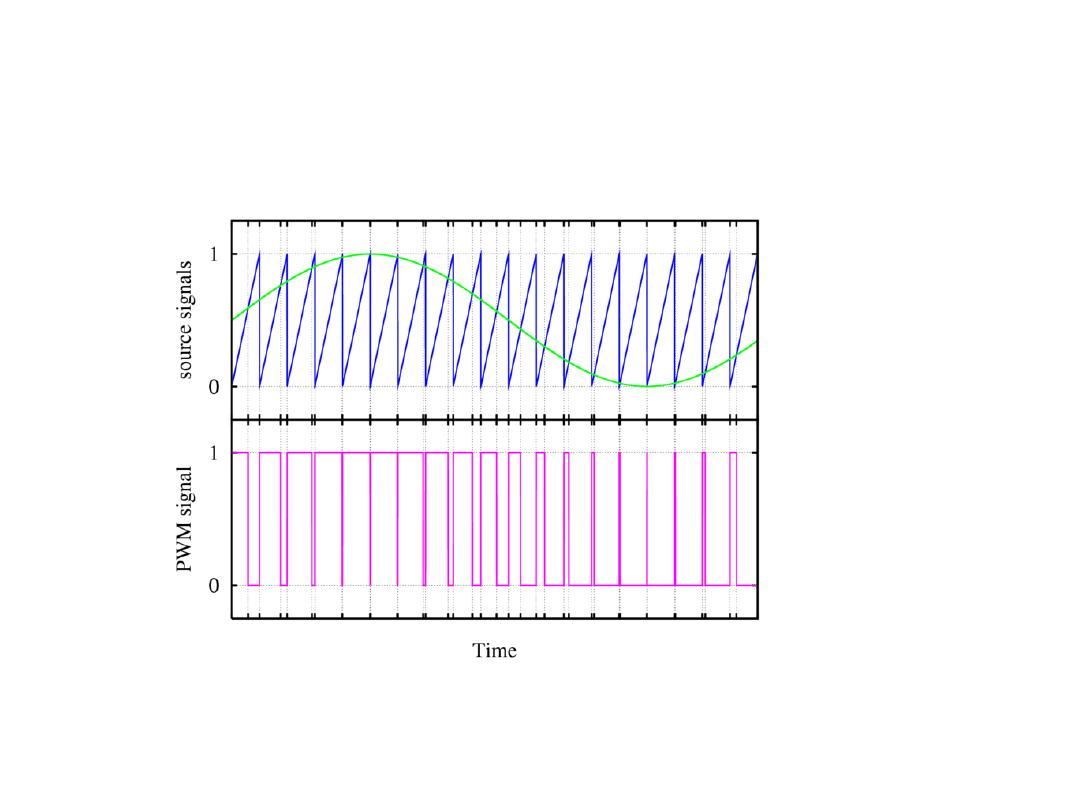
Pulse-Width Modulation - PWM

Pulse-Width Modulation - PWM

Przetwornik D/A 1-bitowy

przykład obrazu

Oryginał

Nieoptymalne

Optymalne

podobnie jak PWM

Delta-

Sigma

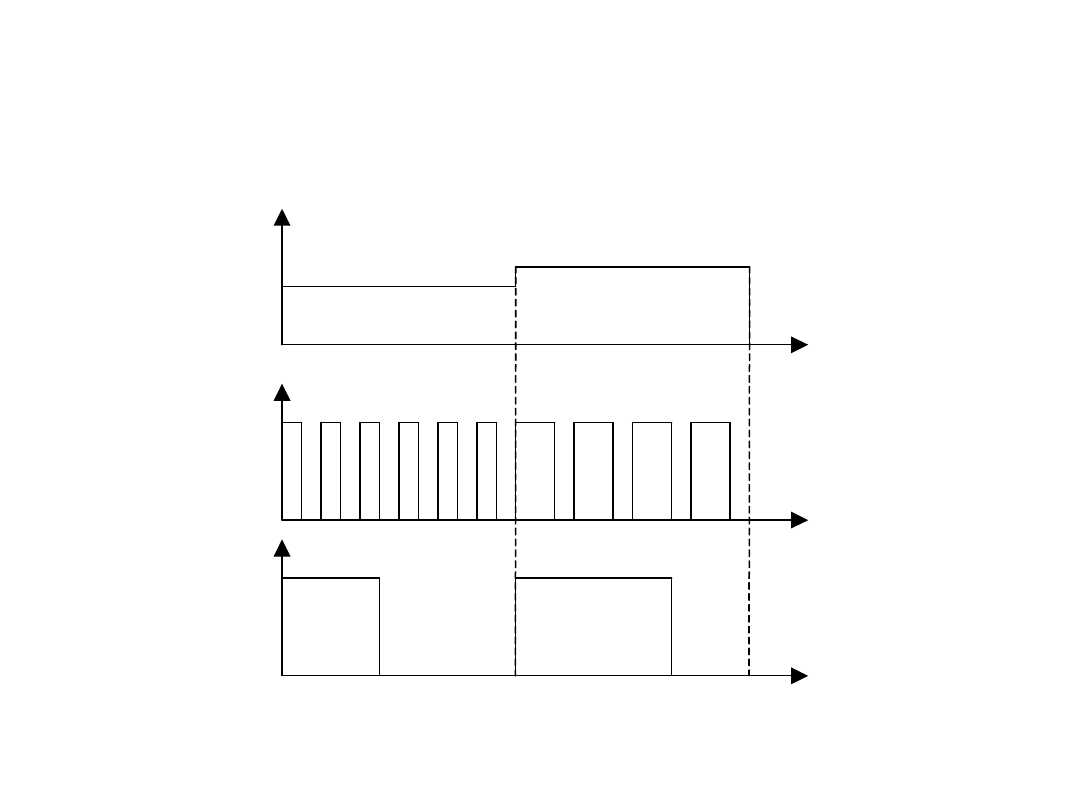
PWM a Sigma-Delta

V

in

Signa-Delta

PWM

Wypełnienie
= V

in

/V

FS

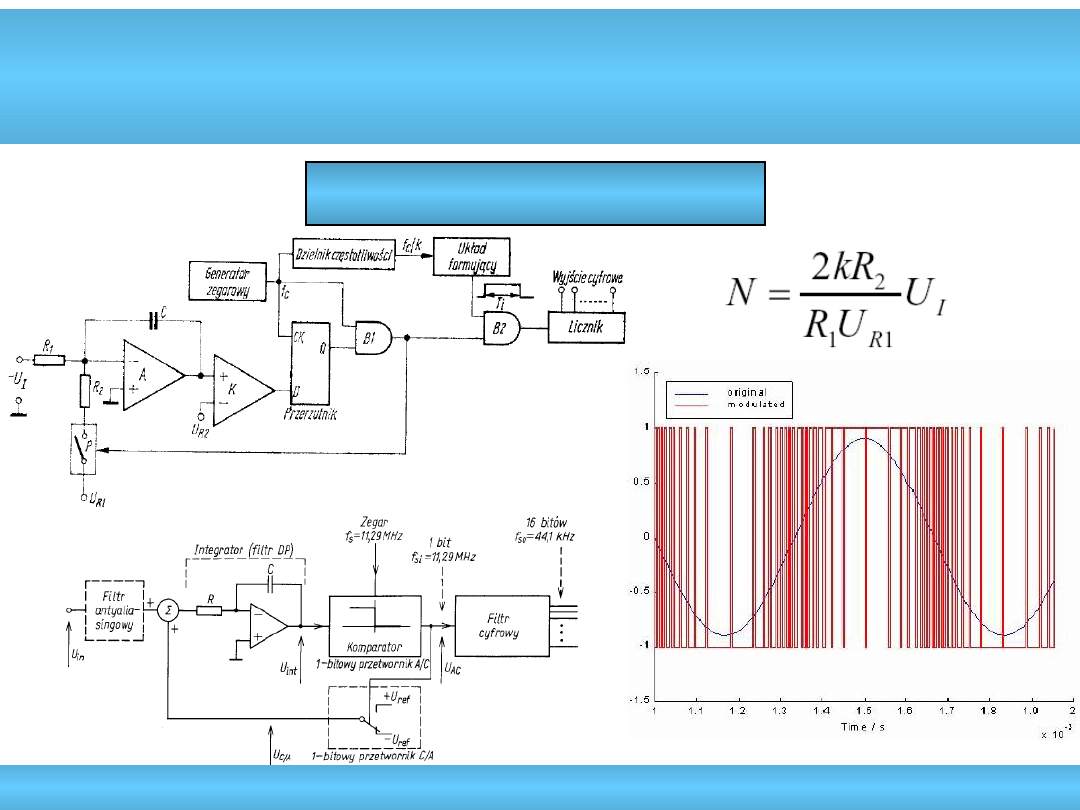
Metoda częstotliwościowa

Metoda częstotliwościowa

Katedra Elektroniki AGH

Katedra Elektroniki AGH

Delta sigma A/C

Delta sigma A/C

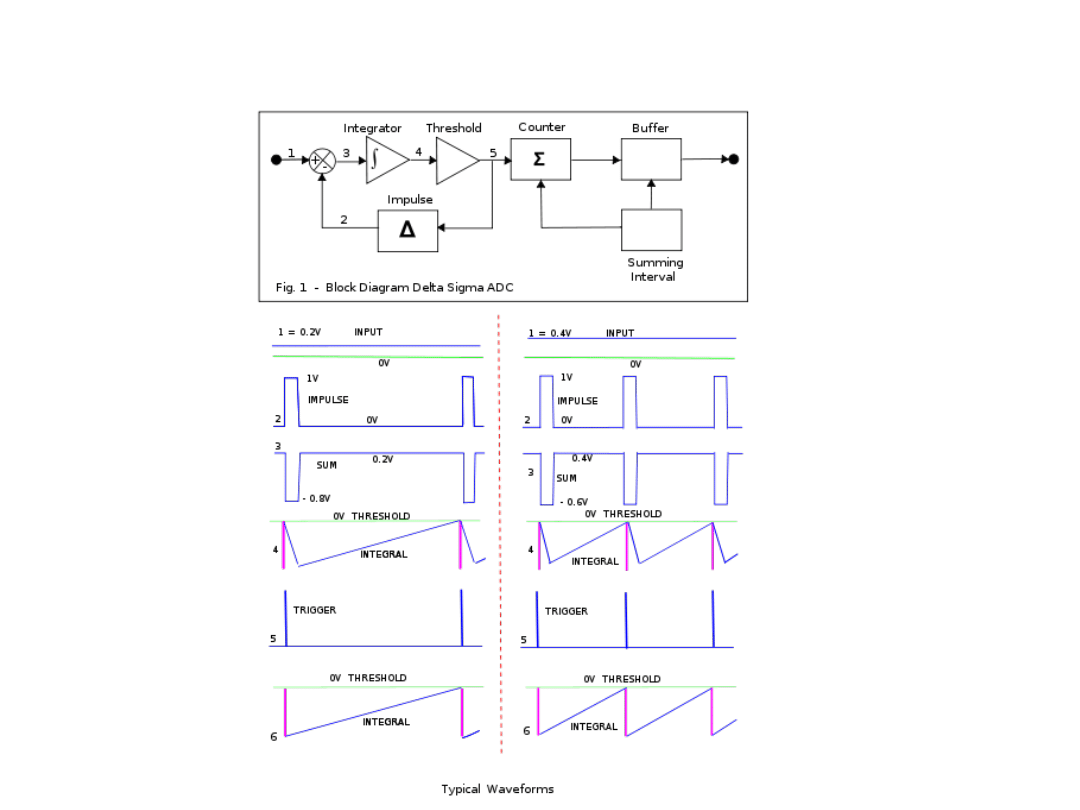
Delta-Sigma A/C c.d.

http://en.wikipedia
.org/wiki/Sigma_d
elta

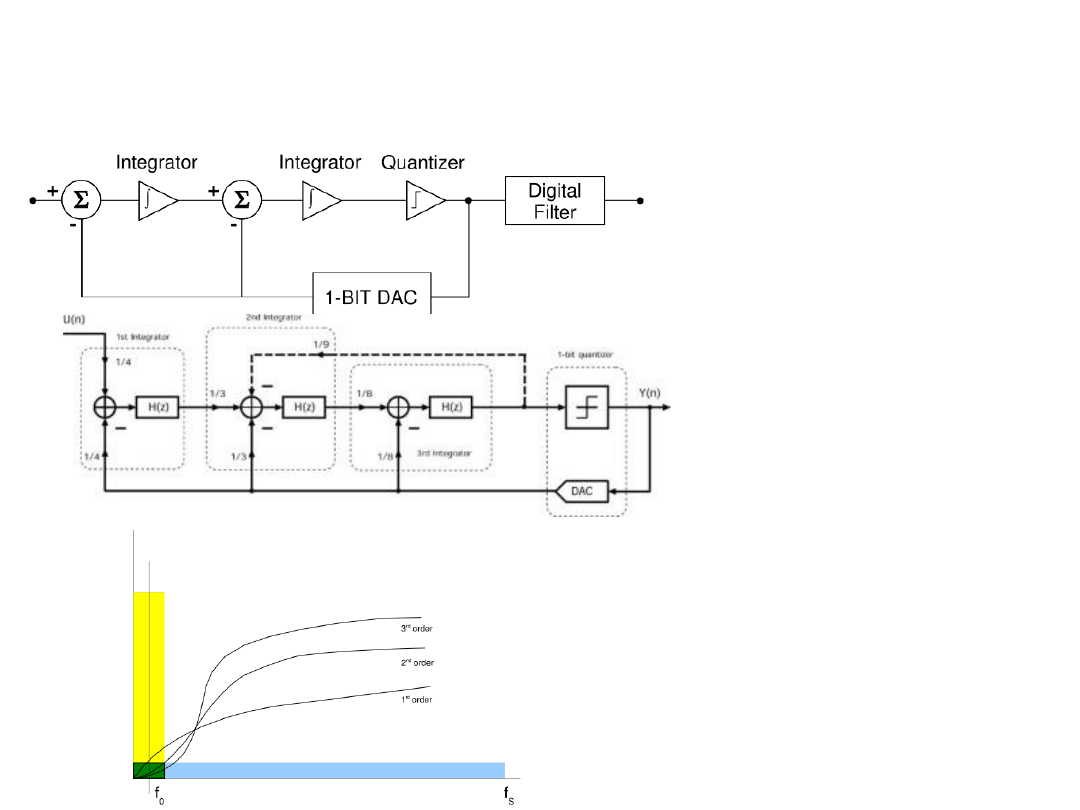
Delta-Sigma wyższego

rzędu

2-gi
rząd

3-rząd

Szumy dla różnych
częstotliwości

Nadpróbkowanie

http://en.wikipedia.org/wiki/Oversamplin
g

Możliwe jest uzyskanie większej rozdzielczości bitowej poprzez
nadpróbkowanie (próbkowanie z większą częstotliwością niż
częstotliwość Nynquist’a.

N= ½ log

2

(n)

N – dodatkowa rozdzielczość bitowa
n – współczynnik nadpróbkowania

Przykład: n= 4  N=1; n=16  N=2
Założenie to wynika z błędu standardowego który maleje
odwrotnie proporcjonalnie z pierwiastkiem liczby pomiarów
(założenie braku korelacji)