Konstrukcja modelu
Konstrukcja modelu
ekonometrycznego i estymacja
ekonometrycznego i estymacja
parametrów modelu
parametrów modelu
ekonometrycznego
ekonometrycznego
1.
1.
Wybór postaci analitycznej
Wybór postaci analitycznej
2.
2.
Estymacja - Metoda
Estymacja - Metoda
najmniejszych kwadratów
najmniejszych kwadratów
Dr Krystyna Melich-
Iwanek
Katedra Ekonometrii
melich@ue.katowice.
pl
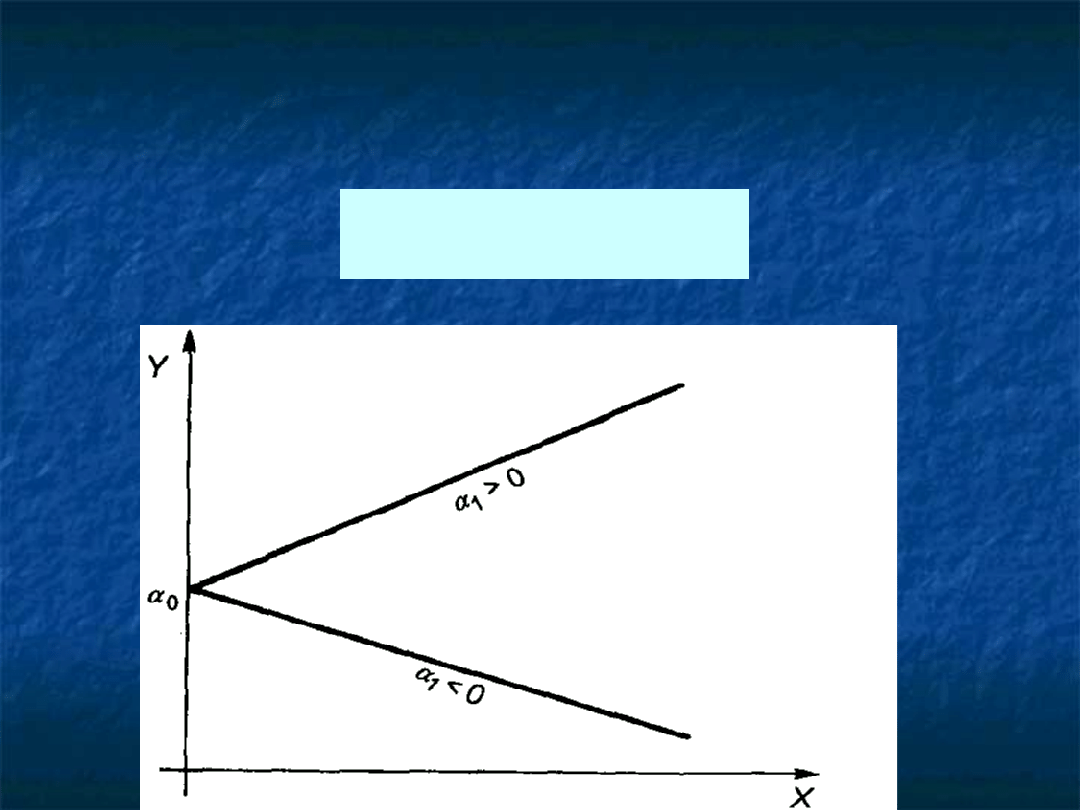
Postać analityczna równania -
Postać analityczna równania -
FUNKCJA LINIOWA
FUNKCJA LINIOWA
yt
0
α
X
1
α
Y
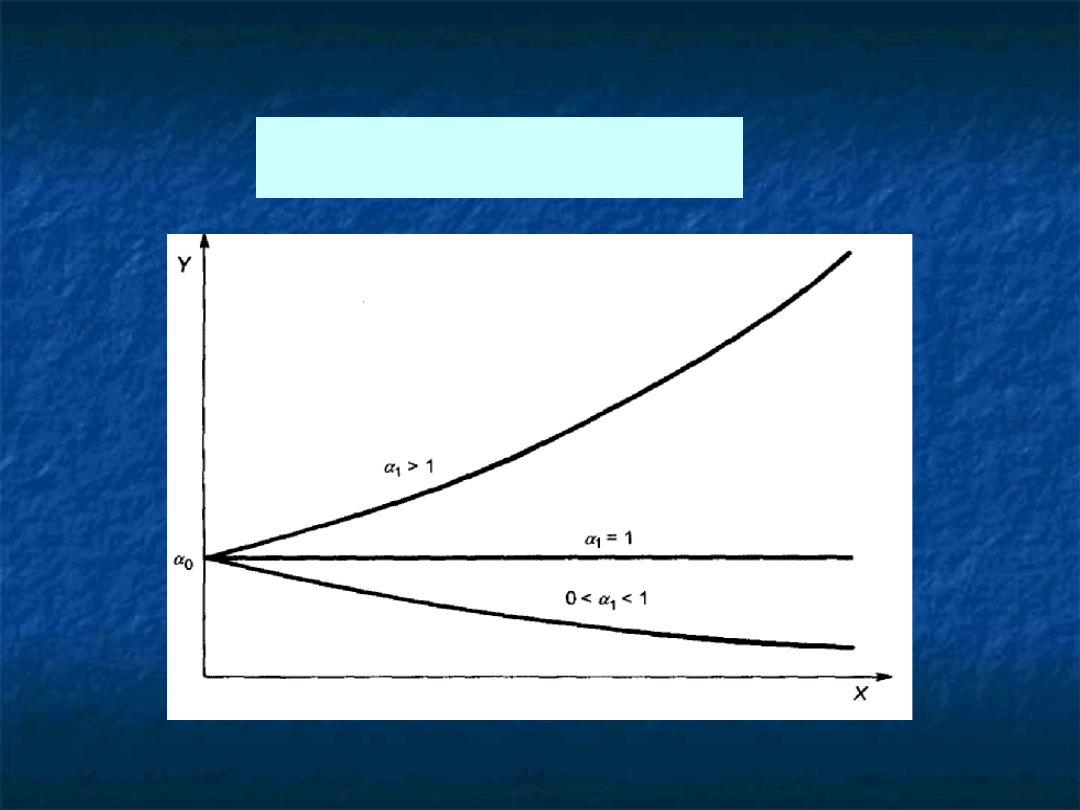
FUNKCJA WYKŁADNICZA
FUNKCJA WYKŁADNICZA
0
1
α
X
1
α
0
α
Y
,
•a
o
, podobnie jak w przypadku funkcji
liniowej, interpretowany jest jako poziom
zmiennej endogenicznej Y, gdy zmienna
objaśniająca X przyjmuje wartość zero.
•a
l
nazywane jest stopą wzrostu, tzn. wzrost
wartości zmiennej objaśniającej X o
jednostkę powoduje zmianę poziomu
zmiennej objaśnianej Y o (a
l
- 1) 100%.
(większe od jedności wartości a
l
oznaczają
wzrost wartości zmiennej objaśnianej)
Inne postacie funkcji
wykładniczej
,
X
1
α
0
α
Y
e
,
X
1
α
0
α
Y
10
Funkcja jest
rosnąca
,
gdy
1
Funkcja jest
malejąca
,
gdy
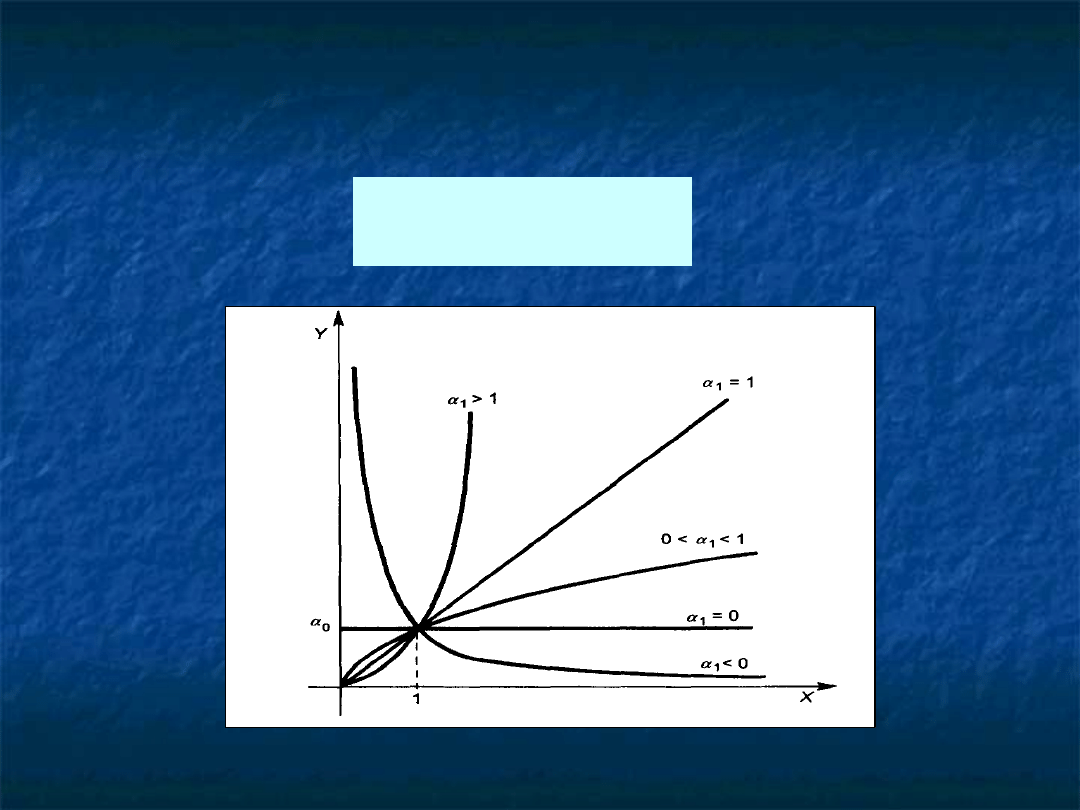
FUNKCJA POTĘGOWA
FUNKCJA POTĘGOWA
1
α
0
X
α
Y
to wartość zmiennej Y,
gdy X=1
1
to elastyczność zmiennej
Y względem zmiennej X i
oznacza w przybliżeniu
procentową zmianę Y
spowodowaną zmiana X o
1%
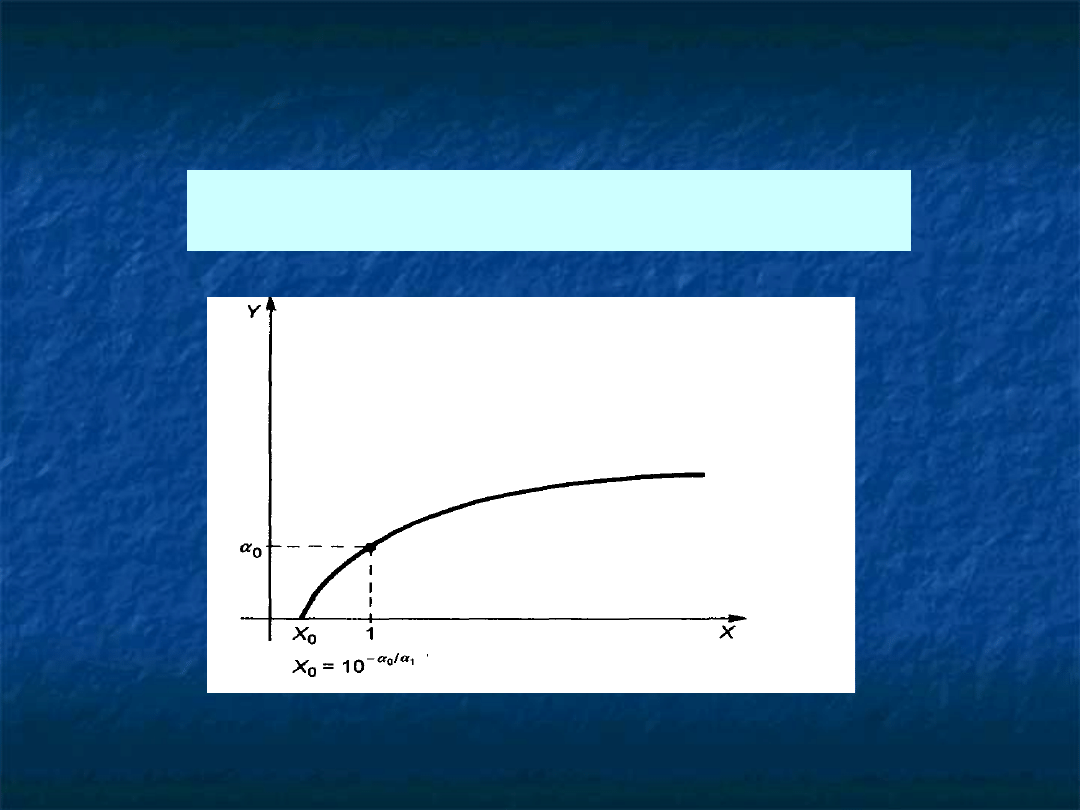
FUNKCJA LOGARYTMICZNA
FUNKCJA LOGARYTMICZNA
0
0
1
0
1
0
α
α
logX,
α
α
Y
,
to wartość zmiennej Y, gdy X=1
ESTYMACJA MODELI EKONOMETRYCZNYCH
ESTYMACJA MODELI EKONOMETRYCZNYCH
METODA NAJMNIEJSZYCH KWADRATÓW (MNK)
METODA NAJMNIEJSZYCH KWADRATÓW (MNK)
MNK – POLEGA NA ZNAJDOWANIU TAKICH
WARTOŚCI OCEN PARAMETRÓW
STRUKTURALNYCH MODELU, BY SUMA
KWADRATÓW ODCHYLEŃ ZAOBSERWOWANYCH
(EMPIRYCZNYCH) WARTOŚCI ZMIENNEJ Y
t
OD JEJ
WARTOŚCI TEORETYCZNYCH WYZNACZONYCH
PRZEZ MODEL BYŁA NAJMNIEJSZA.
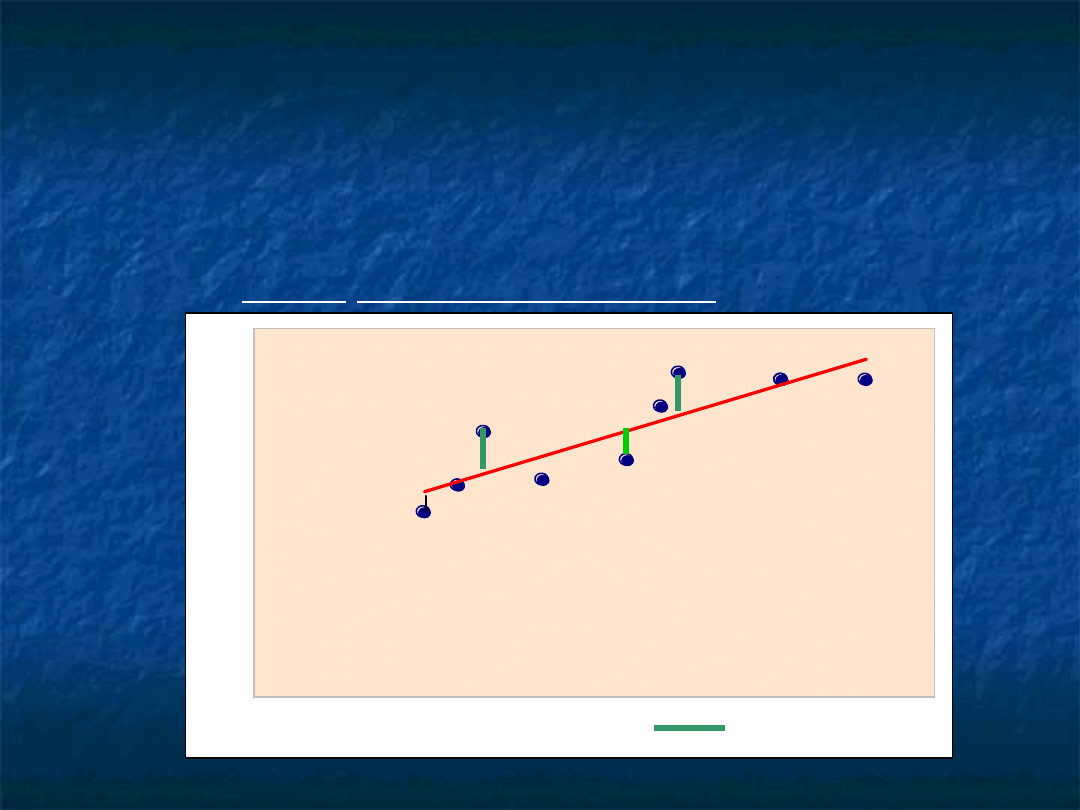
MNK w przypadku jednej zmiennej objaśniającej,
MNK w przypadku jednej zmiennej objaśniającej,
czyli dla modelu
czyli dla modelu
y
y
t
t
=
=
1
1
X
X
t
t
+
+
+
+
t
t
.
.
y = a
1
x - a
o
x
Y
reszty
POLEGA NA ZNAJDOWANIU TAKIEJ PROSTEJ, KTÓRA
JEST NAJLEPIEJ DOPASOWANA DO WSZYSTKICH
PUNKTÓW EMPIRYCZNYCH, CZYLI MINIMALIZOWANA
SUMA KWADRATÓW RESZT (ut).
x
a
y
a
x
x
y
y
x
x
a
n
t
t
n
t
t
t
0
2
1
1
1
,
)
(
)
)(
(
Reszta modelu :
u
t
= y
t
-y
t
*
= y
t
– a
1
x
t
- a
0
Oznaczenia - zapis skalarny
Oznaczenia - zapis skalarny
Model :
t
it
X
i
k
i
t
Y
lub
,
t
t
X
t
X
t
X
t
Y
1
0
3
3
2
2
1
1
Model
oszacowany:
t
u
it
X
i
a
k
i
t
Y
1
Reszta
modelu:
it
X
i
a
k
i
t
y
t
y
t
y
t
u
1
*
y
t
* - wartość teoretyczna
zmiennej Y
t
ZAPIS MACIERZOWY
ZAPIS MACIERZOWY
reszt
wektor
Xa,
y
u
oszacowany
model
u,
Xa
y
model
ξ,
Xα
y
y
(n x 1)
, X
(n x k)
,
(k x 1)
,
a
(k x 1)
,
(n x 1)
, u
(n x 1)
.
WARUNEK MNK
WARUNEK MNK
min
min
)
(
)
(
min,
Xa
T
X
T
a
Xa
T
y
y
T
y
Q
Xa
y
T
Xa
y
u
T
u
Q
czyli
n
t
a
t
x
a
t
x
a
t
y
Q
2
2
1
0
2
2
1
1
ZAPIS MACIERZOWY -WARUNEK KONIECZNY
ZAPIS MACIERZOWY -WARUNEK KONIECZNY
MINIMUM
MINIMUM
0
2
2
Xa
T
X
y
T
X
a
Q
a stąd
,
Xa
T
X
y
T
X
X
T
X
dodatnio
określona
Rozwiązanie układu równań
y
T
X
X
T
X
a
1
)
(
WARUNEK DOSTATECZNY MINIMUM
WARUNEK DOSTATECZNY MINIMUM
)
X
T
X
(
a
Q 2
2
2
W punkcie a=(X
T
X)
–1
X
T
y,
funkcja Q ma ekstremum minimum
Przykład- zapis skalarny
Przykład- zapis skalarny
Niech będzie dany model liniowy z dwoma
zmiennymi objaśniającymi
y
t
=
1
X
1t
+
X
2t
+
t
Po oszacowaniu model powinien mieć postać:
y
t
= a
X
1t
+ a
X
2t
+ a
u
t,
czyli
y
t
= y
t
*
u
t
gdzie:
y
t
*
- wartość teoretyczna zmiennej
endogenicznej
u
t
- reszta modelu w okresie t.
Warunek MNK
min
2
1
3
2
2
1
1
2
1
*
n
t
a
t
x
a
t
x
a
t
y
n
t
t
y
t
y
Q
Aby wyznaczyć min funkcji Q należy ją
trzykrotnie
zróżniczkować, tj. obliczyć pochodne cząstkowe
względem a
i
a następnie
przyrównać je do zera.
Pochodne:
1
1
3
2
2
1
1
2
3
2
1
3
2
2
1
1
2
2
1
1
3
2
2
1
1
2
1
n
t
a
t
x
a
t
x
a
t
y
a
Q
t
x
n
t
a
t
x
a
t
x
a
t
y
a
Q
t
x
n
t
a
t
x
a
t
x
a
t
y
a
Q
Po przyrównaniu pochodnych do zera i
uporządkowaniu równań
otrzymujemy tzw. układ równań normalnych
2
/
0
1
3
2
2
1
1
2
2
/
0
2
1
3
2
2
1
1
2
2
/
0
1
1
3
2
2
1
1
2
n
t
a
t
x
a
t
x
a
t
y
t
x
n
t
a
t
x
a
t
x
a
t
y
t
x
n
t
a
t
x
a
t
x
a
t
y
n
t
t
y
n
a
n
t
t
x
n
t
a
t
x
a
n
t
t
y
t
x
n
t
t
x
a
n
t
t
x
n
t
a
t
x
t
x
a
n
t
t
y
t
x
n
t
t
x
a
n
t
t
x
t
x
n
t
a
t
x
a
1
3
1 2
1
2
1
1
1 2
1 2
3
1
2
2
1
2
1
2
1
1 1
1 1
3
1
2
1
1
2
2
1
1
n
t
t
y
n
t
t
y
t
x
n
t
t
y
t
x
a
a
a
n
n
t
t
x
n
t
t
x
n
t
t
x
n
t
t
x
n
t
t
x
t
x
n
t
t
x
n
t
t
x
t
x
n
t
t
x
1
1 2
1 1
3
2
1
1 2
1 1
1 2
1
2
2
1
1
2
1 1
1
2
1
1
2
1
y)
(X
a
X)
(X
T
T
y
T
X
X
T
X
a
1
)
(
Estymator
wektora
parametrów
strukturalnych
modelu
KLASYCZNE ZAŁOŻENIA MNK
KLASYCZNE ZAŁOŻENIA MNK
•Zmienne objaśniające są nielosowe i
niewspółliniowe, k<n,
•Istnieje n populacji składników
losowych, o na - dziejach E(
t
)=0
i
stałych wariancjach, o skoń-czonych
wartościach
D
2
(
t
)=const ,
t=1,2,....,n
•Realizacje zmiennych tworzą proces
czysto losowy, tzn., że następujące po
sobie realizacje składnika losowego są
nieskorelowane, czyli
t
,
s
)=0, dla ts,
•Składniki losowe są nieskorelowane
ze zmiennymi objaśniającymi
Jeżeli spełnione są klasyczne
założenia MNK to estymatory
są:
1.Nieobciążone
2.Efektywne
3.Zgodne
ESTYMACJA PRZEDZIAŁOWA
ESTYMACJA PRZEDZIAŁOWA
Szacowanie nieznanych wartości parametrów
poprzez podanie przedziałów liczbowych, o
których zakłada się, że będą zawierać
prawdziwe wartości poszukiwanych
parametrów z ustalonym z góry
prawdopodobieństwem
1
-
współczynnik ufności,
Przedział ufności dla parametru
i
P{ a
i
- t
d(a
i
)
i
< a
i
+ t
d(a
i
) } =
t
wartość krytyczna dla zmiennej losowej
o rozkładzie
t – Studenta dla n-k stopni swobody, przy
ustalonym poziomie istotności .