1

Podstawy 
spektroskopii
cząsteczkowej

2

Co to jest spektroskopia cząsteczkowa?

Spektroskopia  molekularna  zajmuje  się 
oddziaływaniem 

promieniowania 

elektromagnetycznego  z  cząsteczkami,  na 
skutek którego dochodzi do absorpcji, emisji 
lub  rozproszenia  fotonów  światła  przez 
badane 

cząsteczki. 

Charakter 

tego 

oddziaływania określa mechanika kwantowa

Wynik  takiego  oddziaływania  obserwuje 
się  jako  widmo  badanej  cząsteczki  z 
charakterystycznym  zbiorem  maksimów 
(pasm)  o  różnych  częstościach,  kształcie  i 
intensywności.

3

MOLEKUŁA

STRUKTURA MOLEKULARNA

SPEKTROSKOPIA MOLEKULARNA

4

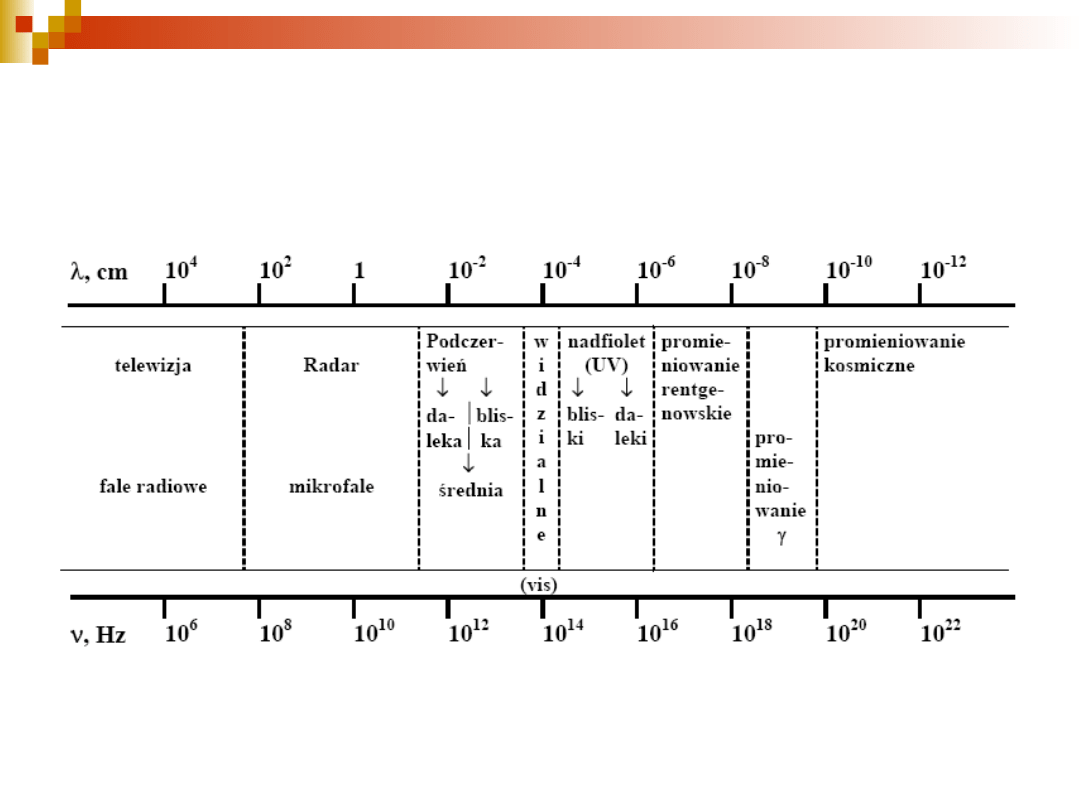
Zakresy promieniowania elektromagnetycznego

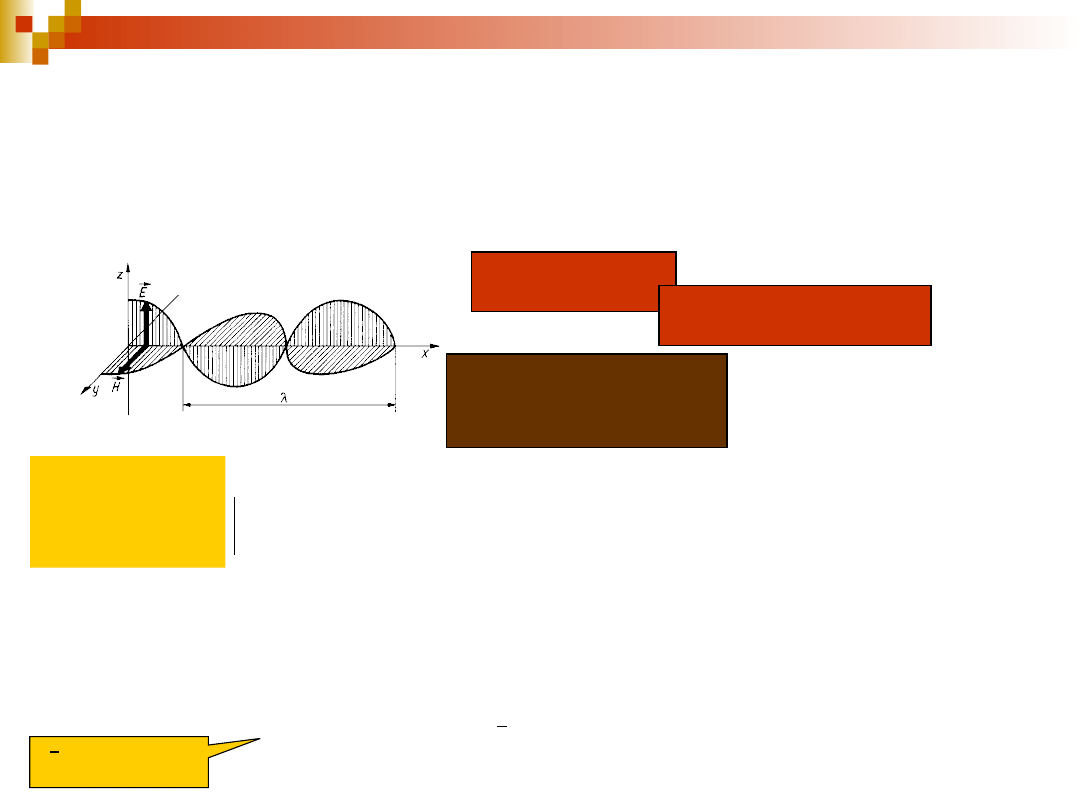
5

Natura promieniowania 
elektromagnetycznego



promieniowanie elektromagnetyczne – drganie pola elektrycznego, 
któremu towarzyszy drganie pola magnetycznego

c = 3·10

8

 m·s

-1

w próżni

u  c

w ośrodku materialnym



długość fali ( [cm]) – odcinek drogi 

promieniowania, na którym mieści się jeden 
okres drgania pola, czyli jedno drganie 



częstość ( [s

-1

]) – liczba drgań przypadająca na 

sekundę



liczba falowa ( [cm

-1

]) – liczba drgań 

przypadająca na 1 cm drogi promieniowania

 = 

 

/

c 

= 

1

/



E = E

0 

cos2t

H = H

0

 cos2t

Promieniowan

ie 

spolaryzowan

e liniowo

6

Cechy promieniowania i jego widmo



energia 1 mola fotonów – ajnsztajn – równy jest N

A

h, gdzie 

N

A

  jest  liczbą  Avogadra  (6.022·10

23

);  ajnsztajn  energii  jest 

zbliżony  do  energii  wiązań  chemicznych  w  obszarze 

promieniowania widzialnego i nadfioletu

E = h = hc

zależność Plancka

6.62·10

-34

 J·s

zależność Plancka jednoczy naturę falową 

i korpuskularną promieniowania



intensywność promieniowania (I) – energia przechodząca w 

ciągu  1  sekundy  przez  1  m

2

  powierzchni  prostopadłej  do 

kierunku biegu promieniowania



gęstość promieniowania () – energia lub proporcjonalna do 

niej  liczba  fotonów  monochromatycznych  zawarta  w  1  m

3

 

napromieniowanego 

układu 

(stężenie 

objętościowe 

fotonów)

I = c = 

c

/

n

n – współczynnik załamania światła

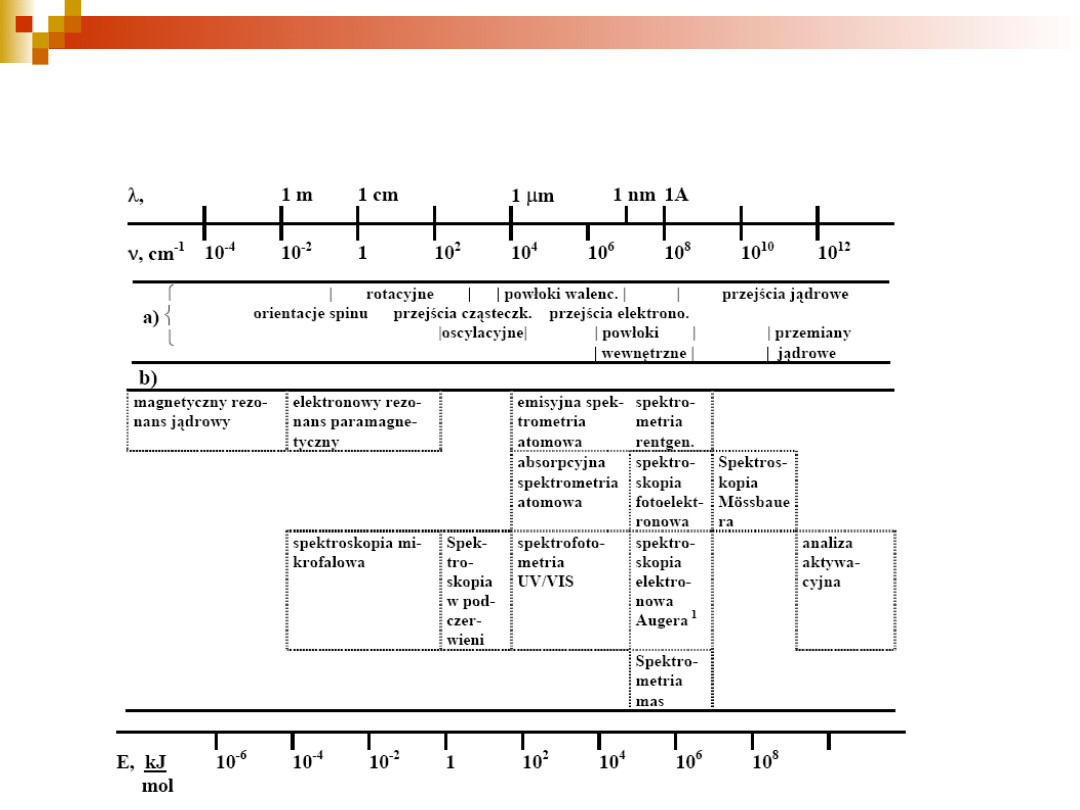
7

Zakresy promieniowania 
elektromagnetycznego używanego w różnych 
metodach spektroskopowych

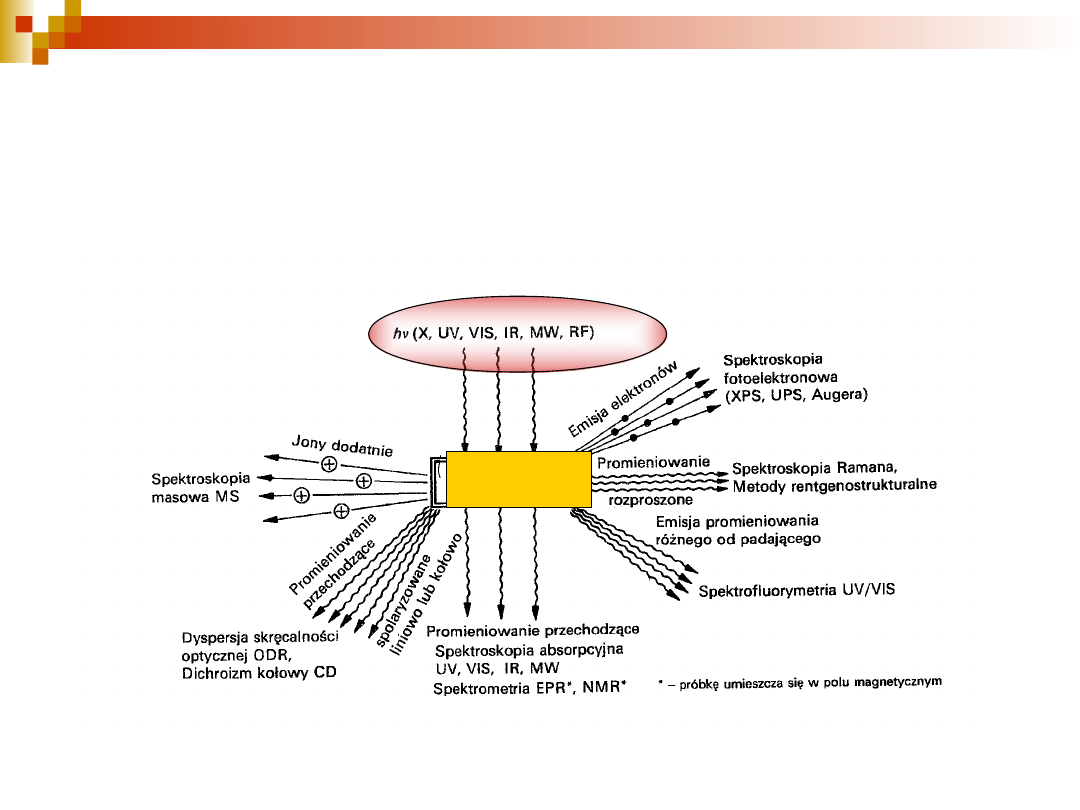
8

Oddziaływanie promieniowania 
elektromagnetycznego z materią

próbka

9

Energia molekuł

[J·molekuła

-1

]

[J·mol

-1

]

[eV]

[cm

-1

]

[Hz]

[J·molekuła

-1

]

1

6.02·10

23

6.24·10

18

5.03·10

22

1.51·10

33

[J·mol

-1

]

1.66·10

-24

1

1.04·10

-5

8.35·10

-2

2.51·10

9

[eV]

1.60·10

-19

9.65·10

4

1

8066

2.42·10

14

[cm

-1

]

1.99·10

-23

12.0

1.24·10

-4

1

3·10

10

[Hz]

6.62·10

-34

3.98·10

-10

4.13·10

-15

3.33·10

-11

1

Energię odnosi się do jednej molekuły lub do jednego mola.

10

Zakres energii dla poszczególnych przejść

Rodzaj poziomów

Orientacyjny zakres

Poziomy elektronowe

kilka – tysiące eV

Poziomy oscylacyjne

0.02 – 0.05 eV

Poziomy rotacyjne

ułamki eV (100 – 0.1 cm

-

1

)

Poziomy energetyczne w zewnętrznych polach 

magnetycznych

kilka cm-1

Poziomy energetyczne w zewnętrznych polach 

elektrycznych

zależy od siły 

zewnętrznego pola 

elektrycznego

11

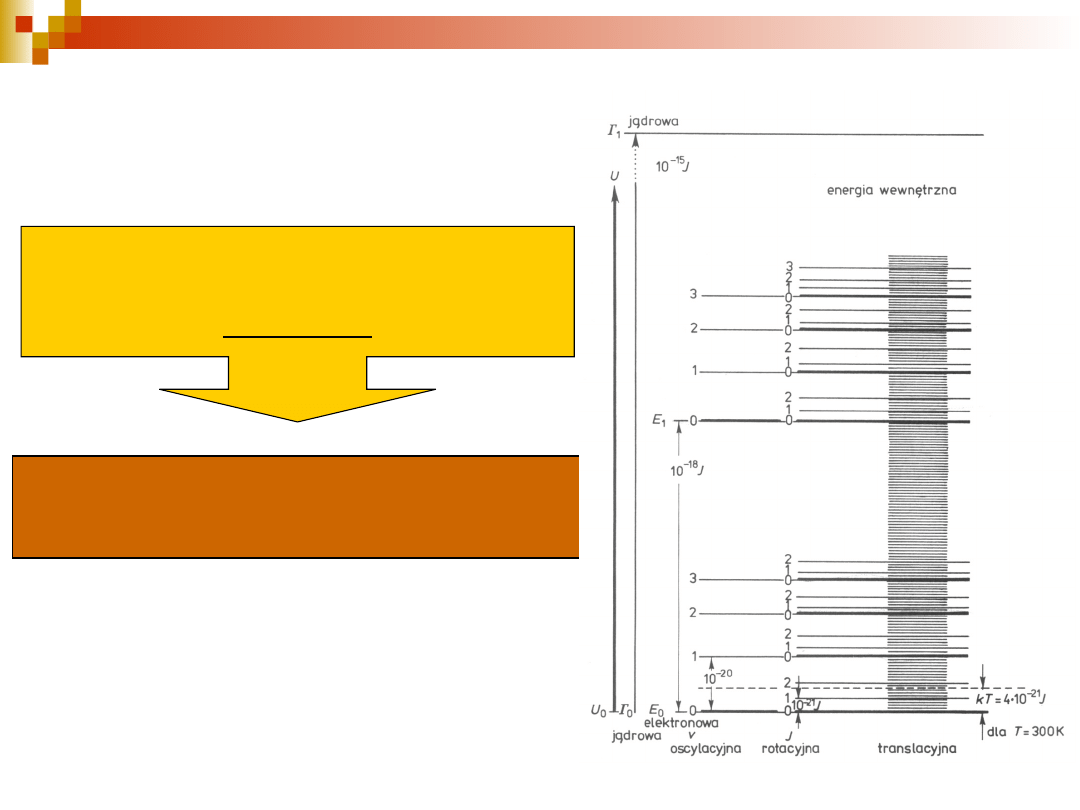
Energia wewnętrzna 
molekuł

E = E

translacyjna

 + E

rotacyjna

 + E

oscylacyjna

 + 

E

elelektronowa

 + E

jądrowa

Każdy z rodzajów energii molekuły może przyjmować 

tylko

 nieciągłe (dyskretne,

kwantowane) wartości nazywane poziomami energii.

E

translacyjna

 =  

kT

2

3

Średnia  energia  translacji  molekuły 
dzieli się
równomiernie  na  stopnie  swobody  i  na 
każdy przypada ½ kT

w 298 K:
E

tr

 = 6,210

-21

 J/molekuła (         )

E

tr

 = 3,710

3

 J/mol           (           )

kT

2

3

A

kTN

2

3

Energia translacyjna jest bardzo słabo kwantowana

J

ma

h

E

tr

40

2

2

10

1

8











10

19

 poziomów

translacyjnych



cząstka w pudle

a = rozmiar pudła = średnia odległość między molekułami

Dla N

2

:

 

w T = 298K – 62000 poziomów translacyjnych; w T = 1K – 5 poziomów translacyjnych

12

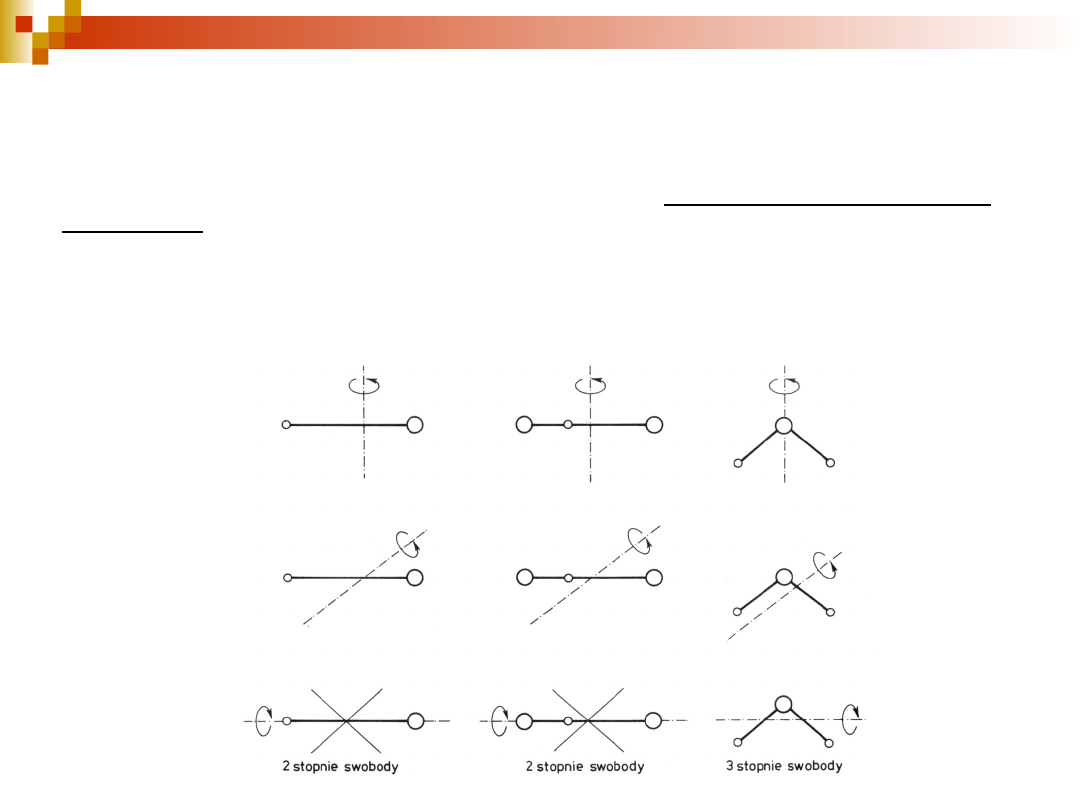
E

rotacyjna

 - wynika z wirowania molekuły wokół własnej osi. Ruch ten 

przypominający bąka można rozłożyć na składowe rotacje wokół 

dwóch lub trzech osi wzajemnie do siebie prostopadłych w zależności 

od struktury molekuły, czyli przypisać mu dwa lub trzy stopnie 

swobody. Na każdy stopień swobody  przypada pewna ilość energii 

rotacji.

T = 400-500 K  zasada ekwipartycji energii  na każdy stopień swobody rotacji przypada 

1

/

2

kT 

energii rotacyjnej

13

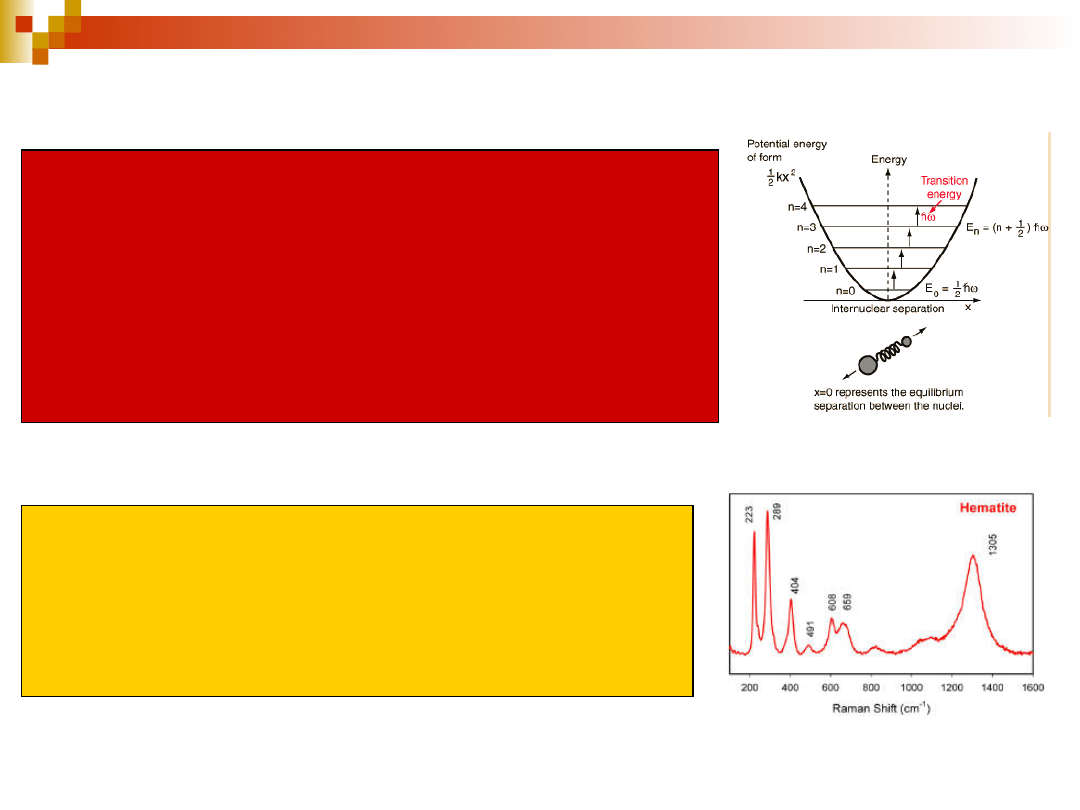
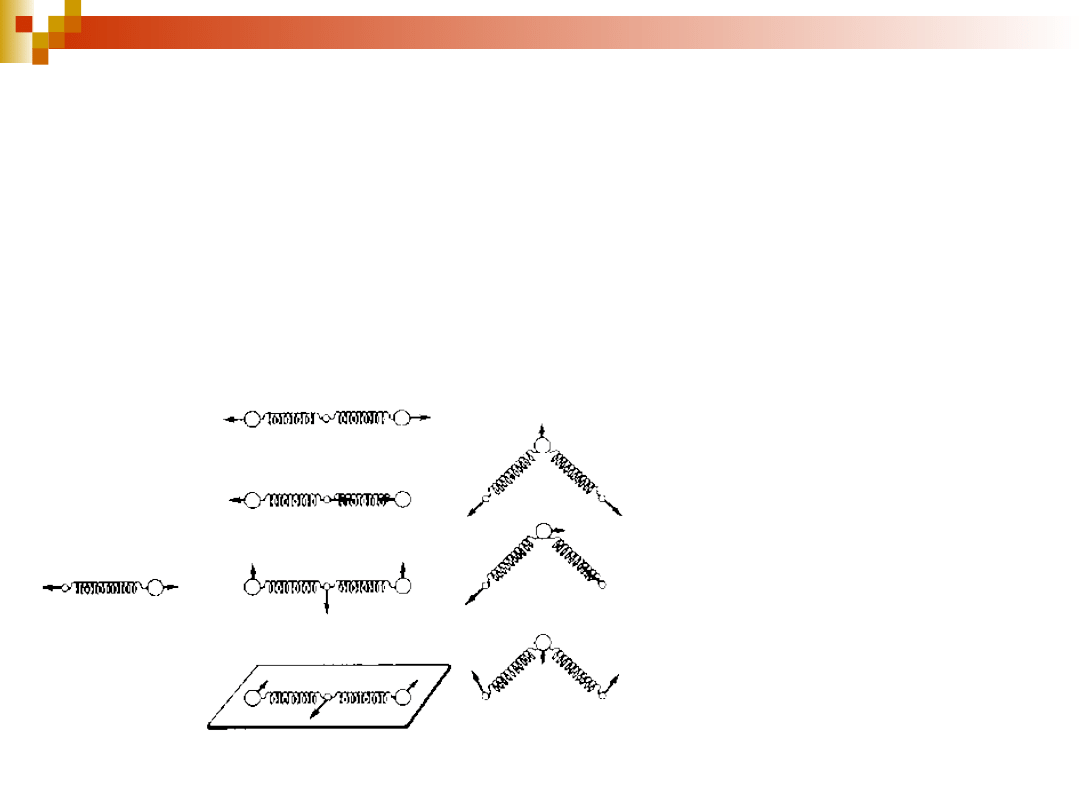
E

oscylacyjna

  -  atomy  w  molekule  połączone  są  wiązaniami  utworzonymi  przez 

elektrony  walencyjne.  Wiązania  zachowują  się  jak  sprężyny,  które  wiążą 
zręby  atomowe,  czyli  jądra  otoczone  zamkniętymi  powłokami  elektronów 
nie  biorących  udziału  w  wiązaniach.    „Sprężynujące”  wiązania  wywołują 
drgania zrębów atomowych – oscylacje wokół położeń równowagi.

3n – 3 – 3  = 3n – 6  (w molekułach nieliniowych)

3n – 3 – 2 = 3n – 5 (w molekułach liniowych)

 n – liczba atomów w molekule

1 stopień swobody        4 stopnie swobody         3 stopnie 
swobody

14



E

elektronowa

 – energia kinetyczna ruchu elektronów w 

molekule i energia przyciągania elektronów przez 
jądra i odpychania ich przez sąsiadujące elektrony.



 

E

jądrowa

 – kinetyczna i potencjalna energia 

nukleonów tworzących jądra molekuły.

15

Kwantowanie 
energii

dana molekuła może oddać otoczeniu swą 

energię tylko charakterystycznymi porcjami – 

kwantami

energia w mikroświecie jest skwantowana

16

Zadanie 1

Jeden  mol  gazu  doskonałego  w  temperaturze 

298 K i pod ciśnieniem 1 bar zajmuje objętość 2.48·10

-

2

  m

3

,  odległość  średnia  między  molekułami  wynosi 

więc

a = (2.48·10

-2

/N

A

)

1/3

 m = 3.45·10

-9

 m

W  przypadku  molekuł  azotu,  których  masa

m=4.65·10

-26

  kg,  h

2

/8ma

2

    10

-25

  J,  a  więc  na  wartość 

średniej  energii  translacji  3/2kT  przypada  62  600 
poziomów translacyjnych. 

Podobne  obliczenie  dla  T  =  1K  i  ciśnienia  1  bar 

daje  5  poziomów  translacyjnych    w  obrębie  średniej 
energii  translacyjnej  wynoszącej  3/2kT  =  2·10

-23

 

J·molekuła

-1

.

17

Obsadzenie poziomów energetycznych

 E

wyższa

E

niższa

 E

w

 – E

n

 = E = h

W stanie równowagi termicznej:

]

exp[

]

exp[

kT

h

kT

E

n

n

n

w













funkcja rozkładu energii Boltzmanna

Przenoszenie się molekuł na wyższe poziomy energetyczne kosztem
energii translacji przekazywanej w zderzeniach

4

e

n

e

rg

ia

0

1

0

1

2

3

kT

18

Analiza funkcji 

Boltzmanna

I.            

E=0 lub T= 

1



n

w

n

n

poziomy pokrywają się ze sobą

nieskończenie wysoka temperatura

przypadek graniczny



Im bliżej siebie leżą poziomy lub im wyższa T, tym bardziej wyrównane obsadzenie.

II. 

               E=  lub T=0

0



n

w

n

n

przypadek graniczny



Im bardziej odległe od siebie poziomy lub im niższa T, tym mniej obsadzony poziom wyższy.

III. 

      

nie ma sensu dla poziomów o tym samym stopniu degeneracji,

        bez dopływu energii z zewnątrz

1



n

w

n

n

]

exp[

kT

E

g

g

n

n

n

w

n

w







Zablokowanie drogi powrotu molekuł na niższy stan prowadzi do inwersji obsadzeń, a bodziec
może  spowodować  lawinowy  spadek  molekuł  na  niższy  poziom  i  emisję  wiązki  fotonów
(akcja laserowa).

19

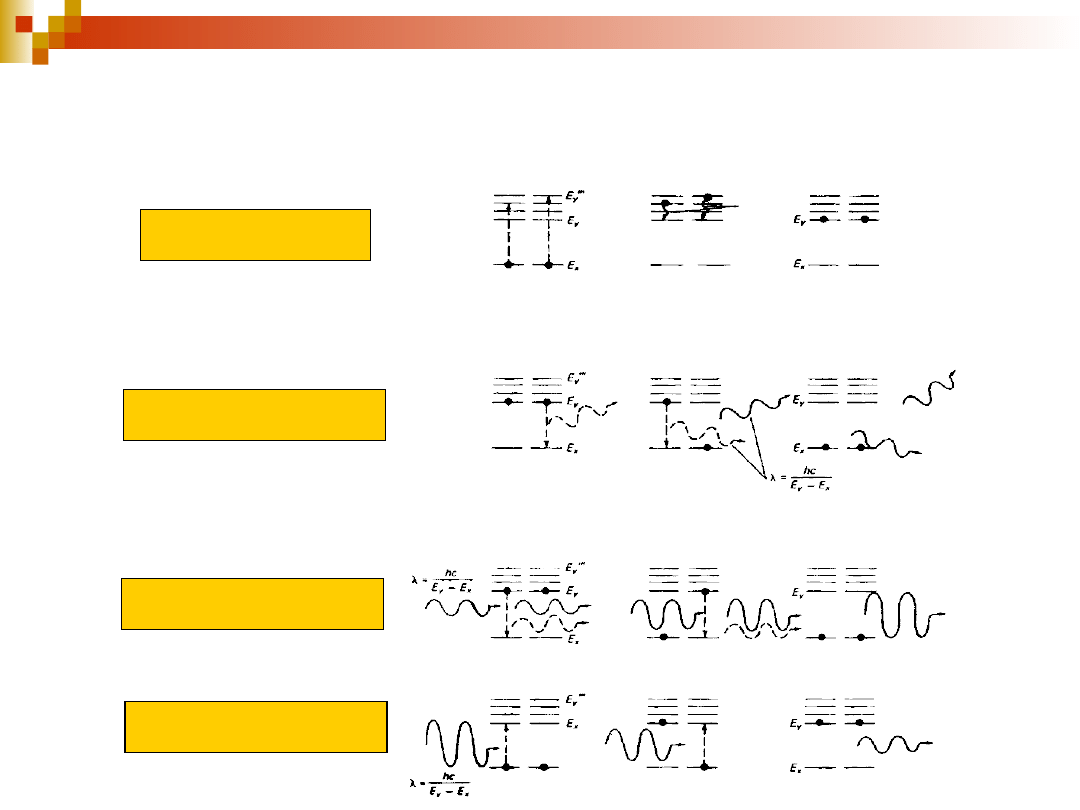
Procesy ważne dla powstania akcji 
laserowej

pompowanie

emisja spontaniczna

emisja wymuszona

absorpcja

20

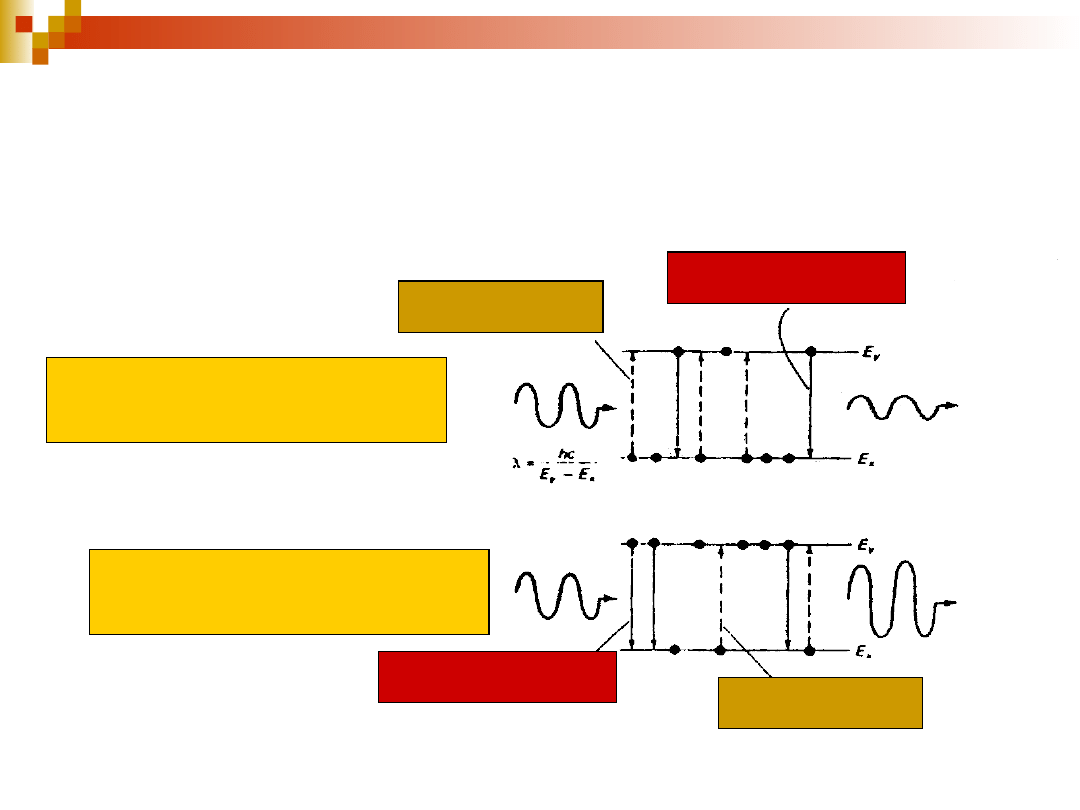
Oddziaływanie promieniowania z 
układem bez inwersji i z inwersją 
obsadzenia stanu wzbudzonego

absorpcja

emisja spontaniczna

emisja wymuszona

absorpcja

brak inwersji obsadzeń stanów 

inwersja obsadzeń stanów 

21

Gęstość

promieniowania

Prawdopodobieństwo absorpcji 
i emisji promieniowania

E = h

a

b

so

rp

cj

a

e

m

is

ja

 

sp

o

n

ta

n

ic

zn

a

e

m

is

ja

 

w

y

m

u

sz

o

n

a

Z

nw

 = B

nw

 n

n

 



liczba przejść 

absorpcyjnych 

w jednostce 

czasu

prawdopodobieństwo 

absorpcji wymuszone – 

współczynnik absorpcji 

Einsteina

Z’

wn

 = A

wn

 n

w

liczba przejść 

emisji 

spontanicznej w 
jednostce czasu

prawdopodobieństwo 

emisji spontanicznej – 

współczynnik 

Einsteina emisji 

spontanicznej

Z

wn

 = B

wn

 n

w

 



liczba przejść 

emisji wymuszonej 

w jednostce czasu

prawdopodobieństwo 

emisji wymuszonej – 

współczynnik 

Einsteina emisji 

wymuszonej

w

n

22



Dynamiczny stan równowagi 
obsadzeń poziomów

B

nw

 n

n

 



 = A

wn

 n

w

 + B

wn

 n

w 





 



 

= 

A

wn

B

nw

      - B

wn

n

n

n

w

Współczynniki Einsteina absorpcji i wymuszonej emisji są sobie równe, gdy poziomy n i w 

mają ten sam stopień degeneracji, czyli g

n

 = g

w

  

B

nw

 = B

wn

    

= exp 

[

         

]

n

n

n

w

h

kT



 

=   

A

wn

B

nw

(exp[      ] -1)

h

kT



 

=   

1

(exp[      ] -1)

h

kT

8h

3

c

3

ciało doskonale czarne – wzór Plancka

 A

wn

    8h

3

 B

nw        

 c

3

=

23

rodzaj 

spektroskopii

częstość 

promieniowania

[Hz]

A

wn

B

nw

jądrowy rezonans 

magnetyczny

10

8

6·10

-34

elektronowy 

rezonans 

paramagnetyczny

10

10

6·10

-28

rotacyjna

10

12

6·10

-22

oscylacyjna

10

14

6·10

-16

elektronowa

10

15

6·10

-13

Wartości A

wn

/B

nw

 dla częstości charakteryzujących promieniowanie używane 

w różnych spektroskopiach wskazują, że współczynnik A

wn

 jest znacznie 

mniejszy od współczynników absorpcji i emisji wymuszonej i stosunek ten 

szybko rośnie ze wzrostem częstości przejść pomiędzy poziomami 

energetycznymi.

24



Równanie Schrödingera zależne od czasu 
pozwala wyznaczyć współczynnik B

nw

 B

nw

 =        |R

nw

|

2

 

8

3

3h

2

|R

nw

| =  

n

*

 Op 

w

 d

+

-

moment 

przejścia

funkcje falowe 

stanów niższego i 

wyższego

operator przejścia

25

spektros-

kopia

rodzaj energii 

wewnętrzenej, 

która zmienia 

energię 

zaabsorbowane

go 

promieniowania 

E

kJ/mol

N

w

/N

n

populacja 

stanu 

wzbudzone

-go

%

czas życia 

stanu 

wzbudzon

e-go

s

obliczono 

dla

NMR

energia spinów 

jądrowych w 

polu 

magnetycznym

4·10

-6

0,99999

8

49,999

9

~10

=100 

MHz

EPR

energia spinów 

niesparowanych 

elektronów w 

polu 

magnetycznym

4·10

-3

0,999

8

49,9

~10

-3

=10

10

 

MHz

MW

energia rotacji 

cząsteczek

4·10

-3

0,999

8

49,9

~10

-3

=10

10

 

MHz

IR

energie 

oscylacji i 

rotacji 

cząsteczek

20

0,00015

0,01

~10

-8

=170 cm

-

1

UV/VIS

energia 

elektronów

3·10

3

0

znikom

a

~10

-9

=400 

nm

26

Ważne!



Nawet, jeśli stosunek N

w

/N

n

=0.99998, to i tak w 

takim przypadku istnieje znaczący nadmiar 

molekuł (jąder) na niższych poziomach 

energetycznych. W 1 molu cząsteczek taki stosunek 

obsadzenia poziomów energetycznych odpowiada 

nadmiarowi rzędu 

10

17

 cząsteczek

 znajdujących 

się na niższym poziomie energetycznym. 



Dzięki temu nadmiarowi procesy absorpcji 

(wymuszonej) mają przewagę nad procesami 

emisji!!

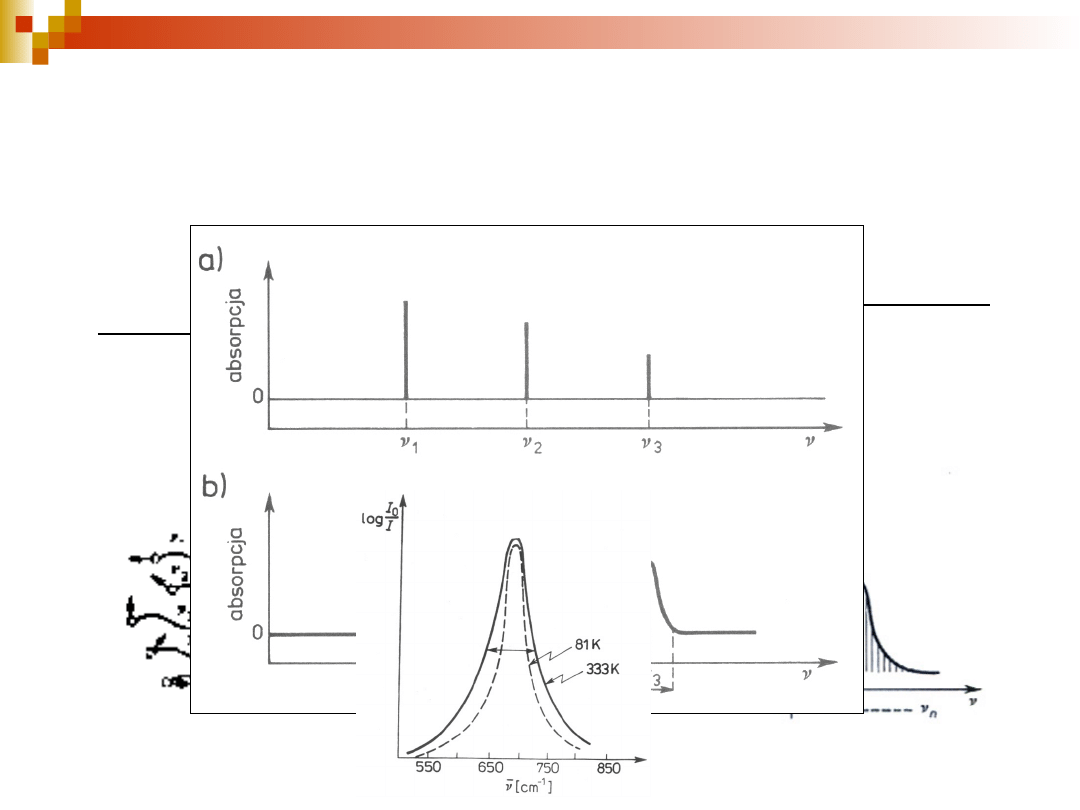
27

Czynniki determinujące kształt i szerokość 
konturu pasma



rozmycie skwantowanych poziomów energetycznych, 

między którymi zachodzi przejście absorpcyjne lub 

emisyjne; rozmycie to tłumaczy zasada nieoznaczoności 

Heisenberga (·  ħ/2)



efekt Dopplera



szczątki gałęzi rotacyjnych w pasmach oscylacyjno-

rotacyjnych układów skondensowanych



chwilowe różnice otoczenia molekuł w fazie 

skondensowanej



zderzenia molekuł w fazie gazowej powodujące jej 

deformacje

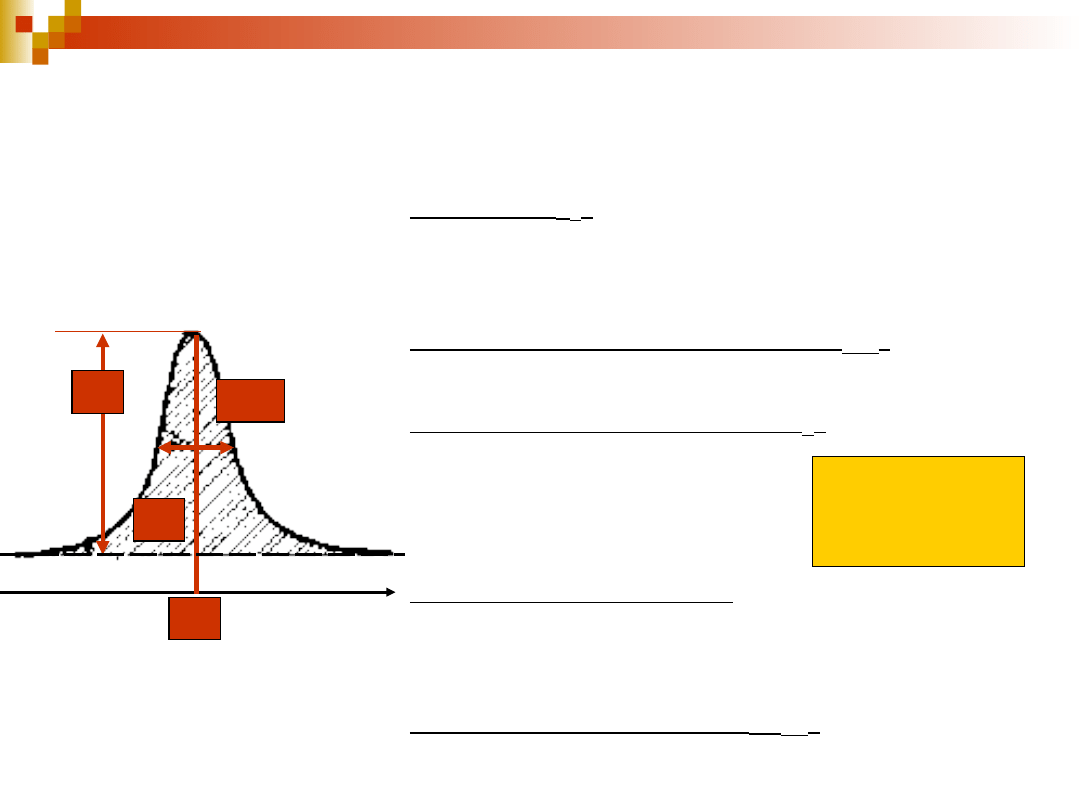
28

Parametry pasma 
spektralnego



częstość (

0

) – częstość osi symetrii konturu, 

która charakteryzuje położenie pasma względem 

innych pasm w widmie i pozwala zidentyfikować 

obiekt dający pasmo



intensywność w maksimum (I

max

) – wysokość 

konturu pasma mierzona od tła pasma



intensywność integralna (I



) – powierzchnia 

ograniczona konturem pasma i tłem



intensywność molowa (w maksimum lub 

integralna) – stosunek zmierzonej intensywności 

do stężenia substancji, której pasmo badamy, 

wyrażona w molach na jednostkę objętości



szerokość połówkowa (

1/2

) – szerokość 

konturu zmierzona w połowie jego wysokości

I





1    



2



1/2



0

tło

I

max

I



 =  I d



2



1

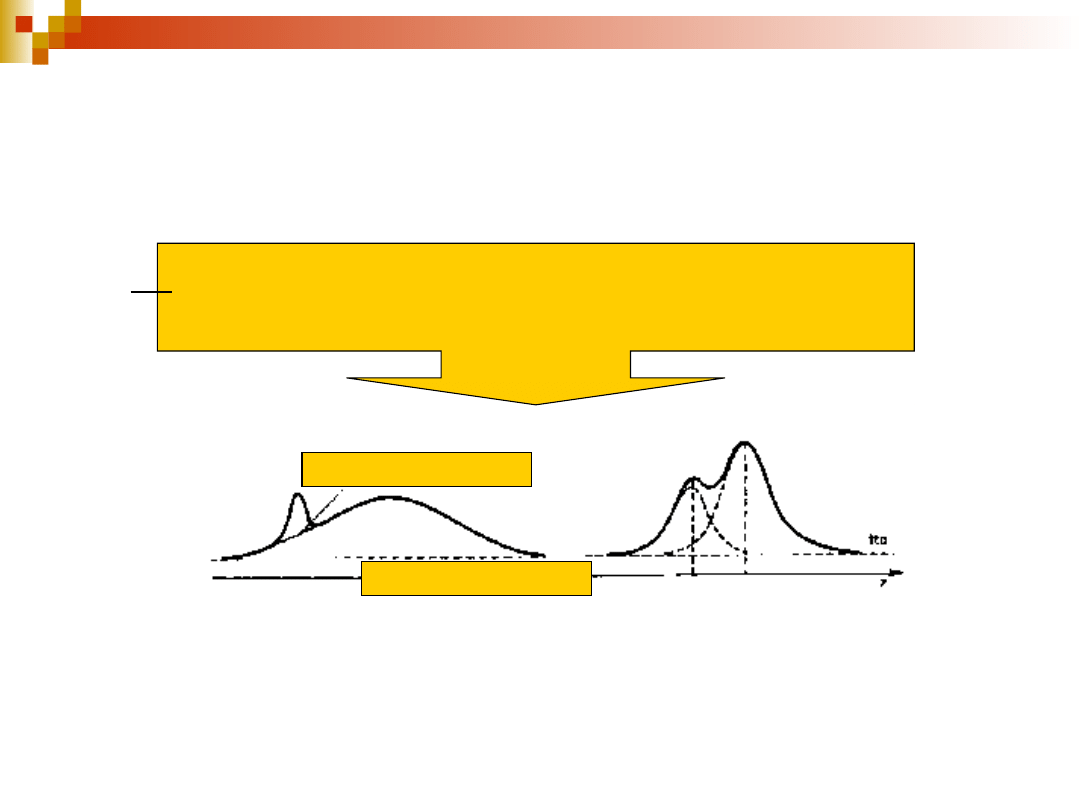
29

tło pasma wąskiego

tło pasma szerokiego

tło – intensywność widma poza obszarem badanego pasma

 i innych pasm znajdujących się w bezpośrednim sąsiedztwie

 

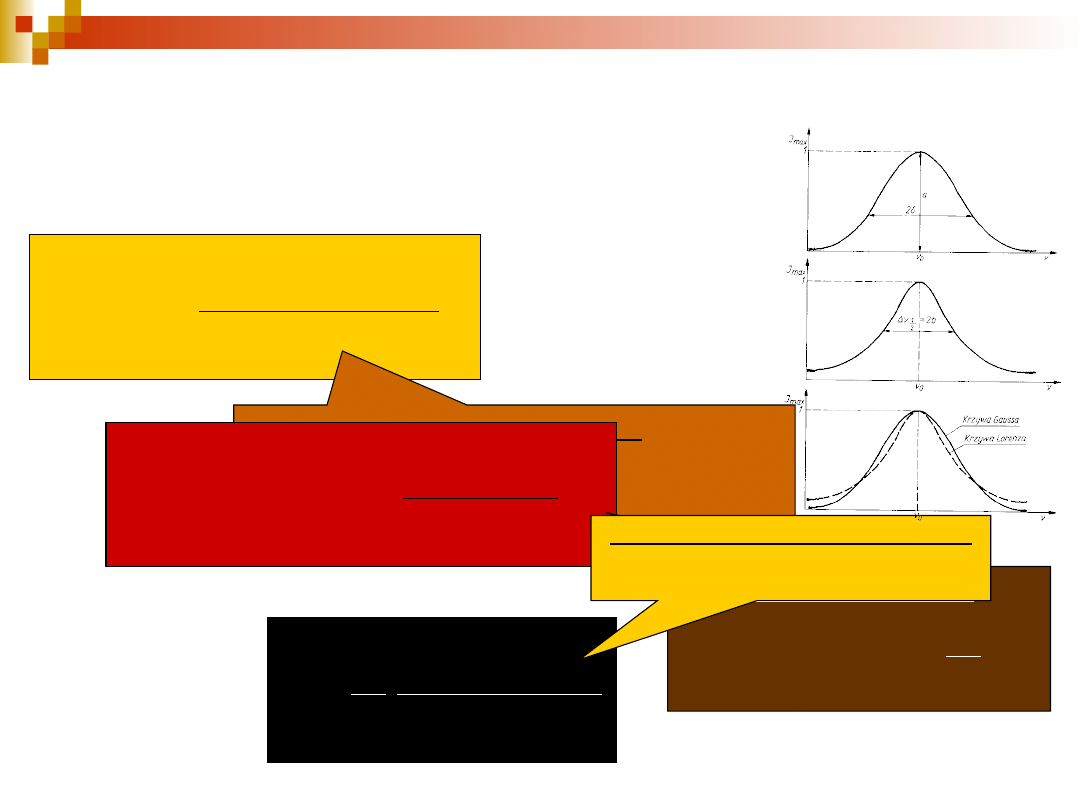
30

Funkcje analityczne opisujące 
kontur pasma

    I() = 

a

( - 

0

)

2

 + b

2

funkcja Lorentza

b – połowa szerokości połówkowej konturu (

1/2

 = 

2b)

I

max

 = a/b

2

I



= a/b

 I() = a’ exp[ -               ] 

( - 

0

)

2

q

2

funkcja Gaussa

q – połowa szerokości konturu na 

wysokości 1/e, a’ – wysokość 

konturu (I

max

 = a’), 

1/2

 = 2q ln2

I



=a’q

 r = 

   

1/2

 · I

max

2         I



współczynnik kształtu konturu

r = 1  funkcja Lorentza

r =  ln2 = 1.47  funkcja Gaussa

31

Kryteria podziału spektroskopii molekularnej

I. Sposób oddziaływania promieniowania z układem 

molekularnym:



spektroskopia absorpcyjna,



spektroskopia emisyjna,



spektroskopia rozproszenia.

II. Rodzaj wzbudzeń wywołanych prze oddziaływania 

promieniowania z układem:



spektroskopia elektronowa,



spektroskopia oscylacyjna,



spektroskopia rotacyjna,



spektroskopia elektronowego rezonansu 

paramagnetycznego,



spektroskopia magnetycznego rezonansu jądrowego.

32

III. Wykorzystanie informacji zawartej w widmie:

     A. Spektroskopia klasyczna:



parametry geometrii molekuły (długości wiązań, kąty walencyjne),



stałe siłowe i energie dysocjacji wiązania,



charakter 

i 

wielkość 

oddziaływania 

między- 

i 

wewnątrzmolekularnych,



energia drgań,



rozkład gęstości elektronowej,



identyfikacja ilościowa i jakościowa związków chemicznych.

    B. Spektroskopia kształtu pasma:



wyznaczenie reorientacyjnych i wibracyjnych czasów korelacji,



wartość bariery aktywacyjnej dla ruchu reorientacyjnego molekuł.