
SPEKTROSKOPIA
CZĄSTECZKOWA
Spektroskopia emisyjna
Spektroskopia absorpcyjna
Spektroskopia Ramana
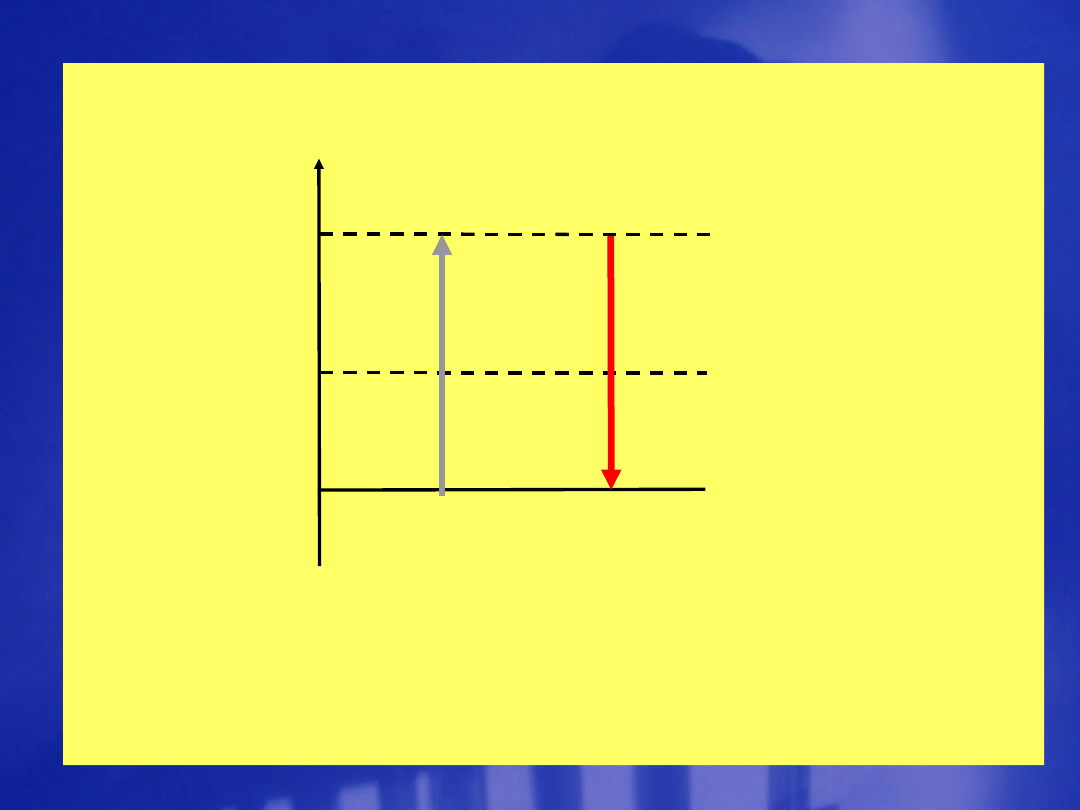
energ
ia
a
b
so
rp
c
ja
e
m
is
ja
W spektroskopii absorpcyjnej i
emisyjnej
E
1
E
2

Warunek Bohra:
h
= E
1
- E
2
h – stała Plancka ( = 6,626 *10
-34
J*s)
- częstość
c /
- długość fali
- liczba falowa
~
1
c
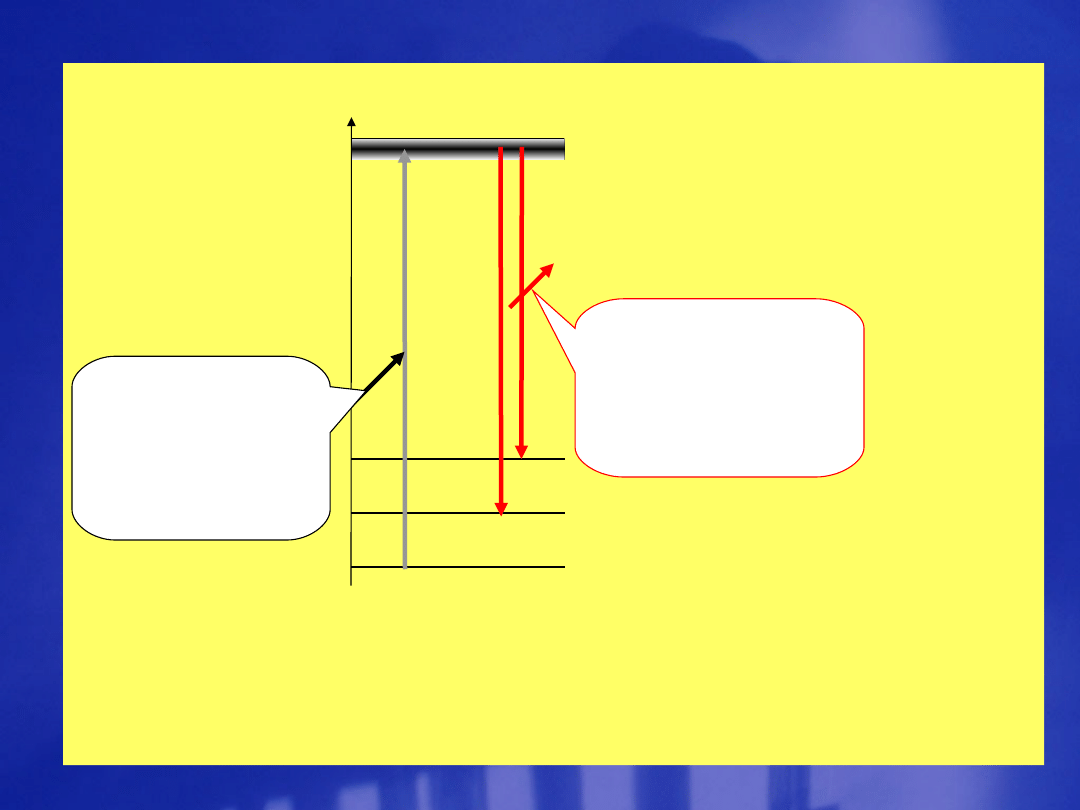
energi
a
Promieniow
a-nie
padające o
wyższej
częstości
Promieniowa
nie
rozproszone
o niższej
częstości
W spektroskopii ramanowskiej
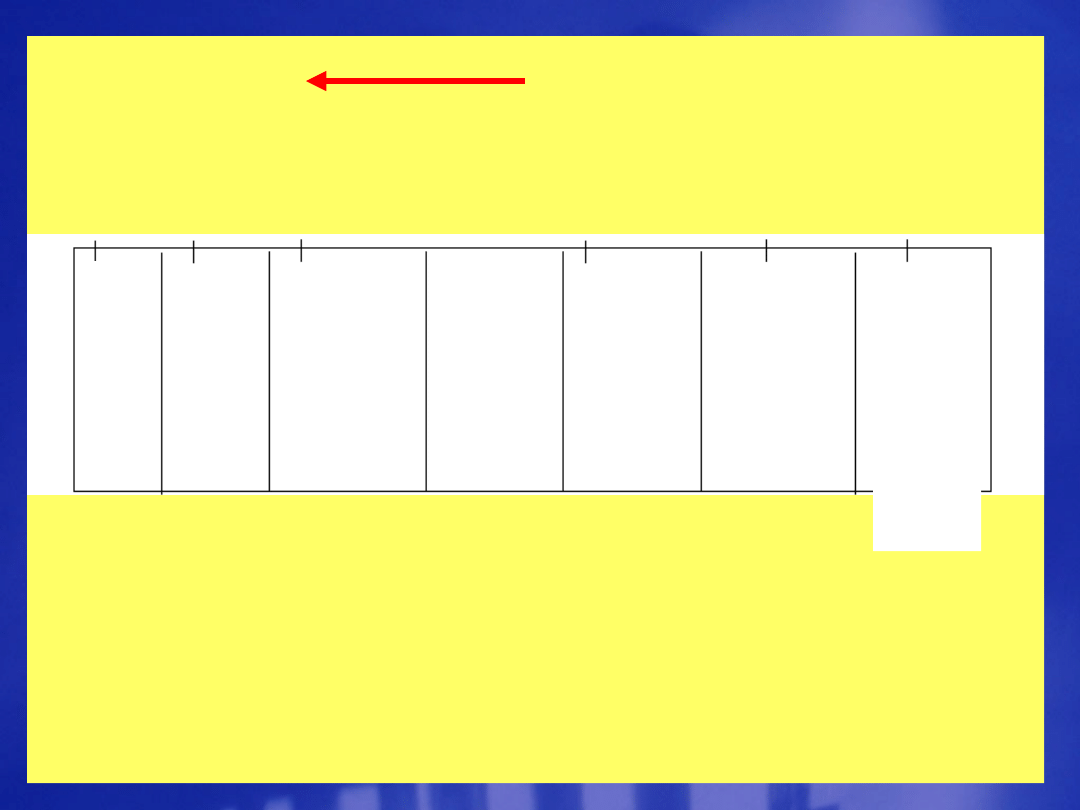
Widmo promieniowania
elektromagnetycznego i klasyfikacja
jego obszarów
Częstość promieniowania,
w hercach
10
20
10
18
10
16
10
14
10
12
10
10
10
-10
10
-8
10
-6
10
-4
10
-2
1
Długość fali,
w cm
Energ
ia
g
a
m
m
a
X
UV
VIS
IR
Mikr
o-
fale
Fal
e
rad-
iow
e

Źródło
światła
Próbka
analizowa
na
Detektor
System
analizowa
nia
wyników
TECHNIKI
DOŚWIADCZALNE
Aparatura w spektroskopii
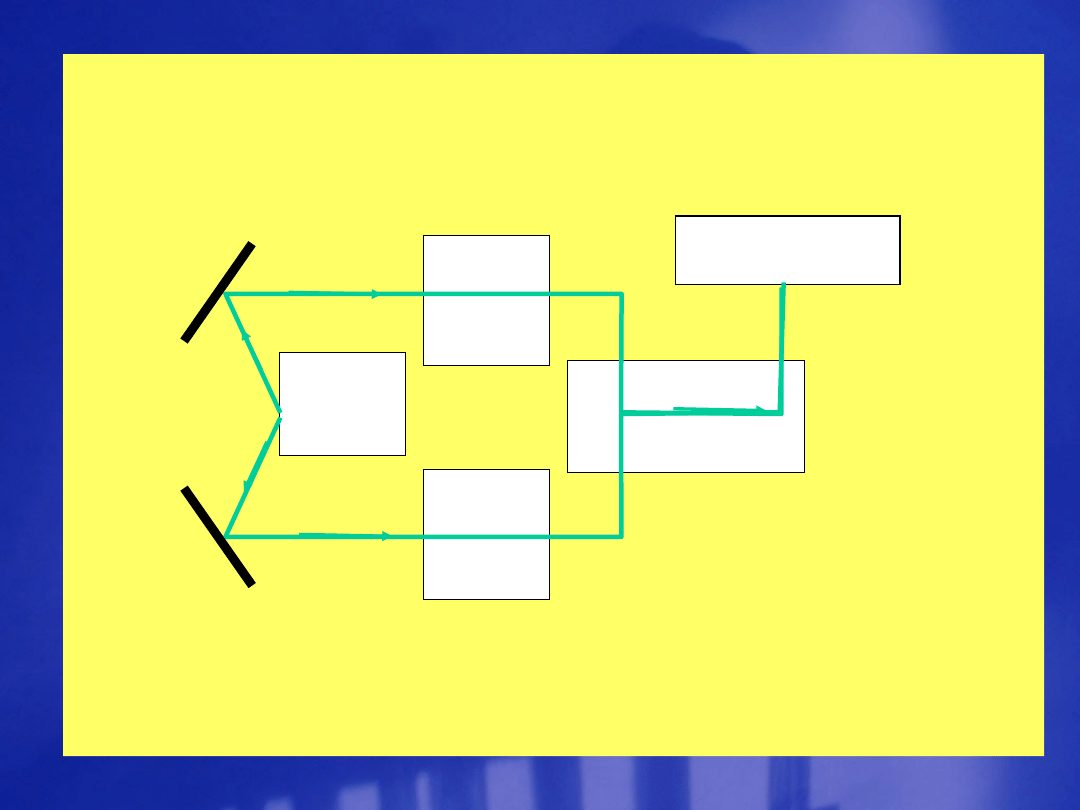
Układ
optyczny
Odno
ś-nik
Źródł
o
świat
ła
Prób
ka
anali
zowa
na
Detektor
TECHNIKI
DOŚWIADCZALNE
Aparatura w spektroskopii

Źródło światła: łuk rtęciowy, pręt
(włókno) Nernsta, żarówka halogenowa,
lampa deuterowa, klistron
Układ dyspersyjny: pryzmat, siatka
dyfrakcyjna
Rozszczepienie
promieniowania
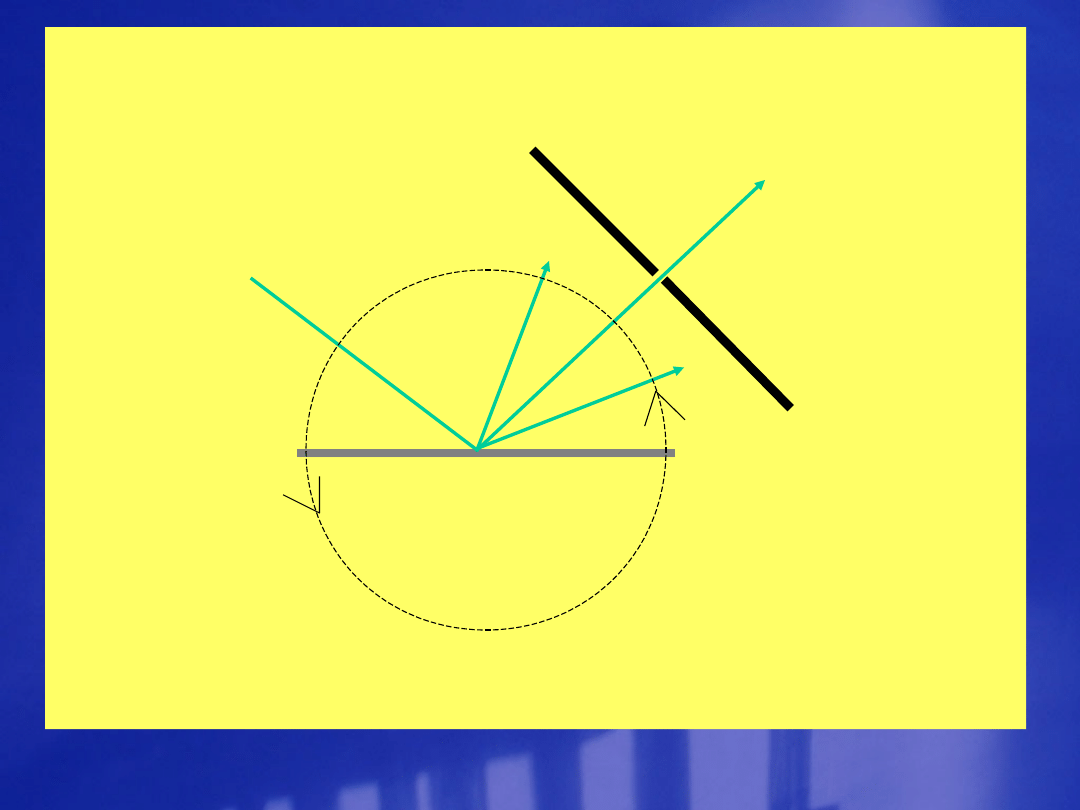
Siatka
dyfrakcyjna
Promieni
o-wanie
padające
Do
detektora
λ
1
λ
2
λ
3

Detektor: fotopowielacz, fotodioda,
termoogniwa, bolometry termistorowe
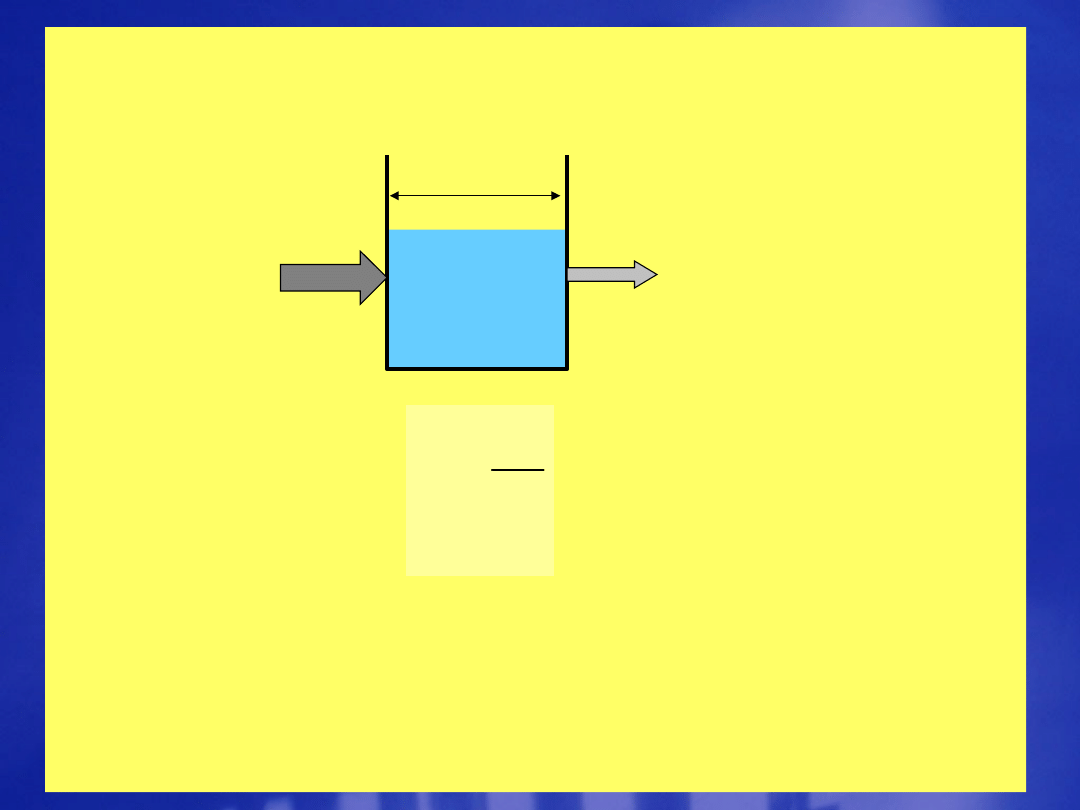
Miary absorpcji promieniowania
[J]
l
I
O
O
I
I
T
T - transmitancja
I
O
- natężenie promieniowania
padającego
I - natężenie promieniowania
przechodzącego

- molowy współczynnik absorpcji
[J] – stężenie substancji
l - grubość warstwy absorpcyjnej
log T = -
[J] l
Wymiarem
jest 1/(stężenie *
długość)
[mol
-1
* dcm
3
* cm
-1
]

A
[J]
A =
[J] l
A -
absorbancja
[J] = A /
l
log 1/T =
[J] l
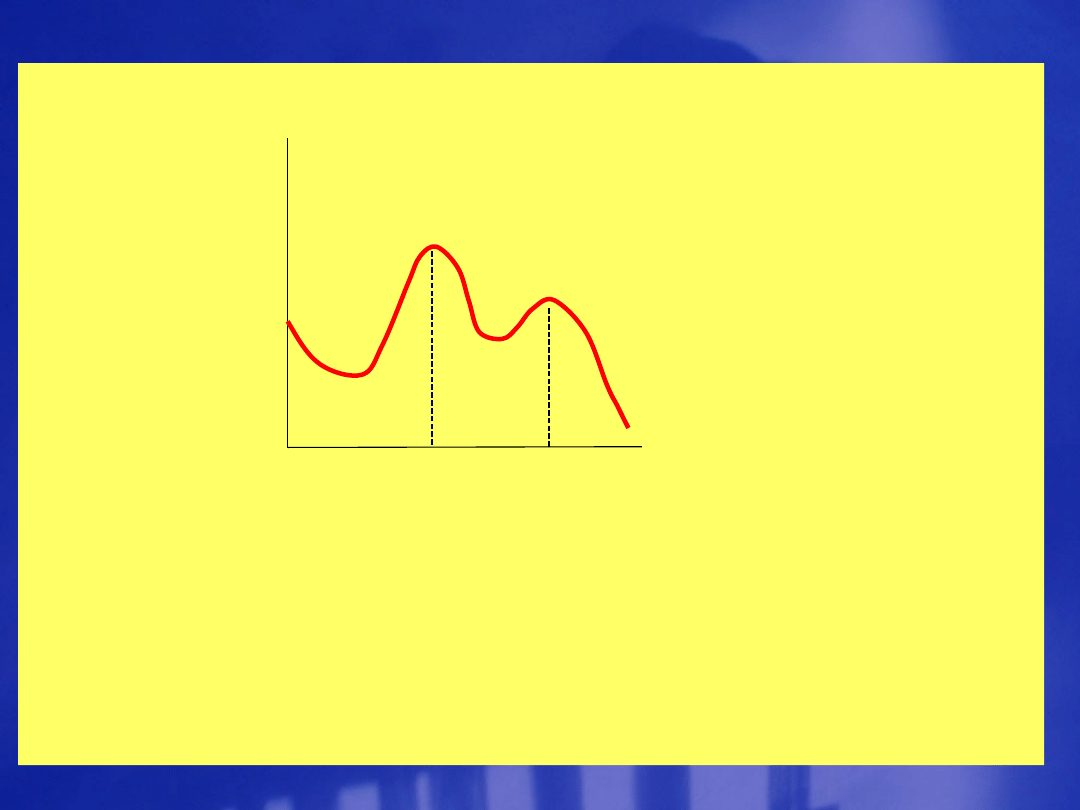
A
b
so
rb
a
n
cj
a
,
A
Długość fali,
Określanie stężeń dwóch składników A
i B
w
roztworze
A
1
A
2

A = A
A
+ A
B
=
A
[A] l +
B
[B] l
= (
A
[A] +
B
[B])l
A
1
= (
A1
[A] +
B1
[B])l
A
2
= (
A2
[A] +
B2
[B])l

Intensywność i szerokość linii
Efekt Dopplera:
Częstość,
’, postrzegana przez
obserwatora, gdy źródło promieniowania
oddala się:
'
/
/
/
1
1
1 2
s c
s c
- częstość
s - prędkość oddalania się źródła od
obserwatora
c – prędkość rozchodzenia się fali (np.
świetlnej lub głosowej)

Częstość,
’, postrzegana przez
obserwatora, gdy źródło promieniowania
przybliża się:
'
/
/
/
1
1
1 2
s c
s c
s – prędkość zbliżania się źródła do
obserwatora
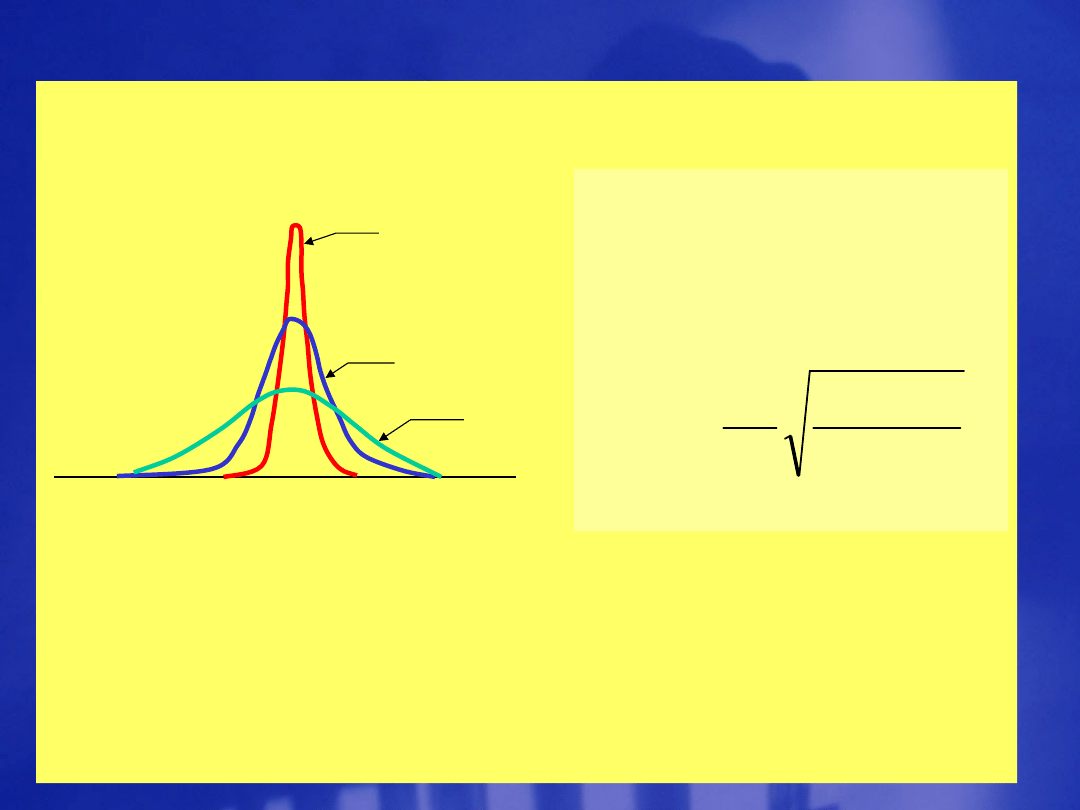
T/
3
T
3T
Wielkość
poszerzenia w
połowie wysokości
profilu widma:
2
2
2
c
RT
M
ln
Kształt linii widmowej poszerzonej
dopplerowsko dla różnych temperatur

Czas życia stanów uczestniczących w
przejściu
E
ħ /
- czas życia stanu
E – rozmycie energii
Czas życia stanów wzbudzonych
zależy od:
- dezaktywacji zderzeniowej,
- emisji spontanicznej

SPEKTROSKOPIA ROTACYJNA
widma rotacyjne - przejścia
niskoenergetyczne - zakres
mikrofalowy

Poziomy energii rotacyjnej cząsteczek
model rotatora sztywnego
-
rotator liniowy (np.: HCl, CO
2
, HCCH)
E
J
= hcBJ(J + 1) J = 0, 1, 2, .....
B = ħ / 4
cI
B - stała rotacyjna
I - moment bezwładności
I =
R
2
m m
m
m
A
A
B
B

30 5
20
4
12
3
6
2
2
1
0
0
E
n
e
rg
ia
(h
cB
)
56
7
42
6
J(J+1) J
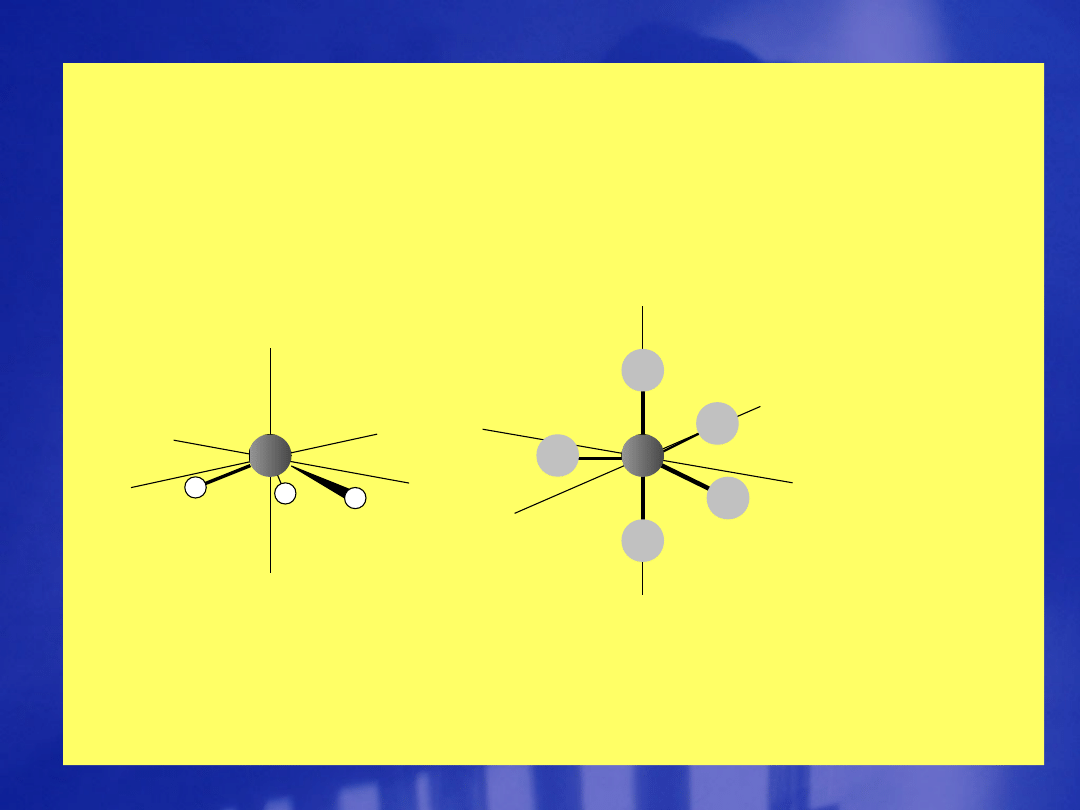
- model rotatora sztywnego
modelem cząsteczki jest kształt bąka
symetrycznego
(np.: amoniak, pięciochlorek fosforu)
NH
3
PCl
5

E
JK
= hcBJ(J + 1) + hc(A – B)K
2
J = 0, 1, 2, ...
K = J, J – 1, ...., -J
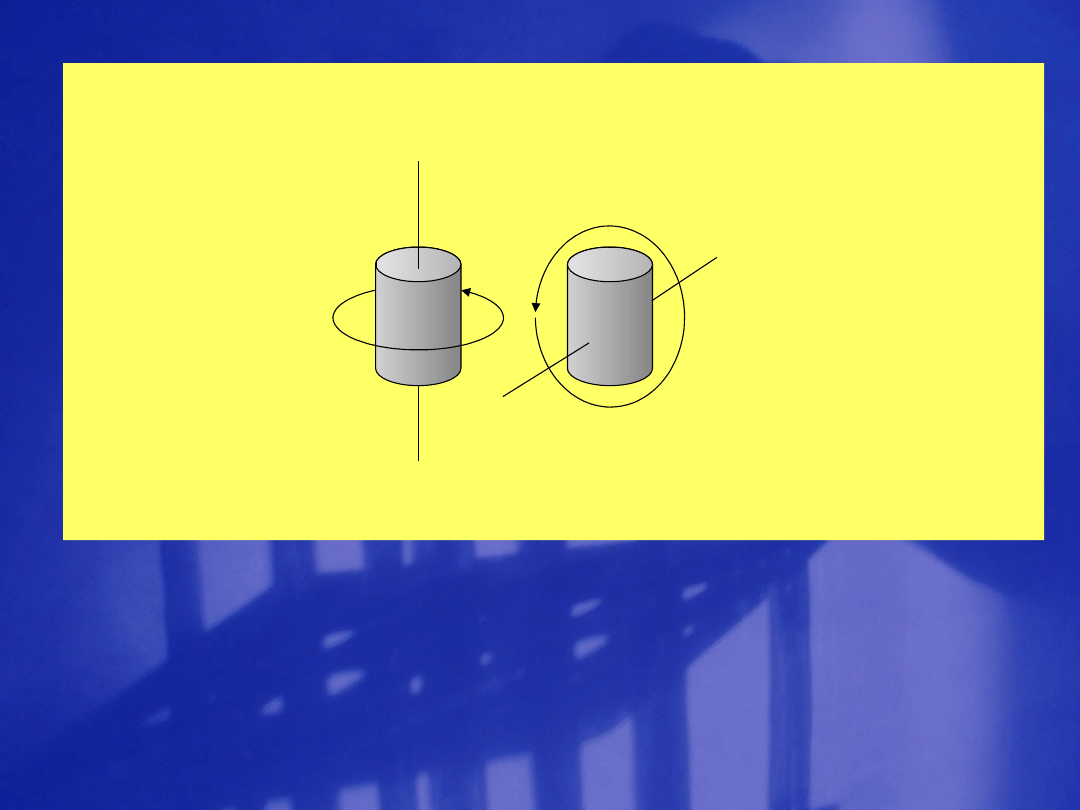
K = J
K = 0

Przejścia rotacyjne i spektroskopia
mikrofalowa
warunek absorpcji lub emisji fotonu o
częstości
reguły wyboru:
- ogólna reguła wyboru
cząsteczki muszą być polarne
- szczegółowa reguła wyboru
J = 1 K = 0

E = E
J +1
+ E
J
= hcB(J + 1)(J + 2) – J(J + 1)
= 2hcB(J + 1)
Zatem energie dozwolonych przejść wynoszą:
2hcB, 4hcB, 6hcB .....

E
n
e
rg
ia
/h
c
B
Dozwolone
przejścia rotacyjne
(absorpcyjne) w
polarnej
cząsteczce liniowej
90
9
72
8
56
7
42
6
30
5
20
4
12
3
6
2
2
1
0
0
J
Rotacyjne widma Ramana
źródło
próbka
detekt
or
Schematyczne przedstawienie aparatury
do obserwacji efektu Ramana

Linie o częstości mniejszej od
częstości światła wzbudzającego to
tzw. linie stokesowskie.
Linie o częstości większej od
częstości światła wzbudzającego to
tzw. linie antystokesowskie.

Reguły wyboru:
ogólna reguła wyboru
-by polaryzowalność cząsteczki była
anizotropowa
szczegółowe reguły wyboru
dla cząsteczek liniowych mają
postać:
J = +2 (linie
stokesowskie)
J = -2 (linie
antystokesowskie)

tzn. gdy cząsteczka podlega przejściu J
J +2 zmiana energii wynosi:
E = hcB(J + 2)(J + 3) - hcBJ(J + 1)
= 2hcB(2J + 3)
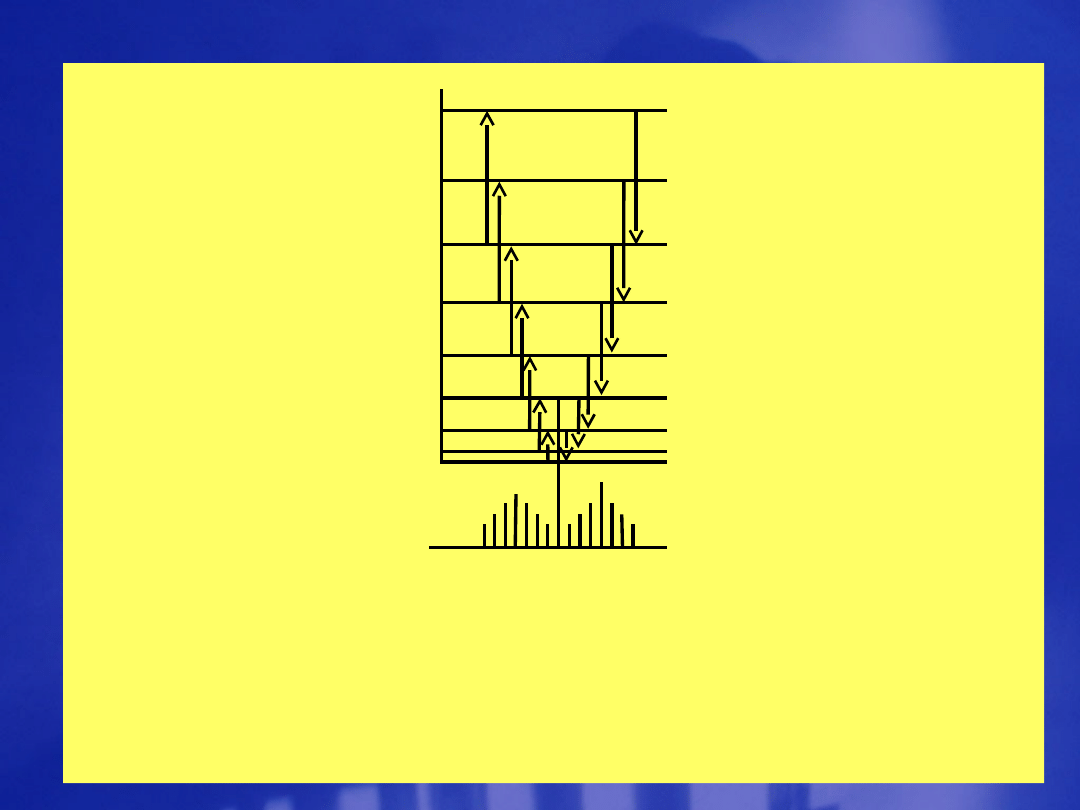
E
n
e
rg
ia
/h
cB
72
8
56
7
42
6
30
5
20
4
12
3
6
2
2
1 0
0
J
P r o m i e n i o w a n i e
stokesowskie
antystokesowskie
Przejścia odpowiedzialne za linie
stokesowskie i antystokesowskie w
rotacyjnym widmie Ramana cząsteczki
liniowej
liczba falowa

WIDMA OSCYLACYJNE
(SPEKTROSKOPIA OSCYLACYJNA)
-drgania (oscylacje) atomów w
cząsteczce

Rodzaje oscylacji w cząsteczce zależą
od:
liczby atomów,
rodzaju atomów,
rodzaju wiązań między atomami.
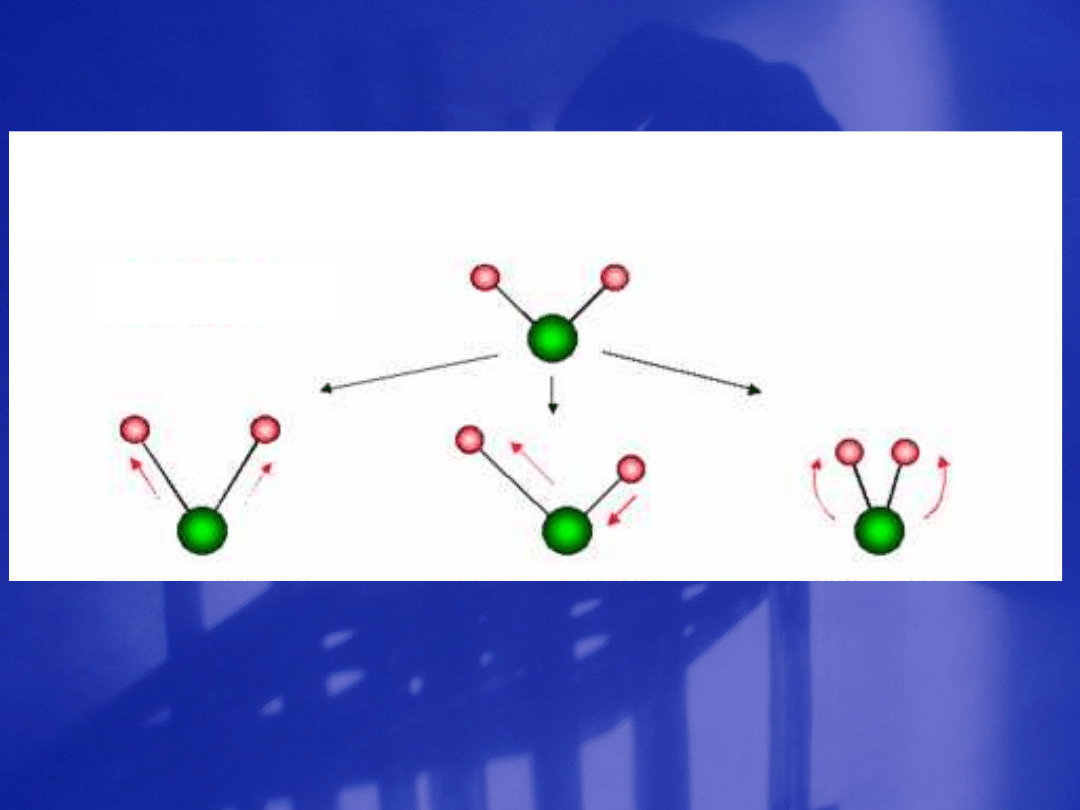
Każda cząsteczka może wykazywać wiele
rodzajów oscylacji
Przykłady:

Widma oscylacyjne cząsteczek
wieloatomowych
-cząsteczki dwuatomowe wykazują drgania
jednego rodzaju,
-cząsteczki nieliniowe wieloatomowe (N)
wykazują 3N – 6
drgań
-cząsteczki liniowe wieloatomowe (N) wykazują
3N – 5
drgań

Poziomy energetyczne oscylacji
E = (
+ ½) ħ
= 0, 1, 2,
.....
k
mm
m
m
1
2
1
2
k - stała siłowa
- kołowa częstość oscylatora,
= 2
- masa efektywna
m – masa atomu

7
6
5
4
3
2
1
0
energia
9/2ħ
7/2 ħ
5/2 ħ
3/2 ħ
1/2 ħ
0
Energia promieniowania wzbudzająca oscylacje
cząsteczek obejmuje zakresie podczerwieni.
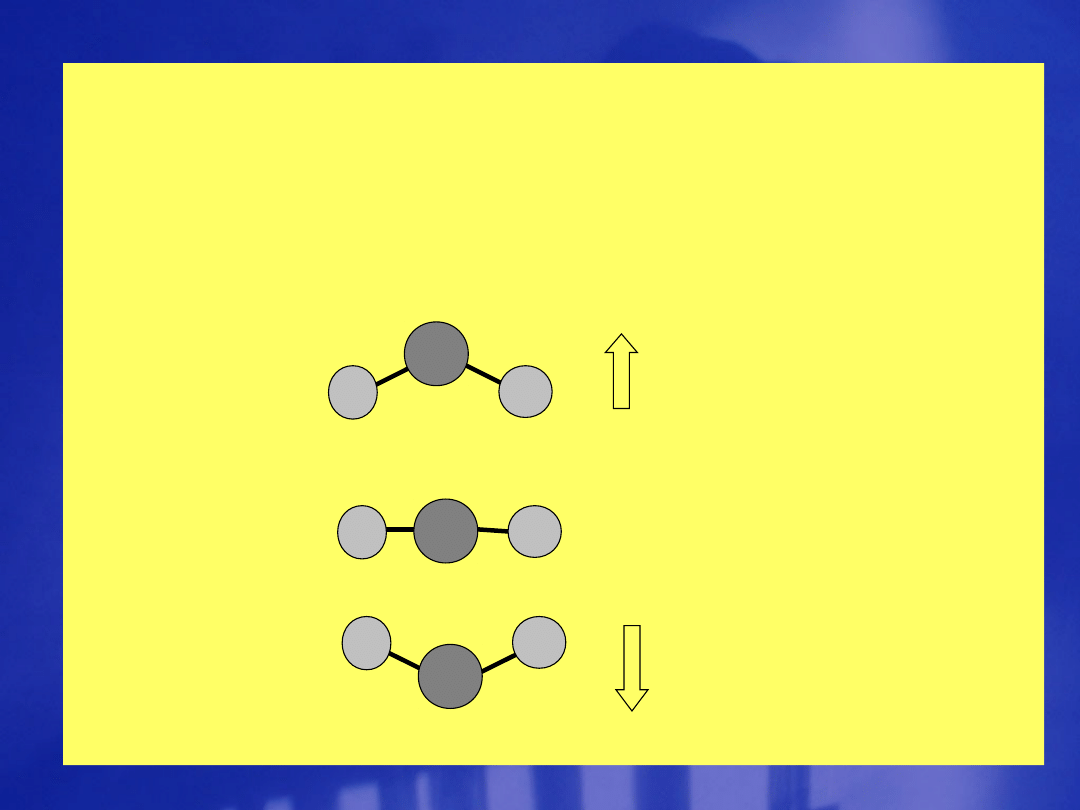
Przejścia oscylacyjne (dozwolone)
ogólna reguła wyboru
- cząsteczki muszą posiadać moment dipolowy
trwały lub chwilowy (np. cząsteczka CO
2
)

szczegółowa reguła wyboru :
= 1
E = (
+ 3/2) ħ
- (
+ ½) ħ
= ħ
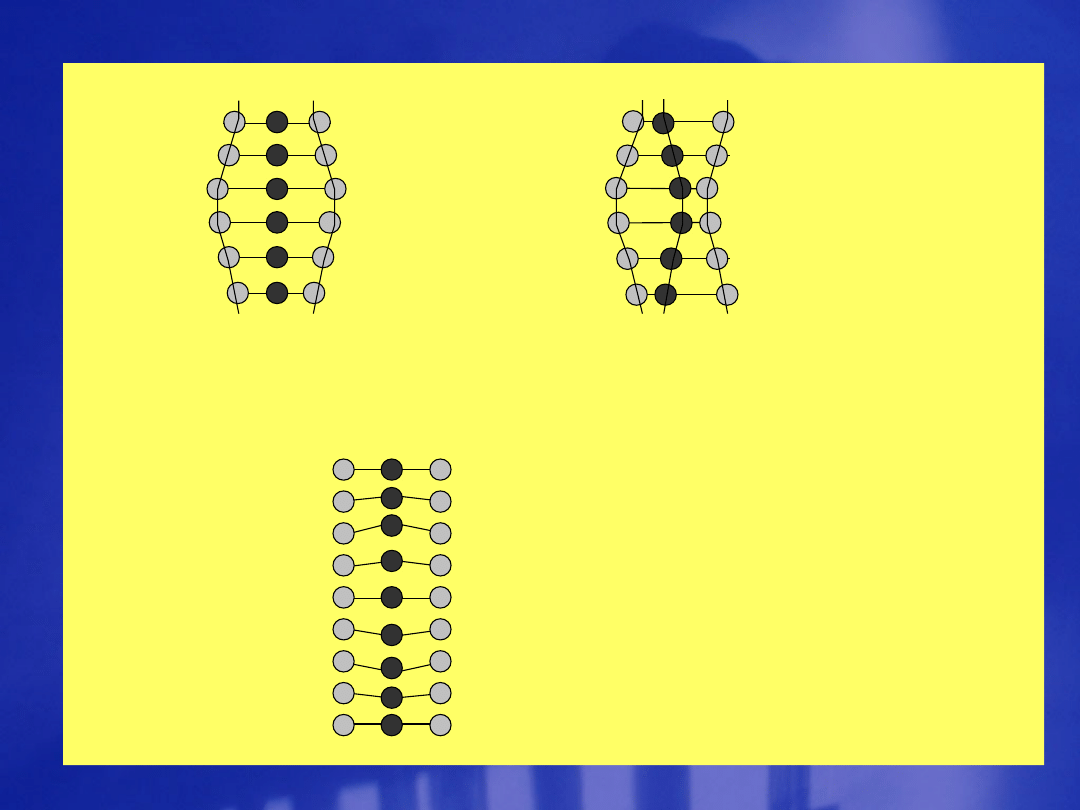
CO
2
Drgania symetryczne Drgania
antysymetryczne
rozciągające rozciągające
Drgania
zginające
cząsteczki CO
2

T
ra
n
sm
it
a
n
cj
a
,
(%
)
4000 3000 2000
1000
Typowe widmo oscylacyjne w podczerwieni
próbki w postaci pastylki z KBr
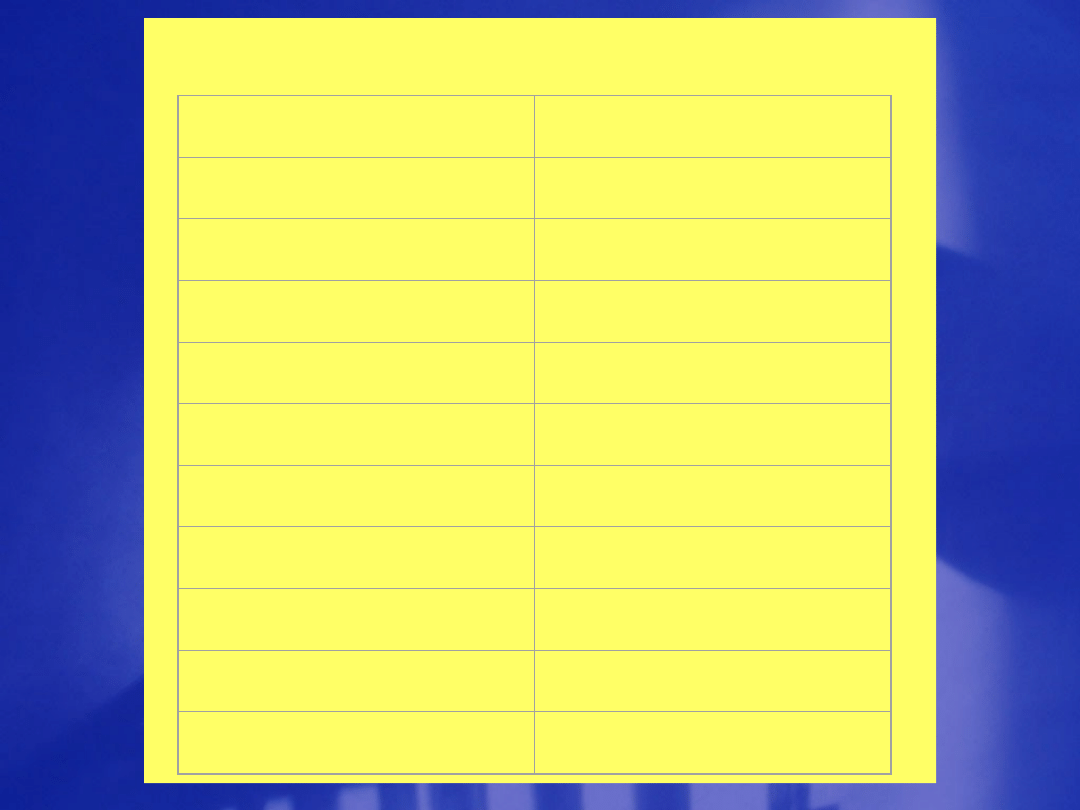
Typowe wartości liczb falowych
oscylacji
Rodzaj drgania
Liczba falowa, , (cm
-
1
)
C-H rozciągające
2850 – 2960
C-H zginające
1340 – 1465
C-C rozciągające,
zginające
700 - 1250
C=C rozciągające
2100 – 2260
CC rozciągające
2100 – 2260
O-H rozciągające
3590 – 3650
C=O rozciągające
1640 – 1780
CN rozciągające
2215 – 2275
N-H rozciągające
3200 – 3500
Wiązania wodorowe
3200 – 3570
~

Oscylacyjne widma Ramana cząsteczek
dwuatomowych
ogólna reguła wyboru:
-wymaga by w trakcie oscylacji ulegała
zmianie polaryzowalność cząsteczki
szczegółowa reguła wyboru:
= 1
Oscylacyjne widma Ramana cząsteczek
wieloatomowych
- zmiana polaryzowalności cząsteczki w wyniku jej
oscylacji to warunek występowania oscylacyjnego
widma Ramana
Z a k a z a l t e r n a t y w n y: żadne drganie
(oscylacja) cząsteczki symetrycznej względem
operacji inwersji nie wykazuje jednoczesnej
aktywności w podczerwieni i widmie Ramana, ale
może być nieaktywne w obu.
Operacja inwersji

In
te
n
sy
w
n
o
ść
1500
1000
500
Przykład oscylacyjnego widma
Ramana
~ ~(
)
O
cm
1

Spektroskopia przejść elektronowych,
widma w obszarze widzialnym i nadfiolecie
Barwa Długość fali Częstość Liczba
falowa
~
Barwa
, nm
, 10
14
Hz
,
10
4
cm
-1
Podczerw
ień
1000
3,00
1,00
Czerwona
700
4,28
1,43
Fioletowa
420
7,14
2,38
Bliski
nadfiolet
300
10,0
3,33
Daleki
nadfiolet
200
15,0
5,00

Koło barw, barwy wzajemnie
dopełniające
a
b
so
rb
a
n
cj
a
400
600 800
(nm)

Masy jąder atomowych znacznie przewyższają
masę elektronu, przejścia elektronowe zachodzą
szybciej niż zdąży na nie zareagować układ
jąder.
a
b
so
rb
a
n
cj
a
Długość fali,
Elektronowe pasmo
absorpcyjne

W fazie gazowej brak
rozpuszczalnika
powoduje minimalny
efekt wpływu
oddzialywań
międzycząsteczkowy

Wpływ
rozpuszczalnika
Faza
gazowa
W
heksanie
W wodzie

R ó ż n e t y p y p r z e j ś ć e l e k t r o n
o w y c h
Orbitale
*
(antywiążące)
Orbitale
*
(antywiążące)
Orbitale n
(niewiążące)
Orbitale
(wiążące)
Orbitale
(wiążące)
S
ta
n
y
w
zb
u
d
zo
n
e
S
ta
n
y
p
o
d
st
a
w
o
w
e
E
=
h
=
h
c/
n
*
*
n
*
*
*

Przejście n
*
Przejście n
*
Przejście
*
Przejście
*
Przejście
*
Przejście
*
Przejście z przeniesieniem
ładunku.

Chromofory - grupy atomów
wykazujące charakterystyczne
pasmo absorpcji:
-NO
2
, >CO, -N=O, >C=S,
-N=N-,
>C=C-C=C, (-C=C-)
3
, (-
C=C-)
4
,
(-C=C-)
5
, benzen, naftalen,
difenyl)

*
*
*, 175
nm
*
*
n n
*, 280
nm
*, 185
nm
>C=C< E =
h
>C=O:: E =
h

*
*
n n
*,
170 nm
*
*
n
*, 120
nm
CH
3
-Cl::: E = h
CH
4
E
= h
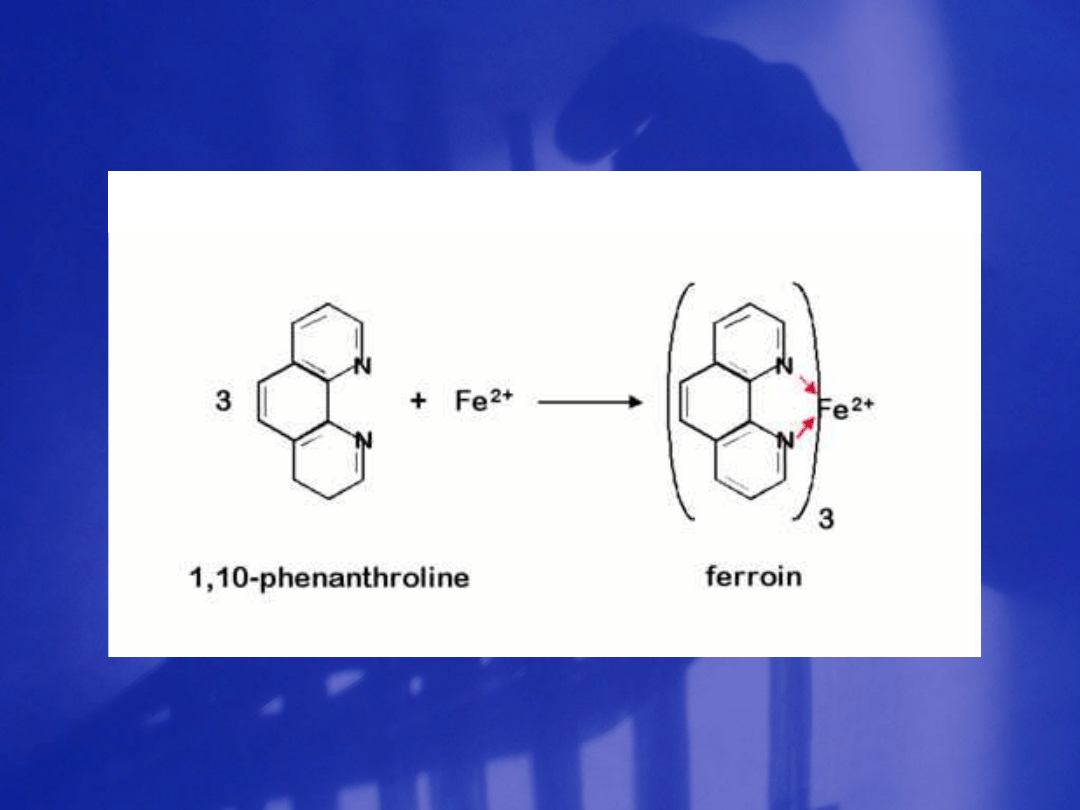
Kompleks z przeniesieniem ładunku

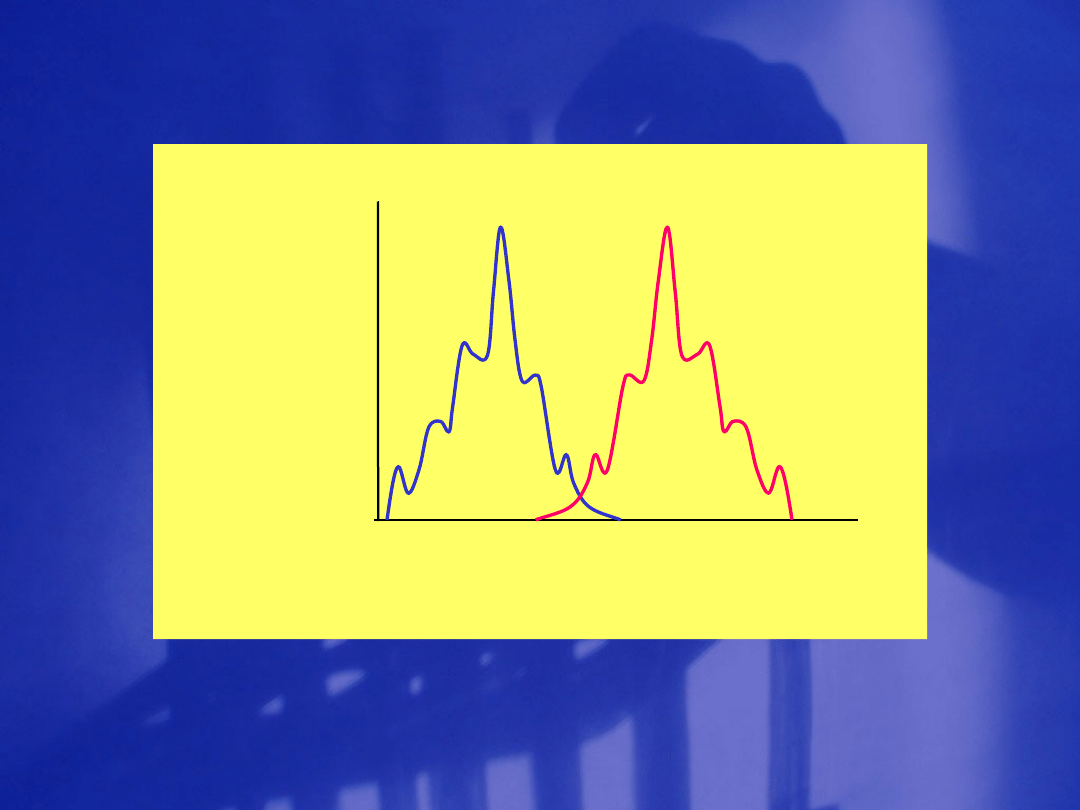
Zanik promienisty
F l u o r e s c e n c j a
F o s f o r o s c e n c j a
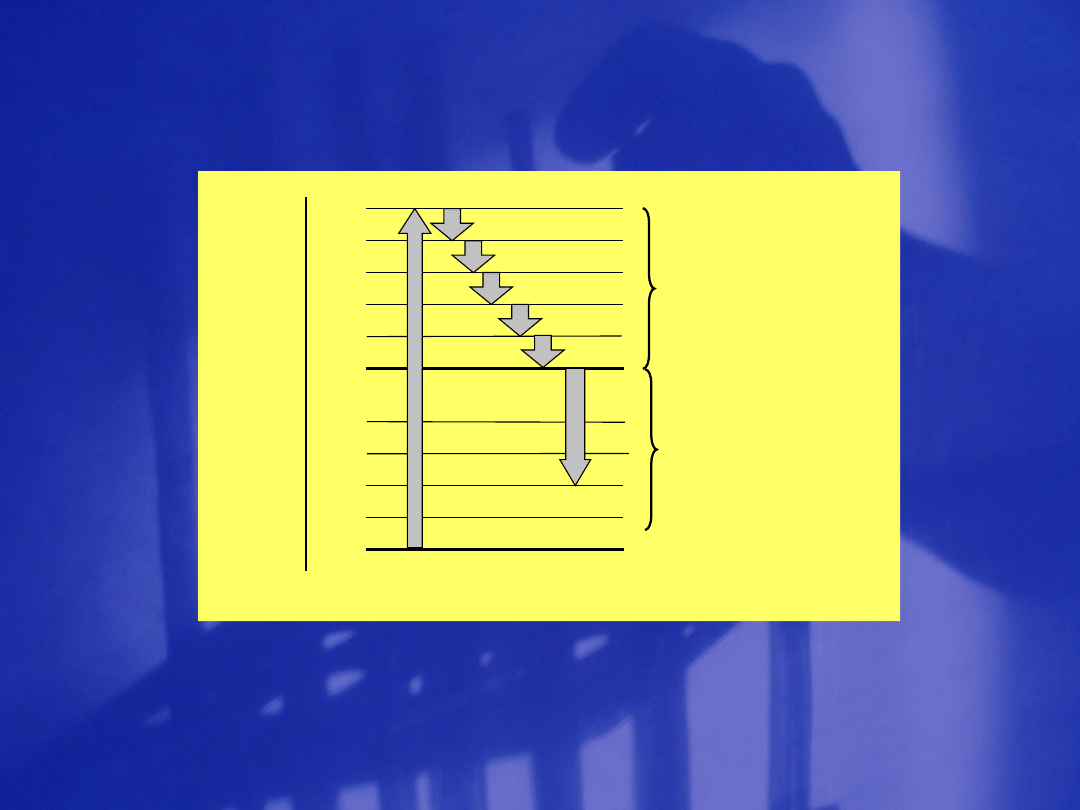
e
n
e
r
g
i
a
a
b
s
o
r
p
c
j
a
re
la
k
sa
cj
a
o
sc
yl
a
cy
j
n
a
f
u
o
re
sc
e
n
cj
a
In
te
n
sy
w
-n
o
ść
a
b
so
rp
c
ji
l
u
b
e
m
is
ji
absorp
cja
fuorescenc
ja
Długość fali,
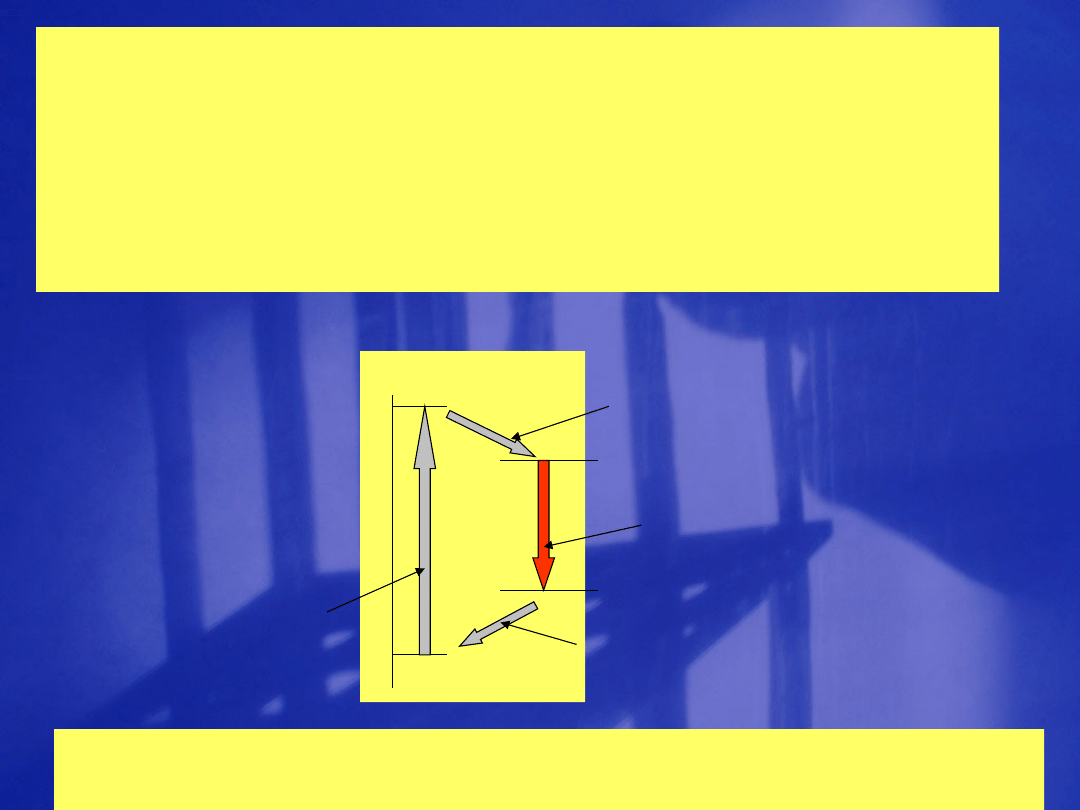
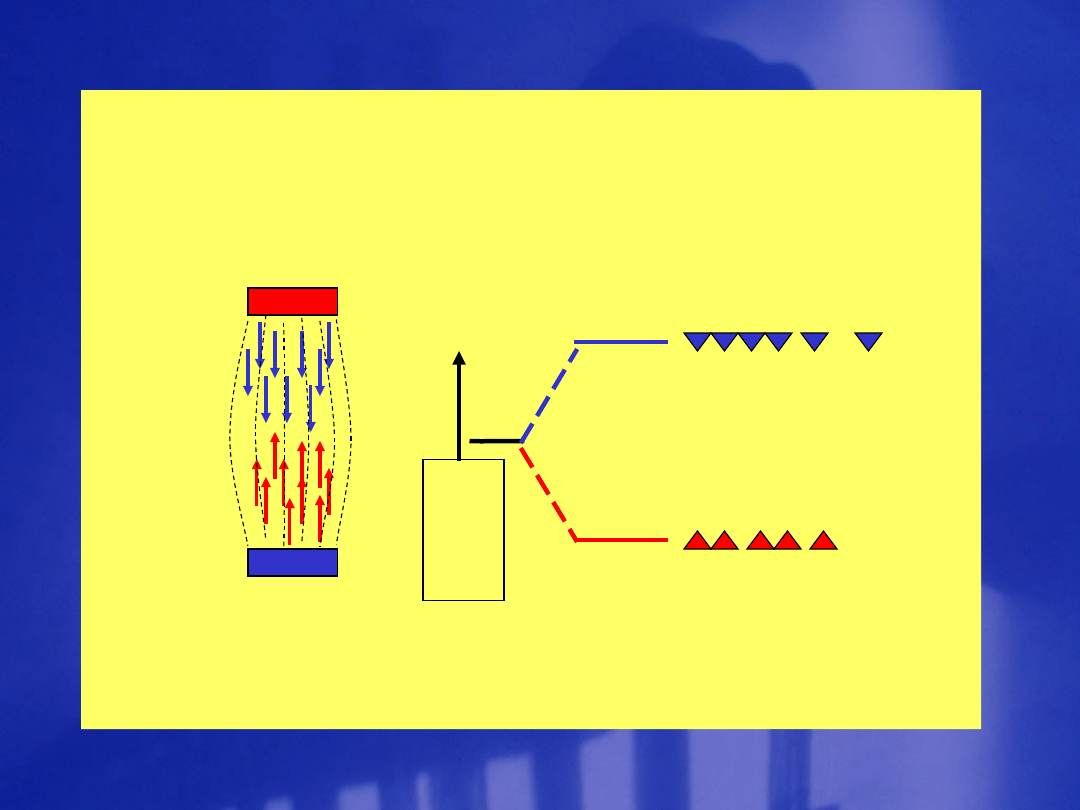
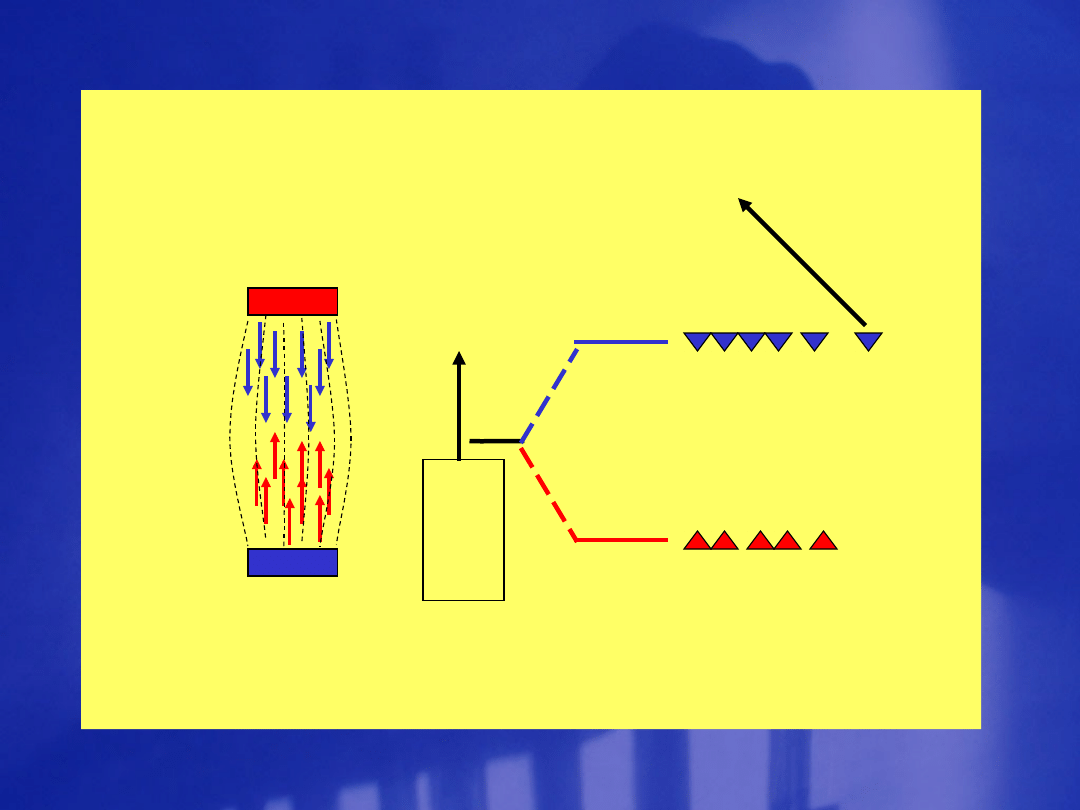
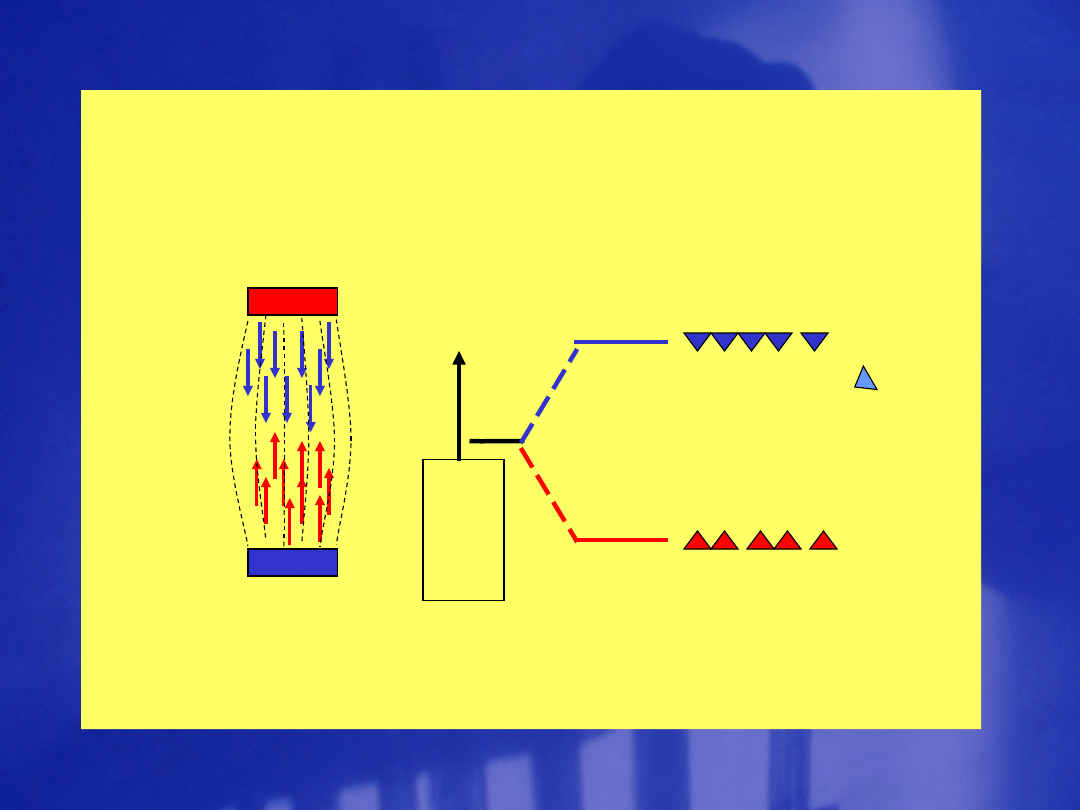
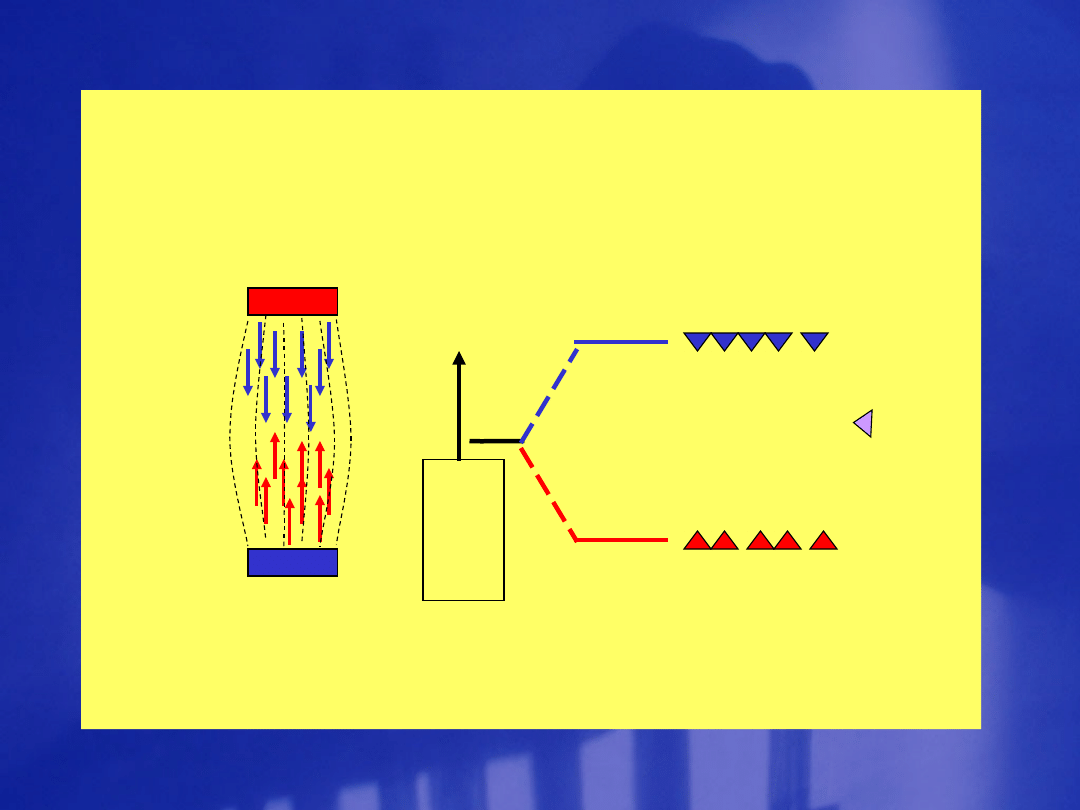
L a s e r y
Emisja wymuszana – proces przebiegający w
laserach
Przejście
bezpromieniste
E
n
e
rg
i
a
X
I
Pompowa
nie
optyczne
Przejście
bezpromien
iste
Przejśc
ie
lasero
we
Relaksac
ja
B
A
Przejścia energetyczne zachodzące w laserze
czteropoziomowym

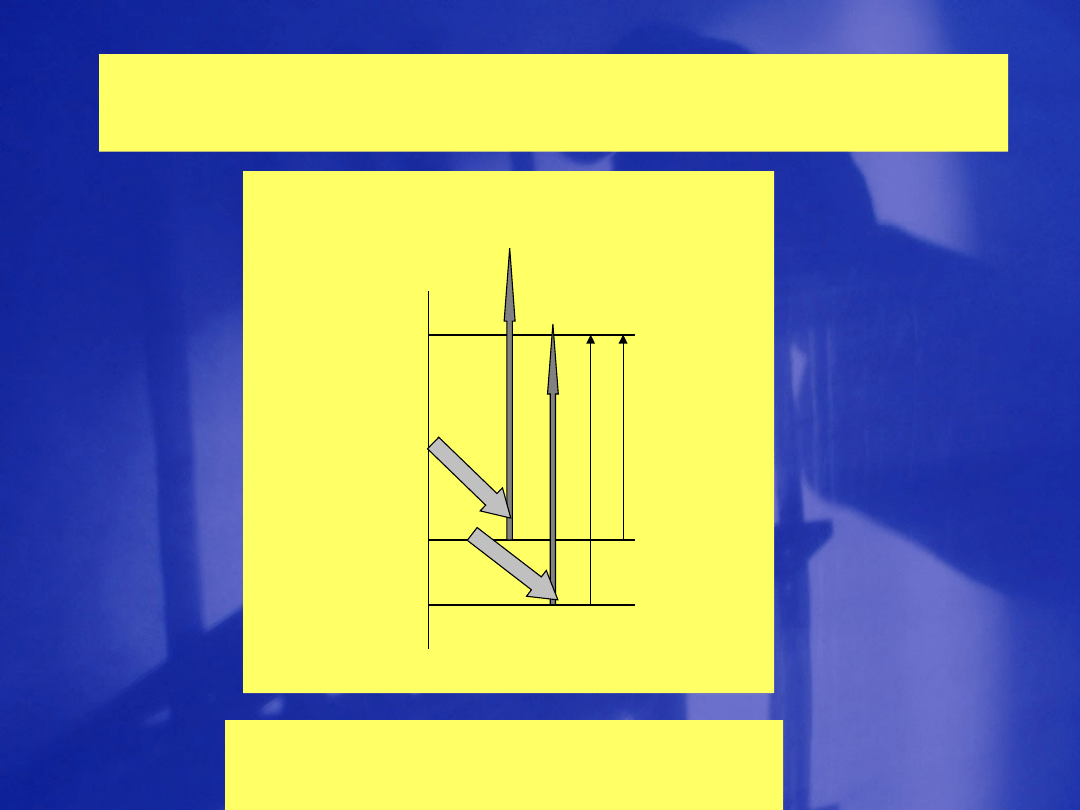
Laser trójstopniowy
Elektron
jest
pompowany
do wyższego
poziomu
energetyczn
ego
Elektron
schodzi na
niższy
poziom i
wyzwala
foton
wytwarzają
dwa fotony
o tej samej
energii i
fazie
Elektron
przeskakuje na
nieco niższy
poziom
energetyczny
Światło i
elektron na
poziomie
wzbudzenia
energetycznego
....
Lustro odbija
fotony
1
2
3
4
5
6
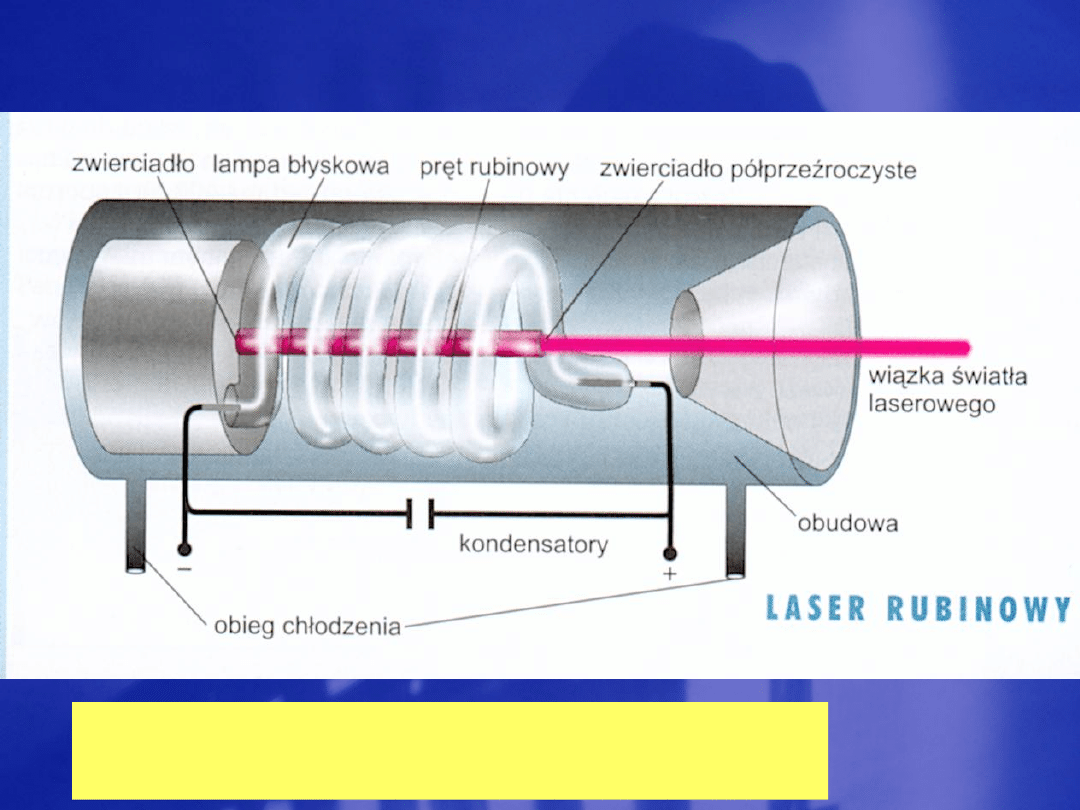
Pierwszy laser: Theodore Maiman
(1960 r.)

Warunki akcji laserowej:
- stan wzbudzony o dostatecznie długim
czasie życia
-
- obsadzenie wyższego stanu
energetycznego większe
niż stanu
niższego


S p e k t r o s k o p i a f o t o e l e k t r o n
ó w
energi
a
elektron
szybki
l
1
l
2
Zasada spektroskopii
fotoelektronów

Różnice między spektroskopią elektronową a
spektroskopią fotoelektronów
Fotoemisja – wybicie z cząsteczki elektronu na skutek
działania promieniowania o dużej częstości.
Fotoelektrony – energia fotoelektronów
h
= I + 0,5 m
e
2
energia jonizacji - I ,
energia kinetyczna: 0,5 m
e
2
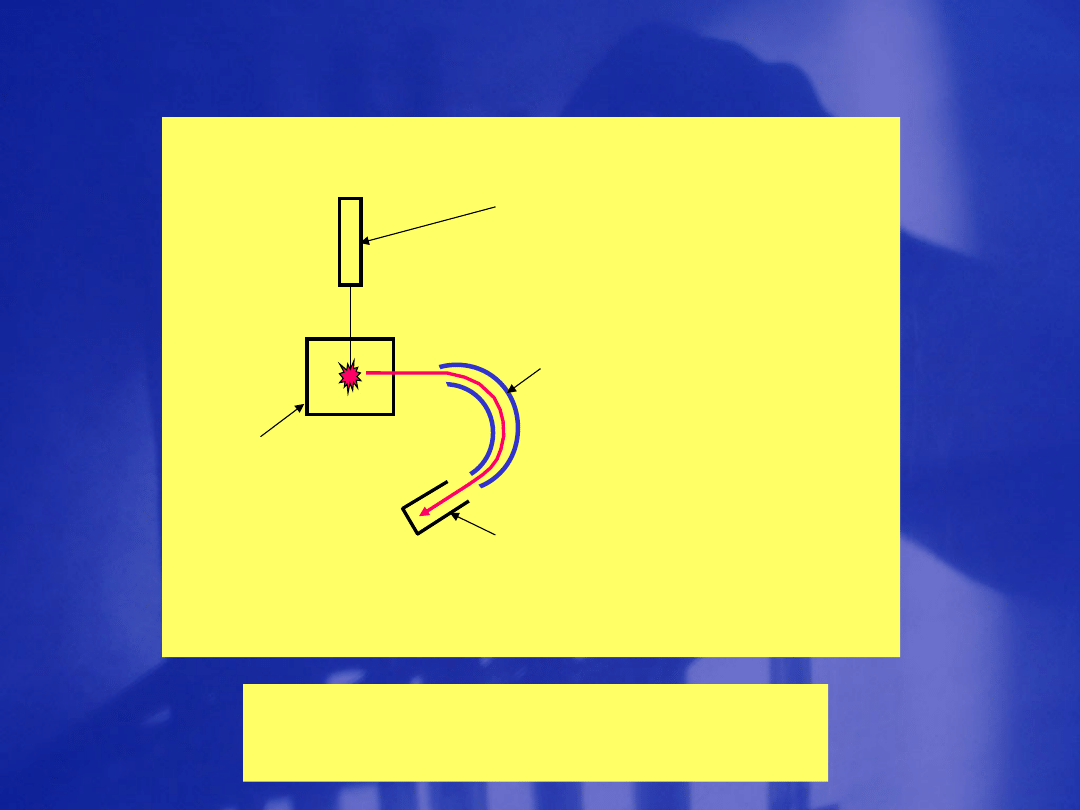
Źródło
promieniowania
jonizującego
Analizator
elektrostatyc
zny
Komora
jonizacji
Detekt
or
Schemat spektrometru
fotoelektronów

Sygna
ł
I
(eV)
17 15 13 11
9
Widmo fotoelektronów
HBr

Jądrowy rezonans magnetyczny (NMR)
Jądra niektórych izotopów obracają się wokół
swojej osi
i mają jądrowy moment pędu czyli spin jądrowy, I,
który może przyjąć
2I + 1
różnych orientacji względem arbitralnie
wybranej osi różniących się wartością liczby
kwantowej:
m
I
= I, I-1, ..., -I
Jądra o parzystej liczbie protonów i neutronów
mają spin równy 0 i nie są aktywne w NMR.
Dla protonu I = ½ ( m
I
= ½, i m
I
= -1/2)

E n e r g i a j ą d e r w p o l a c h m a g n e t
y c z n y c h:
E
mI
= -g
I
N
B
m
I
B – indukcja pola magnetycznego
g – stała charakterystyczna dla danego jądra
N
- magneton jądrowy
m
P
- masa protonu
1
27
10
051
,
2
2
JT
P
N
m
h
e

Pole
wyłączo
ne
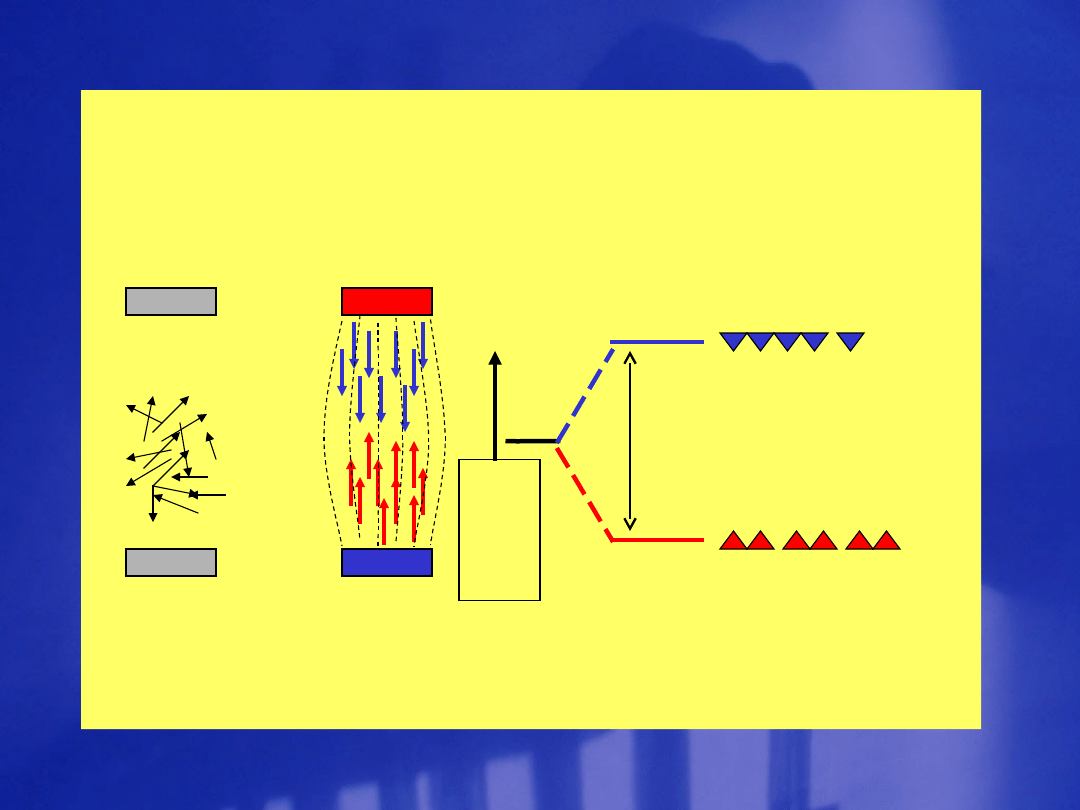
en
er
gia
E
- E
= g
I
N
B
Pole
wyłączo
ne
Pole
włączone
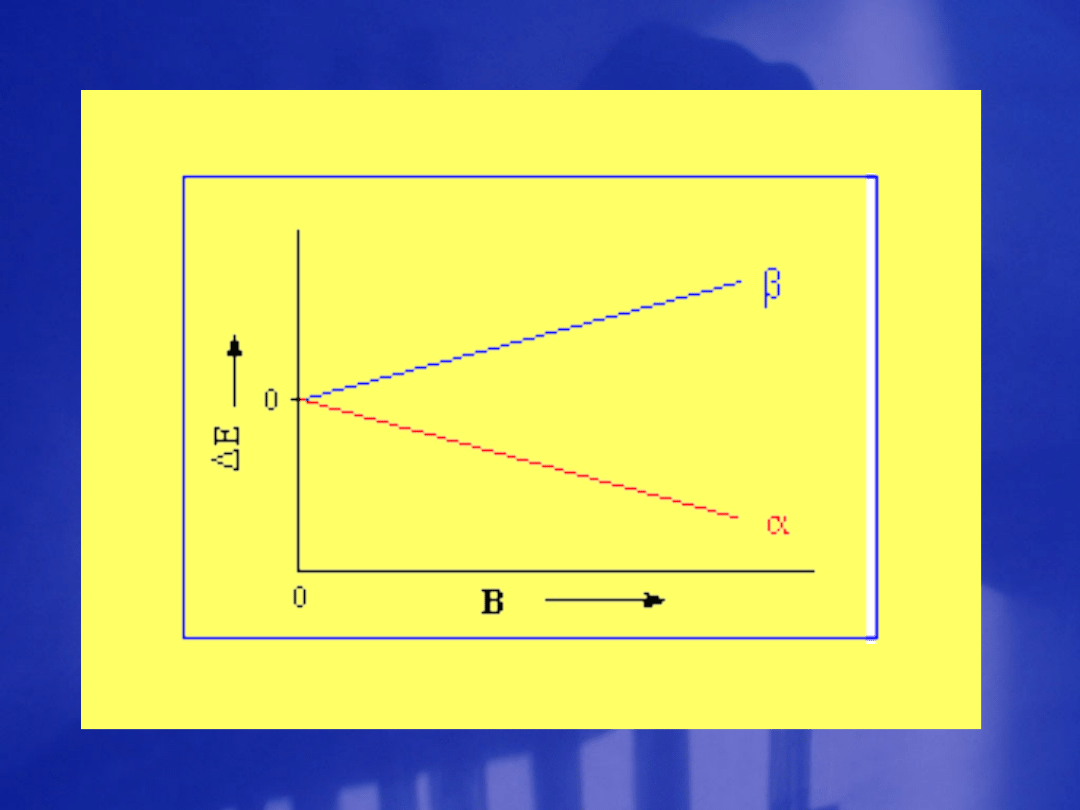
E
- E
= g
I
N
B
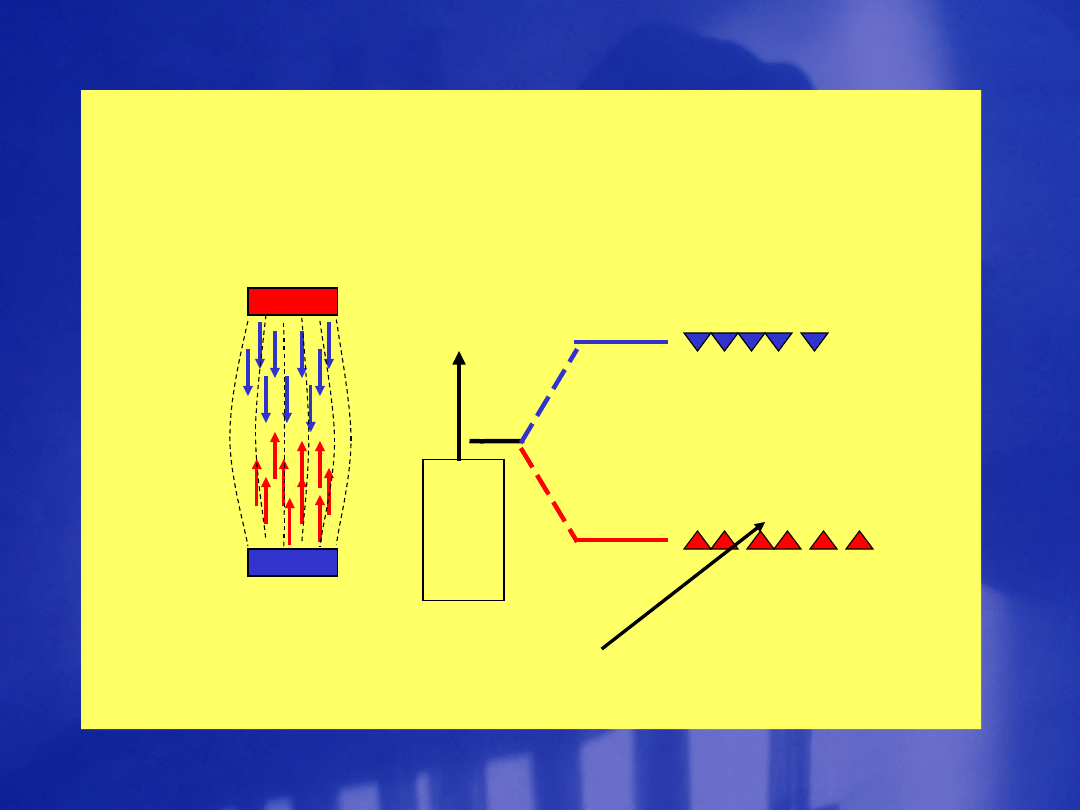
en
er
gia
h
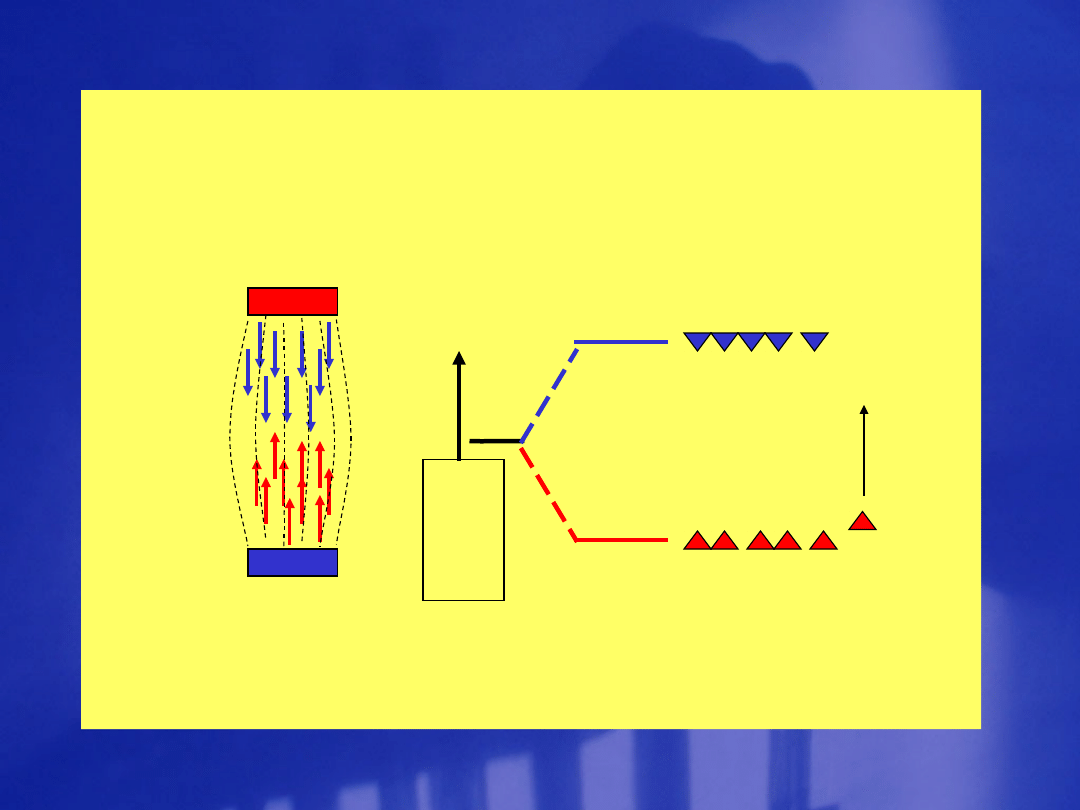
en
er
gia
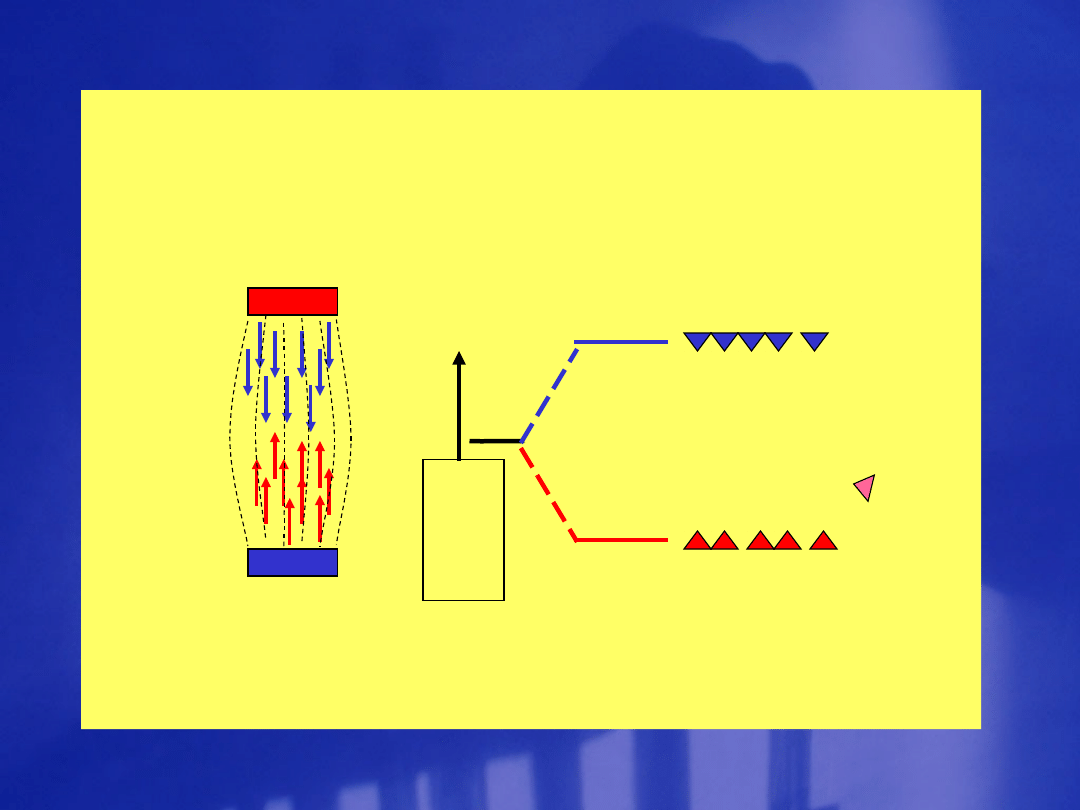
en
er
gia
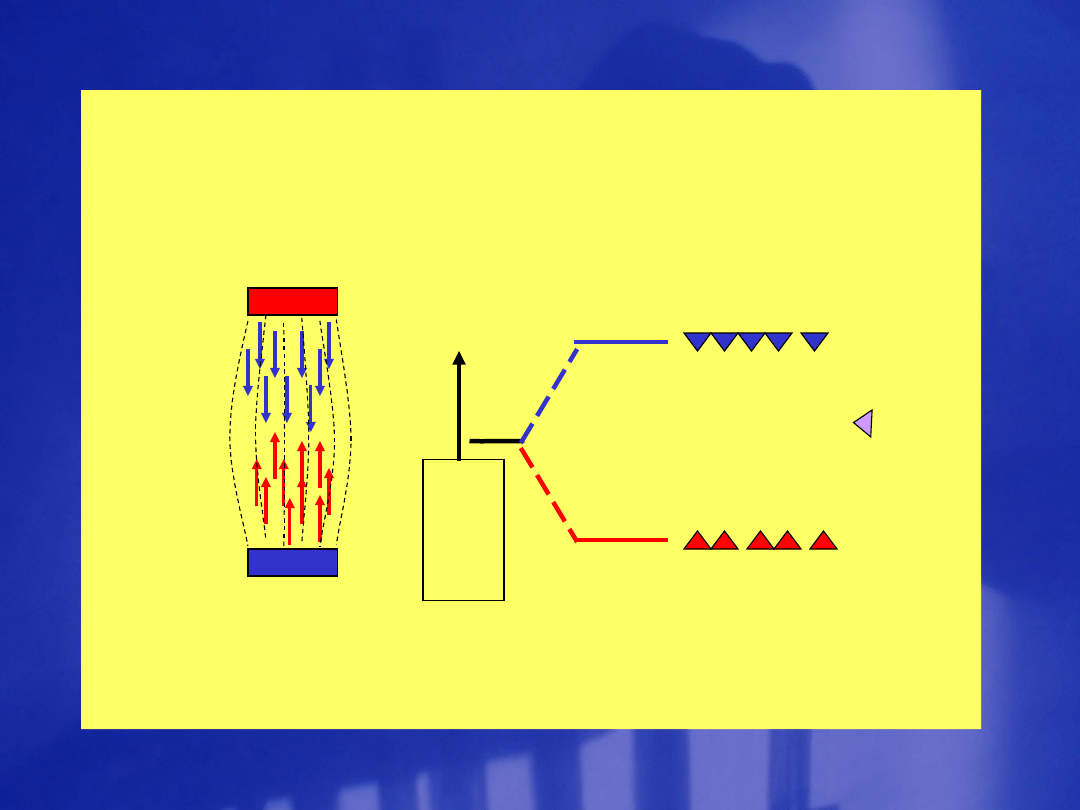
en
er
gia
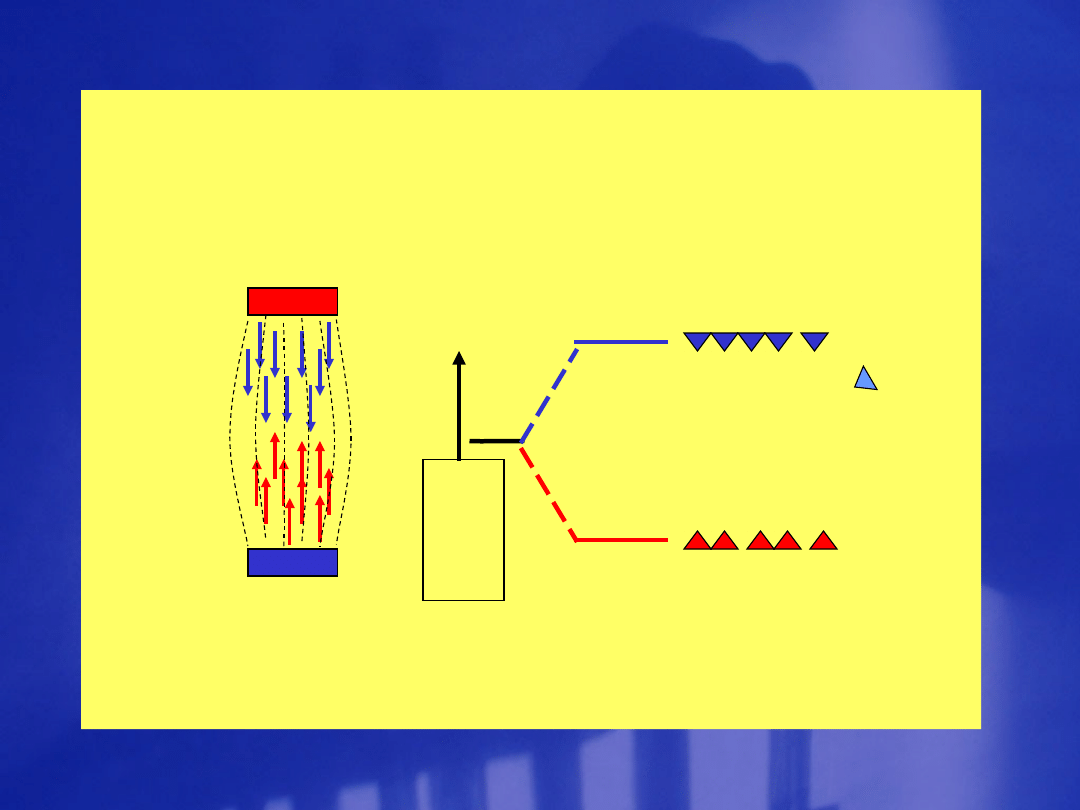
en
er
gia
en
er
gia
en
er
gia
h
en
er
gia
en
er
gia
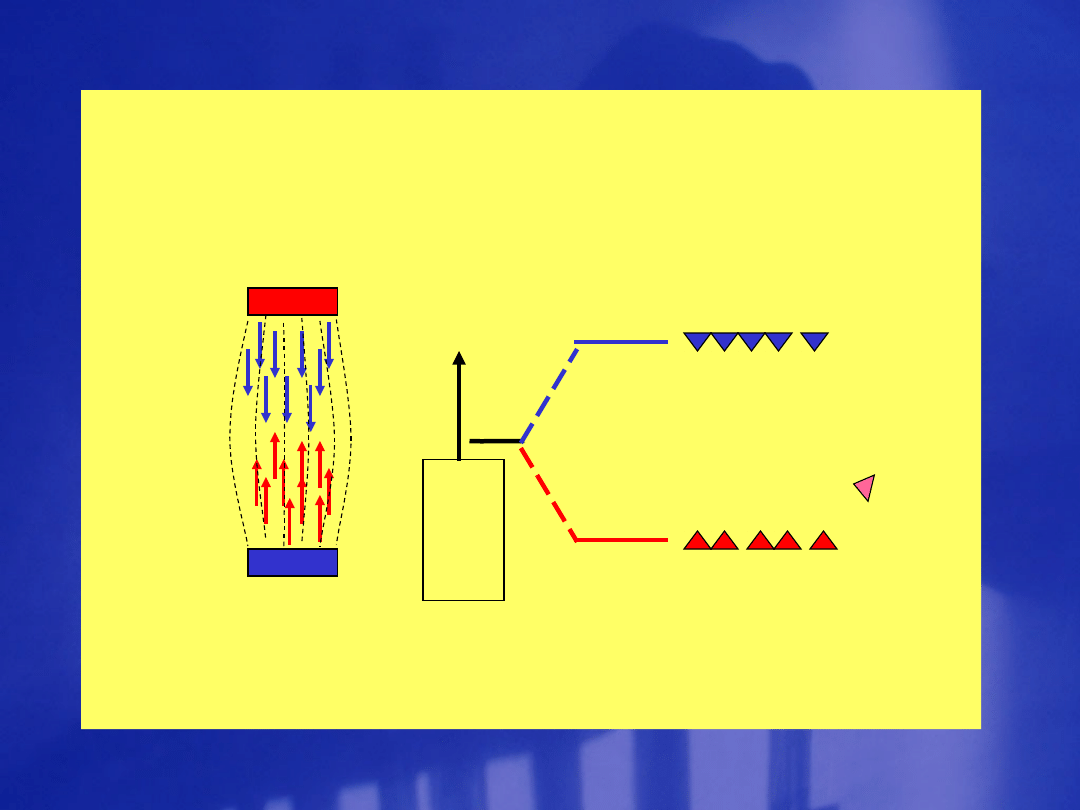
en
er
gia
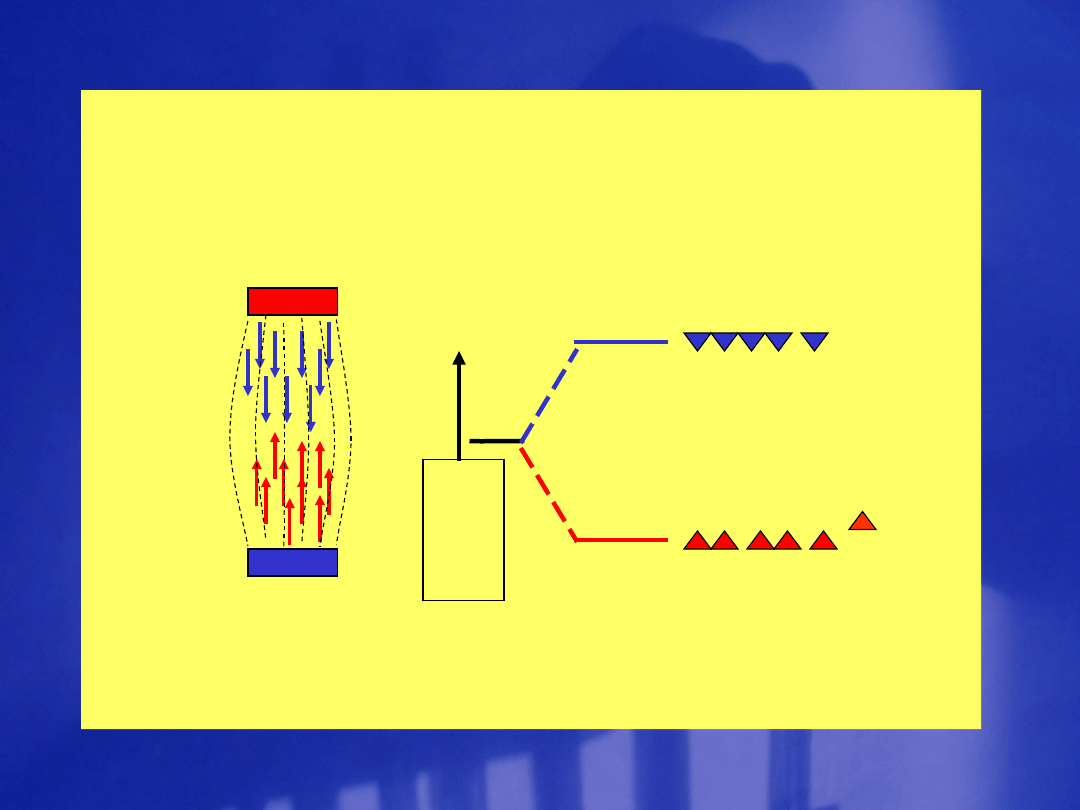
en
er
gia
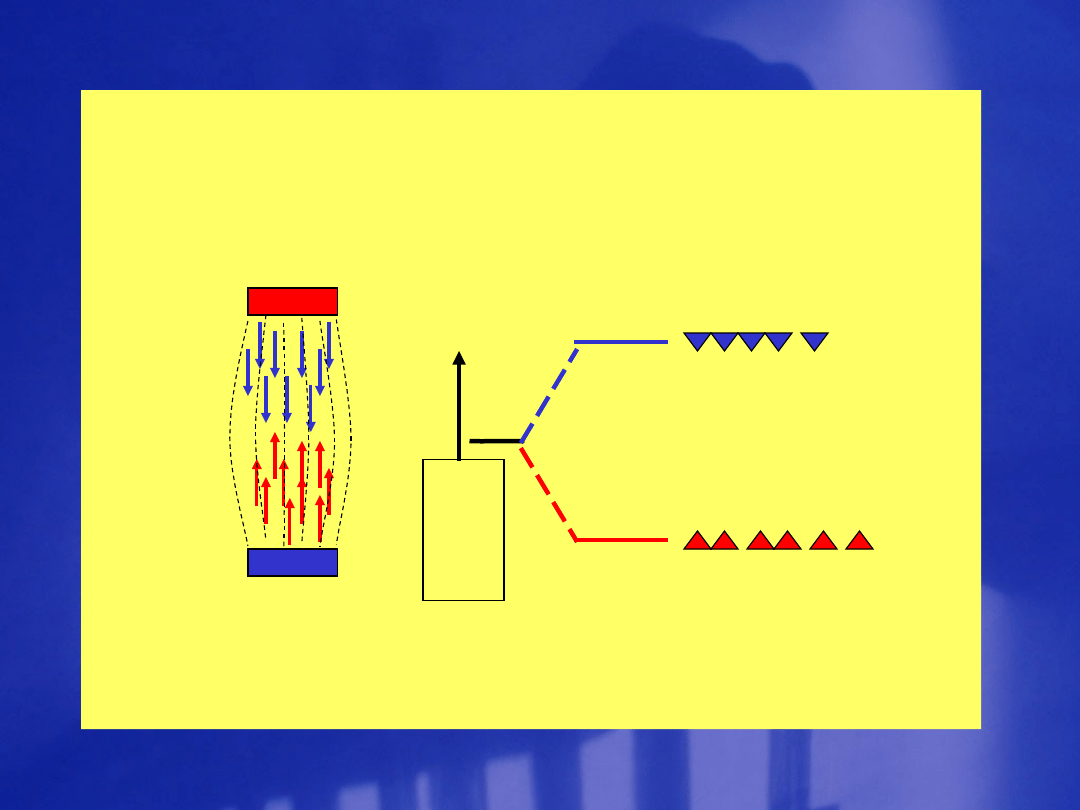
en
er
gia
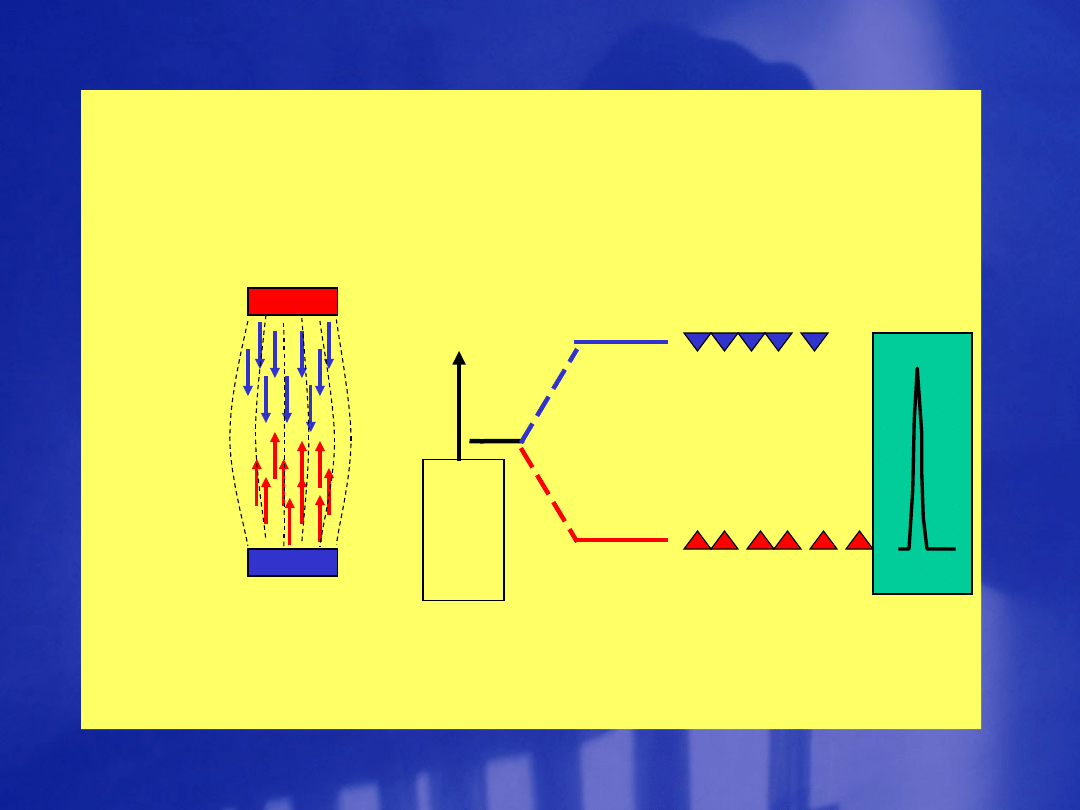
en
er
gia
N
S
h
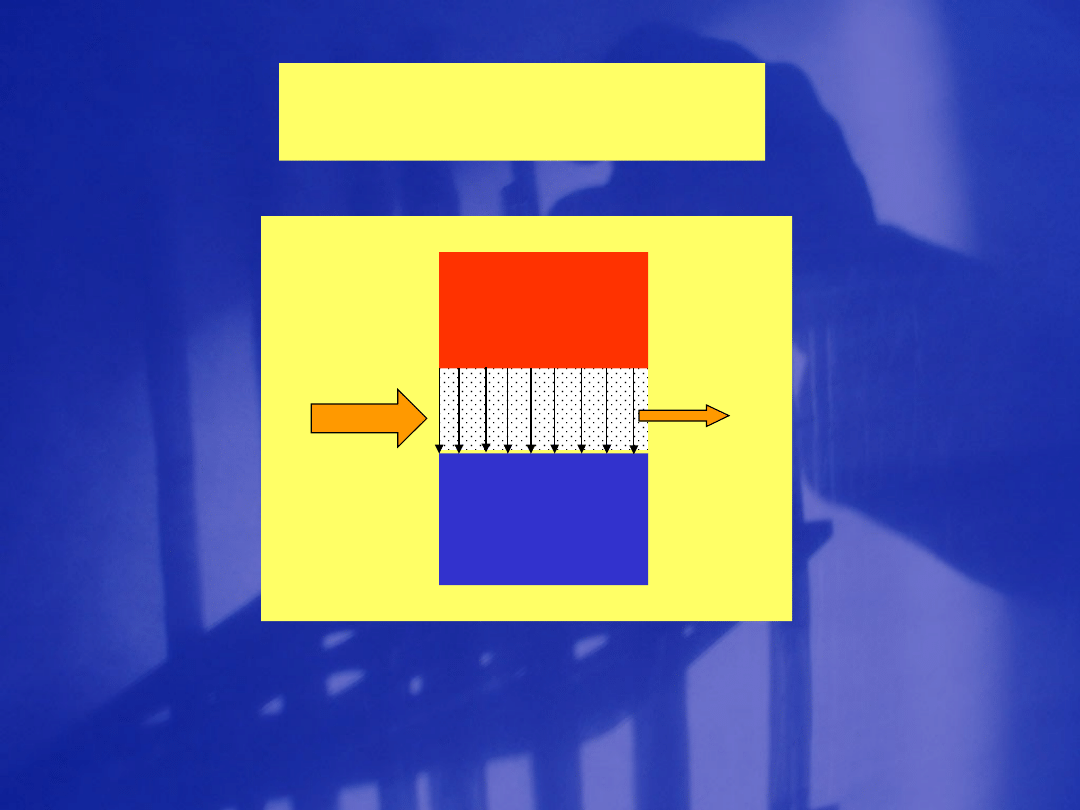
T e c h n i k a p o m i a
r ó w
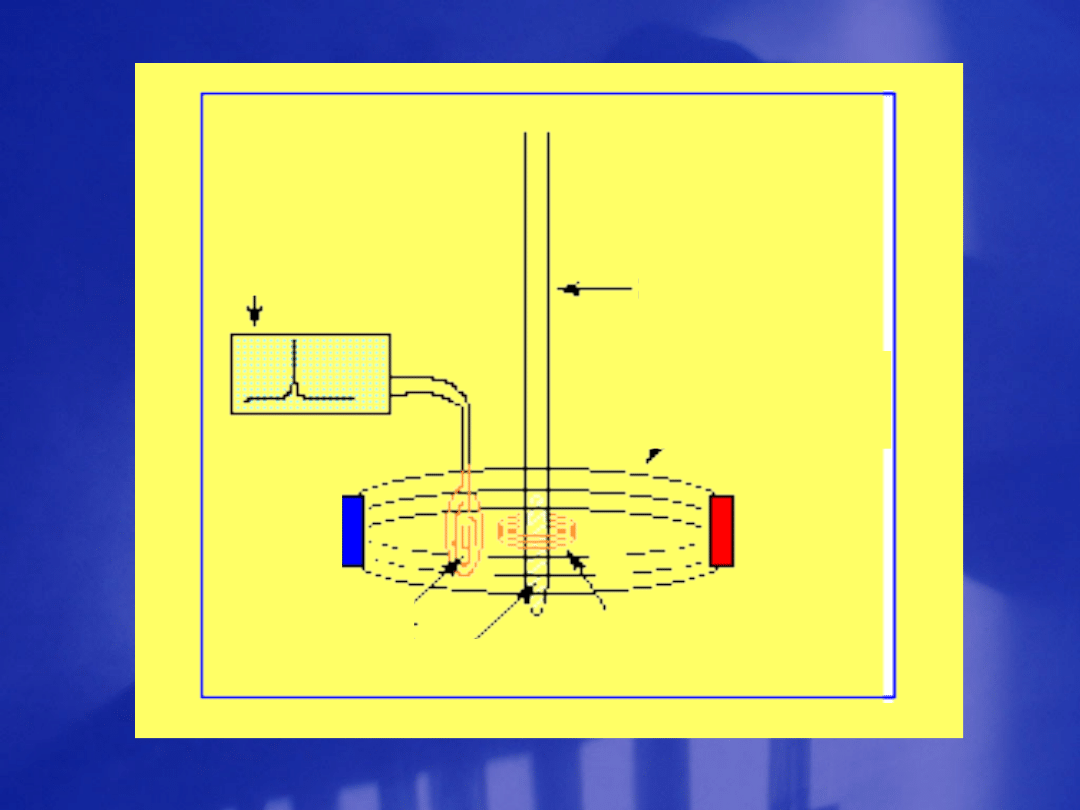
rurka
Pole
magnetyczne
Bieg
un N
Biegu
n S
Odbiorni
k RF
Próbka
Nadajnik RF
Rejestra
tor
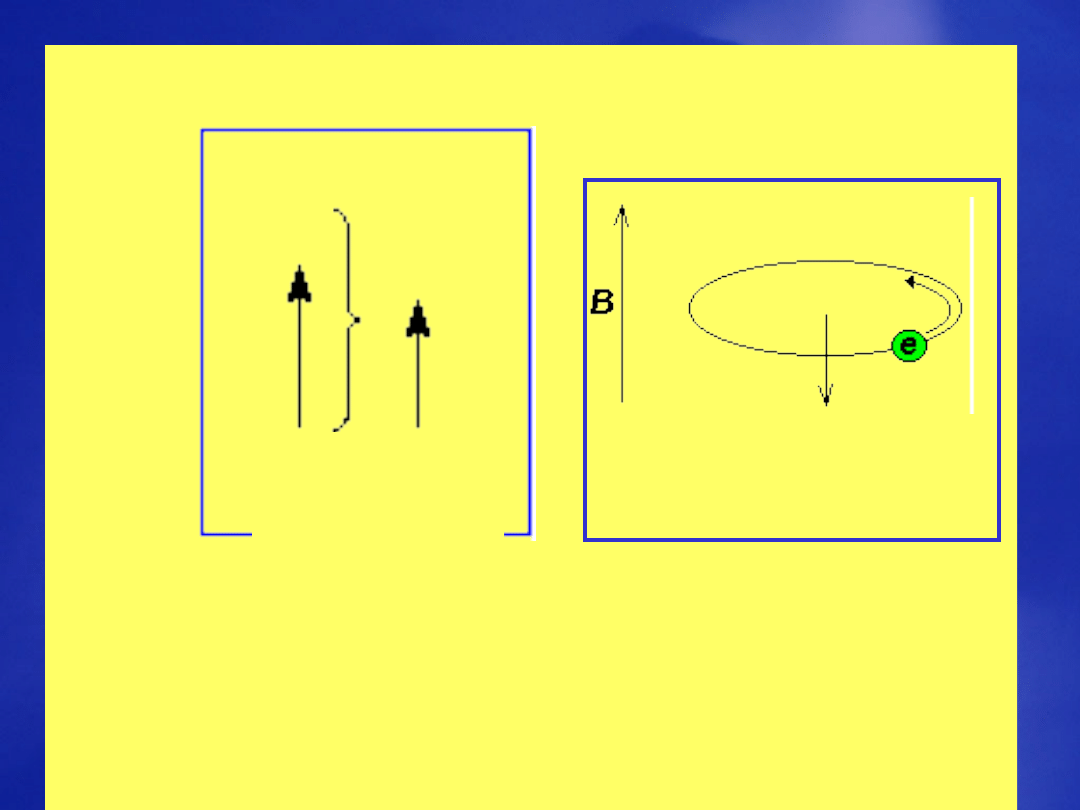
Informacje uzyskiwane w
spektroskopii NMR
B
lok
= B +
B = (1 - )B
h
= g
I
N
B
lok
B
B
lok
B
e
Pole magnetyczne
wytwarzane przez
elektron

Przesunięcie chemiczne,
,
jakiegoś
jądra w widmie NMR to różnica
pomiędzy częstością rezonansową dla
tego jądra a częstością rezonansową dla
substancji wzorcowej (tetrametylosilan,
TMS, Si(CH
3
)
4
, dla rezonansu
protonowego).
o
– częstość rezonansowa wzorca
6
10
O
O
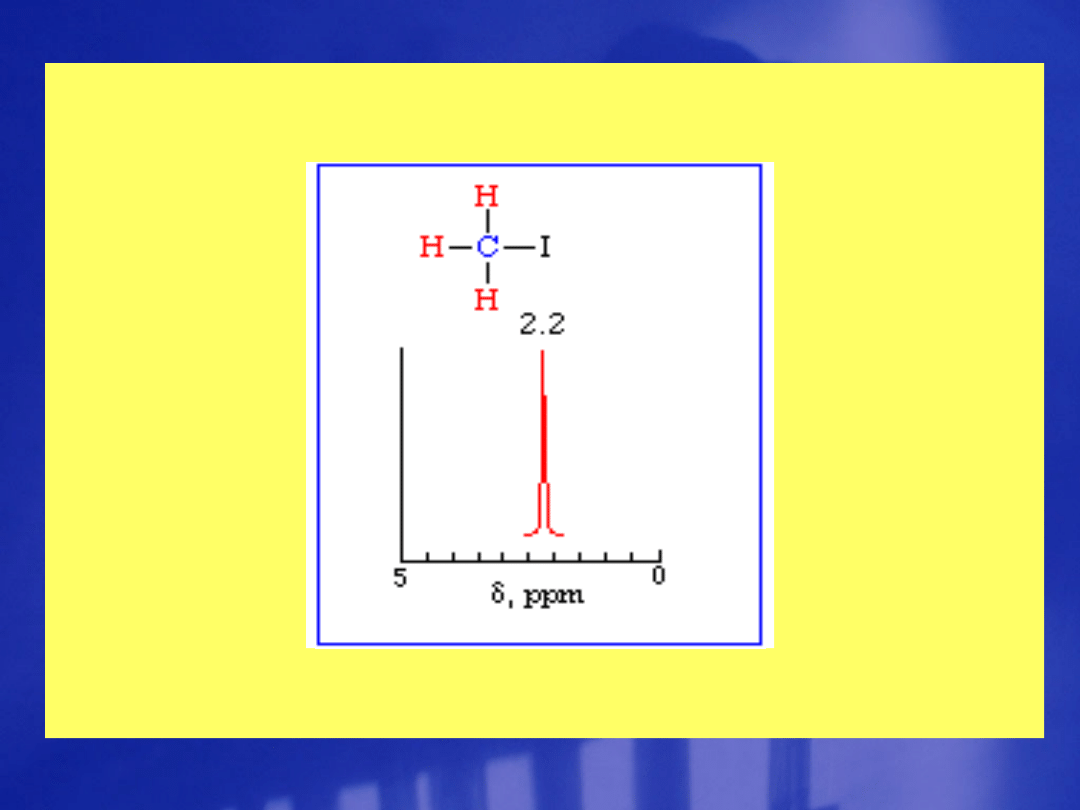
Widma HNMR prostych
substancji
Większa gęstość elektronowa w atomach wodoru –
większa zmiana częstości rezonansowej (większe
przesunięcie chemiczne)

6 5 4 3 2 1
0
OH
CH
2
CH
3
Widmo NMR protonów etanolu. Słaba
rozdzielczość.
Stosunek powierzchni pików 1 : 2 : 3
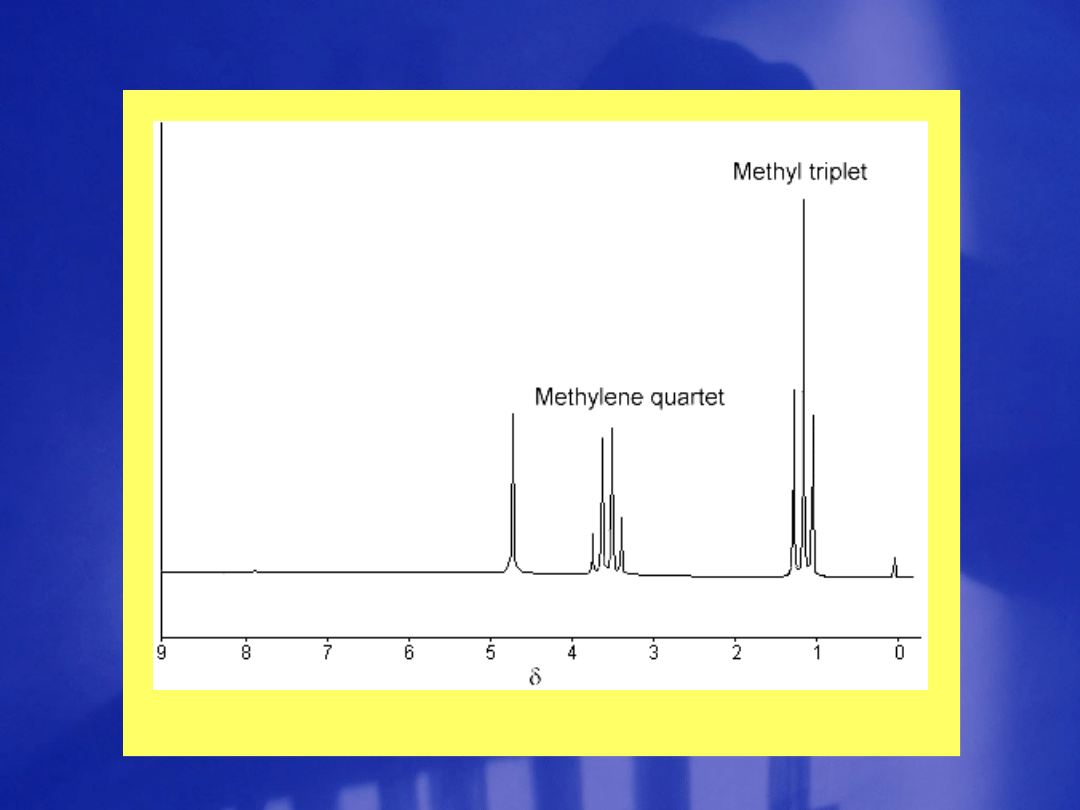
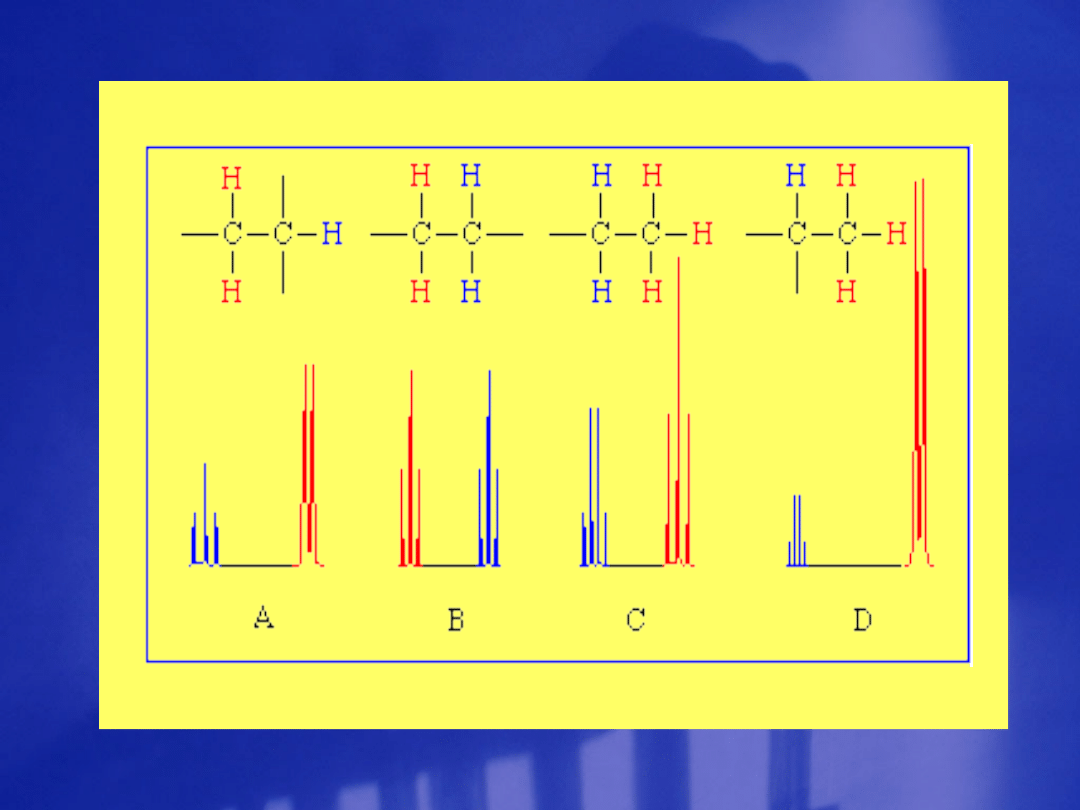
Widmo NMR protonów etanolu. Wysoka rozdzielczość.
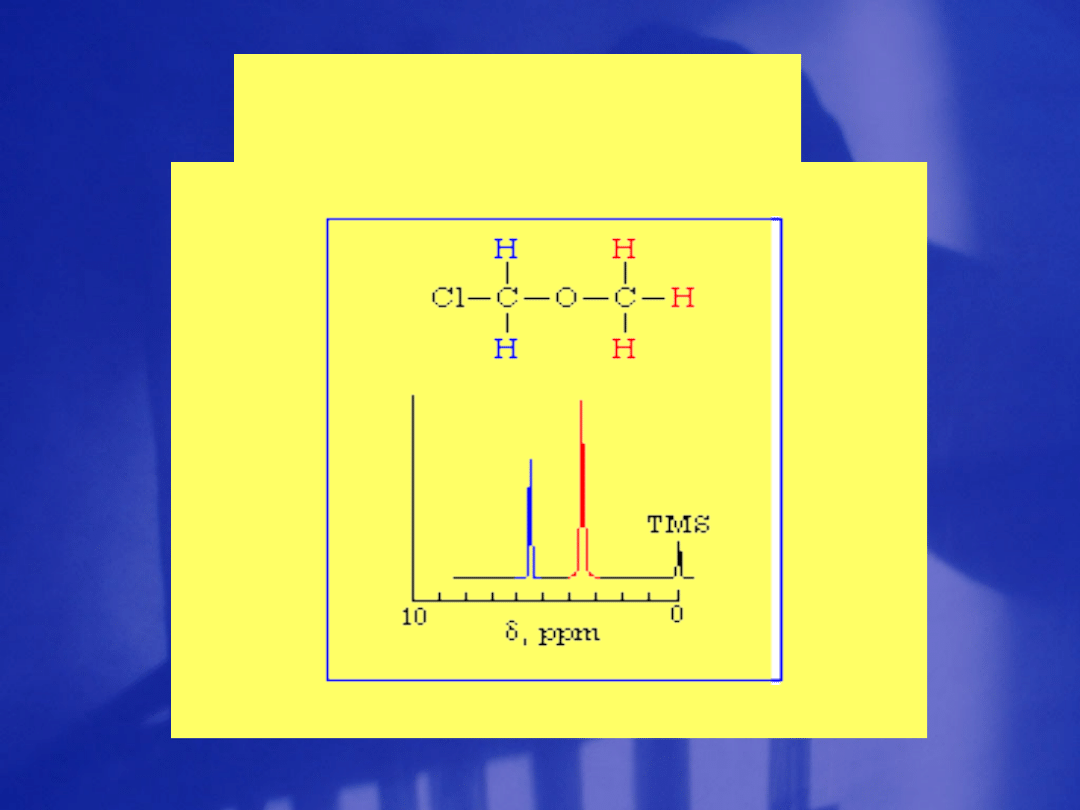
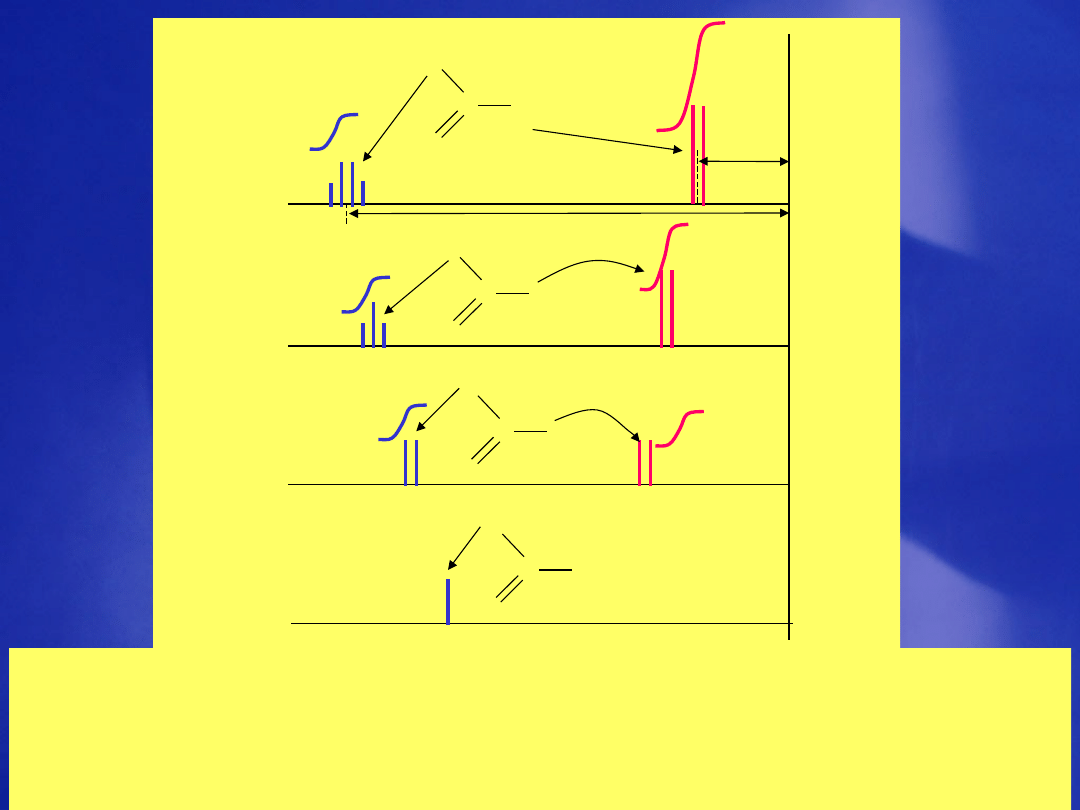
Sprzężenie spinowo -
spinowe
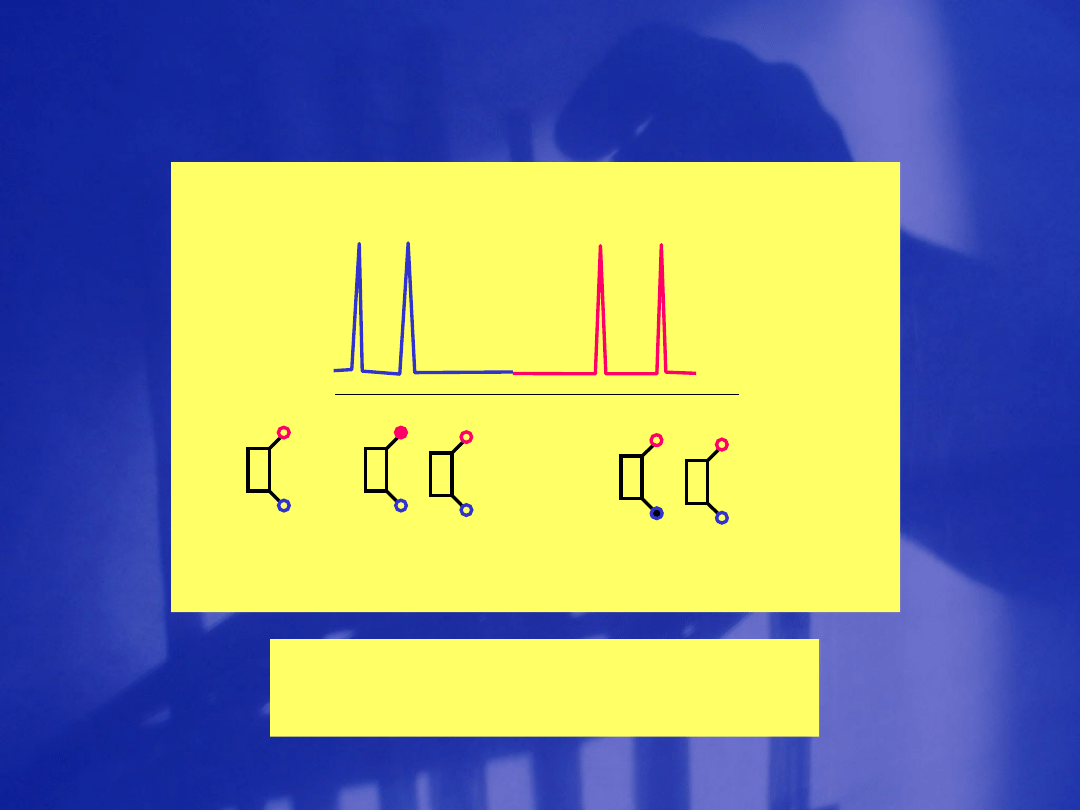
X
Y
Rezonans
Y
Rezonans
X
Powstanie dubletu jądra X i
jądra Y
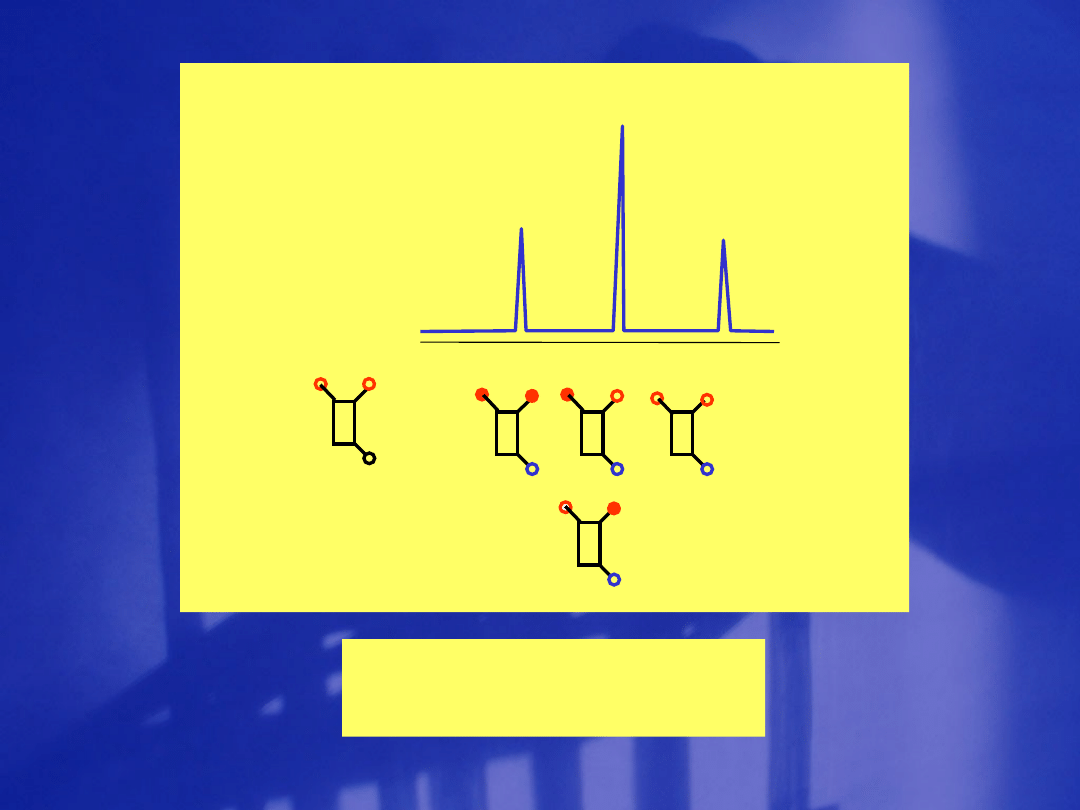
X X
Y
Rezonans
Y
Powstanie trypletu
jądra Y
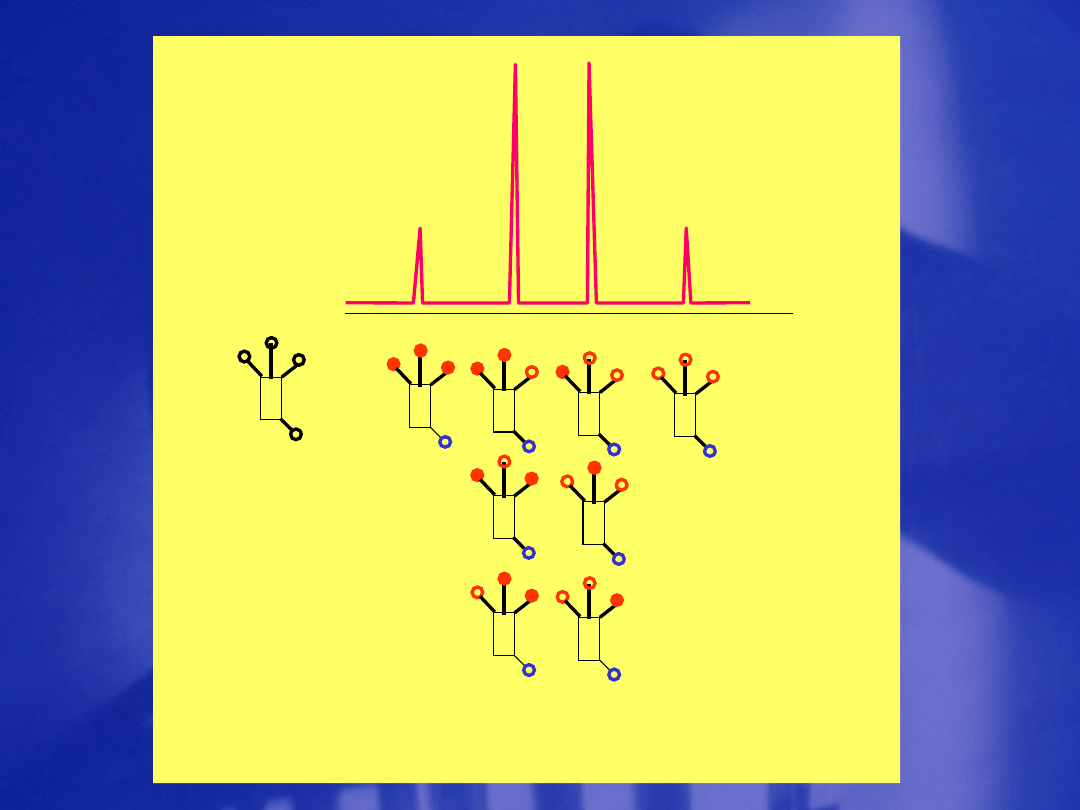
X X X
Y
Powstanie kwartetu
jądra Y

1
1 1
1
2 1
1 3
3 1
1 4 6 4
1
Trójkąt Pascala
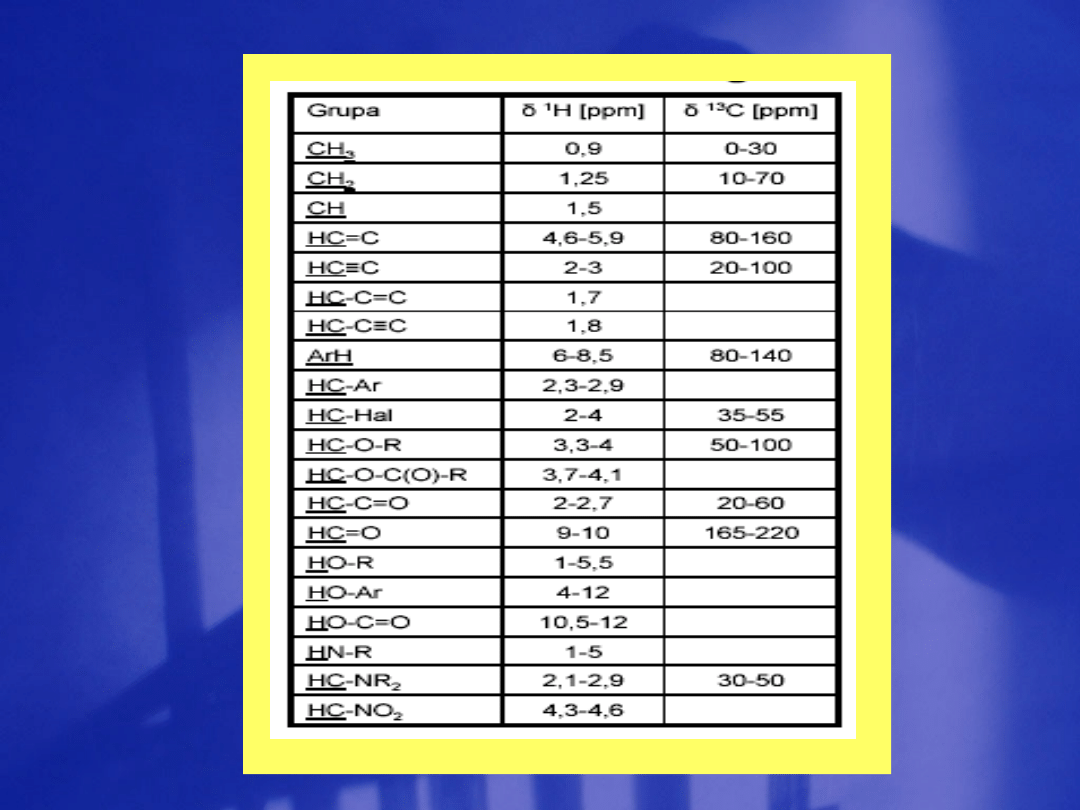
C
C
H
3
O
H
C C
H
2
Cl
O
H
C
C
H
Cl
2
O
H
C
CCl
3
O
H
1
3
1
2
1
1
B
=
0
Zmiana składowych sygnału NMR protonu wraz ze
zmianą liczby sąsiadów. Należy zwrócić uwagę na
zmianę przesunięcia chemicznego wraz z liczbą
wprowadzonych elektroujemnych atomów
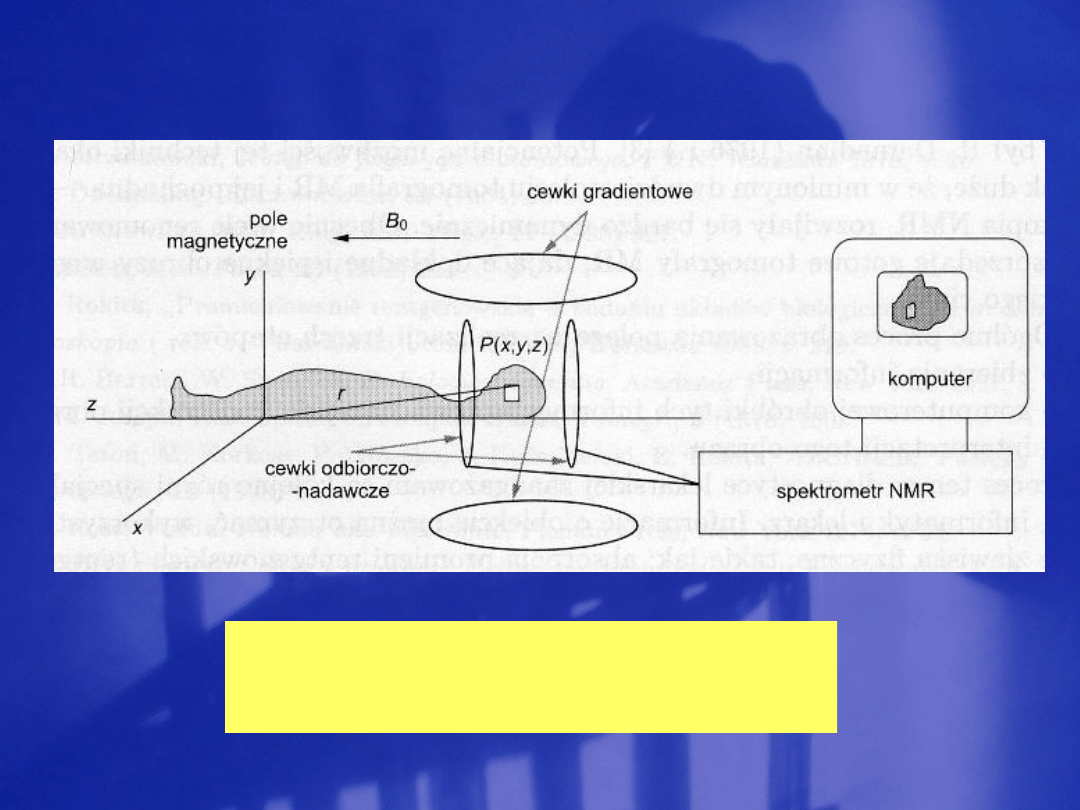
Schemat ideowy tomografu
NMR
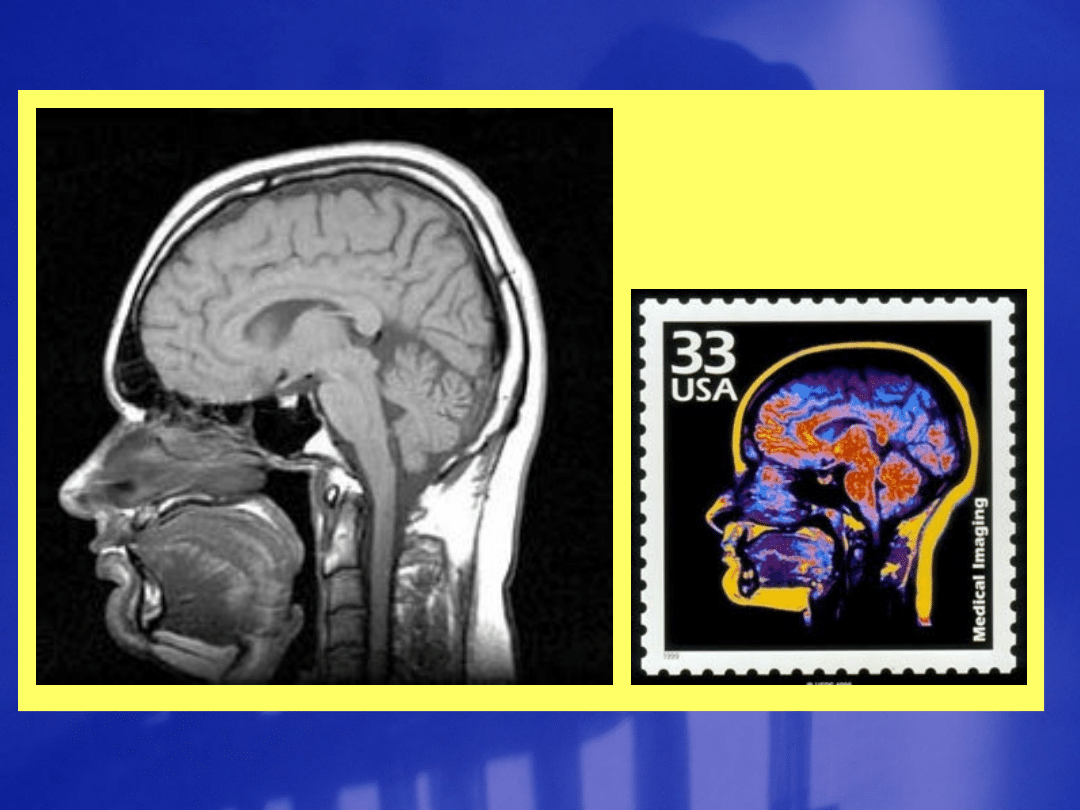
NMR
w MEDYCYNIE
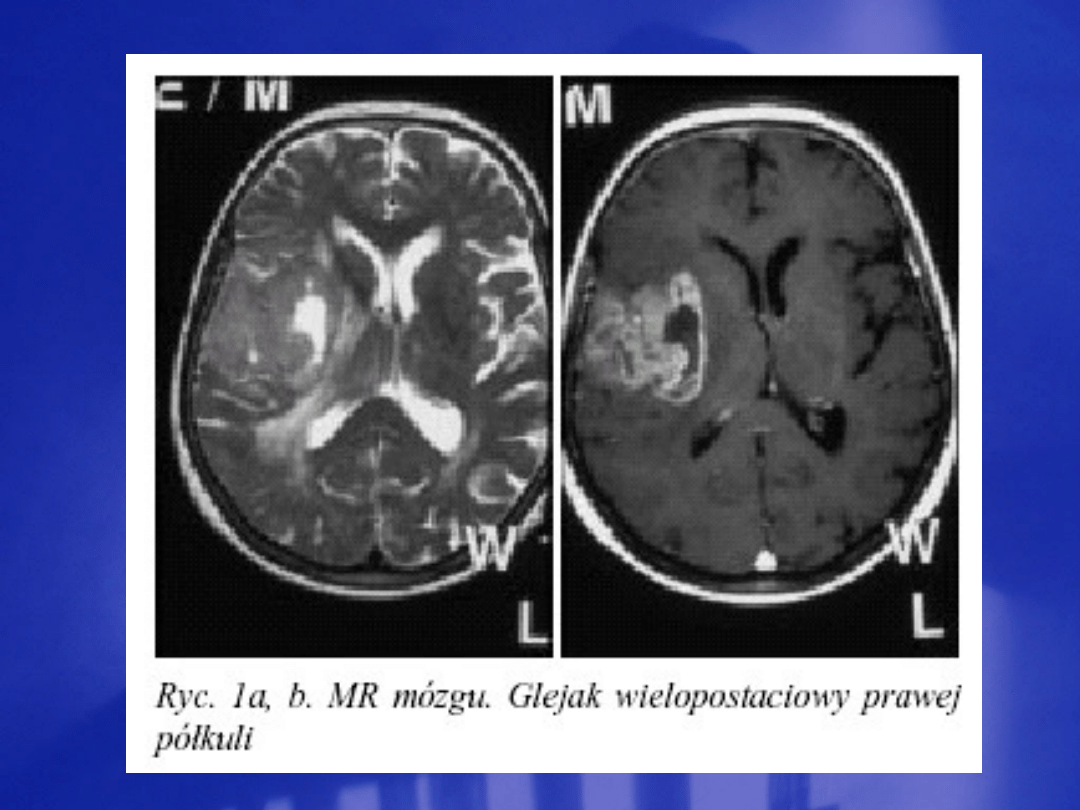
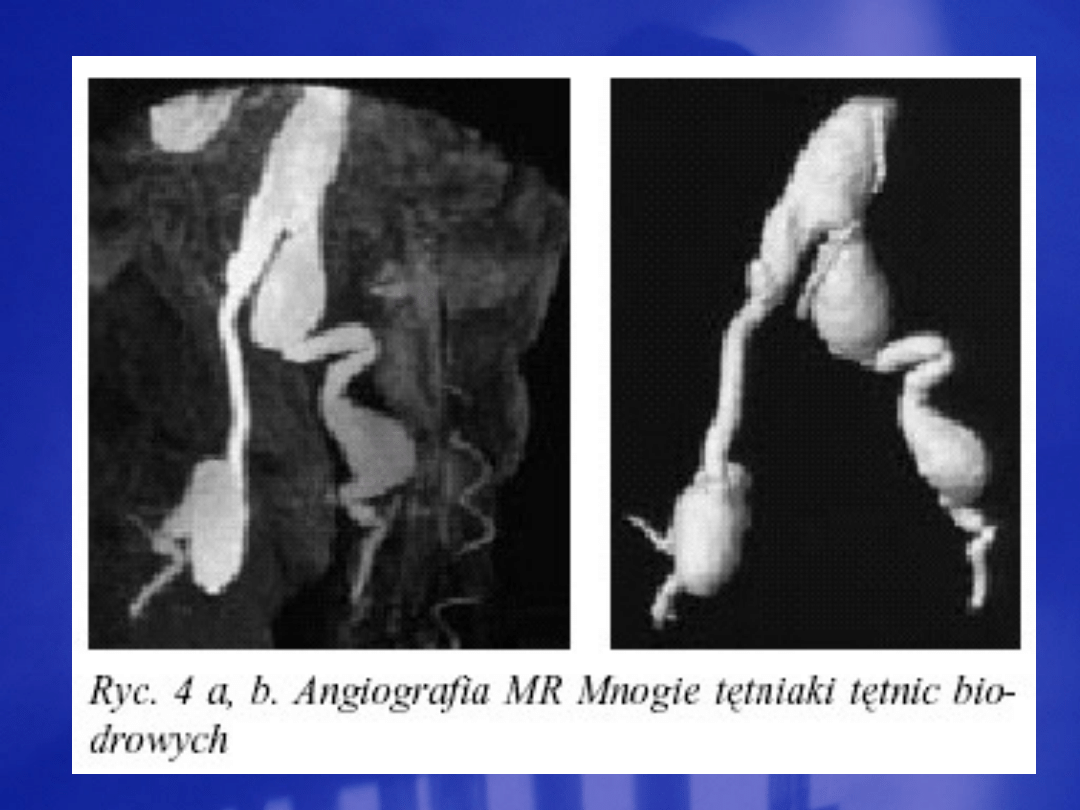
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
- Slide 58
- Slide 59
- Slide 60
- Slide 61
- Slide 62
- Slide 63
- Slide 64
- Slide 65
- Slide 66
- Slide 67
- Slide 68
- Slide 69
- Slide 70
- Slide 71
- Slide 72
- Slide 73
- Slide 74
- Slide 75
- Slide 76
- Slide 77
- Slide 78
- Slide 79
- Slide 80
- Slide 81
- Slide 82
- Slide 83
- Slide 84
- Slide 85
- Slide 86
- Slide 87
- Slide 88
- Slide 89
- Slide 90
- Slide 91
- Slide 92
- Slide 93
- Slide 94
- Slide 95
- Slide 96
- Slide 97
- Slide 98
- Slide 99
- Slide 100
- Slide 101
- Slide 102
- Slide 103
- Slide 104
- Slide 105
- Slide 106
- Slide 107
- Slide 108
- Slide 109
Wyszukiwarka
Podobne podstrony:
Absorpcyjna Spektrofotometria czasteczkowa
Podstawy spektroskopii cząsteczkowej
Absorpcyjna Spektrofotometria czasteczkowa
C5 (X7) B1KT0102P0 12 30 06 2014 Modyfikacja Dodatek do paliwa a filtr cząstek stałych
wykład 12 pamięć
Figures for chapter 12
Mechanika techniczna(12)
Socjologia wyklad 12 Organizacja i zarzadzanie
Spektroskopia NMR
CALC1 L 11 12 Differenial Equations
zaaw wyk ad5a 11 12
budzet ue 11 12
zapotrzebowanie ustroju na skladniki odzywcze 12 01 2009 kurs dla pielegniarek (2)
Stomatologia czesc wykl 12
więcej podobnych podstron