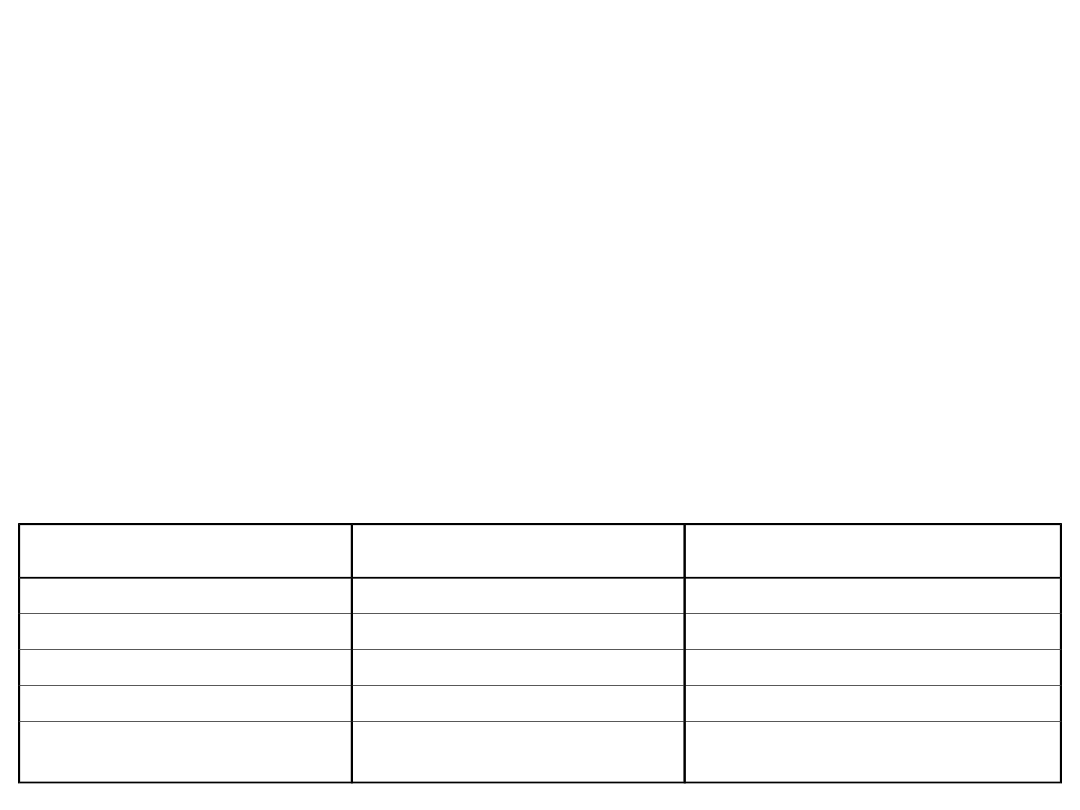
Systemy Liczbowe
Systemy Liczbowe
Podstawa p
System liczbowy
Cyfry używane w systemie
liczbowym
2
Dwójkowy
0, 1
3
Trójkowy
0, 1, 2
8
Ósemkowy
0, 1, 2, 3, 4, 5, 6, 7
10
Dziesiętny
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
16
Szesnastkowy
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B,
C, D, E, F
1
0
0
0
1
1
2
2
1
1
...
n
i
i
i
n
n
n
n
p
a
p
a
p
a
p
a
p
a
lub w skróconej postaci:
lub w skróconej postaci:
p
n
n
a
a
a
a
0
1
2
1
...
gdzie:
p – podstawa systemu, którą jest liczbą
całkowitą dodatnią,
n – numer pozycji
a
i
– cyfry z zakresu od 0 do p – 1.
Algorytm zamiany liczby binarnej z systemu dwójkowego na
system dziesiętny:
(c
i
... c
1
c
0
,c
-1
c
-2
…c
-j
)
(nb)
=c
i
*2
i
+...+
c
1
*2
1
+c
0
*2
0
+c
-1
*2
-1
+c
-2
*2
-2
+…+c
-j
*2
-
j
= n
(10)
Przykład 1
110011
2
= 1* 2
5
+ 1* 2
4
+ 0* 2
3
+ 0* 2
2
+ 1* 2
1
+
1* 2
0
= 32+16+2+1= 51
10
1001,1101
2
=(1 x 2
3
)+(0 x 2
2
)+(0 x 2
1
)+(1 x
2
0
)+(1 x 2
-1
) +(1 x 2
-
2
)+(0 x 2
-3
)+(1 x 2
-4
) =
8+1+0,5+0,25+0,0625=9,8125
10
Algorytm zamiany liczby naturalnej z systemu
dziesiętnego na system dwójkowy:
Przykład 1
N
10
=
83
83 : 2
=41 reszta
1 c
0
41 : 2
=20
1 c
1
20 : 2
=10
0 c
2
10 : 2
=5
0 c
3
5 : 2
=2
1 c
4
2 : 2
=1
0 c
5
1 : 2
=0
1 c
6
Ostatecznie otrzymujemy:
83
(10)
=1010011
(NB)
Przykład 2
N
10
= 9,8125
9 : 2 = 4 reszta
1 (LSB)
c
0
4 : 2 = 2
0
c
1
2 : 2 = 1
0
c
2
1 : 2 = 0
1 (MSB)
c
3
0,8125 x 2 = 1,625 0,625 nadmiar
1
(MSB)
c
-1
0,6250 x 2 = 1,250 0,25
1
c
-2
0,2500 x 2 = 0,500
0
c
-3
0,5000 x 2 = 1,000 0,0
1 (LSB)
c
-4
Ostatecznie otrzymujemy:
9,8125
10
= 1001,1101
2
Przykład 3
N
10
= 12,33
12 : 2 = 6 reszta
0 (LSB)
c
0
6 : 2 = 3
0
c
1
3 : 2 = 1
1
c
2
1 : 2 = 0
1 (MSB)
c
3
0,33 x 2 = 0,66
0 (MSB)
c
-1
0,66 x 2 = 1,32
0,32 nadmiar
1
c
-2
0,32 x 2 = 0,64
0
c
-3
0,64 x 2 = 1,28
0,28
1
c
-4
0,28 x 2 = 0,56
0
c
-5
0,56 x 2 = 1,12
0,12
1
c
-6
0,12 x 2 = 0,24
0
c
-7
0,24 x 2 = 0,48
0
c
-8
0,48 x 2 = 0,96
0
c
-9
0,96 x 2 = 1,92
0,92
1 (LSB)
c
-10
Ostatecznie otrzymujemy:
12,33
10
= 1100,0101010001
2
.
Algorytm zamiany liczby szesnastkowej na liczbę z systemu
dziesiętnego:
Niech liczba wyrażona w systemie szesnastkowym ma postać:
F3A,C8
16
Równoważną jej liczbą dziesiętną jest liczba o postaci:.
(15 x 16
2
) + (3 x 16
1
) + (10 x 16
0
) + (12 x 16
-1
) + (8 x 16
-2
) =
3898,78125
10
Konwersji dziesiętno - szesnastkowej można dokonać na drodze
wielokrotnego dzielenia na 16 części całkowitej oraz mnożenia
przez 16 części ułamkowej przetwarzanej liczby dziesiętnej
Algorytm zamiany liczby naturalnej z systemu
dziesiętnego na system szesnastkowy:
Przykład 1
N
10
=
3898
3898 : 16 =243
reszta
10=A
c
0
243 : 16=15
3=3 c
1
15 : 16=0
15=F c
2
Ostatecznie otrzymujemy:
3898
(10)
=F3A
(16)
Przykład 2
N10 = 2,33
2 : 16 = 0 reszta
2 c0
0,33 x 16 = 5,28
5
c-1
0,28 x 16 = 4,48
4
c-2
0,48 x 16 = 7,68
7
c-3
0,68 x 16 = 10,88
10=A
c-4
0,88 x 16 = 14,08
14=E
c-5
Ostatecznie otrzymujemy:
2,3310 = 2,547AE
16
Algebra Boole’a
.
KODY
Kodem
nazywamy
reguły
uporządkowujące
poszczególne
kombinacje zmiennych. Parametry określające kod to:
długość m – jest to liczba bitów informacji albo liczba zmiennych,
pojemność P – jest to liczba kombinacji wartości zmiennych
występujących w kodzie.
Kody możemy podzielić na:
W zależności od parametru P
Kody zupełne i niezupełne:
kody zupełne, które zawierają wszystkie możliwe kombinacje
wartości zmiennych,
kody niezupełne, które nie wykorzystują wszystkich kombinacji.
Kody systematyczne i niesystematyczne:
kody systematyczne tworzy się na podstawie reguły formalnej, w
której każda kombinacja wartości zmiennych jest zdefiniowana w
sposób jednoznaczny, do kodów systematycznych zaliczamy m.in.
wszystkie kody wagowe,
kody niesystematyczne wymagają podania tabeli, która określa
kolejność poszczególnych kombinacji występujących w dowolnym
porządku, do kodów niesystematycznych zaliczamy kod Watha,
dalekopisowy i inne.
Kody dwójkowe wagowe i niewagowe.
Algebra Boole’a
Systemy Liczbowe
Systemy Liczbowe
.
Kod Dwójkowy
Kod BCD
Kod Graya
A B C D
8 4 2 1
8421
8421
X Y W Z
Niewagowy
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
0001 0 0 0 0
0001 0 0 0 1
0001 0 0 1 0
0001 0 0 1 1
0001 0 1 0 0
0001 0 1 0 1
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0 0 0 0
0 0 0 1
0 0 1 1
0 0 1 0
0 1 1 0
0 1 1 1
0 1 0 1
0 1 0 0
1 1 0 0
1 1 0 1
1 1 1 1
1 1 1 0
1 0 1 0
1 0 1 1
1 0 0 1
1 0 0 0
Algebra Boole’a
Systemy Liczbowe
Systemy Liczbowe
.
Jedną z postaci algebry Boole’a jest znany rachunek zdań, gdzie
zamiast znaków sumy + stosuje się łącznik lub, zamiast znaku iloczynu
– łącznik i, a do negacji używamy słowa nie. Algebra Boole’a posługuje
się szeregiem praw i tożsamości.
W algebrze Boole’a obowiązują następujące podstawowe prawa:
Prawo przemienności mnożenia i dodawania:
A+B = B+A
A · B = B · A
Prawo łączności:
A+B+C = A+(B+C) = (A+B)+C
A · B · C = A · (B · C) = (A · B) ·C
Prawo rozdzielczości:
A ·(B + C) = A · B + A · C
A + B · C = (A + B) · (A + C)
Prawa podstawowe:
A + 1 = 1 A · 1 = A A + 0=A A · 0 = 0 A + A = A A · A = A
Prawa de Morgana:
...
...
C
B
A
C
B
A
...
...
C
B
A
C
B
A
Algebra Boole’a
Układy kombinacyjne i sekwencyjne
Układy kombinacyjne i sekwencyjne
.
Do układów przełączających logicznych zaliczamy:
układy kombinacyjne,
układy sekwencyjne.
Cechą odróżniającą układy kombinacyjne i sekwencyjne jest
właściwość pamiętania stanów logicznych, które charakteryzują
się układy sekwencyjne, a której są pozbawione układy
kombinacyjne.
Układ kombinacyjny służy do przetwarzania informacji
dyskretnej dwuwartościowej. Informacja dyskretna składa się ze
znaków, którymi mogą być zarówno litery, cyfry, jak i inne
symbole.
W układzie kombinacyjnym każda kombinacja sygnałów
wejściowych określa jednoznacznie kombinację sygnałów
wyjściowych. Sygnały wejścia i sygnały wyjścia przyjmują
skończoną liczbę kombinacji i skończoną liczbę wartości.
Kombinacje sygnałów wejściowych są to stany wejść układu, a
kombinacje sygnałów wyjściowych – stany wyjść układu.
Algebra Boole’a
Układy kombinacyjne i sekwencyjne
Układy kombinacyjne i sekwencyjne
.
Układ sekwencyjny jest to układ dyskretny, którego stan
wyjścia nie tylko zależy od stanu wejścia, ale także od
wcześniejszego stanu wyjścia. Inaczej mówiąc stan wyjścia
zależy od stanu wejścia i stanu wyjścia w chwili T. Oprócz
zmiennych wejściowych i wyjściowych, istnieją tzw. stany
wewnętrzne Q, a zbiór stanów wewnętrznych określa pamięć
układu Q
1
, Q
2
,...
Układy sekwencyjne dzielimy na:
układy synchroniczne
układy asynchroniczne.
Układ synchroniczny to układ, w którym zmiany stanów
wewnętrznych i stanów wyjścia odbywa się w ściśle określonych
interwałach czasu, czyli w takt impulsu zegarowego.
Układ asynchroniczny to układ, w którym sygnały na wejściu
bezpośrednio oddziałują na stany wewnętrzne układu i stany na
wyjściu. Układ ten pracuje z szybkością wyznaczoną przez
opóźnienie elementów wewnętrznych układu.
Algebra Boole’a
Układy kombinacyjne i sekwencyjne
Układy kombinacyjne i sekwencyjne
.
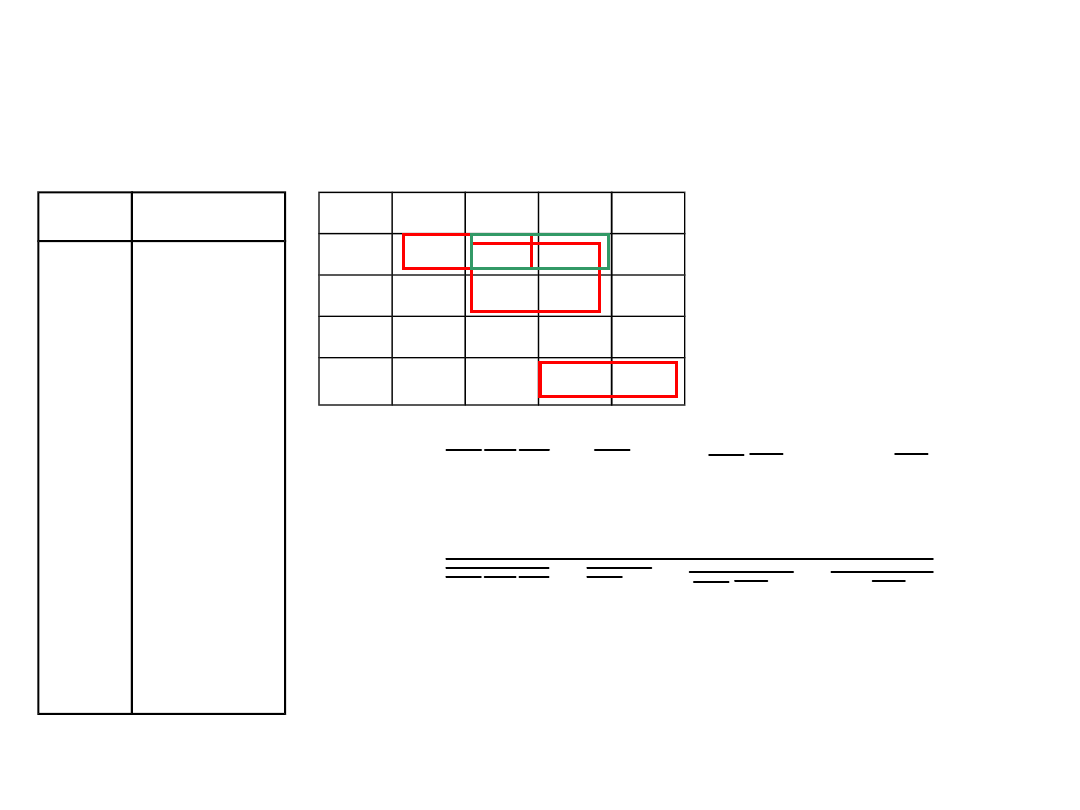
00
01
11
10
00
1
1
1
0
01
0
1
1
0
11
0
0
0
0
10
0
0
1
1
Y
DCBA
1
1
0
1
0
1
0
1
0
0
1
1
0
0
0
0
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
BA
DC
B
C
D
A
C
D
A
D
B
C
D
Y
B
C
D
A
C
D
A
D
B
C
D
Y
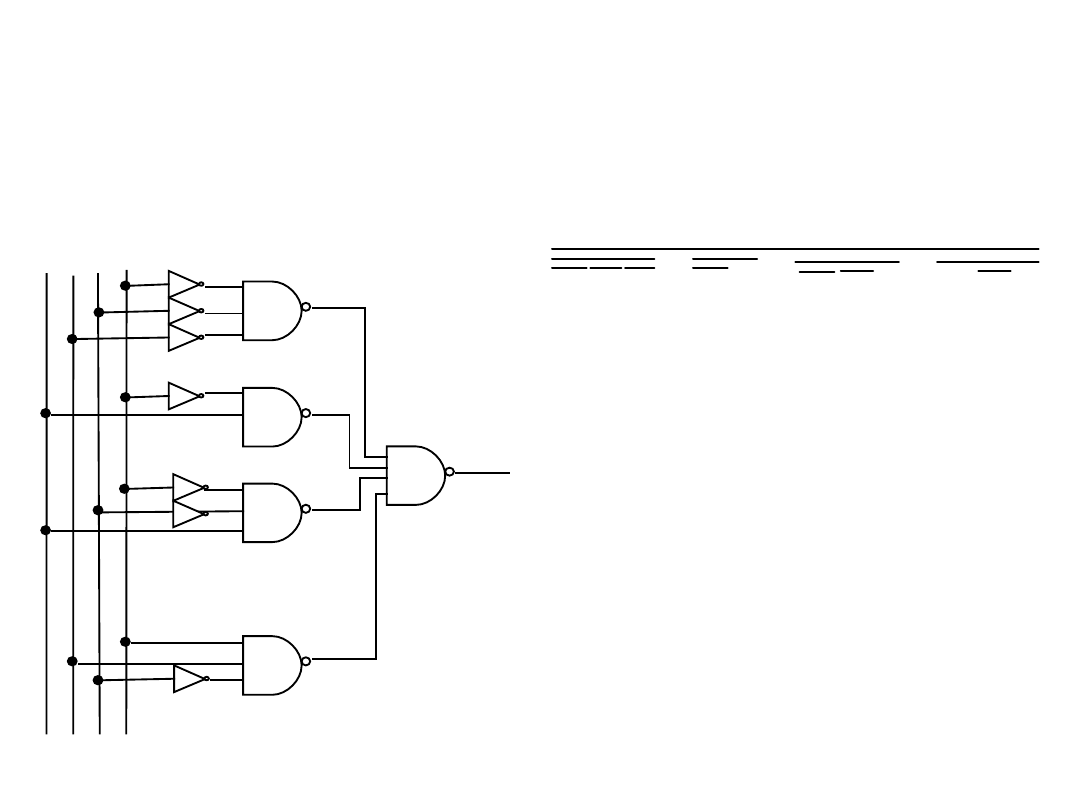
Algebra Boole’a
Układy kombinacyjne i sekwencyjne
Układy kombinacyjne i sekwencyjne
A B C
D
B
C
D
A
C
D
A
D
B
C
D
Y
Document Outline