KINETYKA
CHEMICZNA

Szybkość =

Zmiana
stężenia

czas

v =
±

c

t

v = – =

dc

dt

dx

dt

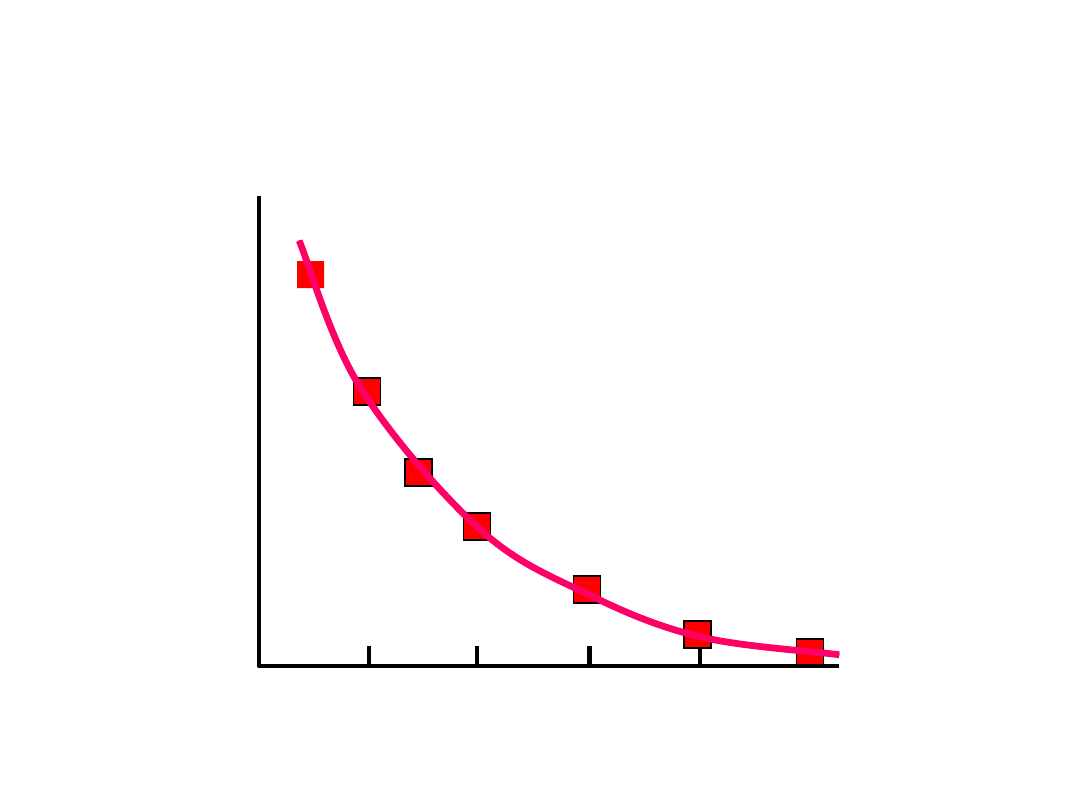
S

tę

że

n

ie

(



g

/m

l)

80

60

40

20

0

0 2 4 6 8

Czas (h)

A  B

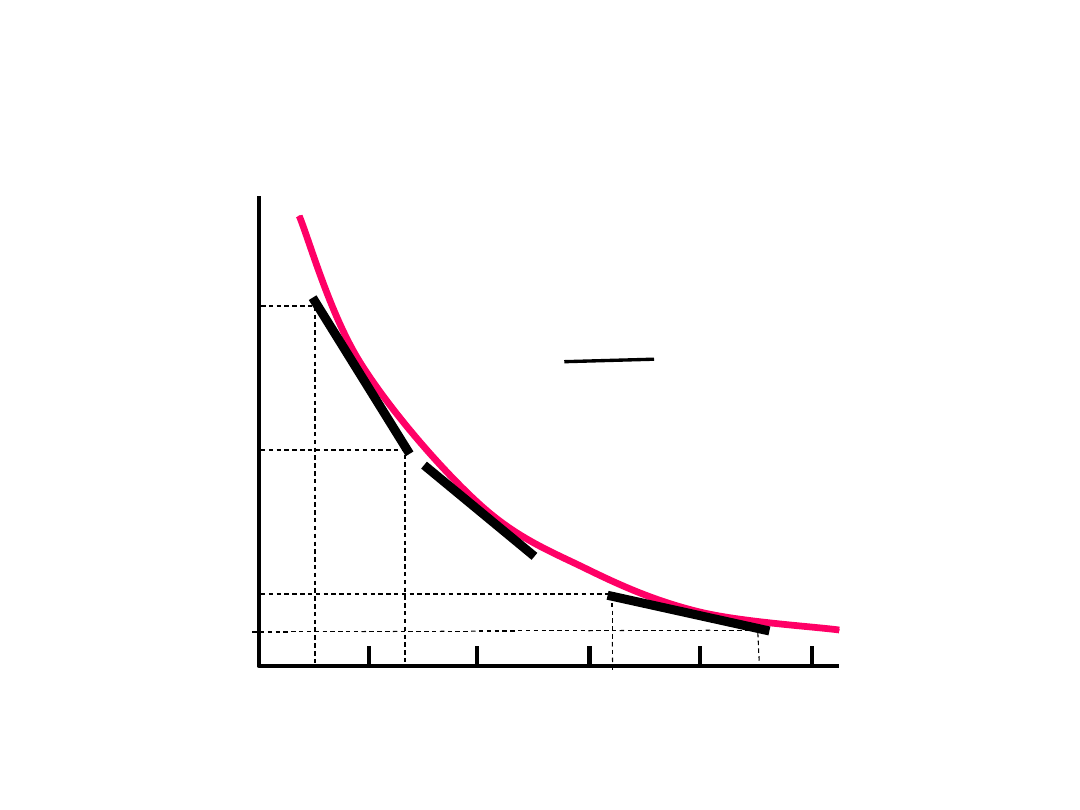
S

tę

że

n

ie

(



g

/m

l)

80

60

40

20

0

0 2 4 6 8

Czas (h)

v =
–

dc

dt

Przykład:

Jeżeli stężenie jonów wodorowych maleje o
0,01 M w ciągu 1 ns, to jaka jest średnia
szybkość reakcji? (mol/dm

3

)

Szybkość = 0,01 M / 1* 10

-9

s = 1,00 * 10

7

M/s

Szybkość =

Zmiana
stężenia

czas



v

n

i

i

C

v 



Rzędowość reakcji

Br

2

= Br + Br

v = k * [Br

2

]

reakcja pierwszego

rzędu

H

2

+ I

2

= 2HI

v = k * [H

2

] * [I

2

]

całkowity rząd

reakcji 2

2NO + Cl

2

= 2NOCl

v = k * [NO]

2

* [Cl

2

]

całkowity rząd

reakcji 3

H

2

+ Br

2

= 2HBr

Całkowity rząd reakcji nieokreślony

]

[

]

[

]

][

[

'

2

2

/

3

2

2

HBr

k

Br

Br

H

k

v





Natomiast, gdy [Br

2

] >> k’ * [HBr]:

2

/

1

2

2

]

][

[

Br

H

k

v 

Równania kinetyczne

Reakcja zerowego rzędu

A  B

v = k [A]

0

k

x

a

k

dt

dx

v









0

)

(

Po scałkowaniu:

kt

x 

k

A

2

0

2

/

1





Reakcja pierwszego rzędu:

)

(

x

a

k

dt

dx

v







Po scałkowaniu:

















x

a

a

t

k

ln

1

















x

a

a

t

k

log

303

,

2

kt

a

x

a







ln

)

ln(

Okres półtrwania (połowicznej przemiany)
reakcji rzędu pierwszego:

k

693

,

0

2

/

1





Kinetyka rozpadu promieniotwórczego
Przykład:
Nuklid

226

88

Ra 

222

86

Rn +

4

2

He

Wiedząc, że 1 g radu emituje w ciągu 1 s

3,70*10

10

cząstek  oblicz:

a) Stałą szybkości rozpadu,
b) Czas połowicznego rozpadu (okres

półtrwania),

c) Procent początkowej ilości radu, który

pozostaje w próbce po upływie 1000 lat,

d) Czas po którym rozpadnie się 99,9%

początkowej ilości radu.

a) Wyznaczane stałej szybkości rozpadu

1 g radu zawiera 6,023*10

23

/206,05 =2,664

*10

21

atomów.

Liczbie rozpadów odpowiada - N.

k = 3,70*10

10

/2,664*10

21

*1s = 1,388*10

-11

s

-1

Ponieważ 1 rok = 3,156*10

7

s,

to k = 4,38*10

-4

rok

-1

kN

t

N







)

*

/(

t

N

N

k







b) Czas połowicznego rozpadu obliczamy ze
wzoru:



1/2

= 0,6931 / 4,38*10

-4

rok

-1

= 1580 lat

k

693

,

0

2

/

1





c) Liczbę atomów, która nie uległa rozpadowi,
obliczamy ze wzoru:

W próbce pozostanie 64,5% początkowej ilości
(liczby atomów) radu.

645

,

0

)

/

(

438

,

0

1000

*

10

*

38

,

4

)

/

ln(

*

)

/

ln(

0

1

4

0

0

















N

N

lat

rok

N

N

t

k

N

N

d) Obliczamy czas, po którym rozpadnie
się 99,9% początkowej ilości radu:

lat

t

rok

k

N

N

t

158000

10

*

38

,

4

/

)

999

,

0

1

ln(

/

)

/

ln(

1

4

0















Reakcja drugiego rzędu (przypadek, gdy
stężenia obu reagentów są jednakowe)

Po scałkowaniu:

Okres półtrwania:

2

)

(

x

a

k

dt

dx

v







kt

a

x

a

x

a

a

x

t

k











1

1

)

(

1

ka

1

2

/

1





Reakcja trzeciego rzędu (przypadek, gdy
stężenia obu reagentów są jednakowe)

Po scałkowaniu:

lub:

Okres półtrwania:

3

)

(

x

a

k

dt

dx

v

























2

2

1

)

(

1

2

1

a

x

a

t

k

kt

a

x

a

2

1

)

(

1

2

2







2

2

/

1

2

1

ka





Metody wyznaczania rzędu reakcji

1) Podstawiania do wzoru:

t

x

k 

















x

a

a

t

k

log

303

,

2

)

(

1

x

a

a

x

t

k























2

2

1

)

(

1

2

1

a

x

a

t

k

Rząd:

0

1

2

3

2 Graficzna:

kt

x 

kt

a

x

a







ln

)

ln(

kt

a

x

a







1

1

kt

a

x

a

2

1

)

(

1

2

2







3) Ostwalda

1

2

/

1

1





n

a



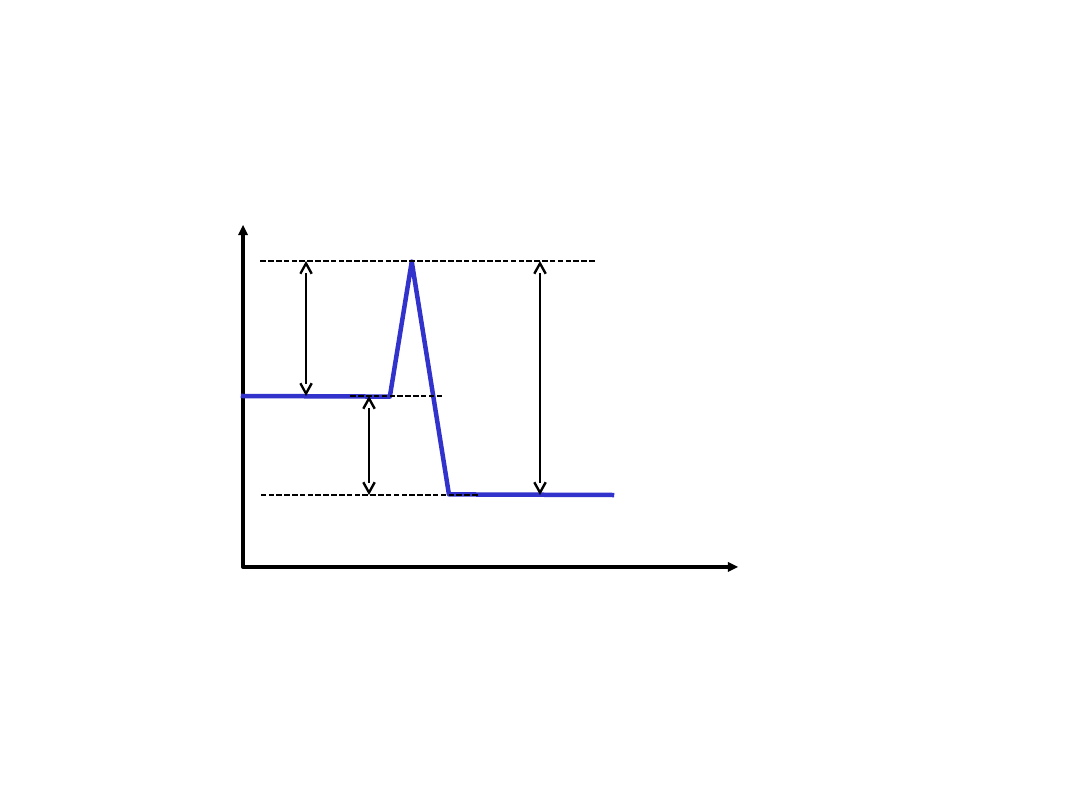
A  B

Energi
a

Postęp
reakcji

K

L

M

E

1

H

E

2

Teoria zderzeń aktywnych

Liczba cząsteczek o energii równej lub
większej niż energia aktywacji dana jest
rozkładem

statystycznym

Maxwella-

Boltzmanna:

kT

E

e

N

N





0

*

N* jest liczbą cząsteczek o energii

większej niż energia aktywacji E

a

,

N

0

całkowitą liczbą cząsteczek,

k stała Boltzmanna
T temperatura w skali bezwzględnej

(Kelvina)

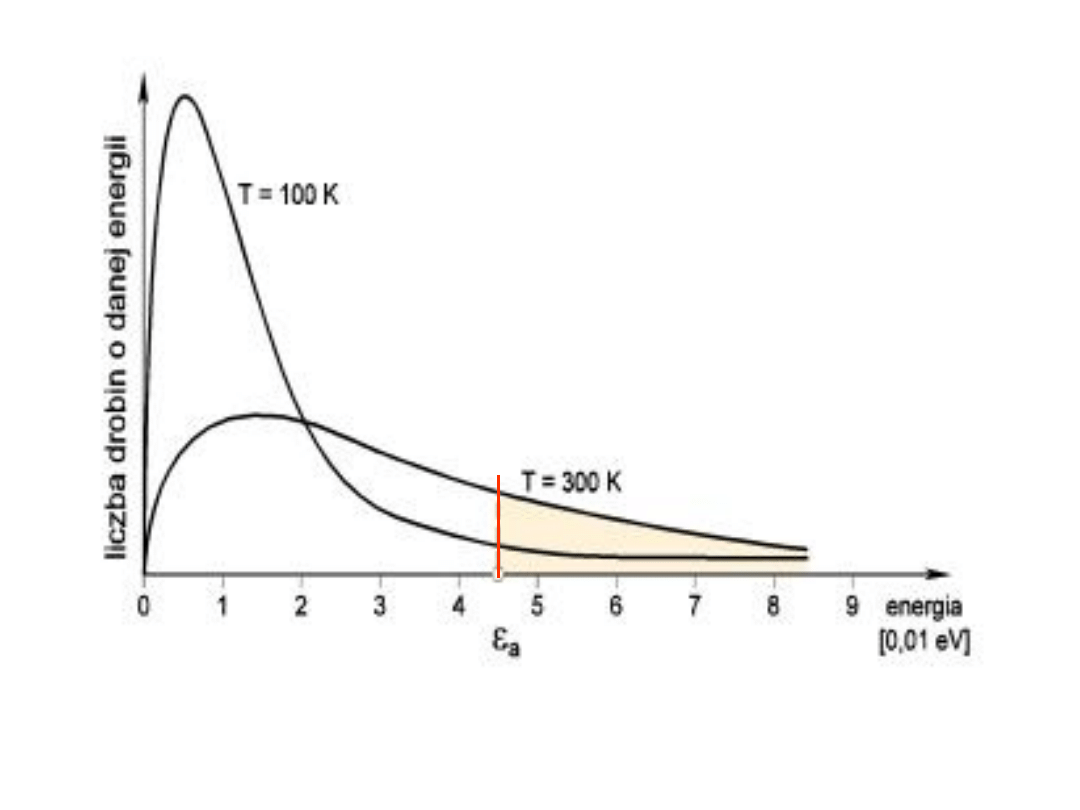
Rozkład prawdopodobieństwa występowania
cząsteczek o energii E

Szybkość

reakcji

chemicznej

jest

proporcjonalna do ilości zderzeń aktywnych,
a więc do ilości cząsteczek o energii równej
lub większej od energii aktywacji E

a

:

                                                                      

kT

E

a

e

N

k

N

k

v







0

0

0

*

Jeżeli liczbę cząsteczek zastąpimy liczbą moli
(n

0

) to:

RT

E

a

e

n

k

n

k

v







0

0

0

*

Gdzie:

A

N

N

n

/



A

kN

R

RT

E

a

e

n

k

n

k

v







0

0

0

*

A 

B

RT

E

a

e

v





]

[A

]

[A

k

v 

RT

E

a

e

k





RT

E

a

e

k

k





0

RT

E

a

e

k

k





0

RT

E

k

k

a





0

ln

ln

Energia
potencja
lna

Bieg reakcji

A + BC  AB + C

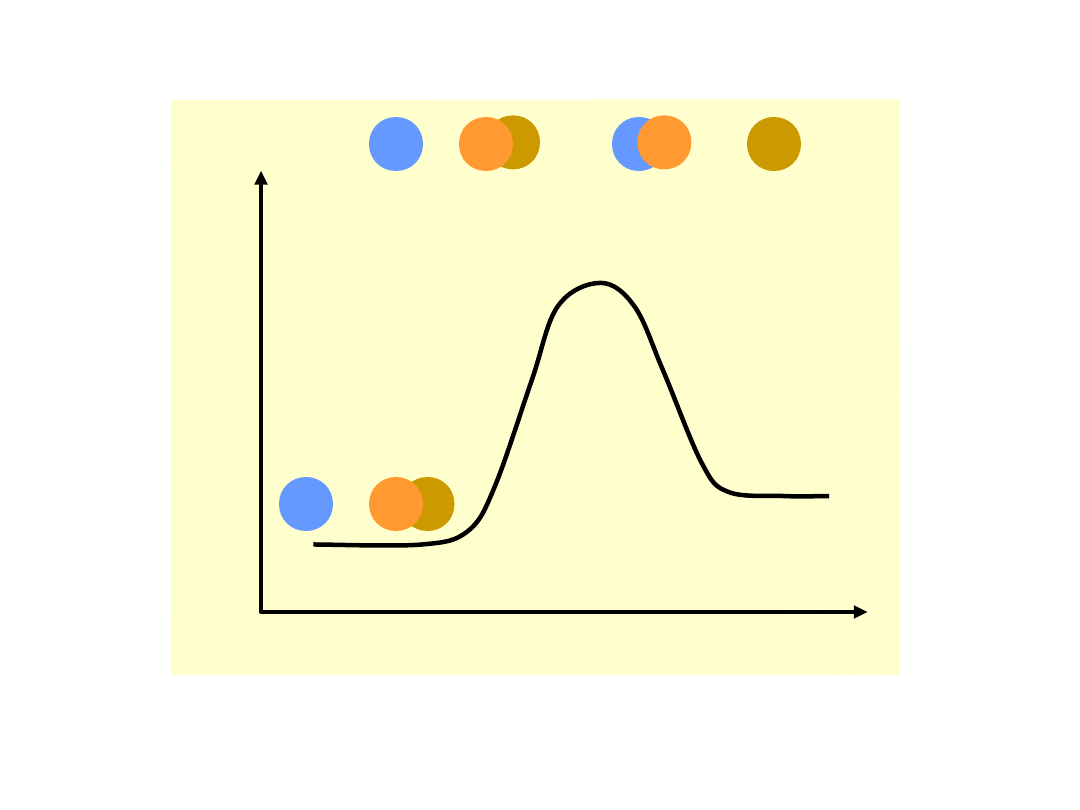
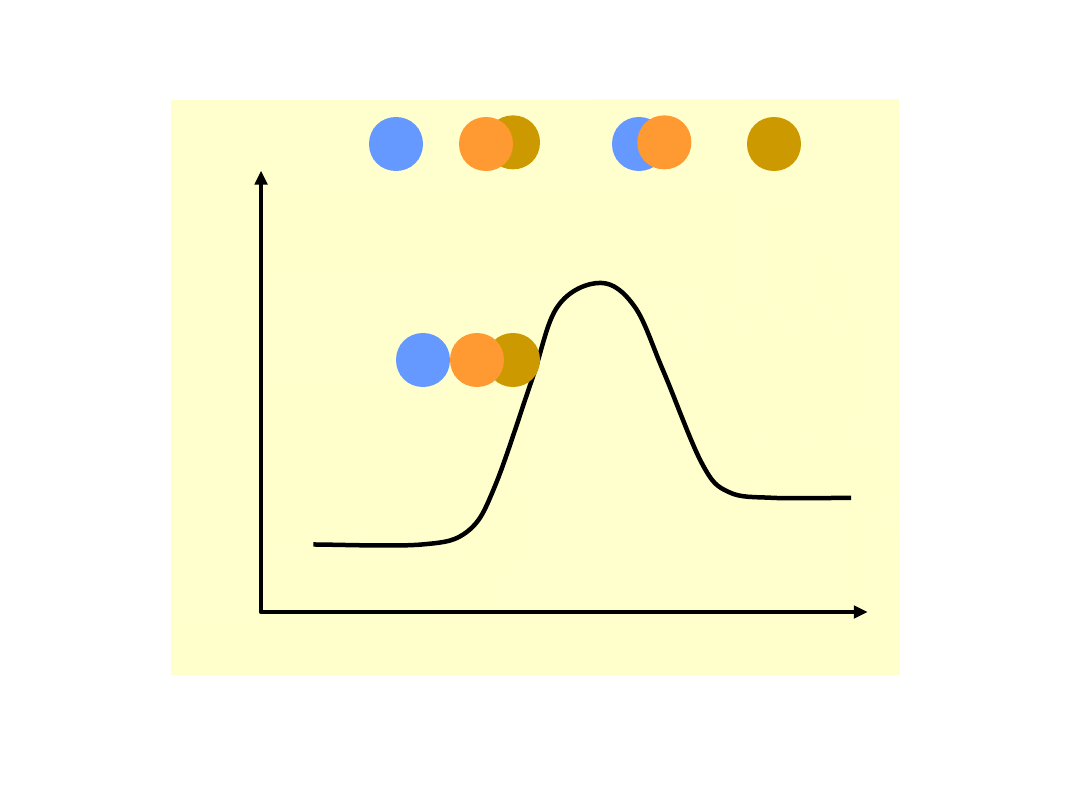
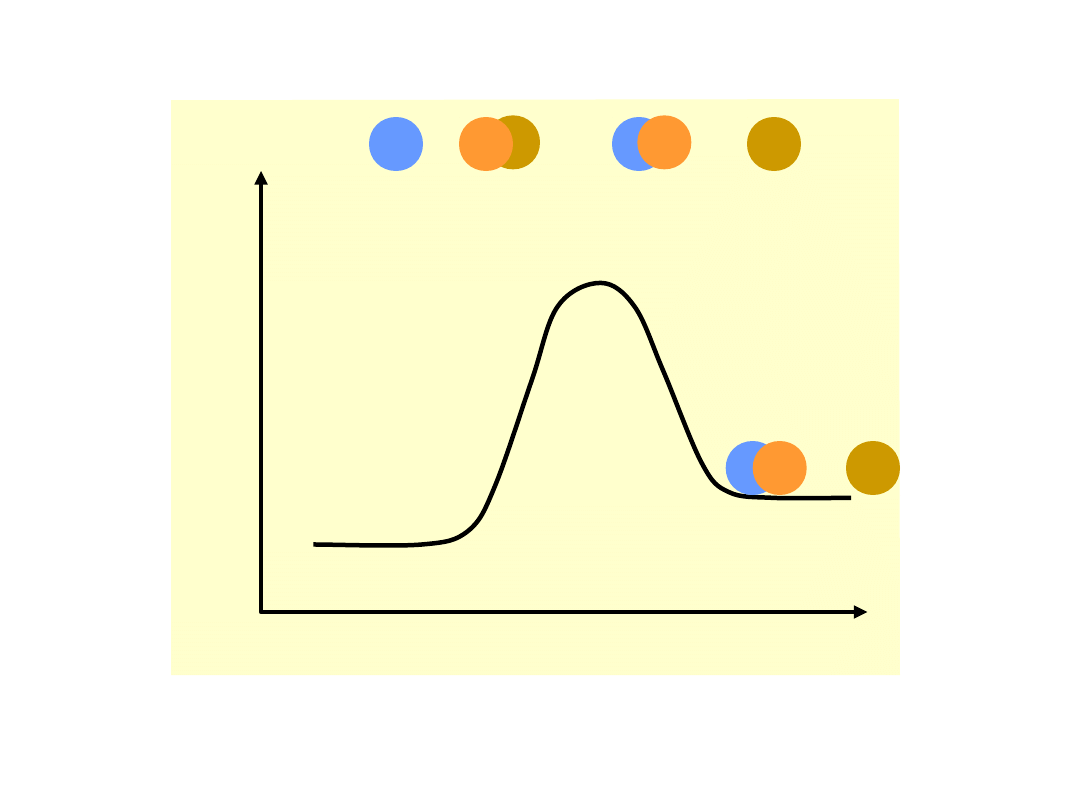
Teoria kompleksu aktywnego (stanu
przejściowego)

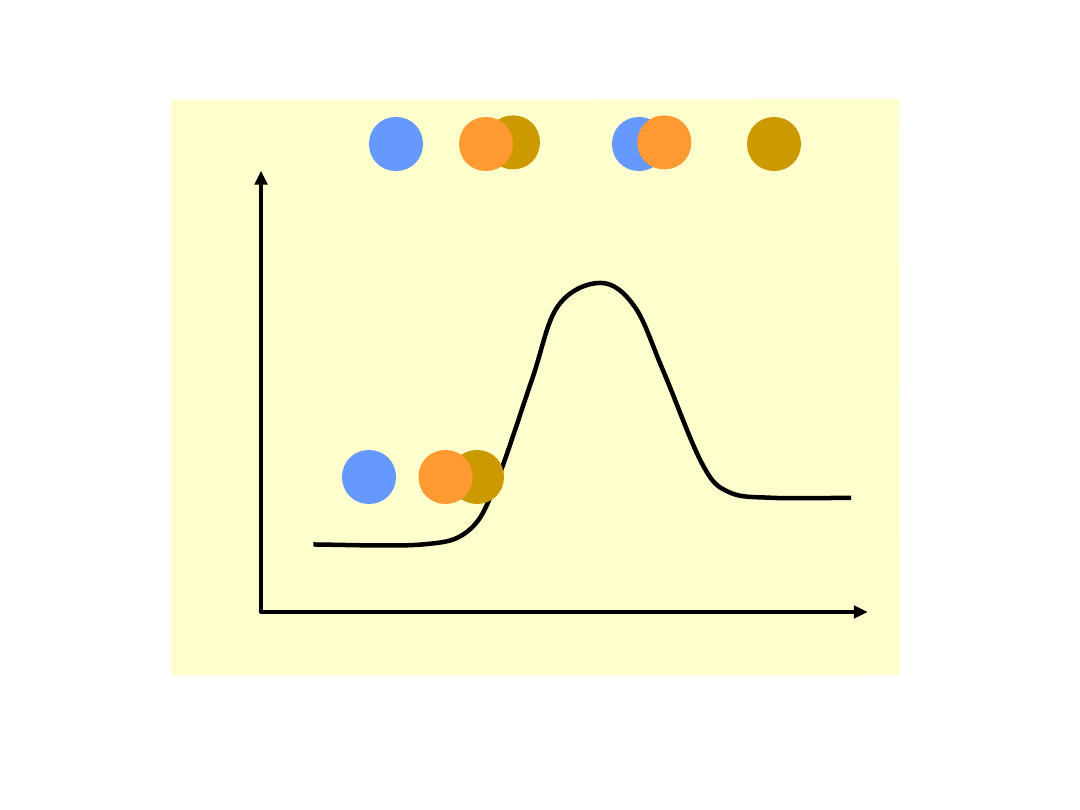
Energia
potencja
lna

Bieg reakcji

A + BC  AB + C

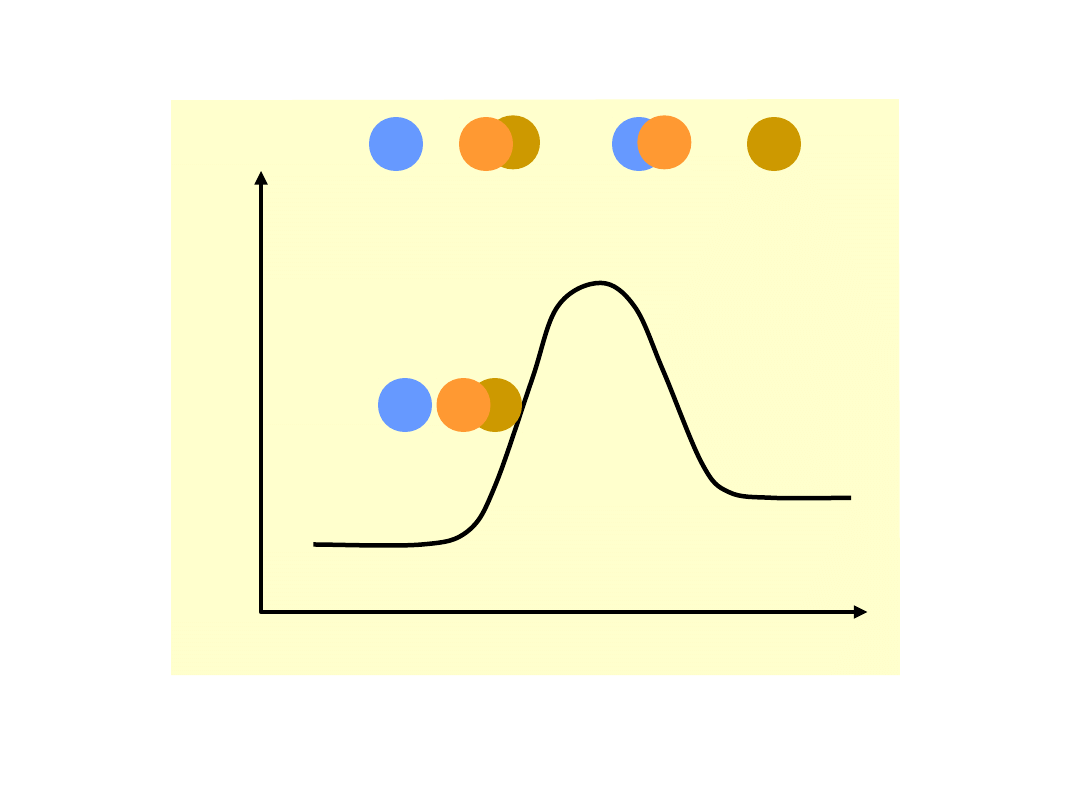
Energia
potencja
lna

Bieg reakcji

A + BC  AB + C

Energia
potencja
lna

Bieg reakcji

A + BC  AB + C

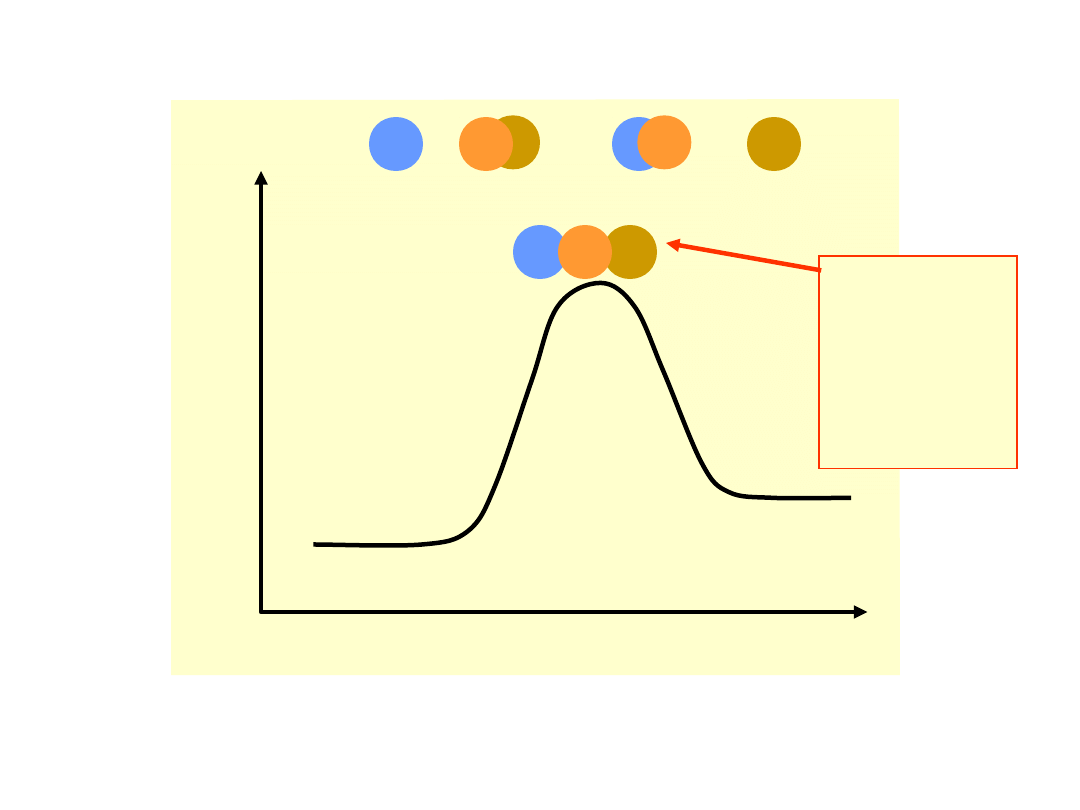
Energia
potencja
lna

Bieg reakcji

Komple
ks
aktywn
y

A + BC  AB + C

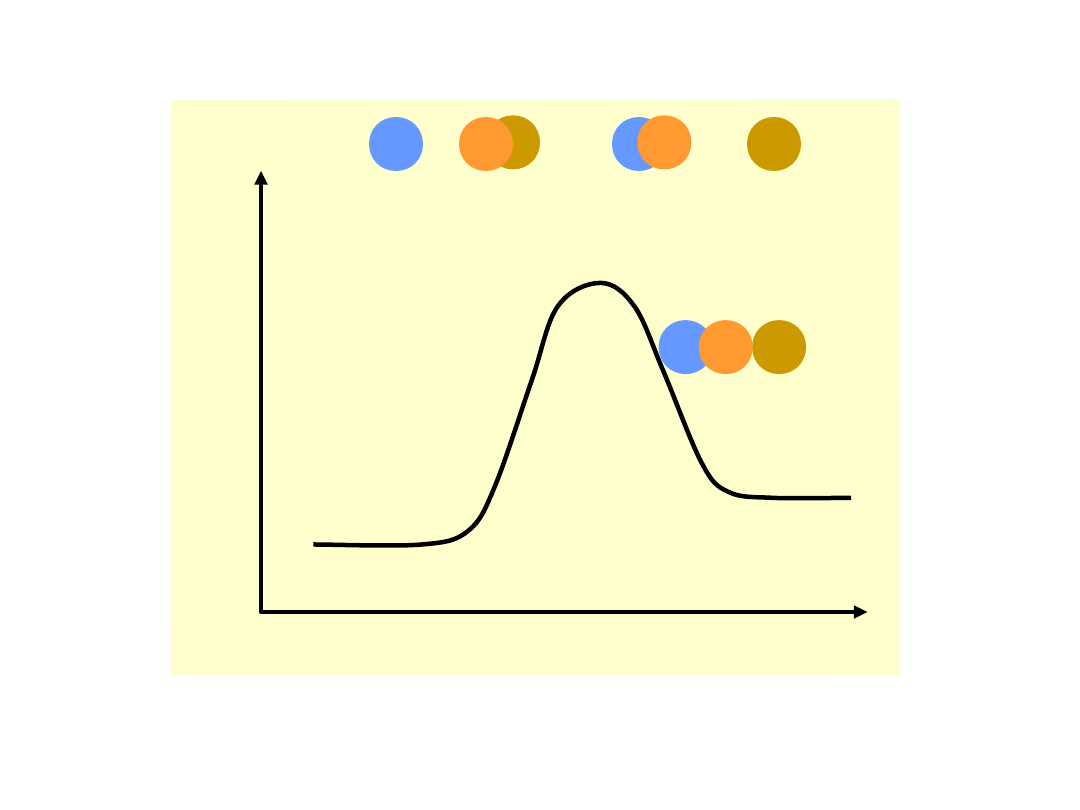
Energia
potencja
lna

Bieg reakcji

A + BC  AB + C

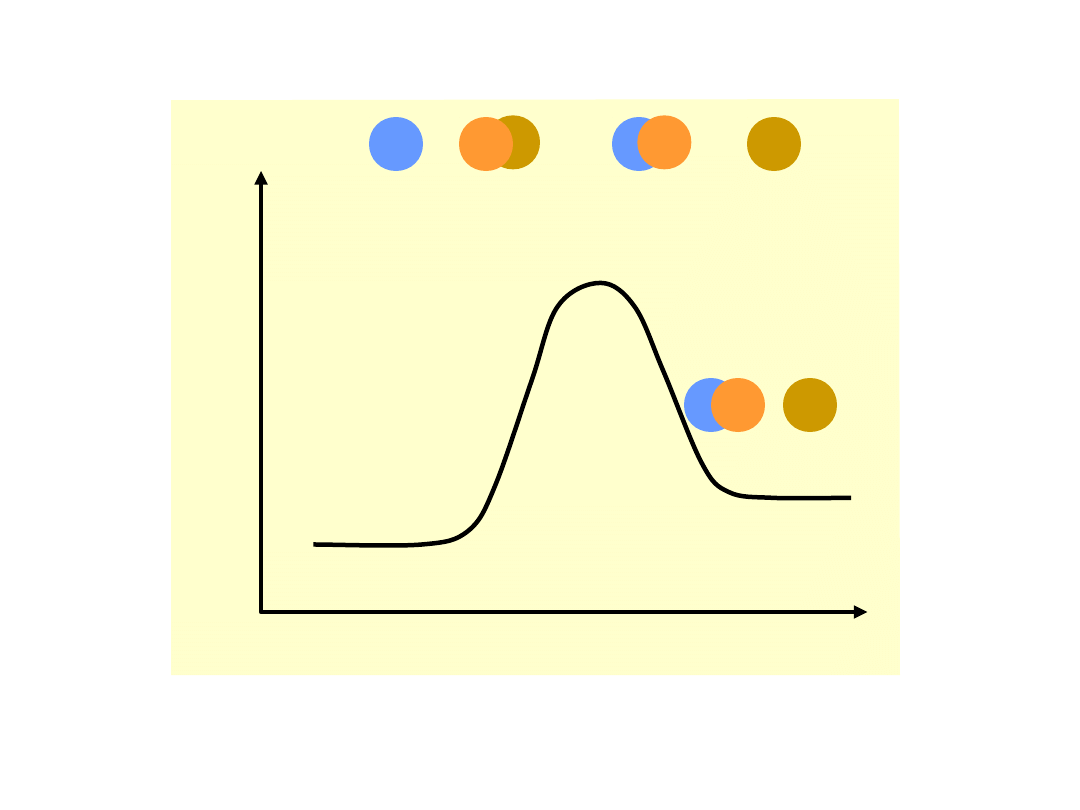
Energia
potencja
lna

Bieg reakcji

A + BC  AB + C

Energia
potencja
lna

Bieg reakcji

A + BC  AB + C

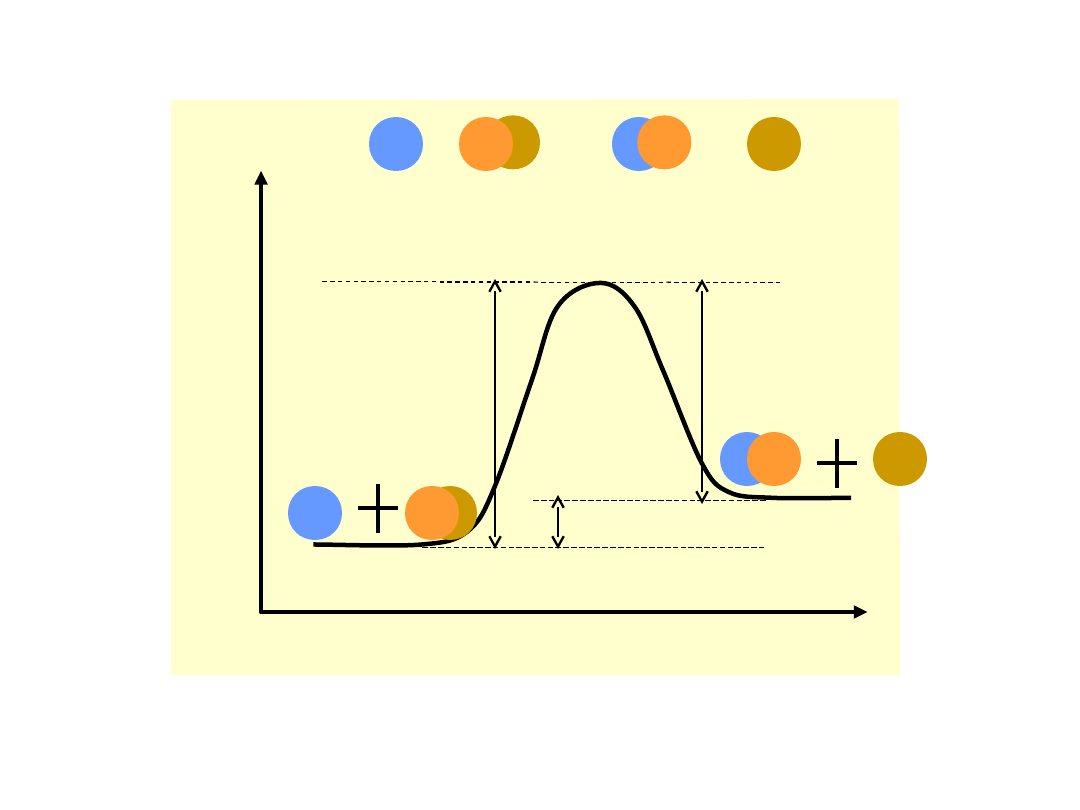
Energia
potencja
lna

Bieg reakcji

H

E

a1

E

a2

A + BC  AB + C

Energia

aktywacji

E

a1

jest

równa

wysokości bariery energetycznej, którą
muszą pokonać reagujące cząsteczki na
drodze reakcji, E

a2

– energia aktywacji

reakcji odwrotnej. Różnica pomiędzy
stanem

energetycznym

produktów

i

substratów E jest równa ciepłu reakcji

H.

Koncepcja kompleksu aktywnego pozwala
zdefiniować energię aktywacji,
cząsteczkowość reakcji, oraz wyprowadzić
wyrażenie opisujące wpływ temperatury na
szybkość reakcji .

A + BC  AB + C
A + BC  ABC*  AB + C

]

][

[

]

[

BC

A

ABC

K







]

][

[

]

][

[

]

[

BC

A

k

v

BC

A

K

v

ABC

v

PROD

PROD

PROD











Z ostatnich dwóch zależności wynika
proporcjonalność stałej równowagi tworzenia
kompleksu aktywnego i stałej k.

Stała równowagi K



jest związana z entalpią

swobodną równaniem:

RT

H

R

S

k

e

k

e

K

S

T

H

G

e

K

K

RT

G

RT

S

T

H

RT

S

T

H

RT

G















































































ln

ln

/

)

(

/

)

(

/

Mechanizm reakcji chemicznej

Cząsteczkowość reakcji

Mechanizm reakcji jest bardziej

skomplikowany niż to wynika z zapisu
stechiometrycznego

H

2

+ Br

2

= 2HBr

Przebieg reakcji:

1) Br

2

= 2Br*

2) Br* + H

2

= HBr + H*

3) H* + Br

2

= HBr + Br* itd..

4) H* + Br* = HBr

Każdy akt elementarny następuje w wyniku
efektywnych zderzeń dwóch lub najwyżej
trzech cząsteczek.

Przykładowo szybkość reakcji:

                                                         

opisuje równanie kinetyczne:

                                            

2HI + H

2

O

2

 I

2

+

2H

2

O

v = k · c

HI

·

c

H2O2

Taką postać równania kinetycznego, w którym

stężenie jodowodoru jest w potędze pierwszej,
można wyjaśnić przyjmując dwu-etapowy
mechanizm reakcji:

                      

                                   

etap I – powolny

etap II – szybki

HI + H

2

O

2

 HIO +

H

2

O

HIO + HI  H

2

O

+ I

2

Reakcja jednoetapowa:

H

2

+ I

2

= 2HI

Reakcje mające co najmniej po jednym
produkcie pośrednim (czyli składające się co
najmniej z dwóch aktów elementarnych) są
nazywane reakcjami wieloetapowymi lub
złożonymi.

Tylko

na

drodze

badań

doświadczalnych możemy stwierdzić czy
dana reakcja jest prostą czy złożoną.

 

                                                       

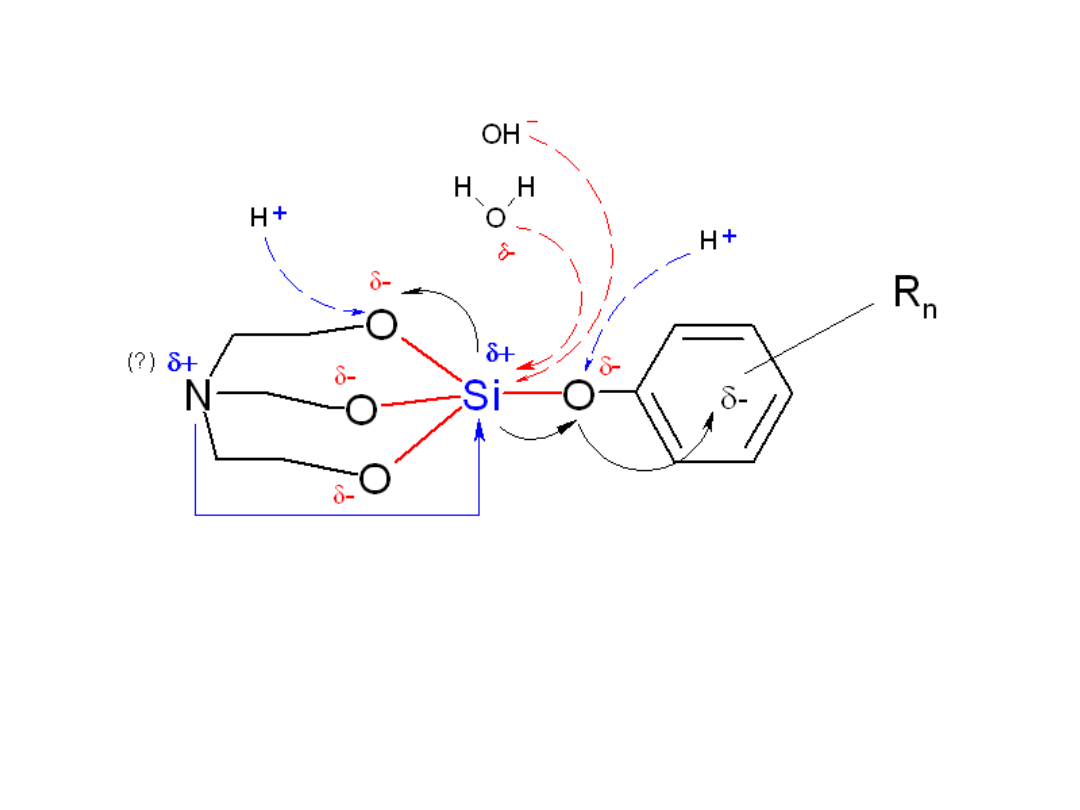
                           Struktura cząsteczki i

różnice w elektroujemnościach atomów

poszczególnych pierwiastków pozwalają

zaproponować podany powyżej rozkład

ładunków w cząsteczce związku.

Reakcje złożone

1) równoległe,

2) sprzężone,

3) następcze,

4) odwracalne.

v

1

v

2

x

a

a

t

k

k







ln

1

2

1

Ad 1) r-cje równoległe:

B

A

C

2

1

v

v

v





v = v

1

+ v

2

+ ........ + v

i

= Σv

i

Ad. 2) r-cje sprzężone:

a) A + B  M
b) A + C  N

Ad. 3) r-cje następcze:

A  B  C

v

1

v

2

2

1

1

1

1

v

v

v





2

1

1

1

1

v

v

v





2

1

2

1

1

v

v

v

v

v





2

1

2

1

v

v

v

v

v





i

v

v

v

v

1

......

1

1

1

2

1







Inna reakcja następcza:

1) A + B  AB powoli
2) AB + B  AB

2

szybko

3) A + 2B  AB

2

r-cja

sumaryczna

v

2

>> v

1

2

1

2

1

v

v

v

v

v





v

= v

1

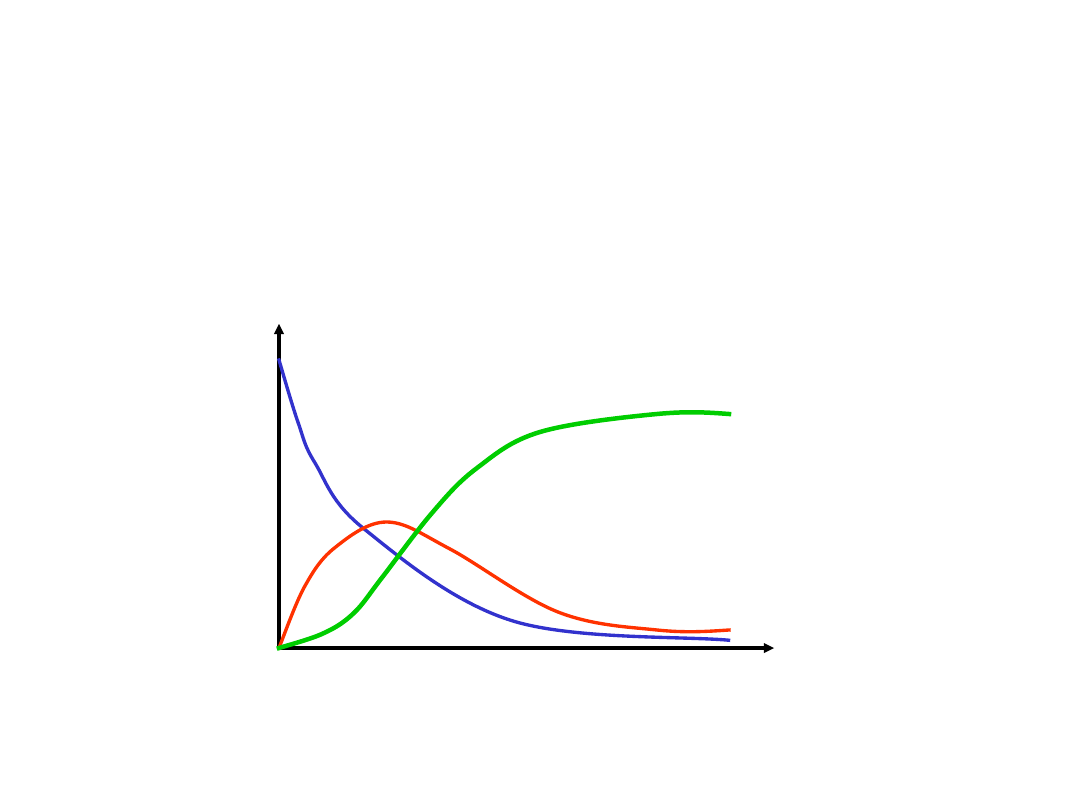
stężenie

czas

A

B

C

Zmiana stężeń reagentów w reakcji
następczej

A  B  C

cd. Ad. 3) r-cje następcze:

reakcje łańcuchowe

Ad. 4) r-cje odwracalne

rozważmy przypadek, gdy obie

reakcje są pierwszego rzędu:

A B

f

r

k

k





]

[

]

[

]

[

B

k

A

k

dt

A

d

r

f











Po scałkowaniu:

eq

eq

o

r

f

A

A

A

A

k

k

t











log

303

,

2

r

f

eq

eq

eq

eq

k

k

A

A

A

B

K









1

Szybkość reakcji jest cechą charakterystyczną
dla danego zespołu reagentów i zależy od
wielu czynników. Najważniejsze z nich to:

·  stężenie reagentów,
·  temperatura,
·  ciśnienie (gdy reakcja przebiega w fazie
gazowej),
·  promieniowanie elektromagnetyczne (r-
cje

fotochemiczne),

·  rozwinięcie powierzchni (reakcje
powierzchniowe)
·  obecność katalizatora lub inhibitora,
. środowisko reakcji (pH, elektrolity,
rozpuszczalniki

organiczne)

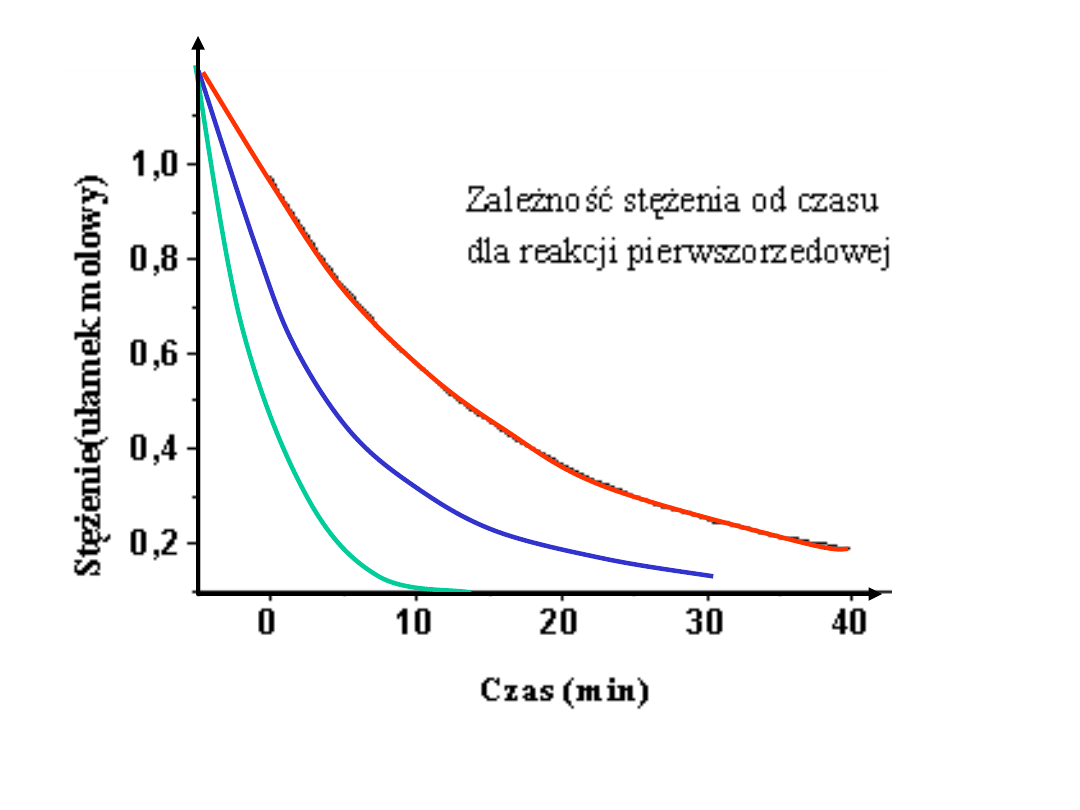
Wpływ
stężenia

k małe

k
średnie

k
duże

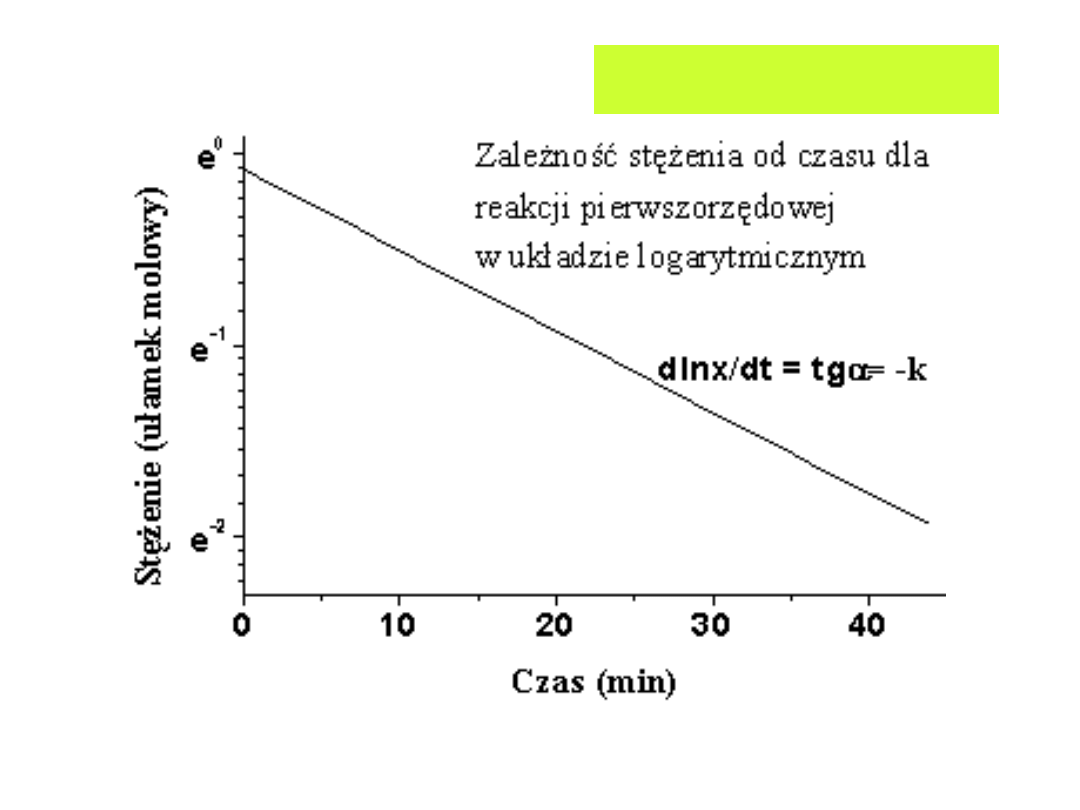
kt

a

x

a







ln

)

ln(

Wpływ
stężenia

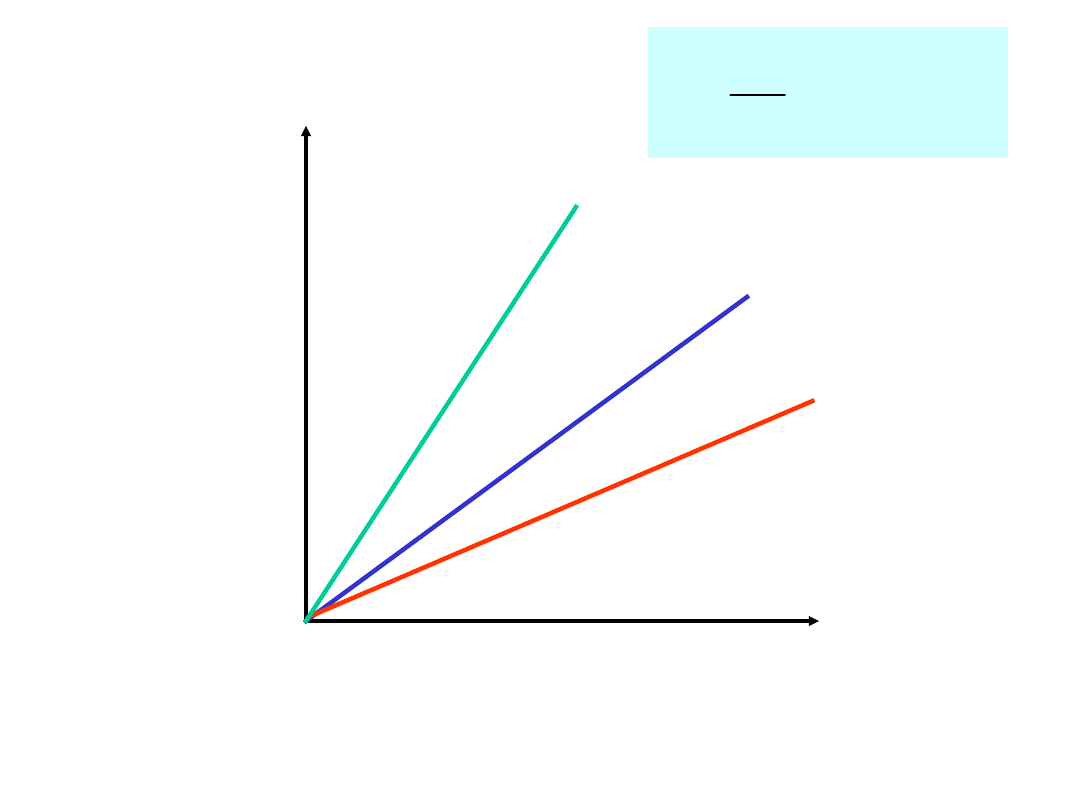
Szybkoś
ć

Stężenie (a –
x)

Wpływ
stężenia

)

(

x

a

k

dt

dx

v







k małe

k
średnie

k
duże

k małe

k
średnie

k
duże

Wpływ
stężenia

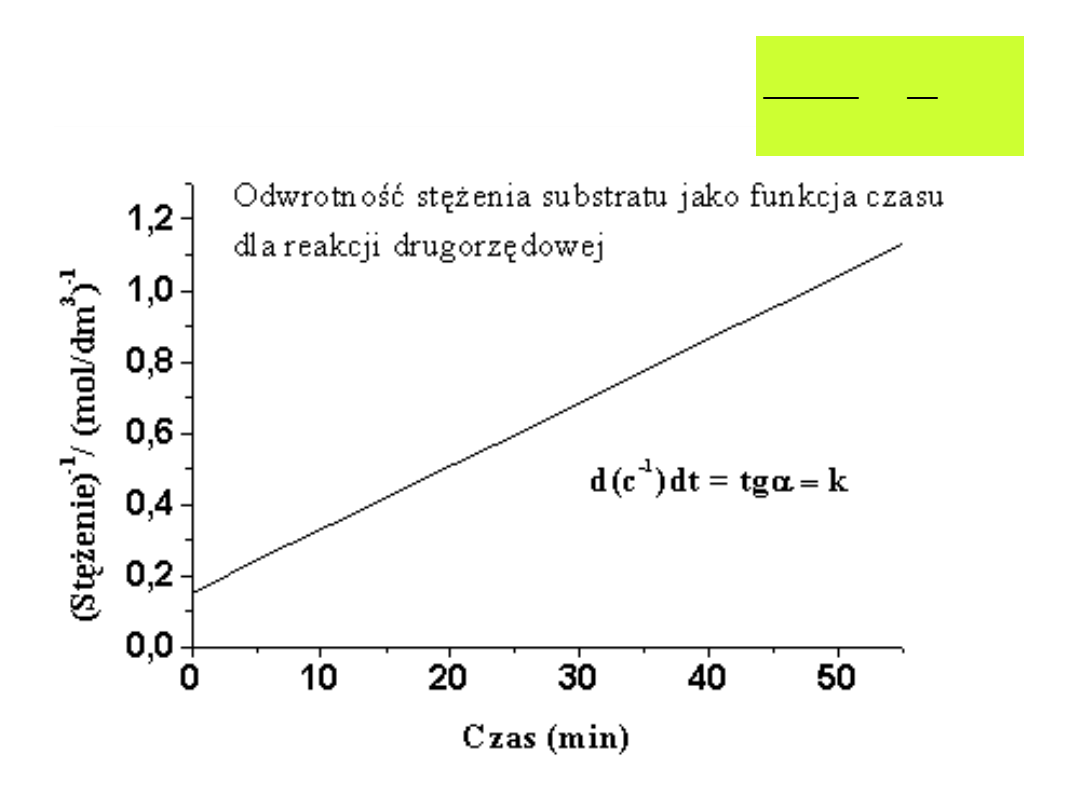
kt

a

x

a







1

1

Wpływ
stężenia

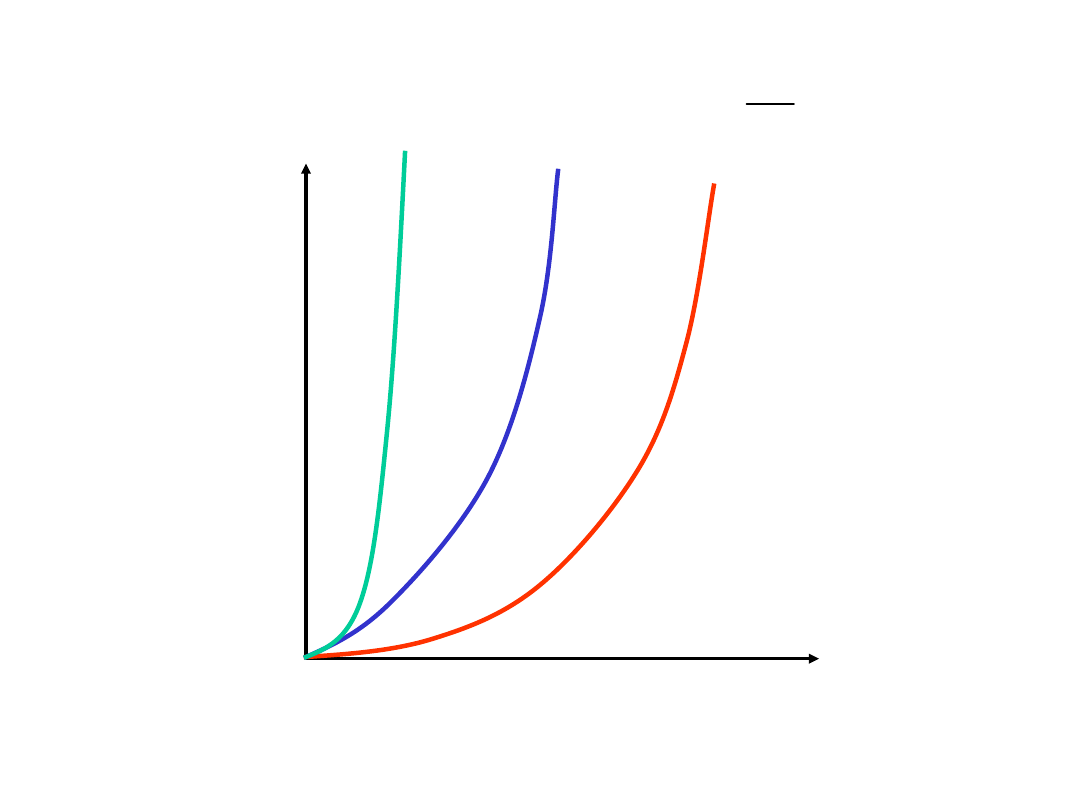
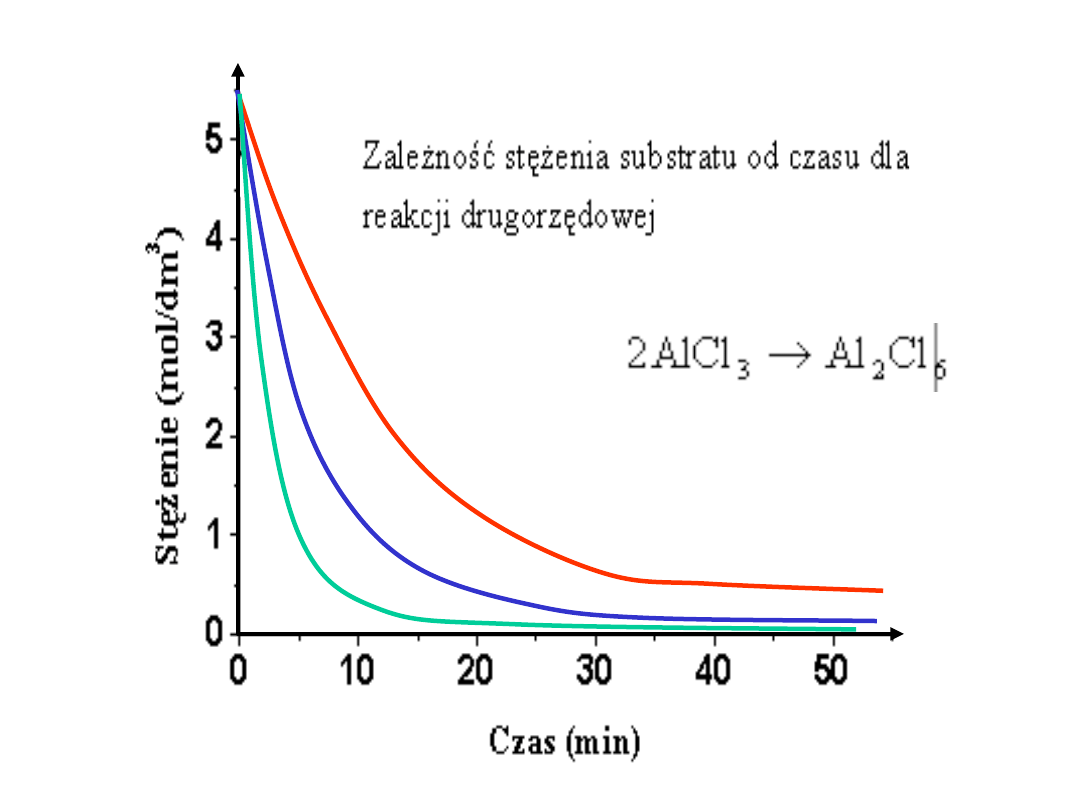
2

)

(

x

a

k

dt

dx

v







Szybkoś
ć

Stężenie (a – x)

Wpływ
stężenia

k małe

k
średnie

k
duże

Wpływ temperatury na szybkość reakcji
chemicznej

zwykle opisuje się poprzez

przedstawianie

zależności stałej k od

temperatury

Empiryczna reguła van’t Hoffa:

T

K

T

T

K

T

k

k

v

v

Q

10

10

10









Równanie Arrheniusa

RT

E

a

a

a

e

k

k

RT

E

k

k

k

A

R

E

B

T

B

A

k

/

0

0

0

ln

ln

ln

'

'

ln

















Równanie Arrheniusa

RT

E

a

a

a

e

k

k

RT

E

k

k

k

A

R

E

B

T

B

A

k

/

0

0

0

ln

ln

ln

'

'

ln

















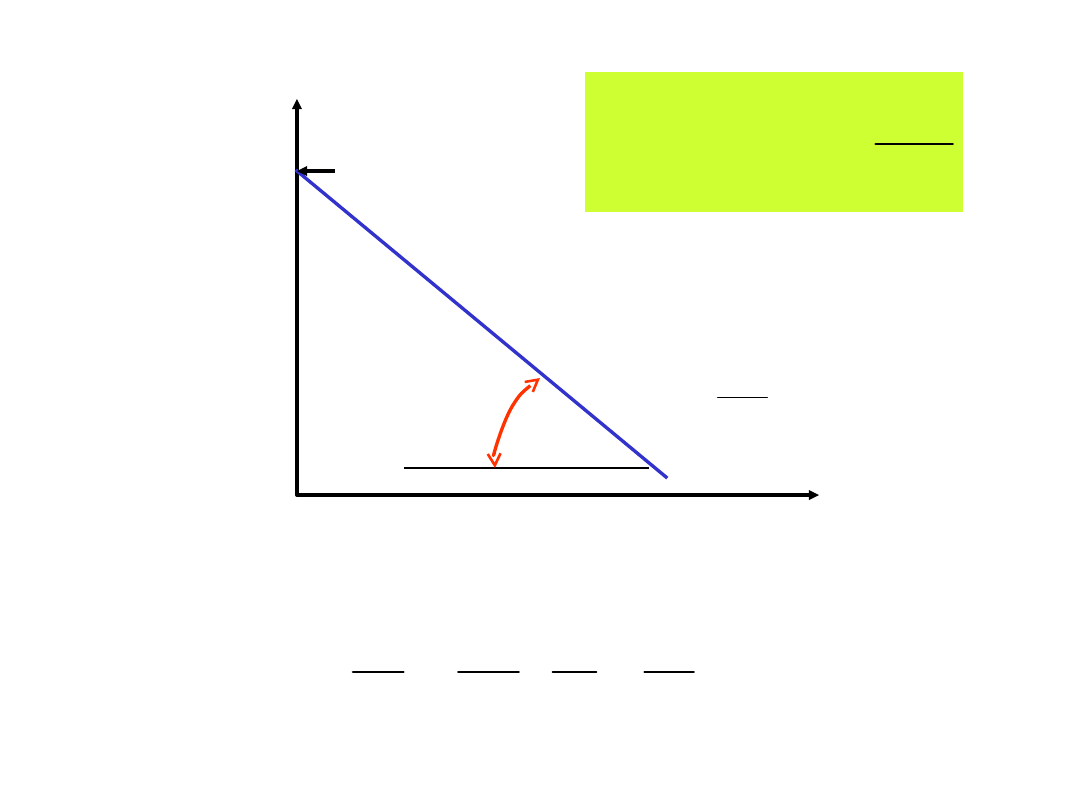
ln k

1/T

















2

1

1

2

1

1

ln

T

T

R

E

k

k

a



R

E

a







tg

RT

E

k

k

a





0

ln

ln

ln k

0

Przykład:
Obliczyć ile razy wzrośnie stała szybkości
reakcji w wyniku ogrzania układu reagującego
od temperatury 0C do temp. 100C, jeżeli

energia aktywacji reakcji jest równa : a) 50
kJ/mol, oraz b) 200 kJ/mol.
 

ln k = ln k

o

– E

A

/ RT

ln (k

T2

)/(k

T1

) = = – E

A

/ R ( 1/T

2

– 1/ T

2

)

ln (k

T2

)/(k

T1

) = (E

A

/ R) ( T

2

– T

1

) / (T

1

* T

2

)

ln (k

373,2 K

)/(k

273,3 K

) = (50000/8,314) * 100 /

(373,2 * 273,2) = 5,898

czyli (k

373,2 K

)/(k

273,3 K

) = 365

Dla E

A

= 200 kJ/ mol (k

373,2 K

)/(k

273,3 K

) = 1,78 *

10

10

 

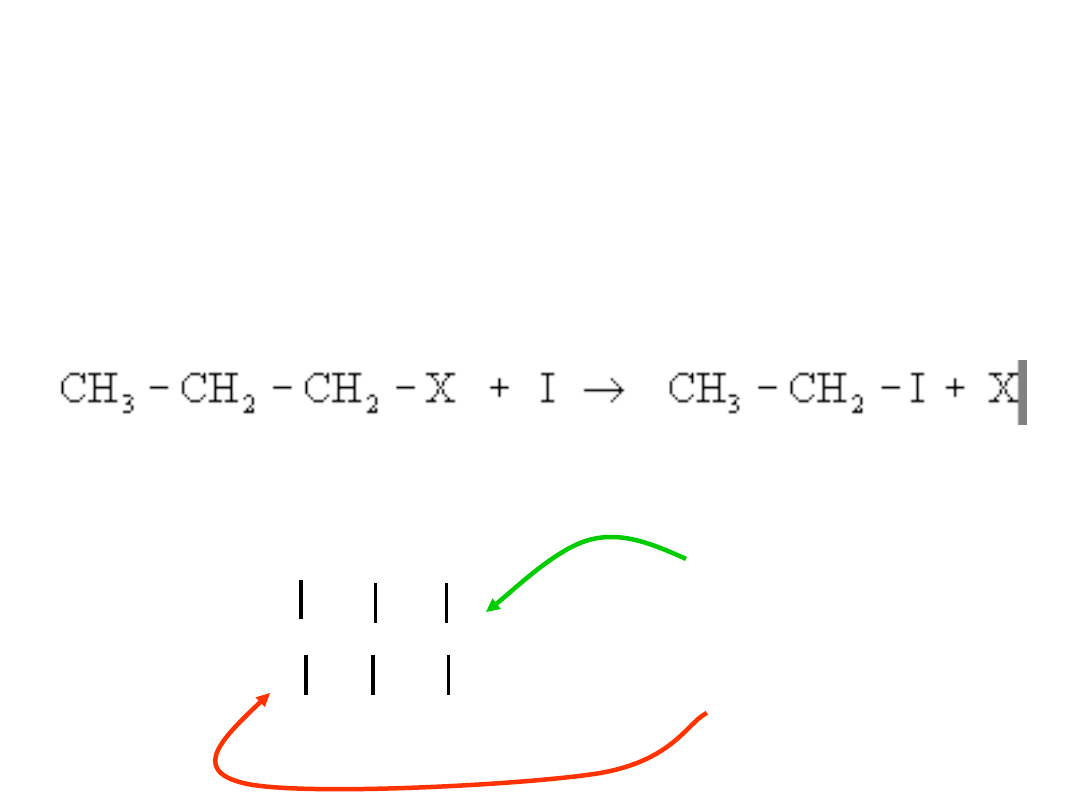
Wpływ orientacji cząsteczek na szybkość
reakcji chemicznej

Aby zderzenie było efektywne cząsteczki
muszą się zderzyć odpowiednimi miejscami,
np. w reakcji:       

                      
drobina I musi uderzyć atom węgla związany
z grupą X:

H H H
I

H – C – C – C – X

H H H

Zderzenie
efektywne

Zderzenie
nieefektywne

Katalizatorem danej reakcji nazywamy
substancję, która wprowadzona do układu
reagującego

zwiększa

szybkość

tej

reakcji, a sama nie ulega przemianom
chemicznym

w

ostatecznym

wyniku

reakcji.

Wpływ katalizatora

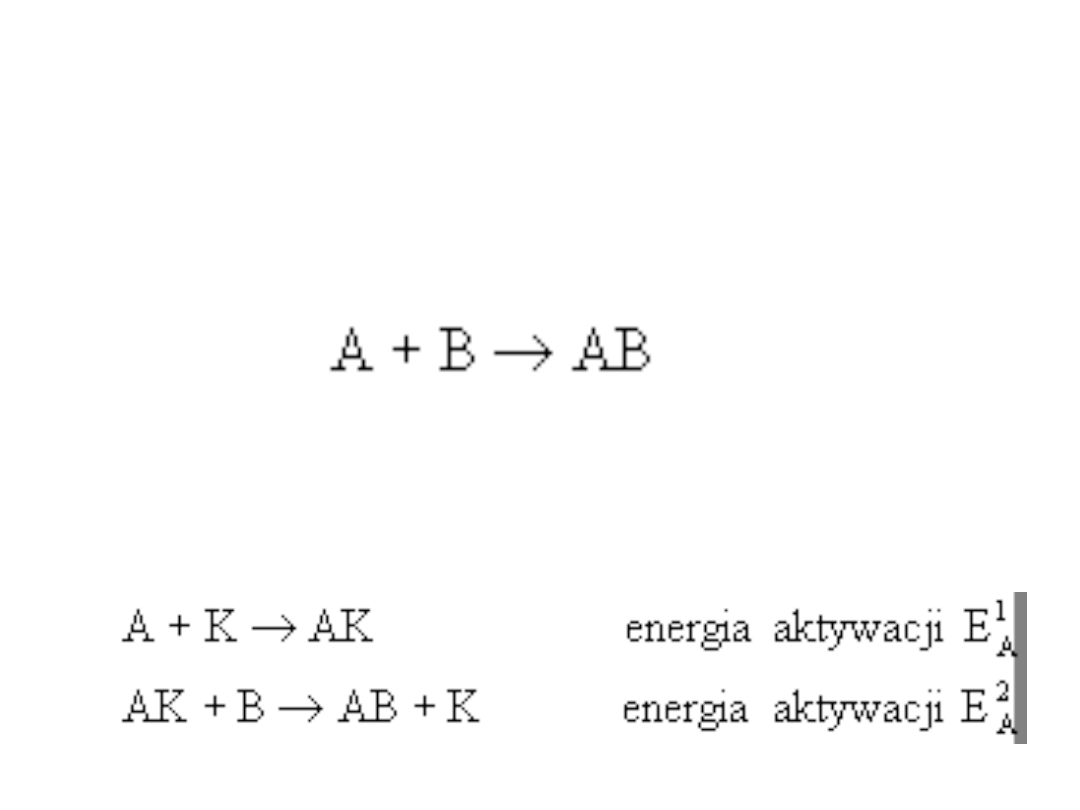
Przyśpieszenie reakcji przez katalizator

polega na zmniejszeniu energii aktywacji w
porównaniu z reakcją nie katalizowaną. Dla
reakcji zachodzącej bez katalizatora:

                            

mamy energię aktywacji E

A

. Tą samą

reakcję

przebiegającą

przy

udziale

katalizatora K można opisać równaniami:

                                                                        
                            

Wpływ katalizatora

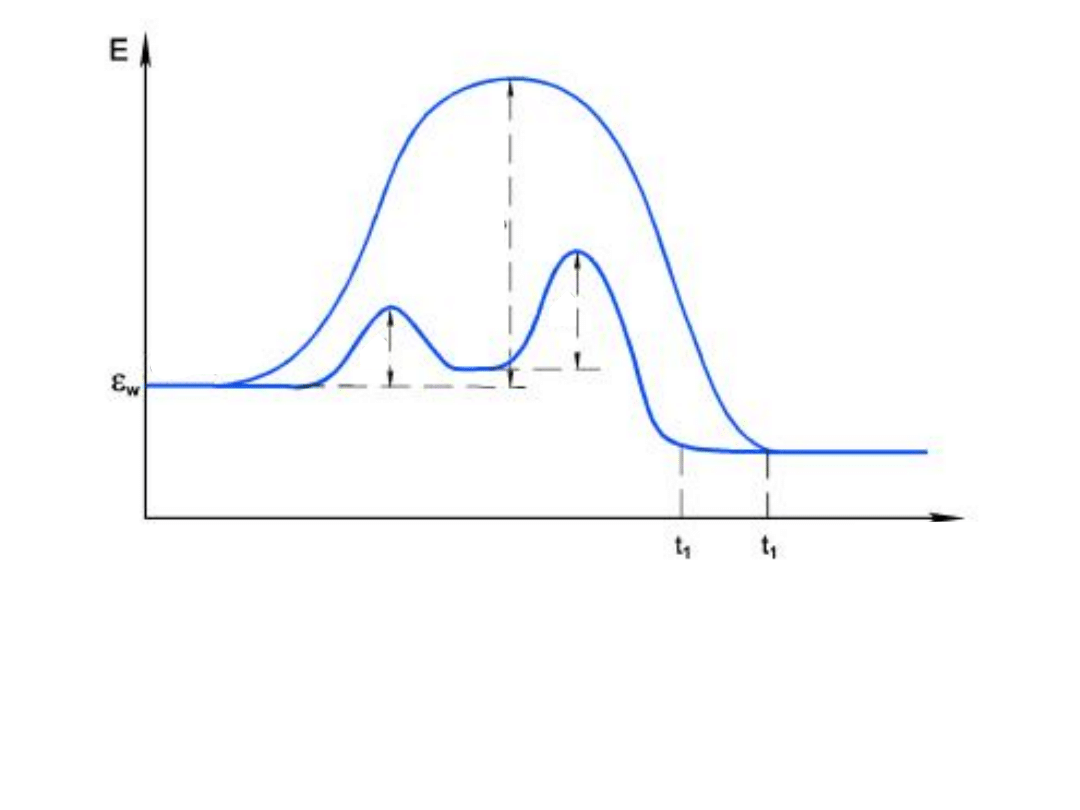
Jeżeli reakcja bez katalizatora wymaga energii
aktywacji E

A

to w obecności katalizatora K,

dwie reakcje wykazują energię aktywacji E

1

i

E

2

przy czym każda z nich jest mniejsza od E

A

AB, K

E

A

A, B,
K

E

1

E

2

Czas

Wpływ katalizatora

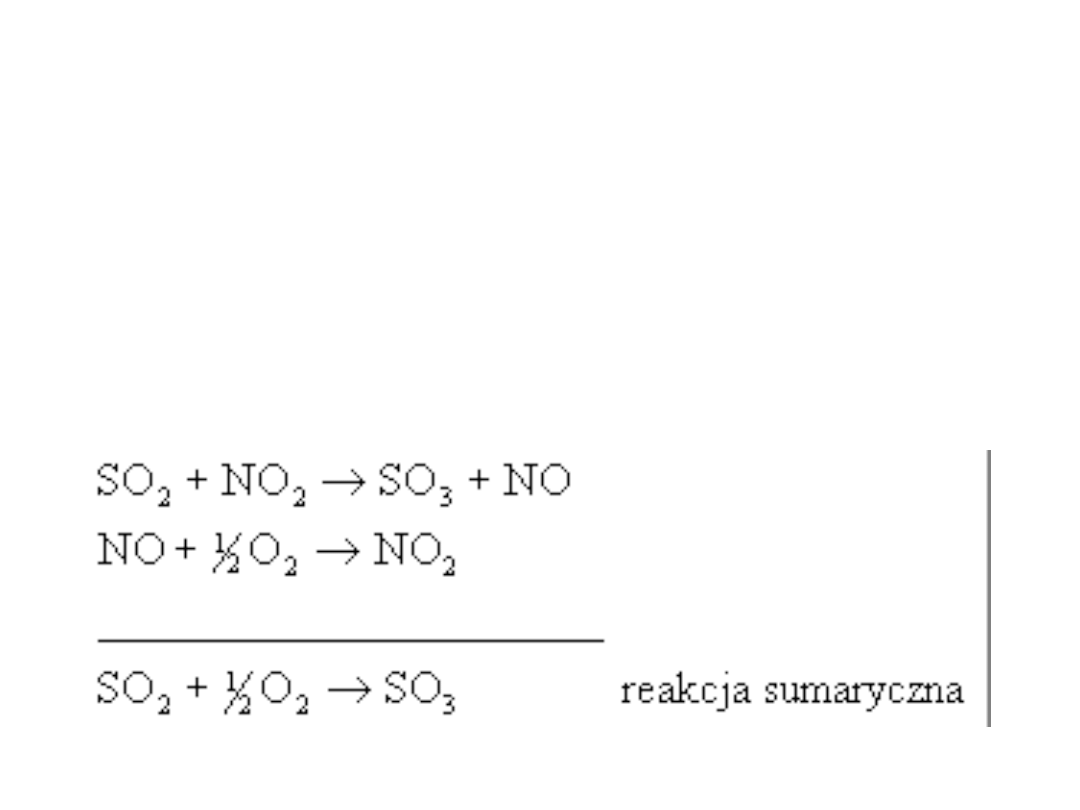
Kataliza homogeniczna

Katalizator

może

stanowić

jeden

ze

składników jednorodnej fazy (gazowej lub
ciekłej) w której zachodzi reakcja - mówimy
wówczas

o

katalizie

homogenicznej,

jednorodnej, jednofazowej.

Kataliza heterogeniczna

Jeśli katalizator stanowi odrębną fazę w
układzie reagującym, to katalizowana reakcja
przebiega na granicy faz i wówczas mamy do
czynienia

z

katalizą

niejednorodną

(heterogeniczną, wielofazową).

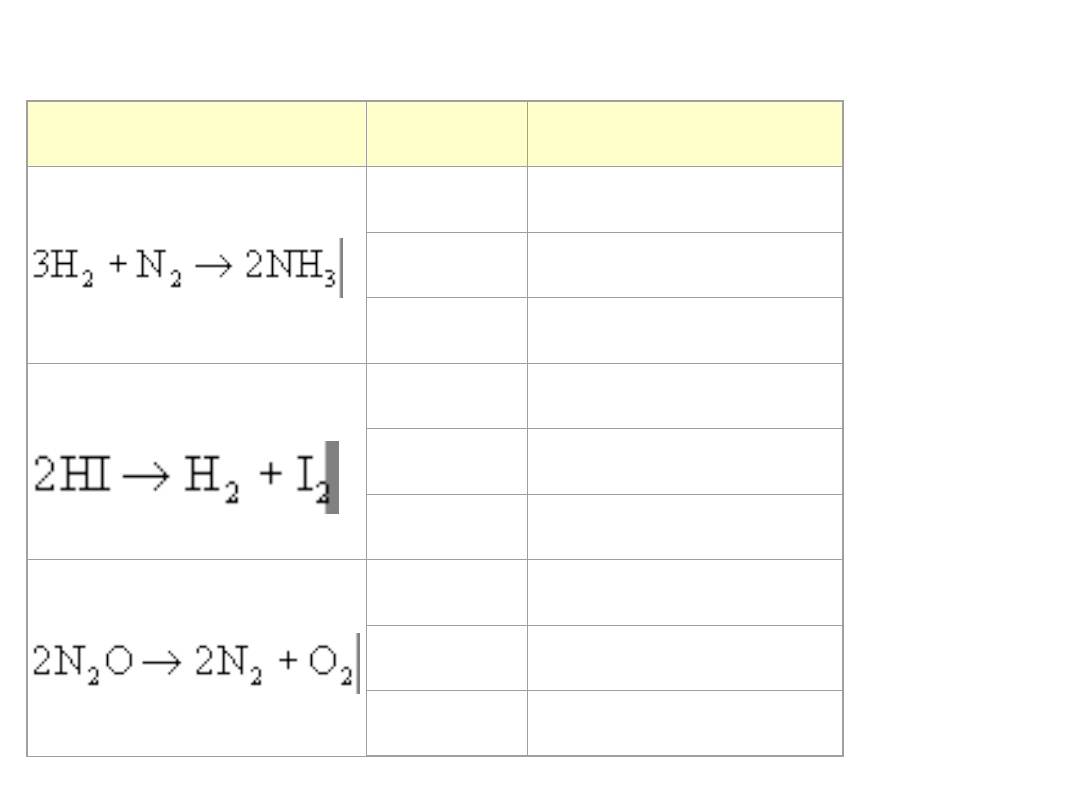
Wartości Ea (energii aktywacji) dla wybranych reakcji

Reakcja

Kat.

Ea [kJ/mol]

 

 

                                         

brak

335

wolfra
m

163

osm

197

 

 

                               

brak

184

platyn
a

105

złoto

59

 

 

                                         

brak

247

platyn
a

138

złoto

121

Mechanizm katalitycznego uwodorniania
etylenu

C

2

H

2

zgodnie

z

reakcją:                                                        

Przebieg procesu odbywa się w czterech
etapach 

CH

2

=CH

2

+ H

2

 CH

3

-

CH

3

 

                                                                                                         

 

                                                                                                         

 

                                                                                                         

 

                                                                                                         

 

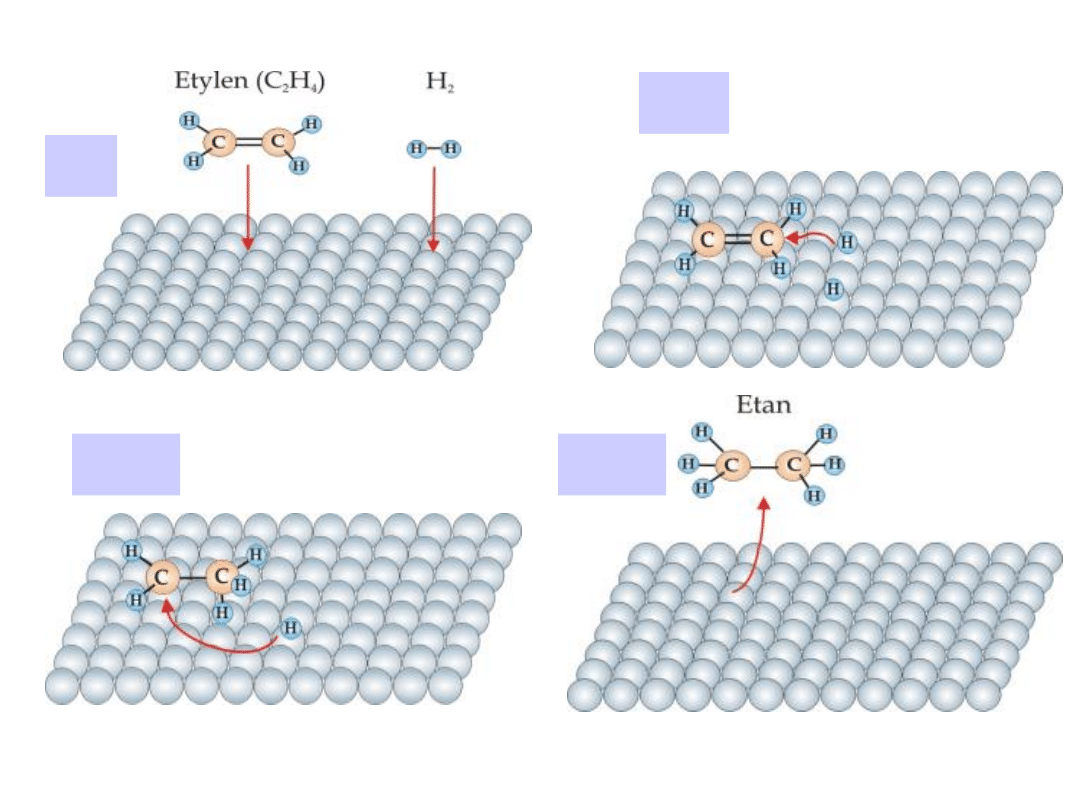
(I)

(II)

(III)

(IV)

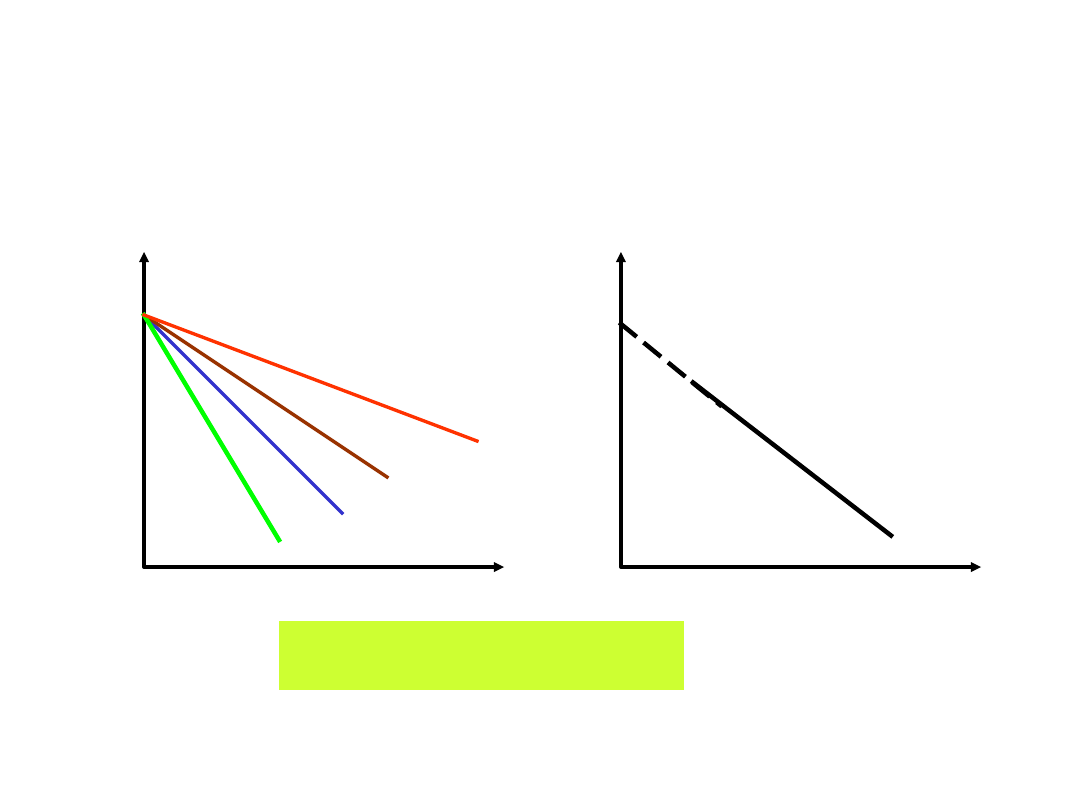
Badanie trwałości leków metodą

przyśpieszonego starzenia

log
c

czas

T

4

T

3

T

2

T

1

log k

1/T

kt

a

x

a







ln

)

ln(

Znając k można wyznaczyć czas
przechowywania leku

Kinetyka reakcji enzymatycznych





]

[

]

[

]

[

1

1

3

1

2

S

ES

E

k

v

P

E

ES

S

E

k

k

k













[E] – [ES] - stężenie wolnego enzymu

[S] - stężenie substratu

]

[

]

[

3

3

2

2

ES

k

v

ES

k

v





W stanie równowagi mamy:

3

2

1

v

v

v





Po podstawieniu:





]

[

]

[

]

[

]

[

]

[

3

2

1

ES

k

ES

k

S

ES

E

k











m

K

k

k

k

ES

S

ES

E









1

3

2

]

[

]

[

]

[

]

[

Jeżeli stan równowagi tworzenia kompleksu
ES ustala się bardzo szybko, wtedy k

2

>> k

3

i wzór upraszcza się:

oraz:

Jeżeli stężenie substratu jest odpowiednio
duże, wtedy wszystkie cząsteczki enzymu są
związane w kompleks ES, a szybkość reakcji
osiąga wartość maksymalną:

1

2

k

k

K

m



]

[

3

3

ES

k

v

v





]

[

3

max

E

k

v



Ostatnie dwa równania pozwalają na
podstawienie wyrażeń za [E] i [ES] w
równaniu na K

m

:

]

[

]

[

max

S

K

S

v

v

m





Stała K

m

(stała Michaelisa) jest marą

powinowactwa enzymu do substratu.

Stałą K

m

można wyznaczyć z powyższego

równania.

Równanie

Michaelisa

–

Menten

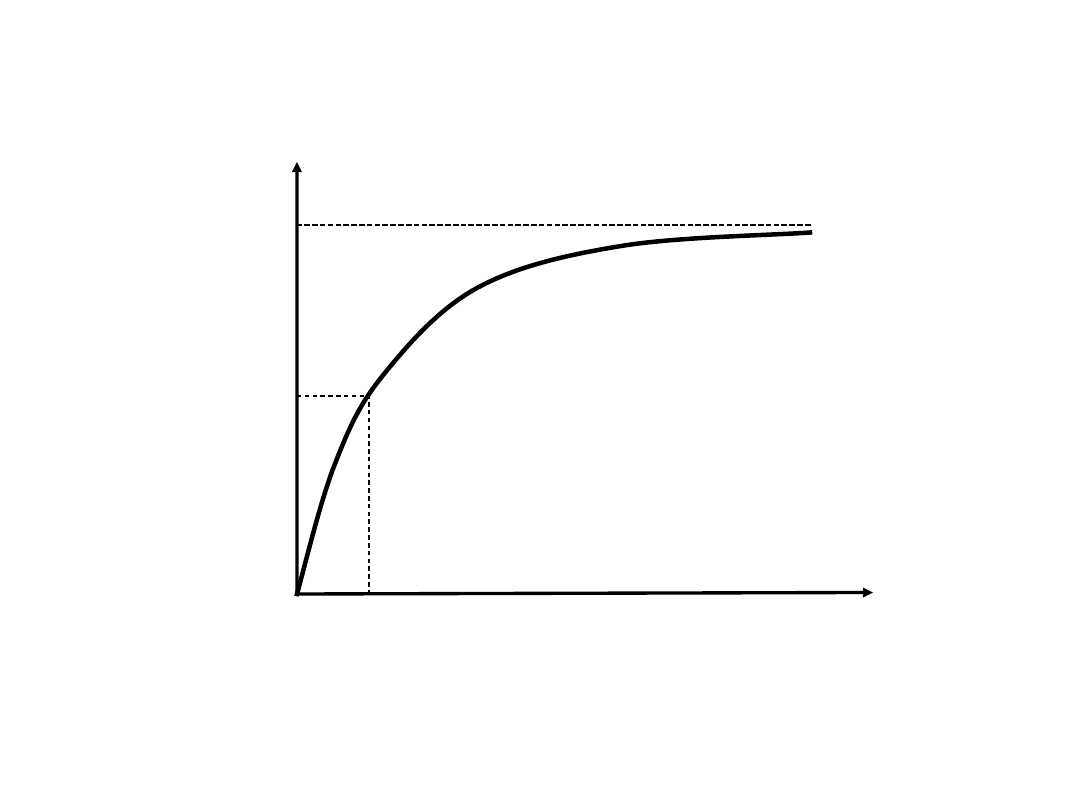
v

v

max

v

max

/

2

K

m

[S]

Graficzne

przedstawienie

równania

Michaelisa – Menten

]

[

]

[

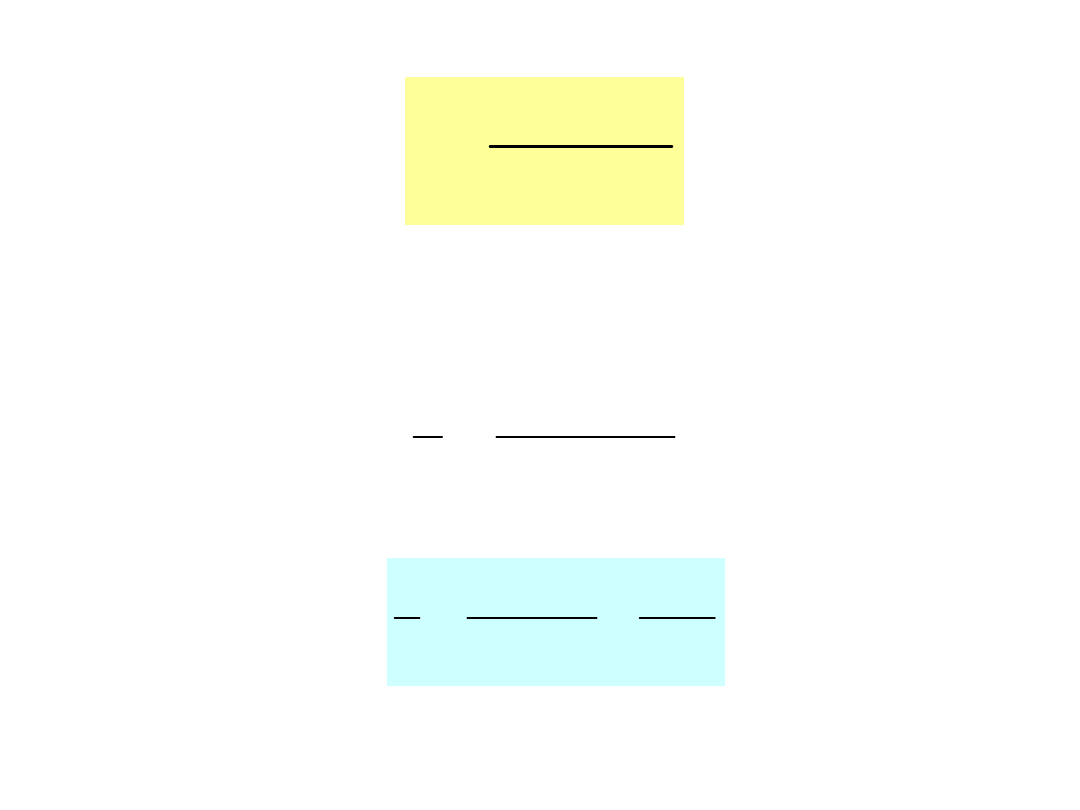
1

max

S

v

S

K

v

m





max

max

1

]

[

1

v

S

v

K

v

m





Równanie Lineweavera –
Burka

]

[

]

[

max

S

K

S

v

v

m





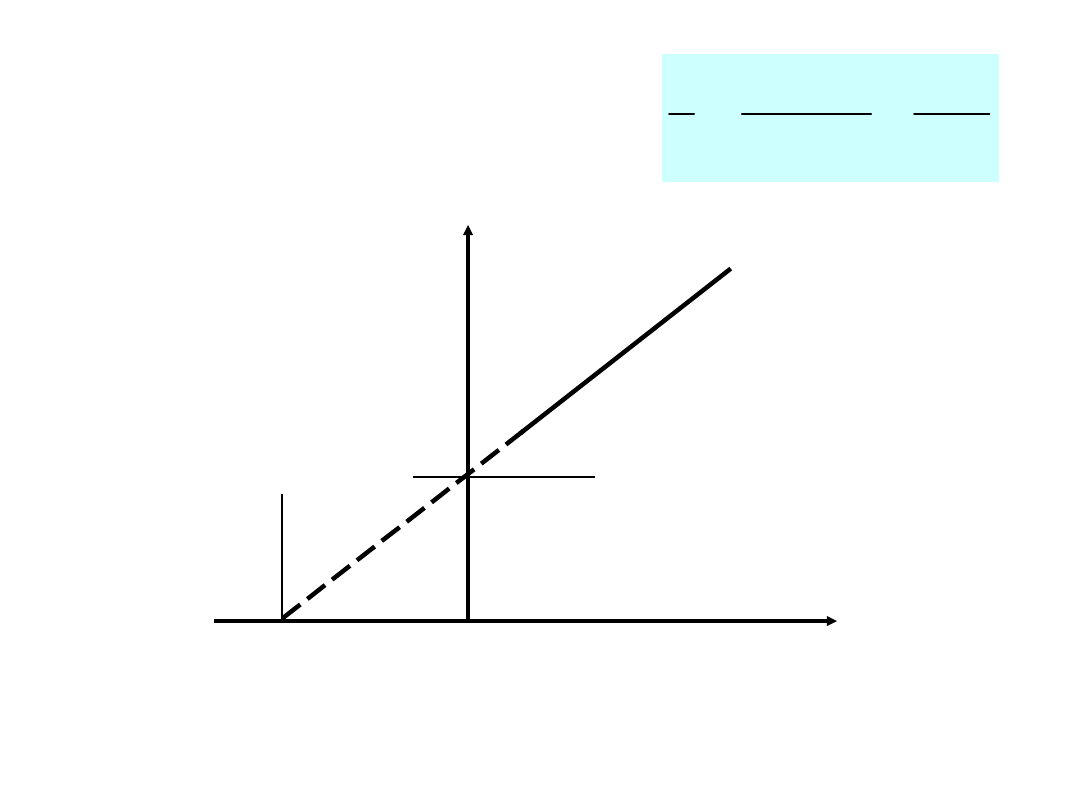
1/v

1/
[S]

1/v

ma

x

-
1/K

m

max

max

1

]

[

1

v

S

v

K

v

m





Graficzne przedstawienie równania
Lineweavera – Burka

Fotochemia

AB +h







 +  A +

B

Prawo Starka – Einsteina:

Każda cząsteczka biorąca udział w
pierwotnym procesie fotochemicznym
absorbuje jeden foton.

Wydajność kwantowa pierwotnego procesu
fotochemicznego,



:

liczba cząsteczek substratu tworzących

określony produkt pierwotny na każdy

zaabsorbowany kwant.

Wydajność kwantowa całkowitego procesu:

liczba cząsteczek substratu
przeprowadzonych w produkt w wyniku
absorpcji jednego kwantu promieniowania.



=

Liczba cząsteczek ulegających przemianie
fotochemicznej

Liczba pochłoniętych kwantów
promieniowania

Przykłady reakcji fotochemicznych:

HI +h





H + HI  H

2

+ I





I + I  I

2

O

2

+ h





































Cl

2

+ h



 Cl + Cl

Cl + H

2

 HCl + H

H + Cl

2

 HCl + Cl

Cl + H

2

 HCl + H itd.

Br

2

= 2Br

Br + H

2

= HBr + H

H + Br

2

= HBr + Br itd.

H* + Br* = HBr

CH

2

-COOH + H

2

O  CH

2

-COOH + HCl

Cl OH

6CO

2

+ 6H

2

O  C

6

H

12

O

6

+

6O

2

h



Szybkość rozpuszczania się
ciał stałych

Równanie
Boguskiego:

)

(

x

a

kS

dt

dx

V





V - objętość cieczy,

S – powierzchnia rozpuszczanego ciała,

a – początkowe stężenie roztworu,

x – stężenie substancji rozpuszczonej w
chwili t.

Po scałkowaniu w przedziałach od t

1

do t

2

oraz x

1

do x

2

otrzymujemy:

2

1

1

2

log

)

(

303

,

2

x

a

x

a

S

t

t

V

k









Przy uwzględnieniu stężenia roztworu
nasyconego zamiast stężenia początkowego,
równanie może przyjąć postać:

)

(

'

C

C

S

k

dt

dC

nas



