INSTYTUT INŻYNIERII ŚRODOWISKA UNIWERSYTET ZIELONOGÓRSKI
		CHEMIA FIZYCZNA LABORATORIUM
III ROK INŻYNIERII ŚRODOWISKA STUDIA DZIENNE GRUPA 36 C		25.04.2003 TYDZIEŃ 4
KINETYKA CHEMICZNA. WYZNACZANIE STAŁEJ SZYBKOŚCI I RZĘDU REAKCJI. TEMAT V AUTORZY OPRACOWANIA: TOMASZ GACEK ARKADIUSZ KARPACZ ERNEST STECKIEWICZ MAREK ŻEBROWSKI

CZĘŚĆ TEORETYCZNA

Szybkość reakcji definiujemy za pomocą pochodnych stężenia substratu lub produktu względem czasu

gdzie c - stężenie substratu, x - stężenie produktu.

Znak minus przed pierwszą pochodną oznacza, że stężenie substratu maleje w czasie.

Szybkość reakcji jest funkcją stężenia poszczególnych reagentów A, B, C ... i jeżeli reakcja jest jednokierunkowa

...

to współczynniki potęgowe a, b, c są charakterystyczne dla danej reakcji i określają rząd reakcji względem danych reagentów.

Suma współczynników potęgowych określa rząd reakcji. Nie można go mylić ze współczynnikami stechiometrycznymi reakcji i tzw. cząsteczkowością reakcji. Cząsteczkowość określa liczbę cząsteczek uczestniczących w elementarnej przemianie chemicznej.

O kinetyce procesu decydują najpowolniejsze etapy, ale niekoniecznie tylko jeden z nich, dlatego też równanie kinetyczne może przyjmować bardzo złożoną postać ze współczynnikami potęgowymi różniącymi się zasadniczo od współczynników stechiometrycznych.

Ponieważ liczba cząsteczek biorących udział w elementarnej przemianie jest z reguły mała (dwie cząsteczki, rzadziej jedna lub trzy), to też i rzędy reakcji osiągają małe wartości. Analizę ogranicza się zwykle do reakcji o rzędowości mniejszej niż 3. Rząd może być ułamkowy, jak również zerowy.

Rozważając przykład, kiedy w reakcji bierze udział tylko jeden substrat, równania kinetyczne dla reakcji rzędu pierwszego, drugiego i trzeciego mają wtedy postać

Scałkowanie tych równań prowadzi do użytecznych w praktyce równań kinetycznych.

Dla reakcji I rzędu:

gdzie c₀ jest stężeniem początkowym. To samo równanie w formie wykładniczej ma postać

Charakterystyczna jest liniowa zależność lg c od czasu. Taką graficzną prezentację kinetyki reakcji I rzędu stosuje się często w praktyce:

Równanie to pozwala w prosty sposób sprawdzić, czy dana reakcja jest pierwszego rzędu, pozwala wyznaczyć stałą szybkości k₁ z nachylenia lg c = f(t).

Z równania możemy znaleźć wyrażenie na tzw. czas połówkowy reakcji, tj. czas po upływie którego stężenie substratu spada do połowy wartości stężenia początkowego c₀. Jeżeli więc wstawimy do równania c= ½ c₀, to czas połówkowy t_1/2 wyniesie

Wynika stąd, że czas połówkowy zupełnie nie zależy od stężenia początkowego c₀. Dla danej reakcji połowa substratu przereagowuje zawsze w tym samym czasie.

Dla reakcji II rzędu, całkowanie równania prowadzi do wyniku:

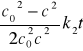
W tym przypadku odwrotność stężenia jest liniową funkcją czasu

,

natomiast czas połówkowy takiej reakcji II rzędu zależy od c₀, zgodnie z wyrażeniem

.

Dla reakcji III rzędu, całkowanie równania (3) prowadzi do równania kinetycznego:

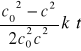
z którego wynika, że od czasu zależy liniowo odwrotność kwadratu stężenia substratu, a czas połówkowy określa wyrażenie

Jeżeli porównamy czasy połówkowe dla reakcji poszczególnych rzędów, to dochodzimy do wniosku, że są one związane z rzędem reakcji n ogólnym wzorem

Dla reakcji zerowego rzędu czas połówkowy będzie proporcjonalny do stężenia początkowego.

Równania na szybkość reakcji dla poszczególnych rzędów w ogólnym przypadku lepiej zapisać w następujący sposób:

I rząd:

II rząd:

III rząd:

gdzie a, b, c oznaczają stężenie początkowe substratów, a x - przyrost stężenia produktu.

Całkowanie powyższych równań prowadzi do ogólnie stosowanych wzorów:

I rząd:

II rząd:

III rząd:

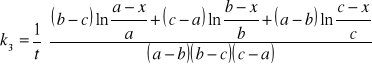
W przypadku równania n-tego rzędu, dla takich samych stężeń substratów, tzn. gdy

całkowanie prowadzi do wyrażenia:

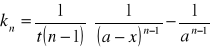
Rząd reakcji wyznacza się następująco:

• Metoda graficzna. Polega na wykorzystaniu scałkowanych postaci równań kinetycznych i graficznej prezentacji wyników pomiarów. Dla reakcji I rzędu spełniona jest liniowa zależność między lg c a czasem, dla reakcji II rzędu między odwrotnością stężenia a czasem, dla reakcji III rzędu między odwrotnością kwadratu stężenia a czasem. Spełnienie jednej z podanych relacji wskazuje na właściwie dobrany rząd.

• 
  Metoda różniczkowa van't Hoffa. Polega na pomiarze szybkości reakcji dla t=0, przy różnych stężeniach początkowych. Nie jest rzeczą łatwą uchwycić zmiany stężeń w chwili początkowej, zwłaszcza, gdy reakcja jest dość szybka. Trzeba wtedy ekstrapolować nachylenie stycznej do krzywej przebiegu reakcji do czasu zerowego.

x

t

Po wyznaczeniu szybkości reakcji dla dwu różnych stężeń początkowych a₁ i a₂ otrzymujemy

i

Po zlogarytmowaniu i przekształceniu dochodzimy do wyrażenia

• Metoda całkowa. W metodzie tej wykorzystuje się pomiar czasu, w ciągu którego przereagowuje określony ułamek substratu. Oznaczamy przez r ułamek nieprzereagowanego substratu:

Podstawiając wartości
i
do równania (6) otrzymujemy:

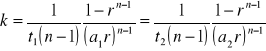
Po przekształceniu i uproszczeniu dochodzimy do relacji

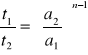
skąd wynika

W równaniu tym można w szczególności wykorzystać pomiar czasu połówkowego.

• W przypadku gdy w reakcji bierze udział szereg reagentów, wówczas konieczne okazuje się stosowanie metody izolacyjnej Ostwalda. W metodzie tej stosujemy duży nadmiar wszystkich składników w stosunku do jednego. Szybkość reakcji jest wtedy zależna od stężenia tylko tego jednego składnika. Rząd reakcji tego właśnie składnika możemy wyznaczyć jedną z trzech ww metod. Metoda ta jest powszechnie stosowana do badań mechanizmu reakcji złożonych.

CZĘŚĆ OBLICZENIOWA

• Metodyka

Zadanie polegało na wyznaczeniu rzędu reakcji utleniania jonów Fe²⁺ jonami ClO₃^- środowisku kwaśnym, zachodzącej według sumarycznego równania:

Stwierdzono, że etapem decydującym o kinetyce jest reakcja:

Stosowano metodę polegającą na określeniu czasu, w ciągu którego przereagowuje zadany ułamek substratów.

Przebieg reakcji śledzono przez fotometryczny pomiar stężenia jonów Fe³⁺ pod postacią kompleksu rodankowego. Pomiar prowadzono dla dwóch serii roztworów o różnym stężeniu początkowym , przy czym stężenia reagentów były takie same.

• Materiały

Aparatura:

spektrofotometr Spekol; ultratermostat U-10; szkło laboratoryjne.

Odczynniki:

roztwór soli żelazowej Fe²⁺ o stężeniu 0,002 mol/dm³ i 0,004 mol/dm³ ;

roztwór chloranu ClO₃^- o stężeniu 0,002 mol/dm³ i 0,004 mol/dm³ ;

25%-owy roztwór rodanku amonowego; 0,1m HCl

• Wykonanie ćwiczenia

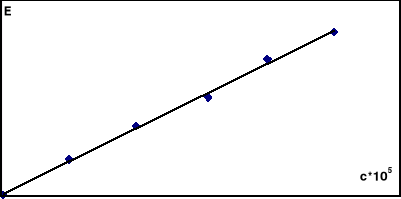
Sporządzono roztwory reagentów w 0,1n HCl i umieszczono je w termostacie nastawionym na ustaloną z góry temperaturę 25°C. Bezpośrednio przed rozpoczęciem pomiarów mieszano w stosunku 1:1 roztwory jonów Fe²⁺ i ClO₃^- o stężeniach 0,002 mol/dm³. Z naczynia reakcyjnego pobrano do kolbki 2 cm³ mieszaniny, rozcieńczono 18 cm³ 0,1 n HCl i dodano 2cm³ rodanku. Czas odczytu określono w momencie rozcieńczenia. Dalsze pomiary wykonano przy tej samej długości fali w 10-cio minutowych odstępach. Podobnie postępowano z roztworem sporządzonym z mieszaniny Fe²⁺ i ClO₃^- o stężeniach 0,004 mol/dm³. W międzyczasie sporządzić krzywą cechowania stężenia jonów Fe³⁺dla długości fali λ=480nm na podstawie pomiaru ekstynkcji kompleksu rodankowego. Krzywą cechowania przedstawiono na wykresie.

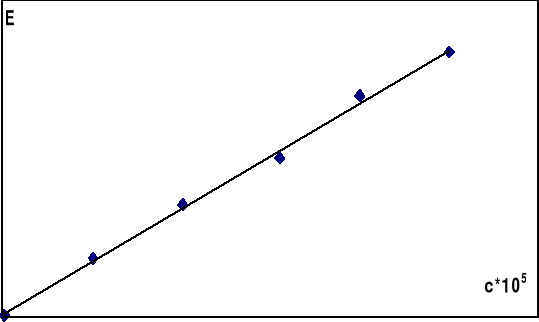
Wykres 1: Krzywa cechowania E(c) dla jonów Fe³⁺ przy λ=480nm

• Przedstawienie wyników pomiarów

Wyniki odczytów ekstynkcji pobieranych próbek w miarę postępu reakcji i znalezionych z krzywej cechowania stężeń x jonów Fe³⁺ przedstawiono odpowiednio w tabelach nr 1 i 2. Tabele te zawierają także wartości stężenia substratu c oraz liczby postępu reakcji x′, która jest stosunkiem x do stężenia początkowego substratu c_o.

Wyniki pomiaru szybkości utleniania jonów Fe²⁺ przy stężeniu początkowym c_o=0,002mol/dm³.

t[s]	0	600	1200	1800	3000
E	0,109	0,121	0,129	0,132	0,144
x • 10^5	35,33	39,21	41,81	42,78	46,67
c • 10^4	16,47	16,08	15,82	15,72	15,33
(1/c) • 10^-4	0,0607	0,0622	0,0632	0,0636	0,0652
x′	0,177	0,196	0,209	0,214	0,233

(*) Wartości znalezione /metodą najmniejszych kwadratów/ na podstawie zmierzonych ekstynkcji były mnożone przez 11, aby uwzględnić efekt rozcieńczenia, przy czym :

c = c_o- x

x′ = x/c_o

Wyniki pomiaru szybkości utleniania jonów Fe²⁺ przy stężeniu początkowym c_o=0,004mol/dm³

t[s]	0	600	1200	1800	3000
E	0,162	0,187	0,211	0,243	0,261
x • 10^5	52,51	60,61	68,39	78,76	84,59
c • 10^4	34,75	33,94	33,16	32,12	31,54
(1/c) • 10^-4	0,0288	0,0295	0,0302	0,0311	0,0317
x′	0,131	0,152	0,171	0,197	0,211

Na podstawie uzyskanych wyników sporządzono wykres zależności 1/c od

czasu, w myśl równania reakcji II rzędu (dla równych ilości substratów):

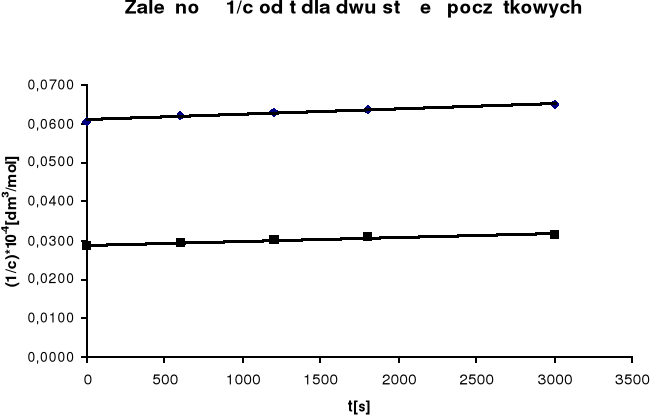
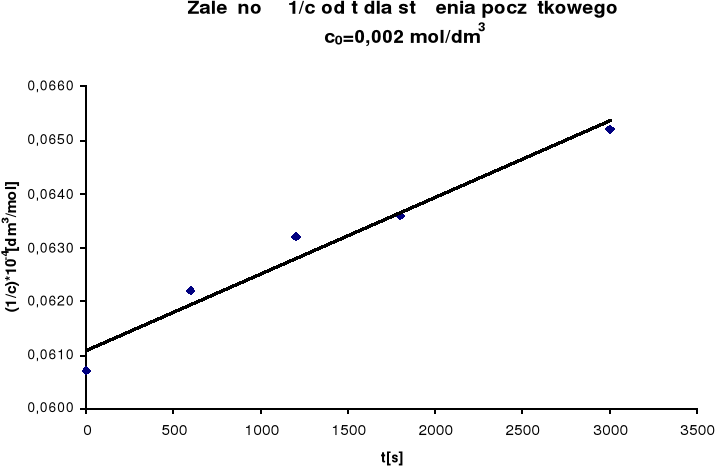
Z nachylenia prostej obliczono stałą szybkości reakcji k:

więc:

k = 0,021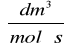

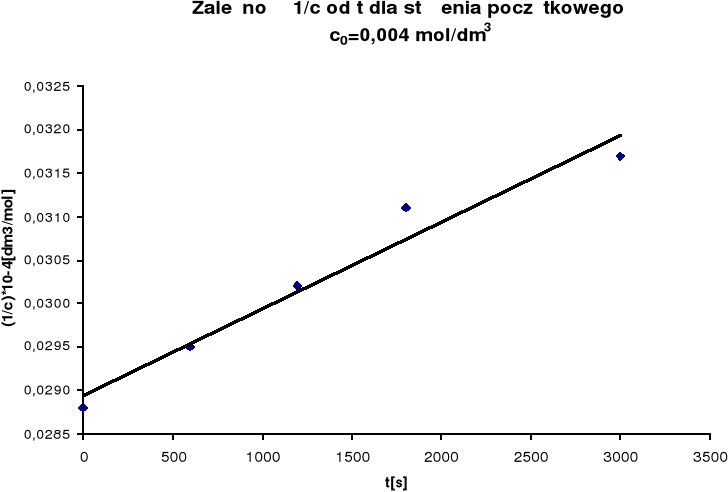
Z nachylenia prostej obliczono stałą szybkości reakcji k:

więc:

k = 0,01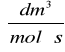

Do określenia rzędu reakcji zastosowano metodę całkową. W tym celu sporządzono wykresy zależności liczby postępu reakcji od czasu. Przebiegi x′=f(t) dla obu stężeń początkowych przedstawia na wykresie :

Z wykresu odczytujemy wartości t₁ i t₂ dla dowolnej wartości liczby postępu reakcji i wstawiamy do poniższego równania

gdzie a₁ i a₂ - stężenie początkowe substratu

Stężenia początkowe substratów: a₁ = 0,004 mol/dm³ , a₂ = 0,002 mol/dm³

= 2,26

WNIOSKI:

Celem ćwiczenia było wyznaczenie rzędu reakcji utleniania jonów Fe²⁺ jonami ClO₃^- w środowisku kwaśnym. Analizując przeprowadzone badanie możemy stwierdzić, iż wraz z upływem czasu stężenie jonów żelaza rosło, oraz wraz z upływem czasu rósł także postęp reakcji. Analizując wykres przedstawiający zależności x^` od t dla dwu stężeń początkowych obliczono rząd reakcji, który wyniósł n=2,26.

LITERATURA

• Pigoń K., Ruziewicz Z., „Chemia fizyczna”, PWN Warszawa

• Sobczyk I., Kisza A., Gatner K., Kroll A., „Eksperymentalna chemia fizyczna”, PWN Warszawa

8

---