Metodologia badań

Metodologia badań

 i statystyka

 i statystyka

Wojciech Grabowski

wgrabowski@aps.edu

.pl

spotkanie trzecie

 

 

 

Populacja

Każda 

dowolna 

zbiorowość 

względnie 

jednorodnych elementów.

Inaczej:

 

Zbiór dowolnej wielkości, w którym obiekty mają 
przynajmniej jedną cechę wspólną.

Przykłady:

• populacja ludzi na świecie;
• populacja dorosłych Polaków;
• populacja studentów danej szkoły;
• populacja samochodów danej firmy.

 

 

Próba

Przykłady:

• grupa 

15 

nauczycieli, 

z 

którymi 

przeprowadzono wywiady;

• grupa 100 ankietowanych osób;
• grupa 30 uczniów poddanych obserwacji.

Jest  to  konkretna  część  populacji,  czyli  grupa 
poddana obserwacji lub pomiarowi.

 

 

Strategia 

badań

Polega na tym, że próba 
jest 

jednocześnie 

populacją.

Oznacza  to,  że  badamy 
każdy 

element 

populacji, 

np. 

wszystkich 

uczniów 

danej szkoły. 

Strategia badań 

pełnych

Strategia badań 

reprezentatywnych

Polega na tym, że:

1. Z  populacji  losujemy 

próbę 
reprezentatywną. 

2. Przeprowadzamy 

na 

niej badania. 

3. Dokonujemy jej opisu.

4. Za 

pomocą 

wnioskowania 
statystycznego 
ustalamy 

prawdopodobieństwo, z 
jakim  możemy  odnieść 
wyniki 

do 

całej 

populacji

.

• Wnioski są 

pewne, 

dokładne

.

 

 

Reprezentatywność próby

Decydują o tym dwa czynniki:

• dostatecznie  duża  wielkość  próby  w  stosunku 

do całej populacji;

• sposób pobrania próby z populacji.

Jest  to  zdolność  próby  do  odzwierciedlania 
właściwości całej populacji.

Generalnie  rzecz  biorąc,  próba  reprezentatywna 
to  dostatecznie  duża  próba  wylosowana  z 
populacji.

 

 

Próba reprezentatywna

warstwowa

prosta

systematyczna

zespołowa

 

 

Próba reprezentatywna 

prosta

Powstaje  wtedy,  gdy  każdy 
element 

populacji 

ma 

jednakową  szansę  trafienia  do 
próby.

Przykład:

losowanie z 
urny 
(totolotek).

Próba reprezentatywna 

systematyczna

Powstaje,  gdy  do  próby 
włączamy 

co 

n-tą 

jednostkę z listy.

Przykład:

co 

dziesiąta 

osoba 

z 

listy 

alfabetycznej.

 

 

Próba reprezentatywna 

warstwowa

Pobieramy 

ją, 

gdy 

populacja 

jest 

niejednorodna.

1. Identyfikujemy 

istniejące 

podgrupy 

(warstwy).

2. Losujemy  w  każdej 

warstwie  z  osobna, 
proporcjonalnie  do  jej 
wielkości.

Próba reprezentatywna 

zespołowa

Powstaje,  gdy  losujemy 
nie  jednostki,  ale  całe 
zespoły

.

Przykład: w czasie badań 
na  uczelni  stwierdzamy, 
że  są  tam  studenci 
dzienni,  wieczorowi  i 
zaoczni.

Na 

przykład: 

klasy, 

szkoły, gminy, parafie...

 

 

Cecha (zmienna)

porządkowa

ilościowa na 

skali 

stosunkowej

ilościowa na 

skali 

interwałowej

jakościowa 

na skali 

nominalnej

Każda  dowolna  właściwość,  która  może  być 
obserwowana lub mierzona.

 

 

Cechy ilościowe wyrażone 

na skali stosunkowej 

(ilorazowej)

Charakteryzują  się  pomiarem  ilościowym  (z 
precyzyjną  jednostką  pomiaru)  mierzonym  od 
zera  rzeczywistego,  z  dokładnością  do  stałości 
ilorazu. 

Przykłady:

• czas;
• długość;
• temperatura w skali 

Kelvina;

• liczba przeczytanych 

książek.

Oznacza  to, 
że 

można 

określić 
zarówno  o  ile 
jednostek 
dwie 
wielkości  się 
różnią,  jak  i 
ile  razy  się 
różnią.

 

 

Cechy ilościowe na skali 

interwałowej 

(przedziałowej)

Przykłady:

• liczba punktów z 

kwestionariusza;

• wysokość nad poziom morza;
• temperatura w skali Celsjusza;
• iloraz inteligencji.

Charakteryzują 

się 

pomiarem 

ilościowym 

mierzonym  od  zera  umownego  z  dokładnością 
do przekształcenia liniowego.

Oznacza to, że 
zapewnione są 
równe 
przedziały.

Antyprzykłady:

•oceny szkolne;
•siła wiatru.

 

 

Cechy porządkowe

Przykłady:

• pozycja w 

rankingu;

• miejsce na mecie;
• stopień 

złośliwości;

• poziom bałaganu;
• siła wiatru.

Charakteryzują  się  pomiarem  nie  dającym 
konkretnej 

wartości 

liczbowej, 

lecz 

umożliwiającym ustalenie kolejności.

Operacją  pomiarową  jest 
rangowanie, 

czyli 

ustalenie 

kolejności 

wszystkich  obiektów  w 
próbie  ze  względu  na 
nasilenie mierzonej cechy.

 

 

Cechy jakościowe

Przykłady:

• marka samochodu;
• ocena szkolna;
• gatunek sera;
• numer linii autobusowej.

Charakteryzują  się  tym,  że  nie  dają  się  wyrazić 
ilościowo  lub  wynik  ilościowy  ma  znaczenie 
jedynie opisowe.

 

 

Cechy ilościowe (łącznie)

dyskretn

e

ciągłe

w przybliżeniu 

ciągłe

 

 

Cechy porządkowe – podział

stymulant

y

destymulanty

nominanty

Pozytywnie 

wartościowane 

jest 

największe 

nasilenie 

cechy.

Pozytywnie 

wartościowane 

jest 

najmniejsze 

nasilenie cechy.

Pozytywnie 

wartościowane 

jest środkowe 

nasilenie 

cechy.

•uroda;
•poziom 

zdolności.

•złośliwość;
•poziom 

spróchnienia 
zębów.

•stopień 

opiekuńczości;

•poziom zadbania 

o własne 
interesy.

 

 

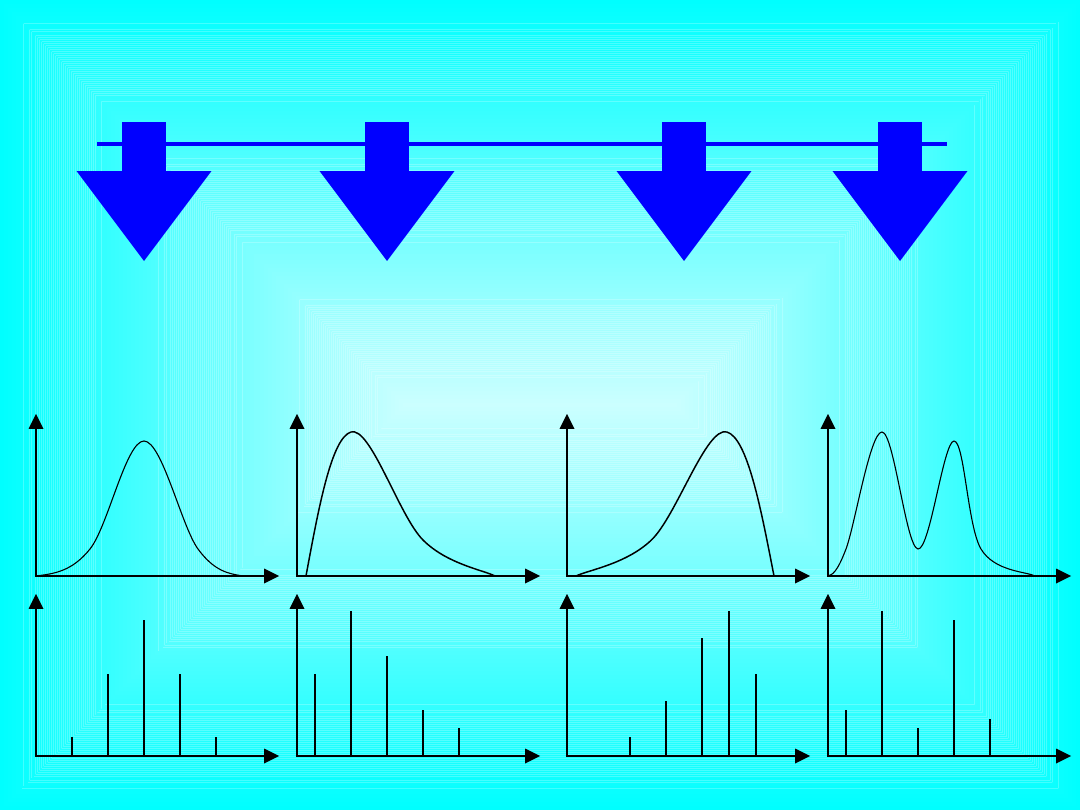
Rozkład cechy

Skośny 

ujemny 

(lewoskośny)

Symetryczn

y 

(normalny, 

typowy)

Skośny 

dodatni 

(prawoskośn

y)

Dwumodalny

 

 

Uwaga na dane 

jakościowe!

Brak klasyfikacji 

zupełnej

• nieuwzględnienie w 

badaniach części 
przypadków, np. 
odrzucenie danych 
niepasujących do 
założenia badacza.

Każda  sytuacja,  w  której  nie  jest  zachowana 
klasyfikacja zupełna i rozłączna oraz brak jest 
odpowiedniej  tego  interpretacji  grozi 

poważnym 

zafałszowaniem 

wyników.

Brak klasyfikacji 

rozłącznej

• liczenie tych samych 

danych klika razy.

 

 

Czy statystyka kłamie?

Nadmierne 

uśrednianie 

danych

Wynik testu 

jest tylko 

prawdopodob

ny

Świadome 

manipulacje

Statystyka kłamie w takim stopniu, w jakim młotek sam 
z  siebie  wali  po  palcach.  Za  wszelkie  przekłamania 
odpowiedzialna  jest  nie  statystyka,  ale  ludzie  ją 
stosujący.

Najczęstsze przyczyny błędów i zafałszowań

Kiedy idę na 
spacer z psem, 
każdy z nas ma 
średnio 3 nogi i 
pół ogona.

W badaniach 
reprezentatywny
ch zawsze 
istnieje ryzyko 
błędu.

•zmiana kategorii 

w trakcie 
badania;

•wybór 

niewłaściwej 
podstawy 
porównań.

 

 

Tablica klasyfikacyjna

wybranych wskaźników opisu 

statystycznego

wsk.

położenia

rozproszenia 

(zróżnicowania

)

skośności, 

asymetrii

zależności

jakościowe

porządkow

e

ilościowe

cechy

• kategoria 

modalna (kostka)

• częstość 

kategorii 
modalnej 

C

m

• dyspersja 

względna 
klasyfikacji 

h

– 

• współczynnik 

siły związku 

r

p

• mediana 

Me

• rozstęp

• współczynnik 

korelacji 
rangowej 

R

s

 

Spearmana

• dominanta 

D

• mediana 

Me

• średnia 

arytmetyczna

x

• rozstęp
• wariancja 

s

2

• odchylenie 

standardowe 

s

• współczynnik 

zmienności 

V

• współczynnik 

skośności 

W

sk

• współczynnik 

asymetrii 

A

• współczynnik 

korelacji 
liniowej 

r

 Pearsona

 

 

Wskaźniki położenia

 

dla danych 

jakościowych

Na przykładzie pytania ankietowego:

Czy podoba Ci się zwyczaj malowania tagów na murach?

Nazw

a 

kostki

++

bardzo

+

raczej tak

?

to zależy

– 

nie

– – 

zdecydo-

wanie nie

RAZEM

Liczba 

osób

7

21

3

40

69

%

N = 

140

15 %

5 %

2,1 % 28,6 % 49,3 %

100 %

100

n

C

N

= �

1

7

100

140

C =

�

5

69

100

140

C =

�

...

Kategoria modalna to kategoria 
najliczniejsza 

tutaj:

•kategoria modalna to „

-

 

-

” lub 

„

zdecydowanie nie

”

•liczebność kategorii modalnej to 

69

 

•częstość kategorii modalnej: 

C

m 

= 49,3%

 

 

Interpretacja C

m

Ich siła dominacji w próbie jest umiarkowana.

49,3% badanej próby to zdecydowani przeciwnicy 
tagów.

Siła dominacji kategorii 

modalnej

Wartością  maksymalną  C

m

  jest  zawsze 

100%.  Wartość  minimalna  jest  zmienna  i 
zależy 

od 

liczby 

kategorii. 

Wartość 

minimalna  C

m

  to  umowne  zero  siły 

dominacji kategorii modalnej.

k

min C

m

2

50 %

3

33,3 %

4

25 %

5

20 %

6

16,7 %

7

14,3 %

8

12,5 %

9

11,1 %

10

10 %

0

20%

40%

60%

80%

100%

C

m

 = 

49,3%

słaba

umiarko

-wana

dość 

duża

bardzo 

duża

 

 

Dyspersja względna klasyfikacji

Wskaźnik rozproszenia (zróżnicowania) dla danych 

jakościowych

(

)

(

)

[ ]

2

2

1

1

k

j

j

h

j

n

k

N

=

=

-

�

-

�

�

N – liczebność próby

k – liczba kategorii

j – numer kolejnej 
kategorii

[] – uporządkowanie 

danych ze względu 
na wielkość

n – liczebność 

poszczególnych kostek

Σ – sumowanie danych

2

k

j=

�

– sumowanie od 

kategorii drugiej do 
ostatniej

gdzie:

 

 

Liczenie dyspersji

(

)

(

)

[ ]

2

2

1

1

k

j

j

h

j

n

k

N

=

=

-

�

-

�

�

j

n

[j]

1

6
9

2

4
0

3

2
1

4

7

5

3

5 140

2. Uporządkowanie danych w szereg 

nierosnący.

3. Odrzucenie pierwszej kategorii.

4. Podstawienie do wzoru.

h=

2

(

5

-1)

.

140

(

2

-

1)

(

. 

40

+(

3

-

1)

. 

21

+(

4

-

1)

. 

7

+(

5

-

1)

. 

3

)

h=

2

4

. 

140

(

1

 . 

40 + 2

 . 

21 + 3

 . 

7 + 

4

 . 

3

)

. 

115

=

2

4

. 

140

= 
0,41

1. Sprawdzenie zupełności i rozłączności.

 

 

Interpretacja dyspersji

h = 
0,41

wartość

zróżnicowani

e

0

brak

0,01 – 

0,20

bardzo słabe

0,21 – 

0,40

dość słabe

0,41 – 

0,60

umiarkowan

e

0,61 – 

0,80

dość silne

0,81 – 

0,99

bardzo silne

1

pełne

UWAGA !

Zawsze:   0  h  1

Występuje 

umiarkowan

e 

zróżnicowanie 

ze względu 

na 

odpowiedź 

na pytanie 

ankietowe.

 

 

Ćwiczenia

W pewnej szkole zbadano dwie klasy po 30 uczniów. 
W  każdej  uczniów  podzielono  na  3  kategorie: 
uczniowie  słabi,  przeciętni  i  zdolni.  Otrzymano 
wyniki:

Klasa 1

S

P

Z

Liczba 
osób

1

28

1

Klasa 2

S

P

Z

Liczba 
osób

9

12

9

1. Wskaż w której z klas występuje większe 

zróżnicowanie.

2. Wskaż kategorię modalną, policz i zinterpretuj jej 

częstość oraz policz i zinterpretuj dyspersję 
klasyfikacji (w każdej z klas z osobna).