Metodologia badań

Metodologia badań

i statystyka

i statystyka

Wojciech Grabowski

[e-mail]

.pl

spotkanie czwarte

Badanie zależności

cech nominalnych

Badanie zależności cech nominalnych rozpoczynamy
od zestawienia danych z próby w wielodzielczej tabeli
krzyżowej.

Dla dwóch cech dychotomicznych będzie to tabela 4-
polowa.

pierwsza

cecha

d

ru

g

a

ce

ch

a

1

1

2

2

n

1,1

n

2,1

n

1,2

n

2,2

N

Tabela 4-polowa musi mieć

klasyfikację

zupełną

i

rozłączną

. Weryfikuje się to

tak, że:

suma z wierszy = suma z
kolumn

co daje całkowitą liczebność.

sum
a

sum
a

Zalecane jest, aby liczebność żadnej kostki nie była
mniejsza od 5.



2



czteropolówka)

Przykład:

Czy istnieje zależność pomiędzy opinią

o tagach a wiekiem respondentów?

opinie

w

ie

k

++ / +

starsi

młodz

i

reszta

suma

suma

a

b

c

d

73

8

20

39

14

0

N

14

0

14

0

(

)

(

) (

) (

) (

)

2

2

ad bc

N

a b c d a c b d

c

-

�

=

+

+

+

+



2

=

(

8

.

39

-

20

.

73

)

2

.

140

81

a+b

59

c+d

28

a+
c

11

2

b+d

81

.

59

.

28

.

112

=

(312 – 1460)

2 .

140

81

.

59

.

28

.

112

=
12,31



2

przyjmuje wartość minimalną 0, ale nie ma

ograniczenia z góry.

Współczynnik siły związku

(wariant uproszczony)

Ponieważ współczynnik 

2

nie ma

maksymalnej

wartości,

nie

można

go

bezpośrednio

zinterpretować. Aby określić siłę
związku, 

2

przelicza się na inne

współczynniki, np. na r

p

.

2

2

2

p

r

N

c

c

=

+

r

p

zależność

 0

brak

0,05 –

0,20

bardzo słaba

0,21 –

0,40

dość słaba

0,41 –

0,60

umiarkowan

a

0,61 –

0,80

dość silna

0,81 –

0,99

bardzo silna

1

pełna





r

p

=

2

.

12,31

12,31+14
0

=
0,40

Występuje

dość

słaba

zależność pomiędzy opinią
o

tagach

a

wiekiem

respondentów.

Interpretacja:

Poprawka Yates’a

Jeżeli w tabeli 4-polowej wystąpi kostka o liczebności
mniejszej niż 5, zaleca się wtedy stosowanie poprawki
Yates’a.

23
27

28 22

50

19

4

9 18

18,

5

4,5

9,5 17,

5

23
27

28

22

50

1. Znaleźć silniejszą przekątną
2. Od każdej wartości na silniejszej

przekątnej odjąć po 0,5

3. Do każdej wartości na słabszej

przekątnej dodać po 0,5

4. Policzyć według dotychczasowej

procedury

1

9

-

0

,5

1

8

-

0

,5

9

+

0

,5

4

+

0

,5



2

=

(18,5

.

17,5 – 4,5

.

9,5)

2 .

50 23

.

27

.

28

.

22

=
10,32

Bez Yates’a:



2

=

12,24

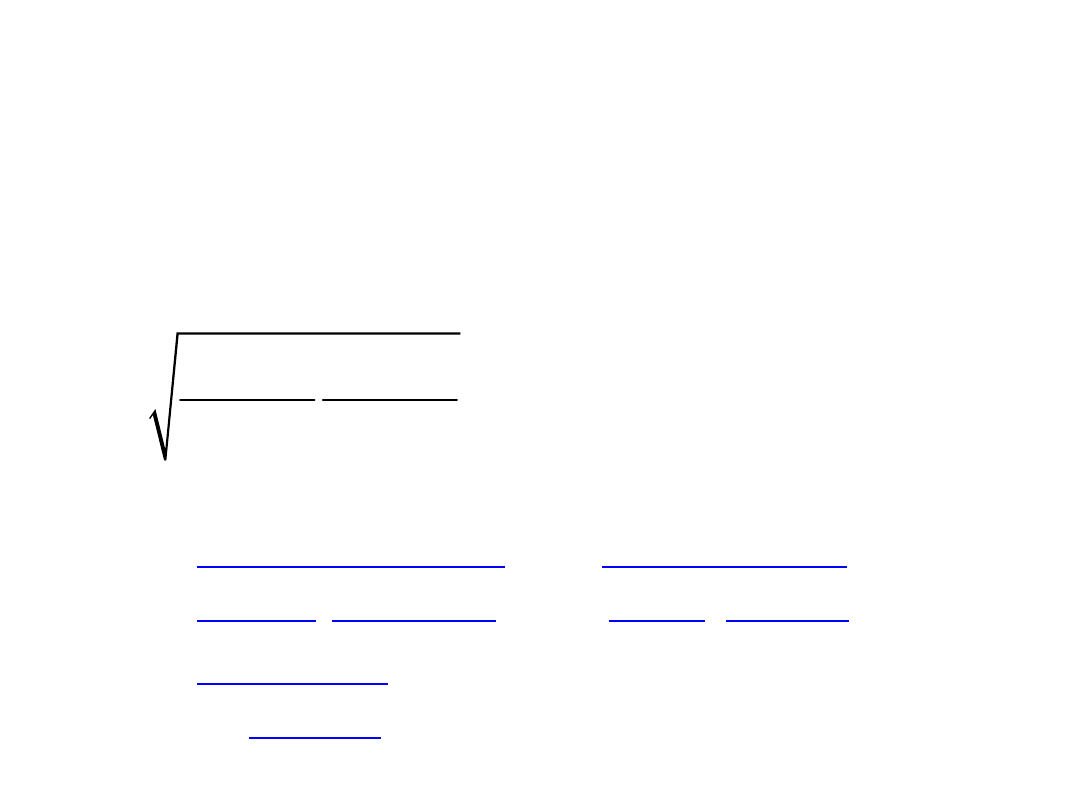
Współczynnik siły związku

(wariant podstawowy)

Jeżeli badamy zależność większej niż dwie liczby cech,
lub najmniejsza liczba kategorii wszystkich cech jest
większa niż 2, to stosuje się wtedy wzór podstawowy
na współczynnik r

p

.

1

2

1

2

1

m

p

m

k

r

k

N

c

c

-

-

=

-

+

gdzie:

m – liczba badanych cech

k – najmniejsza liczba
kategorii

Dla danych z poprzedniego
slajdu:

r

p

=





2

2

-1

–

1

2

2

-1

10,32+5

0

10,32

=





2

– 1

2

60,32

10,32

r

p

=





60,32

10,32

2

=
0,58



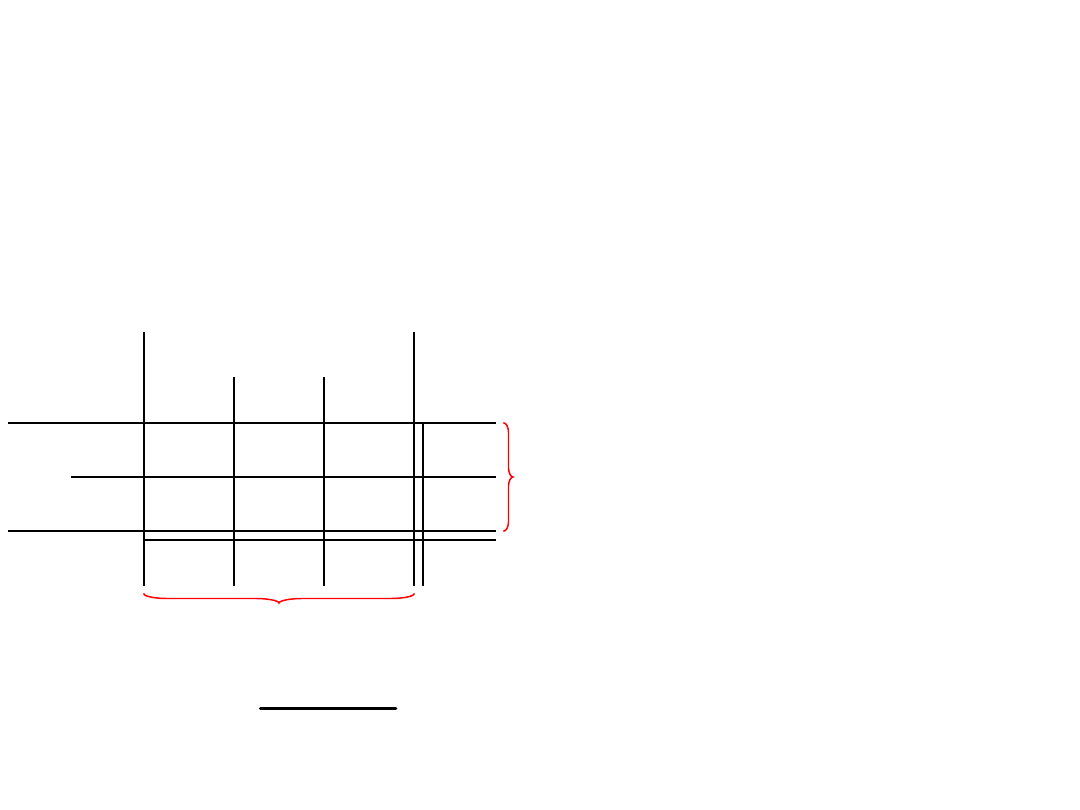
2



wariant pełny)

Przykład:

W ankiecie zadano pytanie: „Czy biją Państwo
swoje dzieci? (tak/nie)” Ustalono również
wykształcenie (wyższe, średnie, podstawowe)
respondentów. Czy istnieje zależność między
tymi cechami?

b

ic

i

e

tak

nie

wykształceni

e

W

Ś

P

24

10

6

30

8

12

1. Wyznaczenie

liczebności brzegowych
i sprawdzenie równości
sum.

36

18

36

90

90

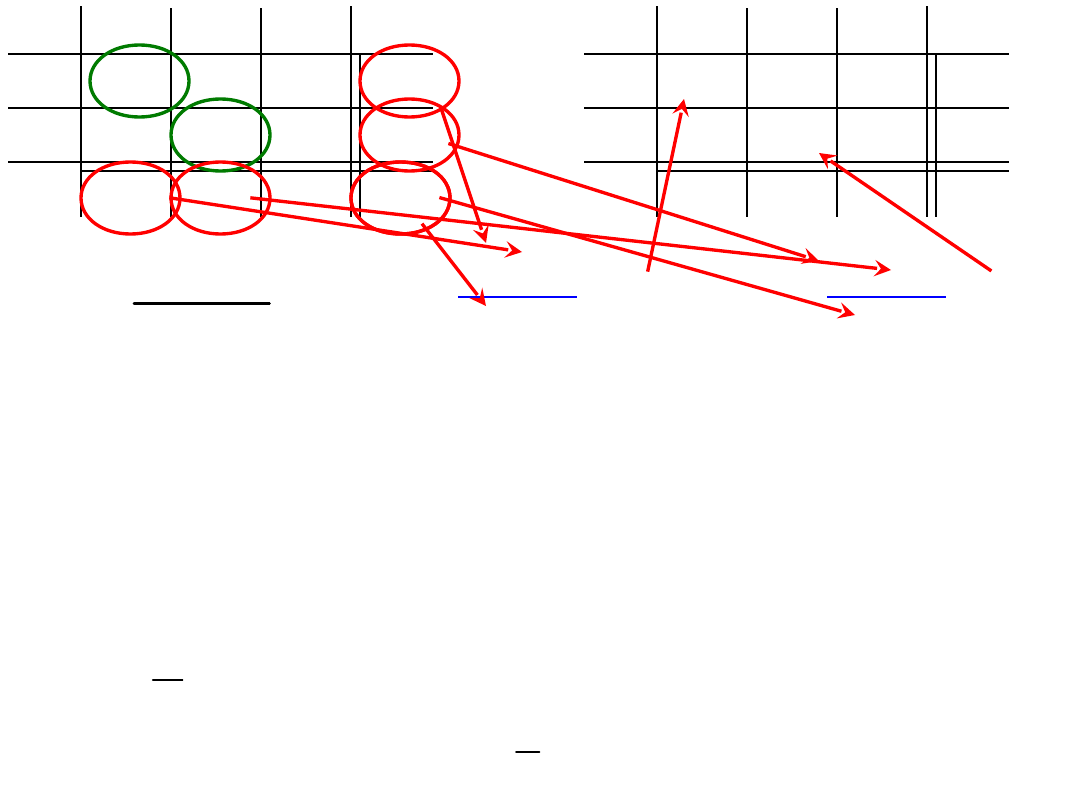
2. Wyznaczenie

liczebności
oczekiwanych
(teoretycznych)

dla

każdej kostki z osobna.

Liczebności oczekiwane
to rozkład w tabeli dla


2

= 0.

ˆ

n

*

*

ˆ

i

i

j

n n

n

N

�

=

1

2

3

4

5

6

40

50

90

N

n

1*

n

2*

n

*1

n

*2

n

*3

*

*

ˆ

i

i

j

n n

n

N

�

=

tak

nie

W

Ś

P

24

10

6

30

8

12

36

18

36

1

2

3

4

5

6

40

50

90

N

n

1*

n

2*

n

*1

n

*2

n

*3

tak

nie

W

Ś

P

36

18

36

40

50

90

n

ˆ

n

1

ˆ

n =

4
0

.

36

9
0

=

16

16

5

ˆ

n =

5
0

.

18

9
0

=

10

10

16

8

20

20

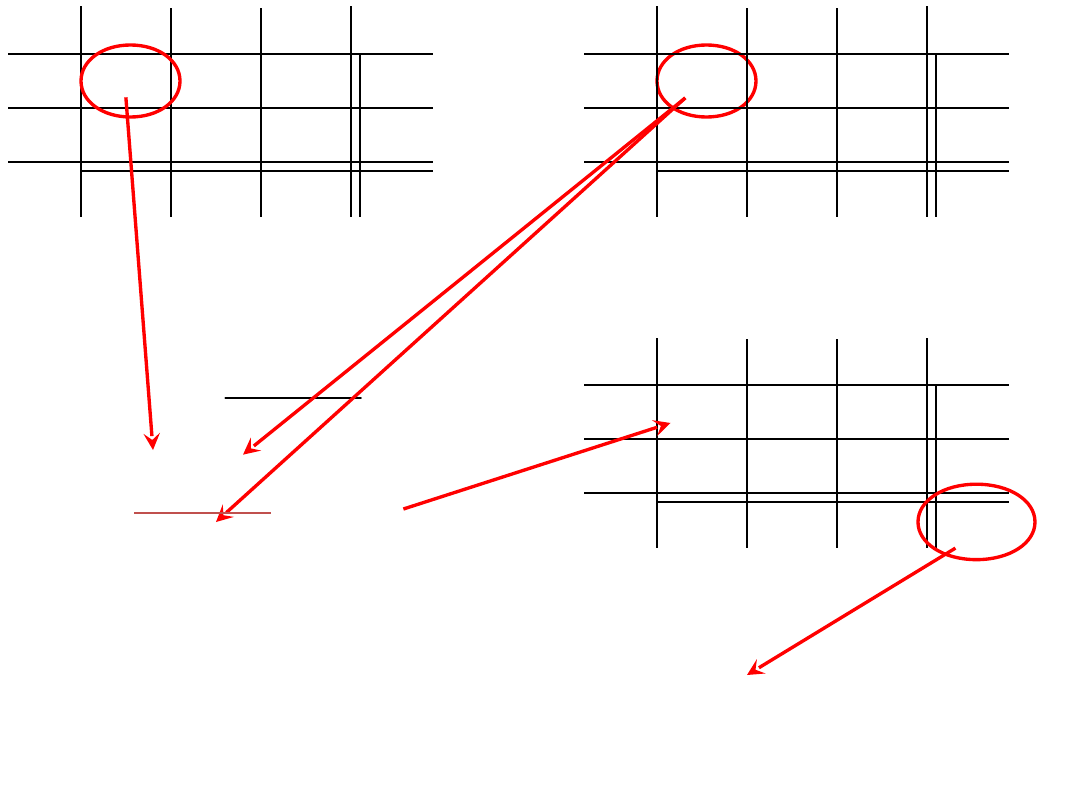
Suma wiersza, w którym znajduje się dana kostka
pomnożona przez sumę odpowiedniej kolumny i
podzielona przez liczebność próby.

3.

Sprawdzenie,

czy

liczebność

próby

jest

wystarczająca do badań.

4

ˆ 3

n

m

� +

gdzie

m

to liczba badanych

cech.

Tutaj:

m = 2

.

Zatem:

4

ˆ 3

2

n� +

czyli:

ˆ 5

n�

tak

nie

W

Ś

P

24

10

6

30

8

12

36

18

36

1

2

3

4

5

6

40

50

90

n

4.

Wyznaczenie 

2

cząstkowych dla każdej kostki z

osobna.

11,2

5

0,9

7,2

10,7
5

8,6

19,35

6,2
5

0,4

4

0,5

5

3,2

tak

nie

W

Ś

P

2

c

(

)

2

2

ˆ

ˆ

i

i

i

i

n n

n

c

-

=

2

1

c

=

(

6

tak

nie

W

Ś

P

36

18

36

40

50

90

ˆ

n

16

10

16

8

20

20

1

2

3

4

5

6

-

16

)

2

16

= 6,25

5.

Wyznaczenie 

2

docelowego.

2

2

i

i

c

c

=

�



2

=

19,3
5

tak

nie

W

Ś

P

24

10

6

30

8

12

36

18

36

1

2

3

4

5

6

40

50

90

n



2

= 19,3

5

2

2

2

p

r

N

c

c

=

+

r

p

=

2

.





=
0,59

+

90

19,35

19,3
5

6.

Interpretacja.

Aby móc zinterpretować 

2

,

musimy

wyznaczyć

inny

współczynnik,

np.

współczynnik r

p.

W naszym przykładzie mamy
dwie cechy, z których jedna ma
2, a druga 3 kategorie. Mniejsza
liczba kategorii nie jest większa
od dwóch, zatem możemy
skorzystać z uproszczonego
wzoru na r

p

.

r

p

zależność

 0

brak

0,05 –

0,20

bardzo słaba

0,21 –

0,40

dość słaba

0,41 –

0,60

umiarkowan

a

0,61 –

0,80

dość silna

0,81 –

0,99

bardzo silna

1

pełna

W

próbie

występuje

umiarkowana

zależność

między skłonnością do bicia
dzieci a wykształceniem.

Współczynnik zależności cech

dla danych porządkowych

 Współczynnik korelacji rangowej R

s

Spearmana

(

)

2

2

6

1

1

ij

s

d

R

N N

�

= -

-

�

gdzie:

N – liczebność próby

d

ij

– różnica

w

kolejnych

rangach

szeregu i oraz

szeregu j

Zawsze:

-1  R

s



1

Interpretacja współczynnika R

s

składa się z dwóch

części.

1. Wartość bezwzględna współczynnika R

s

oznacza

siłę zależności. Interpretuje się ją zgodnie z tabelką
dla współczynnika r

p

.

2. Znak wskazuje, że cechy rosną razem

(+)

, lub że

jedna z cech maleje wtedy, kiedy druga rośnie

(–)

.

Liczenie współczynnika R

s

Przykład:

Zapytano pięcioro studentów jak określiliby
swój poziom zmęczenia po dobiegnięciu do
autobusu oraz o ich wagę ciała.

l.p. wag

a

zmęczenie rangi

i

rangi

j

d

ij

= i –

j

d

ij

2

1

50

marginalne

2

38

straszne

3

80

umiarkowan

e

4

60

niewielkie

5

102

zgon

N=

5

1

2

3

4

5

1

2

3

4

5

1

– 3

1
1
0

1
9
1
1

0

0 !

12

R

s

= 1 –

6

.

12

5

.

(

5

2

– 1)

= 1 –

5

.

24

6

.

12

= 1 –

72

120

= 1 –
0,6

=

+

0,4

Występuje dość słaba zależność dodatnia polegająca
na tym, że wraz ze wzrostem wagi rośnie poziom
zmęczenia.

(

)

2

2

6

1

1

ij

s

d

R

N N

�

= -

-

�