Wprowadzenie

do ekonometrii

i prognozowania

(7)

Prognozowanie zjawisk

jakościowych na podstawie

modeli ekonometrycznych

Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa

W praktyce często zarówno zmienna objaśniana jak i

zmienne objaśniające mogą mieć charakter jakościowy. Mogą
one przyjmować skończoną liczbę wartości objaśnianej, która
może przyjmować skończoną liczbę wariantów. Takie zmienne
można wyrazić zawsze za pomocą pewnej liczny

sztucznych

zmiennych zero-jedynkowych

.

Prezentowany dalej liniowy model prawdopodobieństwa

dla zmiennych zero-jedynkowych

, oparty na sztucznych

zmiennych zero-jedynkowych, służy do opisywania sytuacji, w
których decydent ma do wyboru dwie alternatywne decyzje,
którym przyporządkowuje wartość

1

, a drugiej –

0

. Takie

modele można też wykorzystywać do opisywania częstości
występowania (bądź nie) określonej własności wśród
elementów badanej zbiorowości.

2

GK (WEiP(8) - 2014)

Model

. Niech będzie dana i-ta grupa decydentów o liczności

n

i

(i=1,2,…,r).

Każdy z decydentów ma możliwość podjęcia lub

odrzucenia określonej, tej samej dla wszystkich decydentów,
decyzji. Zmienna opisująca działania decydenta jest zmienną
zero-jedynkową (np.

1

– podjęcie decyzji,

0

– niepodjęcie

decyzji). Przyjmuje się także, że decydenci przy podejmowaniu
decyzji kierują się

k

czynnikami, których wartości tworzą

k

-

elementowy wierszowy wektor

x

i

wartości zmiennych

objaśniających charakteryzujących podejmowaną decyzję.
Niech

y

i

decydentów spośród

n

i

decydentów w

i

-tej grupie

podjęło decyzję. Bada się prawdopodobieństwo, z którym jest
podejmowana rozważana decyzja. Przyjmuje się, że to
prawdopodobieństwo

p

i

, z którym jest podejmowana decyzja w

i

-tej grupie decydentów, jest funkcją liniową zmiennych

objaśniających, tj.





.

α

x

f

p

i

i

,

~ 

Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa

3

GK (WEiP(8) - 2014)

Niech oznacza współczynnik struktury z próby, tj.
empiryczną częstość,

z którą była podejmowana decyzja w i-tej grupie decydentów.
Zakład się, że:

tj, że empiryczna częstość podejmowania decyzji jest
obarczona pewnym błędem



i

, różnym dla różnych grup

decydentów. Stąd wynika, że liniowy model
prawdopodobieństwa jest postaci

w którym estymacji podlegają parametry kombinacji liniowej,
tj. elementy wektora kolumnowego



.

,

...

~

,r

1,2,

i

,

ε

p

p

i

i

i







i

i

i

n

y

p 

Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa





,

...

,

,r

1,2,

i

,

ε

α

x

f

p

i

i

i







4

GK (WEiP(8) - 2014)

O składniku losowym rozpatrywanego modelu zakłada się, że:



wartość oczekiwana składników losowych jest równa zeru, tj.

E(



i

) = 0

, co oznacza, że współczynnik struktury z próby

p

i

stanowi nieobciążone oszacowania prawdopodobieństwa



składniki losowe nie są ze sobą skorelowane, tj.

co oznacza, że składniki losowe nie są ze sobą związane
zależnością liniową.
Przytoczone założenia są analogiczne do założeń dotyczących
składników losowych klasycznego modelu ekonometrycznego, ale
nie wyczerpują wszystkich założeń odnoszących się do
składników losowych.

,

~

i

p





 

,

0

,ε

ε

cov

j

i

,r

1,2,

i,j

j;

i









...

Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa

5

GK (WEiP(8) - 2014)

Ponieważ zmienna

y

i

, wyrażająca liczbę decydentów

należących do

i

-tej grupy decydentów, którzy podjęli decyzję, ma

rozkład dwumianowy, więc

Ponieważ , więc

Ze względu na to, że

zachodzi

 

 





,r.

1,2,

i

oraz

,

p

1

p

n

y

D

p

n

y

E

i

i

i

i

2

i

i

i

...

~

~

~









i

i

i

n

y

p 

 

 





,r.

1,2,

i

oraz

,

n

p

1

p

p

D

p

p

E

i

i

i

i

2

i

i

...

~

~

~









,

...

~

,r

1,2,

i

,

ε

p

p

i

i

i







Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa

 





.

,r

1,2,

i

,

n

p

1

p

ε

D

i

i

i

i

2

...

~

~







6

GK (WEiP(8) - 2014)

Oznacza to, że wariancje składników losowych dla
poszczególnych grup decydentów są różne, zatem składniki
losowe liniowego modelu prawdopodobieństwa są
heteroskedastyczne, co rodzi określone konsekwencje przy
estymacji parametrów strukturalnych tego modelu, który
przyjmuje postać:

W zapisie macierzowym liniowy model prawdopodobieństwa
przyjmuje postać:

gdzie:

p

–

n

-wymiarowy wektor kolumnowy empirycznych częstości

podejmowania wyróżnionej decyzji,

X

–

(n

 (k+1))-

wymiarowa macierz wartości zmiennych

objaśniających (każdy wiersz macierzy dotyczy innej grupy
decydentów podejmujących decyzję),



-

(k+1)

-wymiarowy wektor kolumnowy parametrów

strukturalnych modelu,



-

n

-wymiarowy wektor kolumnowy składników losowych.

.

k

0,1,2,...,

j

;

r

1,2,...,

i

,

ε

α

x

p

i

ij

i

j









Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa

,

ε

Xα

p





7

GK (WEiP(8) - 2014)

Ze względu na heteroskedastyczność składników

losowych, estymacja parametrów strukturalnych liniowego
modelu prawdopodobieństwa jest dokonywana za pomocą

UMNK

(Uogólnionej Metody Najmniejszych Kwadratów)

po

zastosowaniu, której otrzymuje się następujący wektor
oszacowań

W rozpatrywanym przypadku macierz



jest postaci:





.

p

Ω

X

X

Ω

X

a

1

T

1

1

T

















.

~

~

...

...

...

...

...

~

~



































r

r

r

1

1

1

n

p

1

p

0

0

n

p

1

p

Ω

Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa

8

GK (WEiP(8) - 2014)

Ze względu na to, że macierz



jest macierzą

diagonalną,

Uogólniona Metoda Najmniejszych Kwadratów

redukuje się do

Ważonej Metody Najmniejszych Kwadratów

(WMNK)

. W takim przypadku elementy diagonalne pełnią rolę

wag niwelujących efekt heteroskedastyczności składnika
losowego.

Ponieważ nie są znane prawdopodobieństwa , więc

nie jest możliwe wyznaczenie wartości elementów macierzy



.

W praktyce korzysta się z oszacowań tego prawdopodobieństwa,
które można uzyskać na dwa sposoby:

sposób 1

– za oszacowanie prawdopodobieństw przyjmuje się

częstości empiryczne

p

i

, co daje macierz



postaci:

W tym przypadku parametry liniowego modelu
prawdopodobieństwa szacuje się za pomocą

UMNK

z zależności:

i

p

~

Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa

i

p

~









.

n

p

1

p

...

0

...

...

...

0

...

n

p

1

p

Ω

r

r

r

1

1

1



































(

)

-1

T

T

-1

a= X

X X

p,

W

W

- 1

9

GK (WEiP(8) - 2014)

sposób 2

– do budowy macierzy



wykorzystuje się

wartości

teoretyczne liniowego modelu prawdopodobieństwa

(

tylko, gdy

wszystkie z nich należą do przedziału [0,1

]

) oszacowane za

pomocą KMNK z modelu liniowego:

gdzie

co daje macierz



postaci:









,

p

X

X

X

a

T

1

T

KMNK





(

)

(

)

KMNK

KMNK

ˆp

Xa

,

=

(

)

(

)

(

)

(

)

(

)

(

)

KMNK

KMNK

1

1

1

KMNK

KMNK

KMNK

r

r

r

ˆ

ˆ

p

1 p

...

0

n

...

Ω

...

...

...

.

ˆ

ˆ

p

1 p

0

...

n

�

�

-

�

�

�

�

�

�

=�

�

�

�

-

�

�

�

�

�

�

Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa

10

GK (WEiP(8) - 2014)

W tym przypadku parametry liniowego modelu
prawdopodobieństwa szacuje się z zależności:

W jednym i w drugim przypadku teoretyczne prawdopodobieństw
są elementami wektora

Poważnym mankamentem rozpatrywanego
modelu jest to, że wartości teoretyczne
prawdopodobieństw mogą przyjmować wartości
spoza przedziału [0,1]. Tego mankamentu są
pozbawione modele

probitowe

i

logitow

e.

(

)

1

T

1

T

1

KMNK

KMNK

a

XΩ

X

X Ω

p.

-

-

-

=

.

Xa

p

ˆ 

Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa

11

GK (WEiP(8) - 2014)

Przykład.

Przebadano 200 gospodarstw domowych w celu

zebrania danych dotyczących dochodu w gospodarstwie oraz
zakupu sprzętu AGD. Materiał badawczy zgrupowano w tabeli:

Lp.

Średni

dochód

[tys. zł.]

Liczba

badanych

gospodarstw

domowych

Liczba rodzin

kupujących

sprzęt AGD

1

3,0

10

1

2

4,0

20

6

3

5,0

30

18

4

6,0

35

23

5

7,0

40

28

6

8,0

30

22

7

9,0

25

22

8

10,0

10

9

Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa

12

GK (WEiP(8) - 2014)

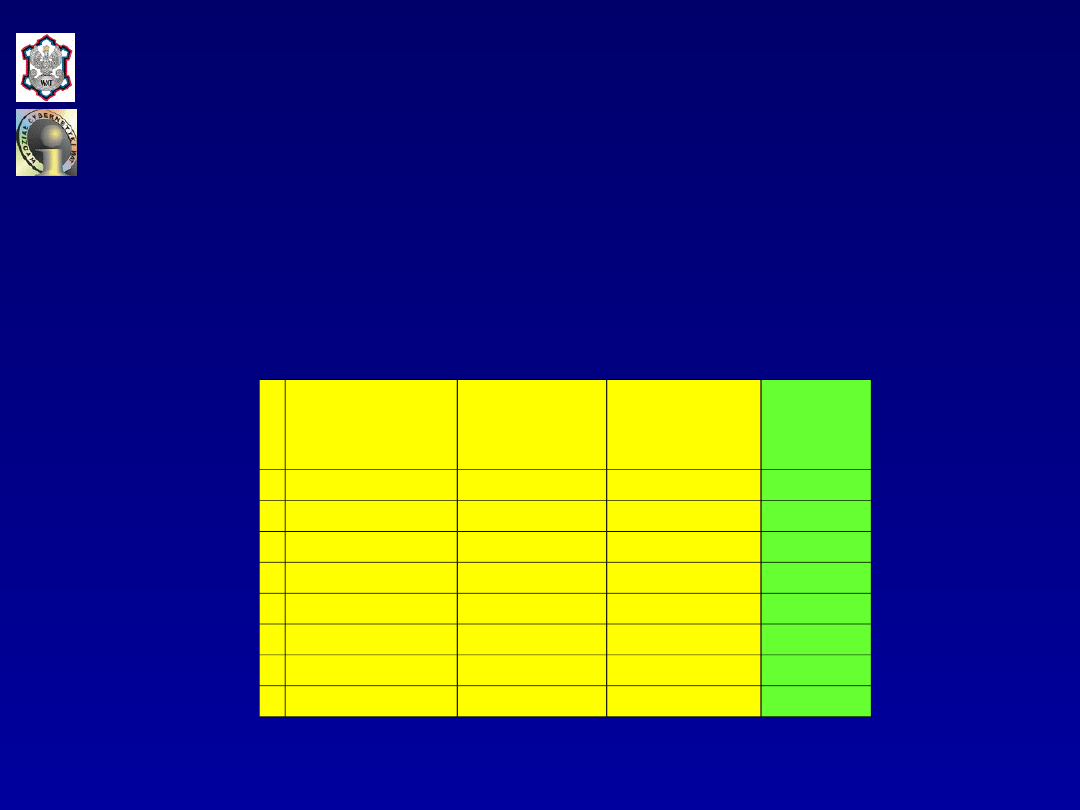
Przyjmując, że zależność pomiędzy prawdopodobieństwem
zakupu sprzętu AGD a średnim dochodem gospodarstwa
domowego jest opisana za pomocą liniowego modelu
prawdopodobieństwa, oszacować jego parametry strukturalne.

Rozwiązanie.

Na podstawie danych zawartych w tabeli obliczono

częstotliwości zakupu sprzętu AGD, jako oszacowania
prawdopodobieństwa zakupu tego sprzętu.

L
p

.

Średni dochód

[tys. zł.]

Liczba

badanych

gospodarstw

domowych

Liczba rodzin

kupujących

sprzęt AGD

Częstość
zakupów

1

3,0

10

1

0,10

2

4,0

20

6

0,30

3

5,0

30

18

0,60

4

6,0

35

23

0,66

5

7,0

40

28

0,70

6

8,0

30

22

0,73

7

9,0

25

22

0,88

8

10,0

10

9

0,90

Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa

13

GK (WEiP(8) - 2014)

Przyjmuje się, że rozpatrywany dalej liniowy model
prawdopodobieństwa jest postaci:

gdzie zmienna objaśniająca

x

oznacza średni dochód w

gospodarstwie domowym.

Do oszacowania parametrów strukturalnych tego modelu,

ze względu na heteroskedastyczność składnika losowego,
zostanie wykorzystana

Uogólniona Metoda Najmniejszych

Kwadratów (UMNK)

, która daje następującą zależność do

wyznaczania oszacowań parametrów strukturalnych modelu:

ε

x

α

α

p

1

0











.

p

Ω

X

X

Ω

X

a

1

T

1

1

T









Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa

14

GK (WEiP(8) - 2014)

Przyjmuje się, że oszacowanie elementów macierzy



niwelującej efekt heteroskedastyczności składnika losowego
zostanie oparte na teoretycznych wartościach
prawdopodobieństw uzyskanych z liniowego modelu
prawdopodobieństwa, w którym parametry strukturalne zostały
oszacowane za pomocą KMNK, tj:

Oszacowania parametrów strukturalnych liniowego

modelu prawdopodobieństwa za pomocą KMNK:









.

Xa

p

ˆ

KMNK

KMNK











.

0,10631

0,08226

p

X

X

X

a

T

1

T

KMNK



















Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa

15

GK (WEiP(8) - 2014)

Teoretyczne wartości prawdopodobieństw (zmiennej objaśnianej
modelu):









.

0,9808

0,8745

0,7682

0,6619

0,5556

0,4493

0,3430

0,2367

Xa

p

ˆ

KMNK

KMNK

























































Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa

16

GK (WEiP(8) - 2014)

Elementy macierzy



:

oraz cała macierz



:













,r

1,2,

i

,

n

p

1

p

i

KMNK

i

KMNK

i

i

...

ˆ

ˆ









 =

0,0180

67

0

0

0

0

0

0

0

0

0,011268

0

0

0

0

0

0

0

0

0,008248

0

0

0

0

0

0

0

0

0,007055

0

0

0

0

0

0

0

0

0,005595

0

0

0

0

0

0

0

0

0,005936

0

0

0

0

0

0

0

0

0,00439

0

0

0

0

0

0

0

0

0,001883

Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa

17

GK (WEiP(8) - 2014)

Elementy macierzy



--1

:

55,348

58

0

0

0

0

0

0

0

0

88,7504

4

0

0

0

0

0

0

0

0

121,246

7

0

0

0

0

0

0

0

0

141,752

8

0

0

0

0

0

0

0

0

178,740

3

0

0

0

0

0

0

0

0

168,474

2

0

0

0

0

0

0

0

0

227,79

1

0

0

0

0

0

0

0

0

531,029

1

Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa

18

GK (WEiP(8) - 2014)

Wektor a ocen parametrów strukturalnych modelu i ostateczna
postać modelu:

Teoretyczne wartości prawdopodobieństw i reszty modelu:





.

0,0884

0,0461

p

Ω

X

X

Ω

X

a

1

T

1

1

T























e

0,0884X

0,0461

p







Lp.

Średni

dochód

[tys. zł.]

Prawdopodobieńst

wa (wartości

empiryczne)

Prawdopodobień

stwa (wartości

teoretyczne)

Reszty

modelu

1

3,0

0,10

0,3113

-0,2113

2

4,0

0,30

0,3997

-0,0997

3

5,0

0,60

0,4881

0,1119

4

6,0

0,66

0,5765

0,0835

5

7,0

0,70

0,6649

0,0351

6

8,0

0,73

0,7533

-0,0233

7

9,0

0,88

0,8417

0,0383

8

10,0

0,90

0,9301

-0,0301

Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa

19

GK (WEiP(8) - 2014)

Prognozowane wartości prawdopodobieństwa zakupu sprzętu
AGD w gospodarstwach domowych w zależności od ich średniego
dochodu:



Lp.

Średni

dochód

[tys. zł.]

Prawdopodobie

ństwa (wartości

prognozowane)

1

0,5

0,0903

2

2,0

0,2229

3

11,0

1,0185

4

12,0

1,1069

Prognozowanie zjawisk

jakościowych

liniowy model

prawdopodobieństwa

20

GK (WEiP(8) - 2014)

Prognozowanie na podstawie

modeli probitowych

Modele

probitowe

są jednym ze sposobów modelowania

zmiennej objaśnianej, która może przyjmować skończoną
liczbę wariantów.

Rozpatruje się przypadek, gdy zmienna objaśniana jest

zmienna jakościową przyjmującą dwa warianty, natomiast
zmienne objaśniające nie są zmiennymi jakościowymi. W tym
przypadku wykorzystuje się sztuczną zero-jedynkową zmienną
objaśniającą

Y

,

przyjmującą wartości

1

i

0

, gdy:

o następującym rozkładzie prawdopodobieństwa:

przy czym

p

oznacza prawdopodobieństwo przyjęcia przez

zmienną objaśnianą wariantu oznaczonego wartością

1

.









wystąpi,

nie

wariant

dany

jeżeli

wystąpi,

wariant

dany

jeżeli

0,

1,

Y









p.

1

q

0

Y

P

p,

1

Y

P













21

GK (WEiP(8) - 2014)

Jeżeli wystąpienie bądź niewystąpienie rozważanego

wariantu zmiennej objaśniającej ma charakter losowy, można
zbudować następujący model ekonometryczny wyznaczający
wartość oczekiwaną zmiennej

Y

:

gdzie:

X

1

,…,X

k

– zmienne objaśniające;



0

,



1

,…,



k

– parametry

strukturalne modelu;



- składnik losowy;

F

– rosnąca funkcja

kombinacji liniowej zmiennych objaśniających i składnika
losowego.

W rozpatrywanym modelu wartość oczekiwana zmiennej

objaśnianej

Y

jest prawdopodobieństwem przyjęcia przez

zmienną losową wyróżnionego wariantu.

W zależności od postaci funkcji

F

rozróżnia się kilka

rodzajów modeli spośród, których są najbardziej znane są
modele

probitowe

i

logitowe

.

 





ε

X

α

X

α

α

F

p

q

0

p

1

Y

E

k

k

1

1

0





















...

Prognozowanie na podstawie

modeli probitowych

22

GK (WEiP(8) - 2014)

W modelu

probitowym

funkcja

F

jest dystrybuantą

standardyzowanego rozkładu normalnego

N(0,1)

:

Wartości funkcji odwrotnej do

(p)

tj.



-1

(p)

nazywają się

normitami

natomiast wartości



-1

(p) + 5

–

probitami (Pr)

, tj.

W modelach

probitowych

najczęściej wykorzystywana jest

zależność liniowa wiążąca zmienne objaśniające. W tym
przypadku model przyjmuje postać:

Estymacja tego modelu musi uwzględniać fakt, że ze względu na
specyfikę zmiennej

Y

i konstrukcję modelu, składnik losowy



nie jest homoskedastyczny, zatem stosowanie KMNK daje
niewłaściwe oszacowania parametrów strukturalnych modelu
(

a

).





.

...

ε

X

α

X

α

α

Φ

p

k

k

1

1

0











 









5.

1

Y

P

Φ

5

p

Φ

Pr

1

1















ε.

X

α

X

α

α

Pr

k

k

1

1

0











...

Prognozowanie na podstawie

modeli probitowych

23

GK (WEiP(8) - 2014)

Parametry strukturalne rozpatrywanego modelu są

estymowane na ogół za pomocą

Uogólnionej Metody

Najmniejszych Kwadratów

. W takim przypadku wektor

a

oszacowań parametrów strukturalnych dla modelu

probitowego

wyznaczany jest z zależności:

gdzie:

,

a

r

jest liczbą rozpatrywanych grup w modelu.





Pr

Ω

X

X

Ω

X

a

1

T

1

1

T









 

 

 















































































kr

2r

1r

k2

22

12

k1

21

11

k

1

0

r

2

1

x

x

x

1

x

x

x

1

x

x

x

1

X

,

α

α

α

α

,

p

Pr

p

Pr

p

Pr

Pr

...

...

...

...

...

...

...

...

...

...

Prognozowanie na podstawie

modeli probitowych

24

GK (WEiP(8) - 2014)

Elementami wektora zmiennej objaśnianej

Pr

(wektor

probitów

) są zaobserwowane wartości

probitów

, obliczone na

podstawie danych empirycznych z zależności:

przy czym:

•n

i

– liczba obserwacji w

i

-tej grupie,

•y

i

– liczba obserwacji w

i

-tej grupie, dla których obserwowany

wariant zmiennej objaśnianej wystąpił, tj. dla których

Y = 1

.

 

 

,r

1,2,

i

i

i

i

i

1

i

n

y

p

5,

p

Φ

p

Pr

...

,











Prognozowanie na podstawie

modeli probitowych

25

GK (WEiP(8) - 2014)

Macierz



jest macierzą diagonalną o następującej budowie:

w której na głównej przekątnej znajdują się oszacowane wartości
wariancji składników losowych:

przy czym

(x)

oznacza funkcję gęstości standaryzowanego

rozkładu normalnego

N(0,1)

.

Obliczenie

ω

i

wymaga znajomości prawdopodobieństw

p

i

zamiast, których najczęściej przyjmuje się znane częstości
empiryczne.

,

...

...

...

...

...

...

...

...



























r

2

1

0

0

0

0

0

0

0

0

0

Ω











 

,r

1,2,

i

,

p

n

p

1

p

ω

i

2

i

i

i

i

...









Prognozowanie na podstawie

modeli probitowych

26

GK (WEiP(8) - 2014)

Oszacowanie parametrów strukturalnych modelu pozwala

na uzyskanie teoretycznych wartości

probitów

, a następnie na ich

podstawie – teoretycznych wartości prawdopodobieństw przyjęcia
przez zmienną objaśnianą wyróżnionego wariantu. Teoretyczne
wartości prawdopodobieństw otrzymuje się z zależności:

Prognozowanie na podstawie

modeli probitowych

 

 

 





,r.

1,2,

i

,

5

r

P

Φ

p

Xa

p

r

P

p

r

P

p

r

P

r

P

i

i

r

2

1

...

ˆ

ˆ

ˆ

...

ˆ

ˆ

ˆ









































27

GK (WEiP(8) - 2014)

Przykład.

Przebadano

200

gospodarstw domowych w celu

zebrania danych dotyczących średniego dochodu w
gospodarstwie i faktu zakupu sprzętu AGD. Materiał badawczy
zgrupowano w tabeli:

Lp.

Średni dochód

w

gospodarstwie

[tys. zł.]

Liczba

badanych

gospodarstw

domowych

Liczba

gospodarstw, w

których

zakupiono

sprzęt AGD

1

3,0

10

1

2

4,0

20

6

3

5,0

30

18

4

6,0

35

23

5

7,0

40

28

6

8,0

30

22

7

9,0

25

22

8

10,0

10

9

Prognozowanie na podstawie

modeli probi

towych

28

GK (WEiP(8) - 2014)

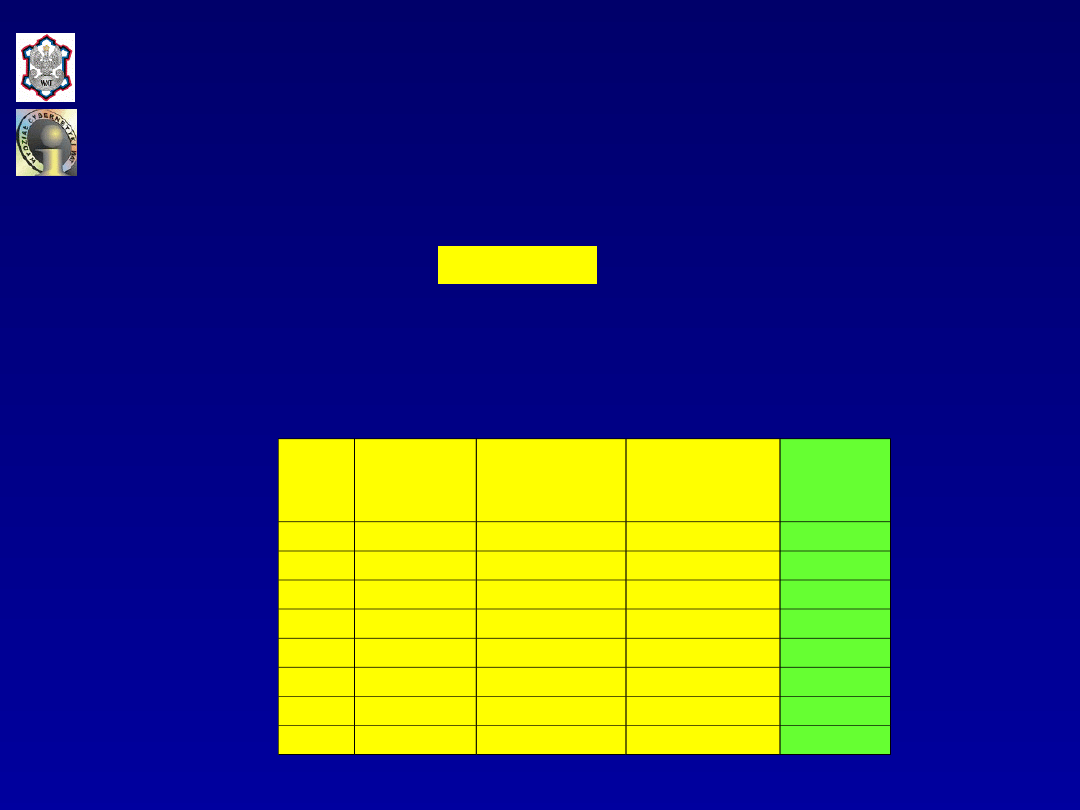
Przyjmując, że zależność pomiędzy prawdopodobieństwem
zakupu sprzętu AGD a średnim dochodem gospodarstwa
domowego

X

jest opisana za pomocą modelu

probitowego

postaci:

oszacować jego parametry strukturalne i wyznaczyć prognozę
dla następujących wartości zmiennej

X

w okresie prognozy:

x

*

= {0.5, 2.0, 11.0, 12.0}

.

Rozwiązanie. Na podstawie danych zawartych w tabeli
obliczono częstości zakupu sprzętu AGD, jako oszacowanie
prawdopodobieństwa zakupu tego sprzętu:

Lp.

Średni

dochód

[tys. zł.]

Liczba

badanych

gospodarstw

domowych

Liczba rodzin

kupujących

sprzęt AGD

Częstość
zakupów

1

3,0

10

1

0,10

2

4,0

20

6

0,30

3

5,0

30

18

0,60

4

6,0

35

23

0,66

5

7,0

40

28

0,70

6

8,0

30

22

0,73

7

9,0

25

22

0,88

8

10,0

10

9

0,90

Prognozowanie na podstawie

modeli probitowych

ε

x

α

α

Pr

1

0







29

GK (WEiP(8) - 2014)

W celu oszacowania parametrów tego modelu obliczono probity
postaci:

 

 

,r

1,2,

i

i

i

i

i

1

i

n

y

p

5,

p

Φ

p

Pr

...

,











Lp.

Średni

dochód

[tys. zł.]

Częstość

zakupów

Probity

1

3,0

0,10

3,7184

2

4,0

0,30

4,4756

3

5,0

0,60

5,2533

4

6,0

0,66

5,4125

5

7,0

0,70

5,5244

6

8,0

0,73

5,6128

7

9,0

0,88

6,1750

8

10,0

0,90

6,2816

Prognozowanie na podstawie

modeli probitowych

30

GK (WEiP(8) - 2014)

Ze względu na heteroskedastyczność składnika losowego

, estymacja parametrów strukturalnych modelu zostanie

przeprowadzona z wykorzystaniem Uogólnionej Metody
Najmniejszych Kwadratów (UMNK), która korzysta z
następującej macierzy



, niwelującej skutki tej

heteroskedastyczności:

Lp.

Często

ść

zakup

ów

Wartości

funkcji

gęstości

rozkładu

normaln

ego

1

0,10

0,3970

2

0,30

0,3814

3

0,60

0,3332

4

0,66

0,3209

5

0,70

0,3123

6

0,73

0,3056

7

0,88

0,2709

8

0,90

0,2661

Prognozowanie na podstawie

modeli probitowych

31

GK (WEiP(8) - 2014)

Elementy macierzy



:

Po wykonaniu obliczeń macierz



przyjmie postać:





 

.

...,r

1,2,

i

,

p

n

p

1

p

ω

i

2

i

i

i

i









0,1146

34

0

0

0

0

0

0

0

0

0,0774

58

0

0

0

0

0

0

0

0

0,0742

88

0

0

0

0

0

0

0

0

0,0685

06

0

0

0

0

0

0

0

0

0,0573

63

0

0

0

0

0

0

0

0

0,0635

56

0

0

0

0

0

0

0

0

0,0598

2

0

0

0

0

0

0

0

0

0,0265

95

Prognozowanie na podstawie

modeli probitowych

32

GK (WEiP(8) - 2014)

Macierz



--1

:

8,723415

39

0

0

0

0

0

0

0

0

12,9102223

0

0

0

0

0

0

0

0

13,4611243

0

0

0

0

0

0

0

0

14,5972616

0

0

0

0

0

0

0

0

17,43284

0

0

0

0

0

0

0

0

15,7341557

0

0

0

0

0

0

0

0

16,7168171

0

0

0

0

0

0

0

0

37,6010528

Prognozowanie na podstawie

modeli probitowych

33

GK (WEiP(8) - 2014)

Wektor a ocen parametrów strukturalnych modelu i
ostateczna postać modelu:

Teoretyczne wartości probitów i reszty modelu:





.

0,3003

3,3643

Pr

Ω

X

X

Ω

X

a

1

T

1

1

T























.

e

0,3003x

3,3643

Pr







Lp.

Średni

dochó

d [tys.

zł.]

Probity

(wartości

empiryczn

e)

Probity

(wartości

teoretyczne)

Reszt

y

mode

lu

1

3,0

3,7184

4,2652

-

0,546

8

2

4,0

4,4756

4,5655

-

0,089

9

3

5,0

5,2533

4,8658

0,387

5

4

6,0

5,4125

5,1661

0,246

4

5

7,0

5,5244

5,4664

0,058

6

8,0

5,6128

5,7667

-

0,153

9

7

9,0

6,1750

6,0670

0,108

8

10,0

6,2816

6,3673

-

0,085

7

Prognozowanie na podstawie

modeli probitowych

34

GK (WEiP(8) - 2014)

Prognozowane wartości prawdopodobieństwa zakupu

sprzętu AGD w gospodarstwach domowych w zależności od ich
średniego dochodu:



Lp.

Średni

dochód

[tys. zł.]

Probity

(wartości

prognozowa

ne)

Prawdopodobień

stwa

(wartości

prognozowane)

1

0,5

3,5145

0,0687

2

2,0

3,9649

0,1503

3

11,0

6,6676

0,9523

4

12,0

6,9679

0,9755

Prognozowanie na podstawie

modeli probitowych

35

GK (WEiP(8) - 2014)

Model

logitowy

jest konstruowany podobnie do modelu

probitowego

, ale w modelu

logitowym

funkcja

F

jest

dystrybuantą rozkładu logistycznego, a model przyjmuje postać:

W tym przypadku funkcja odwrotna do funkcji

F

nosi nazwę

logitu

i wyraża się zależnością:

a model przyjmuje postać:

Estymacja tego modelu musi uwzględniać fakt, że ze względu na
specyfikę zmiennej objaśnianej i konstrukcję modelu składnik
losowy



nie jest homoskedastyczny, zatem stosowanie KMNK

daje niewłaściwe oszacowania

a

parametrów strukturalnych

modelu.









.

ε

X

α

X

α

α

exp

1

ε

X

α

X

α

α

exp

p

k

k

1

1

0

k

k

1

1

0





















...

...

,

p

1

p

ln

L





ε.

X

α

X

α

α

L

k

k

1

1

0











...

Prognozowanie na podstawie

modeli logitowych

36

GK (WEiP(8) - 2014)

Parametry strukturalne rozpatrywanego modelu są

estymowane na ogół za pomocą

Uogólnionej Metody

Najmniejszych Kwadratów

. W takim przypadku wektor

a

oszacowań parametrów strukturalnych dla modelu

logitowego

wyznaczany jest z zależności:

gdzie:

,

a

r

jest liczbą rozpatrywanych grup w modelu.





L

Ω

X

X

Ω

X

a

1

T

1

1

T









 

 

 















































































kr

2r

1r

k2

22

12

k1

21

11

k

1

0

r

2

1

x

x

x

1

x

x

x

1

x

x

x

1

X

,

α

α

α

α

,

p

L

p

L

p

L

L

...

...

...

...

...

...

...

...

...

...

Prognozowanie na podstawie

modeli logitowych

37

GK (WEiP(8) - 2014)

Elementami wektora zmiennej objaśnianej

L

(wektor

logitów

) są zaobserwowane wartości

logitów

, obliczone na

podstawie danych empirycznych z zależności:

przy czym:

•n

i

– liczba obserwacji w

i

-tej grupie,

•y

i

– liczba obserwacji w

i

-tej grupie, dla których obserwowane

zjawisko wystąpiło, tj. dla których

Y = 1

.

 

,r

1,2,

i

i

i

i

i

i

i

n

y

p

,

p

1

p

ln

p

L

...

,









Prognozowanie na podstawie

modeli logitowych

38

GK (WEiP(8) - 2014)

Macierz



jest macierzą diagonalną o następującej budowie:

w której na głównej przekątnej znajdują się oszacowane wartości
wariancji składników losowych:

Obliczenie

ω

i

wymaga znajomości prawdopodobieństw

p

i

zamiast, których najczęściej przyjmuje się znane częstości
empiryczne.

,

...

...

...

...

...

...

...

...



























r

2

1

0

0

0

0

0

0

0

0

0

Ω











.

...,r

1,2,

i

,

p

1

p

n

1

ω

i

i

i

i







Prognozowanie na podstawie

modeli logitowych

39

GK (WEiP(8) - 2014)

Oszacowanie parametrów strukturalnych modelu pozwala

na uzyskanie teoretycznych wartości

logitów

, a następnie na ich

podstawie – teoretycznych wartości prawdopodobieństw przyjęcia
przez zmienną objaśnianą wyróżnionego wariantu. Teoretyczne
wartości prawdopodobieństw otrzymuje się z zależności:

 

 

 

 





.

,r

...

1,2,

i

,

p

Lˆ

exp

1

1

p

ˆ

Xa

p

Lˆ

...

p

Lˆ

p

Lˆ

Lˆ

i

i

r

2

1











































Prognozowanie na podstawie

modeli logitowych

40

GK (WEiP(8) - 2014)

Przykład.

Dane do przykładu takie same jak w przykładzie dla

modelu probitowego. Przyjmując, że zależność pomiędzy
prawdopodobieństwem zakupu sprzętu AGD a średnim
dochodem gospodarstwa domowego

X

jest opisana za pomocą

modelu logitowego postaci:

oszacować jego parametry strukturalne i wyznaczyć prognozę
dla następujących wartości zmiennej

X

w okresie prognozy:

x

*

= {0.5, 2.0, 11.0, 12.0}

.

Prognozowanie na podstawie

modeli logitowych

ε

X

α

α

L

1

0







41

GK (WEiP(8) - 2014)

Rozwiązanie.

Na podstawie danych zawartych w tabeli

obliczono częstotliwości zakupu sprzętu AGD, jako
oszacowania prawdopodobieństwa zakupu tego sprzętu:

Lp.

Średni

dochód

[tys. zł.]

Liczba

badanych

gospodarstw

domowych

Liczba rodzin

kupujących

sprzęt AGD

Częstość

zakupów

1

3,0

10

1

0,10

2

4,0

20

6

0,30

3

5,0

30

18

0,60

4

6,0

35

23

0,66

5

7,0

40

28

0,70

6

8,0

30

22

0,73

7

9,0

25

22

0,88

8

10,0

10

9

0,90

Prognozowanie na podstawie

modeli logitowych

42

GK (WEiP(8) - 2014)

W celu oszacowania parametrów tego modelu obliczono

logity

postaci:

Prognozowanie na podstawie

modeli logitowych

 

,r

1,2,

i

i

i

i

i

i

i

n

y

p

,

p

1

p

ln

p

L

...

,









Lp

.

Średn

i

dochó

d [tys.

zł.]

Częstość

zakupów

Logity

1

3,0

0,10

-2,1972

2

4,0

0,30

-0,8473

3

5,0

0,60

0,4055

4

6,0

0,66

0,6633

5

7,0

0,70

0,8473

6

8,0

0,73

0,9946

7

9,0

0,88

1,9924

8

10,0

0,90

2,1972

43

GK (WEiP(8) - 2014)

Ze względu na heteroskedastyczność składnika losowego



estymacja parametrów strukturalnych zostanie
przeprowadzona z wykorzystaniem Uogólnionej Metody
Najmniejszych Kwadratów (UMNK), która opiera się na
macierzy



, niwelującej skutki tej heteroskedastyczności:

Elementy macierzy



:

Po wykonaniu obliczeń macierz



przyjmie postać:

Prognozowanie na podstawie

modeli logitowych





.

...,r

1,2,

i

,

p

1

p

n

1

ω

i

i

i

i







0,5534

86

0

0

0

0

0

0

0

0

0,22187

6

0

0

0

0

0

0

0

0

0,13471

9

0

0

0

0

0

0

0

0

0,11571

7

0

0

0

0

0

0

0

0

0,11171

3

0

0

0

0

0

0

0

0

0,18719

4

0

0

0

0

0

0

0

0

0,36446

6

0

0

0

0

0

0

0

0

5,31029

1

44

GK (WEiP(8) - 2014)

Macierz



--1

:

Prognozowanie na podstawie

modeli logitowych

1,806

73

0

0

0

0

0

0

0

0

4,5070

22

0

0

0

0

0

0

0

0

7,4228

58

0

0

0

0

0

0

0

0

8,6417

73

0

0

0

0

0

0

0

0

8,951

51

0

0

0

0

0

0

0

0

5,3420

52

0

0

0

0

0

0

0

0

2,743

74

0

0

0

0

0

0

0

0

0,1883

14

45

GK (WEiP(8) - 2014)

Wektor a ocen parametrów strukturalnych modelu i
ostateczna postać modelu:

Teoretyczne wartości

logitów

i reszty modelu:

Prognozowanie na podstawie

modeli logitowych





.

0,5014

2,596

L

Ω

X

X

Ω

X

a

1

T

1

1

T























.

e

0,5014X

2,596

L









Lp.

Średni

dochó

d [tys.

zł.]

Logity

(wartości

empiryczn

e)

Logity

(wartości

teoretyczne)

Reszt

y

mode

lu

1

3,0

-2,1972

-1,0918

-

1,105

4

2

4,0

-0,8473

-0,5904

-

0,256

9

3

5,0

0,4055

-0,0890

0,494

5

4

6,0

0,6633

0,4124

0,250

9

5

7,0

0,8473

0,9138

-

0,066

5

6

8,0

0,9946

1,4152

-

0,420

6

7

9,0

1,9924

1,9166

0,075

8

8

10,0

2,1972

2,4180

-

0,220

8

46

GK (WEiP(8) - 2014)

Prognozowane wartości prawdopodobieństwa zakupu

sprzętu AGD w gospodarstwach domowych w zależności od ich
średniego dochodu:



Prognozowanie na podstawie

modeli logitowych

Lp.

Średni

dochód

[tys. zł.]

Logity

(wartości

prognozowa

ne)

Prawdopodobień

stwa

(wartości

prognozowane)

1

0,5

-2,3453

0,0874

2

2,0

-1,5932

0,1689

3

11,0

2,9194

0,9488

4

12,0

3,4208

0,9683

47

GK (WEiP(8) - 2014)

Porównanie prognoz uzyskanych z modelu

probitowego

i

modelu

logitowego

dla tych samych danych empirycznych:



Prognozowanie na podstawie

modeli probitowych i logitowych

Lp.

Średni

dochó

d [tys.

zł.]

Prawdopodobieństw

a (wartości

prognozowane wg

modelu

probitowego

)

Prawdopodobie

ństwa

(wartości

prognozowane

wg modelu

logitowego)

1

0,5

0,0687

0,0874

2

2,0

0,1503

0,1689

3

11,0

0,9523

0,9488

4

12,0

0,9755

0,9683

48

GK (WEiP(8) - 2014)

Ocena dopasowania modelu do danych empirycznych oraz

dokładność oszacowania parametrów strukturalnych
rozpatrywanych modeli opiera się na oszacowanej wariancji
resztowej oraz macierzy wariancji-kowariancji parametrów
strukturalnych modelu:

 













.

p

p

p

p

1

R

,

X

Ω

X

S

a

D

,

1

k

n

e

Ω

e

S

,

p

p

e

r

1

i

2

i

i

r

1

i

2

i

i

2

1

1

T

2

e

2

1

T

2

e

i

i

i



































ˆ

ˆ

Prognozowanie na podstawie

modeli probitowych i logitowych

49

GK (WEiP(8) - 2014)

Wartości prognoz opartych na modelach

probitowych

i

logitowych

wyznacza się tak samo, jak dla liniowych modeli

ekonometrycznych. Uzyskane wartości prognoz przekształca się
następnie na przewidywane prawdopodobieństwa zajścia
interesującego wariantu zmiennej objaśnianej (prognozowanej).
Zwykle prognozowanie według rozpatrywanych modeli jest
stosowane w przypadku, gdy należy uzyskać odpowiedź na jedno
z następujących pytań:

•jakie jest prawdopodobieństwo przyjęcia określonego wariantu
przez zmienną objaśnianą przy założeniu, że zmienne
objaśniające będą miały określone wartości,

•jakie wartości powinny przyjąć zmienne objaśniające, aby
uzyskać określone prawdopodobieństwo przyjęcia określonego
wariantu przez zmienną objaśnianą.

Prognozowanie na podstawie

modeli probitowych i logitowych

50

GK (WEiP(8) - 2014)

51

GK (WEiP(8) - 2014)