Seria: Informatyka
Elementy teorii
niezawodności Wykład 5
Niezawodność systemów

dr hab. inż. Tadeusz Nowicki prof.

nadzw. WAT

e-mail: [e-mail],

tel. [phone]





n

i

e

e

e

e

e

E

,...,

,...,

,

,

3

2

1



zbiór elementów
struktury
niezawodnościowej
systemu

 

1

,

0

Y

,

X

,

Y

,

X

i

i







Y

X

,

,

S

1

i



















n

i

R

Y

X

...

X

:

)

(

f

R

n

1

(n)









x

zbiory stanów
niezawodnoś-ciowych
elementów i systemu

struktura
niezawodnościo-wa
systemu

Rozpatrujemy systemy o elementach dwustanowych w
sensie nieza-wodności uszkadzających się niezależnie
(podejście klasyczne). Zatem strukturalna funkcja
niezawodnościowa systemu ma postać:

 

 

1

,

0

1

,

0

:

)

(

f

(n)



n

x

Dla elementów i systemu
dwustano-wych w sensie
niezawodności

Przypomnienie

Wyrażenie bulowskie nie zawierające znaku działania negacji
nazywane jest wyrażeniem alternatywno-koniunkcyjnym (wak).
Każdą funkcje monotoniczną (koherentną) można przedstawić
za pomocą wak.

Oznaczmy symbolem „

+”

alternatywę, a symbolem „

·”

koniunkcję. Wtedy przykładem takiej funkcji może być poniższy
zapis

4

3

1

2

3

2

1

(4)

x

)

x

x

(

x

x

x

x

(x)

f









Każde wak można przedstawić w postaci

formuły

alternatywnej

(sumoiloczyn) lub w postaci

formuły koniunkcyjnej

(iloczyn

sum)

4

3

4

1

2

3

2

1

(4)

x

x

x

x

x

x

x

x

(x)

f









)

x

x

)(

x

x

(x

)

x

x

x

)(

x

x

(x

(x)

f

4

2

4

2

1

4

3

2

3

2

1

(4)





















Analityczny zapis struktur
niezawodnościowych

Minimalną

formułą

alternatywną

(mfa)

funkcji

monotonicznej nazywamy formułę alternatywną o
najmniejszej liczbie składników sumy (nieredukowalną)

(mfa)

x

x

x

x

x

(x)

f

4

3

4

1

2

(4)







Minimalną formułą koniunkcyjną

(mfk) funkcji

monotonicznej nazywamy formułę koniunkcyjną o
najmniejszej liczbie czynników (sum)

(mfk)

)

x

x

)(

x

x

(x

(x)

f

4

2

3

2

1

(4)









Analityczny zapis struktur
niezawodnościowych

Podzbiór W  E elementów systemu nazywa się

ścieżką

zdatności

, jeśli przy zdatności wszystkich elementów należących

do W system jest w stanie zdatności niezależnie od stanu
pozostałych elementów systemu.

Ścieżka zdatności jest

minimalną

, jeśli nie zawiera żadnej innej

ścieżki zdatności.

Minimalna formuła alternatywna (mfa) określa jednoznacznie
zbiór wszystkich minimalnych ścieżek zdatności - każdemu
składnikowi

sumy

(iloczynowi)

odpowiada

wzajemnie

jednoznacznie minimalna ścieżka zdatności.

Podzbiór C  E elementów systemu nazywa się

cięciem

(przekrojem), jeśli przy niezdatności wszystkich elementów
należących do C system jest w stanie niezdatności niezależnie
od stanu pozostałych elementów systemu.

Cięcie jest

minimalne

, jeśli nie zawiera żadnych innych cięć.

Minimalna formuła koniunkcyjna (mfk) określa jednoznacznie
zbiór wszystkich minimalnych cięć - każdemu czynnikowi
(sumie) odpowiada wzajemnie jednoznacznie minimalne cięcie.

Ścieżki zdatności i cięcia w
systemie

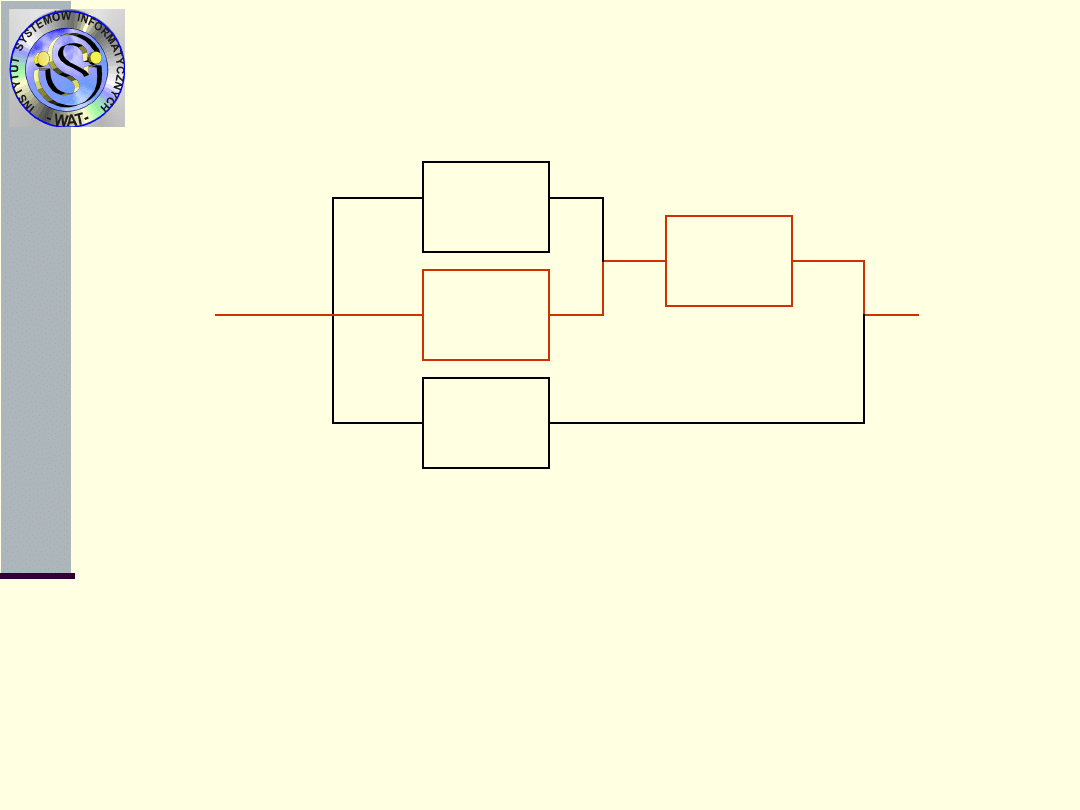
(mfa)

x

x

x

x

x

(x)

f

4

3

4

1

2

(4)







(mfk)

)

x

x

)(

x

x

(x

(x)

f

4

2

3

2

1

(4)









x

1

x

3

x

2

x

4

Przykład

Schemat blokowy struktury

niezawodnościowej

Ścieżki zdatności i cięcia w
systemie

Dla każdej struktury monotonicznej (koherentnej)
określonej przez f

(n)

(x) istnieje dualna struktura

koherentna określona przez funkcję monotoniczna f

(n)

D

(x).

Wyrażenie bulowskie, określające funkcję dualną
otrzymujemy w ten sposób, że w wyrażeniu bulowskim,
określającym

f

(n)

(x),

zamieniamy

wszystkie

znaki

alternatywy na znaki koniunkcji, a znaki koniunkcji na
znaki alternatywy. Dla funkcji

4

3

1

2

3

2

1

(4)

x

)

x

x

(

x

x

x

x

(x)

f









Funkcja dualna ma postać

)

x

x

x

)(

x

)(

x

x

(x

(x)

f

4

3

1

2

3

2

1

(4)

D









Z definicji wynika, że mfa funkcji

f

(n)

D

(x)

otrzymujemy

bezpośrednio z mfk funkcji

f

(n)

(x),

a mfk funkcji

f

(n)

D

(x)

bezpośrednio z mfk

f

(n)

(x). Przykład :

)

x

x

)(

x

x

)(

(x

(x)

f

4

3

4

1

2

(4)

D







x

x

x

x

x

(x)

f

4

2

3

2

1

(4)

D





Struktury dualne

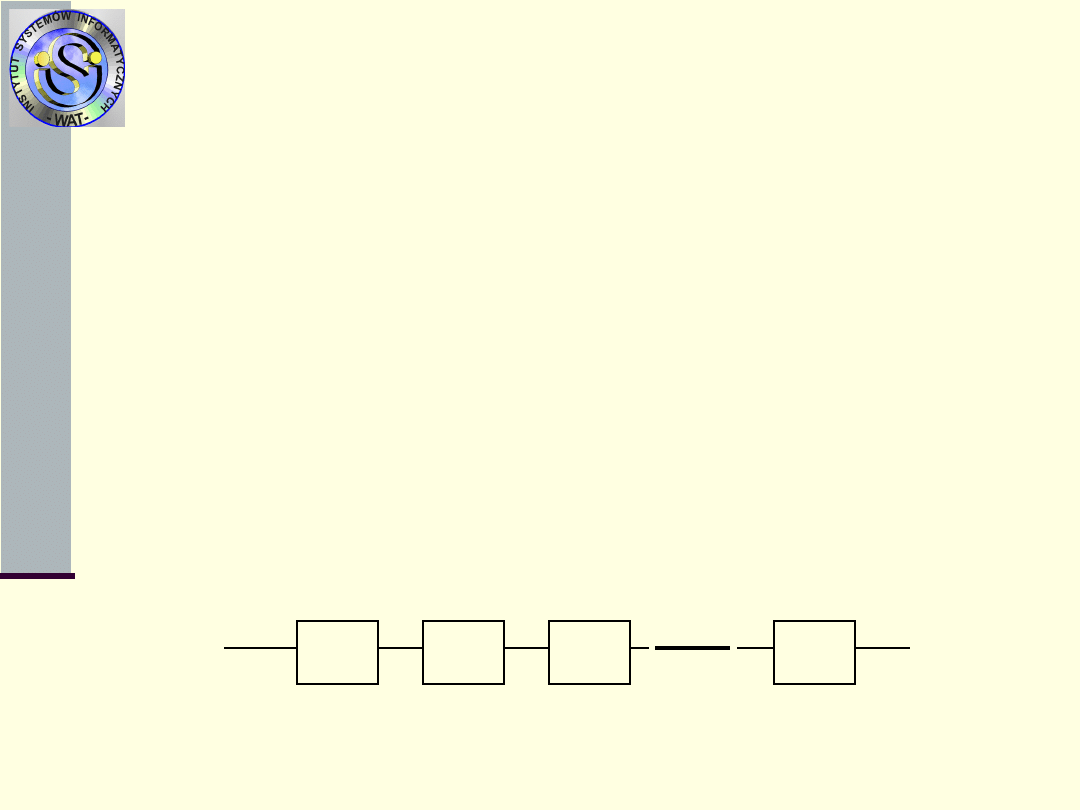
Wyróżnia się niektóre podstawowe struktury, które mogą
być podstrukturami bardziej złożonych struktur.

1. Struktura szeregowa

- gdy niezdatność dowolnego

elementu struktury powoduje niezdatność całego systemu







n

1

i

(n)

x

(x)

f

i

Funkcja dualna dla struktury szeregowej
ma postać







n

1

i

i

(n)

D

x

(x)

f

Schemat blokowy dla struktury szeregowej ma postać

x

1

x

2

x

3

x

n

Elementarne struktury
niezawodnościowe

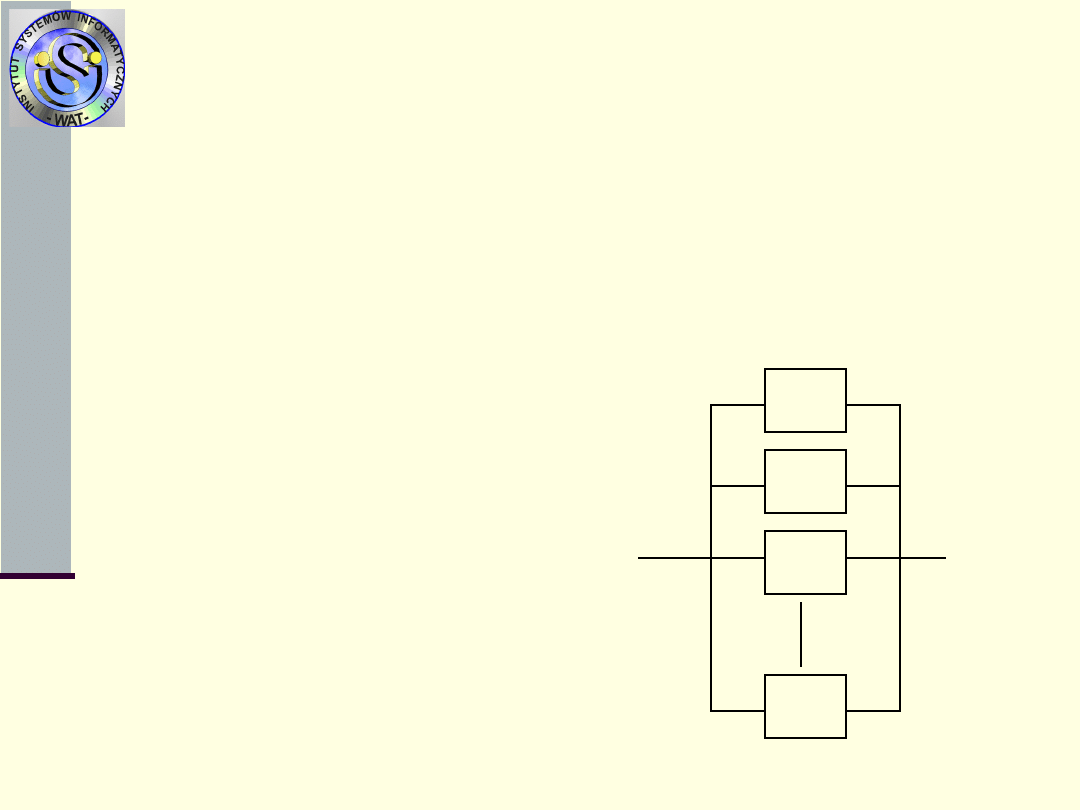
2. Struktura równoległa

- gdy zdatność dowolnego

elementu struktury powoduje zdatność całego systemu







n

1

i

i

(n)

x

(x)

f

Funkcja dualna dla struktury równoległej
ma postać







n

i 1

i

(n)

D

x

(x)

f

Schemat blokowy dla struktury
równoległej ma postać

x

1

x

2

x

3

x

n

Elementarne struktury
niezawodnościowe

3. Struktury progowe

(tak zwane struktury „k z n”)- gdy

zdatność dowolnych co najmniej k elementów struktury
powoduje zdatność całego systemu.
Przykładem może być struktura progowa „2 z 3”

3

2

3

1

2

1

(3)

x

x

x

x

x

x

(x)

f







Funkcja dualna dla tej struktury ma
postać

)

x

)(x

x

)(x

x

x

(

(x)

f

3

2

3

1

2

1

(3)

D









Schemat blokowy dla struktury progowej nie istnieje !

Oznacza to, że nie zawsze można skonstruować schematy
blokowe dla struktur niezawodnościowych.

Uwaga: zauważmy, że

struktura progowa „1 z n” jest
strukturą
struktura progowa „n z n” jest
strukturą

równoległ
ą
szeregową

Elementarne struktury
niezawodnościowe

Stany niezawodnościowe elementów są binarnymi
procesami stochastycznymi x

i

(t). Argument funkcji f

(n)

(x)

jest

dla

ustalonej

chwili

t

n-wymiarową zmienną losową

n

i

1

X

,...,

X

,...,

X

X 

To znaczy binarnym wektorem losowym o odpowiednim
rozkładzie prawdopodobieństwa. Oznaczmy









1..n

i

,

p

-

1

q

0

X

P

,

p

1

X

P

i

i

i

i

i













oraz

n

i

1

x

,...,

x

,...,

x

x 

wektor

binarny.

Wtedy

otrzymujemy





)

x

-

(1

i

n

1

i

x

i

i

i

q

p

X

P







x

że w

ustalonej

chwili stany niezawodnościowe

elementów są takie, jak określono to w wektorze x.

co jest
prawdopodobieństwem tego,

Probabilistyczny model
niezawodnościowy

Stan niezawodnościowy systemu jest bulowską zmienną
losową Y, określoną jako funkcja bulowska wektora
losowego X



































1

X

x

)

i

x

-

(1

i

n

1

i

i

x

i

1

X

x

(n)

q

p

x

X

P

1

(X)

f

P

1

Y

P

(X)

f

Y

(n)



Zatem rozkład zmiennej losowej Y jest jednoznacznie
określony przez rozkład wektora losowego X

Gdzie X

1

jest podzbiorem tych wszystkich wektorów

binarnych x, dla których zachodzi f

(n)

(x) = 1. Gdy

oznaczymy X

0

jako podzbiór tych wszystkich wektorów

binarnych x, dla których zachodzi f

(n)

(x) = 0, to









 





















0

X

x

)

i

x

-

(1

i

n

1

i

i

x

i

0

X

x

q

p

1

x

X

P

1

1

Y

P

Probabilistyczny model
niezawodnościowy

Prawdopodobieństwa p

i

oraz q

i

określone zostały dla

wybranej, ustalonej chwili t. Co zrobić, gdy chcemy znać
charakterystyki niezawodnościowe systemu nie tylko dla
ustalonych momentów czasu. Rozpatrzmy poniższe
przypadki.

1.

Elementy

systemu

są

elementami

prostymi

nieodnawialnymi

Wtedy prawdopodobieństwa p

i

oraz q

i

zastępujemy

odpowiednio funkcjami





t







i

i

i

T

P

(t)

R

p

funkcja niezawodności
elementu prostego
nieodnawialnego

 

t







i

i

i

T

P

(t)

F

q

dystrybuanta elementu
prostego nieodnawialnego

Wtedy otrzymujemy











 



)

x

-

(1

i

X

x

n

1

i

x

i

(n)

i

1

i

(t)

F

(t)

R

1

(X(t))

f

P

1

Y(t)

P

















Probabilistyczny model
niezawodnościowy

2. Elementy systemu są elementami prostymi
odnawialnymi

Zauważmy, że muszą być to elementy z niezerową
odnową, bo w przeciwnym przypadku system byłby
zawsze w stanie zdatności.Wtedy prawdopodobieństwa p

i

oraz q

i

zastępujemy odpowiednio funkcjami





1

(t)

X

P

(t)

k

p

i

i

g

i







współczynnik gotowości
elementu odnawialnego z
niezerową odnową





0

(t)

X

P

(t)

k

-

1

q

i

i

g

i







Wtedy otrzymujemy











 



)

x

-

(1

i

g

X

x

n

1

i

x

i

g

(n)

i

1

i

(t)

k

1

(t)

k

1

(X(t))

f

P

1

Y(t)

P



















Probabilistyczny model
niezawodnościowy

3. Elementy systemu są mieszane, niektóre są
elementami prostymi nieodnawialnymi, a niektóre są
elementami prostymi odnawialnymi

Wtedy prawdopodobieństwa p

i

oraz q

i

zastępujemy

odpowiednio





1

(t)

X

P

(t)

k

p

i

i

g

i











0

(t)

X

P

(t)

k

-

1

q

i

i

g

i







Dla elementów nieodnawialnych
prostych

natomiast dla elementów odnawialnych prostych o niezerowej
odnowie





t







i

i

i

T

P

(t)

R

p

 

t







i

i

i

T

P

(t)

F

q

Probabilistyczny model
niezawodnościowy

Czy nie będziemy mieli żadnych kłopotów
w wyznaczeniu wartości P{f

(n)

(X(t)) = 1}?

Niestety, będziemy mieli. Wynika to z
następującego faktu:

liczności zbiorów X

1

oraz X

0

są olbrzymie

.

Istnieją metody wyznaczania formuł o
minimalnej postaci służące obliczaniu
wartości
P{f

(n)

(X(t)) = 1}.

(Przeczytać skrypt Korzana - punkt 6.11).
Warto zauważyć, że można obliczyć takie
wartości dla elementarnych struktur
niezawodnościowych i uogólnić to dla
struktur bardziej złożonych.

Obliczanie prawdopodobieństwa
zdatności systemu













t

T

,...,

T

,

T

min

P

T

P

(t)

R

n

2

1

s

s









t

1. Struktury szeregowe (elementy nieodnawialne proste)

Niech T

i

oznacza czas zdatności elementu i-tego,

natomiast T

s

oznacza czas zdatności systemu. Wtedy

mamy





n

1,2,...,

i

,

T

min

T

i

s





co daje w
efekcie

co dla niezależności uszkodzeń elementów powoduje równość
powyższego z

















(t)

R

(t)

R

t

T

P

t

T

t,...,

T

t,

T

P

t

T

,...,

T

,

T

min

P

S

n

1

i

i

n

1

i

i

n

2

1

n

2

1





























Z kolei dla dystrybuant otrzymujemy formułę
postaci





 

















n

1

i

i

s

s

t

F

-

1

1

t

T

P

(t)

F

Obliczanie prawdopodobieństwa
zdatności systemu













t

T

,...,

T

,

T

max

P

T

P

(t)

F

n

2

1

s

s









t

2. Struktury równoległe (elementy nieodnawialne proste)

Niech T

i

oznacza czas zdatności elementu i-tego,

natomiast T

s

oznacza czas zdatności systemu. Wtedy

mamy





n

1,2,...,

i

,

T

max

T

i

s





co daje w
efekcie

co dla niezależności uszkodzeń elementów powoduje równość
powyższego z













 

(t)

F

(t)

F

t

T

P

t

T

t,...,

T

t,

T

P

t

T

,...,

T

,

T

max

P

S

n

1

i

i

n

1

i

i

n

2

1

n

2

1





























Z kolei dla funkcji niezawodności otrzymujemy
formułę postaci





 

















n

1

i

i

s

s

t

R

-

1

1

t

T

P

(t)

R

Obliczanie prawdopodobieństwa
zdatności systemu





 

 

  













































n

k

i

D

j)

(i,

D

c

D

l

l

c

s

s

t

F

t

R

t

T

P

(t)

R

i

j

3. Struktury progowe (elementy nieodnawialne proste)

Dla przypadku ogólnego struktur progowych musimy
obliczyć wszystkie możliwe kombinacje dla poprawnych
co najmniej k elementów z n możliwych :

gdzie (i,j)D oznacza wszystkie możliwe kombinacje

par (i,j) spełniające i+j=n oraz założenie, że i oznacza
liczbę elementów zdatnych, a j liczbę elementów
niezdatnych, natomiast zbiory D

i

oraz D

j





n

,...,

2

,

1

D

D

,

j

D

,

i

D

j

i

j

i









Obliczanie prawdopodobieństwa
zdatności systemu

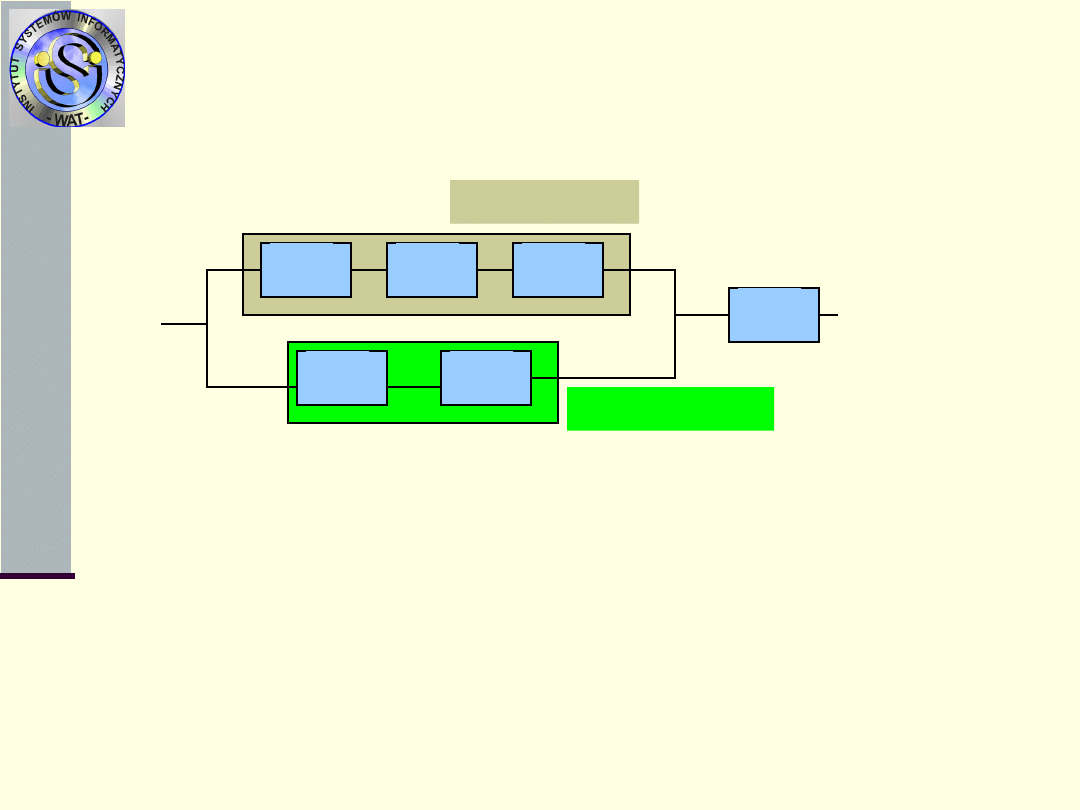
4. Struktury szeregowo-równoległe lub równoległo-
szeregowe

Dekomponujemy wtedy cały system na podsystemy
szeregowe i równo-ległe stosując otrzymane formuły.
Przykład

x

1

x

2

x

3

x

4

x

5

x

6

Podsystem II

Podsystem I

Otrzymujemy teraz formuły
składowe

))

(t

(t)])(R

R

-

(t)][1

R

-

[1

-

(1

))

(t

(t)(R

R

(t)

R

6

II

I

6

II

-

I

s





(t)

(t)F

F

(t)

F

II

I

II

-

I



(t)

(t)R

(t)R

R

(t)

R

3

2

1

I



(t)

(t)R

R

(t)

R

5

4

II



)

(t)

R

-

1

(t)

F

:

uwaga

(

II

-

I

II

-

I



Obliczanie prawdopodobieństwa
zdatności systemu

5. Struktury z elementami prostymi odnawialnymi o
niezerowej odnowie

Jeśli pewne elementy (lub nawet wszystkie) są elementami
odnawialnymi, to stosujemy podstawienie

)

(

k

1

(t)

F

,

)

(

k

(t)

R

i

g

i

i

g

i

t

t







i-te elementy są

odnawialne

Ciąg dalszy Przykładu (jeśli elementy o numerach 1, 5 i 6 są
odnawialne, to system jest nieodnawialny (w końcu uszkodzą się
elementy 2, 3 oraz 4 i nie będzie dla dużych t żadnej ścieżki
zdatności o zdatnych wszystkich elementach). Podsystemy I i II
są obiektami nieodnawialnymi. Zatem system jest nieodna-
wialny i liczymy dla niego charakterystyki (np. R

s

(t)) jak dla

obiektu nieodna-wialnego

))

(t

(t)])(k

R

-

(t)][1

R

-

[1

-

(1

))

(t

(t)(k

R

(t)

R

6

g

II

I

6

g

II

-

I

s





(t)

(t)F

F

(t)

F

II

I

II

-

I



(t)

(t)R

(t)R

k

(t)

R

3

2

1

g

I



(t)

(t)k

R

(t)

R

5

g

4

II



Obliczanie prawdopodobieństwa
zdatności systemu

W przypadku, gdy mamy do czynienia z identycznymi w
sensie rozkładu elementami ( R(t) = R

i

(t), i=1..n ) to wiele

formuł upraszcza się znacznie.

1. Struktury szeregowe o identycznych elementach









n

S

n

S

F(t)

-

1

1

(t)

F

,

R(t)

(t)

R







2. Struktury równoległe o identycznych elementach









n

S

n

S

R(t)

-

1

1

(t)

R

,

F(t)

(t)

F







3. Struktury progowe





 





 

 

























n

k

i

i

n

i

s

s

t

F

t

R

i

n

t

T

P

(t)

R

Wzór ten dla struktur „n-1 z n” upraszcza się do postaci

 





 





n

1

-

n

s

t

R

1)

-

(n

t

R

n

(t)

R





Systemy o jednakowych elementach

Założenia: elementy dwustanowe w sensie niezawodności o
wykładniczych rozkładach czasów poprawnej pracy i odnowy
(model

Markowa);

system

wielostanowy

w

sensie

niezawodności, a jego stany definiowane są stanami elementów.

Dowolny stan systemu opisany jest stanami jego elementów,
czyli wektorem:

n

i

1

x

,...,

x

,...,

x

x 

Poszczególne, zdefiniowane wcześniej stany niezawodnościowe
systemu stanowią podzbiory stanów jego elementów, czyli
podzbiory wektorów x. Zatem przechodzenie procesu zmian
stanów

systemu

wynika

jednoznacznie

z

procesów

przechodzenia elementów pomiędzy swoimi stanami. Przy
założeniu o wykładniczym charakterze rozkładu czasu
przechodzenia do kolejnych stanów i przebywania w stanach
rozkłady łączne procesu zmian definiuje się za pomocą
macierzy intensywności przejść. W efekcie uzyskać można
metodą równań stanów charakterystyki chwilowe lub graniczne
prawdopodobieństw przebywania procesu w poszczególnych
stanach, z których z kolei wyznacza się kolejne istotne wartości
miar niezawodnościowych systemu.

Model systemu wielostanowego
w sensie niezawodności

Metodę tę zilustrujemy przykładem.

Przykład System ma strukturę przedstawioną na schemacie

x

1

x

2

x

3

Czasy poprawnej pracy elementów
x

1

i x

2

mają rozkład wykładniczy z

parametrem a, elementu x

3

z

parametrem b natomiast wszystkie
czasy

odnowy

mają

rozkład

wykładniczy

z

parametrem

c.

Można zatem zdefiniować trzy stany
niezawodnościowe systemu:

Stan pełnej wydajności x

1

= (1,1,1), stany częściowej

wydajności x

2

= (0,1,1), x

3

= (1,0,1) oraz stan awarii x

4

=

(0,0,1), x

5

= (1,1,0), x

6

= (0,1,0), x

7

= (1,0,0), x

8

= (0,0,0).

Oznacza to, że elementy mogą uszkadzać się nawet po
uszkodzeniu systemu, chociaż nie trzeba czynić takiego
założenia. Wtedy po prostu liczba możliwych w realizacji
stanów zmniejszy się istotnie.

Uszkodzony element naprawiany jest przez jednego
konserwatora i najpierw zawsze naprawiany jest element
trzeci (jeśli jest uszkodzony), a następnie któryś z elementów
pozostałych, załóżmy, że pierwszy.

Model systemu wielostanowego w sensie
niezawodności

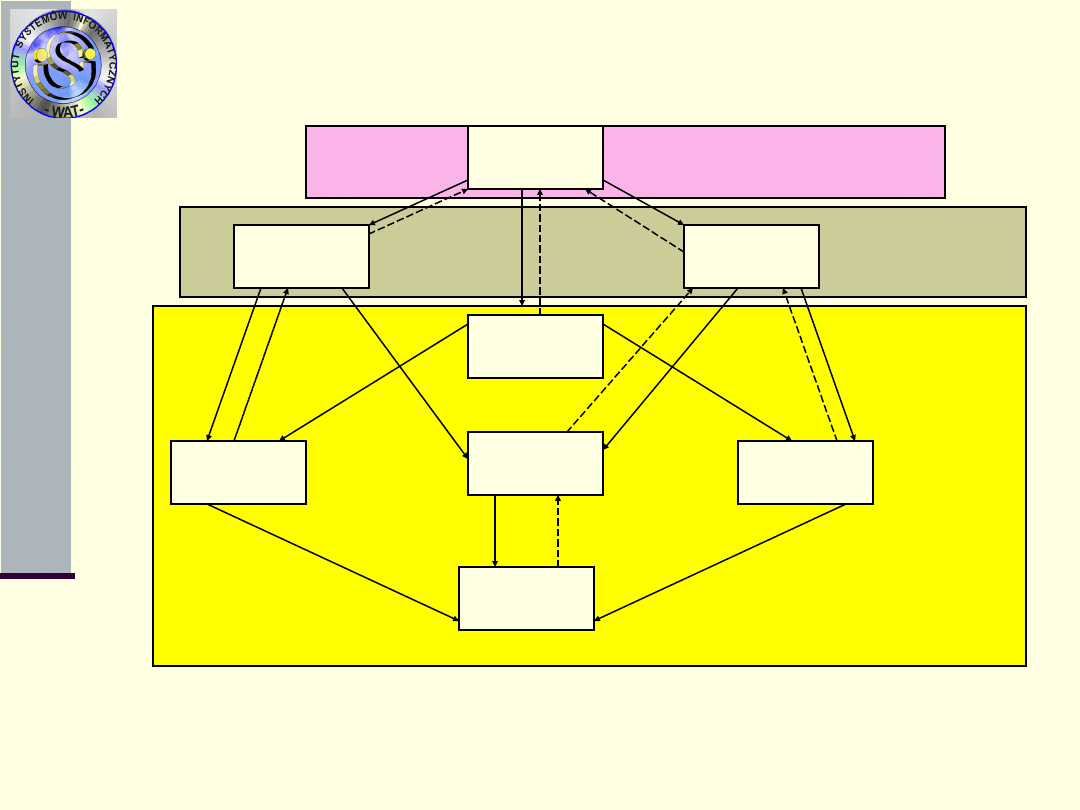
Daje to nam w efekcie następujący graf stanów procesu zmian
stanów elementów i systemu:

(1,1,

1)

(0,1,

1)

(1,0,

1)

(1,1,

0)

(0,0,

1)

(0,1,

0)

(0,0,

0)

(1,0,

0)

a

a

b

b

a

a

a

a

b

a

b

c

c

c

c

c

c

Pełna

wydajność

Częściowa

wydajność

Stan awarii

Uwaga:intensywności (pętle) na wierzchołkach grafu to minus suma
intensywności wychodzących z wierzchołka.

Model systemu wielostanowego w sensie
niezawodności

a

c

(1,1,

1)

(0,1,1),

(1,0,1)

(1,1,

0)

(0,0,1)

2a

b

b

b

c

c

Pełna

wydajność

Częściowa

wydajność

Stan awarii

2a

c

stan1

stan2

stan4

stan5

(1,0,0),

(0,1,0)

(0,0,0)

stan3

stan6

c

c

a

a

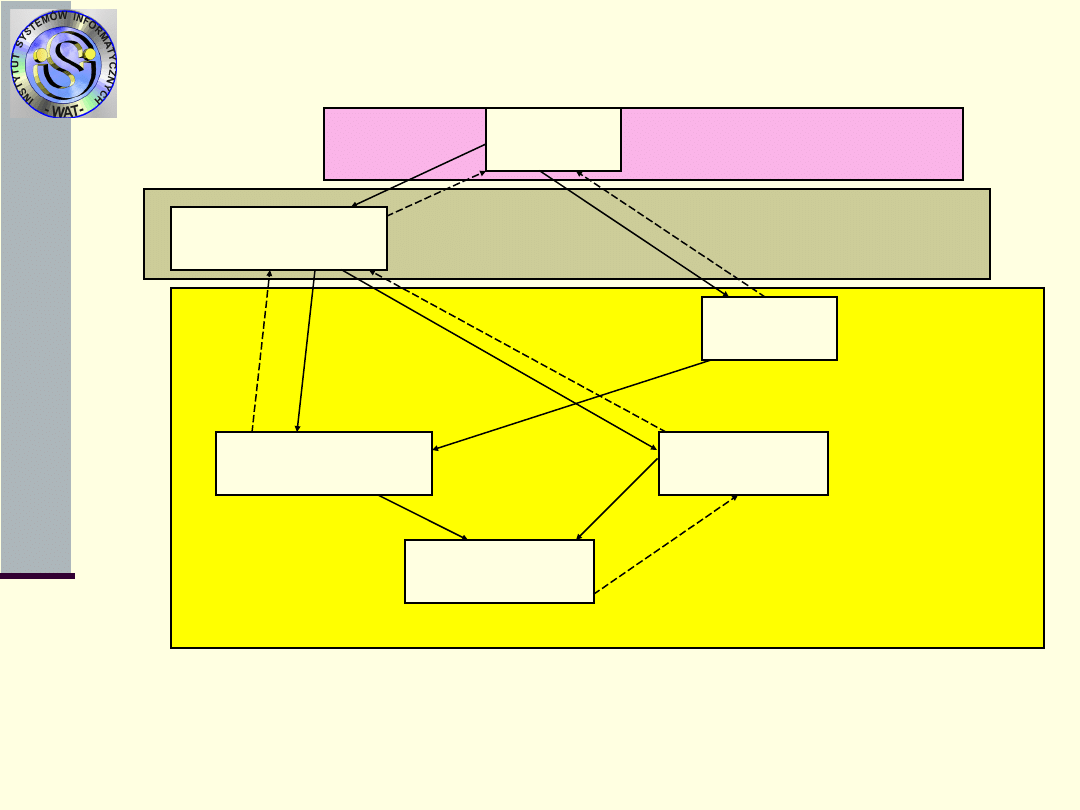
Stany te można zredukować

Uwaga:intensywności (pętle) na wierzchołkach grafu to minus
suma intensywności wychodzących z wierzchołka.

Model systemu wielostanowego w sensie
niezawodności

b

Stąd układ równań różniczkowych stanu (Kołmogorowa) ma
postać :

(t)

cp

(t)

cp

(t)

b)p

a

2

(

(t)

p

dt

d

4

2

1

1











Zamiast jednego z równań (6) dajemy równanie normujące
postaci

(t)

cp

(t)

cp

(t)

c)p

b

(a

-

(t)

p

a

2

(t)

p

dt

d

5

3

2

1

2











(t)

p

2

(t)

c)p

(a

-

(t)

bp

(t)

p

dt

d

4

3

2

3

a







(t)

c)p

a

2

(

(t)

bp

(t)

p

dt

d

4

1

4







1

(t)

p

(t)

p

(t)

p

(t)

p

(t)

p

(t)

p

6

5

4

3

2

1













(t)

cp

(t)

c)p

(b

-

(t)

ap

(t)

p

dt

d

6

5

2

5







)

0

,

0

,

0

,

0

,

0

,

1

(

(0))

p

(0),

p

(0),

p

(0),

p

(0),

p

(0),

(p

p(0)

6

5

4

3

2

1





oraz
warunek
początkow
y

Model systemu wielostanowego w sensie
niezawodności

1

p

p

p

p

p

p

6

5

4

3

2

1













Równania te można rozwiązać stosując transformatę Laplace’a.
Otrzymujemy wtedy wektor p(t)=(p

1

(t), p

2

(t), p

3

(t), p

4

(t), p

5

(t),

p

6

(t))

będący

podstawa

obliczania

charakterystyk

niezawodnościowych wielostanowego w sensie niezawodności
systemu.

Chcąc

uzyskać

charakterystyki

graniczne

przekształcamy uzyskany układ równań (gdzie p

i

= lim p

i

(t)

i=1..6) do postaci:

5

3

2

1

cp

cp

c)p

b

(a

-

p

a

2

0











4

3

2

p

2

c)p

(a

-

bp

0

a







4

1

c)p

a

2

(

bp

0







6

5

2

cp

c)p

(b

-

ap

0







z warunkiem
normującym

4

2

1

cp

cp

b)p

a

2

(

0











Ten układ równań liniowych można rozwiązać np. metodą
Gaussa. Otrzymujemy wtedy wektor p=(p

1

, p

2

, p

3

, p

4

, p

5

, p

6

)

granicznych prawdopo-dobieństw będący podstawa obliczania
granicznych

charakterystyk

nieza-wodnościowych

wielostanowego w sensie niezawodności systemu.

Model systemu wielostanowego w sensie
niezawodności

Należy zawsze dokonać identyfikacji wszystkich

elementów - czy są odnawialne, czy nie; jakie są
ich rozkłady prawdopodobieństwa czasu życia
lub (o ile jest to potrzebne) czasów odnowy, itp.,

należy zbadać ścieżki zdatności i cięcia systemu;

duża liczba ścieżek świadczy o odporności
systemu, a duża liczba cięć świadczy o
wrażliwości systemu; odnosi się to w dużej
mierze do odporności systemu na uszkodzenia
pojedynczych elementów,

należy

ustalić,

czy

system

jest

obiektem

nieodnawialnym,

czy

odnawialnym;

miary

niezawodności obliczane dla systemu muszą być
charakterystyczne dla ustalonej klasy systemu -
obiektu.

Wnioski końcowe