Seria: Informatyka
Elementy teorii niezawodności
Wykład 1
Pojęcia wstępne
dr hab. in
ż
. Tadeusz Nowicki prof. nadzw. WAT
e-mail: tadeusz.nowicki@wat.edu.pl,
tel. 6-837118, kons. wtorek 19.00, pok. 222
Podstawy teorii niezawodności
Niezawodno
ść
jest własno
ś
ci
ą
badanego obiektu
charakteryzuj
ą
ca jego zdolno
ść
do:
•
wykonywania okre
ś
lonych zada
ń
(funkcji),
•
w okre
ś
lonych warunkach,
•
oraz w okre
ś
lonym czasie.
Dowolna
zmiana
powy
ż
szych
trzech
ustale
ń
Dowolna
zmiana
powy
ż
szych
trzech
ustale
ń
powoduje,
ż
e
powinni
ś
my uzna
ć
,
ż
e
badaniu
podlega
ć
zaczyna inny obiekt. Jest on wtedy
innym
od
poprzedniego
obiektem
z
punktu
widzenia bada
ń
niezawodno
ś
ciowych.
Niezawodno
ść
jest cech
ą
kompleksow
ą
i składa
si
ę
na
ni
ą
:
nieuszkadzalno
ść
,
naprawialno
ść
,
trwało
ść
i przechowywalno
ść
.
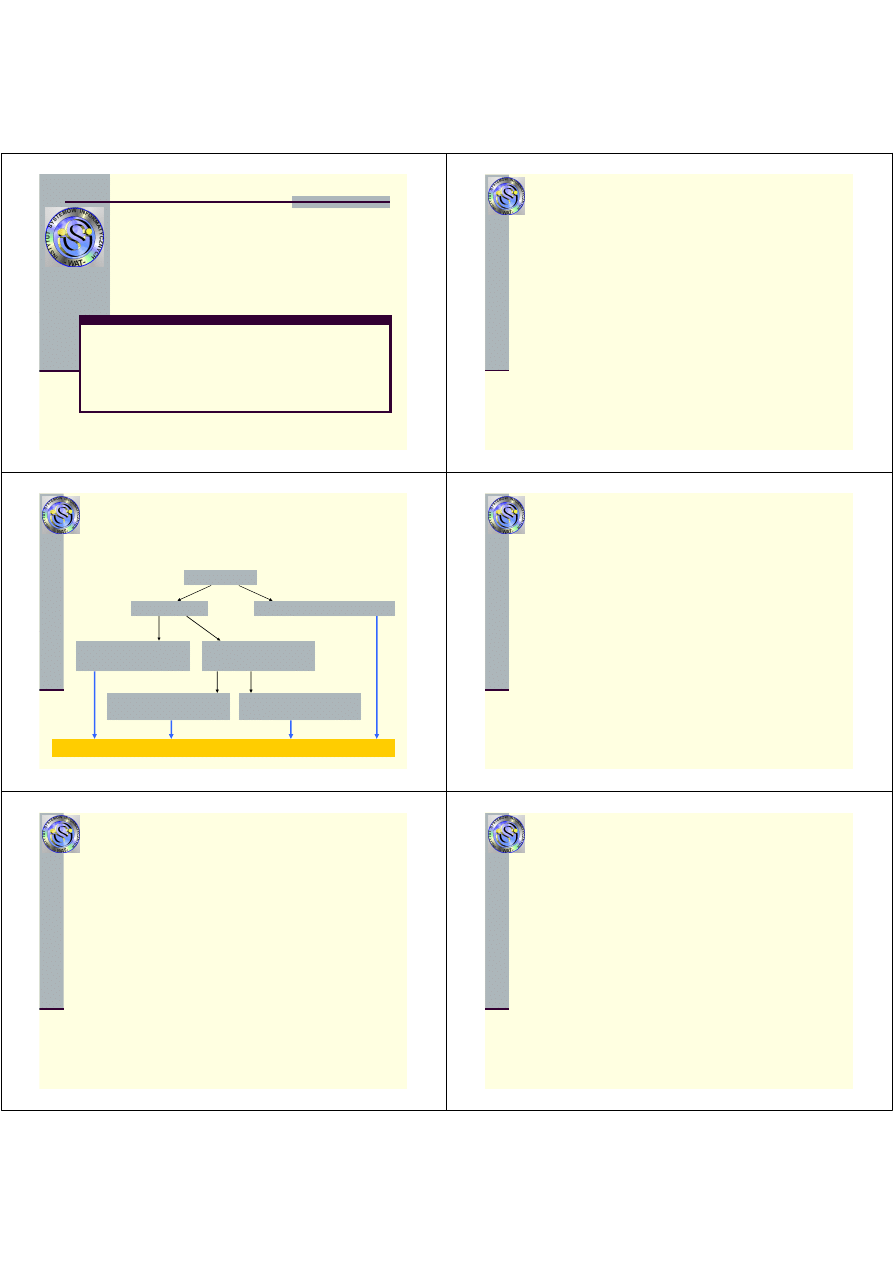
Podstawy teorii niezawodności
Obiekty podlegaj
ą
ce badaniom niezawodno
ś
cio-
wym podzieli
ć
mo
ż
na na klasy według poni
ż
szego
schematu
obiekty
obiekty proste
obiekty złożone (systemy)
obiekty proste
nieodnawialne
obiekty proste
odnawialne
obiekty pr. odnawialne
z zerową odnową
obiekty pr. odnawialne
z niezerową odnową
Określenie i wybór miar niezawodności
Podstawy teorii niezawodności
•
obiekty proste
to takie, w których badaniu nie
wnikamy w ich struktur
ę
wewn
ę
trzn
ą
,
•
obiekty zło
ż
one
(systemy) to takie, w których
badaniu uwzgl
ę
dniamy ich struktur
ę
wewn
ę
trzn
ą
,
•
obiekty proste nieodnawialne
to takie, dla których
zakłada si
ę
,
ż
e nie s
ą
one odnawialne nawet
zakłada si
ę
,
ż
e nie s
ą
one odnawialne nawet
wtedy, gdy istnieje taka mo
ż
liwo
ść
(odnowa jest
uogólnieniem
poj
ęć
:
wymiana,
naprawa,
dostrojenie, itp.),
•
obiekty proste odnawialne
– zakładamy,
ż
e s
ą
one
odnawialne,
•
obiekty proste odnawialne z zerow
ą
odnow
ą
–
zakłada si
ę
,
ż
e odnowa jest pomijalnie krótka,
Podstawy teorii niezawodności
•
obiekty proste odnawialne z niezerow
ą
odnow
ą
–
zakłada si
ę
,
ż
e odnowa nie jest pomijalnie krótka i
nale
ż
y uwzgl
ę
dni
ć
j
ą
w badaniu charakterystyk
niezawodno
ś
ciowych obiektu,
Warto pami
ę
ta
ć
,
ż
e obiekty mog
ą
mie
ć
bogat
ą
struktur
ę
wewn
ę
trzn
ą
, jednak to decyzja analityka
struktur
ę
wewn
ę
trzn
ą
, jednak to decyzja analityka
powoduje ich traktowanie jako obiektów prostych
lub zło
ż
onych. Podobnie jest z nieodnawialno
ś
ci
ą
obiektów. Pomijanie czasu odnowy wynika cz
ę
sto z
faktu wzgl
ę
dnie krótkiego czasu odnowy w stosunku
do czasu eksploatacji obiektu. Zatem pewnie czas
odnowy dla jednych obiektów jest pomijalny, a dla
innych musi by
ć
uwzgl
ę
dniany w badaniach.
Podstawy teorii niezawodności
W
badaniach
niezawodno
ś
ciowych
nale
ż
y
stosowa
ć
nast
ę
puj
ą
cy schemat post
ę
powania:
-
okre
ś
lenie własno
ś
ci obiektu,
-
okre
ś
lenie własno
ś
ci składowych (o ile taka
istnieje potrzeba),
-
okre
ś
lenie miar własno
ś
ci (tu: niezawodno
ś
ci),
-
okre
ś
lenie miar własno
ś
ci (tu: niezawodno
ś
ci),
-
okre
ś
lenie metod pozyskiwania warto
ś
ci miar
niezawodno
ś
ci,
-
analiza niezawodno
ś
ciowa obiektu.
Seria: Informatyka
Elementy teorii niezawodności
Wykład 2
Obiekty proste nieodnawialne
dr hab. in
ż
. Tadeusz Nowicki prof. nadzw. WAT
e-mail:tadeusz.nowicki@wat.edu.pl, tel. 6-837118
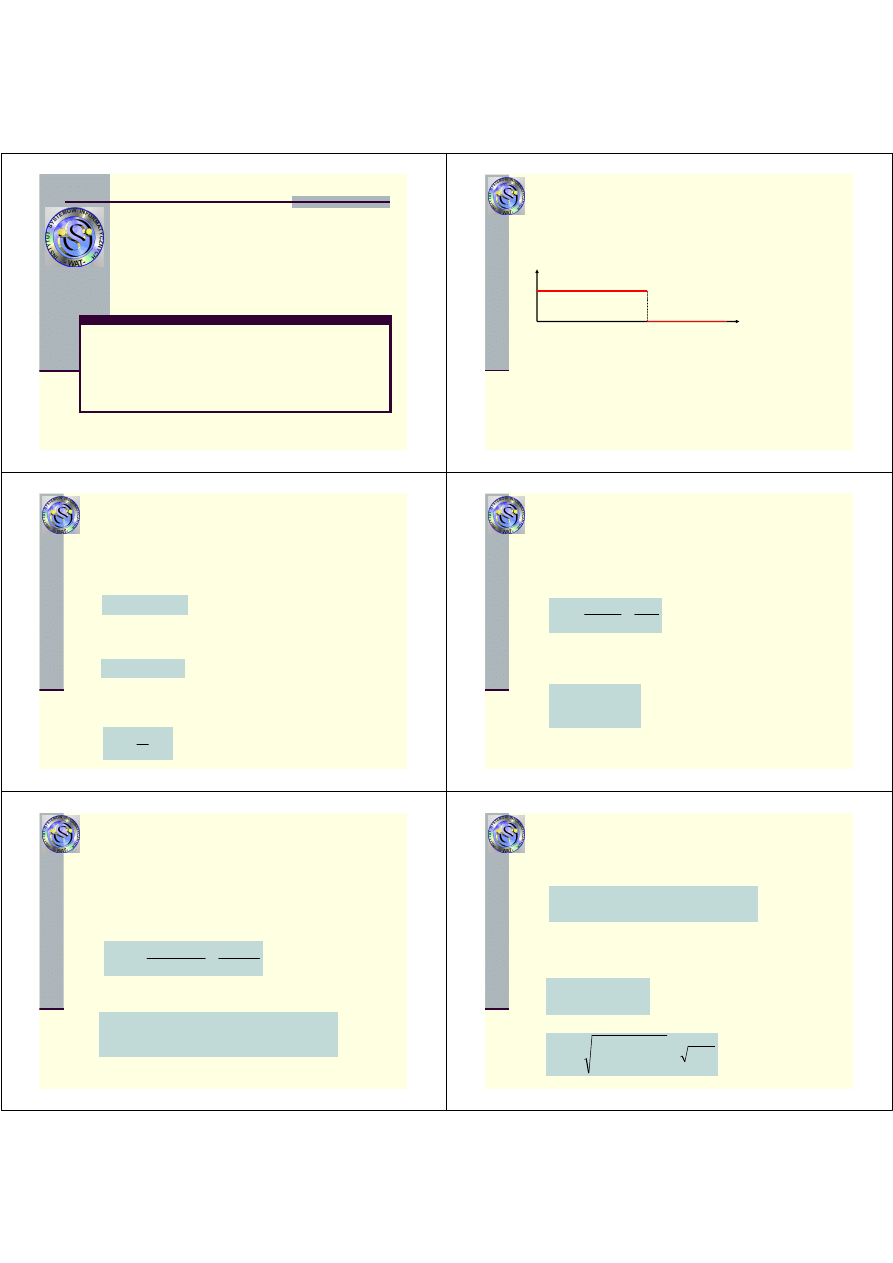
Model niezawodnościowy
Jedynym
istotnym
zdarzeniem
w
eksploatacji
obiektu
prostego nieodnawialnego jest chwila jego uszkodzenia.
Wtedy traci on własno
ść
realizacji przewidzianych funkcji
(zada
ń
).
T
1
1- oznacza zdatno
ść
obiektu do
wykonywania funkcji
0 – oznacza jego niezdatno
ść
Zmienna T jest
ci
ą
gł
ą
i dodatni
ą
zmienn
ą
losow
ą
oznaczaj
ą
c
ą
czas
ż
ycia
obiektu, zatem czas do jego uszkodzenia. Jest ona
modelem
niezawodno
ś
ciowym
obiektu
prostego
nieodnawialnego. Charakterystyki tej zmiennej losowej s
ą
zatem
miarami niezawodno
ś
ciowymi
obiektu.
t
t
1
0
0 – oznacza jego niezdatno
ść
Miary niezawodności
Miary funkcyjne (zale
ż
ne od upływaj
ą
cego czasu)
1.
Dystrybuanta F(t) zmiennej losowej T –
prawdopodobie
ń
stwo,
ż
e czas do uszkodzenia
obiektu jest mniejszy od zadanej chwili t
2.
Funkcja niezawodno
ś
ci R(t) -
prawdopodobie
ń
stwo,
ż
e czas do uszkodzenia
{
}
t
T
P
)
t
(
F
<
=
prawdopodobie
ń
stwo,
ż
e czas do uszkodzenia
obiektu jest wi
ę
kszy od zadanej chwili t
3.
G
ę
sto
ść
zmiennej losowej T – pokazuje
rozło
ż
enie masy prawdopodobie
ń
stwa na
posczególnych warto
ś
ciach zmiennej losowej
{
}
t
T
P
)
t
(
R
≥
=
)
t
(
F
dt
d
)
t
(
f
=
Miary niezawodności
4.
Funkcja
λλλλ
(t) intensywno
ś
ci uszkodze
ń
zmiennej
losowej T – warunkowa g
ę
sto
ść
rozkładu
prawdopodobie
ń
stwa czasu powstania
uszkodzenia w chwili t
)
t
(
R
)
t
(
f
)
t
(
F
1
)
t
(
f
)
t
(
=
−
=
λ
5.
Funkcja wiod
ą
ca
Λ
Λ
Λ
Λ
(t) – skumulowany wska
ź
nik
bazuj
ą
cy na chwilowej charakterystyce
λλλλ
(t)
∫
λ
=
Λ
t
0
du
)
u
(
)
t
(
Miary niezawodności
6.
Warunkowa funkcja niezawodno
ś
ci R
t
(
ττττ
) –
prawdopodobie
ń
stwo warunkowe zdarzenia
polegaj
ą
cego na tym,
ż
e obiekt zachowa stan
zdatno
ś
ci jeszcze przez odcinek czasu o
długo
ś
ci co najmniej
ττττ
pod warunkiem,
ż
e do
chwili t nie uszkodził si
ę
.
{
}
)
t
(
R
t
T
P
)
(
R
τ
+
=
τ
+
≥
=
τ
7.
Bezwarunkowe prawdopodobie
ń
stwo P(t,t+
ττττ
)
braku uszkodzenia w przedziale czasu (t,t+
ττττ
)
[
]
)
t
(
R
)
t
(
R
1
du
)
u
(
f
)
t
,
t
(
P
t
t
τ
+
−
−
=
=
τ
+
∫
τ
+
{
}
{
}
)
t
(
R
)
t
(
R
t
T
P
t
T
P
)
(
R
t
τ
+
=
≥
τ
+
≥
=
τ
Miary niezawodności
Miary liczbowe (niezale
ż
ne od upływaj
ą
cego czasu)
8.
Warto
ść
oczekiwana E{T} zmiennej losowej T
Uwaga: całkujemy od 0 – dodatnie zmienne losowe
9.
Wariancja zmiennej losowej T – miara rozrzutu
{ }
[
]
∫
∫
∫
∞
∞
∞
=
−
=
⋅
=
θ
=
0
0
0
dt
)
t
(
R
dt
)
t
(
F
1
dt
)
t
(
f
t
T
E
9.
Wariancja zmiennej losowej T – miara rozrzutu
wokół warto
ś
ci oczekiwanej
10.
Odchylenie standardowe
{ }
∫
∞
θ
−
=
0
2
dt
)
t
(
f
)
t
(
T
V
{ }
{ }
T
V
dt
)
t
(
f
)
t
(
T
0
2
=
θ
−
=
σ
∫
∞

Miary niezawodności
11.
Kwantyl t
p
zmiennej losowej T – jest chwil
ą
, dla
której dystrybuanta F(t) osi
ą
ga warto
ść
p,
zatem jest rozwi
ą
zaniem równania:
{ }
p
t
F
p
=
Interpretacja geometryczna kwantyla
t
F(T)
t
P
p
Typowe rozkłady czasów zdatności
W teorii i praktyce niezawodno
ś
ci obiektów technicznych
rozwa
ż
a
si
ę
szereg
typowych
rozkładów
prawdopodo-
bie
ń
stw, jakie przyjmuje si
ę
dla czasów zdatno
ś
ci obiektów:
1. Rozkład wykładniczy
0
t
,
e
1
)
t
(
F
t
≥
−
=
λ
−
0
t
,
e
)
t
(
R
t
≥
=
λ
−
0
t
,
e
)
(
R
t
≥
=
τ
λτ
−
{ }
=
1
T
E
{ }
2
1
0
t
,
e
)
t
(
R
t
≥
=
λ
−
0
t
,
e
)
t
(
f
t
≥
λ
=
λ
−
0
t
,
)
t
(
≥
λ
=
λ
t
t
,
t
)
t
(
≥
λ
=
Λ
{ }
λ
=
1
T
E
{ }
2
1
T
V
λ
=
{ }
λ
=
σ
1
T
Uwaga: prosz
ę
zapozna
ć
si
ę
z podstawowymi rozkładami czasów
zdatno
ś
ci ze skryptu Korzana. Pomija
ć
dalej b
ę
dziemy fakt,
ż
e t
≥≥≥≥
0
dla charakterystyk czasowych.
( )
s
s
f
+
λ
λ
=
∗
transformata Laplace’a
g
ę
sto
ś
ci zmiennej losowej
Typowe rozkłady czasów zdatności
2. Rozkład Erlanga n-tego rz
ę
du z parametrem
λλλλ
1
0
(
)
( )
1
,
0
!
i
n
t
i
t
F t
e
t
i
λ
λ
−
−
=
= −
≥
∑
{ }
λ
=
θ
=
n
T
E
{ }
2
n
T
V
λ
=
1
0
(
)
( )
!
i
n
t
i
t
R t
e
i
λ
λ
−
−
=
=
∑
1)!
-
(n
(n)
,
e
)
n
(
t
)
t
(
f
t
1
n
n
=
Γ
Γ
λ
=
λ
−
−
{ }
λ
=
σ
n
T
0
!
i
i
=
( )
n
s
s
f
+
λ
λ
=
∗
1
1
1
0
(
)
( )
( )
!
n n
i
n
i
t
t
t
n
i
λ
λ
λ
−
−
−
=
=
Γ
∑
Typowe rozkłady czasów zdatności
3. Rozkład gamma z parametrami
αααα
i
λλλλ
dx
e
x
)
n
(
1
)
t
(
F
t
0
x
1
∫
λ
−
−
α
α
λ
Γ
=
{ }
λ
α
=
θ
=
T
E
dx
e
x
)
n
(
1
)
t
(
R
t
x
1
∫
∞
λ
−
−
α
α
λ
Γ
=
dx
e
x
)
(
0
x
1
∫
∞
−
−
α
=
α
Γ
t
1
e
)
(
t
)
t
(
f
λ
−
−
α
α
α
Γ
λ
=
{ }
2
T
V
λ
α
=
{ }
λ
α
=
σ
T
( )
α
∗
+
λ
λ
=
s
s
f
dx
e
x
e
t
)
t
(
t
x
1
t
1
∫
∞
λ
−
−
α
λ
−
−
α
=
λ
)
n
(
t
∫
Γ
Typowe rozkłady czasów zdatności
4. Rozkład Weibulla (
αααα
,
ββββ
)
α
β
−
−
=
t
e
1
)
t
(
F
α
β
−
−
α
αβ
=
t
1
e
t
)
t
(
f
α
β
−
=
t
e
)
t
(
R
5. Rozkład Rayleigha (
λλλλ
)
2
t
e
1
)
t
(
F
λ
−
−
=
2
t
te
2
)
t
(
f
λ
−
λ
=
2
t
e
)
t
(
R
λ
−
=
1
t
)
t
(
−
α
αβ
=
λ
α
β
=
Λ
t
)
t
(
{ }
α
−
β
α
+
Γ
=
1
)
1
1
(
T
E
te
2
)
t
(
f
λ
=
t
2
)
t
(
λ
=
λ
{ }
λ
π
=
2
1
T
E
2
t
)
t
(
λ
=
Λ
{ }
λ
π
−
=
4
4
T
V
Typowe rozkłady czasów zdatności
6. Rozkład normalny z parametrami (m,
σσσσ
)
(
)
dx
e
2
1
)
t
(
F
t
2
m
x
2
2
∫
∞
−
σ
−
−
π
σ
=
{ }
m
T
E
=
θ
=
{ }
2
T
V
σ
=
{ }
σ
=
σ
T
(
)
dx
e
2
1
)
t
(
R
t
2
m
x
2
2
∫
∞
σ
−
−
π
σ
=
(
)
2
2
2
m
x
e
2
1
)
t
(
f
σ
−
−
π
σ
=
2
t
∫
π
σ
(
)
(
)
1
t
2
m
x
2
m
x
dx
e
e
)
t
(
2
2
2
2
−
∞
σ
−
−
σ
−
−
=
λ
∫
Uwaga:
rozkład ten stosowa
ć
mo
ż
na jedynie wtedy, gdy m>3
σσσσ
. Wtedy
ujemne warto
ś
ci realizacji zmiennej losowej praktycznie nie wyst
ę
puj
ą
.
W innym przypadku stosujemy rozkład normalny uci
ę
ty w zerze.

Typowe rozkłady czasów zdatności
7.Rozkład normalny uci
ę
ty w zerze (m,
σσσσ
)
We
ź
my pod uwag
ę
rozkład warunkowy zmiennej losowej X,
o rozkładzie normalnym z dystrybuant
ą
F
X
(x), przy czym
warunek ten jest nast
ę
puj
ą
cy: X>0. Wtedy
{
} {
}
{
}
)
0
(
F
1
)
0
(
F
)
t
(
F
0
X
P
t
X
0
P
0
X
/
t
X
P
X
X
−
−
=
≥
≤
≤
=
≥
<
Taka
dystrybuanta
spełnia
warunki
dystrybuanty
czasu
zdatno
ś
ci T, a rozkład T nazywa si
ę
rozkładem normalnym
uci
ę
tym w zerze
{
}
)
0
(
F
1
0
X
P
X
−
≥
0
t
,
)
0
(
F
1
)
0
(
F
)
t
(
F
)
t
(
F
X
X
X
≥
−
−
=
Typowe rozkłady czasów zdatności
Je
ś
li przyjmiemy,
ż
e
to otrzymujemy dalej
8.
Rozkład mieszaniny
Je
ś
li mamy n dystrybuant F
k
(t) oraz prawdo-podobie
ń
stwa p
i
c
1
)
0
(
F
1
X
=
−
[
]
)
0
(
F
)
t
(
F
c
)
t
(
F
X
X
−
=
)
t
(
cf
)
t
(
f
X
=
)
t
(
cR
)
t
(
R
X
=
)
t
(
c
)
t
(
X
λ
=
λ
Je
ś
li mamy n dystrybuant F
k
(t) oraz prawdo-podobie
ń
stwa p
i
takie,
ż
e
to mieszanin
ą
zmiennych losowych nazywa si
ę
zmienn
ą
losow
ą
T o dystrybuancie F(t)
1
p
n
1
k
k
=
∑
=
)
t
(
F
p
)
t
(
F
k
n
1
k
k
∑
=
=
)
t
(
f
p
)
t
(
f
k
n
1
k
k
∑
=
=
)
t
(
R
p
)
t
(
f
p
)
t
(
k
n
1
k
k
k
n
1
k
k
∑
∑
=
=
=
λ
)
t
(
R
p
)
t
(
R
k
n
1
k
k
∑
=
=
Seria: Informatyka
Elementy teorii niezawodności
Wykład 3
Obiekty proste odnawialne
z zerowym czasem odnowy
z zerowym czasem odnowy
dr hab. in
ż
. Tadeusz Nowicki prof. nadzw. WAT
e-mail:tadeusz.nowicki@wat.edu.pl, tel. 6-837118
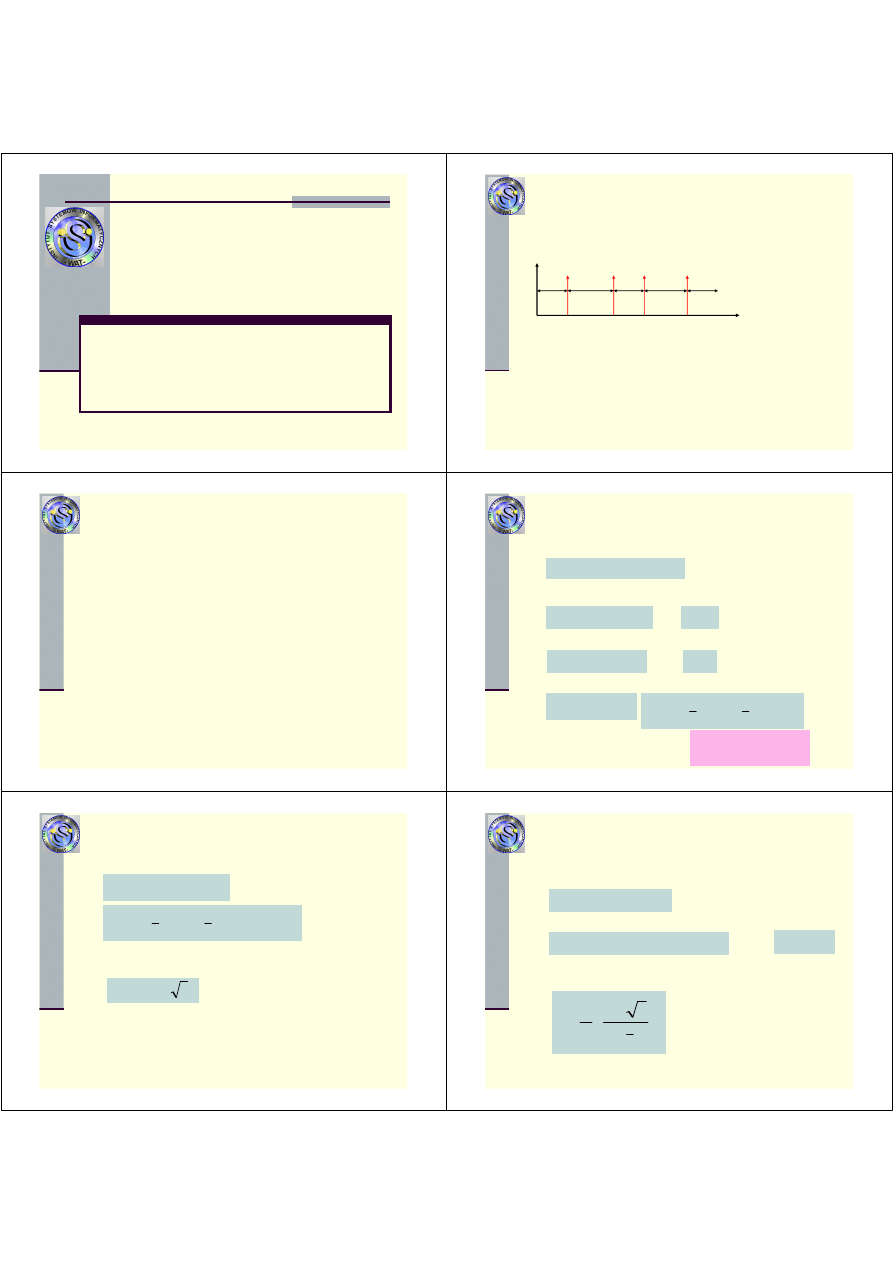
Model niezawodnościowy
Jedynymi istotnymi zdarzeniami w eksploatacji obiektu
prostego
odnawialnego
z
zerowa
odnow
ą
s
ą
chwile
uszkodze
ń
, które przy zerowej odnowie, s
ą
jednocze
ś
nie
chwilami odnów.
T
1
T
2
T
3
T
4
T
5
Ci
ą
g zmiennych losowych T
1
, T
2
, T
3
, ... stanowi
ą
cy strumie
ń
odnów jest modelem niezawodno
ś
ciowym obiektu prostego
odnawialnego z zerowym czasem odnowy. Zmienne T
i
s
ą
ci
ą
głymi i dodatnimi
zmiennymi losowymi oznaczaj
ą
cymi
czasy pomi
ę
dzy kolejnymi uszkodzeniami (jednocze
ś
nie
odnowami)
obiektu,
zatem
czas
do
jego
uszkodzenia.
Charakterystyki tych zmiennych losowych s
ą
zatem
miarami
niezawodno
ś
ciowymi
obiektu.
t
Strumienie odnów
Strumienie odnów dzielimy na:
Proste:
wszystkie zmienne losowe T
1
, T
2
, T
3
, ... maj
ą
identyczne
rozkłady okre
ś
lone dystrybuant
ą
F(t), g
ę
sto
ś
ci
ą
f(t), transformat
ą
Laplace’a f*(s), warto
ś
ci
ą
oczekiwan
ą
θθθθ
oraz
odchyleniem standardowym
σσσσ
.
Ogólne:
wszystkie zmienne losowe T
2
, T
3
, T
4
, ... maj
ą
identyczne rozkłady okre
ś
lone dystrybuant
ą
F(t), g
ę
sto
ś
ci
ą
identyczne rozkłady okre
ś
lone dystrybuant
ą
F(t), g
ę
sto
ś
ci
ą
f(t), transformat
ą
Laplace’a f*(s), warto
ś
ci
ą
oczekiwan
ą
θθθθ
oraz
odchyleniem standardowym
σσσσ
, natomiast dopuszczamy,
ż
e
pierwsza zmienna losowa T
1
ma inny rozkład
okre
ś
lony
dystrybuant
ą
F
1
(t), g
ę
sto
ś
ci
ą
f
1
(t), transformat
ą
Laplace’a
f
1
*(s),
warto
ś
ci
ą
oczekiwan
ą
θθθθ
1
oraz
odchyleniem
standardowym
σσσσ
1
.
Miary niezawodności
1.
Czas S
r
do r-tej odnowy (uszkodzenia) – zmienna losowa
spełniaj
ą
ca:
Jej dystrybuanta wyznaczana jest na podstawie
r
3
2
1
r
T
...
T
T
T
S
+
+
+
+
=
{ }
)
s
(
K
L
)
t
(
K
r
1
r
∗
−
=
)
s
(
K
r
∗
- transformata Laplace’a
dystrybuanty
a g
ę
sto
ść
gdzie dla strumienia prostego
{ }
)
s
(
k
L
)
t
(
k
r
1
r
∗
−
=
)
s
(
k
r
∗
- transformata Laplace’a
g
ę
sto
ś
ci
( )
)
s
(
f
)
s
(
k
r
r
∗
∗
=
( )
)
s
(
f
s
1
)
s
(
k
s
1
)
s
(
K
r
r
r
∗
∗
∗
=
=
Uwaga: transformata Laplace’a funkcji g(x):
∫
∞
∞
−
−
∗
=
dx
e
)
x
(
g
)
s
(
g
sx
Miary niezawodności
a dla strumienia ogólnego:
dla czasów odpowiednio du
ż
ych (t
→∞
→∞
→∞
→∞
) zmienna losowa
( )
)
s
(
f
)
s
(
f
)
s
(
k
1
r
1
r
−
∗
∗
∗
=
( )
)
s
(
f
)
s
(
f
s
1
)
s
(
k
s
1
)
s
(
K
1
r
1
r
r
−
∗
∗
∗
∗
=
=
dla czasów odpowiednio du
ż
ych (t
→∞
→∞
→∞
→∞
) zmienna losowa
S
r
d
ąż
y do rozkładu normalnego
(
)
r
,
r
N
⋅
σ
θ
⋅
Miary niezawodności
2.
Proces stochastyczny N(t) – liczba odnowie
ń
do chwili t
Mo
ż
na pokaza
ć
,
ż
e
i po elementarnych przekształceniach
gdzie
( )
{
} {
}
t
S
r
t
N
r
>
≡
<
( )
{
}
)
t
(
K
)
t
(
K
r
t
N
P
1
r
r
+
−
=
=
1
)
t
(
K
0
≡
Mo
ż
na pokaza
ć
,
ż
e dla du
ż
ych t (odpowiednio du
ż
a liczba
odnowie
ń
) proces N(t) d
ąż
y do
( )
{
}
)
t
(
K
)
t
(
K
r
t
N
P
1
r
r
+
−
=
=
0
t
,
t
N
2
3
θ
⋅
σ
θ

Miary niezawodności
3.
Funkcja odnowy H(t) – oczekiwana liczba odnowie
ń
do
chwili t
oraz
( )
{ }
t
N
E
)
t
(
H
=
( )
{
}
∑
∑
∑
∞
=
∞
=
∞
=
=
+
=
=
=
⋅
=
2
r
r
1
1
r
r
0
r
)
t
(
K
)
t
(
F
)
t
(
K
r
t
N
P
r
)
t
(
H
ale
gdzie
- splot funkcji K
r
(t) i f(t)
∑
∞
=
+
+
=
1
r
1
r
1
)
t
(
K
)
t
(
F
∫
⊗
=
τ
τ
τ
−
=
+
t
0
r
r
1
r
)
t
(
f
K
d
)
(
f
)
t
(
K
)
t
(
K
)
t
(
f
K
r
⊗
Miary niezawodności
Zatem
Z twierdzenia o splocie funkcji otrzymujemy:
równanie odnowy
)
s
(
f
)
s
(
H
(s)
F
)
s
(
H
∗
∗
∗
∗
⋅
+
=
[
]
)
t
(
f
)
t
(
H
)
t
(
F
)
t
(
f
)
t
(
K
)
t
(
F
)
t
(
H
1
1
r
r
1
⊗
+
=
⊗
+
=
∑
∞
=
równanie odnowy
St
ą
d otrzymujemy
dla strumienia ogólnego
dla strumienia prostego
)
s
(
f
)
s
(
H
(s)
F
)
s
(
H
1
⋅
+
=
)
s
(
f
1
(s)
f
s
1
)
s
(
f
1
(s)
F
)
s
(
H
1
1
∗
∗
∗
∗
∗
−
=
−
=
)
s
(
f
1
(s)
f
s
1
)
s
(
f
1
(s)
F
)
s
(
H
∗
∗
∗
∗
∗
−
=
−
=
Miary niezawodności
oraz dalej
4.
G
ę
sto
ść
odnowy h(t)
( )
t
H
dt
d
)
t
(
h
=
{ }
)
s
(
H
L
)
t
(
H
1
∗
−
=
Mo
ż
na pokaza
ć
,
ż
e
dla strumienia ogólnego
dla strumienia prostego
dt
)
s
(
f
1
(s)
f
)
s
(
h
1
∗
∗
∗
−
=
)
s
(
f
1
(s)
f
)
s
(
h
∗
∗
∗
−
=
Miary niezawodności
Mo
ż
na pokaza
ć
,
ż
e dla du
ż
ych t zachodz
ą
twierdzenia
zatem dla du
ż
ych t
Tw. Blackwella
θ
=
∞
→
1
t
)
t
(
H
lim
t
θ
=
t
)
t
(
H
[
]
θ
α
=
−
α
+
∞
→
)
t
(
H
)
t
(
H
lim
t
dla du
ż
ych t oczekiwana liczba odnów w przedziale (t,t+
αααα
) nie
zale
ż
y od t.
Tw. Smitha
Gdy g(x) jest nierosn
ą
c
ą
funkcj
ą
monotoniczn
ą
i całkowaln
ą
w przedziale (0,
∞
∞
∞
∞
), to
w
ę
złowe
twierdzenie
odnowy
θ
∞
→
t
∫
∫
∞
∞
→
θ
=
−
0
t
0
t
du
)
u
(
g
1
dx
)
x
(
h
)
x
t
(
g
lim
Miary niezawodności
5.
P(t,t+
ττττ
) – prawdopodobie
ń
stwo tego,
ż
e w przedziale
(t,t+
ττττ
) nie b
ę
dzie uszkodzenia
a dla du
ż
ych t (korzystaj
ą
c z tw. Smitha) otrzymujemy
[
]
∫
−
τ
+
−
+
τ
+
−
=
τ
+
t
0
1
dx
)
x
(
h
)
x
t
(
F
1
)
t
(
F
1
)
t
,
t
(
P
a dla du
ż
ych t (korzystaj
ą
c z tw. Smitha) otrzymujemy
charakterystyk
ę
graniczn
ą
[
]
∫
∞
τ
∞
→
−
θ
=
τ
+
=
τ
dy
)
y
(
F
1
1
)
t
,
t
(
P
lim
)
(
P
t
Miary niezawodności
6.
Pozostały czas zdatno
ś
ci
ξξξξ
t
– je
ś
li od ostatniej odnowy (r-tej)
min
ą
ł czas t, to ta zmienna losowa jest resztowym czasem do
kolejnej odnowy (r+1-szej)
Mo
ż
na pokaza
ć
,
ż
e
a jej dystrybuanta
t
S
1
r
t
−
=
ξ
+
{ } (
)
τ
+
=
ξ
t
,
t
P
P
t
a jej dystrybuanta
Przy du
ż
ych t mamy
a warto
ść
oczekiwana
(
)
[
]
∫
−
τ
+
−
+
τ
+
−
=
τ
+
=
τ
ξ
t
0
1
dx
)
x
(
h
)
x
t
(
F
1
)
t
(
F
1
t
,
t
P
)
(
F
t
[
]
∫
τ
ξ
θ
=
τ
0
dy
)
y
(
R
1
)
(
F
θ
σ
+
θ
=
τ
τ
=
ξ
∫
∞
2
2
d
)
(
P
)
(
E
2
0
Seria: Informatyka
Elementy teorii niezawodności
Wykład 4
Obiekty proste odnawialne
z niezerowym czasem odnowy
z niezerowym czasem odnowy
dr hab. in
ż
. Tadeusz Nowicki prof. nadzw. WAT
e-mail:tadeusz.nowicki@wat.edu.pl, tel. 6-837118
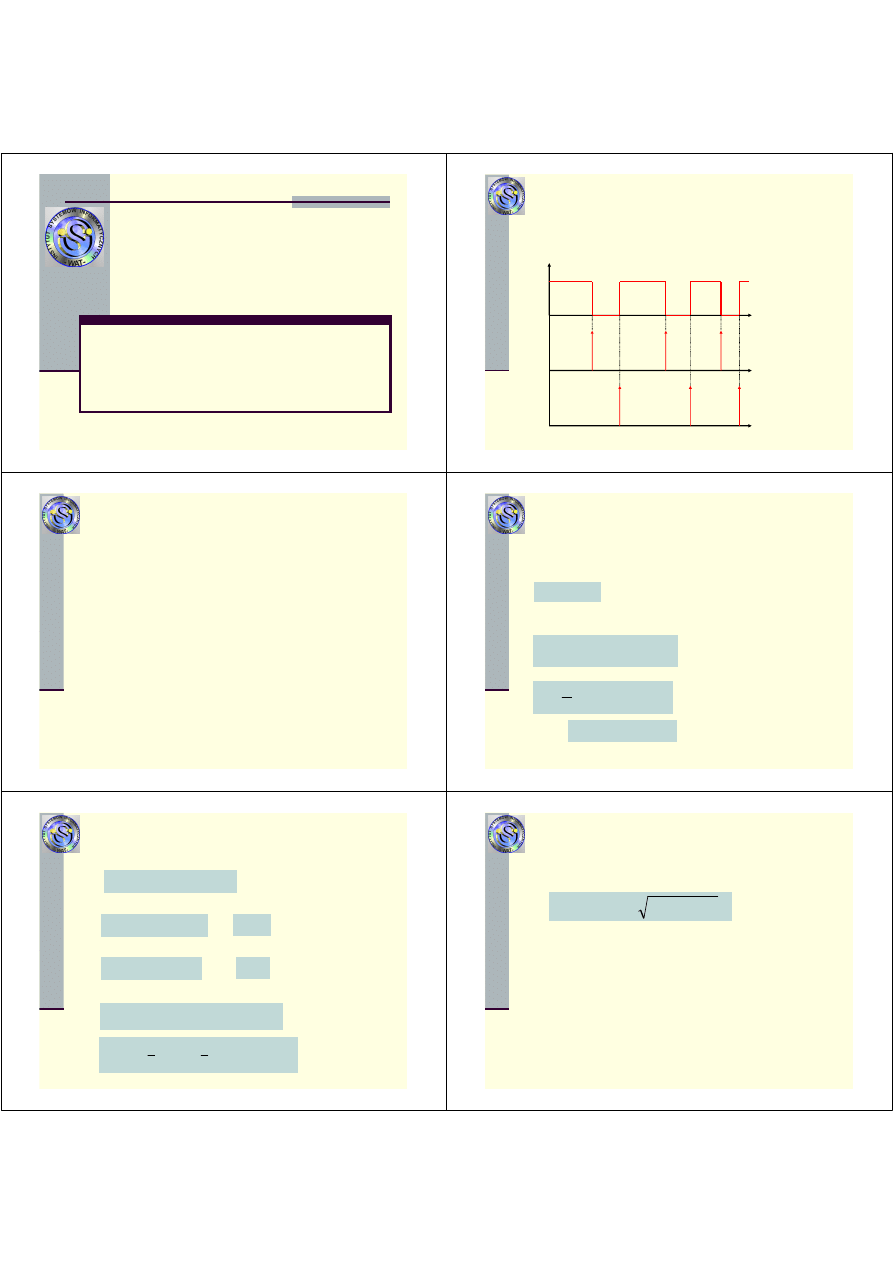
Model niezawodnościowy
Jedynymi istotnymi zdarzeniami w eksploatacji obiektu
prostego odnawialnego z niezerowa odnow
ą
s
ą
chwile
uszkodze
ń
i chwile odnowie
ń
, które przy niezerowej odnowie,
s
ą
chwilami ró
ż
nymi.
T
1
T
2
T
3
T
4
1
0
ηηηη
1
ηηηη
2
ηηηη
3
X(t)
t
0
ηηηη
1
ηηηη
2
ηηηη
3
N
1
(t)
N
2
(t)
strumie
ń
uszkodze
ń
strumie
ń
odnowie
ń
Model niezawodnościowy
Naprzemienny ci
ą
g zmiennych losowych:
T
1
,
ηηηη
1
, T
2
,
ηηηη
2
, T
3
,
ηηηη
3
, ...
czasów poprawnej pracy i czasów
odnów obiektów jest modelem niezawodno
ś
ciowym
obiektu prostego odnawialnego z niezerowym czasem
odnowy.
Zmienne T
i
s
ą
zmiennymi losowymi oznaczaj
ą
cymi
kolejne czasy poprawnej pracy obiektu okre
ś
lone
dystrybuant
ą
F(t), g
ę
sto
ś
ci
ą
f(t), transformat
ą
Laplace’a
kolejne czasy poprawnej pracy obiektu okre
ś
lone
dystrybuant
ą
F(t), g
ę
sto
ś
ci
ą
f(t), transformat
ą
Laplace’a
f*(s),
warto
ś
ci
ą
oczekiwan
ą
θθθθ
1
oraz
odchyleniem
standardowym
σσσσ
1
.
Zmienne
ηηηη
i
s
ą
zmiennymi losowymi oznaczaj
ą
cymi
kolejne czasy odnów obiektu okre
ś
lone dystrybuant
ą
G(t),
g
ę
sto
ś
ci
ą
g(t),
transformat
ą
Laplace’a
g*(s),
warto
ś
ci
ą
oczekiwan
ą
θθθθ
2
oraz
odchyleniem
standardowym
σσσσ
2
.
Charakterystyki tych zmiennych losowych s
ą
zatem
miarami niezawodno
ś
ciowymi
obiektu.
Zmienna losowa
ττττ
Załó
ż
my,
ż
e zmienna losowa
ττττ
r
jest sum
ą
zmiennych
losowych oznaczaj
ą
cych czas poprawnej r-tej pracy obiektu i
czas r-tej odnowy obiektu.
Zmienne losowe
ττττ
1
,
ττττ
2
,
ττττ
3
, ... maj
ą
identyczny rozkład
o dystrybuancie
r
r
r
T
η
+
=
τ
o dystrybuancie
i g
ę
sto
ś
ci
zatem
{
}
∫
−
=
<
τ
=
Φ
t
0
r
dx
)
x
(
g
)
x
t
(
F
t
P
)
t
(
∫
−
=
Φ
=
ϕ
t
0
dx
)
x
(
g
)
x
t
(
f
)
t
(
dt
d
)
t
(
)
s
(
g
)
s
(
f
)
s
(
∗
∗
∗
⋅
=
ϕ
Miary procesu odnowień N
2
(t)
1.
Czas t
”
r
do r-tej odnowy– zmienna losowa spełniaj
ą
ca:
Jej dystrybuanta wyznaczana jest na podstawie
a g
ę
sto
ść
r
3
2
1
"
r
...
t
τ
+
+
τ
+
τ
+
τ
=
{
}
)
s
(
L
)
t
(
r
1
r
∗
−
Φ
=
Φ
)
s
(
r
∗
Φ
- transformata Laplace’a
dystrybuanty
a g
ę
sto
ść
gdzie
{ }
)
s
(
L
)
t
(
r
1
r
∗
−
ϕ
=
ϕ
)
s
(
r
∗
ϕ
- transformata Laplace’a
g
ę
sto
ś
ci
( ) (
)
)
s
(
g
)
s
(
f
)
s
(
)
s
(
r
r
r
∗
∗
∗
∗
⋅
=
ϕ
=
ϕ
(
)
)
s
(
g
)
s
(
f
s
1
)
s
(
s
1
)
s
(
r
r
r
∗
∗
∗
∗
⋅
=
ϕ
=
Φ
Miary procesu odnowień N
2
(t)
dla czasów odpowiednio du
ż
ych (t
→∞
→∞
→∞
→∞
) zmienna losowa
t
”
r
d
ąż
y do rozkładu normalnego
(
)
(
)
(
)
r
,
r
N
2
2
2
1
2
1
⋅
σ
+
σ
θ
+
θ
⋅

Miary procesu odnowień N
2
(t)
2.
Proces stochastyczny N
2
(t) – liczba odnowie
ń
do chwili t
Mo
ż
na pokaza
ć
,
ż
e
Mo
ż
na pokaza
ć
,
ż
e dla du
ż
ych t (odpowiednio du
ż
a liczba
odnowie
ń
) proces N
2
(t) d
ąż
y do
( )
{
}
)
t
(
)
t
(
r
t
N
P
1
r
r
2
+
Φ
−
Φ
=
=
odnowie
ń
) proces N
2
(t) d
ąż
y do
(
)
(
)
t
,
t
N
2
3
2
1
2
2
2
1
2
1
θ
+
θ
⋅
σ
+
σ
θ
+
θ
Miary procesu odnowień N
2
(t)
3.
Funkcja odnowy H
2
(t) – oczekiwana liczba
odnowie
ń
do chwili t
oraz
( )
{
}
t
N
E
)
t
(
H
2
2
=
(s)
g
(s)
f
1
)
s
(
H
∗
∗
∗
⋅
⋅
=
{ }
)
s
(
H
L
)
t
(
H
1
∗
−
=
4.
G
ę
sto
ść
odnowy h
2
(t)
(s)
g
)
s
(
f
1
s
)
s
(
H
2
∗
∗
∗
⋅
−
⋅
=
(s)
g
)
s
(
f
1
(s)
g
(s)
f
)
s
(
h
2
∗
∗
∗
∗
∗
⋅
−
⋅
=
{ }
)
s
(
H
L
)
t
(
H
2
1
2
∗
−
=
{ }
)
s
(
h
L
)
t
(
h
2
1
2
∗
−
=
Miary procesu uszkodzeń N
1
(t)
5.
Czas t
’
r
do r-tego uszkodzenia– zmienna losowa spełnia:
Jej dystrybuanta wyznaczana jest na podstawie
a g
ę
sto
ść
r
3
2
1
'
r
...
T
t
τ
+
+
τ
+
τ
+
=
{
}
)
s
(
L
)
t
(
r
1
r
∗
−
Ψ
=
Ψ
)
s
(
r
∗
Ψ
- transformata Laplace’a
dystrybuanty
a g
ę
sto
ść
gdzie
{ }
)
s
(
L
)
t
(
r
1
r
∗
−
ψ
=
ψ
)
s
(
r
∗
ψ
- transformata Laplace’a
g
ę
sto
ś
ci
(
)
)
s
(
g
)
s
(
f
)
s
(
f
)
s
(
1
r
r
−
∗
∗
∗
∗
⋅
=
ψ
(
)
)
s
(
g
)
s
(
f
)
s
(
f
s
1
)
s
(
s
1
)
s
(
1
r
r
r
−
∗
∗
∗
∗
∗
⋅
=
ψ
=
Ψ
Miary procesu uszkodzeń N
1
(t)
dla czasów odpowiednio du
ż
ych (t
→∞
→∞
→∞
→∞
) zmienna losowa
t
’
r
d
ąż
y do rozkładu normalnego
(
)
(
)
(
)
r
,
r
N
2
2
2
1
2
1
⋅
σ
+
σ
θ
+
θ
⋅
Miary procesu uszkodzeń N
1
(t)
6.
Proces stochastyczny N
1
(t) – liczba uszkodze
ń
do chwili t
Mo
ż
na pokaza
ć
,
ż
e
Mo
ż
na pokaza
ć
,
ż
e dla du
ż
ych t (odpowiednio du
ż
a liczba
odnowie
ń
) proces N
1
(t) d
ąż
y do
( )
{
}
)
t
(
)
t
(
r
t
N
P
1
r
r
1
+
Ψ
−
Ψ
=
=
odnowie
ń
) proces N
1
(t) d
ąż
y do
(
)
(
)
t
,
t
N
2
3
2
1
2
2
2
1
2
1
θ
+
θ
⋅
σ
+
σ
θ
+
θ
Miary procesu uszkodzeń N
1
(t)
7.
Funkcja odnowy H
1
(t) – oczekiwana liczba
uszkodze
ń
do chwili t
oraz
( )
{
}
t
N
E
)
t
(
H
1
1
=
(s)
f
1
)
s
(
H
∗
∗
⋅
=
{ }
)
s
(
H
L
)
t
(
H
1
∗
−
=
8.
G
ę
sto
ść
odnowy h
1
(t)
(s)
g
)
s
(
f
1
s
)
s
(
H
1
∗
∗
∗
⋅
−
⋅
=
(s)
g
)
s
(
f
1
(s)
f
)
s
(
h
1
∗
∗
∗
∗
⋅
−
=
{ }
)
s
(
H
L
)
t
(
H
1
1
1
∗
−
=
{ }
)
s
(
h
L
)
t
(
h
1
1
1
∗
−
=

Miary niezawodności łączne dla strumieni
9.
Współczynnik gotowo
ś
ci k
g
(t) - prawdopodobie
ń
stwo
poprawnej pracy obiektu w chwili t
Mo
ż
na pokaza
ć
,
ż
e
{
}
1
)
t
(
X
P
)
t
(
k
g
=
=
[
]
∫
−
−
+
−
=
t
2
g
du
)
u
t
(
F
1
)
u
(
h
)
t
(
F
1
)
t
(
k
Stosuj
ą
c przekształcenie Laplace’a
lub
i oczywi
ś
cie:
∫
0
[
][
]
(s)
g
)
s
(
f
1
(s)
f
1
s
1
)
s
(
h
1
)
s
(
f
1
s
1
)
s
(
k
2
g
∗
∗
∗
∗
∗
∗
⋅
−
−
⋅
=
−
−
=
s
1
)
s
(
H
)
s
(
H
)
s
(
k
1
2
g
+
−
=
∗
∗
∗
{ }
)
s
(
k
L
)
t
(
k
g
1
g
∗
−
=
Miary niezawodności łączne dla strumieni
Zatem
Dla du
ż
ych t otrzymujemy:
[
]
∫
∞
∞
→
−
⋅
θ
+
θ
=
=
g
t
g
du
)
u
(
F
1
1
)
t
(
k
lim
K
1
)
t
(
H
)
t
(
H
)
t
(
k
1
2
g
+
−
=
ale
zatem
[
]
∫
∞
→
−
⋅
θ
+
θ
=
=
0
2
1
g
t
g
du
)
u
(
F
1
)
t
(
k
lim
K
[
]
1
0
du
)
u
(
F
1
θ
=
−
∫
∞
2
1
1
g
K
θ
+
θ
θ
=
Miary niezawodności łączne dla strumieni
10.
P(t,t+
ττττ
) – prawdopodobie
ń
stwo tego,
ż
e w przedziale
(t,t+
ττττ
) nie b
ę
dzie uszkodzenia
a dla du
ż
ych t (korzystaj
ą
c z tw. Smitha) otrzymujemy
[
]
∫
−
τ
+
−
+
τ
+
−
=
τ
+
t
0
2
dx
)
x
t
(
F
1
)
x
(
h
)
t
(
F
1
)
t
,
t
(
P
a dla du
ż
ych t (korzystaj
ą
c z tw. Smitha) otrzymujemy
charakterystyk
ę
graniczn
ą
[
]
∫
∞
τ
∞
→
θ
+
θ
=
τ
+
=
τ
dy
)
y
(
R
1
)
t
,
t
(
P
lim
)
(
P
2
1
t
Seria: Informatyka
Elementy teorii niezawodności
Wykład 5
Niezawodność systemów
dr hab. in
ż
. Tadeusz Nowicki prof. nadzw. WAT
e-mail:tadeusz.nowicki@wat.edu.pl, tel. 6-837118
{
}
n
i
e
e
e
e
e
E
,...,
,...,
,
,
3
2
1
=
zbiór elementów struktury
niezawodnościowej systemu
{ }
1
,
0
Y
,
X
,
Y
,
X
i
i
=
U
U
Y
X
,
,
S
i
=
ℵ
ℵ
=
n
R
zbiory stanów niezawodnoś-
ciowych elementów i systemu
struktura niezawodnościo-
wa systemu
Przypomnienie
U
U
Y
X
,
,
S
1
i
=
ℵ
ℵ
=
=
i
R
Y
X
...
X
:
)
(
f
R
n
1
(n)
→
×
×
≡
x
wa systemu
Rozpatrujemy systemy o elementach dwustanowych w sensie nieza-
wodności uszkadzających się niezależnie (podejście klasyczne). Zatem
strukturalna funkcja niezawodnościowa systemu ma postać:
{ } { }
1
,
0
1
,
0
:
)
(
f
(n)
→
n
x
Dla elementów i systemu dwustano-
wych w sensie niezawodności
Wyrażenie bulowskie nie zawierające znaku działania negacji nazywane jest
wyrażeniem alternatywno-koniunkcyjnym (wak). Każdą funkcje monotoniczną
(koherentną) można przedstawić za pomocą wak.
Oznaczmy symbolem „
+”
alternatywę, a symbolem „
·”
koniunkcję. Wtedy
przykładem takiej funkcji może być poniższy zapis
4
3
1
2
3
2
1
(4)
x
)
x
x
(
x
x
x
x
(x)
f
+
+
+
=
Każde wak można przedstawić w postaci
formuły alternatywnej
Analityczny zapis struktur niezawodnościowych
Każde wak można przedstawić w postaci
formuły alternatywnej
(sumoiloczyn) lub w postaci
formuły koniunkcyjnej
(iloczyn sum)
4
3
4
1
2
3
2
1
(4)
x
x
x
x
x
x
x
x
(x)
f
+
+
+
=
)
x
x
)(
x
x
(x
)
x
x
x
)(
x
x
(x
(x)
f
4
2
4
2
1
4
3
2
3
2
1
(4)
+
+
+
⋅
⋅
+
+
+
+
=
Minimalną formułą alternatywną
(mfa) funkcji monotonicznej nazywamy
formułę
alternatywną
o
najmniejszej
liczbie
składników
sumy
(nieredukowalną)
(mfa)
x
x
x
x
x
(x)
f
4
3
4
1
2
(4)
+
+
=
Minimalną formułą koniunkcyjną
(mfk) funkcji monotonicznej
Analityczny zapis struktur niezawodnościowych
Minimalną formułą koniunkcyjną
(mfk) funkcji monotonicznej
nazywamy formułę koniunkcyjną o najmniejszej liczbie czynników
(sum)
(mfk)
)
x
x
)(
x
x
(x
(x)
f
4
2
3
2
1
(4)
+
+
+
=
Podzbiór W
⊂
E elementów systemu nazywa się
ś
cieżką zdatności
, jeśli przy
zdatności wszystkich elementów należących do W system jest w stanie zdatności
niezależnie od stanu pozostałych elementów systemu.
Ś
cieżka zdatności jest
minimalną
, jeśli nie zawiera żadnej innej ścieżki zdatności.
Minimalna formuła alternatywna (mfa) określa jednoznacznie zbiór wszystkich
minimalnych ścieżek zdatności - każdemu składnikowi sumy (iloczynowi)
odpowiada wzajemnie jednoznacznie minimalna ścieżka zdatności.
Ścieżki zdatności i cięcia w systemie
Podzbiór C
⊂
E elementów systemu nazywa się
cięciem
(przekrojem), jeśli przy
niezdatności wszystkich elementów należących do C system jest w stanie
niezdatności niezależnie od stanu pozostałych elementów systemu.
Cięcie jest
minimalne
, jeśli nie zawiera żadnych innych cięć.
Minimalna formuła koniunkcyjna (mfk) określa jednoznacznie zbiór wszystkich
minimalnych cięć - każdemu czynnikowi (sumie) odpowiada wzajemnie
jednoznacznie minimalne cięcie.
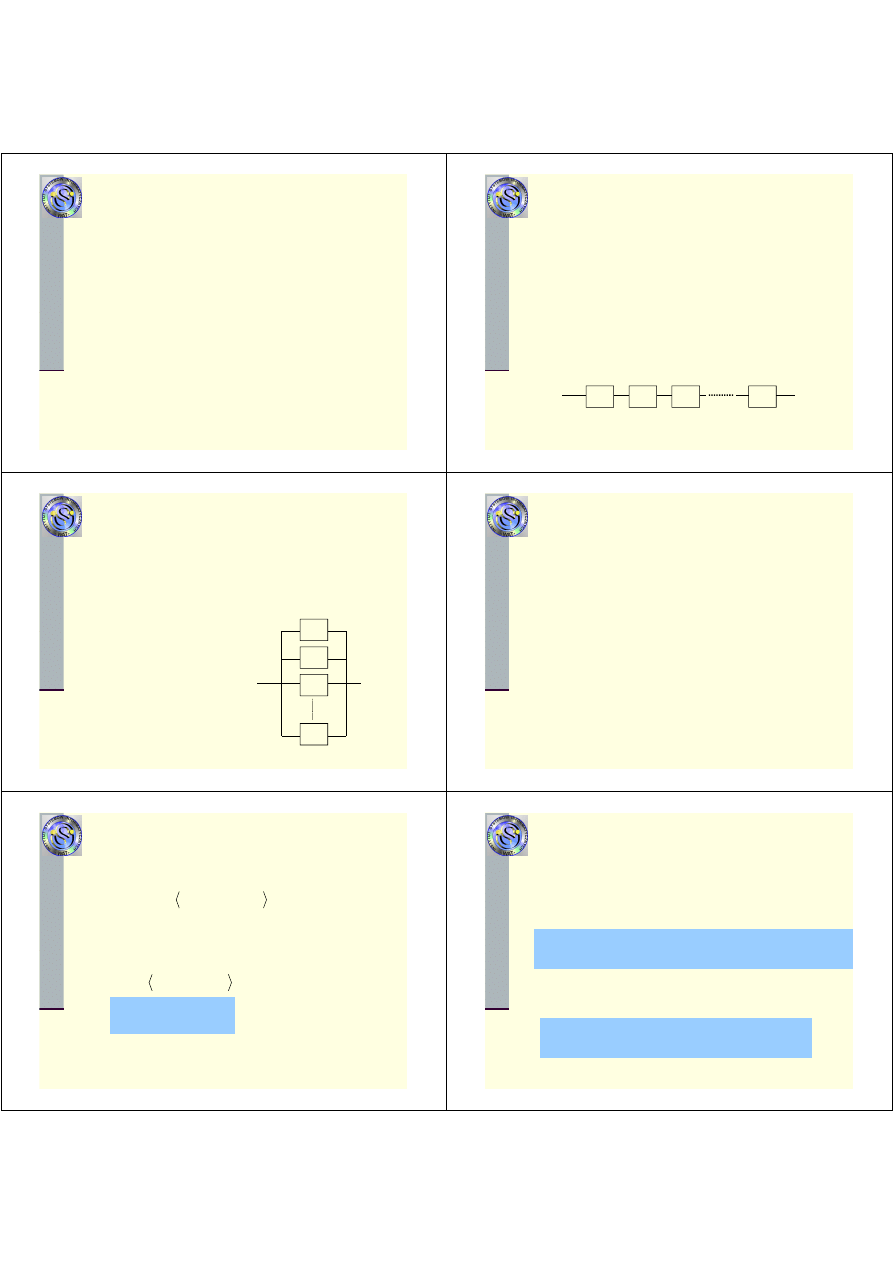
x
1
x
3
x
x
4
Przykład
Ścieżki zdatności i cięcia w systemie
(mfa)
x
x
x
x
x
(x)
f
4
3
4
1
2
(4)
+
+
=
(mfk)
)
x
x
)(
x
x
(x
(x)
f
4
2
3
2
1
(4)
+
+
+
=
x
2
Schemat blokowy struktury niezawodnościowej
Dla każdej struktury monotonicznej (koherentnej) określonej przez f
(n)
(x)
istnieje
dualna
struktura
koherentna
określona
przez
funkcję
monotoniczna f
(n)
D
(x). Wyrażenie bulowskie, określające funkcję dualną
otrzymujemy w ten sposób, że w wyrażeniu bulowskim, określającym
f
(n)
(x)m, zamieniamy wszystkie znaki alternatywy na znaki koniunkcji, a
znaki koniunkcji na znaki alternatywy. Dla funkcji
4
3
1
2
3
2
1
(4)
x
)
x
x
(
x
x
x
x
(x)
f
+
+
+
=
Funkcja dualna ma postać
Struktury dualne
Funkcja dualna ma postać
)
x
x
x
)(
x
)(
x
x
(x
(x)
f
4
3
1
2
3
2
1
(4)
D
+
+
+
=
Z definicji wynika, że mfa funkcji
f
(n)
D
(x)
otrzymujemy bezpośrednio z mfk
funkcji
f
(n)
(x),
a mfk funkcji
f
(n)
D
(x)
bezpośrednio z mfk
f
(n)
(x). Przykład :
)
x
x
)(
x
x
)(
(x
(x)
f
4
3
4
1
2
(4)
D
+
+
=
x
x
x
x
x
(x)
f
4
2
3
2
1
(4)
D
+
=
Wyróżnia
się
niektóre
podstawowe
struktury,
które
mogą
być
podstrukturami bardziej złożonych struktur.
1. Struktura szeregowa
- gdy niezdatność dowolnego elementu struktury
powoduje niezdatność całego systemu
∏
=
=
n
1
i
(n)
x
(x)
f
i
Funkcja dualna dla struktury szeregowej ma postać
Elementarne struktury niezawodnościowe
Funkcja dualna dla struktury szeregowej ma postać
∑
=
=
n
1
i
i
(n)
D
x
(x)
f
Schemat blokowy dla struktury szeregowej ma postać
x
1
x
2
x
3
x
n
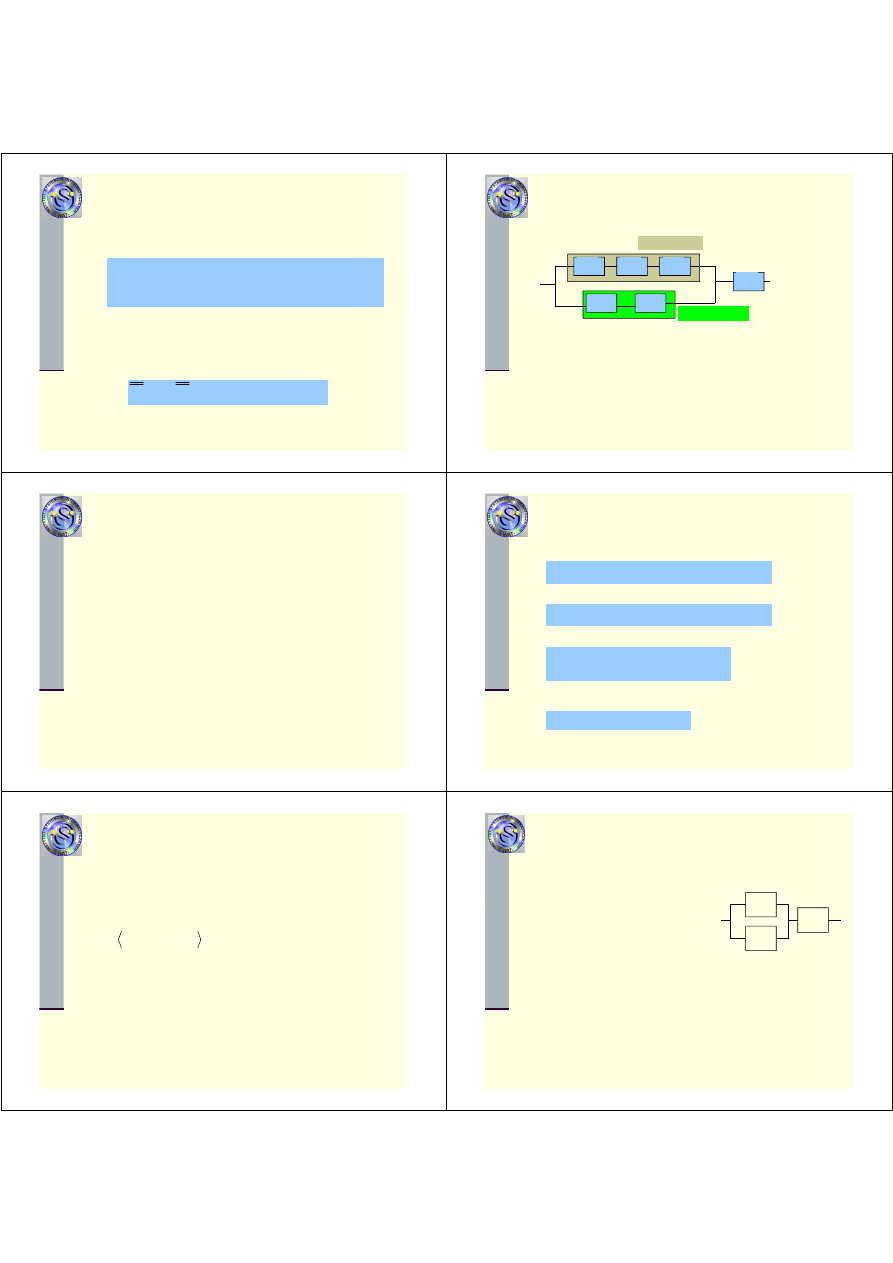
2. Struktura równoległa
- gdy zdatność dowolnego elementu struktury
powoduje zdatność całego systemu
∑
=
=
n
1
i
i
(n)
x
(x)
f
Funkcja dualna dla struktury równoległej ma postać
∏
=
=
n
i 1
i
(n)
D
x
(x)
f
x
1
Elementarne struktury niezawodnościowe
=
i 1
Schemat blokowy dla struktury
równoległej ma postać
x
1
x
2
x
3
x
n
3. Struktury progowe
(tak zwane struktury „k z n”)- gdy zdatność
dowolnych co najmniej
k
elementów struktury powoduje zdatność
całego systemu.
Przykładem może być struktura progowa „2 z 3”
3
2
3
1
2
1
(3)
x
x
x
x
x
x
(x)
f
+
+
=
Funkcja dualna dla tej struktury ma postać
Elementarne struktury niezawodnościowe
)
x
)(x
x
)(x
x
x
(
(x)
f
3
2
3
1
2
1
(3)
D
+
+
+
=
Schemat blokowy dla struktury progowej nie istnieje !
Oznacza to, że nie zawsze można skonstruować schematy blokowe dla
struktur niezawodnościowych.
Uwaga: zauważmy, że
struktura progowa „1 z n” jest strukturą
struktura progowa „n z n” jest strukturą
równoległą
szeregową
Stany
niezawodnościowe
elementów
są
binarnymi
procesami
stochastycznymi x
i
(t). Argument funkcji f
(n)
(x) jest dla ustalonej chwili t
n-wymiarową zmienną losową
n
i
1
X
,...,
X
,...,
X
X
=
To znaczy binarnym wektorem losowym o odpowiednim rozkładzie
prawdopodobieństwa. Oznaczmy
[
]
[
]
1..n
i
,
p
-
1
q
0
X
P
,
p
1
X
P
=
=
=
=
=
=
Probabilistyczny model niezawodnościowy
[
]
[
]
1..n
i
,
p
-
1
q
0
X
P
,
p
1
X
P
i
i
i
i
i
=
=
=
=
=
=
oraz
n
i
1
x
,...,
x
,...,
x
x
=
wektor binarny. Wtedy otrzymujemy
[
]
)
x
-
(1
i
n
1
i
x
i
i
i
q
p
X
P
∏
=
=
=
x
ż
e w ustalonej chwili stany niezawodnościowe elementów są takie, jak
określono to w wektorze x.
co jest prawdopodobieństwem tego,
Stan niezawodnościowy systemu jest bulowską zmienną losową Y,
określoną jako funkcja bulowska wektora losowego X
[
]
[
]
[
]
∑
∏
∑
=
=
=
=
=
=
)
i
x
-
(1
i
n
i
x
i
(n)
q
p
x
X
P
1
(X)
f
P
1
Y
P
(X)
f
Y
(n)
=
Zatem rozkład zmiennej losowej Y jest jednoznacznie określony przez
rozkład wektora losowego X
Probabilistyczny model niezawodnościowy
[
]
[
]
[
]
∑
∏
∑
∈
=
∈
=
=
=
=
=
=
1
X
x
i
1
i
i
1
X
x
q
p
x
X
P
1
(X)
f
P
1
Y
P
Gdzie X
1
jest podzbiorem tych wszystkich wektorów binarnych x, dla
których zachodzi
f
(n)
(x) = 1. Gdy oznaczymy X
0
jako podzbiór tych
wszystkich wektorów binarnych x, dla których zachodzi f
(n)
(x) = 0, to
[
]
[
]
∑
∏
∑
∈
=
∈
−
=
=
−
=
=
0
X
x
)
i
x
-
(1
i
n
1
i
i
x
i
0
X
x
q
p
1
x
X
P
1
1
Y
P
Prawdopodobieństwa p
i
oraz q
i
określone zostały dla wybranej, ustalonej
chwili t. Co zrobić, gdy chcemy znać charakterystyki niezawodnościowe
systemu nie tylko dla ustalonych momentów czasu. Rozpatrzmy poniższe
przypadki.
1. Elementy systemu są elementami prostymi nieodnawialnymi
Wtedy prawdopodobieństwa p
i
oraz q
i
zastępujemy odpowiednio
funkcjami
Probabilistyczny model niezawodnościowy
funkcjami
{
}
t
≥
=
⇒
i
i
i
T
P
(t)
R
p
funkcja niezawodności elementu
prostego nieodnawialnego
{ }
t
〈
=
⇒
i
i
i
T
P
(t)
F
q
dystrybuanta elementu prostego
nieodnawialnego
Wtedy otrzymujemy
[
]
[
]
[
] [ ]
)
x
-
(1
i
X
x
n
1
i
x
i
(n)
i
1
i
(t)
F
(t)
R
1
(X(t))
f
P
1
Y(t)
P
∑
∏
∈
=
⋅
=
=
=
=
2. Elementy systemu są elementami prostymi odnawialnymi
Zauważmy, że muszą być to elementy z niezerową odnową, bo w
przeciwnym przypadku system byłby zawsze w stanie zdatności.Wtedy
prawdopodobieństwa p
i
oraz q
i
zastępujemy odpowiednio funkcjami
{
}
1
(t)
X
P
(t)
k
p
i
i
g
i
=
=
⇒
współczynnik gotowości elementu
odnawialnego z niezerową odnową
{
}
0
(t)
X
P
(t)
k
-
1
q
=
=
⇒
Probabilistyczny model niezawodnościowy
{
}
0
(t)
X
P
(t)
k
-
1
q
i
i
g
i
=
=
⇒
Wtedy otrzymujemy
[
]
[
]
[ ] [
]
)
x
-
(1
i
g
X
x
n
1
i
x
i
g
(n)
i
1
i
(t)
k
1
(t)
k
1
(X(t))
f
P
1
Y(t)
P
−
⋅
=
=
=
=
∑
∏
∈
=
3. Elementy systemu są mieszane, niektóre są elementami prostymi
nieodnawialnymi, a niektóre są elementami prostymi odnawialnymi
Wtedy prawdopodobieństwa p
i
oraz q
i
zastępujemy odpowiednio
Dla elementów nieodnawialnych prostych
{
}
t
≥
=
⇒
i
i
i
T
P
(t)
R
p
{ }
t
〈
=
⇒
T
P
(t)
F
q
Probabilistyczny model niezawodnościowy
{
}
1
(t)
X
P
(t)
k
p
i
i
g
i
=
=
⇒
{
}
0
(t)
X
P
(t)
k
-
1
q
i
i
g
i
=
=
⇒
natomiast dla elementów odnawialnych prostych o niezerowej odnowie
{ }
t
〈
=
⇒
i
i
i
T
P
(t)
F
q
Czy nie będziemy mieli żadnych kłopotów w
wyznaczeniu wartości P{f
(n)
(X(t)) = 1}? Niestety,
będziemy mieli. Wynika to z następującego faktu:
liczności zbiorów X
1
oraz X
0
są olbrzymie
.
Istnieją metody wyznaczania formuł o minimalnej
postaci służące obliczaniu wartości
Obliczanie prawdopodobieństwa zdatności systemu
postaci służące obliczaniu wartości
P{f
(n)
(X(t)) = 1}.
(Przeczytać skrypt Korzana - punkt 6.11).
Warto zauważyć, że można obliczyć takie wartości
dla elementarnych struktur niezawodnościowych i
uogólnić to dla struktur bardziej złożonych.
{
}
{
}
{
}
t
T
,...,
T
,
T
min
P
T
P
(t)
R
n
2
1
s
s
≥
=
≥
=
t
1. Struktury szeregowe (elementy nieodnawialne proste)
Niech T
i
oznacza czas zdatności elementu i-tego, natomiast T
s
oznacza
czas zdatności systemu. Wtedy mamy
{
}
n
1,2,...,
i
,
T
min
T
i
s
=
=
co daje w efekcie
co dla niezależności uszkodzeń elementów powoduje równość powyższego z
Obliczanie prawdopodobieństwa zdatności systemu
co dla niezależności uszkodzeń elementów powoduje równość powyższego z
{
}
{
} {
}
{
}
(t)
R
(t)
R
t
T
P
t
T
t,...,
T
t,
T
P
t
T
,...,
T
,
T
min
P
S
n
1
i
i
n
1
i
i
n
2
1
n
2
1
=
=
≥
=
=
≥
≥
≥
=
≥
∏
∏
=
=
Z kolei dla dystrybuant otrzymujemy formułę postaci
{ }
( )
[
]
∏
=
−
=
〈
=
n
1
i
i
s
s
t
F
-
1
1
t
T
P
(t)
F
{ }
{
}
{
}
t
T
,...,
T
,
T
max
P
T
P
(t)
F
n
2
1
s
s
〈
=
〈
=
t
2. Struktury równoległe (elementy nieodnawialne proste)
Niech T
i
oznacza czas zdatności elementu i-tego, natomiast T
s
oznacza
czas zdatności systemu. Wtedy mamy
{
}
n
1,2,...,
i
,
T
max
T
i
s
=
=
co daje w efekcie
co dla niezależności uszkodzeń elementów powoduje równość powyższego z
Obliczanie prawdopodobieństwa zdatności systemu
co dla niezależności uszkodzeń elementów powoduje równość powyższego z
{
}
{
} {
}
{ }
(t)
F
(t)
F
t
T
P
t
T
t,...,
T
t,
T
P
t
T
,...,
T
,
T
max
P
S
n
1
i
i
n
1
i
i
n
2
1
n
2
1
=
=
〈
=
=
〈
〈
〈
=
〈
∏
∏
=
=
Z kolei dla funkcji niezawodności otrzymujemy formułę postaci
{
}
( )
[
]
∏
=
−
=
≥
=
n
1
i
i
s
s
t
R
-
1
1
t
T
P
(t)
R
{
}
( )
( )
∑ ∑
∏
∏
=
∈
∈
∈
=
≥
=
n
k
i
D
j)
(i,
D
c
D
l
l
c
s
s
t
F
t
R
t
T
P
(t)
R
i
j
3. Struktury progowe (elementy nieodnawialne proste)
Dla przypadku ogólnego struktur progowych musimy obliczyć wszystkie
możliwe kombinacje dla poprawnych co najmniej k elementów z n
możliwych :
Obliczanie prawdopodobieństwa zdatności systemu
gdzie (i,j)
∈
D oznacza wszystkie możliwe kombinacje par (i,j)
spełniające
i+j=n oraz założenie, że i oznacza liczbę elementów
zdatnych, a j liczbę elementów niezdatnych, natomiast zbiory D
i
oraz
D
j
{
}
n
,...,
2
,
1
D
D
,
j
D
,
i
D
j
i
j
i
=
=
=
U
4. Struktury szeregowo-równoległe lub równoległo-szeregowe
Dekomponujemy wtedy cały system na podsystemy szeregowe i równo-
ległe stosując otrzymane formuły. Przykład
x
1
x
2
x
3
x
4
x
5
x
6
Podsystem II
Podsystem I
Obliczanie prawdopodobieństwa zdatności systemu
Podsystem II
Otrzymujemy teraz formuły składowe
))
(t
(t)])(R
R
-
(t)][1
R
-
[1
-
(1
))
(t
(t)(R
R
(t)
R
6
II
I
6
II
-
I
s
=
=
(t)
(t)F
F
(t)
F
II
I
II
-
I
=
(t)
(t)R
(t)R
R
(t)
R
3
2
1
I
=
(t)
(t)R
R
(t)
R
5
4
II
=
)
(t)
R
-
1
(t)
F
:
uwaga
(
II
-
I
II
-
I
=
5. Struktury z elementami prostymi odnawialnymi o niezerowej odnowie
Jeśli pewne elementy (lub nawet wszystkie) są elementami odnawialnymi, to
stosujemy podstawienie
)
(
k
1
(t)
F
,
)
(
k
(t)
R
i
g
i
i
g
i
t
t
−
⇒
⇒
i-te elementy są odnawialne
Ciąg dalszy Przykładu (jeśli elementy o numerach 1, 5 i 6 są odnawialne, to
system jest nieodnawialny (w końcu uszkodzą się elementy 2, 3 oraz 4 i nie będzie
dla dużych t żadnej ścieżki zdatności o zdatnych wszystkich elementach).
Obliczanie prawdopodobieństwa zdatności systemu
dla dużych t żadnej ścieżki zdatności o zdatnych wszystkich elementach).
Podsystemy I i II są obiektami nieodnawialnymi. Zatem system jest nieodna-
wialny i liczymy dla niego charakterystyki (np. R
s
(t) ) jak dla obiektu nieodna-
wialnego
))
(t
(t)])(k
R
-
(t)][1
R
-
[1
-
(1
))
(t
(t)(k
R
(t)
R
6
g
II
I
6
g
II
-
I
s
=
=
(t)
(t)F
F
(t)
F
II
I
II
-
I
=
(t)
(t)R
(t)R
k
(t)
R
3
2
1
g
I
=
(t)
(t)k
R
(t)
R
5
g
4
II
=
W przypadku, gdy mamy do czynienia z identycznymi w sensie rozkładu
elementami ( R(t) = R
i
(t), i=1..n ) to wiele formuł upraszcza się znacznie.
1. Struktury szeregowe o identycznych elementach
( )
(
)
n
S
n
S
F(t)
-
1
1
(t)
F
,
R(t)
(t)
R
−
=
=
2. Struktury równoległe o identycznych elementach
( )
(
)
n
S
n
S
R(t)
-
1
1
(t)
R
,
F(t)
(t)
F
−
=
=
Systemy o jednakowych elementach
3. Struktury progowe
{
}
( )
[ ] ( )
[ ]
∑
=
−
=
≥
=
n
k
i
i
n
i
s
s
t
F
t
R
i
n
t
T
P
(t)
R
Wzór ten dla struktur „n-1 z n” upraszcza się do postaci
( )
[ ]
( )
[ ]
n
1
-
n
s
t
R
1)
-
(n
t
R
n
(t)
R
−
=
Założenia: elementy dwustanowe w sensie niezawodności o wykładniczych
rozkładach czasów poprawnej pracy i odnowy (model Markowa); system
wielostanowy w sensie niezawodności, a jego stany definiowane są stanami
elementów.
Dowolny stan systemu opisany jest stanami jego elementów, czyli wektorem:
n
i
1
x
,...,
x
,...,
x
x
=
Model systemu wielostanowego w sensie
niezawodności
Poszczególne, zdefiniowane wcześniej
stany
niezawodnościowe
systemu
stanowią podzbiory stanów jego elementów, czyli podzbiory wektorów
x.
Zatem przechodzenie procesu zmian stanów systemu wynika jednoznacznie z
procesów przechodzenia elementów pomiędzy swoimi stanami. Przy założeniu o
wykładniczym charakterze rozkładu czasu przechodzenia do kolejnych stanów i
przebywania w stanach rozkłady łączne procesu zmian definiuje się za pomocą
macierzy intensywności przejść. W efekcie uzyskać można metodą równań
stanów
charakterystyki
chwilowe
lub
graniczne
prawdopodobieństw
przebywania procesu w poszczególnych stanach, z których z kolei wyznacza się
kolejne istotne wartości miar niezawodnościowych systemu.
Metodę tę zilustrujemy przykładem.
Przykład System ma strukturę przedstawioną na schemacie
x
1
x
2
x
3
Czasy poprawnej pracy elementów x
1
i x
2
mają rozkład wykładniczy z parametrem a,
elementu x
3
z parametrem b natomiast
wszystkie
czasy
odnowy
mają
rozkład
wykładniczy z parametrem c. Można zatem
zdefiniować trzy stany niezawodnościowe
systemu:
Model systemu wielostanowego w sensie niezawodności
systemu:
Stan pełnej wydajności x
1
= (1,1,1), stany częściowej wydajności x
2
= (0,1,1),
x
3
= (1,0,1) oraz stan awarii x
4
= (0,0,1), x
5
= (1,1,0), x
6
= (0,1,0), x
7
= (1,0,0),
x
8
= (0,0,0). Oznacza to, że elementy mogą uszkadzać się nawet po
uszkodzeniu systemu, chociaż nie trzeba czynić takiego założenia. Wtedy po
prostu liczba możliwych w realizacji stanów zmniejszy się istotnie.
Uszkodzony element naprawiany jest przez jednego konserwatora i najpierw
zawsze naprawiany jest element trzeci (jeśli jest uszkodzony), a następnie
któryś z elementów pozostałych, załóżmy, że pierwszy.
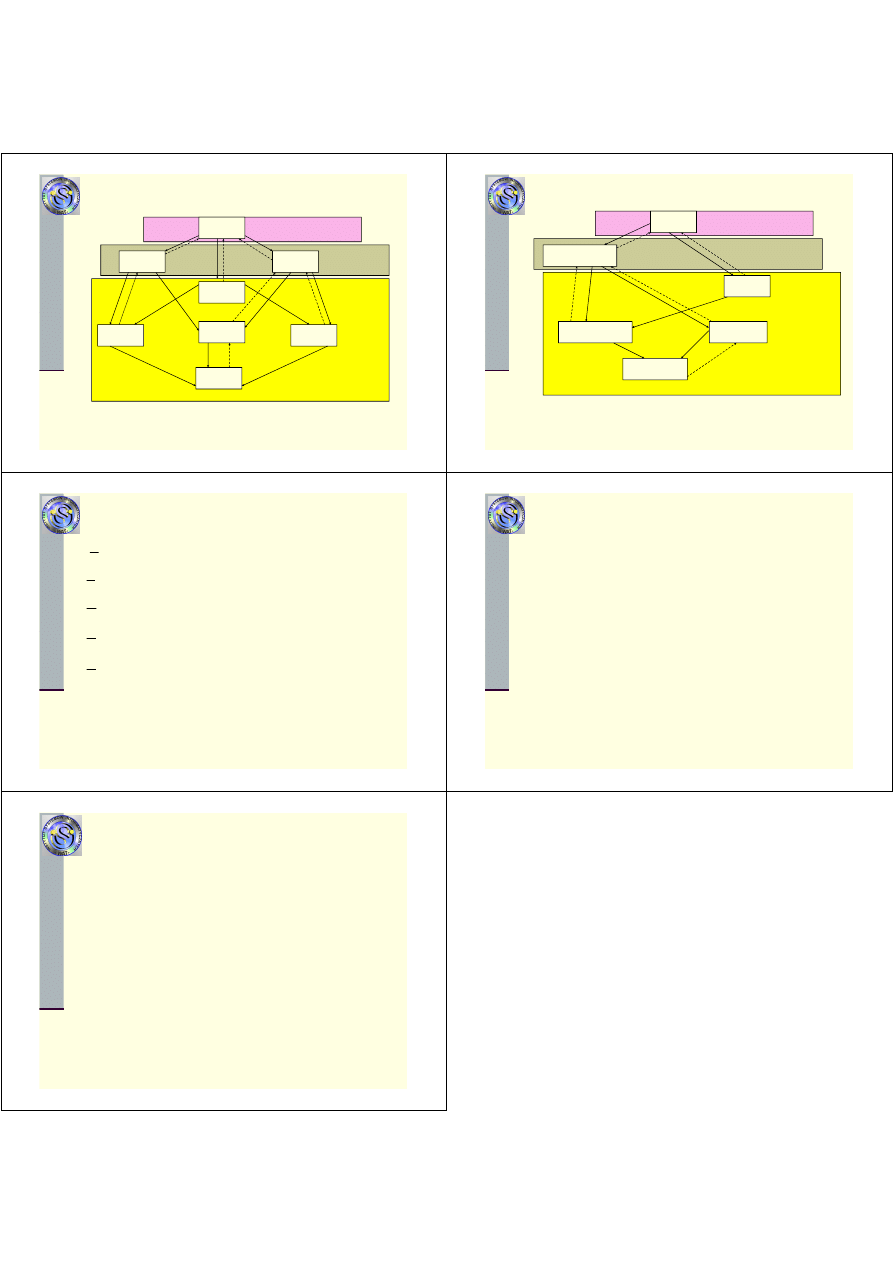
Daje to nam w efekcie następujący graf stanów procesu zmian stanów elementów
i systemu:
(1,1,1)
(0,1,1)
(1,0,1)
(1,1,0)
a
a
b
b
a
a
a
b
c
c
c
c
c
Pełna wydajność
Częściowa
wydajność
Model systemu wielostanowego w sensie niezawodności
a
c
(0,0,1)
(0,1,0)
(0,0,0)
(1,0,0)
a
a
a
b
c
Stan awarii
Uwaga:intensywności (pętle) na wierzchołkach grafu to minus suma intensywności
wychodzących z wierzchołka.
a
(1,1,1)
(0,1,1), (1,0,1)
(1,1,0)
2a
b
b
c
c
Pełna wydajność
Częściowa
wydajność
2a
c
stan1
stan2
stan4
c
a
Stany te można zredukować
Model systemu wielostanowego w sensie niezawodności
b
(0,0,1)
b
Stan awarii
2a
stan5
(1,0,0),(0,1,0)
(0,0,0)
stan3
stan6
c
a
Uwaga:intensywności (pętle) na wierzchołkach grafu to minus suma intensywności
wychodzących z wierzchołka.
Stąd układ równań różniczkowych stanu (Kołmogorowa) ma postać :
(t)
cp
(t)
cp
(t)
b)p
a
2
(
(t)
p
dt
d
4
2
1
1
+
+
+
−
=
(t)
cp
(t)
cp
(t)
c)p
b
(a
-
(t)
p
a
2
(t)
p
dt
d
5
3
2
1
2
+
+
+
+
=
(t)
p
2
(t)
c)p
(a
-
(t)
bp
(t)
p
dt
d
4
3
2
3
a
+
+
=
d
+
−
=
Model systemu wielostanowego w sensie niezawodności
Zamiast jednego z równań (6) dajemy równanie normujące postaci
(t)
c)p
a
2
(
(t)
bp
(t)
p
dt
d
4
1
4
+
−
=
1
(t)
p
(t)
p
(t)
p
(t)
p
(t)
p
(t)
p
6
5
4
3
2
1
=
+
+
+
+
+
(t)
cp
(t)
c)p
(b
-
(t)
ap
(t)
p
dt
d
6
5
2
5
+
+
=
)
0
,
0
,
0
,
0
,
0
,
1
(
(0))
p
(0),
p
(0),
p
(0),
p
(0),
p
(0),
(p
p(0)
6
5
4
3
2
1
=
=
oraz warunek
początkowy
Równania te można rozwiązać stosując transformatę Laplace’a. Otrzymujemy
wtedy wektor p(t)=(p
1
(t), p
2
(t), p
3
(t), p
4
(t), p
5
(t), p
6
(t)) będący podstawa
obliczania
charakterystyk
niezawodnościowych
wielostanowego
w
sensie
niezawodności
systemu.
Chcąc
uzyskać
charakterystyki
graniczne
przekształcamy uzyskany układ równań (gdzie p
i
= lim p
i
(t) i=1..6) do postaci:
5
3
2
1
cp
cp
c)p
b
(a
-
p
a
2
0
+
+
+
+
=
4
3
2
p
2
c)p
(a
-
bp
0
a
+
+
=
3
2
1
cp
cp
b)p
a
2
(
0
+
+
+
−
=
Model systemu wielostanowego w sensie niezawodności
1
p
p
p
p
p
p
6
5
4
3
2
1
=
+
+
+
+
+
4
3
2
p
2
c)p
(a
-
bp
0
a
+
+
=
4
1
c)p
a
2
(
bp
0
+
−
=
6
5
2
cp
c)p
(b
-
ap
0
+
+
=
z warunkiem normującym
Ten układ równań liniowych można rozwiązać np. metodą Gaussa. Otrzymujemy
wtedy wektor p=(p
1
, p
2
, p
3
, p
4
, p
5
, p
6
) granicznych prawdopo-dobieństw będący
podstawa
obliczania
granicznych
charakterystyk
nieza-wodnościowych
wielostanowego w sensie niezawodności systemu.
Nale
ż
y zawsze dokona
ć
identyfikacji wszystkich elementów -
czy s
ą
odnawialne, czy nie; jakie s
ą
ich rozkłady
prawdopodobie
ń
stwa czasu
ż
ycia lub (o ile jest to
potrzebne) czasów odnowy, itp.,
nale
ż
y zbada
ć ś
cie
ż
ki zdatno
ś
ci i ci
ę
cia systemu; du
ż
a liczba
ś
cie
ż
ek
ś
wiadczy o odporno
ś
ci systemu, a du
ż
a liczba
ci
ęć ś
wiadczy o wra
ż
liwo
ś
ci systemu; odnosi si
ę
to w
du
ż
ej mierze do odporno
ś
ci systemu na uszkodzenia
pojedynczych elementów,
Wnioski końcowe
pojedynczych elementów,
nale
ż
y ustali
ć
, czy system jest obiektem nieodnawialnym,
czy odnawialnym; miary niezawodno
ś
ci obliczane dla
systemu musz
ą
by
ć
charakterystyczne dla ustalonej klasy
systemu - obiektu.
Seria: Informatyka
Elementy teorii niezawodności
Wykład 6
Niezawodność systemów
komputerowych
komputerowych
dr hab. in
ż
. Tadeusz Nowicki prof. nadzw. WAT
e-mail:tadeusz.nowicki@wat.edu.pl, tel. 6-837118
Pojedynczy
element
elektroniczny
wchodz
ą
cy
w
skład
komputera przybli
ż
a si
ę
wykładniczym rozkładem czasu do
uszkodzenia. Przyjmuje si
ę
zało
ż
enie i
ż
ka
ż
dy taki element jest
nieodnawialny.
Niech
oznacza czas do uszkodzenia pojedynczego elementu. Wówczas
prawdopodobie
ń
stwo tego,
ż
e czas ten b
ę
dzie krótszy od
Charakterystyki niezawodno
ś
ciowe
elementów elektronicznych
T
e
prawdopodobie
ń
stwo tego,
ż
e czas ten b
ę
dzie krótszy od
zadanej warto
ś
ci t , dane jest wzorem:
0
,
)
(
}
{
P
≥
=
<
t
t
t
F
T
e
e
gdzie
jest intensywno
ś
ci
ą
uszkodzenia si
ę
elementu.
λ
e
Intensywno
ść
uszkadzania si
ę
elementów rozumiana jest nie jako
liczba uszkodze
ń
liczna na jednostk
ę
czasu, lecz w inny sposób.
Je
ś
li dystrybuanta czasu do uszkodzenia si
ę
elementu jest funkcj
ą
{ }
0
t
,
T
P
(t)
F
e
e
≥
〈
=
t
To
funkcj
ę
niezawodno
ś
ci
tego
elementu
okre
ś
la
funkcja
Charakterystyki niezawodno
ś
ciowe
elementów elektronicznych
{
}
0
t
,
T
P
(t)
R
e
e
≥
≥
=
t
To
funkcj
ę
niezawodno
ś
ci
tego
elementu
okre
ś
la
funkcja
rzeczywista
Natomiast
g
ę
sto
ść
zmiennej
losowej
oznaczaj
ą
cej
czas
do
uszkodzenia si
ę
elementu jest funkcj
ą
0
t
,
dt
(t)
dF
(t)
f
e
e
≥
=
Teraz można użyć określenia intensywność uszkodzeń
zmiennej losowej oznaczającej czas do uszkodzenia się
elementu
0
t
,
)
(
R
(t)
f
(t)
e
e
e
≥
=
t
λ
Charakterystyki niezawodno
ś
ciowe
elementów elektronicznych
)
(
R
e
t
Intensywność
uszkodzeń
elementu
jest
więc
funkcją
rzeczywistą określającą jedynie „żywotność”
elementu,
będącą warunkową gęstością zmiennej losowej oznaczającej
czas do jego uszkodzenia się [Korzan]
Zatem: intensywność uszkodzeń elementu nie zmienia się,
jest jego własnością określoną funkcją.
Można
pokazać,
ż
e
pojedynczy
element
elektroniczny
charakteryzuje się czasem do uszkodzenia o wykładniczym
rozkładzie prawdopodobieństwa
0
,
1
)
(
}
{
P
≥
−
=
=
<
−
t
t
t
t
e
F
T
e
e
e
λ
Charakterystyki niezawodno
ś
ciowe
elementów elektronicznych
Wykładniczy charakter rozkładu czasu do uszkodzenia
posiadają również bardziej złożone elementy elektroniczne:
układy scalone, monitory ekranowe, silniki elektryczne,
pamięci dyskowe, napędy dyskowe, pamięci elektroniczne,
zasilacze, transformatory, itp.
Podzespół komputera składa si
ę
z elementów. Je
ś
li jeden element
zepsuje si
ę
, to cały podzespół zazwyczaj te
ż
uwa
ż
a si
ę
za zepsuty.
Wynika to z praktyki i obserwacji skutków uszkadzania si
ę
elementów elektronicznych komputerów. Wprowadza si
ę
zatem
zało
ż
enie,
ż
e podzespół komputera posiada szeregowa struktur
ę
niezawodno
ś
ciow
ą
. Niech p oznacza numer podzespołu
,
Charakterystyki niezawodno
ś
ciowe
elementów elektronicznych
Niech
oznacza czas do uszkodzenia podzespołu zło
ż
onego z elementów.
}
,
...
,
3
,
2
,
1
{
P
p
=
∈
P
T
p
Podzespół składa się z
elementów, tzn.:
L
p
}
,
...
,
,
,
{
3
2
1
e
e
e
e
E
L
p
p
=
Wówczas można zapisać, iż prawdopodobieństwo tego, że
Charakterystyki niezawodno
ś
ciowe
elementów elektronicznych
Wówczas można zapisać, iż prawdopodobieństwo tego, że
czas do uszkodzenia podzespołu jest krótszy od zadanej
wartości t , dane jest wzorem:
P
p
T
T
T
T
T
Lp
e
e
e
e
p
,
1
,
}
,...,
,
,
{
3
2
1
min
=
=
Czas do uszkodzenia się podzespołu ma dystrybuantę:
=
<
=
<
=
}
}
,
...
,
,
,
{
min
{
}
{
)
(
3
2
1
F
t
P
t
P
t
T
T
T
T
T
Lp
e
e
e
e
p
p
=
≥
−
=
}
}
,
...
,
,
,
{
min
{
1
3
2
1
t
P
T
T
T
T
Lp
e
e
e
e
=
≥
≥
≥
≥
−
=
}
,
...
,
,
,
{
1
3
2
t
t
t
t
P
T
T
T
T
eLp
e
e
e
Charakterystyki niezawodno
ś
ciowe
elementów elektronicznych
=
≥
≥
≥
≥
−
=
}
,
...
,
,
,
{
1
3
2
1
t
t
t
t
P
T
T
T
T
eLp
e
e
e
=
≥
−
=
∏
=
}
{
1
1
t
P
T
ei
Lp
i
=
−
∏
=
)
(
1
1
t
Lp
i
ei
R
=
−
−
=
∏
=
Lp
i
e
e
t
i
1
1
λ
=
∑
−
=
−
e
Lp
i
ei
t
1
1
λ
e
t
p
λ
−
−
1
∑
=
=
Lp
i
ei
p
1
λ
λ
gdzie
Wykładniczy
typ rozkładu
Otrzymano w ten sposób wynik świadczący o tym, że
podzespół składający się z elementów o wykładniczym
rozkładzie czasu do uszkodzenia i szeregowej strukturze
niezawodnościowej, ma również wykładniczy rozkład czasu
do jego uszkodzenia.
Charakterystyki niezawodno
ś
ciowe
elementów elektronicznych
Komputer.
Zakłada
się,
ż
e
oprogramowanie
zainstalowane
na
komputerze, zarówno systemowe, jak i użytkowe jest niezawodne. W
praktyce zakłada się również, że rozpatrywane będą tylko te elementy
(podzespoły)
komputera,
które
mają
istotny
wpływ
na
jego
funkcjonalność, tzn. pomija się stacje dyskietek, kartę dźwiękową,
drukarkę. Przyjmuje się, że struktura niezawodnościowa jest również
szeregowa, tzn. awaria jednego z podzespołów powoduje niezdatność
Charakterystyki niezawodnościowe komputerów
Charakterystyki niezawodno
ś
ciowe
komputerów
szeregowa, tzn. awaria jednego z podzespołów powoduje niezdatność
całego
komputera.
Wykorzystując
powyższe
wyprowadzenia
(dla
podzespołu), dla komputera otrzymuje się takie same wzory.
Niech
oznacza czas do uszkodzenia komputera złożonego z P podzespołów.
T
k
Wówczas:
}
,
{
min
P
p
T
T
p
k
∈
=
zatem, mając na uwadze poprzednie rozważania otrzymujemy:
∑
∑
∑
Lp
P
P
λ
λ
λ
Charakterystyki niezawodno
ś
ciowe
komputerów
∑
∑
∑
=
=
=
=
=
Lp
i
ei
P
p
P
p
p
k
1
1
1
λ
λ
λ
e
T
F
t
t
P
t
T
k
k
k
λ
−
−
=
<
=
1
}
{
)
(
oraz
Przypadek wielu komputerów
Rozpatrujemy systemy złożone z wielu komputerów
uszkadzających się zwykle w sposób zależny. Zatem mamy
do czynienia ze strukturalną funkcją niezawodnościową
systemu dla elementów i systemu dwustanowych w sensie
niezawodności ma postać:
{ } { }
→
n
{ } { }
1
,
0
1
,
0
:
)
(
f
(n)
→
n
x
Możemy
mieć
do
czynienia
z
wieloma
różnymi
przypadkami struktur niezawodnościowych systemów z
wieloma komputerami. Elementami systemu są zatem
komputery realizujące różne zadania. Związki pomiędzy
zadaniami definiują nam jednoznacznie tę strukturę.
Załóżmy, że mamy do czynienia z systemem komputerowym złożonym z
p komputerów. Dla każdego z nich tworzymy procedury jego uszkadzania
się (fizycznego) niezależnego.
Symulacyjny model uszkadzania się komputerów
PROCEDURE Komputer p-ty
BEGIN
LOOP
Hold For Time (Rnd Wyk (lambda));
l(p):=0; Action (jeśli taka jest wymagana);
IF NOT Active(Sterowanie) THEN Reactivete Process (Sterowanie);
Hold For Time (Rnd Wyk (beta));
l(p):=1; Action (jeśli taka jest wymagana);
IF NOT Active(Sterowanie) THEN Reactivete Process (Sterowanie);
END LOOP;
END;
Znając strukturalną funkcję niezawodnościową systemu (zależność pracy
komputerów
określającą
np.
fakt
zdatności
systemu)
możemy
wykorzystać znajomość poprawnej pracy komputerów lub całego systemu
PROCEDURE Sterowanie
BEGIN
FOR p=1 TO P DO L(p):=1; END
REPEAT
Symulacyjny model uszkadzania się komputerów
IF f(l(p), p=1,P) THEN Action (jeśli taka jest wymagana dla systemu); END;
FOR p=1 TO P DO
IF zmiana (l(p) THEN Action (jeśli taka jest wymagana dla komputera p-tego);
END;
END;
Pasivate;
UNTIL Czas symulacji <= Chwila zakończenia eksperymentu;
END;
WNIOSKI KOŃCOWE
Przyjmujemy
rozkłady
wykładnicze
czasów
ż
ycia
elementów
i
podzespołów
komputerów
obliczaj
ą
c
charakterystyki niezawodno
ś
ciowe poszczególnych z
nich
nale
ż
y
zawsze
dokona
ć
identyfikacji
wszystkich
elementów - mam na my
ś
li komputerów tzn. czy s
ą
odnawialne,
czy
nie;
jakie
s
ą
ich
rozkłady
odnawialne,
czy
nie;
jakie
s
ą
ich
rozkłady
prawdopodobie
ń
stwa czasu
ż
ycia lub (o ile jest to
potrzebne) czasów odnowy, itp.,
nale
ż
y ustali
ć
, czy system jest obiektem nieodnawialnym,
czy odnawialnym; miary niezawodno
ś
ci obliczane dla
systemu musz
ą
by
ć
charakterystyczne dla ustalonej
klasy systemu - obiektu.
WNIOSKI KOŃCOWE
trzeba skonstruowa
ć
strukturaln
ą
funkcj
ę
niezawodno
ś
ciow
ą
systemu
wynikaj
ą
c
ą
z
zale
ż
nej
pracy
komputerów
(poniek
ą
d z zale
ż
no
ś
ci zada
ń
cz
ą
stkowych realizowanych
na tych komputerach),
nale
ż
y zbada
ć ś
cie
ż
ki zdatno
ś
ci i ci
ę
cia systemu; du
ż
a liczba
ś
cie
ż
ek
ś
wiadczy o odporno
ś
ci systemu, a du
ż
a liczba
ci
ęć ś
wiadczy o wra
ż
liwo
ś
ci systemu; odnosi si
ę
to w
du
ż
ej mierze do odporno
ś
ci systemu na uszkodzenia
pojedynczych elementów,
nale
ż
y
obliczy
ć
wymagane
charakterystyki
systemu
zło
ż
onego z wielu komputerów; o ile da si
ę
analitycznie,
to wy
ś
mienicie, cz
ęś
ciej trzeba zrobi
ć
to za pomoc
ą
eksperymentu symulacyjnego.
Wyszukiwarka
Podobne podstrony:
Kolokwium wyklad do kola id 736 Nieznany
Antropologia Slowa do druku id Nieznany (2)
odpowiedzi do testu id 332437 Nieznany
Montaz zamka do drzwi id 307578 Nieznany
mnozenie do 25 2[1] id 304290 Nieznany
DO Gimn 1 id 137870 Nieznany
dodawanie do 10 4 id 138940 Nieznany
PRZ OPI wyklad 3 v2 pdf id 4033 Nieznany
F Zadania do kol 1 id 167111 Nieznany
Droga Polski do NATO id 142564 Nieznany
mechanika do poprawki id 290847 Nieznany
piae wyklad3 12 13 id 356381 Nieznany
DO P gimn 4 id 137938 Nieznany
od bollanda do deminga id 33072 Nieznany
więcej podobnych podstron